Analysis of a Stochastic Programming Model for Optimal Hydropower System Operation under a Deregulated Electricity Market by Considering Forecasting Uncertainty
Abstract
1. Introduction
2. Methodology
2.1. Conflicting Decisions on Energy Production and Energy Purchase
2.2. Quantification of Revenue from Energy Production Delivery and Cost from Energy Purchase
2.3. Stochastic Programming Model for Conflict Resolution
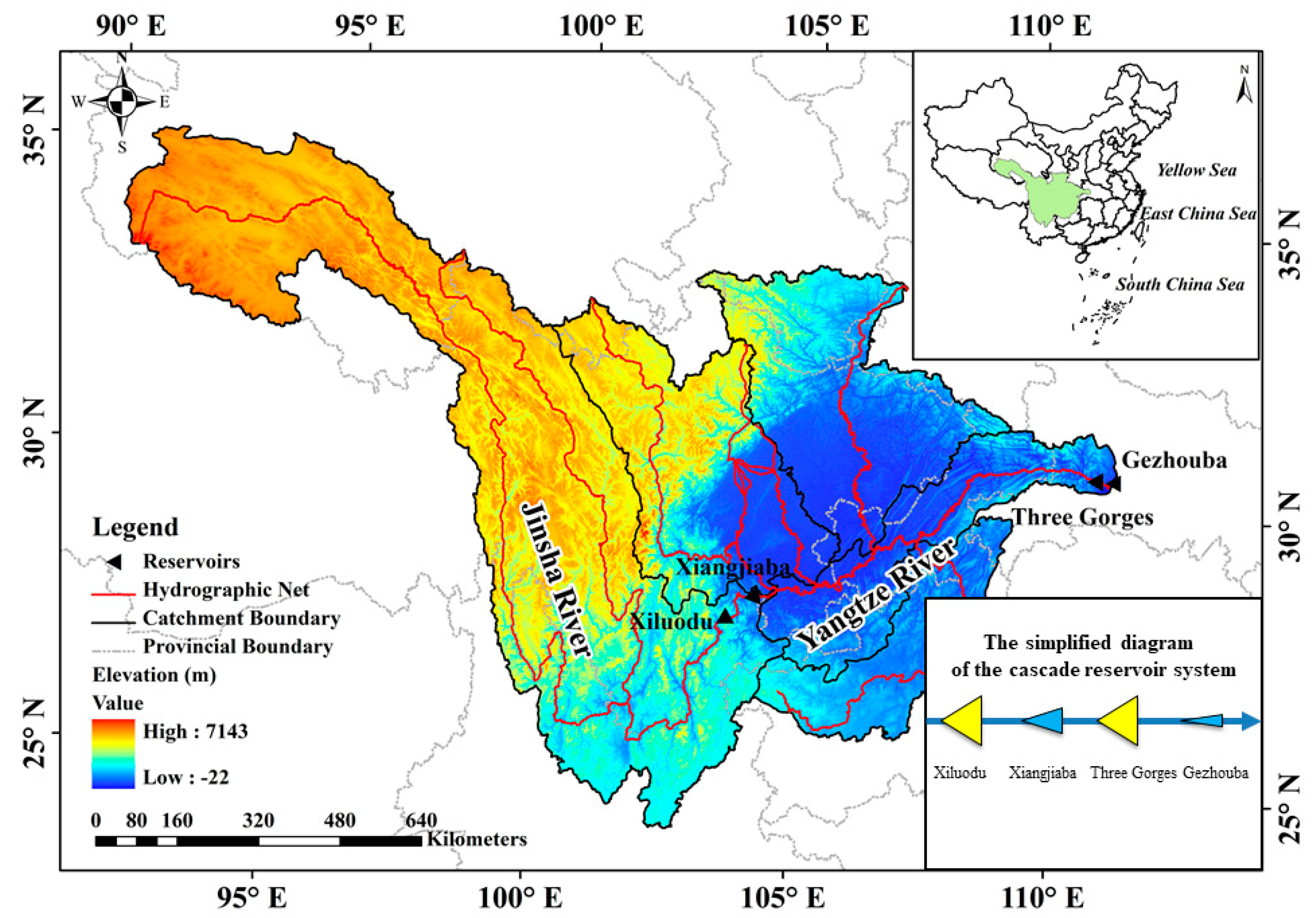
3. Overview of the Cascade Hydropower System
4. Results
4.1. Tradeoffs under Streamflow Uncertainty
4.2. Net Revenue Results
- From the horizontal view, the results of the net revenue under different levels of energy purchase level show that the difference between the highest net revenue and the lowest net revenue from each curve varies greatly with the specific level of . The difference is the cost of making the worst decision. For example, when the actual value of is low ( CNY/kWh), but decision makers overestimate the value of such that a most conservative decision () on energy purchase level is made, the reservoirs system would lose a net revenue of 1.65 × 108 CNY compared with the results given a perfect information on . The corresponding highest reduction in net revenue would be 11.52 × 108 CNY when the actual value of is extremely high ( CNY/kWh), but decision makers underestimate and make a most progressive decision (). For the medium level of ( CNY/kWh), the highest reduction in net revenue would be 2.5 × 108 CNY. Therefore, if an inaccurate information on is used, the loss in net revenue would be high, especially when is high.
- From the vertical view, when the results of net revenue under different levels of but the same level of energy purchase level, the deviated magnitude of the net revenue between the results of and would increase with the energy purchase level. This finding could be applied to decision-making when no reliable predicted information on can be used. For example, if all the scenarios of are assumed equally likely to occur, the expectation of net revenue under all possible scenarios can be used as the target. Consequently, the optimal level of energy purchase would be 14.56% and the corresponding expected value of net revenue would be 209.27 × 108 CNY. Therefore, medium-level energy purchase rather than a high-level or low-level energy purchase should be determined to balance revenue and cost if no predicted information of can be used.
5. Discussion
6. Conclusions
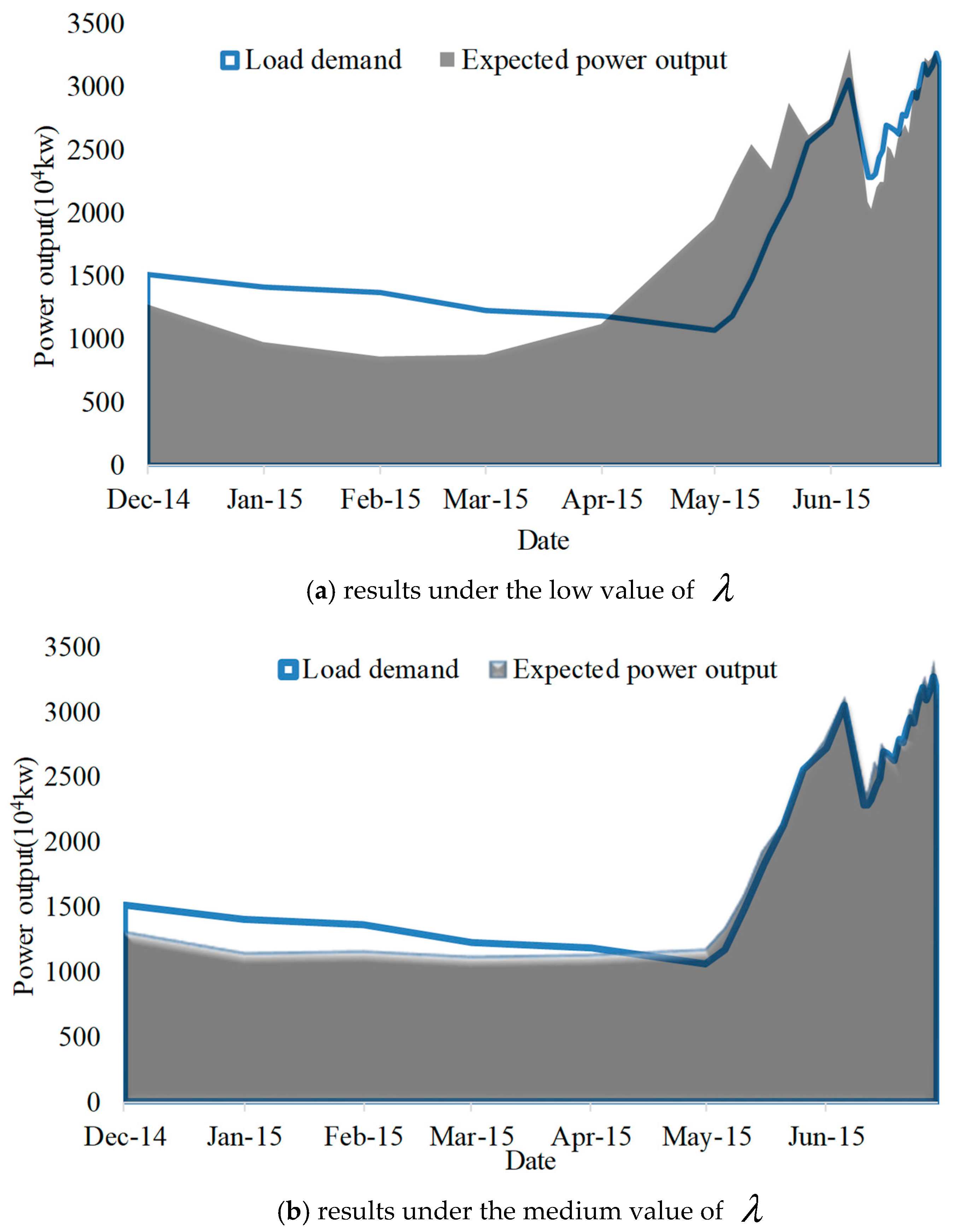
- An increase in expected total revenue adversely affects the reduction of expected energy shortfall percentage or energy purchase level because the mechanism of maximizing the hydropower generation could deviate from the mechanism of minimizing the energy purchase level over sequences of periods. In this case study, maximizing the hydropower generation yields a postponed drawdown policy for increasing water head. This finding generates heterogeneous energy production that intensifies the energy purchase level.
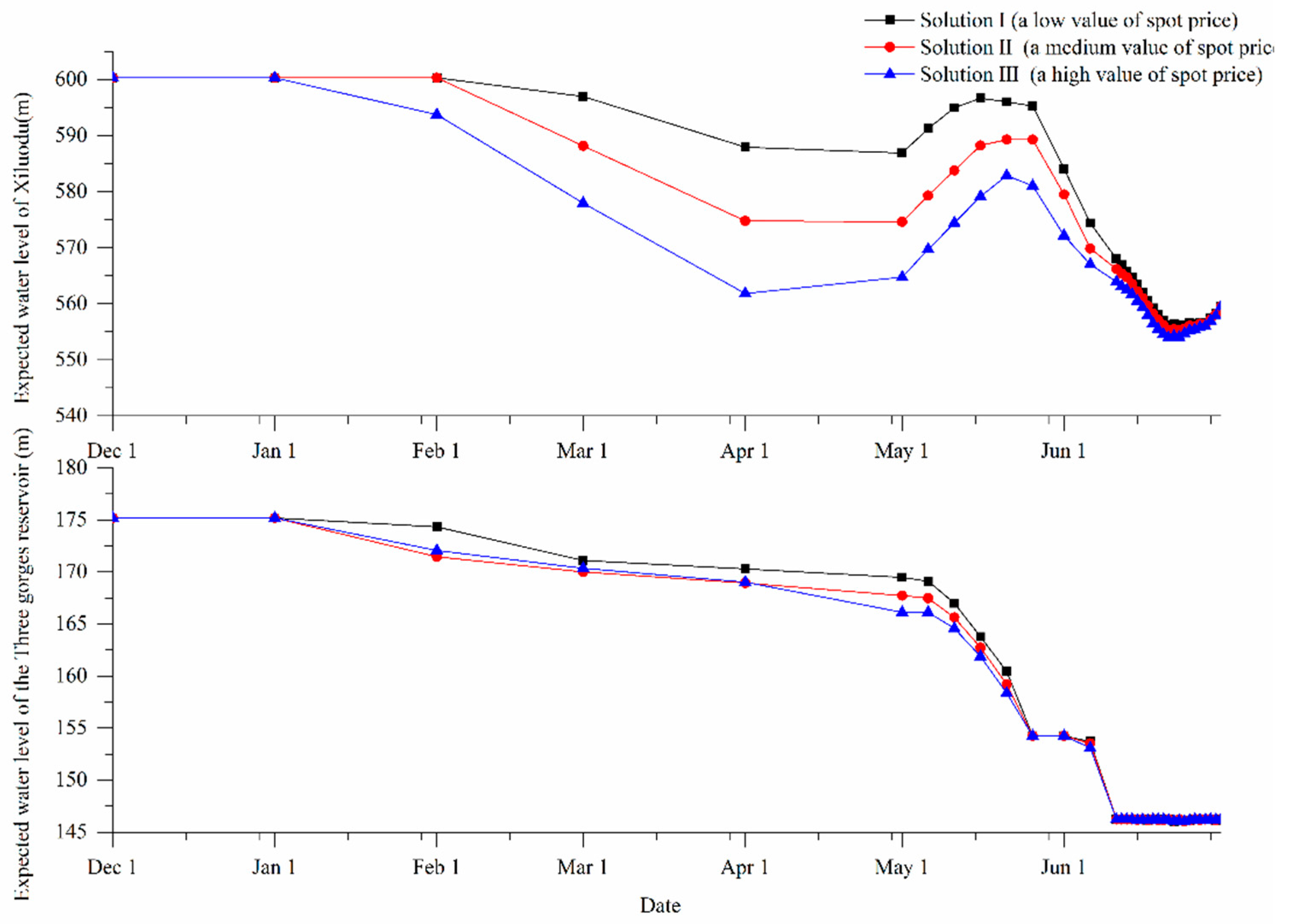
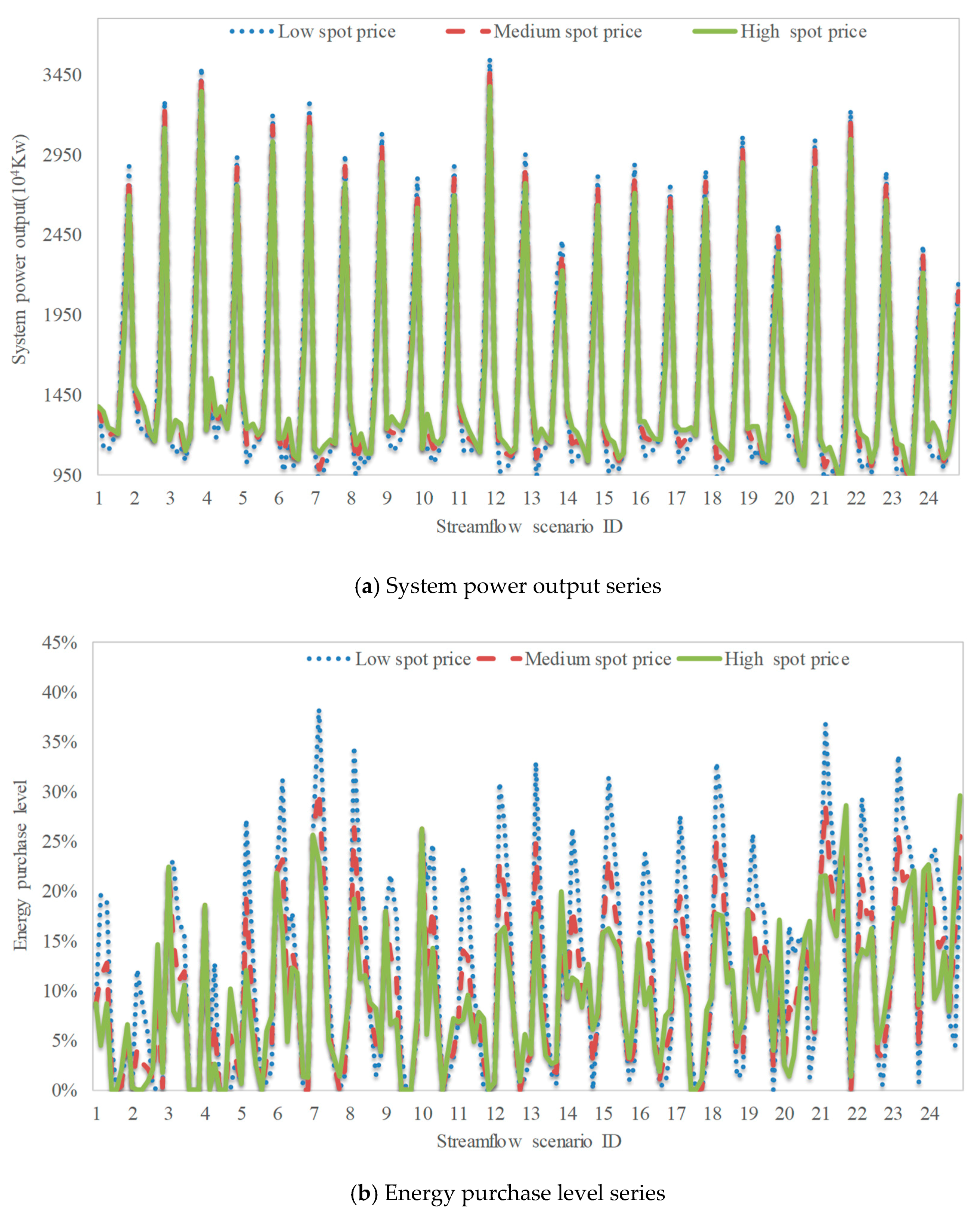
- An increase in spot energy price decreases the expected energy production and energy purchase level because of its direct influence on the drawdown operation policy and the cost of energy purchase. However, this phenomenon does not apply to all streamflow scenarios.
- A precise forecast on the spot energy price provides valuable information regarding its influence on the net revenue. By contrast, sustaining a medium-level energy purchase could outperform the choices of a high-low-level energy purchase in terms of expected value of net revenue over different price scenarios if no accurate predicted information on the spot energy price can be obtained.
- The nonlinear tradeoff results of energy surplus and energy shortfall provide valuable information for determining the compromise of benefit and cost, and the model could yield the optimal policy considering both terms and the influences of inflow and price uncertainties.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chang, X.; Liu, X.; Zhou, W. Hydropower in China at present and its further development. Energy 2010, 35, 4400–4406. [Google Scholar] [CrossRef]
- World Energy Council. World Energy Resources Hydropower|2016; World Energy Council: London, UK, 2016; pp. 1–53. [Google Scholar]
- Xu, B.; Boyce, S.E.; Zhang, Y.; Liu, Q.; Guo, L.; Zhong, P. Stochastic programming with a joint chance constraint model for reservoir refill operation considering flood risk. J. Water Resour. Plan. Manag. 2017, 143, 4016067. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.; Stanko, Z.; Zhao, Y.; Yeh, W.W.G. A multiobjective short-term optimal operation model for a cascade system of reservoirs considering the impact on long-term energy production. Water Resour. Res. 2015, 51, 3353–3369. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.; Wan, X.; Zhang, W.; Chen, X. Dynamic feasible region genetic algorithm for optimal operation of a multi-reservoir system. Energies 2012, 5, 2894–2910. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Cheng, C.; Wu, X. Optimization of hydropower system operation by uniform dynamic programming for dimensionality reduction. Energy 2017, 134, 718–730. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J.; Liu, P.; Lei, X. Evaluating the marginal utility principle for long-term hydropower scheduling. Energy Convers. Manag. 2015, 106, 213–223. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.; Zhao, Y.; Zhu, Y.; Zhang, G. Comparison between dynamic programming and genetic algorithm for hydro unit economic load dispatch. Water Sci. Eng. 2014, 7, 420–432. [Google Scholar]
- Li, X.; Li, T.J.; Wei, J.H.; Wang, G.Q.; Yeh, W.W. Hydro unit commitment via mixed integer linear programming: A case study of the Three Gorges project, China. IEEE Trans. Power Syst. 2014, 29, 1232–1241. [Google Scholar] [CrossRef]
- Li, J.Q.; Marino, M.A.; Ji, C.M.; Zhang, Y.S. Mathematical models of inter-plant economical operation of a cascade hydropower system in electricity market. Water Resour. Manag. 2009, 23, 2003–2013. [Google Scholar] [CrossRef]
- Kern, J.D.; Characklis, G.W.; Doyle, M.W.; Blumsack, S.; Whisnant, R.B. Influence of deregulated electricity markets on hydropower generation and downstream flow regime. J. Water Resour. Plan. Manag. 2012, 138, 342–355. [Google Scholar] [CrossRef]
- Wolfgang, O.; Haugstad, A.; Mo, B.; Gjelsvik, A.; Wangensteen, I.; Doorman, G. Hydro reservoir handling in Norway before and after deregulation. Energy 2009, 34, 1642–1651. [Google Scholar] [CrossRef]
- Liu, H.L.; Jiang, C.W.; Zhang, Y. A review on risk-constrained hydropower scheduling in deregulated power market. Renew. Sustain. Energy Rev. 2008, 12, 1465–1475. [Google Scholar]
- Zhong, P.A.; Zhang, W.; Xu, B. A risk decision model of the contract generation for hydropower generation companies in electricity markets. Electr. Power Syst. Res. 2013, 95, 90–98. [Google Scholar] [CrossRef]
- Mo, B.; Gjelsvik, A.; Grundt, A. Integrated risk management of hydro power scheduling and contract management. IEEE Trans. Power Syst. 2001, 16, 216–221. [Google Scholar] [CrossRef]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer Science & Business Media: New York, NY, USA, 2011; p. 485. [Google Scholar]
- Xu, B.; Zhong, P.A.; Zambon, R.C.; Zhao, Y.; Yeh, W.W.G. Scenario tree reduction in stochastic programming with recourse for hydropower operations. Water Resour. Res. 2015, 51, 6359–6380. [Google Scholar] [CrossRef]
- Latorre, J.M.; Cerisola, S.; Ramos, A. Clustering algorithms for scenario tree generation: Application to natural hydro inflows. Eur. J. Oper. Res. 2007, 181, 1339–1353. [Google Scholar] [CrossRef]
- Côté, P.; Leconte, R. Comparison of stochastic optimization algorithms for hydropower reservoir operation with ensemble streamflow prediction. J. Water Res. Plan. Manag. 2015, 2, 04015046. [Google Scholar] [CrossRef]
- Tilmant, A.; Kelman, R. A stochastic approach to analyze trade-offs and risks associated with large-scale water resources systems. Water Resour. Res. 2007, 43, W064256. [Google Scholar] [CrossRef]
- Kelman, J.; Stedinger, J.R.; Cooper, L.A.; Hsu, E.; Yuan, S.Q. Sampling stochastic dynamic-programming applied to reservoir operation. Water Resour. Res. 1990, 26, 447–454. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Chen, X. Multistage scenario-based interval-stochastic programming for planning water resources allocation. Stoch. Environ. Res. Risk Assess. 2009, 23, 781–792. [Google Scholar] [CrossRef]
- Si, Y.; Li, X.; Yin, D.; Liu, R.; Wei, J.; Huang, Y.; Li, T.; Liu, J.; Gu, S.; Wang, G. Evaluating and optimizing the operation of the hydropower system in the Upper Yellow River: A general LINGO-based integrated framework. PLoS ONE 2018, 13, e191483. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Qiu, J. Multi-objective reservoir optimization balancing energy generation and firm power. Energies 2015, 8, 6962–6976. [Google Scholar] [CrossRef]
- You, J.; Cai, X. Hedging rule for reservoir operations: 1. A theoretical analysis. Water Resour. Res. 2008, 44, 1–9. [Google Scholar] [CrossRef]
- Draper, A.J.; Lund, J.R. Optimal hedging and carryover storage value. J. Water Resour. Plan. Manag. 2004, 130, 83–87. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.; Huang, Q.; Wang, J.; Yu, Z.; Zhang, J. Optimal hedging rules for water supply reservoir operations under forecast uncertainty and conditional value-at-risk criterion. Water 2017, 9, 568. [Google Scholar] [CrossRef]
- Chen, F.; Liu, B.; Cheng, C.; Mirchi, A. Simulation and regulation of market operation in hydro-dominated environment: The Yunnan case. Water 2017, 9, 623. [Google Scholar] [CrossRef]
- Dhaubanjar, S.; Davidsen, C.; Bauer-Gottwein, P. Multi-objective optimization for analysis of changing trade-offs in the Nepalese water-energy-food nexus with hydropower development. Water 2017, 9, 162. [Google Scholar] [CrossRef]
- Shamshad, A.; Bawadi, M.; Wanhussin, W.; Majid, T.; Sanusi, S. First and second order Markov chain models for synthetic generation of wind speed time series. Energy 2005, 30, 693–708. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.; Chen, Y.; Zhao, Y. The multi-objective and joint operation of Xiluodu cascade and Three Gorges cascade reservoirs system. Sci. Sin. Technol. 2017, 47, 823–831. (In Chinese) [Google Scholar]
- Wang, Y.Y.; Huang, G.H.; Wang, S. CVaR-based factorial stochastic optimization of water resources systems with correlated uncertainties. Stoch. Environ. Res. Risk Assess. 2016, 31, 1543–1553. [Google Scholar] [CrossRef]




| Marketing Conditions | Model Types | Special Features and Advantages | Limitations | Reference |
|---|---|---|---|---|
| Regulated market | Revenue maximization models | To maximize the energy production or revenue from energy production with fixed operational cost. | Either the energy production can be entirely consumed by the market, or the demand load should be strictly satisfied by the hydropower producer. Market factors are neglected. | Xu et al. [3,4,5]; Feng et al. [6] Zhao et al. [7] |
| Cost minimization models | To minimize the unit commitment cost over turbine units or hydropower stations with given load demand processes. | Xu et al. [8] Li et al. [9,10] | ||
| Deregulated market | Simulation models | To simulate the results of revenue and risk of failing to deliver adequate energy for a hydropower producer based on reservoir operation rules and given probability distribution function of uncertain factors. | The optimality condition of the operation policy is not guaranteed. | Kern et al. [11] Zhong et al. [14] |
| Optimization models | To optimize the synthesized revenue or cost of a hydropower system with consideration of both inflow and price uncertainty. | Modeling complexity intensifies when all uncertain factors are addressed with probability distributions. | Wolfgang et al. [12]; Liu et al. [13]; Mo et al. [15]; |
| Reservoirs ) | (108 m3) | (108 m3) | (108 m3) | (108 m3) | (104 kW) | (104 kW) | (CNY/kWh) | (m/day) | (CNY/kWh) | (108 kWh) |
|---|---|---|---|---|---|---|---|---|---|---|
| Xiluodu | 115.72 | 69.23 | 115.72 | 51.12 | 120 | 1260 | 0.28 | 2 | 0.317, 0.356, 0.48 a | 818.29 |
| Xiangjiaba | 49.767 | 40.74 | 49.767 | 40.73 | 82 | 600 | 1 | |||
| Three Gorges | 393.05 | 178.96 | 393.05 | 171.5 | 166 | 2250 | 0.6 | |||
| Gezhouba | 7.1 | 7.1 | 7.1 | 6.25 | 25 | 295 | 3 |
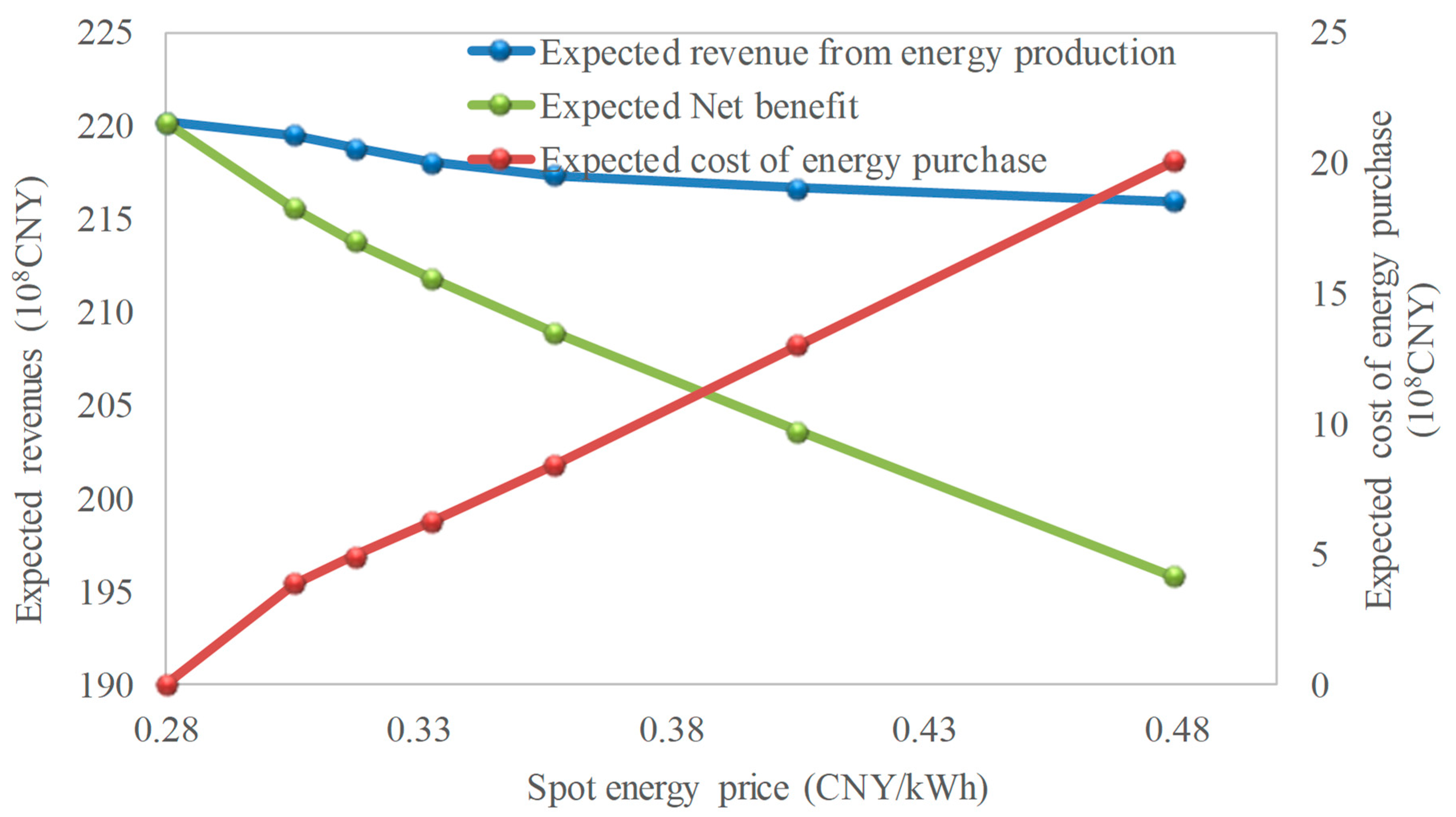
| Expected Revenue from Energy Production (108 CNY) | Expected Energy Purchase Level (%) | Spot energy Price (CNY/kWh) | Expected Cost of Energy Purchase (108 CNY) | Expected Net Revenue (108 CNY) |
|---|---|---|---|---|
| 220.21 | 21.97 | 0.28 | 0 | 220.21 |
| 219.49 | 18.56 | 0.306 | 3.89 | 215.60 |
| 218.78 | 16.22 | 0.317 | 4.96 | 213.82 |
| 218.06 | 14.56 | 0.332 | 6.25 | 211.82 |
| 217.35 | 13.42 | 0.357 | 8.41 | 208.94 |
| 216.64 | 12.72 | 0.405 | 13.02 | 203.62 |
| 215.92 | 12.28 | 0.48 | 20.06 | 195.87 |
| Models | Expected Revenue from Energy Production (108 CNY) | Expected Cost of Energy Purchase (108 CNY) | Expected Net Revenue (108 CNY) |
|---|---|---|---|
| Energy production maximization | 220.21 | 5.11 | 215.10 |
| Energy shortfall minimization | 214.49 | 1.51 | 212.98 |
| Net revenue maximization | 217.35 | 1.91 | 215.45 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Zhong, P.-A.; Du, B.; Chen, J.; Liu, W.; Li, J.; Guo, L.; Zhao, Y. Analysis of a Stochastic Programming Model for Optimal Hydropower System Operation under a Deregulated Electricity Market by Considering Forecasting Uncertainty. Water 2018, 10, 885. https://doi.org/10.3390/w10070885
Xu B, Zhong P-A, Du B, Chen J, Liu W, Li J, Guo L, Zhao Y. Analysis of a Stochastic Programming Model for Optimal Hydropower System Operation under a Deregulated Electricity Market by Considering Forecasting Uncertainty. Water. 2018; 10(7):885. https://doi.org/10.3390/w10070885
Chicago/Turabian StyleXu, Bin, Ping-An Zhong, Baoyi Du, Juan Chen, Weifeng Liu, Jieyu Li, Le Guo, and Yunfa Zhao. 2018. "Analysis of a Stochastic Programming Model for Optimal Hydropower System Operation under a Deregulated Electricity Market by Considering Forecasting Uncertainty" Water 10, no. 7: 885. https://doi.org/10.3390/w10070885
APA StyleXu, B., Zhong, P.-A., Du, B., Chen, J., Liu, W., Li, J., Guo, L., & Zhao, Y. (2018). Analysis of a Stochastic Programming Model for Optimal Hydropower System Operation under a Deregulated Electricity Market by Considering Forecasting Uncertainty. Water, 10(7), 885. https://doi.org/10.3390/w10070885






