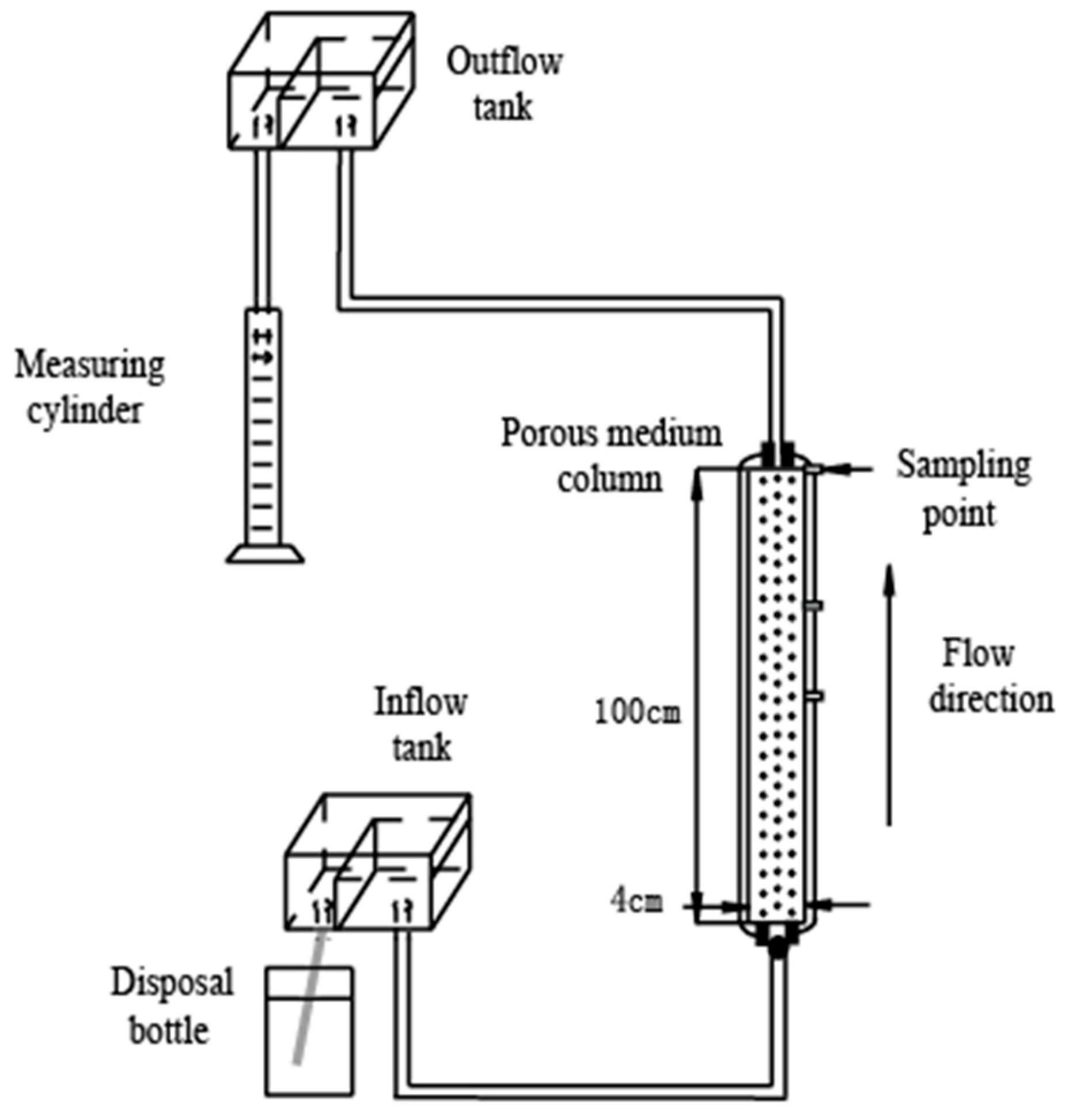
5.1. Comparison of Transport Models
The transport models discussed in
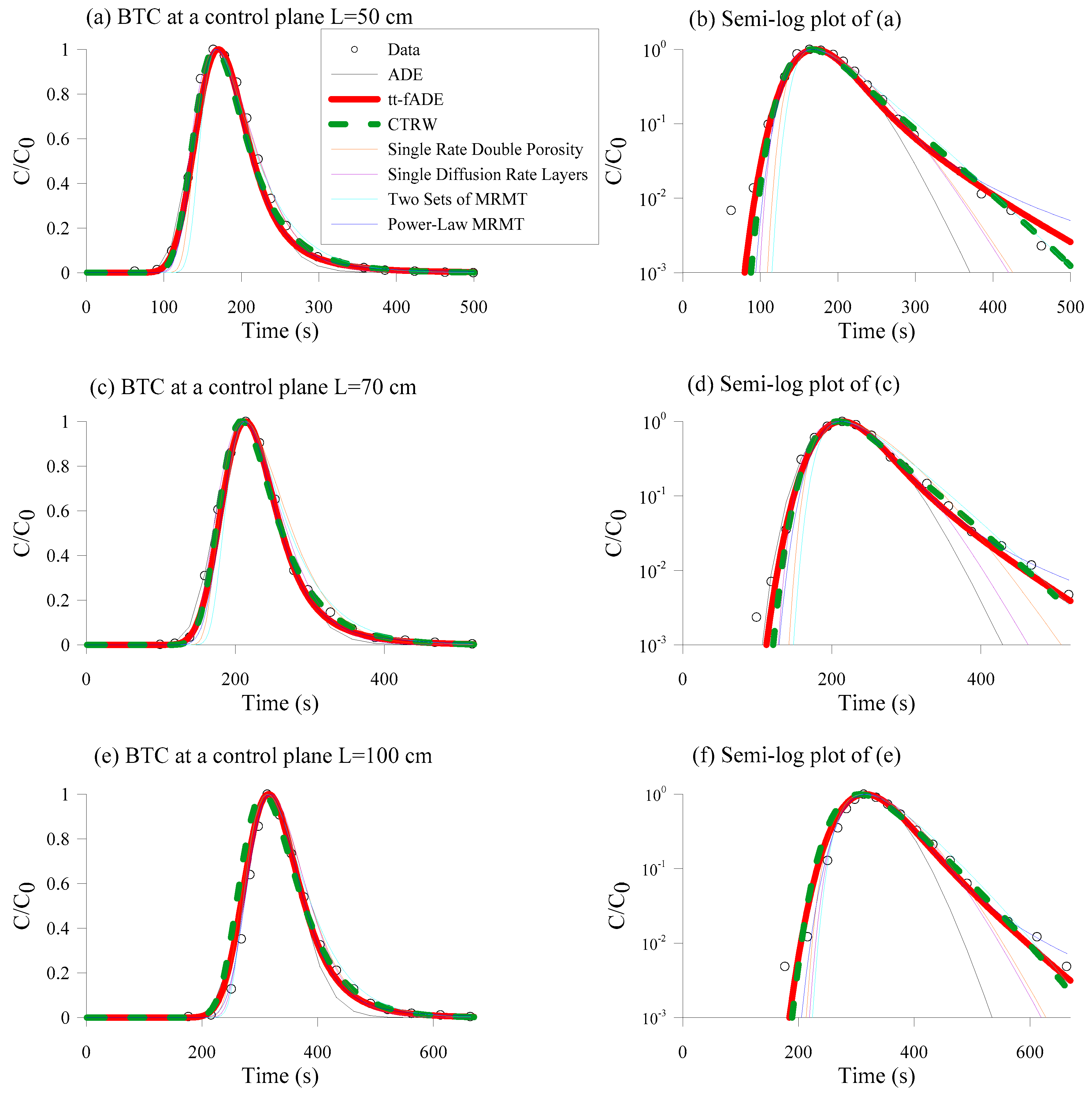
Section 4 can be classified into two main groups. The first group includes the ADE with equilibrium adsorption, the single mass-transfer rate MIM model, and the single diffusion rate MRMT model, which capture the observed early-time BTC and its peak, but underestimate the persistent late-time tail of each BTC. The second group includes the MRMT model with two or a power-law distributed rate coefficients, the tt-fADE, and the CTRW model with a truncated power-law memory function, which can capture the overall trend and positive skewness of the BTCs. The two rate coefficients in the MRMT model, however, might not be adequate to capture heavy late-time tailing for solute transport observed in the field. There is no efficient way to predict the capacity coefficient and the mass transfer rate in the MRMT model, especially when there are multiple sets of mass transfer rates due to various retention capabilities in natural soils with spatial variable hydraulic properties. In contrast, the tt-fADE and the CTRW model parameters are more directly relatable to physical features [
29].
MRMT model: As articulated by [
24], the MRMT model relates closely to the CTRW framework in capturing solute retention times. Particularly, the mean transition time
t1 in the CTRW framework is related to the inverse of the mean rate coefficient in the MRMT model with power-law distributed rate coefficients. Our fitting exercise in
Section 4.4 shows that the BTC is not sensitive to
αmax. The mean transition time
t1 in the CTRW framework and the maximum boundary
αmax used in the MRMT model might not be needed when capturing the late-time tailing of solute transport (note that the cutoff time
t2 in the CTRW model or the minimum rate coefficient
αmin in the MRMT model play a more important role than
t1 or
αmax in affecting the late-time BTC), and therefore they may be removed from the fitting parameters to simplify the model applications. Note that the tt-fADE model does not need the lower-bound of retention times. In addition, the MRMT model with power-law distributed rate coefficients tends to slightly overestimate the late-time tailing in BTCs (
Figure 2 and
Figures S6–S10), implying that the actual mass transfer rates may decline faster than a power-law function at late times.
CTRW model: The CTRW framework has a complex relationship to the tt-fADE model. On one hand, as discussed in
Section 2.3 and checked in
Section 4.4, the power-law exponent
ξ in the CTRW framework is functionally equivalent to the scale index
γ in the tt-fADE, and the cutoff time scale
t2 in CTRW is equivalent to the inverse of the truncation parameter
λ in the tt-fADE. On the other hand, the velocity and dispersion coefficient in the CTRW framework significantly differ from those in the tt-fADE model. Similarly, they are not directly related to the solution of the traditional ADE. Applications in
Section 4.4 show that the average CTRW transport velocity
vψ (1.303 mm/s) is ~59% less than the average real peak velocity (3.18 mm/s) of the observed BTC and ~62% less than the average best-fit velocity (3.39 mm/s) in the tt-fADE model at the flow rate
Q = 1.4 mL/s. For the field tracer tests, the CTRW transport velocity
vψ (0.3 mm/s) is two orders of magnitude larger than the real peak velocity (0.003 mm/s) of the observed BTC, which is similar to the best-fit velocity (0.004 mm/s) in the tt-fADE model. The velocity used in the tt-fADE model can be calculated by using Equation (38), instead of fitting. This procedure further eliminates the number of parameters in the tt-fADE model and makes the fitting more convenient. In addition, the dispersion coefficient in the CTRW framework
Dψ cannot be kept constant under the same flow rate for different travel distances like the dispersion coefficient in the tt-fADE model for both laboratory experiments and field tracer tests. Therefore, the spatially averaged velocity defined by Formula (19) for the CTRW framework may differ from the actual pore-scale velocity. In the CTRW model, different from the traditional ADE, the advective, dispersive, and diffusive transport mechanisms are combined in the random walk formalism. The advective component and the dispersive component are calculated by spatial moments of the same joint probability density function (PDF) for particle transitions and hence cannot be disconnected [
21]. In particular, according to Equation (19), velocity in the CTRW model can be estimated by determining the characteristic time and mean distance, which is the first moment of the PDF of transition displacement. It is, however, difficult to predict the effective velocity
vψ without detailed knowledge of the porous medium. It is also noteworthy that the generalized master Equation (21) does not separate the effects of the spatially varying velocity field on solute particle displacement into an advective part and a dispersive part. The concept of CTRW therefore does not build an explicit relationship between real velocity and model velocity, and the same is true for the dispersion coefficient. In addition, the power-law exponent
ξ can also affect the overall magnitude of solute plume expansion, an effect that intermingles with the dispersion coefficient
Dψ and the effective velocity
vψ. The above analysis is consistent with the result in [
40] that many parameters, particularly
vψ and
ξ, in the CTRW model are correlated with each other. Their fitting exercises showed that different parameter combinations can lead to the same mean Eulerian velocity predicted by the model, implying that the estimated model parameters were not unique.
tt-fADE model: In the tt-fADE model, the best-fit velocity
v can be larger than the plume peak’s velocity
vpeak because the effective velocity used in the tt-fADE is adjusted by the elapsed time for solutes spent in retention, as represented by the fractional-order capacity coefficient
β on the right-hand side of Equation (38). In this study, laboratory experiments with six flow rates and field tracer tests show that the best-fit velocity in the tt-fADE model is close to the measured BTC’s peak velocity, since the capacity coefficient shown in Equation (38) is relatively small. Because the transport velocity used in the tt-fADE model (10) and (11) is not significantly different from the BTC’s peak velocity, the tt-fADE model uses an independent parameter, the time index
γ, to control the power-law distribution of the late-time BTC. This parameterization of the tailing is relatively simple as compared to the CTRW model, with three parameters,
vψ,
Dψ, and
ξ that contribute to time-nonlocal non-Fickian dispersion. We calculate the root mean square error (RMSE) for the laboratory experiments. Comparison of the RMSE (see
Table 1,
Table 6 and
Table 7) of the two models and the ADE model demonstrates that they both perform better than the standard ADE, especially in describing tailing behavior in a heterogeneous medium. When the Formula (38) is used, the tt-fADE model is more convenient to apply in practice than the CTRW framework, since the former contains fewer parameters.
Why the fitted four-parameter tt-fADE model may provide the best performance? This might be due to two reasons. First, according to the physical derivation of the tt-fADE in
Section 2.2, the tt-fADE separates motion in the mobile zone (using the basic transport parameters
v and
D to define advection and Gaussian diffusive displacement) and retention in the immobile domains. When the tracer particle moves in the mobile domain, its average speed is
v, with a finite time required to finish the jump. This physical separation might be reasonable in hydrogeological media. In the CTRW framework, the memory function defines the random waiting time between two subsequent jumps, while the motion can finish instantaneously (in other words, no physical time is required for the tracer particle to move). This physical discrepancy may also cause the discrepancy of the two basic transport parameters
v and
D between the two models, in addition to the spatial average parameters required by the CTRW framework. Second, the tt-fADE does not specify the lower-bound of the waiting time (using an additional parameter such as the lower-limit
t1 in the CTRW framework), since the slow advection can also affect the late-time BTC tail. Mass exchange can apparently affect the late-time BTC tail only when the diffusive time scale is much longer than the advective time scale, as pointed out by [
16]. This may explain why
t1 might not be needed in the CTRW framework. Further real-world tests are needed to check the above hypotheses.
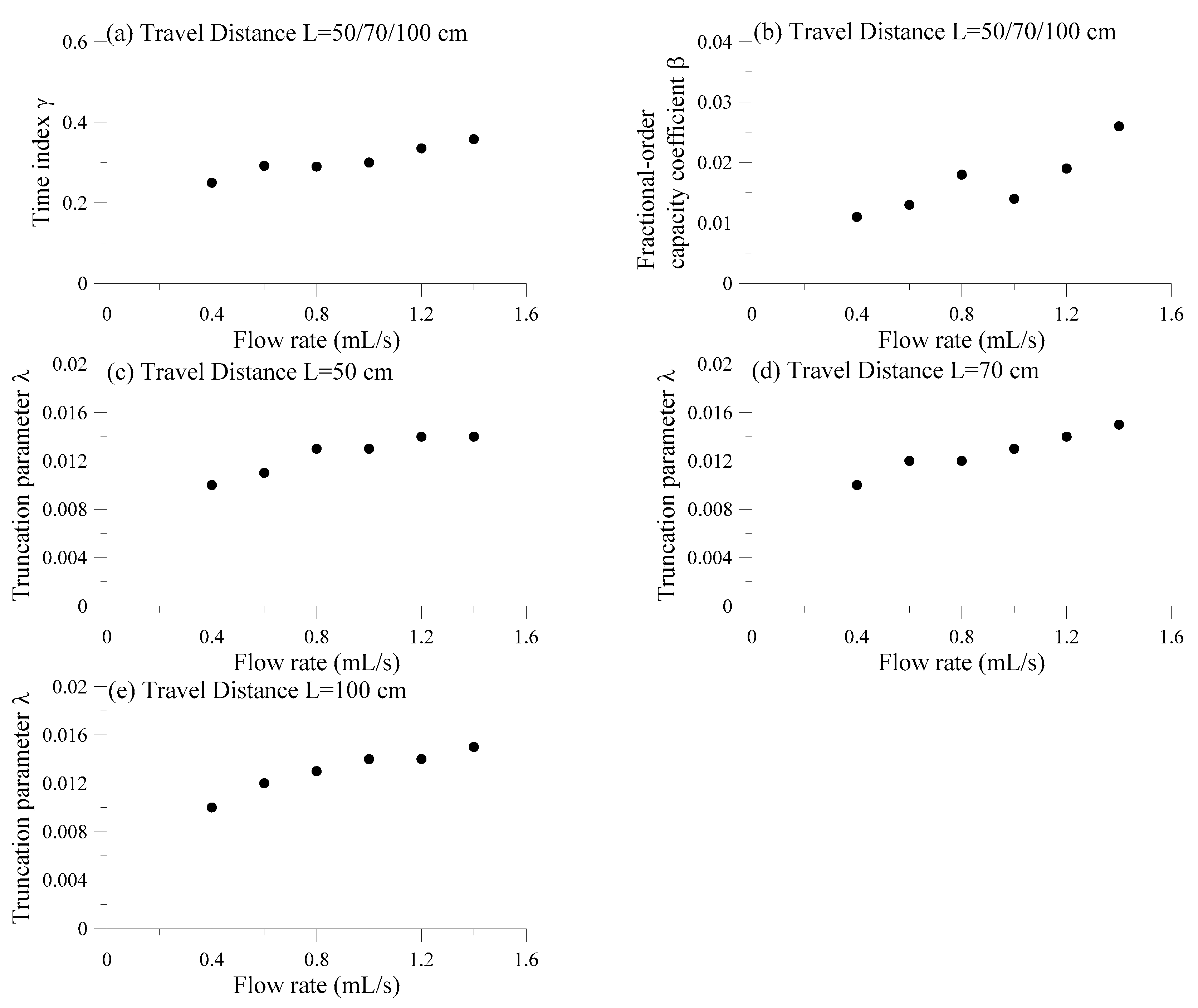
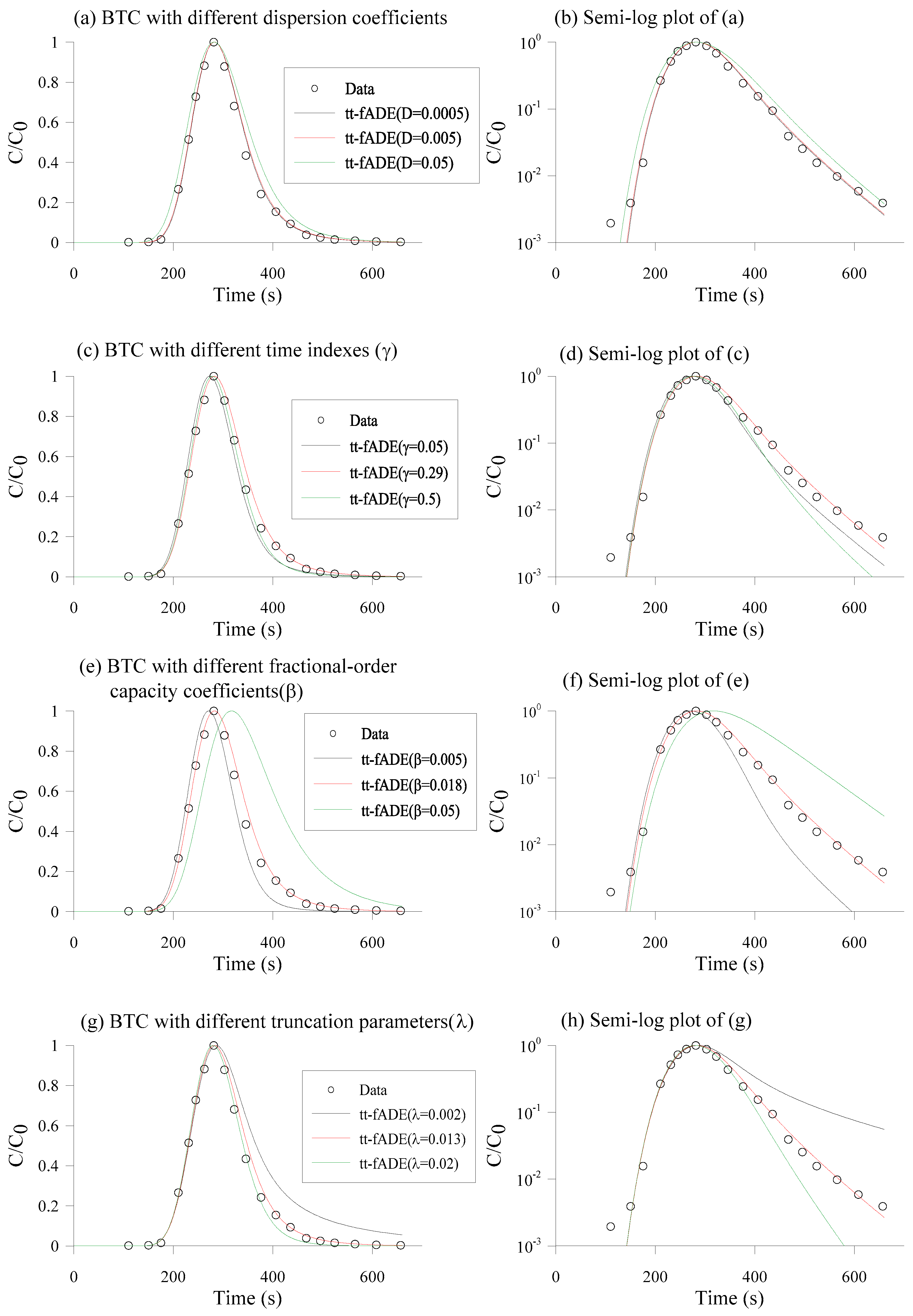
5.2. Parameter Sensitivity
One example of parameter sensitivity is tested here for the tt-fADE (10) and (11). Sensitivity of the BTCs to variations of the four main parameters (
D,
γ,
β,
λ) in the tt-fADE model is shown in
Figure 7.
First, the dispersion coefficient
D has a subtle impact on the overall shape of BTCs. Decreasing
D from 0.005 cm
2/s to 0.0005 cm
2/s results in similar BTCs after normalization (i.e., re-scaling), implying that trapping due to the immobile zones may account at least partially for the spatial expansion of solute plumes. When
D increases from 0.005 cm
2/s to 0.05 cm
2/s, the BTC becomes wider and its shape slightly changes (
Figure 7a,b).
Second, the time index
γ controls the power-law slope of the late-time BTC. For example, when
γ increases from 0.29 to 0.50 (representing the decrease of probability for long retention times), the late-time BTC becomes steeper, approaching relatively fast to its Gaussian asymptote (
Figure 7c,d). When
γ decreases from 0.29 to 0.05, the BTC’s late-time tail becomes heavier (i.e., with a gentler slope), although the overall BTC looks narrower (likely due to the normalization of BTCs). The simulated BTC with the time index
γ equal to 0.29 gives the best fit.
Third, the fractional-order capacity coefficient
β shifts the BTC and expands the BTC’s late-time tail. When
β decreases (representing a decrease of the immobile zone volume or the immobile solute mass at equilibrium), the BTC becomes narrower and shifts to the left (representing a larger effective velocity). A faster drop is apparent in the late-time BTC tail with a smaller
β. An opposite change of the BTC can be seen for an increasing
β (
Figure 7e,f).
Fourth, the truncation parameter
λ affects the speed for the late-time BTC to transfer from a heavy tailed, power-law slope to an exponential tail. A larger truncation parameter means an earlier transform from non-Fickian to Fickian transport (
Figure 7g,h). For the largest
λ tested, the resultant BTC is the closest to the solution of the ADE model, as expected because the tt-fADE reduces to the ADE model for
λ → ∞.
5.3. Application to Field Transport
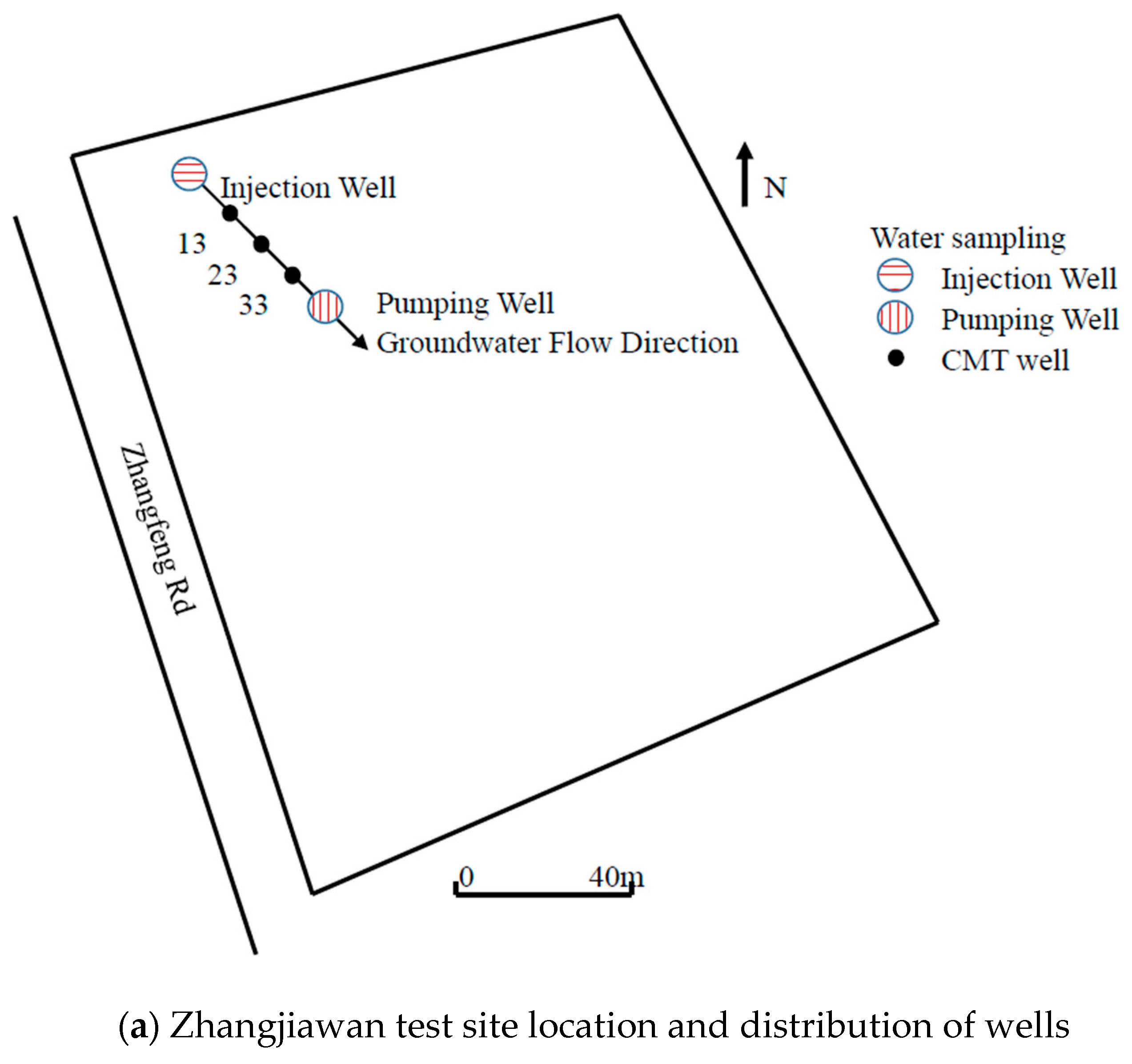
A field trace transport test was conducted recently by Zheng [
41], which provides field data to evaluate further the time nonlocal transport models and compare with the laboratory column experiments. The test site is in the Zhangjiawan Village, Zhangjiawan Town, southeast of the Tongzhou District, Beijing, China, with the longitude of 116.72° and latitude 39.848°. This experimental site is in the Chaobai River alluvial plain. The average annual precipitation in the vicinity is about 533 mm, and the evaporation is 1822 mm. It has a multi-layer aquifer structure. The aquifer is composed of gravelly coarse sand, coarse sand, fine sand, silty clay and clay layer in the test field and surrounding area. The hydraulic conductivity coefficient shows obvious heterogeneity, indicating that the aquifer develops a small-scale preferential flow channel network.
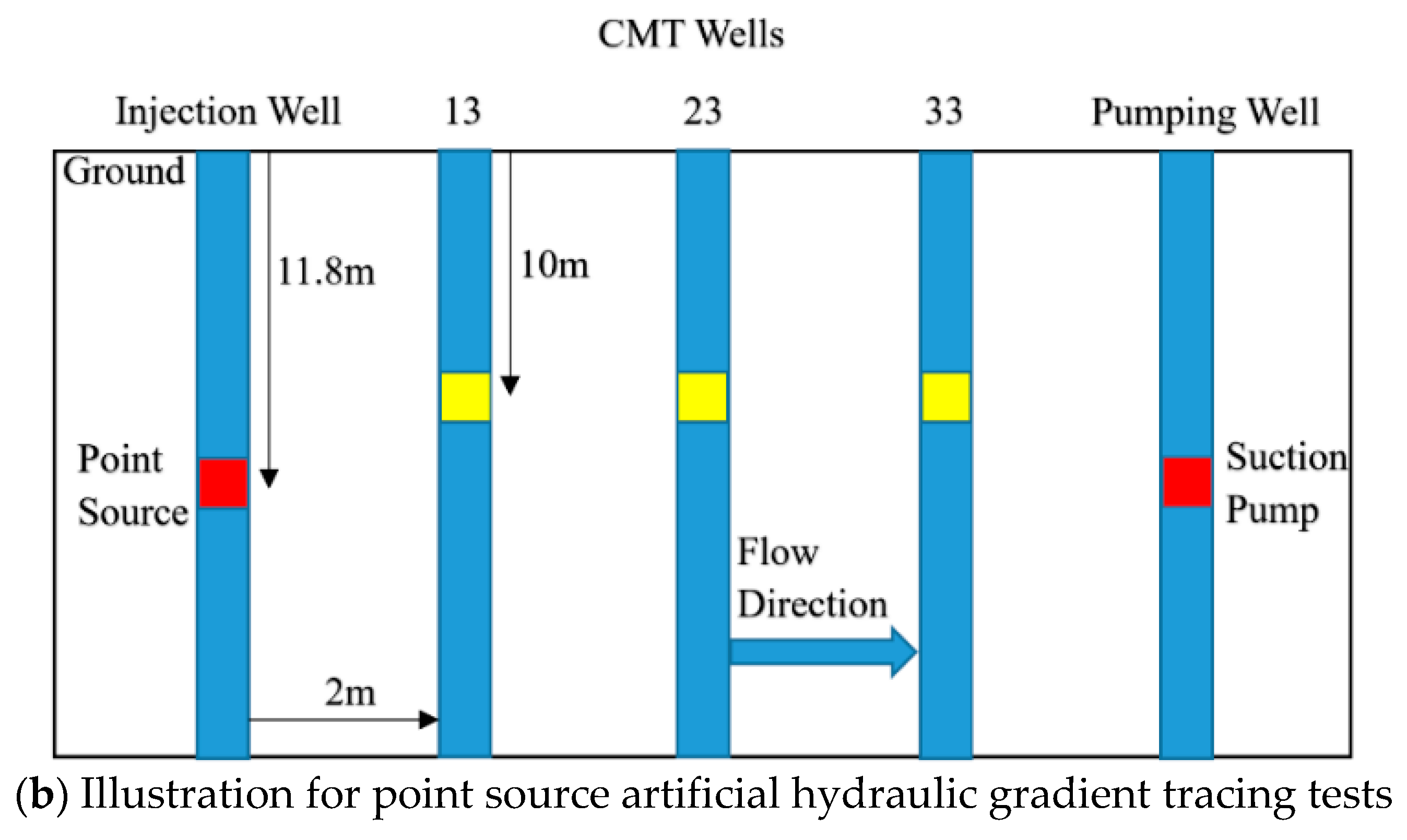
The subsurface network consisted of one injection well, one pumping well, and three monitoring wells with continuous multi-tubing (denoted as well 13, 23, and 33, respectively) (see
Figure 8 for the study site).
All the five wells are along the same line of the general groundwater flow direction, and therefore a one-dimensional model may be used to approximate the overall transport. The injection well and the pumping well are separated by 8 m, and the three observation wells have a uniform interval of 2 m. Groundwater flows from the injection well to well 13, 23, 33, and to the pumping well.
Sodium bromide, a commonly used conservative tracer, was injected into the injection well at a depth of 11.8 m, and groundwater samples were taken from the three observation wells (Well 13, 23, 33) located downstream at a depth of ~10 m. The concentration of the injected solution was 1288 mg/L. The injection rate was about 0.3 m3/h, and the injection duration was 6 h. A peristaltic pump was used to collect the samples in a chronological order, and the sample concentration was measured using a MP523-06 bromide ion concentration meter.
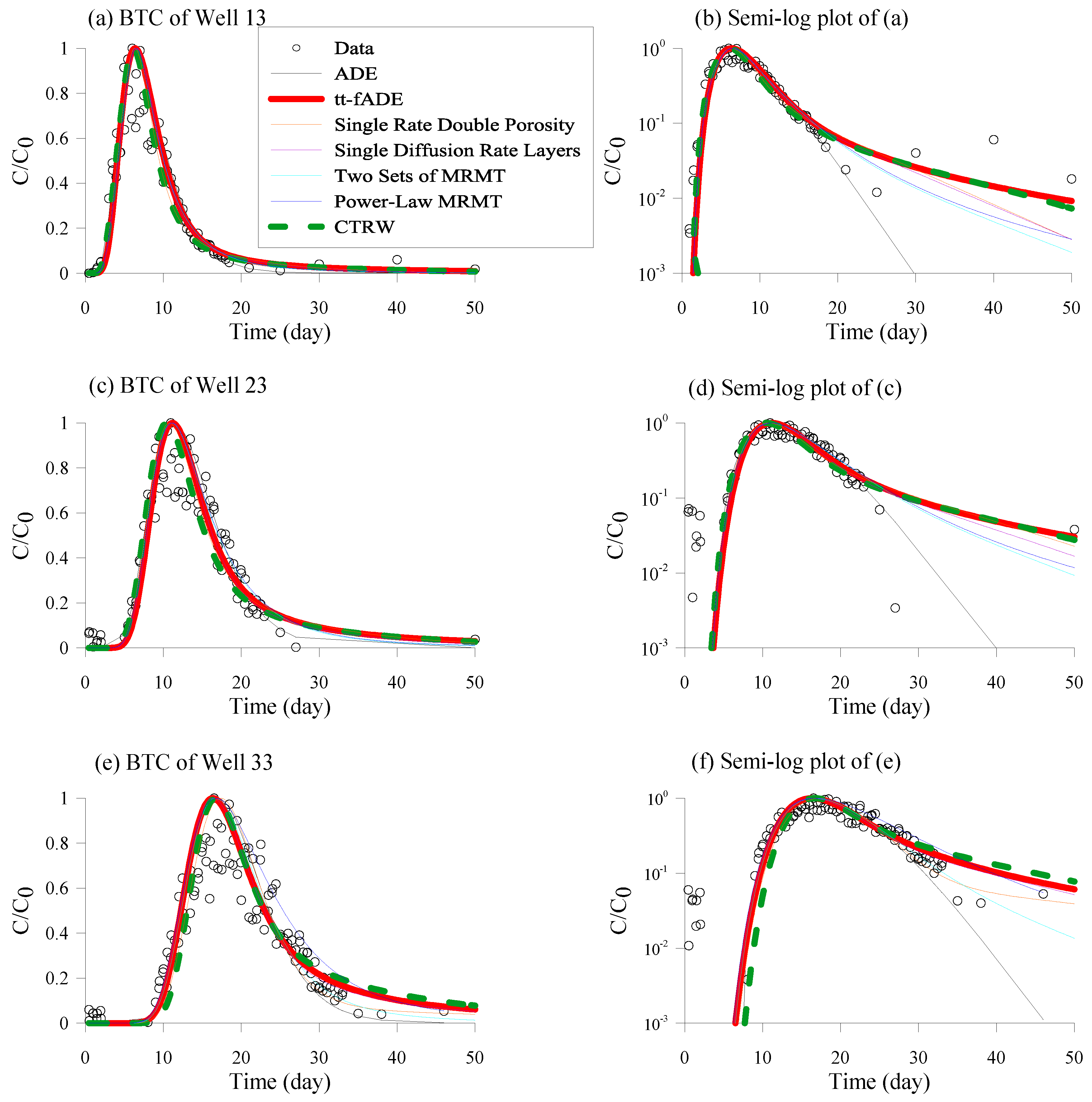
The measured BTCs exhibit apparent late-time tailings (see
Figure 9), similar to that observed in the laboratory column transport. Applications show that the time nonlocal models can capture part of the late-time BTC tail, but not the whole tail of BTC containing apparent noise. Due to the noise, it is also impossible to obtain a reliable RMSE. Although the apparent noise causes high uncertainty in model fitting, both the CTRW framework and the tt-fADE can capture a heavier late-time tail than the MRMT model with two sets of rate coefficients, and the measured BTCs do contain a high concentration at the very end of the sampling period (
Figure 9).
In addition, all the measured BTCs show apparent early time tail, which cannot be captured by the tt-fADE or the CTRW framework with the time index between 0 and 1. It is, however, not a surprise, since the early arrivals are most likely due to fast motion of tracer particles along preferential flow paths, while the delayed arrivals are caused by solute retention due to mass exchange between the mobile and relatively immobile zones. At the field site, high-permeable sand constitutes the layer connecting the injection well and the three monitoring wells, likely forming the preferential channels. The time nonlocal transport models considered in this study were developed to capture solute retention, hence missing the early tail of the BTC. The spatiotemporal fADE may capture both the early and late time tails in the BTC [
28,
42], which will be explored in a future study.
It is also noteworthy that the flow velocity in real aquifers is several orders of magnitude smaller than that used in the laboratory experiments. Hence, the field transport is diffusion dominated, while the laboratory transport is advection dominated. This discrepancy might imply that the late-time BTC tail persists for groundwater flow with a broad range of Peclet numbers, which can be characterized by the time nonlocal models. However, for groundwater flow with a small Peclet number and potential preferential flow paths, the early time BTC tail may occur, which cannot be efficiently captured by the time nonlocal transport models such as the tt-fADE or the CTRW framework with an index less than 1.