A Comparative Study of Groundwater Level Forecasting Using Data-Driven Models Based on Ensemble Empirical Mode Decomposition
Abstract
1. Introduction
2. Methods
2.1. Ensemble Empirical Mode Decomposition
- Step 1. Identify all local maxima and minima points of the time series ;
- Step 2. Interpolate between all local maxima and minima points of to form the upper envelope and lower envelope ;
- Step 3. Compute the mean envelope between the upper envelope and the lower envelope ;
- Step 4. Calculate the IMF candidate;
- Step 5. Determine whether or not satisfies the two conditions of IMF. Is an IMF?
- Step 6. Continue until the final residue meets some predefined stopping criteria.
- Step 1. Initialize the ensemble number and the amplitude of the added white noise.
- Step 2. Add random white noise to produce the noise-added data.
- Step 3. Identify the local maxima and minima and obtain the upper and lower envelopes.
- Step 4. Compute the mean of the upper and lower envelopes.
- Step 5. Decompose the data with added random white noise into IMFs.
- Step 6. Repeat step 3 to step 5 until the stopping criteria. After the shift processing, the IMFs and the residue are obtained.
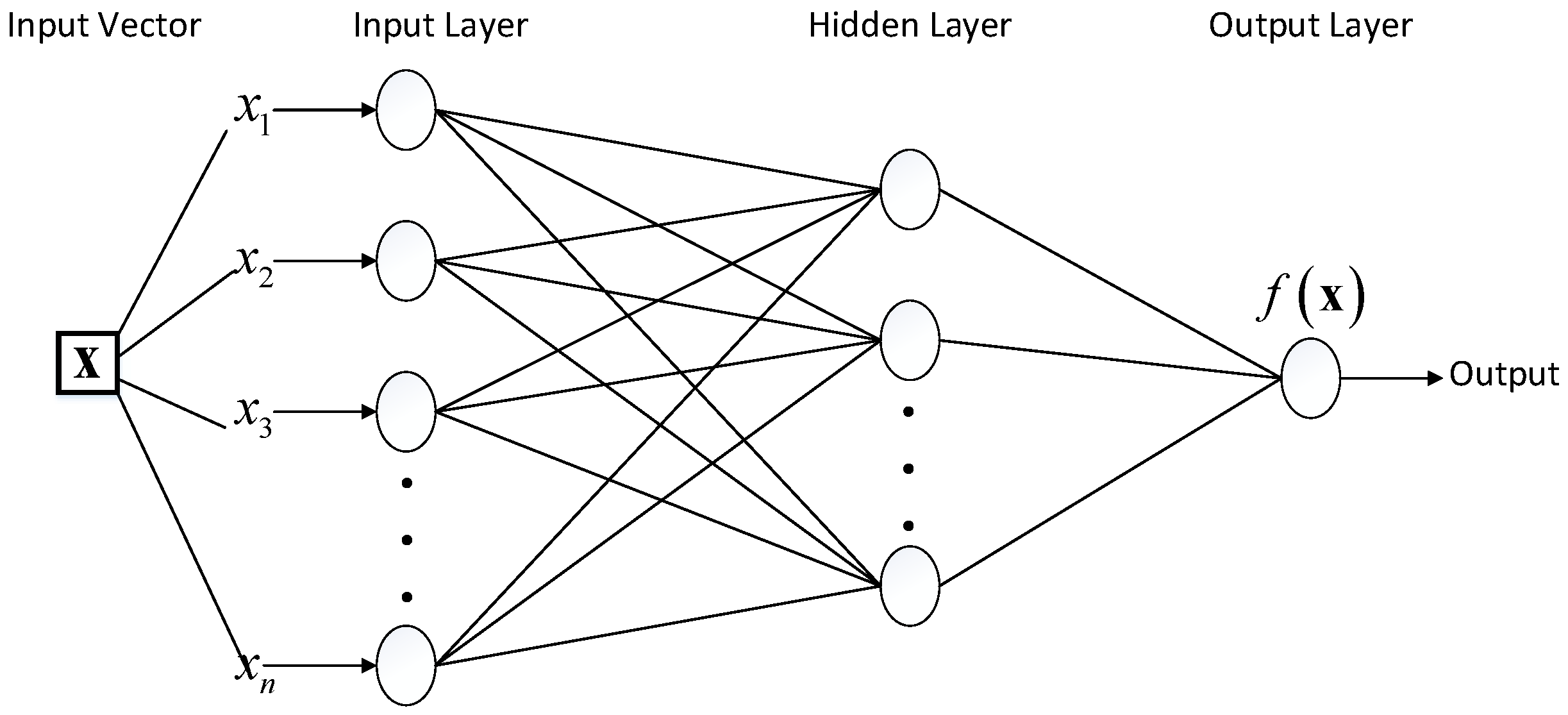
2.2. Artificial Neural Network
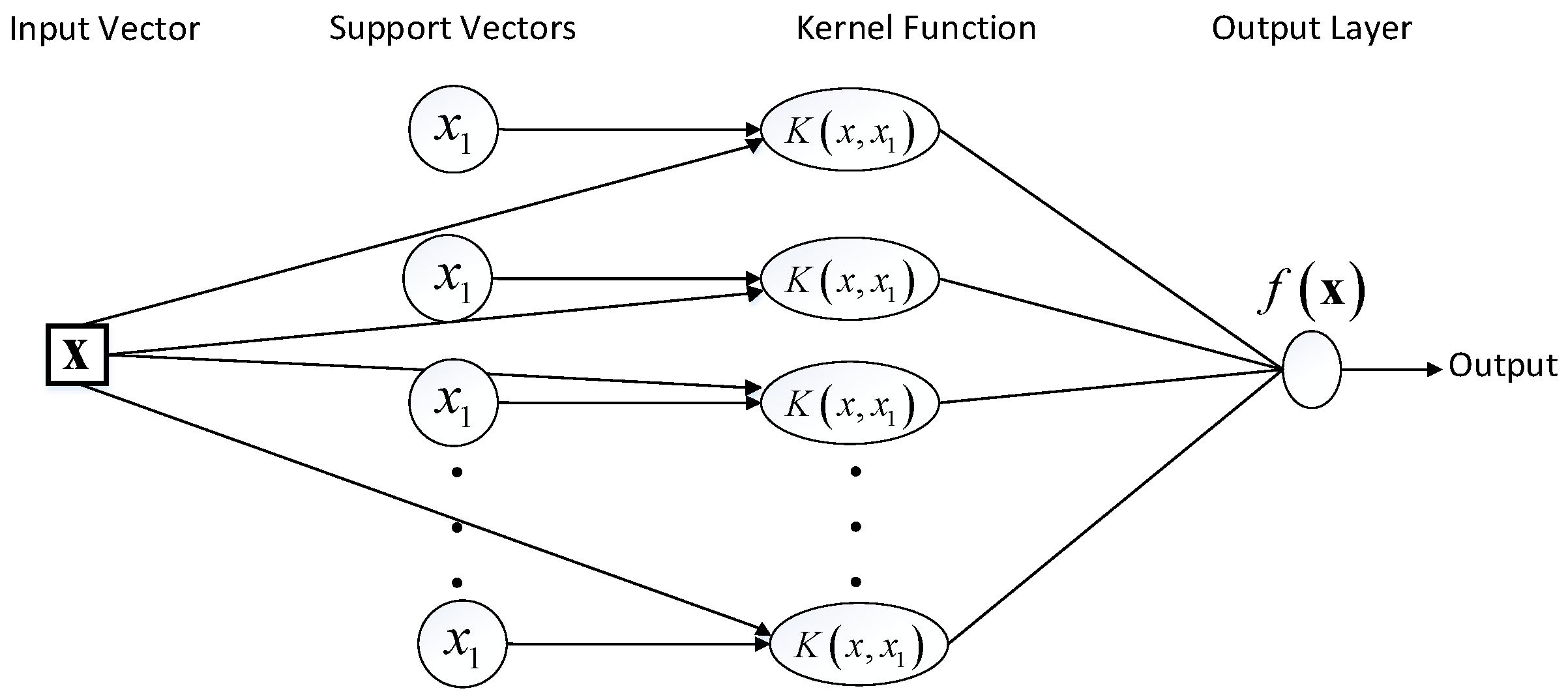
2.3. Support Vector Machine
2.4. Adaptive Neuro Fuzzy Inference System
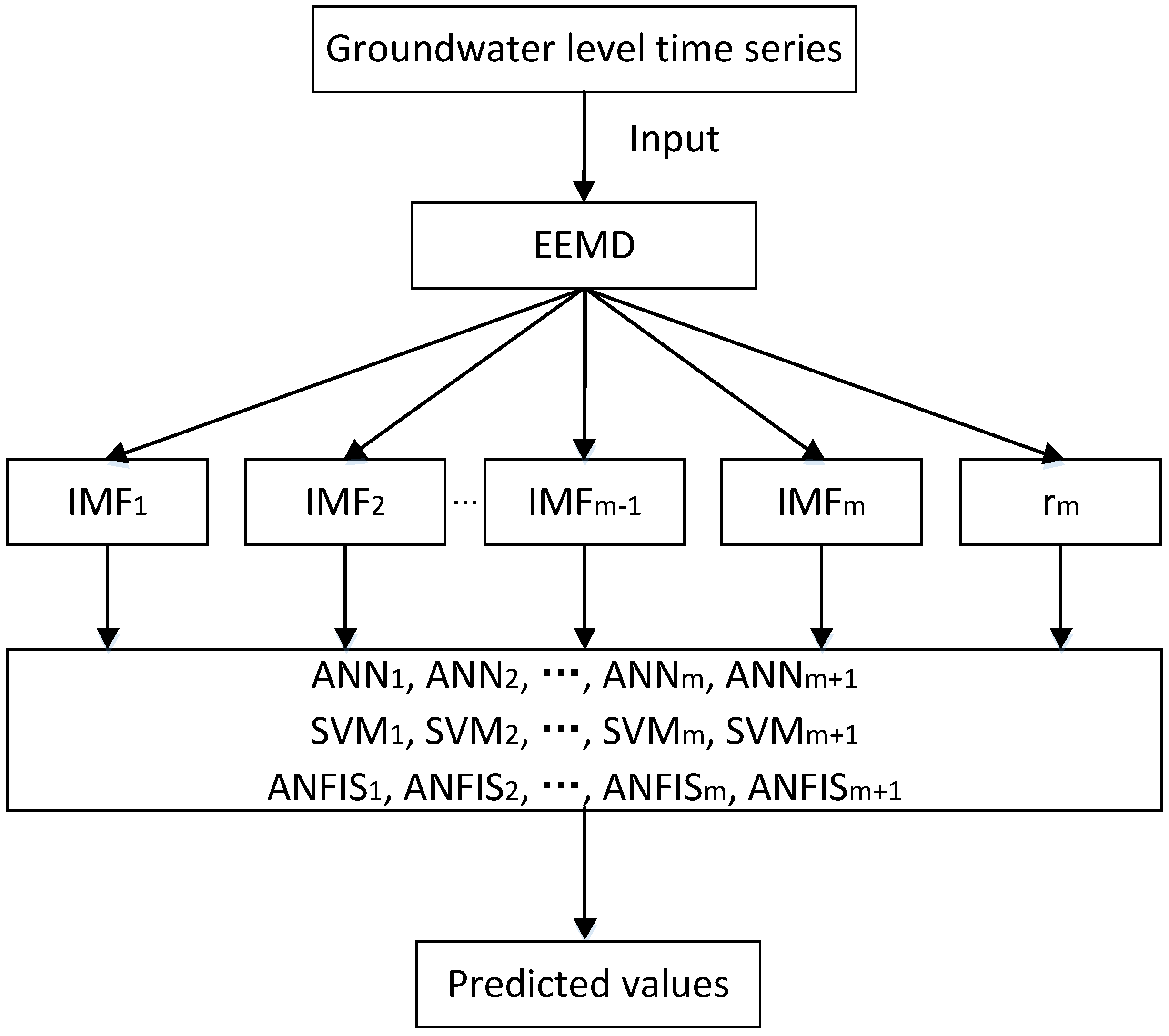
2.5. The Hybrid EEMD-ANN, EEMD-SVM and EEMD-ANFIS Forecasting Models
- (1)
- Firstly, use the EEMD technique to decompose the original groundwater level fluctuation time series into an IMF component and one residual component .
- (2)
- Secondly, the three data driven models ANN, SVM and ANFIS are developed to make the corresponding prediction using extracted IMF component and the residual component, respectively.
- (3)
- Finally, all of the predicting results from the ANN, SVM and ANFIS models are combined to obtain the new output values, which are the final forecasting result for the groundwater level prediction.
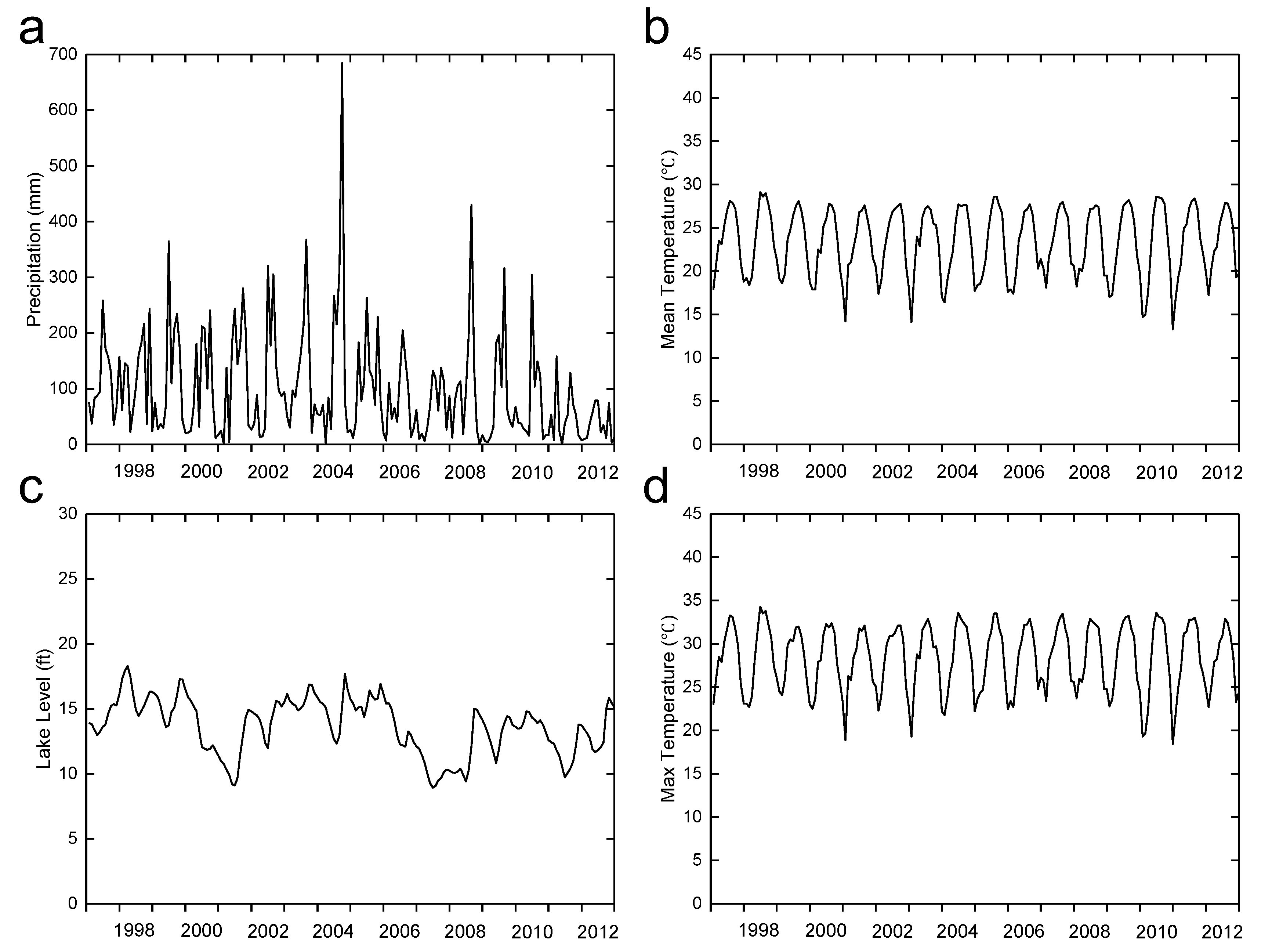
3. Study Area and Available Data
3.1. Study Site and Data Preprocessing
3.2. Performance Criteria
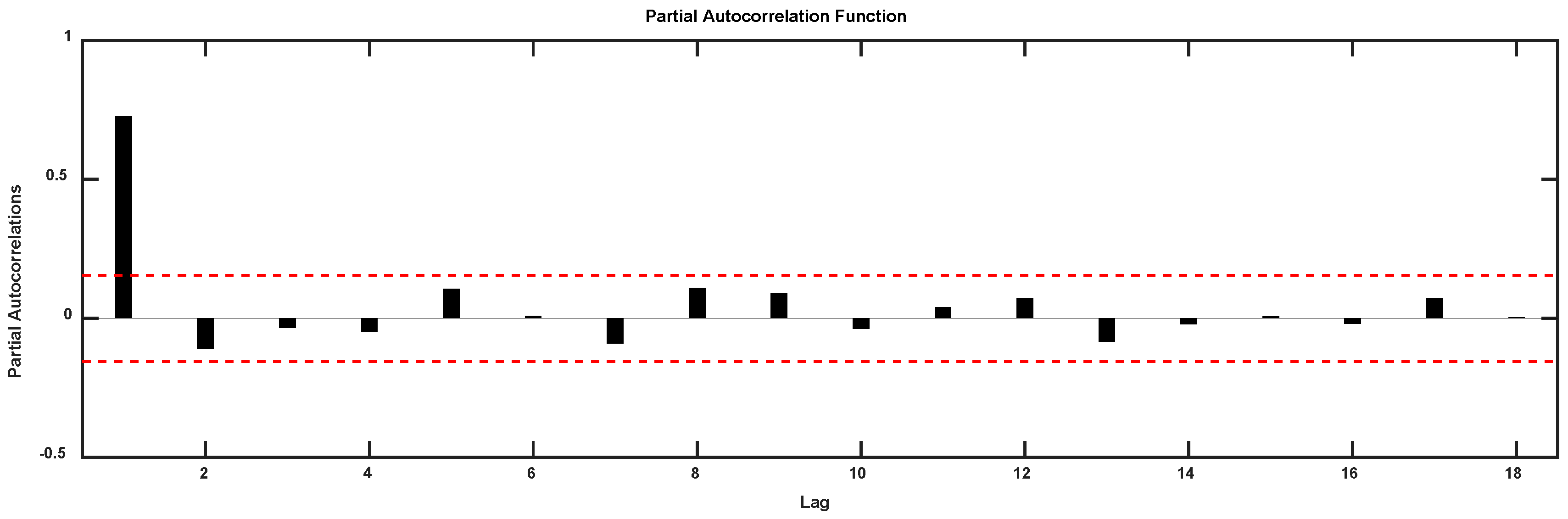
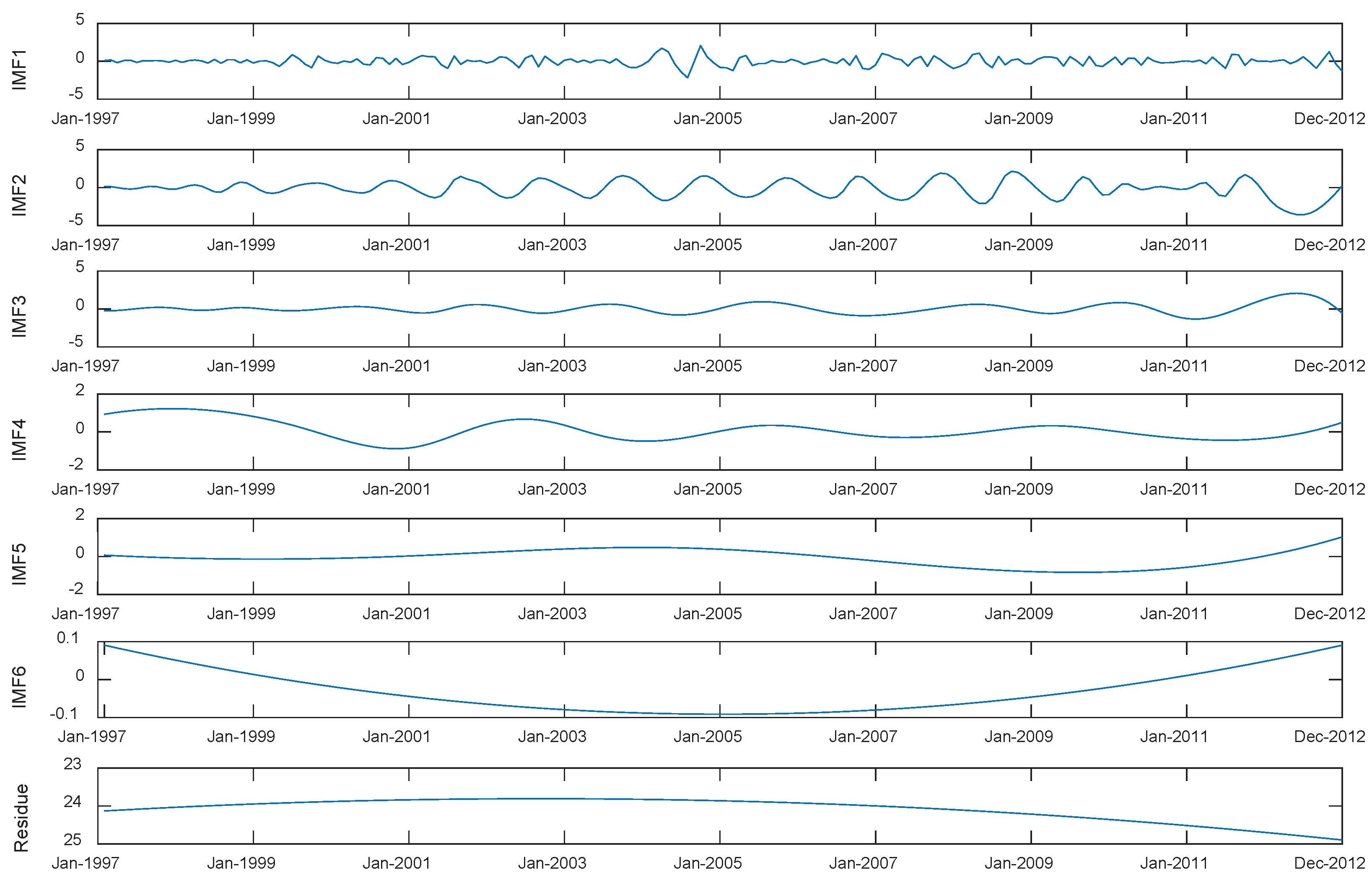
4. Decomposing, Modeling and Application
5. Results and Discussion
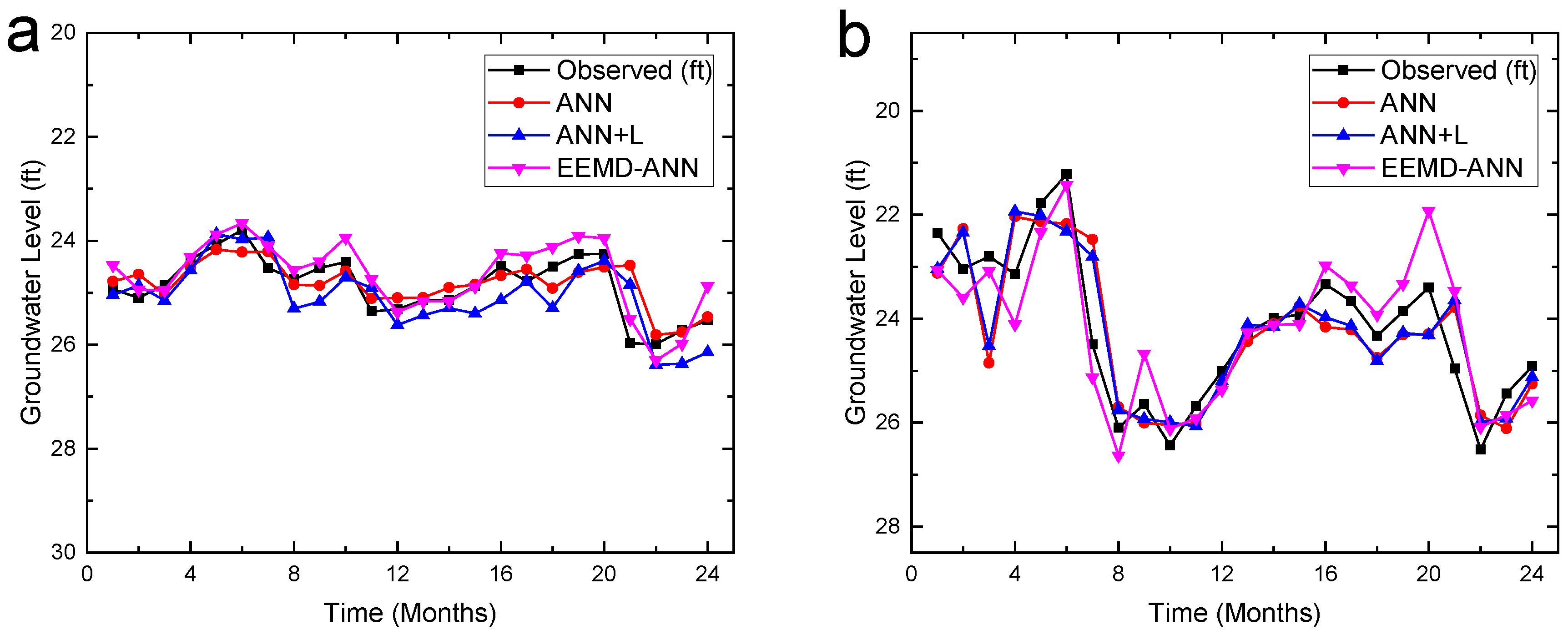
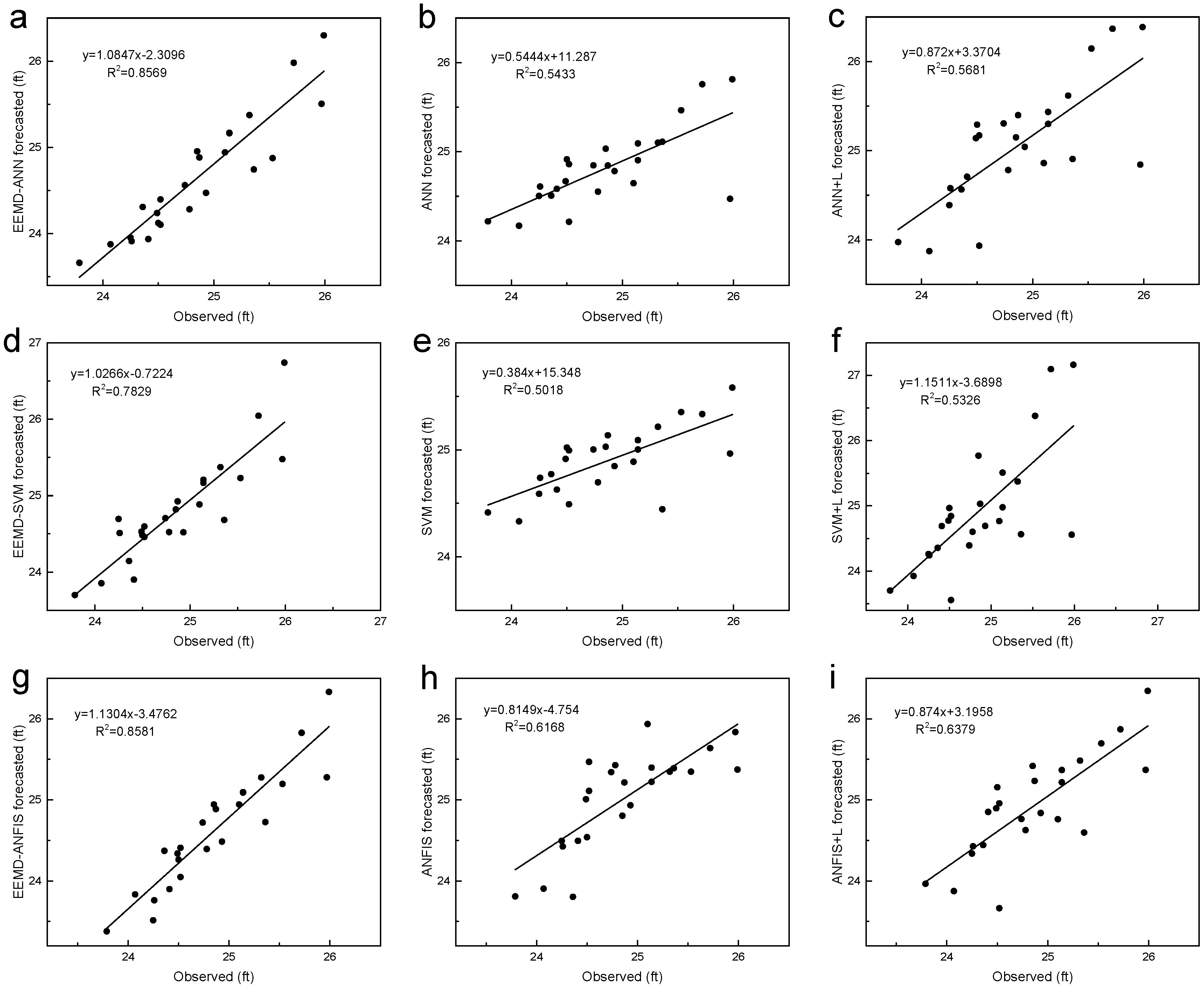
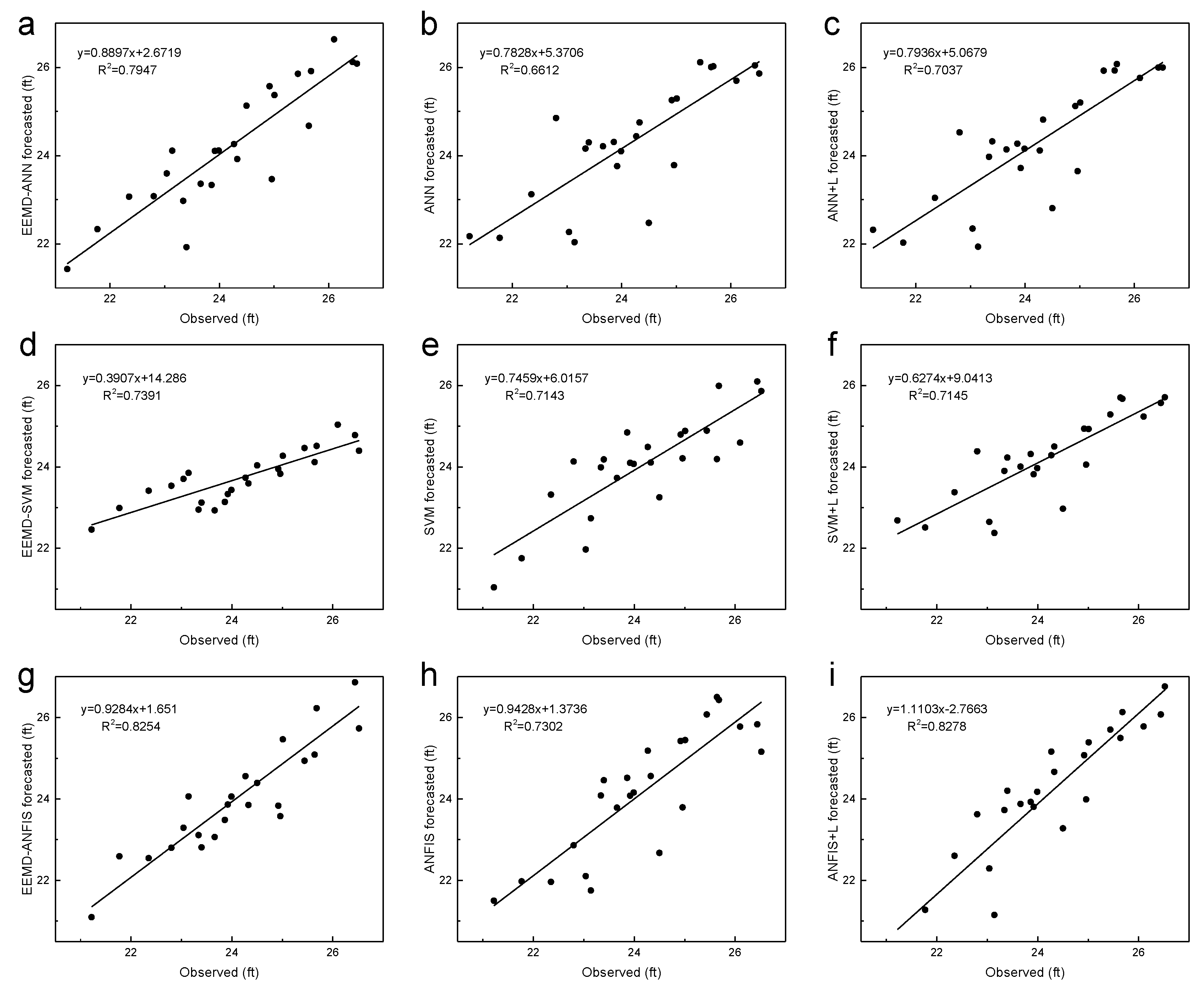
5.1. EEMD-ANN and ANN Models
5.2. EEMD-SVM and SVM Models
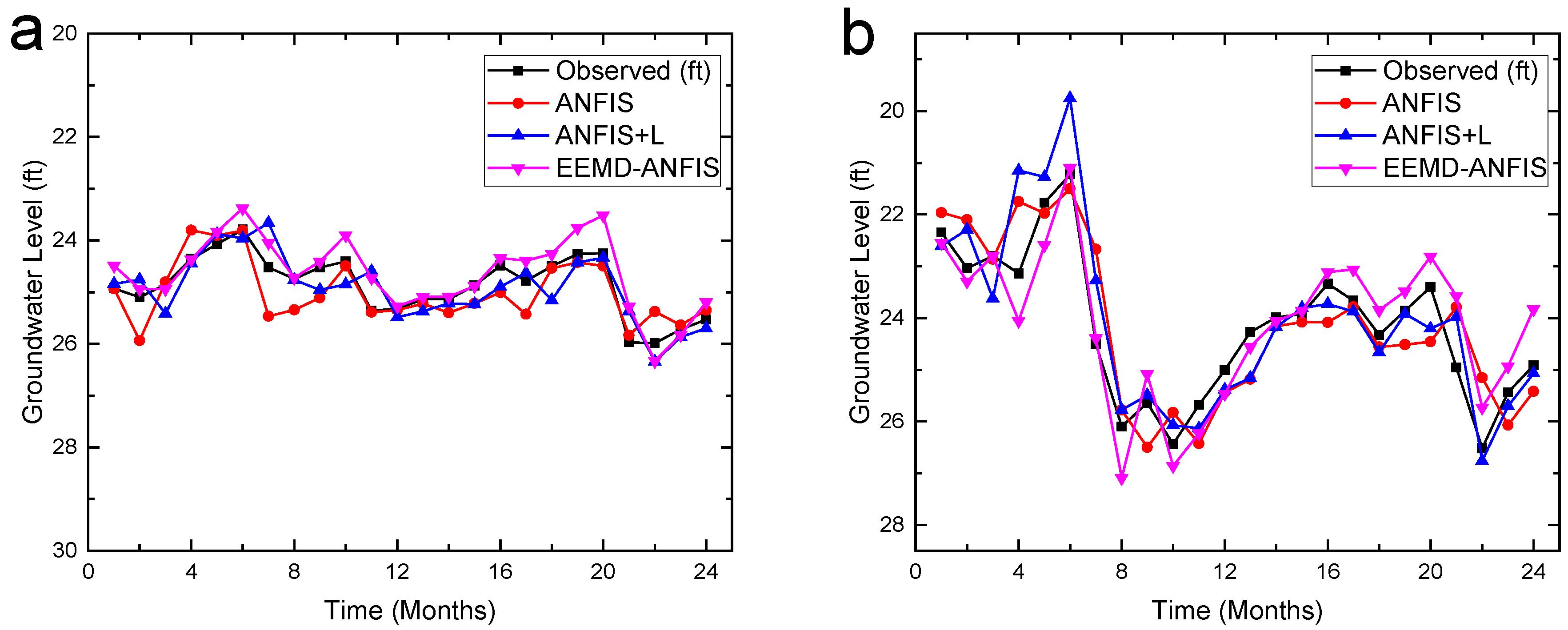
5.3. EEMD-ANFIS and ANFIS Models
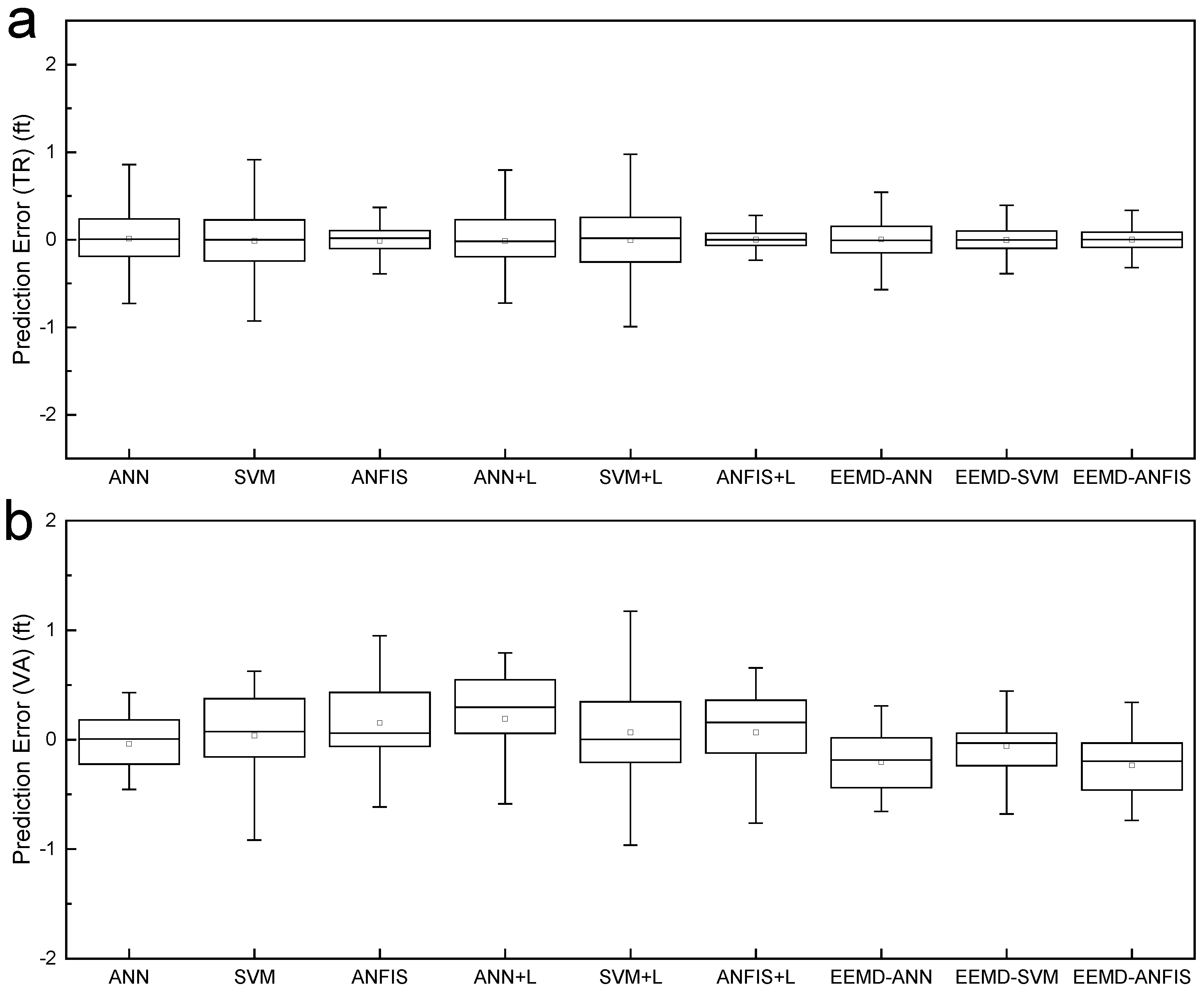
5.4. Comparison of EEMD-ANN, EEMD-SVM and EEMD-ANFIS
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Chang, F.J.; Chang, L.C.; Huang, C.W.; Kao, I.F. Prediction of monthly regional groundwater levels through hybrid soft-computing techniques. J. Hydrol. 2016, 541, 965–976. [Google Scholar] [CrossRef]
- Chang, J.; Wang, G.; Mao, T. Simulation and prediction of suprapermafrost groundwater level variation in response to climate change using a neural network model. J. Hydrol. 2015, 529, 1211–1220. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Moslemi, K.; Karami, G. Prediction the groundwater level of bastam plain (Iran) by artificial neural network (ANN) and adaptive neuro-fuzzy inference system (ANFIS). Water Resour. Manag. 2014, 28, 5433–5446. [Google Scholar] [CrossRef]
- Yoon, H.; Hyun, Y.; Ha, K.; Lee, K.-K.; Kim, G.-B. A method to improve the stability and accuracy of ANN- and SVM-based time series models for long-term groundwater level predictions. Comput. Geosci. 2016, 90, 144–155. [Google Scholar] [CrossRef]
- Yoon, H.; Jun, S.C.; Hyun, Y.; Bae, G.O.; Lee, K.K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Fallah-Mehdipour, E.; Bozorg Haddad, O.; Mariño, M.A. Prediction and simulation of monthly groundwater levels by genetic programming. J. Hydro-Environ. Res. 2013, 7, 253–260. [Google Scholar] [CrossRef]
- Nourani, V.; Alami, M.T.; Vousoughi, F.D. Wavelet-entropy data pre-processing approach for ANN-based groundwater level modeling. J. Hydrol. 2015, 524, 255–269. [Google Scholar] [CrossRef]
- Suryanarayana, C.; Sudheer, C.; Mahammood, V.; Panigrahi, B.K. An integrated wavelet-support vector machine for groundwater level prediction in visakhapatnam, india. Neurocomputing 2014, 145, 324–335. [Google Scholar] [CrossRef]
- Jiang, Q.; Tang, Y. A general approximate method for the groundwater response problem caused by water level variation. J. Hydrol. 2015, 529, 398–409. [Google Scholar] [CrossRef]
- Shirmohammadi, B.; Vafakhah, M.; Moosavi, V.; Moghaddamnia, A. Application of several data-driven techniques for predicting groundwater level. Water Resour. Manag. 2013, 27, 419–432. [Google Scholar] [CrossRef]
- Moosavi, V.; Vafakhah, M.; Shirmohammadi, B.; Behnia, N. A wavelet-ANFIS hybrid model for groundwater level forecasting for different prediction periods. Water Resour. Manag. 2013, 27, 1301–1321. [Google Scholar] [CrossRef]
- Shiri, J.; Kişi, Ö. Comparison of genetic programming with neuro-fuzzy systems for predicting short-term water table depth fluctuations. Comput. Geosci. 2011, 37, 1692–1701. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the arma, arima, and the autoregressive artificial neural network models in forecasting the monthly inflow of dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Xu, T.; Valocchi, A.J.; Choi, J.; Amir, E. Use of machine learning methods to reduce predictive error of groundwater models. Ground Water 2014, 52, 448–460. [Google Scholar] [CrossRef] [PubMed]
- Asefa, T.; Kemblowski, M.; Urroz, G.; Mckee, M. Support vector machines (SVMs) for monitoring network design. Ground Water 2005, 43, 413–422. [Google Scholar] [CrossRef] [PubMed]
- White, S.; Robinson, J.; Cordell, D.; Jha, M.; Milne, G. Urban Water Demand Forecasting and Demand Management: Research Needs Review and Recommendations; Water Services Association of Australia: Melbourne, Australia, 2003. [Google Scholar]
- Wang, Y.-H.; Yeh, C.H.; Young, H.W.V.; Hu, K.; Lo, M.T. On the computational complexity of the empirical mode decomposition algorithm. Phys. A Stat. Mech. Appl. 2014, 400, 159–167. [Google Scholar] [CrossRef]
- Ghalehkhondabi, I.; Ardjmand, E.; Young, W.A., II; Weckman, G.R. Water demand forecasting: Review of soft computing methods. Environ. Monit. Assess. 2017, 189, 313. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition:A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Chi, C.T.; Liu, H.H. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Xu, D.M.; Chen, X.Y. Improving forecasting accuracy of annual runoff time series using arima based on EEMD decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Qiu, L.; Chen, Y.B. Improving forecasting accuracy of medium and long-term runoff using artificial neural network based on EEMD decomposition. Environ. Res. 2015, 139, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.-C.; Xu, D.-M.; Chau, K.-W.; Chen, S. Improved annual rainfall-runoff forecasting using PSO–SVM model based on EEMD. J. Hydroinform. 2013, 15, 1377–1390. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.-Q.; Li, Y.-F. Comparison of new hybrid feemd-mlp, feemd-ANFIS, wavelet packet-mlp and wavelet packet-ANFIS for wind speed predictions. Energy Convers. Manag. 2015, 89, 1–11. [Google Scholar] [CrossRef]
- Duan, W.Y.; Han, Y.; Huang, L.M.; Zhao, B.B.; Wang, M.H. A hybrid emd-svr model for the short-term prediction of significant wave height. Ocean Eng. 2016, 124, 54–73. [Google Scholar] [CrossRef]
- Ausati, S.; Amanollahi, J. Assessing the accuracy of ANFIS, EEMD-GRNN, PCR, and MLR models in predicting PM 2.5. Atmos. Environ. 2016, 142, 465–474. [Google Scholar] [CrossRef]
- Napolitano, G.; Serinaldi, F.; See, L. Impact of emd decomposition and random initialisation of weights in ann hindcasting of daily stream flow series: An empirical examination. J. Hydrol. 2011, 406, 199–214. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Nagesh Kumar, D. Predictability of nonstationary time series using wavelet and emd based arma models. J. Hydrol. 2013, 502, 103–119. [Google Scholar] [CrossRef]
- Hawinkel, P.; Swinnen, E.; Lhermitte, S.; Verbist, B.; Van Orshoven, J.; Muys, B. A time series processing tool to extract climate-driven interannual vegetation dynamics using ensemble empirical mode decomposition (EEMD). Remote Sens. Environ. 2015, 169, 375–389. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A.; Abraham, P.; Mahe, G. Analysis of laser speckle contrast images variability using a novel empirical mode decomposition: Comparison of results with laser doppler flowmetry signals variability. IEEE Trans. Med. Imaging 2015, 34, 618–627. [Google Scholar] [CrossRef] [PubMed]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. An unconstrained optimization approach to empirical mode decomposition. Digit. Signal Process. 2015, 40, 164–175. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- ASCE. Artificial neural networks in hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar]
- ASCE. Artificial neural networks in hydrology. II: Hydrologic applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar]
- Gong, Y.; Zhang, Y.; Lan, S.; Wang, H. A comparative study of artificial neural networks, support vector machines and adaptive neuro fuzzy inference system for forecasting groundwater levels near lake okeechobee, florida. Water Resour. Manag. 2016, 30, 375–391. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Platt, J.C. Fast training of support vector machines using sequential minimal optimization. In Advances in Kernel Methods; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Scholkopf, B.; Smola, A.J. Learning with Kernels: SUPPORT Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Chang, C.C.; Lin, C.J. Libsvm: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive ne twork based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Valizadeh, N.; El-Shafie, A. Forecasting the level of reservoirs using multiple input fuzzification in ANFIS. Water Resour. Manag. 2013, 27, 3319–3331. [Google Scholar] [CrossRef]
- Akrami, S.A.; El-Shafie, A.; Jaafar, O. Improving rainfall forecasting efficiency using modified adaptive neuro-fuzzy inference system (MANFIS). Water Resour. Manag. 2013, 27, 3507–3523. [Google Scholar] [CrossRef]
- Nourani, V.; Komasi, M. A geomorphology-based ANFIS model for multi-station modeling of rainfall–runoff process. J. Hydrol. 2013, 490, 41–55. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, AC-19, 716–723. [Google Scholar] [CrossRef]
- The Math Works; Matlab; Version 9.0.0; The Math Works Inc.: Natick, MA, USA; Available online: http://www.mathworks.com (accessed on 3 March 2016).
- Shu, C.; Ouarda, T.B.M.J. Regional flood frequency analysis at ungauged sites using the adaptive neuro-fuzzy inference system. J. Hydrol. 2008, 349, 31–43. [Google Scholar] [CrossRef]







| Training | Validation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R | NMSE | RMSE | NS | AIC | R | NMSE | RMSE | NS | AIC | ||
| EEMD-ANN | 0.932 | 0.131 | 0.234 | 0.869 | −488.040 | 0.926 | 0.317 | 0.329 | 0.669 | −53.350 | |
| M1255 | ANN | 0.808 | 0.345 | 0.380 | 0.653 | −325.009 | 0.737 | 0.442 | 0.389 | 0.538 | −45.377 |
| ANN+L | 0.816 | 0.333 | 0.374 | 0.665 | −330.668 | 0.754 | 0.675 | 0.480 | 0.296 | −35.246 | |
| EEMD-ANN | 0.977 | 0.044 | 0.281 | 0.955 | −426.784 | 0.891 | 0.208 | 0.646 | 0.783 | −20.979 | |
| STL185 | ANN | 0.869 | 0.244 | 0.659 | 0.754 | −140.343 | 0.813 | 0.353 | 0.842 | 0.632 | −8.239 |
| ANN+L | 0.872 | 0.239 | 0.651 | 0.760 | −144.026 | 0.839 | 0.298 | 0.774 | 0.689 | −12.323 | |
| Training | Validation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R | NMSE | RMSE | NS | AIC | R | NMSE | RMSE | NS | AIC | ||
| EEMD-SVM | 0.948 | 0.102 | 0.206 | 0.898 | −530.463 | 0.885 | 0.292 | 0.315 | 0.696 | −55.373 | |
| M1255 | SVM | 0.786 | 0.450 | 0.434 | 0.548 | −280.434 | 0.7089 | 0.508 | 0.416 | 0.470 | −42.067 |
| SVM+L | 0.758 | 0.424 | 0.421 | 0.574 | −290.376 | 0.730 | 1.149 | 0.626 | −0.199 | −22.467 | |
| EEMD-SVM | 0.972 | 0.073 | 0.360 | 0.927 | −343.467 | 0.860 | 0.507 | 1.009 | 0.471 | 0.447 | |
| STL185 | SVM | 0.931 | 0.134 | 0.488 | 0.865 | −241.064 | 0.845 | 0.283 | 0.755 | 0.704 | −13.512 |
| SVM+L | 0.858 | 0.273 | 0.696 | 0.725 | −121.615 | 0.845 | 0.284 | 0.756 | 0.703 | −13.441 | |
| Training | Validation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R | NMSE | RMSE | NS | AIC | R | NMSE | RMSE | NS | AIC | ||
| EEMD-ANFIS | 0.968 | 0.063 | 0.162 | 0.937 | −611.840 | 0.926 | 0.379 | 0.360 | 0.605 | −49.100 | |
| M1255 | ANFIS | 0.918 | 0.157 | 0.257 | 0.842 | −457.099 | 0.785 | 0.496 | 0.412 | 0.482 | −42.602 |
| ANFIS+L | 0.971 | 0.058 | 0.156 | 0.942 | −624.287 | 0.799 | 0.443 | 0.389 | 0.538 | −45.341 | |
| EEMD-ANFIS | 0.982 | 0.035 | 0.249 | 0.965 | −466.512 | 0.909 | 0.183 | 0.606 | 0.809 | −24.035 | |
| STL185 | ANFIS | 0.940 | 0.117 | 0.455 | 0.883 | −264.408 | 0.855 | 0.318 | 0.799 | 0.668 | −10.756 |
| ANFIS+L | 0.980 | 0.039 | 0.264 | 0.961 | −447.574 | 0.910 | 0.262 | 0.726 | 0.726 | −15.360 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Y.; Wang, Z.; Xu, G.; Zhang, Z. A Comparative Study of Groundwater Level Forecasting Using Data-Driven Models Based on Ensemble Empirical Mode Decomposition. Water 2018, 10, 730. https://doi.org/10.3390/w10060730
Gong Y, Wang Z, Xu G, Zhang Z. A Comparative Study of Groundwater Level Forecasting Using Data-Driven Models Based on Ensemble Empirical Mode Decomposition. Water. 2018; 10(6):730. https://doi.org/10.3390/w10060730
Chicago/Turabian StyleGong, Yicheng, Zhongjing Wang, Guoyin Xu, and Zixiong Zhang. 2018. "A Comparative Study of Groundwater Level Forecasting Using Data-Driven Models Based on Ensemble Empirical Mode Decomposition" Water 10, no. 6: 730. https://doi.org/10.3390/w10060730
APA StyleGong, Y., Wang, Z., Xu, G., & Zhang, Z. (2018). A Comparative Study of Groundwater Level Forecasting Using Data-Driven Models Based on Ensemble Empirical Mode Decomposition. Water, 10(6), 730. https://doi.org/10.3390/w10060730




