An Interval Quadratic Fuzzy Dependent-Chance Programming Model for Optimal Irrigation Water Allocation under Uncertainty
Abstract
:1. Introduction
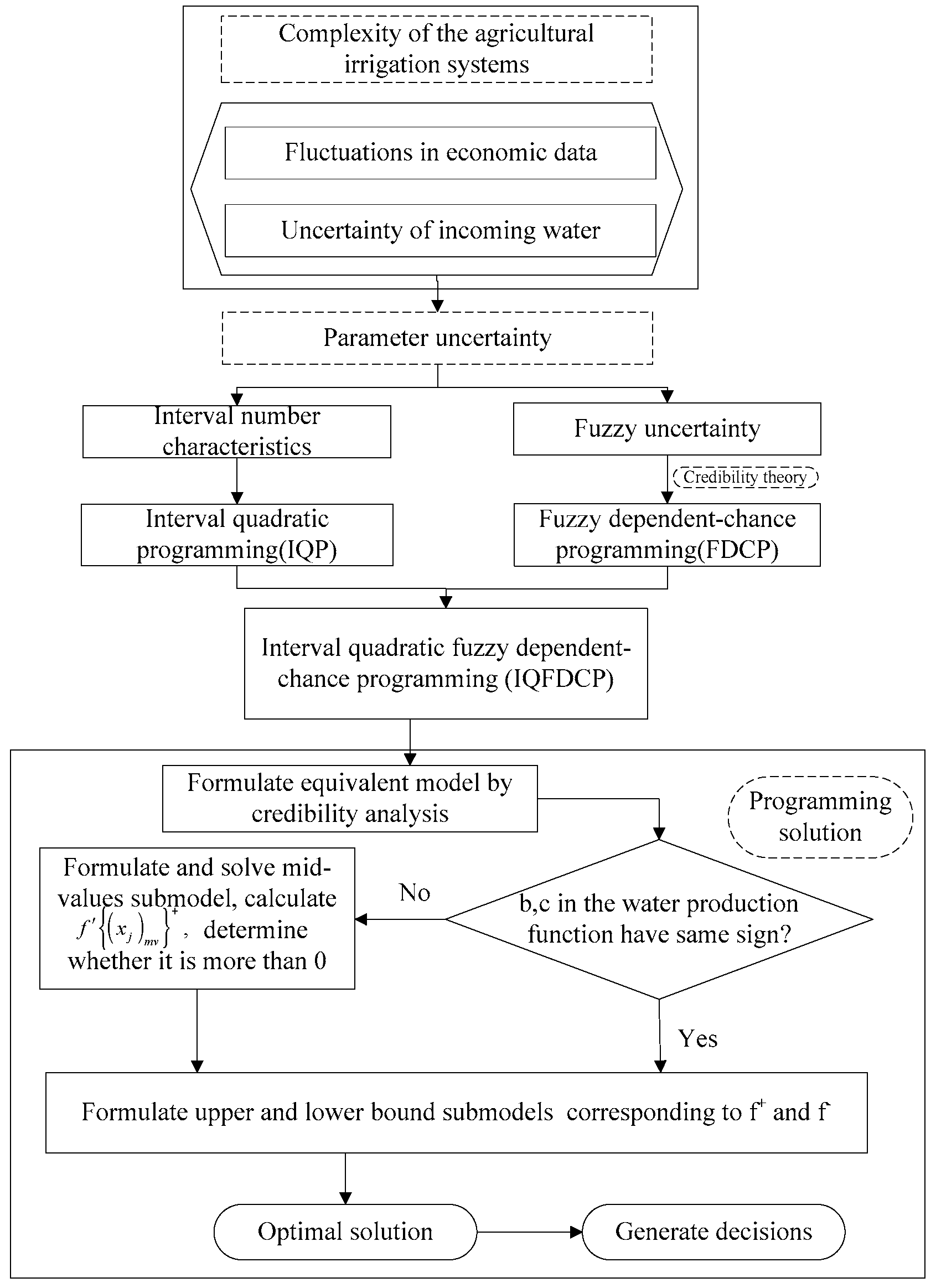
2. Methodology
2.1. Interval Quadratic Programming (IQP)
2.2. Fuzzy Dependent-Chance Programming Theory (FDCP)
2.3. Interval Quadratic Fuzzy Dependent-Chance Programming (IQFDCP) Model
- (1)
- Determine the input parameters of the model and its fuzzy membership functions.
- (2)
- Analyze the credibility level of the model. According to the triangular fuzzy membership functions, the developed model can be transformed into its equivalent model.
- (3)
- If the , in interval quadratic function have the same sign, we can formulate the upper and lower bound submodels corresponding to and .
- (4)
- If the , in interval quadratic function have different signs, we should formulate and solve mid-values model first, have and or and whether is more than 0.
- (5)
- Solve the above submodels and obtain the optimal objective function and the decision variables.
3. Case Study
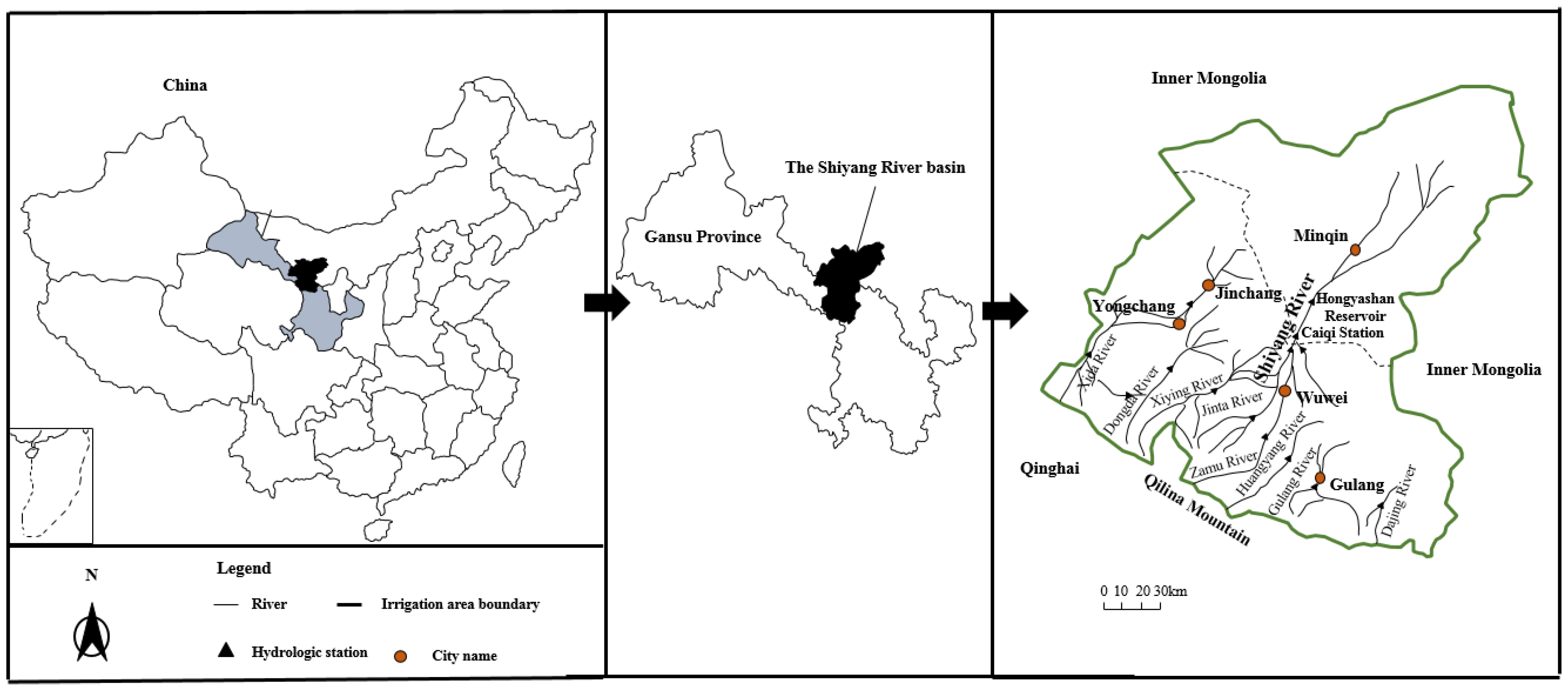
3.1. Study Area
3.2. Problem Statement
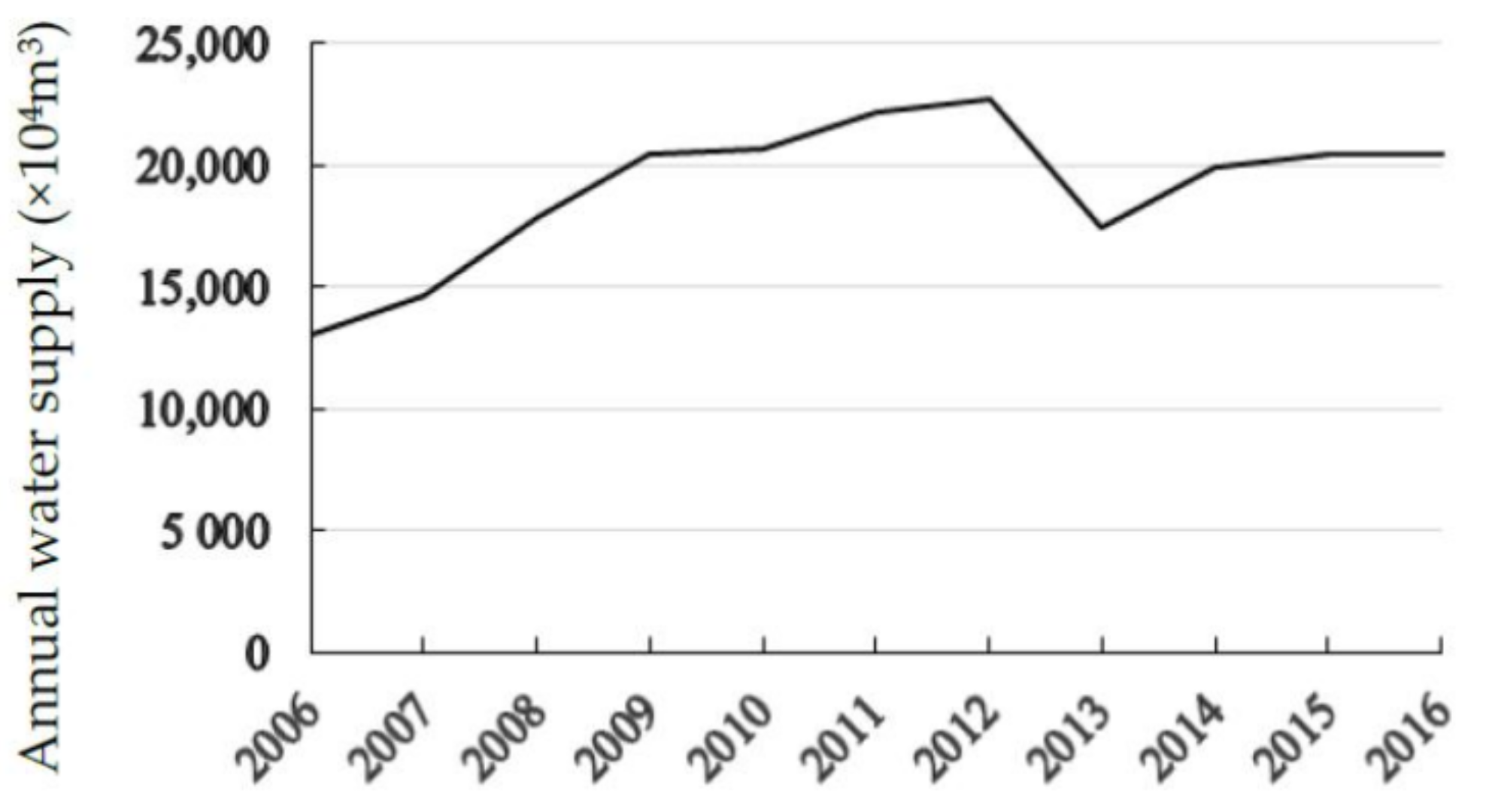
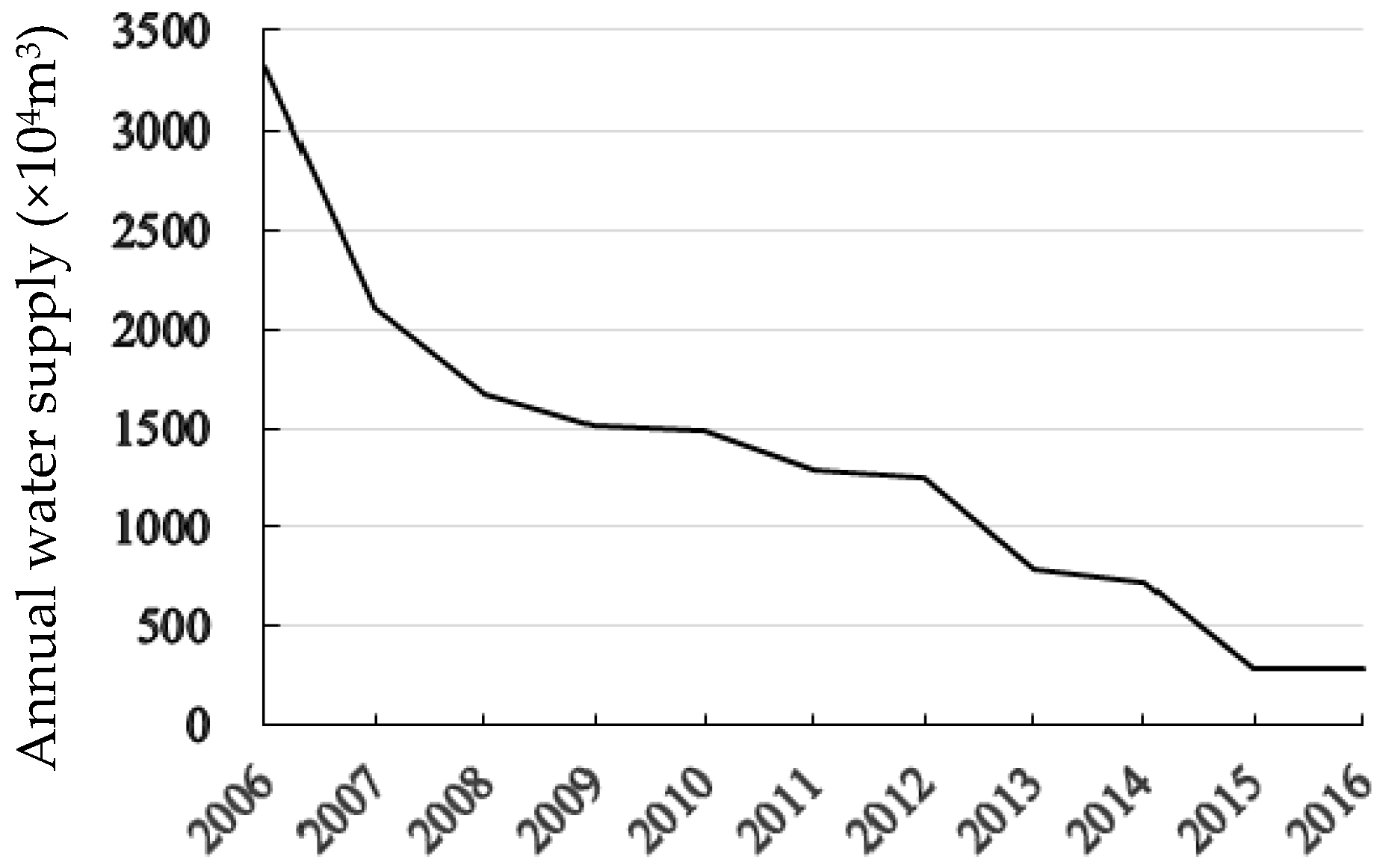
3.3. Data Collection and Processing
3.4. Application of IQFDCP Model
4. Result Analysis
- (1)
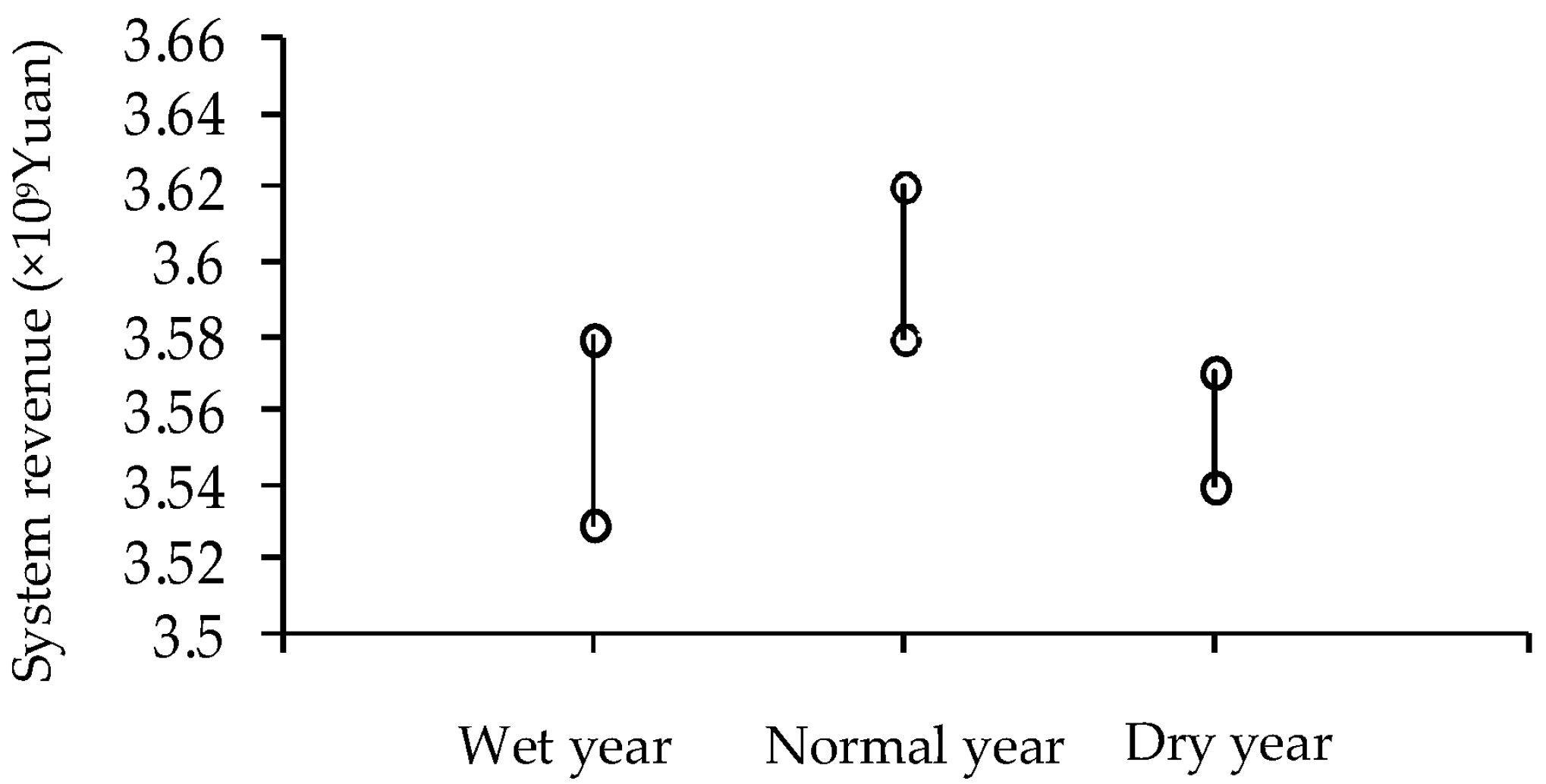
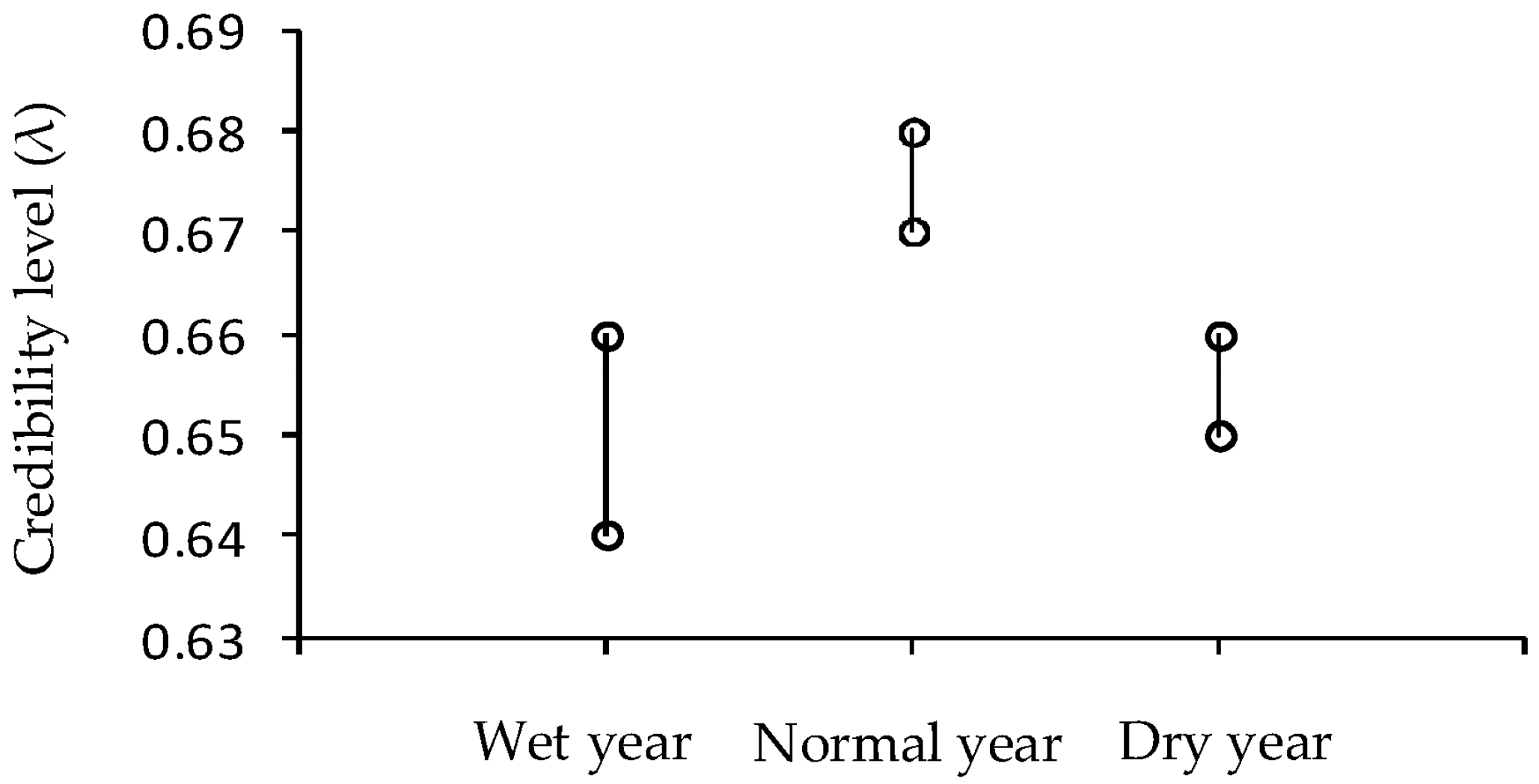
- Compared with the actual situation, the interval of the system revenue of the triangular fuzzy number is too big, especially for obtaining r3. The planting area and the price take a more optimistic value. It is difficult to achieve in the actual situation, causing the lower level of credibility of system revenue.
- (2)
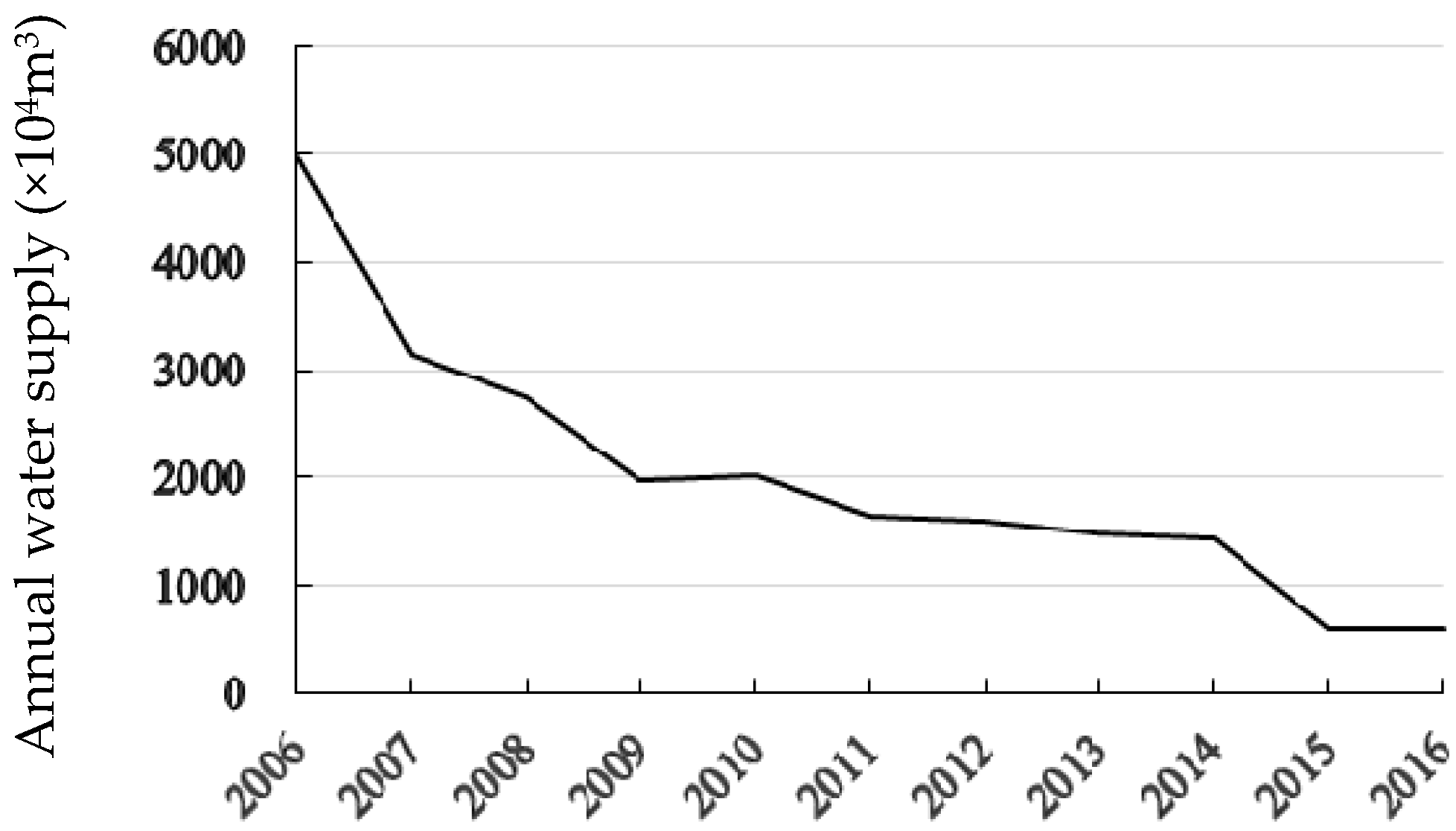
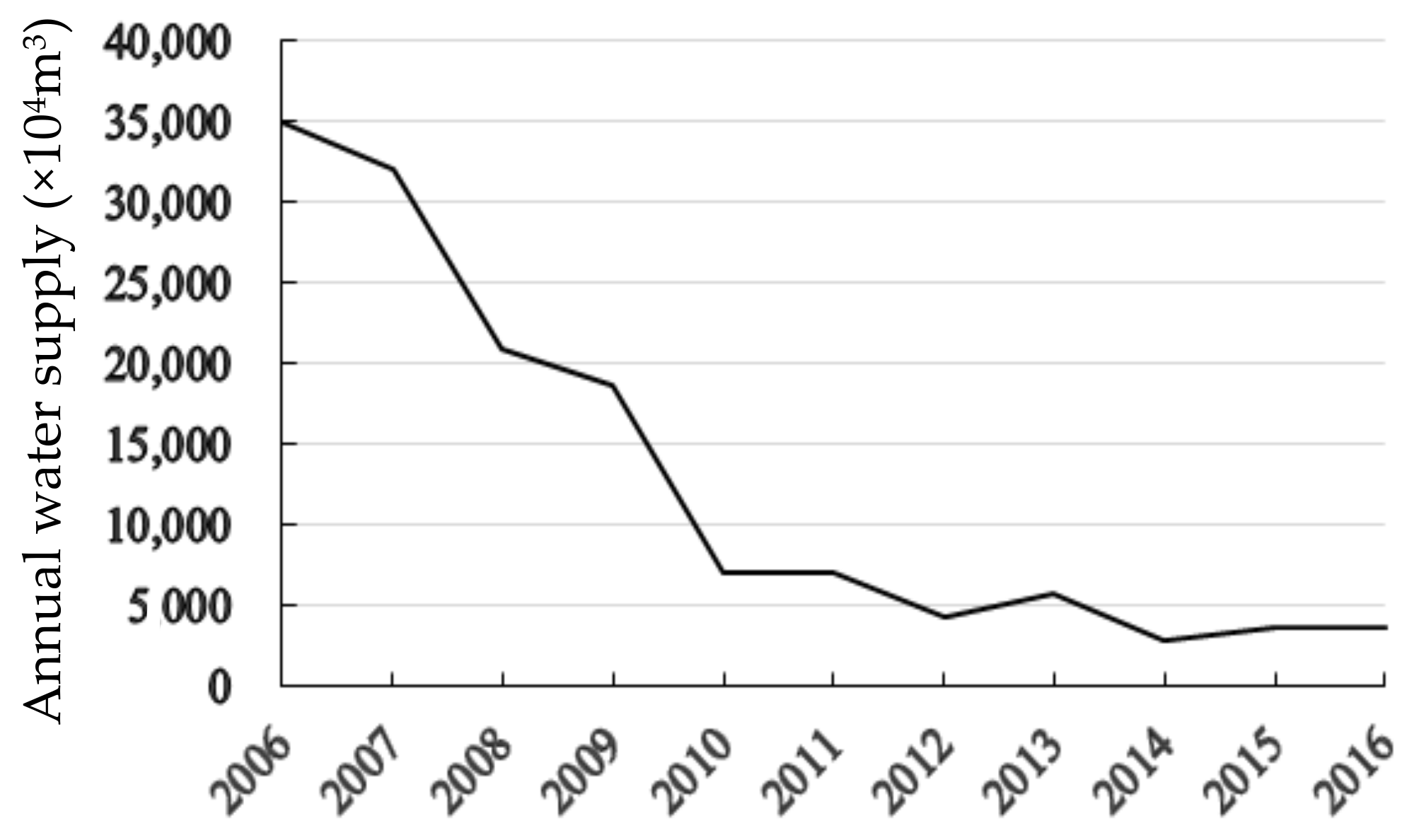
- For three irrigation districts in Minqin Oasis, the CN and HH districts are irrigated by only groundwater. In order to decrease groundwater extraction, irrigation water is reduced, resulting in lower crop yield under the low amount of groundwater availability compared to HYS. Thus, low system revenue is obtained in Minqin Oasis and the credibility level is decreased.
- (3)
- There is no cotton in CN and HH. The main crops are spring wheat and maize. However, cotton is a major source of income for system, resulting in low system revenue, causing the low credibility level.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kang, S.; Hao, X.; Du, T.; Tong, L.; Su, X. Improving agricultural water productivity to ensure food security in China under changing environment: From research to practice. Agric. Water Manag. 2016, 179, 5–17. [Google Scholar] [CrossRef]
- Borrego-Marin, M.M.; Gutiérrez-Martín, C.; Berbel, J. Water Productivity under Drought Conditions Estimated Using SEEA-Water. Water 2016, 8, 138. [Google Scholar] [CrossRef]
- Postel, S. Forging a sustainable water strategy. In State of the World; Worldwatch Institute: Washington, DC, USA, 1996. [Google Scholar]
- Foster, T.; Brozović, N.; Butler, A.P. Effects of initial aquifer conditions on economic benefits from groundwater conservation. Water Resour. Res. 2017, 53, 744–762. [Google Scholar] [CrossRef]
- Tan, Q.; Zhang, S.; Li, R. Optimal Use of Agricultural Water and Land Resources through Reconfiguring Crop Planting Structure under Socioeconomic and Ecological Objectives. Water 2017, 9, 488. [Google Scholar] [CrossRef]
- Hrozencik, R.A.; Manning, D.T.; Suter, J.F.; Goemans, C.; Bailey, R.T. The Heterogeneous Impacts of Groundwater Management Policies in the Republican River Basin of Colorado. Water Resour. Res. 2017, 53, 10757–10778. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Ren, C. Water Resources Management Models Based on Two-Level Linear Fractional Programming Method under Uncertainty. J. Water Resour. Plan. Manag. 2015, 141, 05015001. [Google Scholar] [CrossRef]
- Brown, P.D.; Cochrane, T.A.; Krom, T.D. Optimal on-farm irrigation scheduling with a seasonal water limit using simulated annealing. Agric. Water Manag. 2010, 97, 892–900. [Google Scholar] [CrossRef]
- Zhang, F.; Tan, Q.; Zhang, C.; Guo, S.; Guo, P. A Regional Water Optimal Allocation Model Based on the Cobb-Douglas Production Function under Multiple Uncertainties. Water 2017, 8, 923. [Google Scholar] [CrossRef]
- Frizzone, J.A.; Coelho, R.D.; Dourado Neto, D.; Soliani, R. Linear programming model to optimize the water resource use in irrigation projects: An application to the Senator Nilo Coelho Project. Sci. Agric. 1997, 54, 136–148. [Google Scholar] [CrossRef]
- Burgschweiger, J.; Dig, B.; Steinbach, M.C. Nonlinear programming techniques for operative planning in large drinking water networks. Open Appl. Math. J. 2009, 3, 14–28. [Google Scholar] [CrossRef]
- Keramatzadeh, A.; Chizari, A.H.; Moore, R. Economic optimal allocation of agriculture water: Mathematical programming approach. J. Agric. Sci. Technol. 2011, 13, 477–490. [Google Scholar]
- Ahmad, I.; Tang, D. Multi-objective linear programming for optimal water allocation based on satisfaction and economic criterion. Arab. J. Sci. Eng. 2016, 41, 1421–1433. [Google Scholar] [CrossRef]
- Loucks, D.P.; Van Beek, E. Water Resources Systems Planning and Management—Exercises; United Nation Educational, Scientific and Cultural Organization (Unesco): Paris, France, 2005. [Google Scholar]
- Meng, C.; Wang, X.; Li, Y. An Optimization Model for Water Management Based on Water Resources and Environmental Carrying Capacities: A Case Study of the Yinma River Basin, Northeast China. Water 2018, 10, 565. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Tanaka, H. Multiobjective programming in optimization of the interval objective function. Eur. J. Oper. Res. 1990, 48, 219–225. [Google Scholar] [CrossRef]
- Guo, P.; Huang, G.H.; He, L.; Zhu, H. Interval-parameter two-stage stochastic semi-infinite programming: Application to water resources management under uncertainty. Water Resour. Manag. 2009, 23, 1001–1023. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Yang, Z.F.; Nie, S.L. IFMP: Interval-fuzzy multistage programming for water resources management under uncertainty. Resour. Conserv. Recycl. 2008, 52, 800–812. [Google Scholar] [CrossRef]
- Maqsood, I.; Huang, G.H.; Yeomans, J.S. An interval-parameter fuzzy two-stage stochastic program for water resources management under uncertainty. Eur. J. Oper. Res. 2005, 167, 208–225. [Google Scholar] [CrossRef]
- Liu, B. Fuzzy Dependent-Chance Programming. In Theory and Practice of Uncertain Programming; Physica-Verlag HD: Heidelberg, Germany, 2002; pp. 197–208. [Google Scholar]
- Liu, B. Dependent-chance programming in fuzzy environments. Fuzzy Sets Syst. 2000, 109, 97–106. [Google Scholar] [CrossRef]
- Liang, R.; Gao, J. Dependent-chance programming models for capital budgeting in fuzzy environments. J. Tsinghua Univ. Nat. Sci. Ed. 2008, 13, 117–120. [Google Scholar] [CrossRef]
- Peng, H.; Zhou, H. A fuzzy-dependent chance multi-objective programming for water resources planning of a coastal city under fuzzy environment. Water Environ. J. 2011, 25, 40–54. [Google Scholar] [CrossRef]
- Huang, G.H.; Li, Y.P.; Xiao, H.N.; Qin, X.S. An inexact two-stage quadratic program for water resources planning. J. Environ. Inform. 2007, 10, 99–105. [Google Scholar] [CrossRef]
- Huanga, Y.; Lib, Y.P.; Chenc, X.; Mad, Y.G. Optimization of the irrigation water resources for agricultural sustainability in Tarim River Basin, China. Agric. Water Manag. 2012, 107, 74–85. [Google Scholar] [CrossRef]
- Chen, M.J.; Huang, G.H. A derivative algorithm for inexact quadratic program—Application to environmental decision-making under uncertainty. Eur. J. Oper. Res. 2001, 128, 570–586. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Singh, V.P.; Zhao, J. Irrigation Water Allocation Using an Inexact Two-Stage Quadratic Programming with Fuzzy Input under Climate Change. JAWRA J. Am. Water Resour. Assoc. 2016, 52, 667–684. [Google Scholar] [CrossRef]
- Liu, B. Random fuzzy dependent-chance programming and its hybrid intelligent algorithm. Inf. Sci. 2002, 141, 259–271. [Google Scholar] [CrossRef]
- Huang, G.H.; Loucks, D.P. An Inexact Two-Stage Stochastic Programming Model for Water Resources Management under Uncertainty. Civ. Eng. Environ. Syst. 2000, 17, 95–118. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, P. A generalized fuzzy credibility-constrained linear fractional programming approach for optimal irrigation water allocation under uncertainty. J. Hydrol. 2017, 553, 735–749. [Google Scholar] [CrossRef]
- Hu, X.J.; Xiong, Y.C.; Li, Y.J.; Wang, J.X.; Li, F.M. Integrated water resources management and water users’ associations in the arid region of northwest China: A case study of farmers’ perceptions. J. Environ. Manag. 2014, 145, 162–169. [Google Scholar] [CrossRef] [PubMed]
- Li, T. Study on Basin Water Environment Management Optimization Based on Water Quality Simulation under Uncertain Conditions. Doctoral Dissertation, North China Electric Power University, Zhuhai, China, 2013. [Google Scholar]
- Xiao, D.N.; Li, X.Y.; Song, D.M.; Yang, G.J. Temporal and spatial dynamical simulation of groundwater characteristics in Minqin Oasis. Chin. Sci. Earth Sci. 2007, 50, 261–273. [Google Scholar] [CrossRef]
- Zhao, J.; Li, M.; Guo, P.; Zhang, C.; Tan, Q. Agricultural Water Productivity Oriented Water Resources Allocation Based on the Coordination of Multiple Factors. Water 2017, 9, 490. [Google Scholar] [CrossRef]
- Gui, Z.; Li, M.; Guo, P. Simulation-Based Inexact Fuzzy Semi-Infinite Programming Method for Agricultural Cultivated Area Planning in the Shiyang River Basin. J. Irrig. Drainage Eng. 2016, 143, 05016011. [Google Scholar] [CrossRef]
- Minqin Water Bureau (MWB). Minqin Oasis Annual Division of Water Industry Statistics Table; Minqin Water Bureau: Beijing, China, 2016.
- Wuwei Statistics Bureau (WSB). Wuwei Statistical Yearbook; Wuwei Statistics Bureau: Wuwei, China, 2015.
- Tong, F.; Guo, P. Simulation and optimization for crop water allocation based on crop water production functions and climate factor under uncertainty. Appl. Math. Model. 2013, 37, 7708–7716. [Google Scholar] [CrossRef]
| Typical Year | Crop | Precipitation (P)/mm | Water Demand (ETmax)/mm |
|---|---|---|---|
| Wet year (2002) | Spring wheat | (98.6, 120.6) | 658.0 |
| Maize | (124.1, 151.7) | 561.0 | |
| Cotton | (135.8, 166.0) | 375.3 | |
| Normal year (1998) | Spring wheat | (77.0, 94.2) | 677.4 |
| Maize | (79.8, 97.6) | 590.6 | |
| Cotton | (90.5, 110.6) | 396.8 | |
| Dry year (2013) | Spring wheat | (34.1, 41.7) | 695.9 |
| Maize | (68.9, 84.3) | 589.8 | |
| Cotton | (76.0, 92.8) | 398.5 |
| Irrigation Area | Crop | Acreage/ha | Price/Yuan | Surface Water/×104 m3 | Ground Water/×104 m3 |
|---|---|---|---|---|---|
| CN | Spring wheat | 153.4 | (2.4, 2.7) | 0 | (260, 289) |
| Maize | 530.3 | (2.5, 2.8) | |||
| Cotton | 0 | (7.0, 8.0) | |||
| HH | Spring wheat | 439.7 | (2.4, 2.7) | 0 | (530, 589) |
| Maize | 1214.7 | (2.5, 2.8) | |||
| Cotton | 0 | (7.0, 8.0) | |||
| HYS | Spring wheat | 3764.9 | (2.4, 2.7) | (20180, 22422) | (3231, 3590) |
| Maize | 6868.2 | (2.5, 2.8) | |||
| Cotton | 709.1 | (7.0, 8.0) |
| Parameters and Variables | Meaning and Description |
|---|---|
| The credibility level of the event | |
| The upper and lower limits of the parameters | |
| System revenue (×109 Yuan) | |
| Different irrigation areas | |
| Different crop types | |
| Acreage (hm2) | |
| Purchase price (Yuan/kg) | |
| The parameters of the crop water production function | |
| The total amount of surface water in the whole growth period (mm), the decision variables | |
| The total amount of groundwater in the whole growth period (mm), the decision variables | |
| The availability factor of surface water | |
| The availability factor of groundwater | |
| The precipitation during the whole growth period (mm) | |
| Maximum water demand (mm) | |
| Minimum water demand (mm) | |
| The amount of available surface water (m3) | |
| The amount of available groundwater (m3) | |
| The minimum grain demand of per capita (kg) | |
| The total population of research area |
| Irrigation District | Typical Year | Irrigation Sources | Irrigation Water Allocation for Different Crops | ||
|---|---|---|---|---|---|
| Spring Wheat | Maize | Cotton | |||
| CN | Wet year | Surface water | 0 | 0 | 0 |
| Groundwater | (267.2, 279.4) | (293.3, 289.8) | 0 | ||
| Normal year | Surface water | 0 | 0 | 0 | |
| Groundwater | (275.9, 286.5) | (290.7, 287.7) | 0 | ||
| Dry year | Surface water | 0 | 0 | 0 | |
| Groundwater | (320.2, 322.8) | (278.0, 277.2) | 0 | ||
| HH | Wet year | Surface water | 0 | 0 | 0 |
| Groundwater | (250.3, 262.2) | (239.1, 234.8) | 0 | ||
| Normal year | Surface water | 0 | 0 | 0 | |
| Groundwater | (258.8, 259.2) | (236.1, 232.3) | 0 | ||
| Dry year | Surface water | 0 | 0 | 0 | |
| Groundwater | (302.2, 304.7) | (220.3, 219.4) | 0 | ||
| HYS | Wet year | Surface water | (459.9, 481.9) | (278.4, 306.4) | (186.4, 212.8) |
| Groundwater | 0 | (130.9, 130.5) | (22.9, 26.7) | ||
| Normal year | Surface water | (486.3, 503.4) | (364.4, 380.0) | (242.1, 282.4) | |
| Groundwater | 0 | (128.7, 130.8) | (44.2, 24.0) | ||
| Dry year | Surface water | (538.8, 546.4) | (374.1, 388.3) | (287.3, 315.7) | |
| Groundwater | 0 | (131.4, 132.6) | (18.4, 6.9) | ||
| Irrigation District | Crop | Irrigation Water Amount | Water Saving Amount | Optimized System Revenue (×108 Yuan) | Actual System Revenue (×108 Yuan) | |
|---|---|---|---|---|---|---|
| Optimization | Actual | |||||
| CN | Spring wheat | (275.9, 286.5) | 410 | (134.1, 123.5) | (3.58, 3.62) | 3.2 |
| Maize | (290.7, 287.7) | 405 | (114.3, 117.3) | |||
| Cotton | 0 | 0 | 0 | |||
| HH | Spring wheat | (258.8, 259.2) | 410 | (151.2, 150.8) | ||
| Maize | (236.1, 232.3) | 405 | (168.9, 172.7) | |||
| Cotton | 0 | 0 | 0 | |||
| HYS | Spring wheat | (486.3, 503.4) | 536 | (49.7, 32.6) | ||
| Maize | (493.1, 510.8) | 563 | (69.9, 52.2) | |||
| Cotton | (286.3, 306.4) | 323 | (36.7, 16.6) | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, C.; Guo, P. An Interval Quadratic Fuzzy Dependent-Chance Programming Model for Optimal Irrigation Water Allocation under Uncertainty. Water 2018, 10, 684. https://doi.org/10.3390/w10060684
Wang H, Zhang C, Guo P. An Interval Quadratic Fuzzy Dependent-Chance Programming Model for Optimal Irrigation Water Allocation under Uncertainty. Water. 2018; 10(6):684. https://doi.org/10.3390/w10060684
Chicago/Turabian StyleWang, Hang, Chenglong Zhang, and Ping Guo. 2018. "An Interval Quadratic Fuzzy Dependent-Chance Programming Model for Optimal Irrigation Water Allocation under Uncertainty" Water 10, no. 6: 684. https://doi.org/10.3390/w10060684
APA StyleWang, H., Zhang, C., & Guo, P. (2018). An Interval Quadratic Fuzzy Dependent-Chance Programming Model for Optimal Irrigation Water Allocation under Uncertainty. Water, 10(6), 684. https://doi.org/10.3390/w10060684





