1. Introduction
The European Urban Waste Water Treatment Directive requires the European Union (EU) members to set up sewer systems and biological wastewater treatment plants (WWTP). In addition, it also demands that sensitive areas, i.e., those whose water suffers from eutrophication or are to be used for human consumption such as bathing or drinking, must be defined, since a more stringent treatment is needed to eliminate nutrients (mainly nitrogen and/or phosphorus) before the processed wastewater is discharged into water courses.
This is the reason why organic matter and nutrient removal has been broadly studied in Europe in the last years. In fact, the European Commission issues a biennial report concerning the performance of these processes [
1], the last of which appeared in April 2016. It was highlighted in it that regulations concerning wastewater collection are met for 94.9% of the overall pollution load, while those regarding the total suspended solids and organic matter removal are met for 86% and, finally, the more stringent treatment obligations are met only for 50.5%. Therefore, it may be stated that it is necessary to improve the nutrient removal performance and, to a lesser extent, that related to the total suspended solid and organic matter.
In this context, several treatment processes have been developed in order to achieve the aforementioned regulations. They all are based on concentrating specific microorganisms in a controlled environment to efficiently carry out pollutant removal. Currently, a distinction is made between fixed film attached processes and suspended growth processes, in accordance with the way the microbial population is present. Their main difference is related to the contact between pollutants and bacteria, which is deeper in the suspended growth process since the attached process limits the contact to the surface of the fixed film. Thus, taking into account that nutrients are mainly dissolved substances, the suspended growth process is the most widely used to carry out nutrient removal in wastewater treatment. Activated sludge is the most common one among the suspended growth processes. It is based on a stirred vessel where the microbial population is in contact with pollutants to carry out their metabolic activities. Then, the mixed liquor flows to another vessel, known as secondary clarifier, where the microbial population settles and the clarified water, the effluent, flows over its top. This process was defined in 1904 and, based on its principles, many configurations have been defined. Those most widely used in urban wastewater treatment are: oxidization ditch configuration [
2,
3], alternating cycles processes [
4,
5], pre-anoxic or anaerobic-anoxic-aerobic configurations [
6,
7], or post-anoxic configurations [
8]. In industrial wastewater treatment those most widely used are: Sequential Biological Reactor (SBR), where the main vessel and the secondary clarifier form a single vessel, and Membrane Biological Reactor (MBR), where the secondary clarifier is replaced by a suction membrane.
In addition, several control strategies have been developed to adhere to legal regulations. They are mainly based on studying the dissolved oxygen profiles [
9,
10], ORP profiles [
11,
12], pH profiles [
13], or ammonia and nitrogen profiles [
14]. Nevertheless, it is important to bear in mind that neither the vessel configuration nor the control strategies carry out the pollutant removing process, rather it is the microorganisms. Therefore, if the goals in question are to be achieved, it is necessary to study and characterize the behavior of these microorganisms in order to select the best microorganism load in the vessel and to improve the control strategy performance.
Regardless of the biological nutrient removal configuration, i.e., the type of vessel, the microorganisms which carry out nitrogen and phosphorus removal are very sensitive to both weather (temperature and hydraulic load) and operating (pH, conductivity, dissolved oxygen, oxidation reduction potentials) conditions. Nevertheless, while these last ones can be directly or indirectly modified by technicians in charge of plant government, the former cannot be. Therefore, the control of the WWTP can be very complex and the biological removal efficiency may not achieve the expected removal performance. So, it will be necessary to develop new key parameters based on measures provided by probes usually installed in actual treatment plants in order to quantify the weather and operating conditions. These key parameters will allow identification of changes in the treatment process dynamics related to changes in those weather and operating conditions. Once those changes are identified, based on the new key parameters, it is possible to modify the WWTP operation to improve the biological nutrient removal performance.
In addition, different working conditions of the treatment process based on the values of those parameters should be also defined in order to propose different and specific control strategies for each working condition which, as a whole, must provide a more efficient control than a general nonspecific control law.
Many features related to the treatment process dynamics can be obtained from the analysis of the data provided by the probes usually used in WWTPs, whose number is increasing due to the development of new key parameters [
15]. Nevertheless, the huge amount of data that may be obtained from actual plants needs to be processed in order to identify relevant and useful information from the whole set of available data. In other words, it would be necessary to extract variables and parameters providing relevant information about the microbiological activity which may be subsequently used to characterize the process and then to define an effective control system. There are several multivariate statistical processes (MSP) that can be used for knowledge extraction and monitoring of WWTPs, but an artificial intelligent tool, the Self Organizing Map (SOM), has experienced increasing popularity because of its ability to identify and classify relations between data in highly complex systems that are difficult to describe by deterministic models [
16,
17]. It is a neural network model which is easily trained to identify patterns among data without previous knowledge of possible relations between them. An important feature of SOM is that it shows its response graphically, a fact that highly improves the classification processes because correlations between patterns are easily seen [
18]. A detailed analysis of those correlations may provide valuable information about which are the most significant variables to characterize the system’s behavior.
SOM is a powerful tool used to extract information from a large data set in order to analyze and classify them. It is able to reduce the high dimensionality of a large data set, providing valuable information about behavior patterns among the data. In Ref. [
19], it was proved that SOM outperforms principal component analysis (PCA) because SOM provides a very easily interpreted visual representation. In addition, SOM provides information regarding the original variables while that from PCA is shown in terms of principal components (the variables or a linear combination of them). In addition, while PCA provides a linear reduction of dimensionality, SOM provides a nonlinear one, a fact that should imply that SOM ought to provide a better performance when dealing with nonlinear systems such as WWTPs. So, many authors have used this tool to analyze wastewater treatment processes [
20,
21,
22,
23]. It has been also used to analyze other water treatment processes, such as that of drinking water [
16], or to study the water quality of rivers [
17,
24,
25,
26]. They all analyze the water properties by studying both the component planes and the SOM output, providing information about treatment process dynamics or the water properties.
SOM provides a nonlinear dimensionality reduction of large data sets by grouping them into representative classes in a 2D map (each class is represented by a node, a neuron, in that map). Often, those classes may be further grouped after analyzing the information provided by SOM in order to provide a simplified classification of the information obtained so that it can be more easily interpreted. On the other hand, the analysis of the behavior of the variables describing each pattern could make it possible to identify those with a higher influence in the characteristics of each pattern, in other words, those variables better describing the system dynamics. It is worth noting that the lower the number of classes a dataset may be classified into, the more efficient and easy to use the obtained classification will be. By applying this idea to the problem at hand, it may be stated that a reduced number of patterns along with a low number of significant variables representing the system dynamics will provide an easier to implement control strategy. Several algorithms from the literature may be used to carry out this task. One of the most commonly used is that known as K-means [
27] because it is well suited to provide a “spherical” clustering of data, such as that present in the SOM map, and also because its clustering process is based on the distance concept used by SOM to classify data. Therefore, it has been selected in this work to carry out that clustering process. Other works have also used SOM and K-means to carry out a detailed study of the wastewater treatment process [
16,
19,
20,
22].
In this work, values of dissolved oxygen (DO) and ORP were recorded form an actual plant and then were processed in order to obtain a set of wastewater key parameter indicators (KPI) which characterize process behavior. Seven new parameters were defined to complement those previously defined in Ref. [
15] (9 parameters), providing a set of sixteen. All the available data were first processed by the box-plot tool in order to reject those which could be defined as “outliers”. Then, the remaining data were treated by SOM with a two-fold aim: identification of correlations between parameters in order to select a reduced set which could efficiently characterize the system dynamics and clustering of the data in order to identify behavior patterns. The first aim was carried out by analyzing the weight maps associated with each parameter. This study revealed that only three parameters (which will be defined below) were required to characterize the aeration and aeration/non-aeration transition stages of the biological process. Regarding the second aim, it is worth noting that the network provided an excessively large set of behavior patterns (one for each neuron). Therefore, a clustering algorithm, the K-means, was applied to the map provided by the SOM in order to reduce the number of classes so that they may be meaningful and easy to use in a subsequent control strategy. Four classes were so obtained: standard wet and dry weather operation and organic and hydraulic overload.
The process is suitable for defining the operation states of activated sludge processes in any configuration. In this way, the three selected KPIs may provide enough information to technicians in charge of plant management to efficiently adjust the control laws in order to improve nutrient removal by efficiently adapting to seasonal load variations as defined by the aforementioned classes.
2. Materials and Methods
2.1. Reactor Operation
Usually WWTPs are designed to efficiently remove organic matter. In those designed to also remove nitrogen and phosphorus, the organic matter load (defined as Food to Microorganism Load, F/M) ought to be rather low in order to allow nutrient removal bacteria (ordinary heterotrophic organisms: OHO) to carry out their metabolic activity, avoiding the problem of competition for oxygen with nitrification bacteria or for the readily biodegradable organic matter with phosphorous removal bacteria. Consequently, the vessel volume must be quite large. In this context, and according to the Environmental Protection Agency (EPA) criteria design [
28], in the plant design stage, once its volume is stated, based on the definition of a low F/M, designers have to check whether the calculated SRT, once the MLSS (Mixed Liquor Suspended Solids) in the vessel are defined, reaches a proper value which ensures that microorganisms properly remove organic matter, nitrogen, and phosphorus. In order to provide a proper SRT, the plant designers estimate the SRT with the previously selected volume and MLSS and then check whether or not this SRT is higher than a certain high value, usually 20 days. If this condition is met, the volume is assumed as appropriate; otherwise, designers have to increase its value.
Prior to carrying out this work, fifty design projects were evaluated and all of them used this criteria design instead of the ATV one [
29], which is based on defining the minimum SRT to reach the nitrification process. It may be stated that the vessel volume obtained by using the same MLSS with the EPA criteria was 25% higher than that obtained by using the ATV criteria. Therefore, as those WWTPs in urban agglomerations with population over 2000 inhabitants were built on the basis of the EPA criteria, the impact of their over-dimension in their microorganism kinetic, effluent quality, and energy saving was very high. In order to resolve this problem, upgrading the aeration system management of the plant by means of alternating aeration cycles appears to be most effective option [
4,
5] to avoid high investment costs instead of others, such as reducing the working volume to ensure the proper treatment of organic and nutrient peaks or industrial discharges or replacing the aeration systems.
This type of plant is very common in Spanish WWTPs designed to treat lower than 50,000 inhabitants equivalent (IE) loads. A typical plant of this kind is that of La Albuera, a small town in the southwest of Spain. Its pollution profile is characterized by urban, agricultural, and food industries pollution. It was monitored over twenty-four months to obtain the data used in this work. It is based on the oxidation ditch configuration, with more than 20 days of SRT. Its operation conditions are summarized in
Table 1, where the difference between them and the design are shown. So, this plant may be assumed to be over-dimensioned, a very common situation in Spanish WWTPs designed to treat lower than 50,000 IE loads. As has been stated above, the alternating aeration process (AAP) is usually used to control the biological nutrient removal in this kind of WWTPs to avoid the problems arising from their over-dimensioned design. In this work, a system was used in which the aeration control was carried out based on the information obtained from the DO and ORP profiles. Neither pH nor SRT were considered to define that control because pH variations were very small due to the high vessel volume, and SRT demanded a high number of suspended probes to measure the flow of solids in the system. The ammonia profile could also be considered, nevertheless it demands the use of specific probes based on an ion-selective electrode (ISE) which needs expensive and regular maintenance. In addition, they provide low precision measurements in high volume reactors. Therefore, its use was discarded. On the other hand, DO and ORP profiles were provided on-line by low cost probes and are widely used in WWTPs of the type studied in this work. Therefore, they were only considered to define the process control.
DO was used to control the aeration phase, which extended until a threshold of 2 mg L−1 was reached, a value that was considered to be enough to ensure the nitrification process was properly carried out. When this threshold was reached, the control entered a stand-by state to measure the non-oxidized organic matter in the vessel by using the oxygen uptake rate (OUR). When this value was assumed to be high, the control drove the system into a new aeration phase, whereas it kept aeration off when it decided that that value was low. Its length was controlled by the ORP profile. DO and ORP were selected as system variables to control the process because the probes measuring their values are quite common in WWTPs, with a proved technology and low acquisition and maintenance costs when compared with other probes also used in those plants.
2.2. Wastewater Key Parameter Indicators
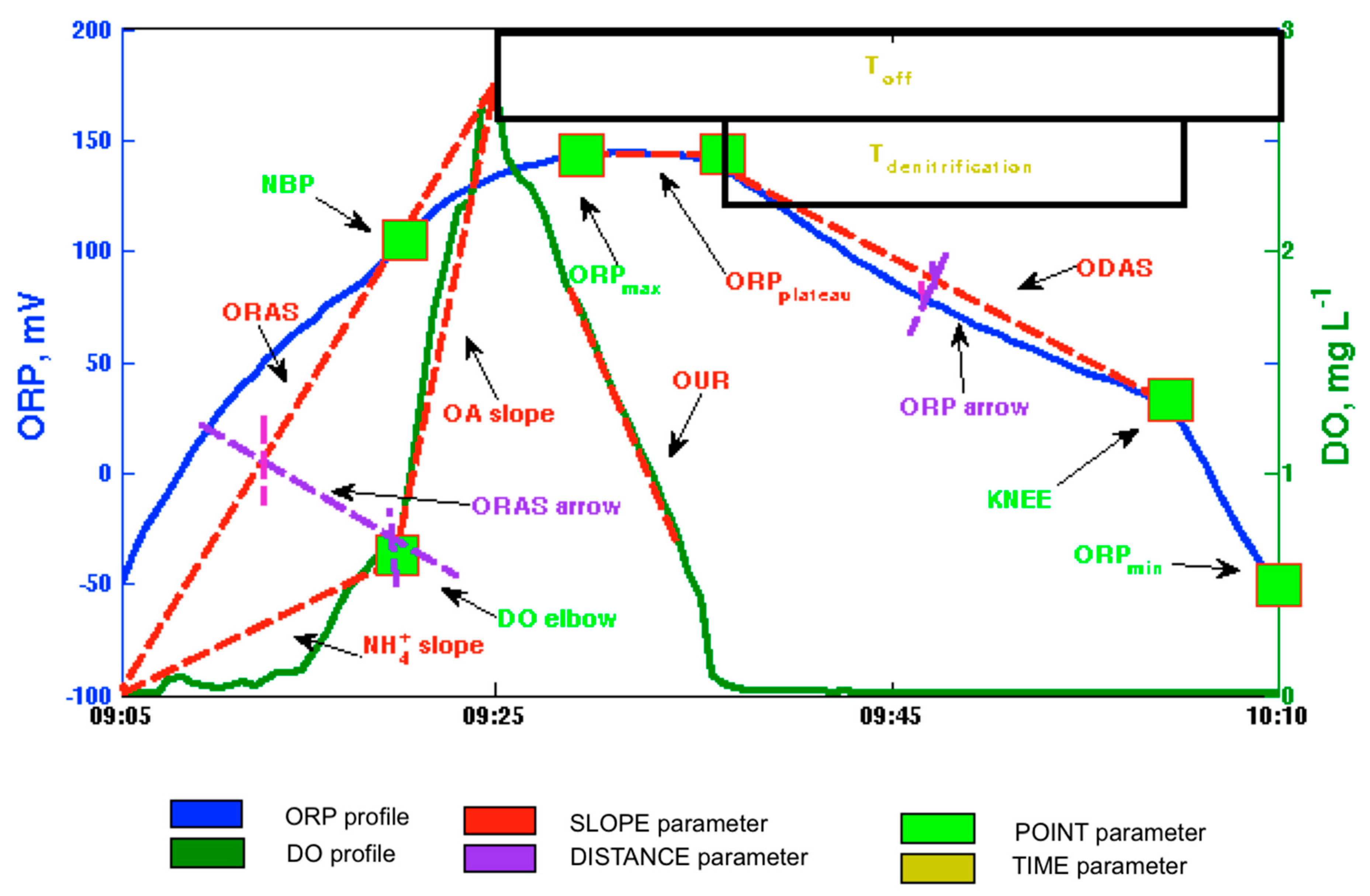
Sixteen parameters have been obtained from the DO and ORP profiles, nine of which have been already described in Reference [
15]: ORP knee (
Knee), oxygen uptake rate (
OUR),
ORParrow, oxygen rise average slope (
ORAS),
ORPmax,
ORPmin, time the aeration is off (
toff), time of denitrification (
tdn), and temperature (
T). Their graphical interpretation is shown in
Figure 1. This figure shows a typical aeration/non-aeration cycle in an alternating cycle process where three states may be seen: aeration, transition, and non-aeration. During the aeration phase, the DO profile (green line) rises until the aeration system is switched off. At this moment, the aeration state ends and the DO profile begins to decrease. However, as the ORP profile (blue line) maintains a slight rising trend, this stage is considered a transition state. Finally, the non-aeration phase begins when the ORP profile shows a decreasing trend. The three states allow one to study the slopes (red lines) and the distances between them and the real profiles (purple lines). So, a new characterization of the DO and ORP profiles in wastewater is provided, because it includes the key points and introduces slopes and distances. The new seven parameters proposed here are described below.
ORASarrow: This parameter measures the maximum distance between the rising DO profile and the linear approximation of the DO profile during the aeration phase:
where (
ton, DOon) defines the start of the aeration phase, (
toff,
DOoff) is the end of the aeration phase, and (
ti,
DOi) is the DO actual value at time
ti.
DOelbow defines the end of nitrification and the start of the over-aeration phase. It is usually calculated as the change in the rise slope of the DO profile [
30]. However, in this work, it has been obtained based on
ORASarrow, in order to guarantee that its value is more accurate and less sensitive to outliers: the DO value, in its rising profile, for which the
ORASarrow is a maximum.
Nitrate break point (NBP) represents the value of the ORP profile when DOelbow appears.
NH4+slope measures the DO slope between the start of the aeration phase and
DOelbow:
Over-aeration slope (OAslope) measures the DO slope between
DOelbow and the maximum DO value:
ORPplateau measures the change rate in ORP between the oxidation phase (where oxygen is the electron acceptor) and the anoxic phase (where nitrate is the acceptor). It is defined as the ORP slope between the maximum ORP and the ORP for which DO is lower than 0.1 mg L
−1:
ORP decrease average slope (ODAS) represents the linearization of the ORP profile while the denitrification process is carried out (during tdn).
2.3. Box-Plots
A box-plot is a graphical depiction of the statistical distribution of a data set. It is defined by five parameters: median (
), first quartile (
), third quartile (
, maximum value, and minimum value. The last two parameters are assumed to not be the maximum and minimum values of the data but two statistical values defined by [
31]:
Once the data have been represented in a box-plot, they may be studied and their distribution analyzed. In this work, it will be used to identify outlier data, that is to say, those beyond the maximum and minimum values. As they represent abnormal values, they might come from erroneous measurements or calculations. If that were the case, they should be removed in order to guarantee that the information describing the time evolution of each measured or calculated variable is reliable, as erroneous data has been rejected. Nevertheless, before removing them, an analysis concerning their origin must be carried out in order to determine whether they come from erroneous measurements or calculations, or are actual high or low data representing an unusual system state.
2.4. Self-Organizing Map (SOM)
Neural networks are artificial intelligence tools widely used to extract information from data in order to reproduce the behavior of the system from which they were obtained, to forecast its evolution, to classify them, or, in a general sense, to extract valuable information from them. They are made up of basic processing elements (neurons) arranged in 2D layers trying to mimic the brain structure so that some of its intelligent skills may be reproduced. A neural network may have several layers so that each neuron carries out the weighted sum of all the outputs provided by those in the previous layer (some neural models carry out a comparison of the input data with weights instead of a weighted sum). This sum (or the result of the comparison) may be further processed by an activation function which is usually nonlinear. The ability of a neural network to carry out the aforementioned tasks is provided by its learning capability, that is to say, they are trained to learn to perform a certain task from a set of data. They are presented to the network and a learning algorithm adapts the weights to minimize the error provided by the outputs of the neurons. To do that, a desired set of outputs must be provided along with the data presented to the network for learning. After the network has been trained, a validation dataset is usually presented to the network (along with their desired outputs) in order to validate the network performance, in order to find out how well the trained network is able to carry out the task it has learned. Once it has been validated, it can be used to carry out the task it was designed for. This learning process is known as “supervised” as it uses “good” neural responses to calculate an error (the difference between the neuron output and the desired one) which will be used by the learning algorithm to adapt the neuron’s weights. Some neural models are designed to adapt their weights without a desired output (that is to say, only the inputs to the network are provided to train it). Therefore the learning algorithm will adapt the neuron’s weights in order to obtain relations among data. These neural models are known as “unsupervised”, as no desired (“good”) responses are provided to obtain an output error. Therefore the network automatically self-adapts to look for relations among data. So, a validation stage may not be performed.
SOM [
32] is an “unsupervised” neural model. It is made up of only one layer which classifies the input vectors it receives into a class defined by the neural weights. Therefore, the neuron will have as many weights as inputs it receives. The neurons in the network will compete between them to find out which of them most closely resembles the input pattern. The winner will be the neuron providing the least distance between the input pattern and its weight vector. It is usually known as the “best matching unit” (BMU).
The network can be viewed as an
×
matrix with a square or hexagonal structure. Nowadays, the latter is the most widely used [
24,
25] because it provides a denser connection between neurons, a fact that provides more interactions between them during competition. There is not an “a priori” rule which can provide the best network structure and different ones must be tested in order to find that which performs the best. Nevertheless, in order to reduce the number of structures to be tested, a heuristic rule has been proposed to estimate a number of neurons close to the optimum [
26,
33]:
where
M is the number of neurons and
N is the number of input data. An expression has been also proposed to estimate the matrix dimensions [
20]:
where
and
are the numbers of rows and columns in the network and
and
are the eigenvalues of the matrix made up with all the input vectors.
As these expressions only provide an approximation to the optimum network size and structure and several structures close to them must be tested. Two indices have been proposed [
24] to find out which performs the best: the topographic error to evaluate how well the data structure is reproduced in the network structure (topology preserving) and the quantization error to measure how well an input pattern is classified by the network.
The topographic error is provided by:
where
N is the number of input vectors,
is one of them, and
is a function which is equal to 1 when the first and second better adapted neurons for
are not direct neighbors of each other and 0 otherwise. Therefore, the lower the value of
, the better the network reproduces the data structure.
The quantization error is given by:
where
N is the number of input vectors,
is one of them, and
is the weight vector of the BMU. As this parameter provides a mean value of how well an input patter is classified, networks with low values will provide a more accurate classification than those with higher ones.
The ability of SOM to properly classify input vectors is acquired in a previous learning process, where a set of training vectors, , are presented to the network and it autonomously (unsupervised learning) adapts their neuron weights so that they all are properly classified, reproducing their topological distribution.
Once the network has been trained, it may be used to classify input patterns different from those used for training. Nevertheless, this process is sometimes not carried out because only the classification of a dataset is required: that used for training. In that case, once the network has been trained, it may be analyzed in order to obtain information about the different classes the vectors are classified into. To do that, the so-called U-matrix may be obtained. It represents the mean distance from the weight vector of a neuron to those of the neurons surrounding it, so that neurons close to one another and with low values may be considered as forming a cluster, while those with high values may be assumed to define borders between them. As the interpretation of these results is rather subjective, many classification methods should be used to help detect possible clusters between neurons.
On the other hand, as each weight component is associated to one system parameter of the input vector, a complementary analysis of the weight vectors may be carried out in order to find possible correlations between their components, that is to say, correlations between the system parameters that each weight component represents. To do that, as many maps may be generated as components the weight vector has , so that each position in those maps represents the value its corresponding weight component has in each neuron (obviously, these maps must have the same dimension as SOM).
2.5. K-Means Clustering
It has been pointed out above that often several neurons (each one defining a class) may have similar characteristics, suggesting that they may be grouped together into a cluster. Several tools are available to help carry out this process. They are known as clustering methods. It is not easy to provide a crisp categorization of them as usually a certain procedure may share features of several categories. Nevertheless, for the sake of clarity, they may be classified into four classes [
34]: partitioning, hierarchical, density-based, and grid methods. Partitioning methods define K groups and assign every data to one of them based on a distance criterion. The second one performs a hierarchical decomposition that may either start with all the data grouped into a single cluster which is successively split into smaller clusters (divisive approach) or with each datum defining a cluster which will be merged into bigger ones (agglomerative approach). The algorithm stops when a certain criterion is accomplished. Density-based methods group data into one cluster based on a density criterion so that neighbor points are grouped together when a density threshold is exceeded. The last method divides the data space following a grid structure so that the clustering process is carried out inside each data group, allowing a multiresolution process. Therefore, it may integrate any other clustering procedure.
Partitioning and hierarchical methods provide a good classification into “spherical” clusters, while the density-based ones are better fitted for arbitrary shaped clusters. On the other hand, hierarchical and density-based methods provide a more robust processing of outliers than the partitioning ones. As the SOM provides (as it will be seen later) clusters of “spherical” shape, density-based methods were discarded. On the other hand, as outliers have been rejected with the preprocessing carried out with box-plots and the hierarchical methods do not allow undoing a merge or split operation once it is carried out, a partitioning method was selected to carry out the clustering process. It was the so-called K-means because, as previously mentioned, it has been widely used with SOM. As this algorithm needs the number of classes be fixed prior to starting the clustering process, several options must be tested and evaluated to find out that which provides the best classification. Two indices have been used to carry out that evaluation: the Davies–Bouldin [
35] and the silhouette [
36].
The first one provides a measure of how compact the clusters are, that is to say, how close the elements inside a cluster are to each other and how far they are from the other clusters. It is given by the expression:
where
K is the number of clusters,
σi the mean distance between the elements inside the
i-th cluster and its centroid
ci,
σj is the mean distance between those elements and the centroids
ci of the other clusters, and
d(
ci,
cj) is the distance between the cluster centroids. For this index, the lower its value, the better the clustering process will be.
The silhouette provides a measure of the resemblance of each data with those inside its own cluster compared with those inside the other clusters [
37]. It is provided by the expression:
where
a(
i) represents the mean distance between the
i-th element and those inside the same cluster and
b(
i) is the lowest mean distance from an element to those inside the other clusters. This expression has values between −1 and 1, so that the closer its value is to 1, the better the data is classified into its cluster and the closer to −1, the worse the data is classified. A near-zero value means that the datum is on the border of two clusters.
Now, if the silhouette of each datum inside a cluster is represented in decreasing order, for all the clusters a graphic representation of the quality of the allocation of data inside them is provided. The mean value of the silhouettes for all the clusters will provide a measure of the quality of the clustering carried out, so that the higher its value, the better the classification will be.
Therefore the K-means algorithm will be run for several values of K and that providing the best performance will be selected. It begins by fixing the number of clusters K and their corresponding centroids [
38]. Then, each data is classified into a cluster when its distance to the centroid defining that class is a minimum. Once they all have been classified, every centroid is recalculated as the value providing the lowest distance to all the members of its class. As the centroids have changed, the distance between each datum and the centroids must be calculated again so that they will be reassigned to the closest cluster. The process will be repeated until no improvement in the classification process is obtained.
3. Results
The WWTP of La Albuera was monitored over twenty-four months from January 2009 to June 2010 and from March 2013 to August 2013. DO and ORP measures were recorded every minute of every day throughout these twenty four months. A total amount of 1,051,200 measures of each variable were recorded. The aeration/non-aeration profiles were obtained from them by finding consecutive minima in the ORP data set so that a profile was generated with data between those minima. The corresponding DO profile were generated with the data inside the time interval defined by the aforementioned minima. In this way, a total of 3200 cycles were obtained. They all were processed in order to obtain the aforementioned 16 parameters for each one so that 3200 data vectors with 16 components were generated.
Data were processed with specific programs developed with Matlab 2012a both to obtain the data vectors and to treat them with box-plots, SOM, and K-means.
3.1. Data Preprocessing
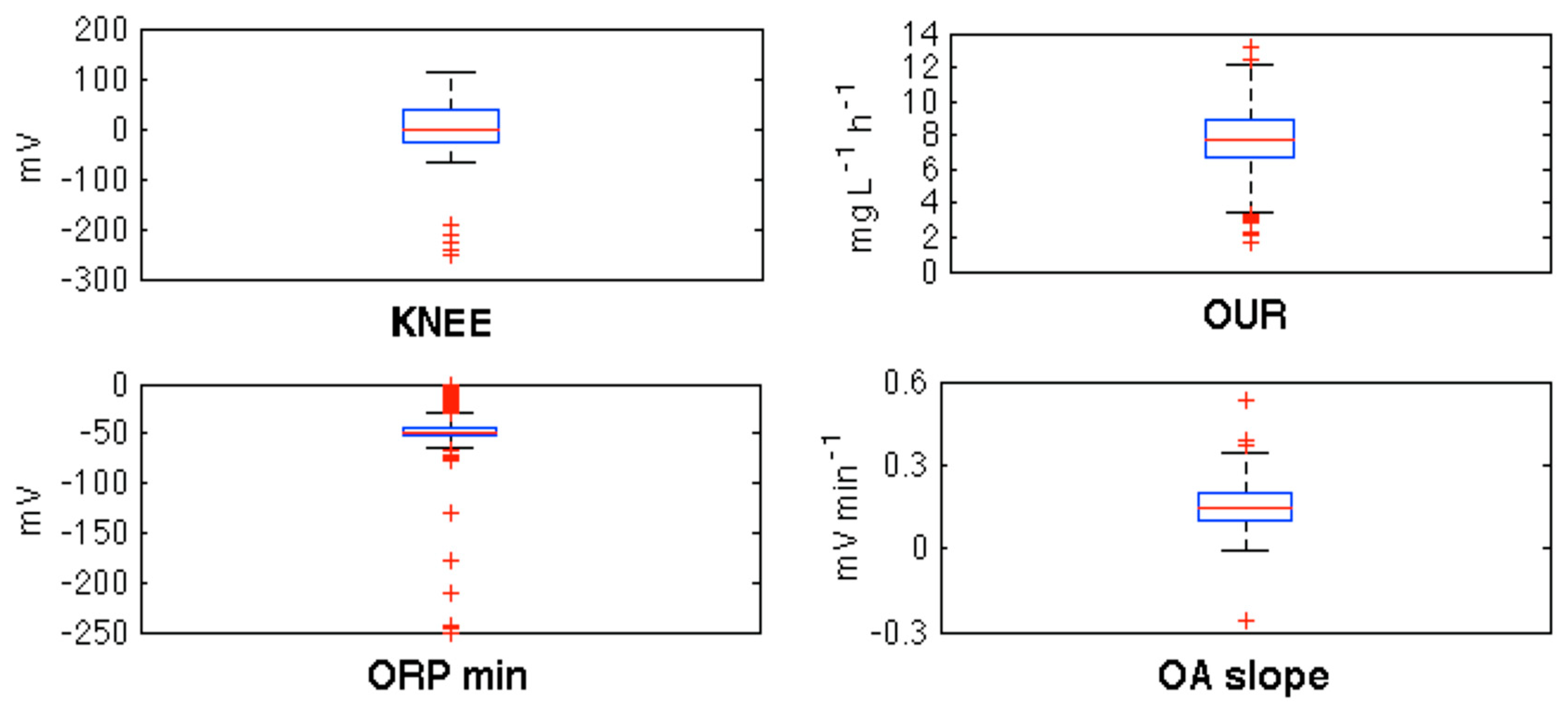
Before processing the data vectors with SOM, all data corresponding to each component of those vectors (16 data sets) were processed with box-plots in order to decide whether abnormally high or low values (outliers) are to be rejected (they are erroneous data) or not (they represent extreme working conditions that the plant must deal with). Only in four parameters was erroneous data detected (
Figure 2):
Knee: As the data presented a compact distribution, extreme values may be considered as erroneous data provided by imprecise calculations. So, those input vectors whose Knee values were considered as outliers were rejected.
OUR: Only very low values were rejected because, as endogenous respiration prevents the appearance of very low values of OUR, those extreme values could be assumed as erroneous calculations. On the other hand, as very high values may be assumed as provided by a charge stress in the reactor they were not rejected. So, only vectors with very low values of OUR were rejected.
ORPmin: As ORP had a predefined minimum value used as a reference in the control implemented in the plant, outliers should be assumed as caused by erroneous calculations and therefore vectors owning these outliers were rejected. It is worth noting that vectors rejected because of outliers in Knee also had outliers in ORPmin. On the other hand, rejecting these vectors meant those corresponding to outliers in toff were also rejected, as ORPmin controlled the time the pumps were switched off.
OAslope: Only vectors with negative values of this parameter were rejected as it may only be positive.
After processing the 3200 data vectors with box-plots, 310 of them were rejected. The 2890 remaining were then used to train the SOM.
3.2. Representative Parameters Identification with SOM
In this work, SOM was used with a two-fold goal: identification of behavior patterns in data and identification of correlations between parameters to identify those most representative. The first one was directly accomplished by properly training SOM, while the second needs a more detailed analysis. This latter will be studied first. In order to identify relations between parameters, 16 maps with the same SOM structure were generated, one for each component of the weight vector, so that each one represented the value of that component in each neuron. If the same color scale is associated with the whole range of values of each parameter, the maps may be used to find out similar patterns in different maps [
20], as parameters with similar patterns may be assumed as correlated and then only one of them is needed to characterize system behavior.
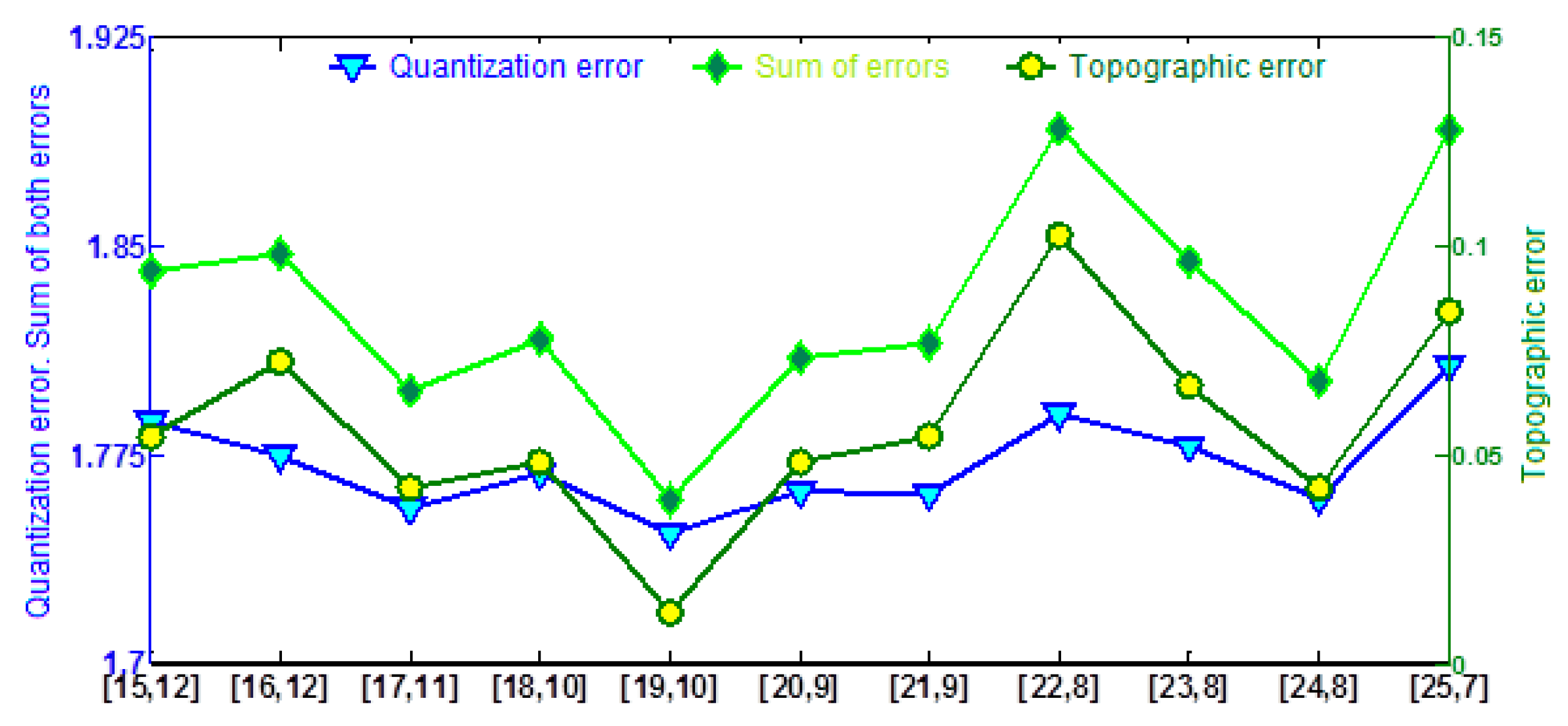
The process started by training SOM with the 2890 data remaining after they all were processed with box-plots. First of all, the network size must be determined. Both the number of neurons and their distribution were obtained from expressions (9) and (10), which provided a network with 268 neurons and a column/row ratio of 1.87. As these values were only an estimation of the best structure, this should be obtained from a trial and error procedure. Different networks with sizes and structures around those defined by (9) and (10) were trained and their performance measured with the topographic and quantization errors provided by (11) and (12) (
Figure 3). The structure providing the best performance was 19 × 10. These values mean that although the best network has a column/row ratio almost equal to that provided by (10), the number of neurons (and therefore the number of classes) is noticeably lower.
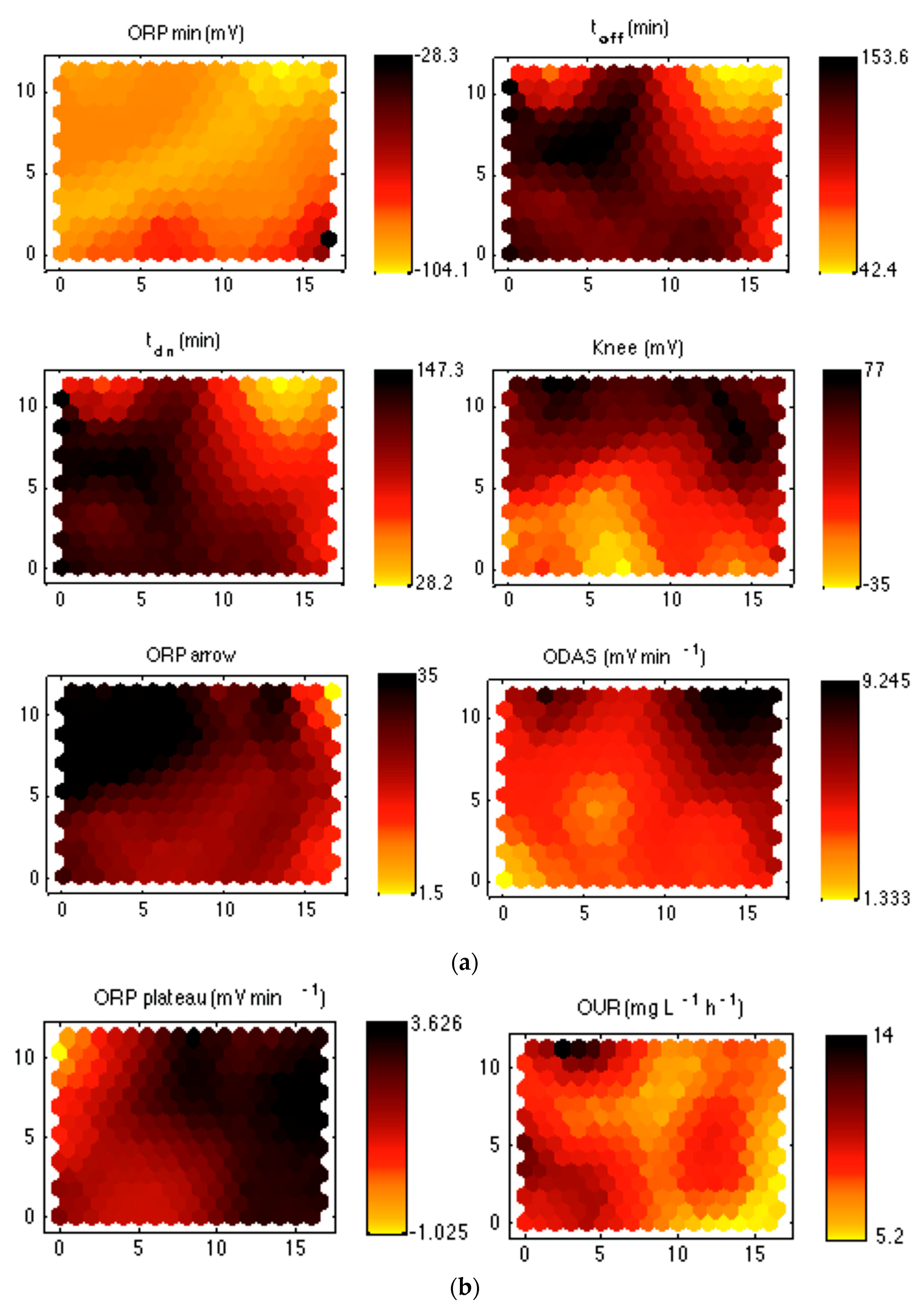
Once the best structure was obtained, their weights could be studied in order to find out correlations between parameters. Comparing the 16 maps to find out graphical resemblances between them may become a very hard task. In order to simplify this process, the maps were grouped based on the aeration/non-aeration process stage each parameter was related to. So, three groups were defined: one for those describing the aeration-oxidation process (
Figure 4), another for the non-aeration-reduction process (
Figure 5a), and finally, the third for the oxidation-reduction transition (
Figure 5b). The first one comprised parameters:
ORPmax,
T,
ORAS,
ORASarrow,
NBP,
NH4+solpe,
OAslope, and
DOelbow; the second:
ORPmin,
toff,
tdn,
knee,
ORParrow, and
ORAS; the third:
OUR and
ORPplateau. 3.2.1. Aeration-Oxidation Parameters
Three parameters showed a clear direct relation as they have very similar map structures: T, ORPmax, and NBP. A first conclusion that may be obtained from this correlation is that high temperatures provide high oxidation levels. As temperature has a clear seasonal dependence, it may be inferred that a high input charge appears with hot weather, when organic input concentration rises because of a lack of rain. Nevertheless, no information about the aeration efficiency may be obtained from this correlation. It is worth noting that as aeration is controlled by the technicians in charge of the plant’s management, it would be desirable to find out a possible correlation between parameters related to both aeration and oxidation processes. As NBP marks the end of nitrification and oxidation of organic matter, it should be checked whether or not the aeration systems were able to transfer enough oxygen to efficiently carry out these processes. To do that, NBP should be compared with the parameter measuring oxygen consumption for nitrification: NH4+slope. Both maps present a clear inverse correlation: a high nitrification rate was associated with a low input charge, while low nitrification rates appear for high charges. This means that the control was able to carry out an efficient nitrification for low charges. Nevertheless, it is not clear whether or not the system was able to correctly manage the scene of high input charge by providing enough aeration to guarantee that organic matter oxidation and nitrification were properly carried out (a fact which involves that extra-assimilation of phosphorous has been also carried out). To answer this question, the NH4+slope map should be compared with that showing the oxygen levels reached after nitrification: DOelbow. This comparison suggests that there is not a correlation between both parameters. Nevertheless, as the question at hand is the system behavior when a low value of the nitrification process is measured, it may be stated that those low NH4+slope values match with medium–high DOelbow values, so that the system increases the time at which aeration is switched on to provide enough oxygen to the process.
Now, it is necessary to analyze the behavior of the parameter measuring the oxygen concentration evolution after nitrification, OAslope, which will give a clear idea of the over-aeration process. Nevertheless, its map shows no correlation with the others. On the other hand, it may be stated that both NH4+slope and OAslope may be assumed as included in ORAS, as this last one represents the oxygen rise average slope (the slope between the beginning and the end of the aeration process) and the nitrification and the over-aeration slopes, as the first spans between the beginning of the aeration cycle and DOelbow, while the second goes from this point to the end of aeration. When comparing ORAS with NBP, an inverse correlation may be seen, in which more color shades are detected. So, this correlation looks more detailed than that shown by NBP and NH4+slope.
Finally, it may be noted that after comparing ORASarrow with the other parameters, no relation was detected. This is hardly surprising as this parameter neither has a direct relation with the length of the aeration process nor provides information about nitrification.
It may be concluded that ORAS presents a clear direct correlation with T, ORPmax, and NBP and an inverse correlation with NH4+slope. On the other hand, no relation was detected with OAslope, DOelbow, and ORASarrow, but while the information provided by OAslope may be complemented with that provided by NH4+slope and DOelbow to define ORAS, no relation may be stated between ORASarrow and the other parameters and, consequently, it may be ignored to define this process. Therefore, the parameter selected to represent the aeration-oxidation process was ORAS.
3.2.2. Non-Aeration-Reduction Parameters
At first glance, an almost perfect correlation between toff and tdn appears when analyzing these six maps. This may be easily explained by the fact that tdn almost always lagged about 10 min behind toff in the DO an ORP profiles studied. On the other hand, a clear inverse correlation may be observed between these two parameters and Knee. This relation is hardly surprising as the lower the value of Knee, the higher the value of tdn, as this last parameter measures the time elapsed between when the blowers were switched off and the appearance of Knee.
It would be interesting to relate these parameters to the denitrification speed, a value which may be provided by ODAS. It presents an almost perfect inverse correlation with tdn, as would be expected, since they both were measured between the same time limits. This fact implies that a system with a fast denitrification process (high values of ODAS) will need less time to carry it out (low values of tdn) and vice versa: low values of ODAS will imply high values of tdn.
These parameters clearly characterize the denitrification process, whose end is marked by the parameter
Knee. Nevertheless, it would be interesting to study the possible inhibition of the denitrification process by a lack of organic matter, a fact that is pointed out by
ORParrow [
15]. High values of this parameter mean that the denitrification process must be extended because of a lack of organic matter, which must be provided by the affluent to complete the denitrification process. Although a clear correlation between
ORParrow and the aforementioned parameters does not appear, it may be pointed out that, after comparing with the
ODAS map, high values of
ORParrow provide low values of
ODAS, while low values of the first one generate high values of the second. Therefore, despite the clear correlation between
toff,
tdn,
Knee, and
ODAS, the parameter selected to represent de non-aeration-reduction process was
ORParrow because it provides a clear idea of the needs of organic matter to efficiently carry out the denitrification process that the other parameters do not provide, a very significant fact for the technicians managing the plant to improve the nitrogen removal efficiency.
Finally it is worth noting that ORPmin has not been compared with the other parameters because it had an almost constant value, a fact that prevents finding any kind of correlation with them and provides no information about the process.
3.2.3. Oxidation-Reduction Transition Parameters
As a certain inverse correlation may be observed between the two parameters it may be stated that they both provide valuable information about the transition from the oxidation state to that of reduction. OUR measures the oxygen consumption rate after aeration has been switched off and, therefore, provides additional information about the carbonaceous matter remaining in the reactor after aeration was switched off. So, low values of this variable will mean that a little amount of organic matter remains in the reactor and the process will need more time to consume all the dissolved oxygen. This fact will make ORPplateau have a positive value. On the other hand, when enough organic matter remains in the reactor after the end of aeration, OUR will have a high value and ORPplateau will be negative. As OUR presents a higher variation in its values, which provides a more detailed information about the process, it will be selected as representative of this state.
3.3. Cluster Analysis with K-Means
Once SOM has classified the whole set of data into classes, it is clear that its number is too high: 190, one for each neuron. Therefore, a procedure must be applied to the map in order to group classes with similar characteristics into clusters so that the total number of classes is reduced to an appropriate value which is manageable and representative. Therefore, the goal is to group the neuronal weight vectors into a reduced set of clusters which could provide representative information about behavior patterns of the system dynamics. It is usual, when working with SOM, to do that by analyzing the U-matrix, nevertheless, as it has been pointed out above, this clustering process is rather subjective and a more systematic and objective one should be used. In this work, the K-means algorithm was selected to do that. Therefore, it was applied to the 19 × 10 features map provided by SOM.
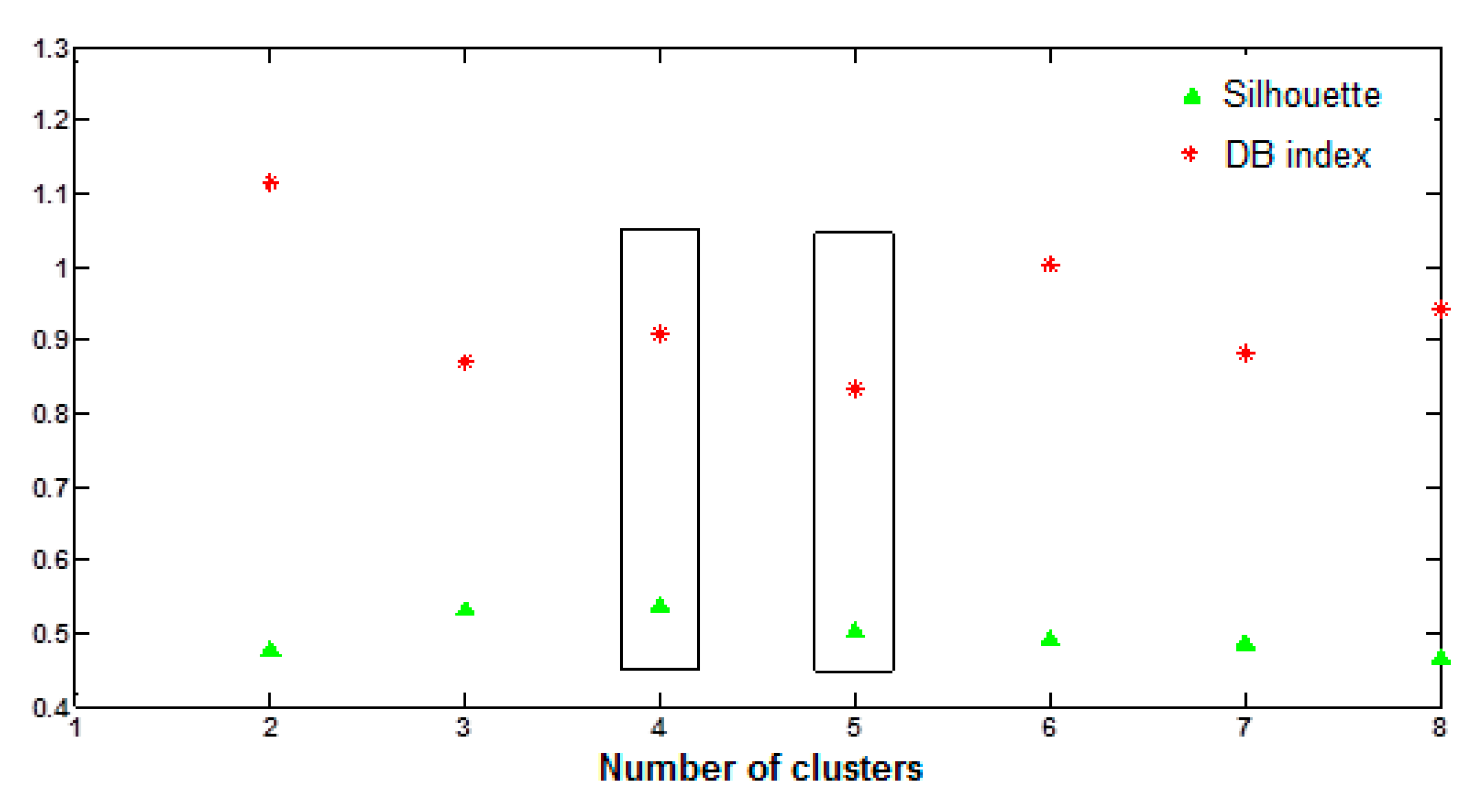
As it has been previously stated, the first step when applying this algorithm is to find a suitable number of clusters, a value that must be obtained by a trial and error process in which the performance of each option will be measured by its Davis–Bouldin index and silhouette. The number of clusters must not be too high in order to guarantee that the classification obtained is both useful and meaningful. Therefore, all the options between 2 and 8 were tested (
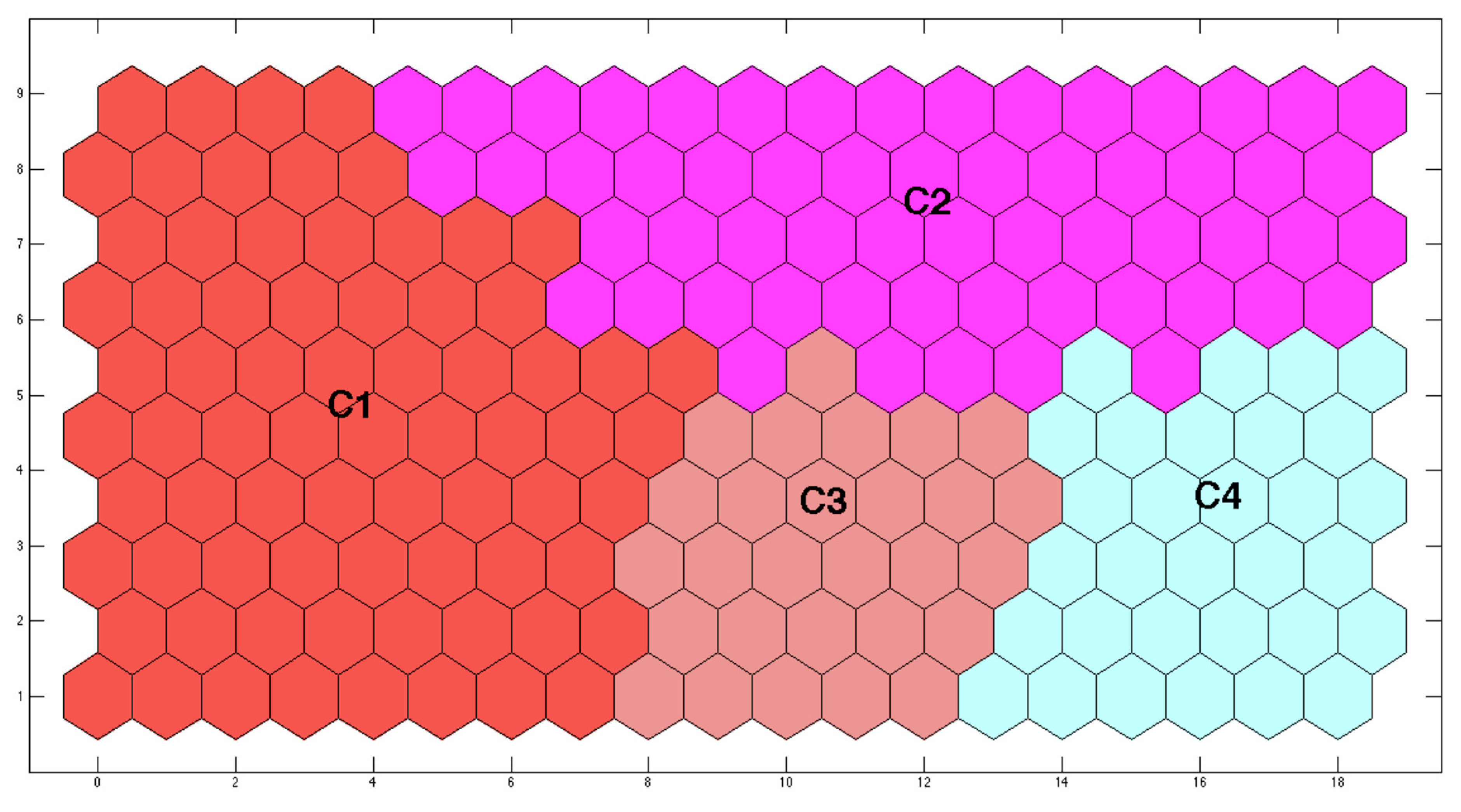
Figure 6). Two of them appeared to be considered as the best: 4 and 5 clusters. The decision of which one is the best was not clear because although the option with 5 clusters provided a better Davis–Bouldin index, that with 4 provided a better silhouette. Although a better Davis–Bouldin index ensures a more compact classification, a better silhouette guarantees a higher resemblance between the elements inside a cluster, that is to say, it will provide fewer misclassifications. Therefore, 4 clusters was the option selected. The results are shown in
Figure 7. The values of the 16 parameters associated to each of the centroids defining the four clusters are detailed in
Table 2.
These four clusters may also be roughly grouped into two sets related to the seasonality defined by temperature: lower for the wet season (clusters C1 and C2) and higher for the dry season (clusters C3 and C4). Nevertheless, temperature was not one of the parameters selected to characterize the treatment process. ORAS was the parameter selected to represent the set when temperature was included: the aeration-oxidation process. Therefore, it must be related to the seasonal behavior defined by temperature. To do that, it must be taken into account that ORAS provides an indirect measurement of the incoming organic matter and ammonia concentrations, as low values of this parameter means that aeration takes a long time to raise the oxygen concentration because of its high consumption by bacteria to process a high amount of incoming organic matter and to carry out a high nitrification. On the other hand, higher values will imply that a low organic matter concentration has entered the reactor and aeration needs less time to reach the switch-off level. From these facts, it may be stated that the two lowest values of ORAS (those in clusters C1 and C2) may be classified as corresponding to the “Dry Season” (because of a high concentration of the incoming pollution caused by the lack of rain) while those with the highest values (C3 and C4) correspond to the “Wet Season” (the rainy season will favor a more diluted affluent).
The study of the features of these four clusters by means of the three representative parameters previously selected to characterize the working states may provide additional information about the biological nutrient and organic matter removal rates (
Table 3). The main aim of showing those removal rates is to ensure that the values of these parameters for each cluster are related to high removal rates, reaching the UE effluent quality standards.
3.3.1. Dry Season
During this season, the plant receives less wastewater because of a lack of rain, but with a higher pollutant concentration. Two cases are possible, both defined by the value of ORAS: Dry Standard Working Conditions (C2) and Organic Overload (C1). The latter is that with the lowest value of ORAS, provided by a long aeration time, which was needed to oxidize a large amount of organic matter. The first one, that with the highest value, was characterized by a lower incoming concentration (a more usual situation) which demands a shorter aeration time and achieves high removal rates.
In cluster C1 (Organic Overload), despite the high input charge, a large aeration time was able to hold a high organic matter removal rate (92% of COD removal). Its high organic matter concentration allows a high amount of it to remain in the reactor after aeration was switched off, as the high OUR value shows. In the same way, it may be stated that the high pollutant concentration received by the plant means that the ammonia concentration was also high and, therefore, a high concentration of nitrates has been also generated (the value measured for NBP proves this claim) as the high ORParrow value shows (a longer time is needed to carry out the denitrification process). This is the reason why the anaerobic phases in the non-aeration period were smaller and the phosphorus removal rates were lower than in the Dry Standard Working Conditions represented by cluster C2.
3.3.2. Wet Season
During this season, the plant receives a large water volume with a low pollutant concentration because of heavy rains. Now, the largest value of ORAS defines a Hydraulic Overload (C3) since the low organic matter concentration needs a short time to be oxidized, while the lowest value (C4) represents the Wet Standard Working Conditions (it is worth noting that this value is close to that of cluster C2, so that defining both states as standard is meaningful).
During Hydraulic Overload (C3) the high value of OUR means that the organic matter is quickly oxidized, but it is also quickly replaced by the incoming flow (high because of hydraulic overload) so that a significant amount of organic matter remains in the reactor after the aeration is switched off, providing a high value of OUR and high nitrogen and phosphorous removal rates. Nevertheless, the low concentration of organic matter leads to a low production of nitrates, a fact that causes an inhibition of the reduction process because of the lack of electron acceptors, as the high value of ORParrow points out.
In the Wet Standard Working Condition (C4), the low input flow provides a relatively high concentration of organic matter which demands a long aeration time, as the low value of OUR points out. Moreover, the low input flow provides a slower replacement of the oxidized organic matter, so that a low amount of it remains in the reactor after the aeration is switched off, as the low value of OUR proves.
4. Discussion
As it has been previously stated, the data used in this work were recorded from an actual WWTP and have been processed to find out a reduced set of parameters (OUR, ORParrow, and ORAS) which may be used to identify the plant state and to identify working conditions (Dry Standard Working Conditions, Organic Overload, Wet Standard Working Conditions, and Hydraulic Overload) which characterize the plant inputs. This information may be useful not only to provide a detailed knowledge of the process dynamics, but also to define control strategies to be implemented in actual plants similar to that studied in this work. The three representative parameters may be used to identify the process states, providing information for a control algorithm to decide how to act on the plant in order to obtain an efficient depuration (in the plant studied in this work the controllers adjusted the process aeration by switching on and off air pumps). On the other hand, the four working conditions may help to adapt the control algorithms to typical working conditions in order to provide more efficient processing. It is worth noting that the information regarding the treatment process obtained when analyzing the SOM component maps can be helpful to properly and efficiently define those controllers.
As the plant studied belongs to a very common class used in the south of Spain, it can be stated that the information obtained in this work may be used in a lot of actual plants. Of course, each controller should be defined taking into account the special features of each plant, but the overall definition of the controller may be based on the information presented in this work. The reduced number of parameters to be measured and the working states allow the definition of efficient controllers because the lower the number of those parameters and working conditions, the easier and more robust the controller definition will be. Nevertheless, it is not necessary to use all this information to develop controllers. It may also be directly used by technicians in charge of plant management to manually adjust aeration or control parameters in the controllers installed in their plants by basing their decisions on the information concerning the depuration process obtained from the study of the system dynamics carried out to find out correlations between variables or to define working states. On the other hand, it may be stated that the method presented in this work may also be applied to process data from any other WWTP in order to obtain information about their dynamics and to cluster them to discover behavior patterns that may allow managing those plants. Therefore, the analytical process described in this work may be applied to both suspended and biofilm systems to obtain a reduced set of parameters and working conditions that may be used to control and manage the process, adjust the aeration system, and improve the removal performance. It is only necessary to install DO and ORP probes and carry out the data analysis described here. It is worth noting that although the reduced set of parameters used to describe the process could be the same (the three KPIs selected in this work), the working conditions defined by the four classes may be different (with more or less classes) as they greatly depend on the input pollution characteristics.
In this work, SOM’s capability to provide a nonlinear dimension reduction of a large set of data by clustering into representative classes has been used in an alternative way: the reduction of the number of components of data. Each datum was a 16-component vector. Each one was obtained from the analysis of DO and ORP profiles. Nevertheless, so much information is difficult to be used and is probably unnecessary. So, the vector dimension should be reduced to both an easy to use and meaningful number of components. As SOM has been used to reduce the dimension of the dataset by classifying them all into classes, it may also be used to reduce the number of components of the data vectors. To do that, the component maps have been analyzed by looking for correlations (direct or inverse) between them, which appeared as similar color distributions (or inverted with respect to the corresponding color scale) in each map. Those parameters which present any kind of correlation may be represented by only one of them. That study was carried out by associating the parameters to three oxidation-reduction states: aeration-oxidation, non-aeration-reduction, and oxidation-reduction transition. The aim was the identification and characterization of those stages of the alternating aeration process carried out in the actual plant. One parameter was associated to each stage: ORAS to aeration-oxidation, ORParrow to non-aeration-reduction, and OUR to the oxidation-reduction transition. In this way, the whole aeration-non-aeration process may be monitored by following only the evolution of those three parameters. In addition, it is possible to improve the nutrient removal efficiency by adapting the WWTP operational conditions to the seasonal influent load variations. This process may be efficiently carried out taking into account only the information provided by those parameters. The reduction of the number of representative parameters represents the novel contribution of this work.