Evaluation of Multi-Satellite Precipitation Products for Streamflow Simulations: A Case Study for the Han River Basin in the Korean Peninsula, East Asia
Abstract
1. Introduction
2. Materials and Methods
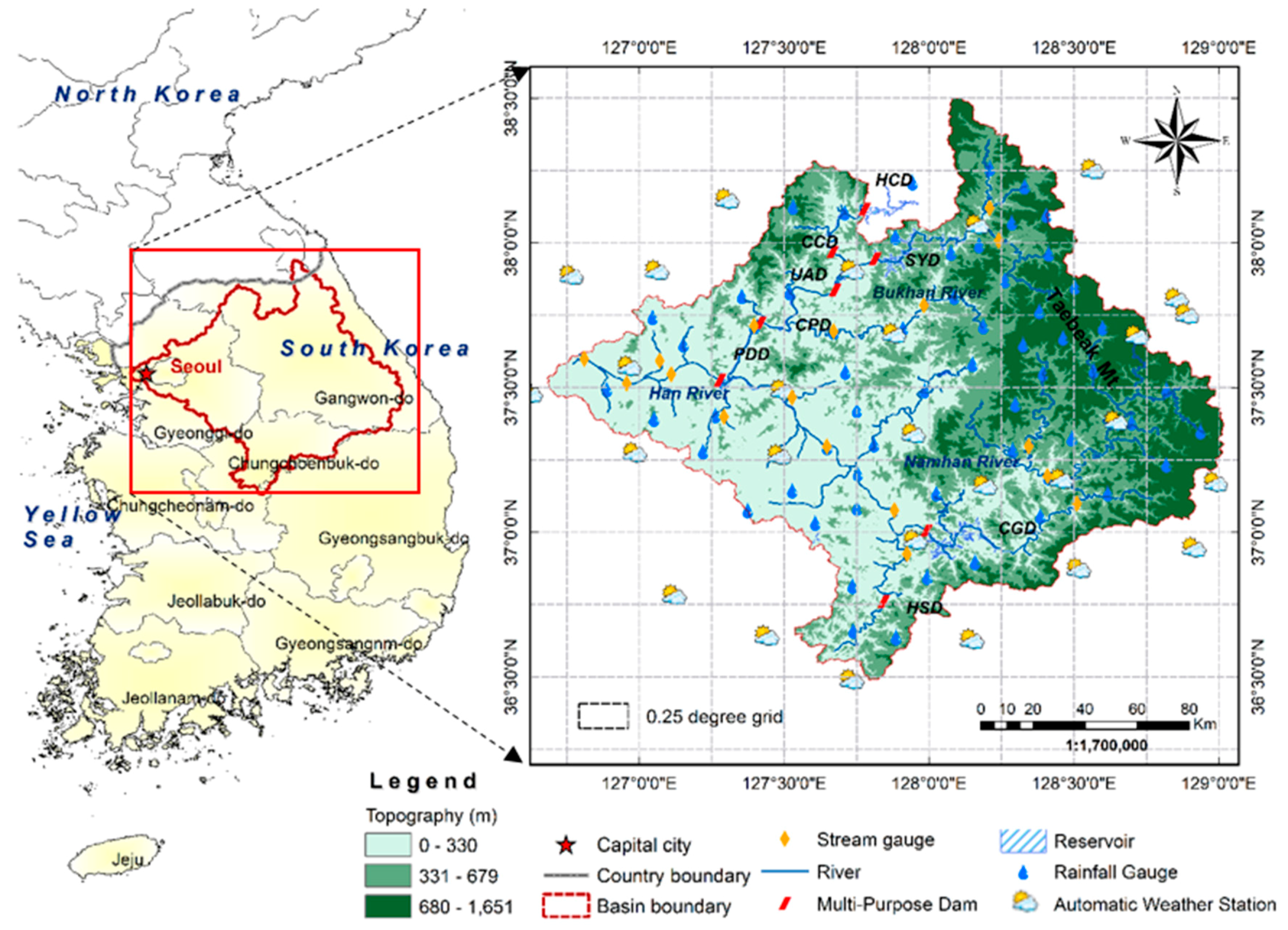
2.1. Study Area
2.2. Precipitation Data from Rain Gauges
2.3. Satellite-Derived Precipitation Products
2.3.1. TRMM 3B42 Precipitation Products
2.3.2. PERSIANN and PERSIANN-CDR Products
2.3.3. CMADS Precipitation Products
2.4. SWAT Model
2.5. Statistical Measures for Precipitation and Runoff
3. Results
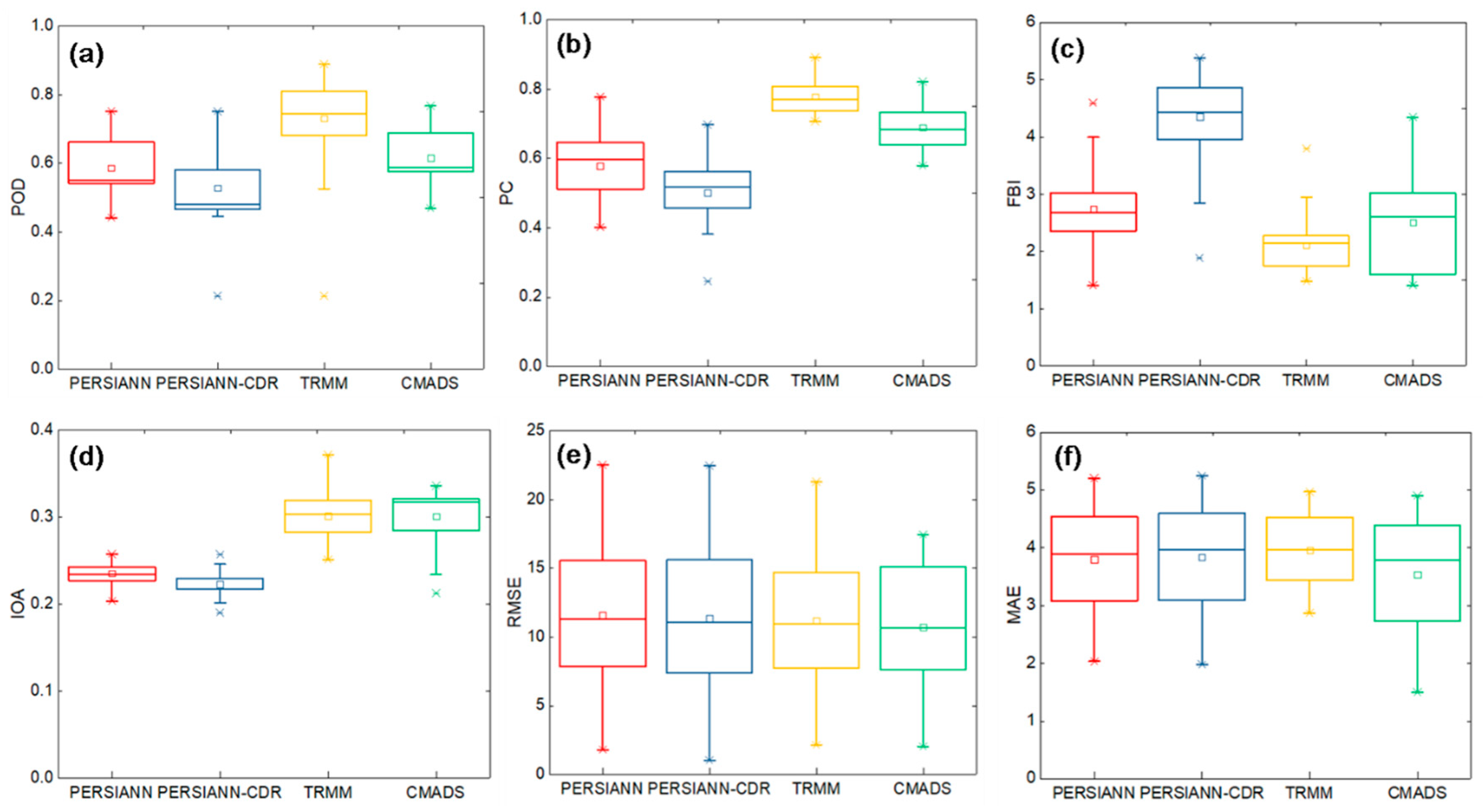
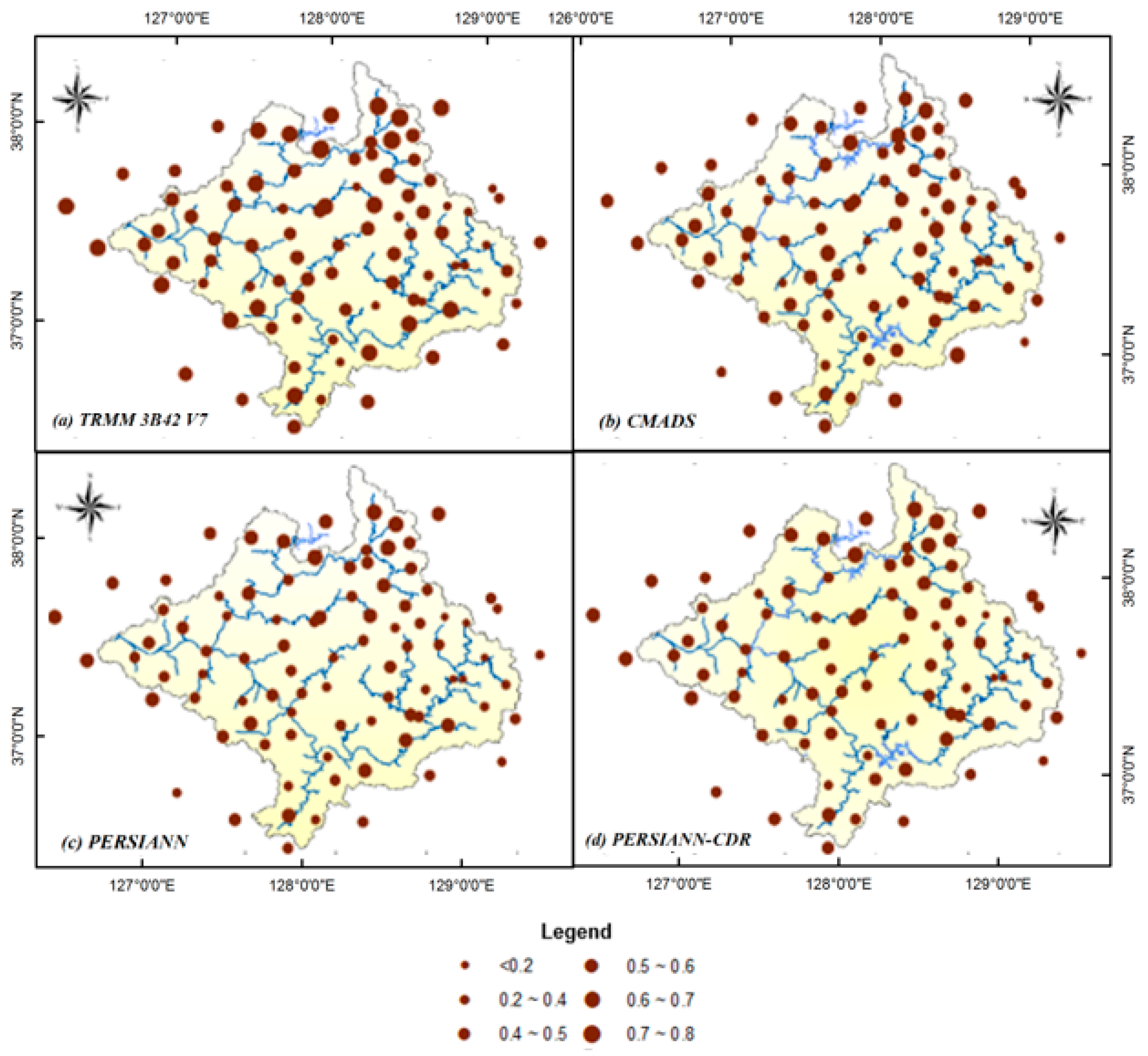
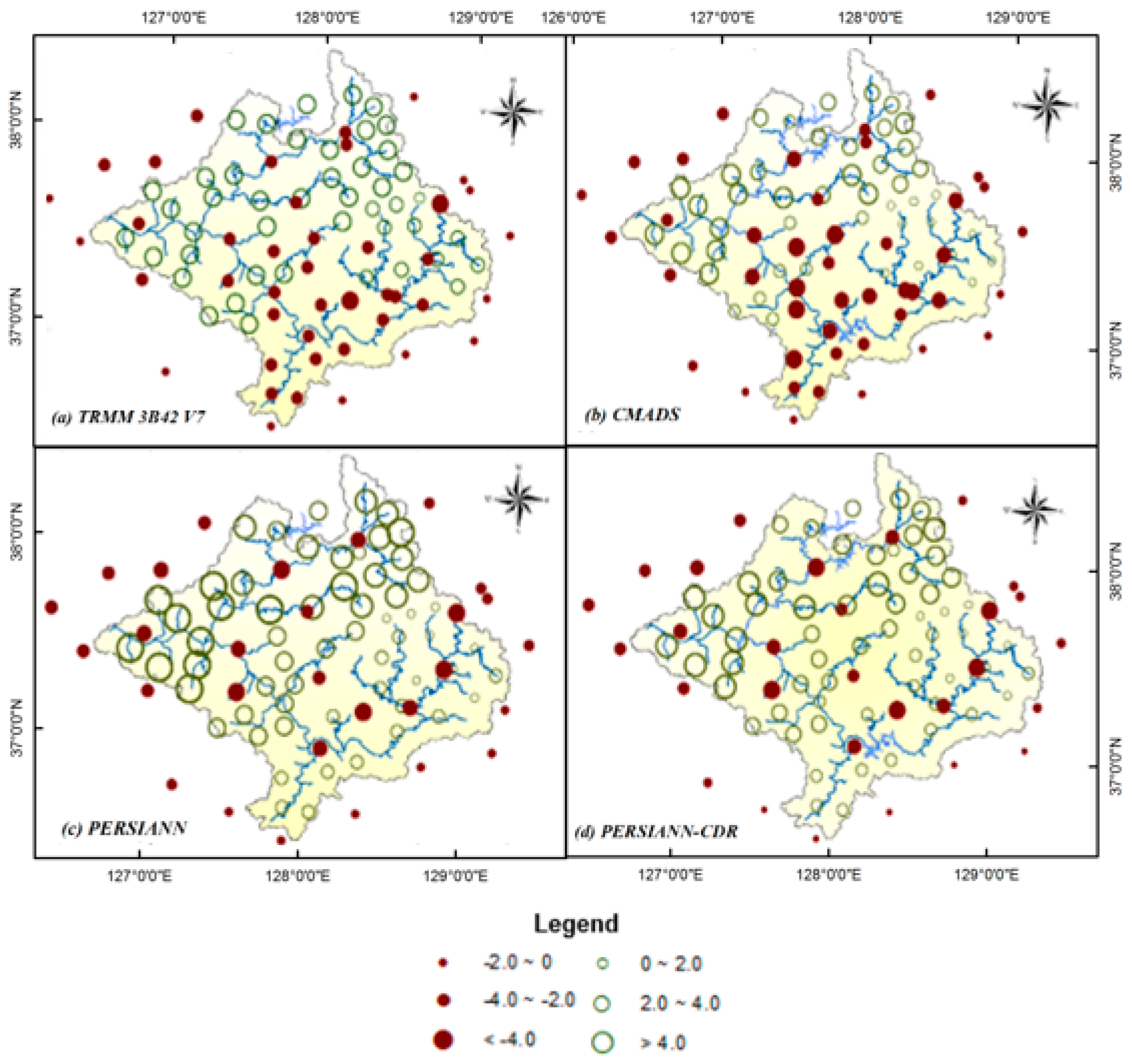
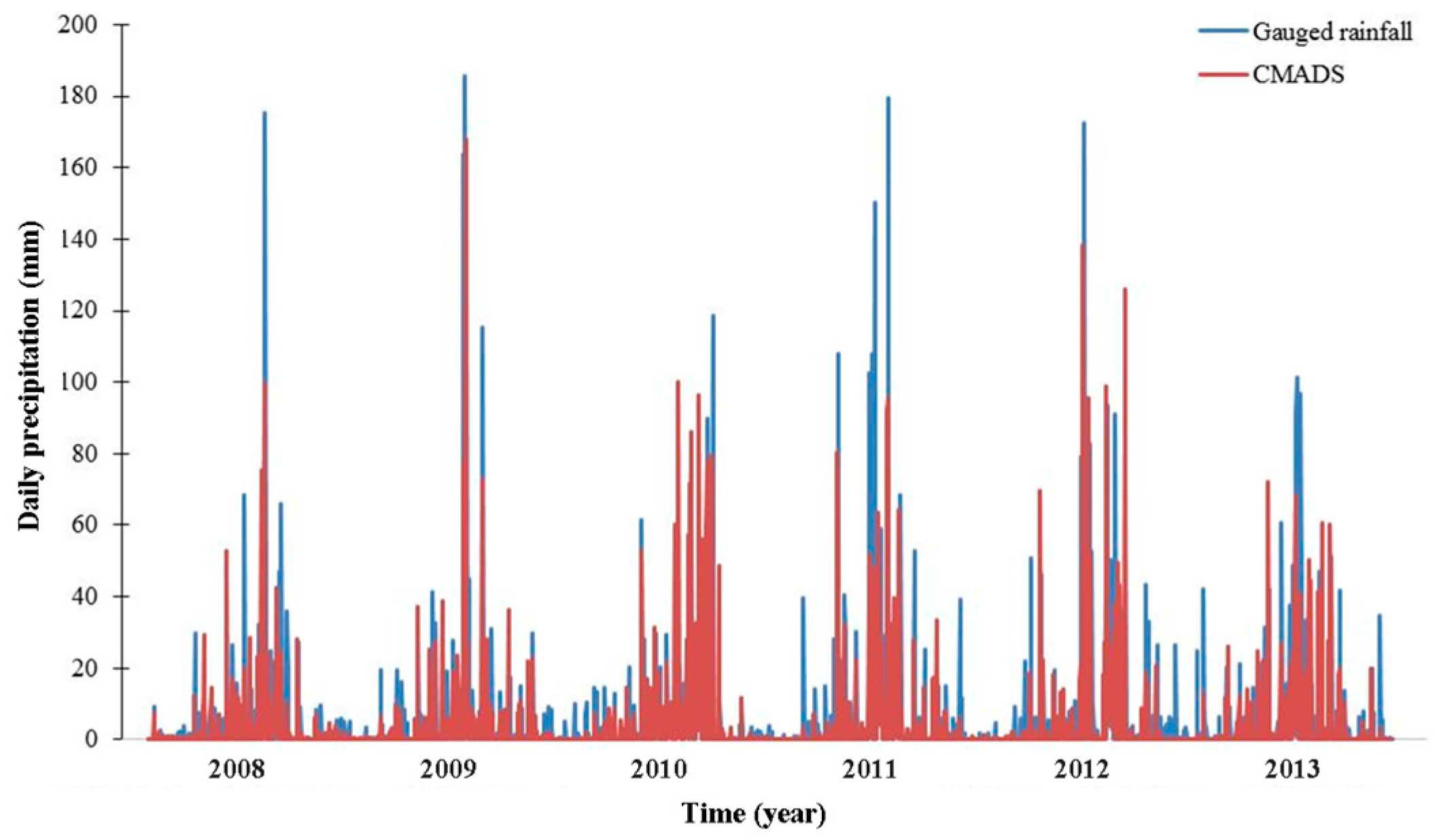
3.1. Evaluation of Different Satellite-Derived Precipitation Data
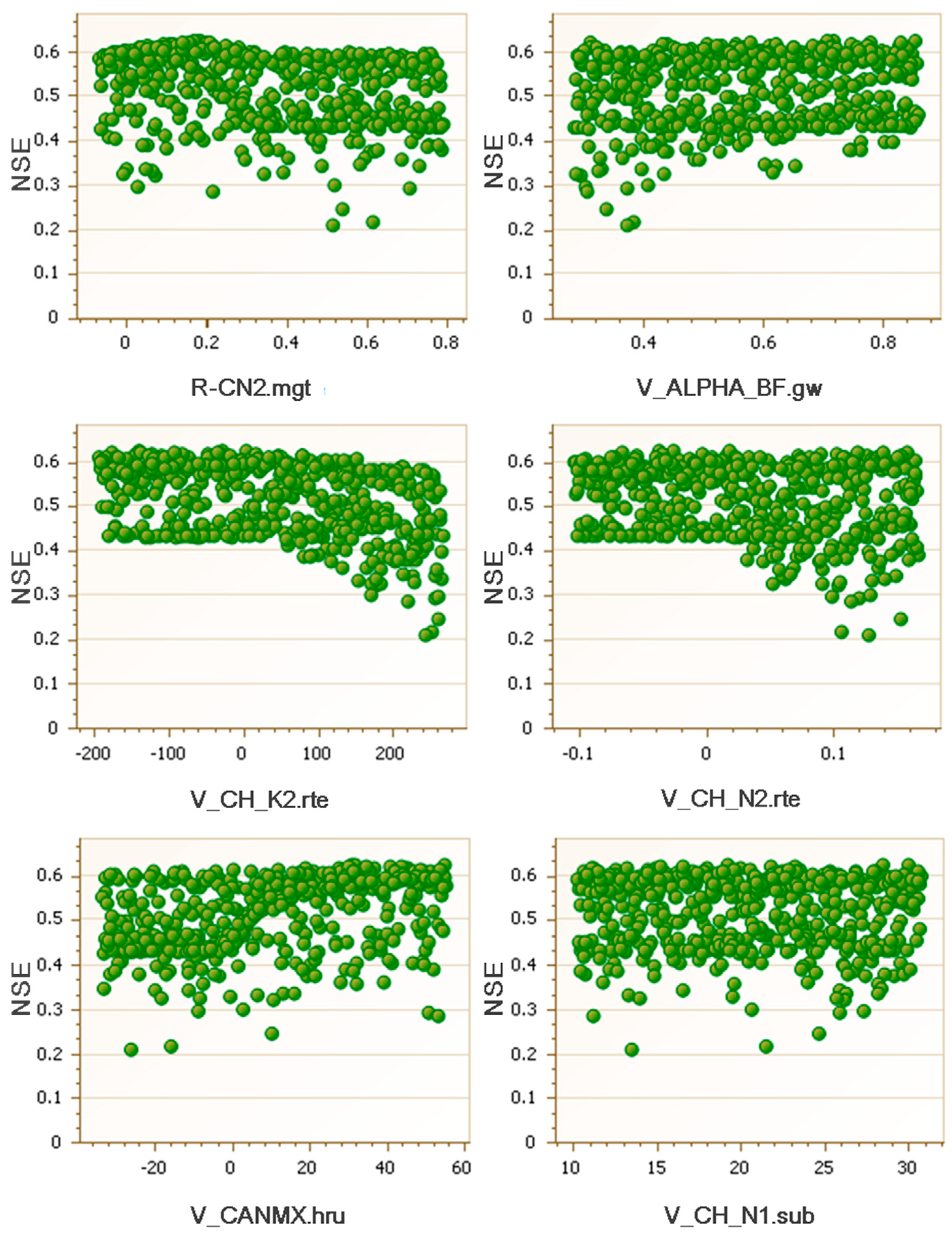
3.2. SWAT Calibration and Validation
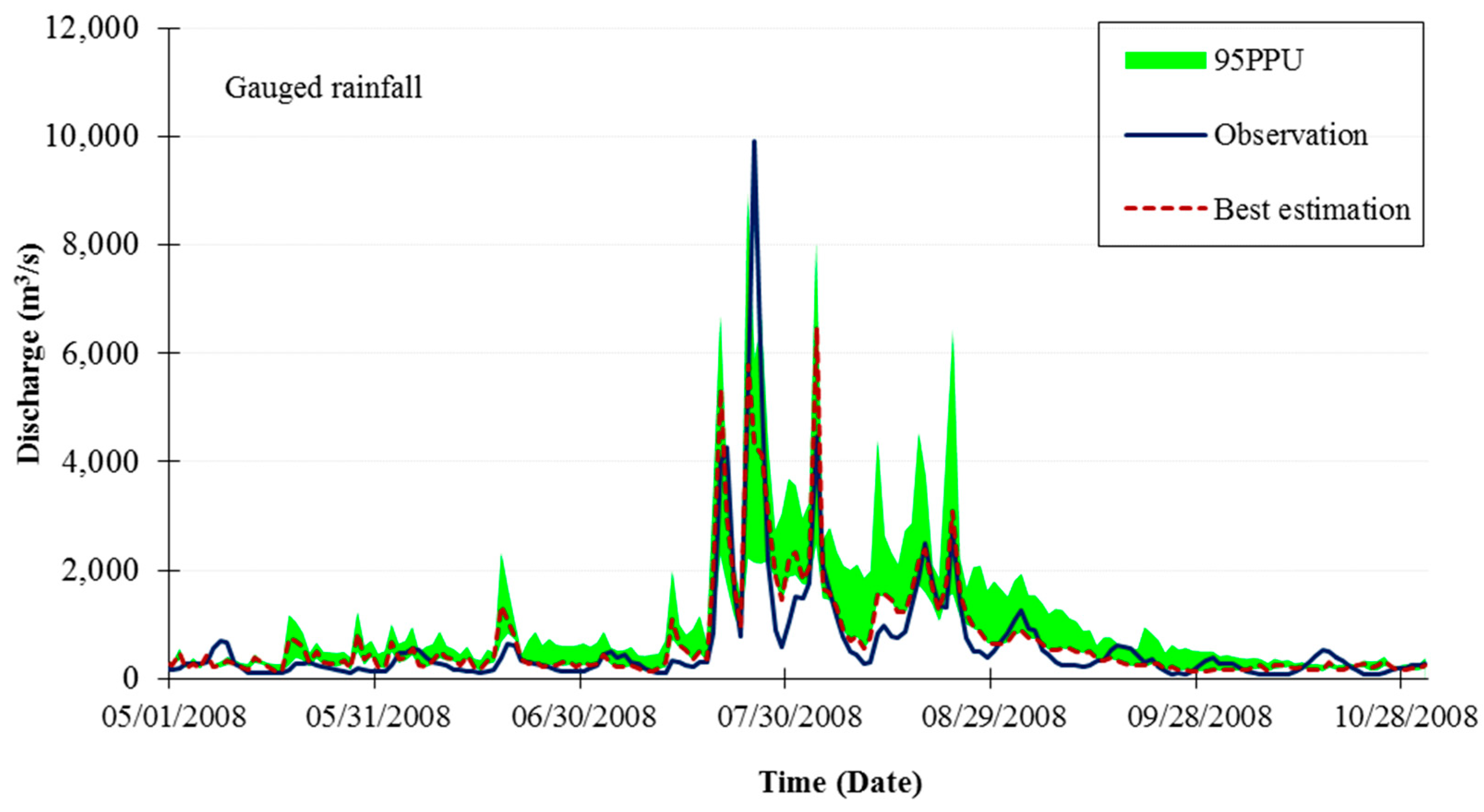
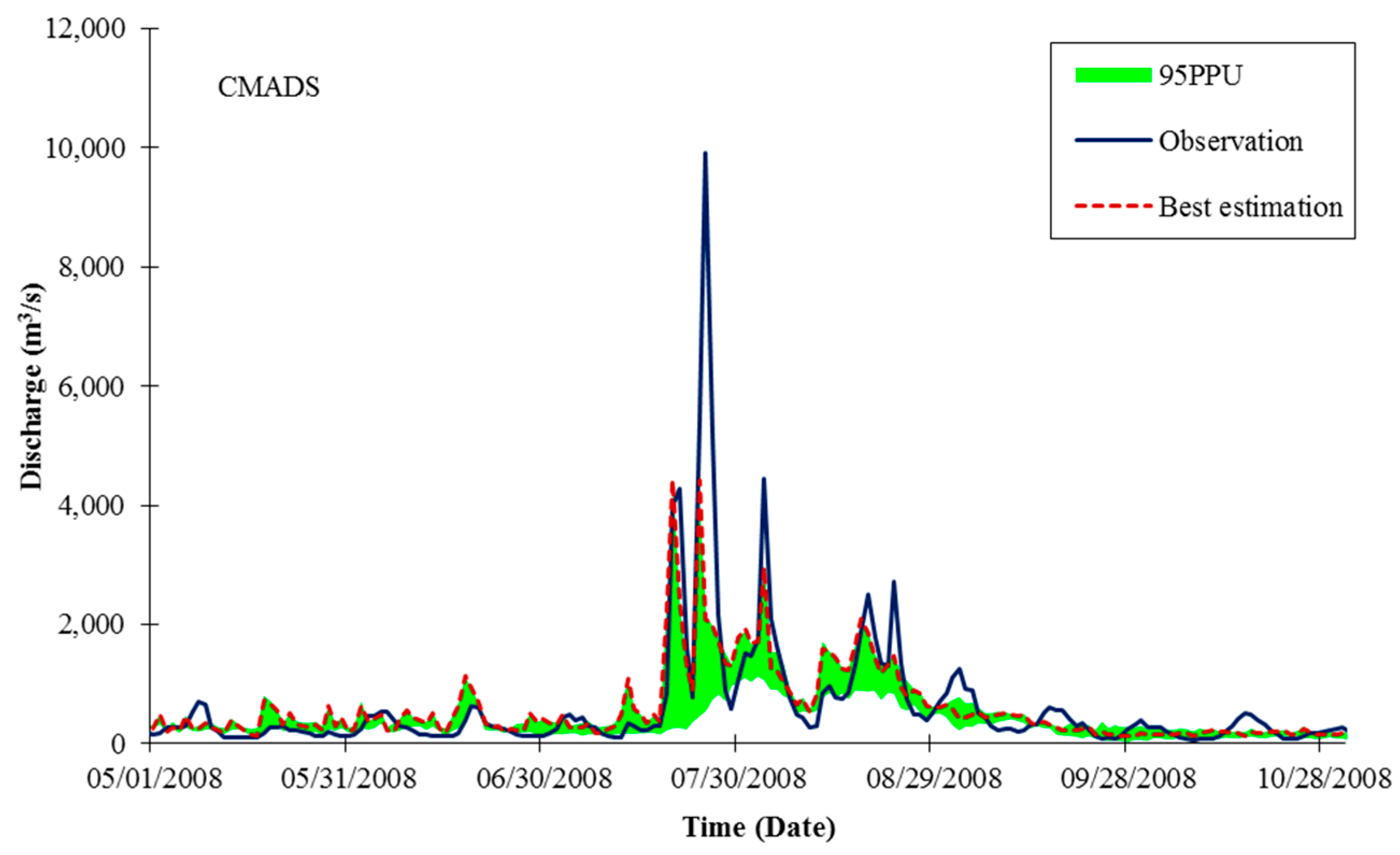
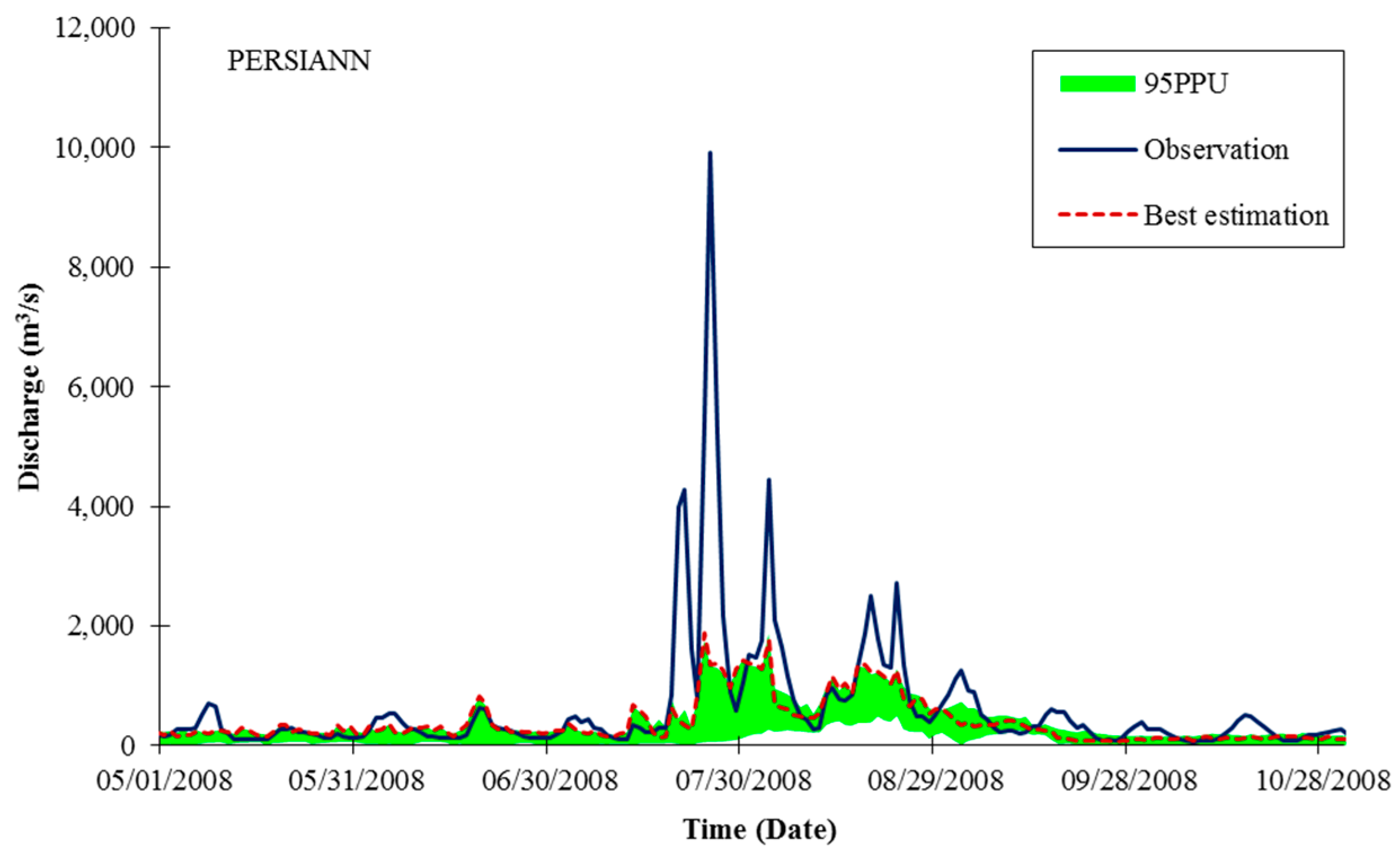
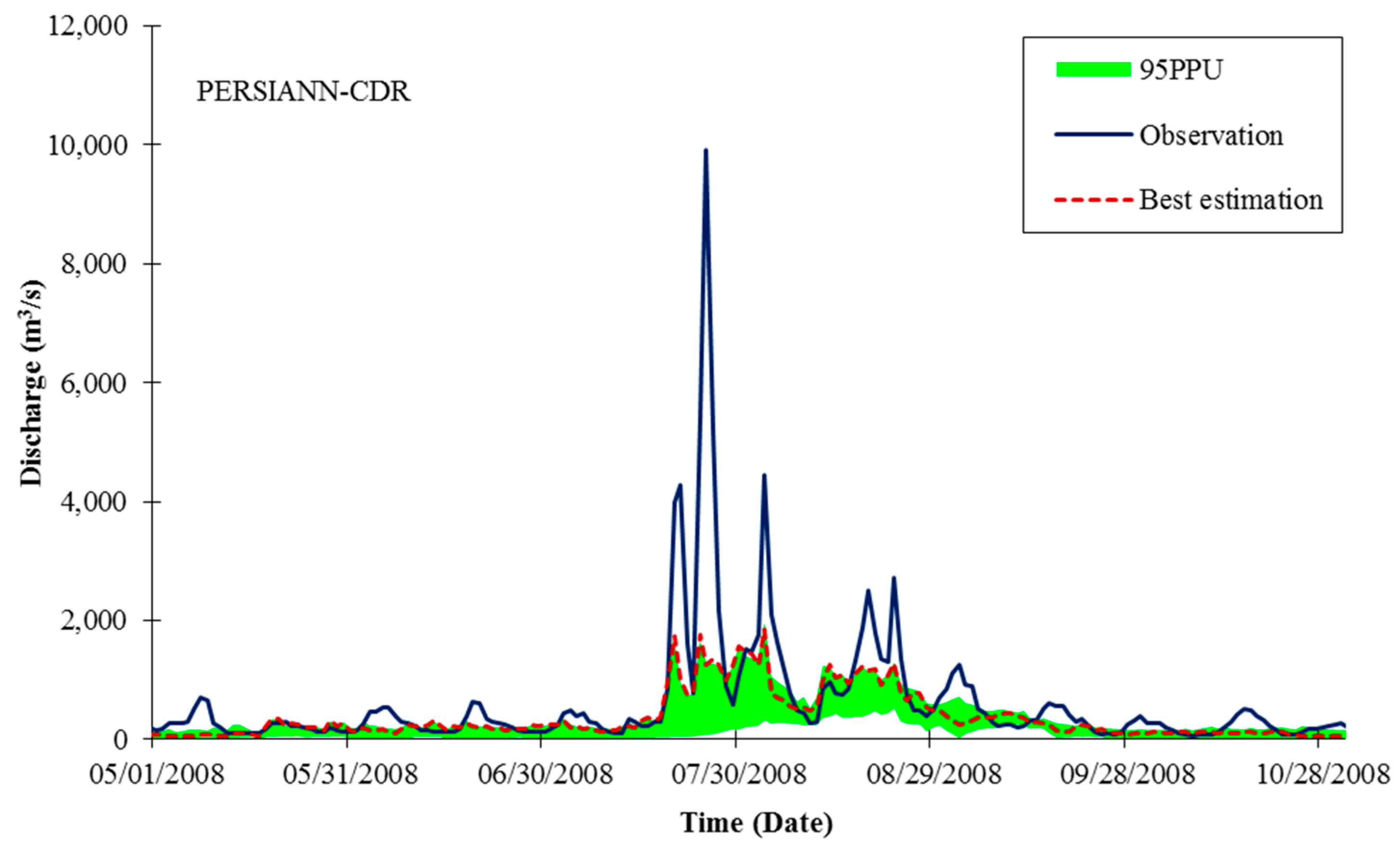
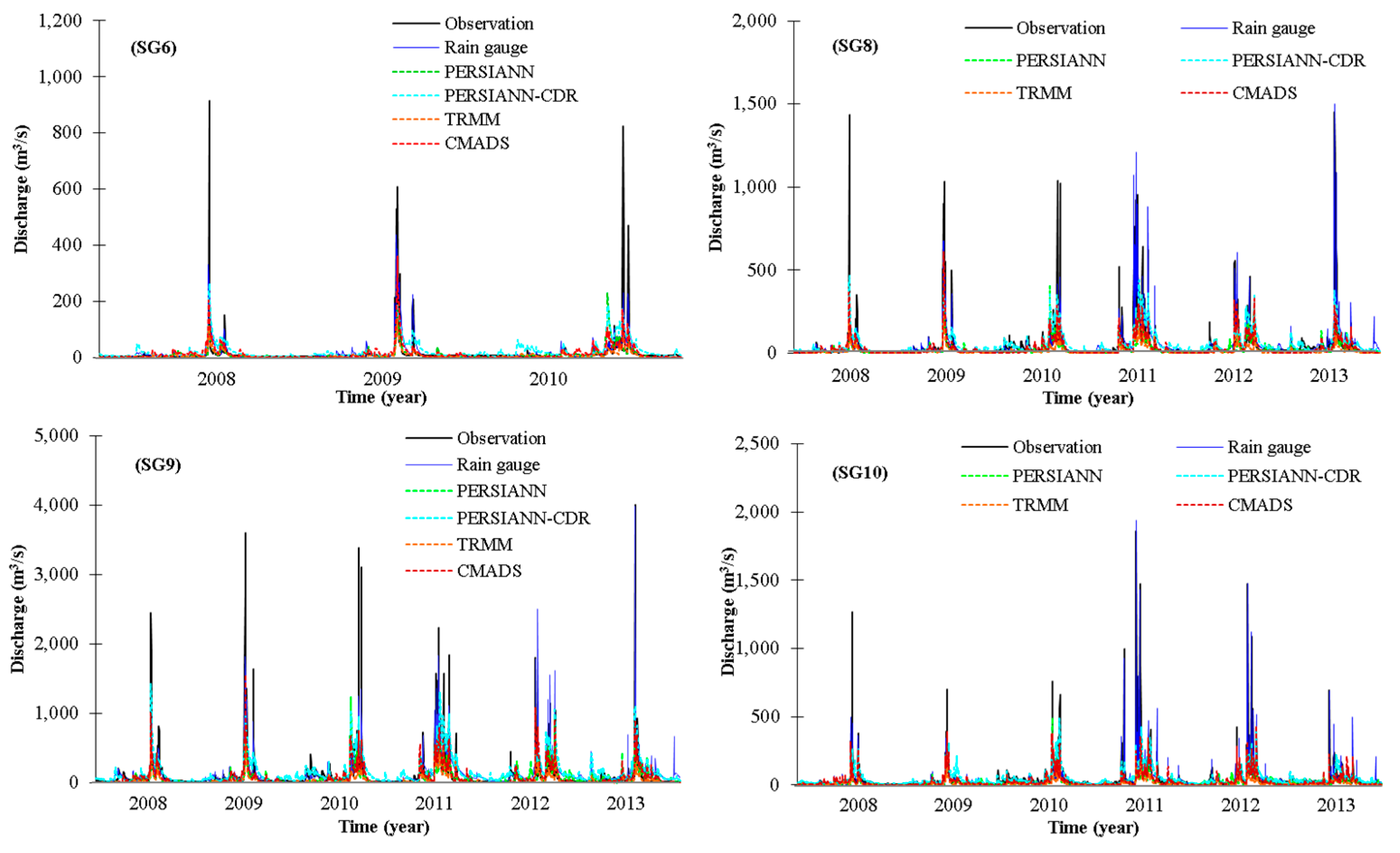
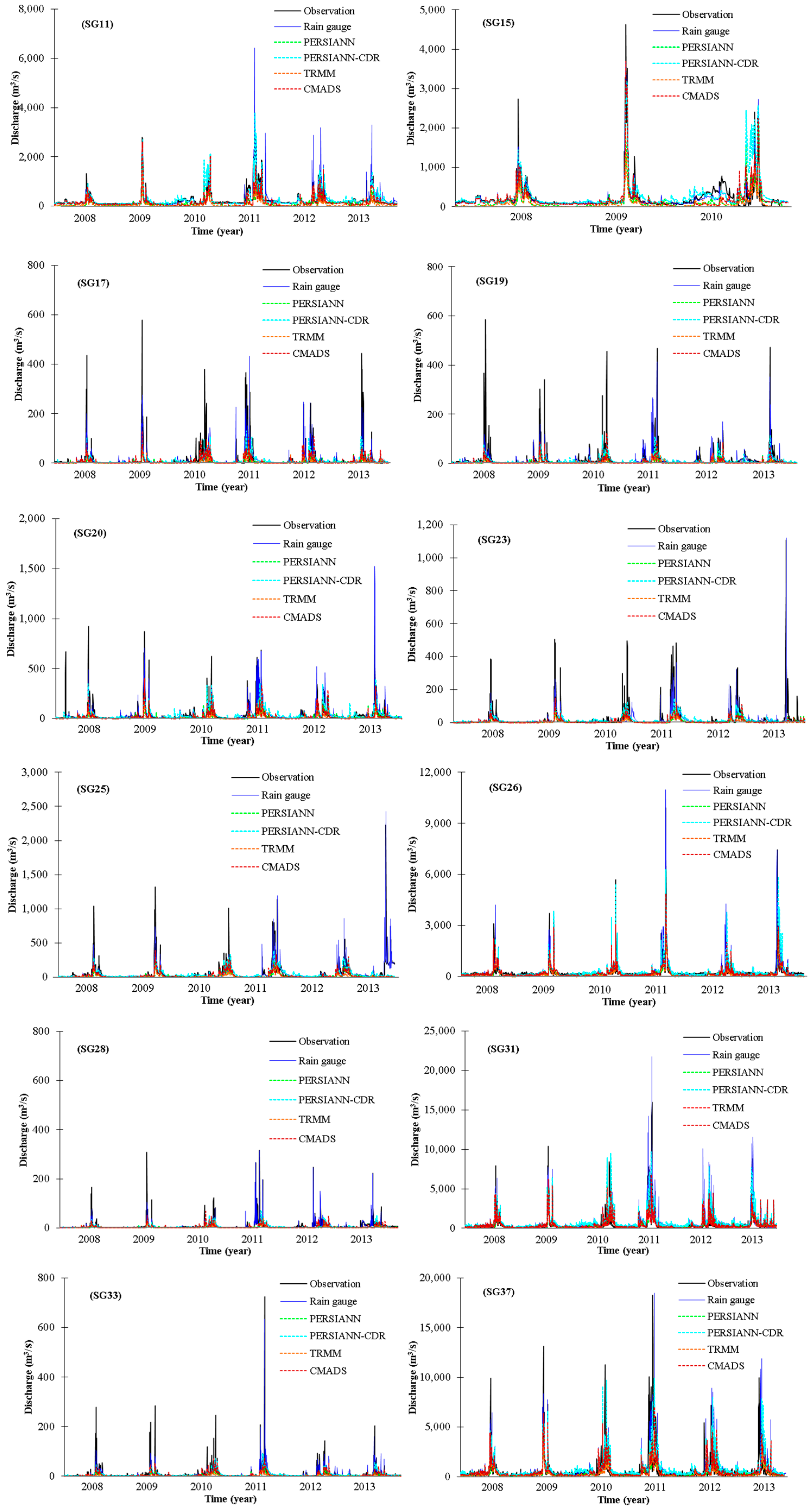
3.3. Streamflow Simulation Using Four Satellite-Derived Rainfall Datasets
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- González-Rouco, J.F.; Jiménez, J.L.; Quesada, V.; Valero, F. Quality control and homogeneity of precipitation data in the southwest of Europe. J. Clim. 2001, 14, 964–978. [Google Scholar] [CrossRef]
- Price, K.; Purucker, S.T.; Kraemer, S.R.; Babendreier, J.E.; Knightes, C.D. Comparison of radar and gauge precipitation data in watershed models across varying spatial and temporal scales. Hydrol. Process. 2014, 28, 3505–3520. [Google Scholar] [CrossRef]
- Sikorska, A.; Seibert, J. Importance of precipitation data quality for streamflow predictions. Geophys. Res. Abstr. 2015, 17, 13369. [Google Scholar]
- Buarque, D.C.; De Paiva, R.C.D.; Clarke, R.T.; Mendes, C.A.B. A comparison of Amazon rainfall characteristics derived from TRMM, CMORPH and the Brazilian national rain gauge network. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Kidd, C.; Bauer, P.; Turk, J.; Huffman, G.J.; Joyce, R.; Hsu, K.L.; Braithwaite, D. Intercomparison of high-resolution precipitation products over northwest Europe. J. Hydrometeorol. 2012, 13, 67–83. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; Veldhuis, M.C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Westrick, K.J.; Mass, C.F.; Colle, B.A. The limitation of the WSR-88D radar network for quantitative precipitation measurement over the coastal western United States. Bull. Am. Meteorol. Soc. 1999, 80, 2289–2298. [Google Scholar] [CrossRef]
- Rico-Ramirez, M.A.; Liguori, S.; Schellart, A.N.A. Quantifying radar-rainfall uncertainties in urban drainage flow modeling. J. Hydrol. 2015, 528, 17–28. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Su, F.; Hong, Y.; Lettenmaier, D.P. Evaluation of TRMM multisatellite precipitation analysis (TMPA) and its utility in hydrologic prediction in the La Plata basin. J. Hydrometeorol. 2008, 9, 622–639. [Google Scholar] [CrossRef]
- Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the Amazon basin using TRMM rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
- Scheel, M.L.M.; Rohrer, M.; Huggel, C.; Villar, D.S.; Huffman, G.J. Evaluation of TRMM multi-satellite precipitation analysis (TMPA) performance in the Central Andes region and its dependency on spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2011, 15, 2649–2663. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Owiti, T.; Kibiiy, J.; Ouma, Y.O.; Tateishi, R.; Kipkorir, E. Multitemporal comparative analysis of TRMM-3B42 satellite-estimated rainfall with surface gauge data at basin scales: Daily, decadal and monthly evaluations. Int. J. Remote Sens. 2012, 33, 7662–7684. [Google Scholar] [CrossRef]
- Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based multi-satellite precipitation analysis over the Wangchu Basin of Bhutan: Are the latest satellite precipitation products ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I. Evaluation of remote-sensing-based rainfall products through predictive capability in hydrological runoff modelling. Hydrol. Process. 2010, 24, 879–891. [Google Scholar] [CrossRef]
- Behrangi, A.; Khakbaz, B.; Jaw, T.C.; AghaKouchak, A.; Hsu, K.; Sorooshian, S. Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrol. 2011, 397, 225–237. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Ha, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Gebremichael, M.; Hopson, T. Evaluation of high-resolution satellite precipitation products over very complex terrain in Ethiopia. J. Appl. Meteorol. Climatol. 2010, 49, 1044–1051. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H. Significance of the China meteorological assimilation driving datasets for the SWAT model (CMADS) of East Asia. Water (Switzerland) 2017, 9, 765. [Google Scholar] [CrossRef]
- Meng, X.Y.; Wang, H.; Lei, X.H.; Cai, S.Y.; Wu, H.J. Hydrological modeling in the Manas River Basin using Soil and Water Assessment Tool driven by CMADS. Teh. Vjesn. 2017, 24, 525–534. [Google Scholar]
- Setegn, S.G.; Donoso, M.C. Sustanability of Intergrated Water Resources Management: Water Governace, Climate and Ecohydrology; Springer: Basel, Switzerland, 2015. [Google Scholar]
- Bicknell, B.R.; Imhoff, J.C.; Kittle, J.L.; Donigian, A.S.; Johanson, R.C. Hydrologic Simulation Program—Fortran: User’s Manual for Release 11; Environmental Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency: Athens, GA, USA, 1996.
- Refsgaard, J.C.; Storm, B. MIKE SHE. In Computer Models of Watershed Hydrology; Sing, V.P., Ed.; Water Resource Publications: Highland Ranch, CO, USA, 1995; pp. 806–846. [Google Scholar]
- USACE. HEC-5 Simulation of Flood Control and Conservation System; US Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 1998. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Sivapalan, M.; Takeuchi, K.; Franks, S.W.; Gupta, V.K.; Karambiri, H.; Lakashmi, V.; Liang, X.; McDonnell, J.J.; Mendiondo, E.M.; O’connell, P.E.; et al. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef]
- Eckhardt, K.; Arnold, J.G. Automatic calibration of a distributed catchment model. J. Hydrol. 2001, 251, 103–109. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and ground water recharge from streamflow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- White, K.L.; Chaubey, I. Sensitivity analysis, calibration, and validations for a multisite and multivariable SWAT model. J. Am. Water Resour. Assoc. 2005, 41, 1077–1089. [Google Scholar] [CrossRef]
- Kang, M.S.; Park, S.W.; Lee, J.J.; Yoo, K.H. Applying SWAT for TMDL programs to a small watershed containing rice paddy fields. Agric. Water Manag. 2006, 79, 72–92. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT-MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Bae, D.H.; Jung, I.W.; Lettenmaier, D.P. Hydrologic uncertainties in climate change from IPCC AR4 GCM simulations of the Chungju Basin, Korea. J. Hydrol. 2011, 401, 90–105. [Google Scholar] [CrossRef]
- Kim, N.W.; Lee, J.E.; Kim, J.T. Assessment of flow regulation effects by dams in the Han River, Korea, on the downstream flow regimes using SWAT. J. Water Resour. Plan. Manag. 2012, 131, 24–35. [Google Scholar] [CrossRef]
- Shope, C.L.; Maharjan, G.R.; Tenhunen, J.; Seo, B.; Kim, K.; Riley, J.; Arnhold, S.; Koellner, T.; Ok, Y.S.; Peiffer, S.; et al. Using the SWAT model to improve process descriptions and define hydrologic partitioning in South Korea. Hydrol. Earth Syst. Sci. 2014, 18, 539–557. [Google Scholar] [CrossRef]
- Cho, K.H.; Pachepsky, Y.A.; Kim, M.; Pyo, J.; Park, M.H.; Kim, Y.M.; Kim, J.W.; Kim, J.H. Modeling seasonal variability of fecal coliform in natural surface waters using the modified SWAT. J. Hydrol. 2016, 535, 377–385. [Google Scholar] [CrossRef]
- Kim, J.P.; Jung, I.; Park, K.W.; Yoon, S.K.; Lee, D. Hydrological utility and uncertainty of multi-satellite precipitation products in the mountainous region of South Korea. Remote Sens. 2016, 8, 608. [Google Scholar] [CrossRef]
- Smith, P.J.; Panziera, L.; Beven, K.J. Forecasting flash floods using data-based mechanistic models and NORA radar rainfall forecasts. Hydrol. Sci. J. 2014, 59, 1343–1357. [Google Scholar] [CrossRef]
- KOWACO. The Pre-Investigation Report for Groundwater Resources; Korea Water Resources Corporation: Daejeon, Korea, 1993; p. 340. [Google Scholar]
- Korea Meteorological Administration. Annual Report 2016; Korea Meteorological Administration: Seoul, Korea, 2016; p. 49.
- Kim, J.S.; Jain, S.; Yoon, S.K. Warm season streamflow variability in the Korean Han River Basin: Links with atmospheric teleconnections. Int. J. Climatol. 2012, 32, 635–640. [Google Scholar] [CrossRef]
- Lee, K.S.; Bong, Y.S.; Lee, D.; Kim, Y.; Kim, K. Tracing the sources of nitrate in the Han River watershed in Korea, using δ15N-NO3 and δ18O-NO3 values. Sci. Total Environ. 2008, 395, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Heo, B.-H.; Kim, K.-E.; Kang, S.-G. Removals of noises from automatic weather station data and radial velocity data of doppler weather radar using modified median filter. J. Korean Meteorol. Soc. 1999, 35, 127–135. [Google Scholar]
- Li, D.; Christakos, G.; Ding, X.; Wu, J. Adequacy of TRMM satellite rainfall data in driving the SWAT modeling of Tiaoxi catchment (Taihu lake basin, China). J. Hydrol. 2018, 556, 1139–1152. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM multi-satellite precipitation analysis (TMPA): Quasi-global, multi-year, combined-sensor precipitation estimates at fine scale. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN system satellite-based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Narsimlu, B.; Gosain, A.K.; Chahar, B.R.; Singh, S.K.; Srivastava, P.K. SWAT model calibration and uncertainty analysis for streamflow prediction in the Kunwari River Basin, India, using sequential uncertainty fitting. Environ. Process. 2015, 2, 79–95. [Google Scholar] [CrossRef]
- Wu, H.; Chen, B. Evaluating uncertainty estimates in distributed hydrological modeling for the Wenjing River watershed in China by GLUE, SUFI-2, and ParaSol methods. Ecol. Eng. 2015, 76, 110–121. [Google Scholar] [CrossRef]
- Khoi, D.N.; Thom, V.T. Parameter uncertainty analysis for simulating streamflow in a river catchment of Vietnam. Glob. Ecol. Conserv. 2015, 4, 538–548. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Baik, J.; Choi, M. Spatio-temporal variability of remotetely sensed precipitation data from COMS and TRMM: Case study of Korean peninsula in East Asia. Adv. Space Res. 2015, 56, 125–1138. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Dai, A. Precipitation characteristics in eighteen coupled climate models. J. Clim. 2006, 19, 4605–4630. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzambwa, S.; Ceccato, P.; Connor, S.J.; Ropelewski, C.F. Validation of high-resolution satellite rainfall products over complex terrain. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- Ma, L.; Ascough Ii, J.C.; Ahuja, L.R.; Shaffer, M.J.; Hanson, J.D.; Rojas, K.W. Root Zone Water Quality Model sensitivity analysis using Monte Carlo simulation. Trans. ASAE 2000, 43, 883–895. [Google Scholar] [CrossRef]
- Hromadka, T.V.; McCuen, R.H. Uncertainty estimates for surface runoff models. Adv. Water Resour. 1998, 11, 2–14. [Google Scholar] [CrossRef]
- Maskey, S.; Guinot, V.; Price, R.K. Treatment of precipitation in rainfall-runoff modelling: A fuzzy set approach. Adv. Water Resour. 2004, 27, 889–898. [Google Scholar] [CrossRef]
- Jones, P.D.; Lister, D.H.; Wilby, R.L.; Kostopoulou, E. Extended riverflow reconstructions for England and Wales, 1865–2002. Int. J. Climatol. 2006, 25, 219–231. [Google Scholar] [CrossRef]
- Andreassian, V.; Perrin, C.; Michel, C.; Usart-Sanchez, I.; Lavabre, J. Impact of imperfect rainfall knowledge on the efficency and the parameters of watershed models. J. Hydrol. 2001, 250, 206–223. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Hossain, F. Understanding the dependence of satellite rainfall uncertainty on topography and climate for hydrologic model simulation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 704–718. [Google Scholar] [CrossRef]
- Xu, S.G.; Niu, Z.; Shen, Y. Understanding the dependence of the uncertainty in a satellite precipitation data set on the underlying surface and a correction method based on geogrphically weighted reggression. Int. J. Remote Sens. 2014, 35, 6508–6521. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Assessment of satellite rainfall products for streamflow simulation in medium watersheds of the Ethiopian highlands. Hydrol. Earth Syst. Sci. 2011, 15, 1147–1155. [Google Scholar] [CrossRef]
- Artan, G.; Gadain, H.; Smith, J.L.; Asante, K.; Bandaragoda, C.J.; Verdin, J.P. Adequacy of satellite derived rainfall data for streamflow modeling. Nat. Hazards 2007, 43, 167–185. [Google Scholar] [CrossRef]

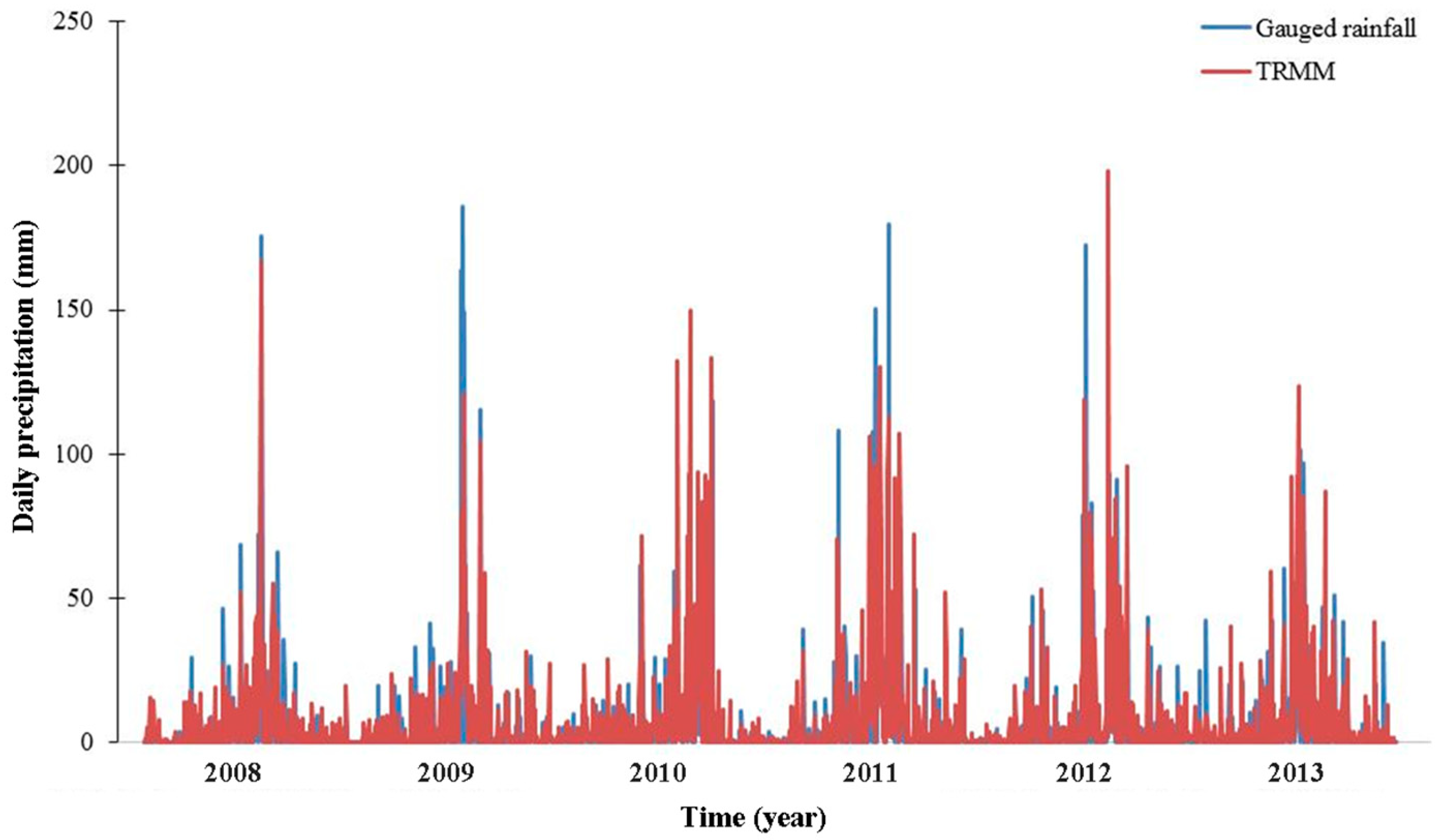
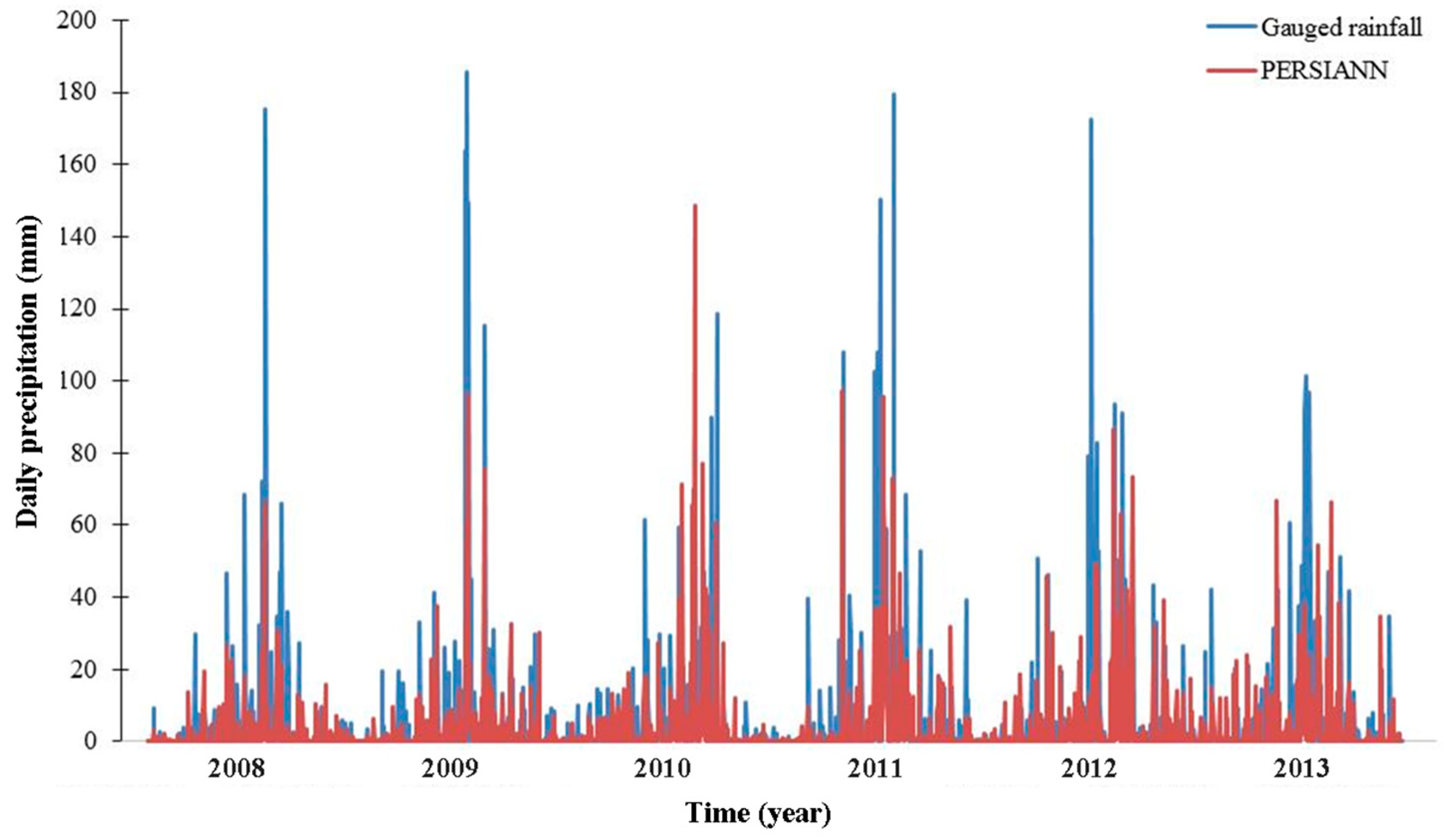
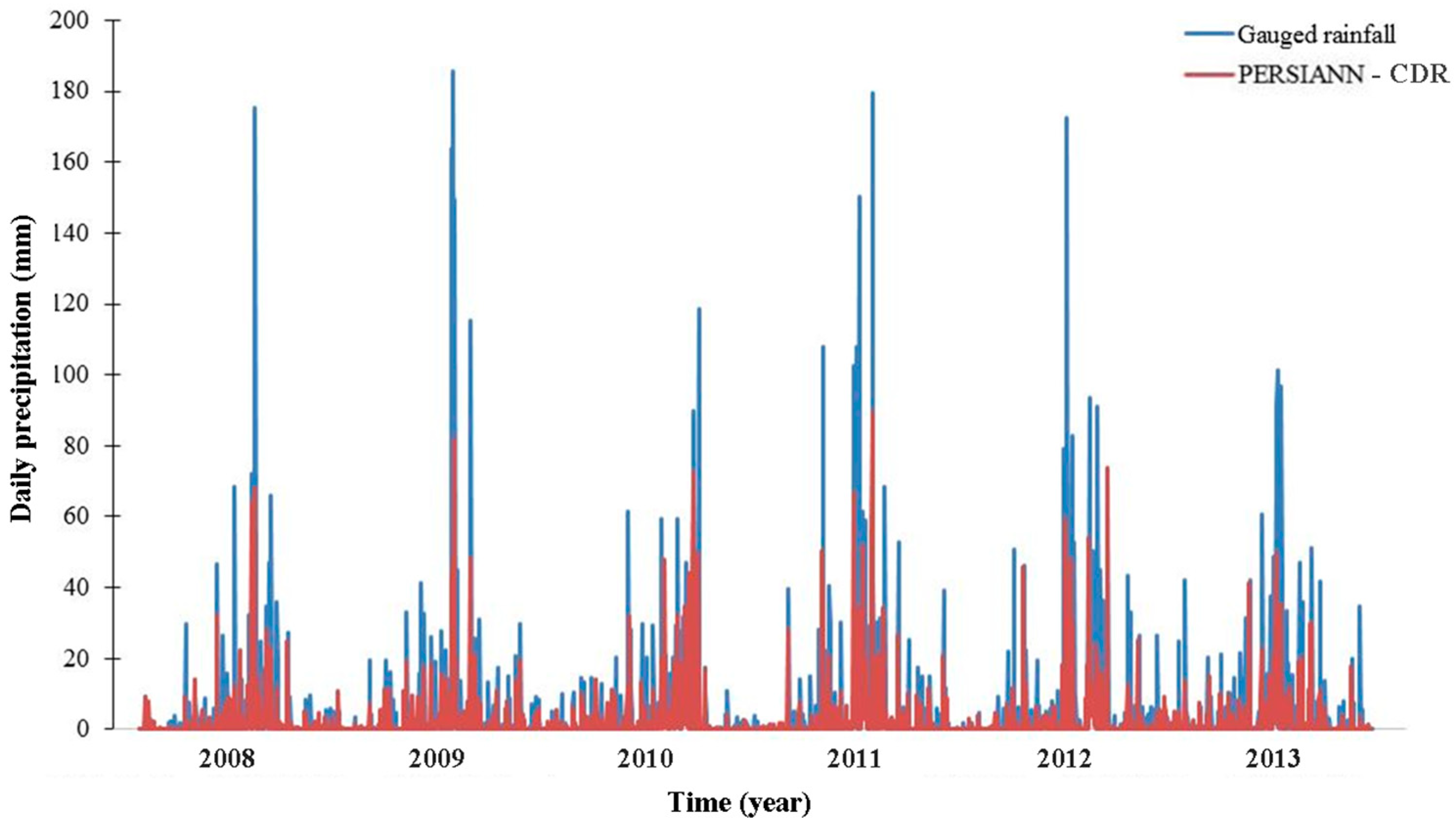
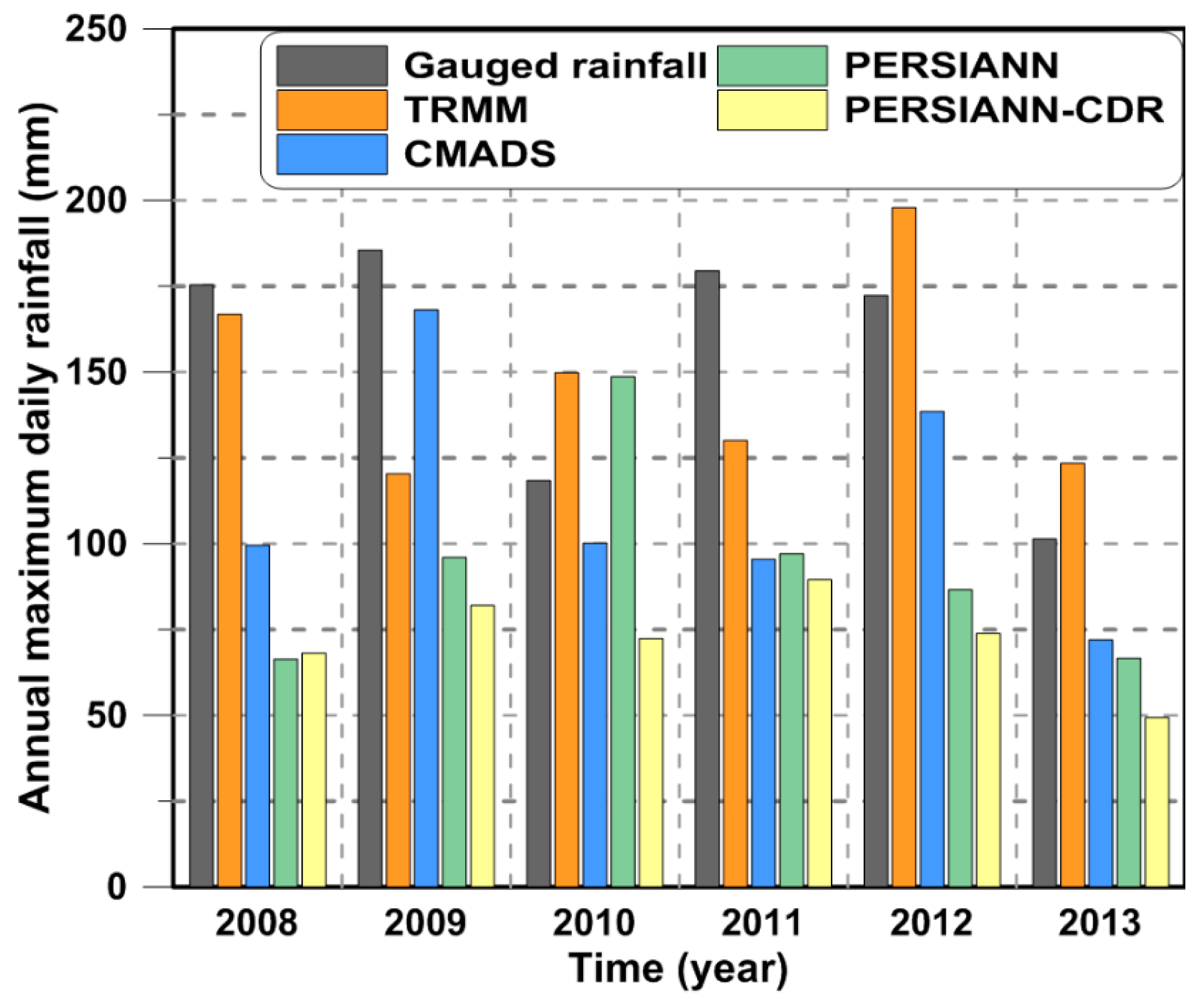
| Dataset | Version | Spatial/Temporal Resolution | Areal Coverage | Time Coverage | Sources |
|---|---|---|---|---|---|
| TRMM | 3B42 V7 | 0.250/daily | Near Global | 1998–present | Huffman et al. [47] |
| PERSIANN | - | 0.250/daily | Near Global | 2000–present | Sorooshian et al. [48] |
| PERSIANN-CDR | CDR | 0.250/daily | Near Global | 1983–2017 | Ashouri et al. [49] |
| CMADS | V1.1 | 0.250/daily | East Asia | 2008–2014 | Meng [22] |
| Data Type | Data Description | Scale | Data Source |
|---|---|---|---|
| Topography map | Digital elevation map (DEM) | 90 m | USGS-HydroSHEDS |
| Land-use/Land cover map | Land use/Land cover classification 2010 | 1:1,250,000 | Korea Ministry of Environment |
| Soil map | Soil types (2007) | 10 km | Food and Agriculture Organization |
| Meteorology | Daily precipitation, Minimum and maximum temperature, Solar radiation, Relative humidity, Wind speed | 1990–2013 | Korea Meteorological Administration and Water Resources Management Information System |
| Hydrological data | Discharge, Dam operation, Reservoir characteristics | 2008–2013 | Water Resources Management Information System |
| Satellite Event | Observation Event | Marginal Total | |
|---|---|---|---|
| Yes (p ≥ 1.0 mm) | No (p < 1.0 mm) | ||
| Yes (p ≥ 1.0 mm) | a | b | a + b |
| No (p < 1.0 mm) | c | d | c + d |
| Marginal total | a + c | b + d | n = a + b + c + d |
| Parameters | Parameter Description | Initial Range | Calibrated Range | Best Value |
|---|---|---|---|---|
| r CN2 | Initial SCS CN II value | −0.20 to 0.20 | −0.07 to 0.79 | 0.18 |
| v ALPHA_BF | Baseflow alpha factor | 0.0035 to 0.80 | 0.28 to 0.80 | 0.72 |
| v CH_K2 | Effective hydraulic conductivity of the main channel | −0.01 to 500 | −0.01 to 268 | 4.65 |
| v CH_N2 | Manning’s value for main channels | −0.01 to 0.30 | −0.10 to 0.17 | 0.03 |
| v CANMX | Maximum canopy storage | 0 to 100 | 0 to 55.40 | 55.19 |
| v CH_N1 | Manning’s value for tributary channels | 0.01 to 30 | 10 to 30 | 28.46 |
| Code | Station | Calibration (2008–2010) | Validation (2011–2013) | ||||
|---|---|---|---|---|---|---|---|
| NSE | R2 | PBIAS (%) | NSE | R2 | PBIAS (%) | ||
| SG6 | PanUn | 0.53 | 0.54 | −7.50 | - | - | - |
| SG8 | YeongWeol1 | 0.57 | 0.59 | 14.70 | 0.64 | 0.72 | −33.41 |
| SG9 | YeongChun | 0.59 | 0.59 | 3.50 | 0.61 | 0.71 | −26.99 |
| SG10 | DalCheon | 0.63 | 0.67 | 24.30 | 0.75 | 0.78 | −17.19 |
| SG11 | Mokgyegyo | 0.94 | 0.95 | 14.70 | 0.61 | 0.73 | −10.10 |
| SG15 | Yeojudaegyo | 0.82 | 0.82 | −0.20 | - | - | - |
| SG17 | Heukcheongyo | 0.51 | 0.53 | 20.00 | 0.61 | 0.61 | −7.73 |
| SG19 | WeonTong | 0.53 | 0.67 | 11.30 | 0.50 | 0.51 | 21.47 |
| SG20 | NaeLinCheon | 0.69 | 0.70 | 17.10 | 0.58 | 0.66 | −12.44 |
| SG23 | Jueumchigyo | 0.50 | 0.51 | 16.90 | 0.56 | 0.56 | 18.90 |
| SG25 | Bangokgyo | 0.67 | 0.71 | 24.20 | 0.58 | 0.63 | −6.78 |
| SG26 | Daeseongri | 0.71 | 0.73 | 0.60 | 0.61 | 0.73 | −14.71 |
| SG28 | Sumthlgyo | 0.63 | 0.67 | 20.50 | 0.75 | 0.78 | 20.77 |
| SG31 | Gwangjingyo | 0.56 | 0.63 | −14.10 | 0.56 | 0.77 | −24.96 |
| SG33 | Jungranggyo | 0.56 | 0.58 | 18.40 | 0.90 | 0.90 | −11.80 |
| SG37 (outlet) | Haengjudaegyo | 0.58 | 0.59 | −13.00 | 0.77 | 0.81 | −38.80 |
| Statistics | Gauged Rainfall (Calibration) | Gauged Rainfall (Validation) | TRMM | CMADS | PERSIANN | PERSIANN-CDR |
|---|---|---|---|---|---|---|
| P-factor | 0.54 | 0.47 | 0.51 | 0.40 | 0.39 | 0.33 |
| R-factor | 0.47 | 0.56 | 0.42 | 0.42 | 0.37 | 0.43 |
| Code | Station | Product | R2 | NSE | PBIAS (%) |
|---|---|---|---|---|---|
| SG6 | PanUn | Rain gauge | 0.54 | 0.53 | −7.50 |
| PERSIANN | 0.44 | 0.23 | 55.70 | ||
| PERSIANN-CDR | 0.21 | 0.19 | 35.00 | ||
| TRMM 3B42 V7 | 0.48 | 0.42 | −52.70 | ||
| CMADS | 0.39 | 0.37 | 11.20 | ||
| SG8 | YeongWeol1 | Rain gauge | 0.66 | 0.61 | −9.36 |
| PERSIANN | 0.55 | 0.21 | 67.20 | ||
| PERSIANN-CDR | 0.55 | 0.21 | 67.20 | ||
| TRMM 3B42 V7 | 0.46 | 0.45 | −18.40 | ||
| CMADS | 0.49 | 0.43 | 23.20 | ||
| SG9 | YeongChun | Rain gauge | 0.65 | 0.60 | −11.75 |
| PERSIANN | 0.49 | 0.25 | 59.50 | ||
| PERSIANN-CDR | 0.28 | 0.25 | 31.30 | ||
| TRMM 3B42 V7 | 0.59 | 0.54 | −33.00 | ||
| CMADS | 0.44 | 0.42 | 20.90 | ||
| SG10 | DalCheon | Rain gauge | 0.73 | 0.69 | 3.56 |
| PERSIANN | 0.41 | 0.15 | 68.90 | ||
| PERSIANN-CDR | 0.29 | 0.23 | 46.30 | ||
| TRMM 3B42 V7 | 0.33 | 0.33 | −14.80 | ||
| CMADS | 0.36 | 0.33 | 10.10 | ||
| SG11 | Mokgyegyo | Rain gauge | 0.84 | 0.78 | 2.30 |
| PERSIANN | 0.61 | 0.18 | 71.10 | ||
| PERSIANN-CDR | 0.60 | 0.42 | 50.10 | ||
| TRMM 3B42 V7 | 0.81 | 0.79 | −7.30 | ||
| CMADS | 0.70 | 0.62 | 35.50 | ||
| SG15 | Yeojudaegyo | Rain gauge | 0.82 | 0.82 | −0.20 |
| PERSIANN | 0.06 | 0.04 | 40.50 | ||
| PERSIANN-CDR | 0.05 | 0.03 | 31.20 | ||
| TRMM 3B42 V7 | 0.60 | 0.43 | −13.57 | ||
| CMADS | 0.31 | 0.31 | −29.30 | ||
| SG17 | Heukcheongyo | Rain gauge | 0.57 | 0.56 | 6.14 |
| PERSIANN | 0.08 | 0.03 | 69.90 | ||
| PERSIANN-CDR | 0.06 | 0.03 | 58.80 | ||
| TRMM 3B42 V7 | 0.48 | 0.42 | 12.70 | ||
| CMADS | 0.30 | 0.38 | 41.80 | ||
| SG19 | WeonTong | Rain gauge | 0.59 | 0.52 | 16.39 |
| PERSIANN | 0.40 | 0.04 | 83.20 | ||
| PERSIANN-CDR | 0.44 | 0.17 | 71.20 | ||
| TRMM 3B42 V7 | 0.59 | 0.58 | 28.30 | ||
| CMADS | 0.57 | 0.49 | 27.10 | ||
| SG20 | NaeLinCheon | Rain gauge | 0.68 | 0.64 | 2.33 |
| PERSIANN | 0.32 | 0.12 | 72.60 | ||
| PERSIANN-CDR | 0.23 | 0.17 | 54.10 | ||
| TRMM 3B42 V7 | 0.59 | 0.58 | −4.50 | ||
| CMADS | 0.31 | 0.45 | 19.50 | ||
| SG23 | Jueumchigyo | Rain gauge | 0.52 | 0.51 | 17.90 |
| PERSIANN | 0.04 | 0.02 | 73.80 | ||
| PERSIANN-CDR | 0.04 | 0.02 | 59.90 | ||
| TRMM 3B42 V7 | 0.58 | 0.42 | 11.30 | ||
| CMADS | 0.50 | 0.43 | 22.90 | ||
| SG25 | Bangokgyo | Rain gauge | 0.67 | 0.63 | 8.71 |
| PERSIANN | 0.14 | 0.02 | 73.70 | ||
| PERSIANN-CDR | 0.08 | 0.02 | 62.00 | ||
| TRMM 3B42 V7 | 0.56 | 0.55 | 16.00 | ||
| CMADS | 0.47 | 0.41 | 20.70 | ||
| SG26 | Daeseongri | Rain gauge | 0.73 | 0.66 | −7.06 |
| PERSIANN | 0.45 | 0.35 | 48.90 | ||
| PERSIANN-CDR | 0.50 | 0.44 | 36.00 | ||
| TRMM 3B42 V7 | 0.55 | 0.51 | −8.90 | ||
| CMADS | 0.53 | 0.51 | 24.30 | ||
| SG28 | Sumthlgyo | Rain gauge | 0.73 | 0.69 | 20.64 |
| PERSIANN | 0.13 | 0.20 | 75.30 | ||
| PERSIANN-CDR | 0.07 | 0.10 | 67.40 | ||
| TRMM 3B42 V7 | 0.62 | 0.57 | 25.10 | ||
| CMADS | 0.59 | 0.55 | 23.90 | ||
| SG31 | Gwangjingyo | Rain gauge | 0.70 | 0.56 | −14.53 |
| PERSIANN | 0.08 | 0.05 | 38.10 | ||
| PERSIANN-CDR | 0.06 | 0.01 | 12.70 | ||
| TRMM 3B42 V7 | 0.57 | 0.44 | −51.20 | ||
| CMADS | 0.49 | 0.42 | −10.70 | ||
| SG33 | Jungranggyo | Rain gauge | 0.74 | 0.73 | 3.30 |
| PERSIANN | 0.19 | 0.04 | 75.80 | ||
| PERSIANN-CDR | 0.30 | 0.15 | 62.50 | ||
| TRMM 3B42 V7 | 0.29 | 0.27 | 13.40 | ||
| CMADS | 0.39 | 0.30 | 21.80 | ||
| SG37 (Outlet) | Haengjudaegyo | Rain gauge | 0.70 | 0.68 | −25.90 |
| PERSIANN | 0.23 | 0.16 | 52.60 | ||
| PERSIANN-CDR | 0.18 | 0.16 | 32.90 | ||
| TRMM 3B42 V7 | 0.46 | 0.47 | −32.50 | ||
| CMADS | 0.22 | 0.32 | 14.60 | ||
| Average | Rain gauge | 0.68 | 0.64 | 0.31 | |
| PERSIANN | 0.29 | 0.13 | 64.18 | ||
| PERSIANN-CDR | 0.25 | 0.16 | 48.66 | ||
| TRMM 3B42 V7 | 0.54 | 0.49 | −8.13 | ||
| CMADS | 0.44 | 0.42 | 17.34 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, T.T.; Li, L.; Jun, K.S. Evaluation of Multi-Satellite Precipitation Products for Streamflow Simulations: A Case Study for the Han River Basin in the Korean Peninsula, East Asia. Water 2018, 10, 642. https://doi.org/10.3390/w10050642
Vu TT, Li L, Jun KS. Evaluation of Multi-Satellite Precipitation Products for Streamflow Simulations: A Case Study for the Han River Basin in the Korean Peninsula, East Asia. Water. 2018; 10(5):642. https://doi.org/10.3390/w10050642
Chicago/Turabian StyleVu, Thom Thi, Li Li, and Kyung Soo Jun. 2018. "Evaluation of Multi-Satellite Precipitation Products for Streamflow Simulations: A Case Study for the Han River Basin in the Korean Peninsula, East Asia" Water 10, no. 5: 642. https://doi.org/10.3390/w10050642
APA StyleVu, T. T., Li, L., & Jun, K. S. (2018). Evaluation of Multi-Satellite Precipitation Products for Streamflow Simulations: A Case Study for the Han River Basin in the Korean Peninsula, East Asia. Water, 10(5), 642. https://doi.org/10.3390/w10050642





