Fast Simulation of Large-Scale Floods Based on GPU Parallel Computing
Abstract
:1. Introduction
2. Methodologies
2.1. Hydrodynamic Model
2.1.1. Governing Equations
2.1.2. Numerical Method
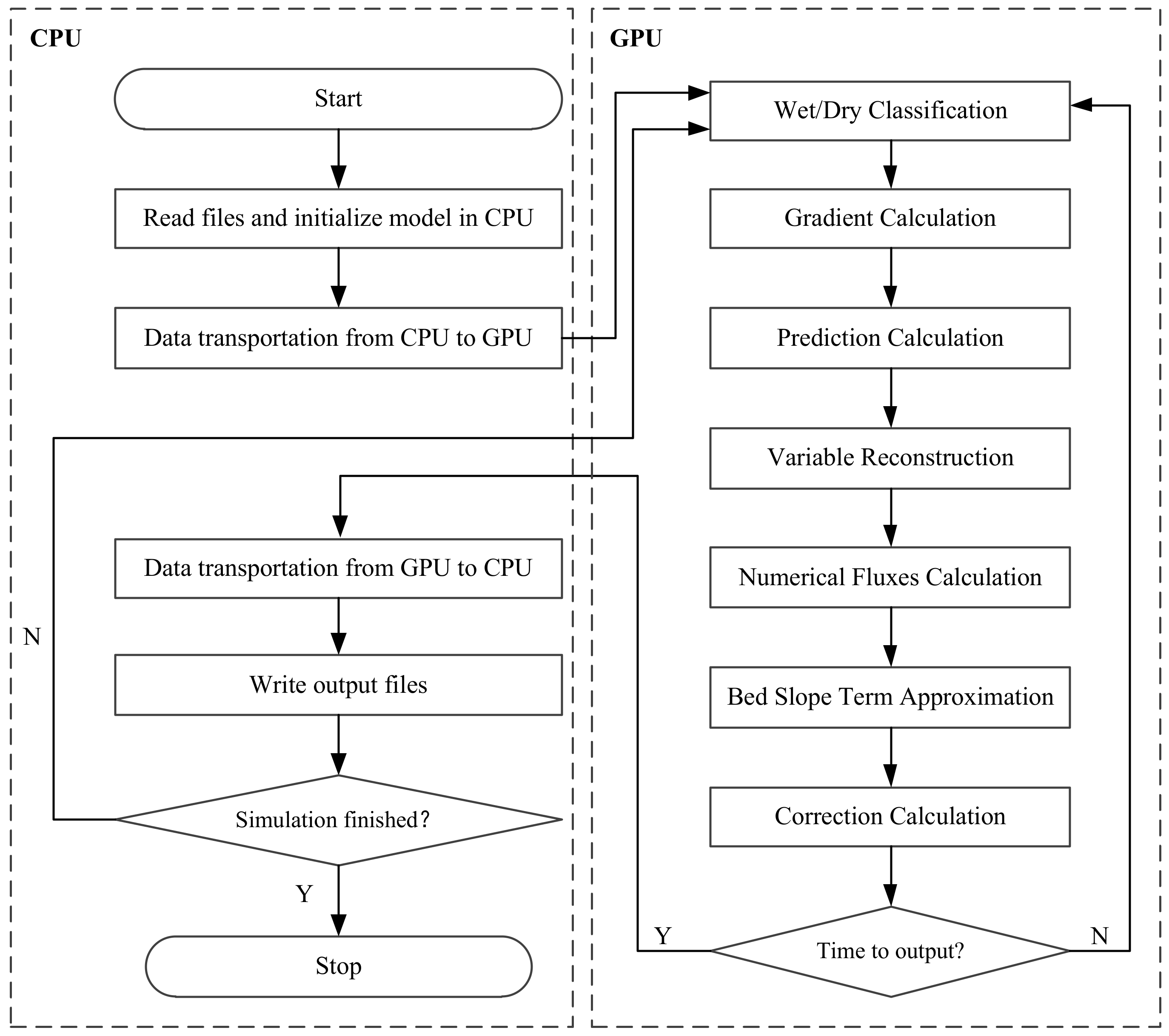
2.2. GPU Parallel Computing
3. Model Validations
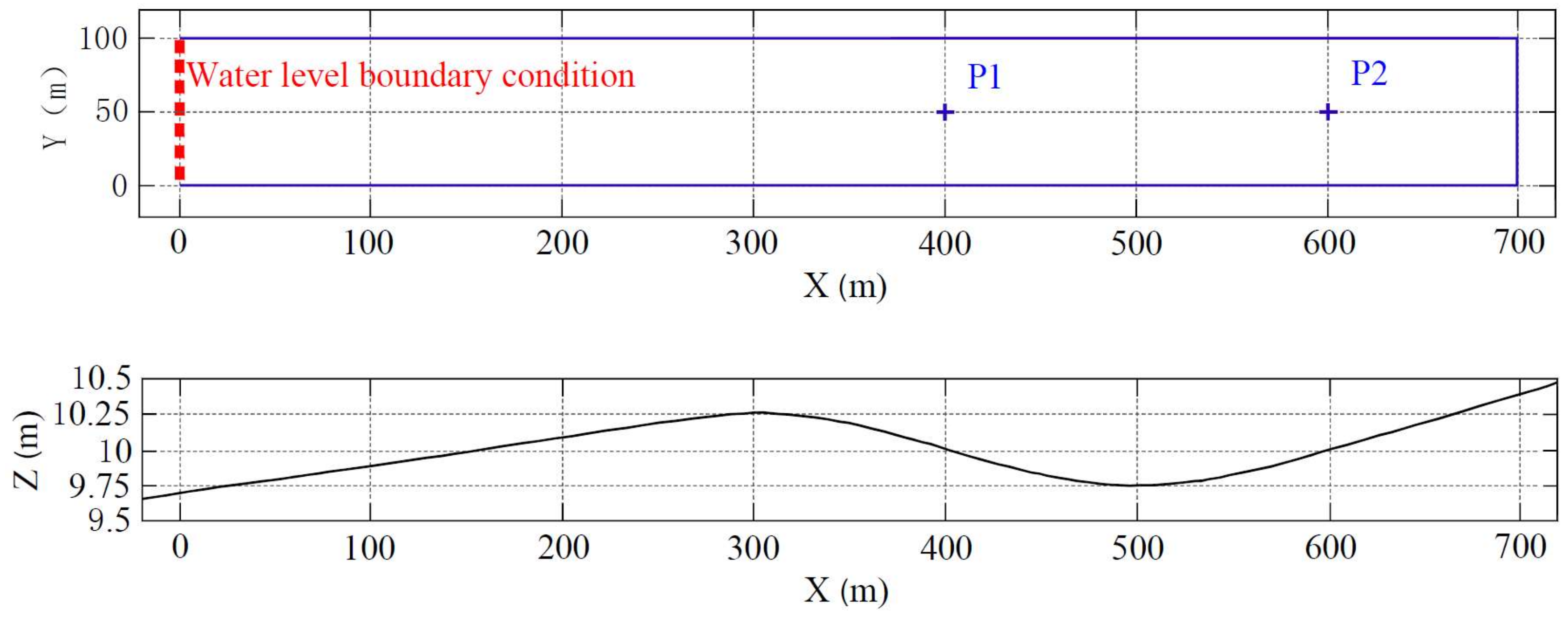
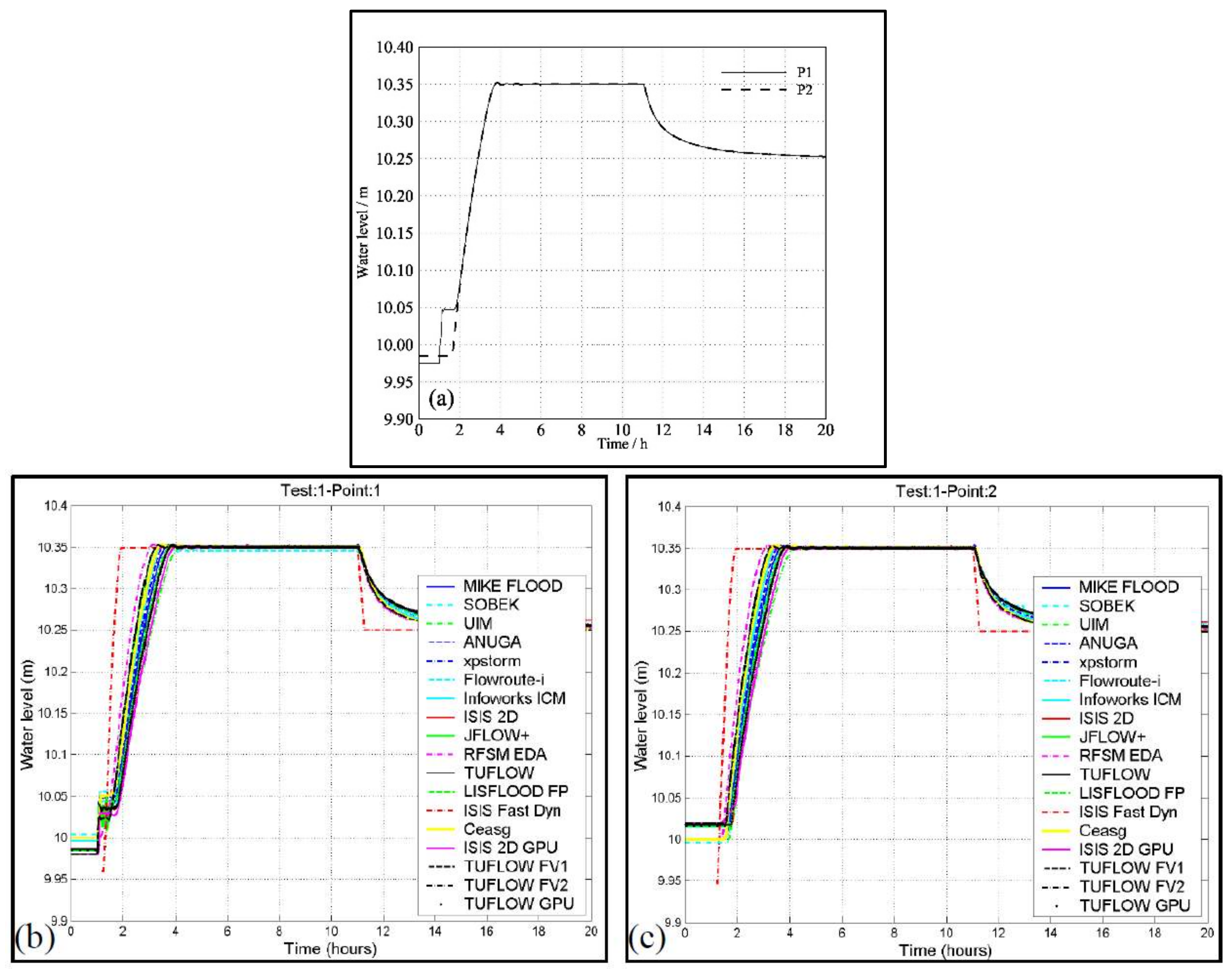
3.1. Flooding a Disconnected Water Body
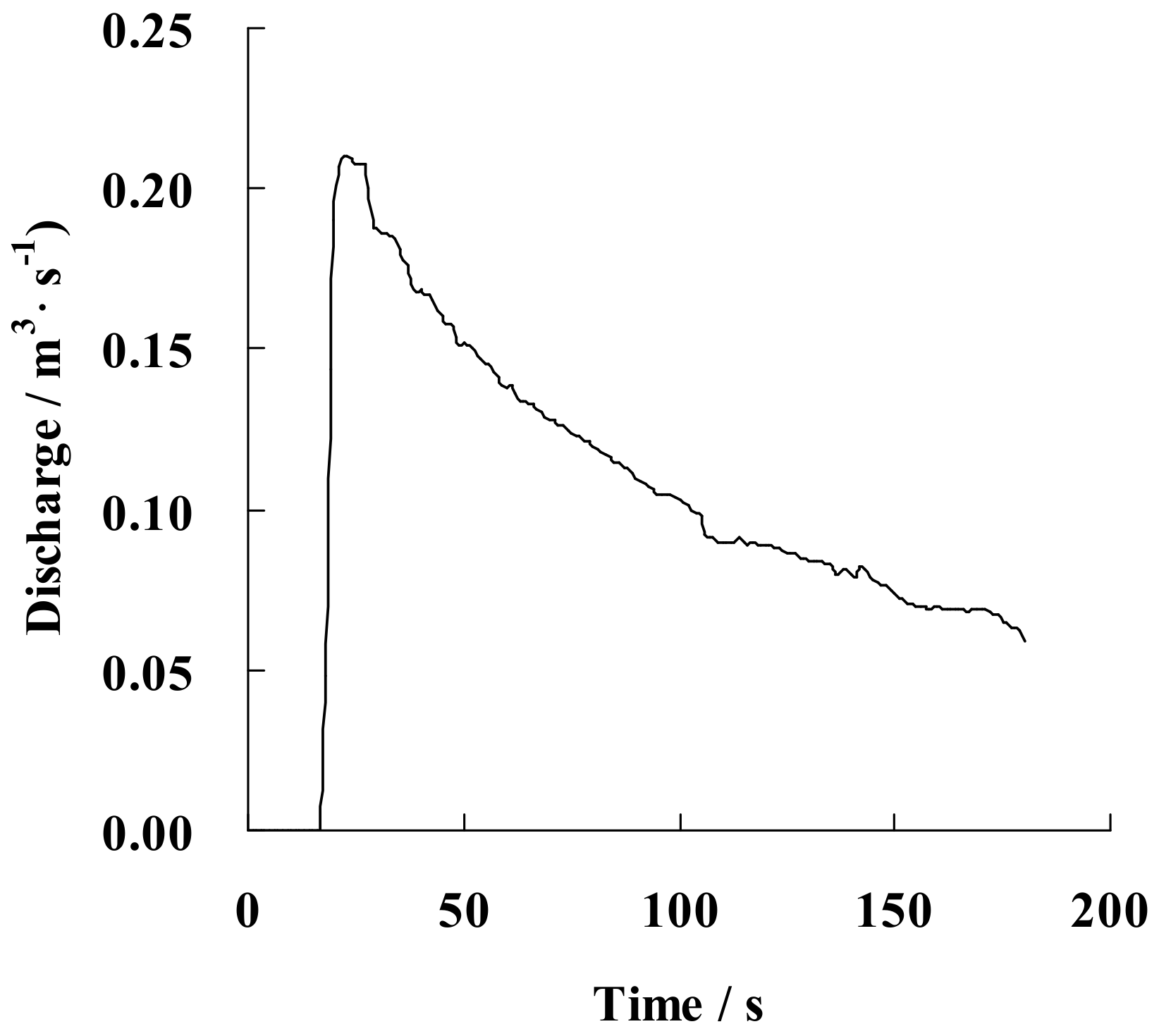
3.2. The Toce River Dam-Break Case with Overtopping
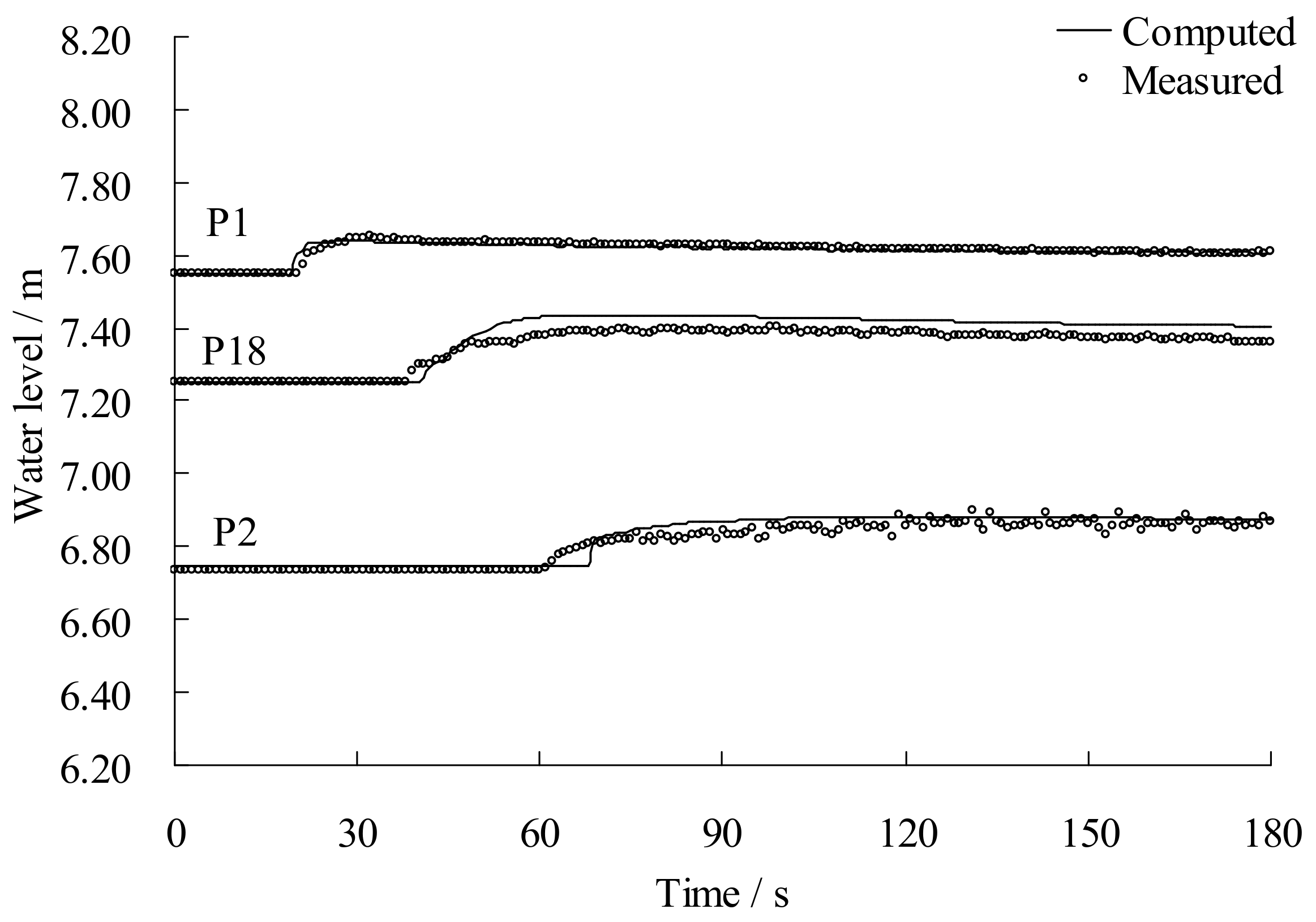
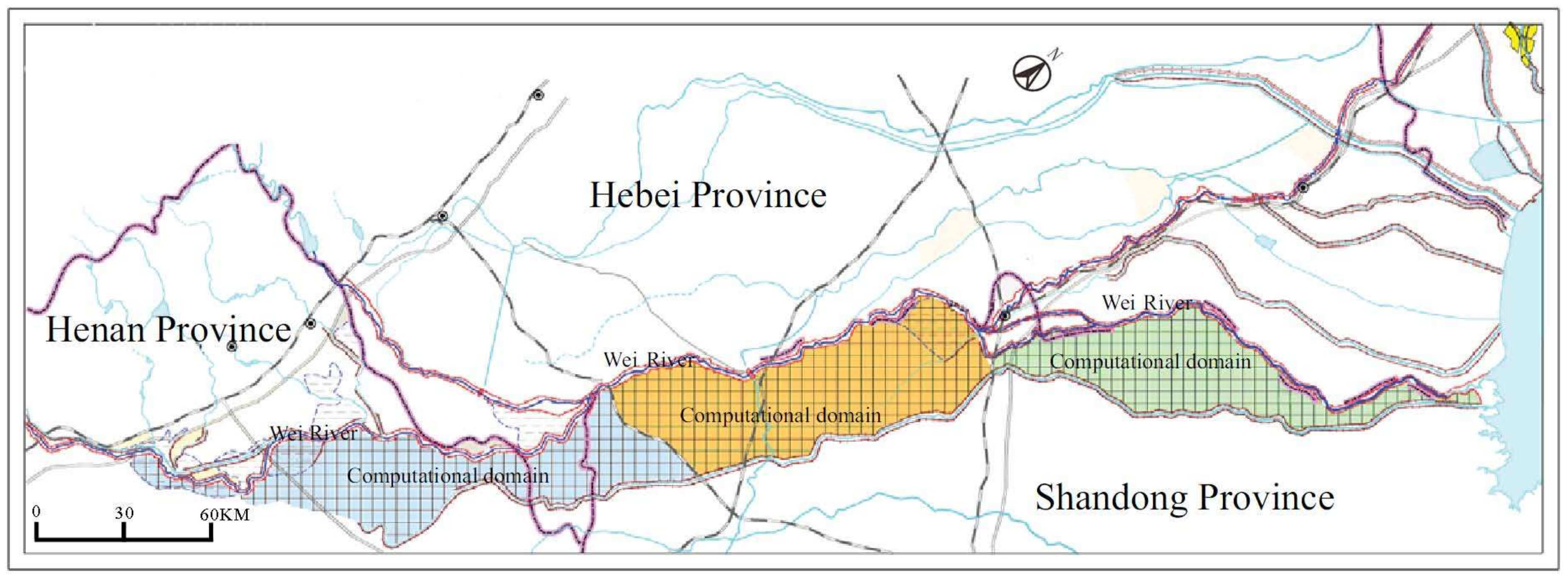
4. Case Study: A Real Flood Simulation in the Wei River
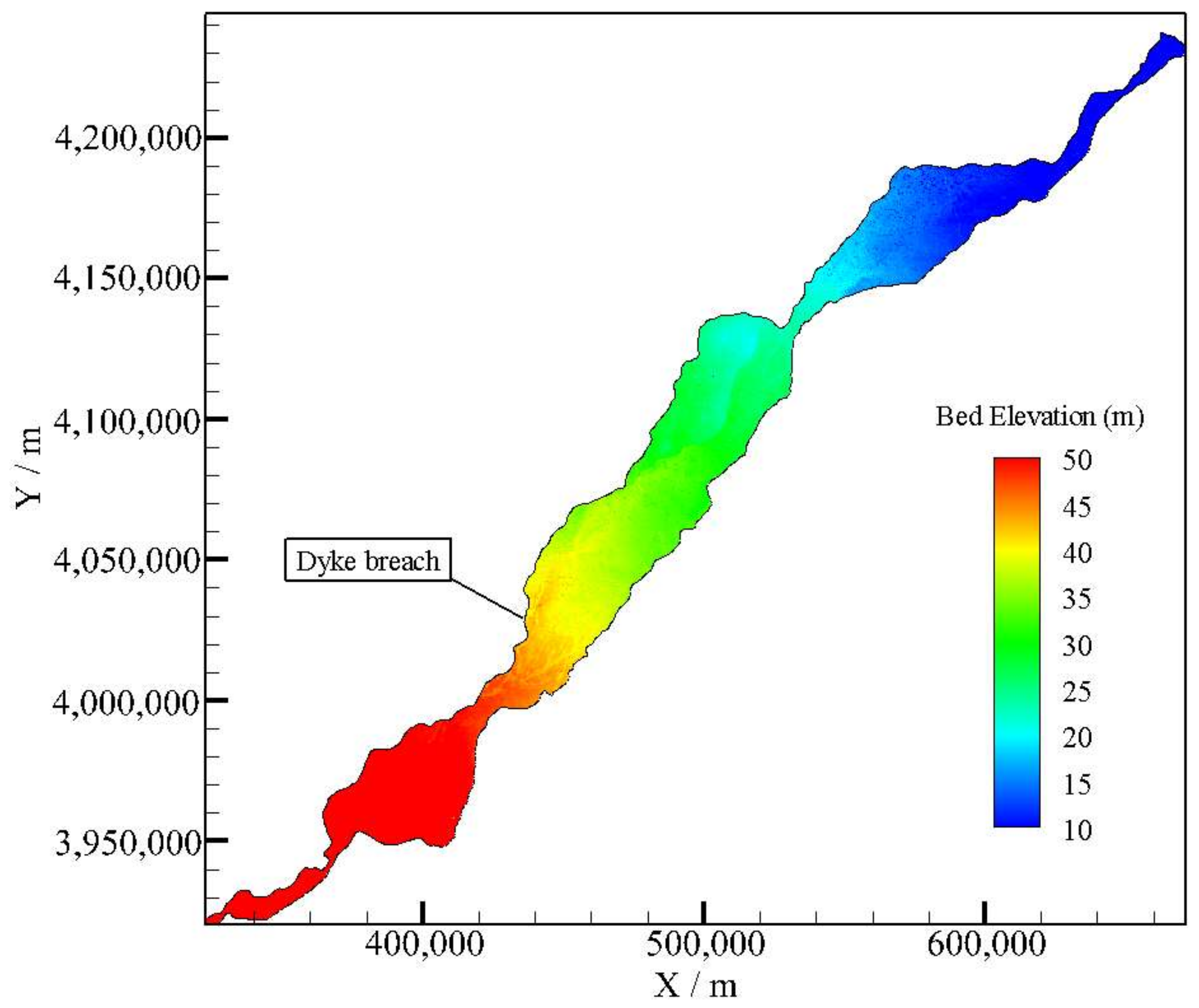
4.1. Study Area
4.2. Computational Mesh
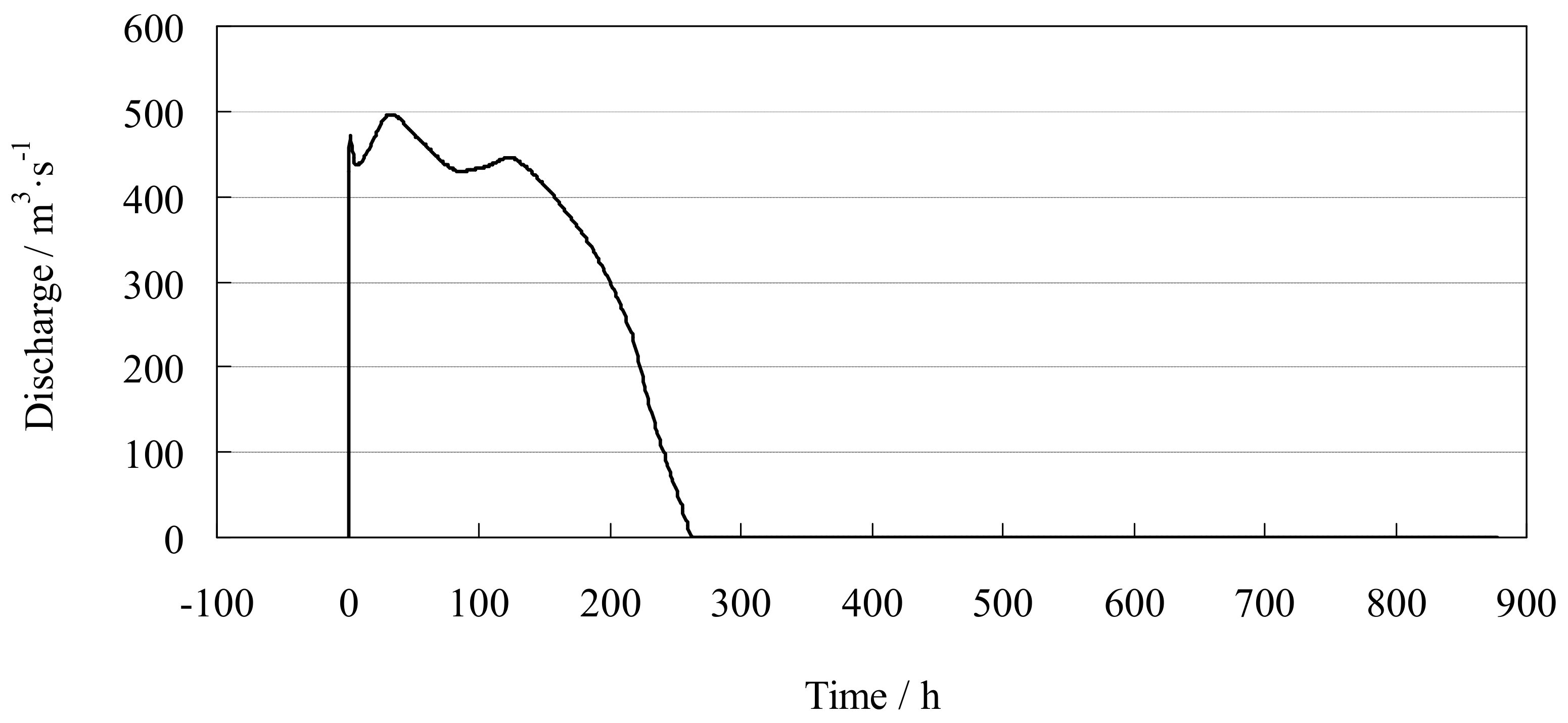
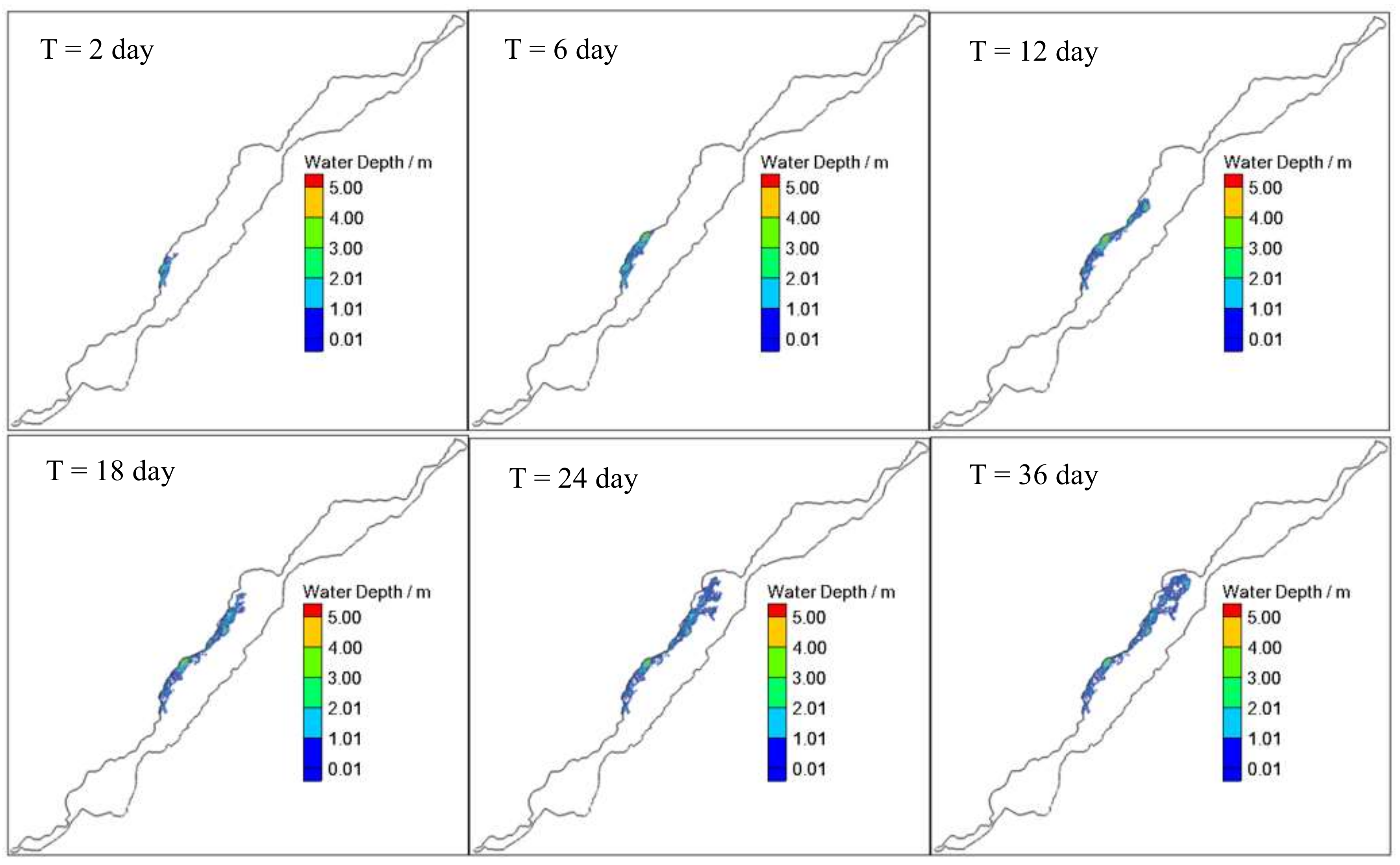
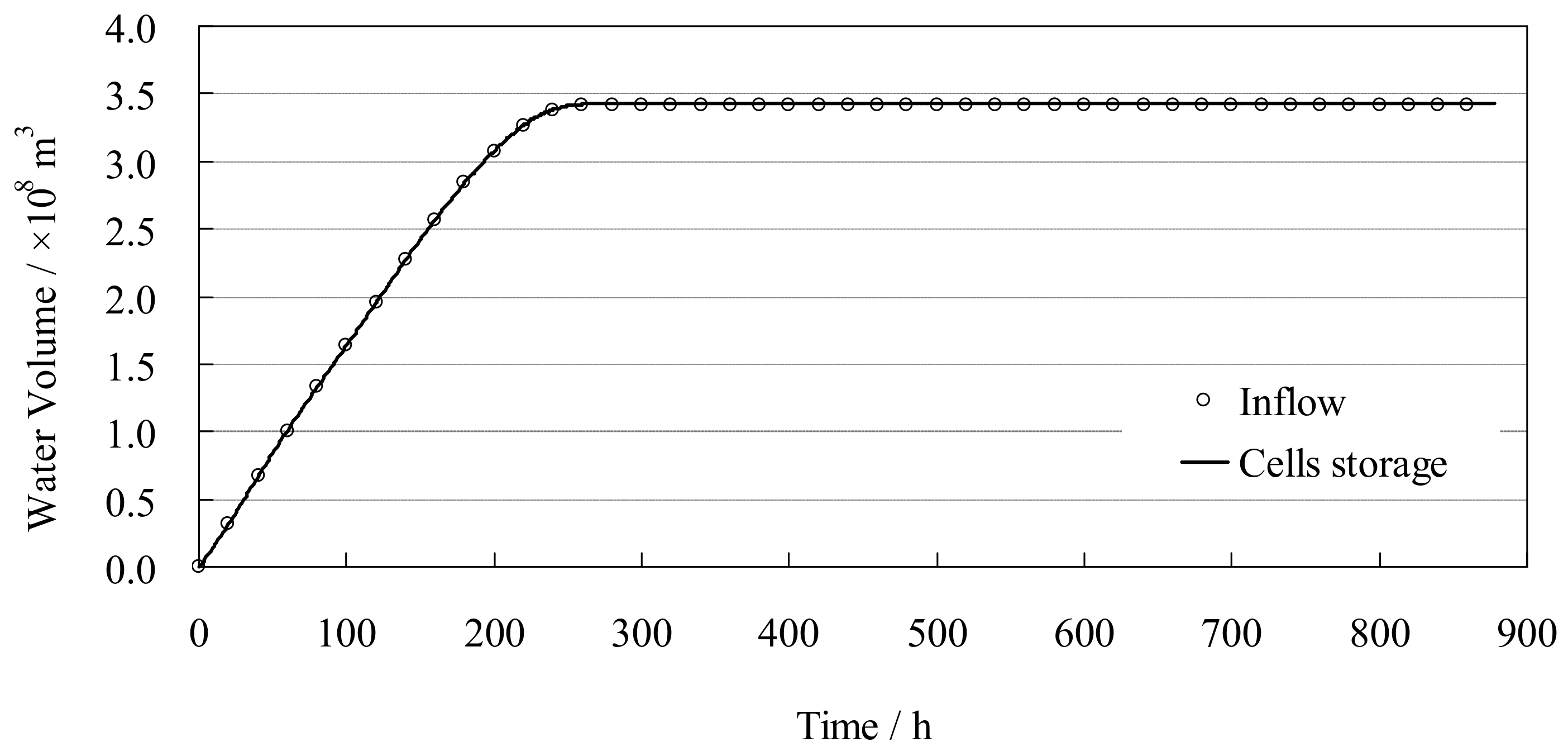
4.3. Dyke-Break Flood Simulation
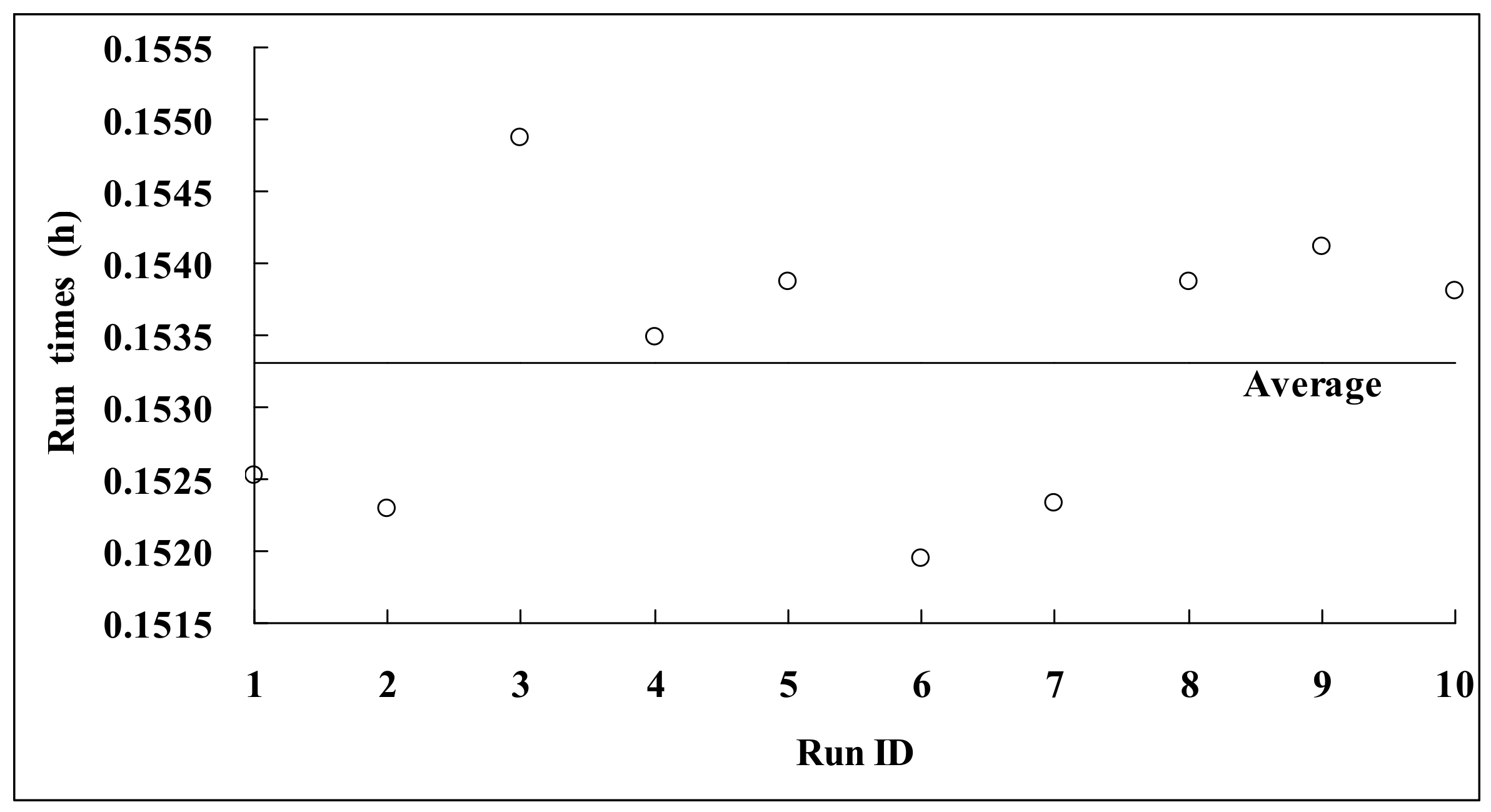
4.4. Parallel Performance Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Song, L.; Zhou, J.; Guo, J.; Zou, Q.; Liu, Y. A robust well-balanced finite volume model for shallow water flows with wetting and drying over irregular terrain. Adv. Water Resour. 2011, 34, 915–932. [Google Scholar] [CrossRef]
- Bi, S.; Zhou, J.; Liu, Y.; Song, L. A finite volume method for modeling shallow flows with Wet-Dry fronts on adaptive cartesian grids. Math. Probl. Eng. 2014, 2014, 805–808. [Google Scholar] [CrossRef]
- Wu, G.; He, Z.; Liu, G. Development of a cell-centered godunov-type finite volume model for shallow water flow based on unstructured mesh. Math. Probl. Eng. 2014, 2014, 1–15. [Google Scholar] [CrossRef]
- Liu, Q.; Qin, Y.; Zhang, Y.; Li, Z. A coupled 1D–2D hydrodynamic model for flood simulation in flood detention basin. Nat. Hazards 2015, 75, 1303–1325. [Google Scholar] [CrossRef]
- Rehman, K.; Cho, Y.S. Novel slope source term treatment for preservation of quiescent steady states in shallow water flows. Water 2016, 8, 488. [Google Scholar] [CrossRef]
- Kvočka, D.; Ahmadian, R.; Falconer, R.A. Flood inundation modelling of flash floods in steep river basins and catchments. Water 2017, 9, 705. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.-A.; Wang, M.-L.; Zhu, F.-L.; Wan, X.-Y.; Zhang, Y. A risk-based model for real-time flood control operation of a cascade reservoir system under emergency conditions. Water 2018, 10, 167. [Google Scholar] [CrossRef]
- Sanders, B.F.; Schubert, J.E.; Detwiler, R.L. ParBreZo: A parallel, unstructured grid, Godunov-type, shallow-water code for high-resolution flood inundation modeling at the regional scale. Adv. Water Resour. 2010, 33, 1456–1467. [Google Scholar] [CrossRef]
- Lai, W.; Khan, A.A. A parallel two-dimensional discontinuous galerkin method for shallow-water flows using high-resolution unstructured meshes. J. Comput. Civ. Eng. 2016, 31, 04016073. [Google Scholar] [CrossRef]
- Wang, X.; Shangguan, Y.; Onodera, N.; Kobayashi, H.; Aoki, T. Direct numerical simulation and large eddy simulation on a turbulent wall-bounded flow using lattice boltzmann method and multiple GPUs. Math. Probl. Eng. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X. Sensitivity analysis of the surface runoff coefficient of HiPIMS in simulating flood processes in a Large Basin. Water 2018, 10, 253. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, R.; Wu, Y.; Yi, Y. Parallel computation of a dam-break flow model using OpenACC applications. J. Hydraul. Eng. 2016, 143, 04016070. [Google Scholar] [CrossRef]
- Zhang, S.; Li, W.; Jing, Z.; Yi, Y.; Zhao, Y. Comparison of three different parallel computation methods for a two-dimensional dam-break model. Math. Probl. Eng. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Liang, Q.; Xia, X.; Hou, J. Catchment-scale high-resolution flash flood simulation using the GPU-based technology. Procedia Eng. 2016, 154, 975–981. [Google Scholar] [CrossRef]
- Zhao, X.D.; Liang, S.X.; Sun, Z.C.; Zhao, X.Z.; Sun, J.W.; Liu, Z.B. A GPU accelerated finite volume coastal ocean model. J. Hydrodyn. 2017, 29, 679–690. [Google Scholar] [CrossRef]
- Chen, T.Q.; Zhang, Q.H. GPU acceleration of a nonhydrostatic model for the internal solitary waves simulation. J. Hydrodyn. 2013, 25, 362–369. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, H.; Yang, R.; Dalrymple, R.A.; Hérault, A. Numerical modeling of dam-break flood through intricate city layouts including underground spaces using GPU-based SPH method. J. Hydrodyn. 2013, 25, 818–828. [Google Scholar] [CrossRef]
- Néelz, S.; Pender, G. Benchmarking the Latest Generation of 2D Hydraulic Modelling Packages; Environment Agency: Bristol, UK, 2013. [Google Scholar]
- Ying, X.; Khan, A.A.; Wang, S.S.Y. Upwind conservative scheme for the Saint Venant equations. J. Hydraul. Eng. 2004, 130, 977–987. [Google Scholar] [CrossRef]

| Model | In All | Water Depth Intervals | ||||
|---|---|---|---|---|---|---|
| 0.05–0.5 m | 0.5–1 m | 1–2 m | 2–3 m | ≥3 m | ||
| MIKE21 FM | 864.26 | 370.35 | 234.5 | 200.34 | 50.14 | 8.93 |
| The proposed model | 856.28 | 364.62 | 241.19 | 193.46 | 47.03 | 9.98 |
| Relative error (%) | −0.92% | −1.55% | 2.85% | −3.43% | −6.20% | 11.76% |
| Mesh Type | Grid Number | Average Grid Area (m2) | TCPU (h) | TGPU (h) | S | TS (%) |
|---|---|---|---|---|---|---|
| Mesh-1 | 179,296 | 53,000 | 1.70 | 0.15 | 11.3 | 91 |
| Mesh-2 | 717,184 | 13,250 | 10.69 | 0.62 | 17.2 | 94 |
| Mesh-3 | 2,868,736 | 3313 | 86.72 | 2.79 | 31.1 | 97 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Qin, Y.; Li, G. Fast Simulation of Large-Scale Floods Based on GPU Parallel Computing. Water 2018, 10, 589. https://doi.org/10.3390/w10050589
Liu Q, Qin Y, Li G. Fast Simulation of Large-Scale Floods Based on GPU Parallel Computing. Water. 2018; 10(5):589. https://doi.org/10.3390/w10050589
Chicago/Turabian StyleLiu, Qiang, Yi Qin, and Guodong Li. 2018. "Fast Simulation of Large-Scale Floods Based on GPU Parallel Computing" Water 10, no. 5: 589. https://doi.org/10.3390/w10050589
APA StyleLiu, Q., Qin, Y., & Li, G. (2018). Fast Simulation of Large-Scale Floods Based on GPU Parallel Computing. Water, 10(5), 589. https://doi.org/10.3390/w10050589





