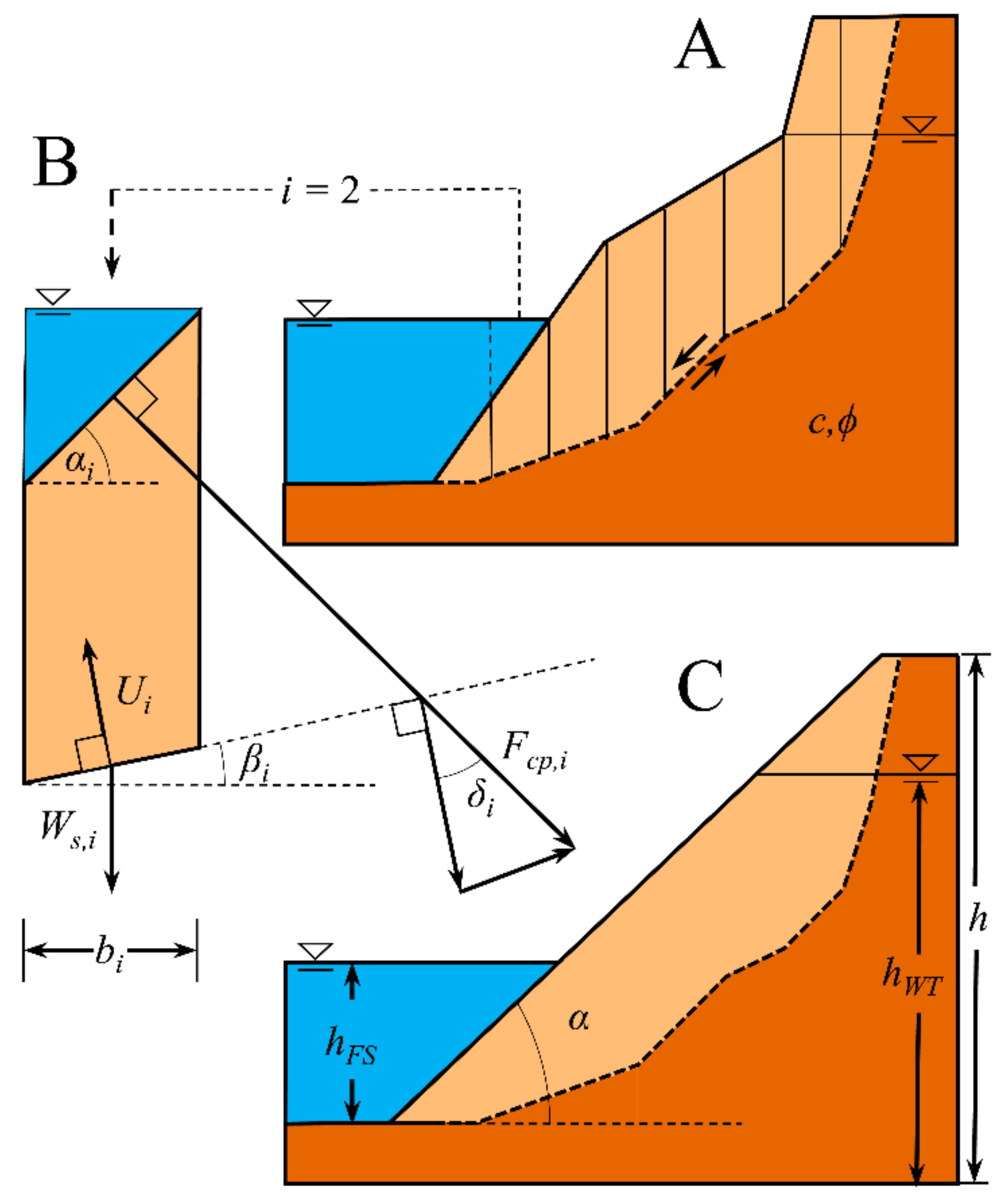
1. Introduction
Despite increasing reliance on numerical modelling to simulate flow hydraulics, sediment transport, and bank erosion in rivers [
1,
2,
3,
4], several challenges remain when investigating natural channels. These are attributed to the complexity and spatial heterogeneity of processes related to soil properties, bank morphology, hydrology, and riparian vegetation [
5,
6].
Knowledge gains on lateral adjustments in natural channels have often emerged from studies undertaken at the scale of a single bank or river reach (e.g., [
7,
8]). The manner in which findings are presented in these studies may give the impression that alluvial river channels are affected in a similar way by external forces, independent of their scale and biophysical context. For instance, generalizations have been made such as soil cohesion increasing river bank stability [
2,
9] or vegetation stabilizing banks due to mechanical reinforcement [
10,
11,
12]. On the contrary, the surcharge imposed by mature trees on a river bank can have a destabilizing effect [
13], in particular during the falling limb of a hydrograph [
14]. However, because each finding likely applies to limited river contexts (i.e., similar to the river from which they were drawn), the relative importance of biophysical variables may in fact differ considerably between river channels [
15]. Given the diversity of soil characteristics and heterogeneity of the floodplain with respect to biophysical conditions [
16], there is an urgent need to develop tools that can be used with ease to evaluate the evolution of a diversity of alluvial and semi-alluvial river reaches [
17].
In the last 10‒15 years, several laboratory studies have examined the role of vegetation on increased cohesion in meander formation (e.g., [
18,
19,
20]). Previous laboratory studies also used cohesive substrate, such as clay (e.g., [
21,
22,
23]). However, most modelling (e.g., [
4,
24]) and flume-based studies (e.g., [
25,
26]) on meandering rivers involve sand beds and banks, whereas the meandering process typically occurs in cohesive floodplains [
27]. In particular, the mechanisms responsible for the development of meandering channels in a laboratory channel (e.g., [
2]) may differ from those observed in nature, even if these channels share similar physiological traits. In addition, model validation is often achieved broadly with respect to visual elements captured using airborne imagery, such as channel planform and dynamics (e.g., [
28,
29]), with only a few modelling parameters representing the broad characteristics of soil and vegetation cover. For instance, bank material can be attributed to an erodibility coefficient [
28], while plants are represented by a density value. The problem of how transferrable findings obtained at a given scale for a particular river type are to other channels remains scarcely documented. For example, are the key physical parameters contributing equally to bank stability in all river contexts? Very few studies have attempted to calibrate a model against data from a natural river channel/floodplain to help answer this question ([
30,
31,
32] being exceptions), and none, to the best of our knowledge, have compared parameter values between river channels. This could be attributed to weaknesses in the physics behind meander dynamics models, which do not take into account channel morphology (including bars) and vegetation [
33]. It may also be related to the substantial computational power required by these models [
34] and to the scarcity or incompleteness of field datasets, owing to limitations in financial resources, time, available technologies, and data accessibility [
35,
36]. This is particularly the case for bank retreat models [
31].
River bank retreat involves a sequence of processes operating simultaneously at different timescales [
37,
38]. For example, bend migration process is generally associated with periods that are much larger than that of the flow [
39]. Indeed, river banks are subject to slow transformations involving tension cracking [
40], basal erosion by the flow [
41], and riparian vegetation cover [
42,
43] and assemblage [
13]. Bank failures occur as soon as bank strength drops below a critical value. From a modelling point of view, this duality is challenging, and it has been addressed by at least two contrasting approaches. A linear framework—relying on near-bank excess velocity and an empirical representation of bank resistance (known as the HIPS formulation, from [
44,
45])—makes it possible to examine channel dynamics at long spatiotemporal scales (e.g., [
46]). However, the consideration of basic flow and soil properties (velocity, cohesion), combined with the lack of a groundwater hydrology model and the impossibility to take into account complex channel and floodplain bathymetry [
33,
47], are serious limitations when analysing lateral retreat along natural river channels [
16]. A second popular approach is the use of enhanced computational fluid dynamics (CFD) models (e.g., [
4,
5,
31]). The primary limitations of this approach are that it is computationally demanding and applicable to short spatiotemporal scales. They are also usually designed for curvilinear meshes (e.g., [
48,
49]), which often prevents their use with multithreaded channels [
50].
This paper compares the sensitivity of river bank retreat to geotechnical parameter values between two natural river channels of different scale and geomorphological contexts in Quebec and Ontario (Canada). Both modelling investigations were undertaken with the hydrodynamic solver TELEMAC-2D [
51] and sediment transport solver SISYPHE [
52] from the suite open TELEMAC-MASCARET [
53] v7.0. They were coupled to a physics-based geotechnical module that considers a broader set of soil properties than is commonly included in most bank erosion models [
54]. This research was based on three methodological novelties: (i) the use of a coupled CFD–geotechnical numerical model to examine the morphodynamics of a multithreaded river reach at the kilometre scale, (ii) the use of sedimentological and bathymetric data to calibrate models of river bank retreat, and (iii) the inclusion of groundwater hydrology into a coupled CFD–geotechnical numerical model and study. These lad to two main novel applications: (i) the identification of a set of biophysical conditions that fit observations of bank retreat for two different natural river channels, and (ii) a comparison of simulated bank retreat evolution between two natural river channels of different scales and geomorphological contexts.
4. Discussion
The two conceptual novelties of this study are the identification of a set of biophysical conditions that fit observations of bank retreat for two different natural river channels, and a comparison of simulated bank retreat between two natural river channels of different scales and geomorphological contexts.
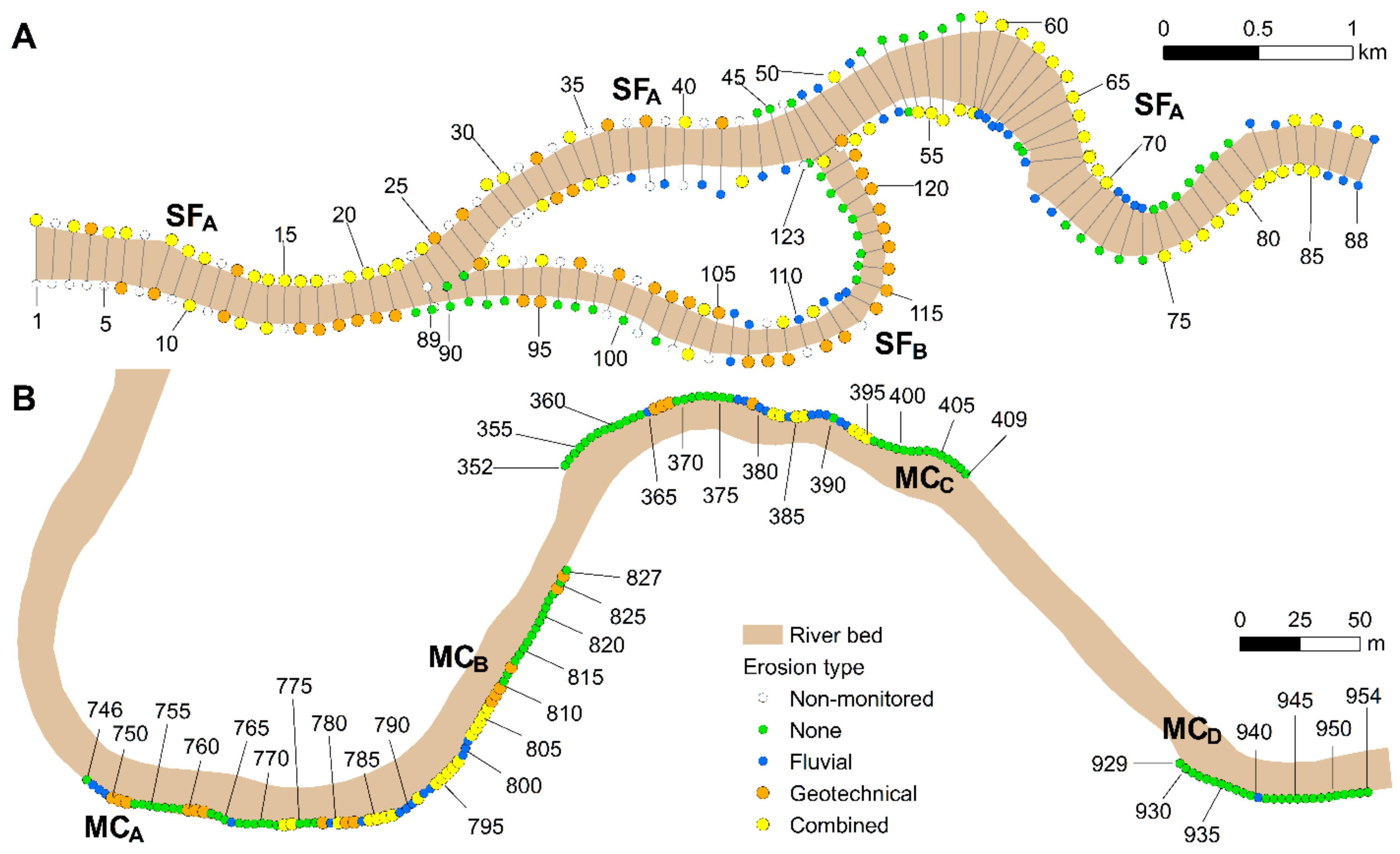
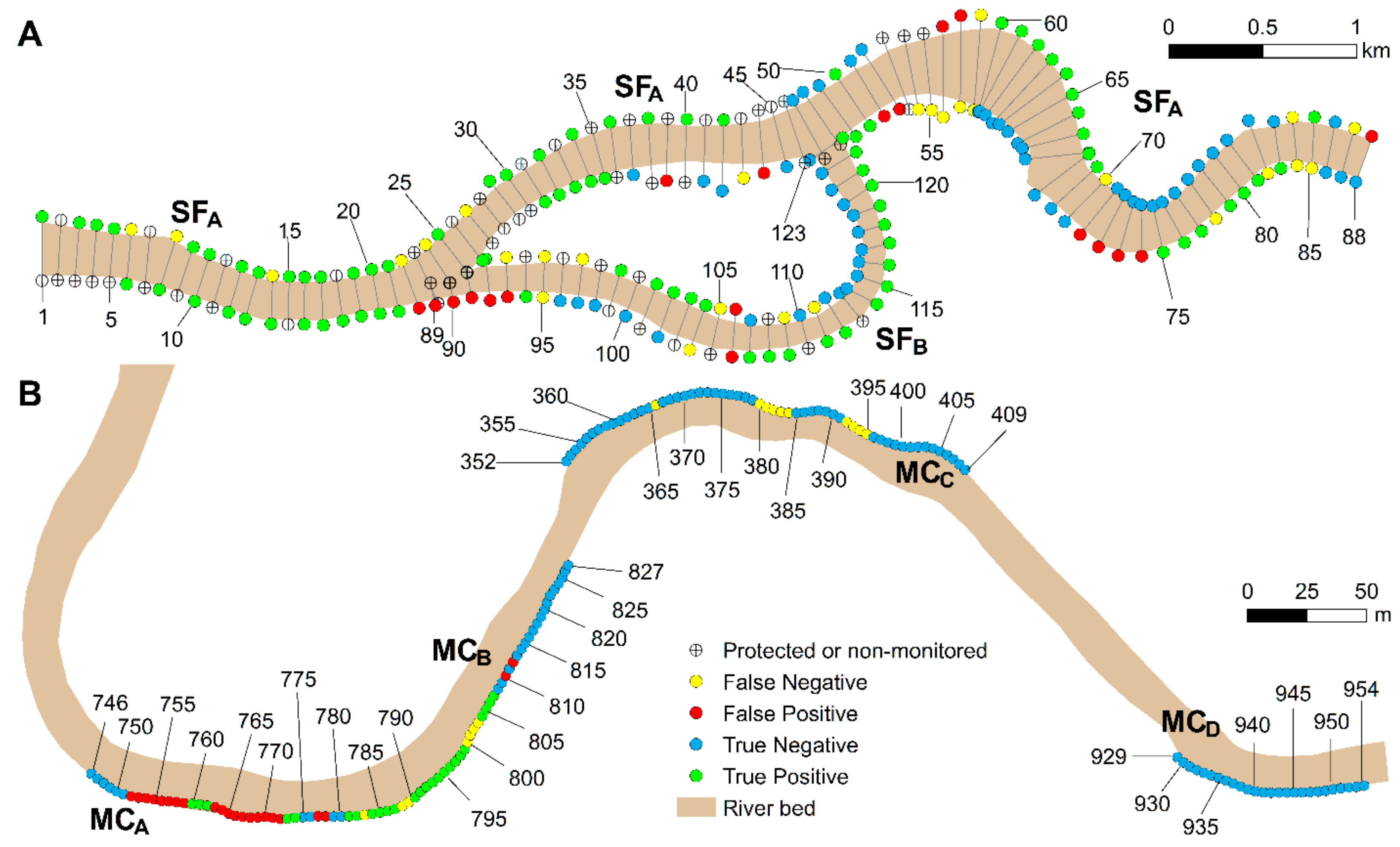
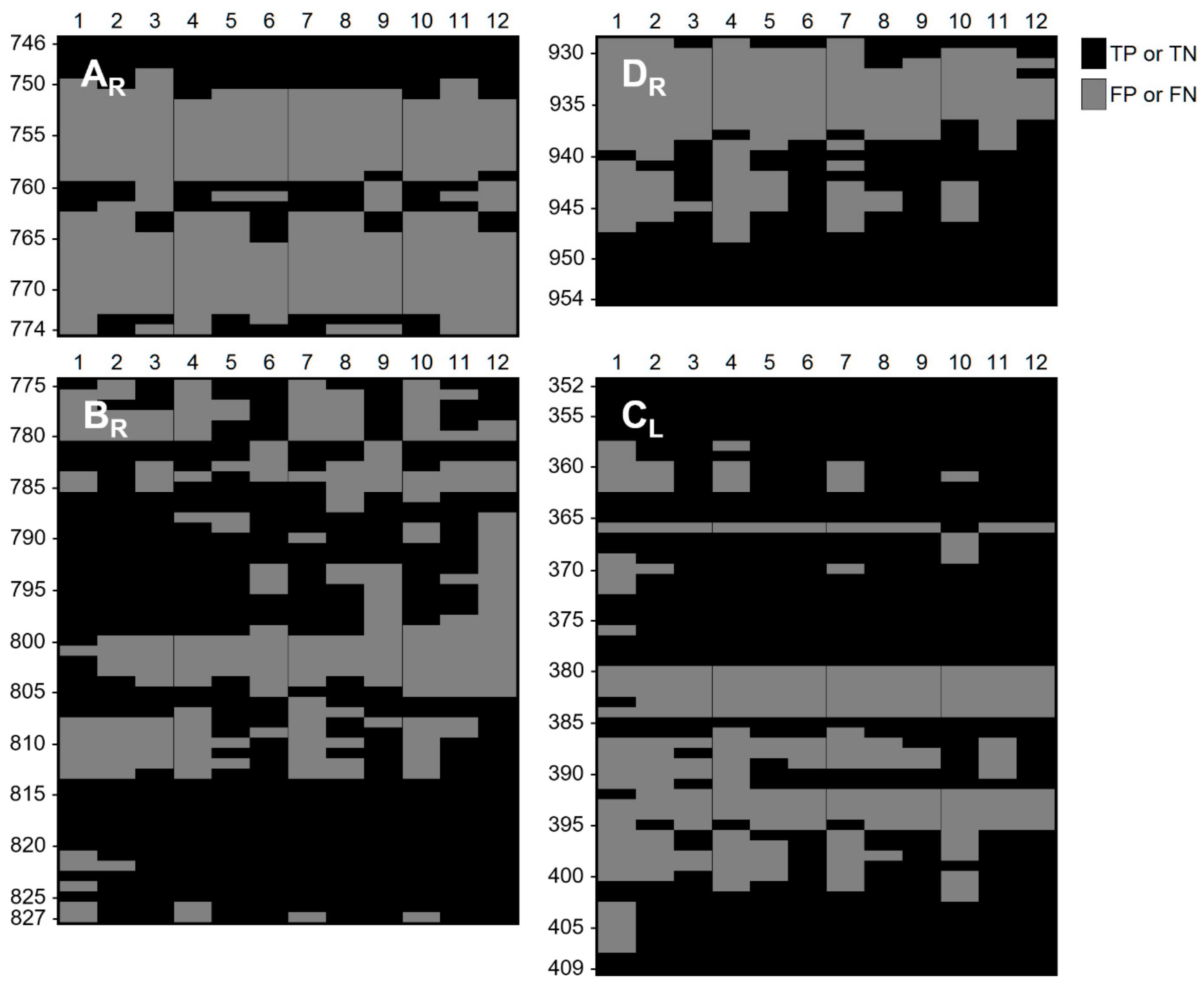
The fact that the biophysical parameter values producing the best fit between observed and simulated bank retreat at site MC varies between sub-reaches suggests a variation in bank material composition over a relatively short distance. Indeed, each sub-reach at MC exhibits distinctive texture and layering (
Figure 10). In sub-reach B, a sandy layer overlays glacial till, which also forms the channel bed. In sub-reach D, sediments are more thoroughly mixed vertically. Conversely, the analysis of two soil columns by [
55] revealed a vertical profile consisting primarily of sand, but separated by a few silty sand, sandy silt, and silt layers. The greater uniformity of bank material in the latter case may explain that a stronger fit was obtained for SF (
J = 50.2 in
Table 9) than for MC (
J = 22.5 in
Table 8). Note that the presence of sedimentary strata was not considered in the model. The cohesion values that maximize model fit with river bank evolution at study sites are at least one order of magnitude lower than those commonly encountered in nature despite the fact that the model’s ability to quantify stability was a priori tested against known problems of translational and rotational failures. For instance, [
55] measured a cohesion of 13 kPa at the toe of a bank at SF (for a silty sample), which is ~100 times larger than the value associated with the parameter set that produced the best fit (
Table 9). This seems to indicate that the model, even if it is physics-based, does not take into account a number of aspects of natural river banks that contribute to bank failures. The analysis of relatively homogeneous soil samples free of tension cracks in a laboratory may overestimate the overall strength of bank material found in nature. Finally, the fact that the observed lateral retreat corresponds to a timescale (2 and 3 years, respectively, for SF and MC) much larger than the simulation time (8 and 2.75 h, respectively, for SF and MC) may explain why a reduced cohesion value is required for the simulation outcome to fit observations.
A marked difference in the cohesion value that maximizes fit was noted between MC sub-reaches (
Table 7 and
Table 8). This may, at least partially, be attributed to the mechanical effects of the plant cover, which are lumped into the soil cohesion parameter. The model did not introduce spatial variations in soil characteristics; cohesion was identical at all nodes but varied between simulations. In natural rivers, the vertical variation in root density is such that the apparent cohesion is greater in the upper soil layer for several species [
74,
75], whereas the distribution of plant species and assemblage introduces a horizontal variation in soil strength, even assuming homogeneous soil material [
13]. The most unstable sub-reach at MC is B; it is densely vegetated but associated with the lowest cohesion value (
Table 8). At this location, the removal of vegetation by floods, combined with the surcharge imposed by mature trees, seems to have triggered bank retreat. Conversely, sub-reach D is associated with the highest cohesion and friction angle (
Table 8), perhaps owing to a vegetation stand consisting of herbaceous plants and young trees (
Figure 10d), offering enhanced cohesion for little surcharge. However, an exposed bank section (upstream of the location shown in
Figure 10d) was very stable during the observation period. Therefore, riparian vegetation seems to have a greater effect on bank stability in sub-reach B, even if it is less than 500 m away from sub-reach D. Similarly, spatial variations in root reinforcement may be responsible for the large number of false positives obtained in sub-reach A of site MC (transects 752‒772). This steep bluff is topped by mature trees that may prevent its collapse. Failures have been observed in this area (
Figure 10), but they are usually limited in extent to the area around a tree trunk falling off the bluff. For this sub-reach, the parameter set associated with the strongest agreement indicates that soil is moderately cohesive (
c = 0.5) in this sub-reach, compared to sub-reaches B and D.
A better fit with observations is obtained by associating a set of parameter values to each river bank segment or floodplain patch with homogeneous biophysical conditions (soil characteristics, vegetation assemblage, etc.). For instance, the best overall fitness climbs from
J = 22.5% to 41.8% for MC when considering the best parameter set at each sub-reach (A, B, C, and D). For SF, Youden’s
J only increases by 5.3% when varying parameter values spatially, which suggests more homogeneous soil characteristics at the SF field site, relative to MC. The suggestion to integrate floodplain heterogeneity into planform evolution models [
26] would not only serve in improving the fit between observations and simulation results but would make the model more independent of input parameter values; the parameter set would remain valid throughout a simulation. However, care is required to avoid overfitting a model, which would otherwise compromise its capacity to be validated against a second dataset. Here, the possibility of overfitting comes from the fact that soil cohesion, despite the physics basis of the model, still represents the combined effect of at least two components, namely, soil and vegetation. This model characteristic would render the model less representative of the system with time if vegetation cover was to change. More work on complex river systems such as MC is needed to determine if, for practical purposes, a reduced complexity modelling approach would be more appropriate; it may not be realistic to attempt gathering biophysical data at the level of details required to obtain an acceptable fit.
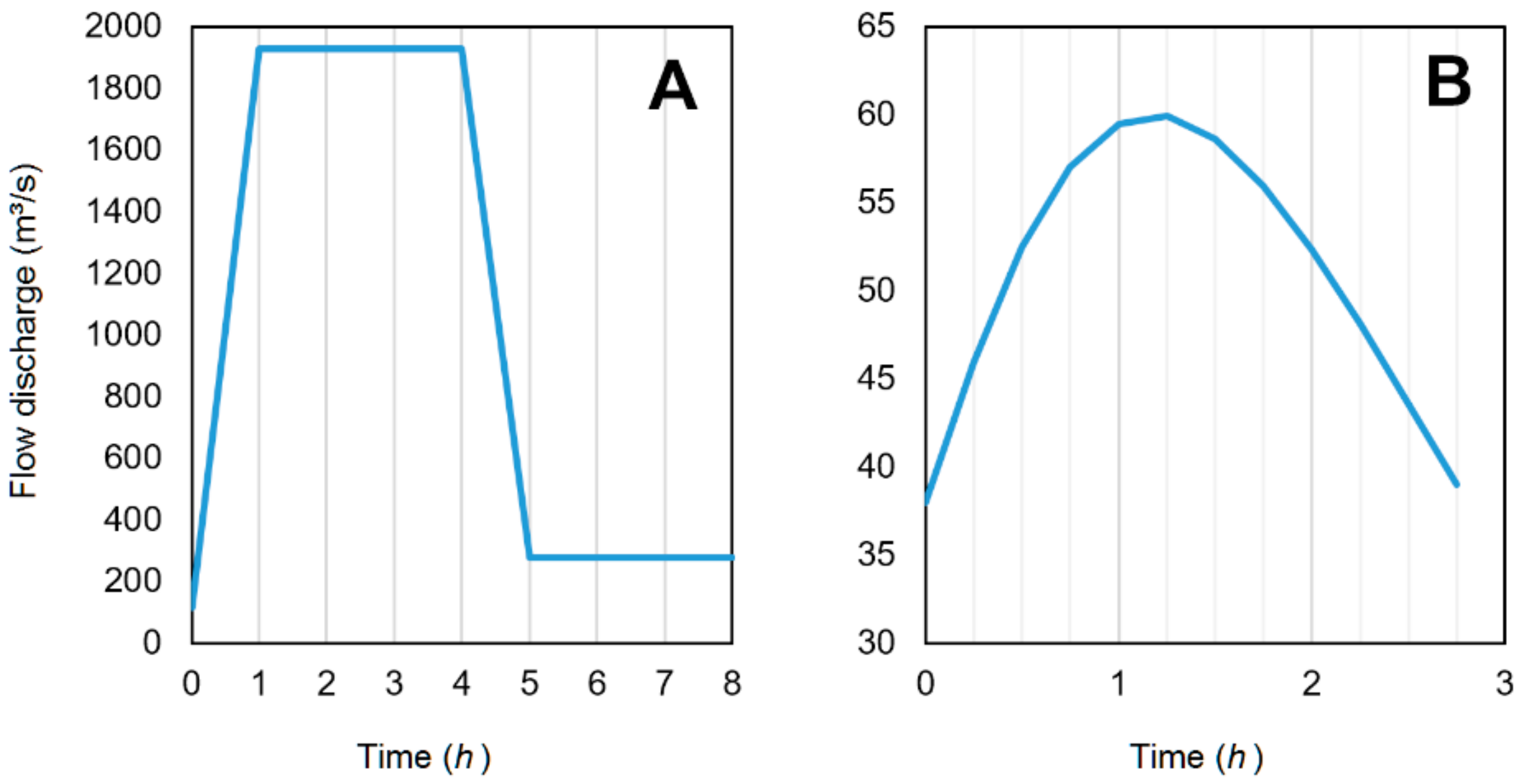
Downstream conditions also differ between the sites. Both the inlet and outlet of the MC site are directly related to flow discharge. However, although the free surface at the inlet of SF is also related to the imposed flow discharge, the second half of the reach depends on the level of the St. Lawrence River in which the SF river drains. The selected free surface elevation at the outlet of this domain corresponds to the elevation recorded at a gauging station during the simulated event. During the observation period, a large number of combinations of inlet-outlet free surfaces have been encountered, but a single one of these combinations is examined in this study. We acknowledge that the differences in imposed hydrographs and boundary conditions between sites SF and MC, arising from the differences in scale and location of the sites compared, may affect results. However, free surface elevation (
hFS) and water table elevation (
hWT) were found to be less influential than geotechnical parameters (
Table 6). It is thus unlikely that selecting a different event would have led to significantly different results. In addition, a good fit was obtained with respect to bank retreat for site SF.
One of the most important limitations of the coupled model is that it assumes that water table adjusts solely as a function of variations in the free surface of the flow. By doing so, it neglects the fact that banks may be fully saturated. This situation may explain the presence of false negatives between transects 380‒395 at site MC. The area north of sub-reach
C is partially submerged during the spring due to snowmelt, and a pond drains to the river by the remnants of a meander bend that was abandoned prior to 1942 (entering the floodplain at transects 377‒384 and exiting at transects 403‒410 and beyond) (
Figure 6 and
Figure 10c). It is quite possible that the disagreement between simulated and observed failures in this area be attributed to the lack of a physics-based hydrological component that can be set up to consider realistic water table elevations across the floodplain. The presence of vegetation at the field site during failure events could have been detrimental when the soil was saturated, the mechanical effects of plants being outweighed by hydrological effects, as suggested by [
16]. Therefore, the fact that soil moisture content did not vary longitudinally along the bank according to preferential groundwater flows in the coupled model may have contributed to overestimating bank stability.
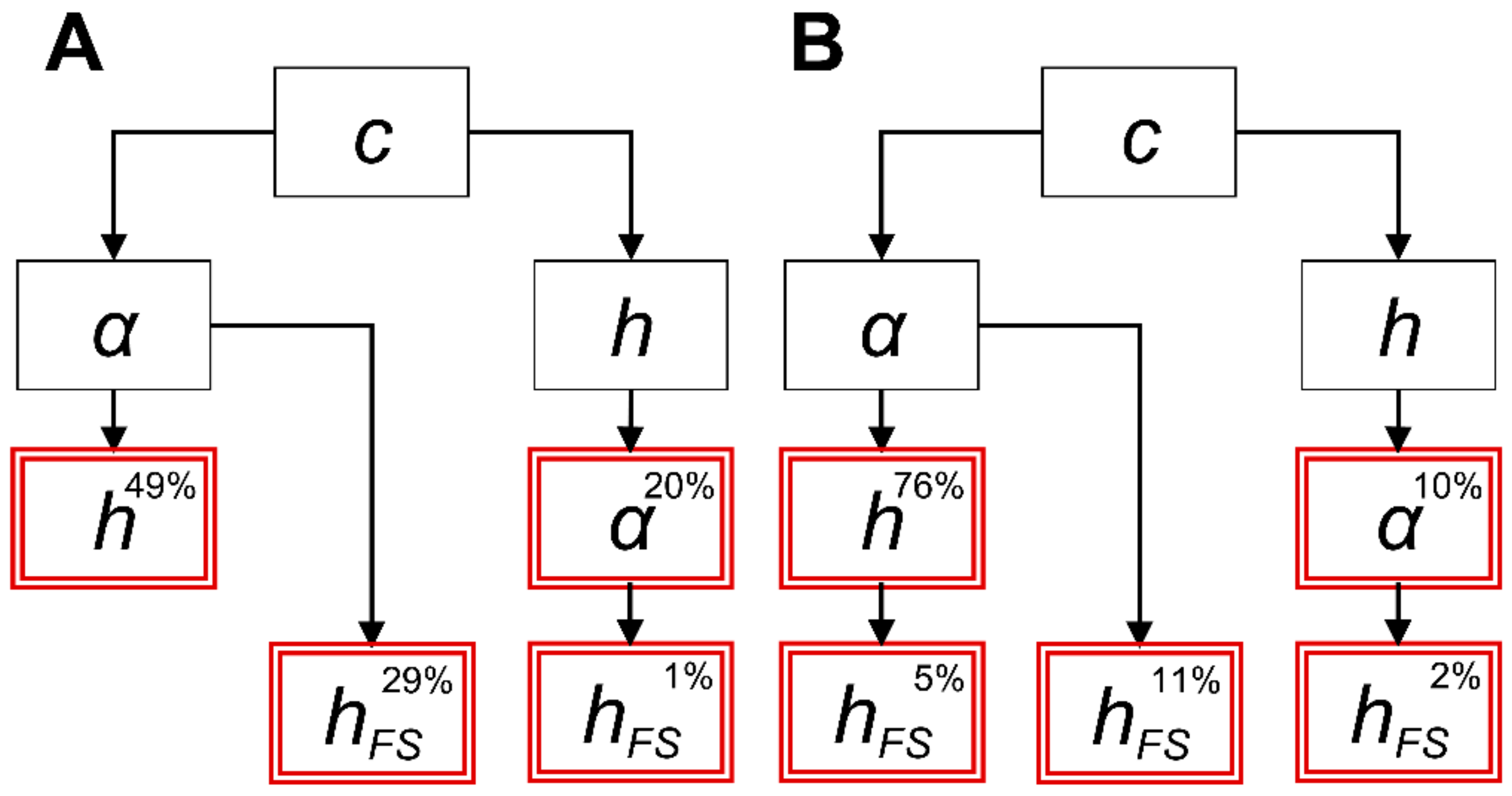
Calibrating a morphodynamic model can be time consuming, and detailed field data on bank retreat are seldom available. The integration of a geotechnical module, combined with large uncertainty regarding the value of geotechnical parameters to be used for a field site, renders the process more tedious as a larger number of trial simulations needs to be run to adjust model outcomes to observations. Here, a statistics-assisted calibration based on tree classification was completed to determine the range of parameter values leading to a safety factor near unity. Similar agreements were obtained with the geotechnical stability (without bank retreat) model and coupled model (with bank retreat) (see
Section 3.4), which seem to indicate that initial channel bathymetry and biophysical conditions can be sufficient to estimate the location of bank retreat, without the need to consider hydrodynamics and sediment transport. However, caution is required, as these two model types generated slightly different parameter values (see
Section 3.4). This difference could be attributed to the lag effect between water table and free surface elevations and to the consideration of complex bank morphologies by the coupled model. In contrast, water table elevation is equal to the free surface elevation, and bank profile is always straight with the geotechnical stability model. The coupled model also allows for one or several subsequent failures to occur in different portions of the slope. A potential application of machine learning algorithms would be to allow the geotechnical module to recognize and use the rules emerging from a decision tree directly into a coupled model. This would substantially reduce computation time. The module would remain partially physics-based, as the rules would have been pre-established using the geotechnical module.
5. Conclusions
This study sought to identify the most sensitive parameters in a morphodynamic model capable of taking into account mass wasting in a physics-based manner, and to verify whether the sensitivity to key geotechnical parameters differs between two contrasting fluvial environments. Our results indicate that lateral erosion is very sensitive to soil cohesion and friction angle and, to a lesser extent, to mass density of the bank material. A few combinations of these parameters resulted in a good agreement between simulation results and field observations, particularly in the alluvial St. François River case, where biophysical parameters of river banks and floodplain are more homogeneous. However, the agreement with field observations, and thus sensitivity, varies substantially from a parameter set to another, between sub-reaches, and between the two study sites. Sensitivity was also greater in some sub-reaches of the more complex semi-alluvial channel of Medway Creek.
The secondary objective was to devise a calibration method adapted to morphodynamic modelling that requires running as few simulations as possible. A pre-calibration phase, which used tree classification, and based on the assumption that the combined selected parameters values must bring the safety factor near unity, was used to estimate parameter values that are likely to result in an agreement with field observations. An iterative process was then used to run morphodynamic simulations within the coupled model, each time slightly varying the value of key geotechnical parameters in order to explore model behaviour and to improve fit with observations.
The primary implication of the substantial degree of sensitivity found at both field sites is that morphodynamic models must account for spatial variations in geotechnical properties along a channel and must be reductionist enough to describe the complexity of the fluvial environment that they represent. For a highly complex semi-alluvial channel incised in glacial till, such as Medway Creek, it may be unrealistic to achieve this level of reductionism, and a reduced-complexity modelling approach may be considered. For less complex alluvial systems, such as the St. François River, the model employed in this study possesses these desirable characteristics, in particular, its physical base and ability to manipulate geotechnical variables to better represent bank material. In all cases, allowing to vary geotechnical properties across the floodplain should be the next step to improve morphodynamic models.