Assessment of the Spatiotemporal Effects of Land Use Changes on Runoff and Nitrate Loads in the Talar River
Abstract
1. Introduction
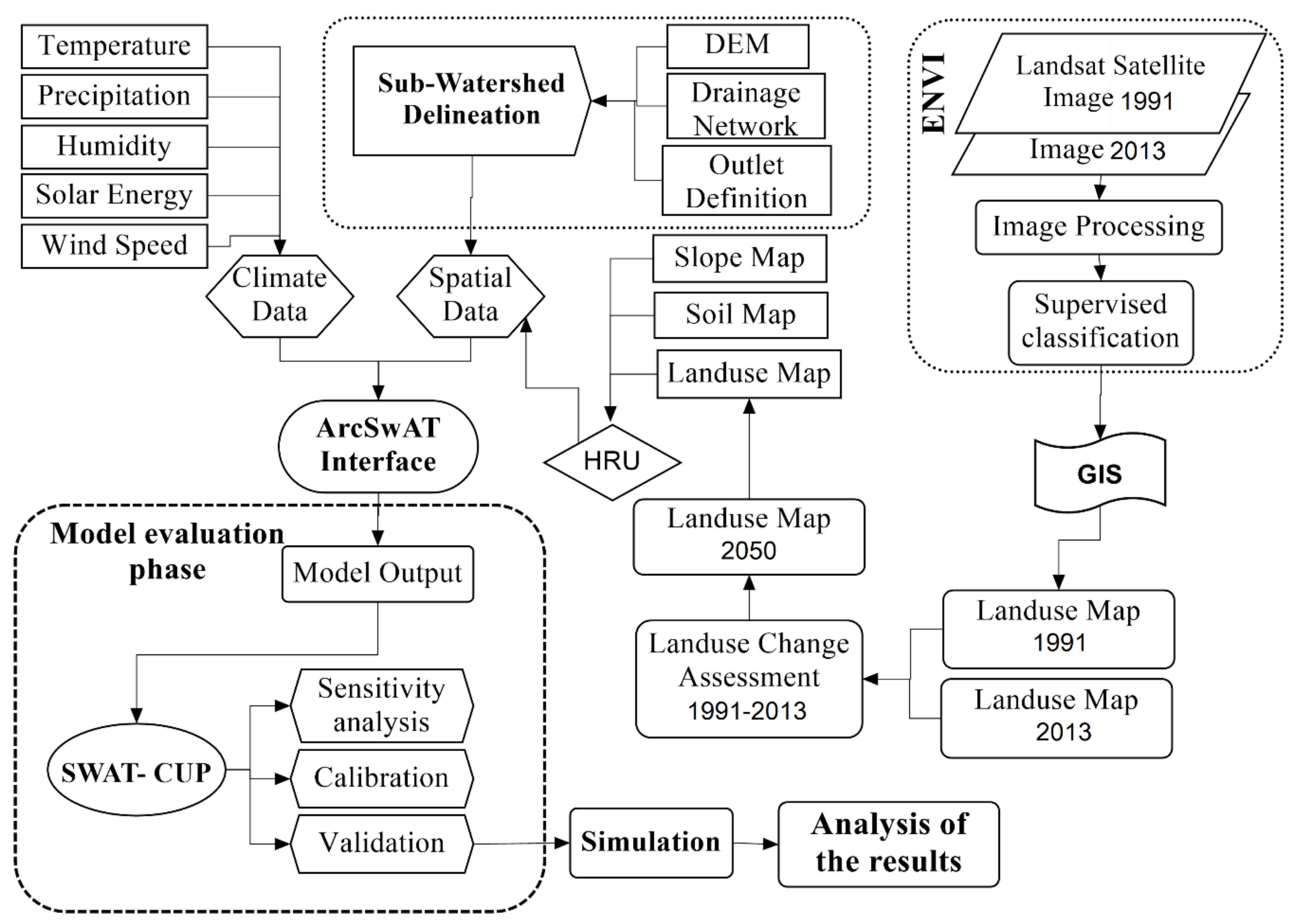
2. Materials and Methods
2.1. Study Area
2.2. SWAT Model
2.3. Data Collection
2.4. Model Performance Evaluation
2.4.1. Coefficient of Determination (R2)
2.4.2. Nash-Sutcliffe Efficiency (NSE)
2.4.3. Percent Bias (PBIAS)
2.4.4. Sensitivity Analysis
3. Results and Discussion
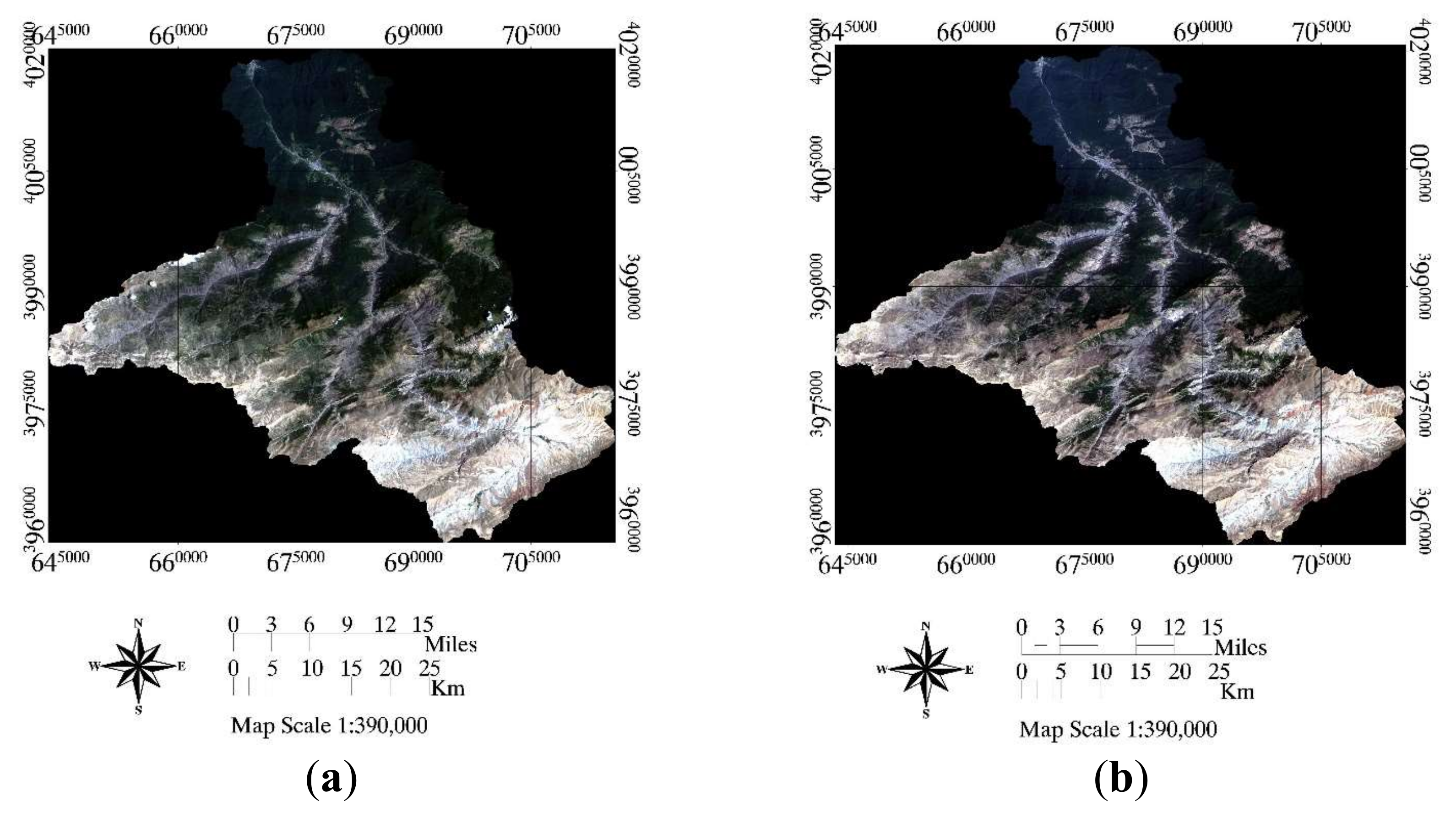
3.1. Accuracy Assessment of Land Use Classification
3.2. Land Use Changes from 1991 to 2013
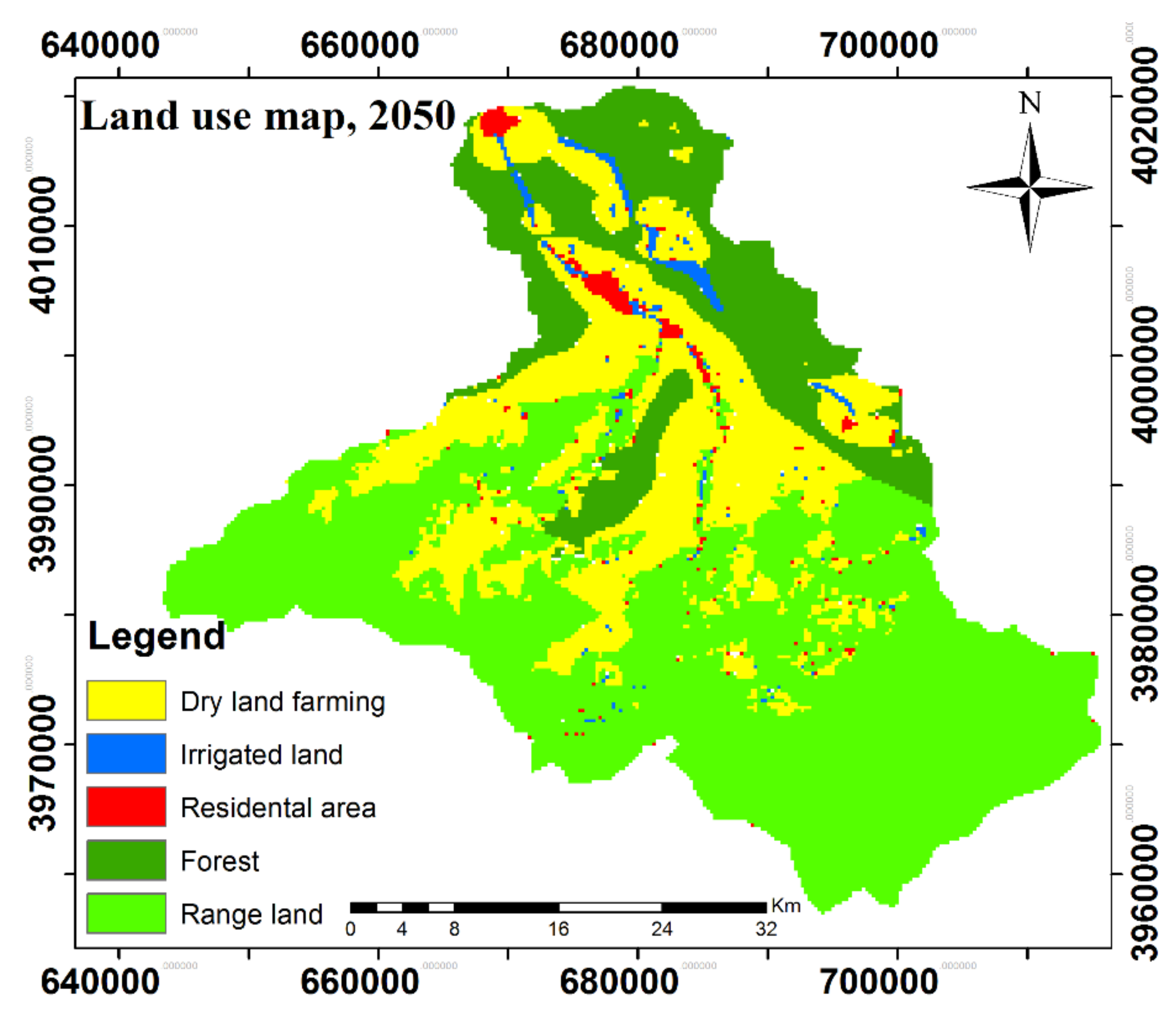
3.3. Land-Use Scenario in Year 2050
3.4. Model Calibration and Validation
3.4.1. Sensitivity Analysis
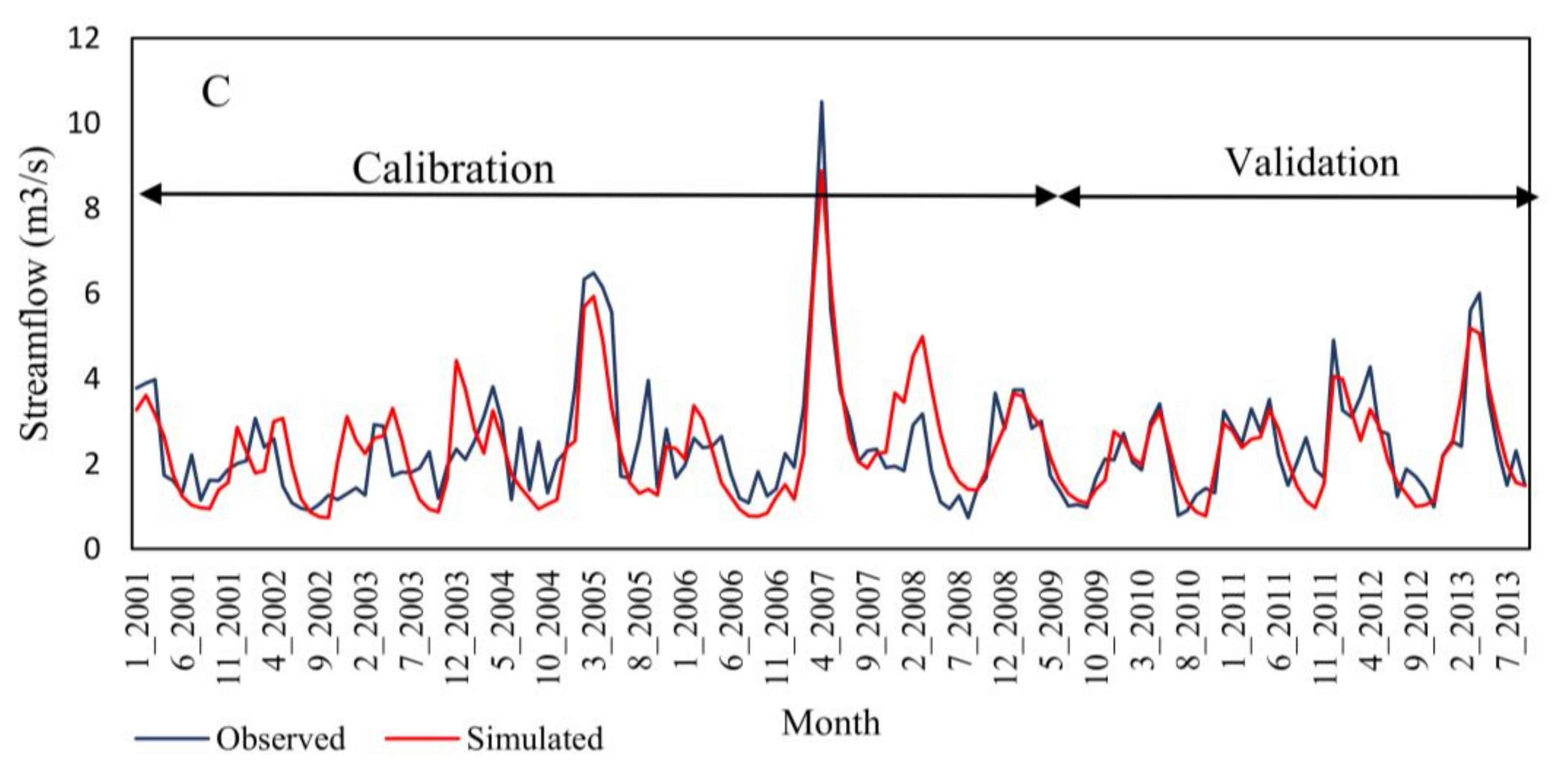
3.4.2. Stream Flow Simulations
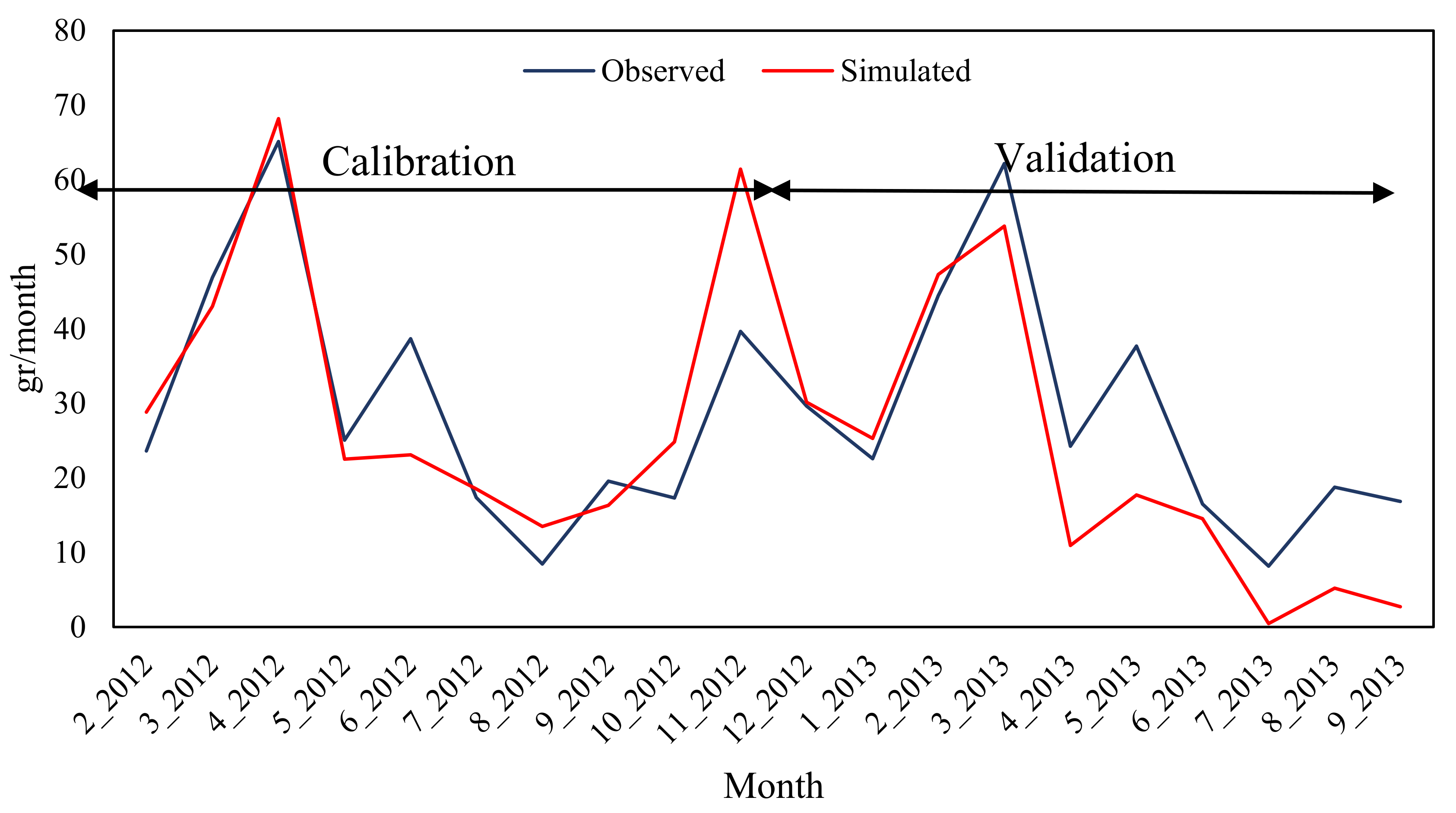
3.4.3. Nitrate Simulations
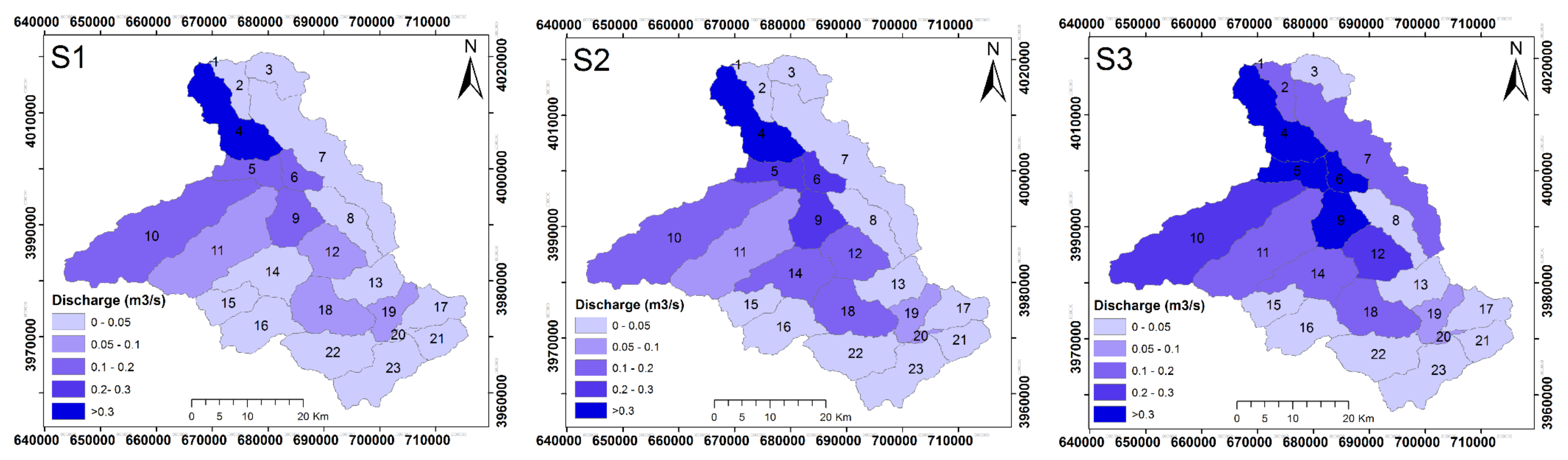
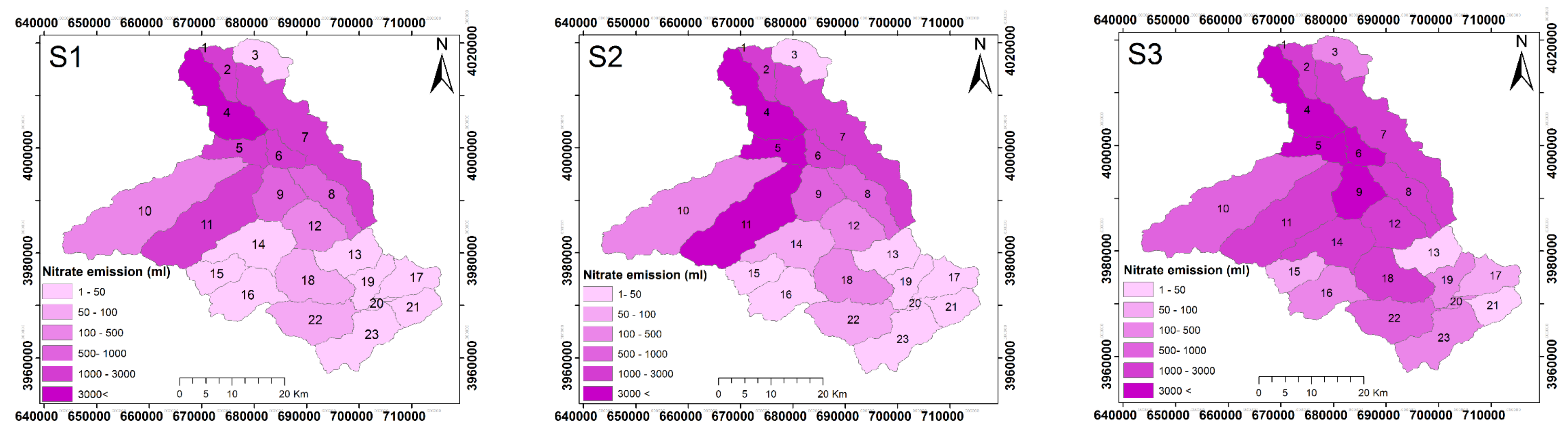
3.5. Discharge and Nitrate Responses to Land Use Changes
3.6. Broader Impact
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Keesstra, S.D. Impact of natural reforestation on floodplain sedimentation in the Dragonja basin, SW Slovenia. Earth Surf. Process. Landf. 2007, 32, 49–65. [Google Scholar] [CrossRef]
- Mohajerani, H.; Kholghi, M.; Mosaedi, A.; Farmani, R.; Sadoddin, A.; Casper, M. Application of bayesian decision networks for groundwater resources management under the conditions of high uncertainty and data scarcity. Water Resour. Manag. 2017, 31, 1859–1879. [Google Scholar] [CrossRef]
- Bertalan, L.; Tóth, C.A.; Szabó, G.; Nagy, G.; Kuda, F.; Szabó, S. Confirmation of a theory: Reconstruction of an alluvial plain development in a flume experiment. Erdkunde 2016, 70, 271–285. [Google Scholar] [CrossRef]
- Abdollahi, Z.; Kavian, A.; Sadeghi, S.H.R. Spatio-temporal changes of water quality variables in a highly disturbed river. Glob. J. Environ. Sci. Manag. 2017, 3, 243–256. [Google Scholar] [CrossRef]
- Steffan, J.J.; Brevik, E.C.; Burgess, L.; Cerdà, A. The effect of soil on human health: An overview. Eur. J. Soil Sci. 2017, 69, 159–171, In press. [Google Scholar] [CrossRef] [PubMed]
- Jafarian, Z.; Kavian, A. Effects of Land-Use Change on Soil Organic Carbon and Nitrogen. Commun. Soil Sci. Plant Anal. 2013, 44, 339–346. [Google Scholar] [CrossRef]
- Pulido Moncada, M.; Gabriels, D.; Cornelis, W.; Lobo, D. Comparing Aggregate Stability Tests for Soil Physical Quality Indicators. Land Degrad. Dev. 2015, 26, 843–852. [Google Scholar] [CrossRef]
- Khaledian, Y.; Kiani, F.; Ebrahimi, S.; Brevik, E.C.; Aitkenhead-Peterson, J. Assessment and monitoring of soil degradation during land use change using multivariate analysis. Land Degrad. Dev. 2016, 28, 128–141. [Google Scholar] [CrossRef]
- Schultz, B. Impacts of man-Induced Changes in Land use and Climate Change on Living in Coastal and Deltaic Areas. Irrig. Drain. 2016. [Google Scholar] [CrossRef]
- Pulido, M.; Schnabel, S.; Lavado Contador, J.F.; Lozano-Parra, J.; González, F. The Impact of Heavy Grazing on Soil Quality and Pasture Production in Rangelands of SW Spain. Land Degrad. Dev. 2018, 29, 219–230. [Google Scholar] [CrossRef]
- Jacobson, C.R. Identification and quantification of the hydrological impacts of imperviousness in urban catchments: A review. J. Environ. Manag. 2011, 92, 1438–1448. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Hernández, C.; Rodrigo-Comino, J.; Romero-Díaz, A. Impact of lithology and soil properties on abandoned dryland terraces during the early stages of soil erosion by water in south-east Spain. Hydrol. Process. 2017, 31, 3095–3109. [Google Scholar] [CrossRef]
- Pfister, L.; Kwadijk, J.; Musy, A.; Bronstert, A.; Hoffmann, L. Climate change, land use change and runoff prediction in the Rhine–Meuse basins. River Res. Appl. 2004, 20, 229–241. [Google Scholar] [CrossRef]
- Kavian, A.; Golshan, M.; Abdollahi, Z. Flow discharge simulation based on land use change predictions. Environ. Earth Sci. 2017, 76, 588. [Google Scholar] [CrossRef]
- Wang, W.; Shao, Q.; Yang, T.; Peng, S.; Xing, W.; Sun, F.; Luo, Y. Quantitative assessment of the impact of climate variability and human activities on runoff changes: A case study in four catchments of the Haihe River basin, China. Hydrol. Process. 2012, 27, 1158–1174. [Google Scholar] [CrossRef]
- Angrill, S.; Petit-Boix, A.; Morales-Pinzón, T.; Josa, A.; Rieradevall, J.; Gabarrell, X. Urban rainwater runoff quantity and quality—A potential endogenous resource in cities? J. Environ. Manag. 2017, 189, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Shamir, E.; Rimmer, A.; Georgakakos, K.P. The use of an orographic precipitation model to assess the precipitation spatial distribution in Lake Kinneret watershed. Water 2016, 8, 591. [Google Scholar] [CrossRef]
- Germer, S.; Neill, C.; Vetter, T.; Chaves, J.; Krusche, A.V.; Elsenbeer, H. Implications of long-term land-use change for the hydrology and solute budgets of small catchments in Amazonia. J. Hydrol. 2009, 364, 349–363. [Google Scholar] [CrossRef]
- Giertz, S.; Junge, B.; Diekkrüger, B. Assessing the effects of land use change on soil physical properties and hydrological processes in the sub-humid tropical environment of West Africa. Phys. Chem. Earth Parts A/B/C 2005, 30, 485–496. [Google Scholar] [CrossRef]
- Zema, D.A.; Denisi, P.; Taguas Ruiz, E.V.; Gómez, J.A.; Bombino, G.; Fortugno, D. Evaluation of Surface Runoff Prediction by AnnAGNPS Model in a Large Mediterranean Watershed Covered by Olive Groves. Land Degrad. Dev. 2015, 27, 811–822. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; Cerdà, A. Improving stock unearthing method to measure soil erosion rates in vineyards. Ecol. Indic. 2018, 85, 509–517. [Google Scholar] [CrossRef]
- Lin, B.; Chen, X.; Yao, H.; Chen, Y.; Liu, M.; Gao, L.; James, A. Analyses of landuse change impacts on catchment runoff using different time indicators based on SWAT model. Ecol. Indic. 2015, 58, 55–63. [Google Scholar] [CrossRef]
- Beasley, D.B.; Huggins, L.F.; Monke, E.J. ANSWERS: A Model for Watershed Planning. Trans. ASAE 1980, 23, 938–944. [Google Scholar] [CrossRef]
- Young, R.A.; Onstad, C.A.; Bosch, D.D.; Anderson, W.P. AGNPS: A nonpoint-source pollution model for evaluating agricultural watersheds. J. Soil Water Conserv. 1989, 44, 168–173. [Google Scholar]
- Bicknell, B.; Imhoff, J.; Kittle, J.; Donigian, A.; Johanson, R. Hydrologic Simulation Program-Fortran: User’s Manual for Release 10; U.S. EPA Environmental Research Laboratory Athens: Athens, GA, USA, 1993.
- Nearing, M.A.; Foster, G.R.; Lane, L.J.; Finkner, S.C. A Process-Based Soil Erosion Model for USDA-Water Erosion Prediction Project Technology. Trans. ASAE 1989, 32, 1587–1593. [Google Scholar] [CrossRef]
- Williams, J.R.; Nicks, A.D.; Arnold, J.G. Simulator for Water Resources in Rural Basins. J. Hydraul. Eng. 1985, 111, 970–986. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part i: Model development1. JAWRA J. Am. Water Resour. Assoc. 2007, 34, 73–89. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, Y.; Pan, Y.; Yu, Z. Land use pattern optimization based on CLUE-S and SWAT models for agricultural non-point source pollution control. Math. Comput. Model. 2013, 58, 588–595. [Google Scholar] [CrossRef]
- Tong, S.T.Y.; Liu, A.J.; Goodrich, J.A. Assessing the water quality impacts of future land-use changes in an urbanising watershed. Civ. Eng. Environ. Syst. 2009, 26, 3–18. [Google Scholar] [CrossRef]
- Chaplot, V.; Saleh, A.; Jaynes, D.B.; Arnold, J. Predicting Water, Sediment and NO3-N Loads under Scenarios of Land-use and Management Practices in a Flat Watershed. Water Air Soil Pollut. 2004, 154, 271–293. [Google Scholar] [CrossRef]
- Kigira, F.K.; Gathenya, J.M.; Home, P.G. Modeling the Influence of Land Use/Land Cover Changes on Sediment Yield and Hydrology in Thika River Catchment Kenya, Using SWAT Model. In Proceedings of the 2007 JKUAT Scientific, Technological and Industrialisation Conference, JKUAT, Kenya, 25–26 October 2007. [Google Scholar]
- Lam, Q.D.; Schmalz, B.; Fohrer, N. The impact of agricultural Best Management Practices on water quality in a North German lowland catchment. Environ. Monit. Assess. 2011, 183, 351–379. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, W.; Song, K.; Wang, X.; Hao, F. Non-point source pollution dynamics under long-term agricultural development and relationship with landscape dynamics. Ecol. Indic. 2014, 45, 579–589. [Google Scholar] [CrossRef]
- Li, Y.; Chang, J.; Wang, Y.; Jin, W.; Guo, A. Spatiotemporal Impacts of Climate, Land Cover Change and Direct Human Activities on Runoff Variations in the Wei River Basin, China. Water 2016, 8, 220. [Google Scholar] [CrossRef]
- Giri, S.; Nejadhashemi, A.P.; Woznicki, S.; Zhang, Z. Analysis of best management practice effectiveness and spatiotemporal variability based on different targeting strategies. Hydrol. Process. 2012, 28, 431–445. [Google Scholar] [CrossRef]
- Stehr, A.; Debels, P.; Romero, F.; Alcayaga, H. Hydrological modelling with SWAT under conditions of limited data availability: Evaluation of results from a Chilean case study. Hydrol. Sci. J. 2008, 53, 588–601. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Tuffour, H.; Bagherzadeh, A.; Duraisamy, V. Spatial and Fractal Characterization of Soil Properties across Soil Depth in an Agricultural Field, Northeast Iran. Eur. J. Soil Sci. 2018, 7, 35–45. [Google Scholar]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Finke, P. Comparing the efficiency of digital and conventional soil mapping to predict soil types in a semi-arid region in Iran. Geomorphology 2017, 285, 186–204. [Google Scholar] [CrossRef]
- Kavian, A.; Sabet, S.H.; Solaimani, K.; Jafari, B. Simulating the effects of land use changes on soil erosion using RUSLE model. Geocarto Int. 2017, 32, 97–111. [Google Scholar] [CrossRef]
- Luo, P.; He, B.; Chaffe, P.L.B.; Nover, D.; Takara, K.; Rozainy, M.A.Z.M.R. Statistical analysis and estimation of annual suspended sediments of major rivers in Japan. Environ. Sci. Process. Impacts 2013, 15, 1052–1061. [Google Scholar] [CrossRef] [PubMed]
- Luo, P.; He, B.; Takara, K.; Xiong, Y.E.; Nover, D.; Duan, W.; Fukushi, K. Historical assessment of Chinese and Japanese flood management policies and implications for managing future floods. Environ. Sci. Policy 2015, 48, 265–277. [Google Scholar] [CrossRef]
- Luo, P.; He, B.; Duan, W.; Takara, K.; Nover, D. Impact assessment of rainfall scenarios and land-use change on hydrologic response using synthetic Area IDF curves. J. Flood Risk Manag. 2015, 11, S84–S97. [Google Scholar] [CrossRef]
- Comprehensive studies of Talar watershed. Office of Watersheds Studies Evaluation; Jahad Engineering Services Company: Sari, Mazandaran, Iran, 2001. [Google Scholar]
- Jimmy, R. Williams Flood Routing With Variable Travel Time or Variable Storage Coefficients. Trans. ASAE 1969, 12, 100–103. [Google Scholar] [CrossRef]
- Neitsch, S.; Arnold, J.; Kiniry, J.; Williams, J. Soil and Water Assessment Tool Theoretical Documentation; Version 2000; Texas Water Resources Institute: College Station, TX, USA, 2009. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the swat model on a large rwer basin with point and nonpoint sources. J. Am. Water Resour. Assoc. 2007, 37, 1169–1188. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondízio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Butzer, K.W. Environmental history in the Mediterranean world: Cross-disciplinary investigation of cause-and-effect for degradation and soil erosion. J. Archaeol. Sci. 2005, 32, 1773–1800. [Google Scholar] [CrossRef]
- García-Ruiz, J.M.; Nadal-Romero, E.; Lana-Renault, N.; Beguería, S. Erosion in Mediterranean landscapes: Changes and future challenges. Geomorphology 2013, 198, 20–36. [Google Scholar] [CrossRef]
- Panagos, P.; Meusburger, K.; Ballabio, C.; Borrelli, P.; Alewell, C. Soil erodibility in Europe: A high-resolution dataset based on LUCAS. Sci. Total Environ. 2014, 479–480, 189–200. [Google Scholar] [CrossRef] [PubMed]
- Benvenuti, S.; Bretzel, F. Agro-biodiversity restoration using wildflowers: What is the appropriate weed management for their long-term sustainability? Ecol. Eng. 2017, 102, 519–526. [Google Scholar] [CrossRef]
- Dawson, L.; Elbakidze, M.; Angelstam, P.; Gordon, J. Governance and management dynamics of landscape restoration at multiple scales: Learning from successful environmental managers in Sweden. J. Environ. Manag. 2017, 197, 24–40. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.; Cai, Q.; Liu, R.; Cao, M. The influence of topography and land use on water quality of Xiangxi River in Three Gorges Reservoir region. Environ. Geol. 2009, 58, 937–942. [Google Scholar] [CrossRef]
- Barbier, E.B.; Delacote, P.; Wolfersberger, J. The economic analysis of the forest transition: A review. J. For. Econ. 2017, 27, 10–17. [Google Scholar] [CrossRef]
- Bravo-Espinosa, M.; Mendoza, M.E.; CarlóN Allende, T.; Medina, L.; Sáenz-Reyes, J.T.; Páez, R. Effects of converting forest to avocado orchards on topsoil properties in the trans-Mexican volcanic system, Mexico. Land Degrad. Dev. 2014, 25, 452–467. [Google Scholar] [CrossRef]
- Vaezi, A.R.; Abbasi, M.; Keesstra, S.; Cerdà, A. Assessment of soil particle erodibility and sediment trapping using check dams in small semi-arid catchments. CATENA 2017, 157, 227–240. [Google Scholar] [CrossRef]
- Yousefi, S.; Sadeghi, S.H.; Mirzaee, S.; van der Ploeg, M.; Keesstra, S.; Cerdà, A. Spatio-temporal variation of throughfall in a hyrcanian plain forest stand in Northern Iran. J. Hydrol. Hydromech. 2018, 66, 97–106. [Google Scholar] [CrossRef]
- Mohammadkhan, S.; Ahmadi, H.; Jafari, M. Relationship between soil erosion, slope, parent material, and distance to road (Case study: Latian Watershed, Iran). Arab. J. Geosci. 2011, 4, 331–338. [Google Scholar] [CrossRef]
- López-Vicente, M.; Quijano, L.; Palazón, L.; Gaspar, L.; Navas, A. Assessment of soil redistribution at catchment scale by coupling a soil erosion model and a sediment connectivity index (central spanish pre-pyrenees). Cuad. Investig. Geogr. 2015, 41, 127–147. [Google Scholar] [CrossRef]
- Feng, T.; Wei, W.; Chen, L.; Rodrigo-Comino, J.; Die, C.; Feng, X.; Ren, K.; Brevik, E.C.; Yu, Y. Assessment of the impact of different vegetation patterns on soil erosion processes on semiarid loess slopes. Earth Surf. Process. Landf. 2018. [Google Scholar] [CrossRef]
- Frey, C.H.; Sumeet, P.R. Identification and Review of Sensitivity Analysis Methods. Risk Anal. 2002, 22, 553–578. [Google Scholar] [CrossRef] [PubMed]
- Parajuli, P.B.; Duffy, S.E. Quantifying Hydrologic and Water Quality Responses to Bioenergy Crops in Town Creek Watershed in Mississippi. J. Sustain. Bioenergy Syst. 2013, 03, 202. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Lenhart, T.; Eckhardt, K.; Fohrer, N.; Frede, H.-G. Comparison of two different approaches of sensitivity analysis. Phys. Chem. Earth Parts A/B/C 2002, 27, 645–654. [Google Scholar] [CrossRef]
- Zhai, X.; Zhang, Y.; Wang, X.; Xia, J.; Liang, T. Non-point source pollution modelling using Soil and Water Assessment Tool and its parameter sensitivity analysis in Xin’anjiang catchment, China. Hydrol. Process. 2012, 28, 1627–1640. [Google Scholar] [CrossRef]
- Cibin, R.; Sudheer, K.P.; Chaubey, I. Sensitivity and identifiability of stream flow generation parameters of the SWAT model. Hydrol. Process. 2010, 24, 1133–1148. [Google Scholar] [CrossRef]
- Taguas, E.V.; Yuan, Y.; Licciardello, F.; Gómez, J.A. Curve numbers for olive orchard catchments: Case study in Southern Spain. J. Irrig. Drain. Eng. 2015, 141, 05015003. [Google Scholar] [CrossRef]
- Cao, W.; Bowden, W.B.; Davie, T.; Fenemor, A. Multi-variable and multi-site calibration and validation of SWAT in a large mountainous catchment with high spatial variability. Hydrol. Process. 2006, 20, 1057–1073. [Google Scholar] [CrossRef]
- Wu, H.; Chen, B. Evaluating uncertainty estimates in distributed hydrological modeling for the Wenjing River watershed in China by GLUE, SUFI-2, and ParaSol methods. Ecol. Eng. 2015, 76, 110–121. [Google Scholar] [CrossRef]
- Xu, H.; Taylor, R.G.; Kingston, D.G.; Jiang, T.; Thompson, J.R.; Todd, M.C. Hydrological modeling of River Xiangxi using SWAT2005: A comparison of model parameterizations using station and gridded meteorological observations. Quat. Int. 2010, 226, 54–59. [Google Scholar] [CrossRef]
- Pongpetch, N.; Chandraseka, P.; Yossapol, C. Dasananda Assessment the Critical Areas and Nonpoint Source Pollution Reduction best Management Practices in Lam Takong River Basin, Thailand. Environ. Asia 2015, 8, 41–52. [Google Scholar]
- Ribarova, I.; Ninov, P.; Cooper, D. Modeling nutrient pollution during a first flood event using HSPF software: Iskar River case study, Bulgaria. Ecol. Model. 2008, 211, 241–246. [Google Scholar] [CrossRef]
- Ahearn, D.S.; Sheibley, R.W.; Dahlgren, R.A.; Anderson, M.; Johnson, J.; Tate, K.W. Land use and land cover influence on water quality in the last free-flowing river draining the western Sierra Nevada, California. J. Hydrol. 2005, 313, 234–247. [Google Scholar] [CrossRef]
- Behera, S.; Panda, R.K. Evaluation of management alternatives for an agricultural watershed in a sub-humid subtropical region using a physical process based model. Agric. Ecosyst. Environ. 2006, 113, 62–72. [Google Scholar] [CrossRef]
- Mohammad, A.G.; Adam, M.A. The impact of vegetative cover type on runoff and soil erosion under different land uses. CATENA 2010, 81, 97–103. [Google Scholar] [CrossRef]
- Castillo, M.M.; Allan, J.D.; Brunzell, S. Nutrient Concentrations and Discharges in a Midwestern Agricultural Catchment. J. Environ. Qual. 2000, 29, 1142–1151. [Google Scholar] [CrossRef]
- Basnyat, P.; Teeter, L.D.; Flynn, K.M.; Lockaby, B.G. Relationships Between Landscape Characteristics and Nonpoint Source Pollution Inputs to Coastal Estuaries. Environ. Manag. 1999, 23, 539–549. [Google Scholar] [CrossRef]
- Shrestha, S.; Kazama, F. Assessment of surface water quality using multivariate statistical techniques: A case study of the Fuji river basin, Japan. Environ. Model. Softw. 2007, 22, 464–475. [Google Scholar] [CrossRef]
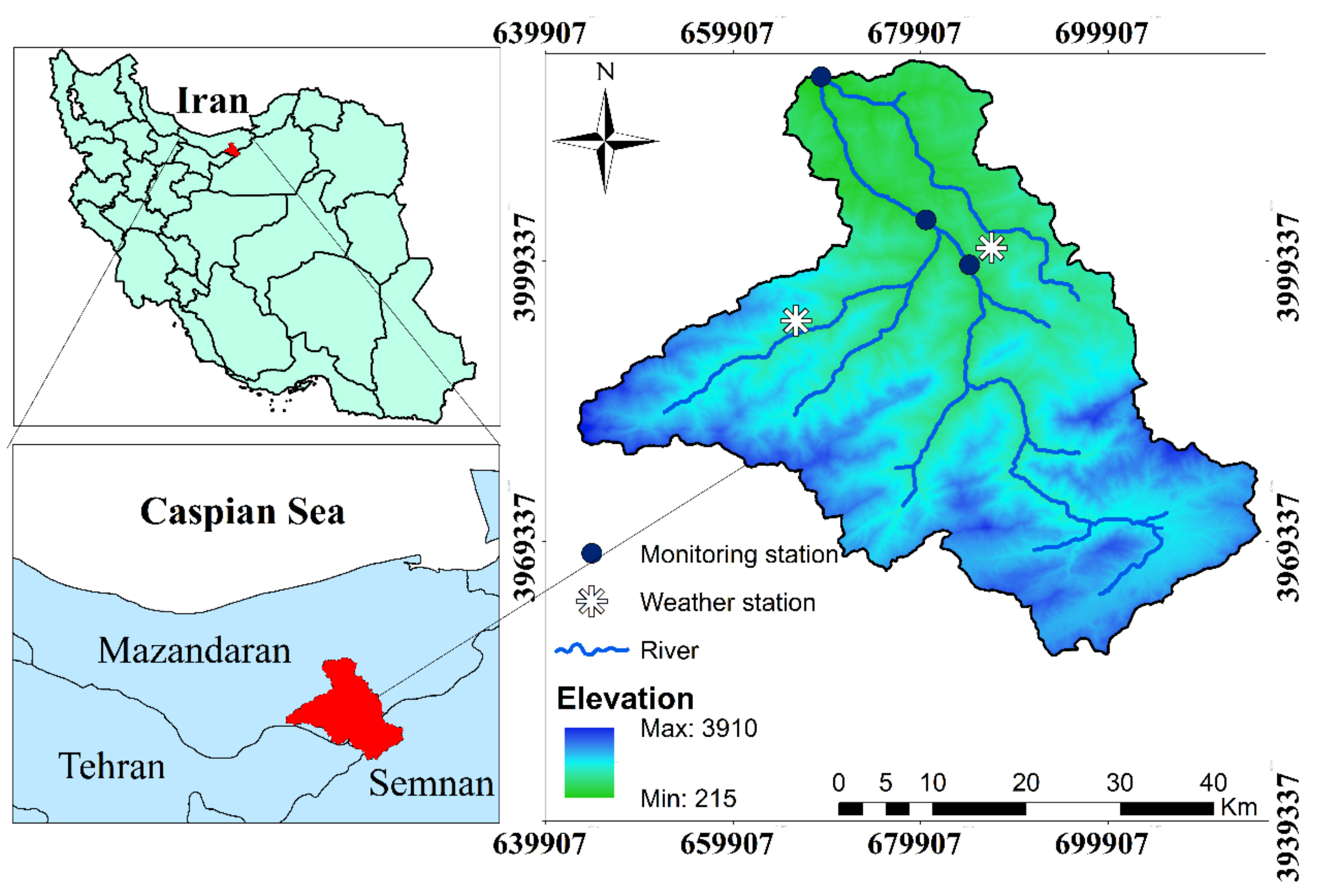


| Data | Data Item | Station | Data Period | Sources |
|---|---|---|---|---|
| Weather data | Precipitation Max./Min. Temperature Solar radiation Wind speed | Gharakheil, Polsefid, | 2000–2013 | Iran meteorological organization |
| Relative humidity | Allasht (Synoptic stations) | |||
| Hydrological data (measured daily) | Discharge | Shirgah, Kerikola, Polsefid, | 2000–2013 | Iran Water Resources Management Company |
| Water quality data | Nitrate | Shirgah | 2012–2013 | Iran Water Resources Management Company |
| Soil map | Soil physical and chemical properties | - | 2008 | Forests, Range and Watershed Management. IR of Iran |
| Land use | Satellite images (Landsat) | - | 1991–2013 | http://earthexplorer.usgs.gov/ |
| Performance Rating | NSE | Percent Bias (PBIAS) | |
|---|---|---|---|
| Stream Flow | Nitrate | ||
| Very good | 0.75 < NSE < 1.00 | PBIAS < ±10 | PBIAS < ±25 |
| Good | 0.65 < NSE < 0.75 | ±10 < PBIAS < ±15 | ±25 < PBIAS < ±40 |
| Satisfactory | 0.50 < NSE < 0.65 | ±15 < PBIAS < ±25 | ±40 < PBIAS < ±70 |
| Unsatisfactory | NSE < 0.50 | PBIAS > ±25 | PBIAS > ±70 |
| Land Use | Forest | Irrigated Land | Dry Land Farming | Residential Area | Range Land | Total | Producer Accuracy (%) |
|---|---|---|---|---|---|---|---|
| Forest | 472 | 0 | 0 | 0 | 0 | 472 | 100 |
| Irrigated land | 0 | 72 | 0 | 0 | 0 | 72 | 100 |
| Dryland farming | 0 | 0 | 23 | 0 | 4 | 27 | 85.2 |
| Residential Area | 0 | 0 | 0 | 42 | 27 | 69 | 60.9 |
| Range land | 0 | 0 | 0 | 0 | 297 | 297 | 100 |
| Total | 472 | 72 | 23 | 42 | 328 | 937 | - |
| Overall accuracy = 96.69% and Kappa index = 0.94. | |||||||
| Land Use | Forest | Range Land | Irrigated Land | Dry Land Farming | Residential Area | Total | Producer Accuracy (%) |
|---|---|---|---|---|---|---|---|
| Forest | 1257 | 0 | 0 | 0 | 0 | 1257 | 100 |
| Range land | 2 | 987 | 0 | 0 | 0 | 990 | 99.8 |
| Irrigated land | 0 | 0 | 80 | 0 | 0 | 80 | 100 |
| Dry land farming | 7 | 357 | 5 | 116 | 13 | 498 | 23.3 |
| Residential area | 0 | 0 | 2 | 0 | 179 | 181 | 98.9 |
| Total | 1266 | 1345 | 87 | 116 | 192 | 3006 | 100 |
| Overall accuracy = 87.15% and Kappa index = 0.80. | |||||||
| Land Use | 1991 | 2013 | Change | |||
|---|---|---|---|---|---|---|
| Area (%) | Area (ha) | Area (%) | Area (ha) | Area (%) | Area (ha) | |
| Forest | 40.8 | 83,902.75 | 34.8 | 71,424.71 | −14.9 | −12,478.04 |
| Irrigated land | 0.5 | 1017.82 | 0.7 | 1493.82 | +46.8 | +476 |
| Dry land farming | 11.3 | 23,272.06 | 14.8 | 30,520.31 | +31.1 | +7248.25 |
| Range land | 46.6 | 95,826.45 | 48.8 | 10,0307.5 | +4.7 | +4481.05 |
| Residential area | 0.8 | 1563.77 | 0.9 | 1837.72 | +17.5 | +273.95 |
| Land-Use Type | Land-Use 1991 (ha) | Land-Use 2013 (ha) | Change (1991–2013) | Change Annual Rate (ha) | Scenario 2050 (ha) | Change (1991–2050) |
|---|---|---|---|---|---|---|
| Forest | 83,902.75 | 71,424.71 | −12,478.04 | −542.52 | 51,351.47 | −32,551.28 |
| Irrigated land | 1017.82 | 1493.82 | +476 | +20.70 | 2259.72 | +1241.90 |
| Dry land farming | 23,272.06 | 30,520.31 | +7248.25 | +315.14 | 42,180.49 | +18,908.43 |
| Range land | 95,826.45 | 100,307.5 | +4481.07 | +194.83 | 107,516.21 | +11,689.76 |
| Residential Area | 1563.77 | 1837.72 | +273.95 | +11.91 | 2278.39 | +714.62 |
| Sensitive Parameters | Definition | Final Parameter Value |
|---|---|---|
| CN2 | SCS runoff curve number for moisture condition II | 0.57 |
| SMTMP | Snow melt base temperature | −2.09 |
| SOL_BD | Moist bulk density | −0.32 |
| SFTMP | Snowfall temperature | 8.68 |
| ALPHA_BNK | Base flow alpha factor for bank storage | 0.11 |
| SOL_K | Soil hydraulic conductivity | 0.51 |
| SMFMN | Melt factor for snow in December 21 | 1.73 |
| SOL_AWC | Soil available water storage capacity | 0.05 |
| SLSUBBSN | Average slope length | 1.81 |
| REVAPMN | Threshold depth of water in the shallow aquifer for “revap” to occur | 249.23 |
| LAT_TTIME | Lateral flow travel time | −15.50 |
| CANMX | Maximum canopy storage | 34.93 |
| TIMP | Snow pack temperature lag factor | 0.92 |
| CH_N2 | Manning’s “n” value for the main channel | 0.52 |
| GWQMN | Threshold depth of water in the shallow aquifer required for return flow to occur | 3652.82 |
| SURLAG | Surface runoff lag time | 0.78 |
| TLAPS | Temperature lapse rate | 67.63 |
| ESCO | Outflow simulation option | 0.47 |
| GW_REVAP | Groundwater “revap” coefficient | 0.12 |
| ALPHA_BF | Baseflow alpha factor | −0.42 |
| SDNCO | Denitrification threshold water content | 0.50 |
| ERORGN | Organic N enrichment ratio for loading with sediment | 0.94 |
| SOL_NO3 | Initial NO3 concentration in the soil layer | 25.69 |
| SOL_ORGN | Initial organic N concentration in the soil layer | 75.09 |
| Item | Station | Period | Mean | NSE | R2 | PBIAS | |
|---|---|---|---|---|---|---|---|
| Observed | Simulated | ||||||
| Streamflow | Shirgah | Calibration | 4.83 | 4.72 | 0.67 | 0.68 | 4.2 |
| Validation | 5.01 | 5.19 | 0.62 | 0.65 | 5.3 | ||
| Kerikkola | Calibration | 1.86 | 1.98 | 0.57 | 0.63 | 6.2 | |
| Validation | 1.48 | 1.70 | 0.71 | 0.75 | 13 | ||
| Polseffid | Calibration | 2.25 | 2.43 | 0.60 | 0.62 | 7.4 | |
| Validation | 2.02 | 2.08 | 0.75 | 0.76 | 1.3 | ||
| Nitrate load | Shirgah | Calibration | 30,116.8 | 31,850 | 0.74 | 0.75 | 5.4 |
| Validation | 27,924.1 | 19,762.33 | 0.62 | 0.83 | −39.3 | ||
| Sub-Basin | Discharge Change (%) | Nitrate Change (%) | ||||
|---|---|---|---|---|---|---|
| S1-S2 | S2-S3 | S1-S3 | S1-S2 | S2-S3 | S1-S3 | |
| 1 | +21.4 | +43.6 | +74.4 | +18.2 | +163.8 | +211.9 |
| 2 | +13.2 | +883.5 | +1013 | +2.9 | +4 | +7 |
| 3 | 0 | 0 | 0 | 0 | +846 | +846 |
| 4 | +27.8 | +43.3 | +83.2 | +23.6 | +210.6 | +283.9 |
| 5 | +32.5 | +56.2 | +107.0 | +31.9 | +73.7 | +129.1 |
| 6 | +69.1 | +53.1 | +158.9 | +10.2 | +470.4 | +528.5 |
| 7 | +4.2 | +899.6 | +941.8 | +3.2 | −20.8 | −18.3 |
| 8 | 0 | +0.4 | +41.7 | 0 | +300.2 | +300.2 |
| 9 | +84.6 | +49.7 | +176.2 | +11.8 | +512 | +626.9 |
| 10 | +60.5 | +51.3 | +142.8 | +36.8 | +568 | +813.7 |
| 11 | +3.8 | +99.0 | +106.6 | +32.8 | −5.8 | +25.1 |
| 12 | +81.3 | +19.5 | +116.6 | +126.6 | +661.9 | +1626.5 |
| 13 | +197.9 | 0 | +197.9 | +613.5 | 0 | +613.5 |
| 14 | +241.9 | +20.4 | +311.7 | +74.2 | +1968.7 | +2469.1 |
| 15 | +229.4 | +24.6 | +310.4 | +11.4 | +1277.6 | +1433.8 |
| 16 | +3.6 | +11.9 | +404.4 | −1.8 | +1240.5 | +1216 |
| 17 | +1.2 | +19.8 | +147 | +294.8 | +1087.3 | +4587.8 |
| 18 | +62.7 | +14.3 | +85.9 | +115.2 | +817.4 | +1873.9 |
| 19 | +43.2 | +8.7 | +55.6 | +250.3 | +1000.8 | +3767.4 |
| 20 | +47.9 | +8.7 | +60.8 | +257.3 | +809.8 | +3151.1 |
| 21 | 0 | +0.6 | +56.9 | +514.9 | +6.1 | +551.9 |
| 22 | +936.6 | +6.2 | +1001.2 | +80.1 | +452.4 | +894.9 |
| 23 | +37.5 | +6.8 | +46.8 | +106.7 | +3820.7 | +8003.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kavian, A.; Mohammadi, M.; Gholami, L.; Rodrigo-Comino, J. Assessment of the Spatiotemporal Effects of Land Use Changes on Runoff and Nitrate Loads in the Talar River. Water 2018, 10, 445. https://doi.org/10.3390/w10040445
Kavian A, Mohammadi M, Gholami L, Rodrigo-Comino J. Assessment of the Spatiotemporal Effects of Land Use Changes on Runoff and Nitrate Loads in the Talar River. Water. 2018; 10(4):445. https://doi.org/10.3390/w10040445
Chicago/Turabian StyleKavian, Ataollah, Maziar Mohammadi, Leila Gholami, and Jesús Rodrigo-Comino. 2018. "Assessment of the Spatiotemporal Effects of Land Use Changes on Runoff and Nitrate Loads in the Talar River" Water 10, no. 4: 445. https://doi.org/10.3390/w10040445
APA StyleKavian, A., Mohammadi, M., Gholami, L., & Rodrigo-Comino, J. (2018). Assessment of the Spatiotemporal Effects of Land Use Changes on Runoff and Nitrate Loads in the Talar River. Water, 10(4), 445. https://doi.org/10.3390/w10040445







