Abstract
Water Distribution Networks (WDNs) can be regarded as complex networks and modeled as graphs. In this paper, Complex Network Theory is applied to characterize the behavior of WDNs from a topological point of view, reviewing some basic metrics, exploring their fundamental properties and the relationship between them. The crucial aim is to understand and describe the topology of WDNs and their structural organization to provide a novel tool of analysis which could help to find new solutions to several arduous problems of WDNs. The aim is to understand the role of the topological structure in the WDNs functioning. The methodology is applied to 21 existing networks and 13 literature networks. The comparison highlights some topological peculiarities and the possibility to define a set of best design parameters for ex-novo WDNs that could also be used to build hypothetical benchmark networks retaining the typical structure of real WDNs. Two well-known types of network ((a) square grid; and (b) random graph) are used for comparison, aiming at defining a possible mathematical model for WDNs. Finally, the interplay between topology and some performance requirements of WDNs is discussed.
1. Introduction
Biological and chemical systems, brain neural networks, social interacting species, the Internet and the World Wide Web, and the multiple and interconnected infrastructures that provide several services to consumers in the cities are network shaped [1,2]. It seems that the efficiency of the systems largely depends on their ability to create (if they are natural) or to have (in the case of man-made structures) multiple links between the units. On the one hand, it ensures better performance and self-recovering function in the case of failure of an element thanks to a redundant structure. On the other hand, it makes it difficult to understand the principles of their functioning and behavior. In this regard, a suitable approach to capture the local and the global properties of network systems is to model them as graphs, where the nodes represent the units, and the links stand for the interactions between them.
The study of networks is known as graph theory, and, since its birth in 1736 by the Swiss mathematician Leonhard Euler, graph theory has solved several practical problems revealing interesting properties of many systems [3]. In the past decades, two important papers [4,5] established the mathematical bases of a new movement of interest and research in the study of complex networks, i.e., networks with irregular, complex, and dynamically evolving structure. The main focus was to provide tools for the analysis of irregular systems with thousands or millions of nodes.
The huge analysis of networks from different fields produced a series of unexpected and interesting results about their behaviors that led to the identification of a series of unifying principles and statistical properties. The effort was the definition of new concepts and measures to characterize the topology and the structure of real networks, to help in understanding their behavior and dynamic development. For example, it was shown how the robustness of the network systems to perturbations (such as failures and attacks) strongly depends on topology [6]; the functioning of the Internet network is studied from a topological point of view by Faloutsos et al. [7]; for the understanding of cancer cell growth mechanism, the analysis of the p53 gene and protein, and also the study of the whole network interacting with them, was proposed by Vogelstein et al. [8]. Consequently, a topological approach has become crucial in the last years, helping to characterize quantitatively certain local and global aspects of systems.
Based on the successful application of the Complex Network Theory to several fields (e.g., the Internet, neuroscience, computer science, biology, social science, medicine, etc.), in this paper, Water Distribution Networks (WDNs) are regarded as complex systems, modeled as graphs, and studied within the approach of the Complex Network Theory. In fact, WDNs can be considered as complex networks [9], as they are often constituted of thousands of elements, are strongly looped and show irregular shape, since they follow the layout of the city they serve. Water distribution networks have been successfully modeled as graphs to design an optimal sub-region layout [10], to study their global robustness [11,12,13], to evaluate their vulnerability to single pipe failures [14], to make a spectral analysis of the system [15,16], or to investigate possible benchmark values for the information entropy [17]. In general, strong correlations have been shown to exist among graph theory metrics and performance measures of model planar networks [18]; hence, the complex systems approach has been proposed as a framework to design and implement sustainable and hybrid water systems [19,20].
The complex and meshed structure of WDNs allows the system to recover from failures, exploiting the topological redundancy provided by closed loops, so that the flow could reach a given node through different paths. This redundant design approach gives the system an intrinsic capability of overcoming perturbations (e.g., local pipe failures or peaks of water demand), and, together with pipe diameters larger than those strictly necessary to fulfill the design pressure at the network nodes, to guarantee a power surplus to be dissipated [21,22]. In [21], Todini introduced a resilience index which accounts for the power surplus for an assigned network layout without any information about topology. More recently, Prasad and Park [23] proposed the concept of network resilience, which combines the effects of surplus power and reliable loops, but with a very simplified approach. Even if there is awareness that topology affects the performance and behavior of WDNs, this effect has not been quantified yet. Defining the topology of a WDN is a layout problem aimed at ensuring robustness and reliability [24] and represents one of the most difficult tasks in the design [25].
In fact, WDNs are critical infrastructures, whose reliable, robust, and efficient operation greatly affects national economic prosperity and people everyday life. It has been widely agreed that there are inseparable interdependencies between the robust structure of WDNs, their efficiency, as well as that of directly and indirectly related infrastructure operations. Therefore, the understanding of complex infrastructure systems needs a balance between holistic and reductionist methodologies [26]. This requires predictability of the complex network topology, behavior, and evolution dynamics over time, through a novel analysis framework.
In the last years, several new methodologies and metrics have been proposed in the scientific literature to better understand, describe, measure and optimize the topology of complex networks (a wide review is provided in [3,27]). Previous studies on real infrastructure networks indicated that they do not present small-world features (i.e., the presence of short geodesic distances between each nodes, meaning that it takes only a few steps to go from one node to another [4], and so the most part of the communication cross these hub nodes [5]). This is because, generally, infrastructure networks are planar networks with significant spatial limitation.
In this paper, the major and basic complex network metrics are applied to a large set of real and synthetic WDNs of various size. Then, the relationships between the obtained values of the metrics and the topology of WDNs are analyzed. The focus is identifying typical values for the topological metrics of WDNs to define a range of benchmark values and a general model of WDN structure, seeking possible relationships among these metrics and some indices of performance of WDNs. This topological framework could be a preliminary and alternative tool to the classical methods of analysis and design of WDNs, especially in the case of incomplete or lacking information about the system, since a calibrated hydraulic simulation model is not required. Furthermore, two well-known types of networks are considered, exploring the same number of nodes as the studied WDNs, namely the square grid and the random graph. For these networks, the topological metrics are calculated and used as a comparison to find possible relations and benchmark values. The results can help to define a mathematical model to describe the structure and the topology of WDNs. Finally, the clear relationships between some of the adopted topological metrics allows limiting the set of metrics needed to successfully describe the taxonomy of WDNs and so which of them should be further investigated and adopted as efficiently made for power grids by [28]. In this way, the paper can be seen as a contribution to the understanding, from a topological point of view, of WDNs, which could serve as a guidance for planning and monitoring practices.
2. Methods
From a topological and mathematical point of view, WDNs can be modeled as link-node planar (e.g., networks forming vertices wherever two edges cross) spatially organized weighted graphs , where junctions, water sources and water demand points are represented by the set V of n nodes (hereinafter assumed as a measure of network size), while pipes and valves are represented by the set E of m edges, and w is a function that assigns to each edge a weight characterizing the physical characteristics of the pipe or of the valve [14]. In particular, WDNs belong to the class of networks strongly constrained by their geographical embedding [3], for which connections between distant nodes are unlikely to be found, due to physical and economic constraints [29]. In particular, the long range connections in a spatial network are constrained by the Euclidean distance, having important consequences on the network statistical properties. In addition, the number of edges that can be connected to a single node is limited by the physical space to connect them (it is evident for urban streets, where only a small number of streets can cross in an intersection).
Generally, a complete representation of a network is provided by its adjacency matrix A which indicates which of the vertices are connected (adjacent): element indicates that there is a link between nodes i and j, otherwise. For an undirected network, the A matrix is symmetric since . A weighted graph can be represented by its weighted adjacency matrix W where indicates the intensity of the link between nodes i and j, and if nodes i and j are disconnected. In the case of WDNs, the weight of the links could be hydraulic and/or geometric characteristics of the pipes (e.g., length, diameter, hydraulic resistance, flow, etc.) if available. From the adjacency matrix, the Laplacian matrix can be defined [30], where and is called the degree of the node i. In the case of a weighted graph, . The matrices A and L described above represent two of the major and most frequently used graph matrices, the spectra of which, together with topological metrics defined and computed from them appear in many real case applications. In the following, the definitions of several topological metrics used in the paper are given. It is worth highlighting that most quantify the connectivity and the communication rate within a network. Hence, their meaning is diametrically opposed if network sectorization is discussed in terms of its effect on water flows or on potential contaminant transmission.
2.1. Link Density q
The link density q is the ratio between the total number m of network edges and the maximum number of edges of a network with n nodes:
For most real networks, the link density value is low [27], since they are sparse, indicating that they are not fully connected.
2.2. Average Node Degree k
One of the simplest, and most important characteristics of a node is its degree , defined as the total number of edges concurring in the node. The node degree counts the number of neighbors of node. The average value of over all nodes n:
providing immediate information on the organization and structure of network, and its connectivity. The higher is the value of the average node degree, the better is the communication between the nodes.
2.3. Diameter D
The diameter D is defined as:
where is defined as the shortest path from node i to node j, computed as the number of edges along the shortest path connecting them (when there is no path between a pairs of nodes, the distance is assumed infinite). The diameter D is defined as the maximum shortest distance (the maximum geodesic length) between any pair of vertices [31]. It expresses how cohesive a system is.
2.4. Average Path Length l
The average path length l is the average number of steps along the shortest paths for all possible pairs of nodes in the network, determining the average degree of separation between any pair of nodes:
It measures the mean distance between two nodes, averaged over all pairs of nodes [4]. The geodesic length provides an optimal path way, since one would achieve a fast transfer and save system resources. The average path length gives information about the flow communication between any pairs of nodes.
2.5. Spectral Radius (or Spectral Index)
The spectral radius corresponds to the largest eigenvalue of the adjacency matrix A of a graph and it is related to the mean value of vertex degrees, taking into account not only immediate neighbors of vertices but also the neighbors of the neighbors [32]. Spectral radius plays an important role in abstract models for computer virus spreading through a network. In particular, the smaller the radius, the larger the network robustness against the spread of viruses is [33]. In this regard, Wang et al. [28] showed that the epidemic threshold (i.e., once exceeded, the infection survives and becomes an epidemic) in virus spreading is proportional to . This fact can be explained as the number of walks in a connected graph is proportional to . The greater is the number of walks of a network, the easier is the spread of the “moving substance” through it. Conversely, the higher is the spectral radius, the better is the communication within a network.
2.6. Spectral Gap
The spectral gap is the difference between the first and second eigenvalue of the adjacency matrix A. Low values of this spectral metric indicate the presence of bottlenecks (articulation points or bridges) in the network [34], which hence can be easily split into sub-regions by removing few nodes or links [6].
2.7. Algebraic Connectivity
The algebraic connectivity corresponds to the second smallest eigenvalue of graph Laplacian matrix L [30], and quantifies the strength of network connections even if the graph is sparse (“how strong” are network connections). Its properties are extensively discussed in [35] with regard to its application to the analysis of graph robustness in terms of node and link failures, and proneness to clustering. Consequently, the larger the algebraic connectivity is, the more difficult it is to split the network into independent components.
2.8. Eigengap
The eigengap corresponds to the difference between the eigenvalue and the eigenvalue of the Laplacian matrix:
where s is the number of clusters in which the network is intrinsically shaped. Choosing the proper number s of clusters is a general problem for all clustering algorithms, and, in the case of water distribution networks, it constitutes the arduous problem of water network partitioning [36]. A tool which is particularly designed for spectral clustering [35], but can also be applied successfully to other clustering algorithms, is the eigengap heuristic, which chooses the number of proper clusters such that all eigenvalues are small, but is relatively large. In other words, a simple indication of the proper number of clusters , from a topological point of view, is given by the first eigengap which results significantly larger than the previous ones. An explanation for this procedure, based on perturbation theory, is that, in the ideal case of c completely disconnected clusters, the 0 eigenvalue has multiplicity , and there is a gap to the eigenvalue, that is [37]. It is worth highlighting that the more pronounced is the cluster structure in the network, the better is the eigengap works.
3. Materials
To represent the topology of typical water systems, publicly available datasets of real and synthetic WDNs were used. These model networks are reported in the literature and their data-files are accessible on-line. Furthermore, to conduct the analysis and explore the structural properties of WDNs from a wide size range, we also compared the value of the above introduced topological metrics with that concerning square grids and random regular graphs. In Table 1, the name, the number of nodes n, the number of pipes m, the type (real or synthetic) and the data-file sources are reported for all networks used in the paper.

Table 1.
Name of network, number of nodes n, number of pipes m, number of loops r, type and data-file sources for all WDNs.
Square grids: A lattice graph, mesh graph, or grid graph is a graph whose drawing, embedded in some Euclidean space , forms a regular tiling [3]. This type of graph may more shortly be called just a lattice, mesh, or grid. A particular type of two-dimensional lattice graph (indicated with , and also known as square grid graph) is the graph whose vertices correspond to the points in the plane with integer coordinates, x-coordinates being in the range , y-coordinates being in the range , and two vertices are connected by an edge wherever the corresponding points are at distance 1 from each other (see Figure 1a). In other words, it is a unit distance graph for the described point set. A two-dimensional grid graph, also known as a square grid graph, is an lattice graph . In this paper, the two-dimensional square grid graph was considered, with a number of nodes equal to , 100, 1024, 10000, and 34969 (respectively, named SG1, SG2, SG3, SG4, and SG5). In this way, a benchmark value was obtained for the entire size range of the studied networks. In fact, the largest considered square lattice has a number of nodes similar to the largest WDN considered in the paper (Chihuahua, for which ).
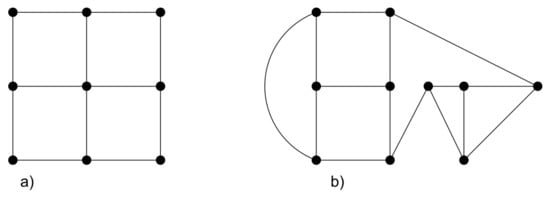
Figure 1.
Examples of the synthetic networks used for comparison: (a) a small square grid with 9 nodes and 12 edges; and (b) a small random 3-regular graph with 10 nodes and 15 edges.
: The systematic study of random graphs was initiated by Erdos and Renyi [58]. The term random graph refers to the disordered arrangement of links between nodes. In particular, they considered graphs obtained by uniform sampling of all possible graphs with n vertices and m edges. In practice, random graphs are generated by connecting couples of randomly selected nodes (prohibiting multiple connections), until the number of edges equals m (see Figure 1b). It is clear that a given graph is only one realization of all the possible combinations of connections. A particular class of random graphs is the random k-regular graph, for which each node has the same number of neighbors (e.g., every node has the same degree k). A 3-regular graph is known as a cubic graph. Some important characteristics are: (a) a graph is regular if and only if it exists an eigenvector of the Adjacency matrix A whose eigenvalue is the constant degree k of the graph; and (b) a regular graph of degree k is connected if and only if the eigenvalue k has multiplicity one. Since k-regular graphs are subject to constraints, to generate them efficiently while ensuring an unbiased sampling one can resort either to the algorithm, implementing the most general configuration model [59], or to a refinement of such algorithm [60].
In the present paper, to compare with the water networks explored, k-regular graphs with and with a number of nodes equal to n = 10, 100, 1000, 10000, and 35000 were considered (respectively, named RG1, RG2, RG3, RG4, and RG5).
4. Results and Discussion
In recent years, several researchers studied the statistical and topological properties of several systems and infrastructures to provide novel solutions and understand what kind of network is needed to support and optimize the functioning of the systems themselves. In this regard, in this paper, the topological characteristics of WDNs are studied, based on some real-world and synthetic systems. In the following, the topological metrics defined in Section 2 are calculated for the networks described in Section 3, and then they are displayed as function of the number of nodes of each WDN. The results are reported in Table 2.

Table 2.
Topological metric values calculated for all case studies: link density q, average node degree , graph diameter D, average path length l, spectral gap , algebraic connectivity , inverse spectral radius , optimal cluster number .
In Figure 2, the relationship between the link density q and the number of nodes n for the analyzed WDNs is plotted in log–log scale. It can be noticed that the two groups of WDNs (synthetic and real) follow the same trend with . Specifically, for increasing n, the link density tends to zero and closely follows a power-law with exponent , as reported in [27] for other real-world networks (linguistic systems, power grids, actor networks and biological systems). The link density shows a well defined scaling behavior, resulting inversely proportional to the network size n. It is worth highlighting that both square grids and random regular graphs show the same trend, meaning that water distribution networks are equally sparse in these two types of graph. In fact, link density is strongly related to the average node degree, which is not significantly different for WDNs, SG, and the considered RG. Such a similar behavior can be interpreted by means of Equation (1). In fact, introducing in Equation (1) the well-known topological relationship , linking the number of pipes m, nodes n, and loops r of a network, it results . As in WDNs it is r << (n− 1), the second term is always smaller than the first, so that q = 2/n. SG and RG are instead more looped than most WDNs. In fact, in Figure 1, it is clear that the link density is slightly higher for SG and RG, which is due to the presence of a greater number of loops (according to the above relationship), as shown in Table 1. In this regard, since the number of loops can be regarded as a robustness metric, clearly the link density can be used as a surrogate metric for the robustness of WDNs. In fact, it takes into account the number of nodes, pipes and, implicitly, the number of loops.
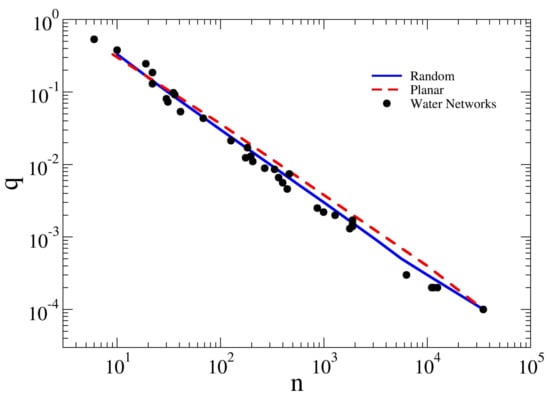
Figure 2.
Relationship between the link density q and the network size n. The data points follow a trend that can be fitted with a power law decrease . Both water networks, random regular graphs and planar square lattice show a similar scaling expected for sparse networks. The blue continuous line and the broken red line refer to random graph and square grids, respectively. The black dots represent the studied WDNs. For numerical values, please see Table 2.
In Figure 3, the average node degree —the coarsest characteristic of node interconnections [27]—is plotted in semi-log scale as a function of the size n. We observe that the average node degree is nearly invariant with respect to the network size n—perhaps with a slightly decreasing trend—confirming that water distribution networks are sparsely connected. Such a behavior is expected for real networks with economic and geographic constraints [16,29]. It is possible to identify a range of values from to that are the typical small values of WDNs. In fact, the lower bound () corresponds to simple line graphs, which have the lowest topological robustness, as the failure of a single pipe leads to a complete network disconnection. An important aspect is that the nearly invariant trend is also observed for the square grids, for which the average node degree seems to tend, as the number of nodes increases, to an asymptotic value of . For the random graph, the average node degree is obviously constant and equal to for all networks (cubic graphs were chosen for the comparison). The small variations of the average node degree for the two groups of WDNs (synthetic and real) is another aspect of the trend observed for link density in Figure 2; in fact, . Another important aspect to highlight is that the node degree distribution is almost homogeneous [61], i.e., almost all nodes have the same degree.
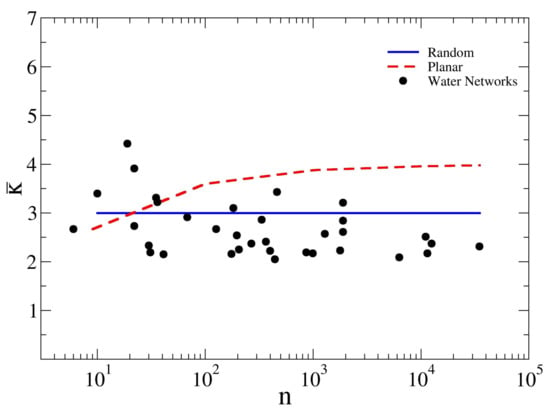
Figure 3.
Relationship between the average node degree and the network size n compared to the case of random regular networks and planar square grids. Notice that, due to boundary effects, the square grids approach their theoretical value only for large network sizes n. The blue continuous line and the broken red line refer to random graph and square grids, respectively. The black dots represent the studied WDNs. For numerical values, please see Table 2.
Hence, water distribution networks are not characterized by the presence of hubs—nodes with very high degree—that happens in the case of scale free networks. This leads to the immediate consequence that generally WDNs are almost equally robust against both intentional and accidental pipe breaks. In this case, by taking into account the relationship , it is possible to better interpret the typical values shown by WDNs. It results , which implies that is the lowest possible value for WDNs (i.e., no loops), and that values above 2 are related to the number of loops and thus to the ratio . In this respect, the average node degree can be used as a surrogate measure of robustness, quantifying how a WDN is far from a line shaped network (for which ).
In Figure 4, the diameter D is plotted in log–log scale as a function of the number of nodes n. It is clear that the graph diameter, for both synthetic and real WDNs, increases as the network size increases, following a power law, with . Thus, differently from communication systems, WDNs do not represent the peculiar features of Small-World networks, for which—similar to in random networks—. Such a feature leads to robustness in communications, since the average shortest path between two nodes increases very slowly with the network size. The larger diameter graph for the WDNs is due to economic and physical/geographic constraints that generally do not allow the presence of long-range links, except in rare cases [29]. In fact, it is well known that even a small fraction of links between distant nodes in a network can significantly shorten the path lengths [4]. It is clear that, also from a communication point of view, square grids and WDNs show a similar structure. In fact, in the SG, the nodes are always linked to the adjacent neighborhoods. It means that, from a global communication point of view, the possible presence of few long-range links in WDNs is not enough to reduce D, which also corresponds to the maximum of the shortest paths between nodes. Conversely, the random regular graphs, with the same number of nodes and with an average node degree close to WDNs, show a significantly lower diameter. In particular, they can be well fitted by a , as expected in general for random graphs [58].
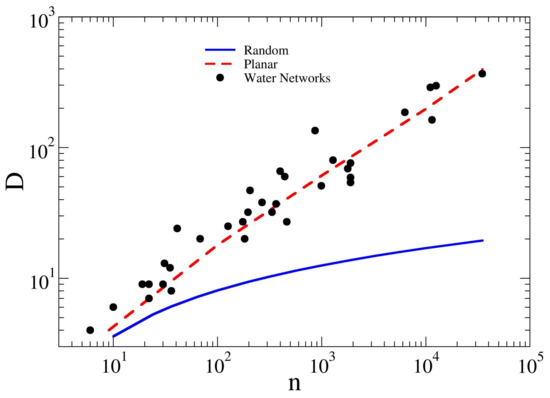
Figure 4.
Plot of the diameter D versus the network size n for synthetic and real water networks, planar square grids and random graphs. Notice that, similar to planar square grids, water networks also show the scaling that is expected for planar spatial networks. The blue continuous line and the broken red line refer to random graph and square grids, respectively. The black dots represent the studied WDNs. For numerical values, please see Table 2.
In Figure 5, the average path length l is plotted in log–log scale as a function of the number of nodes n. The trend clearly resembles that of the diameter, as shown in Figure 3. In particular, l increases as the network size increases following a power law, with , for the same reasons described above. In this case, the square grids follow a trend very close to WDNs, while the random graphs confirm their better flow communication, showing a logarithmic increase of the average path length. It can be observed that the scaling of D and l in WDNs reflects their embedding in a 2D-spatial environment. Very differently, the randomness of the cubic graphs provides the possibility to also have long-range connections that drastically reduce the length of the shortest paths between each pair of nodes. In this case, the global communication of the WDNs is strongly influenced by the fact that most nodes are linked to the adjacent neighborhoods, which makes them very similar to the SG, for which all the nodes are always and only linked to the adjacent neighborhoods.
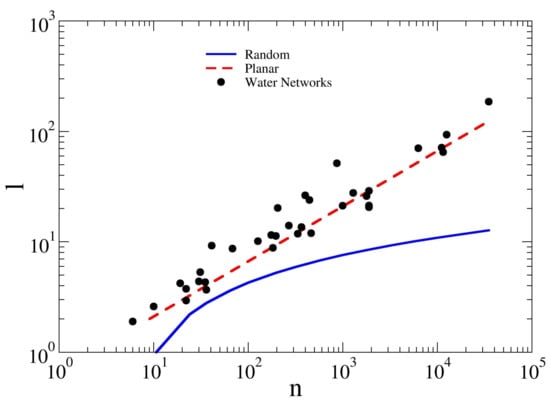
Figure 5.
Plot of the average path length l versus the network size n for synthetic and real water networks, square grids and random graphs. Notice that, similar to planar square grids, water networks also show the scaling that is expected for planar spatial networks. The blue continuous line and the broken red line refer to random graph and square grids, respectively. The black dots represent the studied WDNs. For numerical values, please see Table 2.
In Figure 6, the inverse of the spectral index is plotted in semi-log scale as a function of the water distribution network size n. It is possible to identify a typical WDN range with , and so for , which is related to the general relationship according to which [33]. For this reason, the inverse spectral radius of cubic random graphs assumes the constant value , while for square grids it tends asymptotically to (for these networks the maximum node degree is equal to 4 and the larger the number of the network nodes, the fewer of them are boundary nodes, which have a degree smaller than 4). Finally, for the water distribution networks, is nearly invariant with the size of the network. It means that, even if the size of the water network increases, the topology does not vary. Since the spectral radius is linked to the “velocity of spread” of a substance in the presence of percolation dynamics, it means that for WDNs it is possible to define a characteristic value of the intrinsic capacity of being crossed by a substance, water flow or contaminant. In this regard, the nearly invariant value of the spectral index suggests that, in general, the probability of the spreading of a contaminant from a point to another in a WDN does not depend on its dimension, as, apart from the hydraulic characteristics of the system, it is strongly related to the number of connections of each node. The value of the spectral index for WDNs falls between that of RG and SG as the number of nodes increases. It can be observed that the SG are the most vulnerable in terms of substance spreading, since most of the nodes have a degree equal to 4, while the RG, having a degree equal to 3 for all nodes, show the lowest value of . For WDNs, even if the average node degree is usually lower than RG, the small fraction of nodes with a degree higher than 3 gives WDNs a higher capability of being crossed by a substance. It can also be observed that the relation indicates that the spectral radius simultaneously quantifies global and local connectivity of the network. In fact, the lowest bound is related to the number of loops, while the highest is related to the presence of hubs.
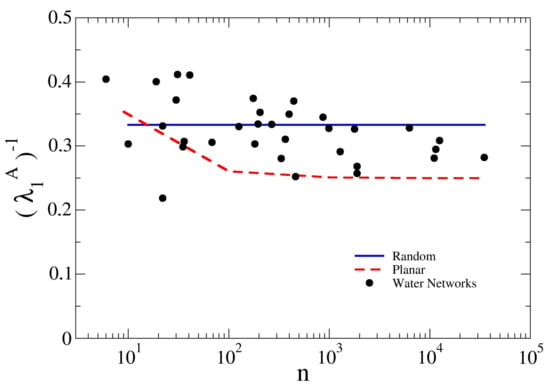
Figure 6.
Relationship between the inverse of the spectral index and the network size n for water networks, random cubic networks and planar square grids. The blue continuous line and the broken red line refer to random graph and square grids, respectively. The black dots represent the studied WDNs. For numerical values, please see Table 2.
In Figure 7, the behavior of the spectral gap is plotted in log–log scale as a function of the network size n. A decreasing trend of the spectral metric with increasing size is visible for all the studied networks, which could be fitted with a power scaling law . While, for square grids and random graphs, the trends are quite clear—respectively, a power law decay and an exponential decay to a plateau—for WDNs, the trend with network size is less clearly defined. However, the dots representing the studied WDNs fall between the trend lines of square grids and random graphs. As a small indicates high probability of having articulation points or bridges (the failure of which can cause the disconnection of the network in more sub-regions), this result points out that large WDNs tend to be increasingly less robust against disconnection. It is also clear that random graphs show a higher robustness than the square grids, since they show a higher value of the spectral gap . This is due first to the fact that the chosen cubic graphs have constant average node degree which guarantees that all nodes are linked to other three nodes. Furthermore, their randomness ensures the presence of long-range links that lead to a more cohesive and compact structure. Clearly, this metric does not depend on the number of connections, but rather on how nodes are connected to each other. In fact, the SG have highest , but at the same time they show the smallest spectral gap. In this respect, the possible presence of few long-range links gives some randomness to WDNs, thus resulting more similar to RG. This behavior resembles the concept of Pseudorandom graph (e.g., Torres et al. [18]), in which random connections are allowed only between neighboring nodes.
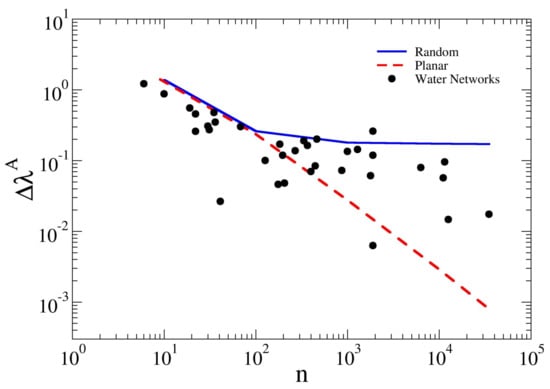
Figure 7.
Relationship between the spectral gap and the network size n. For the water networks, the fit of the data points is a power law ; for the random networks, thick line is fitting to an exponential approach to a plateau value of ; and, for the square grids, to a power law . The blue continuous line and the broken red line refer to random graph and square grids, respectively. The black dots represent the studied WDNs. For numerical values, please see Table 2.
In Figure 8, the behavior of the algebraic connectivity is plotted in log–log scale as a function of the network size n. A clear decrease of the connectivity metric with increasing size can be seen for all the networks, confirming the results of the spectral gap, but with clearer trends. Specifically, the water distribution networks and the square grids show a power law behavior, respectively, and , thus both curves tend to zero for increasing system size. This implies that the robustness of these networks, and in particular of WDNs, decreases as the number of nodes increase, with a high probability to have bottlenecks that can be easily broken with small effort (low value of ). The algebraic connectivity of WDNs results always smaller than for the square grids, implying in general lower robustness, owing to the smaller number and less regularity of the connections between nodes. On the other hand, the randomness of the k-regular graphs provides a higher robustness to the system: in fact, the algebraic connectivity shows an exponential trend , approaching a plateau value of = 0.17; hence, fragility does not increase with system size but stabilizes at a constant value. Hence, the algebraic connectivity indicates that large WDNs can be easily subdivided (i.e., create clusters with high density intra-clusters and low density infra-clusters), meaning that, as suggested by Wang et al. [28] for power grids, WDNs show a nested layout. In other words, it is easy to identify regions with different levels of density that can be isolated from the rest of the network. Clustering seems to constitute an intrinsic topological property of WDNs.
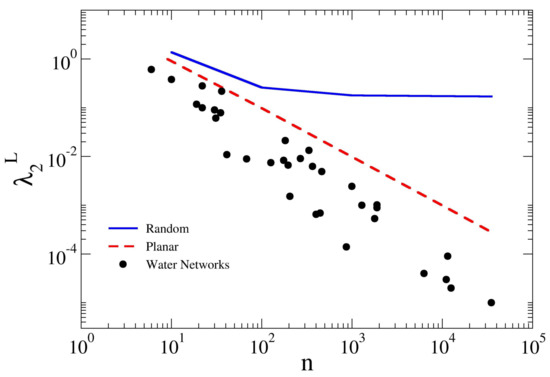
Figure 8.
Relationship between the algebraic connectivity and the network size n. For the water networks, the fit of the data points is a power law ; for the random networks, thick line is fitting to an exponential approach to a plateau value of ; and, for the square grids, to a power law . The blue continuous line and the broken red line refer to random graph and square grids, respectively. The black dots represent the studied WDNs. For numerical values, please see Table 2.
Given a graph , a community (or cluster, or cohesive subgroup) is a sub-graph , whose nodes are tightly connected, i.e., cohesive. The community structure of the complex network systems constitutes a powerful tool for better understanding the functioning of the network itself, as well as for identifying a hierarchy of connections within a complex architecture. Different metrics can lead to different communities; however, for physical networks, one of the most natural methods to partition its graph in reasonable communities is spectral partitioning [62], since it allows the separation into subgraphs minimizing the number of links between such subgraphs. Spectral partitioning uses the eigenvectors of the Laplacian matrix of a graph to determine the subgraphs corresponding to separate communities. To optimize the number of such communities, it is customary to look at the eigengap, i.e., at the maximum jump in the spectrum of the Laplacian matrix. According to such a criterion, only the eigenvectors whose eigenvalue is smaller than the eigengap are used to partition the network; in this regard, it has been shown that the eigengap can constitute a valid and useful tool to solve the problem of establishing a preliminary number of districts for the water network partitioning [16], according to only topological criteria, especially when no other information is available. In Figure 9, the first largest eigengap of the Laplacian matrix is used to calculate the optimal number of cluster as a function of the network size n. It looks clear how the number of clusters in which the water distribution networks are divided according to increases with the system size. In particular, it follows approximatively a power law . Hence, the number of districts grows sub-linearly with the network size, indicating that the optimal number of districts does not increase significantly with system size. It is worth noticing that, since grows sub-linearly, the number of partitions grows more slowly than the number of elements of the network. Hence, for large water networks, the size of optimal districts grows, compared to small water networks. It is worth noting that this result holds for network partitioning only from the topological point of view, while also the aims of the sectorization of the network should be considered in the choice of the optimal dimension of districts. In fact, it is known that the larger districts are, the more difficult is the identification of bursts and leakages from night flow data, although smaller districts imply higher costs for valves, flow meters and maintenance. Conversely, in terms of network safety against accidental or intentional water contamination, the larger is the district, the larger is the number of users potentially exposed to injected pollutants.
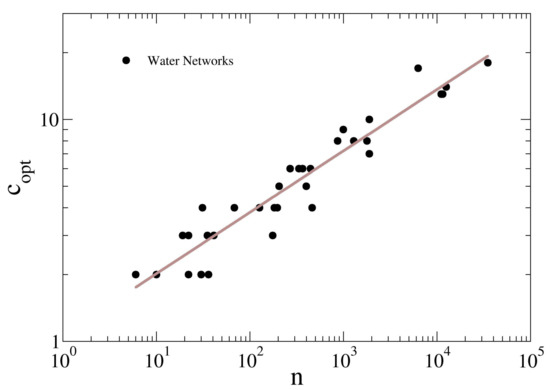
Figure 9.
Relationship between the optimal number of clusters and the network size n. The thick brown line is a power law fit for the analyzed water networks, yielding , providing an indication for the optimal number of District Metered Areas (DMAs) of a water network of given size. The black dots represent the studied WDNs. For numerical values, please see Table 2.
However, the obtained result points out that, in large WDNs, the size of the districts should necessarily increase. Otherwise, the benefits of an easier management guaranteed by smaller districts would be partly nullified by the increased vulnerability (or lower robustness) of the network, caused by the excessive fragmentation.
5. Conclusions
The topological analysis of several real and synthetic water distribution networks shows that such networks tend to be sparse, being characterized by small values of the average degree and of the link density . The nearly homogeneous value of the node degree marks a distance between WDNs and scale-free networks. The studied networks show many characteristics of planar lattices, since both the diameter D and the average path length l scale as . Such power law trends confirm that WDNs, similar to power grids or street networks, cannot be modeled as small world systems. Summarizing, all the evaluated topological connectivity metrics indicate that the graphs of WDNs are far from being totally random, as often claimed in theoretical studies, and rather resemble regular square grids.
The analysis of the spectral metrics, however, points out that WDNs present some randomness which can have a positive effect on their topological robustness, despite the geographical constraints, which make them close to planar graphs. In fact, for large network size, both the spectral index and the spectral gap fall in between the values of random graphs and square grids. On the one side, the spectral index , similar to planar lattices (for which ), results nearly constant with network size, indicating that WDNs are topologically protected from the spread of a contaminant, apart from the hydraulic characteristics of the pipes. On the other side, the decreasing trend of the spectral gap with the network size indicates the presence of bottlenecks and articulation points, but not leading to the complete disintegration of the network, as for regular square grids. In fact, while the strongly decreasing trend of the algebraic connectivity with the network size indicates that the “energy” required to break the network into independent sub-regions becomes lower, the optimal number of clusters , identified by means of the eigengap , grows less than linearly with the network size. Such a sub-linear growth hints that, from a connectivity point of view, the larger the WDN, the larger is the optimal size of DMAs.
The topological analysis of an extensive number of real and synthetic water distribution networks indicates that it is possible to identify a limited set of metrics that completely characterize the topological structure of WDNs. In particular, the average node degree strongly influences the values of the spectral index and of the link density q. Regarding the communication metrics, it is evident that the graph diameter D and the average path length l provide nearly the same information about the topology of a WDN. It seems preferable to use l, since it expresses a mean value over all paths, and because it is more sensitive than D to the addition or removal of an edge. The comparison between the two spectral robustness metrics, the spectral gap and the algebraic connectivity , suggests that, in the case of WDNs, the latter is more significant, both because it is strongly related to the strength needed to split the network into sub-regions, and because it shows a clearer trend with the network size. Finally, from a topological connectivity point of view, the eigengap provides a quick and good estimate of the optimal number of districts for the partitioning of a WDN.
According to the results presented in this study, the topological structure of WDN is very far from the “totally” random networks often used in theoretical studies. Similar to the concept of Nested-Smallworld, introduced for power-grids [28], and to the concept of Pseudorandom graph, introduced by Torres et al. [18], WDNs could be classified as a novel structure defined as Nested-Pseudorandom graph, because they show simultaneously nested and pseudorandom characteristics. In particular, such a model is the result of connecting several pseudorandom sub-networks through few long-range links, also in accordance with the above mentioned intrinsic clustering property of WDNs.
The typical values of the topological metrics calculated in this paper could be used to generate graphs of synthetic water distribution networks, which retain the topological characteristics of real WDNs, e.g., through a graph generating software. This would allow having many test cases for modeling purposes (it is not always easy to have the data and the graph of real WDNs), with realistic topologies and with network size. In this respect, the automatic generation would be a useful tool, as the currently used synthetic WDNs generally have small dimensions.
Acknowledgments
AS thanks CNR-PNR National Project “Crisis-Lab” for support. The contents of the paper do not necessarily reflect the position or the policy of funding parties. This research is part of the Ph.D. project “Water distribution network management optimization through Complex Network theory” within the Doctoral Course “A.D.I.” granted by Universita’ degli Studi della Campania “L. Vanvitelli”.
Author Contributions
All authors contributed equally to the paper.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| WDN | Water Distribution Network |
| CWDN | Complex Water Distribution Network |
| DMAs | District Metered Areas |
References
- Dorogovtsev, S.N.; Mendes, J.F.F. Evolution of Networks: From Biological Nets to the Internet and WWW (Physics); Oxford University Press, Inc.: New York, NY, USA, 2003. [Google Scholar]
- D’Agostino, G.; Scala, A. (Eds.) Networks of Networks: The Last Frontier of Complexity; Understanding Complex Systems; Springer: Berlin, Germany, 2014. [Google Scholar]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabasi, A.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Estrada, E. Network robustness to targeted attacks. The interplay of expansibility and degree distribution. Eur. Phys. J. B Condens. Matter Complex Syst. 2006, 52, 563–574. [Google Scholar] [CrossRef]
- Faloutsos, M.; Faloutsos, P.; Faloutsos, C. On power-law relationships of the Internet topology. Comput. Commun. Rev. 1999, 29, 251–262. [Google Scholar] [CrossRef]
- Vogelstein, B.; Lane, D.; Levine, A.J. Surfing the p53 network. Nature 2000, 408, 307–310. [Google Scholar] [CrossRef] [PubMed]
- Mays, L.W. Water Distribution Systems Handbook; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Tzatchkov, V.G.; Alcocer-Yamanaka, V.H.; Ortiz, V.B. Graph Theory Based Algorithms for Water Distribution Network Sectorization Projects. In Proceedings of the Eighth Annual Water Distribution Systems Analysis Symposium (WDSA), Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Yazdani, A.; Jeffrey, P. Robustness and Vulnerability Analysis of Water Distribution Networks Using Graph Theoretic and Complex Network Principles. In Proceedings of the 12th Annual Conference on Water Distribution Systems Analysis (WDSA), Tucson, AZ, USA, 12–15 September 2010. [Google Scholar]
- Yazdani, A.; Jeffrey, P. Complex network analysis of water distribution systems. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 016111. [Google Scholar] [CrossRef] [PubMed]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F.; Simone, A. Water Distribution System Clustering and Partitioning Based on Social Network Algorithms. Procedia Eng. 2015, 119, 196–205. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Rodriguez Varela, J.; Santonastaso, G.; Simone, A.; Tzatchkov, V. Redundancy Features of Water Distribution Systems. Procedia Eng. 2017, 186, 412–419. [Google Scholar] [CrossRef]
- Herrera, M.F. Improving Water Network Management by Efficient Division into Supply Clusters. Ph.D. Thesis, Universitat Politécnica de Valencia, Valéncia, Spain, 2011. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R.; Santonastaso, G.F. Water Supply Network Partitioning Based On Weighted Spectral Clustering. In Complex Networks & Their Applications V: Proceedings of the 5th International Workshop on Complex Networks and their Applications (COMPLEX NETWORKS 2016); Cherifi, H., Gaito, S., Quattrociocchi, W., Sala, A., Eds.; Springer: Cham, The Netherland, 2017; pp. 797–807. [Google Scholar]
- Santonastaso, G.F.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Greco, R. Scaling-Laws of Flow Entropy with Topological Metrics of Water Distribution Networks. Entropy 2018, 20, 95. [Google Scholar] [CrossRef]
- Torres, J.M.; Duenas-Osorio, L.; Li, Q.; Yazdani, A. Exploring Topological Effects on Water Distribution System Performance Using Graph Theory and Statistical Models. J. Water Resour. Plan. Manag. 2017, 143, 04016068. [Google Scholar] [CrossRef]
- Facchini, A.; Scala, A.; Lattanzi, N.; Caldarelli, G.; Liberatore, G.; Maso, L.D.; Nardo, A.D. Complexity Science for Sustainable Smart Water Grids. In Italian Workshop on Artificial Life and Evolutionary Computation; Springer: Cham, The Netherland, 2017; Volume 708. [Google Scholar]
- Zodrow, K.R.; Li, Q.; Buono, R.M.; Chen, W.; Daigger, G.; Duenas-Osorio, L.; Elimelech, M.; Huang, X.; Jiang, G.; Kim, J.H.; et al. Advanced Materials, Technologies, and Complex Systems Analyses: Emerging Opportunities to Enhance Urban Water Security. Environ. Sci. Technol. 2017, 51, 10274–10281. [Google Scholar] [CrossRef] [PubMed]
- Todini, E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Santonastaso, G.; Savic, D. Simplified Approach to Water Distribution System Management via Identification of a Primary Network. J. Water Resour. Plan. Manag. 2018, 144, 04017089. [Google Scholar] [CrossRef]
- Prasad, T.D.; Park, N.S. Multiobjective Genetic Algorithms for Design of Water Distribution Networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water Distribution Reliability: Analytical Methods. J. Water Resour. Plan. Manag. 1988, 114, 253–275. [Google Scholar] [CrossRef]
- Goulter, I.C.; Bouchart, F. ReliabilityConstrained Pipe Network Model. J. Hydraul. Eng. 1990, 116, 211–229. [Google Scholar] [CrossRef]
- Rouse, W.B. Complex engineered, organizational and natural systems. Syst. Eng. 2007, 10, 260–271. [Google Scholar] [CrossRef]
- Jamakovic, A.; Uhlig, S. On the relationships between topological measures in real-world networks. Netw. Heterog. Media 2008, 3, 345–359. [Google Scholar] [CrossRef]
- Wang, Z.; Scaglione, A.; Thomas, R. Generating Statistically Correct Random Topologies for Testing Smart Grid Communication and Control Networks. IEEE Trans. Smart Grid 2010, 1, 28–39. [Google Scholar] [CrossRef]
- Amaral, L.A.N.; Scala, A.; Barthélémy, M.; Stanley, H.E. Classes of small-world networks. Proc. Natl. Acad. Sci. USA 2000, 97, 11149–11152. [Google Scholar] [CrossRef] [PubMed]
- Fiedler, M. Algebraic Connectivity of Graphs. Czech. Math. J. 1973, 23, 298–305. [Google Scholar]
- Watts, D.J. Small Worlds: The Dynamics of Networks Between Order and Randomness; Princeton University Press: Princeton, NJ, USA, 1999; p. xv. 262p. [Google Scholar]
- Bonacich, P. Power and Centrality: A Family of Measures. Am. J. Sociol. 1987, 92, 1170–1182. [Google Scholar] [CrossRef]
- Arsic, B.; Cvetkovic, D.; Simic, S.K.; Skaric, M. Graph spectral techniques in computer sciences. Appl. Anal. Discret. Math. 2012, 6, 1–30. [Google Scholar] [CrossRef]
- Donetti, L.; Neri, F.; Munoz, M.A. Optimal network topologies: Expanders, cages, Ramanujan graphs, entangled networks and all that. J. Stat. Mech. Theory Exp. 2006, 2006, P08007. [Google Scholar] [CrossRef]
- Von Luxburg, U. A Tutorial on Spectral Clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Perelman, L.S.; Michael, A.; Ami, P.; Mudasser, I.; Whittle, A.J. Automated sub-zoning of water distribution systems. Environ. Model. Softw. 2015, 65, 1–14. [Google Scholar] [CrossRef]
- Chung, F.R.K. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Alperovits, E.; Shamir, U. Design of optimal water distribution systems. Water Resour. Res. 1977, 13, 885–900. [Google Scholar] [CrossRef]
- Gessler, J. Pipe network optimization by enumeration. In Proceedings of Computer Applications for Water Resources, New York; ASCE: Reston, VA, USA, 1985; pp. 572–581. [Google Scholar]
- Murphy, L.; Simpson, A.; Dandy, G. Pipe Network Optimization Using an Improved Genetic Algorithm; Research Report; Rep.109; University of Adelaide, Department of Civil and Environmental Engineering: Adelaide, Australia, 1993. [Google Scholar]
- Kim, J.; Kim, T.; Yoon, Y. A study on the pipe network system design using non-linear programming. J. Korean Water Resour. Assoc. 1994, 27, 59–67. [Google Scholar]
- Walski, T.; Brill, E.; Gessler, J.; Goulter, I.; Jeppson, R.; Lansey, K.; Lee, H.; Liebman, J.; Mays, L.; Morgan, D.; et al. Battle of the network models: Epilogue. J. Water Resour. Plan. Manag. ASCE 1987, 113, 191–203. [Google Scholar] [CrossRef]
- Sherali, H.D.; Subramanian, S.; Loganathan, G. Effective Relaxations and Partitioning Schemes for Solving Water Distribution Network Design Problems to Global Optimality. J. Glob. Optim. 2001, 19, 1–26. [Google Scholar] [CrossRef]
- Fujiwara, O.; Khang, D.B. A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour. Res. 1990, 26, 539–549. [Google Scholar] [CrossRef]
- Lee, S.C.; Lee, S.I. Genetic algorithms for optimal augmentation of water distribution networks. J. Korean Water Resour. Assoc. 2001, 34, 567–575. [Google Scholar]
- Bragalli, C.; D’Ambrosio, C.; Lee, J.; Lodi, A.; Toth, P. On the optimal design of water distribution networks: A practical MINLP approach. Optim. Eng. 2012, 13, 219–246. [Google Scholar] [CrossRef]
- Van Zyl, J.; Savic, D.; Walters, G. Operational optimization of water distribution systems using a hybrid genetic algorithm. J. Water Resour. Plan. Manag. 2004, 130, 160–170. [Google Scholar] [CrossRef]
- Ostfeld, A.; Uber, J.G.; Salomons, E.; Berry, J.W.; Hart, W.E.; Phillips, C.A.; Watson, J.P.; Dorini, G.; Jonkergouw, P.; Kapelan, Z.; et al. The Battle of the Water Sensor Networks (BWSN): A Design Challenge for Engineers and Algorithms. J. Water Resour. Plan. Manag. 2008, 134, 556–568. [Google Scholar] [CrossRef]
- Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Laspidou, C.; Morlando, F.; Santonastaso, G.; Kofinas, D. Spectral analysis and topological and energy metrics for water network partitioning of Skiathos island. Eur. Water 2017, 58, 423–428. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Gisonni, C. La distrettualizzazione delle reti idriche per il controllo delle pressioni (il sito pilota di Monteruscello). In Proceedings of the Atti del XXXI Convegno di Idraulica e Costruzioni Idrauliche, Perugia, Italy, 9–12 Settembre 2008. [Google Scholar]
- Herrera, M.; Canu, S.; Karatzoglou, R.; Perez-Garcia, R.; Izquierdo, J. An approach to water supply clusters by semi-supervised learning. In Proceedings of the International Congress on Environmental Modelling and Software Modelling (iEMSs) 2010 for Environment Sake, Fifth Biennial Meeting, Ottawa, ON, Canada, 5–8 July 2010. [Google Scholar]
- Marchi, A.; Salomons, E.; Ostfeld, A.; Kapelan, Z.; Simpson, A.R.; Zecchin, A.C.; Maier, H.R.; Wu, Z.Y.; Elsayed, S.M.; Song, Y.; et al. Battle of the Water Networks II. J. Water Resour. Plan. Manag. 2014, 140, 04014009. [Google Scholar] [CrossRef]
- Reca, J.; Martinez, J. Genetic algorithms for the design of looped irrigation water distribution networks. Water Resour. Res. 2006, 42, W05416. [Google Scholar] [CrossRef]
- Marchis, M.D.; Fontanazza, C.M.; Freni, G.; Loggia, G.L.; Napoli, E.; Notaro, V. A model of the filling process of an intermittent distribution network. Urban Water J. 2010, 7, 321–333. [Google Scholar] [CrossRef]
- Lippai, I. Colorado Springs Utilities Case Study: Water System Calibration/Optimization. In Pipelines 2005: Optimizing Pipeline Design, Operations, and Maintenance in Today’s Economy; American Society of Civil Engineers: Reston, VA, USA, 2005. [Google Scholar]
- Farmani, R.; Savic, D.A.; Walters, G.A. Evolutionary multi-objective optimization in water distribution network design. Eng. Optim. 2005, 37, 167–183. [Google Scholar] [CrossRef]
- Salomons, E.; Skulovich, O.; Ostfeld, A. Battle of Water Networks DMAs: Multistage Design Approach. J. Water Resour. Plan. Manag. 2017, 143, 04017059. [Google Scholar] [CrossRef]
- Erdos, P.; Renyi, A. On random graphs. Publ. Math. Debr. 1959, 6, 290–297. [Google Scholar]
- Wormald, N.C. Generating random regular graphs. J. Algorithms 1984, 5, 247–280. [Google Scholar] [CrossRef]
- McKay, B.D.; Wormald, N.C. Uniform generation of random regular graphs of moderate degree. J. Algorithms 1990, 11, 52–67. [Google Scholar] [CrossRef]
- Giustolisi, O.; Simone, A.; Ridolfi, L. Network structure classification and features of water distribution systems. Water Resour. Res. 2017, 53, 3407–3423. [Google Scholar] [CrossRef]
- Pothen, A.; Simon, H.D.; Liou, K.P. Partitioning Sparse Matrices with Eigenvectors of Graphs. SIAM J. Matrix Anal. Appl. 1990, 11, 430–452. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).