1. Introduction
The volume of water consumed per unit of time is the operating parameter of each water supply system. Great attention is currently paid to optimizing the pressure conditions in water supply systems. However, a major part of the optimizing approaches is dedicated to reduction of both water loss and energy cost [
1,
2]. The first step in reducing water losses is usually the revision of pressure conditions and their subsequent adjustment, enabling the optimum scope of pressure conditions while maintaining the hydraulic capacity of the mains. In most cases, pressures in the network are decreased to achieve reduced water loss and lower failure rates of the mains. Yet, evidently, with lowered pressure there is also a decrease in the volume of water billed to the individual consumers. Therefore, lowering the pressure in the network has a positive effect on water loss while having a negative effect on the volume of billed water and the economic performance of the company. In our experience in regard to this solution of optimization, waterworks operators stress the following criteria, listed in a decreasing order according to priority: (1) the economic aspect—the problem of water loss is solved strictly from an economic viewpoint. The effectiveness of each proposed measure is always calculated from the economic perspective of the company. Measures with negative economic effects are only implemented under the condition that they generate a significant secondary benefit other than economic (for example, environmental); (2) the environmental viewpoint—in cases where it is a relevant problem within the given situation, the capacity of the water source is considered. Reduction of water loss presents a decreased burdening of the source and the ecosystem as a whole; (3) quality of delivered water—reduction of water loss causes a decreased consumption of water, increasing the age of water in the network and, in specific cases, this may result in a higher frequency of complaints regarding its quality. This point of view is always considered individually with regard to the specific situation; (4) company prestige—last in terms of priorities, yet still a relevant criterion. Performance indicators of water companies are annually published in a country-wide professional almanac. Achieving outstanding results in the category of water loss is a matter of prestige.
In order for such water consumption to be included as a criterion in the optimization of pressure conditions, it is necessary to express it mathematically as a function of pressure. This mathematical description complicates its stochastic nature, as is apparent, for example, from [
3]. It has been proven that many more factors aside from pressure conditions have an effect on water consumption. Several previous studies have shown that water consumption is affected not only by customer price [
4,
5,
6], but also by climate factors [
6,
7,
8] and pressure in the water mains [
2,
5,
9,
10]. For example, in [
11] an analysis of the dependency of water produced for the city of Brno on meteorological factors was conducted and a certain dependency was indicated. This analysis was carried out for the entire water supply system. On the other hand, it should be noted that for each type of user the dependency on factors influencing consumption always varies (see e.g., [
12]). According to [
13] water consumption is divided for the purposes of simulating the changes in water consumption with pressure changes into “inside-the-house” and “outside-the-house”. Both areas of consumption then have different coefficients expressing their dependency on pressure. Subsequently, the average coefficient expressing dependency of pressure for the entire building and for each consumer is calculated. Subsequently, this cumulative coefficient per user is implemented into the FAVAD (Fixed and Variable Discharge) equation according to [
14], or into its simplified form according to [
13].
Nowadays, there are not many
N3 set coefficients within the meaning of [
13] based on real studies. For example the value of the “inside-the-house” consumption coefficient was set at 0.2 for the Johannesburg student campus at the University of Johannesburg in [
15]. Also worth mentioning is the principle of minimum pressure, which must be ensured in the water supply network so that the water supply can be realized. If this value is under-stepped, the volume of water supplied is considered zero [
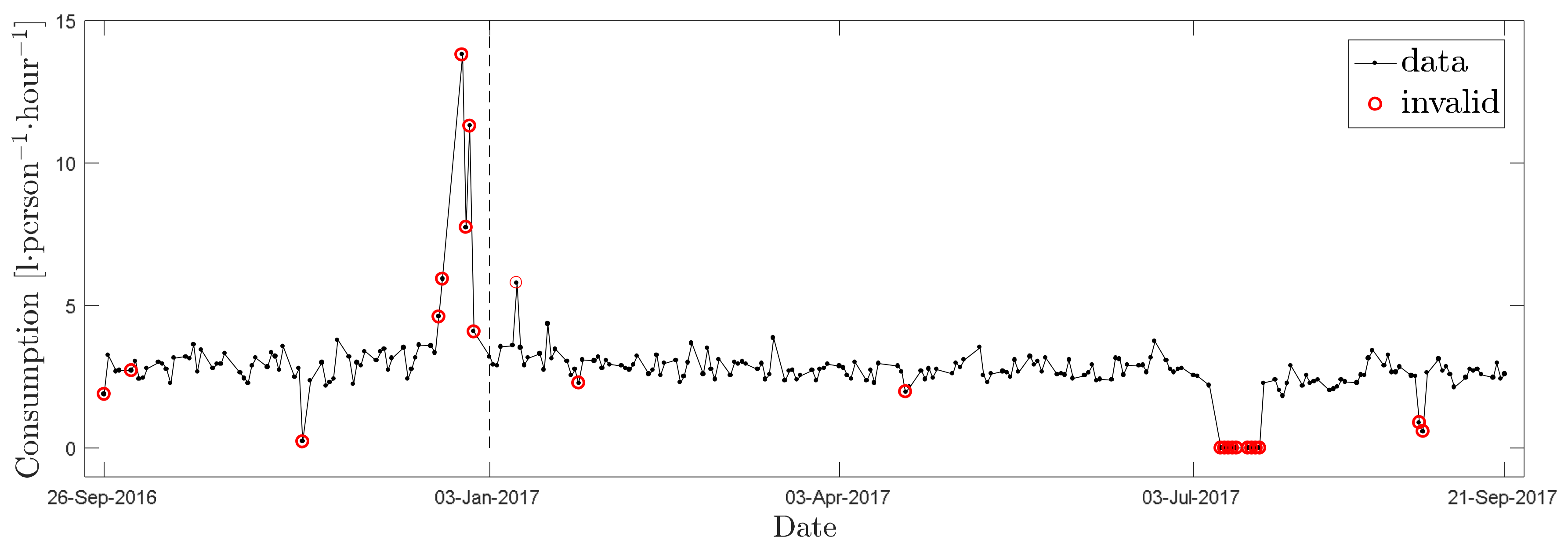
9]. In this study, the results of which are presented here, this limit was defined by valid legislation at 0.15 MPa and was not broken during the experiment.
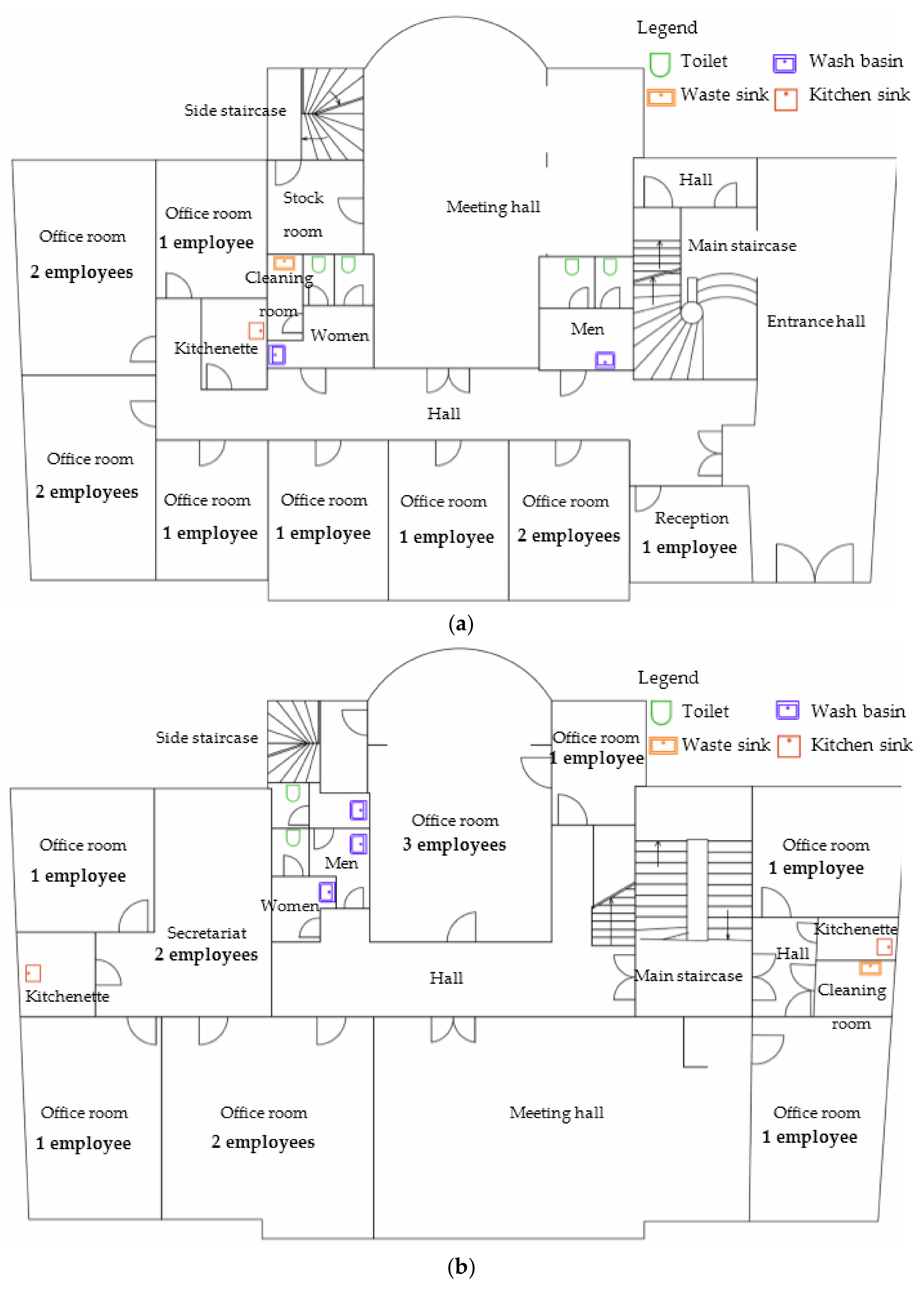
This paper provides information regarding the effect of water pressure and selected climatological factors on water consumption in an administrative building. It had three goals.
The first was to establish the value of the
N3 coefficient used in the FAVAD concept. In the past, a sufficient number of studies used the FAVAD concept, covering the entire spectrum of various types of end users. A new regressive model was not created for this purpose, but an existing model used according to [
13].
The second goal was to verify whether it is possible to predict water consumption under stable pressure conditions (albeit with various levels of pressure) on the basis of climatological factors, using linear regression.
The third goal was to extend the FAVAD concept into the area of water consumption prediction, according to [
13] and stipulate a regressive model with a newly added variable of climatological factor. All regression models were subject to statistical testing to confirm or reject their significance.
4. Discussion
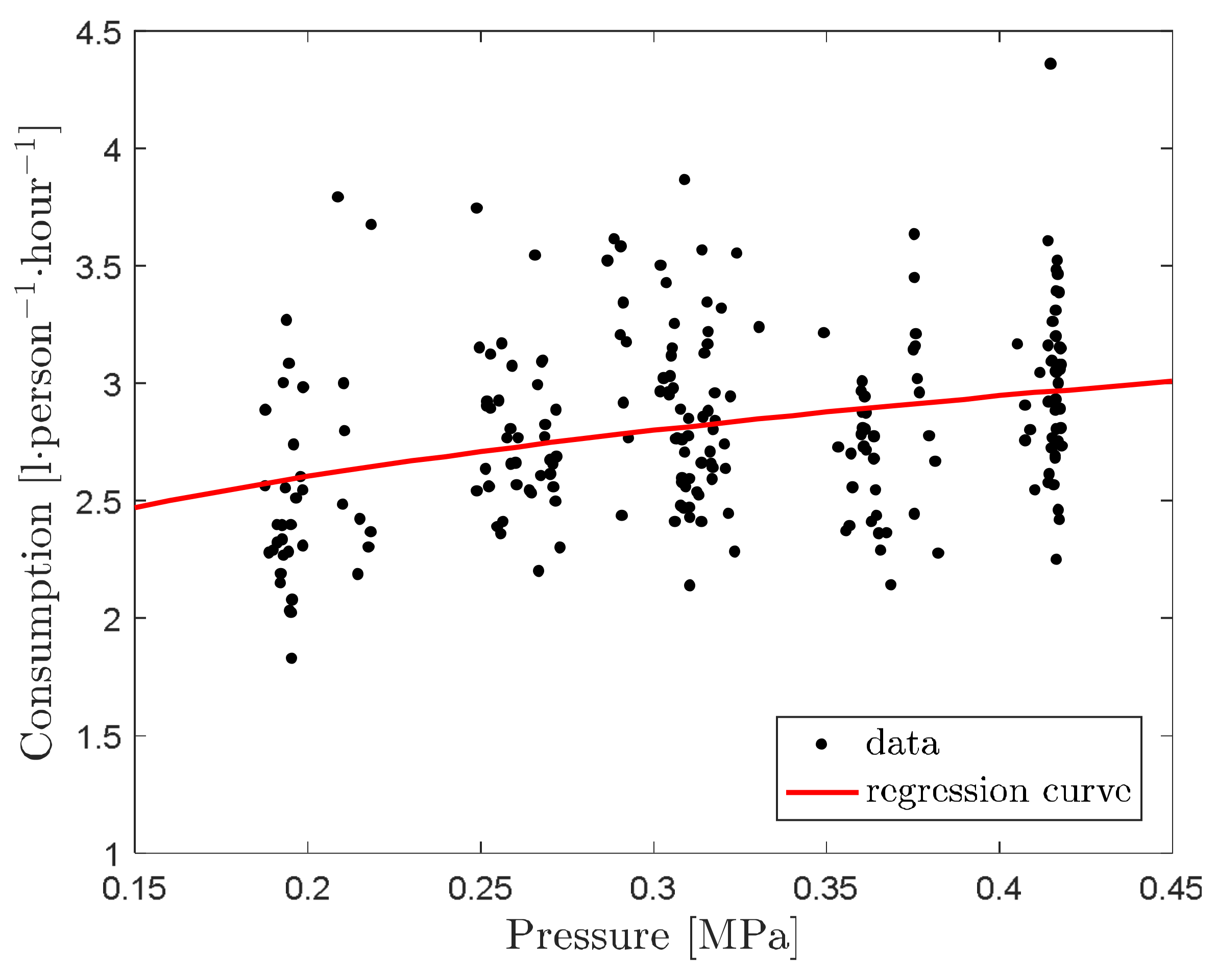
The analysis of data gained through measurement in this case study revealed that the
N3 coefficient value established by the FAVAD concept, according to [
13], for the respective administrative building reaches 0.179. Compared to our expectations, this value is rather high. In administrative buildings, a high percentage of water is used for flushing toilets, while these are often volumetric flushing systems with a pre-stored storage water tank. For example, according to [
32], water consumption for toilets in government and private administrative buildings in Singapore presents 37% of all overall consumption, while another 31% is water for cooling systems. Water consumption for cooling was zero in the building where our case study took place, because a cooling system is not installed. This results in a ratio of water used for flushing toilets to be a minimum of 50%, although this ratio was not specifically established during this study. Therefore, at least 50% of the overall volume of consumed water in this building is not dependent on water pressure in the mains.
The established value of the
N3 coefficient in this study is also rather high in comparison with [
15], where the
N3 value was established at 0.2. Although this is a higher value, the study was performed at a student campus with a considerable ratio of water consumption for personal hygiene purposes, as well as for gardening and irrigation, which are areas of consumption dependent on pressure.
According to a theoretical calculation, in the case of the given building, a reduction of pressure in the water mains to 50% of its original value would result in a decrease of overall consumption (not only during working hours) by 28 m3 year−1. This represents 12% of the overall annual water consumption in the entire building. The user would save approximately 100 € year−1.
However, from the perspective of water suppliers in the CZ in most cases, consumption reduction is undesirable both from an economic perspective and, in particular, concerning the decrease of water quality in the mains. Over the course of the last twenty years, historic development in the field of water mains and sewage experienced a drastic drop in specific water consumption per person and day. While in 1989, this value was approximately 250 L capita−1·day−1, today this value is approximately at half.
This change in water consumption is caused by significant economic and social transformations after 1989, as well as by an increase in the price of water. Water mains built between 1960 and 1990 that continue to fulfil their function today were planned for a considerably higher capacity. Today, with lower water consumption, their capacity is excessive and oversized. In water treatment facilities, this problem is solved relatively quickly by exchanging large pumps for smaller, or lowering the operational levels of water towers.
Unfortunately, in the case of water mains in the CZ that reached the overall length of 77,681 km as of 2016, this is a problem that clearly does not have a quick and cheap solution. Within a natural replacement of the networks, segments with excess capacity are replaced with pipes with smaller diameters and high-quality interior surfaces. Nonetheless, until all oversized networks are replaced, water-treatment operations must deal with problems regarding water quality that often result in both stagnation and excessive age. Further reduction of volumes delivered through the mains system is therefore undesirable, regardless of its economic effect.
As previously mentioned, reduction of water consumption reflects in the volume of invoiced water. With few exceptions, in the CZ each water connection is equipped with an invoicing water meter. The amount of the annual fee for drinking water delivered by the mains to the user is thus established on the basis of measuring the volume of water delivered through the water meter. Therefore, lower water consumption also means a lower collection of income for the water rate on the part of the mains operator.
Evidently, significant costs on the part of the mains operator are fixed and not based on volume produced or invoiced water. There are employee costs and asset depreciation to be considered. Only a smaller part of overall costs are variable, composed mostly of water taken from the sources and the use of chemicals.
A decrease in invoiced water volume must subsequently result in a re-calculation of the unit price of water, because the dominant fixed costs must be distributed across a lesser volume of invoiced water. The final consequence of water consumption reduction is an increase in the unit price of water, which is a trend that has been observed since 1989.
The price of water in the CZ is subject to approval by the Ministry of Finance of the CZ and limited by the socially acceptable price of water, which is close to today’s average water price. Therefore, water consumption reduction fails to bring any economic benefit to water suppliers in the CZ.
From the perspective of its environmental impacts, reduced water consumption clearly presents a positive trend. It decreases costs of energy production and water distribution, going hand-in-hand with decreased production of greenhouse gasses. It must be noted that in the case of a different model of operation and billing, this may also bring economic benefits to the operator.
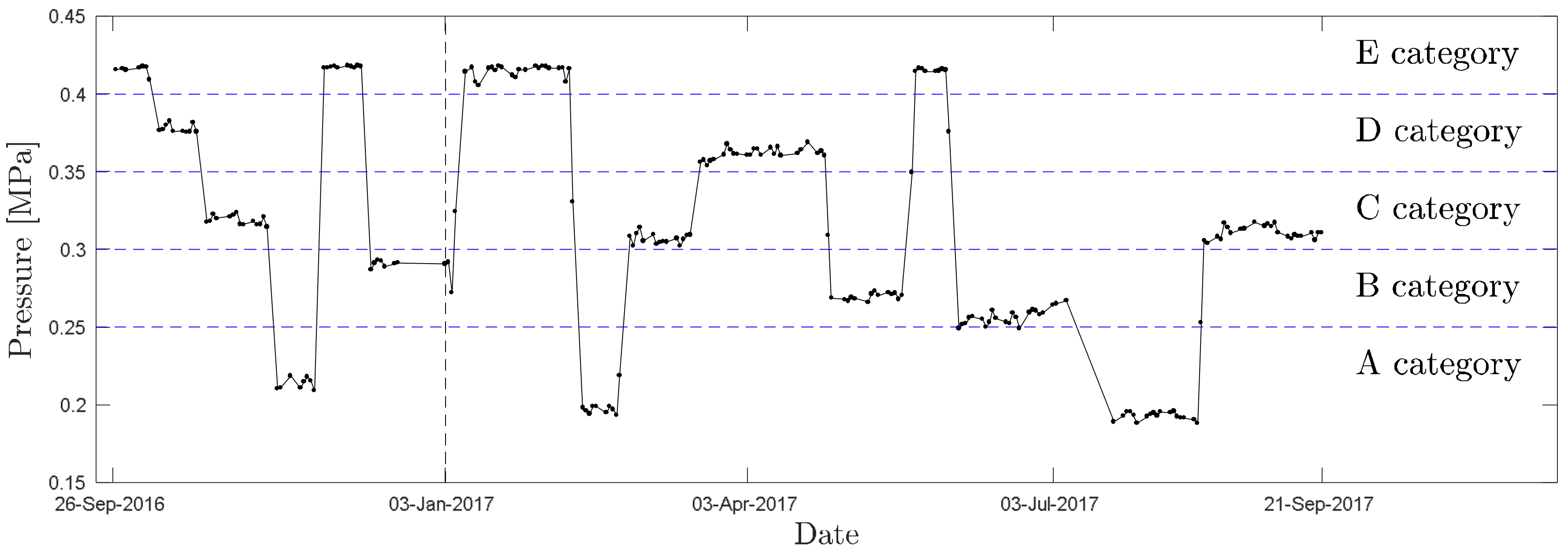
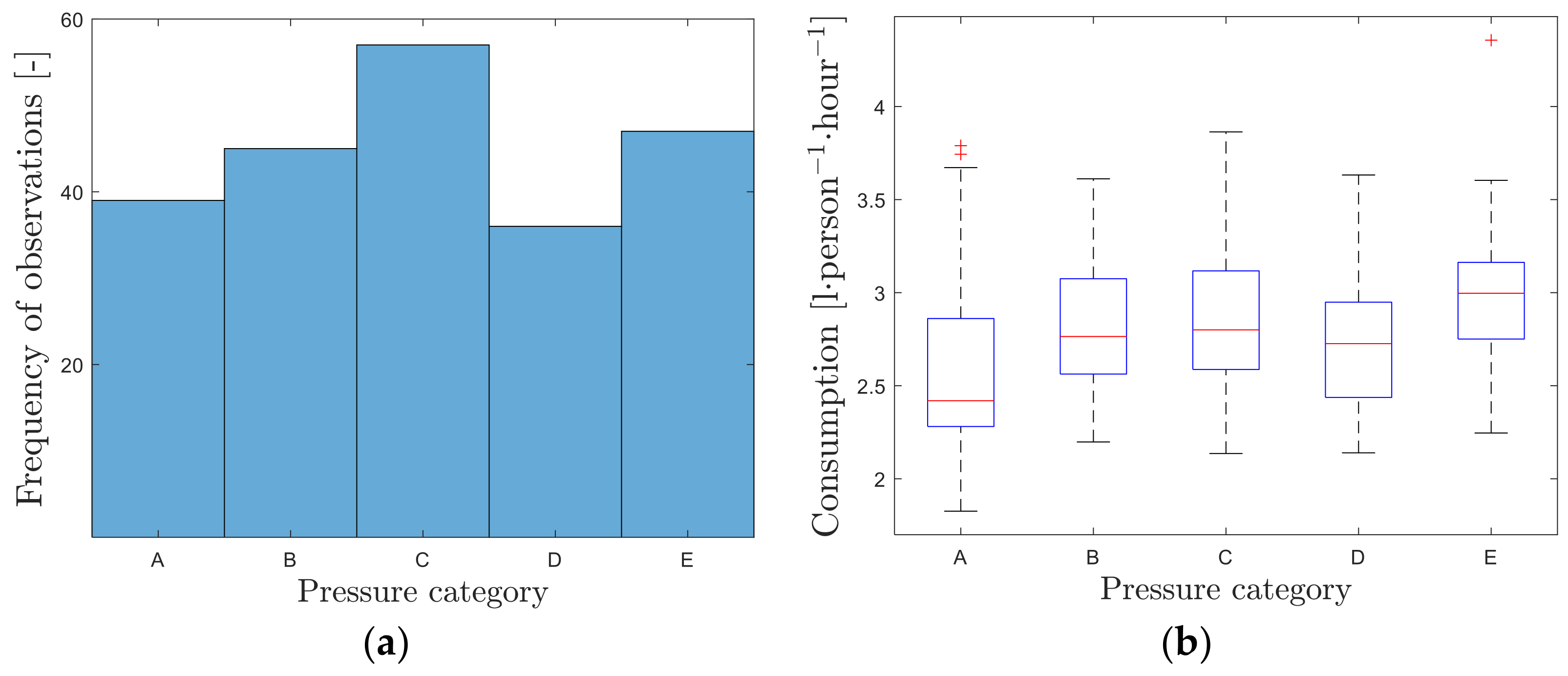
A separate evaluation of the effects of climatological factors in stable pressure conditions (however, at various levels of pressure) identified neither temperature nor humidity as significant variables for all pressure categories (at significance level 0.05). Even so, particularly in the case of temperature (a significant variable for categories A, B, and E), the same trend was apparent for all categories where, along with decreasing temperature, water consumption increased.
This is a rather unusual phenomenon that contradicts studies [
8,
33,
34] and other similar studies. Note that these studies focused more on the overall view of the water mains, rather than consumption in a specific building. This phenomenon can only be explained by the situation in a specific building where no showers were installed or other equipment for overall personal hygiene. Even at high summer air temperatures, water consumption in the building was not affected by more intensive personal hygiene factors.
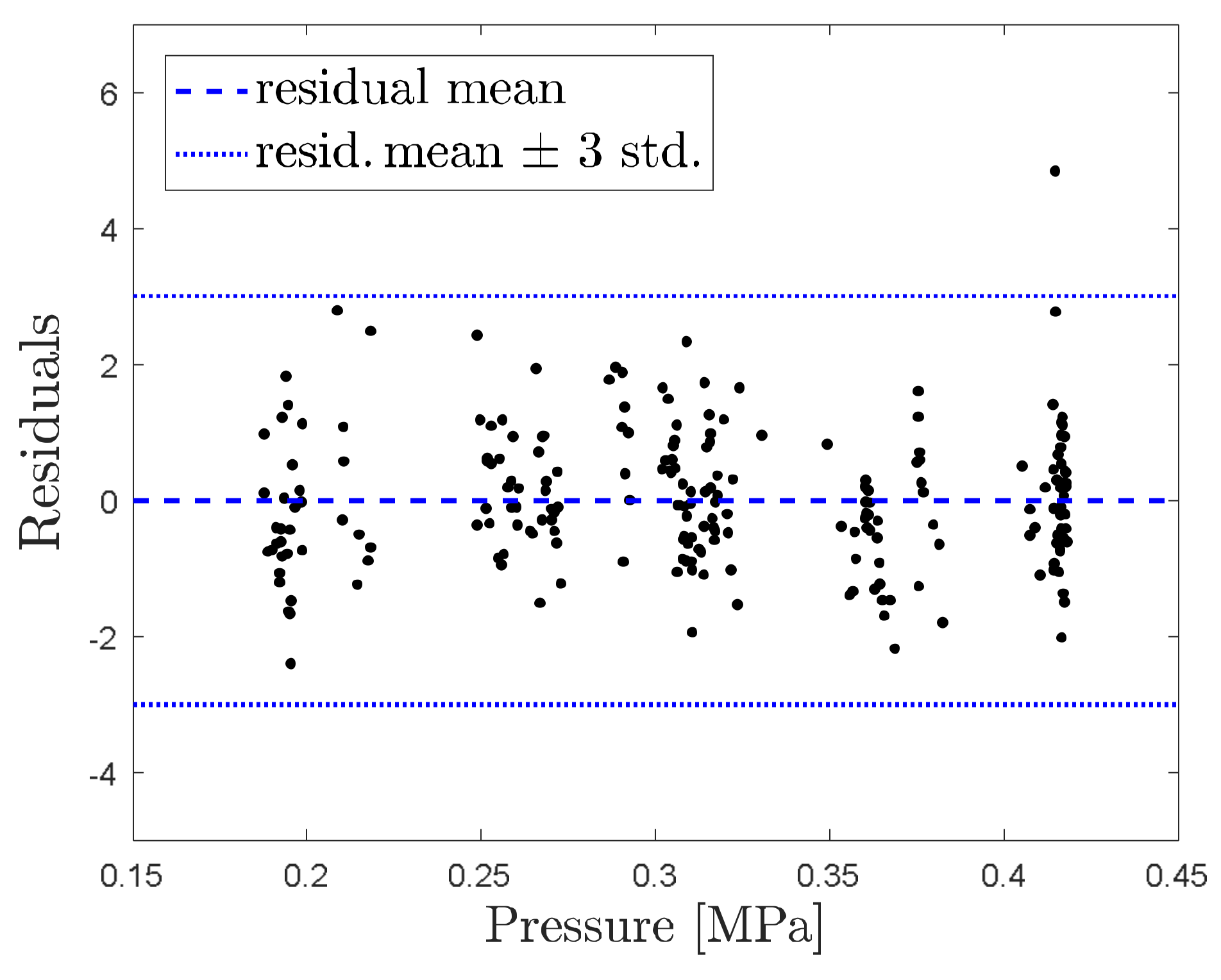
Upon establishing the regressive non-linear model (7), which was the expansion of the FAVAD concept by prediction of water consumption with an added climatological variable, the effect of temperature as a significant variable was confirmed. This also held, regarding a change of pressure. This is valid for air humidity as well, but the dependency of pressure and humidity is not as solid as that of pressure and temperature. This is also apparent from the N3 coefficient (upon using the (7) model), which reaches the value of 0.091 for temperature and 0.178 for humidity.
5. Conclusions
Our study of water consumption within an administrative building concluded that local linearization of the dependency on pressure is less suitable than the power regression function according to [
13], while the value of the
N3 coefficient for an administrative building was established at 0.179. Stipulating this value is important to establish realistic values for multiple types of users, using individual values of the
N3 coefficient for the optimization of pressure conditions in water distribution networks, including water consumption as an optimization criterion according to (3).
This method is not very common to date, although water consumption remains one of the most important performance indicators in systems supplying drinking water. From a long-term perspective of optimization of pressure conditions, the effect of pressure is the most significant, although consumption also depends on other factors. Unlike pressure, climatological factors cannot be influenced. In this situation, it is best to follow the relation (3).
However, our study also confirmed the effect of climatological factors on water consumption, as a regressive model (7) was established for quantifying these mutual interactions. Testing found that temperature has a significantly higher effect on consumption in interaction with pressure. This finding can be used in the form of a regressive model (7) such as in the operative management of pressure conditions in water mains.
Regarding all of the above results, caution must be applied in generalizing these results for entire water main systems. Dependence of water consumption on pressure and climatological factors varies for each type of user. Therefore, it is necessary (and in the future, will likely be a goal of the authors) to perform further similar real-life studies for varied types of users to develop a wide range of realistic N3 coefficient values.