Model-Based Analysis of the Potential of Macroinvertebrates as Indicators for Microbial Pathogens in Rivers
Abstract
1. Introduction
2. Materials and Methods
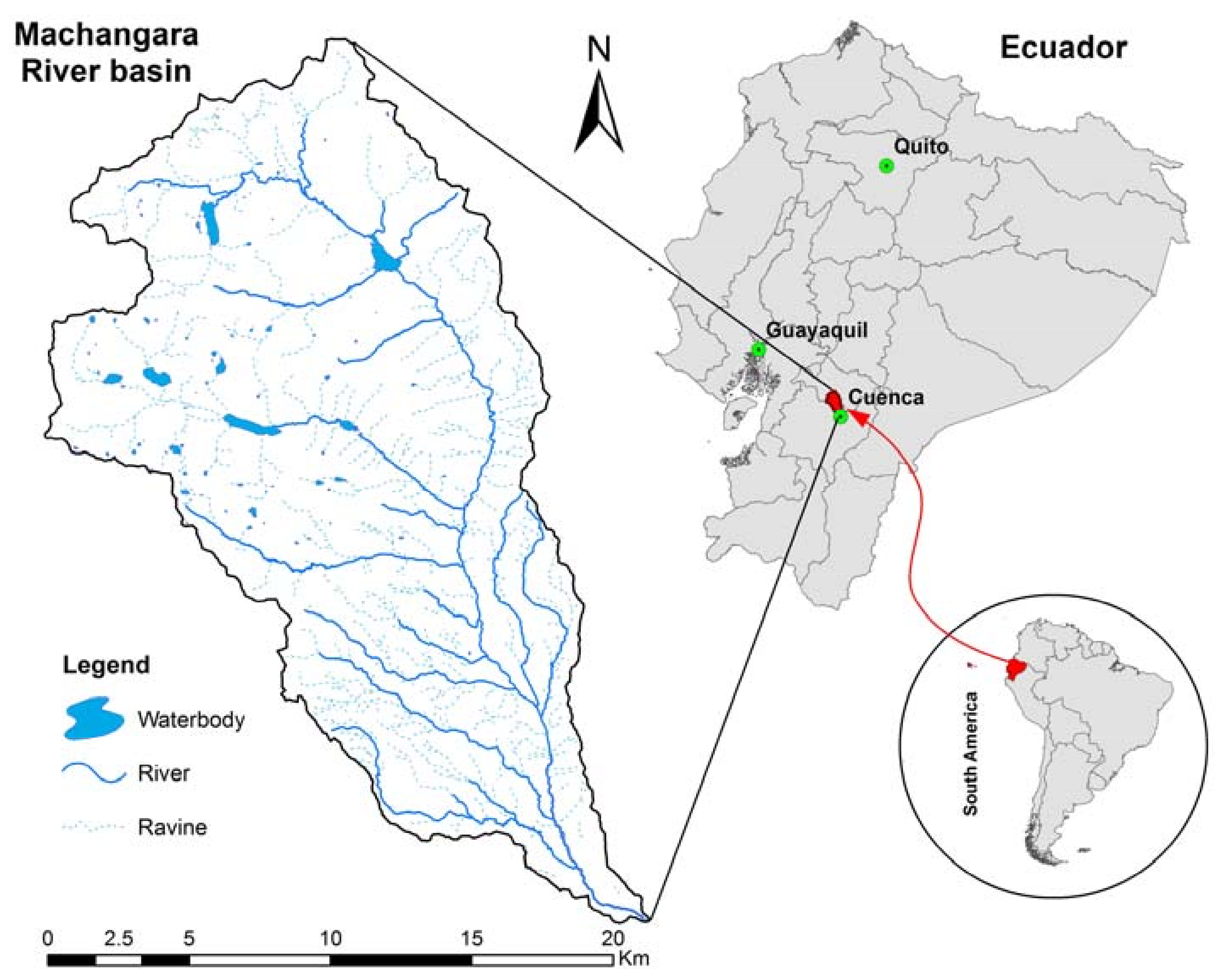
2.1. Study Area
2.2. Data Collection
2.3. Ecuadorian Water Regulation in Relation to Water Use
2.4. Model Development
2.5. Model Optimization
2.6. Modeling and Analysis
3. Results
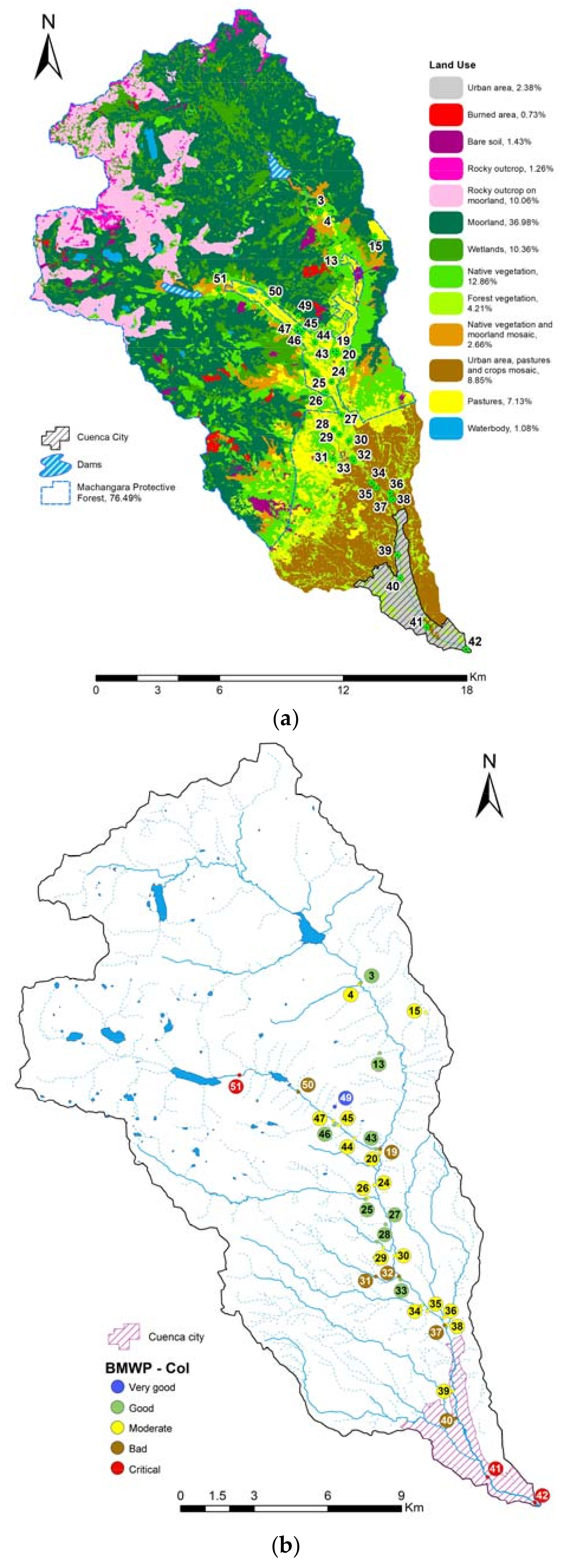
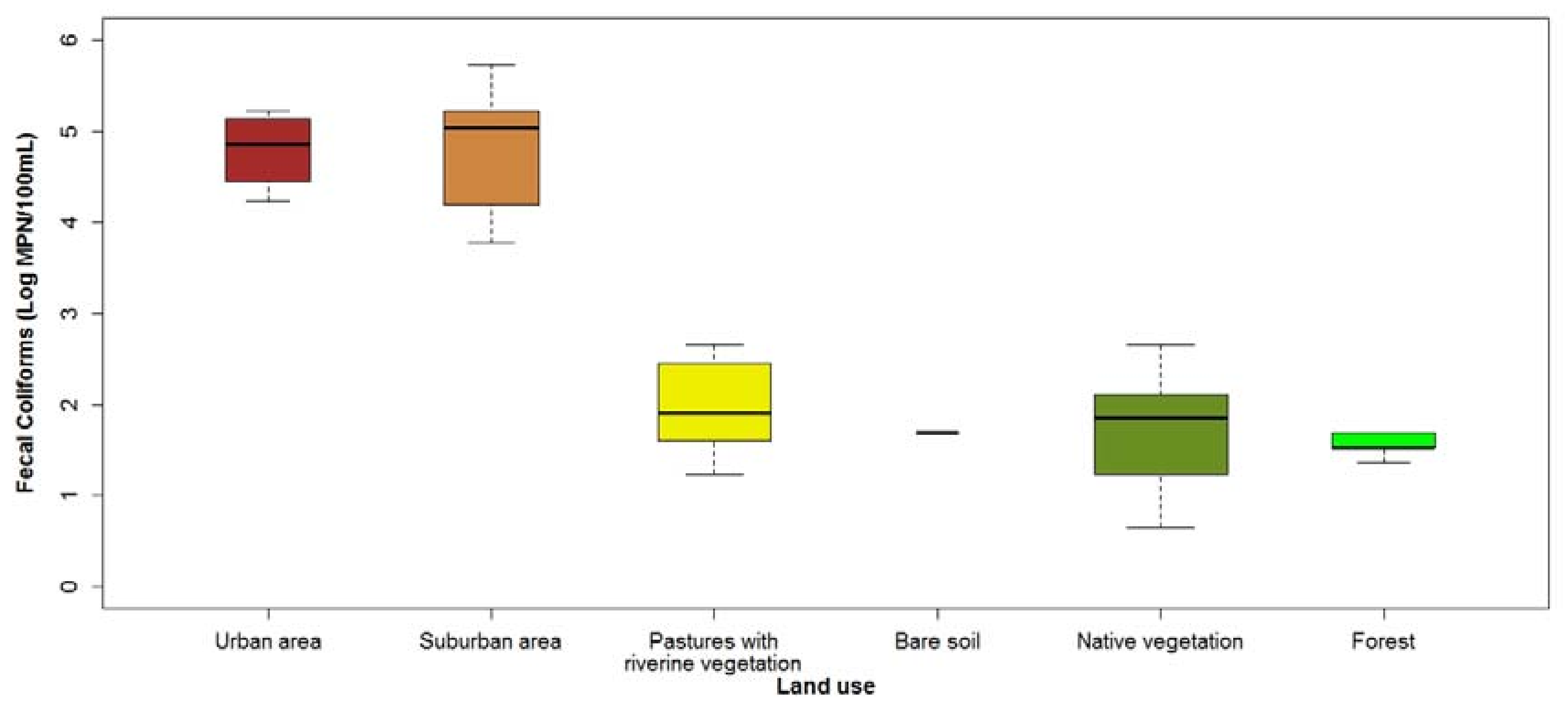
3.1. Current Water Quality Status
3.2. Model Development
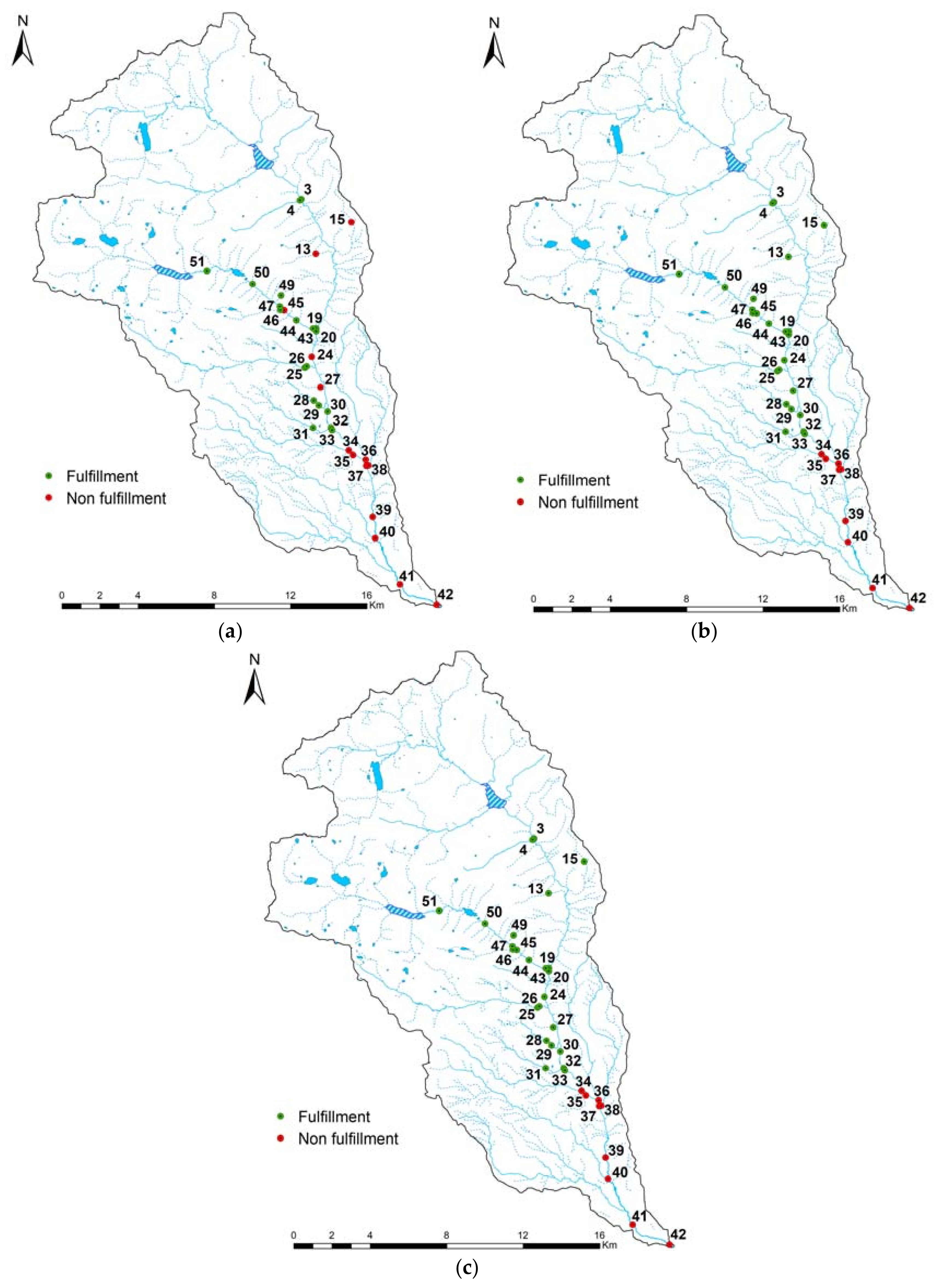
3.3. Model Optimization
4. Discussion
4.1. Model Relevance and Optimization from a Statistical Point of View
4.2. Model Relevance and Optimization from an Ecological Point of View
4.3. A Possible Screening Tool for Microbial Pollution
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BMWP | Biological Monitoring Working Party |
| BMWP-Col | Biological Monitoring Working Party adapted to Colombia |
| BOD5 | Biochemical Oxygen Demand 5 d |
| BWQ | Biological Water Quality |
| CCI | correctly classified instances |
| CEN | confusion entropy of a confusion matrix |
| CMW | cost matrix weights |
| COD | chemical oxygen demand |
| CSC | cost-sensitive classifier |
| CSO | combined sewer overflow |
| CTs | classification trees |
| DO | Dissolved Oxygen |
| DTM | Decision tree model |
| FC | Fecal coliforms |
| fcv | folds cross validation |
| FCR | Fecal coliform regulation |
| FN | false negative |
| FP | false positive |
| ISO | International Organization for Standardization |
| k-fold | three, five or ten-fold |
| m a.s.l. | meters above sea level |
| MPN.100 mL−1 | most probable number per 100 mL |
| PCF | Pruning confidence factor |
| TN | true negative |
| TP | true positive |
| TS | tolerant score |
| SWO | surface water outfalls |
| Weka | Waikato Environment for Knowledge Analysis |
Appendix A
| Parameter | Analysis Method | Units | Mean Value ± Standard Deviation | Min Value | Max Value | Median Value |
|---|---|---|---|---|---|---|
| Mean depth | m | 0.33 ± 0.30 | 0.04 | 1.63 | 0.26 | |
| Flow velocity | m·s−1 | 0.59 ± 0.44 | 0.07 | 1.84 | 0.47 | |
| Temperature | °C | 11.50 ± 1.10 | 9.10 | 13.40 | 11.90 | |
| pH | SM 4500 H B | 7.58 ± 0.45 | 6.33 | 8.36 | 7.70 | |
| Dissolved oxygen (DO) | SM 4500 0-G | mg·L−1 | 9.08 ± 1.47 | 6.65 | 12.60 | 9.54 |
| Total solids | SM 2540 B | mg·L−1 | 89.09 ± 51.65 | 19.00 | 190.00 | 74.00 |
| Turbidity | SM2130B | NTU | 7.68 ± 11.11 | 0.51 | 48.20 | 3.66 |
| True color | SM2120 C | HU | 14.39 ± 8.52 | 0.00 | 40.00 | 14.00 |
| Specific conductivity | SM 2510 B | μS·cm−1 | 91.64 ± 44.12 | 13.20 | 238.00 | 82.30 |
| Phosphates | SM 4500-P-E | mg P·L−1 | 0.07 ± 0.12 | 0.03 | 0.55 | 0.03 |
| Nitrate + Nitrite | SM 4500 N03 E | mg N·L−1 | 0.05 ± 0.12 | BDL | 0.70 | 0.02 |
| Ammonia nitrate | SM 4500 NH3 C | mg·L−1 | 0.02 ± 0.07 | 0.00 | 0.40 | 0.00 |
| Organic nitrogen | SM 4500 Norg B | mg N·L−1 | 0.55 ± 1.21 | 0.00 | 6.55 | 0.14 |
| Biochemical oxygen demand 5 day (BOD5) | SM 5210-B | mg·L−1 | 1.06 ± 2.35 | BDL | 13.00 | 0.40 |
| Chemical oxygen demand (COD) | SM 5220-C | mg·L−1 | 9.94 ± 8.39 | 2.00 | 46.00 | 8.00 |
| Fecal coliforms | SM 9221 E | MPN.100 mL−1 | 3.60 × 104 ± 1.02 × 105 | 4.5 × 100 | 5.4 × 105 | 7.9 × 101 |
| Total coliforms | SM 9221 E | MPN.100 mL−1 | 4.1 × 104 ± 1.1 × 105 | 7.8 × 100 | 5.4 × 105 | 3.3x102 |
| Model No. | FCR a | Dataset Macroinvertebrates | Model Settings | |||||
|---|---|---|---|---|---|---|---|---|
| J4.8 | PCF b | CMW c | ||||||
| TP d | FN e | FP f | TN g | |||||
| * 1hapi1j | Recreational | Presence/absence | 3, 5 and 10 fcv k | 0.25 | ||||
| * 1ap2 | Recreational | Presence/absence | 3, 5 and 10 fcv | 0.10 | ||||
| 1ap3 | Recreational | Presence/absence | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 2 | 0 |
| 1ap4 | Recreational | Presence/absence | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 3 | 0 |
| 1ap5 | Recreational | Presence/absence | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 5 | 0 |
| 1ap6 | Recreational | Presence/absence | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 6 | 0 |
| 1ap7 | Recreational | Presence/absence | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 7 | 0 |
| 1ap8 | Recreational | Presence/absence | 3, 5 and 10 fcv | 0.10 | 0 | 1 | 10 | 0 |
| * 1a1 | Recreational | Abundance | 3, 5, 10 fcv and 66%tr | 0.25 | ||||
| * 1a2 | Recreational | Abundance | 3, 5, 10 fcv and 66%tr | 0.10 | ||||
| 1a3 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 1 | 0 |
| 1a4 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 2 | 0 |
| 1a5 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 3 | 0 |
| 1a6 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 4 | 0 |
| 1a7 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 5 | 0 |
| 1a8 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 7 | 0 |
| 1a9 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 8 | 0 |
| 1a10 | Recreational | Abundance | 3, 5 and 10 fcv | 0.1 | 0 | 1 | 8 | 0 |
| 1a11 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 9 | 0 |
| 1a12 | Recreational | Abundance | 3, 5 and 10 fcv | 0.1 | 0 | 1 | 9 | 0 |
| 1a13 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 10 | 0 |
| 1a14 | Recreational | Abundance | 3, 5 and 10 fcv | 0.1 | 0 | 1 | 10 | 0 |
| 1a15 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 11 | 0 |
| 1a16 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 12 | 0 |
| 1a17 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 15 | 0 |
| 1a18 | Recreational | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 18 | 0 |
| * 2ap1 | Agriculture l | Presence/absence | 3, 5 and 10 fcv | 0.25 | ||||
| * 2ap2 | Agriculture | Presence/absence | 3, 5 and 10 fcv | 0.10 | ||||
| 2ap3 | Agriculture | Presence/absence | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 2 | 0 |
| 2ap4 | Agriculture | Presence/absence | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 3 | 0 |
| 2ap5 | Agriculture | Presence/absence | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 5 | 0 |
| * 2a1 | Agriculture | Abundance | 3, 5, 10 fcv and 66%tr | 0.25 | ||||
| * 2a2 | Agriculture | Abundance | 3, 5, 10 fcv and 66%tr | 0.10 | ||||
| 2a3 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 1 | 0 |
| 2a4 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 2 | 0 |
| 2a5 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 3 | 0 |
| 2a6 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 4 | 0 |
| 2a7 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 5 | 0 |
| 2a8 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 8 | 0 |
| 2a9 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 10 | 0 |
| 2a10 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 12 | 0 |
| 2a11 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 15 | 0 |
| 2a12 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 17 | 0 |
| 2a13 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 18 | 0 |
| 2a14 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 20 | 0 |
| 2a15 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 21 | 0 |
| 2a16 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 22 | 0 |
| 2a17 | Agriculture | Abundance | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 25 | 0 |
| Model No. | FCR a | Model Outcomes | |||
|---|---|---|---|---|---|
| CCI b (%) | Kappa Statistics | Number of Leaves | CEN c | ||
| Mean ± sd | Mean ± sd | Mean ± sd | |||
| * 1eapf1g | Recreational d | 40.40 ± 3.50 | −0.21 ± 0.09 | 6 | 1.03 ± 0.01 |
| * 1ap2 | Recreational | 48.48 ± 3.03 | −0.09 ± 0.07 | 2 | 1.01 ± 0.02 |
| 1apf3g | Recreational | 42.42 ± 6.06 | −0.12 ± 0.13 | 3 | 0.99 ± 0.04 |
| 1ap4 | Recreational | 41.41 ± 7.63 | −0.11 ± 0.17 | 4 | 0.95 ± 0.11 |
| 1ap5 | Recreational | 43.43 ± 1.75 | −0.01 ± 0.02 | 4 | 0.80 ± 0.05 |
| 1ap6 | Recreational | 42.42 ± 3.03 | −0.03 ± 0.05 | 4 | 0.80 ± 0.06 |
| 1ap7 | Recreational | 42.42 ± 3.03 | −0.02 ± 0.05 | 1 | 0.77 ± 0.06 |
| 1ap8 | Recreational | 42.42 ± 0.00 | −0.01 ± 0.01 | 1 | 0.60 ± 0.12 |
| * 1a1 | Recreational | 70.45 ± 1.50 | 0.39 ± 0.05 | 5 | 0.81 ± 0.03 |
| * 1a2 | Recreational | 70.45 ± 1.50 | 0.39 ± 0.05 | 4 | 0.81 ± 0.03 |
| 1a3 | Recreational | 69.70 ± 0.00 | 0.37 ± 0.00 | 5 | 0.83 ± 0.00 |
| 1a4 | Recreational | 72.73 ± 6.05 | 0.44 ± 0.13 | 4 | 0.78 ± 0.09 |
| 1a5 | Recreational | 77.77 ± 4.64 | 0.56 ± 0.09 | 3 | 0.65 ± 0.08 |
| 1a6 | Recreational | 76.78 ± 9.24 | 0.55 ± 0.17 | 3 | 0.65 ± 0.12 |
| 1a7 | Recreational | 77.73 ± 12.24 | 0.56 ± 0.23 | 3 | 0.63 ± 0.17 |
| 1a8 | Recreational | 78.77 ± 8.00 | 0.58 ± 0.15 | 3 | 0.61 ± 0.11 |
| 1a9 | Recreational | 79.80 ± 1.73 | 0.60 ± 0.04 | 3 | 0.63 ± 0.05 |
| 1a10 | Recreational | 79.81 ± 1.74 | 0.60 ± 0.04 | 3 | 0.63 ± 0.05 |
| 1a11 | Recreational | 70.69 ± 7.64 | 0.44 ± 0.14 | 3 | 0.70 ± 0.09 |
| 1a12 | Recreational | 70.69 ± 7.64 | 0.44 ± 0.14 | 3 | 0.70 ± 0.09 |
| 1a13 | Recreational | 66.68 ± 10.92 | 0.36 ± 0.21 | 3 | 0.73 ± 0.15 |
| 1a14 | Recreational | 63.63 ± 12.13 | 0.32 ± 0.20 | 3 | 0.68 ± 0.05 |
| 1a15 | Recreational | 62.62 ± 10.65 | 0.30 ± 0.17 | 3 | 0.71 ± 0.02 |
| 1a16 | Recreational | 58.57 ± 6.30 | 0.24 ± 0.10 | 3 | 0.70 ± 0.02 |
| 1a17 | Recreational | 47.47 ± 8.78 | −0.01 ± 0.01 | 3 | 0.60 ± 0.12 |
| 1a18 | Recreational | 42.42 ± 0.00 | 0.00 ± 0.00 | 1 | 0.53 ± 0.00 |
| * 2ap1 | Agriculture | 66.67 ± 0.00 | 0.17 ± 0.03 | 4 | 0.88 ± 0.01 |
| * 2ap2 | Agriculture | 69.70 ± 3.03 | 0.24 ± 0.00 | 3 | 0.84 ± 0.01 |
| 2ap3 | Agriculture | 75.76 ± 5.25 | 0.47 ± 0.13 | 4 | 0.67 ± 0.15 |
| 2ap4 | Agriculture | 73.74 ± 6.31 | 0.44 ± 0.11 | 3 | 0.70 ± 0.06 |
| 2ap5 | Agriculture | 71.72 ± 9.26 | 0.42 ± 0.18 | 3 | 0.66 ± 0.14 |
| * 2a1 | Agriculture | 86.35 ± 7.99 | 0.68 ± 0.19 | 3 | 0.52 ± 0.20 |
| * 2a2 | Agriculture | 77.25 ± 16.87 | 0.43 ± 0.44 | 3 | 0.67 ± 0.26 |
| 2a3 | Agriculture | 84.86 ± 9.07 | 0.64 ± 0.21 | 3 | 0.57 ± 0.21 |
| 2a4 | Agriculture | 89.88 ± 4.61 | 0.74 ± 0.13 | 3 | 0.47 ± 0.13 |
| 2a5 | Agriculture | 86.86 ± 7.61 | 0.68 ± 0.18 | 3 | 0.54 ± 0.19 |
| 2a6 | Agriculture | 86.86 ± 7.61 | 0.68 ± 0.18 | 3 | 0.54 ± 0.19 |
| 2a7 | Agriculture | 85.86 ± 6.31 | 0.66 ± 0.16 | 3 | 0.57 ± 0.14 |
| 2a8 | Agriculture | 80.83 ± 9.76 | 0.57 ± 0.21 | 3 | 0.63 ± 0.14 |
| 2a9 | Agriculture | 80.81 ± 9.74 | 0.57 ± 0.21 | 3 | 0.63 ± 0.14 |
| 2a10 | Agriculture | 80.81 ± 14.95 | 0.58 ± 0.29 | 3 | 0.60 ± 0.18 |
| 2a11 | Agriculture | 72.74 ± 6.05 | 0.42 ± 0.13 | 3 | 0.70 ± 0.09 |
| 2a12 | Agriculture | 60.60 ± 9.09 | 0.26 ± 0.12 | 3 | 0.71 ± 0.08 |
| 2a13 | Agriculture | 63.63 ± 10.51 | 0.33 ± 0.13 | 3 | 0.66 ± 0.00 |
| 2a14 | Agriculture | 57.56 ± 5.26 | 0.25 ± 0.06 | 2 | 0.67 ± 0.00 |
| 2a15 | Agriculture | 58.57 ± 7.01 | 0.26 ± 0.09 | 2 | 0.67 ± 0.00 |
| 2a16 | Agriculture | 47.48 ± 19.70 | 0.17 ± 0.18 | 2 | 0.60 ± 0.12 |
| 2a17 | Agriculture | 40.39 ± 13.64 | 0.09 ± 0.11 | 2 | 0.59 ± 0.11 |
| (a) Recreational Fecal Coliform Regulation | |
| Model: 1a4 | Models: 1a5, 1a6, 1a7 |
| Baetidae <= 3: A Baetidae > 3 | Perlidae = 0: B | Perlidae > 0 | | Chironomidae <= 3: B | | Chironomidae > 3: A | Baetidae <= 3 | Scirtidae = 1: A | Scirtidae > 1: B Baetidae > 3: B |
| Model: 1a8 | Models: 1a9, 1a10, 1a11, 1a12 |
| Baetidae <= 3 | Elminthidae <= 2: A | Elminthidae > 2: B Baetidae > 3: B | Baetidae <= 3 | Scirtidae <= 4: A | Scirtidae > 4: B Baetidae > 3: B |
| (b) Agriculture fecal coliform regulation | |
| Model: 2ap3 | Models: 2ap4, 2ap5 |
| Perlidae = presence: A Perlidae = absence | Baetidae = presence | | Leptophlebiidae = presence: A | | Leptophlebiidae = absence: B | Baetidae = absence: A | Perlidae = presence: A Perlidae = absence | Baetidae = presence: B | Baetidae = absence: A |
| Models: 2a1, 2a2, 2a3, 2a4, 2a5, 2a6 | Models: 2a7, 2a8, 2a9, 2a10, 2a11 |
| Baetidae <= 4: A Baetidae > 4 | Perlidae = 0: B | Perlidae > 0: A | Perlidae = 0 | Baetidae <= 4: A | Baetidae > 4: B Perlidae > 0: A |
| A: fulfillment; B: non-fulfillment | |
References
- Gofti-Laroche, L.; Demanse, D.; Joret, J.-C.; Zmirou, D. Health risks and parasitical quality of water. J. Am. Water Works Assoc. 2003, 95, 162–172. [Google Scholar] [CrossRef]
- World Health Organization (WHO). Guidelines for Drinking-Water Quality; World Health Organization: Geneva, Switzerland, 2004; Volume 1. [Google Scholar]
- Mallin, M.A.; Johnson, V.L.; Ensign, S.H.; MacPherson, T.A. Factors contributing to hypoxia in rivers, lakes, and streams. Limnol. Oceanogr. 2006, 51, 690–701. [Google Scholar] [CrossRef]
- Arnone, R.D.; Walling, J.P. Waterborne pathogens in urban watersheds. J. Water Health 2007, 5, 149–162. [Google Scholar] [CrossRef] [PubMed]
- Oliver, B.G. Guidelines for Drining-Water Quality, Volume 1: Recommendations; Elsevier: Geneva, Switzerland, 1984; p. 130. [Google Scholar]
- Fewtrell, L.; Bartram, J.; Organization, W.W.H. Water Quality: Guidelines, Standards, and Health: Assessment of Risk and Risk Management for Water-Related Infectious Disease; IWA Publishing: London, UK, 2001. [Google Scholar]
- World Health Organization (WHO). Guidelines for Safe Recreational Water Environments: Coastal and Fresh Waters; World Health Organization: Geneva, Switzerland, 2003; Volume 1. [Google Scholar]
- Dominguez-Granda, L.; Lock, K.; Goethals, P.L. Using multi-target clustering trees as a tool to predict biological water quality indices based on benthic macroinvertebrates and environmental parameters in the Chaguana Watershed (Ecuador). Ecol. Inform. 2011, 6, 303–308. [Google Scholar] [CrossRef]
- De Pauw, N.; Gabriels, W.; Goethals, P.L. River monitoring and assessment methods based on macroinvertebrates. In Biological Monitoring of Rivers: Applications and Perspectives; John Wiley and Son, Ltd.: Chichester, UK, 2006; pp. 113–134. [Google Scholar]
- Gabriels, W.; Lock, K.; De Pauw, N.; Goethals, P.L. Multimetric macroinvertebrate index Flanders (MMIF) for biological assessment of rivers and lakes in Flanders (Belgium). Limnol. Ecol. Manag. Inland Waters 2010, 40, 199–207. [Google Scholar] [CrossRef]
- Džeroski, S.; Demšar, D.; Grbović, J. Predicting chemical parameters of river water quality from bioindicator data. Appl. Intell. 2000, 13, 7–17. [Google Scholar] [CrossRef]
- Griffiths, M. The European water framework directive: An approach to integrated river basin management. Eur. Water Manag. Online 2002, 5, 1–14. [Google Scholar]
- Junqueira, V.; Campos, S. Adaptation of the “BMWP” method for water quality evaluation to Rio das Velhas watershed (Minas Gerais, Brazil). Acta Limnol. Bras. 1998, 10, 125–135. [Google Scholar]
- Mustow, S. Biological monitoring of rivers in Thailand: Use and adaptation of the BMWP score. Hydrobiologia 2002, 479, 191–229. [Google Scholar] [CrossRef]
- Roldán Pérez, G.A. Bioindicación De La Calidad Del Agua En Colombia: Uso Del Método Bmwp/Col; Imprenta Universidad de Antioquia: Medellín, Colombia, 2003. [Google Scholar]
- Wilkinson, J.; Jenkins, A.; Wyer, M.; Kay, D. Modelling faecal coliform dynamics in streams and rivers. Water Res. 1995, 29, 847–855. [Google Scholar] [CrossRef]
- Mahloch, J.L. Comparative analysis of modeling techniques for coliform organisms in streams. Appl. Microbiol. 1974, 27, 340–345. [Google Scholar] [PubMed]
- Ansa, E.; Lubberding, H.; Ampofo, J.; Amegbe, G.; Gijzen, H. Attachment of faecal coliform and macro-invertebrate activity in the removal of faecal coliform in domestic wastewater treatment pond systems. Ecol. Eng. 2012, 42, 35–41. [Google Scholar] [CrossRef]
- Kay, D.; Mcdonald, A. Predicting coliform concentrations in upland impoundments: Design and calibration of a multivariate model. Appl. Environ. Microbiol. 1983, 46, 611–618. [Google Scholar] [PubMed]
- Hoang, T.H.; Lock, K.; Mouton, A.; Goethals, P.L. Application of classification trees and support vector machines to model the presence of macroinvertebrates in rivers in Vietnam. Ecol. Inform. 2010, 5, 140–146. [Google Scholar] [CrossRef]
- Ambelu, A.; Mekonen, S.; Koch, M.; Addis, T.; Boets, P.; Everaert, G.; Goethals, P. The application of predictive modelling for determining bio-environmental factors affecting the distribution of blackflies (diptera: Simuliidae) in the Gilgel Gibe Watershed in southwest Ethiopia. PLoS ONE 2014, 9, e112221. [Google Scholar] [CrossRef] [PubMed]
- Jerves-Cobo, R.; Everaert, G.; Iñiguez-Vela, X.; Córdova-Vela, G.; Díaz-Granda, C.; Cisneros, F.; Nopens, I.; Goethals, P.L. A methodology to model environmental preferences of EPT taxa in the Machangara River basin (Ecuador). Water 2017, 9, 195. [Google Scholar] [CrossRef]
- Holguin-Gonzalez, J.E.; Boets, P.; Alvarado, A.; Cisneros, F.; Carrasco, M.C.; Wyseure, G.; Nopens, I.; Goethals, P.L.M. Integrating hydraulic, physicochemical and ecological models to assess the effectiveness of water quality management strategies for the River Cuenca in Ecuador. Ecol. Model. 2013, 254, 1–14. [Google Scholar] [CrossRef]
- Acosta, R.; Hampel, H. Evaluación Del Estado Ecológico Y Biodiversidad De Macroinvertebrados Bentónicos En La Cuenca Alta Del Río Paute Y Parque Nacional El Cajas; Universidad de Cuenca: Cuenca, Ecuador, 2015; p. 83. [Google Scholar]
- Goethals, P.; Dedecker, A.; Gabriëls, W.; De Pauw, N. Development and application of predictive river ecosystem models based on classification trees and artificial neural networks. In Ecological Informatics; Springer: Berlin, Germany, 2006; pp. 151–167. [Google Scholar]
- Ambelu, A.; Lock, K.; Goethals, P. Comparison of modelling techniques to predict macroinvertebrate community composition in rivers of Ethiopia. Ecol. Inform. 2010, 5, 147–152. [Google Scholar] [CrossRef]
- Dakou, E.; D’Heygere, T.; Dedecker, A.P.; Goethals, P.L.M.; Lazaridou-Dimitriadou, M.; De Pauw, N. Decision tree models for prediction of macroinvertebrate taxa in the river axios (northern greece). Aquat. Ecol. 2007, 41, 399–411. [Google Scholar] [CrossRef]
- Goethals, P. Data Driven Development of Predictive Ecological Models for Benthic Macroinvertebrates in Rivers; Ghent University: Ghent, Belgium, 2005. [Google Scholar]
- Fernandez de Cordova, J.; González, H. Evoluación De La Calidad Del Agua De Los Tramos Bajos De Los Ríos De La Ciudad De Cuenca; ETAPA-EP: Cuenca, Ecuador, 2012. [Google Scholar]
- Instituto Nacional de Estadísticas y Censos del Ecuador (INEC). Proyección De La Población Ecuatoriana, Por Años Calendario, Según Cantones 2010–2020; Instituto Nacional de Estadísticas y Censos del Ecuador: Quito, Ecuador, 2010.
- PROMAS-UCuenca. Información de la Red Meteorológica e Hidrológica. Progarma para el Manejo del Agua y el Suelo; Universidad de Cuenca: Cuenca, Ecuador, 2010. [Google Scholar]
- Aereopuerto-Mariscal-Lamar. Información Meteorológica Aereopuerto Mariscal Lamar Cuenca; Dirección de Aviación Civil del Ecuador: Quito, Ecuador, 2012.
- Estrella, R.; Tobar, V. Hidrologia Y Climatologia—Formulación Del Plan De Manejo Integral De La Subcuenca Del Río Machangara; ACOTECNIC Cia. Ltda.—Consejo de Cuenca del Río Machangara: Cuenca, Ecuador, 2013. [Google Scholar]
- Esquivel, J.C.; Verbeiren, B.; Alvarado, A.; Feyen, J.; Cisneros, F. Preliminary statistical analysis of the water quality database of ETAPA; PROMAS—Universidad de Cuenca: Cuenca, Ecuador, 2008. [Google Scholar]
- Mulliss, R.; Revitt, D.M.; Shutes, R.B.E. The impacts of discharges from two combined sewer overflows on the water quality of an urban watercourse. Water Sci. Technol. 1997, 36, 195–199. [Google Scholar]
- Hvitved-Jacobsen, T. The impact of combined sewer overflows on the dissolved oxygen concentration of a river. Water Res. 1982, 16, 1099–1105. [Google Scholar] [CrossRef]
- Weyrauch, P.; Matzinger, A.; Pawlowsky-Reusing, E.; Plume, S.; von Seggern, D.; Heinzmann, B.; Schroeder, K.; Rouault, P. Contribution of combined sewer overflows to trace contaminant loads in urban streams. Water Res. 2010, 44, 4451–4462. [Google Scholar] [CrossRef] [PubMed]
- Passerat, J.; Ouattara, N.K.; Mouchel, J.-M.; Vincent, R.; Servais, P. Impact of an intense combined sewer overflow event on the microbiological water quality of the seine river. Water Res. 2011, 45, 893–903. [Google Scholar] [CrossRef] [PubMed]
- Novotny, V. Diffuse pollution from agriculture—A worldwide outlook. Water Sci. Technol. 1999, 39, 1–13. [Google Scholar]
- Dohner, E.; Markowitz, A.; Barbour, M.; Simpson, J.; Byrne, J.; Dates, G. Volunteer Stream Monitoring: A Methods Manual; Environmental Protection Agency: Washington, DC, USA, 1997.
- Armitage, P.D.; Moss, D.; Wright, J.F.; Furse, M.T. The performance of a new biological water quality score system based on macroinvertebrates over a wide range of unpolluted running-water sites. Water Res. 1983, 17, 333–347. [Google Scholar] [CrossRef]
- Sutherland, W.J. Ecological Census Techniques: A Handbook; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Alba-Tercedor, J.; Pardo, I.; Prat, N.; Pujante, A. Protocolos de muestreo y análisis para invertebrados bentónicos. In Metodología Para el Establecimiento del Estado Ecológico Según la Directiva Marco del Agua; Ministerio de Medio Ambiente, Confederación Hidrográfica del Ebro: Madrid, España, 2005; pp. 131–175. (in Spanish) [Google Scholar]
- Roldán Pérez, G.A. Guía Para El Estudio De Los Macroinvertebrados Acuáticos Del Departamento De Antioquia; Fondo para la Protección del Medio Ambiente “José Celestino Mutis”: Bogotá, Colombia, 1988.
- Álvarez, L.F. Metodología Para La Utilización De Los Macroinvertebrados Acuáticos Como Indicadores De La Calidad Del Agua; Instituto de Investigación de Recursos Biológicos Alexander von Humboldt: Bogotá, Colombia, 2005. [Google Scholar]
- Encalada, A.C.; Sant, M.R.; Prat i Fornells, N.; Quito, U.S.F.d.; Barcelona, U.d.; Desarrollo, A.E.d.C.I.p.e.; Agua, F.p.l.P.d. Protocolo Simplificado Y Guía De Evaluación De La Calidad Ecológica De Ríos Andinos (Cera-S): text 2. Làmines; Proyecto FUCARA: Quito, Ecuador, 2011. [Google Scholar]
- Zúñiga, M.d.C.; Cardona, W.; Cantera, J.; Carvajal, Y.; Castro, L. Bioindicadores de calidad de agua y caudal ambiental. In Caudal Ambiental: Conceptos, Experiencias y Desafíos; Universidad del Valle: Cali, Colombia, 2009; Volume 1, pp. 303–310. [Google Scholar]
- MAE-Ecuador. Tulas—Texto Unificado de Legislación Secundaria; Ministerio-del-Ambiente, Ed.; EDICION ESPECIAL No. 270 ed.; Acuerdo Ministerial No. 028; Registro Oficial: Quito, Ecuador, 2015.
- Sánchez, L.; Sánchez, A.; Galvis, G.; Latorre, J. Filtración en Múltiples Etapas; IRC International Water and Sanitation Centre: Delft, The Netherlands, 2007; Volume 15. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Quinlan, J.R. Generating production rules from decision trees. In Proceedings of the 10th International Joint Conference on Artificial Intelligence, Milan, Italy, 23–29 August 1987; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1987; pp. 304–307. [Google Scholar]
- Everaert, G.; Boets, P.; Lock, K.; Džeroski, S.; Goethals, P.L. Using classification trees to analyze the impact of exotic species on the ecological assessment of polder lakes in flanders, belgium. Ecol. Model. 2011, 222, 2202–2212. [Google Scholar] [CrossRef]
- Lior, R. Data Mining with Decision trees: Theory and Applications; World Scientific: Singapore, 2014; Volume 81. [Google Scholar]
- Forio, M.A.E.; Van Echelpoel, W.; Dominguez-Granda, L.; Mereta, S.T.; Ambelu, A.; Hoang, T.H.; Boets, P.; Goethals, P.L.M. Analysing the effects of water quality on the occurrence of freshwater macroinvertebrate taxa among tropical river basins from different continents. AI Commun. 2016, 29, 665–685. [Google Scholar] [CrossRef]
- Stockwell, D.R.; Peterson, A.T. Effects of sample size on accuracy of species distribution models. Ecol. Model. 2002, 148, 1–13. [Google Scholar] [CrossRef]
- Yu, R.; Abdel-Aty, M. Utilizing support vector machine in real-time crash risk evaluation. Accid. Anal. Prev. 2013, 51, 252–259. [Google Scholar] [CrossRef] [PubMed]
- Moisen, G. Classification and regression trees. In Encyclopedia of Ecology; Elsevier: Oxford, UK, 2008; pp. 582–588. [Google Scholar]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: San Francisco, CA, USA, 2005. [Google Scholar]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Elsevier: San Mateo, CA, USA, 2014. [Google Scholar]
- Goethals, P.L.; Dedecker, A.P.; Gabriels, W.; Lek, S.; De Pauw, N. Applications of artificial neural networks predicting macroinvertebrates in freshwaters. Aquat. Ecol. 2007, 41, 491–508. [Google Scholar] [CrossRef]
- Fielding, A.H.; Bell, J.F. A review of methods for the assessment of prediction errors in conservation presence/absence models. Environ. Conserv. 1997, 24, 38–49. [Google Scholar] [CrossRef]
- Ting, K.M. An instance-weighting method to induce cost-sensitive trees. IEEE Trans. Knowl. Data Eng. 2002, 14, 659–665. [Google Scholar] [CrossRef]
- Maimon, O.; Rokach, L. Data Mining and Knowledge Discovery Handbook; Springer: New York, NY, USA, 2005; Volume 2. [Google Scholar]
- Kohavi, R.; Provost, F. Glossary of terms. Mach. Learn. 1998, 30, 271–274. [Google Scholar]
- Fukuda, S.; De Baets, B.; Mouton, A.M.; Waegeman, W.; Nakajima, J.; Mukai, T.; Hiramatsu, K.; Onikura, N. Effect of model formulation on the optimization of a genetic takagi–sugeno fuzzy system for fish habitat suitability evaluation. Ecol. Model. 2011, 222, 1401–1413. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.-M.; Yuan, X.-J.; Hu, Q.-H.; Wang, S.-Q. A novel measure for evaluating classifiers. Expert Syst. Appl. 2010, 37, 3799–3809. [Google Scholar] [CrossRef]
- Everaert, G.; Pauwels, I.S.; Boets, P.; Verduin, E.; de la Haye, M.A.A.; Blom, C.; Goethals, P.L.M. Model-based evaluation of ecological bank design and management in the scope of the european water framework directive. Ecol. Eng. 2013, 53, 144–152. [Google Scholar] [CrossRef]
- Everaert, G.; Pauwels, I.S.; Boets, P.; Buysschaert, F.; Goethals, P.L. Development and assessment of ecological models in the context of the european water framework directive: Key issues for trainers in data-driven modeling approaches. Ecol. Inform. 2013, 17, 111–116. [Google Scholar] [CrossRef]
- Džeroski, S.; Grbović, J.; Walley, W.J.; Kompare, B. Using machine learning techniques in the construction of models. Ii. Data analysis with rule induction. Ecol. Model. 1997, 95, 95–111. [Google Scholar] [CrossRef]
- Roldán Pérez, G. Los macroinvertebrados y su valor como indicadores de la calidad del agua. Acad. Colomb. Cienc. 1999, 23, 375–387. [Google Scholar]
- Jacobsen, D. The effect of organic pollution on the macroinvertebrate fauna of ecuadorian highland streams. Archiv für Hydrobiol. 1998, 143, 179–195. [Google Scholar] [CrossRef]
- Ríos-Touma, B.; Encalada, A.C.; Prat Fornells, N. Macroinvertebrate assemblages of an andean high-altitude tropical stream: The importance of season and flow. Int. Rev. Hydrobiol. 2011, 96, 667–685. [Google Scholar] [CrossRef]
- Jacobsen, D. Temporally variable macroinvertebrate–stone relationships in streams. Hydrobiologia 2005, 544, 201–214. [Google Scholar] [CrossRef]
- Burneo, P.C.; Gunkel, G. Ecology of a high andean stream, río Itambi, Otavalo, Ecuador. Limnol. Ecol. Manag. Inland Waters 2003, 33, 29–43. [Google Scholar] [CrossRef]
- Dallas, H.F.; Day, J.A. Natural variation in macroinvertebrate assemblages and the development of a biological banding system for interpreting bioassessment data—A preliminary evaluation using data from upland sites in the south-western Cape, South Africa. Hydrobiologia 2007, 575, 231–244. [Google Scholar] [CrossRef]
- Kauffman, J.B.; Krueger, W.C. Livestock impacts on riparian ecosystems and streamside management implications… A review. J. Range Manag. 1984, 37, 430–438. [Google Scholar] [CrossRef]
- Seyfried, P.; Harris, E. Bacteriological Characterization of Feces and Source Differentiation; Water Resources Branch, Ontario Ministry of the Environment: Toronto, ON, Canada, 1990.
- Leclerc, H.; Mossel, D.; Edberg, S.; Struijk, C. Advances in the bacteriology of the coliform group: Their suitability as markers of microbial water safety. Ann. Rev. Microbiol. 2001, 55, 201–234. [Google Scholar] [CrossRef] [PubMed]
- Tallon, P.; Magajna, B.; Lofranco, C.; Leung, K.T. Microbial indicators of faecal contamination in water: A current perspective. Water Air Soil Pollut. 2005, 166, 139–166. [Google Scholar] [CrossRef]
- Wade, T.J.; Calderon, R.L.; Sams, E.; Beach, M.; Brenner, K.P.; Williams, A.H.; Dufour, A.P. Rapidly measured indicators of recreational water quality are predictive of swimming-associated gastrointestinal illness. Environ. Health Perspect. 2006, 114, 24–28. [Google Scholar] [CrossRef] [PubMed]
- Forio, M.A.E.; Landuyt, D.; Bennetsen, E.; Lock, K.; Nguyen, T.H.T.; Ambarita, M.N.D.; Musonge, P.L.S.; Boets, P.; Everaert, G.; Dominguez-Granda, L.; et al. Bayesian belief network models to analyse and predict ecological water quality in rivers. Ecol. Model. 2015, 312, 222–238. [Google Scholar] [CrossRef]

| Regulations | Water Used for | Fecal Coliforms Limited Value MPN.100 mL−1 |
|---|---|---|
| Recreational | Recreational with primary contact | ≤200 |
| Agriculture | Agriculture and livestock | ≤1000 |
| Raw water | Raw water previous to non-conventional treatment a | ≤2000 |
| Sampled Points in the Machangara River | Points with the Same Taxa | |||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Site | Sensitivity Score ↓ | 3 | 4 | 13 | 15 | 19 | 20 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 49 | 50 | 51 | ||
| Taxa | ||||||||||||||||||||||||||||||||||||
| Biological Water Quality BMWP-Col → | 69 | 57 | 71 | 59 | 35 | 48 | 58 | 82 | 55 | 74 | 63 | 46 | 40 | 29 | 19 | 64 | 55 | 39 | 49 | 33 | 59 | 38 | 34 | 11 | 8 | 67 | 37 | 57 | 82 | 56 | 93 | 29 | 11 | |||
| Land use category → | 5 | 5 | 5 | 3 | 5 | 4 | 3 | 5 | 6 | 3 | 6 | 6 | 3 | 6 | 3 | 6 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 5 | 5 | 5 | 3 | 6 | 5 | 3 | 5 | |||
| Tubificidae | 1 | 38 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 28 | ||||||
| Chironomidae | 2 | 38 | 4 | 1 | 56 | 9 | 4 | 6 | 2 | 4 | 4 | 2 | 1 | 15 | 2 | 40 | 2 | 6 | 9 | 43 | 15 | 8 | 2 | 3 | 2 | 23 | 10 | 4 | 27 | |||||||
| Dytiscidae | 3 | 1 | 1 | |||||||||||||||||||||||||||||||||
| Physidae | 3 | 14 | 1 | 1 | 3 | |||||||||||||||||||||||||||||||
| Glossiphoniidae | 3 | 1 | 1 | 1 | 1 | 3 | 1 | 6 | ||||||||||||||||||||||||||||
| Empididae | 4 | 1 | 1 | |||||||||||||||||||||||||||||||||
| Psychodidae | 4 | 1 | 1 | |||||||||||||||||||||||||||||||||
| Hydrophilidae | 4 | 1 | 1 | |||||||||||||||||||||||||||||||||
| Planorbidae | 4 | 1 | 2 | 2 | ||||||||||||||||||||||||||||||||
| Dixidae | 4 | 1 | 1 | 2 | ||||||||||||||||||||||||||||||||
| Limoniidae | 4 | 3 | 5 | 3 | 3 | |||||||||||||||||||||||||||||||
| Tabanidae | 4 | 1 | 1 | 1 | 3 | |||||||||||||||||||||||||||||||
| Limnaeidae | 4 | 1 | 1 | 2 | 2 | 4 | ||||||||||||||||||||||||||||||
| Ceratopogonidae | 4 | 1 | 1 | 1 | 2 | 1 | 1 | 6 | ||||||||||||||||||||||||||||
| Planariidae | 4 | 6 | 1 | 14 | 2 | 1 | 6 | 1 | 1 | 8 | ||||||||||||||||||||||||||
| Staphylinidae | 5 | 2 | 1 | |||||||||||||||||||||||||||||||||
| Hydropsychidae | 5 | 1 | 1 | 1 | 3 | |||||||||||||||||||||||||||||||
| Muscidae | 5 | 1 | 2 | 1 | 5 | 5 | 2 | 3 | 2 | 3 | 1 | 10 | ||||||||||||||||||||||||
| Tipulidae | 5 | 1 | 6 | 4 | 5 | 2 | 1 | 3 | 1 | 1 | 1 | 3 | 1 | 1 | 1 | 14 | ||||||||||||||||||||
| Baetidae | 5 | 3 | 13 | 37 | 2 | 43 | 16 | 2 | 38 | 3 | 2 | 1 | 1 | 3 | 53 | 7 | 189 | 45 | 108 | 151 | 31 | 17 | 19 | 1 | 3 | 4 | 30 | 140 | 27 | |||||||
| Scirtidae | 6 | 132 | 1 | 1 | 2 | 3 | 1 | 1 | 1 | 1 | 4 | 4 | 2 | 12 | ||||||||||||||||||||||
| Elminthidae | 6 | 2 | 2 | 3 | 16 | 2 | 3 | 1 | 1 | 5 | 1 | 2 | 4 | 1 | 1 | 4 | 1 | 1 | 17 | |||||||||||||||||
| Simuliidae | 6 | 18 | 3 | 3 | 13 | 1 | 21 | 2 | 31 | 26 | 19 | 45 | 8 | 18 | 5 | 14 | 51 | 22 | 10 | 1 | 14 | 2 | 1 | 18 | 1 | 5 | 3 | 15 | 27 | |||||||
| Aeshnidae | 7 | 1 | 1 | 2 | ||||||||||||||||||||||||||||||||
| Tricorythidae | 7 | 25 | 7 | 6 | 2 | 3 | 2 | 8 | 1 | 1 | 14 | 9 | 1 | 2 | 13 | |||||||||||||||||||||
| Hyalellidae | 7 | 88 | 4 | 6 | 30 | 7 | 10 | 1 | 16 | 3 | 2 | 3 | 2 | 1 | 1 | 6 | 2 | 2 | 2 | 116 | 61 | 38 | 5 | 22 | ||||||||||||
| Leptoceridae | 8 | 1 | 1 | 1 | 1 | 1 | 2 | 6 | ||||||||||||||||||||||||||||
| Leptophlebiidae | 8 | 10 | 4 | 1 | 2 | 6 | 5 | 1 | 2 | 56 | 9 | |||||||||||||||||||||||||
| Hydrobiosidae | 8 | 2 | 3 | 6 | 4 | 2 | 1 | 9 | 1 | 1 | 14 | 2 | 2 | 1 | 1 | 1 | 1 | 6 | 17 | |||||||||||||||||
| Helicopsychidae | 9 | 1 | 1 | |||||||||||||||||||||||||||||||||
| Ptilodactylidae | 9 | 1 | 1 | 2 | ||||||||||||||||||||||||||||||||
| Odontoceridae | 9 | 1 | 1 | 2 | ||||||||||||||||||||||||||||||||
| Hydracarina | 10 | 1 | 1 | 2 | ||||||||||||||||||||||||||||||||
| Blepharoceridae | 10 | 1 | 1 | 2 | ||||||||||||||||||||||||||||||||
| Gripopterygidae | 10 | 1 | 1 | 2 | ||||||||||||||||||||||||||||||||
| Calamoceratidae | 10 | 2 | 1 | 1 | 1 | 4 | ||||||||||||||||||||||||||||||
| Perlidae | 10 | 1 | 7 | 6 | 1 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | 9 | 12 | ||||||||||||||||||||||
| Taxa richness → | 12 | 10 | 11 | 10 | 8 | 10 | 9 | 14 | 10 | 13 | 10 | 8 | 7 | 6 | 4 | 12 | 12 | 7 | 11 | 8 | 11 | 7 | 7 | 4 | 3 | 12 | 7 | 11 | 14 | 11 | 14 | 7 | 3 | |||
| Land use category → | 1 | Urban area | 2 | Suburban area, pastures and crops | 3 | Pastures | 4 | Bare soil | 5 | Native vegetation | 6 | Forest vegetation | ||||||||||||||||||||||||
| Biological water quality classification → | Very good | Good | Moderate | Deficient | Bad | |||||||||||||||||||||||||||||||
| Taxa analyzed to construct the models → | Included | Not included | p = Taxa present | |||||||||||||||||||||||||||||||||
| Model No. | FCR a | Model Settings | Model Outcomes | ||||
|---|---|---|---|---|---|---|---|
| CCI c (%) | Kappa Statistics | Number of Leaves | CEN d | ||||
| J4.8 | PCF b | Mean ± sd | Mean ± sd | Mean ± sd | |||
| 1eapf1g | Recreational h | 3, 5 and 10 fcv i | 0.25 | 40.40 ± 3.50 | −0.21 ± 0.09 | 6 | 1.03 ± 0.01 |
| 1ap2 | Recreational | 3, 5 and 10 fcv | 0.10 | 48.48 ± 3.03 | −0.09 ± 0.07 | 2 | 1.01 ± 0.02 |
| 1a1 | Recreational | 3, 5, 10 fcv and 66%tr | 0.25 | 70.45 ± 1.50 | 0.39 ± 0.05 | 5 | 0.81 ± 0.03 |
| 1a2 | Recreational | 3, 5, 10 fcv and 66%tr | 0.10 | 70.45 ± 1.50 | 0.39 ± 0.05 | 4 | 0.81 ± 0.03 |
| 2ap1 | Agriculture | 3, 5 and 10 fcv | 0.25 | 66.67 ± 0.00 | 0.17 ± 0.03 | 4 | 0.88 ± 0.01 |
| 2ap2 | Agriculture j | 3, 5 and 10 fcv | 0.10 | 69.70 ± 3.03 | 0.24 ± 0.00 | 3 | 0.84 ± 0.01 |
| 2a1 | Agriculture | 3, 5, 10 fcv and 66%tr | 0.25 | 86.35 ± 7.99 | 0.68 ± 0.19 | 3 | 0.52 ± 0.20 |
| 2a2 | Agriculture | 3, 5, 10 fcv and 66%tr | 0.10 | 77.25 ± 16.87 | 0.43 ± 0.44 | 3 | 0.67 ± 0.26 |
| Model No. | Model Settings | Model Outcomes | |||||||
|---|---|---|---|---|---|---|---|---|---|
| J4.8 | PCF a | CMW b | CCI g (%) | Kappa Statistics | CEN h | ||||
| TP c | FN d | FP e | TN f | Mean ± sd | Mean ± sd | Mean ± sd | |||
| 1iaj-4k | 3, 5 and 10 fcv l | 0.25 | 0 | 1 | 2 | 0 | 72.73 ± 6.05 | 0.44 ± 0.13 | 0.78 ± 0.09 |
| 1a5 to 1a7 | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 3 to 5 | 0 | 77.43 ± 8.03 | 0.56 ± 0.15 | 0.64 ± 0.11 |
| 1a8 | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 7 | 0 | 78.77 ± 8.00 | 0.58 ± 0.15 | 0.61 ± 0.11 |
| 1a9 to 1a12 | 3, 5 and 10 fcv | 0.1 and 0.25 | 0 | 1 | 8 and 9 | 0 | 74.93 ± 6.93 | 0.51 ± 0.13 | 0.67 ± 0.07 |
| 2ap3 | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 2 | 0 | 75.76 ± 5.25 | 0.47 ± 0.13 | 0.67 ± 0.15 |
| 2ap4 and 2ap5 | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 3 and 5 | 0 | 72.73 ± 7.17 | 0.43 ± 0.13 | 0.68 ± 0.10 |
| 2a3 to 2a6 | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 1 to 4 | 0 | 87.12 ± 6.59 | 0.69 ± 0.16 | 0.53 ± 0.16 |
| 2a7 to 2a11 | 3, 5 and 10 fcv | 0.25 | 0 | 1 | 5 to 15 | 0 | 80.21 ± 9.44 | 0.56 ± 0.19 | 0.63 ± 0.13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jerves-Cobo, R.; Córdova-Vela, G.; Iñiguez-Vela, X.; Díaz-Granda, C.; Van Echelpoel, W.; Cisneros, F.; Nopens, I.; Goethals, P.L.M. Model-Based Analysis of the Potential of Macroinvertebrates as Indicators for Microbial Pathogens in Rivers. Water 2018, 10, 375. https://doi.org/10.3390/w10040375
Jerves-Cobo R, Córdova-Vela G, Iñiguez-Vela X, Díaz-Granda C, Van Echelpoel W, Cisneros F, Nopens I, Goethals PLM. Model-Based Analysis of the Potential of Macroinvertebrates as Indicators for Microbial Pathogens in Rivers. Water. 2018; 10(4):375. https://doi.org/10.3390/w10040375
Chicago/Turabian StyleJerves-Cobo, Rubén, Gonzalo Córdova-Vela, Xavier Iñiguez-Vela, Catalina Díaz-Granda, Wout Van Echelpoel, Felipe Cisneros, Ingmar Nopens, and Peter L. M. Goethals. 2018. "Model-Based Analysis of the Potential of Macroinvertebrates as Indicators for Microbial Pathogens in Rivers" Water 10, no. 4: 375. https://doi.org/10.3390/w10040375
APA StyleJerves-Cobo, R., Córdova-Vela, G., Iñiguez-Vela, X., Díaz-Granda, C., Van Echelpoel, W., Cisneros, F., Nopens, I., & Goethals, P. L. M. (2018). Model-Based Analysis of the Potential of Macroinvertebrates as Indicators for Microbial Pathogens in Rivers. Water, 10(4), 375. https://doi.org/10.3390/w10040375









