Abstract
While the rain-driven evapotranspiration (ET) process has been well-studied in the humid climate, the mixed irrigation and rain-driven ET process is less understood for green roof implementations in dry regions, where empirical observations and model parameterizations are lacking. This paper presents an effort of monitoring and simulating the ET process for an irrigated green roof in a rain-scarce environment. Annual ET rates for three weighing lysimeter test units with non-vegetated, sedums, and grass covers were 2.01, 2.52, and 2.69 mm d−1, respectively. Simulations based on the three Penman–Monteith equation-derived models achieved accuracy within the reported range of previous studies. Compared to the humid climate, the overestimation of high ET rates by existing models is expected to cause a larger error in dry environments, where the enhanced ET process caused by repeated irrigations overlapped with hot, dry conditions often occurs during summer. The studied sedum species did not show significantly lower ET rates than native species, and could not effectively take advantage of the deep moisture storage. Therefore, native species, instead of the shallow-rooted species commonly recommended in humid climates, might be a better choice for green roofs in rain-scarce environments.
1. Introduction
Urbanization can perturb the natural patterns of streamflow, channel morphology, water quality, and ecosystem structure and function [1]. To address such an “urban stream syndrome”, the natural water balance needs to be restored via harvesting, infiltrating, or evapotranspiring the extra stormwater runoff caused by urbanization [1,2]. As one type of green infrastructure (GI), green roofs provide rainfall–runoff retention and stormwater filtration for non-severe storms, and are especially useful in densely built areas where space for stormwater retention measures is limited and expensive [3,4,5]. As a stormwater management strategy applied since the 1960s [6], they have been found to reduce runoff flow rate, volume, and response time—all important for reducing stormwater impacts [6,7,8,9,10,11,12]. Green roofs also bring other environmental benefits to the urban ecosystem, including heat island relief, air quality improvement, habitat and biodiversity provision, and food production [3,6,7,13,14,15,16,17,18,19,20,21].
Green roofs mainly rely on evapotranspiration (ET) to regenerate the retention capacity between rainfall–runoff events [22]. The evaluation of other green roof sustainability objectives (like roof cooling and food production) also requires the accurate estimation of ET. In addition to its insulation [14,16,21], reflection [23], and shading [3] properties, a green roof can act as an evaporative device which uses ET to cool roof surfaces in warm seasons [6,8,9,10,22,24,25]. Evapotranspiration estimation, therefore, is an essential element in the performance modeling for green roofs [26,27,28,29,30], and remains an area for improvement in integrated modeling frameworks [27,31].
Common practices of transforming agricultural ET models or establishing localized empirical models have not been widely validated for different environments. For example, crop coefficients are widely identified by existing studies for the humid climate [32,33,34,35], but are less known in drier regions. The standardized ET equations such studies used generally assumed the surface resistances are fixed for well-watered short grass surfaces. But the surface resistance can be affected by leaf area index varying across the growing stages and stomatal resistance varying across a day with solar radiation, leaf temperature, vapor pressure, leaf water potential, and carbon dioxide [36,37]. Establishing the crop coefficients on a hypothetically fixed surface resistance does not make this workflow completely physically-based. Though most calibration studies are concentrated on wet regions, the empirical aspect of the plant-specific and moisture-based parameters requires calibration for different climates [26,38]. But fundamentally in the long term, models of green roof ET need to be advanced with more physically-based parameters. Parameterization study as well as the uncertainty analysis, therefore, are needed to create that knowledge basis.
The ET process can be conceptualized by two regimes: in the energy-limited regime, ET is independent of moisture supply; in the moisture-limited regime, ET is first-order constrained by moisture supply [39]. Opposite of the general recognition as a water-saving device in the humid environment where the ET process is limited more by the energy availability given enough rainfall inputs [40,41,42,43,44], green roofs have been less applied and less studied in drier regions where the ET process is more limited by water availability. Though widely selected as green roof species for humid regions [32,33,34,35,42,43], the adaptability of sedums has not been thoroughly examined for other climates. The primary challenge with green roofs in less humid regions lies in the hot, dry summer period when irrigation often needs to be supplemented [45,46]. Although irrigation is critical for plant establishment only for the first few years in humid regions [41], non-native plants may need continuous watering in rain-scarce areas. Irrigated green roofs are typically subject to daily cycles that switch between a climate-driven dry state and an irrigation-induced wet state. The impact of this cycling on existing green roof ET models has not been fully examined. The maintenance activities, including irrigation, are one of the key factors characterizing the long-term GI efficiency, but their empirical data are extremely limited and need to be collected [47]. Despite that the potential ET (PET) rate has been long established to determine the ideal amount of irrigation [48], this concept is applied in arid areas only for the traditional types of urban landscape [49,50]. A very limited number of studies has been conducted to estimate the irrigation cost for green infrastructure. The estimation of the irrigation demand for GI is needed and requires further studies [51]. The cost and the public perception of watering green roofs in rain-scarce areas are commonly noted as disadvantages. But applying irrigation to city landscapes tends to enhance urban ET [52,53,54,55,56], especially in hot and dry regions where high atmospheric demands and intensified heat advection prevail. The resulting roof cooling and urban heat island relief create potential energy savings in building operations to compensate for the irrigation cost. As the central role in determining the tradeoff between the cooling gain and irrigation savings, ET estimation becomes closely linked to the life cycle assessment for green roof applications [41]. For the above-mentioned knowledge gaps, additional studies of ET observations and modeling in the dry areas are critical [57,58].
This study aims to help address the general lack of green roof ET empirical observation and modeling studies in dry regions. The specific goal is to quantify the ET performance of an irrigated green roof in a rain-scarce environment via both measurement and estimation. A weighing lysimeter-based experiment was conducted on an intensive green roof on the University of Utah campus in the metropolitan area of Salt Lake City, Utah, USA. The role of the environmental variables, especially the applied irrigation, to the ET process was explored. Three prevalent ET models were parameterized, while the influence of the parameter uncertainty to one model prediction was further analyzed. The research results are expected to contribute to the knowledge base to improve ET modeling and more generally the hydrologic performance evaluation of green roofs in dry regions.
2. Materials and Methods
2.1. Study Site
The study was conducted in Salt Lake City (SLC), UT, USA, which has a hot-summer, sub-humid, continental climate (Dfa) based on the Köppen climate classification without the prevalence of severe storms. From 1980 to 2010, the average annual precipitation was 409 mm and the average annual air temperature was 11.5 °C [59]. July is the hottest (average temperature: 26 °C) and the driest month (average precipitation: 15 mm; average pan evaporation: 366 mm). The winters are cold and snowy, while January and December have the lowest average temperature (−1 °C) and April is usually the wettest month (average precipitation: 51 mm). The primary source of summer precipitation is monsoon moisture moving in from the Gulf of California. In the winter, temperature frequently stays below freezing, and evening fog and daytime haze are common [60]. Salt Lake City utilizes four local sources for its water needs: approximately 57% drawn from City Creek, Parleys Creek, Big Cottonwood Creek, and Little Cottonwood Creek; around 27% from Deer Creek Project, and the rest from wells [61]. As a water-limited region, SLC regulates 80% of trees and shrubs to be drought-tolerant species and restricts turf grass to areas with a ground slope of less than 50% [61].
The study site was an established intensive green roof located on top of the third-floor mezzanine of the University of Utah’s Marriott Library (40.7623° N, 111.8468° W). The green roof had an area of 632 m2, and the growth medium had a depth of 305–457 mm. Half of the entire roof (51%) was planted with primarily herbaceous plants (74% of the grown area) and shrubs (19%). The dominant species was Blue Grama Grass, Bouteloua gracilis, covering 37% of the vegetated area, followed by Russian Sage, Perovskia atriplicifolia (9%), and Hardy Dwarf Broom, Genista Lydia (9%). Sedums, Sedum spurium ‘Red Carpet’ and Sedum kamtschaticum, ranked as the 4th most abundant species (7%). Underneath the plants, the green roof consisted of growth media, Beckett (North Ridgeville, OH, USA) filter fabrics, and AmerGreen (Thousand Oaks, CA, USA) 50RS drainage mats. The Utelite E-Soil® Root Zone Mix growth media was mechanically blended by the Utelite Corporation (Salt Lake City, UT, USA). The blended medium included 33.4% sand, 26.0% silt, and 14.3% clay with 8.0% organic matter. The bulk density was 1.02 g/cm3, the soil porosity was 0.58, the pH was 7.1, and the saturated hydraulic conductivity was 1.4 mm/min.
As a part of the campus landscape, the green roof was managed and irrigated by the university. As requested, the university management provided a consistent irrigation schedule for the green roof and other nearby landscaping. Irrigation was executed automatically via established rotating sprinklers (Rain Bird, Azusa, CA, USA) with a Baseline 3200 controller (Baseline Inc., Boise, ID, USA). While the authors were unable to control the irrigation schedule, the field experiment carefully recorded irrigation amounts and timing via tipping bucket rain gauges. The start and end of each irrigation event were further documented by high-resolution load cells measuring the addition and loss of water to the green roof weighing lysimeters. Identified accordingly, the irrigation was scheduled nightly near midnight with a maximum total duration of 30 min from May to early November. The total irrigation during the experiment was 442 mm. The daily maximums of irrigation and rainfall were 15 mm and 31 mm, respectively. To avoid undesirable irrigation influences on the load cell readings, nightly observations during the irrigation periods were not considered in this study.
2.2. Evapotranspiration Observation
Data collection lasted through the calendar year 2014 (496 mm annual precipitation), which was a slightly wetter than average year (409 mm) (Figure 1). Weighing lysimeters were adopted to measure green roof ET rates, because of their previous successful applications in GI [24,33,62] and their capacity to account for the advection effect. The water balance of a weighing lysimeter is:
where ETa is actual evapotranspiration (mm), P is precipitation (mm), Irrig is irrigation (mm), O is surface overflow (mm), Q is discharge from the underdrain (mm), and ∆S is the change in water storage (mm). The surface overflow was neglected in this study due to the highly pervious soil used and the lack of observed runoff. Infiltration is implicitly tracked by Q and ∆S. During the periods when precipitation, irrigation, surface overflow, and discharge were zero, ET was then determined as the mass change tracked by the weighing lysimeters:
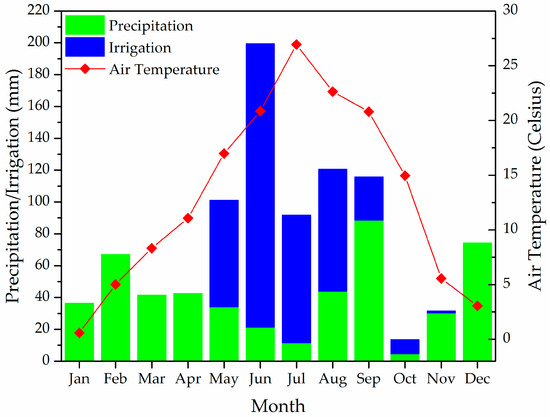
Figure 1.
Monthly precipitation and irrigation amounts, and average 2-m air temperature at the study site in 2014.
The lysimeter shells were rectangular acrylic containers (1.22 m by 0.61 m by 0.36 m) sealed with adhesives and silicone. To match the green roof, an underdrain, made of a bulkhead fitting and a valve, was installed at the bottom of the lysimeter on one side. Each lysimeter contained a replica of layers of the existing green roof at the site. The depth of the growth medium within the container was designed to be 254 mm, 17% less than the depth of the referenced green roof. A deeper lysimeter requires a more costly load cell with a greater loading capacity. Such a load cell, however, would have a lower resolution that affects the accuracy of observed ET rates. Therefore, compared to the referenced green roof, a slightly shallower soil depth was selected to achieve more accurate and economical ET observations.
Three custom-built weighing lysimeters of the type described above were established to contain covers including non-vegetated growing medium (as the control), sedums (Red Carpet Stonecrop, Sedum spurium ‘Red Carpet’ and Russian Stonecrop, Sedum kamtschaticum), and grass (Blue Grama grass, Bouteloua gracilis) (Figure 2). The plants were transplanted into the lysimeters in September 2013, after several years of growth on site as part of the green roof installation. Rice Lake BenchMark HE weighing scales (Rice Lake, WI, capacity: 454 kg, resolution: 0.05 kg ~ 0.06 mm, tolerance: 0.08 kg ~ 0.10 mm) were adopted as the load cells managed by IQ355 indicators (Rice Lake, WI, USA). Buried at the surface (~10 mm deep) and bottom (~360 mm deep) of each lysimeter after lab calibrations, Decagon (Pullman, WA, USA) 5TM sensors were used to measure soil moisture (resolution: 0.08% VWC). Attached to and protected by a PVC pipe on the outside, a tipping bucket rain gauge (TE525, resolution: 0.25 mm, Campbell Scientific, Logan, UT, USA) was half buried underground to monitor the timing of the underdrain discharge for each of the three lysimeters (Figure 3). The observation during the drainage periods could then be tracked and excluded from the analysis. Additional TE525 tipping bucket rain gauges were placed next to each of the lysimeters on the roof in order to measure the precipitation and irrigation. All data were recorded as 5-min averages by a Campbell Scientific CR1000 datalogger (Campbell Scientific, Logan, UT, USA) linked with a Campbell Scientific AM16/32B multiplexer (Campbell Scientific, Logan, UT, USA). The measured 5-min ETa rates were summed to daily values to be used in the following analyses and comparison.

Figure 2.
Photograph of the experimental setup.
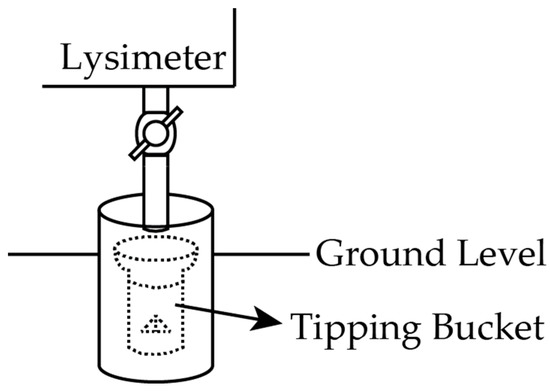
Figure 3.
Schematic (not to scale) of the drainage observation setup underneath the lysimeter.
The micro-meteorological conditions were monitored by a weather station (Met. Tower in Figure 2). A Kipp & Zonen CNR-1 (Delft, The Netherlands) net radiometer was mounted 3 m above the roof level, which measured both incoming and outgoing components of the short and longwave radiation. The 2-m wind speed was monitored by a Campbell Scientific CSAT3 sonic anemometer (20 Hz) (Campbell Scientific, Logan, UT, USA). Four thermocouple probes (Omega HTTC36-T-18G-6, Stamford, CT, USA) were mounted at 0.12 m, 0.60 m, 1.50 m, and 2.50 m above the roof level to determine the vertical air temperature profile. Relative humidity was measured at 2 m using a Campbell Scientific HMP155A probe (Campbell Scientific, Logan, UT, USA). Meteorological data were recorded by a Campbell Scientific CR5000 datalogger (Campbell Scientific, Logan, UT, USA). The whole experiment was powered by directly connected solar panels. Standard operational weather stations (ID: WBB and MTMET) from the nearby campus operated by Mesowest (http://mesowest.utah.edu/) were used to fill the gaps caused by power failures. A Decagon SC-1 Leaf Porometer (Pullman, WA, USA) was employed to measure the diurnal stomatal resistances of sedums and grass in the lysimeters on 17 June 2015, in order to corroborate ET estimates. The leaf area was estimated by branch sampling and image analysis via Easy Leaf Area, which uses the color ratio of image pixels to distinguish leaves from the background [63].
2.3. Evapotranspiration Estimation
Based on the Monin–Obukhov Similarity Theory and the surface energy balance, the Penman equation and its family, including the Penman–Monteith (P–M) equation, were derived for ET estimation. The P–M equation serves as the keystone of other simplified equations like the Priestley–Taylor (P–T) equation [64] and the Advection–Aridity (A–A) equation [65], or revised forms, including the Food and Agriculture Organization (FAO) of the United Nations’ irrigation and drainage method (FAO56) [48] and the American Society of Civil Engineers standardized reference ET scheme [66]. As the P–M equation and its descendants are commonly used for green roof ET estimation in the humid environment [32,33,34,35,42,43], the P–M equation and its two revisions are tested for the two vegetated covers. Non-vegetated cover, without the transpiration part (no crop coefficient and water stress coefficient), was excluded from the ET estimation.
The FAO56 ET scheme has been widely used as the baseline to estimate green roof ET [32,34,43]. It can be calculated by the following workflow. The reference ET (ETo) was first computed as follows [48]:
where ETo is the reference ET corresponding to well-watered short grass (mm h−1), ∆ represents the slope of the saturation–vapor–pressure temperature curve (kPa °C−1), Rn is the net radiation (MJ m−2 h−1), G is the soil heat flux (MJ m−2 h−1), γ is the psychrometric constant (kPa °C−1), T is the air temperature at 2 m (°C), es is saturation vapor pressure (kPa), ea is actual vapor pressure (kPa), and u2 is the mean hourly wind speed at the 2-m height (m s−1). Daily summed reference ET can be further revised by a crop coefficient and a water stress coefficient to compute ETa (mm d−1) [48]:
where Ks is the water stress coefficient, Kc is the crop coefficient (parameterized as monthly constants in this study), and the product of Kc and ETo results in PET (mm d−1). Converted to the volume demand with the green roof area, PET can be directly used to estimate the irrigation cost ($):
where TPj is the tiered water price ($/m3) corresponding to the jth tier, and Vj is the net water demand (m3) of the jth tier during the growth season (April–October), calculated as the residue of subtracting the product of PET and area by the rainfall amounts. The water stress coefficient can be estimated as follows [48]:
where θ is the moisture content (fraction) as the average of the measured surface and the bottom soil moisture contents of the lysimeter, θwp is the wilting point (fraction), θfc is the field capacity (fraction), and p is the average fraction of the available moisture that can be depleted from the root zone before moisture stress occurs. The field capacity (0.35) was determined via lab tests by oven-drying soil samples. There is no established way to measure the wilting point directly other than visual observation, which, however, is difficult to determine and could be inconsistent between observers and cases [29,33]. As no visual wilting was clearly observed, the wilting point of this study was approximated based on the following empirical equations [67,68]:
where θwp is the wilting point (fraction), θ1500t is the moisture content at a tension of 1500 kPa, S is the weight fraction of sand, C is the weight fraction of clay, and OM is the percent organic matter. The fraction p can be estimated as follows [48]:
where pFAO56 is the recommended value from Table 22 in the FAO56 report [48]. The average of the ETa measured from the lysimeter observation was used. The pFAO56 value (0.4) corresponding to bluegrass was used to represent the studied grass. No pFAO56 value was published for sedum species. The fraction p represents the plant’s capability of extracting moisture from the root zone. The documented pFAO56 value (0.5) of cucumber was assumed as that of the sedum, since both are succulent species. Once Ks is determined, the daily Kc can be back-calculated given the computed ETo and the measured ETa. The developed daily Kc time series were summarized into the monthly averages.
The Thornthwaite–Mather equation (T–M), as the second model tested here, has been often used to convert ETo to ETa for green roofs by only adjusting soil moisture variations [33,38]:
The ETo Equation (3) implicitly fixes the surface resistance at 70 s m−1, or at 50 s m−1 for daytime and 200 s m−1 for nighttime. Only representing the short, cool-season, well-watered reference grass, though, such values are presumed for green roofs as a routine [32,33,42,43]. As the cornerstone of all P–M derived methods, the original P–M equation was also examined to estimate ETa after calibrating the surface resistance parameter [69]:
where ρa is the mean air density (kg m−3), cp is the specific heat of the air (MJ kg−1 °C−1), ra is the aerodynamic resistance (s m−1) which can be calculated based on FAO56 scheme [48], λ is the latent heat of vaporization, which can be calculated as λ = 2.501 − 0.00237 × T [70], but 2.45 MJ kg−1 was used in this study, γ is the psychrometric constant (kPa °C−1), and rs is surface resistance (s m−1). Given the tracked ETa and the measured meteorological conditions, the hourly surface resistances could be back-calculated via Equation (11) [71,72].
As a short summary on the parameterizations, back-calculating the FAO-56 method generates the daily time series of Kc, which were then reduced to monthly Kc. Back-calculating for the P–M equation produces the hourly time series of rs, which were then reduced to the hourly rs averaged over the month and over the year. The former gives the hourly surface resistances averaged over the month, and the latter gives the hourly surface resistances averaged over the year. The FAO56 method then took the reduced monthly crop coefficients to estimate the ETa, the T–M method did not need to calibrate any parameters, and the P–M method used the reduced hourly surface resistances averaged over the month (Table 1).

Table 1.
Parameters used for three evapotranspiration estimation methods.
2.4. Statistics
The Kruskal–Wallis Analysis of Variance (ANOVA) test and the Mood’s Median test were used to determine the difference in the ETa observations between covers. Partial least squares (PLS) analysis was made to examine the influence of selected environmental variables (air temperature, relative humidity, wind speed, air pressure, incoming solar radiation, the sum of precipitation and irrigation, surface soil moisture, and bottom soil moisture) on the ET process. To conduct the PLS analyses on a daily basis, the solar radiation and the sum of precipitation and irrigation were aggregated to daily values, while a daily average was used to represent all other measured variables. For all three ETa models, their 5-min ETa estimates were summed to daily amounts to be compared with the ETa daily measurements. The variable importance in projection (VIP) scores summarize the influence of individual variables on the PLS model, and give a measure useful to select the independent variables that contribute the most to the dependent variable’s variance [73]. It is generally accepted in practice that variables having a VIP > 1.0 are highly influential, values between 0.8 < VIP < 1.0 indicate moderately influential variables, and variables with VIP < 0.8 are less important [73,74]. The coefficients of determination (R2), the root mean square error (RMSE), the Nash–Sutcliffe efficiency (NSE) [75], and the percent bias (PBIAS) were calculated to evaluate the goodness of fit of the three ETa models. Model simulation can be judged satisfactory if NSE > 0.65 or PBIAS < ±15% [43]. The statistical analysis was conducted via OriginPro 2015.
To quantify the contributions of the uncertainty of the parameterization process to ETa estimates, the generalized likelihood uncertainty estimation (GLUE) [76] was used in Python 2.7.13 to conduct the uncertainty analysis for the FAO56 model. As only the FAO56 model includes the full suite of parameters of interest (Kc, Ks, and rs for this study), the TM and PM models were not included in the uncertainty analysis. A uniform distribution within a feasible range (Table 2) was assigned to the parameters, as no evidence existed for other statistical distributions [77,78]. The maximum of Kc was set according to the previous observation [79], and the threshold of rs was the maximum value observed in the field. The range of the water stress coefficient was based on the definition of the FAO56 method [48]. A Monte Carlo simulation with 100,000 runs was performed to create a random parameter space for sedum and grass ETa estimates, respectively. Each run was driven by the available hourly meteorological data of 2014 and independently randomized parameters. As a formal likelihood measure could be more problematic due to the subjectivity of choosing the shape factor [80], a less formal likelihood measure (NSE) was used in the form:
where L(θi|Y) is the likelihood measure for the model with the ith parameter set conditioned on the observations Y, is the error variance for the ith model, is the observed variance, and N is the shape factor. As higher N values have the effect of accentuating the weight given to the better simulations and narrowing the confidence limits, N = 1 was used [81]. The simulated and measured daily ETa time series were compared to compute a yearly NSE as the indicator of the model efficiency. Runs with a negative NSE were excluded. Followed by Staudt et al. [77] and Prihodko et al. [78], the top 10% behavioral threshold for NSE was used to select runs for further analysis. The posterior likelihood can be updated by the application of Bayes equation [81]:
where L(Y|θi) is the posterior likelihood for the simulation of Y given the ith parameter set and the scaling constant C, Lo(θi) is the prior likelihood for the parameter set θi. The scaling constant is used to scale the cumulative of the posterior likelihood to equal to unity. Based on the assumed uniform distribution, the prior likelihood for each parameter set was equal. Then the scaling constant could be calculated as [82]:

Table 2.
Range of the prior uniform distribution sampled for the uncertainty analysis.
Predictive uncertainty bounds were determined as the 5% and 95% quantiles of the derived cumulative probability distribution of the ranked model efficiency [83]. The cumulative likelihood of each parameter was also plotted against the uniform distribution. The deviation from the uniform distribution indicates the parameter sensitivity, and the steepest slope in the cumulative likelihood curves reflects the optimal range of the parameter values [77]. The two-sample Kolmogorov–Smirnov (K–S) test [84] was conducted to evaluate the difference between the generated distribution and the uniform distribution. The K–S value was used to rank the sensitivity of parameters [77,78].
3. Results and Discussion
3.1. Evapotranspiration Regime
The average observed ET rates are 2.01 ± 1.16 (standard deviation), 2.52 ± 1.79, and 2.69 ± 1.69 mm d−1 over the one-year study period for the non-vegetated, sedum, and grass covers, respectively (Figure 4). The p values of the Kruskal–Wallis ANOVA test and Mood’s Median test for the daily ET time series are 2.08 × 10−4 and 1.53 × 10−6, respectively, at a significance level of 0.05. Therefore, the observed ET rates are statistically different among the three surface covers. Compared to the non-vegetated roofs, vegetation could elevate ET rates by over 25% on average.
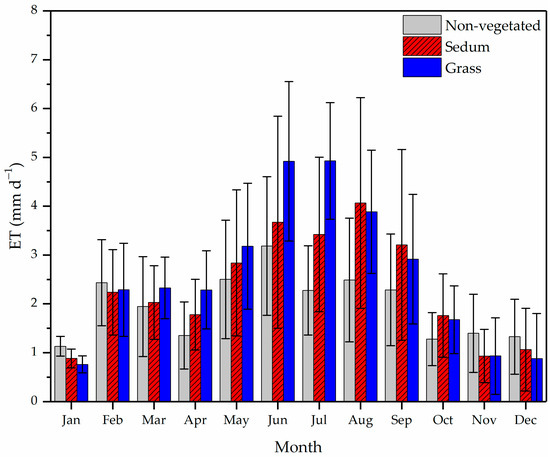
Figure 4.
Monthly averages of observed green roof evapotranspiration (ET) rates of 2014 (error bars represent standard deviations).
The observed ET rates of sedums and grass tend to be slightly higher than most studies conducted in rain-rich environments [23,29,33,85,86,87]. For example, Rezaei [85] observed ET rates of 1.68 mm/d for sedums and 1.06 mm/d for the non-vegetated medium with unlimited water supply in an indoor environment. Marasco et al. [86] measured via a dynamic chamber 1.71 mm/d on average for sedums in New York City, NY with 1078 mm annual rainfall, while DiGiovanni et al. [33] measured via lysimeters 2.27 mm/d for sedums in the Bronx, NY with an average annual rainfall of 1100 mm. In Auckland, New Zealand, Voyde et al. [22] reported 2.21 mm/d for sedums with an annual rainfall of 1240 mm via lysimeter measurements. With a lower water supply (a total of 938 mm water: 496 mm precipitation + 442 mm irrigation) in the studied sub-humid climate compared to the above-listed wetter environments, the values of the observed annual ET rates are not correspondingly smaller. In other words, the rain-scarce region does not necessarily lead to a lower yearly ET rate of the green roof compared to the rain-rich region.
Intuitively, the larger yearly ET rates seem to be caused by the added irrigation only. The maximums of the observed monthly ET averages of the sedum (4.07 mm d−1) and grass (4.93 mm d−1) are higher than the maximum daily rate of 3.4 mm/d from the grass and sedum covers after a 7-day dry period measured in a climate-controlled chamber [29]. Yet, the observed ET rates during the summer with irrigation applied are not always significantly larger than the reported values in the rain-rich environments. The maximum monthly ET rates of the sedum and grass are lower than the maximum monthly average (7 mm d−1) reported by a multi-year study of sedums in Villanova, PA, USA with an annual rainfall of 817–1352 mm [42], but are close to the reported 4.94 mm d−1 in the rain-rich region [86]. There is no consistent relationship between the observed summer ET rates and the reported values. But overall, comparable summer ET rates were found between the studied rain-scarce region and other rain-rich regions. Added irrigation appears to be able to support the energy-limited ET regime in the studied environment.
Four variables were found as the important factors influencing the ET process of the vegetated covers via the PLS analysis (Figure 5). For the sedum cover, the VIP scores for air temperature, surface moisture, relative humidity, and solar radiation are 1.79, 1.26, 1.22, and 0.95, respectively. For the grass cover, the VIP scores for air temperature, solar radiation, surface moisture, and relative humidity are 1.48, 1.33, 1.07, and 1.01, respectively.
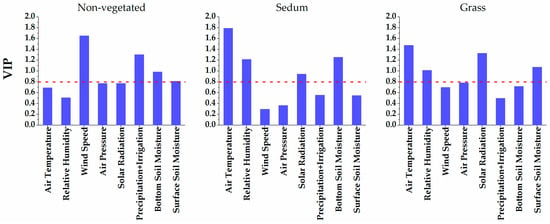
Figure 5.
Variable importance in projection (VIP) plots for partial least squares analysis. Note: the VIP value of the influential variables is larger than 0.8 (red dashed line).
The VIP scores mean that the climate factors play a large role in determining the variations of observed ET rates. Air temperature is discovered to be the most important factor determining ET rates for sedum and grass covers, as it is closely related to other meteorological variables (like vapor pressure deficit) and plant physiological responses (like stomatal conductance). The wind speed has the largest influence on evaporation rates for non-vegetated cover. This is likely a result of the different turbulent flow characteristics associated with bare soil and vegetative canopies.
The important role of climate factors indicates that the ET process of the studied species in the rain-scarce region prevalently had an energy-limited regime due to a combined impact. The climate and irrigation worked together to promote the high ET rates. Applied irrigation could promote an energy-limited regime; within the regime, the ET process would be independent of the irrigation but taken over by climatic factors. With intensified atmospheric demands and prevailing heat advection, the hot, dry summers in the dry regions would have a larger climatic driving force than the summers in the wet regions, for the energy-limited ET regime given the same moisture supply. However, maintaining an energy-limited ET regime in a rain-scarce environment can be costly and may not make sense in terms of water conservation. Native species with stronger drought tolerance, therefore, are recommended as green roof species in a dry environment.
3.2. Design Considerations for Water Conservation
Via PLS analysis, solar radiation is another important contributor to ET rates for both studied plant species (Figure 5). Strategies like shading to reduce the duration and magnitude of sunshine might be helpful for suppressing PET rates. Selecting a rooftop that can be partially shaded by (higher part of or nearby) buildings becomes an important design factor for green roof investments in rain-scarce environments. A heterogeneous landscape design with higher native shrubs being able to shade less drought-resistant grass plants on the nearby roof surface is also recommended. In addition to climatic factors, the moisture storage of green roofs also has a larger influence on ET variations than wetting events (Figure 5). The storage created by the medium pores and drainage mats could delay the response of ET rates corresponding to the wetting events. Increasing the size of this moisture storage (by using, for example, a deeper medium or thicker drainage mats) could help green roofs collect more moisture from the wetting events for use during the drought periods. Therefore, shading and increasing the moisture storage would be recommended for green roof applications in dry regions.
Actual evapotranspiration rates of sedum and grass statistically differ from each other. From an analysis of the vertical moisture profiles, this ET difference is related to the diverse rooting depths between the two species. The surface moisture content of the sedum cover was consistently lower than that of the grass cover during April–July (Figure 6). During this period, however, sedums tended to have lower ET rates than the grass (Figure 4). Seemingly, during the early growing stage, sedums, as succulent species, tended to store moisture rather than releasing it. Since August, when the surface moisture of the sedum cover became close to or even larger than that of the grass, the ET rates of sedums became larger than those of the grass. No consistent relation, however, was found between the moisture content of the bottom layer and the observed ET rates. Even when the deep moisture of the sedum-covered lysimeter, for instance, was highest among all three covers in July, the sedum ET amount was still much lower than the grass ET. These indicate that the ET rates and the survival of the studied sedums are more restricted by the surface moisture. Therefore, though the extra soil depth in an intensive green roof could provide more moisture and heat storage for runoff reduction and roof cooling, sedums may not be able to fully take advantage of the moisture stored in the deep soil. From the perspective of water conservation, sedums may not be the ideal species for green roofs in the rain-scarce regions. However, as a succulent species, sedums need a moist surface soil layer to grow healthily. This has to be satisfied by repeated irrigation when precipitation is limited. Dying sedums were observed from another green roof on the University of Utah campus due to the lack of enough irrigation (according to personal correspondence with the campus irrigation technicians). This also partly explains why native species established more readily than exotic succulent species like sedums under extreme conditions [25], where the capacity of tapping extra deeper moisture becomes necessary.
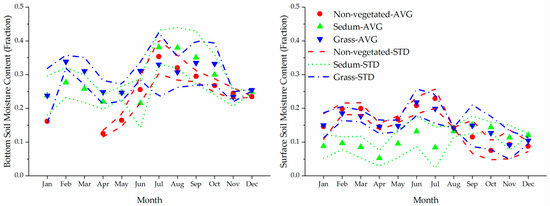
Figure 6.
Monthly averages of soil moisture at the bottom (left) and the surface (right) soil layers. Data are missing from the non-vegetated lysimeter at the bottom soil in February and March due to broken sensors. The point symbols represent monthly averages (AVG), while the lines represent the monthly standard deviations (STD).
3.3. Parameterization for Evapotranspiration Modeling
Calculated yearly averages of crop coefficients are 0.59 ± 0.29 (standard deviation) for sedum and 0.61 ± 0.25 for grass. The sedum Kc found by this study is generally close to and slightly larger than most previous studies conducted in moisture-rich environments. For example, 0.53 was reported for a well-watered sedum canopy measured by a weighing lysimeter of the same base size as this study in Durham, NH, USA [87]. An annual average of 0.51 was reported for different sedums in College Park, MD, USA with a 1004 mm annual rainfall, which was estimated based on moisture contents of green roof platforms (1.31 m2) larger than the area of this study [88], while 0.32–0.45 was reported as the annual averages for three sedum types also in College Park, MD, USA [33]. Similarly, 0.35–0.52 was observed for well-watered sedums calculated based on an energy balance approach for a 1000 m2 green roof in Vicenza, Italy with an approximately 1087 mm annual rainfall [89]. The sedum Kc of this study case is lower than some findings with smaller lysimeters but more moisture supplied. For example, Voyde [90] reported 0.85 for the well-watered sedum measured using 0.072 m2 weighing trays in Auckland, New Zealand; Schneider [79] observed 1.0–1.7 for sedums measured with a 0.21 m2 weighing lysimeter in Villanova, PA; and Rezaei [84] observed 1.35 on average for sedums estimated from 0.56 m2 indoor greenhouse trays.
In spite of the absolute difference, the crop coefficients of sedums estimated by this study are still within the range of the above-listed studies. As the crop coefficients adjust ETo mainly for the characteristics of species and climates, this reinforces that the applied irrigation effectively made up for the lack of rainfall in the studied environment. Notably, the studied sedum species have higher Kc than grass for some months (Figure 7). So, if well-watered, the studied sedum species could consume more water than grass, as also observed by Wolf and Lundholm [91]. Noticeably, both sedums and grass were observed to have higher Kc than the native species [92], indicating the potential application of the native species in green roofs in dry environments given enough soil space for the longer and wider root systems.
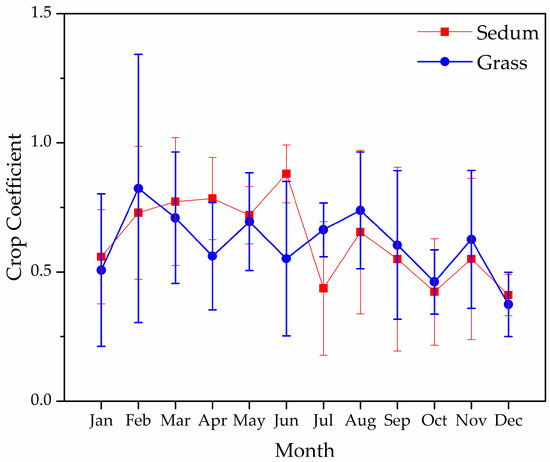
Figure 7.
Parameterized monthly crop coefficients of sedums and grass surface covers for the Food and Agriculture Organization of the United Nations’ irrigation and drainage method (FAO56).
The estimated surface resistances appear to vary widely among different plant covers, different months, and different hours (Figure 8). As no value larger than 2500 s m−1 was ever observed for both species during the diurnal field camp, any simulated surface resistances above this threshold were regarded as indicating the closure of stomata (i.e., negligible ET). Not representing the average resistance in the P–M equation, those infinite values were excluded from this study. The annual surface resistances of sedums and grass were estimated as 678 s m−1 and 651 s m−1, respectively. The corresponding stomatal resistances of sedums and grass during the middle growing stage (as leaf areas keep varying) were estimated as 958 and 606 s m−1, respectively. The estimated stomatal resistance of sedums is higher than previously reported values (250 s m−1 [90] and 750 s m−1 [79]). A diurnal measurement of stomatal resistance was further made on 17 June 2015 for the sedum and grass in the same lysimeters. Their values were converted to surface resistances after leaf areas were measured, and then compared with the hourly averages of estimated values of June 2014. In spite of one year’s difference, the estimated surface resistance still showed a relatively good match to the observed values (Figure 8), validating this parameterization procedure. Notably, the estimated nighttime non-zero resistances in this study seem to be lower than the measured nighttime non-zero resistances. This discrepancy might be because the former calculated the average resistance for the entire plant, while the latter only represented the average resistance of a few sampled leaves.
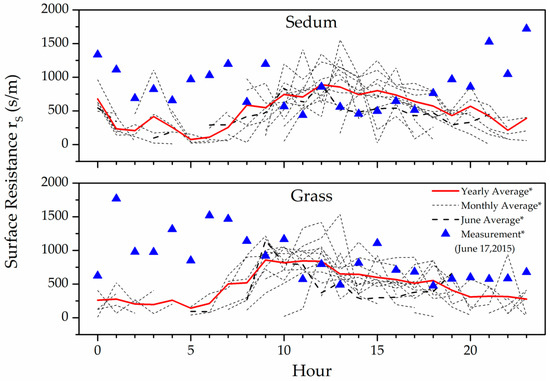
Figure 8.
Parameterized hourly surface resistances averaged over the year (red solid lines) and averaged over every month (short dashed lines, esp. over June: long dashed lines), and measured hourly surface resistances (blue triangles) of the sedum (top) and grass covers (bottom). * Note: values larger than 2500 s m−1 were excluded.
It has been recognized that sedums could have a crassulacean acid metabolism (CAM) mechanism, which shuts down stomata during the daytime to save carbon dioxide and water, and opens stomata to resume metabolism during the cooler and wetter nights [22,71,93,94]. Based on the estimated and measured surface resistances, however, no strong CAM was observed for the sedums in this study, as found by others as well [88,90]. The night irrigation might prevent sedums switching from the C3 mode, with which plants usually open stomata during the daytime, to CAM mode [95,96,97].
3.4. Comparison of Model Estimates
The selected three methods (FAO56, T–M, and P–M) were tested to simulate daily ETa values, which were then compared to the observed ETa time series (Figure 9). In spite of a slightly overall overestimation, all methods are close to the 1:1 line. The T–M method had the lowest R2 for the grass (Table 3). This may be because the T–M method is highly sensitive to the input parameters like the wilting point and field capacity [33], which are often difficult to accurately quantify. The FAO56 method achieved the best fit among the three methods for both vegetated covers. The accuracy of the P–M method was similar to the FAO56 method for grass cover. With less tedious computational work, the P–M method might be used to replace the FAO56 method for estimating ET rates of the grass-covered green roof.
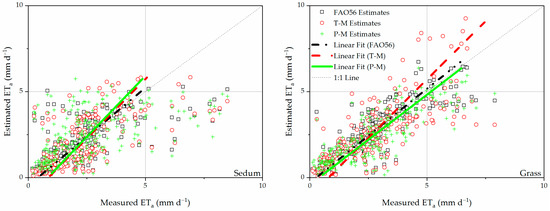
Figure 9.
Evapotranspiration (ETa) estimates based on FAO-56, T–M, and P–M methods plotted against ETa observations for the sedum (left); and grass green roofs (right). Note: FAO56 refers to the Food and Agriculture Organization of the United Nations’ irrigation and drainage method, T–M refers to the Thornthwaite–Mather equation, and P–M refers to the Penman–Monteith equation.

Table 3.
Statistical performance measures of evapotranspiration (ETa) estimations.
Although the model performance statistics are not particularly good, they fall within the range of most previous studies. The corresponding R2 for the sedum cover is slightly lower than the best estimate (R2 = 0.51) of Starry et al. [34] who used the FAO56 scheme to estimate sedum ETa in a rain-rich climate, but falls within their reported range (0.07 < R2 < 0.51). The R2 of sedum ETa simulation is also lower than the reported R2 value of DiGiovanni et al. [33] using the T–M method for sedums in a rain-rich climate, but the linear fitting equation of that study fixed the intercept at zero which could lead to a higher R2 value. The RMSEs of simulated sedum ETa are close to Marasco et al. [35] (1.19 to 1.32 mm d−1), who used a modified P–T equation, an A–A equation, and a storage model to simulate ETa for sedum green roofs in a rain-rich environment. The NSEs and PBIASs of ETa simulations for the studied sedums generally fall within the range of Berretta et al. [43] (NSE: −0.15 to 0.98; PBIAS: −74.02 to 15.13) based on a study also using the FAO56 scheme and the Hargreaves equation for sedums in a rain-rich environment; and NSEs of FAO56 and T–M methods are higher than the reported value (0.31) of Starry et al. [34]. Overall, the results of the tested three methods fall within the normal range of the aforementioned previous studies. The efficiency of the three methods generally follows the pattern of FAO56 > T–M > P–M for sedums, and FAO56 > P–M > T–M for grass.
All three methods generate a better estimation of grass ETa than sedums ETa. But, the three methods couldn’t fully explain the ET variance for the sedum cover, especially for the large ETa rates (over about 5 mm d−1). The underestimation of ETa for high ET-rate days has been observed in previous studies that used a fixed annual Kc [34,35]. The temporal upscaling of the calibrated parameters (i.e., averaging the daily crop coefficients into monthly or yearly values) does not seem to be a satisfactory approach to capture the ET response of sedums to large wetting events. Yearly or monthly constant crop coefficients might not have enough temporal resolution for ET prediction for succulent plants. This issue may be less problematic in wet regions where mild weather with higher humidity usually does not support a high ET rate after rain events. The accuracy of ETa estimation, however, might be more severely affected in dry regions, where frequent irrigation events often occur simultaneously with or right before hot and dry weather that favors high ET rates. Improved (e.g., non-linear) models of Kc and Ks are recommended for dry regions that depend on irrigation.
Most of the observations (overall 78% for sedums and 73% for grass) fell out of the 90% uncertainty envelope especially during the summer period (Figure 10). The NSE values of the top 10% of the runs ranged from 0.05 to 0.26 for sedums, and from 0.3 to 0.67 for grass. The variation in the selected parameters alone could not explain the disagreement between the estimates and measurements. A similar challenge was also found by Poyatos et al. [83], who modeled ET based on a stomatal conductance model in the Mediterranean climate. This deviation of the observed data from the uncertainty envelope might further indicate the fundamental deficiency in the current model structure [98,99]. On the other hand, the estimates also slightly fell out of the uncertainty envelope. This might be due to the lack of seasonality in the GLUE analysis. The sampled parameters with a fixed value were used constantly through a year for one GLUE run. Unlike the calibrated parameters with a finer temporal resolution, the sampled parameters without accounting for the seasonality might not be able to predict the ETa variations with a similar accuracy. As evidence, the observations tend to be closer to the estimates than to the uncertainty bounds (Figure 10). A stratified sampling for different seasons and multi-year observations as the inputs might be necessary for the future uncertainty analysis of ET models.
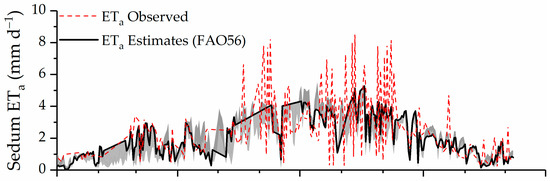
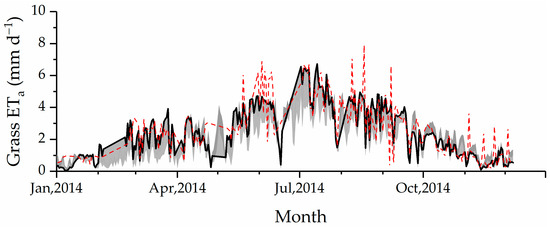
Figure 10.
Observed and estimated daily evapotranspiration (ETa) with the (5% and 95% quantiles) uncertainty bounds (shaded area) for the sedum (upper); and grass green roofs (lower). Note: the Food and Agriculture Organization of the United Nations’ irrigation and drainage method (FAO56) with the parameterized crop coefficients was used here to estimate ETa.
The cumulative likelihood distribution for the model parameters deviates from the uniform distribution (Figure 11), suggesting that the tested model is sensitive to the selected parameters [77]. The current model is sensitive to all three tested parameters via the K–S test at the 0.05 level. While the K–S values of three parameters were found to be close to each other, the model tended to be more sensitive to rs for both sedum and grass (Table 4).
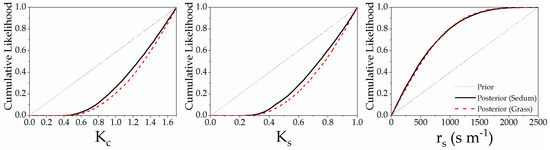
Figure 11.
Prior and posterior cumulative likelihood distribution for the crop coefficient (Kc) (left); water stress coefficient (Ks) (middle); and surface resistance (rs) (right). Note: the Food and Agriculture Organization of the United Nations’ irrigation and drainage method (FAO56) with the parameterized crop coefficients was used here to estimate ETa.

Table 4.
Kolmogorov–Smirnov coefficients for the sensitive parameters at the 0.05 level.
3.5. Irrigation Cost
Since it is a major concern associated with the long-term maintenance cost in water-limited regions, irrigation cost was estimated in this study. The total PET amounts of the growing season (April–October) were calculated as 785 mm and 768 mm for growing sedum and grass, respectively. An extra 174 m3 and 168 m3 water would be required for sedum and grass green roofs (322 m2), respectively, after assuming that the rainfall (246 mm) could be completely used. The estimated irrigation amounts could only be considered as a minimum, due to the assumption of no water loss during the irrigation process. From the water conservation perspective, the non-vegetated roof might be a good alternative to the vegetated green roofs in a dry climate. Based on the tiered water price in Salt Lake City, Utah [100], the total irrigation cost for the studied green roof was $117 for the entire growing season of 2014, which approximately equals to $0.4/m2. This irrigation cost is much less than a longer-term estimate ($2.9/m2) for an extensive green roof [41]. The difference, however, is highly dependent on the local water price.
Of the various environmental benefits that can be provided by green roofs [17,57], only stormwater runoff reduction is considered in this study. The economic returns of runoff reduction could be reflected by the potential to waive the stormwater impact fee, which is based for this study on the policy of Salt Lake City, UT, USA [101]. Given all of the harvested rainwater processed by the green roof, the avoided impact fee for the entire year would be $34. This economic return of using the green roof for runoff reduction would cover only 28% of the irrigation cost. The remaining 72% of irrigation cost would need to be offset by other potential benefits of the green roof, or the irrigation demand would need to be reduced to make projects balance cost and benefits in an economic sense. However, if the native species with the smaller Kc [92] are available to grow in this study setting (i.e., assuming the same PET rates), they could live without any irrigation and harvest a minimum of 60 mm of rainwater for the next year’s use (equal to 22 m3 harvested rainwater for the studied green roof). Also, if a retrofitting is possible, harvesting of discharge water from air conditioning units and other nearby sources can be considered solutions.
4. Conclusions
This study aimed to examine the ET behavior and to parameterize three ET models (FAO56, T–M, and P–M) for green roofs in a rain-scarce environment. A field experiment based on weighing lysimeter units was conducted in Salt Lake City, UT, USA, in 2014. The annual average ET rates of the studied grass, sedums, and non-vegetated covers were observed as 2.69, 2.52, and 2.01 mm d−1, respectively, which tend to be higher than other studies with more moisture-rich environments. Irrigation was able to support the energy-limited ET regime in the studied rain-scarce region. Given enough irrigation, the ET process is determined more by climate conditions than the wetting events during the dry, hot summers. In terms of water conservation, native species with higher drought tolerance are recommended for the rain-scarce environments with less irrigation demand. Shading and increasing the moisture storage capacity are recommended measures for reducing the irrigation demands for green roof plants with deep rooting systems.
The parameters of the ET models determined by the designed experiment generally fell in the range of other studies conducted in more humid environments. The yearly averages of crop coefficients for the sedum and grass covers were found to be 0.59 and 0.61, respectively, while the yearly averages of surface resistances were estimated as 678 and 651 s m−1, accordingly. These values are within the reported ranges for rain-rich areas. The physiological parameters of the sedums were found to be close to those of the grass species in this study. This finding indicates that sedums in the studied climate might not necessarily have a significantly lower ET capacity than other grass species as commonly assumed in humid climates. Extra irrigation would be required for sedums to keep them growing healthily in the dry environments. Furthermore, the studied sedums and possibly other shallow-rooted plants could not effectively utilize the deep moisture storage to survive drought periods like native species. On the other hand, the challenge of depleting the deep moisture storage reflects a less satisfactory runoff reduction capability for severe events compared to the long-rooted plants. Therefore, unlike in a humid climate, sedums may not be the ideal green roof species for a drier climate.
The tested three ET models generated reasonable estimates compared to previous similar studies. The FAO56 method overall achieved the best fit. The temporal upscaling of critical parameters like the crop coefficient may lead to the underestimation of high ET rates for a green roof. Compared to humid regions, where the rainfall-driven ET process is prevalent, this issue may lead to more severe errors for ET estimation in drier regions where the overlapping of repeated irrigation events with hot, dry meteorological conditions would often lead to higher ET rates. Improved ET models, and especially the non-linear models with adjustable parameters (e.g., Kc and Ks) which can simulate low and high ET ranges, are needed for dry regions with an irrigation demand.
The irrigation cost of the studied green roof was estimated at $0.4/m2 per year. This cost, however, is in excess of the savings from the avoided stormwater impact fee. At least 72% of the annual irrigation cost needs to be offset by other environmental benefits unless the irrigation demand can be reduced. Native species with the reported smaller crop coefficients may not need any irrigation in the study setting and, therefore, can be recommended for green roof implementations in dry environments.
Acknowledgments
This research was supported by NSF EPSCoR cooperative agreement IIA-1208732 awarded to Utah State University, as part of the State of Utah EPSCoR Research Infrastructure Improvement Award. Additional support was provided by the Sustainable Campus Initiative Fund and the Global Change and Sustainability Center at the University of Utah. Any opinions, findings, and conclusions or recommendations expressed are those of the authors and do not necessarily reflect the views of the National Science Foundation. The fieldwork could not be accomplished without the help from the Urban Water Research Group (esp. George Elliott and Sara Mitchell), the Environmental Fluid Dynamics Lab, and the personnel of Facility Management (esp. Shem Hobbs, Jeremy Coates, and John Walker) of the University of Utah, as well as Kimberly DiGiovanni from Quinnipiac University.
Author Contributions
All authors conceived and designed the experiments; Y.F. performed the experiments and analyzed the data; E.P. contributed materials and tools; all authors wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Askarizadeh, A.; Rippy, M.A.; Fletcher, T.D.; Feldman, D.L.; Peng, J.; Bowler, P.; Mehring, A.S.; Winfrey, B.K.; Vrugt, J.A.; AghaKouchak, A.; et al. From Rain Tanks to Catchments: Use of Low-Impact Development To Address Hydrologic Symptoms of the Urban Stream Syndrome. Environ. Sci. Technol. 2015, 49, 11264–11280. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Burian, S.; Pomeroy, C. Potential of green infrastructure to restore predevelopment water budget of a semi-arid urban catchment. J. Hydrol. 2016, 542, 744–755. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Reducing Urban Heat Islands: Compendium of Strategies; USEPA: Washington, DC, USA, 2008.
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Burian, S.J.; Pomeroy, C.A. Urban impacts on the water cycle and potential green infrastructure implications. In Urban Ecosystems Ecology; Aitkenhead-Peterson, J., Volder, A., Eds.; American Society of Agronomy, Crop Science Society of America, and Soil Science Society of America: Madison, WI, USA, 2010; Chapter 14. [Google Scholar]
- Levallius, J. Green roofs on municipal buildings in Lund: Modeling potential environmental benefits. In Physical Geography and Ecosystem Science; Lund University: Lund, Sweden, 2005. [Google Scholar]
- Getter, K.L.; Rowe, D.B. The role of extensive green roofs in sustainable development. HortScience 2006, 41, 1276–1285. [Google Scholar]
- VanWoert, N.D.; Rowe, D.B.; Andresen, J.A.; Rugh, C.L.; Fernandez, R.T.; Xiao, L. Green roof stormwater retention: Effects of roof surface, slope, and media depth. J. Environ. Qual. 2005, 34, 1036–1044. [Google Scholar] [CrossRef] [PubMed]
- Jarrett, A.R.; Hunt, W.F.; Berghage, R.D. Evaluating a spreadsheet model to predict green roof stormwater management. In Low Impact Development; American Society of Civil Engineers: Reston, VA, USA, 2009; pp. 252–259. [Google Scholar]
- DiGiovanni, K.; Gaffin, S.; Montalto, F. Green roof hydrology: Results from a small-scale lysimeter setup (Bronx, NY). In Low Impact Development; American Society of Civil Engineers: San Francisco, CA, USA, 2010; pp. 1328–1341. [Google Scholar]
- Berghage, R.D.; Beattie, D.; Jarrett, A.R.; Thuring, C.; Razaei, F.; O’Connor, T.P. Green Roofs for Stormwater Runoff Control; United States Environmental Protection Agency: Washington, DC, USA, 2009.
- Fassman-Beck, E.; Voyde, E.; Simcock, R.; Hong, Y.S. 4 Living roofs in 3 locations: Does configuration affect runoff mitigation? J. Hydrol. 2013, 490, 11–20. [Google Scholar] [CrossRef]
- Scherba, A.; Sailor, D.J.; Rosenstiel, T.N.; Wamser, C.C. Modeling impacts of roof reflectivity, integrated photovoltaic panels and green roof systems on sensible heat flux into the urban environment. Build. Environ. 2011, 46, 2542–2551. [Google Scholar] [CrossRef]
- Barrio, E.P.D. Analysis of the green roofs cooling potential in buildings. Energy Build. 1998, 27, 179–193. [Google Scholar] [CrossRef]
- Wong, N.H.; Chen, Y.; Ong, C.L.; Sia, A. Investigation of thermal benefits of rooftop garden in the tropical environment. Build. Environ. 2003, 38, 261–270. [Google Scholar] [CrossRef]
- Ouldboukhitine, S.-E.; Belarbi, R.; Jaffal, I.; Trabelsi, A. Assessment of green roof thermal behavior: A coupled heat and mass transfer model. Build. Environ. 2011, 46, 2624–2631. [Google Scholar] [CrossRef]
- Saadatian, O.; Sopian, K.; Salleh, E.; Lim, C.H.; Riffat, S.; Saadatian, E.; Toudeshki, A.; Sulaiman, M.Y. A review of energy aspects of green roofs. Renew. Sustain. Energy Rev. 2013, 23, 155–168. [Google Scholar] [CrossRef]
- Wong, N.H.; Cheong, D.K.W.; Yan, H.; Soh, J.; Ong, C.L.; Sia, A. The effects of rooftop garden on energy consumption of a commercial building in Singapore. Energy Build. 2003, 35, 353–364. [Google Scholar] [CrossRef]
- Kosareo, L.; Ries, R. Comparative environmental life cycle assessment of green roofs. Build. Environ. 2007, 42, 2606–2613. [Google Scholar] [CrossRef]
- Smith, K.R.; Roebber, P.J. Green roof mitigation potential for a proxy future climate scenario in Chicago, Illinois. J. Appl. Meteorol. Climatol. 2011, 50, 507–522. [Google Scholar] [CrossRef]
- Castleton, H.F.; Stovin, V.; Beck, S.B.M.; Davison, J.B. Green roofs; building energy savings and the potential for retrofit. Energy Build. 2010, 42, 1582–1591. [Google Scholar] [CrossRef]
- Voyde, E.; Fassman, E.; Simcock, R.; Wells, J. Quantifying evapotranspiration rates for New Zealand green roofs. Hydrol. Eng. 2010, 15, 395–403. [Google Scholar] [CrossRef]
- Tsang, S.W.; Jim, C.Y. Theoretical evaluation of thermal and energy performance of tropical green roofs. Energy 2011, 36, 3590–3598. [Google Scholar] [CrossRef]
- Feller, M. Quantifying Evapotranspiration in Green Infrastructure: A Green Roof Case Study. Master’s Thesis, Department of Civil and Environmental Engineering, Villanova University, Villanova, PA, USA, 2011. [Google Scholar]
- Klein, P.M.; Coffman, R. Establishment and performance of an experimental green roof under extreme climatic conditions. Sci. Total Environ. 2015, 512–513, 82–93. [Google Scholar] [CrossRef] [PubMed]
- Krebs, G.; Kuoppamäki, K.; Kokkonen, T.; Koivusalo, H. Simulation of green roof test bed runoff. Hydrol. Process. 2016, 30, 250–262. [Google Scholar] [CrossRef]
- Feng, Y.; Burian, S. Improving Evapotranspiration Mechanisms in the U.S. Environmental Protection Agency’s Storm Water Management Model. J. Hydrol. Eng. 2016, 21, 06016007. [Google Scholar] [CrossRef]
- Elliott, R.M.; Gibson, R.A.; Carson, T.B.; Marasco, D.E.; Culligan, P.J.; McGillis, W.R. Green roof seasonal variation: Comparison of the hydrologic behavior of a thick and a thin extensive system in New York City. Environ. Res. Lett. 2016, 11, 074020. [Google Scholar] [CrossRef]
- Poë, S.; Stovin, V.; Berretta, C. Parameters influencing the regeneration of a green roof’s retention capacity via evapotranspiration. J. Hydrol. 2015, 523, 356–367. [Google Scholar] [CrossRef]
- Sims, A.W.; Robinson, C.E.; Smart, C.C.; Voogt, J.A.; Hay, G.J.; Lundholm, J.T.; Powers, B.; O’Carroll, D.M. Retention performance of green roofs in three different climate regions. J. Hydrol. 2016, 542, 115–124. [Google Scholar] [CrossRef]
- Peng, Z.; Stovin, V. Independent Validation of the SWMM Green Roof Module. J. Hydrol. Eng. 2017, 22, 04017037. [Google Scholar] [CrossRef]
- Schneider, D.; Wadzuk, B.M.; Traver, R.G. Using a weighing lysimeter to determine a crop coefficient for a green roof to predict evapotranspiration with the FAO standardized Penman-Monteith equation. In World Environmental and Water Resources Congress 2011; American Society of Civil Engineers: Palm Springs, CA, USA, 2011; pp. 3629–3638. [Google Scholar]
- DiGiovanni, K.; Montalto, F.; Gaffin, S.; Rosenzweig, C. Applicability of classical predictive equations for the estimation of evapotranspiration from urban green spaces: Green roof results. J. Hydrol. Eng. 2013, 18, 99–107. [Google Scholar] [CrossRef]
- Starry, O.; Lea-Cox, J.; Ristvey, A.; Cohan, S. Parameterizing a Water-Balance Model for Predicting Stormwater Runoff from Green Roofs. J. Hydrol. Eng. 2016, 21, 04016046. [Google Scholar] [CrossRef]
- Marasco, D.E.; Culligan, P.J.; McGillis, W.R. Evaluation of common evapotranspiration models based on measurements from two extensive green roofs in New York City. Ecol. Eng. 2015, 84, 451–462. [Google Scholar] [CrossRef]
- Allen, R.G.; Pruitt, W.O.; Wright, J.L.; Howell, T.A.; Ventura, F.; Snyder, R.; Itenfisu, D.; Steduto, P.; Berengena, J.; Yrisarry, J.B.; et al. A recommendation on standardized surface resistance for hourly calculation of reference ETo by the FAO56 Penman-Monteith method. Agric. Water Manag. 2006, 81, 1–22. [Google Scholar] [CrossRef]
- Jarvis, P. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Stovin, V.; Poë, S.; Berretta, C. A modelling study of long term green roof retention performance. J. Environ. Manag. 2013, 131, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Carter, T.; Keeler, A. Life-cycle cost–benefit analysis of extensive vegetated roof systems. J. Environ. Manag. 2008, 87, 350–363. [Google Scholar] [CrossRef] [PubMed]
- Sproul, J.; Wan, M.P.; Mandel, B.H.; Rosenfeld, A.H. Economic comparison of white, green, and black flat roofs in the United States. Energy Build. 2014, 71, 20–27. [Google Scholar] [CrossRef]
- Wadzuk, B.; Schneider, D.; Feller, M.; Traver, R. Evapotranspiration from a green-roof storm-water control measure. J. Irrig. Drain. Eng. 2013, 139, 995–1003. [Google Scholar] [CrossRef]
- Berretta, C.; Poë, S.; Stovin, V. Moisture content behaviour in extensive green roofs during dry periods: The influence of vegetation and substrate characteristics. J. Hydrol. 2014, 511, 374–386. [Google Scholar] [CrossRef]
- Spatari, S.; Yu, Z.; Montalto, F.A. Life cycle implications of urban green infrastructure. Environ. Pollut. 2011, 159, 2174–2179. [Google Scholar] [CrossRef] [PubMed]
- Pataki, D.E.; Carreiro, M.M.; Cherrier, J.; Grulke, N.E.; Jennings, V.; Pincetl, S.; Pouyat, R.V.; Whitlow, T.H.; Zipperer, W.C. Coupling biogeochemical cycles in urban environments: Ecosystem services, green solutions, and misconceptions. Front. Ecol. Environ. 2011, 9, 27–36. [Google Scholar] [CrossRef]
- Williams, N.S.G.; Rayner, J.P.; Raynor, K.J. Green roofs for a wide brown land: Opportunities and barriers for rooftop greening in Australia. Urban For. Urban Green. 2010, 9, 245–251. [Google Scholar] [CrossRef]
- Liu, Y.; Engel, B.A.; Flanagan, D.C.; Gitau, M.W.; McMillan, S.K.; Chaubey, I. A review on effectiveness of best management practices in improving hydrology and water quality: Needs and opportunities. Sci. Total Environ. 2017, 601–602, 580–593. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO—Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Sun, H.; Kopp, K.; Kjelgren, R. Water-efficient Urban Landscapes: Integrating Different Water Use Categorizations and Plant Types. HortScience 2012, 47, 254–263. [Google Scholar]
- Litvak, E.; Pataki, D.E. Evapotranspiration of urban lawns in a semi-arid environment: An in situ evaluation of microclimatic conditions and watering recommendations. J. Arid Environ. 2016, 134, 87–96. [Google Scholar] [CrossRef]
- Coutts, A.M.; Tapper, N.J.; Beringer, J.; Loughnan, M.; Demuzere, M. Watering our cities: The capacity for water sensitive urban design to support urban cooling and improve human thermal comfort in the Australian context. Prog. Phys. Geogr. 2013, 37, 2–28. [Google Scholar] [CrossRef]
- Oke, T.R. Advectively-assisted evapotranspiration from irrigated urban vegetation. Bound.-Layer Meteorol. 1979, 17, 167–173. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Urban water balance: 2. Results from a suburb of Vancouver, British Columbia. Water Resour. Res. 1986, 22, 1404–1412. [Google Scholar]
- Dimoudi, A.; Nikolopoulou, M. Vegetation in the urban environment: Microclimatic analysis and benefits. Energy Build. 2003, 35, 69–76. [Google Scholar] [CrossRef]
- Gober, P.; Brazel, A.; Quay, R.; Myint, S.; Grossman-Clarke, S.; Miller, A.; Rossi, S. Using watered landscapes to manipulate urban heat island effects: How much water will it take to cool Phoenix? J. Am. Plan. Assoc. 2009, 76, 109–121. [Google Scholar] [CrossRef]
- House-Peters, L.A.; Chang, H. Modeling the impact of land use and climate change on neighborhood-scale evaporation and nighttime cooling: A surface energy balance approach. Landsc. Urban Plan. 2011, 103, 139–155. [Google Scholar] [CrossRef]
- Oberndorfer, E.; Lundholm, J.; Bass, B.; Coffman, R.R.; Doshi, H.; Dunnett, N.; Gaffin, S.; Köhler, M.; Liu, K.K.Y.; Rowe, B. Green roofs as urban ecosystems: Ecological structures, functions, and services. BioScience 2007, 57, 823–833. [Google Scholar] [CrossRef]
- Berndtsson, J.C. Green roof performance towards management of runoff water quantity and quality: A review. Ecol. Eng. 2010, 36, 351–360. [Google Scholar] [CrossRef]
- NOAA. Salt Lake City Climate Information. 2016. Available online: http://www.wrh.noaa.gov/slc/climate/slcclimate/SLC/index.php (accessed on 23 February 2016).
- Russell, J.; Cohn, R. Climate of Salt Lake City; LENNEX Corp.: Edinburgh, UK, 2012. [Google Scholar]
- Hutchins-Cabibi, T.; Miller, B.; Hern, T.; Schwartz, A. Urban Water on the Wasatch Front: Past, Present, and Future; Western Resource Advocates: Boulder, CO, USA, 2006. [Google Scholar]
- Denich, C.; Bradford, A. Estimation of evapotranspiration from bioretention areas using weighing lysimeters. J. Hydrol. Eng. 2010, 15, 522–530. [Google Scholar] [CrossRef]
- Easlon, H.M.; Bloom, A.J. Easy Leaf Area: Automated digital image analysis for rapid and accurate measurement of leaf area. Appl. Plant Sci. 2014, 2, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Brutsaert, W.; Stricker, H. An advection-aridity approach to estimate actual regional evapotranspiration. Water Resour. Res. 1979, 15, 443–450. [Google Scholar] [CrossRef]
- Walter, I.A.; Allen, R.G.; Elliott, R.; Jensen, M.E.; Itenfisu, D.; Mecham, B.; Howell, T.A.; Snyder, R.; Brown, P.; Echings, S.; et al. ASCE’s Standardized Reference Evapotranspiration Equation. In Watershed Management and Operations Management Conferences 2000, Fort Collins, CO, USA, 20–24 June 2000; American Society of Civil Engineers: Reston, VA, USA, 2000. [Google Scholar]
- Rossman, L.; Huber, W. Storm Water Management Model Reference Manual Volume I–Hydrology (Revised); US Environmental Protection Agency: Cincinnati, OH, USA, 2016.
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. In Symposium of the Society for Experimental Biology, The State and Movement of Water in Living Organisms; Fogg, G.E., Ed.; Academic Press Inc.: Swansea, UK, 1965; pp. 205–234. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer: Dordrecht, The Netherlands, 1988; Volume 13. [Google Scholar]
- Jones, H. Plants and Microclimate: A Quantitative Approach to Environmental Plant Physiology; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Schulze, E.D.; Beck, E.; Müller-Hohenstein, K. Plant Ecology; Springer: Heidelberg, Germany, 2005. [Google Scholar]
- Farrés, M.; Platikanov, S.; Tsakovski, S.; Tauler, R. Comparison of the variable importance in projection (VIP) and of the selectivity ratio (SR) methods for variable selection and interpretation. J. Chemom. 2015, 29, 528–536. [Google Scholar] [CrossRef]
- Gosselin, R.; Rodrigue, D.; Duchesne, C. A Bootstrap-VIP approach for selecting wavelength intervals in spectral imaging applications. Chemom. Intell. Lab. Syst. 2010, 100, 12–21. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Staudt, K.; Falge, E.; Pyles, R.D.; Paw U, K.T.; Foken, T. Sensitivity and predictive uncertainty of the ACASA model at a spruce forest site. Biogeosciences 2010, 7, 3685–3705. [Google Scholar] [CrossRef]
- Prihodko, L.; Denning, A.S.; Hanan, N.P.; Baker, I.; Davis, K. Sensitivity, uncertainty and time dependence of parameters in a complex land surface model. Agric. For. Meteorol. 2008, 148, 268–287. [Google Scholar] [CrossRef]
- Schneider, D. Quantifying Evapotranspiration from a Green Roof Analytically. Master’s Thesis, Villanova University, Villanova, PA, USA, 2011. [Google Scholar]
- Hassan, A.E.; Bekhit, H.M.; Chapman, J.B. Uncertainty assessment of a stochastic groundwater flow model using GLUE analysis. J. Hydrol. 2008, 362, 89–109. [Google Scholar] [CrossRef]
- Freer, J.; Beven, K.; Ambroise, B. Bayesian Estimation of Uncertainty in Runoff Prediction and the Value of Data: An Application of the GLUE Approach. Water Resour. Res. 1996, 32, 2161–2173. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Q.; Xu, Q.; Blanckaert, K. Generalized Likelihood Uncertainty Estimation Method in Uncertainty Analysis of Numerical Eutrophication Models: Take BLOOM as an Example. Math. Probl. Eng. 2013, 2013, 701923. [Google Scholar] [CrossRef]
- Poyatos, R.; Villagarcía, L.; Domingo, F.; Piñol, J.; Llorens, P. Modelling evapotranspiration in a Scots pine stand under Mediterranean mountain climate using the GLUE methodology. Agric. For. Meteorol. 2007, 146, 13–28. [Google Scholar] [CrossRef]
- Sokal, R.; Rohlf, F. Biometry; Freeman: San Francisco, CA, US, 1981; p. 859. [Google Scholar]
- Rezaei, F. Evapotranspiration Rates from Extensive Green Roof Species; Pennsylvania State University: State College, PA, USA, 2005. [Google Scholar]
- Marasco, D.E.; Hunter, B.N.; Culligan, P.J.; Gaffin, S.R.; McGillis, W.R. Quantifying Evapotranspiration from Urban Green Roofs: A Comparison of Chamber Measurements with Commonly Used Predictive Methods. Environ. Sci. Technol. 2014, 48, 10273–10281. [Google Scholar] [CrossRef] [PubMed]
- Sherrard, J.; Jacobs, J. Vegetated Roof Water-Balance Model: Experimental and Model Results. J. Hydrol. Eng. 2012, 17, 858–868. [Google Scholar] [CrossRef]
- Starry, O. The Comparative Effects of THREE SEDUM SPECies on Green Roof Stormwater Retention; University of Maryland: College Park, MA, USA, 2013. [Google Scholar]
- Lazzarin, R.M.; Castellotti, F.; Busato, F. Experimental measurements and numerical modelling of a green roof. Energy Build. 2005, 37, 1260–1267. [Google Scholar] [CrossRef]
- Voyde, E. Quantifying the complete hydrologic budget for an extensive living roof. Ph.D. Thesis, Department of Civil and Environmental Engineering, The University of Auckland, Auckland, New Zealand, 2011. [Google Scholar]
- Wolf, D.; Lundholm, J.T. Water uptake in green roof microcosms: Effects of plant species and water availability. Ecol. Eng. 2008, 33, 179–186. [Google Scholar] [CrossRef]
- Steinwand, A.L.; Harrington, R.F.; Groeneveld, D.P. Transpiration coefficients for three Great Basin shrubs. J. Arid Environ. 2001, 49, 555–567. [Google Scholar] [CrossRef]
- Dvorak, B.; Volder, A. Green roof vegetation for north american ecoregions: A literature review. Landsc. Urban Plan. 2010, 96, 197–213. [Google Scholar] [CrossRef]
- VanWoert, N.D.; Rowe, D.B.; Andresen, J.A.; Rugh, C.L.; Xiao, L. Watering regime and green roof substrate design affect sedum plant growth. HortScience 2005, 40, 659–664. [Google Scholar]
- Starry, O.; Lea-Cox, J.D.; Kim, J.; van Iersel, M.W. Photosynthesis and water use by two sedum species in green roof substrate. Environ. Exp. Bot. 2014, 107, 105–112. [Google Scholar] [CrossRef]
- Kluge, M. Is sedum acre L. a CAM plant? Oecologia 1977, 29, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Gravatt, D.A.; Martin, C.E. Comparative ecophysiology of five species of sedum (crassulaceae) under well-watered and drought-stressed conditions. Oecologia 1992, 92, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, S.; Beven, K.; Freer, J. Multiple sources of predictive uncertainty in modeled estimates of net ecosystem CO2 exchange. Ecol. Model. 2009, 220, 3259–3270. [Google Scholar] [CrossRef]
- Franks, S.W.; Beven, K.J. Bayesian estimation of uncertainty in land surface-atmosphere flux predictions. J. Geophys. Res. Atmos. 1997, 102, 23991–23999. [Google Scholar] [CrossRef]
- Government, S.L.C. Salt Lake City Water Rates. Available online: http://www.slcdocs.com/utilities/PDF%20Files/UtilityRates/WaterrateswebCurrent.pdf (accessed on 8 February 2018).
- Government, S.L.C. Salt Lake City Stormwater Rates. Available online: http://www.slcdocs.com/utilities/PDF%20Files/UtilityRates/StormrateswebCurrent.pdf (accessed on 8 February 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).