Infiltration and Short-Time Recharge in Deep Karst Aquifer of the Salento Peninsula (Southern Italy): An Observational Study
Abstract
1. Introduction
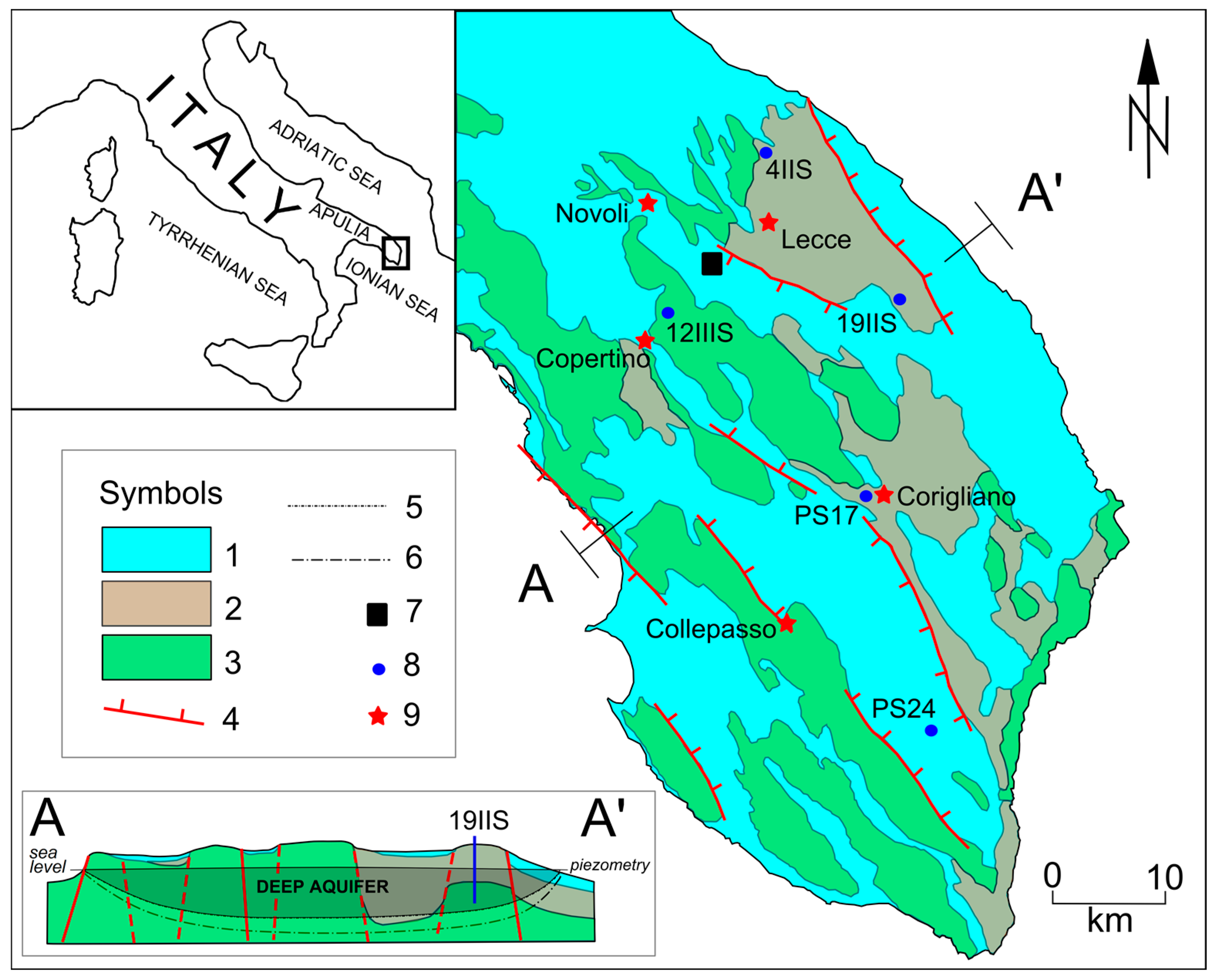
2. Study Area Description
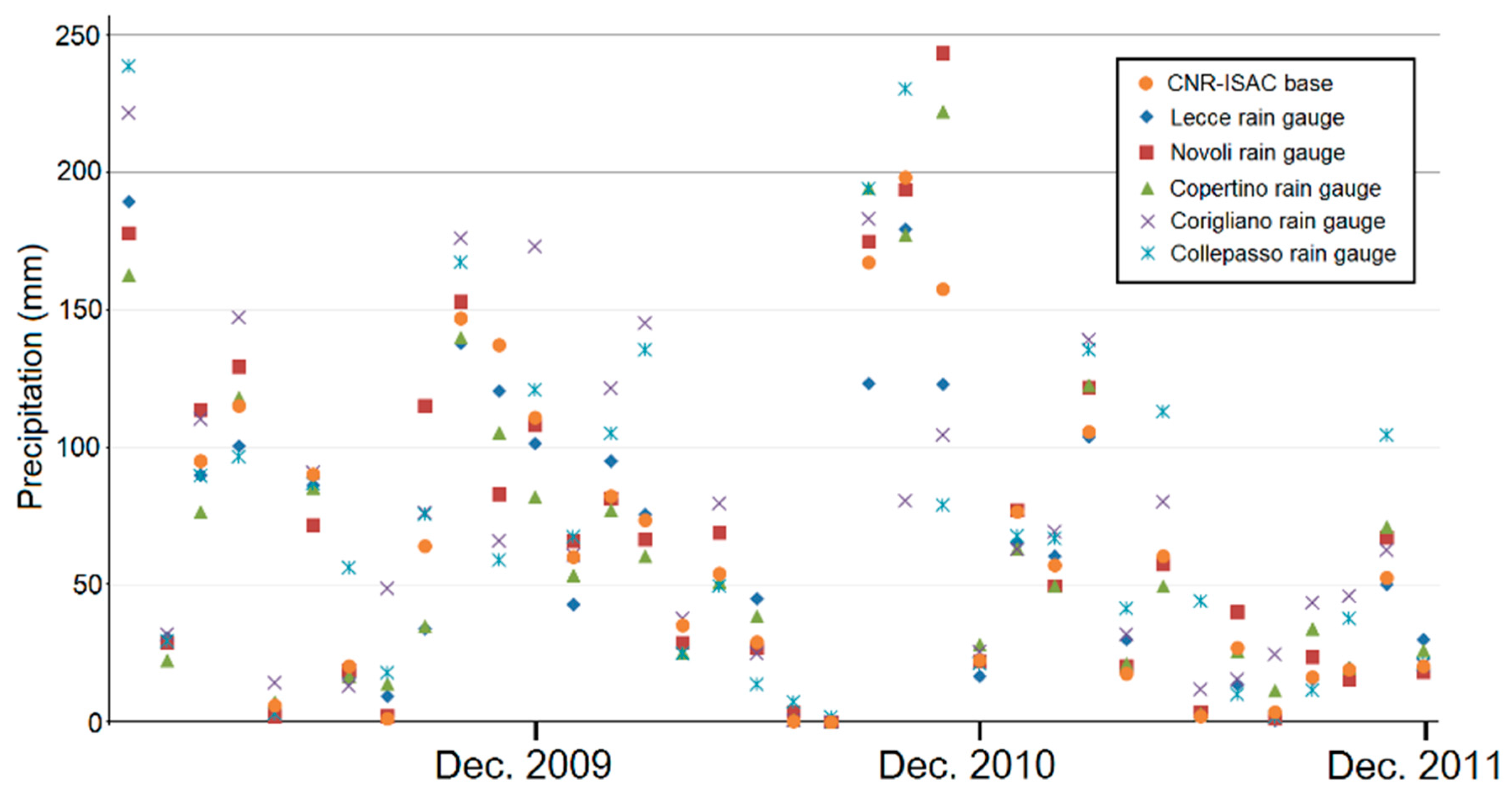
3. Materials and Methods
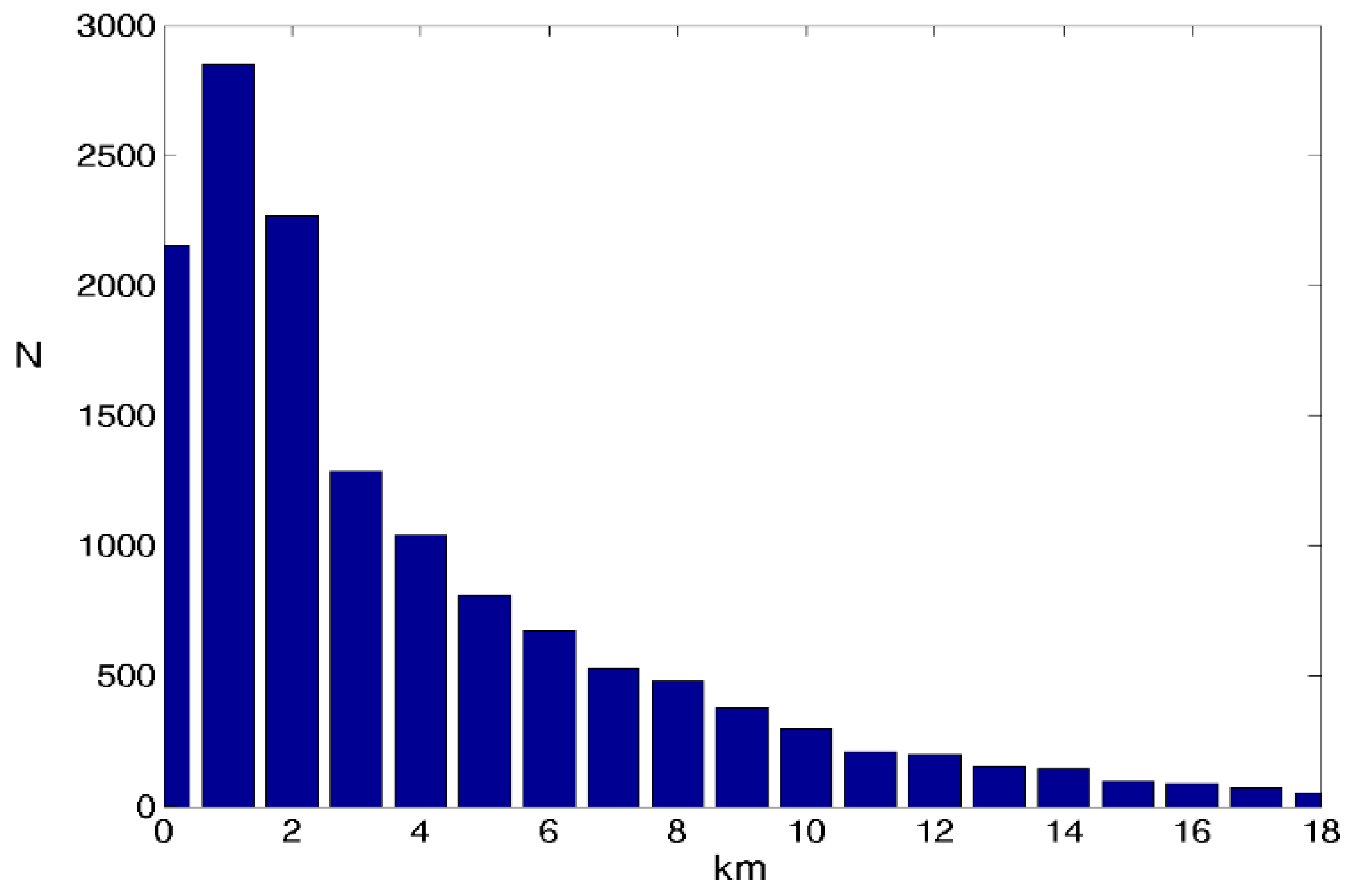
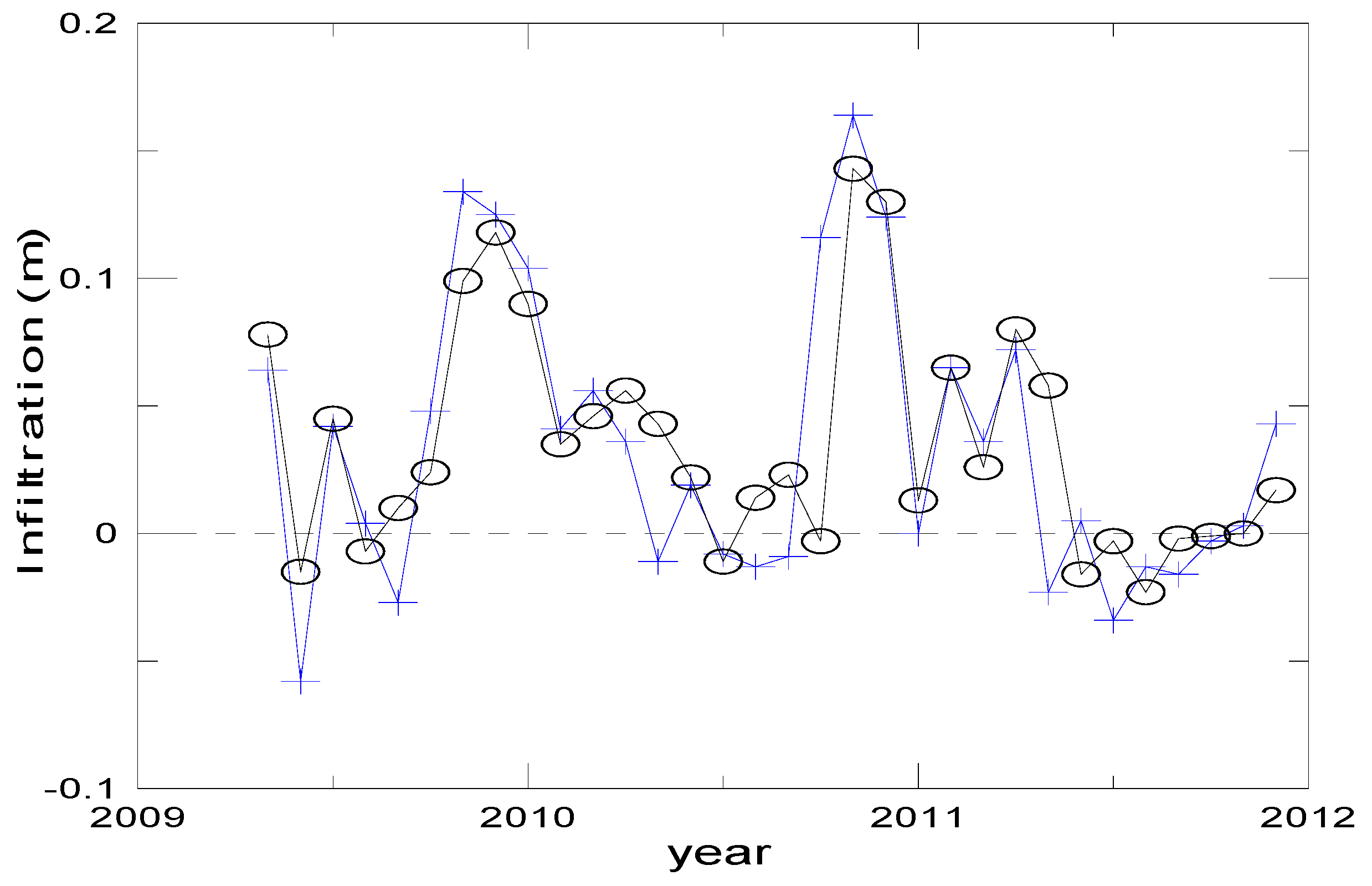
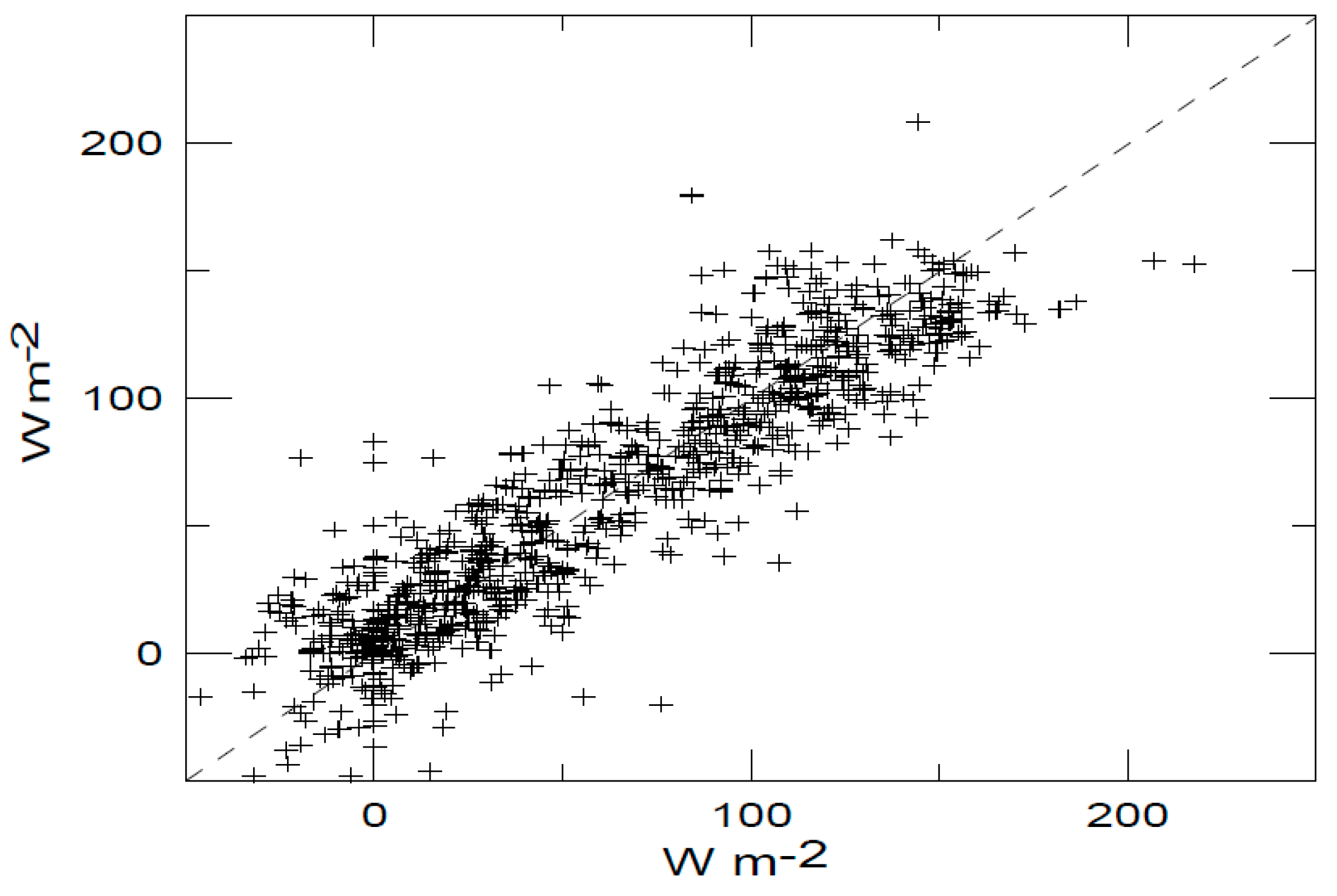
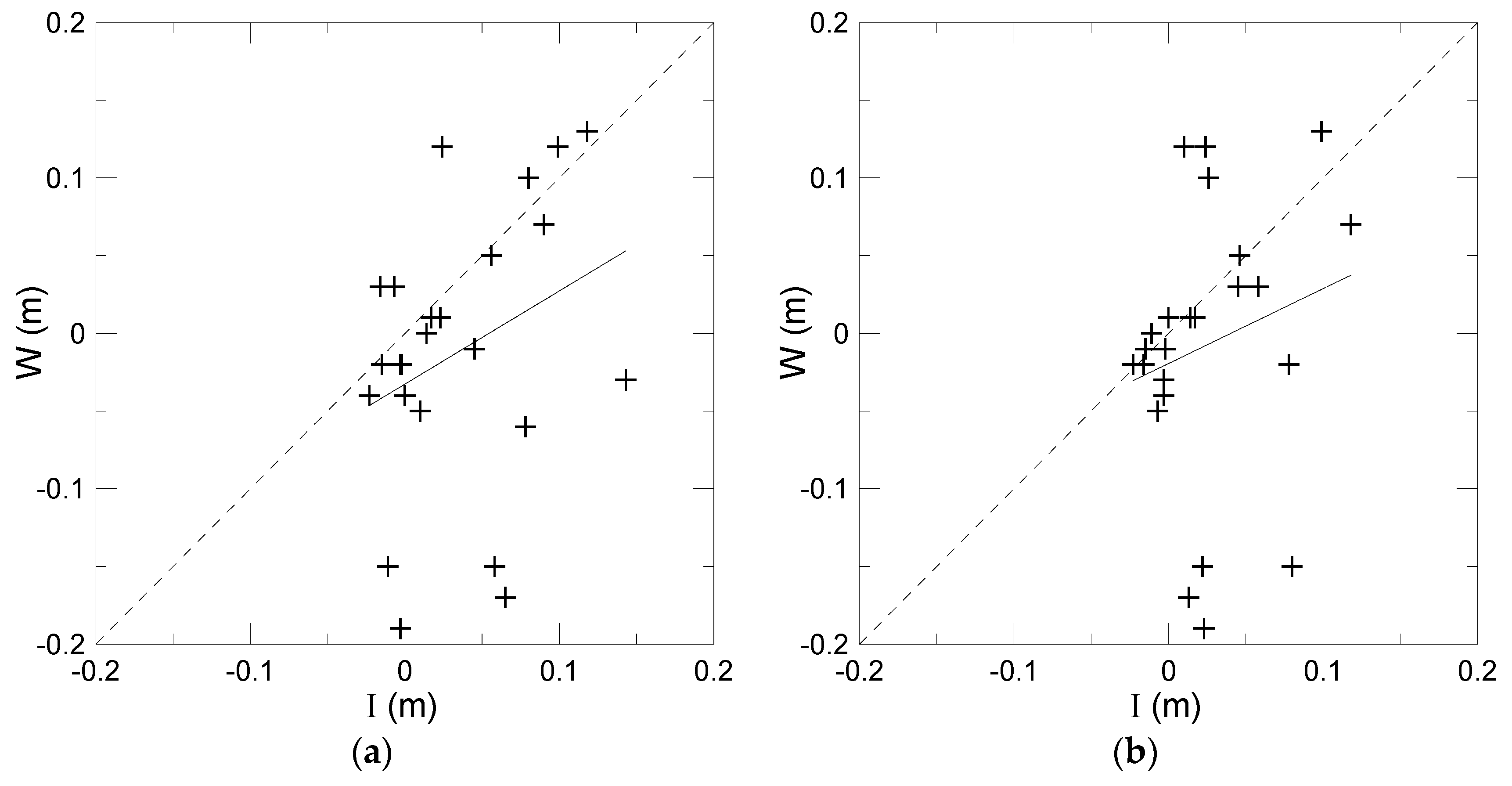
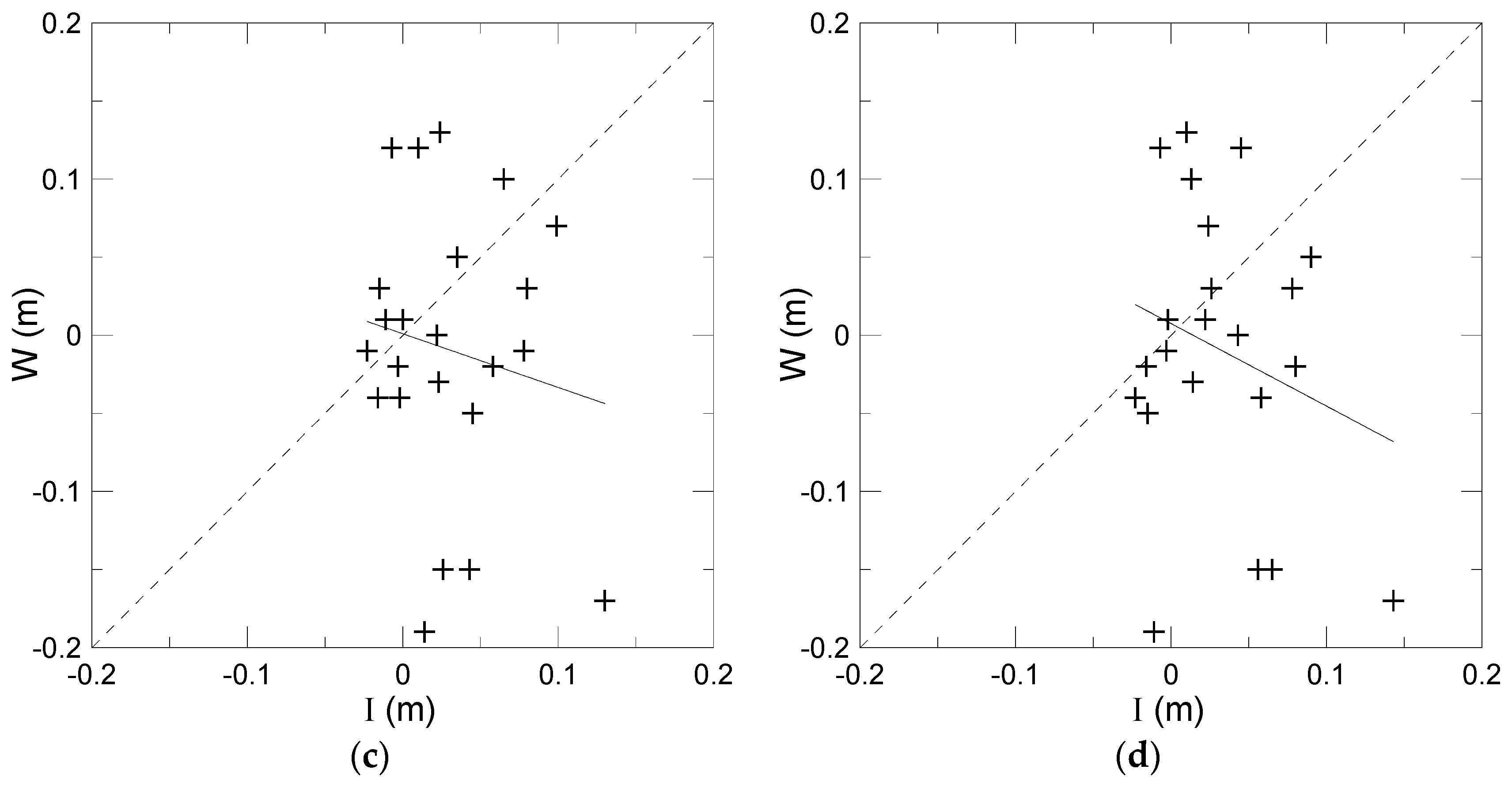
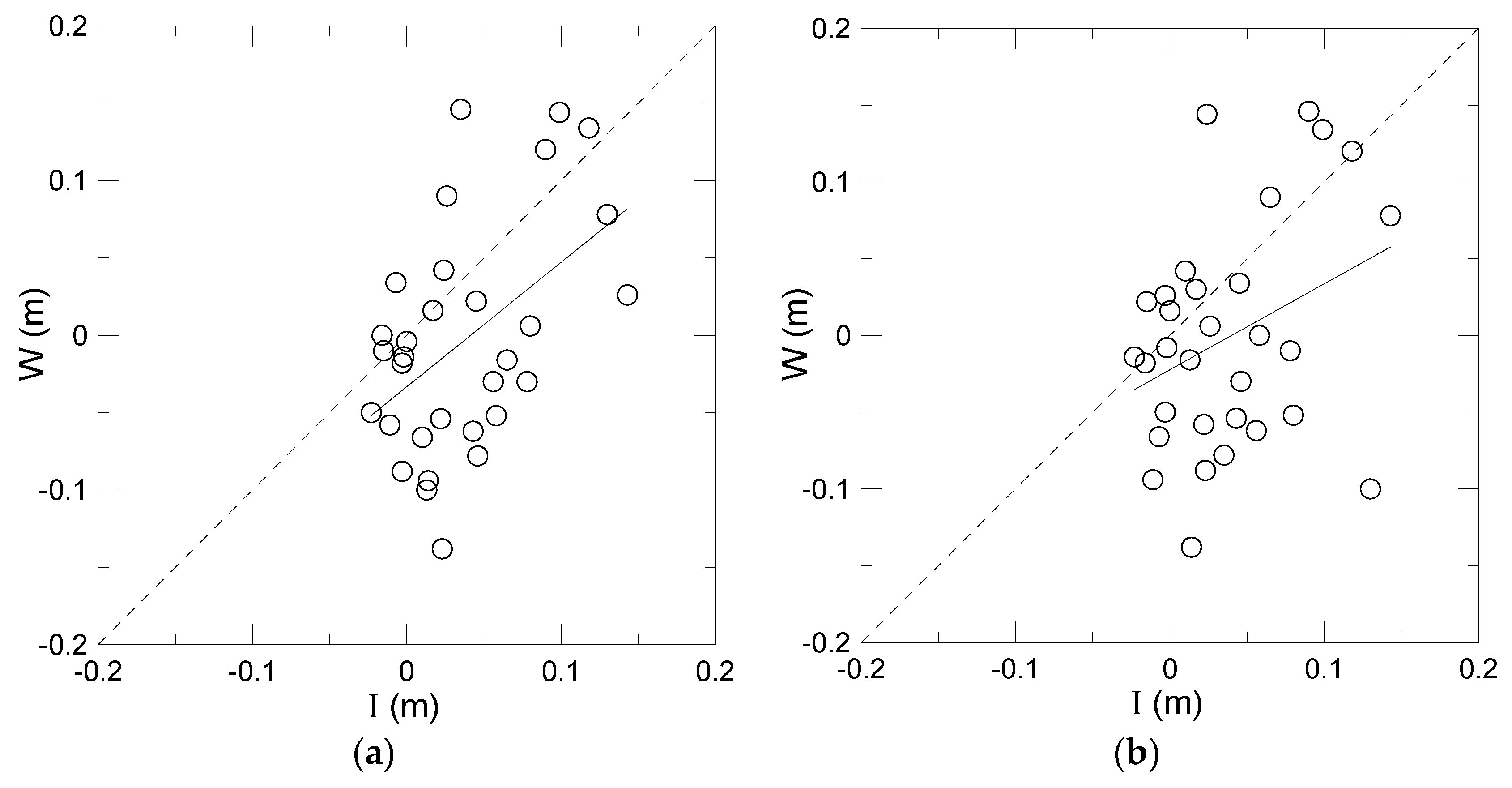
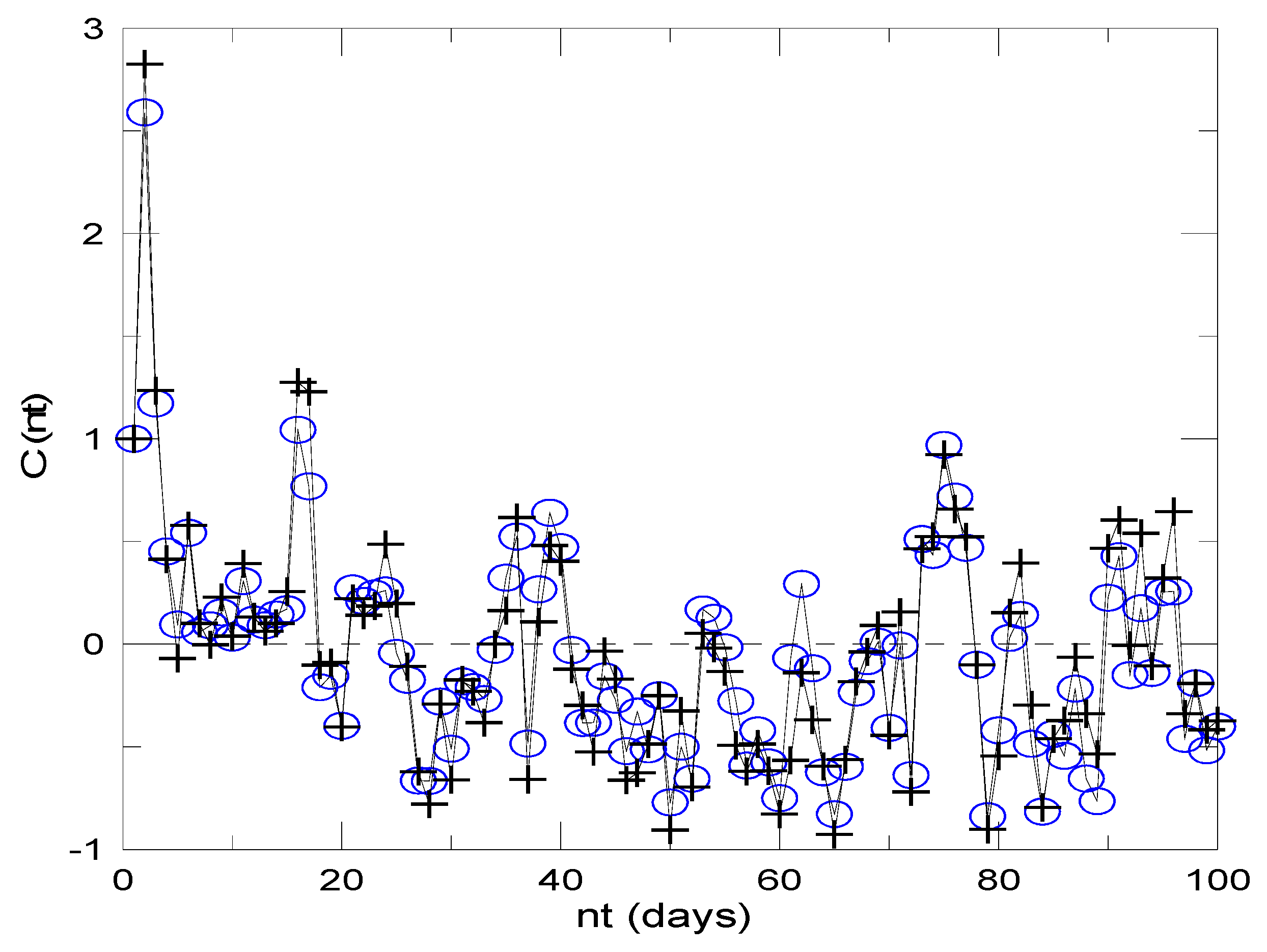
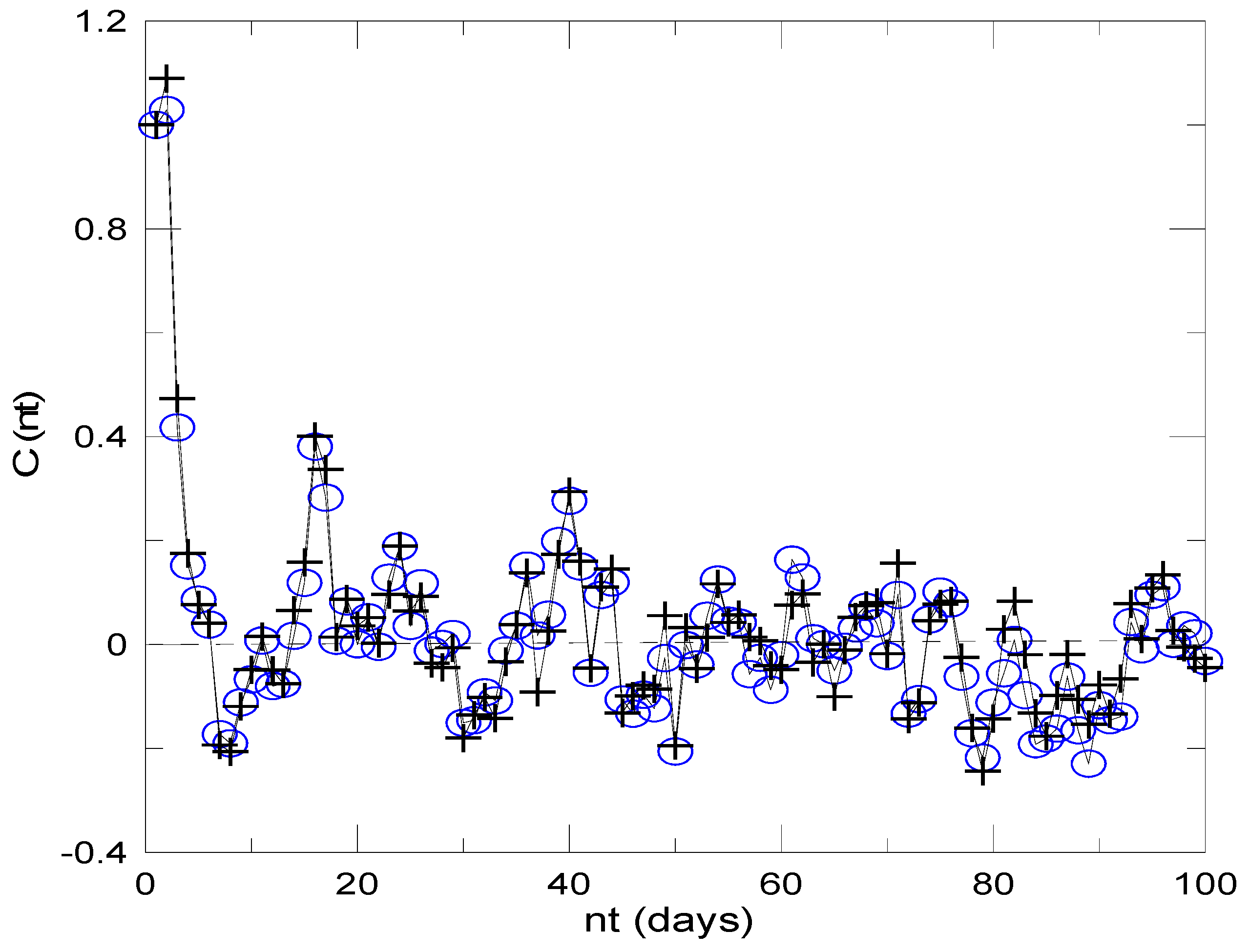
4. Results
5. Discussion
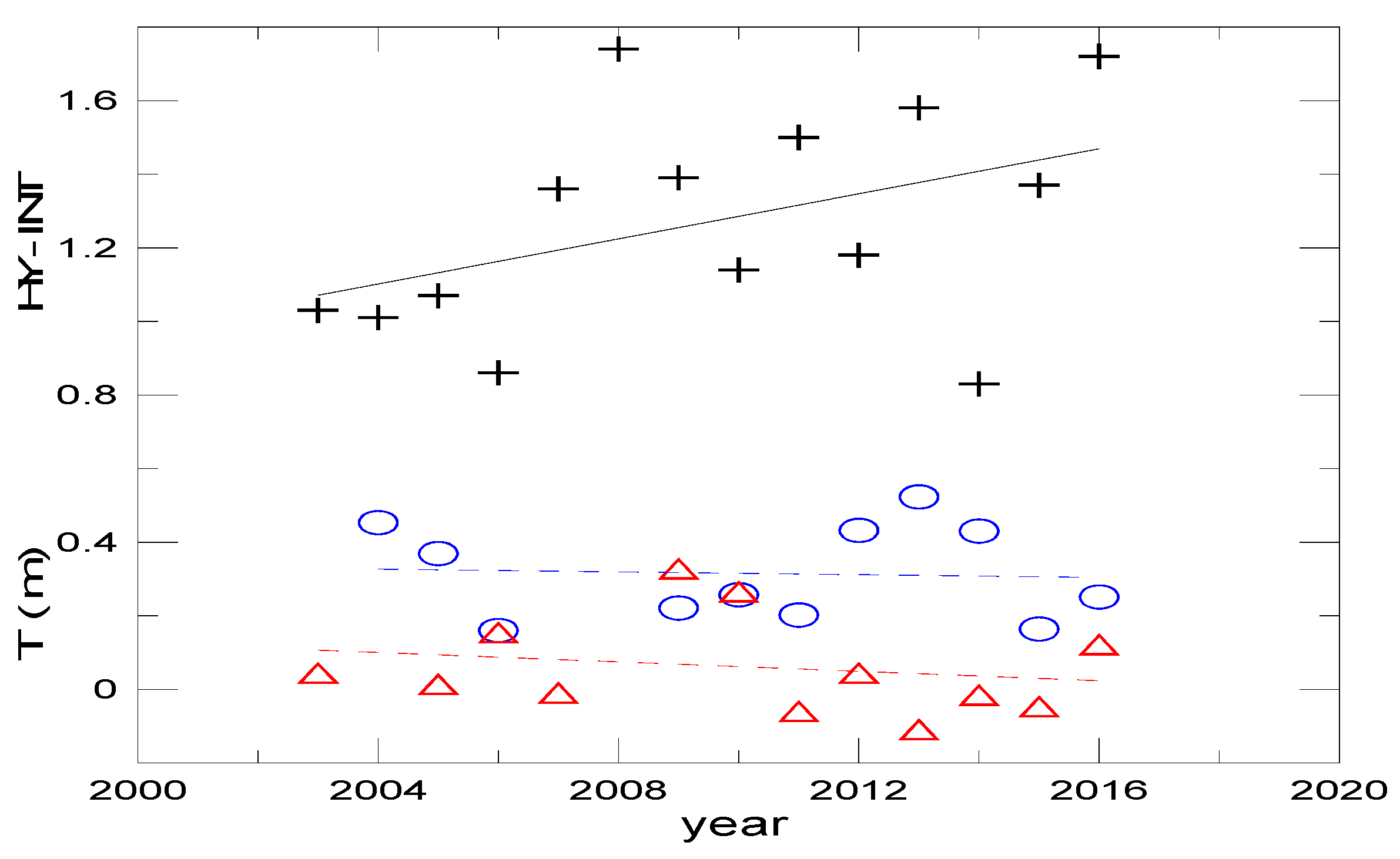
5.1. Estimations of the Seasonal/Yearly Net Infiltration
5.2. Infiltration, Precipitation Distribution and Aquifer Recharge
5.3 Water Management Concerns
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; van Beek, R. and others 21 authors. Ground water and climate change. Nat. Clim. Chang. 2012, 3, 322–329. [Google Scholar] [CrossRef]
- Ries, F.; Lange, J.; Schmidt, S.; Puhlmann, H.; Sauter, M. Recharge estimation and soil moisture dynamics in a Mediterranean, semi-arid karst region. Hydrol. Earth Syst. Sci. 2015, 19, 1439–1456. [Google Scholar] [CrossRef]
- Jemcov, I.; Petric, M. Measured precipitation vs. effective infiltration and their influence on the assessment of karst systems based on results of the time series analysis. J. Hydrol. 2009, 379, 304–314. [Google Scholar] [CrossRef]
- Robertson, W.M.; Sharp, J.M. Estimates of net infiltration in arid basins and potential impacts on recharge and solute flux due to land use and vegetation change. J. Hydrol. 2015, 522, 211–227. [Google Scholar] [CrossRef]
- Bonacci, O. Hazards caused by natural and anthropogenic changes of catchment area in karst. Nat. Hazards Earth Syst. Sci. 2004, 4, 655–661. [Google Scholar] [CrossRef]
- Butscher, C.; Huggenberger, P. Modeling the Temporal Variability of karst groundwater vulnerability with implications for climate change. Environ. Sci. Technol. 2009, 43, 1665–1669. [Google Scholar] [CrossRef]
- Hartmann, A.; Goldscheider, N.; Wagener, T.; Lange, J.; Weiler, M. Karst water resources in a changing world: Review of hydrological modeling approaches. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- Neves, M.C.; Costa, L.; Monteiro, J.P. Climatic and geologic controls on the piezometry of the Querença-Silves karst aquifer, Algarve (Portugal). Hydrogeol. J. 2016, 24, 1015–1028. [Google Scholar] [CrossRef]
- Page, D.; Dillon, P.; Vanderzalm, J.; Toze, S.; Sidhu, J.; Barry, K.; Levet, K.; Kremer, S.; Regel, R. Risk assessment of aquifer storage transfer and recovery with urban stormwater for producing water of a potable quality. J. Environ. Qual. 2010, 39, 2029–2039. [Google Scholar] [CrossRef] [PubMed]
- Somaratne, N. Characteristics of point recharge in karst aquifers. Water 2014, 6, 2782–2807. [Google Scholar] [CrossRef]
- Bacchus, S.T.; Bernardes, S.; Xu, W.; Madden, M. Fractures as Preferential Flowpaths for Aquifer Storage and Recovery (ASR) Injections and Withdrawals: Implications for Environmentally Sensitive Near-Shore Waters, Wetlands of the Greater Everglades Basin and the Regional Karst Floridan Aquifer System. J. Geogr. Geol. 2015, 7, 117–155. [Google Scholar] [CrossRef]
- Xanke, J.; Jourde, H.; Liesch, T.; Goldscheider, N. Numerical long-term assessment of managed aquifer recharge from a reservoir into a karst aquifer in Jordan. J. Hydrol. 2016, 540, 603–614. [Google Scholar] [CrossRef]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1992; 316p, ISBN 0-521-38052-9. [Google Scholar]
- Federer, C.A.; Vorosmarty, C.; Fekete, B. Intercomparison of methods for calculating potential evaporation in regional and global water balance models. Water Resour. Res. 1996, 32, 2315–2321. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crops Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; 300p. [Google Scholar]
- Portoghese, I.; Uricchio, V.; Vurro, M. A GIS tool for hydrogeological water balance evaluation on a regional scale in semi-arid environments. Comput. Geosci. 2005, 31, 15–27. [Google Scholar] [CrossRef]
- Katerji, N.; Rana, G. FAO-56 methodology for determining water requirement of irrigated crops: Critical examination of the concepts, alternative proposals and validation in Mediterranean region. Theor. Appl. Climatol. 2014, 115, 515–536. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: A review. Eur. J. Agron. 2000, 13, 125–153. [Google Scholar] [CrossRef]
- Martano, P. Evapotranspiration Estimates over Non-Homogeneous Mediterranean Land Cover by a Calibrated “Critical Resistance” Approach. Atmosphere 2015, 6, 255–272. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Zito, G.; Ruggiero, L.; Zuanni, F. Aspetti meteorologici e climatici della Puglia. In Proceedings of the First Workshop on “Clima, Ambiente e Territorio nel Mezzogiorno”, Taormina, Italy, 11–12 December 1989; CNR: Roma, Italy, 1991; pp. 43–73. (In Italian). [Google Scholar]
- Martano, P.; Elefante, C.; Grasso, F. Ten years water and energy surface balance from the CNR-ISAC micrometeorological station in Salento peninsula (southern Italy). Adv. Sci. Res. 2015, 12, 121–125. [Google Scholar] [CrossRef]
- Giorgi, F.; Lionello, P. Climate change projections for the Mediterranean region. Glob. Planet. Chang. 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Ladisa, G.; Todorovic, M.; Trisorio Liuzzi, G. A GIS-based approach for desertification risk assessment in Apulia region, SE Italy. Phys. Chem. Earth 2012, 49, 103–113. [Google Scholar] [CrossRef]
- Gianfreda, F.; Miglietta, M.M.; Sansò, P. Tornadoes in Southern Apulia (Italy). Nat. Hazards 2005, 34, 71–89. [Google Scholar] [CrossRef]
- Romera, R.; Gaertner, M.A.; Sánchez, E.; Domínguez, M.; González-Alemá, J.J.; Miglietta, M.M. Climate change projections of medicanes with a large multi-model ensemble of regional climate models. Glob. Planet. Chang. 2017, 151, 134–143. [Google Scholar] [CrossRef]
- Delle Rose, M.; Fidelibus, C. Water resource management in karstic catchments: The case of the Asso Torrent basin (Southern Italy). Environ. Earth Sci. 2016, 75, 892. [Google Scholar] [CrossRef]
- USEPA. A Lexicon of Cave and Karst Terminology with Special Reference to Environmental Karst Hydrology (EPA/600/R-02/003); USEPA: Washington, DC, USA, 2002; 214p.
- Costantini, E.A.C.; Barbetti, R.; Fantappiè, M.; L’Abate, G.; Lorenzetti, R.; Magini, S. Pedodiversity. In The Soils of Italy; Costantini, E.A.C., Dazzi, C., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 105–178. [Google Scholar] [CrossRef]
- Tadolini, T.; Tulipano, L. The evolution of fresh-water/salt-water equilibrium in connection with withdrawals from coastal carbonate and karstic aquifer of the salentine peninsula. Geol. Jaharb. 1981, 29, 69–85. [Google Scholar]
- Carotenuto, L.; Di Pillo, G.; Raiconi, G.; Troisi, S. Mathematical modelling and parameter identification for a coastal aquifer. Adv. Water Resour. 1980, 3, 151–157. [Google Scholar] [CrossRef]
- Delle Rose, M. Geological constraints on the location of industrial waste landfills in Salento karst areas (southern Italy). In Water Pollution VI, Modelling, Measuring and Prediction; Brebbia, C.A., Ed.; Witpress: Southampton, UK, 2001; pp. 57–68. ISBN 1-85312-878-3. [Google Scholar]
- Tulipano, L. Temperature logs interpretation for the identification of preferential flow pathway in the coastal carbonatic and karstic aquifer of the Salento peninsula (southern Italy). In Proceedings of the 21st Congress of International Association of Hydrogeologists, Guilin, China, 10–15 October 1988; Volume 2, pp. 956–961. [Google Scholar]
- Tadolini, T.; Tazioli, G.S.; Tulipano, L. Idrogeologia della zona delle sorgenti Idume (Lecce). Geol. Appl. Idrogeol. 1971, 4, 41–63. (In Italian) [Google Scholar]
- Delle Rose, M. Sedimentological features of the plio-quaternary aquifers of Salento (Puglia). Mem. Descr. Carta Geol. Ital. 2007, 76, 137–146. [Google Scholar]
- Delle Rose, M.; Federico, A.; Fidelibus, C. A computer simulation of groundwater salinization risk in Salento peninsula (Italy). In Risk Analysis II; Brebbia, C.A., Ed.; Witpress: Southampton, UK, 2000; pp. 465–475. ISBN 1-85312-830-9. [Google Scholar]
- Cotecchia, V. Sviluppi della teoria di Ghyben ed Herzberg nello studio idrogeologico dell’alimentazione e dell’impiego delle falde acquifere, con riferimento a quella profonda delle Murge e del Salento. Geotecnica 1958, 6, 301–318. (In Italian) [Google Scholar]
- Aubinet, M.; Vesala, T.; Papale, D. (Eds.) Eddy Covariance. A Practical Guide to Measurement and Data Analysis; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Martano, P.; Elefante, C.; Grasso, F. A database for long term atmosphere-surface transfer monitoring in Salento Peninsula (Southern Italy). Dataset Papers Geosci. 2013, 946431. [Google Scholar] [CrossRef]
- Hsieh, C.I.; Katul, G.G.; Chi, T.W. An approximate analytical model for footprint estimation of scalar fluxes in thermally stratified atmospheric flows. Adv. Water Resour. 2000, 23, 765–772. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skonfronick-Jackson, G.; Kirchbaum, D. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Carrozzo, M.T.; Delle Rose, M.; De Marco, M.; Federico, A.; Forte, F.; Margiotta, S.; Negri, S.; Pennetta, L.; Simeone, V. Pericolosità di allagamento nel Salento leccese. Ital. J. Eng. Geol. Environ. 2003, 2, 77–85. [Google Scholar]
- Forte, F.; Pennetta, L.; Strobl, R.O. Historic records and GIS applications for flood risk analysis in the Salento peninsula (Southern Italy). Nat. Hazards Earth Syst. Sci. 2005, 5, 833–844. [Google Scholar] [CrossRef]
- Giorgi, F.; Im, E.S.; Coppola, E.; Diffenbaugh, N.S.; Gao, X.J.; Mariotti, L.; Shi, Y. Higher Hydroclimatic Intensity with Global Warming. J. Clim. 2011, 24, 5309–5324. [Google Scholar] [CrossRef]
- Regione Puglia. Annali Idrologici. 2009. Available online: http://www.protezionecivile.puglia.it/wp-content/uploads/Annali_I/annale2009.pdf (accessed on 30 November 2017). (In Italian).
- Regione Puglia. Annali Idrologici. 2010. Available online: http://www.protezionecivile.puglia.it/wp-content/uploads/Annali_I/annale2010.pdf (accessed on 30 November 2017). (In Italian).
- Regione Puglia. Annali Idrologici. 2011. Available online: http://www.protezionecivile.puglia.it/wp-content/uploads/Annali_I/annale2011.pdf (accessed on 30 November 2017). (In Italian).
- Palatella, L.; Miglietta, M.M.; Paradisi, P.; Lionello, P. Climate change assessment for Mediterranean agricultural areas by statistical downscaling. Nat. Hazards Earth Syst. Sci. 2010, 10, 1647–1661. [Google Scholar] [CrossRef]
- Alpert, P.; Ben-Gai, T.; Baharad, A.; Benjamini, Y.; Yekutieli, D.; Colacino, M.; Diodato, L.; Ramis, C.; Homar, V.; Romero, R.; et al. The paradoxical increase of Mediterranean extreme daily rainfall in spite of decrease in total values. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Fidelibus, M.D.; Balacco, G.; Gioia, A.; Iacobellis, V.; Spilotro, G. Mass transport triggered by heavy rainfall: The role of endorheic basins and epikarst in a regional karst aquifer. Hydrol. Process. 2017, 31, 394–408. [Google Scholar] [CrossRef]
- Miglietta, P.P.; Toma, P.; Fanizzi, F.P.; De Donno, A.; Coluccia, B.; Migoni, D.; Bagordo, F.; Serio, F. A Grey Water Footprint Assessment of Groundwater Chemical Pollution: Case Study in Salento (Southern Italy). Sustainability 2017, 9, 799. [Google Scholar] [CrossRef]
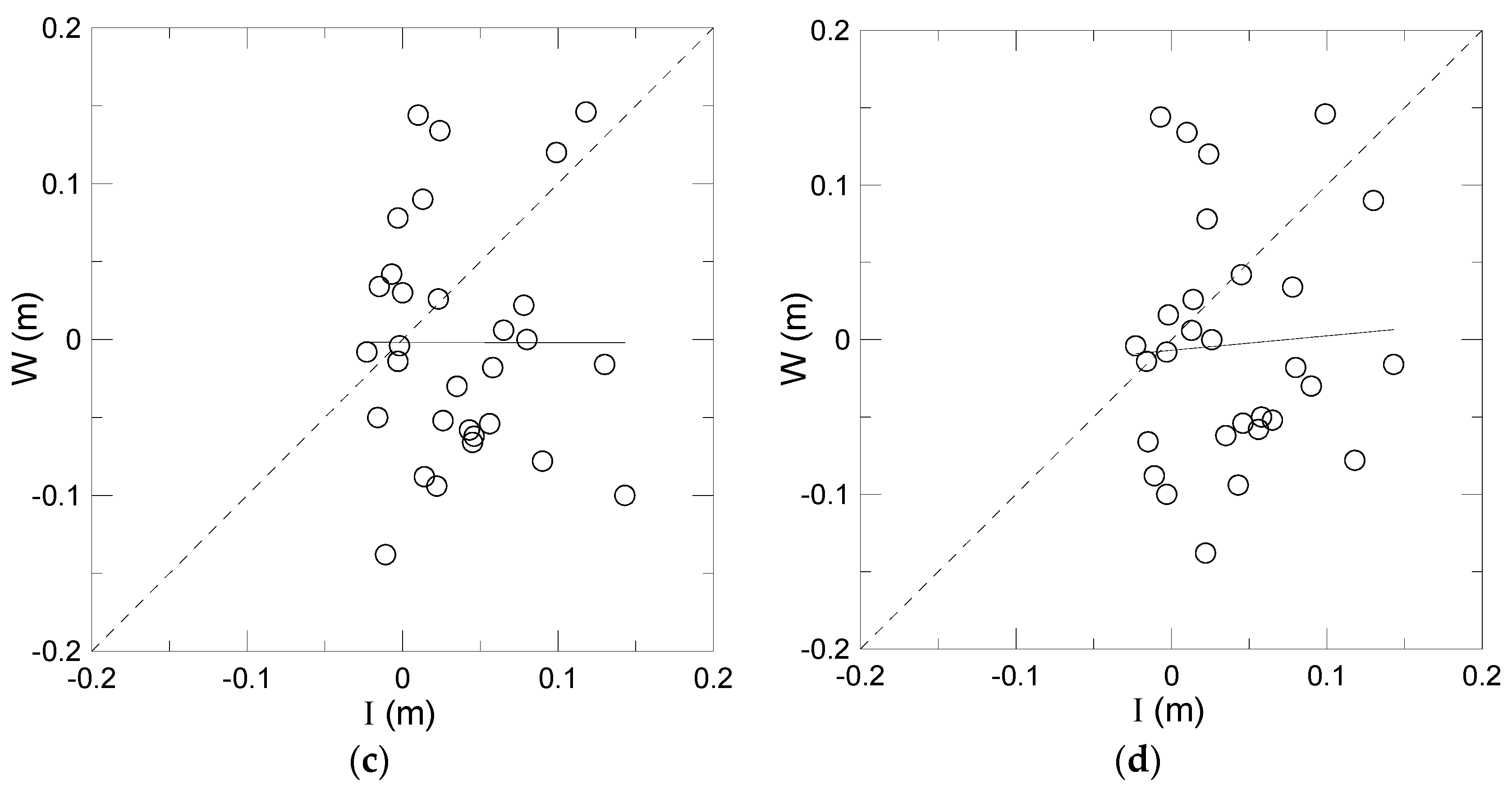
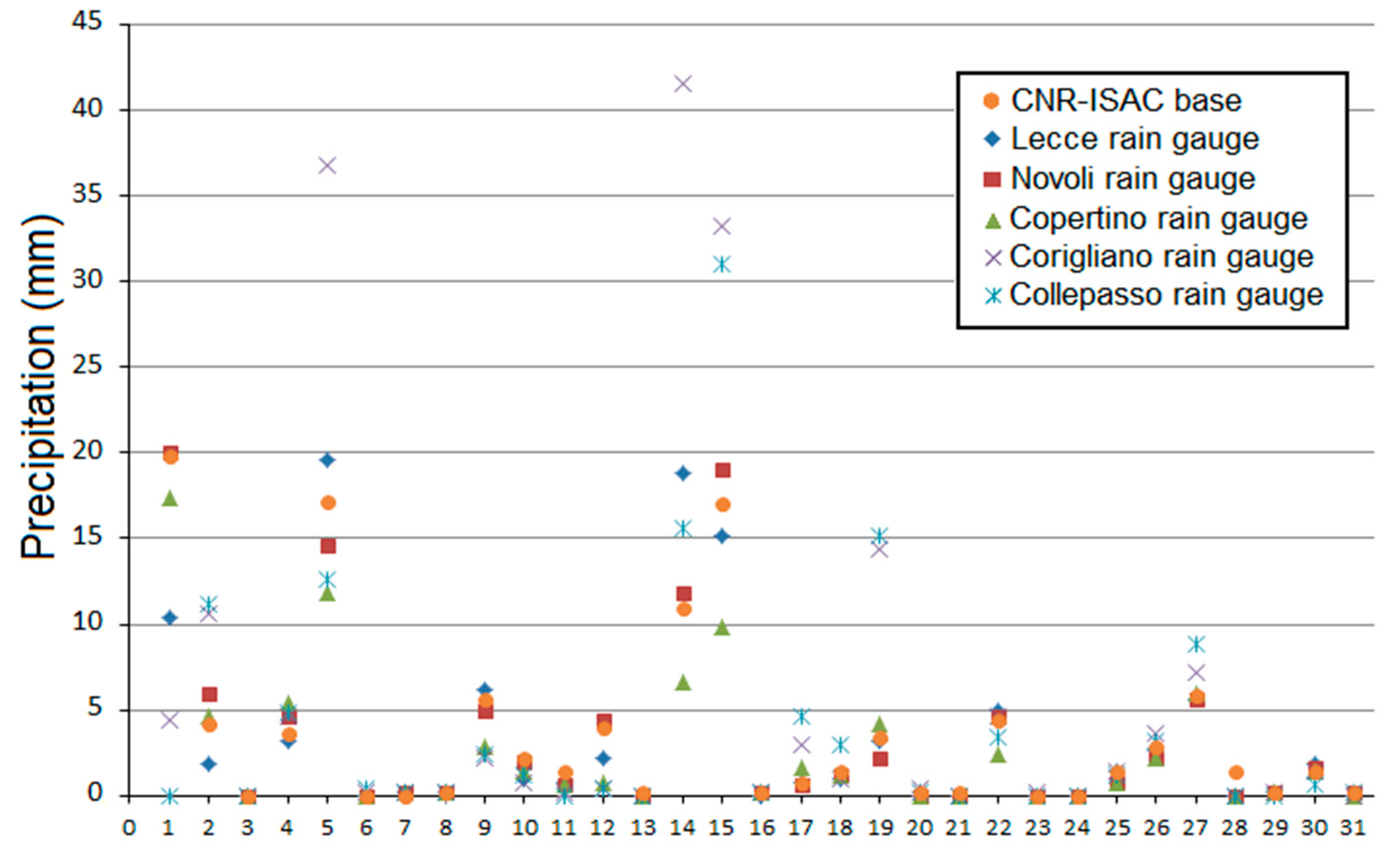
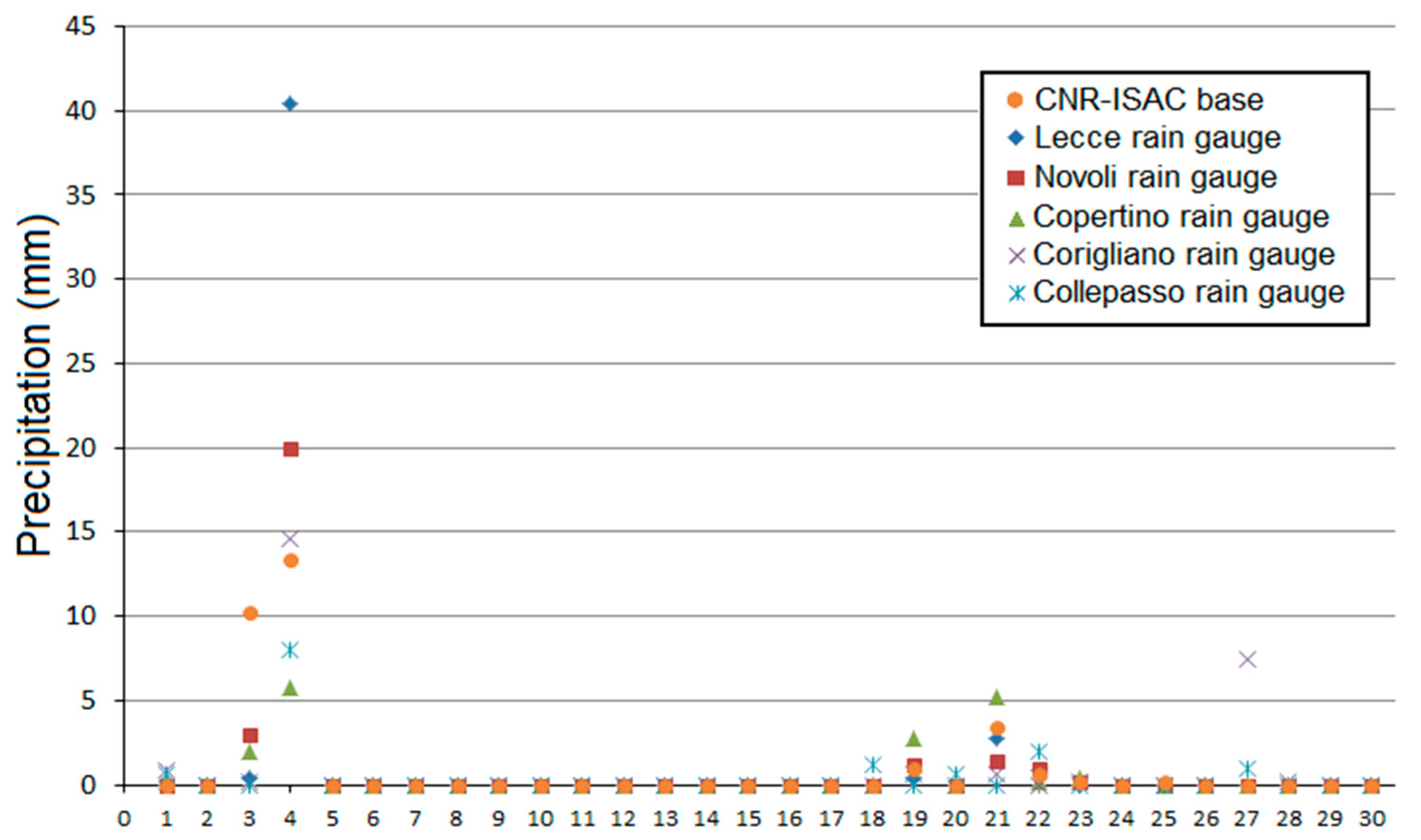
| (2003–2016 Period) | Precipitation (m) | Surface Infiltration (m) | Soil Moisture (m/m) |
|---|---|---|---|
| Dry season (April–September) | 0.25 ± 0.13 | 0.06 ± 0.13 | 0.11 ± 0.05 |
| Wet season (October−March) | 0.45 ± 0.13 | 0.33 ± 0.13 | 0.25 ± 0.05 |
| Year | 0.70 ± 0.13 | 0.39 ± 0.13 | 0.18 ± 0.05 |
| (2009–2011 Period) | Precipitation (m) | Net Infiltration (m) | Soil Moisture (m/m) |
|---|---|---|---|
| Dry season (April–September) | 0.36 ± 0.04 | 0.12 ± 0.04 | 0.14 ± 0.04 |
| Wet season (October–March) | 0.36 ± 0.02 | 0.28 ± 0.02 | 0.23 ± 0.04 |
| Year | 0.72 ± 0.06 | 0.40 ± 0.06 | 0.19 ± 0.04 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delle Rose, M.; Martano, P. Infiltration and Short-Time Recharge in Deep Karst Aquifer of the Salento Peninsula (Southern Italy): An Observational Study. Water 2018, 10, 260. https://doi.org/10.3390/w10030260
Delle Rose M, Martano P. Infiltration and Short-Time Recharge in Deep Karst Aquifer of the Salento Peninsula (Southern Italy): An Observational Study. Water. 2018; 10(3):260. https://doi.org/10.3390/w10030260
Chicago/Turabian StyleDelle Rose, Marco, and Paolo Martano. 2018. "Infiltration and Short-Time Recharge in Deep Karst Aquifer of the Salento Peninsula (Southern Italy): An Observational Study" Water 10, no. 3: 260. https://doi.org/10.3390/w10030260
APA StyleDelle Rose, M., & Martano, P. (2018). Infiltration and Short-Time Recharge in Deep Karst Aquifer of the Salento Peninsula (Southern Italy): An Observational Study. Water, 10(3), 260. https://doi.org/10.3390/w10030260






