Abstract
A dense rain-gauge network within continental Ecuador was used to evaluate the quality of various products of rainfall data over the Pacific slope and coast of Ecuador (EPSC). A cokriging interpolation method is applied to the rain-gauge data yielding a gridded product at 5-km resolution covering the period 1965–2015. This product is compared with the Global Precipitation Climatology Centre (GPCC) dataset, the Climatic Research Unit–University of East Anglia (CRU) dataset, the Tropical Rainfall Measuring Mission (TRMM/TMPA 3B43 Version 7) dataset and the ERA-Interim Reanalysis. The analysis reveals that TRMM data show the most realistic features. The relative bias index (Rbias) indicates that TRMM data is closer to the observations, mainly over lowlands (mean Rbias of 7%) but have more limitations in reproducing the rainfall variability over the Andes (mean Rbias of −28%). The average RMSE and Rbias of 68.7 and −2.8% of TRMM are comparable with the GPCC (69.8 and 5.7%) and CRU (102.3 and −2.3%) products. This study also focuses on the rainfall inter-annual variability over the study region which experiences floods that have caused high economic losses during extreme El Niño events. Finally, our analysis evaluates the ability of TRMM data to reproduce rainfall events during El Niño years over the study area and the large basins of Esmeraldas and Guayas rivers. The results show that TRMM estimates report reasonable levels of heavy rainfall detection (for the extreme 1998 El Niño event) over the EPSC and specifically towards the center-south of the EPSC (Guayas basin) but present underestimations for the moderate El Niño of 2002–2003 event and the weak 2009–2010 event. Generally, the rainfall seasonal features, quantity and long-term climatology patterns are relatively well estimated by TRMM.
1. Introduction
Spatio-temporal analysis of rainfall is crucial for water-resource management including water supply, risk management, sustainable agriculture and hydrological infrastructure. These aspects must be addressed and discussed before promulgating public policies in order to achieve the best climate-adapted development. Over South America, at continental scale, the rainfall distributions and related processes, such as moisture sources and transport, atmospheric circulation over oceans and continents, and the Andes range forcing, are fairly well-documented [1,2,3,4]. At regional scale, the Ecuadorian Pacific slope and coast (EPSC) is an area of particular interest due to its physiographic features (surface, altitudinal range and the considerable horizontal distance from the coastal border to the watershed division on the high Andes) because they have a strong impact on the spatial variability of rainfall. In addition, the El Niño-Southern Oscillation (ENSO) is commonly identified as the main driver of temporal rainfall variability along the Ecuadorian coastal region and how the influence of this is different on the Andes [5].
High-rainfall events over the EPSC, generally associated with El Niño events, are responsible for increases in runoff that cause major floods over Ecuador and Peru. The results of a 35-year simulation of rivers’ runoff over the Pacific Slope and coast of South America (PSCSA) showed that 15% of the total PSCSA runoff comes from the EPSC [6] making it one of the main runoff surfaces over the PSCSA. By comparison, the Peruvian Pacific slope produces 17% of the PSCSA runoff over the area that is six times the area of the EPSC [6]. This highlights the importance of conducting more detailed climatological and hydrological studies over the whole EPSC and also in its two largest basins (the Guayas and Esmeraldas basins) considering different types of ENSO events in terms of strength and seasonality.
The rainfall distribution and anomalous heavy rainfall in the coastal area of Ecuador are known to be related to the strong positive Sea-Surface Temperature Anomalies (SSTA) in the El Niño 1 + 2 region (N1 + 2) located between 0–10° S/80–90° W [7]. The spreading of atmospheric instability in the N1 + 2 Pacific region to the eastern escarpment of the Andes could be a result of the temporary eastward shift of the Walker circulation [8]. Moreover, over the Andes, the rainfall patterns are driven by the influence of both the Pacific Ocean and the Amazon basin [8] and the combinations of regional and local atmospheric processes which interact with the topography [5,7,9,10,11]. Currently, various datasets are available to study different aspects of the Ecuadorian climate, such as the spatio-temporal rainfall patterns over this region. These datasets include the best rainfall estimates from gauge analyses such as the best-estimate precipitation rate with multiple independent precipitation estimates of the Tropical Rainfall Measuring Mission (TRMM) sensors and rain-gauge analysis (TRMM 3B43 monthly Version 7 product) or called TRMM Multi-Satellite Precipitation Analysis (TMPA/3B43) [12] that later we will name only TRMM.
A few studies have investigated the rainfall patterns over Ecuadorian areas [9,13,14], but they do not examine in detail the entire EPSC surface. One of the objectives of this study is to better understand rainfall behavior over the EPSC. A critical step to achieving this goal consists in identifying the best regionally available dataset (e.g., based on synoptic observations from in situ networks, model reanalyzes, or derived from remote sensing) to represent the rainfall patterns over the EPSC. Consequently, this identified dataset will provide a more realistic framework to advance further hydro-climatic studies. Of course, in situ observations, that pass a quality-control process, constitute the most valuable source of information for climate studies. However, post-processing of satellite information contribute to enhancing the products that are only based on in situ observations, particularly on areas where it is too difficult to install a weather station. Over South America, TRMM products were used for regional analyses of rainfall variability already tested, e.g., the Peruvian [15,16,17] and Central Andes [18], Brazil [19], Andean–Amazon River Basins [20,21] or the Amazon Basin [22]. Therefore, this study aims to test whether TRMM information represents the climatological conditions of the EPSC obtained from in situ observations better than the other three datasets (Global Precipitation Climatology Centre (GPCC), Climatic Research Unit–University of East Anglia (CRU), and ERA-Interim Reanalysis). To determine which global dataset provides the better results, a monthly 5-km resolution product was generated from the rain gauge network that covers the entire EPSC region. This product served as reference for the comparison with the four other datasets.
This study is organized as follows: the details of the study area are presented in Section 2, whilst Section 3 presents the data. First, the quality-control process applied to the information of all available rain gauges in Ecuadorian territory that are maintained by the Meteorological and Hydrological National Institute of Ecuador (INAMHI); second, the process to generate the 5-km gridded rainfall dataset applying the cokriging method (COK) to the rain-gauge data; and last, a brief overview of the other rainfall products. Section 4 presents methods for comparing the different products based on statistical metrics, principal component analysis (PCA), and an analysis of selected El Niño rainfall events corresponding to different types and amplitudes. Section 5 is dedicated to the summary of the results. Section 6 presents the discussion. Finally, Section 7 presents the conclusions of this work.
2. Study Area
Ecuador is located in north-western South America, between Colombia and Peru, between 81.03° W–75.16° W, 1.48° N–5.04° S. Ecuador extends from the Pacific coast in the west to the Amazon plain in the east. Following a north–south direction, the Andes range crosses the entire Ecuadorian territory. Along this section, the Andes are divided in two main chains, the western and eastern ranges. These two quasi-parallel lines form an inter-Andean zone characterized by several valleys where many human settlements are found, including the capital of Ecuador, Quito. The highest watershed altitude divides the territory into two large drainage surfaces, with main flow directions towards the Pacific Ocean and the Amazon basin respectively (Figure 1). Over the western Andes slopes, rainfall is produced from moist air coming from the Pacific Ocean, whilst over the western Andes the moisture comes from the Amazon basin and the Atlantic Ocean. The eastern side, through the trade winds, generally receive more moist air than the western slope [5,23]. In addition, the inter-Andean valleys are influenced by both the oceanic and continental air masses [5], the prevailing easterly moisture flow extends across the mountains depending on the speed of trade winds, especially in the south (around 3° S), where the mountain chain is generally lower [10].
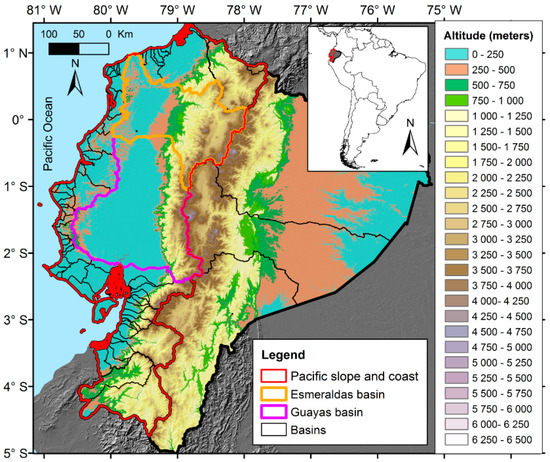
Figure 1.
Topographical map of continental Ecuador obtained using the digital elevation model of the Shuttle Radar Topographic Mission (SRTM) at 1 km of spatial resolution. The Pacific slope and coast (study area) is delineated with a red line and the two largest basins (Esmeraldas and Guayas) with orange and purple lines respectively. The other hydrographic basins are delineated with black lines according to level 5 of the Pfafstetter methodology. There are in total 74 basins for the Pacific slope and coast and three basins for the Amazon slope.
Our study area, the EPSC, is delimited to the west by the Pacific Ocean and to the east by the Andes watershed division. From west to east, the EPSC can be divided into the coastal region, the low-altitude coastal cordillera (extending from 1° N to 2° S, with a maximum altitude of 860 m.a.s.l.), an inland low valley, the western flanks of the Andes, the western high Andes ranges until they reach the tropical glaciers, and finally an inter-Andean region in the north (Figure 1). The EPSC covers an area of ~116,436 km2 and represents about 47% of Ecuadorian territory with a total wide range of altitudes varying from 0 to 5870 m.a.s.l. from the coastal border to the higher Andes summits. Due to the complex topography of the study area, 74 basins are delimited according to level five of the Pfafstetter methodology [24]. The Esmeraldas and Guayas basins are the largest of the EPSC, covering 19,680 km2 and 32,300 km2 respectively, together representing 44.6% of the EPSC surface.
The singular rainfall distribution of the EPSC is related to the two relevant mountains chains. The coastal border is characterized by low rainfall (<600 mm/year); the rainfall amount increases over the low coastal cordillera; and eastwardly, between this chain and the start of the Andes foothills, rainfall amounts reach the maximum of the region (>2000 mm/year). Then, to the east, rainfall decreases with altitude towards the high Andes (~400 to 1200 mm) [25]. Over the entire region, large rainfall variability is associated with the influence of the Pacific Ocean warming during extreme El Niño events [7], which induce extensive floods that can become devastating during the extreme El Niño years [26] over the lowlands.
3. Data
3.1. In Situ Rainfall Data
The in situ observations are composed of the monthly rainfall records from 325 selected meteorological stations (262 gauges on the Pacific slope and coast, and 63 on the Amazon slope) with at least 10 years of data over the 1965–2015 period (Figure 2). The meteorological stations network is managed by INAMHI. The method applied to select the stations with valid long-term records is described in Section 3.1.1.
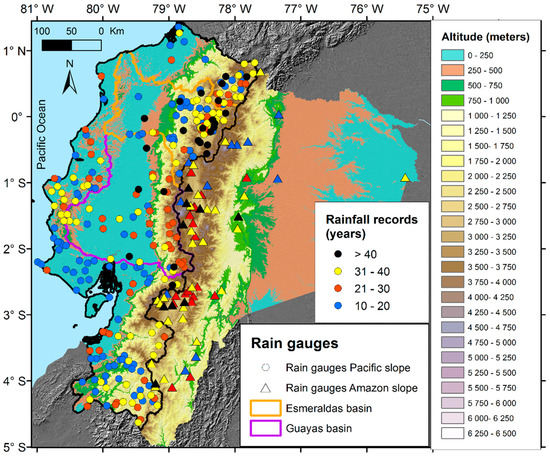
Figure 2.
The rain gauges of the Pacific slope and coast (EPSC) network (the 262 stations are represented using circles and the colors represent the rainfall record length of the stations for the 1965–2015 period). The rain gauges of the Amazon slope (63 stations) are represented using triangles. The study area (EPSC) is delineated using a black and bold line. The Esmeraldas and Guayas basins are delineated using orange and purple lines, respectively. The topography is represented using the digital elevation model (SRTM at 1 km of spatial resolution).
3.1.1. Data Homogenization and Validation
The raw data from the rain gauge network operated by INAMHI (370 gauges) were first quality-checked with the methodology applied in [27,28]. In the following analysis a valid station record should contain at least 10 years of observations and pass the quality-assessment and regionalization processes using the Regional Vector Method (RVM) [29]. The RVM assumes that for the same rainfall regime in a climatic zone, the total annual rainfall presents a pseudo-proportionality (little random variation) associated with the rain distribution in the zone. Based on this method, the coherence of the gauge data was checked grouping the gauges by watersheds and altitudinal ranges. Then, they were regrouped iteratively to check their homogeneity. The main statistical criteria for regrouping stations are based on thresholds applied to the standard deviation of the differences between annual pluviometrical indices of stations and the regional vector indices; and to the correlation coefficient between the regional vector and annual pluviometric values of stations [27,28]. During this process, an exhaustive geographical supervision was conducted using a background isohyet map with all data under review. This allowed excluding stations with doubtful data and those that did not correspond to any group and did not represent real climate zones. After this process, 45 gauges were excluded.
Belonging to the EPSC, 262 stations were grouped and selected; however, due to the low-gauge density over the Amazon region, only 63 stations were taken into account for this region. The information from these stations was used to perform an interpolation of the rainfall for all the Ecuadorian continental territory.
3.1.2. Rainfall Data Interpolation
Mountainous or sparsely populated regions often lack stations, so the meteorological information that represents these places does not exist or is limited. To solve these problems, spatial interpolation methods are convenient approaches. These techniques create continuous data over the region with missing information from sampled point values adjacent to a determined location.
The 325 validated gauges were interpolated using the cokriging method (COK) [30] for the whole Ecuadorian territory but the results are only applied to the EPSC. The Digital Elevation Model (DEM) of the Shuttle Radar Topographic Mission (SRTM) at 1-km resolution, provided by the National Aeronautics and Space Administration–National Geospatial-Intelligence Agency (NASA–NGA) and available at [31] was used as the external covariable for COK. Considering the gauge network density and the covariable resolution, the results of COK were obtained at a spatial resolution of 5 km. The R language and the libraries raster [32], gstat [33], were mainly used to perform the COK on the rainfall records. The library automap [34] was used to get the best fit for the variogram model. The best values to fit the variogram model were selected by testing the following four models: exponential, spherical, Gaussian and Matern–Stein. Considering the whole period, the best-fit indices were obtained with the exponential model, and therefore it was chosen.
The COK method was selected to interpolate the rainfall data because it allows avoiding the instability caused by highly redundant secondary data [35]. Improved results over the Andes have already been shown using this method [36] as well as over complex terrain in general [37]. However, despite the advantages of COK, the main weakness of the Kriging method is the tendency to produce maximum rainfall values over the summits rather than on the slopes [38]. Despite this limitation, the COK interpolation produces better results compared to those obtained in a previous study using simple Kriging and Cressman [39]. The gridded rainfall data obtained with COK represents adequately the rainfall variation by altitude. This better representation is thanks to the DEM data used by the COK method, which allows representing coherent rainfall changes by altitude, especially over the slope and the Andes.
In order to show a brief summary of the EPSC features and the results obtained with the validated gauges, Figure 3a shows the topography of the study area using SRTM (1 km of spatial resolution) and Figure 3b presents a three-dimensional view of the relief. The average annual rainfall map for the 1965–2015 period obtained using the COK spatial rainfall interpolation is presented in Figure 3c. The monthly mean rainfall variability averaged over the whole region is presented in Figure 3d.
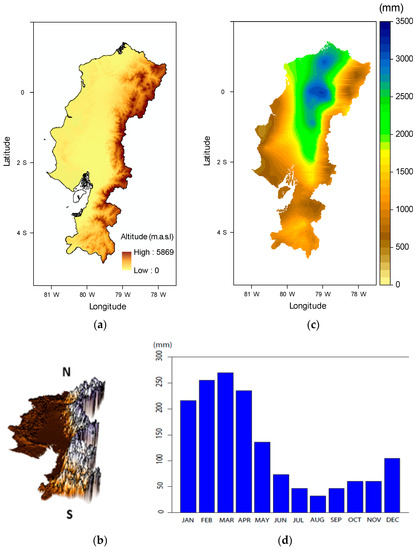
Figure 3.
(a) Pacific slope and coast (EPSC) topography; and (b) south–north perspective 3D-topography view showing the low-altitude costal cordillera (west) and the Andes (east); (c) multiyear average rainfall distribution from 325 rain gauges (262 stations from the EPSC) for the 1965–2015 period obtained with the cokriging interpolation method (COK) at 5 km grid resolution in mm/year; and (d) the rainfall averaged over the whole region (mm/month) for the 1965–2015 period.
The rainfall spatial distribution (Figure 3c) shows the lowest rainfall region (<750 mm/year) located on the central coastal border between latitudes 1° S and 2.5° S. This is associated with the limited displacement of the Inter-Tropical Convergence Zone (ITCZ) to the south in normal conditions, which is truncated by the cold water of the south-west Pacific inhibiting the development of convection processes [40]. Towards to the east, the rainfall increases over the low-altitude coastal cordillera (~750 to 1500 mm/year) and reaches the highest rainfall (~1500 to 3500 mm/year) on an inter-valley between the low coastal cordillera and the Andes (1° N to 1° S and 79.5° W to 78.5° W). Finally, on the eastern side of the EPSC, over the Andes range, the rainfall decreases (~750 to 1750 mm/year).
3.2. Rainfall Products
The gridded in situ rainfall obtained with COK interpolation as described in Section 3.1.2 was used to evaluate four commonly used gridded monthly rainfall datasets. They include two global gridded gauge-analysis products (CRU and GPCC), a reanalysis product (ERA-Interim) and the satellite-based estimate product from the TRMM monthly rainfall estimates with 3B34 algorithm, version 7. The details of the products used are shown in Table 1.

Table 1.
Description of the regional gridded interpolated rain-gauge product and four external rainfall datasets used in this study.
4. Methods
4.1. Evaluation of the Rainfall Products
The interpolated in situ observations obtained with COK were considered as the reference data to assess the quality of the four rainfall products described in Section 3.2. Three standard comparison metrics were used: the Pearson correlations coefficient (Crr), the Root Mean Squared Error (RMSE) and the Relative bias index (Rbias), the latter expressed in percentage (Equations (1)–(3)):
where n is the number of months; P is the monthly observed interpolated rainfall of the grid located at the coordinates in the month t; and , represent respectively the mean and standard deviation of P; , corresponds to the monthly series rainfall of the compared product; and represent, respectively, the mean and standard deviation of x.
The comparisons were performed over the longest time period of common availability by resampling the in situ observations at the same original resolution of the four tested products (see Table 1): for ERA-Interim at 0.125°, for TRMM at 0.25° and for the rainfall products GPCC, CRU at 0.5°.
4.2. Evaluation of the Tropical Rainfall Measuring Mission (TRMM) Rainfall Product
Principal Component Analysis (PCA) (or the Empirical Orthogonal Functions (EOF)) technique [45,46] is a commonly used method to characterize the spatio-temporal variability of physical fields in climate-related studies. It was applied to the centered and deseasonnalized anomalies of the interpolated monthly gridded in situ observations obtained in Section 3.1.2, over the 1965–2015 period. Given that, TRMM shows the best comparison metrics in terms of the criteria presented in 4.1 among the four tested products; we performed a more detailed evaluation of the TRMM data over the overlapping period with the gridded in situ observations (1998–2015). In particular, the PCA was also applied on the centered and deseasonalized anomalies to analyze the spatio-temporal variability of rainfall estimates from TRMM and compare them to those obtained using the gridded in situ observations.
Furthermore, the TRMM estimates were also evaluated during El Niño events over the entire EPSC area and over the two largest river basins (Esmeraldas and Guayas basins). The results of the comparison will be presented for each study region and each El Niño event as the percentage of Rbias of the TRMM rainfall estimates and the total rainfall episodes.
The duration of El Niño rainfall events were selected according to the consecutive positive values of the Southern Oscillation Index (SOI) [47]; El Niño intensity was ranked according to the NOAA Oceanic Niño Index (ONI) [48]; sea-surface temperature anomaly (SSTA) as weak (0.5 °C to 0.9 °C SSTA), moderate (1 °C to 1.4 °C SSTA) and extreme (≥2 °C SSTA). Finally, the events’ ranking was fine-tuned according to the observed rainfall quantity in the study area. The events intensity for the EPSC was also adjusted regarding the SOI values because the ONI only considers the mean of extended reconstructed sea-surface temperature anomalies (ERSST.v4) [49] in the El Niño 3.4 region (5° N–5° S, 120°–170° W). According to these criteria, and for the overlapping data period, the El Niño events selected were: El Niño 1998 (January 1998–September 1998) ranked as extreme, the El Niño of 2002–2003 (January 2002–September 2003), 2007–2008 (September 2007–September 2008) ranked as moderates and El Niño of 2009–2010 (October 2009–September 2010) ranked as weak. It should be noted that only a part of El Niño 1997–1998 (from January 1998) could be analyzed due to the data availability of TRMM.
5. Results
5.1. Rainfall Products Comparison
The first step consists of determining the rainfall product that provides the better rainfall estimates compared with in situ observations. The results of the comparison between in situ observations interpolated with COK and the four rainfall products described in Section 3.2 are presented in Table 2 and Figure 4.

Table 2.
Results of the comparison between the four rainfall products and in situ gridded (interpolated with COK) observations. The monthly time-series comparison is shown, along with the gridded resolution of the comparison, the mean annual precipitation with the mean bias difference of each product with the interpolated observations. Finally, the results of the three comparison metrics: correlation, RMSE and relative bias. The comparison was made in reference to the common temporal periods and the original grid resolutions of the four rainfall products compared (see Table 1).
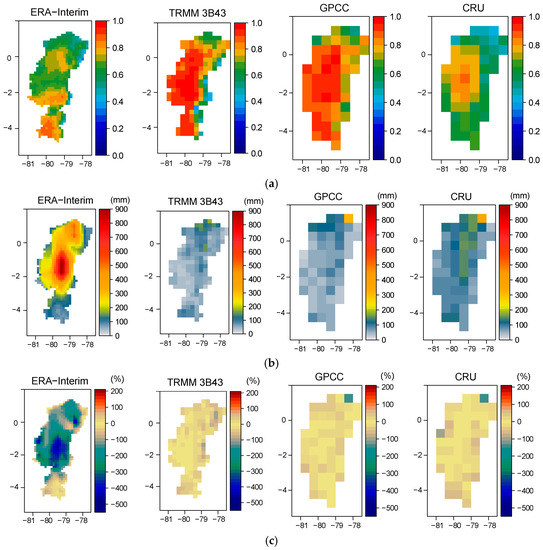
Figure 4.
Maps of (a) linear correlations; (b) root mean squared error (RMSE) (in mm) and; (c) relative bias (in %) between interpolated in situ observations with COK and the four studied rainfall datasets (ERA-Interim, TRMM 3B43 V7, GPCC V7, CRU V3.22).
An analysis of variance (ANOVA) was performed on the four global rainfall products and the in situ one, all resampled at 0.5° of spatial resolution (corresponding to 10,572 samples in the EPSC from 1998 to 2013 at monthly time-scale) in order to determine if the differences between the datasets are significant. The different datasets do not perfectly follow the normal distribution, but they have almost all similar variances (20,388, 14,849, 18,646, 24,670 mm2 for the observations, TRMM, GPCC and CRU, respectively), except ERA-Interim (95,579 mm2). Results of the ANOVA give a F-statistic of 2839 and a p-value close to 0. As the ERA-Interim does not perfectly fit the assumption of the ANOVA and also as the results of the comparison with the in situ data show important differences with the in situ dataset, an ANOVA on the in situ product, TRMM, GPCC and CRU was then performed. A F-statistic of 33.85 and a p-value of 7.6 × 10−22 were obtained. A final ANOVA on the in situ data, TRMM and GPCC was performed as CRU provides quite different results from the other datasets. A F-statistic of 6.78 and p-value of 0.0011 were obtained. In all the cases, the null hypothesis was rejected, showing that the results presented in Table 2 and Figure 4 are statistically significant.
Considering the global products only based on in situ observations, better results are obtained using the GPCC product than the CRU (correlation 0.83 versus 0.66 and RMSE of 69 versus 102 mm). This is likely to be due to the use of a larger number of rain gauges in GPCC than in CRU [42,50]. ERA Interim reanalysis monthly mean data show a large rainfall overestimation over the central region of the EPSC (Guayas basin). This was already observed in other studies in the same latitude range as Ecuador [51] and over the Peruvian Andes [52].
The two rainfall estimates that provide the best results are GPCC and TRMM products with Crr higher than 0.8 and Rbias lower than 6%. The major advantage of TRMM over GPCC is its higher spatial resolution (0.25° against 0.5°) and the availability of more frequently updated data. TRMM underestimates the total rainfall (−12.5%) with a Rbias, mean Crr and RMSE of −2.8%, 0.82 and 68.7, respectively (Table 2). TRMM exhibits the best score in the lowlands, with high correlation, low RMSE and low Rbias compared to the other products (Figure 4). Nevertheless, the performance of TRMM is quite low over the high-altitude regions, as already mentioned in several studies [16,53,54,55,56,57] (Figure 4a,c). This can be explained by the fact that the rainfall data from TRMM are derived through an inverse approach from the brightness temperature at the cloud top [58]. The TRMM processing scheme of microwave and infrared (IR) data has to cope with the highly heterogeneous terrain with varying brightness temperatures which affects the rainfall estimates [18]. Generally, the microwave signal as seen from space is strongly dependent on surface type [17], and is affected by the presence of topography that is especially the case over the Andes [59]. The Andes cause strong scattering of the electromagnetic waves emitted by the Precipitation Radar (PR). This is a large source of error for rainfall estimation [38,44] and also may severely affect the infrared retrieved estimation of rainfall [54].
5.2. Identification of Spatio-Temporal Rainfall Variability with TRMM
As a second step, as showed in 5.1, the TRMM product was chosen among the other rainfall products because of its evaluation scores, which were some of the best, and also because of its higher spatial resolution (0.25° × 0.25°).
PCA was applied on deseasonalized anomalies to both the TRMM product and the gridded interpolated observations averaged at 0.25° of spatial resolution over 1998–2015. According to North’s rule of thumb [60], the first five PCA modes are significant, but only the first three PCA modes will be discussed because the higher-order modes explain a variance lower than 5% and are difficult to interpret. Figure 5 shows these three first modes, which represent 76% (53, 13 and 10%, respectively) of the explained total variance for the gridded observations and 86% (69, 10, and 7%, respectively) for TRMM. The spatial structures of both rainfall products are very similar, especially the first spatial and temporal component, which accounts for the highest explained variance. The explained variances obtained are lower for the observations resampled at the 0.25° × 0.25° resolution than for TRMM. This difference is because the PCA method is less able to represent (as explained variance) the more detailed spatial distribution of observed resampled grid rainfall than the TRMM estimates.

Figure 5.
Comparison of spatial and temporal components of the first (a), second (b) and third (c) first Principal Component Analysis (PCA) modes obtained on the deseasonalised rainfall anomalies for the gridded observations and TRMM estimates. The comparison was performed at the spatial resolution of the TRMM 3B43 V7 product (0.25°) and over the common period of availability of the two datasets (1998–2015).
Very similar spatial and temporal patterns, with Crr = 0.91 and 0.95 and RSME = 55 mm and 0.07 respectively, were found for the first PCA mode (Figure 5a). For the spatial component, small differences can be observed in terms of amplitude. TRMM represents more rainfall variability: lower over the Andes foothills and higher over the lowlands. The temporal component is dominated by the signature of the ENSO events, especially the extreme event of 1998 and the moderate event of 2002–2003. For the second PCA mode, showing a meridional dipole, the spatial patterns are very similar between TRMM and the re-gridded deseasonalized anomalies’ observations (Crr = 0.91, RMSE = 45 mm), although the amplitudes of the dipole centers are smaller for TRMM, especially over the north of the EPSC (ITCZ migration region) and on the coastal center and south border (Humboldt Current influence). The temporal components are quite different (Crr = 0.57 and RMSE = 0.27). In particular, TRMM exhibits a stronger variability with respect to the observations (Figure 5b). Similar spatial and temporal patterns with, respectively, Crr = 0.81 and 0.82 and RSME = 34 mm and 0.19 were found for the third PCA mode. However, a clear east–west gradient is present in the in situ gridded rainfall. It does not appear so clearly for TRMM (Figure 5c).
5.3. Identification of Spatio-Temporal Rainfall Variability during El Niño-Southern Oscillation (ENSO) Events with TRMM
As a third and final step, three regions were studied for extreme, moderate and weak El Niño events selected in Section 4.2 over the whole EPSC and its two largest basins (Esmeraldas and Guayas). Time series and maps of average rainfall (1998–2015 period), as well as temporal events and cumulative rainfall maps over each study area and for each El Niño event are presented in Figure 6.
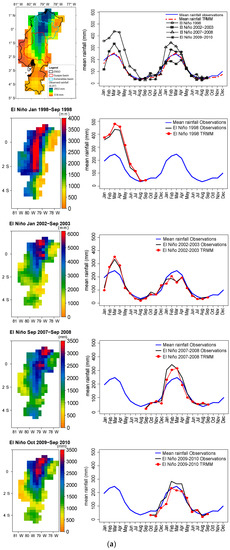
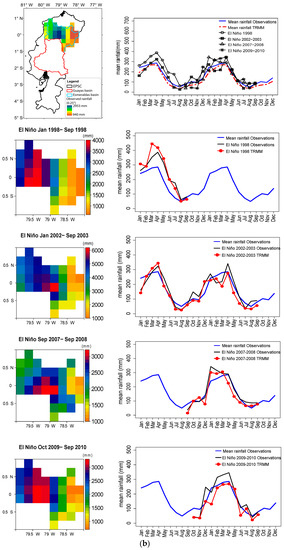
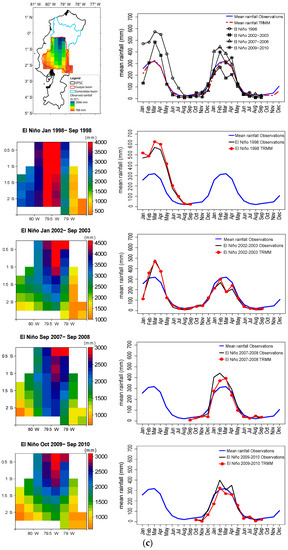
Figure 6.
Rainfall comparison of the gridded observations and TRMM estimates at 0.25° of spatial resolution, during the El Niño events of 1998, 2002–2003, 2007–2008 and 2009–2010. The top image corresponds to the map of the observed pluri-annual monthly average rainfall of the period 1998–2015 and the monthly comparison of four El Niño events with the mean rainfall observed and estimated by TRMM for (a) the Pacific slope and coast, for (b) the Esmeraldas basin, and for (c) the Guayas basin. The other maps are the spatial cumulative rainfall observations and the comparisons of the temporal average series by El Niño event, between observations and TRMM made for the (a) Pacific slope and coast and for (b) the Esmeraldas basin and (c) Guayas basin.
5.3.1. Pacific Slope and Coast
For the EPSC, the monthly averaged time variations of the observed rainfall were well estimated in the TRMM product. They present a low Rbias of −6.9% with respect to the observations. As shown in Table 3, the 1998 El Niño event was the strongest rainfall event of the entire period 1998–2015 over the EPSC with 75.1% above the pluri-annual monthly average rainfall. Next was the moderate El Niño event of 2007–2008, with a cumulative rainfall event of 9.3% above the monthly average. The moderate and weak events of 2002–2003 and 2009–2010, with an average rainfall of −3.5% and −0.8%, respectively, were the closest to the monthly average of the EPSC. The best represented event by TRMM was the moderate 2002–2003 El Niño, and the worst was the weak 2009–2010 El Niño (Figure 6a).

Table 3.
Percentages of cumulated observed rainfall with respect to the monthly average (period 1998–2015) for each El Niño event (1998, 2002–2003, 2007–2008 and 2009–2010) and for each study region (Ecuadorian Pacific Slope and Coast, Esmeraldas and Guayas basins) and the corresponding Rbias (in %) of the TRMM rainfall estimates.
The spatial and temporal results presented in Figure 6a show that the 1998 El Niño, for the 9 months considered, produced a maximum cumulative rainfall event between 3500 and 4000 mm over most of the lowlands and the high rainfall was observed towards the south until 2.5° S. During 2002–2003 El Niño, a maximum cumulative rainfall event of 6000 mm in 21 months was located in the northern region (~1° N to 0.5° S). For the 2007–2008 El Niño, the maximum cumulative rainfall event of 3500 mm in 13 months was located over the north of the region (~1° N to 0.5° S). During the 2009–2010 El Niño, with a duration of 12 months, the maximum cumulative rainfall event of 3500 mm was located in the north (~1° N to 1° S). For all of these four events, high rainfall was delimited at the west and east by the low coastal cordillera and the Andes range, respectively (Figure 6a).
5.3.2. Esmeraldas Basin
In the Esmeraldas basin, the monthly average rainfall was generally underestimated by TRMM, with an average Rbias of −16.4%. The rainfall during El Niño events of 1998, 2002–2003, 2007–2008 and 2009–2010 exceeded by 43.2%, 3.4%, 8.1% and 5.9% the pluri-annual monthly average rainfall observations. The extreme 1998 El Niño was the major rainfall event. The Rbias comparison of rainfall observations and TRMM estimates of El Niño events of 1998, 2002–2003, 2007–2008 and 2009–2010 are presented in Table 3.
The rainfall during the extreme El Niño of 1998 and the weak 2009–2010 El Niño are, respectively, the best and worst estimated using TRMM. The rainfall during the weak 2009–2010 El Niño was the most underestimated by TRMM. Regarding the spatial rainfall distribution of the events (Figure 6b), the maximum accumulated rainfall was observed in the central and southern regions of this basin. The upstream basin (in the Andes) was, in all cases, the region with least rainfall and lower variability. This spatial distribution is in accordance with the zonal rainfall distribution showed by the multiyear average rainfall map and the first spatial PCA mode.
5.3.3. Guayas Basin
In the Guayas Basin, the monthly average rainfall was also underestimated by TRMM, with an average Rbias of −8.5% (lower than in the Esmeraldas basin). El Niño events of 1998, 2002–2003, 2007–2008 and 2009–2010 presented 100.7%, −21.3%, 0.8% and −7.5% more/less rainfall with reference to the average of the basin (Table 3). The extreme 1998 El Niño presented the largest impact on the rainfall variability compared to the EPSC and Esmeraldas basin. The moderate El Niño of 2002–2003 was the best estimated, and the worst was the weak El Niño of 2009–2010.
The distribution of average rainfall (Figure 6c) indicates that it was mostly concentrated in the northern basin region (normal seasonal ITCZ influence). The largest rainfall amounts occurred in the center and along the north–south border of the basin during the 1998 El Niño event. The total rainfall (4000 mm in 9 months) was distributed over most of the lowlands in the region delimited by the Andes and the low-altitude coastal cordillera. For all events, less rainfall was found in the Andean part of the basin. This spatial distribution is in accordance with the multiyear average rainfall distribution and with the zonal and meridional rainfall-variability distribution (N–S increase and W–E decrease) showed by the spatial PCA modes (EOF1 and EOF2) of Figure 5.
6. Discussion
Our work presents a detailed rainfall distribution for the EPSC, which shows a significant correlation with orographic features. The high amount of climatology rainfall is concentrated in the north at the western windward side of the Andes and in the low coastal cordillera due to the intense low-level convergence when the ITCZ is placed on the north of the equator (almost in line with the oceanic ITCZ) in austral winter [4]. The mountain slopes exposed perpendicularly to frequent winds that transport moisture [11] can produce this highest amount of rainfall. This could also be supported by a larger cloud frequency observed in the north (~0) than the south (~4 S) [61]. The spatial rainfall distribution over the EPSC is clearly delimited by its two mountain chains, which act as weather divisions, mainly the Andes, as the major borderline between Pacific and Amazonian climatic influences. These two chains have permanent interactions with tropospheric flow, which is more remarkable during the rainy season due the ITCZ seasonal migration and the interannual ENSO influence periodicity (ranging from 2 to 7 years [62]). The particular case of the coastal border, where the rainfall amount is minimum, can be related to the influence of the SE Pacific anticyclone and the cold water upwelling of the Humboldt Current in austral winter [61]. As for the temporary rainfall distribution over the EPSC, the first rainfall seasons starts in November–December when the ITCZ begins its southern displacement, then a second marked season, due to the direct influence of the ITCZ on convective processes, starts in Jan–May reaching a maximum in March. A third season with lower (minimum) rainfall occurs during Jul–Sep due to the northward shift of the ITCZ, during the northern hemisphere summer, and the intensified Walker circulation that produces advective low cloud [63].
The largest interannual variability within the EPSC region is mostly produced by the ENSO conditions and influenced by the seasonal meridional migration of the ITCZ. This relationship is supported by the fact that the ITCZ migration is delayed (favored) during warm (cool) ENSO phases [64] because the ITCZ generally migrates toward a differentially warming hemisphere [65]. The spatial component of the second EOF mode is consistent with the higher cloud frequency during the ITCZ meridional migration over the EPSC and, therefore, closely related to the ENSO events represented by the first EOF mode. The spatial component of the first EOF specifically reveals the zonal rainfall variability influence of El Niño events, which is highest over the lowlands, specifically higher over the center south (Guayas basin), low over the Andes slope, and very low over the Andes. This was clear, for example, during the extreme 1998 El Niño, with a high rainfall variability impact towards the center-south according to the spatial rainfall variability presented by the first EOF mode and the event rainfall accumulation over the Esmeraldas and Guayas basins. The higher rainfall variability for the Guayas basin (center-south region) than for the Esmeraldas basin (north region) can be accounted for by evidence of historic strong and extreme El Niño events, which clearly separate the moist northern Ecuadorian coast, under the normal influence of the ITCZ, from the south coast of Ecuador, which is the driest region and sensitive to ENSO events [66]. It should be noted that the ITCZ shift during warm ENSO episodes reduces rainfall by about 100 mm/year along the northern edge of the normal ITCZ over the eastern Pacific [67], mostly in December–February (DJF) and March–May (MAM). It is equally important to mention that the western and central Pacific ITCZ shifts southward by about 2° S on typical ENSO conditions, and by about 5° S during strong El Niño events (such as in 1983 and 1998) [65] with the longitudinal ITCZ structure modified by ENSO’s zonal rearrangement of convection [67].
Although the monthly global datasets as GPCC and CRU obtained by interpolating global gauges’ observations allow for fairly good rainfall data for the study region, TRMM 3B34 V7 is the better source among all the datasets considered in this study. TRMM showed good agreement with gauge data compared with GPCC and CRU, and it showed to be superior to the global atmospheric reanalysis of ERA-Interim. Nevertheless, TRMM presents some overestimations over lowlands (mean Rbias of 7%) and has more underestimations over the Andes (mean Rbias of −28%) when compared with in situ gauges. For the El Niño rainfall events, TRMM presents mostly underestimations for the considered El Niño events. This could be explained because the TRMM dataset is the result of the combination of multiple independent precipitation estimates from the TRMM microwave imager (TMI), visible and infrared scanner (VIRS), rain gauge data and the precipitation radar (PR). PR underestimates rainfall rate for extremely intense convective rainfall [68], especially for extreme precipitating systems that contain significant mixed phase and/or frozen hydrometeors [69], as on the Andes. There is also the limitation of the VIRS data that provide information of cloud-top height, which do not correlate well enough with ground precipitation [70]. Different cloud types may have similar cloud-top temperatures and are associated with different amounts of rainfall at the ground [71]; for higher convective cloud there are normally underestimations compared to low-level short convection [72]. Finally, the TMI also missed the light and heavy rainfall because of its small scale (swath width of 758.5 km) [73] and/or type of rainfall according to its nature as, for example, the warm rain (derived from non ice-phase processes in clouds) [74]. As shown by [61], over Ecuadorian territory the average cloud-top height increases from west to east during the wet season (December–May), which means W–E rainfall cloud-top height increases; thus, this results in important underestimation over the Andes against a reasonably small overestimation over lowlands. It could also suggest that during the lower rainfall season (July–September), as shown in [75], TRMM overestimations over the dry areas could be attributed to sub-cloud evaporation.
7. Conclusions
Comparison of the gridded observations with the commonly used rainfall datasets from GPCC, CRU, ERA-Interim reanalysis, and the satellite estimates from TRMM 3B43, showed that the satellite-based rainfall product provides the more reliable estimates. Overall, considering the 1998–2015 period, there is a good agreement between observations and TRMM with an average lowest RMSE of 68.7 mm/year and Rbias of −2.8% for the entire EPSC. We can note that, for the lowlands, the Rbias obtained (7%) are closer (small overestimation) to the observations than for the Andes (−28%) (underestimation). These results can be related to the uncertainties associated with the TRMM 3B43 algorithm and the errors from the different sensors onboard the satellite (TMI, PR and VIRS) which are responsible for underestimations of the rainfall during the wet season (December–May) when top-cloud heights increase from W–E of the EPSC over the Andes slopes and inter-Andean basin.
Very similar spatial and temporal patterns were found, especially for the first mode (Crr = 0.91 and 0.95 and RSME = 55 mm and 0.07 mm), when applying the PCA to deseasonalized anomalies of rainfall from TRMM 3B43 and in situ gridded observations over the EPSC between 1998 and 2015. For the spatial component, some differences can be observed in terms of rainfall variability amplitude and structures form over the Andes foothills (lower for TRMM) and over the lowlands (higher for TRMM). The first temporal component is dominated by the signature of the ENSO events, especially the extreme event of 1998. The first PCA spatial mode clearly shows the location of heavy rainfall impact of El Niño events and their zonal rainfall variability influence, which is highest over the lowland and lower towards the Andes.
The TRMM 3B43 product showed a generally good capability for providing realistic rainfall estimates during extreme El Niño 1998 (mean Rbias of +7.7%), and moderate El Niño of 2002–2003 (mean Rbias of −2.4%) over the EPSC. Nevertheless, rainfall for the El Niño 2007–2008 and 2009–2010 events were underestimated by TRMM (mean Rbias of −11% and −17.1%) over the EPSC and more notably underestimated for the 2009–2010 event for the Esmeraldas (−23.7%) than the Guayas basin (−18.9%). General good agreement was also found over the Esmeraldas basin for the extreme El Niño 1998 (mean Rbias 6.3%) and over the Guayas basins for the extreme 1998 and moderate 2002–2003 El Niño events (mean Rbias of +8.5%, +5.3%) in spite of small overestimations. All these results confirm that TRMM 3B43 V7 reports reasonable levels of heavy rainfall detection over the EPSC and specifically towards the center-south of the EPSC (Guayas basin) but presents a general underestimation for the moderate and weak El Niño events. Over the whole EPSC, the seasonal features and quantity are relatively well estimated by TRMM and the long-term climatology patterns are well represented. The present study validates the use of remotely sensed rainfall data in regions with sparse rain-gauge stations and high rainfall variability, taking into account the potentialities and limitations of satellite estimates.
Acknowledgments
This work was supported by Ecuadorian National Secretary for Higher Education, Science, Technology and Innovation (SENESCYT). Authors would like to thank INAMHI (Meteorological and Hydrological National Institute of Ecuador) for providing the complete hydrometeorological raw dataset. We thank three anonymous reviewers for their constructive comments on our manuscript.
Author Contributions
Bolívar Erazo, Luc Bourrel and Frédéric Frappart conceived, designed the study and processed the data. David Labat, Oscar Chimborazo, Luis Dominguez-Granda, David Matamoros and Raul Mejia were involved in the analysis of the results. All authors contributed to the writing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, J.; Lau, K.M. Principal modes of interannual and decadal variability of summer rainfall over South America. Int. J. Climatol. 2001, 21, 1623–1644. [Google Scholar] [CrossRef]
- Haylock, M.R.; Peterson, T.C.; Alves, L.M.; Ambrizzi, T.; Anunciação, Y.M.T.; Baez, J.; Grimm, A.M.; Karoly, D.; Marengo, J.A.; Marino, M.B.; et al. Trends in Total and Extreme South American Rainfall in 1960–2000 and Links with. J. Clim. 2006, 19, 1490–1513. [Google Scholar] [CrossRef]
- Garreaud, R.D. The Andes climate and weather. Adv. Geosci. 2009, 7, 1–9. [Google Scholar] [CrossRef]
- Garreaud, R.D.; Vuille, M.; Compagnucci, R.; Marengo, J. Present-day South American climate. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 180–195. [Google Scholar] [CrossRef]
- Vuille, M.; Bradley, R.S.; Keimig, F. Climate Variability in the Andes of Ecuador and Its Relation to Tropical Pacific and Atlantic Sea Surface Temperature Anomalies. J. Clim. 2000, 13, 2520–2535. [Google Scholar] [CrossRef]
- Mernild, S.H.; Liston, G.E.; Hiemstra, C.; Beckerman, A.P.; Yde, J.C.; Mcphee, J. The Andes Cordillera. Part IV: Spatio-temporal freshwater run-off distribution to adjacent seas (1979-2014). Int. J. Climatol. 2016. [Google Scholar] [CrossRef]
- Bendix, A.; Bendix, J. Heavy rainfall episodes in Ecuador during El Niño events and associated regional atmospheric circulation and SST patterns. Adv. Geosci. 2006, 6, 43–49. [Google Scholar] [CrossRef]
- Bendix, J.; Trache, K.; Palacios, E.; Rollenbeck, R.; Goettlicher, D.; Nauss, T.; Bendix, A. El Niño meets La Niña—Anomalous rainfall patterns in the “traditional” El Niño region of southern Ecuador. Erdkunde 2011, 65, 151–167. [Google Scholar] [CrossRef]
- Bendix, J.; Lauer, W. Die Niederschlagsjahreszeiten in Ecuador und ihre klimadynamische Interpretation (Rainy Seasons in Ecuador and Their Climate-Dynamic Interpretation). Erdkunde 1992, 46, 118–134. [Google Scholar] [CrossRef]
- Emck, P. A climatology of south Ecuador-with special focus on the major Andean ridge as Atlantic-Pacific climate divide. Ph.D. Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, July 2007. [Google Scholar]
- Rollenbeck, R.; Bendix, J. Rainfall distribution in the Andes of southern Ecuador derived from blending weather radar data and meteorological field observations. Atmos. Res. 2011, 99, 277–289. [Google Scholar] [CrossRef]
- Bolvin, D.T.; Huffman, G.J. Transition of 3B42/3B43 research product from monthly to climatological calibration/adjustment. In NASA Precipitation Measurement Missions Document; NASA: Washington, DC, USA, 2015; pp. 1–11. [Google Scholar]
- Rossel, F.; Mejía, R.; Ontaneda, G.; Pombosa, R.; Roura, J.; Calvez, R.; Cadier, E. Régionalisation de l’influence du El Niño sur les précipitations de l’Equateur. Bulletin d'Institut Français D'études Andines 1998, 27, 643–654, ISSN:0303-7495. [Google Scholar]
- Morán-Tejeda, E.; Bazo, J.; López-Moreno, J.I.; Aguilar, E.; Azorín-Molina, C.; Sanchez-Lorenzo, A.; Martínez, R.; Nieto, J.J.; Mejía, R.; Martín-Hernández, N.; et al. Climate trends and variability in Ecuador (1966–2011). Int. J. Climatol. 2015. [Google Scholar] [CrossRef]
- Lavado, W.; Labat, D.; Guyot, J.L.; Ronchail, J.; Ordoñez, J. TRMM rainfall data estimation over the Peruvian Amazon-Andes basin and its assimilation into a monthly water balance model. In New Approaches to Hydrological Prediction in Data-Sparse Regions; International Association of Hydrological Sciences: London, UK, 2009. [Google Scholar]
- Condom, T.; Rau, P.; Espinoza, J.C. Correction of TRMM 3B43 monthly precipitation data over the mountainous areas of Peru during the period 1998-2007. Hydrol. Process. 2011, 25, 1924–1933. [Google Scholar] [CrossRef]
- Mantas, V.M.; Liu, Z.; Caro, C.; Pereira, A.J.S.C. Validation of TRMM multi-satellite precipitation analysis (TMPA) products in the Peruvian Andes. Atmos. Res. 2014. [Google Scholar] [CrossRef]
- Scheel, M.L.M.; Rohrer, M.; Huggel, C.; Villar, D.S.; Silvestre, E.; Huffman, G.J. Evaluation of TRMM Multi-satellite Precipitation Analysis (TMPA ) performance in the Central Andes region and its dependency on spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2011, 2649–2663. [Google Scholar] [CrossRef]
- Franchito, S.H.; Rao, V.B.; Vasques, A.C.; Santo, C.M.E.; Conforte, J.C. Validation of TRMM precipitation radar monthly rainfall estimates over Brazil. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Negrón Juárez, R.I.; Li, W.; Fu, R.; Fernandes, K.; de Oliveira Cardoso, A. Comparison of Precipitation Datasets over the Tropical South American and African Continents. J. Hydrometeorol. 2009, 10, 289–299. [Google Scholar] [CrossRef]
- Zulkafli, Z.; Buytaert, W.; Onof, C.; Manz, B.; Tarnavsky, E.; Lavado, W.; Guyot, J.-L. A Comparative Performance Analysis of TRMM 3B42 (TMPA) Versions 6 and 7 for Hydrological Applications over Andean–Amazon River Basins. J. Hydrometeorol. 2014, 15, 581–592. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G.; Ronchail, J. Changes in terrestrial water storage versus rainfall and discharges in the Amazon basin. Int. J. Climatol. 2013, 33, 3029–3046. [Google Scholar] [CrossRef]
- Bendix, J.; Rollenbeck, R.; Reudenbach, C. Diurnal patterns of rainfall in a tropical Andean valley of southern Ecuador as seen by a vertically pointing K-band Doppler radar. Int. J. Climatol. 2006, 26, 829–846. [Google Scholar] [CrossRef]
- Pfafstetter, O. Classification of hydrographic basins: Coding methodology. Unpublished work. 1989. [Google Scholar]
- Bourrel, L.; Melo, P.; Vera, A.; Pombosa, R.; Guyot, J.L. Study of the erosion risks of the Ecuadorian Pacific coast under the influence of ENSO phenomenom: Case of the Esmeraldas and Guayas basins. In Proceedings of the International Conference on the Status and Future of the World’s Large Rivers, Vienna, Austria, 11–14 April 2011; pp. 11–14. [Google Scholar]
- Frappart, F.; Bourrel, L.; Brodu, N.; Riofrío Salazar, X.; Baup, F.; Darrozes, J.; Pombosa, R. Monitoring of the Spatio-Temporal Dynamics of the Floods in the Guayas Watershed (Ecuadorian Pacific Coast) Using Global Monitoring ENVISAT ASAR Images and Rainfall Data. Water 2017, 9, 12. [Google Scholar] [CrossRef]
- Bourrel, L.; Rau, P.; Dewitte, B.; Labat, D.; Lavado, W.; Coutaud, A.; Vera, A.; Alvarado, A.; Ordoñez, J. Low-frequency modulation and trend of the relationship between ENSO and precipitation along the northern to centre Peruvian Pacific coast. Hydrol. Process. 2014, 29, 1252–1266. [Google Scholar] [CrossRef]
- Rau, P.; Bourrel, L.; Labat, D.; Melo, P.; Dewitte, B.; Frappart, F.; Lavado, W.; Felipe, O. Regionalization of rainfall over the Peruvian Pacific slope and coast. Int. J. Climatol. 2016. [Google Scholar] [CrossRef]
- Brunet Moret, Y. Homogénéisation des précipitations. ORSTOM 1979, XVI, 147–170. [Google Scholar]
- Cressie, N.; Johannesson, G. Fixed rank kriging for very large spatial data sets. J. R. Stat. Soc. Ser. B Stat. Methodol. 2008, 70, 209–226. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E.; others Hole-filled SRTM for the globe Version 4. Available CGIAR-CSI SRTM 90m Database Httpsrtm Csi Cgiar Org. 2008. Available online: http://www.cgiar-csi.org/data/srtm-90m-digital-elevation-database-v4-1 (accessed on 15 May 2017).
- Hijmans, R.J.; van Etten, J. Raster: Geographic data analysis and modeling. R Package Version 2014, 2, 15. [Google Scholar]
- Pebesma, E. spacetime : Spatio-Temporal Data in R. J. Stat. Softw. 2012, 51, 1–30. [Google Scholar] [CrossRef]
- Hiemstra, P.; Hiemstra, M.P. Package “automap”. Compare 2013, 105, 10. [Google Scholar]
- Schuurmans, J.M.; Bierkens, M.F.P.; Pebesma, E.J.; Uijlenhoet, R. Automatic Prediction of High-Resolution Daily Rainfall Fields for Multiple Extents: The Potential of Operational Radar. J. Hydrometeorol. 2007, 8, 1204–1224. [Google Scholar] [CrossRef]
- Buytaert, W.; Celleri, R.; Willems, P.; De Bièvre, B.; Wyseure, G. Spatial and temporal rainfall variability in mountainous areas: A case study from the south Ecuadorian Andes. J. Hydrol. 2006, 329, 413–421. [Google Scholar] [CrossRef]
- Diodato, N. The influence of topographic co-variables on the spatial variability of precipitation over small regions of complex terrain. Int. J. Climatol. 2005, 25, 351–363. [Google Scholar] [CrossRef]
- Mourre, L.; Condom, T.; Junquas, C.; Lebel, T.; Sicart, J.E.; Figueroa, R.; Cochachin, A. Spatio-temporal assessment of WRF, TRMM and in situ precipitation data in a tropical mountain environment (Cordillera Blanca, Peru). Hydrol. Earth Syst. Sci. 2016, 20, 125–141. [Google Scholar] [CrossRef]
- Cressman, G.P. An Operational Objective Analysis System. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Mitchell, T.P.; Wallace, J.M. The annual cycle in equatorial convection and sea surface temperature. J. Clim. 1992, 5, 1140–1156. [Google Scholar] [CrossRef]
- Schneider, U.; Ziese, M.; Meyer-Christoffer, A.; Finger, P.; Rustemeier, E.; Becker, A. The new portfolio of global precipitation data products of the Global Precipitation Climatology Centre suitable to assess and quantify the global water cycle and resources. Proc. Int. Assoc. Hydrol. Sci. 2016, 374, 29–34. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations–the CRU TS3. 10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T. TRMM and Other Data Precipitation Data Set Documentation; TRMM 3B423B43 Doc; NASA: Greenbelt, MD, USA, 2015; pp. 1–44. [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Phil. Trans. R. Soc. A 2016, 374. [Google Scholar] [CrossRef] [PubMed]
- Preisendorfer, R.W.; Mobley, C.D. Principal Component Analysis in Meteorology and Oceanography; Elsevier: Amsterdam, The Netherlands, 1988; Volume 425. [Google Scholar]
- Southern Oscillation Index (SOI) | Teleconnections | National Centers for Environmental Information (NCEI). Available online: https://www.ncdc.noaa.gov/teleconnections/enso/indicators/soi/ (accessed on 27 July 2017).
- Null, J. El Nino and La Nina Years and Intensities Based on Oceanic Nino index (ONI); NOAA: Silver Spring, MD, USA, 2015.
- Huang, B.; Banzon, V.F.; Freeman, E.; Lawrimore, J.; Liu, W.; Peterson, T.C.; Smith, T.M.; Thorne, P.W.; Woodruff, S.D.; Zhang, H.-M. Extended reconstructed sea surface temperature version 4 (ERSST. v4). Part I: Upgrades and intercomparisons. J. Clim. 2015, 28, 911–930. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.I.F.; Allan, R.P.; Greatrex, H.; Rojas, O.; Leo, O. Evaluation of satellite-based and model re-analysis rainfall estimates for Uganda. Meteorol. Appl. 2013, 20, 308–317. [Google Scholar] [CrossRef]
- Norina, A.; Vegas, F.; Lavado, C. Zappa water resources and climate change impact modelling on a daily time scale in the Peruvian Andes. Hydrol. Sci. J. 2014, 59, 2043–2059. [Google Scholar] [CrossRef]
- Ballari, D.; Castro, E.; Campozano, L. Validation of Satellite Precipitation (TRMM 3B43) in Ecuadorian Coastal Plains, Andean Highlands and Amazonian Rainforest. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 305–311. [Google Scholar]
- Satgé, F.; Bonnet, M.-P.; Gosset, M.; Molina, J.; Lima, W.H.Y.; Zolá, R.P.; Timouk, F.; Garnier, J. Assessment of satellite rainfall products over the Andean plateau. Atmos. Res. 2016, 167, 1–14. [Google Scholar] [CrossRef]
- Manz, B.; Buytaert, W.; Zulkafli, Z.; Lavado, W.; Willems, B.; Robles, L.A.; Rodríguez-Sánchez, J.-P. High-resolution satellite-gauge merged precipitation climatologies of the Tropical Andes. J. Geophys. Res. Atmos. 2016. [Google Scholar] [CrossRef]
- Dinku, T.; Connor, S.J.; Ceccato, P. Comparison of CMORPH and TRMM-3B42 over mountainous regions of Africa and South America. In Satellite Rainfall Applications for Surface Hydrology; Springer: Berlin, Germany, 2010; pp. 193–204. [Google Scholar]
- Espinoza, J.C.; Chavez, S.; Ronchail, J.; Junquas, C.; Takahashi, K.; Lavado, W. Rainfall hotspots over the southern tropical Andes: Spatial distribution, rainfall intensity, and relations with large-scale atmospheric circulation. Water Resour. Res. 2015, 51, 3459–3475. [Google Scholar] [CrossRef]
- Levizzani, V.; Amorati, R.; Meneguzzo, F. A Review of Satellite-Based Rainfall Estimation Methods. In MUSIC–MUltiple-Sensor Precipitation Measurements, Integration, Calibration and Flood Forecasting; European Commission: Brussels, Belgium, 2002; Volume 70. [Google Scholar]
- Mätzler, C.; Standley, A. Technical note: Relief effects for passive microwave remote sensing. Int. J. Remote Sens. 2000, 21, 2403–2412. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling errors in the estimation of empirical orthogonal functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Bendix, J.; Rollenbeck, R.; Göttlicher, D.; Cermak, J. Cloud occurrence and cloud properties in Ecuador. Clim. Res. 2006, 30, 133–147. [Google Scholar] [CrossRef]
- Diaz, H.F.; Markgraf, V. El Niño and the Southern Oscillation: Multiscale Variability and Global and Regional Impacts; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Campozano, L.; Célleri, R.; Trachte, K.; Bendix, J.; Samaniego, E. Rainfall and Cloud Dynamics in the Andes: A Southern Ecuador Case Study. Adv. Meteorol. 2016, 2016. [Google Scholar] [CrossRef]
- Philander, S.G.H.; El Niño, L.N. The Southern Oscillation; Academic Press: San Diego, CA, USA, 1990; pp. 904–905. [Google Scholar]
- Schneider, T.; Bischoff, T.; Haug, G.H. Migrations and dynamics of the intertropical convergence zone. Nature 2014, 513, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Arteaga, K.; Tutasi, P.; Jiménez, R. Climatic variability related to El Niño in Ecuador? A historical background. Adv. Geosci. 2006, 6, 237–241. [Google Scholar] [CrossRef]
- Dai, A.; Wigley, T.M.L. Global patterns of ENSO-induced precipitation. Geophys. Res. Lett. 2000, 27, 1283–1286. [Google Scholar] [CrossRef]
- Iguchi, T.; Kozu, T.; Meneghini, R.; Awaka, J.; Okamoto, K. Rain-profiling algorithm for the TRMM precipitation radar. J. Appl. Meteorol. 2000, 39, 2038–2052. [Google Scholar] [CrossRef]
- Rasmussen, K.L.; Choi, S.L.; Zuluaga, M.D.; Houze, R.A. TRMM precipitation bias in extreme storms in South America. Geophys. Res. Lett. 2013, 40, 3457–3461. [Google Scholar] [CrossRef]
- Nastos, P.T.; Kapsomenakis, J.; Philandras, K.M. Evaluation of the TRMM 3B43 gridded precipitation estimates over Greece. Atmos. Res. 2016, 169, 497–514. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN system satellite–based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Islam, M.N.; Uyeda, H. Use of TRMM in determining the climatic characteristics of rainfall over Bangladesh. Remote Sens. Environ. 2007, 108, 264–276. [Google Scholar] [CrossRef]
- Stano, G.; Krishnamurti, T.N.; Kumar, T.V.; Chakraborty, A. Hydrometeor structure of a composite monsoon depression using the TRMM radar. Tellus A 2002, 54, 370–381. [Google Scholar] [CrossRef]
- Lau, K.M.; Wu, H.T. Warm rain processes over tropical oceans and climate implications. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Connor, S.J. Challenges of satellite rainfall estimation over mountainous and arid parts of east Africa. Int. J. Remote Sens. 2011, 32, 5965–5979. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).