Water Resources and Sustainability Assessment Based on Group AHP-PCA Method: A Case Study in the Jinsha River Basin
Abstract
1. Introduction
2. Methodology
2.1. Selection of Indicators
2.2. Group Analytic Hierarchy Process (AHP)
2.3. Principal Component Analysis (PCA)
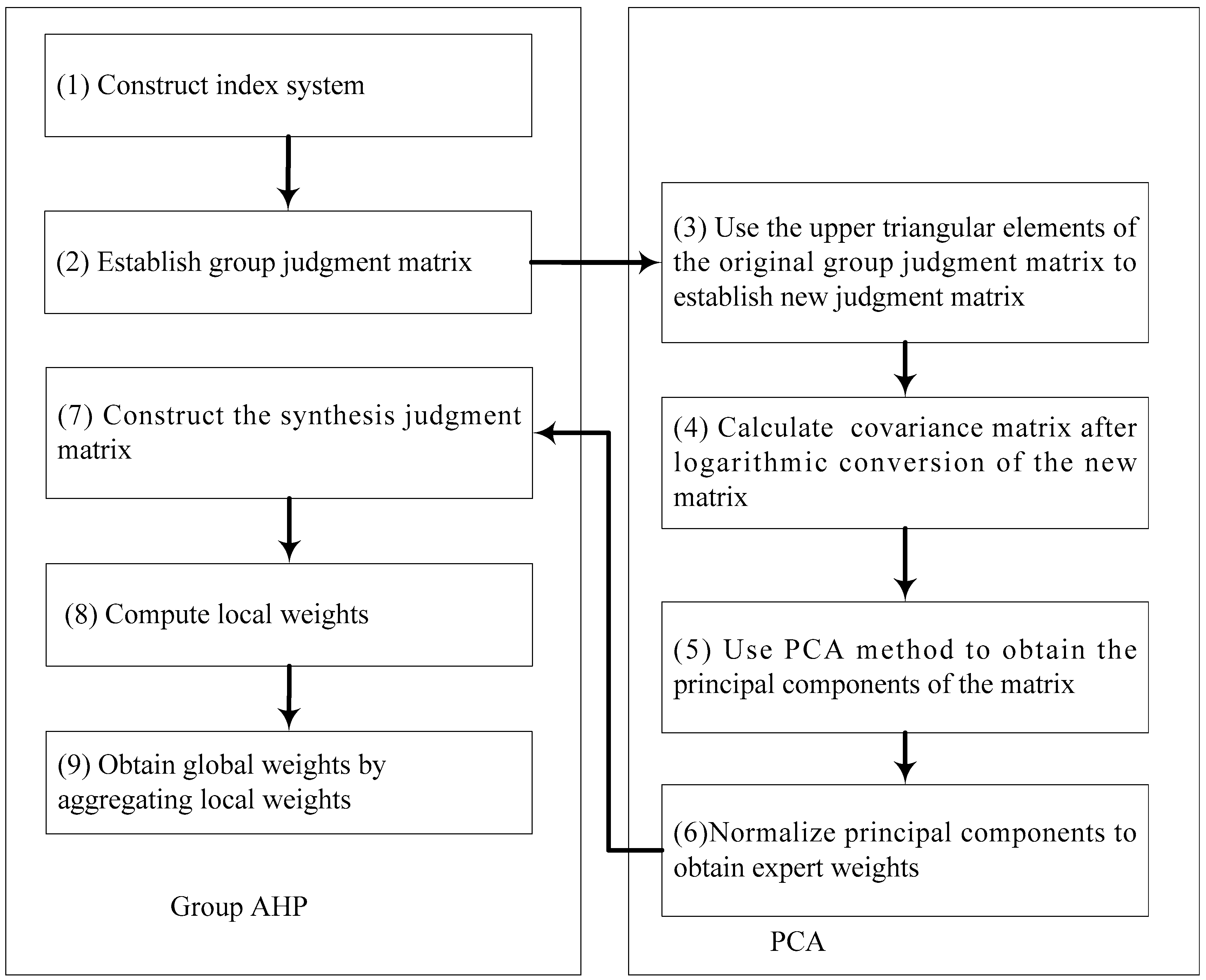
2.4. The Group AHP-PCA
3. Case Study
3.1. Study Area
3.2. Data Collection
3.3. Survey
3.4. Application in the Jinsha River Basin Sustainability Assessment
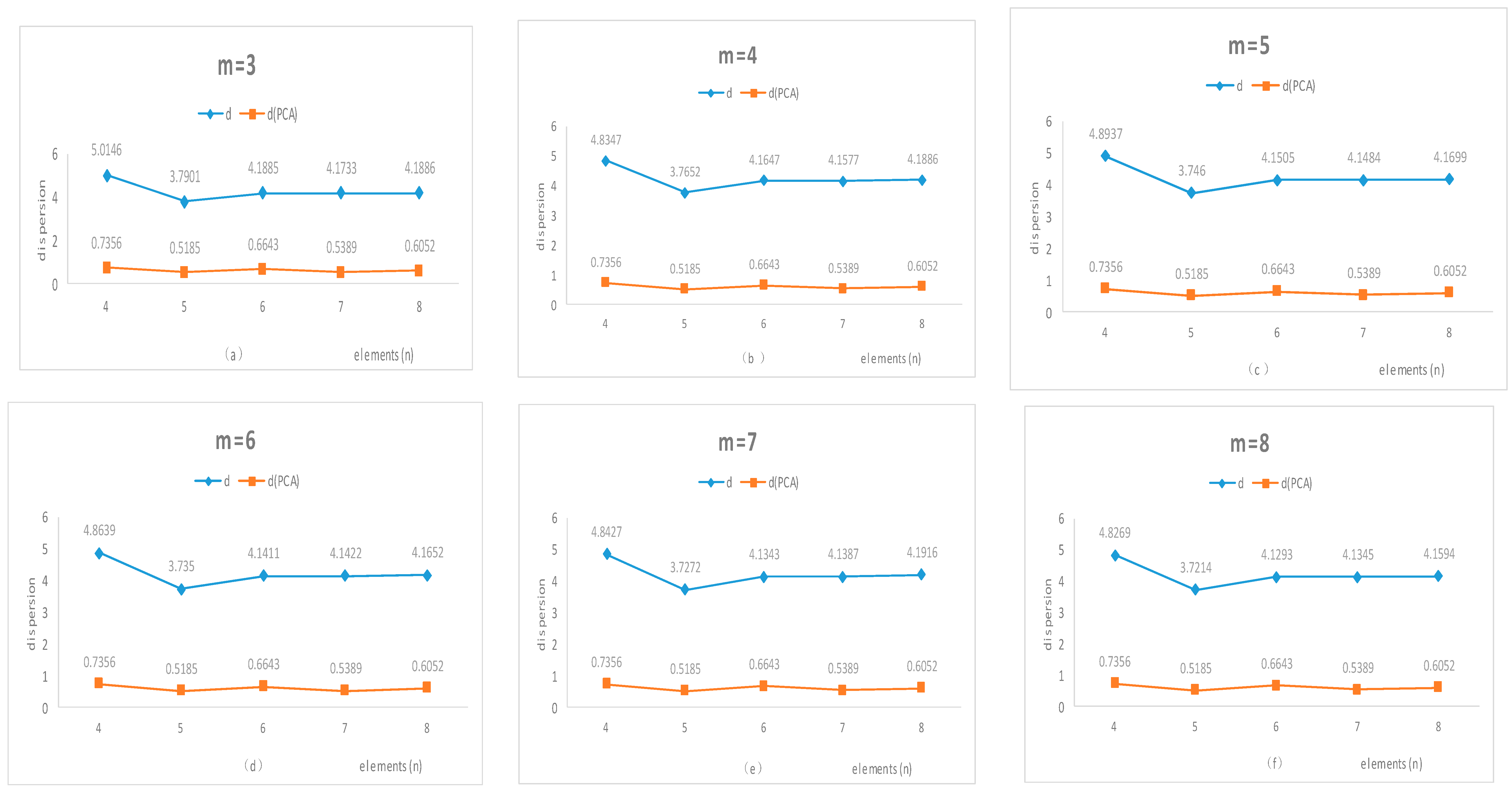
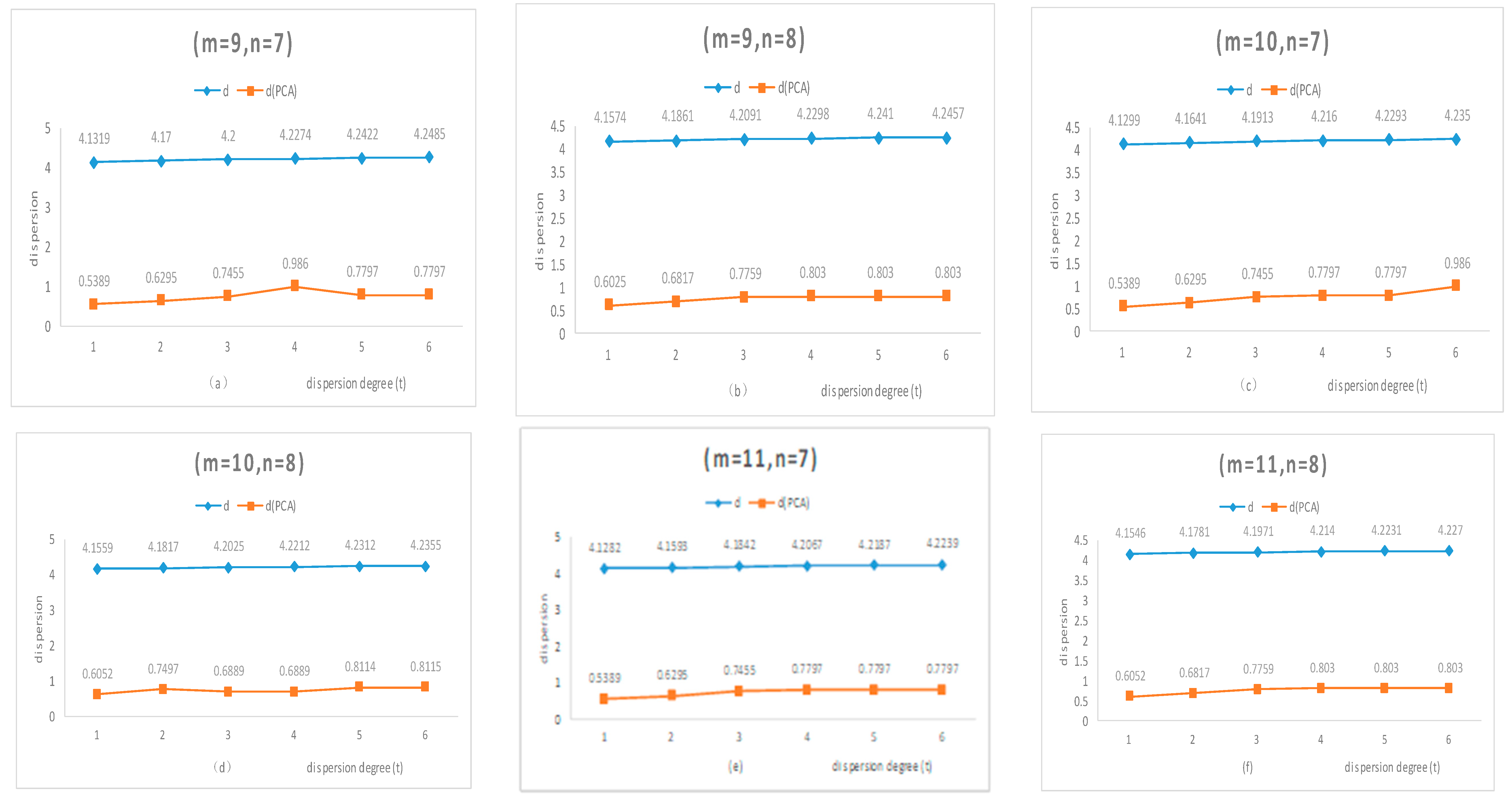
4. Dispersion-Based Simulation
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
| Indicators | Data Sources | Website Remarks |
|---|---|---|
| SWQ | http://www.schj.gov.cn/ | Four provincial environmental protection offices |
| http://www.ynepb.gov.cn/ | ||
| http://www.qhepb.gov.cn/ | ||
| http://www.xzep.gov.cn/ | ||
| EC | http://www.stats.gov.cn/ | National Bureau of Statistic of China |
| GQ | http://www.schj.gov.cn/ | Four provincial environmental protection offices |
| http://www.ynepb.gov.cn/ | ||
| http://www.qhepb.gov.cn/ | ||
| http://www.xzep.gov.cn/ | ||
| EL | http://www.stats.gov.cn/ | National Bureau of Statistic of China |
| ICE | ||
| IWR | ||
| WS | ||
| IWU | http://www.mwr.gov.cn/ | Ministry of Water Resources of China |
| SC | http://www.stats.gov.cn/ | National Bureau of Statistic of China |
| PWSC | ||
| IFM | ||
| AWU | http://www.mwr.gov.cn/ | Ministry of Water Resources of China |
| WQM | http://www.stats.gov.cn/ | National Bureau of Statistic of China |
| SWR | http://www.mwr.gov.cn/ | Ministry of Water Resources of China |
| WI | http://www.stats.gov.cn/ | National Bureau of Statistic of China |
| EB |
| Indicators | Unit | Sichuan | Yunnan | Qinghai | Tibet |
|---|---|---|---|---|---|
| SWQ | Compliance rate | 87.41% | 96.8% | 91% | 100% |
| EC | Area classified as the ‘1st’ grade on the eco-nature index/total area | 17.21% | 7.3% | 31.27% | 33.9% |
| GQ | Compliance rate | 100% | 100% | 100% | 100% |
| EL | Number of persons graduated from high school/population | 0.0060 | 0.0052 | 0.0064 | 0.0060 |
| ICE | Investment amount/population (Yuan per person) | 701 | 920 | 1086 | 1192 |
| IWR | Investment amount/total area (Yuan/hectare) | 12242 | 9098 | 891 | 484 |
| WS | Water saving irrigation area/population (hectare per person) | 3.41 | 3.79 | 3.41 | 7.60 |
| IWU | Billion /total industrial water use × 100 | 68.89 | 26.05 | 3.21 | 1.85 |
| SC | Sewage discharge/population number ( per person) | 42.70 | 37.96 | 46.00 | 18.56 |
| PWSC | /per person | 2843.31 | 4391.67 | 10375.95 | 141746.56 |
| IFM | Reservoir capacity /population number ( per person) | 785 | 88 | 34 | 11 |
| AWU | Area of irrigated paddy fields/total paddy fields × 100 | 155.90 | 105.20 | 19.90 | 26.90 |
| WQM | Achievement rate of objective water quality/annual product per person | 77% | 75% | 74% | 90% |
| SWR | Billion /population number ( per person) | 7.02 | 5.87 | 18.55 | 9.06 |
| WI | Amount of annual water intake/annual product per person (/Yuan) | 573 | 673 | 141 | 1335 |
| EB | Billions of kilowatt-hours/population number (kilowatt-hours per person) | 3452 | 4775 | 5073 | 1474 |
Appendix C. Questionnaire Survey
| The survey was designed and conducted to determine indicator weights and importance priorities for assessment topics. We are researchers from Huazhong University of Science and Technology, Wuhan, China. We would like to know your attitude towards the elements of water resources and sustainability assessment. Tick in the box after the option you want. |
| 1. Gender Male Female |
| 2. What is your name |
| 3. What is your major occupation? : (a). Manager in environmental conservation; (b). Professor in water resources management; (c). Researcher in social equity; (d). Researcher in water resources development; (e). Professor in economics; (f). Other |
| 4. For how long have you been in your job?: (a) 1–15 years; (b) 16–30 years; (c) 31 years and above |
| 5. What is your level of education?: (a). Master; (b) Doctor; (c) Bachelor; (d) Other |
| 6. You are asked to make comparative judgements on the relative importance of each pair of criteria below. A 9-point scale for measuring the relative importance of each criteria is adopted here for the pairwise comparison. 1 represents equal importance, 3 represents weak importance, 5 represents essential or strong importance, 7 represents demonstrated importance, 9 represents absolute importance.2, 4, 6 and 8 are intermediate values between the two adjacent judgements. Reciprocal values are assigned for each reversed pairwise comparison. |
| Environmental conservation and maintenance capacity: (a). 1 2 3 4 5 6 7 8 9 |
| Environmental conservation and social equity: (a). 1 2 3 4 5 6 7 8 9 |
| Environmental conservation and economic efficiency: (a). 1 2 3 4 5 6 7 8 9 |
| Maintenance capacity and social equity: (a). 1 2 3 4 5 6 7 8 9 |
| Maintenance capacity and economic efficiency: (a). 1 2 3 4 5 6 7 8 9 |
| Economic efficiency: (a). 1 2 3 4 5 6 7 8 9 |
| 8. You are asked to make comparative judgements on the relative importance of each pair of indicators below by 9-points scale (the indicators part of questionnaire is shown partly as below for word limitation). |
| Surface water quality and groundwater quality: (a). 1 2 3 4 5 6 7 8 9 |
| Surface water quality and ecosystem conservation: (a). 1 2 3 4 5 6 7 8 9 |
| Groundwater quality and ecosystem conservation: (a). 1 2 3 4 5 6 7 8 9 |
| Education level and investment in culture and education: (a). 1 2 3 4 5 6 7 8 9 |
| Education level and investment in water resources: (a). 1 2 3 4 5 6 7 8 9 |
| Education level and water saving: (a). 1 2 3 4 5 6 7 8 9 |
| Investment in culture and education and investment in water resources: (a). 1 2 3 4 5 6 7 8 9 |
| Investment in culture and education and water saving: (a). 1 2 3 4 5 6 7 8 9 |
| Investment in water resources and water saving: (a). 1 2 3 4 5 6 7 8 9 |
| Do you have other suggestions about indicators of water resources and sustainability assessment? |
| Thank you for your cooperation. |
References
- Wouters, P.; Rieu-Clarke, A. Sustainability criteria for water resource systems. Resour. Policy 2001, 27, 139–140. [Google Scholar] [CrossRef]
- Abadi, L.S.K.; Shamsai, A.; Goharnejad, H. An Analysis of the Sustainability of Basin Water Resources using Vensim Model. KSCE J. Civ. Eng. 2015, 19, 1941–1949. [Google Scholar] [CrossRef]
- Milman, A.; Short, A. Incorporating resilience into sustainability indicators: An example for the urban water sector. Glob. Environ. Chang. 2008, 18, 758–767. [Google Scholar] [CrossRef]
- Sun, S.K.; Wang, Y.B.; Liu, J.; Cai, H.J.; Wu, P.T.; Geng, Q.L.; Xu, L.J. Sustainability assessment of regional water resources under the DPSIR framework. J. Hydrol. 2016, 532, 140–148. [Google Scholar] [CrossRef]
- Juwana, I.; Muttil, N.; Perera, B.J.C. Indicator-based water sustainability assessment—A review. Sci. Total Environ. 2012, 438, 357–371. [Google Scholar] [CrossRef] [PubMed]
- Koop, S.H.A.; Cornelis, J.; Leeuwen, V. Assessment of the Sustainability of Water Resources Management: A Critical Review of the City Blueprint Approach. Water Resour. Manag. 2015, 29, 5649–5670. [Google Scholar] [CrossRef]
- Giacomoni, M.H.; Berglund, E.Z. Complex Adaptive Modeling Framework for Evaluating Adaptive Demand Management for Urban Water Resources Sustainability. J. Water Resour. Plan. Manag. 2015, 141, 04015024. [Google Scholar] [CrossRef]
- Xu, Z.X.; Takeuchi, K.; Ishidaira, H.; Zhang, X.W. Sustainability Analysis for Yellow River Water Resources Using the System Dynamics Approach. Water Resour. Manag. 2002, 16, 239–261. [Google Scholar] [CrossRef]
- Zeng, X.T.; Li, Y.P.; Huang, G.H.; Liu, J. Modeling of Water Resources Allocation and Water Quality Management for Supporting Regional Sustainability under Uncertainty in an Arid Region. Water Resour. Manag. 2017, 31, 3699–3721. [Google Scholar] [CrossRef]
- Peterson, H.M.; Nieber, J.L.; Kanivetsky, R.; Shmagin, B. Water Resources Sustainability Indicator: Application of the Watershed Characteristics Approach. Water Resour. Manag. 2013, 27, 1221–1234. [Google Scholar] [CrossRef]
- Hernandez-Bedolla, J.; Solera, A.; Paredes-Arquiola, J.; Pedro-Monzonis, M.; Andreu, J.; Sánchez-Quispe, S.T. The Assessment of Sustainability Indexes and Climate Change Impacts on Integrated Water Resource Management. Water 2017, 9, 213. [Google Scholar] [CrossRef]
- Ni, X.; Wu, Y.Q.; Wu, J.; Lu, J.; Wilson, P.C. Scenario analysis for sustainable development of Chongming Island: Water resources sustainability. Sci. Total Environ. 2012, 439, 129–135. [Google Scholar] [CrossRef] [PubMed]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Awang, A.; Ghani, A.T.A.; Abdullah, L.; Ahmad, M.F. Global Weights of Coastal Erosion Risk indicators using AHP Method: A Case Study of Setiu Wetlands. Natl. Symp. Math. Sci. 2017, 24, 050014. [Google Scholar]
- Ishizaka, A.; Labib, A. Review of the main developments in the analytic hierarchy process. Expert Syst. Appl. 2011, 38, 14336–14345. [Google Scholar] [CrossRef]
- Kang, M.G.; Lee, G.M. Multicriteria Evaluation of Water Resources Sustainability in the Context of Watershed Management. J. Am. Water Resour. Assoc. 2011, 47, 813–827. [Google Scholar] [CrossRef]
- Shi, S.G.; Cao, J.C.; Feng, L.; Liang, W.Y.; Zhang, L.Q. Construction of a technique plan repository and evaluation system based on AHP group decision-making for emergency treatment and disposal in chemical pollution accidents. J. Hazard. Mater. 2014, 276, 200–206. [Google Scholar] [CrossRef]
- Dragincic, J.; Milica, V. AHP Based Group Decision Making Approach to Supplier Selection of Irrigation Equipment. Water Res. 2013, 41, 782–791. [Google Scholar] [CrossRef]
- Akaa, O.U.; Abu, A.; Spearpoint, M.; Giovinazzi, S. A group-AHP decision analysis for the selection of applied fire protection to steel structures. Fire Saf. J. 2016, 86, 95–105. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Dispersion of group judgments. Math. Comput. Model. 2007, 46, 918–925. [Google Scholar] [CrossRef]
- Lin, S.W.; Lu, M.T. Characterizing disagreement and inconsistency in experts’ judgments in the analytic hierarchy process. Manag. Decis. 2012, 50, 1253–1265. [Google Scholar] [CrossRef]
- Palese, L.L. A random version of principal component analysis in data clustering. Comput. Biol. Chem. 2018, 73, 57–64. [Google Scholar] [CrossRef]
- Yang, L.W.; Eyal, E.; Bahar, I.; Kitao, A. Principal component analysis of native ensembles of biomolecular structures (PCA_NEST): Insights into functional dynamics. Bioinformatics 2009, 25, 606–614. [Google Scholar] [CrossRef] [PubMed]
- Bro, R.; Smilde, A.K. Principle component analysis. Anal. Methods 2014, 6, 2812–2831. [Google Scholar] [CrossRef]
- Zheng, X.Q.; Nie, Y.; Gao, Y.; Huang, B.; Ye, J.H.; Lu, J.L.; Liang, Y.R. Screening the cultivar and processing indicators based on the flavonoid profiles of dry teas using principal component analysis. J. Food Compos. Anal. 2018, 67, 29–37. [Google Scholar] [CrossRef]
- Longo, A.; Federolf, P.; Haid, T.; Meulenbroek, R. Effects of a cognitive dual task on variability and local dynamic stability in sustained repetitive arm movements using principal component analysis: A pilot study. Exp. Brain Res. 2018, 4, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.Y.; Zhou, J.L.; Gan, L.F. Safety assessment in oil drilling work system based on empirical study and Analytic Network Process. Saf. Sci. 2018, 105, 86–97. [Google Scholar] [CrossRef]
- Perez, M.; Tujchneide, O.; Paris, M.; Ela, M.D. Sustainability indicators of groundwater resources in the central area of Santa Fe province, Argentina. Environ. Earth Sci. 2015, 73, 2671–2682. [Google Scholar] [CrossRef]
- Bradfor, A. An ecological flow assessment framework: Building a bridge to implementation in Canada. Can. Water Res. J. 2008, 33, 215–232. [Google Scholar] [CrossRef]
- Spiller, M. Adaptive capacity indicators to assess sustainability of urban water systems—Current application. Sci. Total Environ. 2016, 569, 751–761. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Bai, M.H.; Zhou, S.B.; Zhao, M. Agricultural Water Use Sustainability Assessment in the Tarim River Basin under Climatic Risks. Water 2018, 10, 170. [Google Scholar] [CrossRef]
- Henriksen, H.J.; Troldborg, L.; Højberg, A.L.; Refsgaard, J.C. Assessment of exploitable groundwater resources of Denmark by use of ensemble resource indicators and a numerical groundwater–surface water model. J. Hydrol. 2007, 348, 224–240. [Google Scholar] [CrossRef]
- Ercin, E.; Mekonnen, M.M.; Hoekstra, A.Y. Sustainability of national consumption from a water resources perspective: The case study for France. Ecol. Econ. 2013, 88, 133–147. [Google Scholar] [CrossRef]
- Hoekstra, A.Y. The global dimension of water governance: Why the river basin approach is no longer sufficient and why cooperative action at global level is needed. Water 2011, 3, 21–46. [Google Scholar] [CrossRef]
- Pellicer-Martinez, F.; Marnez-Paz, J.M. The Water Footprint as an indicator of environmental sustainability in water use at the river basin level. Sci. Total Environ. 2017, 571, 561–574. [Google Scholar] [CrossRef]
- Almazán-Gómez, M.Á.; Sánchez-Chóliz, J.; Sarasa, C. Environmental flow management: An analysis applied to the Ebro River Basin. J. Clean. Prod. 2018, 182, 838–851. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic Hierarchy Process: An Overview of Applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Guo, J.W.; Zhou, M.C.; Li, Z.W.; Xie, H.G. Green design assessment of electromechanical products based on group weighted-AHP. Enterp. Inf. Syst. 2015, 9, 878–899. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis; Springer: New York, NY, USA, 2002; pp. 10–28. [Google Scholar]
- Quiroga, J.; Mujica, L.; Villamizar, R.; Ruiz, M.; Camacho, J. PCA Based Stress Monitoring of Cylindrical Specimens Using PZTs and Guided Waves. Sensors 2017, 17, 2788. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Song, M.B.; Li, T.X.; Chen, J.Q. Preliminary Analysis on Rainfall Runoff Features of Jinsha River Watershed. Procedia Eng. 2012, 28, 688–695. [Google Scholar]
- Lidinska, L.; Jablonsky, J. AHP model for performance evaluation of employees in a Czech management consulting company. CEJOR 2018, 26, 239–258. [Google Scholar] [CrossRef]
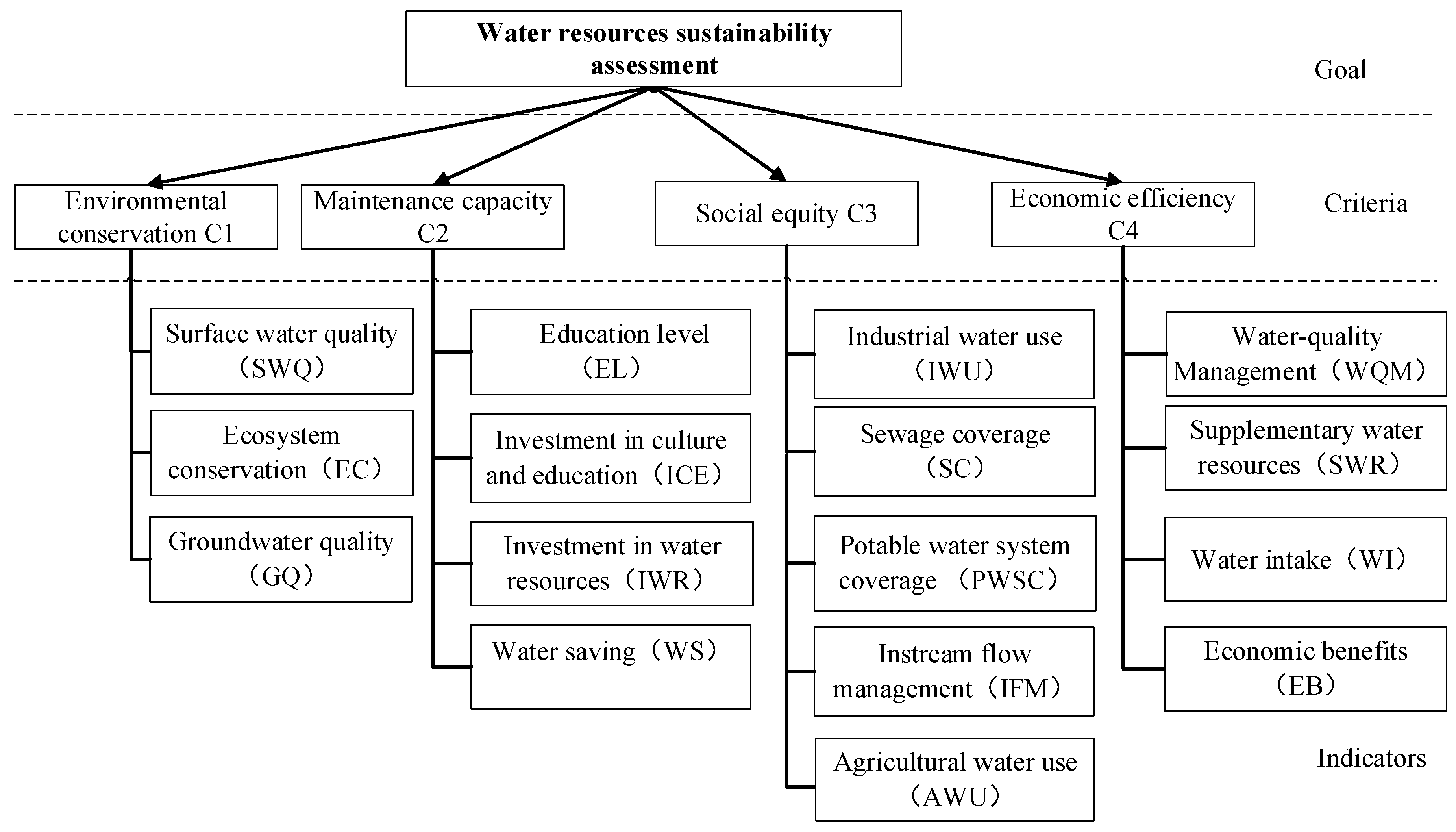
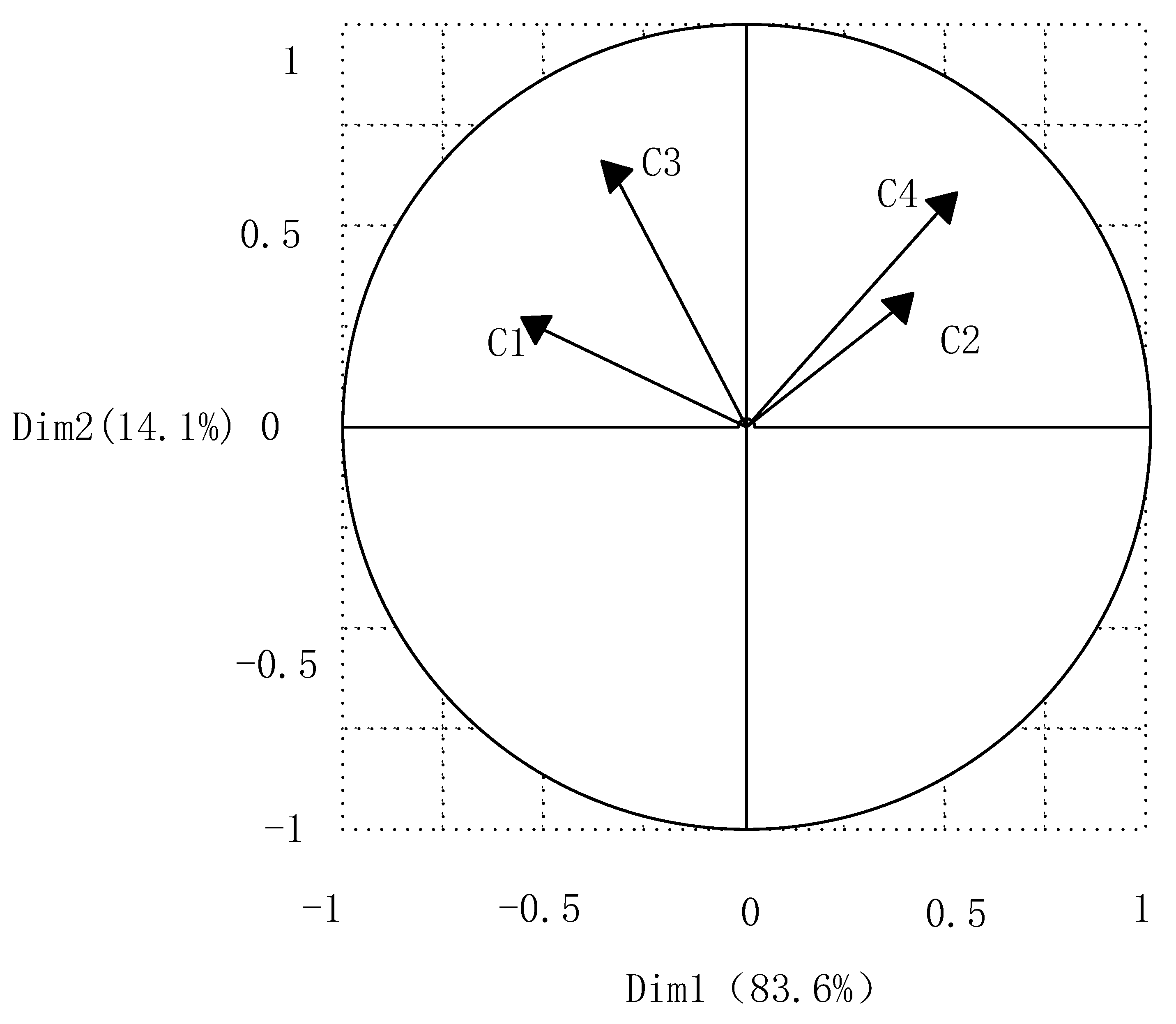
| Criteria | Indicators | Computational Expressions |
|---|---|---|
| Environmental conservation | Surface water quality (SWQ) | Integration of items representing surface water quality |
| Groundwater quality (GQ) | Integration of items representing groundwater quality | |
| Ecosystem conservation (EC) | Integration of items representing groundwater quality | |
| Maintenance capacity | Education level (EL) | Number of persons graduated from high school/population |
| Investment in culture and education (ICE) | Amount of investment in culture and education/population | |
| Investment in water resources (IWR) | Amount of investment in water resources/total area | |
| Water saving (WS) | Amount of water saved/population | |
| Social equity | Industrial water use (IWU) | Industrial water use in a watershed/total industrial water use × 100 |
| Sewage coverage (SC) | Number of persons using sewage/population × 100 | |
| Potable water system coverage (PWSC) | Number of persons using potable water system/population × 100 | |
| Instream flow management (IFM) | Reservoir capacity/population | |
| Agricultural water use (AWU) | Area of irrigated paddy fields/total paddy fields × 100 | |
| Economic efficiency | Water-quality management (WQM) | Achievement rate of objective water quality/annual product per person |
| Supplementary water resources (SWR) | Amount of supplementary water resources/population | |
| Water intake (WI) | Amount of annual water intake/annual product per person | |
| Economic benefits (EB) | Annual economic benefits from water resources/population |
| Numerical Values | Definition |
|---|---|
| 1 | Index is as important as index |
| 3 | Index is slightly more important than index |
| 5 | Index is obviously more important than index |
| 7 | Index is strongly more important than index |
| 9 | Index is extremely more important than index |
| 2, 4, 6, 8 | Middle value of the above adjacent judgments |
| A | x1 | x2 | … | xn |
| x1 | 1 | … | ||
| x2 | 1 | … | ||
| … | … | … | … | … |
| xn | … | 1 |
| ID | Gender | Working Seniority | Profession | Education |
|---|---|---|---|---|
| 1 | Male | 15 | Manager in environmental conservation | Master |
| 2 | Female | 10 | Professor in water resources management | Doctor |
| 3 | Male | 17 | Researcher in social equity | Bachelor |
| 4 | Female | 15 | Researcher in water resources development | Master |
| 5 | Male | 20 | Professor in economics | Doctor |
| C1 | C2 | C3 | C4 | |
| C1 | 1 | |||
| C2 | 1 | |||
| C3 | 1 | |||
| C4 | 1 |
| C1 | C2 | C3 | C4 | Weight | |
| C1 | |||||
| C2 | |||||
| C3 | |||||
| C4 |
| Criteria | Weights (Group AHP-PCA) | Weights (Group AHP) | Indicators | Global Weights (Group AHP-PCA) | Rank (Group AHP-PCA) | Global Weights (Group AHP) | Rank (Group AHP) |
|---|---|---|---|---|---|---|---|
| Environmental conservation | 0.4449 | 0.4026 | SWQ | 0.2167 | 1 | 0.2537 | 1 |
| EC | 0.0387 | 8 | 0.1167 | 3 | |||
| GQ | 0.1121 | 3 | 0.0539 | 7 | |||
| Maintenance capacity | 0.0883 | 0.1027 | EL | 0.0083 | 16 | 0.0089 | 16 |
| ICE | 0.0230 | 12 | 0.0275 | 12 | |||
| IWR | 0.0322 | 9 | 0.0327 | 9 | |||
| WS | 0.0249 | 11 | 0.0303 | 10 | |||
| Social equity | 0.3155 | 0.2967 | IWU | 0.1215 | 2 | 0.1215 | 2 |
| SC | 0.0603 | 6 | 0.0603 | 6 | |||
| PWSC | 0.0288 | 10 | 0.0288 | 11 | |||
| IFM | 0.0138 | 14 | 0.0138 | 14 | |||
| AWU | 0.0802 | 4 | 0.0802 | 4 | |||
| Economic efficiency | 0.1513 | 0.1608 | WQM | 0.0629 | 5 | 0.0629 | 5 |
| SWR | 0.0439 | 7 | 0.0439 | 8 | |||
| WI | 0.0271 | 13 | 0.0271 | 13 | |||
| EB | 0.0129 | 15 | 0.0129 | 15 |
| Indicators | Global Weights | Sichuan | Yunnan | Qinghai | Tibet |
|---|---|---|---|---|---|
| SWQ | 0.2167 | 0.2330 | 0.2580 | 0.2425 | 0.2665 |
| EC | 0.0387 | 0.1919 | 0.0814 | 0.3487 | 0.3780 |
| GQ | 0.1121 | 0.2500 | 0.2500 | 0.2500 | 0.2500 |
| EL | 0.0083 | 0.2542 | 0.2203 | 0.2712 | 0.2542 |
| ICE | 0.0230 | 0.1798 | 0.2360 | 0.2785 | 0.3057 |
| IWR | 0.0322 | 0.5390 | 0.4005 | 0.0392 | 0.0213 |
| WS | 0.0249 | 0.1873 | 0.2081 | 0.1872 | 0.4174 |
| IWU | 0.1215 | 0.6889 | 0.2605 | 0.0321 | 0.0185 |
| SC | 0.0603 | 0.2940 | 0.2614 | 0.3168 | 0.1278 |
| PWSC | 0.0288 | 0.0178 | 0.0276 | 0.0651 | 0.8895 |
| IFM | 0.0138 | 0.8551 | 0.0959 | 0.0370 | 0.0120 |
| AWU | 0.0802 | 0.5063 | 0.3417 | 0.0646 | 0.0874 |
| WQM | 0.0629 | 0.2437 | 0.2373 | 0.2342 | 0.2848 |
| SWR | 0.0439 | 0.1733 | 0.1449 | 0.4580 | 0.2237 |
| WI | 0.0271 | 0.2105 | 0.2472 | 0.0518 | 0.4904 |
| EB | 0.0129 | 0.2336 | 0.3232 | 0.3434 | 0.0998 |
| Final Scores | 0.3002 | 0.2215 | 0.1799 | 0.2057 | |
| 1 | (3, 3, 3) | (5, 5, 5) | (5, 5, 5) |
| 1 | |||
| 1 | |||
| 1 |
| 1 | (3, 3, 3, 3, 3, 3, 3, 3, 3) | (5, 5, 5, 5, 5, 5, 5, 5, 5) | (7, 7, 7, 7, 7, 7, 7, 7, 7) | |||
| 1 | ||||||
| 1 | ||||||
| 1 | ||||||
| 1 | ||||||
| 1 | ||||||
| 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.-L.; Xu, Q.-Q.; Zhang, X.-Y. Water Resources and Sustainability Assessment Based on Group AHP-PCA Method: A Case Study in the Jinsha River Basin. Water 2018, 10, 1880. https://doi.org/10.3390/w10121880
Zhou J-L, Xu Q-Q, Zhang X-Y. Water Resources and Sustainability Assessment Based on Group AHP-PCA Method: A Case Study in the Jinsha River Basin. Water. 2018; 10(12):1880. https://doi.org/10.3390/w10121880
Chicago/Turabian StyleZhou, Jian-Lan, Qin-Qin Xu, and Xian-Yong Zhang. 2018. "Water Resources and Sustainability Assessment Based on Group AHP-PCA Method: A Case Study in the Jinsha River Basin" Water 10, no. 12: 1880. https://doi.org/10.3390/w10121880
APA StyleZhou, J.-L., Xu, Q.-Q., & Zhang, X.-Y. (2018). Water Resources and Sustainability Assessment Based on Group AHP-PCA Method: A Case Study in the Jinsha River Basin. Water, 10(12), 1880. https://doi.org/10.3390/w10121880






