Automated Laboratory Infiltrometer to Estimate Saturated Hydraulic Conductivity Using an Arduino Microcontroller Board
Abstract
1. Introduction
2. Materials and Methods
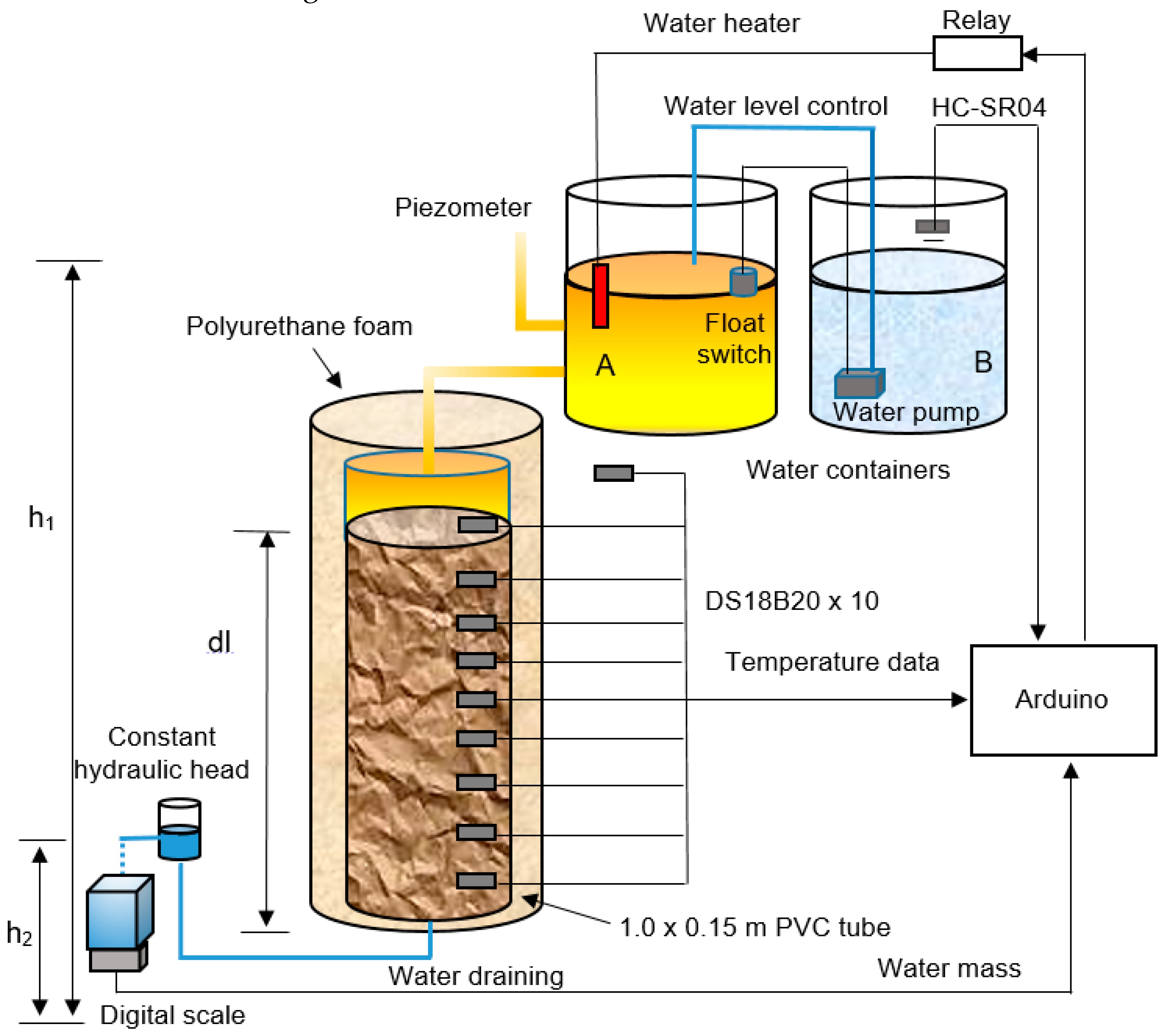
2.1. The Automated Laboratory Infiltrometer
2.2. Data Acquisition System
2.3. Drained Water Flux Rates Measurement
2.4. Water Flux Rates Determination by Measuring Infiltration Rates
2.5. Low Pass Filter
2.6. Water Flux Rates Determination by Using Temperature Time Series
2.6.1. The Heat and Fluid Transport Equation
2.6.2. Dynamic Harmonic Regression (DHR)
2.6.3. Temperature Time Series Processing
2.6.4. Soil Sample Preparation
2.7. Saturated Hydraulic Conductivity
3. Results
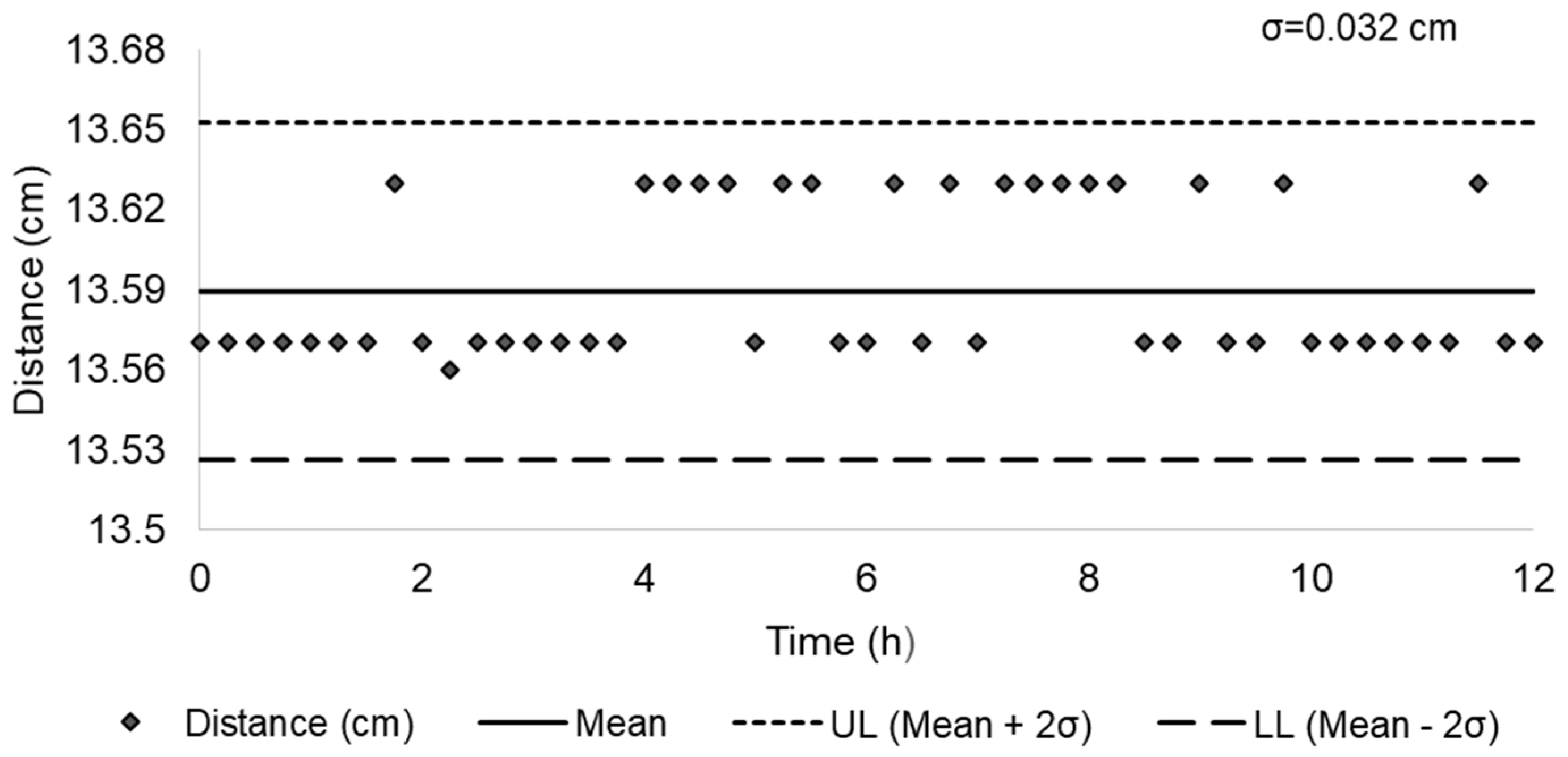
3.1. Hydraulic Boundary Conditions and Data Processing
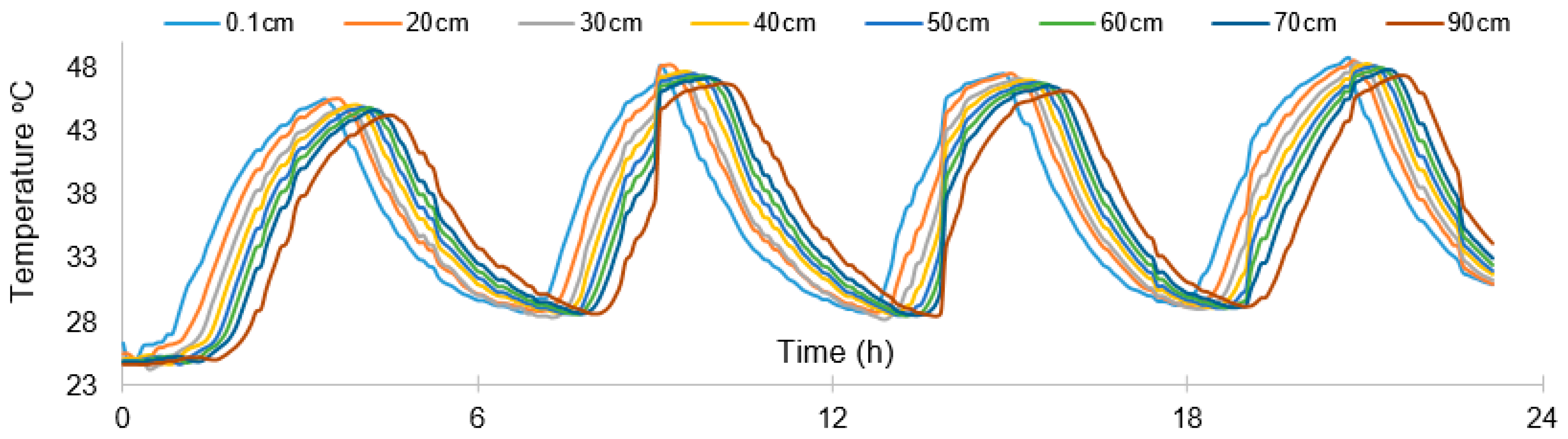
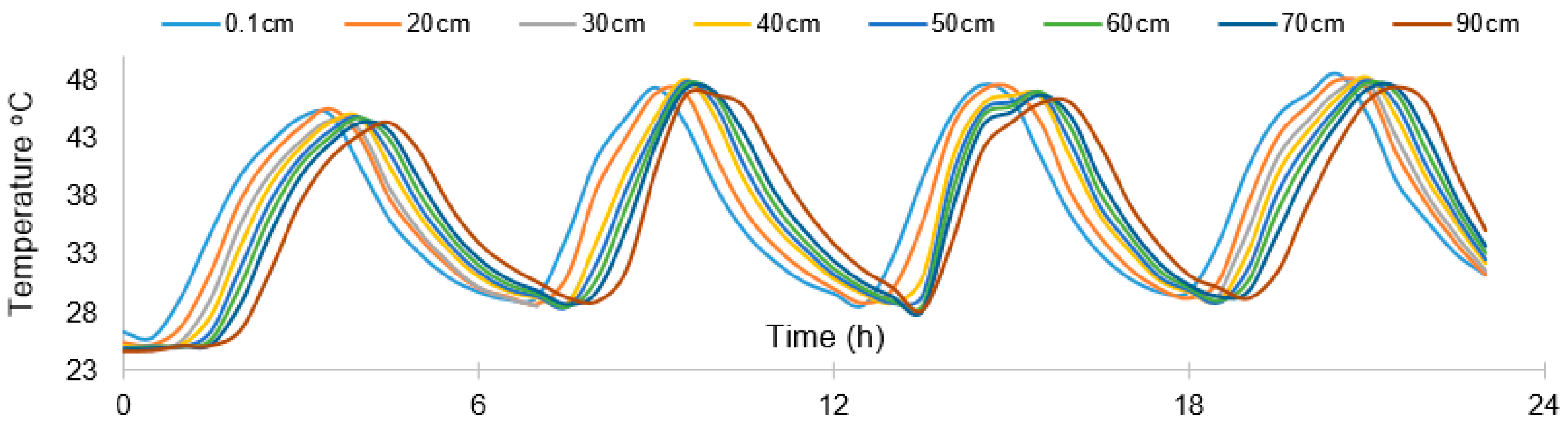
3.2. Temperature Boundary Conditions and Data Processing
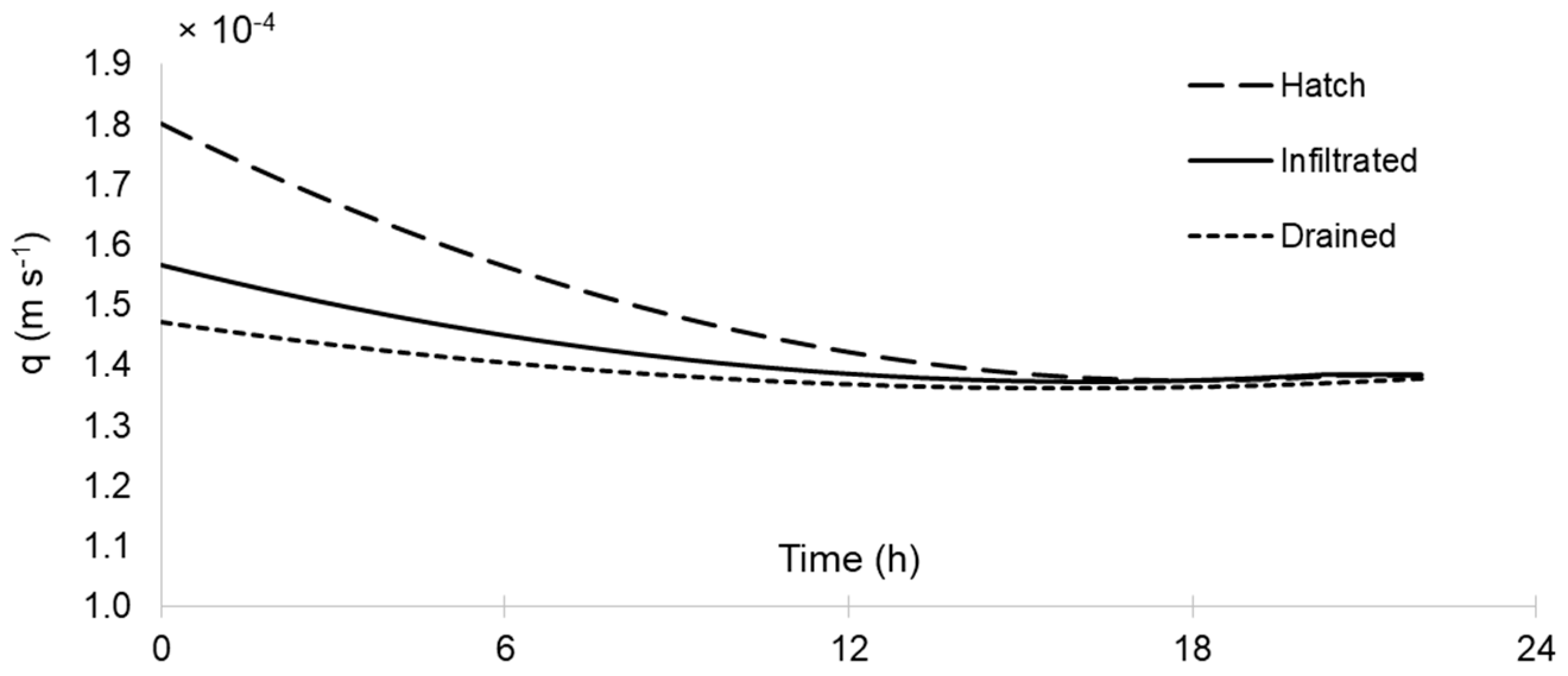
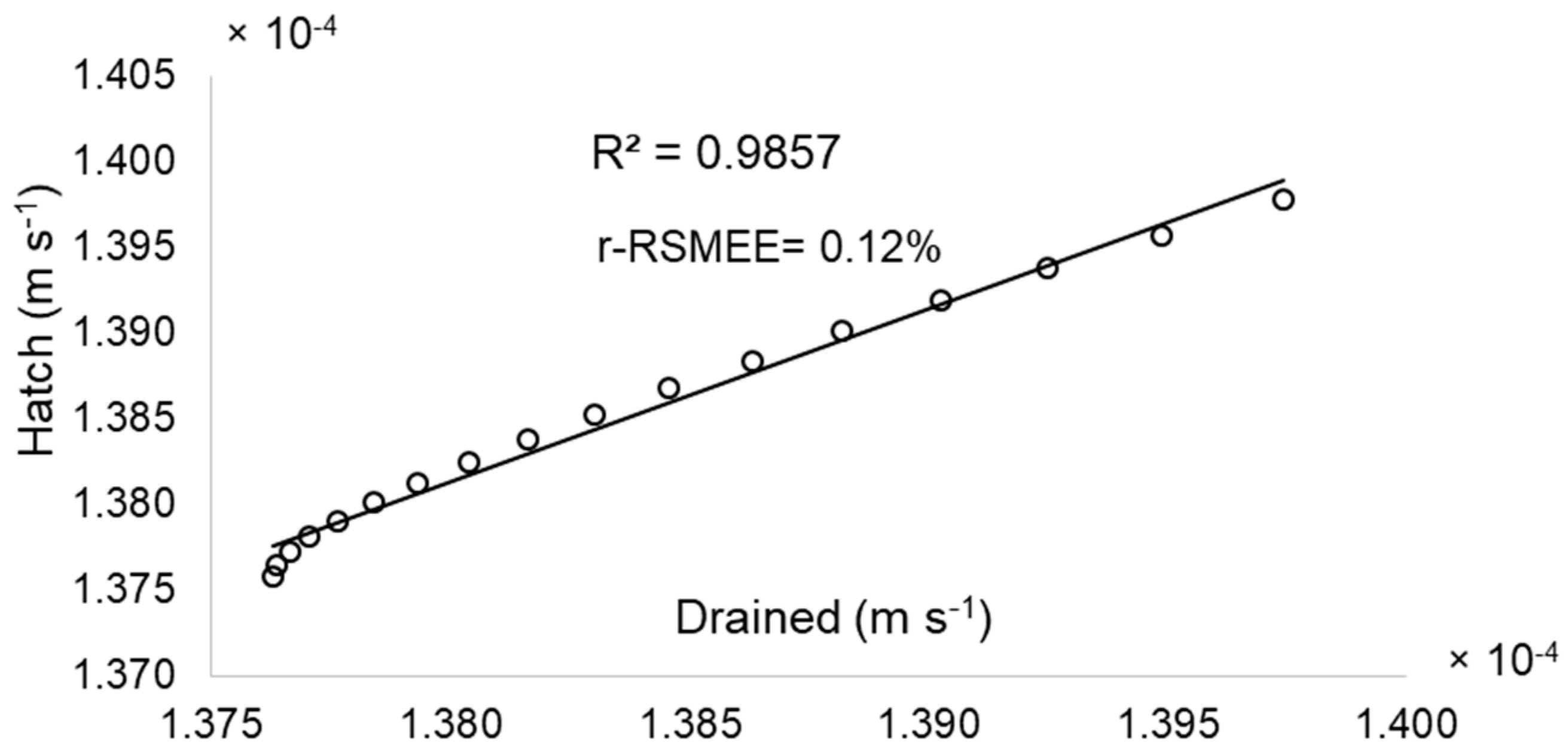
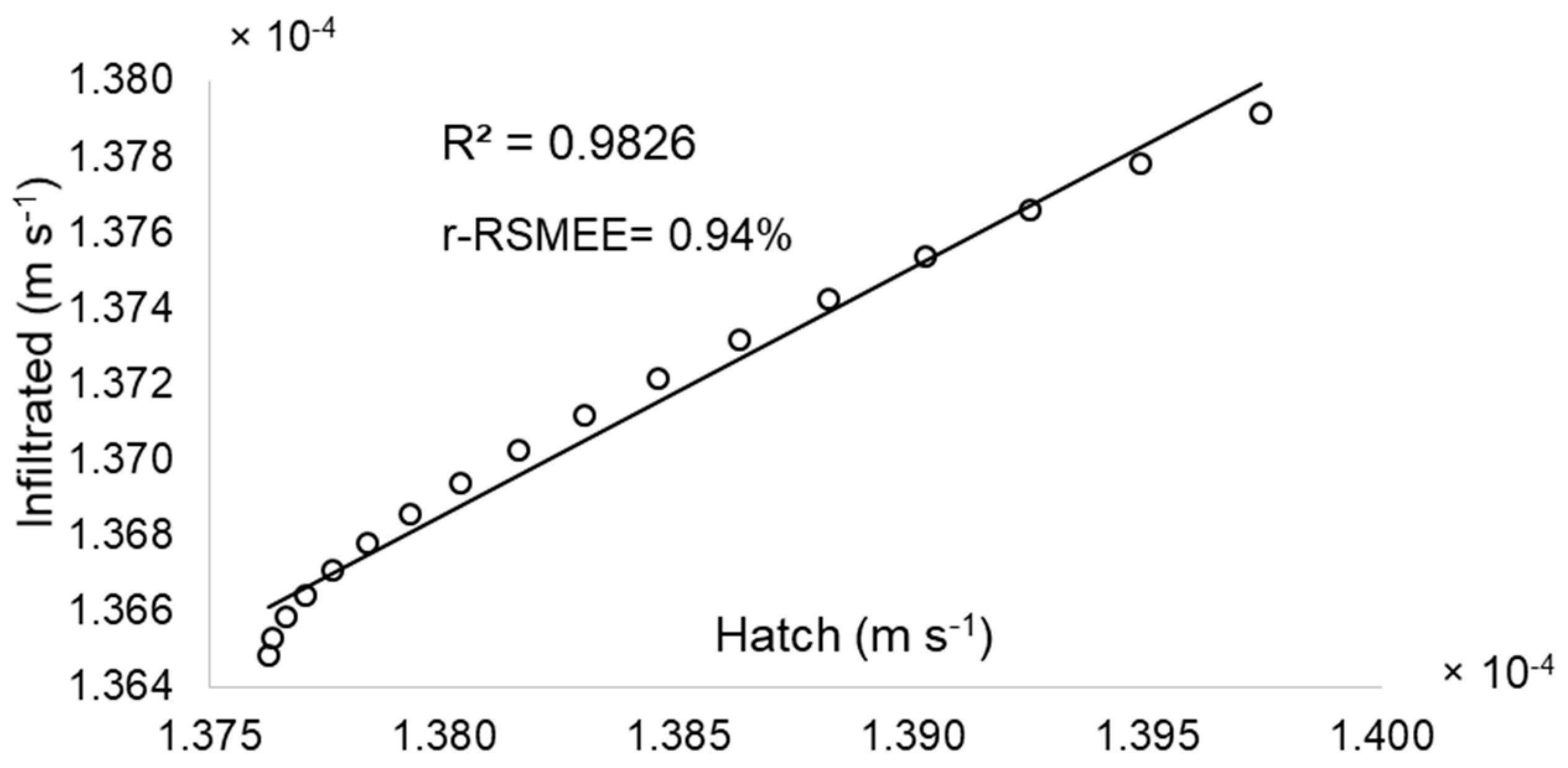
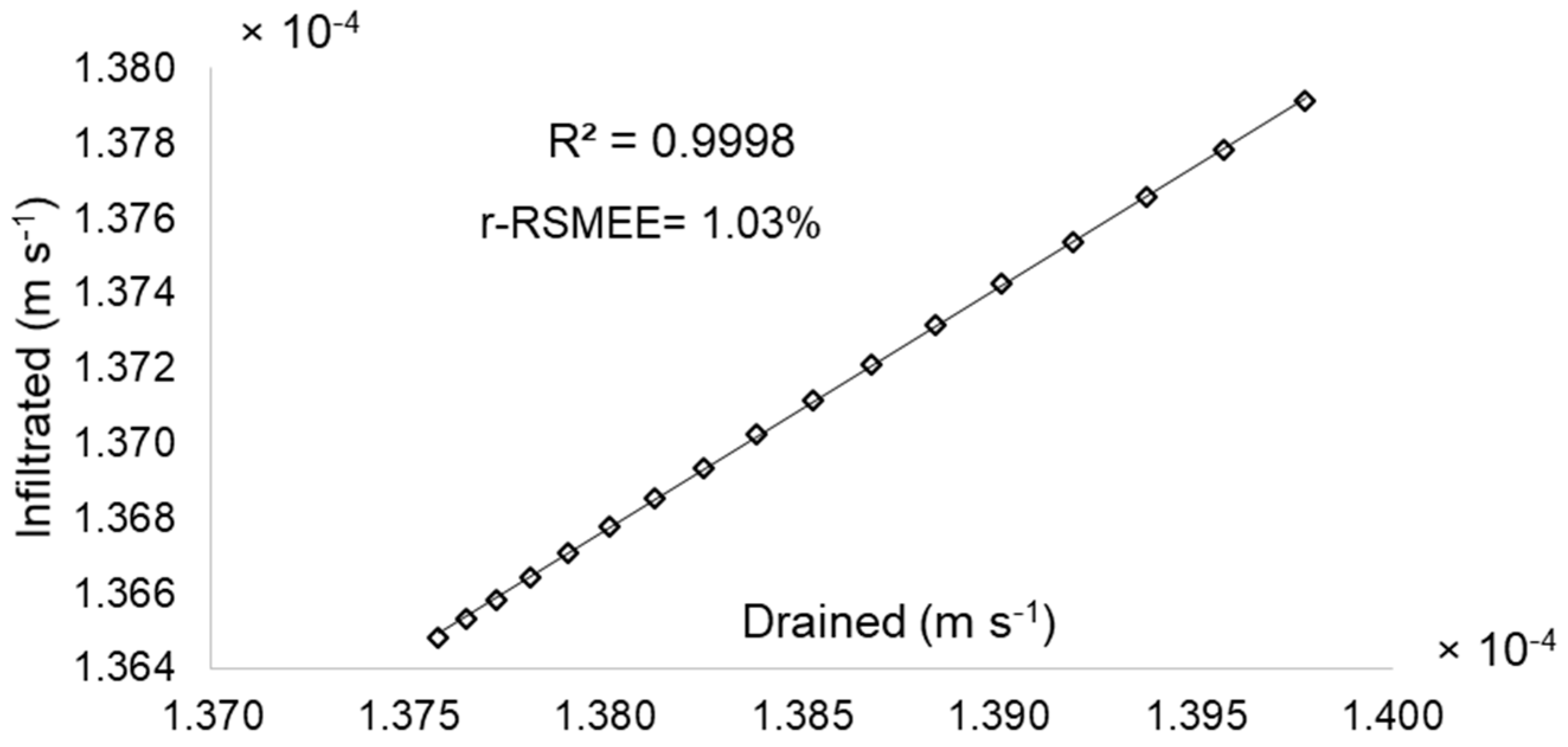
3.3. Water Flux Rates Comparison
3.4. Determination of Saturated Hydraulic Conductivity
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- De Luna, R.M.R.; Garnés, S.J.D.A.; Cabral, J.J.D.S.P.; dos Santos, S.M. Groundwater overexploitation and soil subsidence monitoring on Recife plain (Brazil). Nat. Hazards 2017, 86, 1363–1376. [Google Scholar] [CrossRef]
- Taylor, R.G. Ground water and climate change. Nat. Clim. Chang. 2012, 3, 322–329. [Google Scholar] [CrossRef]
- Custodio, E. Aquifer overexploitation: What does it mean? Hydrogeol. J. 2002, 10, 254–277. [Google Scholar] [CrossRef]
- Fetter, C.; Boving, T.; Kreamer, D. Contaminant Hydrogeology; Waveland Press Inc.: Long Grove, IL, USA, 2017; ISBN 978-14786-3279-5. [Google Scholar]
- Tang, Y.; Zhou, J.; Yang, P.; Yan, J.; Zhou, N. Groundwater Engineering; Tongji University Press/Springer: Shanghai, China, 2016; ISBN 978-981-10-0669-2. [Google Scholar]
- Mertens, J.; Madsen, H.; Feyen, L.; Jacques, D.; Feyen, J. Including prior information in the estimation of effective soil parameters in unsaturated zone modelling. J. Hydrol. 2004, 294, 251–269. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Shanafield, M.; Cook, P.G. Transmission losses, infiltration and groundwater recharge through ephemeral and intermittent streambeds: A review of applied methods. J. Hydrol. 2014, 511, 518–529. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; LaBa ugh, J.W. Field Techniques for Estimating Water Fluxes between Surface Water and Ground Water; USGS: Reston, VA, USA, 2008. Available online: https://pubs.usgs.gov/tm/04d02/ (accessed on 7 December 2018).
- Xu, X.; Lewis, C.; Liu, W.; Albertson, J.D.; Kiely, G. Analysis of single-ring infiltrometer data for soil hydraulic properties estimation: Comparison of BEST and Wu methods. Agric. Water Manag. 2012, 107, 34–41. [Google Scholar] [CrossRef]
- Lai, J.; Luo, Y.; Ren, L. Numerical evaluation of depth effects of double-ring infiltrometers on soil saturated hydraulic conductivity measurements. Soil Sci. Soc. Am. J. 2011, 76, 867–875. [Google Scholar] [CrossRef]
- Kadam, A.S. Determination of infiltration rate for rite selection of artificial water recharge: An experimental study. Int. J. Sci. Res. 2016, 5, 699–705. [Google Scholar] [CrossRef]
- Fatehnia, M.; Paran, S.; Kish, S.; Tawfiq, K. Automating double ring infiltrometer with an Arduino microcontroller. Geoderma 2016, 262, 133–139. [Google Scholar] [CrossRef]
- Vand, A.S.; Sihag, P.; Singh, B.; Zand, M. Comparative evaluation of infiltration models. KSCE J. Civ. Eng. 2018, 22, 4173–4184. [Google Scholar] [CrossRef]
- Nestingen, R.; Asleson, B.C.; Gulliver, J.S.; Hozalski, R.M.; Nieber, J.L. Laboratory Comparison of Field Infiltrometers. J. Sustain. Water Built Environ. 2018, 4. [Google Scholar] [CrossRef]
- Arriaga, F.J.; Kornecki, T.S.K.; Balkcom, K.S.B.; Raper, R.L. A method for automating data collection from a double-ring infiltrometer under falling head conditions. Soil Use Manag. 2010, 26, 61–67. [Google Scholar] [CrossRef]
- Di Prima, S.; Lassabatere, L.; Bagarello, V.; Iovino, M.; Angulo-Jaramillo, R. Testing a new automated single ring infiltrometer for Beerkan infiltration experiments. Geoderma 2015, 262, 20–34. [Google Scholar] [CrossRef]
- Lautz, L.K. Observing temporal patterns of vertical flux through streambed sediments using time-series analysis of temperature records. J. Hydrol. 2012, 464–465, 199–215. [Google Scholar] [CrossRef]
- Salas-García, J.; Garfias, J.; Martel, R.; Bibiano-Cruz, L. A low-cost automated test column to estimate soil hydraulic characteristics in unsaturated porous media. Geofluids 2017, 2017, 6942736. [Google Scholar] [CrossRef]
- IAEA. Use of Artificial Tracers in Hydrology IAEA-TECDOC-601; International Atomic Energy Agency: Vienna, Austria, 1991; ISSN 1011-4289. [Google Scholar]
- Yeh, Y.; Lee, C.; Chen, S. A tracer method to determinate hydraulic conductivity and effective porosity of saturated clays under low gradients. Groundwater 2000, 38, 522–529. [Google Scholar] [CrossRef]
- Hwang, H.; Jeen, S.; Suleiman, A.A.; Lee, K. Comparison of saturated hydraulic conductivity estimated by three different methods. Water 2017, 9, 942. [Google Scholar] [CrossRef]
- Mosthaf, K.; Brauns, B.; Fjordbøge, A.S.; Rohde, M.M.; Kerrn-Jespersen, H.; Bjerg, P.L.; Binning, P.J.; Broholm, M.M. Conceptualization of flow and transport in a limestone aquifer by multiple dedicated hydraulic and tracer tests. J. Hydrol. 2018, 561, 532–546. [Google Scholar] [CrossRef]
- Stonestrom, D.A.; Constantz, J. Heat as a Tool for Studying the Movement of Ground Water near Streams; USGS Circular 1260; USGS: Reston, VA, USA, 2003. Available online: https://pubs.usgs.gov/circ/2003/circ1260/pdf/Circ1260.pdf (accessed on 12 July 2018).
- Ronan, A.D.; Prudic, D.E.; Thodal, C.E.; Constantz, J. Field study and simulation of diurnal temperature effects on infiltration and variably saturated flow beneath an ephemeral stream. Water Resour. Res. 1998, 34, 2137–2153. [Google Scholar] [CrossRef]
- Thomas, C.L.; Steward, A.E.; Constantz, J.E. Determination of Infiltration and Percolation Rates along a Reach of the Santa Fe River near La Bajada New Mexico; U.S. Geological Survey, Water-Resources Investigations Report 00-4141; USGS: Reston, VA, USA, 2000. [CrossRef]
- Arriaga, M.A.; Leap, D.I. Using solver to determine vertical groundwater velocities by temperature variations. Hydrogeol. J. 2006, 14, 253–263. [Google Scholar] [CrossRef]
- Birkel, C.; Soulsby, C.; Irvine, D.I.; Malcolm, I.; Lautz, L.K.; Tetzlaff, D. Heat-based hyporheic flux calculations in heterogeneous salmon spawning gravels. Aquat. Sci. 2016, 78, 203–213. [Google Scholar] [CrossRef]
- Kurylyk, B.L.; Irvine, D.J.; Carey, S.K.; Briggs, M.A. Heat as a groundwater tracer in shallow and deep heterogeneous media: Analytical solution, spreadsheet tool, and field applications. Hydrol. Process. 2017, 31, 2648–2661. [Google Scholar] [CrossRef] [PubMed]
- Irvine, D.J.; Briggs, M.A.; Lautz, L.K.; Gordon, R.P.; McKenzie, J.M.; Cartwright, I. Using Diurnal Temperature Signals to Infer Vertical Groundwater-Surface Water Exchange. Groundwater 2016, 55, 10–26. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Rodríguez, M.; Fernández-Ayuso, A.; Hayashi, M.; Moral-Martos, F. Using water temperature, electrical conductivity, and pH to Characterize surface–groundwater relations in a shallow ponds system (Doñana National Park, SW Spain). Water 2018, 10, 1406. [Google Scholar] [CrossRef]
- Rodríguez, P.; Júnez-Ferreira, H.E.; González, J.; de la Rosa, J.I.; Galván, C.; Burnes, S. Vadose zone hydraulic conductivity monitoring by using an Arduino data acquisition system. In Proceedings of the 2018 International Conference on Electronics, Communications and Computers, Cholula, Mexico, 21–23 February 2018; pp. 80–85. [Google Scholar] [CrossRef]
- Rau, G.C.; Andersen, M.S.; McCallum, A.M.; Roshan, H.; Acworth, R.I. Heat as a tracer to quantify water flow in near-surface sediments. Earth Sci. Rev. 2014, 10, 41–58. [Google Scholar] [CrossRef]
- Halloran, L.J.; Rau, G.C.; Andersen, M.S. Heat as a tracer to quantify processes and properties in the vadose zone: A review. Earth Sci. Rev. 2016, 159, 358–373. [Google Scholar] [CrossRef]
- Programmable Resolution 1-Wire Digital Thermometer. Available online: https://datasheets.maximintegrated.com/en/ds/DS18B20.pdf (accessed on 12 July 2018).
- Product Users Manual HC-SR04 Ultrasonic Sensor. Available online: https://docs.google.com/document/d/1Y-yZnNhMYy7rwhAgyL_pfa39RsB-x2qR4vP8saG73rE/edit (accessed on 12 July 2018).
- Micro Load Cell Datasheet. Available online: https://www.robotshop.com/media/files/pdf/datasheet-3133.pdf (accessed on 12 July 2018).
- Smith, S.W. The Scientist and Engineer’s Guide to Digital Signal Processing. DSP Guide 1997, 423–450. Available online: http://www.dspguide.com/pdfbook.htm (accessed on 12 July 2018). [CrossRef]
- Hatch, C.E.; Fisher, A.T.; Revenaugh, J.S.; Constantz, J.; Ruehl, C. Quantifying surface water-groundwater interactions using time series analysis of streambed thermal records: Method development. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Shanafield, M.; Hatch, C.; Pohll, G. Uncertainty in thermal time series analysis estimates of streambed water flux. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Stallman, R.W. Steady One-Dimensional Fluid Flow in a Semi-Infinite Porous Medium with Sinusoidal Surface Temperature. J. Geophys. Res. 1965, 70, 2821–2827. [Google Scholar] [CrossRef]
- Young, P.; Pedregal, D.; Tych, W. Dynamic harmonic regression. J. Forecast. 1999, 18, 369–394. [Google Scholar] [CrossRef]
- Gordon, R.P.; Lautz, L.K.; Briggs, M.A.; McKenzie, J.M. Automated calculation of vertical pore-water flux from field temperature time series using the VFLUX method and computer program. J. Hydrol. 2012, 420–421, 142–158. [Google Scholar] [CrossRef]
- Munz, M.; Oswald, S.E.; Schmidt, C. Sand box experiments to evaluate the influence of subsurface temperature probe design on temperature based water flux calculation. Hydrol. Earth Syst. Sci. 2011, 15, 3495–3510. [Google Scholar] [CrossRef]
- Loutfi, H.; Bernatchou, A.; Raoui, Y.; Tadili, R. Learning Processes to Predict the Hourly Global, Direct, and Diffuse Solar Irradiance from Daily Global Radiation with Artificial Neural Networks. Int. J. Photoenergy 2017, 2017, 4025283. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Evaluation of empirical models for predicting monthly mean horizontal diffuse solar radiation. Renew. Sustain. Energy Rev. 2016, 56, 246–260. [Google Scholar] [CrossRef]
- Saturated Hydraulic Conductivity in Relation to Soil Texture. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/detail/soils/survey/office/ssr10/tr/?cid=nrcs144p2_074846 (accessed on 12 July 2018).


| Parameters | Determined | Units |
|---|---|---|
| Effective porosity () | 0.28 | dimensionless |
| Volumetric heat capacity of soil () | 0.5 | Cal cm−3 °C−1 |
| Volumetric heat capacity of water () | 1.0 | Cal cm−3 °C−1 |
| Thermal dispersivity () | 0.001 | M |
| Baseline thermal conductivity () | 0.0045 | Cal s−1 cm−1 °C−1 |
| Approach | Ks | Units |
|---|---|---|
| Heat as a tracer a | 8.6318 × 10−5 | m s−1 |
| Infiltrated b | 8.6384 × 10−5 | m s−1 |
| Drained c | 8.5680 × 10−5 | m s−1 |
| USDA d | 4.2 × 10−5 to 1.41 × 10−4 | m s−1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Juárez, P.; Júnez-Ferreira, H.E.; González Trinidad, J.; Zavala, M.; Burnes-Rudecino, S.; Bautista-Capetillo, C. Automated Laboratory Infiltrometer to Estimate Saturated Hydraulic Conductivity Using an Arduino Microcontroller Board. Water 2018, 10, 1867. https://doi.org/10.3390/w10121867
Rodríguez-Juárez P, Júnez-Ferreira HE, González Trinidad J, Zavala M, Burnes-Rudecino S, Bautista-Capetillo C. Automated Laboratory Infiltrometer to Estimate Saturated Hydraulic Conductivity Using an Arduino Microcontroller Board. Water. 2018; 10(12):1867. https://doi.org/10.3390/w10121867
Chicago/Turabian StyleRodríguez-Juárez, Pedro, Hugo E. Júnez-Ferreira, Julián González Trinidad, Manuel Zavala, Susana Burnes-Rudecino, and Carlos Bautista-Capetillo. 2018. "Automated Laboratory Infiltrometer to Estimate Saturated Hydraulic Conductivity Using an Arduino Microcontroller Board" Water 10, no. 12: 1867. https://doi.org/10.3390/w10121867
APA StyleRodríguez-Juárez, P., Júnez-Ferreira, H. E., González Trinidad, J., Zavala, M., Burnes-Rudecino, S., & Bautista-Capetillo, C. (2018). Automated Laboratory Infiltrometer to Estimate Saturated Hydraulic Conductivity Using an Arduino Microcontroller Board. Water, 10(12), 1867. https://doi.org/10.3390/w10121867






