Multivariate Flood Risk Analysis at a Watershed Scale Considering Climatic Factors
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Methodology
2.2.1. Definition of flood risk
2.2.2. Archimedean Copula
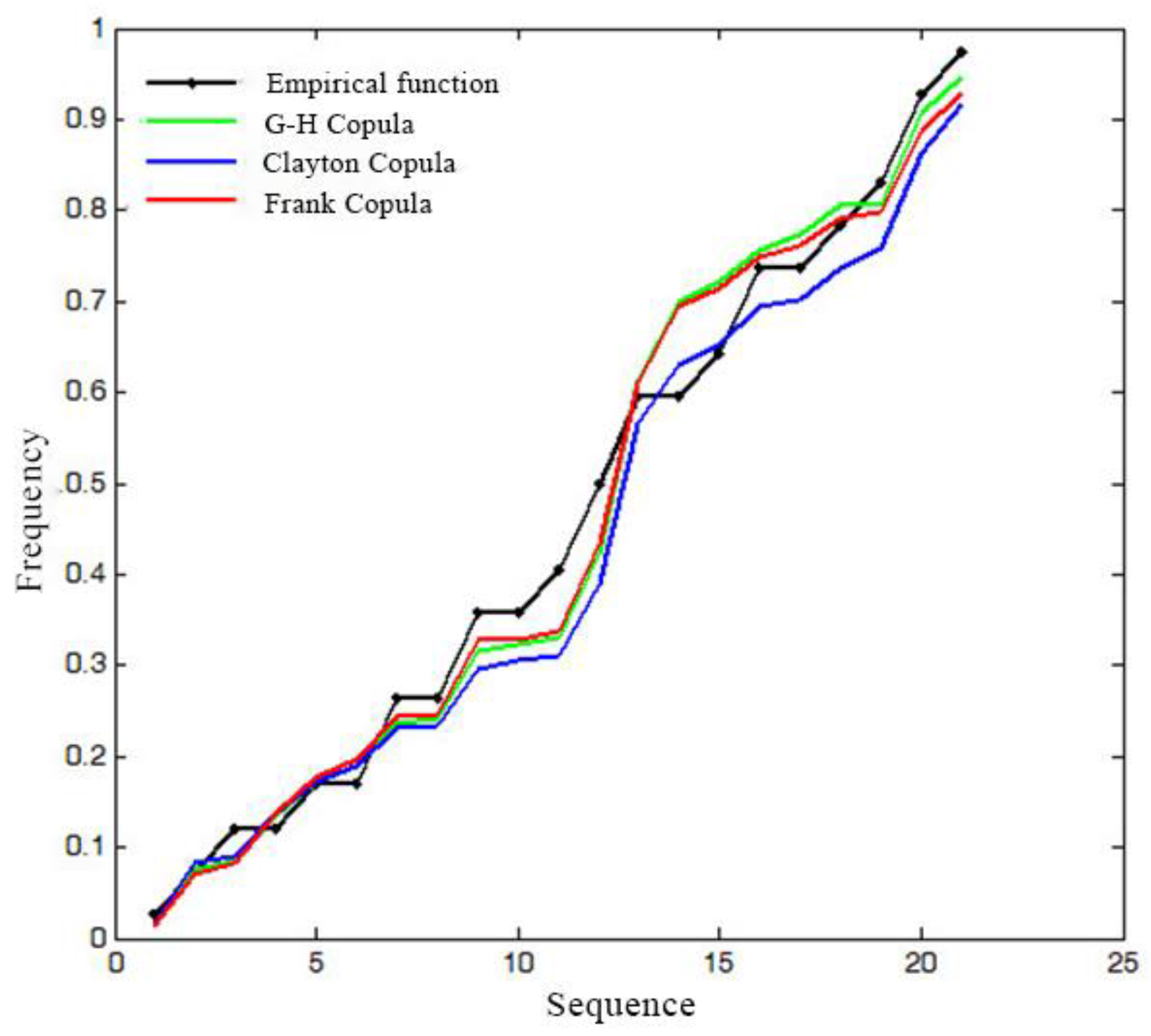
2.2.3. Parameter Estimation and Goodness-of-fit Test
2.2.4. Scenario Hypothesis
2.2.5. Climate Scenarios
3. Results
3.1. Flood Response Analysis Under Different Climate Scenarios
3.2. Hydrological Response of Different Climate Scenarios
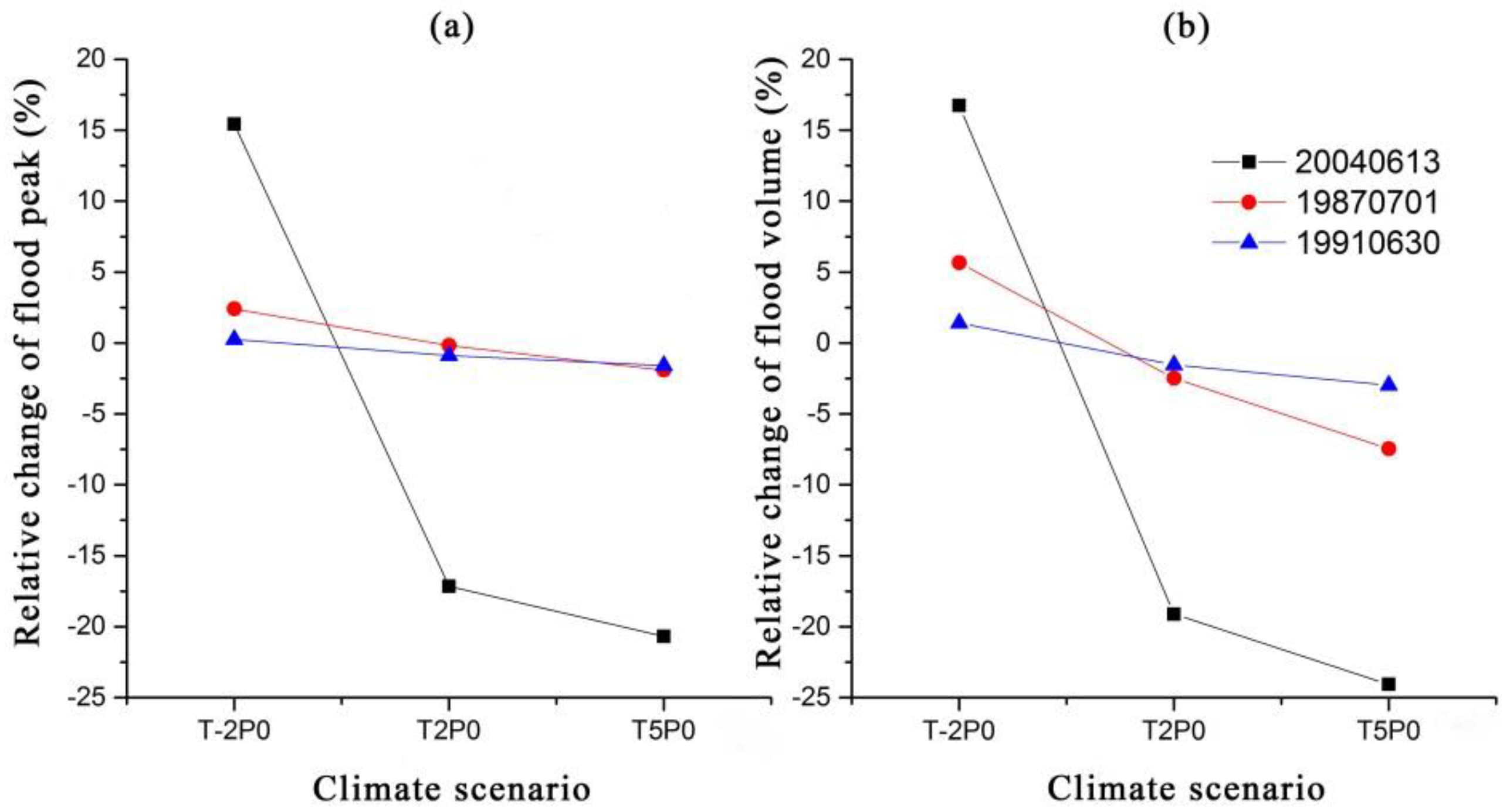
3.2.1. Analysis of the Impact of Temperature Changes on Floods
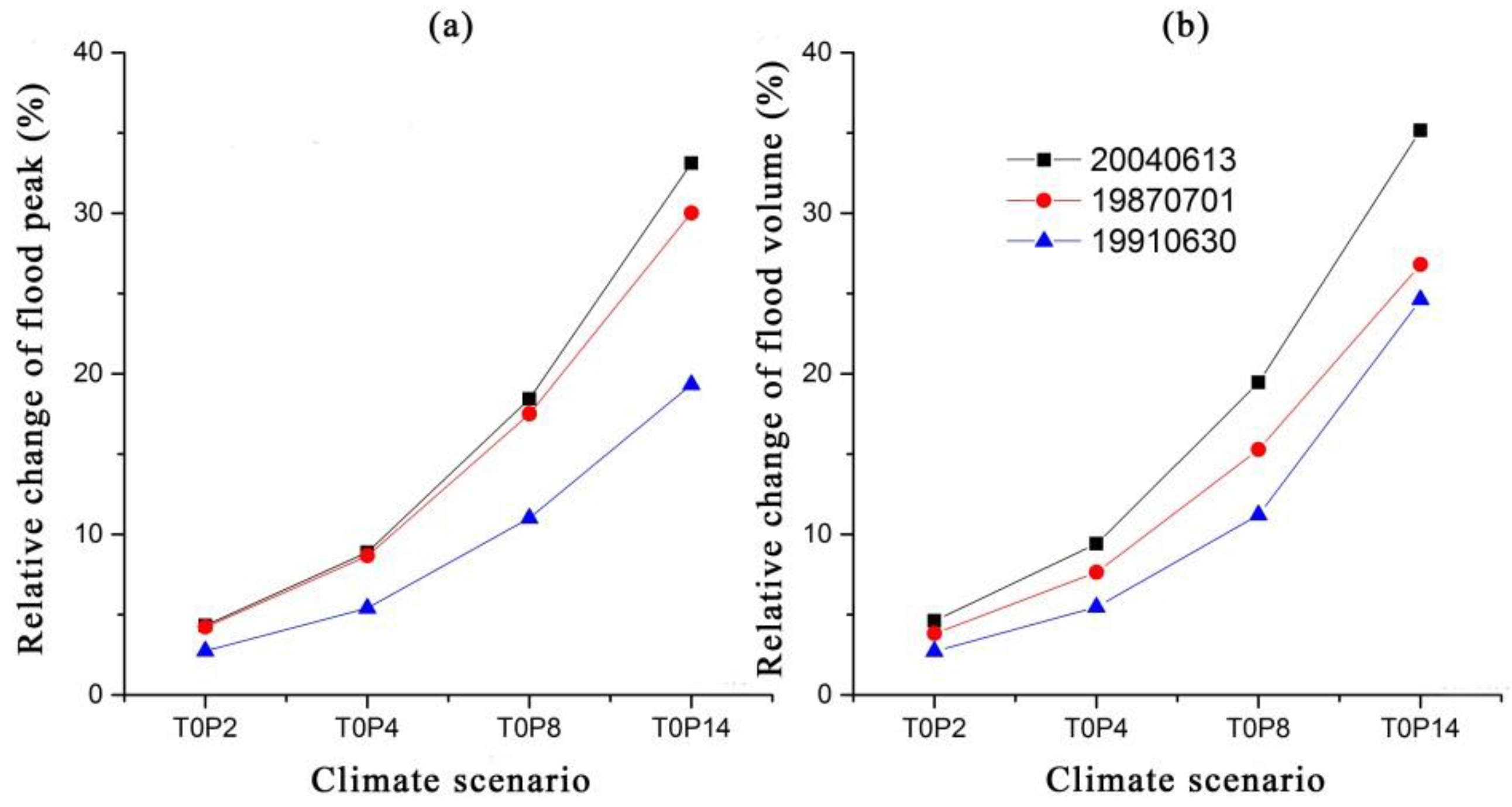
3.2.2. Analysis of the Impact of Rainfall Changes on Floods
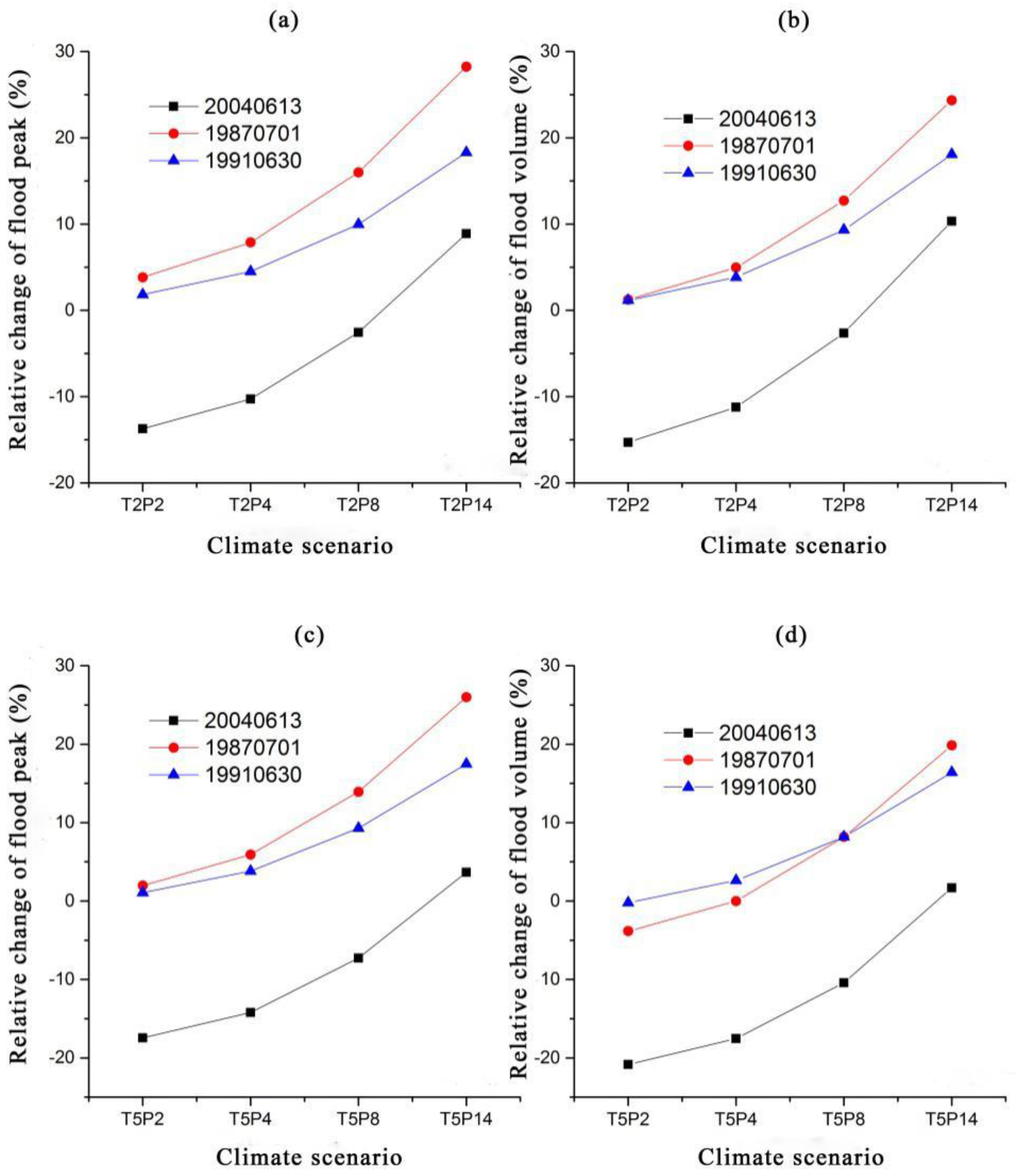
3.2.3. Analysis of the Combined Effects of Temperature and Rainfall
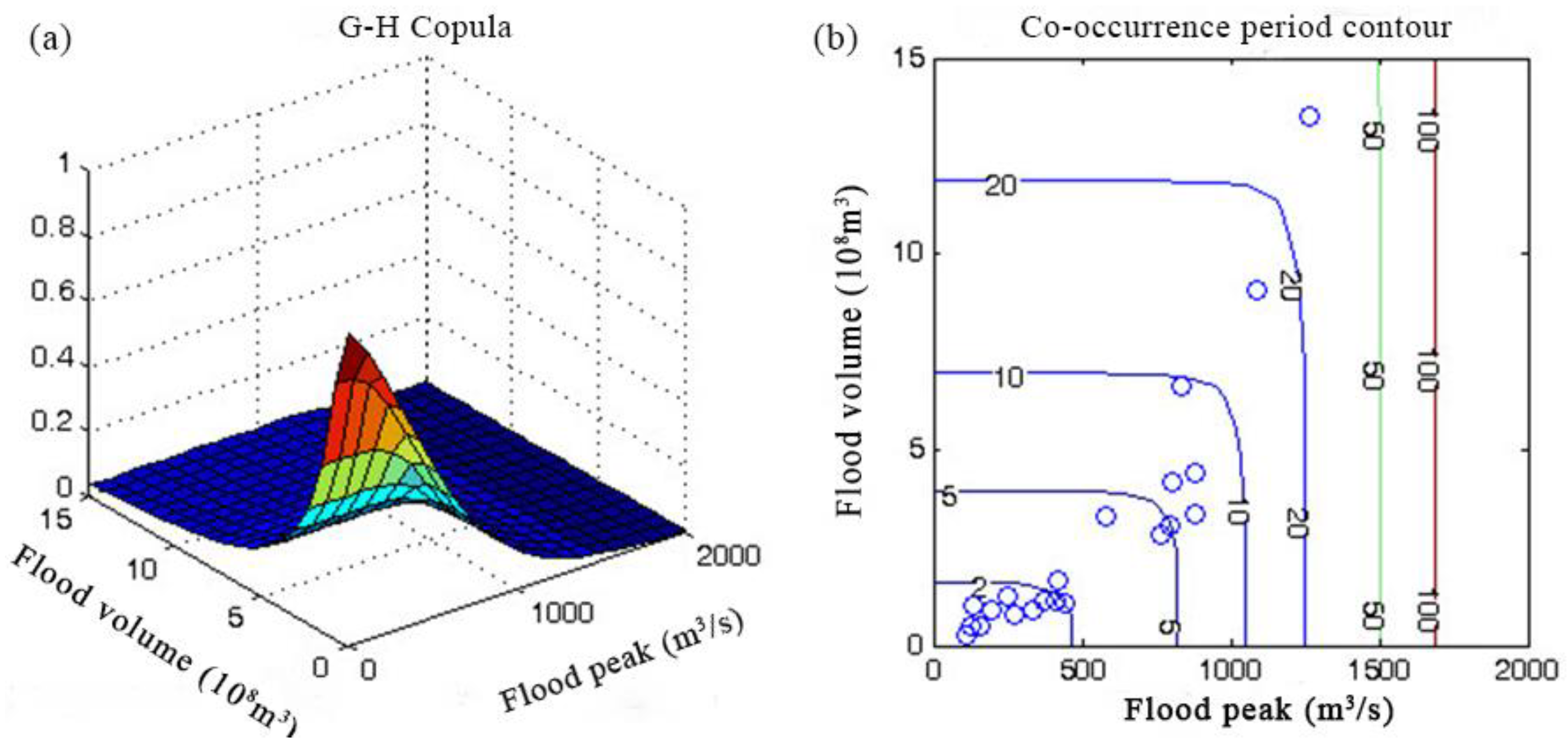
3.3. Copula Function Fitting
4. Discussion
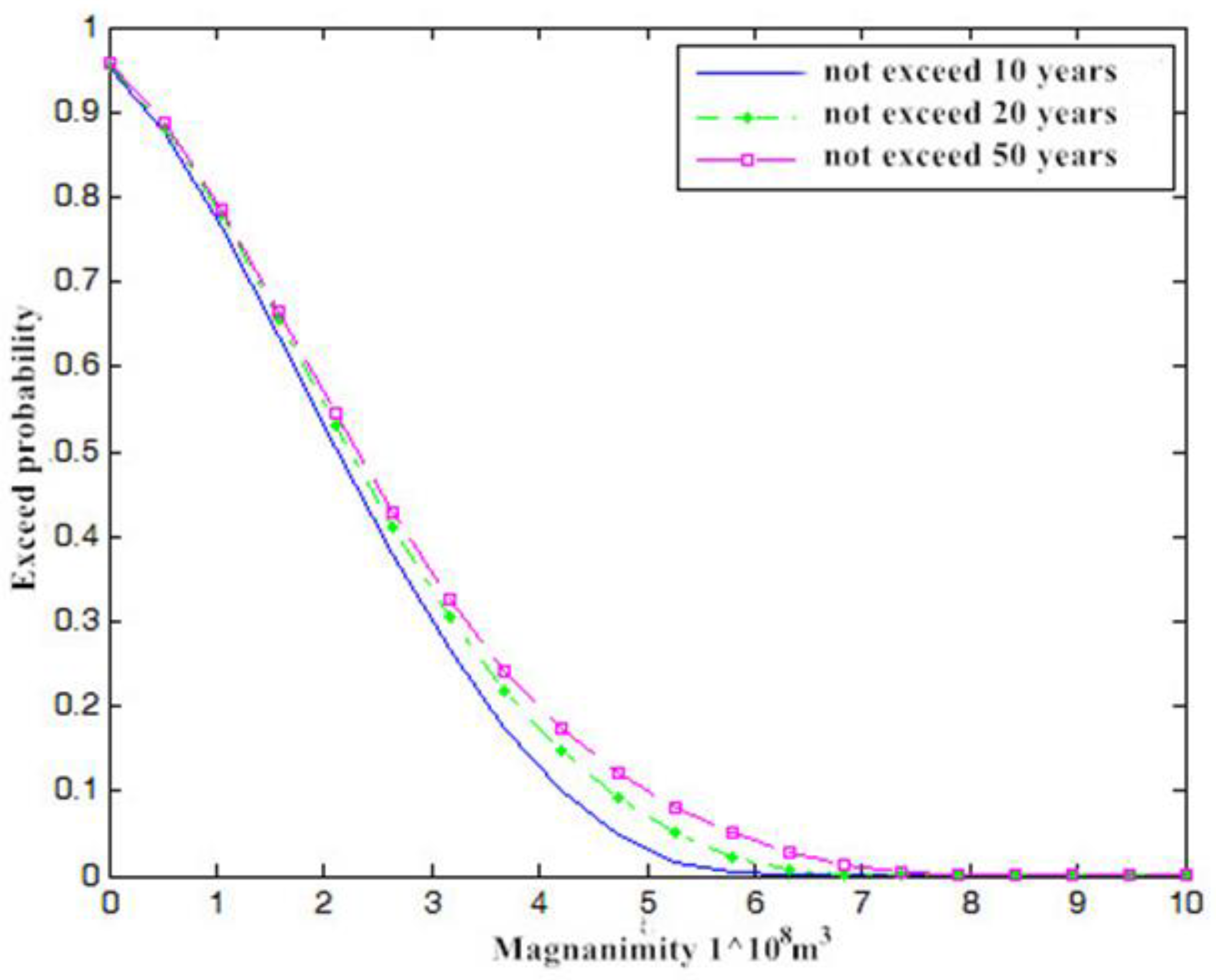
4.1. Multivariate Flood Risk Analysis
4.1.1. Flood Risk Analysis Under Current Situation
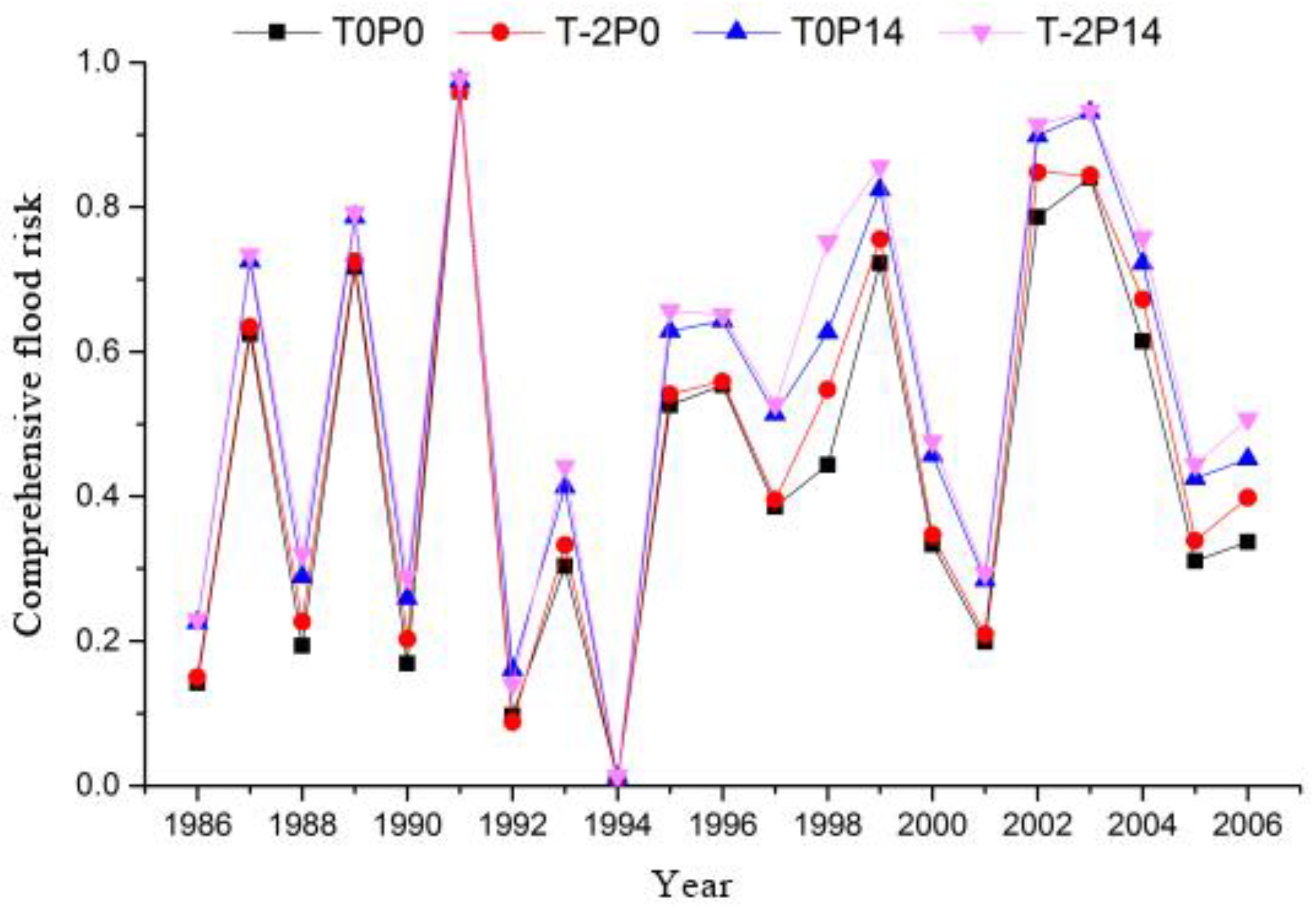
4.1.2. Flood Risk Analysis Considering Climate Change Impact
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Flood | Relative Flood Change (%) | ||||||
|---|---|---|---|---|---|---|---|
| Rank | Number | T-2P0 | T2P0 | T5P0 | |||
| Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | ||
| light | 20040618 | 15.43 | 16.75 | −17.15 | −19.11 | −20.69 | −24.06 |
| medium | 19870701 | 2.40 | 5.65 | −0.16 | −2.48 | −1.91 | −7.45 |
| heavy | 19910630 | 0.25 | 1.41 | −0.89 | −1.55 | −1.59 | −2.98 |
| average | 6.03 | 7.94 | −6.07 | −7.71 | −8.06 | −11.50 | |
| Floods | Relative Flood Change (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rank | Number | T0P2 | T0P4 | T0P8 | T0P14 | ||||
| Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | ||
| light | 20040618 | 4.33 | 4.62 | 8.89 | 9.41 | 18.43 | 19.47 | 33.11 | 35.16 |
| medium | 19870701 | 4.23 | 3.82 | 8.66 | 7.64 | 17.50 | 15.27 | 30.02 | 26.80 |
| heavy | 19910630 | 2.74 | 2.72 | 5.41 | 5.48 | 11.01 | 11.20 | 19.34 | 24.62 |
| average | 3.76 | 3.72 | 7.65 | 7.51 | 15.64 | 15.31 | 27.49 | 28.86 | |
References
- Liu, Z.Y.; Xia, J. Impact of climate change on flood risk in China. Nature 2016, 3, 177–181. [Google Scholar]
- Wang, Y.; Cao, M.K.; Tao, B.; Li, K. The changing characteristics of spatial pattern of precipitation in China under the background of global climate change. Geogr. Res. 2006, 6, 1031–1040. [Google Scholar] [CrossRef]
- Wu, S.H.; Gao, J.B.; Deng, H.Y.; Liu, L.L.; Pan, W. Climate change risk and its quantitative assessment methods. Progr. Geogr. 2018, 1, 28–35. [Google Scholar]
- Yang, Z.; Zhang, L.P.; Qin, L.L.; Yang, Y.R.; Duan, Y.B. The variation characteristics of Danjiangkou Reservoir inflow flood and its response to future climate scenarios. Resour. Environ. Yangtze River Basin 2013, 5, 588–594. [Google Scholar]
- Mani, P. Spatial variability and potential impacts of climate change on flood and debris flow hazard zone mapping and implications for risk management. Nat. Hazards Earth Syst. Sci. 2008, 8, 539–558. [Google Scholar] [CrossRef]
- Ran, Q.X.; Zhang, X. Review on Methods of Multivariate Hydrological Joint Distribution and Copula Function. Water Resour. Power 2010, 9, 8–11. [Google Scholar]
- Jaworski, P.; Durante, F.; Rdle, W.; Karl, H.; Rychlik, T. Copula Theory and Its Applications. In Proceedings of the Copula Theory and Its Applications, Warsaw, Poland, 25–26 September 2009. [Google Scholar]
- Feng, P.; Mao, H.H.; Wang, Y. Hydrological frequency analysis method and its application under multivariable conditions. J. Hydraul. Eng. 2009, 1, 33–37. [Google Scholar]
- Duan, X.L.; Hao, Z.C. Research progress of Copula function in hydrological applications. In Proceedings of the First China Water Forum, Ningbo, Zhejiang, China, 14 October 2010. [Google Scholar]
- Yue, S. The Gumbel Mixed Model Applied to Storm Frequency Analysis. Water Resour. Manag. 2000, 14, 377–389. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Probabilistic assessment of flood risks using trivariate copulas. Theor. Appl. Climatol. 2013, 111, 341–360. [Google Scholar] [CrossRef]
- Chowdhary, H.; Escobar, L.A.; Singh, V.P. Identification of suitable copulas for bivariate frequency analysis of flood peak and flood volume data. Hydrol. Res. 2011, 42, 193–216. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate rainfall frequency distributions using Archimedean copulas. J. Hydrol. 2007, 332, 93–109. [Google Scholar] [CrossRef]
- Favre, A.C.; El Adlouni, S.; Perreault, L.; Thiemonge, N.; Bobee, B. Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Reddy, M.J.; Ganguli, P. Bivariate Flood Frequency Analysis of Upper Godavari River Flows Using Archimedean Copulas. Water Resour. Manag. 2012, 26, 3995–4018. [Google Scholar] [CrossRef]
- Fu, G.T.; Butler, D. Copula-based frequency analysis of overflow and flooding in urban drainage systems. J. Hydrol. 2014, 510, 49–58. [Google Scholar] [CrossRef]
- Gao, Y.Q.; Chen, Y.X.; Zhao, L.M.; Yang, M. Joint Probability Analysis of Different Frequency Rainfall in Qinhuai River Basin. Hydropower Energy Sci. 2016, 3, 1–5. [Google Scholar]
- Gao, Y.Q.; Ye, L.; Lai, L.J. Flood risk analysis of Qinhuai River Basin based on G-H copula function. J. Water Resour. Water Eng. 2018, 1, 172–177. [Google Scholar]
- Hao, Z.C.; Duan, X.L. Two-variable joint distribution and application of floods in flood season. J. Liaoning Techn. Univ 2011, 4, 533–536. [Google Scholar]
- Dung, N.V.; Merz, B.; Bardossy, A.; Apel, H. Handling uncertainty in bivariate quantile estimation—An application to flood hazard analysis in the Mekong Delta. J. Hydrol. 2015, 527, 704–717. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, Q.; Liu, Z.M. Three-variable flood risk assessment based on asymmetric Archimedean Copula. Adv. Water Sci. 2016, 5, 763–771. [Google Scholar]
- Gaal, L.; Szolgay, J.; Kohnova, S.; Hlavcova, K.; Parajka, J.; Viglione, A.; Merz, R.; Bloeschl, G. Dependence between flood peaks and volumes: A case study on climate and hydrological controls. Hydrol. Sci. J.-J. Des. Sci. Hydrol. 2015, 60, 968–984. [Google Scholar] [CrossRef]
- Rui, H. Land Use Change and Its Hydrological Effects in the Qinhuai River Basin; Nanjing University: Nanjing, China, 2012. [Google Scholar]
- Huang, D.P.; Liu, C.; Peng, S.F. Progress on Assessment and Regionalization of Flood Risk. Prog. Geogr. 2007, 26, 11–22. [Google Scholar]
- Sun, Z.L.; Zhu, X.F.; Pan, Y.Z.; Liu, X.F. Flood Risk Analysis: Progress, Challenges and Prospect. J. Catastrophol. 2017, 32, 125–130. [Google Scholar]
- Gumbel, E.J. Bivariate exponential distributions. J. Am. Stat. Assoc. 1960, 55, 698–707. [Google Scholar] [CrossRef]
- Hougaard, P. A class of multivariate failure time distributions. Biometrika 1986, 73, 671–678. [Google Scholar] [CrossRef]
- Clayton, D.G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic desease incidence. Biometrika 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Frank, M.J. On the simultaneous associativity of F(x,y) and x + y − F(x,y). Aequ. Math. 1979, 19, 194–226. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel inference—Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 22, 261–304. [Google Scholar] [CrossRef]
- Kim, D.; Chun, J.A.; Aikins, C.M. An hourly-scale scenario-neutral flood risk assessment in a mesoscale catchment under climate change. Hydrol. Process. 2018, 19, 2427. [Google Scholar] [CrossRef]
- Prudhomme, C.; Wilby, R.L.; Crooks, S.; Kay, A.L.; Reynard, N.S. Scenario-neutral approach to climate change impact studies: Application to flood risk. J. Hydrol. 2010, 390, 198–209. [Google Scholar] [CrossRef]
- Vormoor, K.; Rössler, O.; Bürger, G.; Bronstert, A.; Weingartner, R. When timing matters-considering changing temporal structures in runoff response surfaces. Clim. Chang. 2017, 142, 213–226. [Google Scholar] [CrossRef]

| Distribution | Probability Density Function | Denotes |
|---|---|---|
| P-III | where, | , , are shape scale and location parameter respectively. |
| GEV | k, a and u are shape scale and location parameter respectively. | |
| LN | and are the expectation and variance of the logarithm of the original sample |
| Copula | Expression | |
|---|---|---|
| GH | = | [0, 1] |
| Clayton | = | [−1, 1]\{0} |
| Frank | = | [−1, 1]\{0} |
| ΔT (°C) | ΔP (%) | ||||
|---|---|---|---|---|---|
| 0 | 2% | 4% | 8% | 14% | |
| −2 | T-2P0 | T-2P2 | T-2P4 | T-2P8 | T-2P14 |
| 0 | T0P0 | T0P2 | T0P4 | T0P8 | T0P14 |
| 2 | T2P0 | T2P2 | T2P4 | T2P8 | T2P14 |
| 5 | T5P0 | T5P2 | T5P4 | T5P8 | T5P14 |
| Scenario | Heavy (19910630) | Median (19870701) | Light (20040618) | |||
|---|---|---|---|---|---|---|
| Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | |
| T-2P0 | 1240.3 | 12.21 | 831.5 | 6.00 | 843.1 | 2.80 |
| T-2P2 | 1274.2 | 12.55 | 866.0 | 6.22 | 871.7 | 2.91 |
| T-2P4 | 1308.8 | 12.90 | 901.6 | 6.44 | 900.4 | 3.02 |
| T-2P8 | 1377.3 | 13.69 | 974.3 | 6.88 | 958.5 | 3.24 |
| T-2P14 | 1578.7 | 16.23 | 1081.2 | 7.56 | 1079.0 | 3.64 |
| T0P0 | 1237.2 | 12.04 | 812.0 | 5.68 | 730.4 | 2.40 |
| T0P2 | 1271.0 | 12.37 | 846.3 | 5.90 | 762.0 | 2.51 |
| T0P4 | 1304.1 | 12.70 | 882.3 | 6.11 | 795.3 | 2.63 |
| T0P8 | 1373.3 | 13.39 | 954.1 | 6.55 | 865.0 | 2.87 |
| T0P14 | 1476.4 | 15.00 | 1055.7 | 7.20 | 972.2 | 3.24 |
| T2P0 | 1226.1 | 11.85 | 810.7 | 5.54 | 605.1 | 1.94 |
| T2P2 | 1260.0 | 12.18 | 843.2 | 5.75 | 630.2 | 2.03 |
| T2P4 | 1293.0 | 12.50 | 876.0 | 5.96 | 655.4 | 2.13 |
| T2P8 | 1360.7 | 13.16 | 942.0 | 6.40 | 711.7 | 2.34 |
| T2P14 | 1463.8 | 14.22 | 1041.4 | 7.06 | 795.3 | 2.65 |
| T5P0 | 1217.5 | 11.68 | 796.5 | 5.26 | 579.3 | 1.82 |
| T5P2 | 1250.5 | 12.01 | 828.0 | 5.46 | 602.9 | 1.90 |
| T5P4 | 1284.4 | 12.36 | 860.2 | 5.68 | 626.6 | 1.98 |
| T5P8 | 1352.1 | 13.03 | 925.1 | 6.14 | 677.4 | 2.15 |
| T5P14 | 1453.6 | 14.01 | 1023.1 | 6.81 | 757.1 | 2.44 |
| Scenario | Relative Peak Flow Change (%) | Average | Relative Flood Volume Change (%) | Average | ||||
|---|---|---|---|---|---|---|---|---|
| Light 20040618 | Medium 19870701 | Heavy 19910630 | Light 20040618 | Medium 19870701 | Heavy 19910630 | |||
| T2P2 | −13.7 | 3.8 | 1.80 | −2.70 | −15.30 | 1.20 | 1.20 | −4.30 |
| T2P4 | −10.3 | 7.9 | 4.50 | 0.70 | −11.20 | 5.00 | 3.80 | −0.80 |
| T2P8 | −2.6 | 16 | 10.00 | 7.80 | −2.60 | 12.70 | 9.30 | 6.47 |
| T2P14 | 8.9 | 28.3 | 18.30 | 18.50 | 10.40 | 24.40 | 18.10 | 17.63 |
| T5P2 | −17.5 | 2 | 1.10 | −4.80 | −20.80 | −3.80 | −0.20 | −8.27 |
| T5P4 | −14.2 | 5.9 | 3.80 | −1.50 | −17.50 | 0.00 | 2.60 | −4.97 |
| T5P8 | −7.3 | 13.9 | 9.30 | 5.30 | −10.40 | 8.20 | 8.20 | 2.00 |
| T5P14 | 3.7 | 26 | 17.50 | 15.73 | 1.70 | 19.80 | 16.40 | 12.63 |
| Copula | θ | RMSE | AIC |
|---|---|---|---|
| G-H | 4.9273 | 0.009 | −134.272 |
| Clayton | 3.1097 | 0.011 | −123.354 |
| Frank | 17.7637 | 0.009 | −132.292 |
| Return Period | Univariate Design Value | Bivariate Design Value | Joint Return Period | Co-occurrence Return Period | ||
|---|---|---|---|---|---|---|
| Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | |||
| 5 | 825 | 3.93 | 868 | 4.38 | 4.41 | 5.76 |
| 10 | 1049 | 6.95 | 1089 | 7.72 | 8.76 | 11.66 |
| 20 | 1253 | 11.87 | 1292 | 13.17 | 17.44 | 23.44 |
| 30 | 1367 | 16.11 | 1404 | 17.83 | 26.13 | 35.22 |
| 50 | 1504 | 23.54 | 1541 | 26.09 | 43.50 | 58.78 |
| 100 | 1683 | 39.20 | 1718 | 43.41 | 86.94 | 117.67 |
| Scenario | Flood Risk | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Light (20040618) | Medium (19870701) | Heavy (19910630) | |||||||
| Q (m3/s) | V (108 m3) | Joint | Q (m3/s) | V (108 m3) | Joint | Q (m3/s) | V (108 m3) | Joint | |
| T-2P0 | 0.8251 | 0.6740 | 0.6725 | 0.6342 | 0.8891 | 0.6341 | 0.9649 | 0.9665 | 0.9606 |
| T-2P2 | 0.8356 | 0.6873 | 0.6859 | 0.6499 | 0.8943 | 0.6498 | 0.9681 | 0.9679 | 0.9633 |
| T-2P4 | 0.8456 | 0.6997 | 0.6985 | 0.6654 | 0.8992 | 0.6654 | 0.9711 | 0.9693 | 0.9657 |
| T-2P8 | 0.8639 | 0.7233 | 0.7224 | 0.6951 | 0.9081 | 0.6950 | 0.9761 | 0.9720 | 0.9698 |
| T-2P14 | 0.8954 | 0.7584 | 0.7579 | 0.7342 | 0.9194 | 0.7342 | 0.9865 | 0.9788 | 0.9783 |
| T0P0 | 0.7769 | 0.6170 | 0.6146 | 0.6250 | 0.8782 | 0.6249 | 0.9646 | 0.9657 | 0.9600 |
| T0P2 | 0.7916 | 0.6340 | 0.6319 | 0.6410 | 0.8843 | 0.6409 | 0.9678 | 0.9671 | 0.9627 |
| T0P4 | 0.8061 | 0.6507 | 0.6489 | 0.6571 | 0.8900 | 0.6570 | 0.9707 | 0.9685 | 0.9650 |
| T0P8 | 0.8332 | 0.6819 | 0.6806 | 0.6871 | 0.9002 | 0.6870 | 0.9759 | 0.9711 | 0.9690 |
| T0P14 | 0.8679 | 0.7232 | 0.7224 | 0.7254 | 0.9129 | 0.7253 | 0.9819 | 0.9758 | 0.9748 |
| T2P0 | 0.7080 | 0.5349 | 0.5313 | 0.6243 | 0.8703 | 0.6242 | 0.9635 | 0.9648 | 0.9588 |
| T2P2 | 0.7233 | 0.5528 | 0.5495 | 0.6395 | 0.8771 | 0.6394 | 0.9668 | 0.9663 | 0.9616 |
| T2P4 | 0.7379 | 0.5710 | 0.5679 | 0.6543 | 0.8833 | 0.6542 | 0.9698 | 0.9677 | 0.9640 |
| T2P8 | 0.7677 | 0.6069 | 0.6042 | 0.6822 | 0.8946 | 0.6821 | 0.9750 | 0.9703 | 0.9681 |
| T2P14 | 0.8061 | 0.6534 | 0.6515 | 0.7203 | 0.9089 | 0.7202 | 0.9813 | 0.9737 | 0.9728 |
| T5P0 | 0.6915 | 0.5108 | 0.5073 | 0.6175 | 0.8593 | 0.6173 | 0.9626 | 0.9640 | 0.9578 |
| T5P2 | 0.7067 | 0.5270 | 0.5238 | 0.6325 | 0.8674 | 0.6323 | 0.9659 | 0.9656 | 0.9607 |
| T5P4 | 0.7212 | 0.5433 | 0.5402 | 0.6473 | 0.8749 | 0.6471 | 0.9690 | 0.9671 | 0.9632 |
| T5P8 | 0.7499 | 0.5758 | 0.5732 | 0.6753 | 0.8882 | 0.6752 | 0.9744 | 0.9697 | 0.9675 |
| T5P14 | 0.7894 | 0.6239 | 0.6219 | 0.7136 | 0.9038 | 0.7135 | 0.9807 | 0.9731 | 0.9722 |
| Scenario | Flood Characteristics | Light (20040618) | Medium (19870701) | Heavy (19910630) | |||
|---|---|---|---|---|---|---|---|
| Risk | Relative Change (%) | Risk | Relative Change (%) | Risk | Relative Change (%) | ||
| T0P0 | Q (m3/s) | 0.7769 | - | 0.6250 | - | 0.9646 | - |
| V (108 m3) | 0.6170 | - | 0.8782 | - | 0.9657 | - | |
| Joint | 0.6146 | - | 0.6249 | - | 0.9600 | - | |
| T-2P0 | Q (m3/s) | 0.8251 | 6.21 | 0.6342 | 1.47 | 0.9649 | 0.03 |
| V (108 m3) | 0.6740 | 9.24 | 0.8891 | 1.24 | 0.9665 | 0.08 | |
| Joint | 0.6725 | 9.42 | 0.6341 | 1.47 | 0.9606 | 0.06 | |
| T0P14 | Q (m3/s) | 0.8679 | 11.71 | 0.7254 | 16.06 | 0.9819 | 1.80 |
| V (108 m3) | 0.7232 | 17.21 | 0.9129 | 3.95 | 0.9758 | 1.05 | |
| Joint | 0.7224 | 17.55 | 0.7253 | 16.07 | 0.9748 | 1.54 | |
| T-2P14 | Q (m3/s) | 0.8954 | 15.25 | 0.7342 | 17.48 | 0.9865 | 2.27 |
| V (108 m3) | 0.7584 | 22.91 | 0.9194 | 4.70 | 0.9788 | 1.35 | |
| Joint | 0.7579 | 23.32 | 0.7342 | 17.49 | 0.9783 | 1.91 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Guo, Z.; Wang, D.; Zhang, Z.; Liu, Y. Multivariate Flood Risk Analysis at a Watershed Scale Considering Climatic Factors. Water 2018, 10, 1821. https://doi.org/10.3390/w10121821
Gao Y, Guo Z, Wang D, Zhang Z, Liu Y. Multivariate Flood Risk Analysis at a Watershed Scale Considering Climatic Factors. Water. 2018; 10(12):1821. https://doi.org/10.3390/w10121821
Chicago/Turabian StyleGao, Yuqin, Zichen Guo, Dongdong Wang, Zhenxing Zhang, and Yunping Liu. 2018. "Multivariate Flood Risk Analysis at a Watershed Scale Considering Climatic Factors" Water 10, no. 12: 1821. https://doi.org/10.3390/w10121821
APA StyleGao, Y., Guo, Z., Wang, D., Zhang, Z., & Liu, Y. (2018). Multivariate Flood Risk Analysis at a Watershed Scale Considering Climatic Factors. Water, 10(12), 1821. https://doi.org/10.3390/w10121821




