Abstract
Based on the constructed SWAT model in the Qinhuai River Basin, the hydrological response of flooding under different scenarios of temperature and rainfall change is analyzed. The Copula function is then used to calculate and analyze the multivariate flood risk. The results show that the flood peaks increase with the increase of precipitation and decrease with the increase of temperature. The hydrological response of light floods to temperature changes is stronger than that of medium and heavy floods. Additionally, the temperature drop and the precipitation increase lead to a higher flood risk. The flood risk of flood peaks is more sensitive to changes in precipitation.
1. Introduction
Since the industrial revolution, human activities have intensified and the impact on the climate has become more and more important. In the context of global climate change, the average annual temperature rise in northern China has been relatively significant in the past 50 years, and heat waves in summers have increased. Precipitation in the Yangtze River Basin has generally increased [1,2,3]. Climate change directly affects precipitation, evaporation, runoff, soil moisture, etc., thus affecting streamflow and sedimentation mechanisms. This will further change hydrological cycle processes and the spatial and temporal distribution pattern of water resources. Extreme flood events in southern China have been occurring more frequently recently and the frequency and intensity of flood peaks have also increased [4]. Since the 21th century, the concept of flood management has shifted from flood control to flood management. Flood risk assessment, as a non-engineering disaster reduction measure, is of great significance for strengthening disaster early warning, flood risk management, and decision-making. Understanding the impact of climate change on flood risks can help the scientific management and control of flood risks in river basins [5].
As the actual risk of flood risk becomes more complicated, many scholars have begun to experiment with multivariate hydrological frequency analysis. Common methods include the normal transformation method, empirical frequency method (EFM), non-parametric method, and Copula function method. These methods have their own advantages and disadvantages in different application scopes [6]. The normal transformation method transforms the original data, which is computationally intensive and computationally complex, and may corrupt the data information during the data conversion process. The traditional empirical frequency method heavily relies on measured data and has no extension capability. The type of marginal distribution of joint distribution constructed by the nonparametric method is not clear, and has a poor prediction ability. However, the Copula function describes the correlation of variables by constructing the interdependence structure between variables, neither restricting the marginal distribution types of variables nor requiring the variables to be the same distribution, which greatly solves the joint distribution structure problem of different forms of marginal distribution variables, and is widely applied in hydrology.
The Copula function is the hotspot and frontier direction of hydrological frequency analysis [7,8]. It is mainly used for the joint probability analysis of hydrological and meteorological variables with multiple attributes [9,10]. Ganguli et al. [11] used tri-variate copulas to analyze the flood risk of the Delaware River Basin. Chowdhary et al. [12] applied six Copula functions to study bivariate flood risk analysis and identified the Clayton Copula as the best fitted model for their study area. Zhang et al. [13] used four Archimedean Copulas to study bivariate rainfall frequency. Farve et al. [14] used Copula to study the joint probability problem of the peaks in the Peribonka Basin of Canada and compared copulas with a frequency analysis of individual variables, demonstrating that Copula can better simulate the joint and marginal distribution of variables. Reddy and Ganguli [15] used the Copula function to analyze the flood frequency of the Godavari River Basin in India. Fu et al. [16] studied overflow and flooding in urban drainage systems using Copula frequency analysis. Gao et al. [17,18] analyzed flood risks in the Qinhuai River Basin and developed a joint rainfall and flood return period under a two-dimensional joint distribution. Hao and Duan [19] studied the bivariate joint frequency of flood peaks and volumes. Dung [20] explored the uncertainty in the bivariate flood risk model. Chen et al. [21] analyzed the joint distribution of flood, duration, and flood peaks of various return periods. Gaal [22] studied casual factors, controlling the relationship between flood peaks and volumes, and found that the climate-related factors are more important in controlling the consistency.
Rui (2012), with the support of GIS, RS, and mathematical statistics, used the Qinhuai River Basin as the study area and developed a SWAT hydrological model to simulate hydrological processes under various land-use scenarios. His results demonstrated that the SWAT hydrological model was capable of simulating hydrologic processes of the Qinhuai River Basin [23]. There are many studies on the impacts of climate change on the hydrological processes in the basin. However, there is little research on the quantitative analysis of the impacts of climate change on flood risks. The current study aims to quantitatively examine the climate change impact on flood risks in the Qinhuai River Basin, using 20 climate change scenarios with different temperature and rainfall changes. The climate change impact on peak flow and flood volume is simulated by a well-calibrated and validated SWAT model. The Copula function is applied to calculate the multivariate flood risk. The study provides scientific information for flood control in the basin and regional engineering design and risk assessment.
2. Materials and Methods
2.1. Study Area and Data
The Qinhuai River Basin is located in the Jiangsu Province, China, in the lower reaches of the Yangtze River, with a total drainage area of 2631 km2. The average annual precipitation of the basin is 1031 mm, and the precipitation is unevenly distributed over a year. The rainfall from April to September accounts for 70.6% of the total annual precipitation. The Qinhuai River has two headwaters, that is, the Qinshui River and the Jurong River. The Qinhuai River, with a length of 34 km, starts in a northwestern village of Jiangning District where the Qinshui River meets the Jurong River. The main channel of the Qinhuai River is divided into two branches in Dongshan Town, Jiangning District. The north branch passes through the Wudingmen Gate and the west branch flows into the Yangtze River via the Qinhuaixinhe Gate.
The daily flow of Qinhuaixinhe and Wudingmen Gate at the outlet of the basin for the period of 1986 to 2006 is used in the study. The annual maximum method is used to select the flood sample. The other data used in the study include the 90 m resolution DEM topographic data, latest LUCC data of a 300 m resolution, and one million soil type data. Climate data are form Nanjing Meteorological Station 1978–2007, including air pressure, temperature, relative humidity, precipitation, evaporation, wind speed, sunshine, etc. Daily rainfall data for eight stations, including Zhaocun Reservoir and Wudingmen Gate, from 1986 to 2006, are also used in the study.
2.2. Methodology
2.2.1. Definition of flood risk
Since the introduction of the risk theory into the flood system, there has been a lot of controversy surrounding the definition of flood risk. At present, the academic community has not formed a unified conclusion [24].
Generally speaking, the narrow sense of flood risk analysis is a single-factor analysis of disaster-causing factors or flood loss, and in the broad sense, it is a comprehensive analysis and assessment of all risk components [25]. This paper studies the impact of climate change on flood risk at a watershed scale. Assuming that the vulnerability for the hazard bearing body does not change, which can be not considered when studying flood risk under different climate scenarios, the flood risk is defined as the risk caused by the interaction between disaster deducing factors and the disaster environment. The flood return period is commonly used in visually expressing the degree of flood risk. The greater the return period of the flood is, the greater the flood loss caused will be. The formula of the flood reoccurrence period is:
where, P is the probability that the event does not exceed the set threshold, and the variation trend of the return period T is consistent with the probability P.
T = 1/(1 − P)
The probability that the event does not exceed the set threshold can be used to assess the flood risk. The greater P is, the greater the return period of the event, the greater the possible loss, and thus the higher the risk. The value of the risk degree is between zero and one; that is, the higher the value of the risk degree is, the higher the magnitude of the flood risk is.
2.2.2. Archimedean Copula
The Copula function is a function that connects marginal distributions and multivariate joint distributions. It describes the correlation of variables by constructing a dependent structure between variables. Archimedean Copula is very important and commonly used in hydrology because of its clear method, simple expression, mature parameter estimation, and function optimization. The common Archimedean Copula functions include G-H, Clayton, and Frank Copula, which are shown in Table 1.

Table 1.
Bivariate Archimedean Copula expression.
The Archimedean Copula function has no limitation on the marginal distribution for constructing the joint distribution, and is applied widely in fitting analysis of the joint probability distribution of hydrological events. At present, two commonly used recurrence criteria for describing bivariate flood frequency are the joint recurrence period and co-occurrence period. The difference between the criteria of different recurrence periods is essentially the difference in the way that dangerous events are defined.
Taking flood peak flow (Q) and flood volume (V) as characteristic quantities to represent flood events, for the joint recurrence period TU, the hazardous event EU indicates that one of the variables exceeds the set threshold (Q0 or V0), and the joint recurrence period can be represented by the Copula function as:
where is a parameter of the Copula function; and u and v are the marginal distribution functions of flood peak flow and flood volume, respectively.
For the co-occurrence period T∩, the danger event E∩ denotes that both of the variables exceed the set threshold. The Copula function can be used to represent the co-occurrence recurrence period as:
The recommended marginal distribution of hydrological variables in China’s water conservancy is P-III distribution. However, P-III distribution does not fit well for some extreme events. Generalized extreme value distribution (GEV) and lognormal distribution (LN) are also widely used as marginal distributions. The marginal distribution is shown in Table 2.

Table 2.
Probability density distribution of marginal distribution.
2.2.3. Parameter Estimation and Goodness-of-fit Test
The parameter of bivariate Archimedean Copula can be estimated by its relationship with the Kendall rank correlation coefficient , which is shown in Table 3.

Table 3.
The relationship of the parameter of Archimedean Copula and Kendall .
Statistical methods and graphical methods are generally used to test the goodness-of-fit. In order to verify the degree of fit between Copula and the empirical cumulative probability of the measured samples, a goodness-of-fit test is needed for the constructed model. Commonly used test methods include the RMSE method and the AIC method [30].
where Femp and C are the empirical and theoretical cumulative probability, respectively; and n is the sample size. The smaller the RMSE value, the better the fitting.
where , and m is the number of parameters of the Copula function.
2.2.4. Scenario Hypothesis
A scenario hypothesis is used to simulate the hydrological response of flooding under a certain climate scenario in the future and then analyze the flood risk [31,32,33]. The hydrological response to climate change is the basis of the study on the influence of climate change on flood risk. The hydrological response to climate change is simulated by running the hydrological model of a river basin under manual climatic conditions to quantitatively analyze the effect of climate change on the flood hydrological process. The artificial scenario hypothesis is used to generate different climate scenarios in this study; that is, by artificially setting various combination scenarios of different precipitation and temperature changes, corresponding hydrological processes can be simulated in the hydrological model, to analyse the influence of climate change on the flood hydrology process in a watershed.
2.2.5. Climate Scenarios
According to the results of the IPCC (Intergovernmental Panel on Climate Change) China Climate Change Study, by the end of the 21st century, the average temperature in China is estimated to increase by 2.8~5.3 °C, and the annual precipitation is estimated to increase by 6.4~11%. Combined with the relevant literature research in the Qinhuai River Basin, the increases in rainfall levels of 0%, 2%, 4%, 8%, and 14% are used, and the temperature changes of −2 °C, 0, +2 °C, and +5 °C are used. Three floods of different magnitudes, that is, 199106030 (heavy), 19870701 (medium), and 20040618 (light), are selected to explore the effects of climate change on floods in the Qinhuai River Basin. The SWAT model was used to simulate the daily flow from 1986 to 2006 for the 20 climate scenarios. The P-III distribution and GEV distribution were used to fit the flood peak and flood volume, respectively, and the Copula function was used to analyze the joint probability. The climate scenarios are shown in Table 4.

Table 4.
Climate scenarios of different changes of temperature and precipitation.
3. Results
3.1. Flood Response Analysis Under Different Climate Scenarios
The simulation results of three floods under 20 climate scenarios are shown in Table 5.

Table 5.
The simulated results of floods under 20 climate scenarios.
3.2. Hydrological Response of Different Climate Scenarios
3.2.1. Analysis of the Impact of Temperature Changes on Floods
To examine the impact of temperature changes on different floods, the changes of climate scenarios T-2P0, T2P0, and T5P0 relative to the current situation T0P0 are analyzed. The results are shown in Figure 1, and Appendix A Table A1 for detailed data.
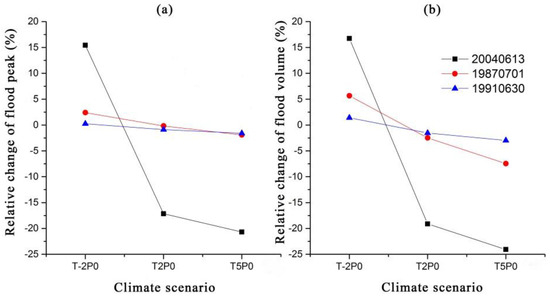
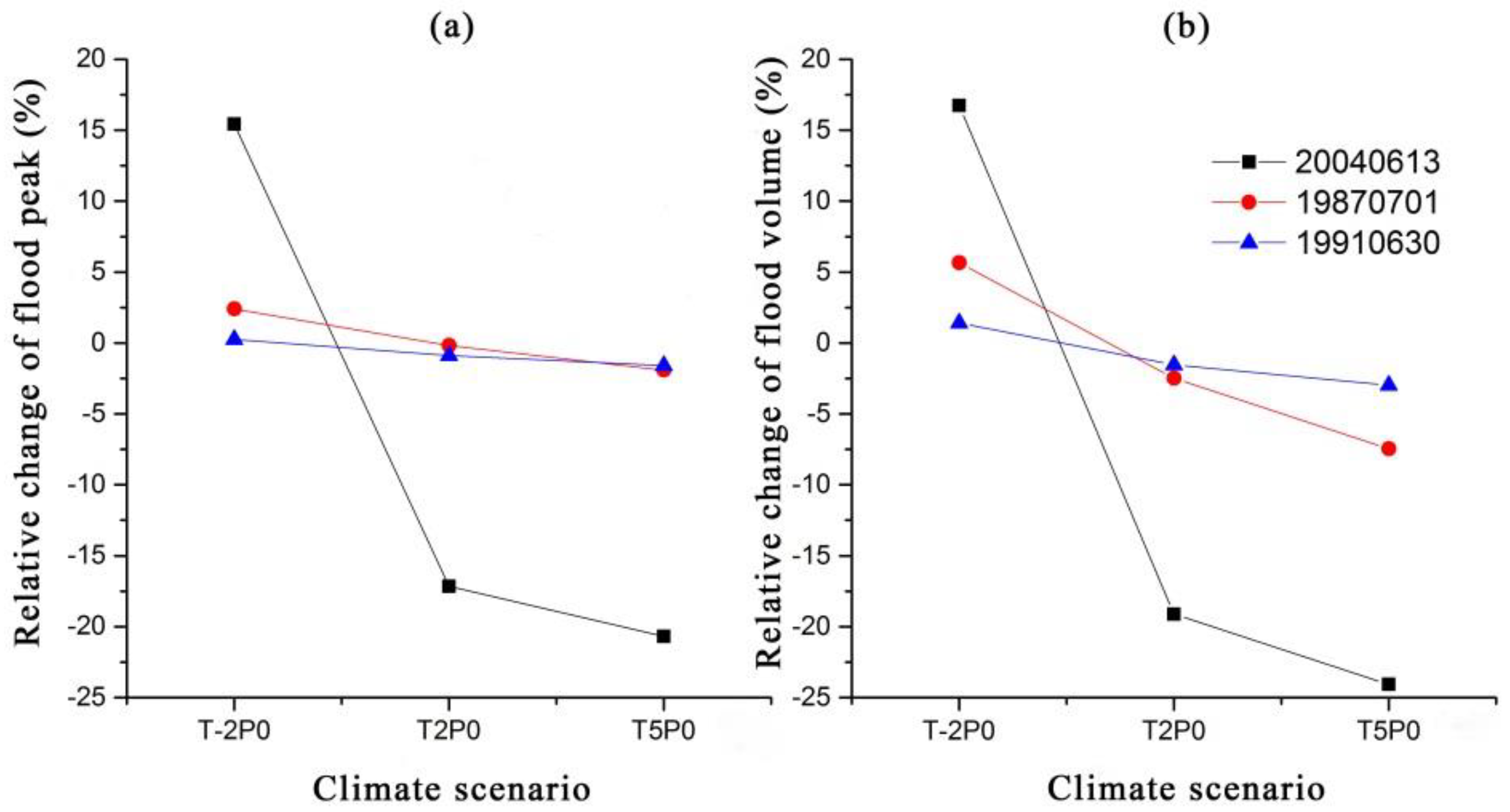
Figure 1.
The hydrological response of temperatures changes for different-scaled floods: (a) Relative change of flood peak under temperature changes; (b) Relative change of flood volume under temperature changes.
As the temperature rises, the peak flow and peak intensity decrease. When the temperature decreases, the peak flow and peak intensity increase. However, as the temperature gradually increases, the degree of influence on flood peaks decreases. The temperature has a greater impact on the magnitude than the flood peak; that is, the flood is more sensitive to temperature changes. When the temperature rises by 2 °C, the flood peaks and flood volumes of three floods are reduced by 6.07% and 7.71%, respectively. When the temperature rises by 5 °C, the flood peaks and flood volumes of three floods are reduced by an average of 8.06% and 11.50%, respectively. The hydrological response of different floods to temperature is different. Taking the temperature rise of 5 °C as an example, the relative changes in peak flow of light, medium, and heavy floods are −20.69%, −1.91%, and −1.59%, respectively. The relative changes in flood volume are −24.06%, −7.45%, and −2.98%. The hydrological response of light floods to temperature changes is significantly stronger than that of medium and heavy floods. It appears that temperature has a greater impact on peak flows and flood volumes for small floods.
3.2.2. Analysis of the Impact of Rainfall Changes on Floods
To analyze the impact of rainfall changes on different floods, the climate scenarios T0P2, T0P4, T0P8, and T0P14 are compared with the current situation T0P0. The results are shown in Figure 2 and Appendix A Table A2.
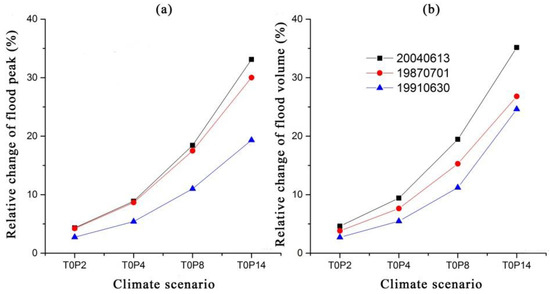
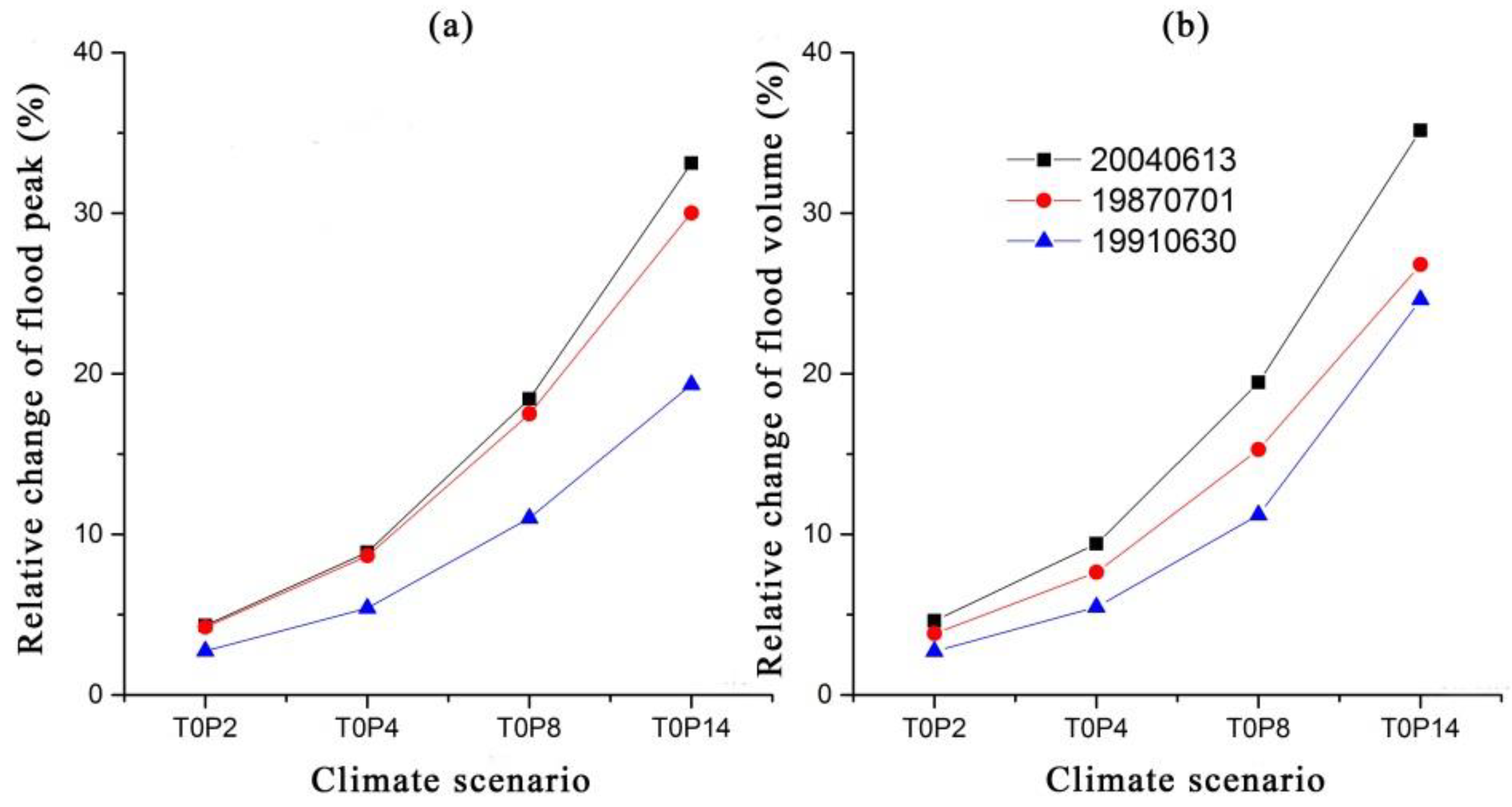
Figure 2.
The hydrological response of precipitation changes for different-scaled floods: (a) Relative change of flood peak under precipitation changes; (b) Relative change of flood volume under precipitation changes.
When rainfall increases, the flood peak increases as well. When the incremental rate in rainfall increased by 2%, 4%, 8%, and 14%, the curve gradually became steep, showing a consistent increasing trend. When the rainfall change was less than 8%, the impact of rainfall change on the flood peak was slightly greater than the flood volume. However, when the rainfall change increased to a certain extent, the impact on the flood volume was more significant than the flood peak. When the rainfall increased by 2%, 4%, 8%, and 14%, the average increase of flood peaks of the three floods was 3.76%, 7.65%, 15.64%, and 27.49%, respectively. When the rainfall increased by 2%, 4%, 8%, and 14%, the average increase of flood volumes of the three floods was 3.72%, 7.51%, 15.31%, and 28.86%, respectively.
The hydrological response to rainfall varies for different floods. Taking the increase of rainfall by 14% as an example, the relative changes of flood peaks are 33.11%, 30.02%, and 19.34%, respectively. The relative changes of flood volume are 35.16%, 26.80%, and 24.62%, respectively. The hydrological response of floods to rainfall is stronger for light floods than for medium- and large-scale floods. Small floods are more sensitive to rainfall changes.
3.2.3. Analysis of the Combined Effects of Temperature and Rainfall
Peak flows and flood volumes decrease with increasing temperature and increase with increasing rainfall. As the temperature rises, its impact weakens, and as the rainfall increases, its impact will intensify. The combined impact of temperature and rainfall is examined in this section using the scenarios of T2P2, T2P4, T2P8, T2P14, T5P2, T5P4, T5P8, and T5P14. The comparisons of these scenarios with the current situation T0P0 are shown in Table 6 and Figure 3.

Table 6.
Relative flood change when both temperature and precipitation increase.
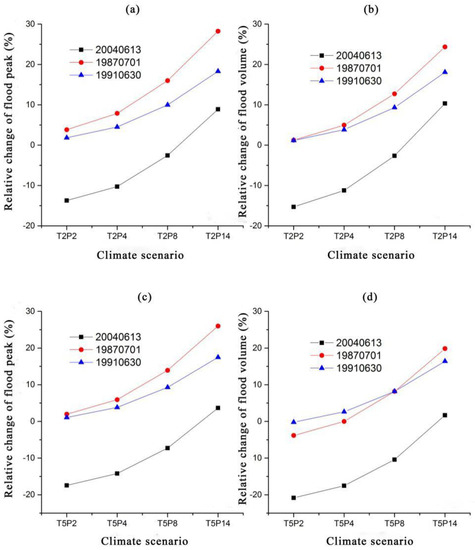
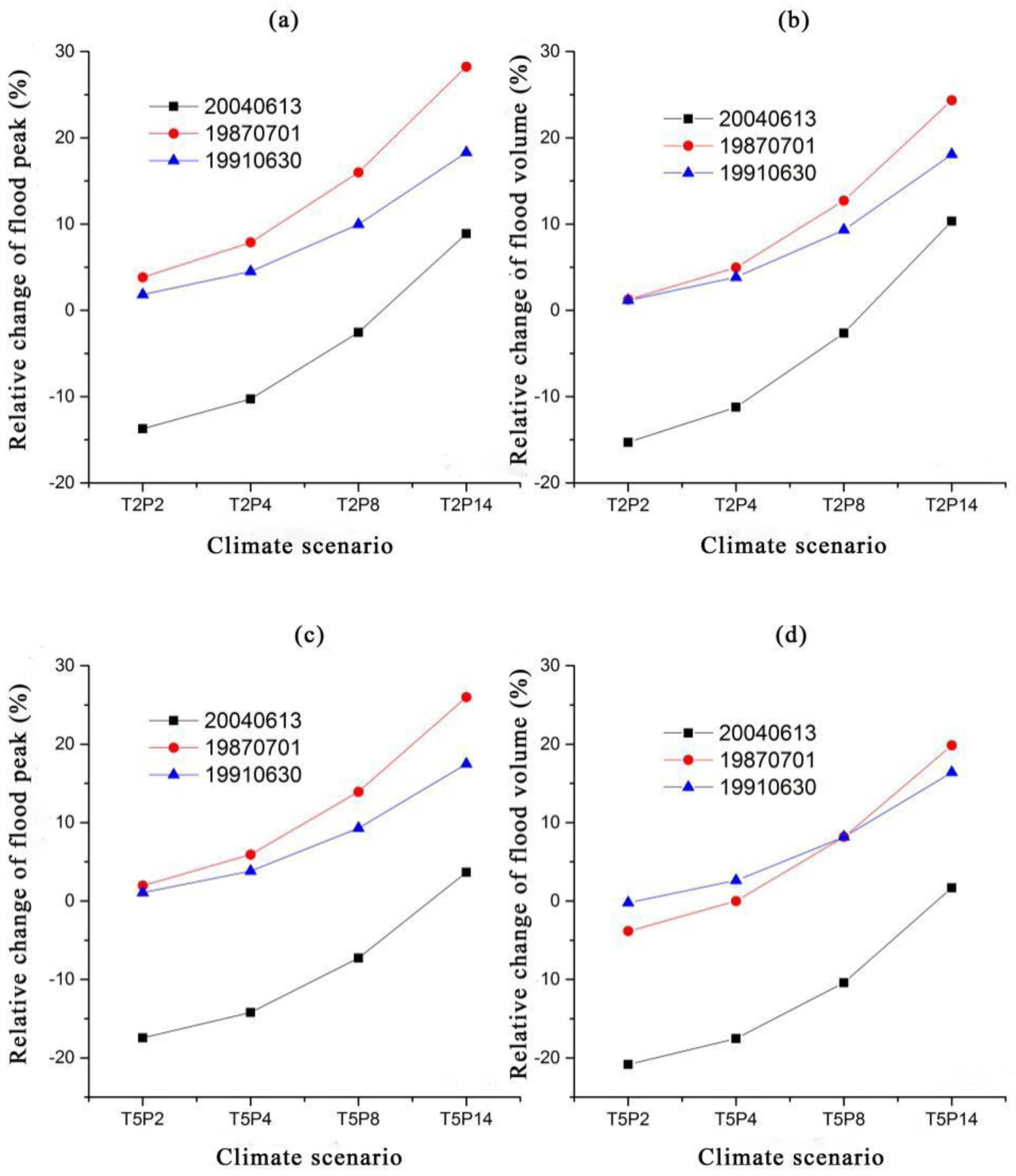
Figure 3.
The hydrological response of increased temperature and precipitation for different-scaled floods: (a) Relative change of flood peak under increased temperature and precipitation scenario (temperature rises 2 °C); (b) Relative change of flood volume under increased temperature and precipitation scenario (temperature rises 2 °C); (c) Relative change of flood peak under increased temperature and precipitation scenario (temperature rises 5 °C); (d) Relative change of flood volume under increased temperature and precipitation scenario (temperature rises 5 °C).
When the temperature and rainfall increase simultaneously, the flood generally shows an increasing trend. This may be because the impact of the temperature rising weakens for a higher temperature rise and the impact of rainfall increases intensifies for higher rainfall increases. In the T2P2, T2P4, T2P8, and T2P14 scenarios, the average flood peaks of light, medium, and heavy floods were −2.7%, 0.7%, 7.8%, and 18.5%, respectively. The average change of flood volume was −4.3%, −0.8%, 6.47%, and 17.63%, respectively. For light floods, temperature change appears to have a greater impact on flood peaks. The relative change values of the flood volume and peak flood are negative, and the peak volume intensity decreases. When the rainfall increase reaches 14%, the relative change of flood peak and flood volume become positive values.
3.3. Copula Function Fitting
The P-III and GEV distribution are selected to describe the marginal distribution of peak flow and flood volume, respectively. The maximum likelihood method is used to estimate the parameters and the goodness of fit is assessed with the KS test. The smaller the KS statistic, the better the fitting. The larger the P value, the more likely that the distribution is accepted. The location, scale, and shape parameters of the P-III distribution of peak flows are −276.240, 0.005, and 4.340, respectively; the location, scale, and shape parameters of the GEV distribution of flood volumes are 1.168, 1.020, and 0.724, respectively. The KS statistics of flood peak flooding are 0.099 and 0.127, and the corresponding P values are 0.737 and 0.78. Therefore, the marginal distributions fit pretty well.
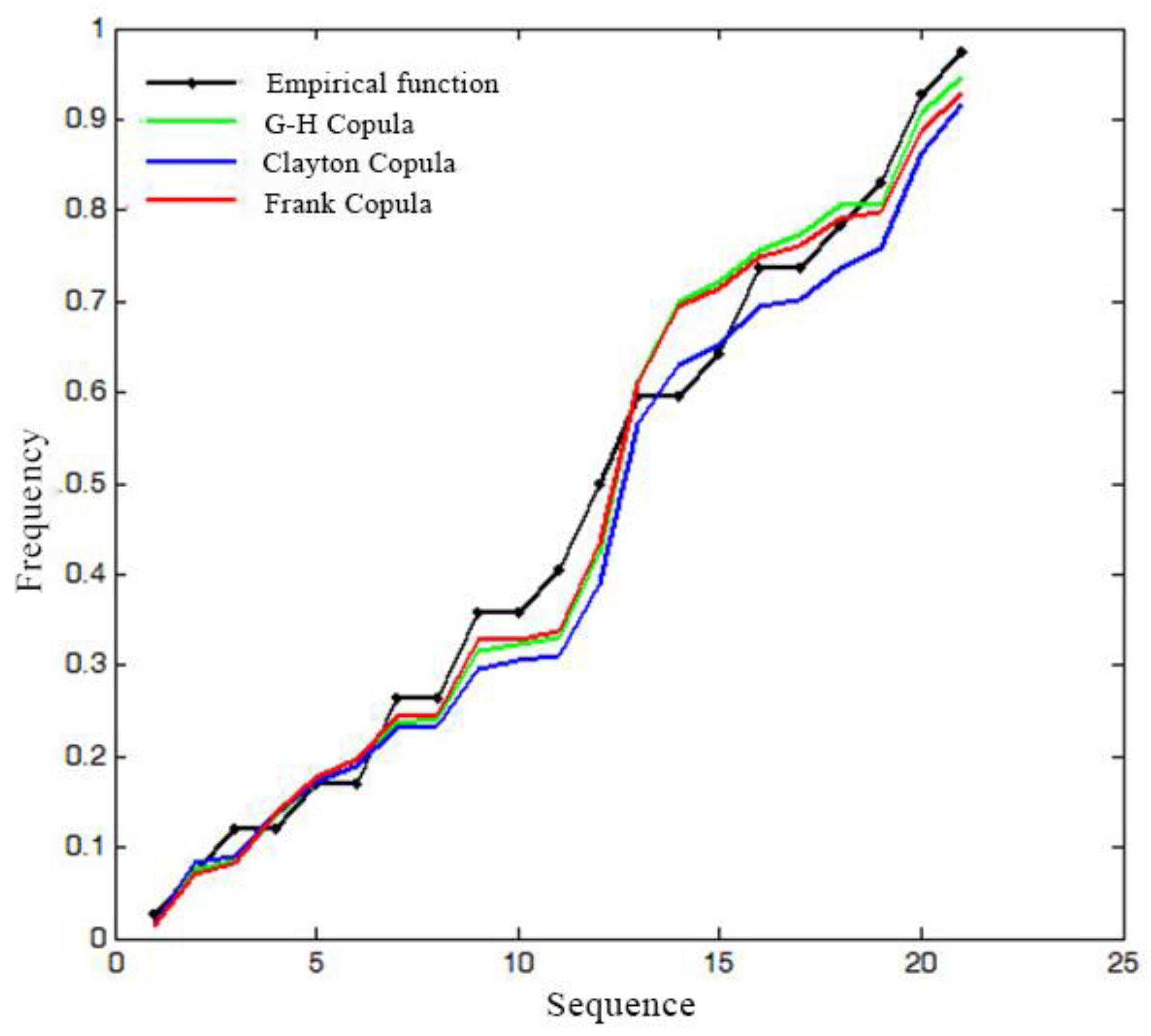
According to the two-dimensional Copula functions in Table 1, the relevance indicator method was used to estimate the parameters. The peak distribution model is established by marginal distributions of each variables. The corresponding parameters of G-H, Clayton, and Frank Copula are 4.9273, 3.1097, and 17.763, respectively. The RMSE and AIC methods were used to assess the goodness of fit. The smaller the RMSE and AIC values, the better the fitting. The results are shown in Table 7. The RMSE value of G-H Copula is the same as that of Frank, but the AIC value is the smallest. Figure 4 shows the fitting of the three Copula functions with the empirical frequency. According to the comparison of the goodness of fit, G-H Copula is selected to develop the joint distribution of peaks.

Table 7.
The goodness-of-fit test for the bivariate Copula function.
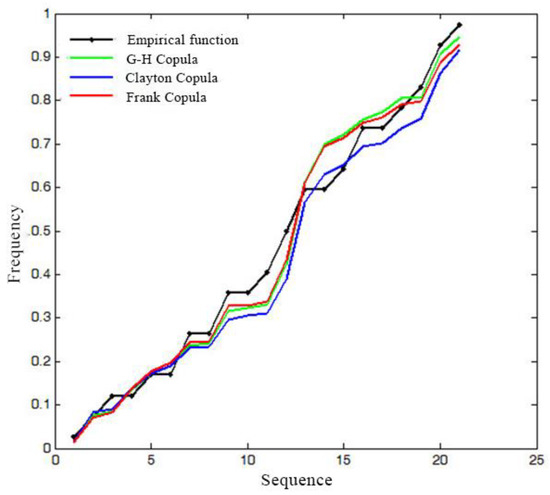
Figure 4.
Comparison of goodness-of-fit for joint distribution of peak flow and flood volume.
4. Discussion
4.1. Multivariate Flood Risk Analysis
4.1.1. Flood Risk Analysis Under Current Situation
According to the estimated peak-volume joint distribution risk model in the previous section, the joint return period, the co-occurrence return period, and the corresponding design values of the same frequency are calculated, with the univariate conditions given as a comparison. The results are shown in Table 8. The probability distributions of peak flows and flood volumes are plotted and corresponding recurring contours are added to the measured data for comparison, as shown in Figure 5 and Figure 6.

Table 8.
Design value for univariate and bivariate distribution.
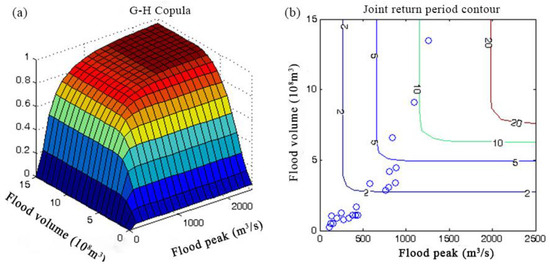
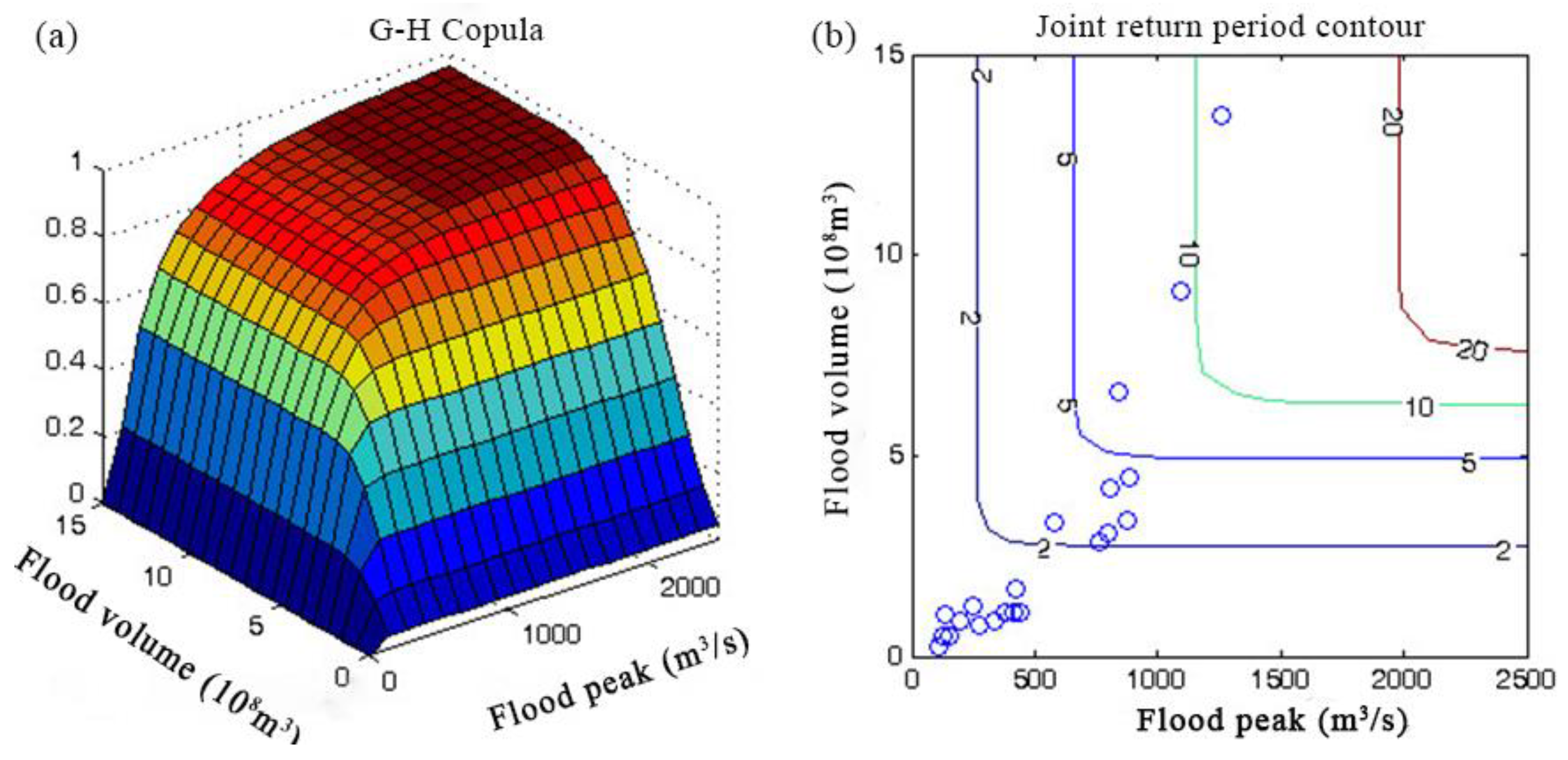
Figure 5.
(a) Peak-volume joint distribution; (b) The contour of peak-volume joint return period.
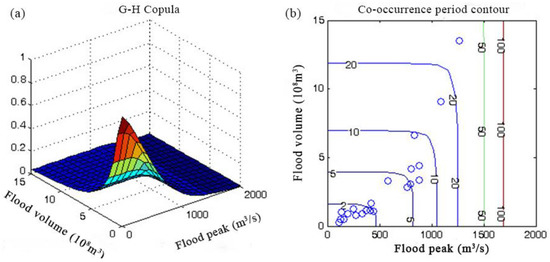
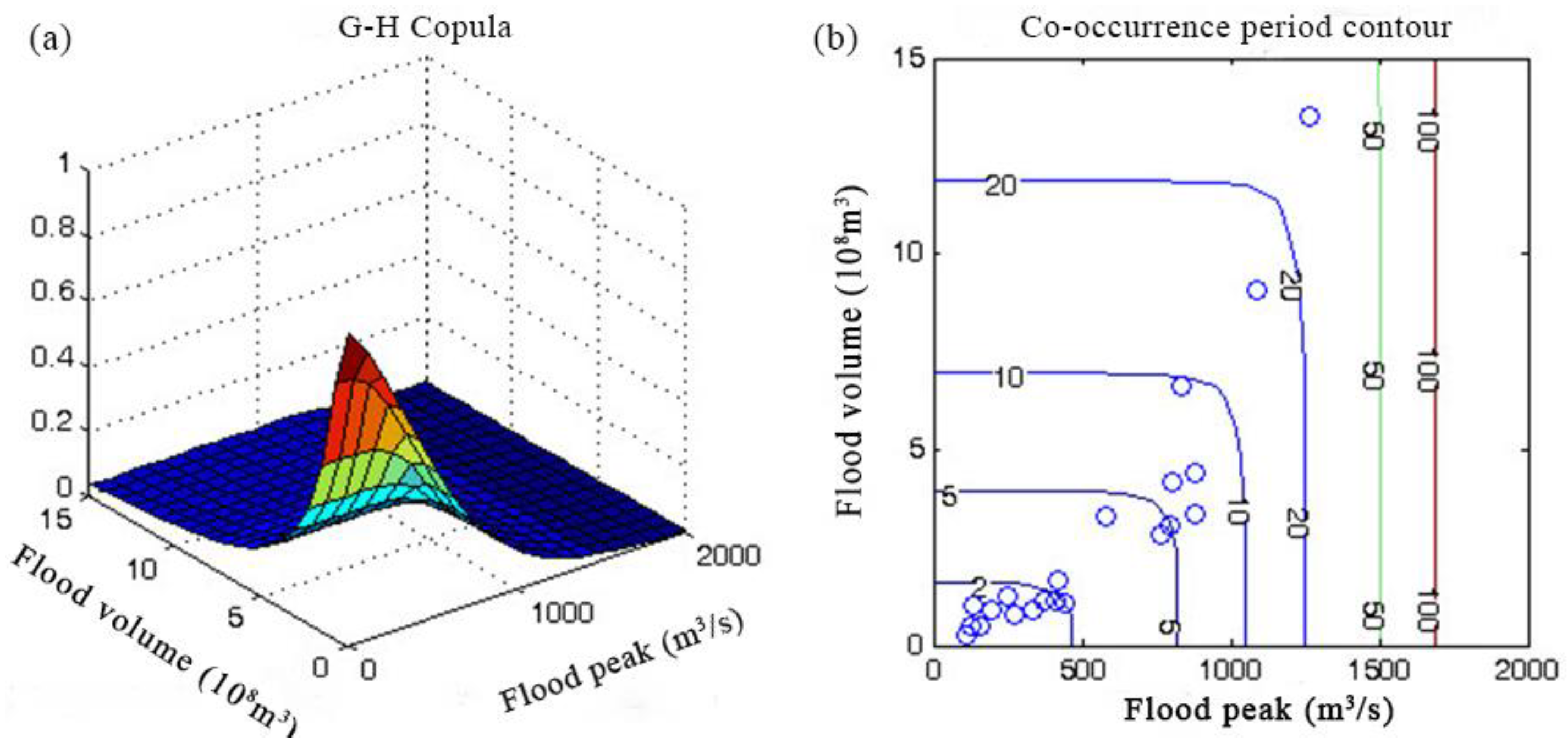
Figure 6.
(a) Peak-volume co-occurrence distribution; (b) The contour of Peak-volume co-occurrence period.
It can be seen that the peak-volume joint design value is greater than its corresponding univariate design value. The maximum joint return period of peak volume in 1986–2006 is about 12 years, and the maximum co-occurrence return period is about 30 years. The joint period is smaller than the univariate return period, and the co-occurrence return period is greater than the univariate return period. The joint recurrence period is smaller than the co-recurrence period; that is, the probability of individual variable exceedance is greater than the probability when both variables simultaneously exceed the threshold. The application of the recurrence period means a large safety margin, but it will increase the cost of flood control. Engineering design can consider the pros and cons of different return periods.
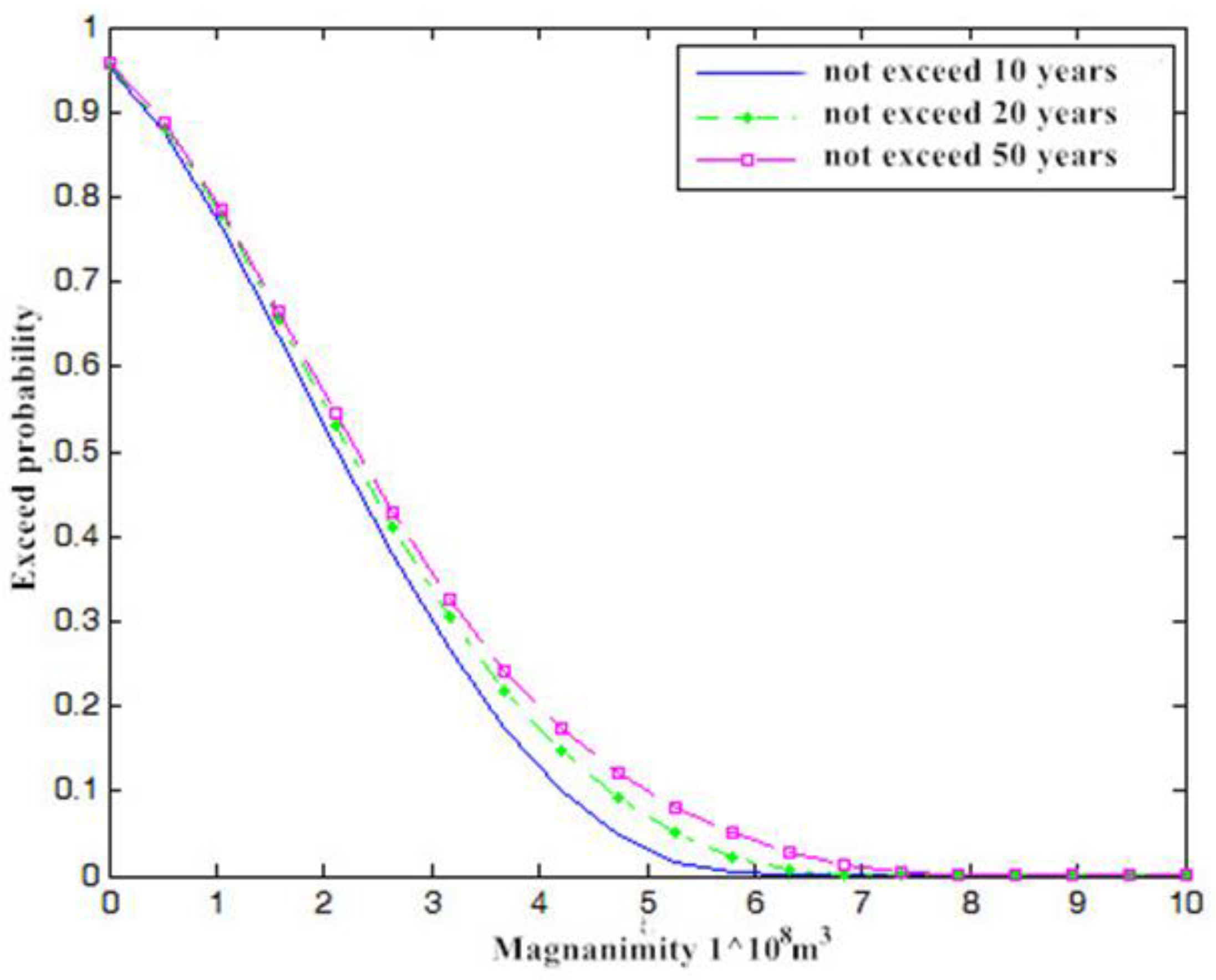
We also analyzed the risk of flood volume exceedance under a given peak flow. The flood volume exceedance probability when the return period of peak flow does not exceed 10 years, 20 years, and 50 years is plotted, as shown in Figure 7. When the peak flow does not exceed the design value of 10 years, 20 years, and 50 years, the probability of the flood volume exceeding five years (3.93 million m3) is 0.1121, 0.1579, and 0.1837, respectively. Given a certain flood threshold, the smaller the magnitude of the flood peak, the smaller the flood exceedance probability. When the flood peak is small, the flood volume is less likely to exceed the threshold.
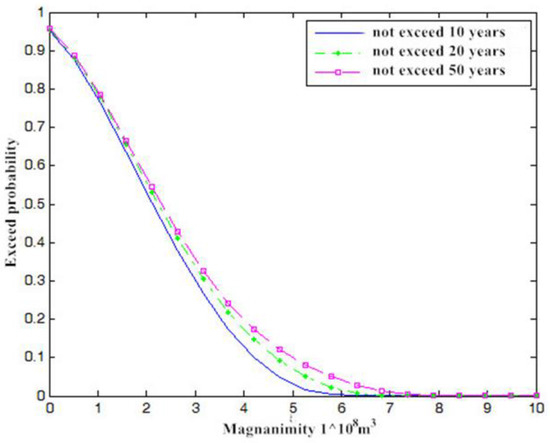
Figure 7.
Flood volume exceedance when peak flow is less than a certain return period.
4.1.2. Flood Risk Analysis Considering Climate Change Impact
The univariate and peak-volume joint flood risk under 20 different scenarios in the Qinhuai River Basin are compared with the baseline condition. Three typical flood processes of different scales were selected for comparative analysis. The results of flood peaks, floods, and joint risk of three floods under the climatic scenario are shown in Table 9.

Table 9.
The watershed flood risk under different climate scenarios.
Flood peaks decrease with increasing temperatures and increase with increasing rainfall. The scenario T-2P0 has the largest temperature drop and the scenario T0P14 has the greatest rainfall increase. The scenario T-2P14 has the largest temperature drop and greatest rainfall increase. It is thus selected to compare with the baseline scenario T0P0. The univariate and bivariate joint risk calculation results and relative risk changes of three floods are shown in Table 10. The comprehensive flood risk comparisons under the four different climate scenarios are shown in Figure 8.

Table 10.
The flood risk and their relative change for different-scaled floods.
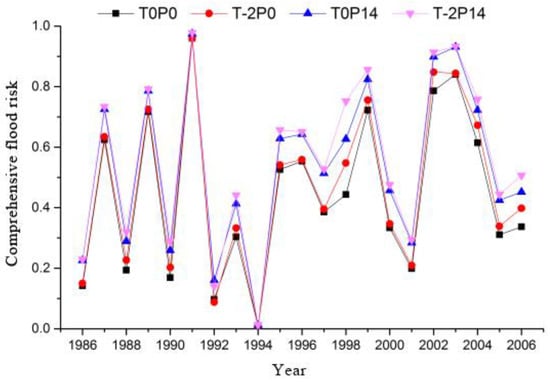
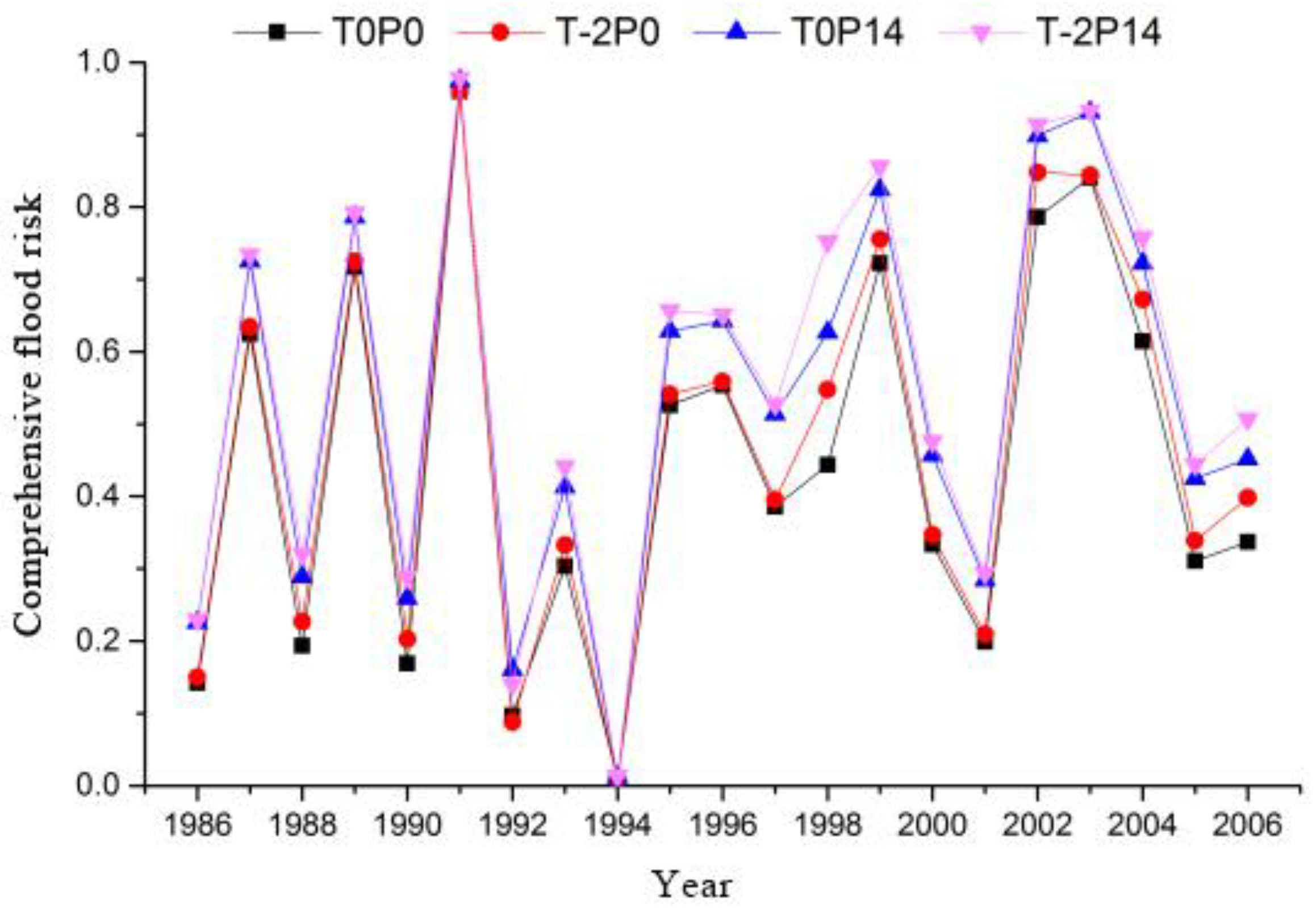
Figure 8.
The comprehensive flood risk comparisons under the four different climate scenarios.
It can be seen that the temperature drop and rainfall increase intensify the flood risk. The relative risks of the overlapped adverse effects caused by the temperature drop and the rainfall increase are the largest. Taking the light flood (20040618) as an example, the relative joint risks for the three climate scenarios T-2P0, T0P14, and T-2P14 are 9.42%, 17.55%, and 23.32%, respectively.
5. Conclusions
The 20 climate scenarios with different combinations of temperature and rainfall changes are employed to explore the hydrological response for different floods under climate change. Based on the simulation results, the following conclusions are reached.
The response of peak flows and flood volumes is similar and consistent under temperature or rainfall change. The peak flow increases with increasing rainfall and decreases with increasing temperature. The impact of temperature changes on flood volume is greater than that of peak flow.
The hydrological response of light floods to temperature changes is significantly stronger than that of medium and heavy floods. As the magnitude of floods decreases, the peak flow and flood volume change more obviously. When temperature rises, the peak-reduction effect will weaken. When rainfall increases, the peak-enhancement effect will become more significant.
The peak-volume joint design value is greater than its corresponding univariate design value. The temperature drop and rainfall increase intensify the flood risk.
Author Contributions
Conceptualization, methodology, and funding acquisition: Y.G.; Writing—Original draft preparation, Writing—Review, and editing: Y.G., Z.G., D.W., and Z.Z.; Modelling: Y.G. and Z.G.; Investigation and Data curation: Y.L.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51309076, 51609261; the Fundamental Research Funds for the Central Universities, grant number 2014B05814; the Fundamental Research Funds for the Natural Science Foundation of Jiangsu Province, grant number BK20181310; and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Relative flood change under different temperature change.
Table A1.
Relative flood change under different temperature change.
| Flood | Relative Flood Change (%) | ||||||
|---|---|---|---|---|---|---|---|
| Rank | Number | T-2P0 | T2P0 | T5P0 | |||
| Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | ||
| light | 20040618 | 15.43 | 16.75 | −17.15 | −19.11 | −20.69 | −24.06 |
| medium | 19870701 | 2.40 | 5.65 | −0.16 | −2.48 | −1.91 | −7.45 |
| heavy | 19910630 | 0.25 | 1.41 | −0.89 | −1.55 | −1.59 | −2.98 |
| average | 6.03 | 7.94 | −6.07 | −7.71 | −8.06 | −11.50 | |

Table A2.
Relative flood change under different precipitation change.
Table A2.
Relative flood change under different precipitation change.
| Floods | Relative Flood Change (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rank | Number | T0P2 | T0P4 | T0P8 | T0P14 | ||||
| Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | Q (m3/s) | V (108 m3) | ||
| light | 20040618 | 4.33 | 4.62 | 8.89 | 9.41 | 18.43 | 19.47 | 33.11 | 35.16 |
| medium | 19870701 | 4.23 | 3.82 | 8.66 | 7.64 | 17.50 | 15.27 | 30.02 | 26.80 |
| heavy | 19910630 | 2.74 | 2.72 | 5.41 | 5.48 | 11.01 | 11.20 | 19.34 | 24.62 |
| average | 3.76 | 3.72 | 7.65 | 7.51 | 15.64 | 15.31 | 27.49 | 28.86 | |
References
- Liu, Z.Y.; Xia, J. Impact of climate change on flood risk in China. Nature 2016, 3, 177–181. [Google Scholar]
- Wang, Y.; Cao, M.K.; Tao, B.; Li, K. The changing characteristics of spatial pattern of precipitation in China under the background of global climate change. Geogr. Res. 2006, 6, 1031–1040. [Google Scholar] [CrossRef]
- Wu, S.H.; Gao, J.B.; Deng, H.Y.; Liu, L.L.; Pan, W. Climate change risk and its quantitative assessment methods. Progr. Geogr. 2018, 1, 28–35. [Google Scholar]
- Yang, Z.; Zhang, L.P.; Qin, L.L.; Yang, Y.R.; Duan, Y.B. The variation characteristics of Danjiangkou Reservoir inflow flood and its response to future climate scenarios. Resour. Environ. Yangtze River Basin 2013, 5, 588–594. [Google Scholar]
- Mani, P. Spatial variability and potential impacts of climate change on flood and debris flow hazard zone mapping and implications for risk management. Nat. Hazards Earth Syst. Sci. 2008, 8, 539–558. [Google Scholar] [CrossRef]
- Ran, Q.X.; Zhang, X. Review on Methods of Multivariate Hydrological Joint Distribution and Copula Function. Water Resour. Power 2010, 9, 8–11. [Google Scholar]
- Jaworski, P.; Durante, F.; Rdle, W.; Karl, H.; Rychlik, T. Copula Theory and Its Applications. In Proceedings of the Copula Theory and Its Applications, Warsaw, Poland, 25–26 September 2009. [Google Scholar]
- Feng, P.; Mao, H.H.; Wang, Y. Hydrological frequency analysis method and its application under multivariable conditions. J. Hydraul. Eng. 2009, 1, 33–37. [Google Scholar]
- Duan, X.L.; Hao, Z.C. Research progress of Copula function in hydrological applications. In Proceedings of the First China Water Forum, Ningbo, Zhejiang, China, 14 October 2010. [Google Scholar]
- Yue, S. The Gumbel Mixed Model Applied to Storm Frequency Analysis. Water Resour. Manag. 2000, 14, 377–389. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Probabilistic assessment of flood risks using trivariate copulas. Theor. Appl. Climatol. 2013, 111, 341–360. [Google Scholar] [CrossRef]
- Chowdhary, H.; Escobar, L.A.; Singh, V.P. Identification of suitable copulas for bivariate frequency analysis of flood peak and flood volume data. Hydrol. Res. 2011, 42, 193–216. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate rainfall frequency distributions using Archimedean copulas. J. Hydrol. 2007, 332, 93–109. [Google Scholar] [CrossRef]
- Favre, A.C.; El Adlouni, S.; Perreault, L.; Thiemonge, N.; Bobee, B. Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Reddy, M.J.; Ganguli, P. Bivariate Flood Frequency Analysis of Upper Godavari River Flows Using Archimedean Copulas. Water Resour. Manag. 2012, 26, 3995–4018. [Google Scholar] [CrossRef]
- Fu, G.T.; Butler, D. Copula-based frequency analysis of overflow and flooding in urban drainage systems. J. Hydrol. 2014, 510, 49–58. [Google Scholar] [CrossRef]
- Gao, Y.Q.; Chen, Y.X.; Zhao, L.M.; Yang, M. Joint Probability Analysis of Different Frequency Rainfall in Qinhuai River Basin. Hydropower Energy Sci. 2016, 3, 1–5. [Google Scholar]
- Gao, Y.Q.; Ye, L.; Lai, L.J. Flood risk analysis of Qinhuai River Basin based on G-H copula function. J. Water Resour. Water Eng. 2018, 1, 172–177. [Google Scholar]
- Hao, Z.C.; Duan, X.L. Two-variable joint distribution and application of floods in flood season. J. Liaoning Techn. Univ 2011, 4, 533–536. [Google Scholar]
- Dung, N.V.; Merz, B.; Bardossy, A.; Apel, H. Handling uncertainty in bivariate quantile estimation—An application to flood hazard analysis in the Mekong Delta. J. Hydrol. 2015, 527, 704–717. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, Q.; Liu, Z.M. Three-variable flood risk assessment based on asymmetric Archimedean Copula. Adv. Water Sci. 2016, 5, 763–771. [Google Scholar]
- Gaal, L.; Szolgay, J.; Kohnova, S.; Hlavcova, K.; Parajka, J.; Viglione, A.; Merz, R.; Bloeschl, G. Dependence between flood peaks and volumes: A case study on climate and hydrological controls. Hydrol. Sci. J.-J. Des. Sci. Hydrol. 2015, 60, 968–984. [Google Scholar] [CrossRef]
- Rui, H. Land Use Change and Its Hydrological Effects in the Qinhuai River Basin; Nanjing University: Nanjing, China, 2012. [Google Scholar]
- Huang, D.P.; Liu, C.; Peng, S.F. Progress on Assessment and Regionalization of Flood Risk. Prog. Geogr. 2007, 26, 11–22. [Google Scholar]
- Sun, Z.L.; Zhu, X.F.; Pan, Y.Z.; Liu, X.F. Flood Risk Analysis: Progress, Challenges and Prospect. J. Catastrophol. 2017, 32, 125–130. [Google Scholar]
- Gumbel, E.J. Bivariate exponential distributions. J. Am. Stat. Assoc. 1960, 55, 698–707. [Google Scholar] [CrossRef]
- Hougaard, P. A class of multivariate failure time distributions. Biometrika 1986, 73, 671–678. [Google Scholar] [CrossRef]
- Clayton, D.G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic desease incidence. Biometrika 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Frank, M.J. On the simultaneous associativity of F(x,y) and x + y − F(x,y). Aequ. Math. 1979, 19, 194–226. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel inference—Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 22, 261–304. [Google Scholar] [CrossRef]
- Kim, D.; Chun, J.A.; Aikins, C.M. An hourly-scale scenario-neutral flood risk assessment in a mesoscale catchment under climate change. Hydrol. Process. 2018, 19, 2427. [Google Scholar] [CrossRef]
- Prudhomme, C.; Wilby, R.L.; Crooks, S.; Kay, A.L.; Reynard, N.S. Scenario-neutral approach to climate change impact studies: Application to flood risk. J. Hydrol. 2010, 390, 198–209. [Google Scholar] [CrossRef]
- Vormoor, K.; Rössler, O.; Bürger, G.; Bronstert, A.; Weingartner, R. When timing matters-considering changing temporal structures in runoff response surfaces. Clim. Chang. 2017, 142, 213–226. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).