A Cost–Benefit Based, Parametric Procedure to Screen Existing Irrigation and Municipal Supply Reservoirs for Wind Energy Storage
Abstract
1. Introduction
2. Materials and Methods
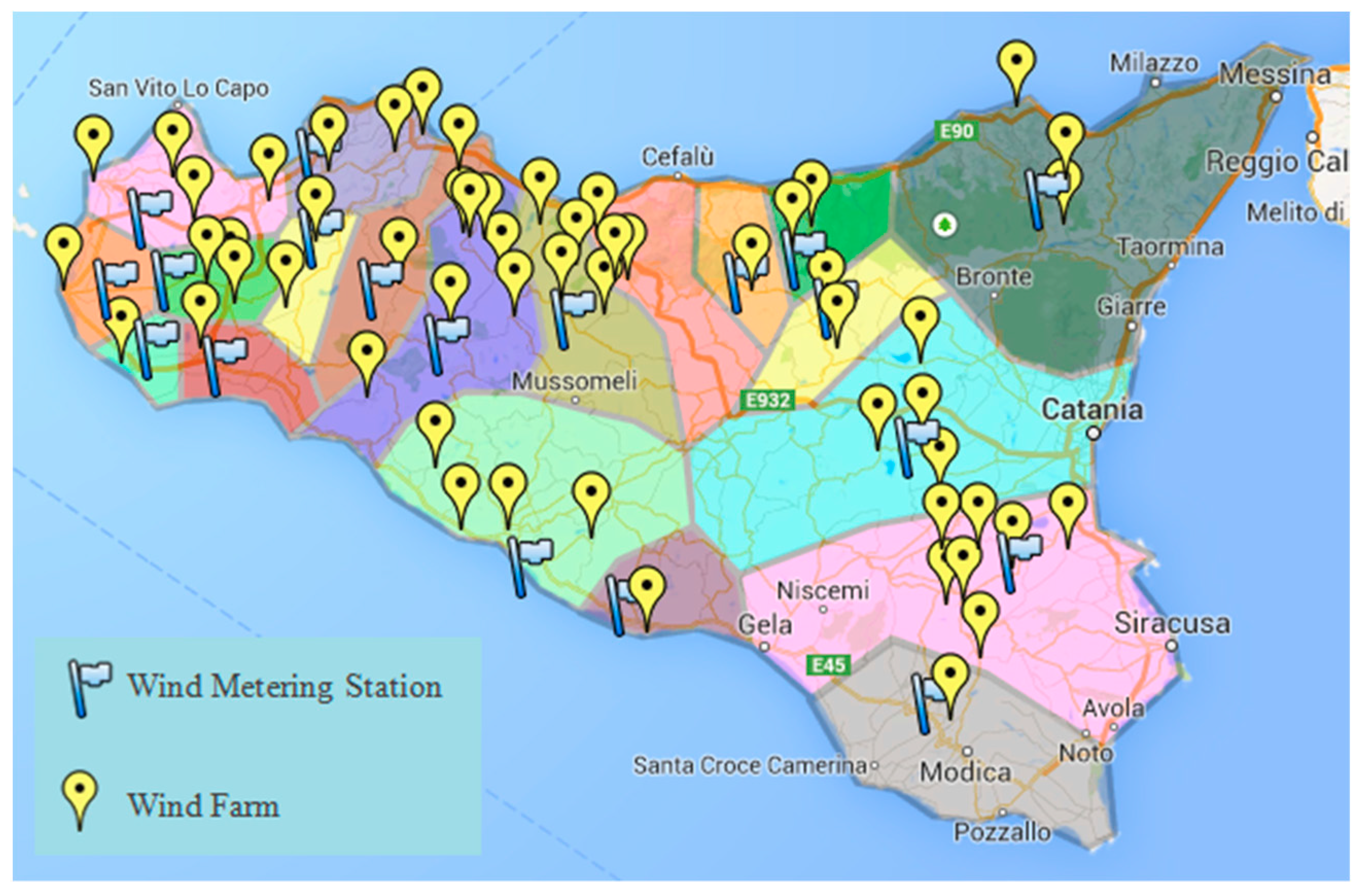
2.1. Estimation of Wind Power Production Data
2.2. Load Data
2.3. The Evaluation Model
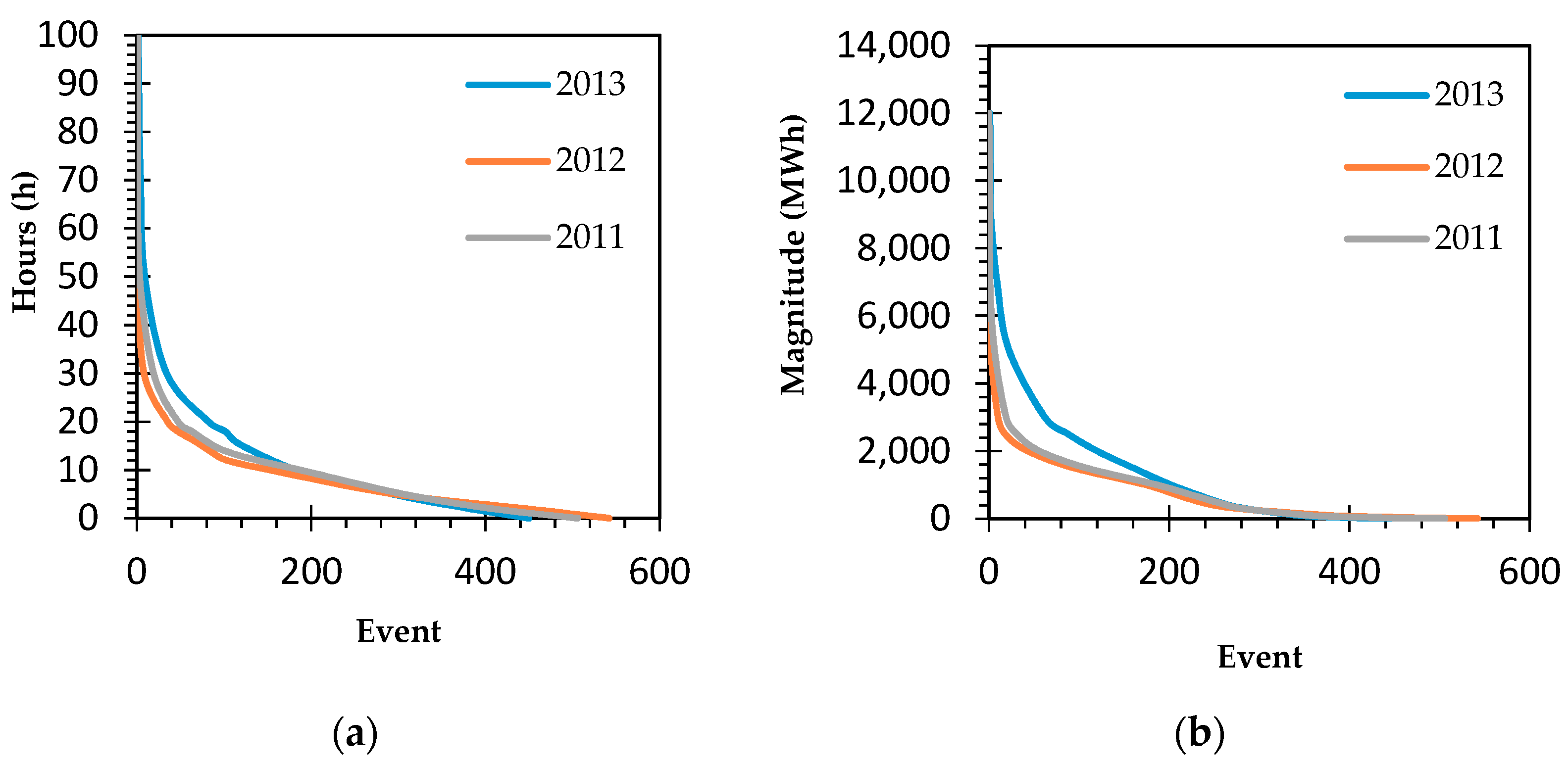
2.3.1. Modelling the Storage–Release Process
2.3.2. Assessing the Economic Indicators of the Plant
- 1)
- NPV of the plant:where C0 is the investment cost, assumed concentrated in year 0, By is the benefit in year y, Cy is the cost in year y and r is the social discount rate (SDR), set equal to 3.5% [30]. The methodology to obtain costs is illustrated in 2.3.3, and benefit estimation is reported at 2.3.4. After N years, at the end of the planning period, a residual value of the existing infrastructure should be considered. In addition, depending on N, the cost for equipment renewal should be concentrated in some year distant from the first one (say the 20th or the 30th). In this analysis, the planning horizon was set equal to 25 years so to avoid considering renewal costs, while residual value was conservatively omitted.
- 2)
- IRR of the plant: the discount rate that makes NPV = 0.
- 3)
- B/C: the ratio between actualized benefits and costs:
- 4)
- LCOE, the levelized cost of energy:where ICy, My and Fy respectively represent investment, operation and maintenance costs (O&M), and fuel expenditures in year y. LCOE has the dimension of a price and is similar to B/C ratio, except that benefits are not quantified explicitly.
- 5)
- Eff = Ereltot/EabstotFinally, a saturation index may be defined, as the ratio between energy produced and the total energy surplus:
- 6)
- Sat = Ereltot/WtotThe first three indicators require an explicit assessment of both costs and benefits of the plant.
2.3.3. Cost Assessment
2.3.4. Benefits Assessment
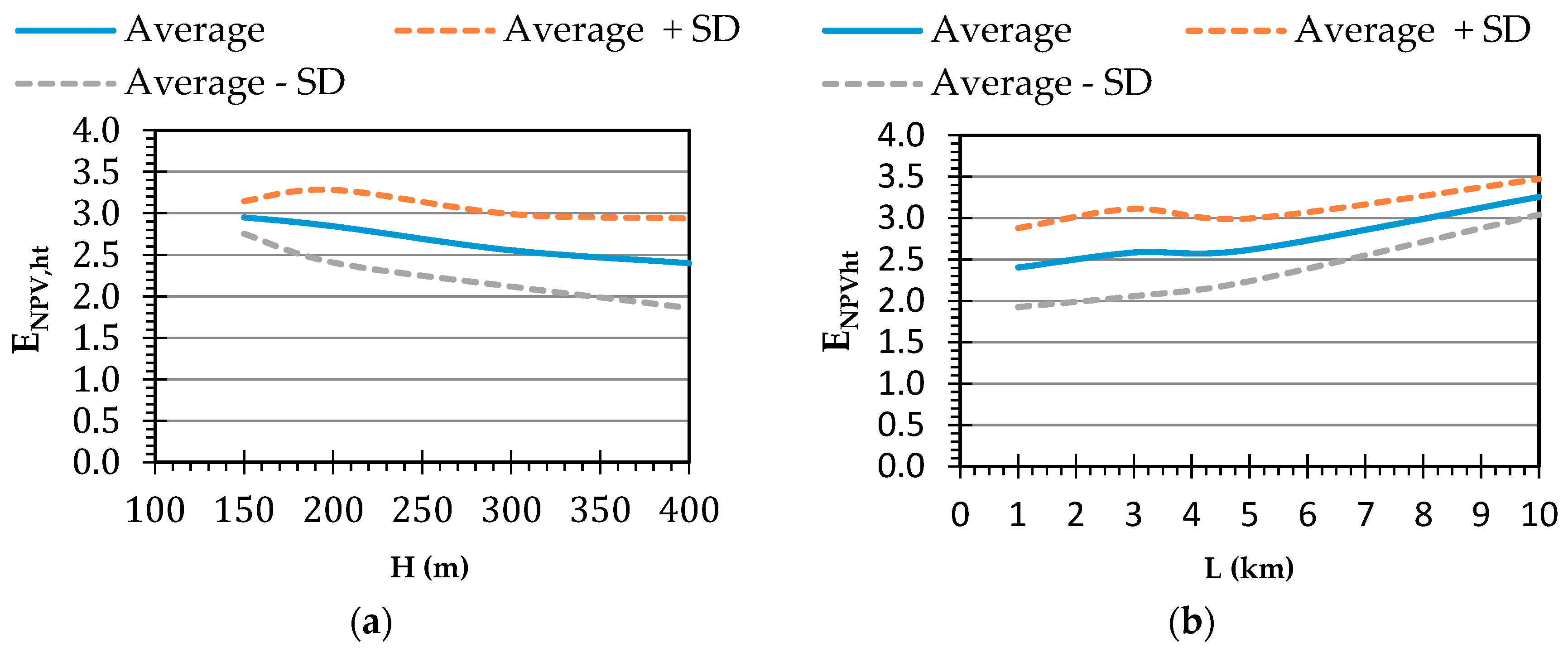
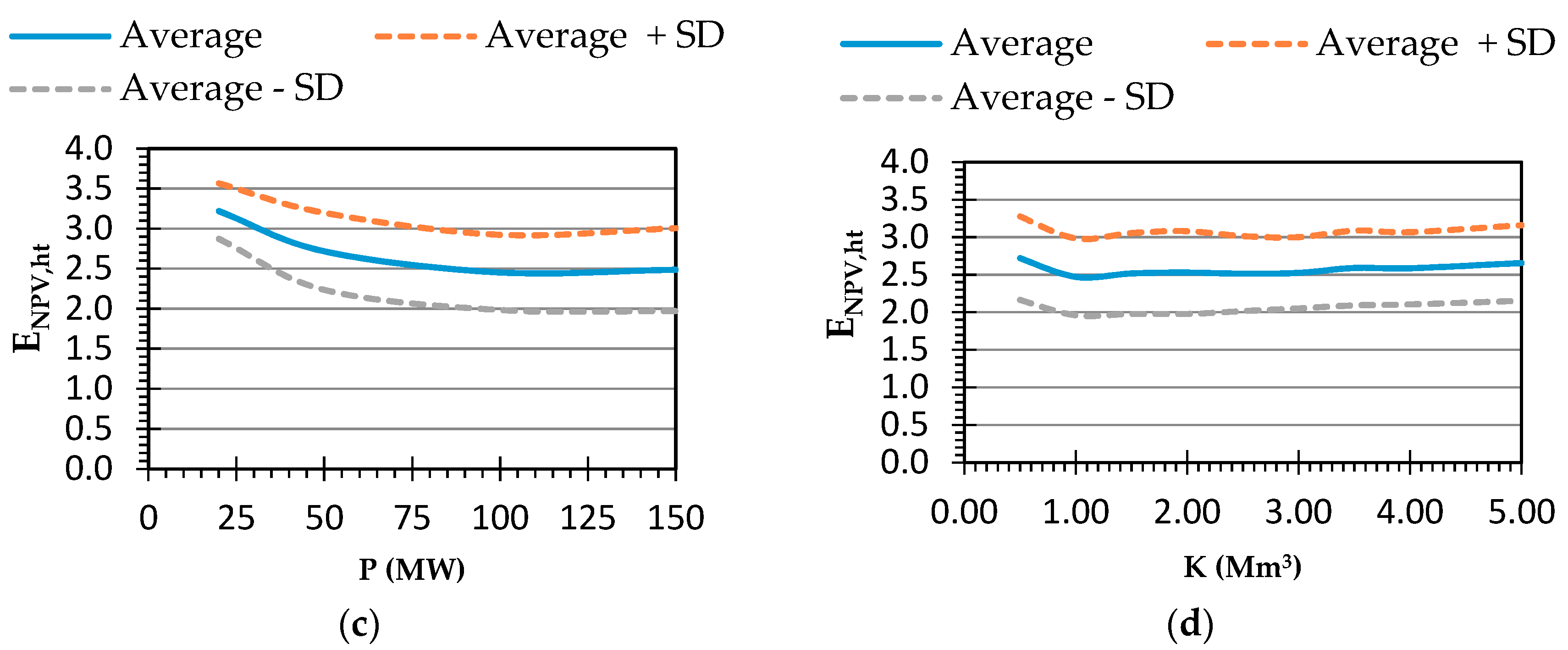
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Electric Power Research Institute, Inc. (EPRI). Electricity Energy Storage Technology Options—A White Paper Primer on Applications, Costs, and Benefits; Electric Power Research Institute, Inc.: Palo Alto, CA, USA, 2010. [Google Scholar]
- Electric Power Research Institute, Inc. (EPRI). Grid Integration of Large-Capacity Renewable Energy Sources and Use of Large-Capacity Electrical Energy Storage—White Paper. 2012. Available online: www.iec.ch (accessed on 4 December 2018).
- National Renewable Energy Laboratory. Renewable Electricity Futures Study; 4 Volumes NREL/TP-6A20-52409; Hand, M.M., Baldwin, S., DeMeo, E., Reilly, J.M., Mai, T., Arent, D., Porro, G., Meshek, M., Sandor, D., Eds.; National Renewable Energy Laboratory: Golden, CO, USA, 2012. [Google Scholar]
- Denholm, P.; Ela, E.; Kirby, B.; Milligan, M. The Role of Energy Storage with Renewable Energy Generation; NREL Technical Report NREL/TP-6A2-47187; National Renewable Energy Laboratory: Golden, CO, USA, 2012. [Google Scholar]
- European Commission—DG ENER. The Future Role and Challenges of Energy Storage, DG-ENER Working Paper. 2013. Available online: http://ec.europa.eu/energy/infrastructure/doc/energy-storage/2013/energy_storage.pdf (accessed on 4 December 2018).
- Strbac, G.; Aunedi, M.; Pudjianto, D.; Djapic, P.; Teng, F.; Sturt, A.; Jackravut, D.; Sansom, R.; Yufit, V.; Brandon, N. Strategic Assessment of the Role and Value of Energy Storage Systems in the UK Low Carbon Energy Future, Report for Carbon Trust; Energy Futures Lab, Imperial College: London, UK, 2012. [Google Scholar]
- Eurelectric. Renewables Action Plan—Annexes. 2011. Available online: www.eurelectric.org (accessed on 4 December 2018).
- Castronuovo, E.D.; Lopes, J.A.P. Optimal operation and hydro storage sizing of a wind-hydro power plant. Electr. Power Energy Syst. 2004, 26, 771–778. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Finn, P.; Mathiesen, B.V.; Leahy, M. Practical operation strategies for pumped hydroelectric energy storage (PHES) utilising electricity price arbitrage. Energy Policy 2011, 39, 4189–4196. [Google Scholar] [CrossRef]
- Parastegari, M.; Hooshmand, R.-A.; Khodabakhshian, A.; Forghani, Z. Joint operation of wind farms and pump-storage units in the electricity markets: Modeling, simulation and evaluation. Simul. Model. Pract. Theory 2013, 37, 56–69. [Google Scholar] [CrossRef]
- Muche, T. Optimal operation and forecasting policy for pump storage plants in day-ahead markets. Appl. Energy 2014, 113, 1089–1099. [Google Scholar] [CrossRef]
- Korpaas, M.; Holen, T.; Hildrum, R. Operation and sizing of energy storage for wind power plants in a market system. Int. J. Electr. Power Energy Syst. 2003, 25, 599–606. [Google Scholar] [CrossRef]
- Yang, C.-J.; Jackson, R.B. Opportunities and barriers to pumped-hydro energy storage in the United States. Renew. Sustain. Energy Rev. 2011, 15, 839–844. [Google Scholar] [CrossRef]
- Ardizzon, G.; Cavazzini, G.; Pavesi, G. A new generation of small hydro and pumped-hydro power plants: Advances and future challenges. Renew. Sustain. Energy Rev. 2014, 31, 746–761. [Google Scholar] [CrossRef]
- Kapsali, M.; Anagnostopoulos, J.S.; Kaldellis, J.K. Wind powered pumped-hydro storage systems for remote islands: A complete sensitivity analysis based on economic perspectives. Appl. Energy 2012, 99, 430–444. [Google Scholar] [CrossRef]
- Papaefthymiou, S.V.; Papathanassiou, S.A. Optimum sizing of wind-pumped-storage hybrid power stations in island systems. Renew. Energy 2014, 64, 187–196. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Zafirakis, D.; Kavadias, K. Techno-economic comparison of energy storage systems for island autonomous electrical networks. Renew. Sustain. Energy Rev. 2009, 13, 378–392. [Google Scholar] [CrossRef]
- Kane, M. Development of Bulk Energy Storage & Natura 2000, Deliverable 3.3. STOre Project. 2012. Available online: www.store-project.eu (accessed on 4 December 2018).
- Genco, M. Ricerca su l’uso delle capacità residue di laghi artificiali esistenti come accumulo di energia elettrica Attività propedeutica Fasi 1 e 2—Rapporto Finale, 2015. Available online: http://www.fondazionamga.it (accessed on 4 December 2018).
- Arántegui, R.L.; Fitzgerald, N.; Leahy, P. Pumped-Hydro Energy Storage: Potential for Transformation from Single Dams, JRC-IET Report EUR 25239 EN; European Union: Luxembourg, 2011. [Google Scholar]
- Connolly, D.; MacLaughin, S.; Leahy, M. Development of a computer program to locate potential sites for pumped hydroelectric energy storage. Energy 2010, 35, 375–381. [Google Scholar] [CrossRef]
- Gimeno-Gutiérrez, M.; Lacal-Arántegui, R. Assessment of the European Potential for Pumped Hydropower Energy Storage; JRC Scientific and Policy reports; European Union: Luxembourg, 2013; ISBN 978-92-79-29511-9. [Google Scholar]
- Bueno, C.; Carta, C. Wind powered pumped hydro storage systems, a means of increasing the penetration of renewable energy in the Canary Islands. Renew. Sustain. Energy Rev. 2006, 10, 312–340. [Google Scholar] [CrossRef]
- Anagnostopoulos, J.; Papantonis, D. Simulation and size optimization of a pumped–storage power plant for the recovery of wind-farms rejected energy. Renew. Energy 2008, 33, 1685–1694. [Google Scholar] [CrossRef]
- Rozali, N.E.M.; Alwi, S.R.W.; Mananam, Z.A.; Klemeš, J.J.; Mohammad Yusri Hassan, M.Y. Optimisation of Pumped-Hydro Storage System for Hybrid Power System Using Power Pinch Analysis. Chem. Eng. Trans. 2013, 35, 85–90. [Google Scholar] [CrossRef]
- Benitez, L.E.; Benitez, P.C.; Van Kooten, G.C. The economics of wind power with energy storage. Energy Econ. 2008, 30, 1973–1989. [Google Scholar] [CrossRef]
- Parfomak, P.W. Energy Storage for Power Grids and Electric Transportation: A Technology Assessment; CRS Report for Congress; Congressional Research Service: Washington, DC, USA, 2012; Available online: https://fas.org/sgp/crs/misc/R42455.pdf (accessed on 4 December 2018).
- Servizio Informativo Agrometeorologico Siciliano. Available online: http://www.sias.regione.sicilia.it (accessed on 4 December 2018).
- Jacobson, N. Basic Algebra 1, 2nd ed.; Dover Publications: Mineola, NY, USA, 2009; ISBN 978-0-486-47189-1. [Google Scholar]
- EC-Directorate General Regional Policy. Guide to Cost-Benefit Analysis of Investment Projects; Publications Office of the European Union, European Union: Luxembourg, 2015; ISBN 978-92-79-34796-2. [Google Scholar]
- Florio, M. Applied Welfare Economics—Cost-Benefit Analysis of Projects and Policies; Routledge: London, UK, 2014; ISBN 978-0-415-85833-5. [Google Scholar]
- Regione Siciliana, Nuovo Prezziario Unico Regionale per i Lavori Pubblici 2013. Available online: https://www.acca.it/prezzario-regione-sicilia (accessed on 27 November 2018).
- Alvarado-Anceida, C.A. Estimating E&M Powerhouse Costs, International Water Power& Dam Construction. 2009. Available online: http://www.waterpowermagazine.com/ (accessed on 4 December 2018).
- Black, M.; Strbac, G. Value of storage in providing balancing services for electricity generation systems with high wind penetration. J. Power Sources 2006, 162, 949–953. [Google Scholar] [CrossRef]
- Denholm, P.; Ela, L.; Kirby, B.; Milligan, M. The Role of Energy Storage with Renewable Electricity Generation; NREL/TP-6A2-47187; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
- Rahimi, E.; Rabiee, A.; Aghaei, J.; Muttaqi, K.M.; Nehzad, A.E. On the management of wind power intermittency. Renew. Sustain. Energy Rev. 2013, 26, 643–653. [Google Scholar] [CrossRef]
- Chang, M.K.; Eichman, D.J.; Mueller, F.; Samuelsen, S. Buffering intermittent renewable power with hydroelectric generation: A case study in California. Appl. Energy 2013, 112, 1–11. [Google Scholar] [CrossRef]
- Nyamdash, B.; Denny, E. The impact of electricity storage on wholesale electricity prices. Energy Policy 2013, 58, 6–16. [Google Scholar] [CrossRef]
- Gast, N.; Le Boudec, J.; Proutiere, A.; Tomozei, D. Impact of storage on the efficiency and prices in real-time electricity markets. In Proceedings of the e-Energy ’13, Berkley, CA, USA, 21–24 May 2013. [Google Scholar]
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Pican, E.; Leahy, M. The technical and economic implications of integrating fluctuating renewable energy using energy storage. Renew. Energy 2012, 43, 47–60. [Google Scholar] [CrossRef]
- Vennemann, P.; Gruber, K.H.; Haaheim, J.U.; Kunsch, A.; Sistenich, H.-P.; Thöni, H.-R. Pumped storage plants—Status and perspectives. VGB PowerTech 2011, 4/2011, 32–38. [Google Scholar]
- Donalek, P.; Clark, H.; Nakata, R.; Stein, J. Application of Adjustable Speed Doubly Fed Machines in Pumped Storage and Conventional Hydroelectric Plants. In Proceedings of the American Power Conference, Chicago, IL, USA, 13–15 April 1993; Volume 55-I, pp. 245–290. [Google Scholar]
- Donalek, P.; Clark, H. Application of Adjustable Speed Machines in Conventional and Pumped Storage Hydro Projects; EPRI: Palo Alto, CA, USA, 1995. [Google Scholar]
- Loucks, D.P.; Van Beek, E. Water Resources Systems Planning and Management—An Introduction to Methods, Models and Applications; UNESCO Publishing: Paris, France, 2005; ISBN 92-3-103998-9. [Google Scholar]
- Schill, W.P.; Kemfert, C. Modeling Strategic Electricity Storage: The Case of Pumped Hydro Storage in Germany. Energy J. 2013, 32, 59–87. [Google Scholar] [CrossRef]
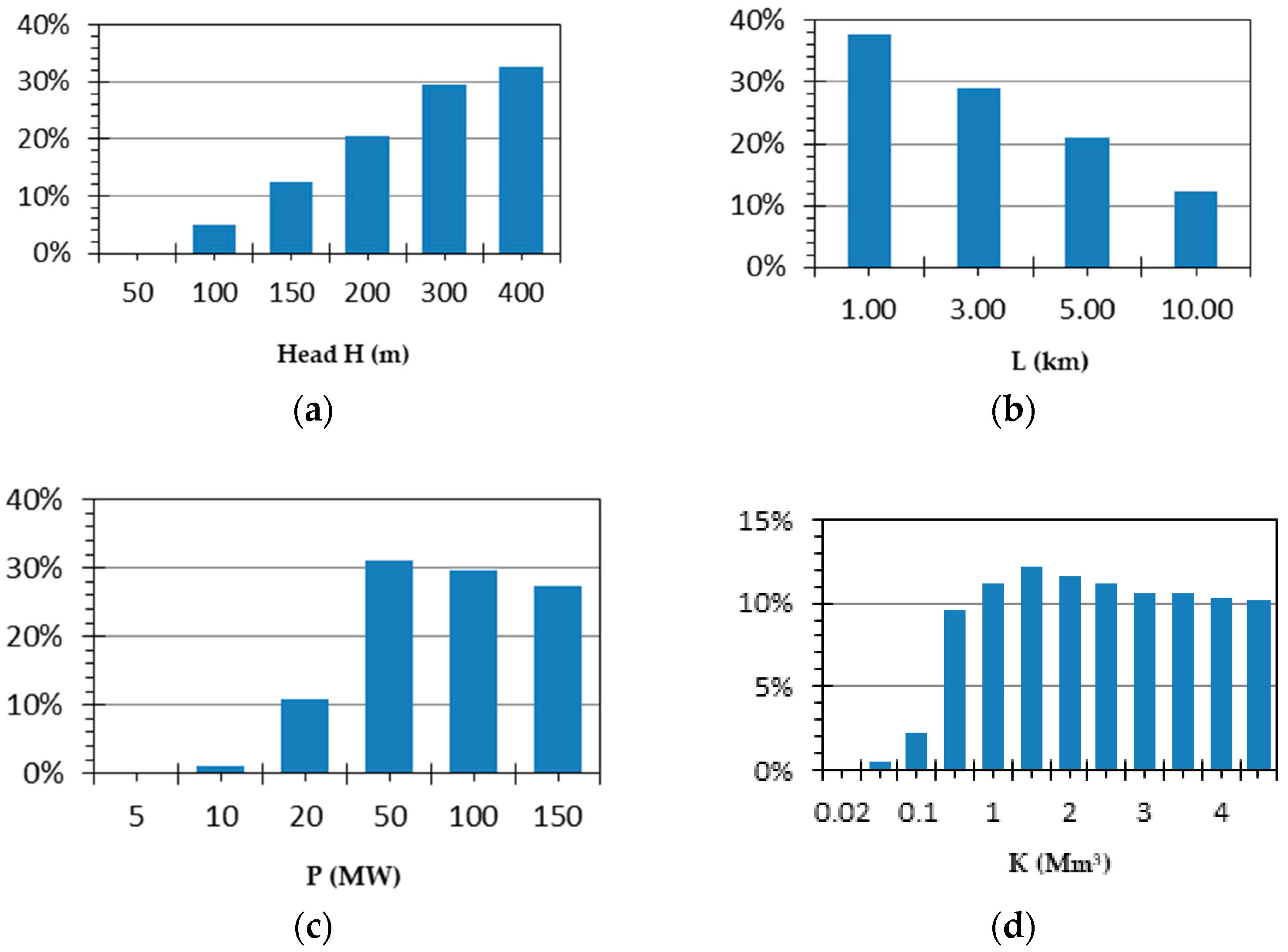
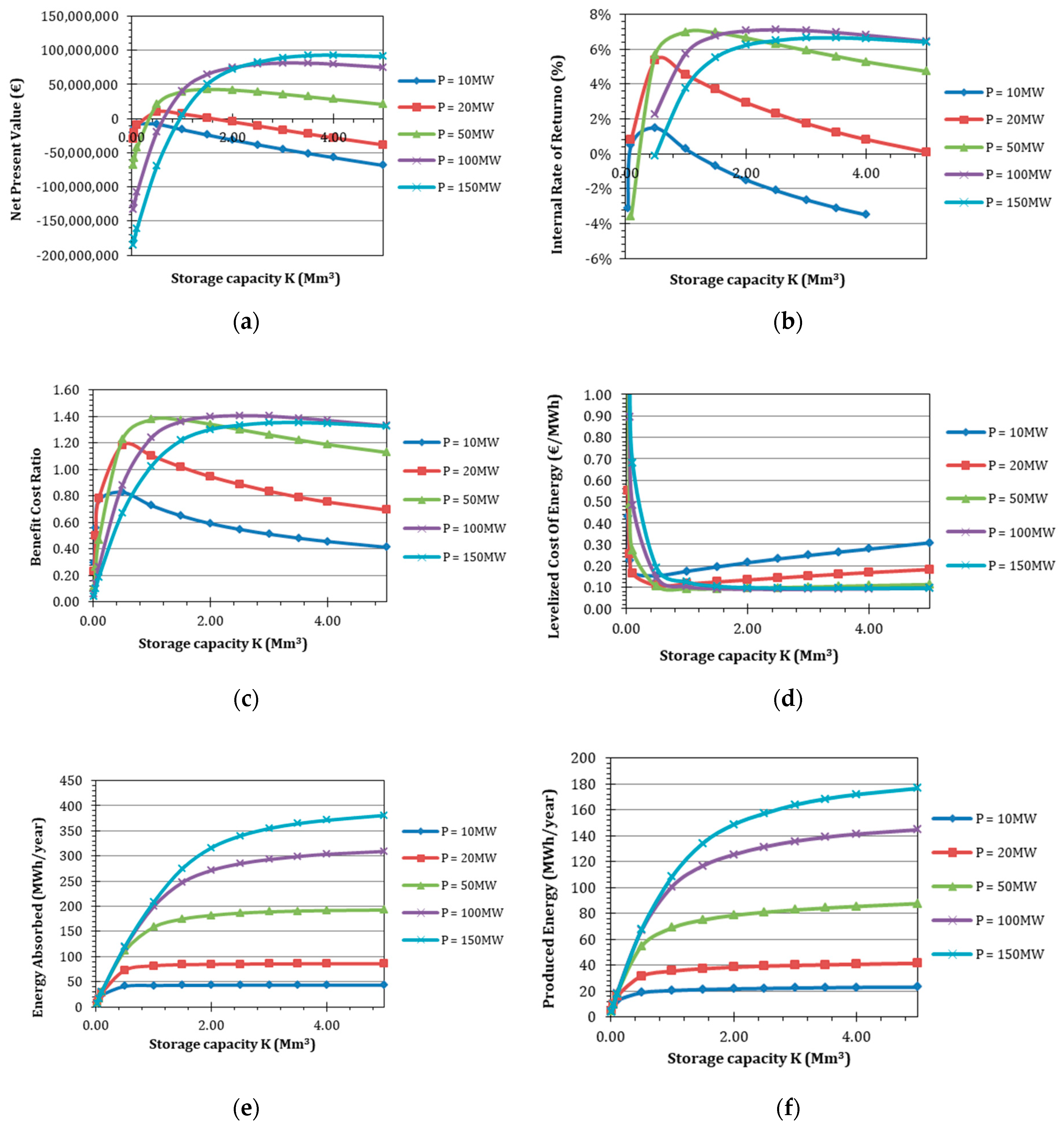
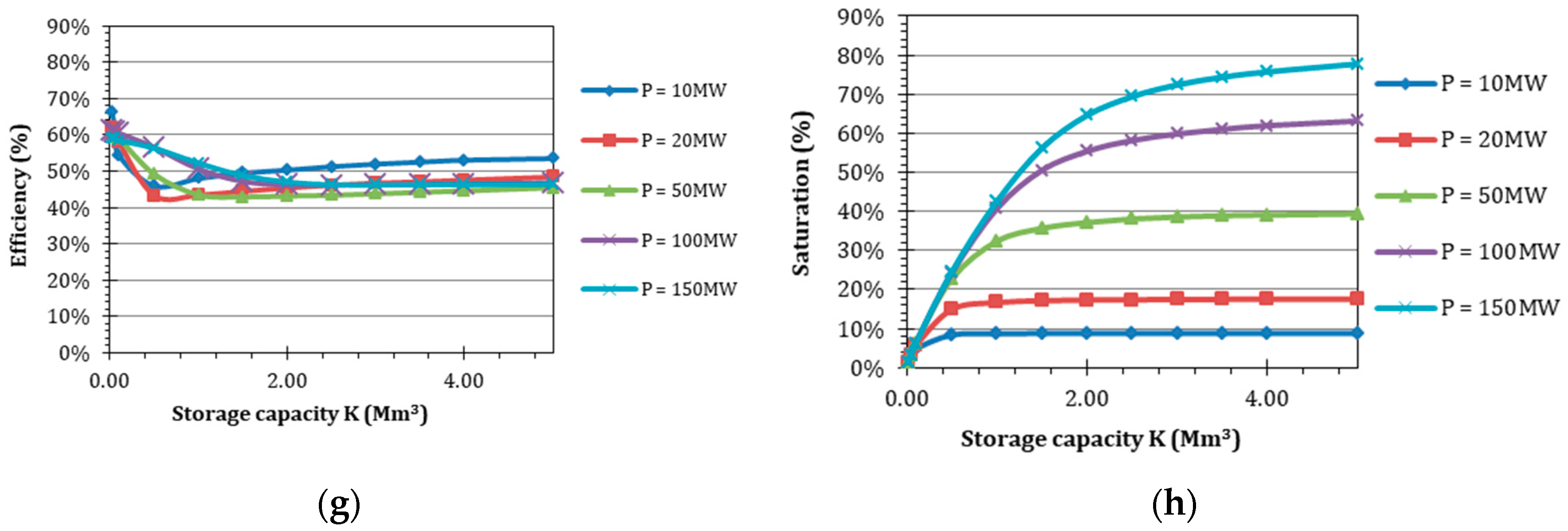
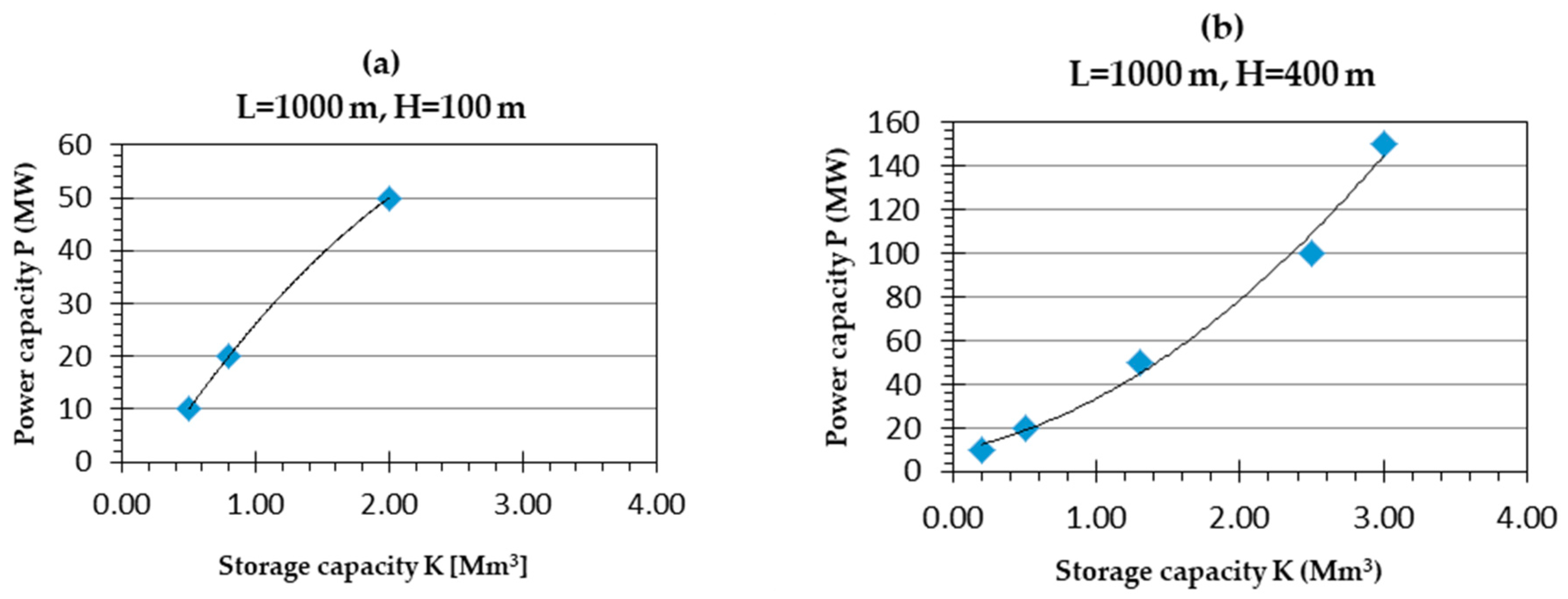
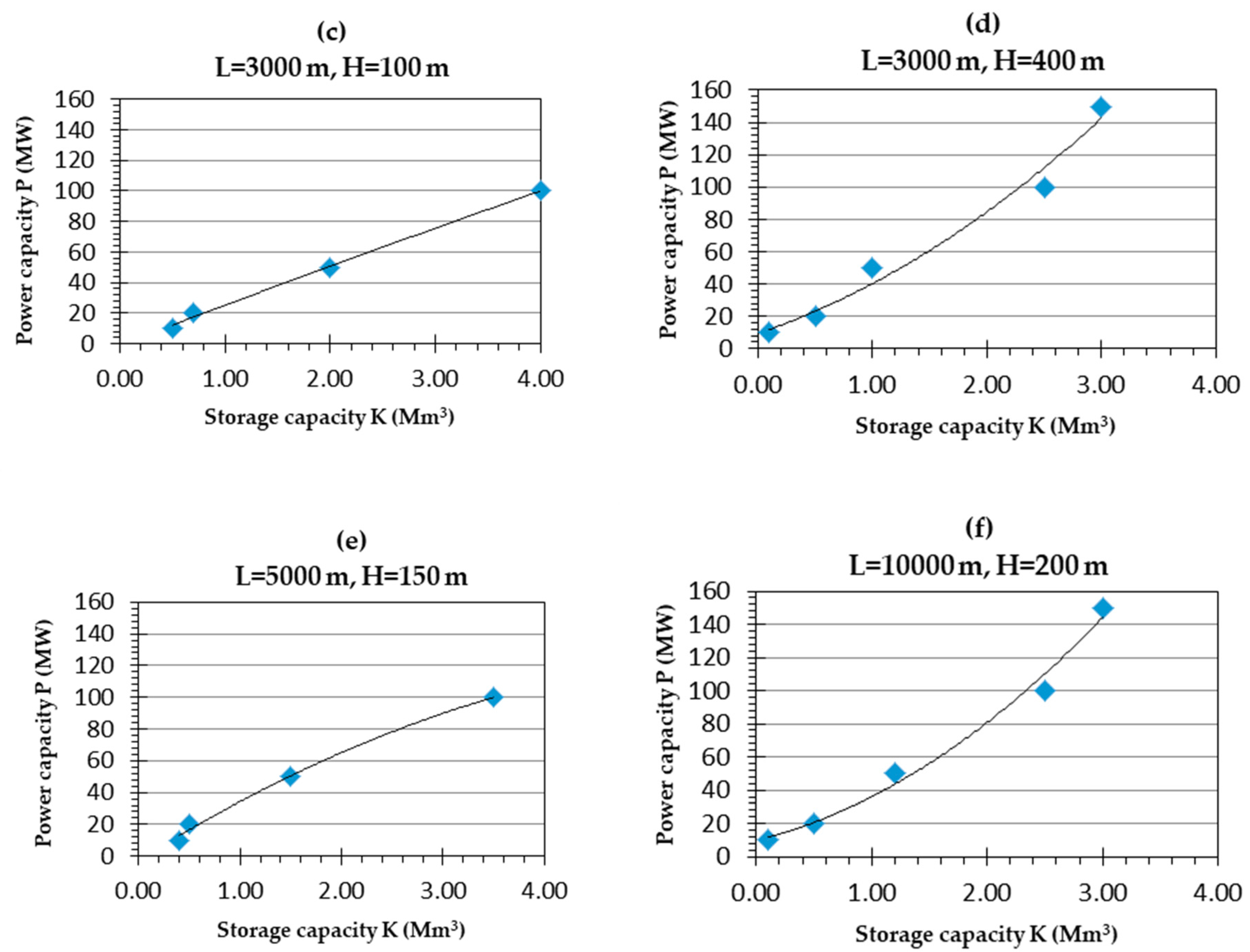
| H (m) | L (km) | P (MW) | K (Mm3) |
|---|---|---|---|
| 50 | 1 | 5 | 0.02 |
| 100 | 3 | 10 | 0.05 |
| 150 | 5 | 20 | 0.10 |
| 200 | 10 | 50 | 0.50 |
| 300 | 100 | 1.00 | |
| 400 | 150 | 1.50 | |
| 2.00 | |||
| 2.50 | |||
| 3.00 | |||
| 3.50 | |||
| 4.00 | |||
| 5.00 |
| Symbol | Cost Item | Parametric Investment Cost Model | Maintenance Costs (€/year) |
|---|---|---|---|
| CK | Upper reservoir | Ck = K × 0.0038 × (K)−0.35/1.275 K (m3) | 0.0025 × CK |
| Cpipes | Pipelines | Cpipes = 0.0375 × (D)1.4562 × NT × L D (mm) L (m) | 0.0015 × Cpipes |
| Cturb | Power Generation (Turbines and equipment) | Cturb = 1.1948 × (P)0.7634 × Nturb × 0.82234 × 106 P(MW) | 0.0030 × Cturb |
| Cpump | Pumping System | 0.5 × Cturb | 0.0040 × Cpump |
| Cacc_res | Reservoir ancillary works (fencing, lighting, access roads etc.) | 0.15 × Cres | 0.0030 × Cacc_res |
| Cacc_turb | Pumping and generation ancillary works (power and pump house, keeper’s house, services etc.) | 0.05 × Cturb | 0.0040 × Cacc-turb |
| CLand | Land | 0.005 × (Cres + Cpipes + Cturb + Cpump) | |
| CS | Electric substation and connection to AC grid | 0.20 × (Cturb + Cpump) | |
| CTE | Technical expenditures | 0.1 × (Cres + Cpipes + Cturb + Cpump+ Cacc_res + Cacc_turb + CLand + Cs) |
| No | Parameter | Parameter Range | |||
|---|---|---|---|---|---|
| Lower Value | Central Value | Upper Value | |||
| 1 | Reservoir cost | CK | 90% | 100% | 110% |
| 2 | Generation equipment cost | Cturb | 90% | 100% | 110% |
| 3 | Pumping system cost | Cpump | 90% | 100% | 110% |
| 4 | Pipelines cost | Cpipes | 90% | 100% | 110% |
| 5 | Total operation cost | Cgtot | 90% | 100% | 110% |
| 6 | Economic value of avoided energy production from the present mix | PUN | 90% | 100% | 110% |
| 7 | Value of avoided CO2 emissions | CO2 | 90% | 100% | 110% |
| 8 | Efficiency of the generation system | ηt | 0.80 | 0.85 | 0.90 |
| 9 | Efficiency of the pumping system | ηp | 0.75 | 0.80 | 0.85 |
| 10 | Maximum water velocity in the pipelines | v | 3 m/s | 4 m/s | 5 m/s |
| Parameter | Cardinality of the Order of Importance | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1° | 2° | 3° | 4° | 5° | 6° | 7° | 8° | 9° | 10° | |
| CK | 0.00 | 0.00 | 0.00 | 0.44 | 0.40 | 0.09 | 0.04 | 0.01 | 0.00 | 0.00 |
| Cpipes | 0.00 | 0.00 | 0.00 | 0.00 | 0.07 | 0.21 | 0.14 | 0.06 | 0.34 | 0.19 |
| Cturb | 0.00 | 0.00 | 0.05 | 0.50 | 0.44 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 |
| Cpump | 0.00 | 0.00 | 0.00 | 0.00 | 0.04 | 0.46 | 0.32 | 0.15 | 0.04 | 0.00 |
| Cgtot | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.27 | 0.70 |
| PUN | 0.00 | 0.97 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| CO2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.04 | 0.26 | 0.52 | 0.18 | 0.00 |
| ηp | 0.00 | 0.03 | 0.92 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| ηt | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| v | 0.00 | 0.00 | 0.00 | 0.01 | 0.05 | 0.18 | 0.24 | 0.23 | 0.18 | 0.12 |
| Order of Importance | 1° | 2° | 3° | 4° | 5° | 6° | 7° | 8° | 9° | 10° |
|---|---|---|---|---|---|---|---|---|---|---|
| Parameters ordered by importance—NPV | PUN | Cturb | Ck | CO2 | Cpump | Ck | Cgtot | v | ||
| Average elasticity value (over the 225 plants)—NPV | 2.56 | 2.22 | 1.79 | −0.51 | −0.52 | 0.35 | −0.25 | −0.20 | −0.15 | −0.06 |
| Parameters ordered by importance—IRR | PUN | Cturb | Ck | Cpump | CO2 | v | Ck | Cgtot | ||
| Average elasticity value (over the 225 plants)—IRR | 1.40 | 1.23 | 0.98 | −0.48 | −0.48 | 0.23 | 0.18 | 0.16 | 0.17 | −0.08 |
| Parameters ordered by importance—B/C | PUN | Cturb | Ck | Cpump | CO2 | v | Cgtot | Ck | ||
| Average elasticity value (over the 225 plants)—B/C | 1.00 | 0.86 | 0.70 | −0.34 | 0.33 | −0.16 | 0.14 | 0.07 | −0.09 | 0.11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arena, C.; Genco, M.; Lombardo, A.; Meli, I.; Mazzola, M.R. A Cost–Benefit Based, Parametric Procedure to Screen Existing Irrigation and Municipal Supply Reservoirs for Wind Energy Storage. Water 2018, 10, 1813. https://doi.org/10.3390/w10121813
Arena C, Genco M, Lombardo A, Meli I, Mazzola MR. A Cost–Benefit Based, Parametric Procedure to Screen Existing Irrigation and Municipal Supply Reservoirs for Wind Energy Storage. Water. 2018; 10(12):1813. https://doi.org/10.3390/w10121813
Chicago/Turabian StyleArena, Claudio, Mario Genco, Alessio Lombardo, Ignazio Meli, and Mario Rosario Mazzola. 2018. "A Cost–Benefit Based, Parametric Procedure to Screen Existing Irrigation and Municipal Supply Reservoirs for Wind Energy Storage" Water 10, no. 12: 1813. https://doi.org/10.3390/w10121813
APA StyleArena, C., Genco, M., Lombardo, A., Meli, I., & Mazzola, M. R. (2018). A Cost–Benefit Based, Parametric Procedure to Screen Existing Irrigation and Municipal Supply Reservoirs for Wind Energy Storage. Water, 10(12), 1813. https://doi.org/10.3390/w10121813




