Calculation Proposal for the Economic Level of Apparent Losses (ELAL) in a Water Supply System
Abstract
:1. Introduction
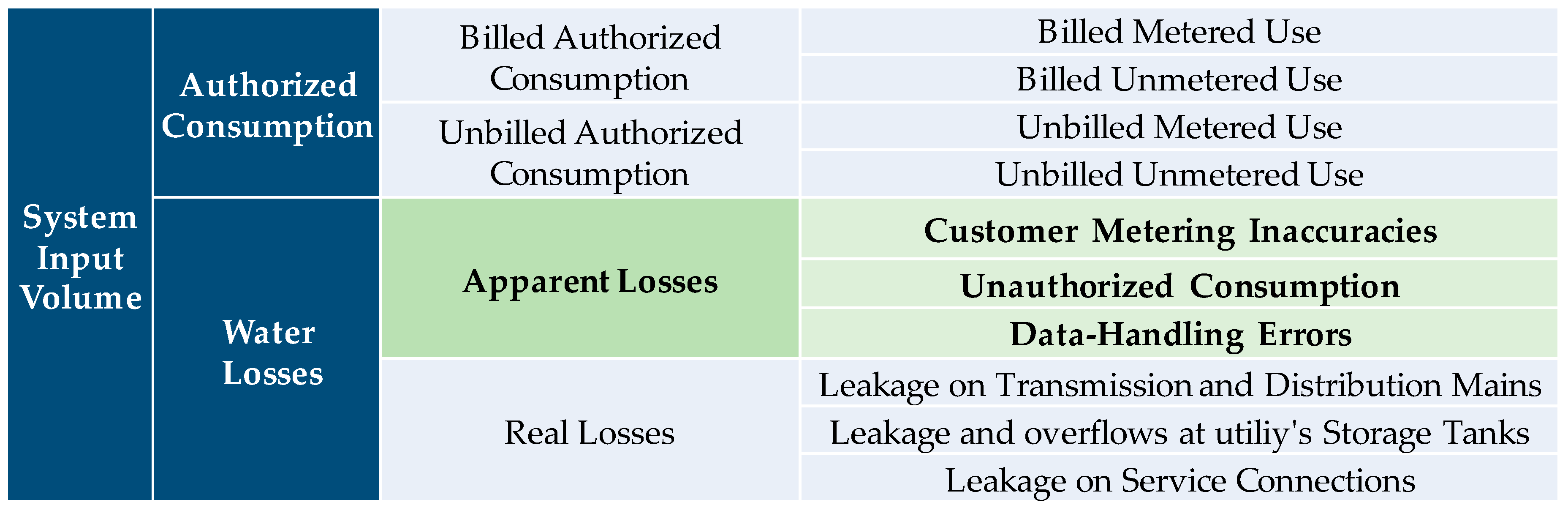
2. Components of Apparent Losses
- Intervention independent apparent losses. This category is related to the unavoidable level of losses in a system, no matter the number and frequency of the interventions regularly carried out. These losses could only be reduced if there is a substantial change in an essential element of the system (water metering technology, installation conditions of the meters, a variation of water meter suppliers quality, etc.), but they would not be affected if, for example, customers’ meters are replaced more frequently. When expressed in annual terms, this category is called the Intervention Independent Annual Apparent Losses (IIAAL, in m3/year).
- Intervention dependent apparent losses. This category is related to the amount of losses that depends on the intervention policies carried out by the water company and grows when interventions are delayed over time. On the contrary, more frequent interventions requiring greater investments by the utility lead to smaller volumes of apparent losses. When expressed in annual terms, this category is called the Intervention Dependent Annual Apparent Losses (IDAAL, in m3/year).
2.1. IIAAL—Intervention Independent Annual Apparent Losses
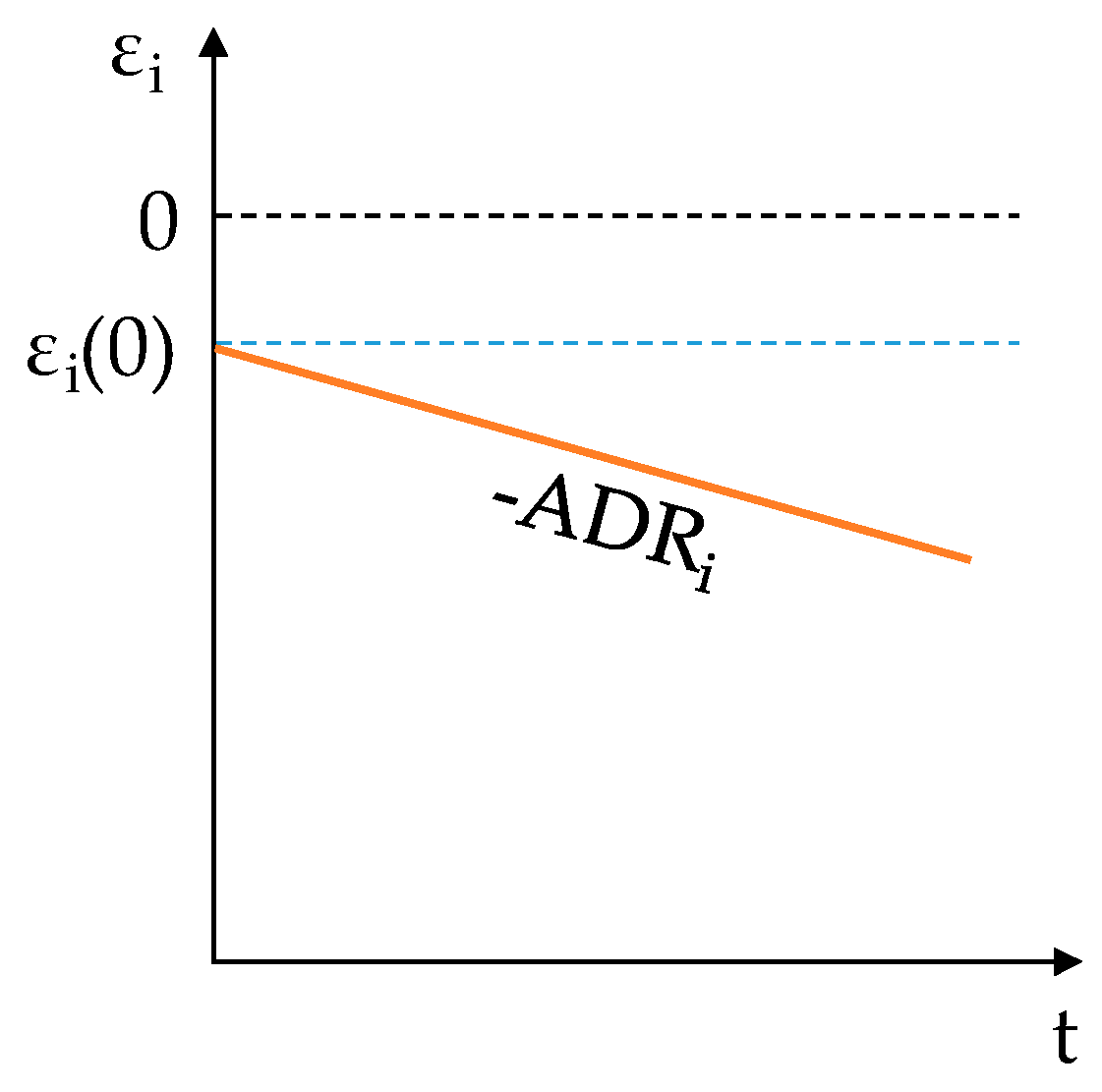
- Unavoidable measuring errors (), which are associated with the minimum (initial) measuring the error of brand new water meters. The magnitude of this term depends not only on the metering technology but also on the consumption characteristics of the users, as defined by their water consumption flow rate probability distribution function [24].
- Unavoidable illegal uses of water (). Even if great effort and resources are put in place to avoid the illegal uses of water, there will always be a minimum volume of water taken from the system without the company’s knowledge or authorization. This minimum volume is mainly related to local socio-cultural and economic conditions.
- Systematic data handling errors (). This component is typically caused by data manipulations performed by the water utility when actual meter readings are not available or are noticeably wrong. Frequently, it is associated with incorrect water consumption calculation procedures and incorrect estimations of meter readings. Consequently, unless these procedures are changed, the magnitude of this term will remain approximately constant over time and be independent of the frequency of the intervention activities. However, only when consumption calculation procedures are extremely imprecise does the magnitude of this component compared to the previous ones prove significant.
2.1.1. IIAALMES—Intervention Independent Annual Apparent Losses Due to Unavoidable Measuring Errors
2.1.2. IIAALILL—Intervention Independent Annual Apparent Losses Due to Illegal Uses of Water
2.1.3. IIAALDH—Intervention Independent Annual Apparent Losses Due to Systematic Data Handling Errors
2.2. IDAAL—Intervention Dependent Annual Apparent Losses
- Intervention Dependent Apparent Losses associated with measuring errors (). This component accounts for the amount of water not registered by a functional water meter. The rate of increase of the volumes not registered by the meters every year depends on the manufacturing and design quality of the meters and the working conditions in the field.
- Intervention Dependent Apparent Losses associated with illegal consumption (). Unauthorized uses of water in the system caused by meter tampering and illegal connections are included within this category. The magnitude of the volume stolen every year from the water company is directly related to the inspection frequency of the connections [38].
2.2.1. IDAALMES—Intervention Dependent Annual Apparent Losses Associated with Measuring Errors
- -
- Employ a single value of the for all meters in the system regardless of their type.
- -
- Use an average meter age for all meters in the system, .
2.2.2. IDAALILL—Intervention Dependent Annual Apparent Losses Associated with Illegal Connections
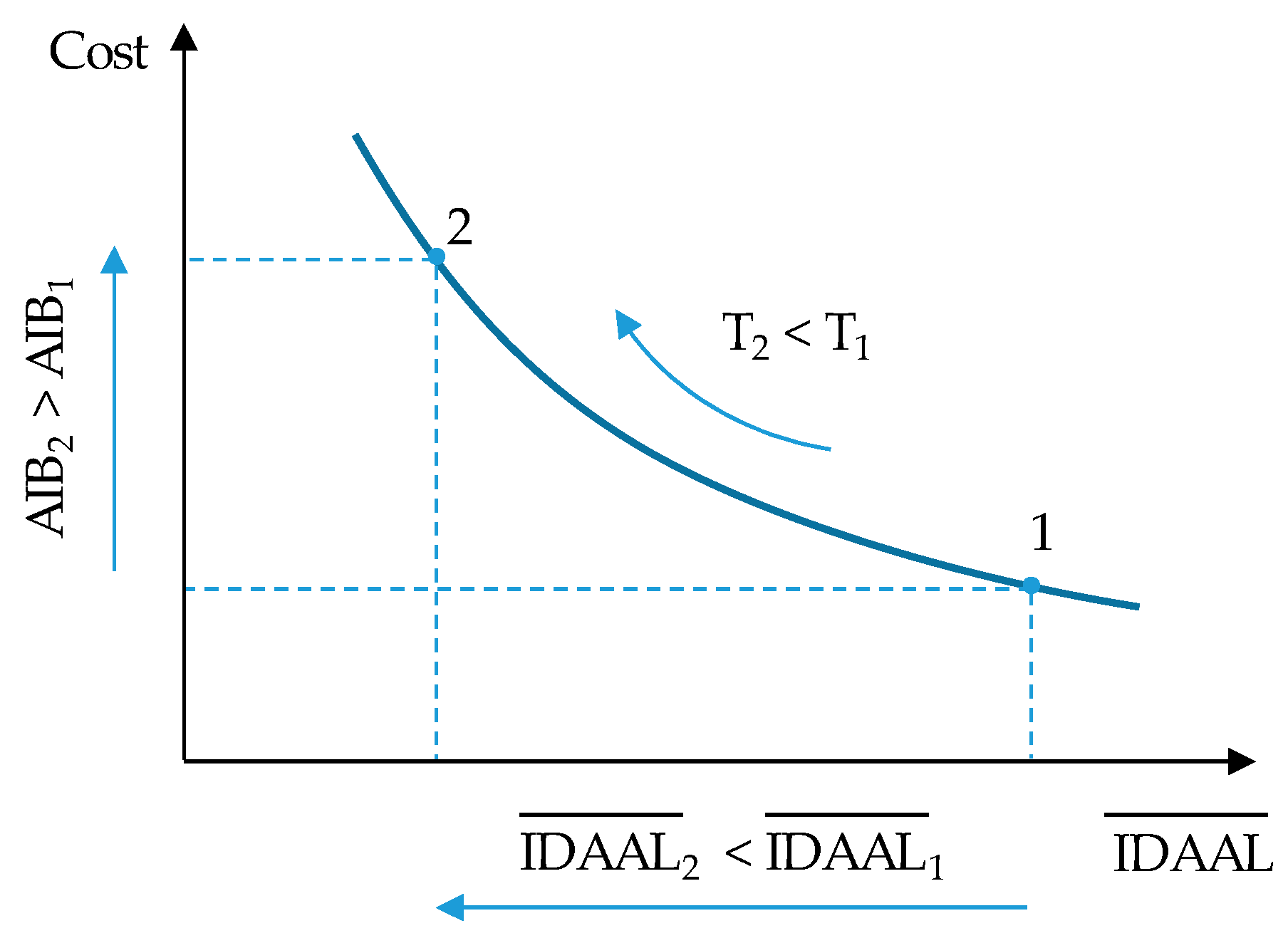
3. Policies to Reduce Apparent Losses and Related Costs
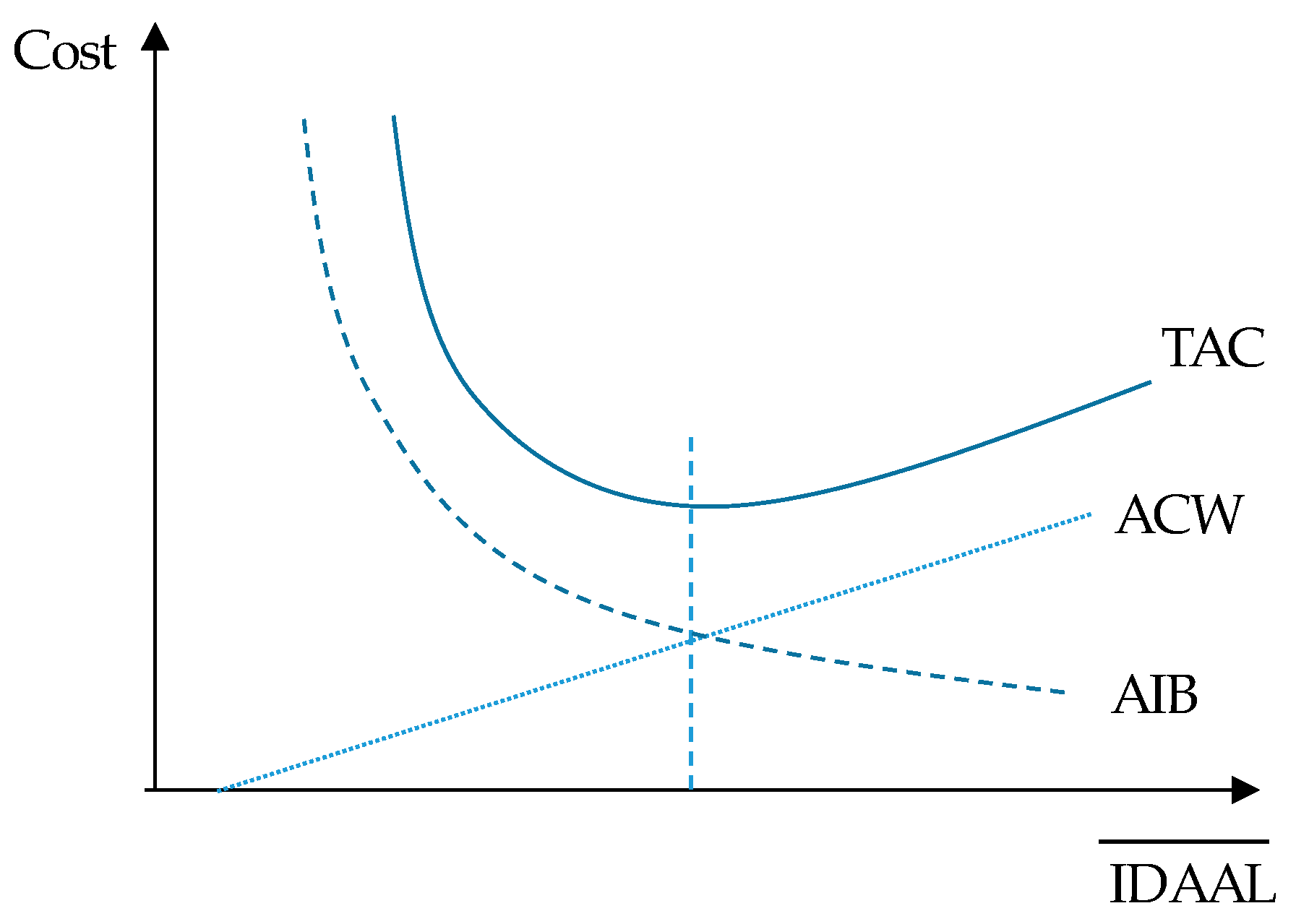
4. Calculation of Economic Level of Apparent Losses
- Intervention costs (from Equation (15) for and Equation (16) for ):
- Optimum intervention periods (from Equations (15), (21), and (24) for , and Equations (16), (22), and (25) for ):
- Percentage of water meters or customers’ connections annually replaced or inspected, respectively, by each policy:
5. Apparent Loss Indicators
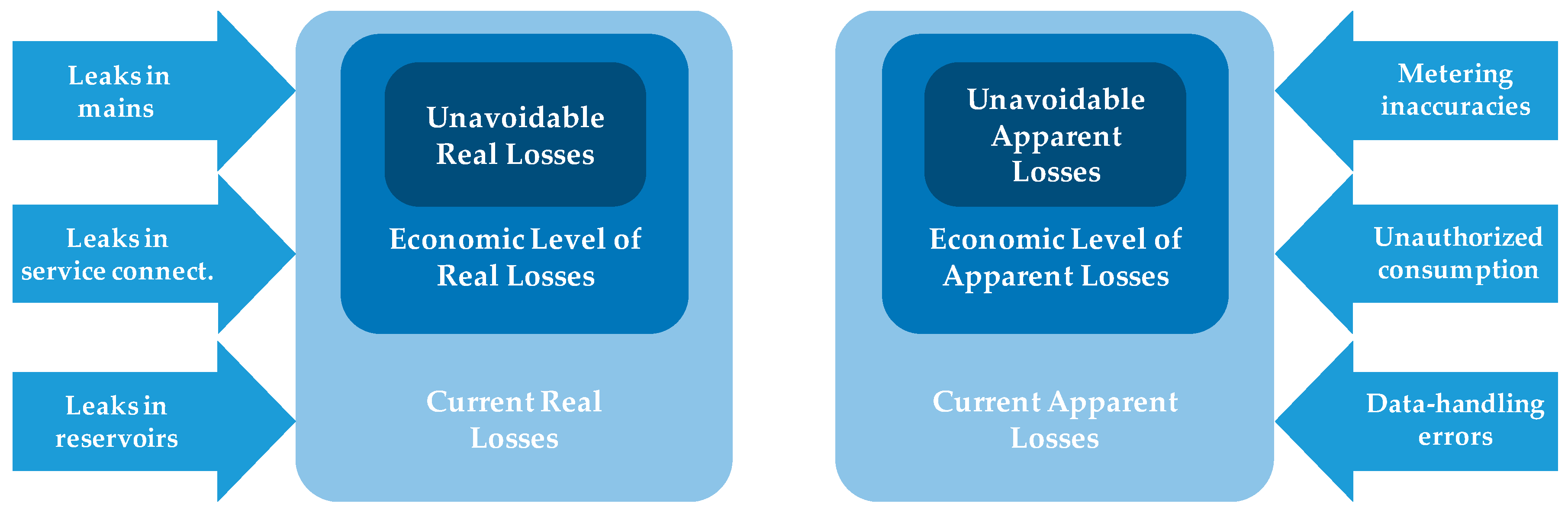
- Apparent Losses Index (). This indicator is a measure of how the current apparent losses compare to the minimum achievable value. This indicator should always be greater than one.
- Apparent Losses Economic Index (). This indicator measures how close the utility losses are with respect to the economic level of losses. The target for a properly managed water utility is to attain a value for the as close to one as possible.
- Apparent Losses Economic Potential Index (). The is not directly related to the water loss management policies of the utility. It measures how far the economic level is from the unavoidable level of losses.
6. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| ACV | Annual Consumption Volume (m3/year); |
| ACWILL | Annual Cost of Water lost due to illegal connections (€/year); |
| ACWMES | Annual Cost of Water lost due to meter inaccuracies (€/year); |
| ADMFAL | Annual Detected Meter Failures Apparent Losses (m3/year); |
| ADR | Annual Degradation Rate of the weighted error (%/year); |
| AIB | Annual Intervention Budget (€/year); |
| AIBILL | Annual Inspection Budget of customers’ connections (€/year); |
| AIBMES | Annual Intervention Budget due to meter replacement (€/year); |
| AICR | Annual Illegal Consumption Increasing Rate (%/year); |
| AIF | Average Illegal use Frequency (%/year); |
| ALEI | Apparent Losses Economic Index (-); |
| ALEPI | Apparent Losses Economic Potential Index (-); |
| ALI | Apparent Losses Index (-); |
| AMFF | Annual Meter Failure Frequency (%/year); |
| ART | Average Repair Time between the occurrence and resolution of a meter failure (years); |
| ARV | Annual Registered Volume (m3/year); |
| CAAL | Current Annual Apparent Losses (m3/year); |
| DHE | Data Handling Error parameter (m3/(meter × year); |
| ELAL | Economic Level of Apparent Losses (m3/year); |
| Average Weighted Error depending on time (%); | |
| Average Initial Weighted Error (%); | |
| i | Meter type; |
| ICF | Infrastructure Condition Factor (-); |
| IDAAL | Intervention Dependent Annual Apparent Losses (m3/year); |
| IDAALILL | Intervention Dependent Annual Apparent Losses due to illegal connections (m3/year); |
| IDAALMES | Intervention Dependent Annual Apparent Losses due to meter inaccuracies (m3/year); |
| IIAAL | Intervention Independent Annual Apparent Losses (m3/year); |
| IIAALDH | Intervention Independent Annual Apparent Losses due to data handling errors (m3/year); |
| IIAALILL | Intervention Independent Annual Apparent Losses due to illegal connections (m3/year); |
| IIAALMES | Intervention Independent Annual Apparent Losses due to meter inaccuracies (m3/year); |
| j | Customer group; |
| NM | Number of Meters installed (meters); |
| NRRALILL | Natural Rate of Rise of Apparent Losses due to illegal connections (m3/year2); |
| NRRALMES | Natural Rate of Rise of Apparent Losses due to meter inaccuracies (m3/ year2); |
| PAIMILL | Percentage of Annually Inspected Meters (%/year); |
| PAIMMES | Percentage of Annually Replaced Meters (%/year); |
| PW | Selling Price of water (€/m3); |
| t | Time Period (years); |
| Time required to inspect all water connections (years); | |
| Time required to replace all water meters (years); | |
| TAC | Total Annual Cost (€/year); |
| TACILL | Total Annual Cost of the policy associated with the inspection of customers’ connections (€/year); |
| TACMES | Total Annual Cost of the policy associated with meter replacements (€/year) |
| TICILL | Total Intervention Cost of inspections (€); |
| TICMES | Total Intervention Cost of replacements (€); |
| UAUV | Unavoidable Annual Unmeasured Volume (m3/year); |
Appendix A. Case Study 1—Example for a Water Utility with Basic Data
Appendix A.1. General Data
| USER TYPE | RESIDENTIAL |
|---|---|
| METER TYPE | VELOCITY |
| NM (meters) | 30,000 |
| ACV (m3/year) | 4,500,000 |
| (%) | −5 |
| AMFF (%/year) | 0.5 |
| ART (years) | 0.7 |
| AIF (%/year) | 0.3 |
| ADR (%/year) | 0.5 |
| AICR (%/year) | 0.15 |
| TMES (years) | 14 |
| TILL (years) | 3 |
| UICMES (€/meter) | 32 |
| UICILL (€/meter) | 5 |
| ICF | 1.21 |
| DHE (m3/(meter × year)) | 0.180 |
| PW (€/m3) | 0.9 |
Appendix A.2. IIAAL—(Current) Intervention Independent Annual Apparent Losses
Appendix A.3. IDAAL—(Current) Intervention Dependent Annual Apparent Losses
Appendix A.4. CAAL—Current Annual Apparent Losses
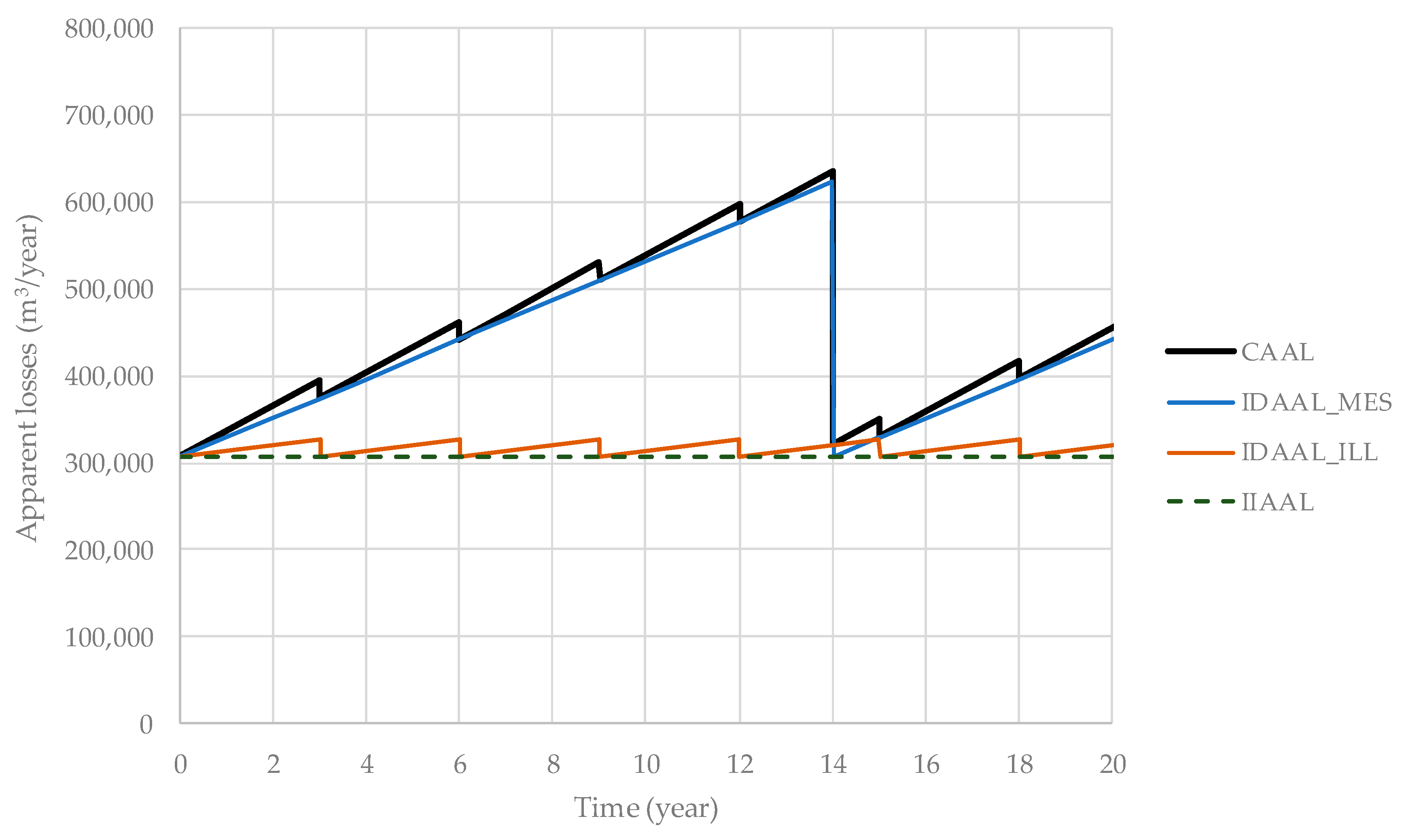
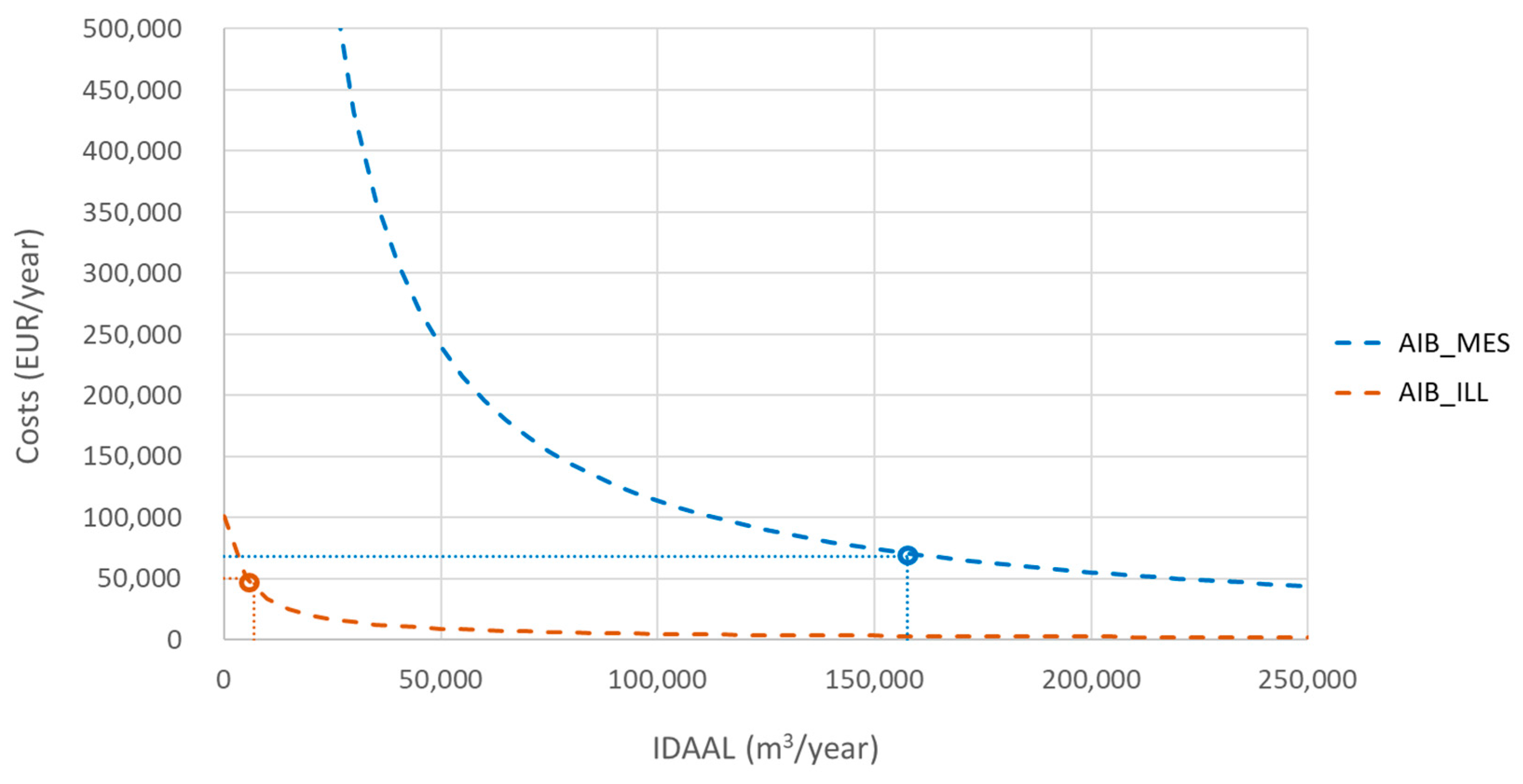
Appendix A.5. TAC—Total Annual Costs of Current Control Policies
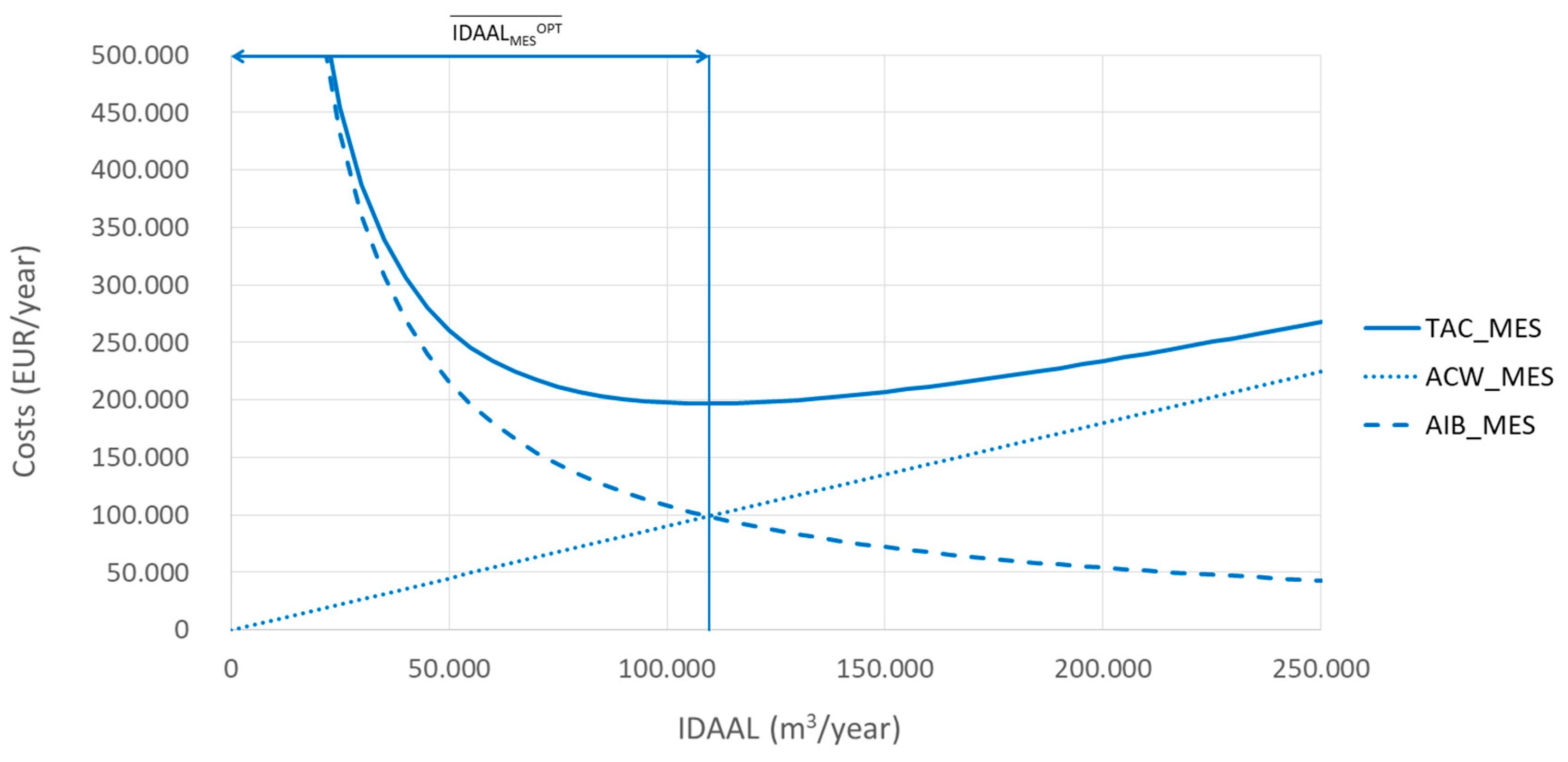
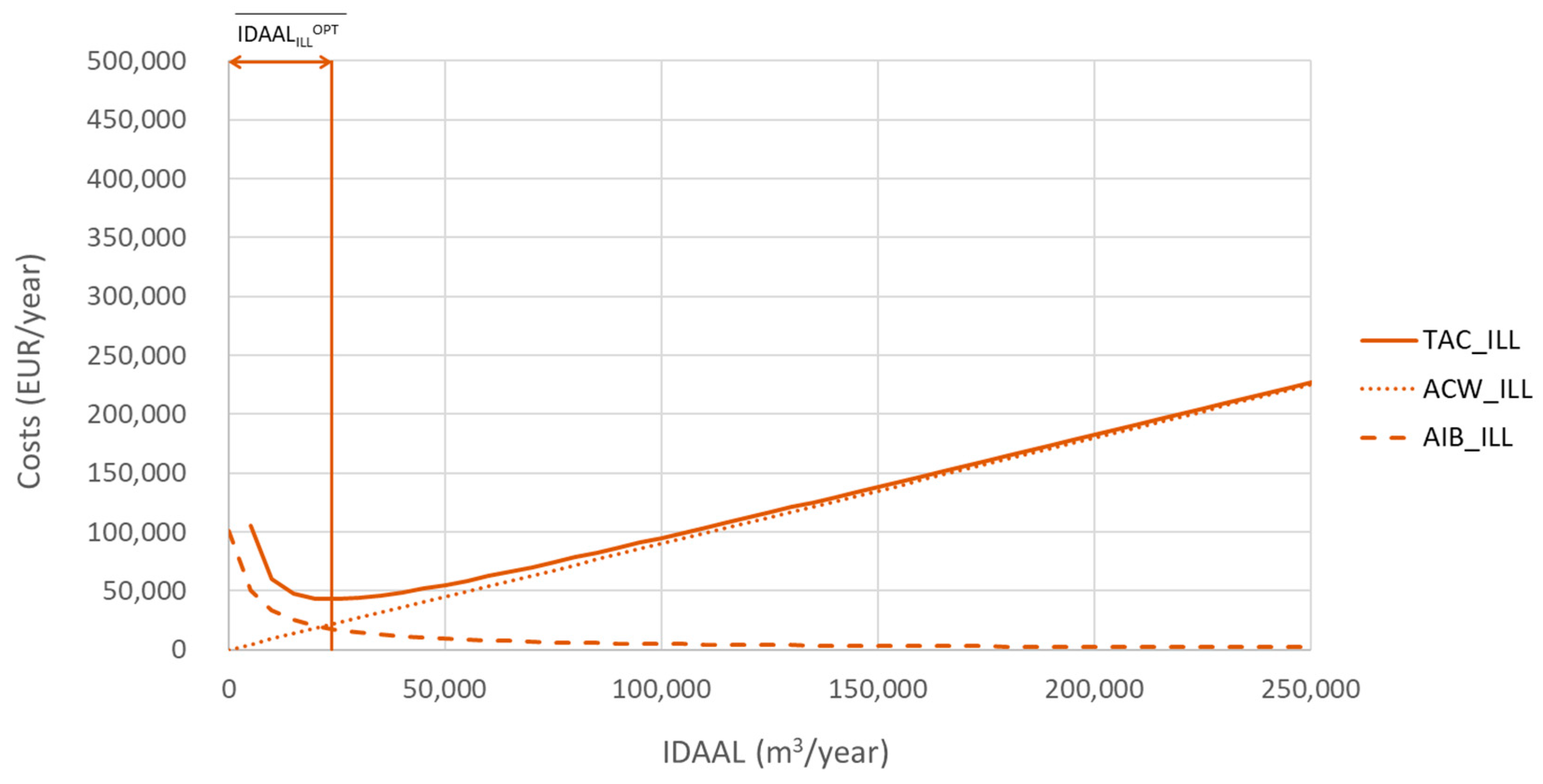
Appendix A.6. ELAL—Control Policies Frequency and the Economic Level of Apparent Losses
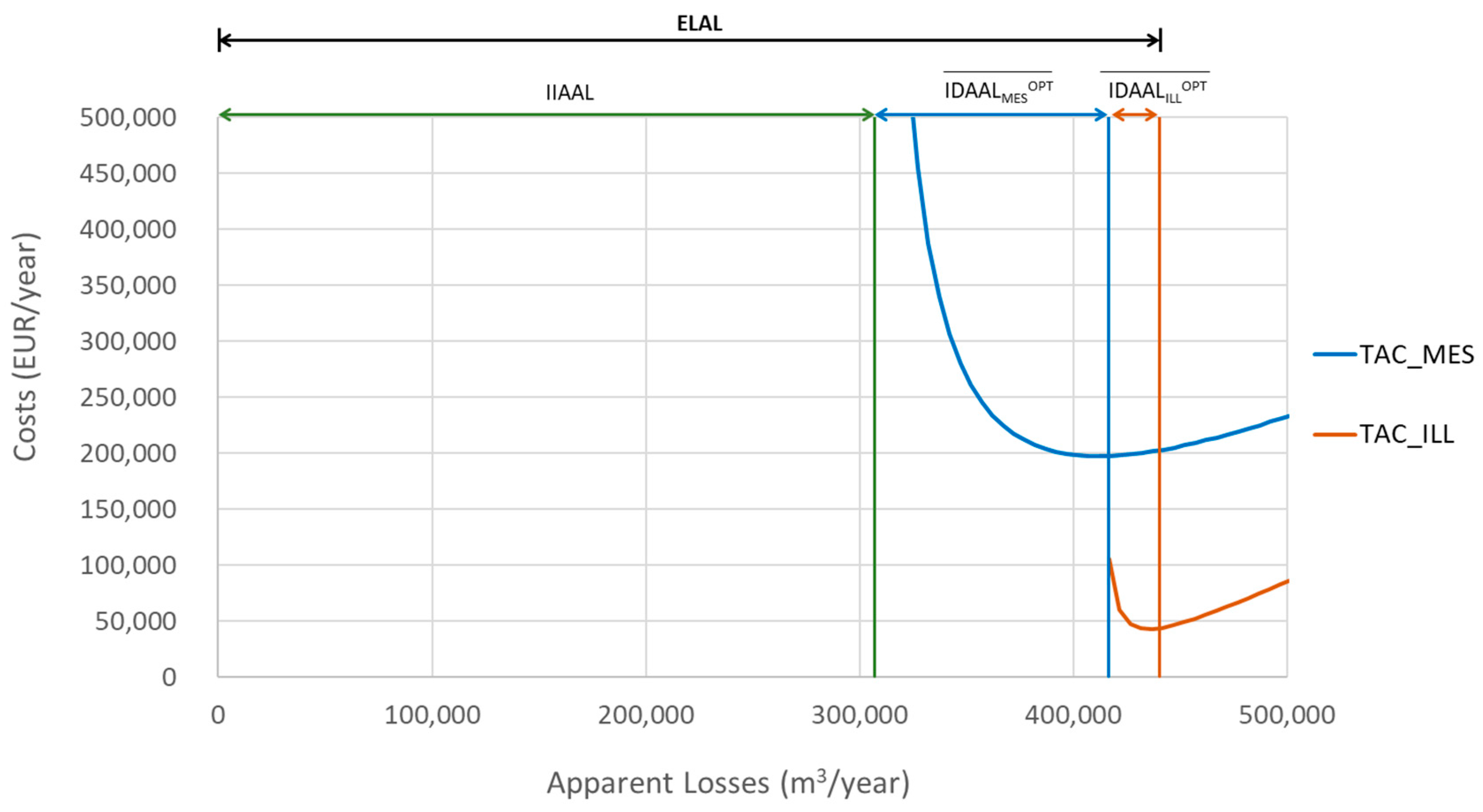
| 288,000 m3/year | ||
| 306,900 m3/year | 13,500 m3/year | |
| 474,525 m3/year | 5400 m3/year | |
| 157,500 m3/year | ||
| 167,625 m3/year | ||
| 10,125 m3/year | ||
| 288,000 m3/year | ||
| 306,900 m3/year | 13,500 m3/year | |
| 440,162 m3/year | 5400 m3/year | |
| 109,545 m3/year | ||
| 133,262 m3/year | ||
| 23,717 m3/year |
| AIBMES (€/year) | AIBILL (€/year) | ACWMES (€/year) | ACWILL (€/year) | TACMES (€/year) | TACILL (€/year) | TAC (€/year) | |
|---|---|---|---|---|---|---|---|
| Current | 68,571 | 50,000 | 141,750 | 9113 | 210,321 | 59,113 | 269,434 |
| Minimized | 98,590 | 21,345 | 98,590 | 21,345 | 197,180 | 42,691 | 239,871 |
| Equation | Variable | Calculation | Result |
|---|---|---|---|
| (31) | 1.55 | ||
| (32) | 1.08 | ||
| (33) | 1.43 |
Appendix A.7. Case Study 1—Conclusions
Appendix B. Case Study 2—Example for a Water Utility with Complete Data
Appendix B.1. General Data
| USER TYPE | RESIDENTIAL | SMALL ICI | MEDIUM-LARGE ICI | |
|---|---|---|---|---|
| METER TYPE | VELOCITY | VOLUMETRIC | VELOCITY | VELOCITY |
| NMi (meters) | 30,000 | 17,250 | 2500 | 250 |
| ACVi (m3/year) | 4,500,000 | 2,587,500 | 1,250,000 | 750,000 |
| (%) | −5 | −1 | −3 | 0 |
| AMFFi (%/year) | 0.5 | 0.5 | 0.5 | 0.2 |
| ARTi (year) | 0.7 | 0.7 | 0.7 | 0.2 |
| AIFj (%/year) | 0.3 | 0.3 | 0.4 | 0 |
| ADRi (%/year) | 0.5 | 0.5 | 0.3 | 0.1 |
| AICRj (%/year) | 0.15 | 0.15 | 0.05 | 0 |
| TMESi (years) | 14 | 14 | 14 | 14 |
| TILLj (years) | 3 | 3 | 3 | 3 |
| UICMESi (€/meter) | 32 | 37 | 62 | 400 |
| UICILLj (€/meter) | 5 | 5 | 5 | 50 |
| ICF | 1.21 | |||
| DHE (m3/(meter × year)) | 0.18 | |||
| PW (€/m3) | 0.9 | |||
Appendix B.2. IIAAL—(Current) Intervention Independent Annual Apparent Losses
Appendix B.3. IDAAL—(Current) Intervention Dependent Annual Apparent Losses
| Equation | Variable | Calculation | Type of Customer/Type of Meter | |||
|---|---|---|---|---|---|---|
| Residential | Small ICI | Med-Large ICI | ||||
| Velocity | Volumetric | Velocity | Velocity | |||
| (8) | 22,500 | 12,938 | 3750 | 750 | ||
| (13) | 157,500 | 90,563 | 26,250 | 5250 | ||
| Equation | Variable | Calculation | Type of Customer | ||
|---|---|---|---|---|---|
| Residential | Small ICI | Med-Large ICI | |||
| (11) | 10,631 | 625 | - | ||
| (14) | 15,947 | 938 | - | ||
Appendix B.4. CAAL—Current Annual Apparent Losses
Appendix B.5. TAC—Total Annual Costs of Current Control Policies
| Equation | Variable | Calculation | Type of Customer/Type of Meter | |||
|---|---|---|---|---|---|---|
| Residential | Small ICI | Med-Large ICI | ||||
| Velocity | Volumetric | Velocity | Velocity | |||
| - | 960,000 | 638,250 | 155,000 | 100,000 | ||
| (15) | 68,571 | 45,589 | 11,071 | 7143 | ||
| (17) | 141,750 | 81,506 | 23,625 | 4725 | ||
| (19) | 210,321 | 127,096 | 34,696 | 11,868 | ||
| Equation | Variable | Calculation | Type of Customer | ||
|---|---|---|---|---|---|
| Residential | Small ICI | Med-Large ICI | |||
| - | 236,250 | 12,500 | 12,500 | ||
| (16) | 78,750 | 4167 | 4167 | ||
| (18) | 14,352 | 844 | 0 | ||
| (20) | 93,102 | 5010 | 4167 | ||
Appendix B.6. ELAL—Control Policies Frequency and the Economic Level of Apparent
| Equation | Variable | Calculation | Type of Customer/Type of Meter | |||
|---|---|---|---|---|---|---|
| Residential | Small ICI | Med-Large ICI | ||||
| Velocity | Volumetric | Velocity | Velocity | |||
| (21) | 109,545 | 67,731 | 17,970 | 6455 | ||
| (27) | 9.74 | 10.47 | 9.58 | 17.21 | ||
| (29) | 10.3% | 9.6% | 10.4% | 5.8% | ||
| Equation | Variable | Calculation | Type of Customer/Type of Meter | |||
|---|---|---|---|---|---|---|
| Residential | Small ICI | Med-Large ICI | ||||
| Velocity | Volumetric | Velocity | Velocity | |||
| (15) | 98,590 | 60,957 | 16,173 | 5809 | ||
| (17) | 98,590 | 60,957 | 16,173 | 5809 | ||
| (19) | 197,180 | 121,915 | 32,346 | 11,619 | ||
| Equation | Variable | Calculation | Type of Customer | ||
|---|---|---|---|---|---|
| Residential | Small ICI | Med-Large ICI | |||
| (22) | 37,354 | 2083 | - | ||
| (28) | 7.03 | 6.67 | - | ||
| (30) | 14.2% | 15.0% | - | ||
| Equation | Variable | Calculation | Type of Customer | ||
|---|---|---|---|---|---|
| Residential | Small ICI | Med-Larg ICI | |||
| (16) | 33,619 | 1875 | - | ||
| (18) | 33,619 | 1875 | - | ||
| (20) | 67,238 | 3750 | - | ||
| 378,415 m3/year | ||
| 413,678 m3/year | 26,263 m3/year | |
| 710,124 m3/year | 9000 m3/year | |
| 279,563 m3/year | ||
| 296,447 m3/year | ||
| 16,884 m3/year | ||
| 378,415 m3/year | ||
| 413,678 m3/year | 26,263 m3/year | |
| 654,815 m3/year | 9000 m3/year | |
| 201,700 m3/year | ||
| 241,138 m3/year | ||
| 39,438 m3/year |
| AIBMES (€/year) | AIBILL (€/year) | ACWMES (€/year) | ACWILL (€/year) | TACMES (€/year) | TACILL (€/year) | TAC (€/year) | |
|---|---|---|---|---|---|---|---|
| Current | 132,375 | 87,083 | 251,606 | 15,196 | 383,981 | 102,279 | 486,261 |
| Minimized | 181,560 | 35,494 | 181,530 | 35,494 | 363,060 | 70,988 | 434,048 |
| Equation | Variable | Calculation | Result |
|---|---|---|---|
| (31) | 1.72 | ||
| (32) | 1.09 | ||
| (33) | 1.58 |
Appendix B.7. ELAL—Sensitivity Analysis
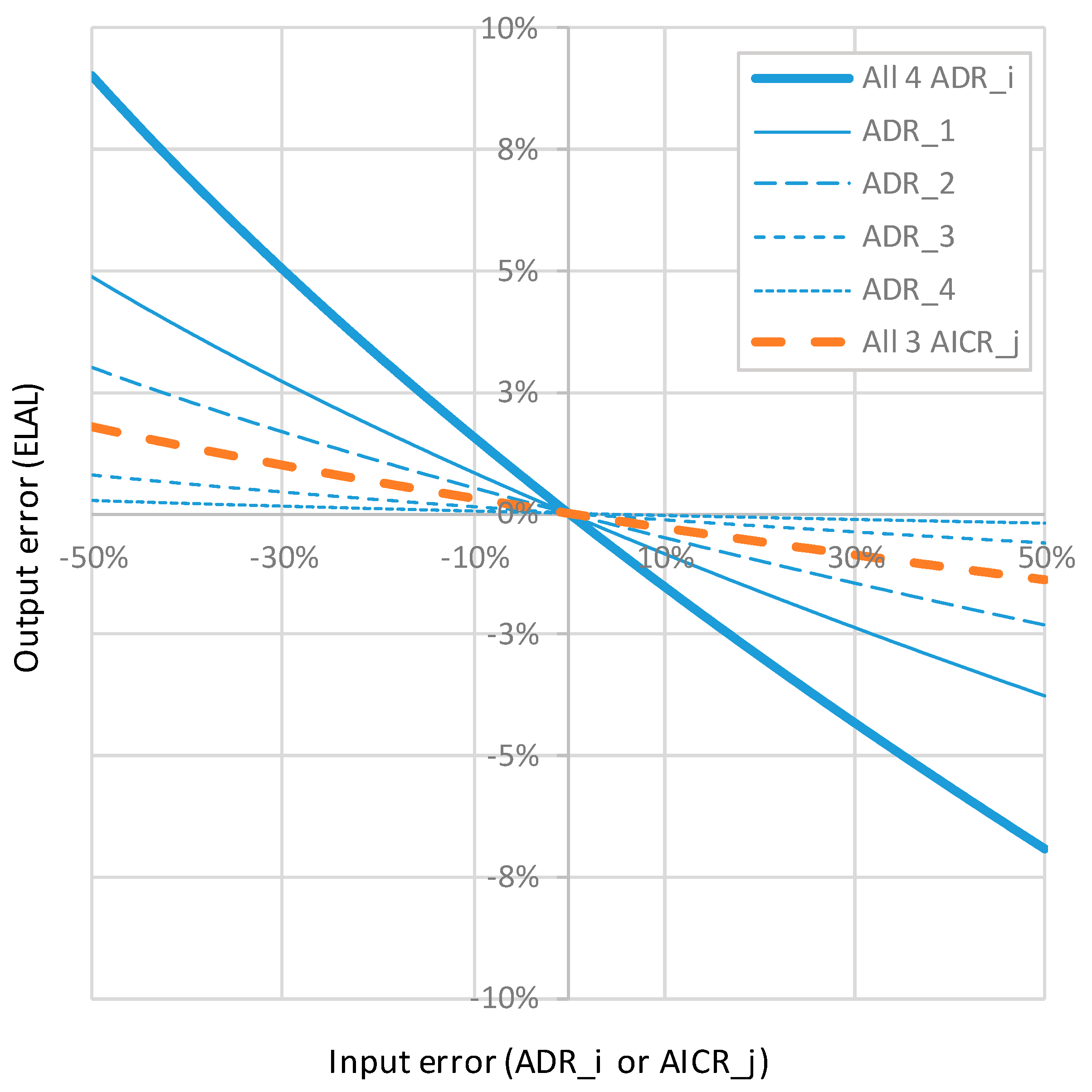
Appendix B.8. Case Study 2—Conclusions
Appendix C. The comparison Between the Variables Used for Calculating the Economic Level of Real Losses vs. Apparent Losses
| Variable | Calculation of the Economic Level of REAL Losses (ELL) | Calculation of the Economic Level of APPARENT Losses (ELAL) | |
| Apparent Losses Due to Meter Ageing | Apparent Losses Due to Illegal Consumption | ||
| Growing trend of losses with time | Natural Rate of Rise of Leakage () | Natural Rise of Apparent Losses due to meter ageing () | Natural Rise of Apparent Losses due to illegal consumption () |
| Intervention to reduce current losses to their initial value | Pipe inspection | Meter replacement | Meter/Connection inspection |
| Unit intervention cost | Pipe inspection cost () | Meter replacement cost () | Meter/Connection inspection cost () |
| Annual intervention cost | Annual budget for intervention () | Annual intervention (replacement) budget () | Annual intervention (inspection) budget () |
| Unit water value | Marginal cost of supply () | Price of water () | Price of water () |
| Total annual costs | Total annual costs () | Total annual intervention (replacement) costs () | Total annual intervention (inspection) costs () |
| Total annual intervention cost () | |||
| Optimized intervention time period | Economic inspection frequency () | Optimum intervention (replacement) period () | Optimum intervention (inspection) period () |
| Economic level of losses | Economic level of real losses () | Economic level of apparent losses () | |
| Main indicator on losses level | Infrastructure leakage level () | Apparent losses indicator () | |
References
- Lambert, A.; Hirner, W. Losses from Water Supply Systems: Standard Terminology and Recommended Performance Measures; IWA Blue Pages; 2000; Available online: https://www.researchgate.net/publication/284884240_Losses_from_water_supply_systems_Standard_terminology_and_recommended_performance_measures (accessed on 7 December 2018).
- Farley, M.; Trow, S. Losses in Water Distribution Networks: A Practitioner’s Guide to Assessment, Monitoring and Control; IWA Publication: London, UK, 2003. [Google Scholar]
- Lambert, A. Assessing non-revenue water and its components: A practical approach. Water 21 Mag. Int. Water Assoc. 2003, 5, 50–51. [Google Scholar]
- Arregui, F.J.; Cabrera, E.J.; Cobacho, R.; García-Serra, J. Key factors affecting water meter accuracy. In Proceedings of the IWA Leakage Conference ‘Leakage 2005’, Halifax, NS, Canada, 12–14 September 2005. [Google Scholar] [CrossRef]
- Fontanazza, C.M.; Notaro, V.; Puleo, V.; Freni, G. The apparent losses due to metering errors: A proactive approach to predict losses and schedule maintenance. Urban Water J. 2015, 12, 229–239. [Google Scholar] [CrossRef]
- Lambert, A.O.; Brown, T.G.; Takizawa, M.; Weimer, D. A review of performance indicators for real losses from water supply systems. J. Water Supply Res. Technol. AQUA 1999, 48, 227–237. [Google Scholar] [CrossRef]
- Canto Ríos, J.; Santos-Tellez, R.U.; Hansen Rodríguez, P.; Antúnez Leyva, E.; Nava Martínez, V. Methodology for the identification of apparent losses in water distribution networks. Procedia Eng. 2014, 70, 238–247. [Google Scholar] [CrossRef]
- Rizzo, A. Apparent Water Loss Control: Theory and Application. In Proceedings of the Water Conference, Ferrara, Italy, 17–19 May 2006. [Google Scholar]
- Mutikanga, H.E.; Sharma, S.K.; Vairavamoorthy, K. Assessment of apparent losses in urban water systems. Water Environ. J. 2011, 25, 327–335. [Google Scholar] [CrossRef]
- Thornton, J.; Sturm, R.; Kunkel, G.A. Water Loss Control; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Kingdom, B.; Liemberger, R.; Marin, P. The Challenge of Reducing Non-Revenue Water (NRW) in Developing Countries. How the Private Sector Can Help: A Look at Performance-Based Service Contracting; Water & Sanitation Discussion Paper No. 8; World Bank Group: Washington, DC, USA, 2006. [Google Scholar]
- Lambert, A.; Charalambous, B.; Fantozzi, M.; Kovac, J.; Rizzo, A.; St John, S.G. 14 Years Experience of using IWA Best Practice Water Balance and Water Loss Performance Indicators in Europe. In Proceedings of the IWA Specialized Conference: Water Loss, Vienna, Austria, 30 April–2 May 2014. [Google Scholar]
- Alkasseh, J.M.A.; Adlan, M.N.; Abustan, I.; Hanif, A.B.M. Achieving an economic leakage level in Kinta Valley, Malaysia. Water Utility J. 2015, 11, 31–47. [Google Scholar]
- Wyatt, A.; Alshafey, M. Non-revenue water: Financial model for optimal management in developing countries—Application in Aqaba, Jordan. Water Sci. Technol. Water Supply 2012, 12, 451–462. [Google Scholar] [CrossRef]
- Trochez-Muñoz, C.; Smout, I.; Kayaga, S. Incorporating energy use into the economic level of Leakage Model. In Proceedings of the World Wide Workshop for Young Environmental Scientists, Arcueil, France, 31 May–4 June 2010. [Google Scholar]
- Munoz-Trochez, C. Inclusion of Energy Externalities in the Economic Level of Leakage (ELL) Model. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2011. [Google Scholar]
- Rimeika, M.; Albrektienė, R. Reduction of Apparent Water Losses. In Proceedings of the 10th International Conference “Environmental Engineering”, Vilnius, Lithuania, 27–28 April 2017. [Google Scholar]
- Criminisi, A.; Fontanazza, C.M.; Freni, G.; La Loggia, G. Evaluation of the apparent losses caused by water meter under-registration in intermittent water supply. Water Sci. Technol. 2009, 60, 2373–2382. [Google Scholar] [CrossRef] [PubMed]
- Fontanazza, C.M.; Freni, G.; La Loggia, G. Implementation of a Numerical Model for the Evaluation of Potential Apparent Losses in a Distribution Network. In Proceedings of the 5th IWA Water Loss Reduction Specialist Conference, Cape Town, South Africa, 26–30 April 2009; pp. 381–389. [Google Scholar]
- Rizzo, A.; Cilia, J. Quantifying meter under-registration caused by the ball valves of roof tanks (for indirect plumbing systems). In Proceedings of the IWA Leakage Conference ‘Leakage 2005’, Halifax, NS, Canada, 12–14 September 2005. [Google Scholar]
- Arregui, F.J.; Palau, C.V.; Gascón, L.; Peris, O. Evaluating domestic water meter accuracy. A case study. In Pumps, Electromechanical Devices and Systems Applied to Urban Water Management; Swets & Zeitlinger B.V.: Leiden, The Netherlands, 2003. [Google Scholar]
- Xin, K.; Tao, T.; Lu, Y.; Xiong, X.; Li, F. Apparent losses analysis in district metered areas of water distribution systems. Water Resour. Manag. 2014, 28, 683–696. [Google Scholar] [CrossRef]
- Arregui, F.; Gavara, F.; Soriano, J.; Pastor-Jabaloyes, L. Performance Analysis of Ageing Single-Jet Water Meters for Measuring Residential Water Consumption. Water 2018, 10, 612. [Google Scholar] [CrossRef]
- Arregui, F.; Cabrera, E., Jr.; Cobacho, R. Integrated Water Meter Management; IWA Publishing: London, UK, 2007. [Google Scholar]
- Vermersch, M.; Carteado, F.; Rizzo, A.; Johnson, E.; Arregui, F.; Lambert, A. Guidance Notes on Apparent Losses and Water Loss Reduction Planning. 2016. Available online: https://www.mcast.edu.mt/227 (accessed on 7 December 2018).
- AWWA. Water Audits and Loss Control Programs; AWWA Manual M36 Third Edition; Manual of Water Supply Practices—M36, Water Audits and Loss Control; American Water Works Association: Denver, CO, USA, 2009; ISBN 978-1-58321-631-6. [Google Scholar]
- Walski, T.M. Real-World Considerations in Water Distribution System Design. J. Water Resour. Plan. Manag. 2015, 141, 02515002. [Google Scholar] [CrossRef]
- Thornton, J. Water Losses Manual, 2nd ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Gonelas, K.; Kanakoudis, V. Reaching economic leakage level through pressure management. Water Sci. Technol. Water Supply 2016. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Gonelas, K. Analysis and Calculation of the Short and Long Run Economic Leakage Level in a Water Distribution System. Water Util. J. 2016, 12, 57–66. [Google Scholar]
- ISO 4064-2:2014—Water Meters for Cold Potable Water and Hot Water—Part 2: Test Methods; International Organization for Standardization: Geneve, Switzerland, 2014.
- Fanner, P.; Thornton, J. The Importance of Real Loss Component Analysis for Determining the Correct Intervention Strategy. In Proceedings of the IWA Leakage Conference ‘Leakage 2005’, Halifax, NS, Canada, 12–14 September 2005. [Google Scholar]
- Yazdandoost, F.; Izadi, A. An asset management approach to optimize water meter replacement. Environ. Model. Softw. 2018, 104, 270–281. [Google Scholar] [CrossRef]
- Rizzo, A.; Pearson, D.; Stephenson, M.; Harper, N. Apparent water loss control: A practical approach. Water 2004, 21, 44–45. [Google Scholar]
- Fanner, P.; Thornton, J.; Liemberger, R.; Sturm, R. Leakage Management Technologies; AWWA/IWA: Denver, CO, USA; London, UK, 2007. [Google Scholar]
- Fanner, P.; Thornton, J.; Liemberger, R.; Sturm, R. Evaluating Water Loss and Planning Loss Reduction Strategies; AWWA/IWA: Denver, CO, USA; London, UK, 2007. [Google Scholar]
- AWWA. Near Final Draft for Water Loss Committee Review: AWWA M36 Publication Rewrite; American Water Works Association: Denver, CO, USA, 2006. [Google Scholar]
- Morote, Á.-F.; Hernández-Hernández, M. Unauthorised Domestic Water Consumption in the City of Alicante (Spain): A Consideration of Its Causes and Urban Distribution (2005–2017). Water 2018, 10, 851. [Google Scholar] [CrossRef]
- Richards, G.L.; Johnson, M.C.; Barfuss, S.L. Apparent losses caused by water meter inaccuracies at ultralow flows. J. Am. Water Works Assoc. 2010, 102, 123–132. [Google Scholar] [CrossRef]
- Male, J.W.; Noss, R.R.; Moore, I.C. Identifying and Reducing Losses in Water Distribution Systems; Noyes Publications: Park Ridge, NJ, USA, 1985. [Google Scholar]
- Lambert, A.O.; Lalonde, A. Using practical predictions of Economic Intervention Frequency to calculate Short-run Economic Leakage Level, with or without Pressure Management. In Proceedings of the IWA Leakage Conference ‘Leakage 2005’, Halifax, NS, Canada, 12–14 September 2005. [Google Scholar]
- Lambert, A.; Myers, S.; Trow, S. Managing Water Leakage; Financial Times Energy Ltd.: London, UK, 1998. [Google Scholar]
- Gavara-Tortes, F.J. Estudio del Comportamiento Metrológico de los Contadores en Abastecimientos de Agua Optimización de su Gestión para la Reducción de las Pérdidas Comerciales. Ph.D. Thesis, Universitat Politècnica de València, Valencia, Spain, 2015. [Google Scholar] [CrossRef]

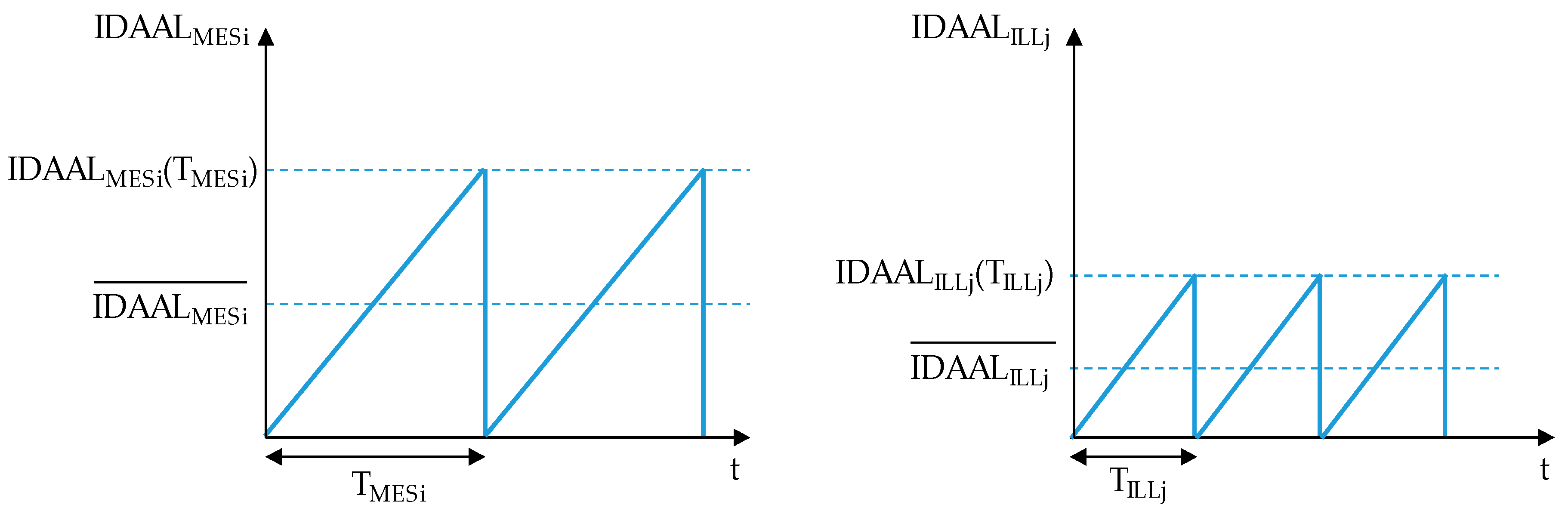
| Worst Case (%) | Best Case (%) | |
|---|---|---|
| Single jet | −5 | −2 |
| Oscillating piston | −1 | +0 |
| AWWA Single-jet | −7 | −3 |
| AWWA Multi-jet | −7 | −3 |
| Fluidic | −7 | −5 |
| Multi-jet | −6 | −2 |
| AWWA Nutating disc | −3 | −1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arregui, F.J.; Cobacho, R.; Soriano, J.; Jimenez-Redal, R. Calculation Proposal for the Economic Level of Apparent Losses (ELAL) in a Water Supply System. Water 2018, 10, 1809. https://doi.org/10.3390/w10121809
Arregui FJ, Cobacho R, Soriano J, Jimenez-Redal R. Calculation Proposal for the Economic Level of Apparent Losses (ELAL) in a Water Supply System. Water. 2018; 10(12):1809. https://doi.org/10.3390/w10121809
Chicago/Turabian StyleArregui, Francisco J., Ricardo Cobacho, Javier Soriano, and Ruben Jimenez-Redal. 2018. "Calculation Proposal for the Economic Level of Apparent Losses (ELAL) in a Water Supply System" Water 10, no. 12: 1809. https://doi.org/10.3390/w10121809
APA StyleArregui, F. J., Cobacho, R., Soriano, J., & Jimenez-Redal, R. (2018). Calculation Proposal for the Economic Level of Apparent Losses (ELAL) in a Water Supply System. Water, 10(12), 1809. https://doi.org/10.3390/w10121809





