An Integrated Multicriteria Analysis Tool for Evaluating Water Resource Management Strategies
Abstract
1. Introduction
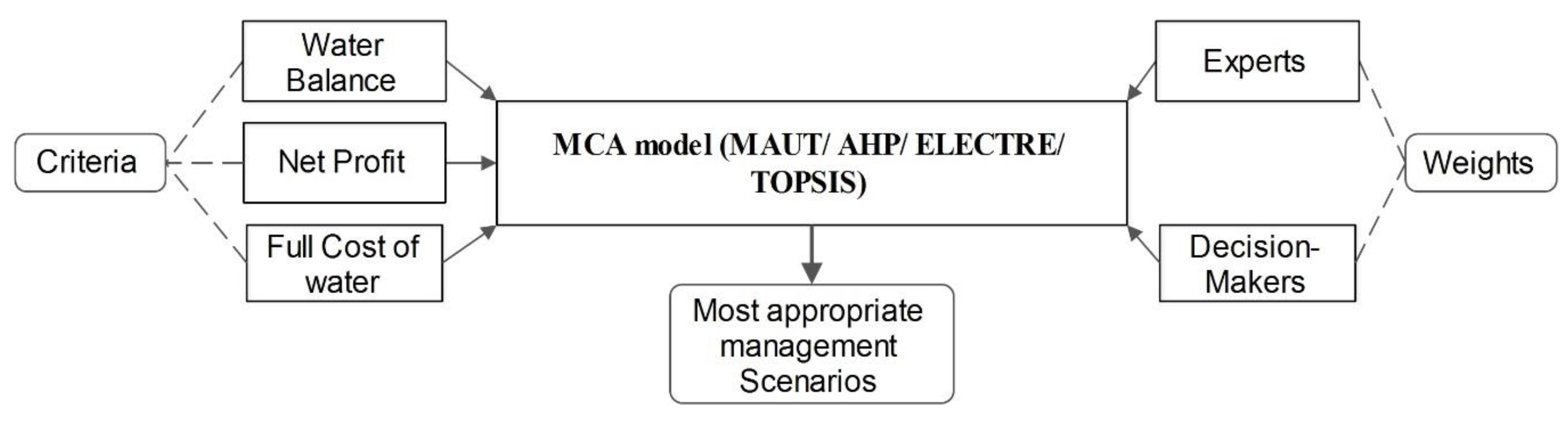
2. The Studied Problem
- Scenario 1a: Reducing water irrigation losses in the current situation. The Karla reservoir is not active yet. Water needs are covered from the groundwater aquifer and from the Pinios River. This can be practically achieved by cleaning and maintaining the irrigation canals.
- Scenario 1b: Replacing irrigation methods with more efficient methods than the current situation. Previous field surveys have shown that the majority of the basin’s farmers are using sprinklers. This scenario was developed based on the assumption that sprinklers are replaced with drip irrigation, which is more efficient.
- Scenario 2: Future situation (operation of the reservoir and the new Karla network). Some new irrigation areas can be served from the reservoir’s surface water (instead of the underlying aquifer). To implement this scenario, the local authorities need to ensure that the water from Pinios will reach to the reservoir.
- Scenario 2a: Replacement of 25% of cotton crops with winter wheat, in Scenario 2.
- Scenario 2b: Replacement 20% of cotton crops with 10% winter wheat and 10% maize. The development of the crop replacement scenarios was based on the crop distribution of the watershed during the past ten years, and on some factors that affect the farmers’ decisions on what to cultivate (e.g., subsidies and product prices timeseries). The trends are also in agreement with the objectives set by the Common Agricultural Policy (CAP 2015–2020), which provides more incentives for cultivating less water consuming crops [44].
- Scenario 2c: Reducing water irrigation losses in Scenario 2, in the same way that was considered in Scenario 1a.
- Scenario 2d: Replacing irrigation methods with more efficient methods in Scenario 2, according to Scenario 1b.
- Criterion 1: Water balance. The water supply, the crop distribution and areas, and the water demand of the watershed was estimated. The irrigation water requirements were calculated by using CROPWAT 8.0. software [45] and were adjusted for the water supply network and the irrigation method efficiency, which were estimated from a field survey. Thus, the water balance was calculated [41].
- Criterion 2: Net Profits. Data concerning crop distribution, average yields, product prices, subsidies, and production costs, were collected. A simple logistic model was developed and implemented in order to calculate the net profits from the agricultural activities [43].
- Criterion 3: Full cost of water. According to the European Framework Directive 2000/60, and of course the Greek Ministry of Environment [44], the full cost of water has to be taken into account in every water resource management plan. It is the sum of the three following costs:
- ○
- Monetary (or direct) cost: the cost for the water supply company. The financial data of the annual balance sheets of Pinios and Karla LALRs were collected and used in order to estimate the capital cost, the cost of maintenance and operation, and the administrative cost (at their present value).
- ○
- Natural resource cost: the cost associated with damage or negative impact on the aquatic environment in terms of water scarcity or resource misallocation. It was treated as: (a) the opportunity cost (lost profits) due to the exploitation of the water resources faster than their natural rate of renewal [46]. This was estimated as the net profit that occurs if the deficit water (from the water balance) is distributed to the existing crop pattern. (b) The opportunity cost, since the water may be not allocated to its optimum use, but to other less profitable uses [46]. Then, the natural resource cost expresses the difference between the current and the optimum water allocation [47]. The optimum use is actually the optimum crop distribution resulting from a net profit maximization problem, with environmental constraints.
- ○
- Environmental cost: the cost associated with the damage of use, or negative impact on the aquatic environment in terms of qualitative degradation. The environmental damage is equal with the cost needed to bring the environment back to its original state [46], and therefore associated with the cost of restoring the quality of the water used in its original condition (maximum allowed pollutant concentrations for irrigation) [44].
3. Methodology
4. Results and Discussion
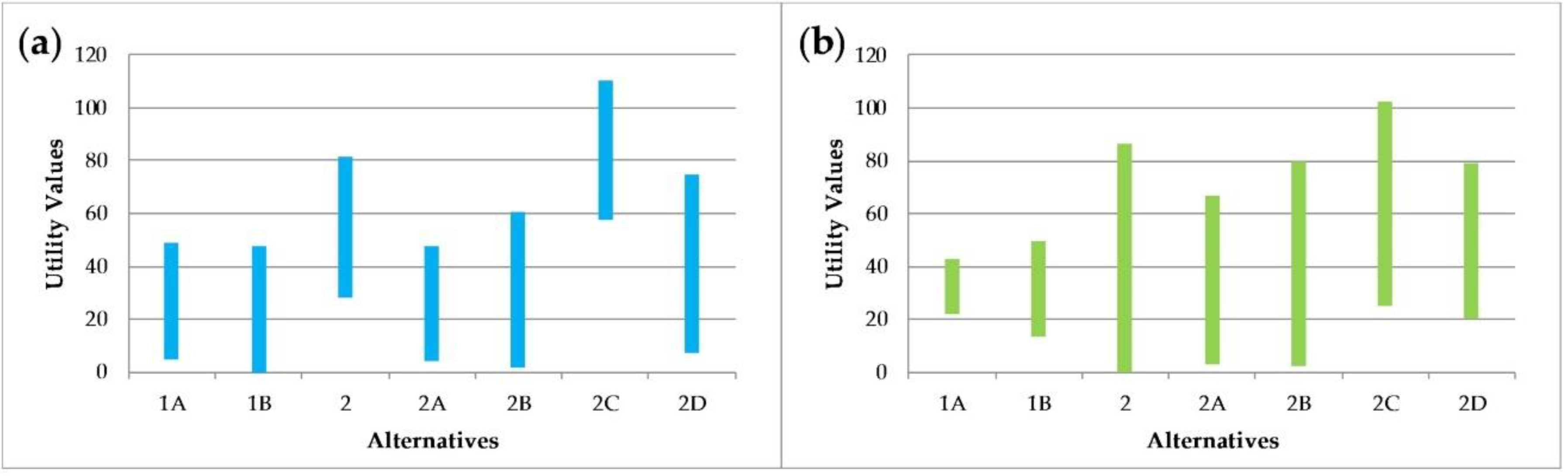
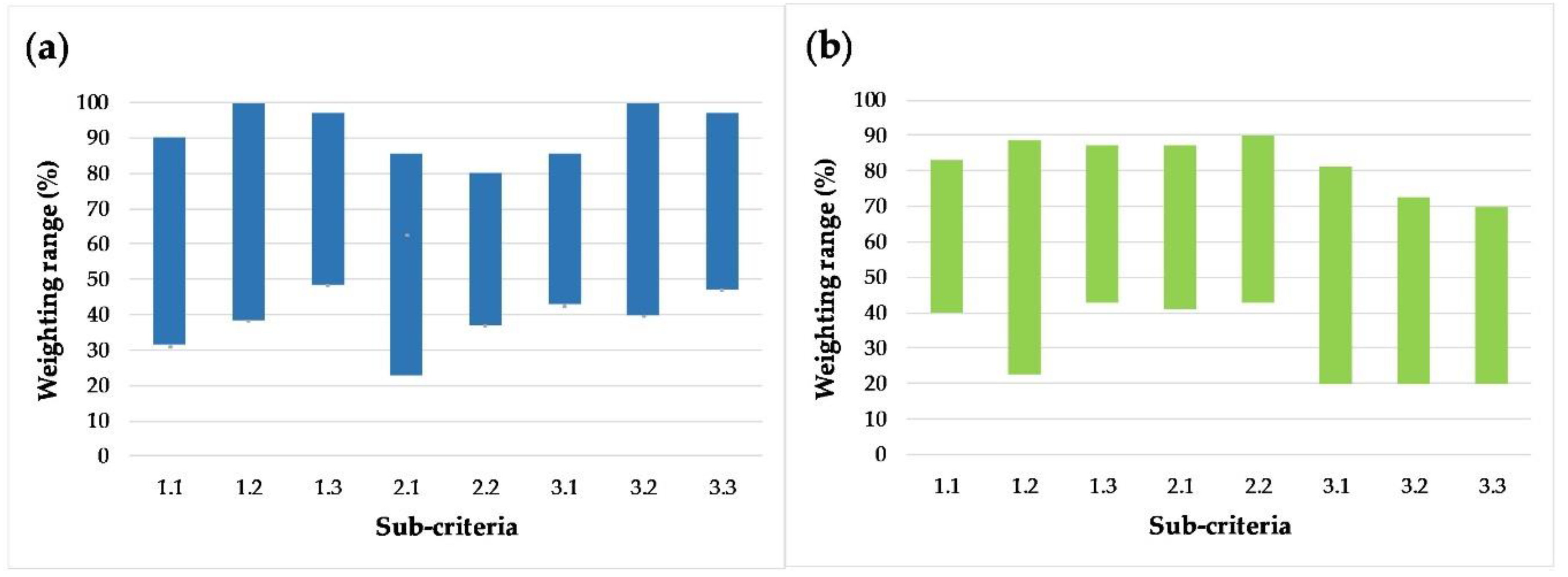
4.1. Results of MAUT Method
4.2. Results of AHP Method
4.3. Results of ELECTRE Method
4.4. Results of TOPSIS Method
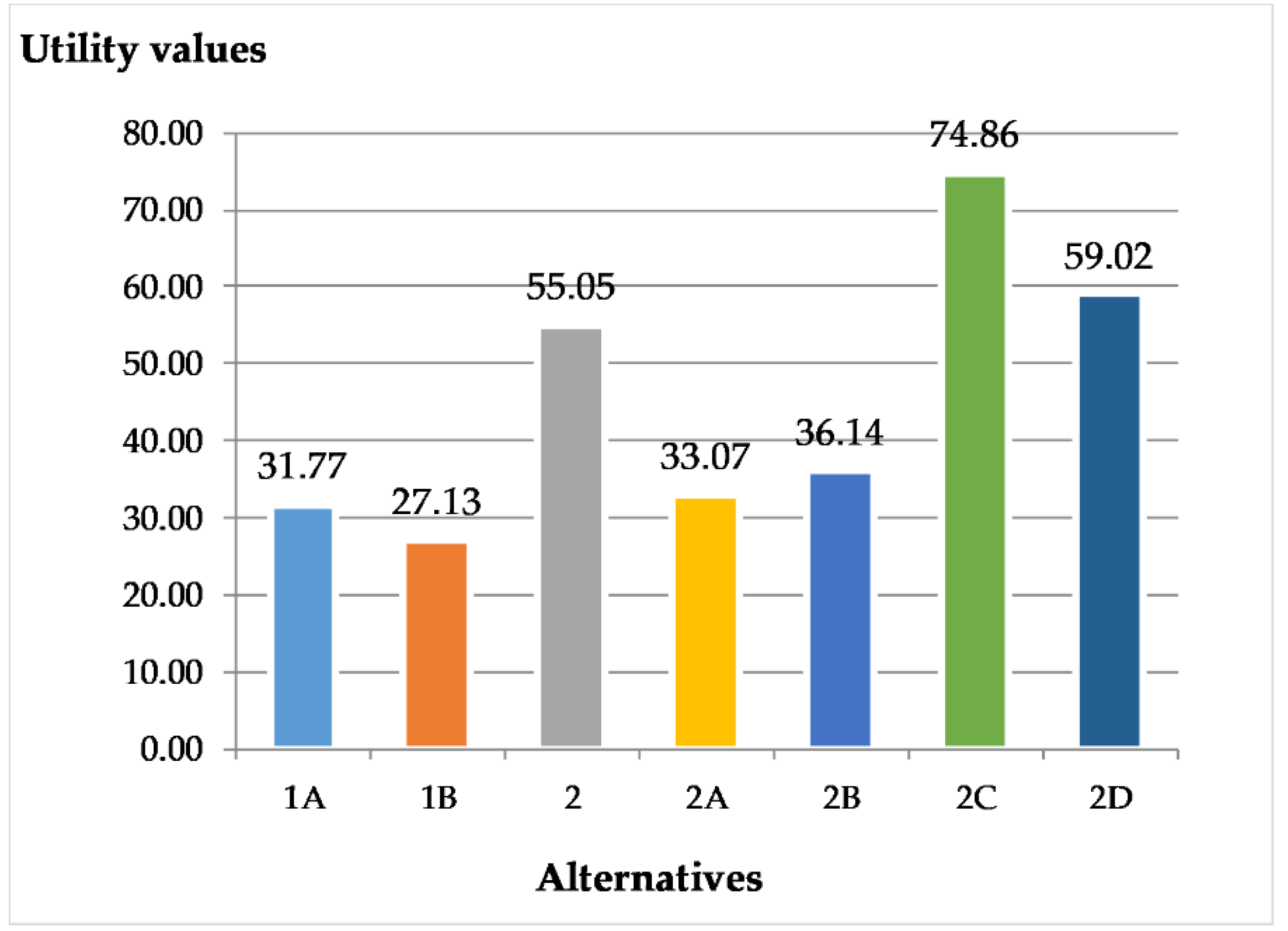
4.5. Overall Results
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Janssen, R. Multiobjective Decision Support for Environmental Management; Kluwer Academic: Dortrecht, The Netherlands, 1992. [Google Scholar]
- Rahman, M.A.; Rusteberg, B.; Uddin, M.S.; Saada, M.A.; Rabi, A.; Sauter, M. Impact Assessment and Multicriteria Decision Analysis of Alternative Managed Aquifer Recharge Strategies Based on Treated Wastewater in Northern Gaza. Water 2014, 6, 3807–3827. [Google Scholar] [CrossRef]
- Voogd, H. Multiple Criteria Evaluation for Urban and Regional Planning; Pion: London, UK, 1983. [Google Scholar]
- Meerkhan, H.; Teixeira, J.; Espinha Marques, J.; Afonso, M.J.; Chaminé, H.I. Delineating Groundwater Vulnerability and Protection Zone Mapping in Fractured Rock Masses: Focus on the DISCO Index. Water 2016, 8, 462. [Google Scholar] [CrossRef]
- Andreoli, M.; Tellarini, V. Farm sustainability evaluation: Methodology and practice. Agric. Ecosyst. Environ. 2000, 77, 43–52. [Google Scholar] [CrossRef]
- Funtowicz, S.O.; Ravetz, J. Uncertainty and Quality in Science for Policy; Kluwer: Dortrecht, The Netherlands, 1990. [Google Scholar]
- Mendoza, G.A.; Prabhu, R. Multiple criteria decision making approaches to assessing forest sustainability using criteria and indicators: A case study. For. Ecol. Manag. 2000, 131, 107–126. [Google Scholar] [CrossRef]
- Brown, C.; Werick, W.; Leger, W.; Fay, D. A decision-analytic approach to managing climate risks: Application to the upper great lakes. J. Amer. Water Res. Assoc. 2011, 47, 524–534. [Google Scholar] [CrossRef]
- Little, J.D.C. Models and Managers: The Concept of a Decision Calculus. Manag. Sci. 1970, 16, B466–B485. [Google Scholar] [CrossRef]
- Keen, P.G.W.; Scott-Morton, M.S. Decision Support Systems: An Organizational Perspective; Addison-Wesley: Reading, MA, USA, 1978; ISBN 0-201-03667-3. [Google Scholar]
- Sprague, R.H.; Carlson, E.D. Building Effective Decision Support Systems; Appeared in DSS News, February 11 2001; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1982; Volume 2. [Google Scholar]
- Andriole, S.J. Handbook for the Design, Development, Evaluation, and Application of Interactive Decision Support Systems; Petrocelli: Princeton, NJ, USA, 1989. [Google Scholar]
- Sage, A.P. Decision Support Systems Engineering; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Adelman, L. Evaluating Decision Support and Expert Systems; xvi+234pp; Wiley: New York, NY, USA, 1992; 234p, ISBN 0-471-54801-4. [Google Scholar]
- Demirel, M.C.; Koch, J.; Mendiguren, G.; Stisen, S. Spatial Pattern Oriented Multicriteria Sensitivity Analysis of a Distributed Hydrologic Model. Water 2018, 10, 1188. [Google Scholar] [CrossRef]
- Mylopoulos, N. Water Resources Management, Teaching Notes; University of Thessaly, Department of Civil Engineering: Volos, Greece, 2006. [Google Scholar]
- Figueira, J.; Salvatore, G.; Ehrgott, M. Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005; p. 1045. [Google Scholar]
- Pohekar, S.D.; Ramachandran, M. Application of multi-criteria decision making to sustainable energy planning—A review. Renew. Sustain. Energy 2004, 8, 365–381. [Google Scholar] [CrossRef]
- Dunning, D.J.; Ross, Q.E.; Merkhofer, M.W. Multiattribute utility analysis; best technology available; adverse environmental impact. Clean Water Act, Section 316(b). Environ. Sci. Policy 2000, 3, 7–14. [Google Scholar] [CrossRef]
- Romero, C.; Rehman, T. Natural resource management and the use of multiple criteria decision making techniques: A review. Eur. Rev. Agric. Econ. 1987, 14, 61–89. [Google Scholar] [CrossRef]
- UNESCO. IWRM Guidelines at River Basin Level—Part 2-1: The Guidelines for IWRM Coordination; unesco.org; UNESCO IHP Secretariat: Paris, France, 2009. [Google Scholar]
- UNESCO. IWRM Guidelines at River Basin Level—Part 2-4: The Guidelines for Managing Environmental Sustainability; unesco.org; UNESCO IHP Secretariat: Paris, France, 2009. [Google Scholar]
- Cohon, J.L.; Marks, D.H. A review evaluation of multiobjective programming techniques. Water Resour. Manag. 1975, 11, 208–220. [Google Scholar] [CrossRef]
- Singh, A. Decision support for on-farm water management and long-term agricultural sustainability in a semi-arid region of India. J. Hydrol. 2010, 391, 63–76. [Google Scholar] [CrossRef]
- Pegram, G.; Li, Y.; Le Quesne, T.; Speed, R.; Li, J.; Shen, F. River Basin Planning: Principles, Procedures and Approaches for Strategic Basin Planning; UNESCO IHP Secretariat: Paris, France, 2013. [Google Scholar]
- UNEP. The UN-Water Status Report on the Application of Integrated Approaches to Water Resources Management; UN-Water Reports; UNEP: Athens, Greece, 2012. [Google Scholar]
- Hajkowicz, S.; Collins, K. A Review of Multiple Criteria Analysis for Water Resource Planning and Management. Water Resour. Manag. 2007, 21, 1553–1566. [Google Scholar] [CrossRef]
- Steuer, R.E.; Na, P. Multiple criteria decision making combined with finance: A categorized bibliographic study. Eur. J. Oper. Res. 2003, 150, 496–515. [Google Scholar] [CrossRef]
- Lee, C.S.; Chang, S.P. Interactive fuzzy optimization for an economic and environmental balance in a river system. Water Res. 2005, 39, 221–231. [Google Scholar] [CrossRef] [PubMed]
- Tecle, A. Selecting a multicriterion decision making technique for watershed resources management. Water Resour. Bull. 1992, 28, 129–140. [Google Scholar] [CrossRef]
- Gershon, M.; Duckstein, L. Multiobjective approaches to river basin planning. J. Water Resour. Plan. Manag. 1983, 109, 13–28. [Google Scholar] [CrossRef]
- Ozelkan, E.C.; Duckstein, L. Analysing water resource alternatives and handling criteria by multi criterion decision techniques. J. Environ. Manag. 1996, 48, 69–96. [Google Scholar] [CrossRef]
- Eder, G.; Duckstein, L.; Nachtnebel, H.P. Ranking water resource projects and evaluating criteria by multicriterion Q-analysis: An Austrian case study. J. Multi-Criteria Decis. Anal. 1997, 6, 259–271. [Google Scholar] [CrossRef]
- Alhumaid, M.; Ghumman, A.R.; Haider, H.; Al-Salamah, I.S.; Ghazaw, Y.M. Sustainability Evaluation Framework of Urban Stormwater Drainage Options for Arid Environments Using Hydraulic Modeling and Multicriteria Decision-Making. Water 2018, 10, 581. [Google Scholar] [CrossRef]
- Fishburn, P.C. Utility theory. Manag. Sci. 1968, 14, 335–378. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Roy, B. The outranking approach and the foundations of ELECTRE methods. Theory Decis. 1991, 31, 49–73. [Google Scholar] [CrossRef]
- Yoon, K.P.; Hwang, C.L. Multiple Attribute Decision Making; Sage Publication: Thousand Oaks, CA, USA, 1995. [Google Scholar]
- Loukas, A.; Mylopoulos, N.; Vasiliades, L. A modeling system for the evaluation of water resources management strategies in Thessaly, Greece. Water Resour. Manag. 2007, 21, 1673–1702. [Google Scholar] [CrossRef]
- Sidiropoulos, P. Groundwater Resources Management under Uncertainty: The Value of Information on Environmentally Degraded Aquifers. PhD Thesis, University of Thessaly, Department of Civil Engineering, Volos, Greece, 2014. [Google Scholar]
- Alamanos, A.; Xenarios, S.; Mylopoulos, N.; Stalnacke, P. Hydroeconomic modeling and management with limited data: The case of Lake Karla Basin, Greece. Eur. Water J. 2016, 54, 3–18. [Google Scholar]
- Alamanos, A.; Xenarios, S.; Mylopoulos, N.; Stalnacke, P. Integrated Water Resources Management in agro-economy using linear programming: The case of Lake Karla Basin, Greece. Eur. Water J. 2017, 60, 41–47. [Google Scholar]
- Alamanos, A.; Fafoutis, C.; Papaioannou, G.; Mylopoulos, N. Extension of an integrated hydroeconomic model of Lake Karla basin, under management, climate and pricing scenario analysis. In Proceedings of the Sixth International Conference on Environmental Management, Engineering, Planning and Economics (CEMEPE), Thessaloniki, Greece, 25–30 June 2017. [Google Scholar]
- Greek Ministry of Environment, Energy and Climate Change, Special Water Secretariat. Water Resources Management Plans for the Water Districts of Thessaly, Epirus and Central Greece, according to the Requirements of the Water Framework Directive 2000/60/EC, the Law 3199/2003 and the Presidential Decree 51/2007; Special Water Secretariat-YPEKA: Athens, Greek, 2012. [Google Scholar]
- FAO. Cropwat. 2015. Available online: http://www.fao.org/nr/water/infores_databases_cropwat.html (accessed on 21 August 2017).
- Common Implementation Strategy Working Group 2 (WATECO). EU Guidance Document: Economics and the Environment. The Implementation Challenge of the Water Framework Directive. August 2002. Available online: http://forum.europa.eu.int/Public/irc/env/wfd/library (accessed on 30 April 2015).
- Tietenberg, T.; Lewis, L. Environmental & Natural Resource Economics, 9th ed.; Pearson: Boston, MA, USA, 2011; ISBN 978-0131392571. [Google Scholar]
- Neumann, J.V.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1953; ISBN 9780691130613. [Google Scholar]
- Churchman, C.W.; Ackoff, R.L.; Arnoff, E.L. Introduction to Operations Research; Wiley: New York, NY, USA, 1957. [Google Scholar]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives; Wiley: New York, NY, USA, 1976; 569p, ISBN 0-521-44185-4. [Google Scholar]
- Fishburn, P.C. A Survey of Multiattribute/11multiple Criteria Evaluation Theories; Multiple Criteria Problem, Solving, Zionts, S., Eds.; Springer: Berlin, Germany, 1978; pp. 181–224. [Google Scholar]
- Fishburn, P.C. Utility Theory for Decision Making; John Wiley and Sons: New York, NY, USA, 1970; Volume 6. [Google Scholar]
- Sintonen, H. An approach to measuring and valuing health states. Soc. Sci. Med. 1981, 15, 55–65. [Google Scholar] [CrossRef]
- Rehman, T.; Romero, C. The application of the MCDM paradigm to the management of agricultural systems: Some basic considerations. Agric. Syst. 1993, 41, 239–255. [Google Scholar] [CrossRef]
- Beinat, E. Value Functions for Environmental Management; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Climaco, J. Multicriteria Analysis. In Proceedings of the XIth International Conference on MCDM, Coimbra, Portugal, 1–6 August 1997; Springer: Berlin, Germany, 1997. [Google Scholar]
- De Montis, A.; De Toro, P.; Droste-Franke, B.; Omann, I.; Stagl, S. Criteria for quality assessment of MCDA methods. In Proceedings of the 3rd Biennial Conference of the European Society for Ecological Economics, Vienna, Austria, 3–6 May 2000. [Google Scholar]
- Hayashi, K. Multicriteria analysis for agricultural resource management: A critical survey and future perspectives. Eur. J. Oper. Res. 2000, 122, 486–500. [Google Scholar] [CrossRef]
- Munier, N. A Strategy for Using Multicriteria Analysis in Decision-Making. A Guide for Simple and Complex Environmental Projects; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; London, UK; New York, NY, USA, 2011; ISBN 978-94-007-1511-0. e-ISBN 978-94-007-1512-7. [Google Scholar] [CrossRef]
- Spanos, S. Analytical Study of Multicriteria Decision Making Methods. Diploma (BSc.) Thesis, School of Electrical and Computer Engineering, National Technical University of Athens, Athina, Greece, 2004. [Google Scholar]
- Galliou, F. Managing a Framework for the Assessment of Small-Scale Sewage Treatment Systems with Multi-Criteria Decision Analysis. Postgraduate Thesis, Agricultural School, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2009. [Google Scholar]
- Roy, B. Classement et choix en présence de points de vue multiples (la méthode ELECTRE). La Revue d’Informatique et de Recherche Opérationelle (RIRO) 1968, 8, 57–75. (In French) [Google Scholar]
- Roy, B. Multicriteria Methodology for Decision Aiding; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Hwang, C.L.; Lai, Y.J.; Liu, T.Y. A new approach for multiple objective decision making. Comput. Oper. Res. 1993, 20, 889–899. [Google Scholar] [CrossRef]
- Luce, R.D. Semiorders and a theory of utility discrimination. Econometrica 1956, 24, 178–191. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981; ISBN 978-3-642-48318-9. [Google Scholar]
- Triantaphyllou, E.; Lin, C. Development and Evaluation of Five Fuzzy Multiattribute Decision-Making Methods. Int. J. Approx. Reason. 1996, 14, 281–310. [Google Scholar] [CrossRef]
- Yoon, K. A reconciliation among discrete compromise situations. J. Oper. Res. Soc. 1987, 38, 277–286. [Google Scholar] [CrossRef]
- Cheng, S.; Chan, C.W.; Huang, G.H. Using multiple criteria decision analysis for supporting decision of solid waste management. J. Environ. Sci. Health 2002, 6 Pt A37, 975–990. [Google Scholar] [CrossRef]
- Kim, G.; Park, C.S.; Yoon, K.P. Identifying investment opportunities for advanced manufacturing systems with comparative-integrated performance measurement. Int. J. Prod. Econ. 1997, 50, 23–33. [Google Scholar] [CrossRef]
- Shih, H.S.; Shyur, H.J.; Lee, E.S. An extension of TOPSIS for group decision making. Math. Comput. Model. 2007, 45, 801–813. [Google Scholar] [CrossRef]
- Wittrup-Jensen, K.U.; Pedersen, K.M. Modelling Danish Weights for the 15D Quality of Life Questionnaire by Applying Multi-Attribute Utility Theory (MAUT); Health Economics Papers; University of Southern Denmark: Odense, Denmark, 2008; Volume 7. [Google Scholar]
- Guarini, M.R.; Battisti, F.; Chiovitti, A. A Methodology for the Selection of Multi-Criteria Decision Analysis Methods in Real Estate and Land Management Processes. Sustainability 2018, 10, 507. [Google Scholar] [CrossRef]
- Guarini, M.R.; Battisti, F.; Chiovitti, A. Public Initiatives of Settlement Transformation: A Theoretical-Methodological Approach to Selecting Tools of Multi-Criteria Decision Analysis. Buildings 2018, 8, 1. [Google Scholar] [CrossRef]
- Alamanos, A.; Mylopoulos, N.; Vasiliades, L.; Loukas, A. Climate change effects on the availability of water resources of Lake Karla watershed for irrigation and Volos city urban water use. In Proceedings of the 14th Protection and Restoration of the Environment (PRE) Conference, Thessaloniki, Greece, 3–6 July 2018. [Google Scholar]

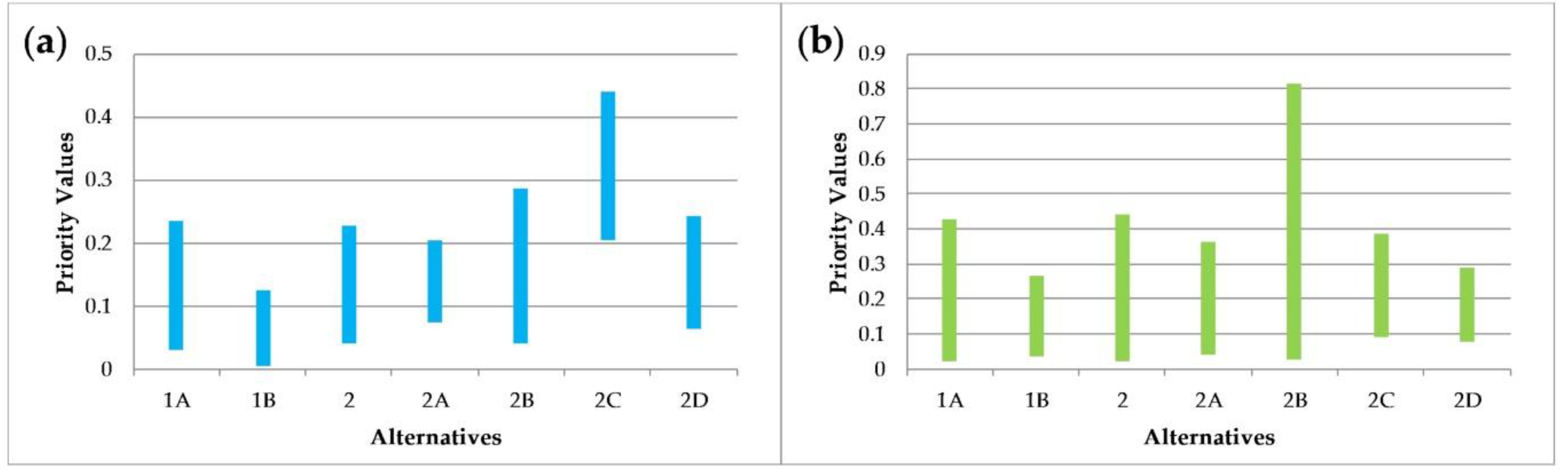
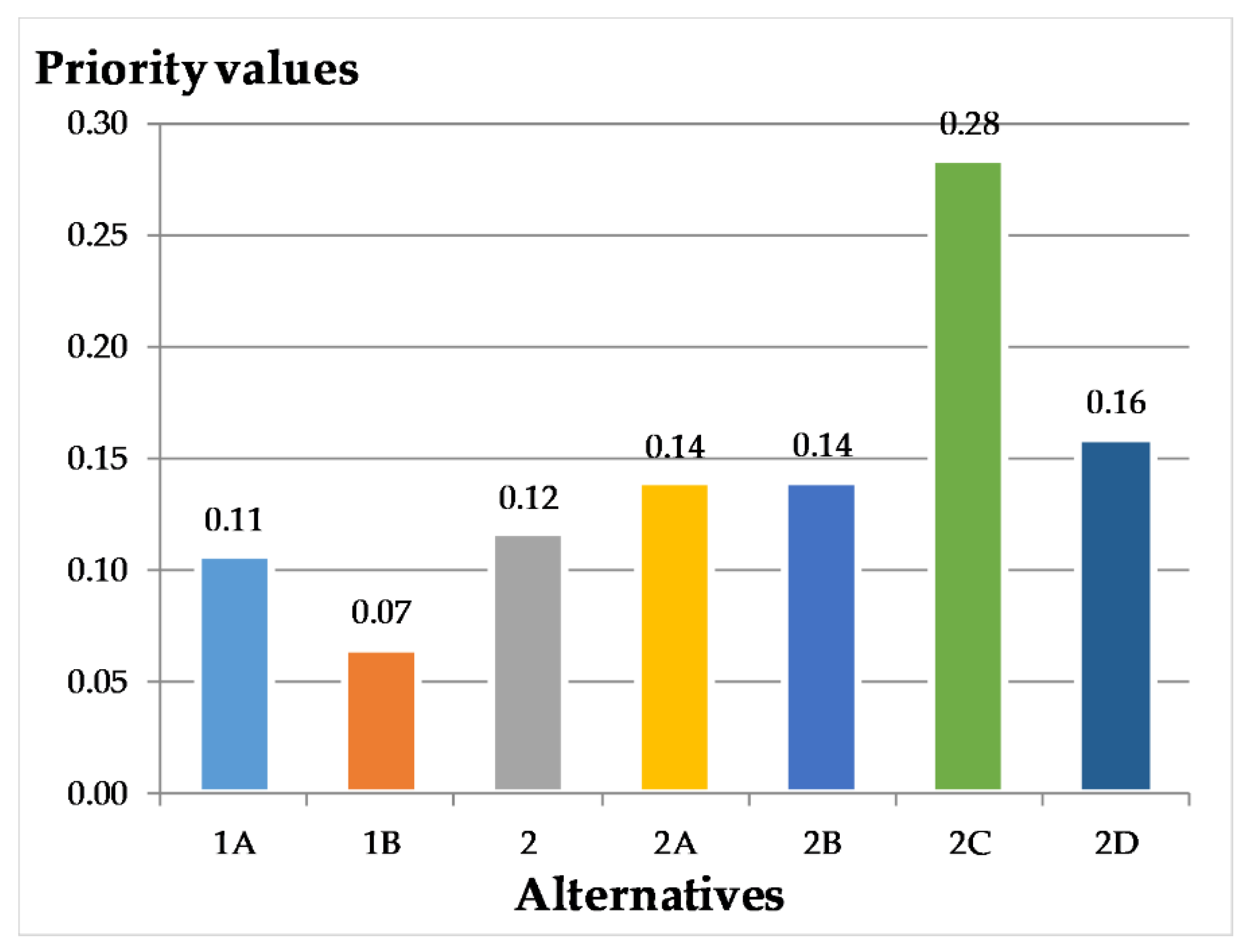

| Alternatives | Criterion 1—Water Balance (hm3) | Criterion 2—Net Profit (mil. €) | Criterion 3—Full Cost of Water (mil. €) |
|---|---|---|---|
| 1A | −71.26 | 47.31 | 27.83 |
| 1B | −142.49 | 47.31 | 34.39 |
| 2 | −99.55 | 49.40 | 25.92 |
| 2A | −78.17 | 47.33 | 23.59 |
| 2B | −90.26 | 48.67 | 24.90 |
| 2C | −10.52 | 49.40 | 22.67 |
| 2D | −81.67 | 49.40 | 26.47 |
| Sub-Criteria/Alternatives | C1.1 (hm3) | C1.2 (hm3) | C1.3 (hm3) | C2.1 (mil. €) | C2.2 (mil. €) | C3.1 (mil. €) | C3.2 (mil. €) | C3.3 (mil. €) |
|---|---|---|---|---|---|---|---|---|
| 1A | 50.2 | −121.46 | 0 | 73.96 | 57.84 | 2.6 | 18.87 | 6.36 |
| 1B | −4.96 | −137.53 | 0 | 73.96 | 57.84 | 7.18 | 21.05 | 6.16 |
| 2 | −10.8 | −102.69 | 13.95 | 108.43 | 59.03 | 4.01 | 15.22 | 6.68 |
| 2A | −1.4 | −92.73 | 15.97 | 101.65 | 54.32 | 4.01 | 13.83 | 5.75 |
| 2B | −6.72 | −98.37 | 13.95 | 104.9 | 56.22 | 4.01 | 13.67 | 7.22 |
| 2C | 50.2 | −79.79 | 19.06 | 108.43 | 59.03 | 2.84 | 11.68 | 8.16 |
| 2D | −4.96 | −92.87 | 16.15 | 108.43 | 59.03 | 6.43 | 13.87 | 6.17 |
| MCA Method | Theory | Weightings | Description |
|---|---|---|---|
| MAUT | Utility Theory | The alternatives are evaluated under each sub-criterion. | The alternatives are ranked according to the sum product of the performances of the alternatives to the respective weights |
| AHP | Hierarchical Theory | Comparing every pair of criteria, and then every pair of alternatives, under each criterion. | Linear algebra is used to extract the overall score for each alternative. The alternatives are ranked in descending order of the resulting priority values, i.e., in order of suitability. |
| ELECTRE I | Outranking Theory | Scores of importance for each criterion | Outranking relations are formed to represent the preferences of the respondents, through pairwise comparisons of the alternatives. |
| TOPSIS | Classification Theory | Scores of importance for each criterion | The alternatives are ordered between the best and the worst solution, based on the distances of their respective performances. A closeness index expresses each alternative’s similarity to the optimal solution. |
| Alternatives | Group of Experts | Group of DMs | Total |
|---|---|---|---|
| 1A | 54.055 | 54.087 | 54.072 |
| 1B | 0.000 | 0.000 | 0.000 |
| 2 | 35.128 | 36.499 | 35.837 |
| 2A | 50.926 | 52.083 | 51.524 |
| 2B | 41.999 | 43.286 | 42.665 |
| 2C | 100.000 | 100.000 | 100.000 |
| 2D | 47.247 | 47.896 | 47.583 |
| Alternatives | MAUT | AHP | ELECTRE I | TOPSIS | Overall |
|---|---|---|---|---|---|
| 1A | 0 | 2 | 0 | 0 | 2 |
| 1B | 0 | 1 | 0 | 0 | 1 |
| 2 | 1 | 4 | 0 | 0 | 5 |
| 2A | 0 | 3 | 0 | 0 | 3 |
| 2B | 3 | 3 | 0 | 0 | 6 |
| 2C | 45 | 39 | 60 | 60 | 174 |
| 2D | 11 | 8 | 0 | 0 | 19 |
| Total runs | 60 | 60 | 60 | 60 | 240 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamanos, A.; Mylopoulos, N.; Loukas, A.; Gaitanaros, D. An Integrated Multicriteria Analysis Tool for Evaluating Water Resource Management Strategies. Water 2018, 10, 1795. https://doi.org/10.3390/w10121795
Alamanos A, Mylopoulos N, Loukas A, Gaitanaros D. An Integrated Multicriteria Analysis Tool for Evaluating Water Resource Management Strategies. Water. 2018; 10(12):1795. https://doi.org/10.3390/w10121795
Chicago/Turabian StyleAlamanos, Angelos, Nikitas Mylopoulos, Athanasios Loukas, and Dimitrios Gaitanaros. 2018. "An Integrated Multicriteria Analysis Tool for Evaluating Water Resource Management Strategies" Water 10, no. 12: 1795. https://doi.org/10.3390/w10121795
APA StyleAlamanos, A., Mylopoulos, N., Loukas, A., & Gaitanaros, D. (2018). An Integrated Multicriteria Analysis Tool for Evaluating Water Resource Management Strategies. Water, 10(12), 1795. https://doi.org/10.3390/w10121795






