Industrial Water Pollution Discharge Taxes in China: A Multi-Sector Dynamic Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Input Dataset
2.2. Water Use Intensity, COD Discharge Rate and Concentration
2.3. Dynamic CGE Model
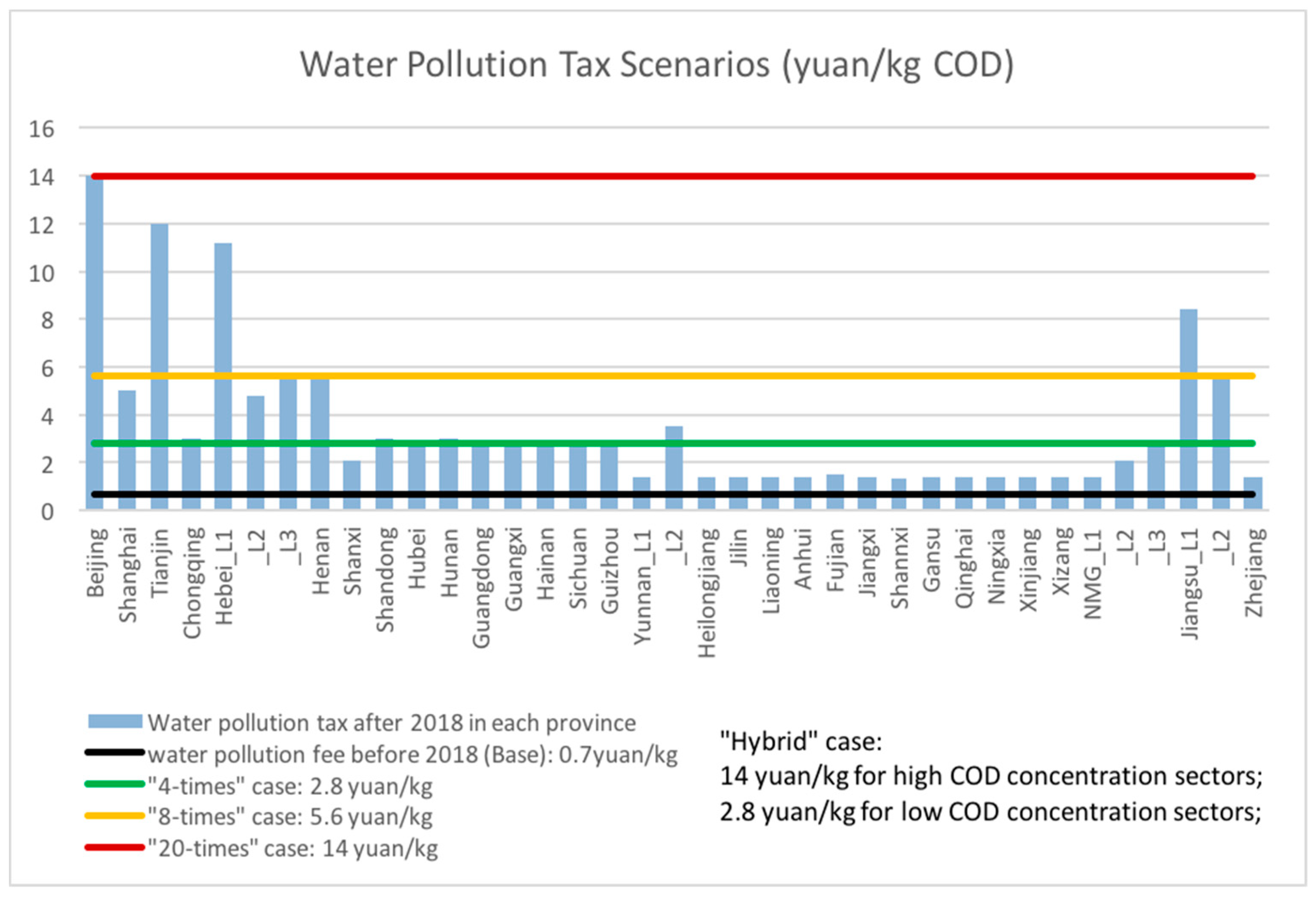
2.4. Water Pollution Tax Scenarios
3. Simulation Results
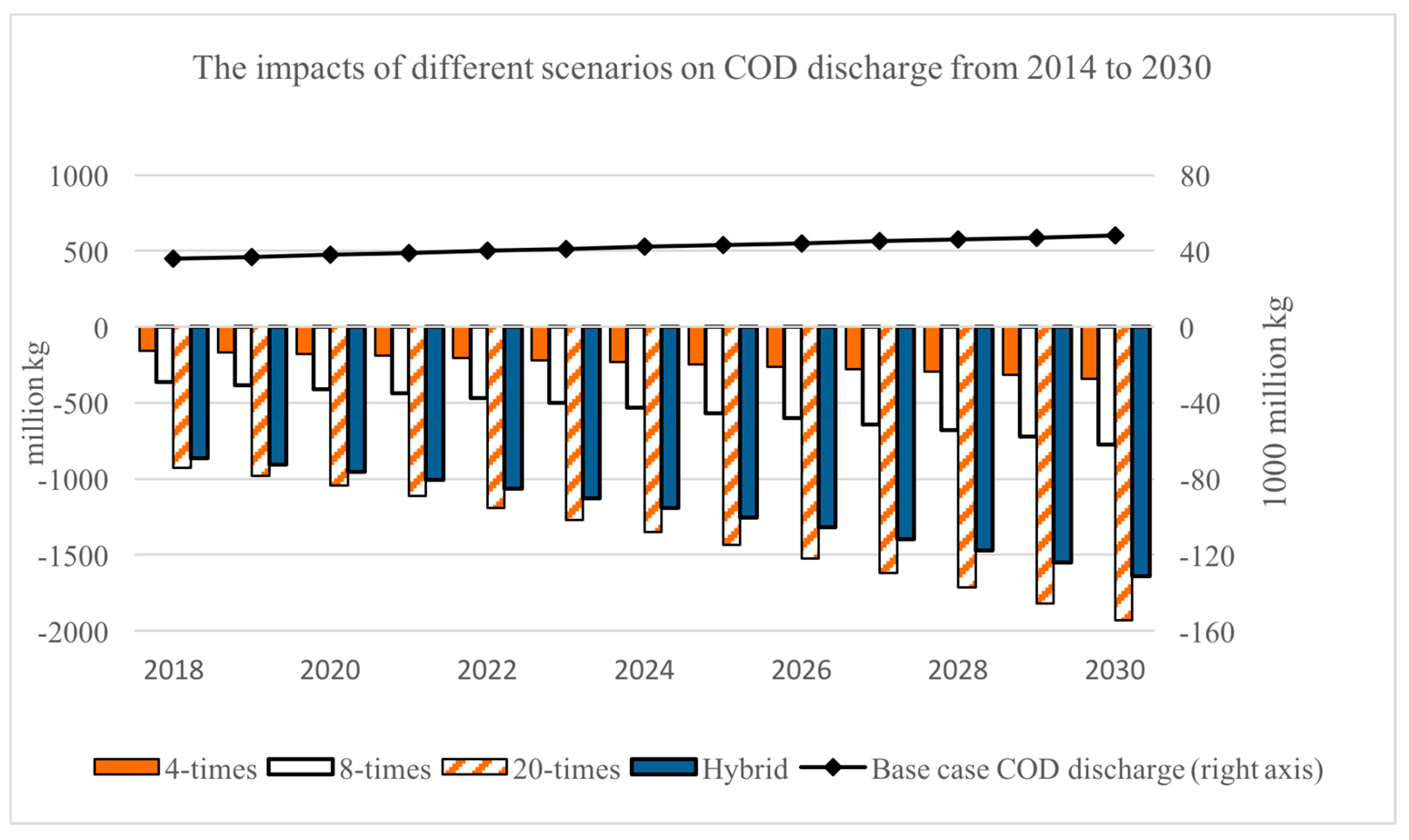
3.1. Baseline
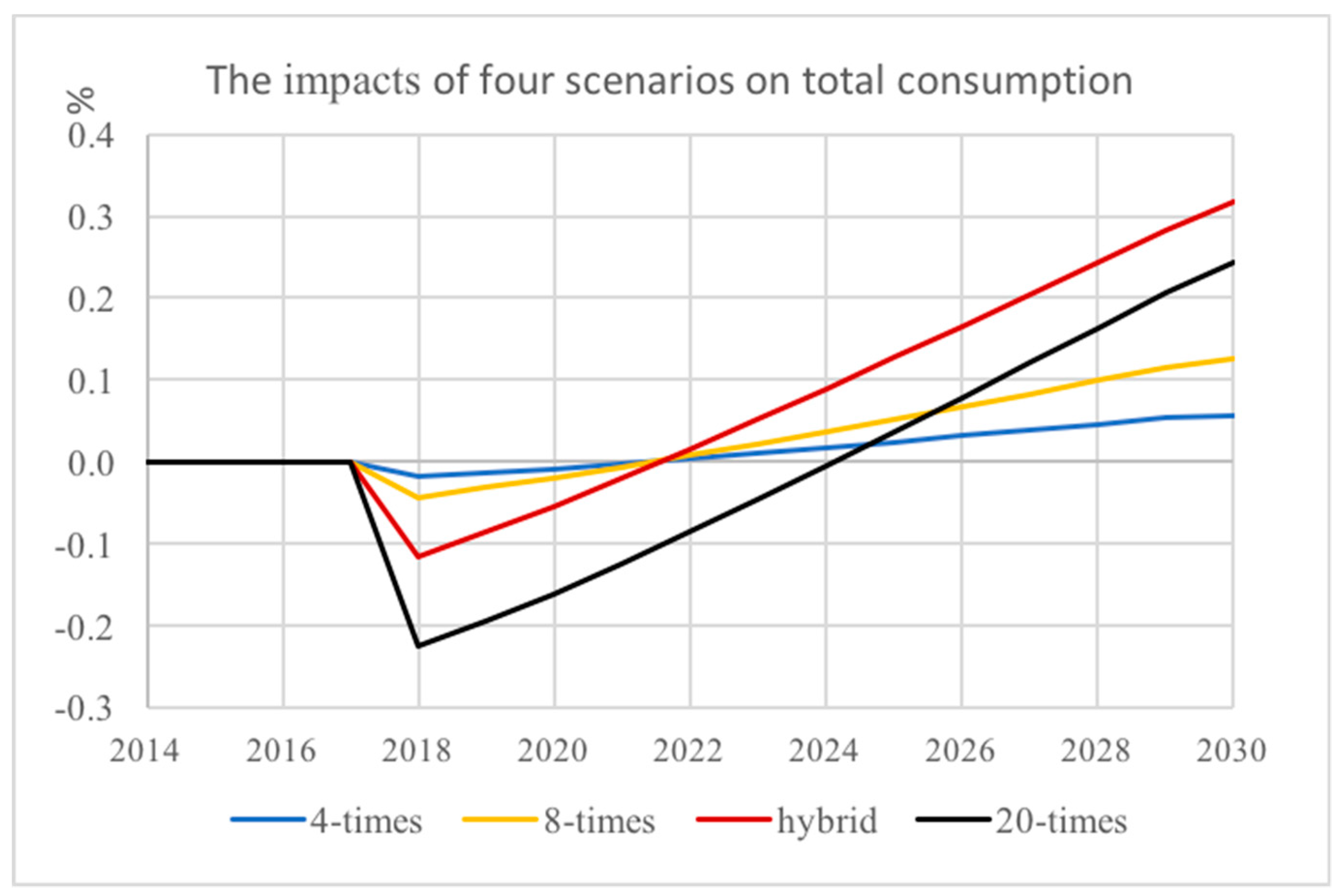
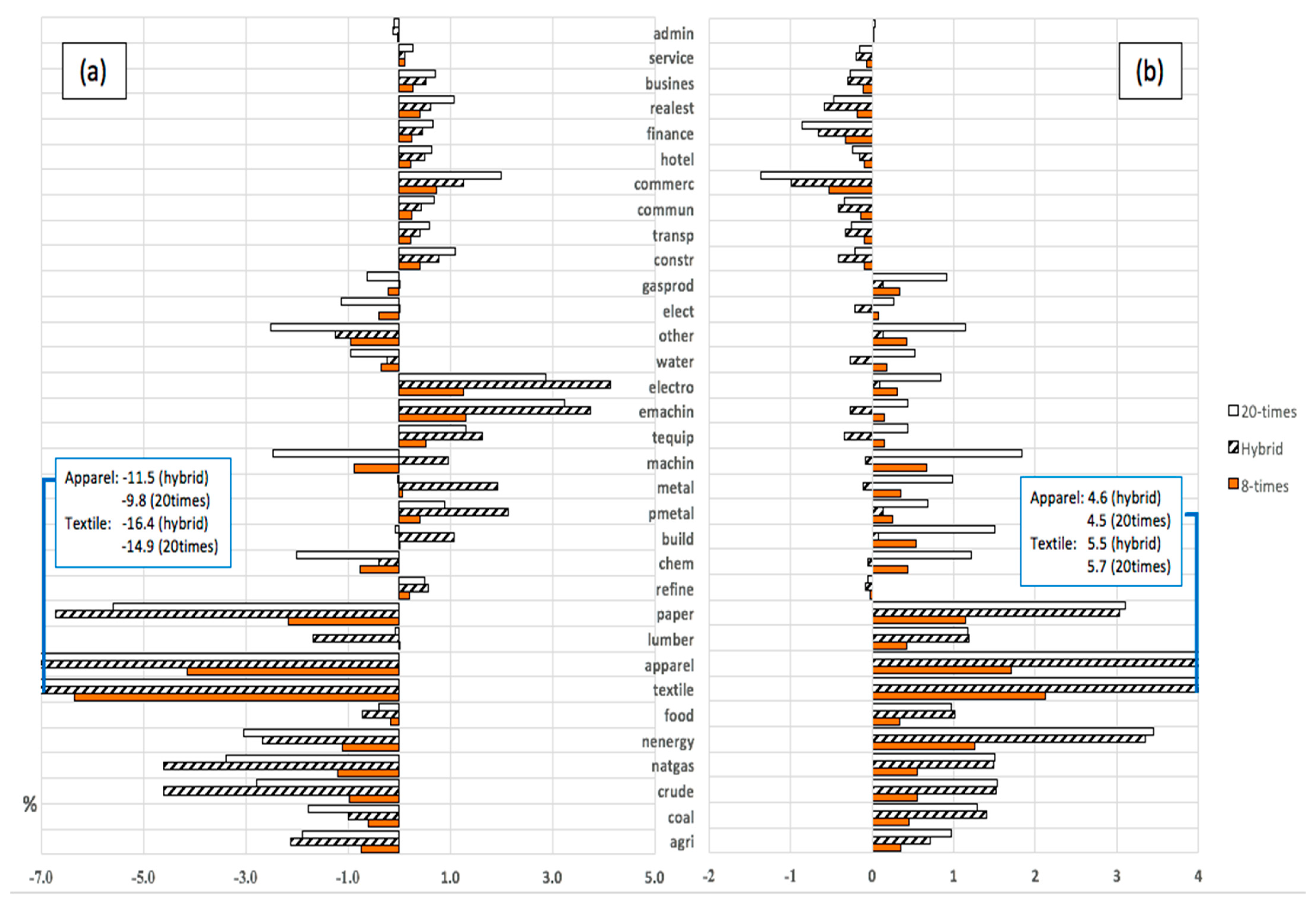
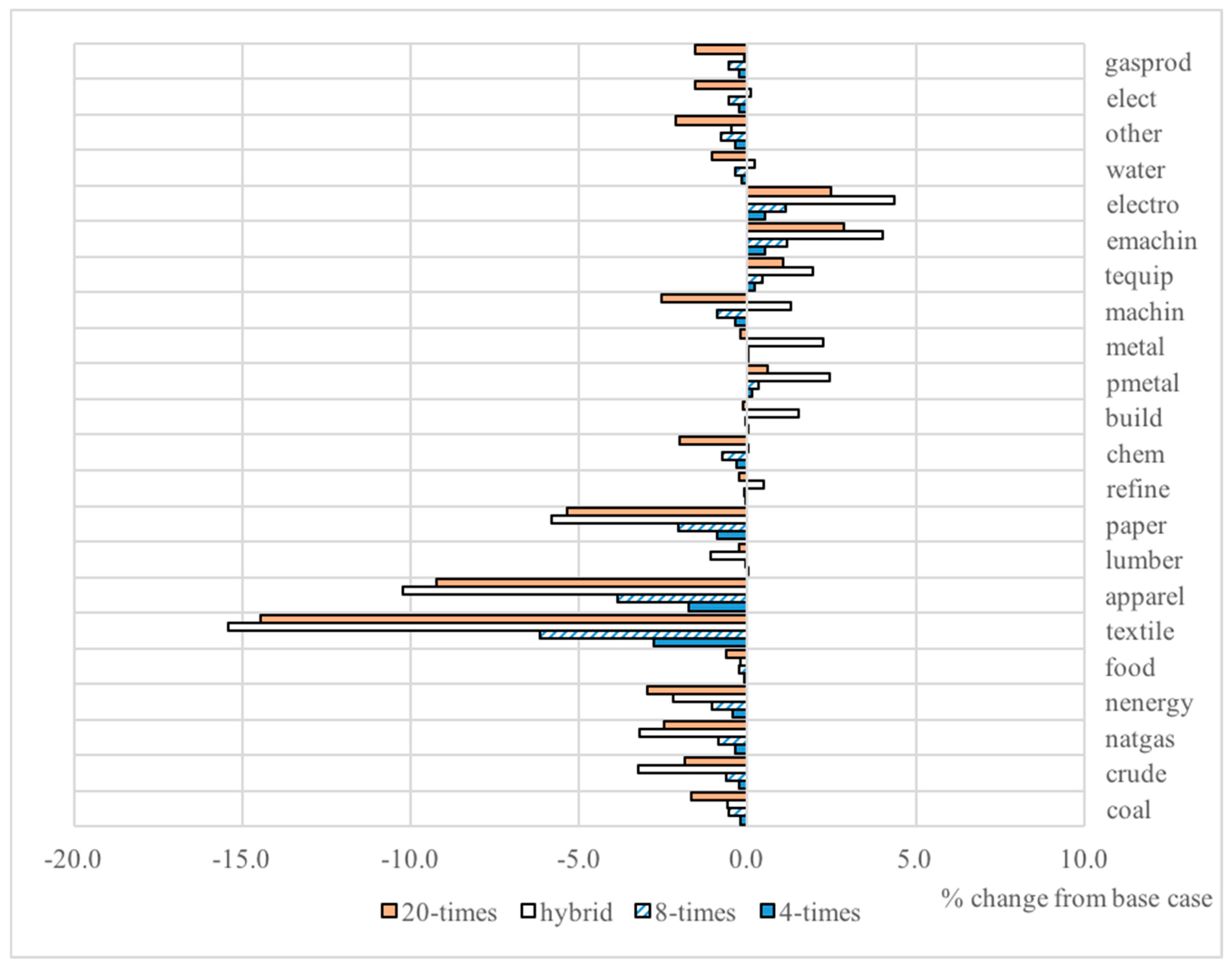
3.2. Impact of Taxes
4. Conclusions
- Output taxes based on water pollution rates would have a positive impact on conserving freshwater use and reducing COD discharge. Raising the tax rate on COD discharge from the current 0.7 yuan/kg by 4 times would lead to a 0.7% reduction in 2030 discharge. An increase by 20 times, to levels observed in the strictest provinces today, could lead to a 4.0% reduction in national COD discharge by 2030.
- If the new COD discharge tax is offset by cutting other taxes, then the loss of economic efficiency would be small. There is a small loss in initial Consumption, but a cut of taxes on enterprises would lead to higher investment and higher future GDP.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Production
| Sector | Sector | ||
|---|---|---|---|
| 1 | Agriculture (Agri) | 18 | Electrical machinery (Emachin) |
| 2 | Coal mining (Coal) | 19 | Commmunication equip, computer, electronic (Electro) |
| 3 | Oil mining (Crude) | 20 | Water utilities (Water) |
| 4 | Natural gas mining (Natgas) | 21 | Other manufacturing, recycling (Other) |
| 5 | Non-energy mining (Nenergy) | 22 | Electricity, steam (Elect) |
| 6 | Food products (Food) | 23 | Gas utilities (Gasprod) |
| 7 | Textiles | 24 | Construction (Constr) |
| 8 | Apparel, leather (Apparel) | 25 | Transportation equipment (Transp) |
| 9 | Sawmills and furniture (Lumber) | 26 | Telecommunications, Software and IT (Commun) |
| 10 | Paper, printing, recording media (Paper) | 27 | Wholesale and Retail (Commerc) |
| 11 | Petroleum processing (Refine) | 28 | Hotels and Restaurants (Hotel) |
| 12 | Chemicals (Chem) | 29 | Finance |
| 13 | Nonmetal mineral products (Build) | 30 | Real estate (Realest) |
| 14 | Primary metals (Pmetal) | 31 | Business services (Busines) |
| 15 | Metal products (Metal) | 32 | Other services (Service) |
| 16 | Machinery (Machin) | 33 | Public administration (Admin) |
| 17 | Transportation equipment (Tequip) |
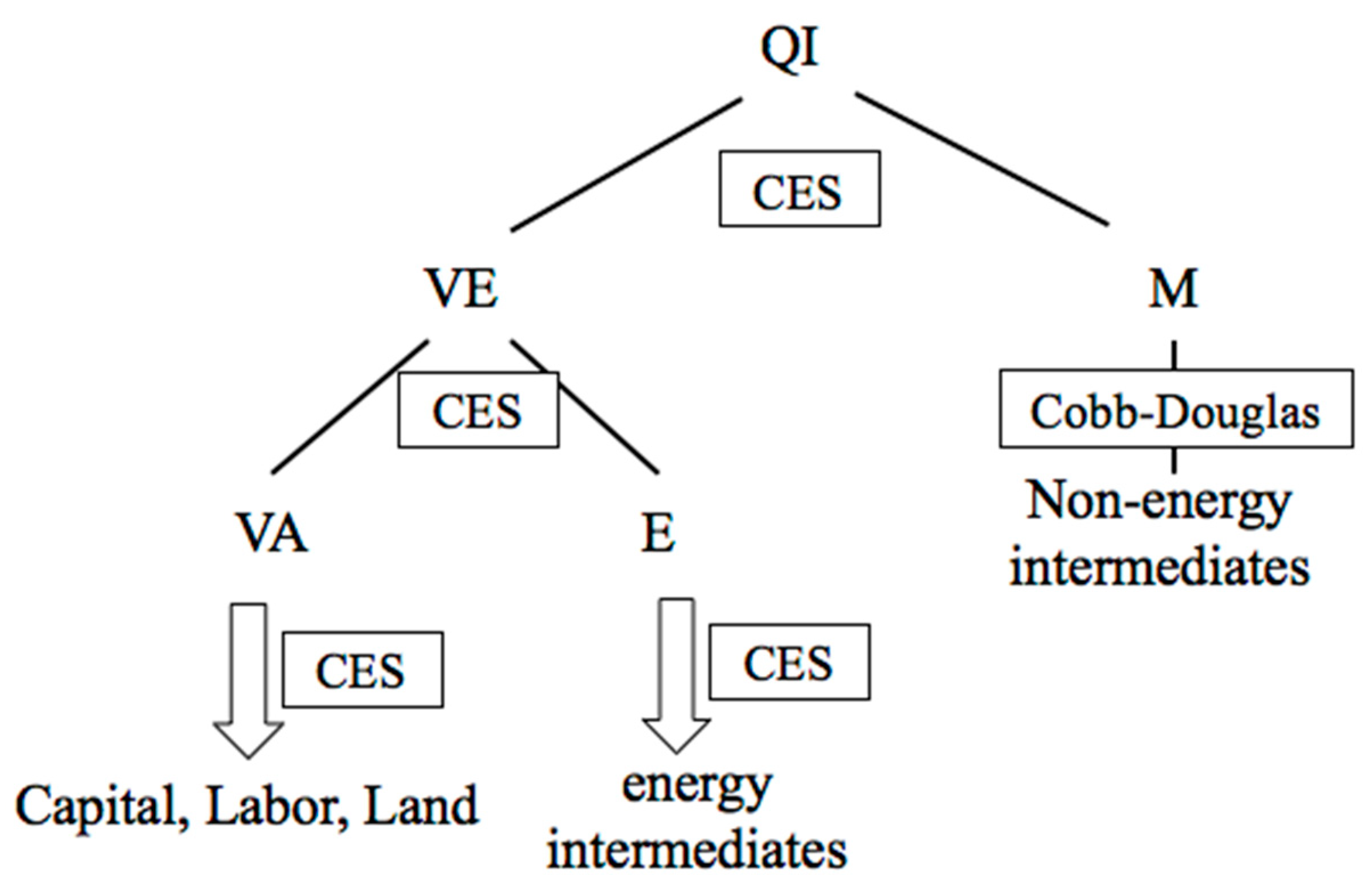
Industries versus Commodities
Appendix A.2. Households
Appendix A.3. Government and Taxes
Appendix A.4. Capital, Investment, and the Financial System
Appendix A.5. The Foreign Sector
Appendix A.6. Markets
References
- Fang, G.; Wang, T.; Si, X.; Wen, X.; Liu, Y. Discharge Fee Policy Analysis: A Computable General Equilibrium (CGE) Model of Water Resources and Water Environments. Water 2016, 89, 413. [Google Scholar] [CrossRef]
- Jiang, L.; Lin, C.; Lin, P. The determinants of pollution levels: Firm-level evidence from Chinese manufacturing. J. Comparat. Econ. 2014, 421, 118–142. [Google Scholar] [CrossRef]
- Pérez-Blanco, C.D.; Standardi, G.; Mysiak, J.; Parrado, R.; Gutiérrez-Martín, C. Incremental water charging in agriculture. A case study of the Regione Emilia Romagna in Italy. Environ. Model. Softw. 2016, 78, 202–215. [Google Scholar] [CrossRef]
- Chan, W. Wastewater: Good to the Last Drop. China Water Risk. Available online: http://chinawaterrisk.org/resources/analysis-reviews/wastewater-good-to-the-last-drop/ (accessed on 22 March 2017).
- Zhang, B.; Cao, C.; Hughes, R.M.; Davis, W.S. China’s new environmental protection regulatory regime: Effects and gaps. J. Environ. Manag. 2017, 187, 464–469. [Google Scholar] [CrossRef] [PubMed]
- Wang, C. Environmental Law: 2 Years On. China Water Risk. Available online: http://chinawaterrisk.org/opinions/environmental-law-2-years-on/ (accessed on 14 June 2017).
- 2016 State of Environment Report Review. China Water Risk. Available online: http://chinawaterrisk.org/resources/analysis-reviews/2016-state-of-environment-report-review/ (accessed on 14 June 2017).
- Liu, M.; Shadbegian, R.; Zhang, B. Does Environmental Regulation Affect Labor Demand in China? Evidence from the Textile Printing and Dyeing Industry. J. Environ. Econ. Manag. 2017, 86, 277–294. [Google Scholar] [CrossRef]
- Hu, F.; Tan, D.; Lazareva, I. 8 Facts on China’s Wastewater. China Water Risk. Available online: http://chinawaterrisk.org/resources/analysis-reviews/8-facts-on-china-wastewater/ (accessed on 12 March 2017).
- Cao, J.; Ho, M.S.; Timilsina, G.R. Impacts of Carbon Pricing in Reducing the Carbon Intensity of China’s GDP; Social Science Electronic Publishing: New York, NY, USA, 2016. [Google Scholar]
- Xu, Y. China’s Water Resource Tax Reform. China Water Risk. Available online: http://chinawaterrisk.org/resources/analysis-reviews/chinas-water-resource-tax-reform/ (accessed on 20 July 2016).
- Franckx, L. Environmental Enforcement with Endogenous Ambient Monitoring. Energy Transp. Environ. Work. Pap. 2005, 302, 195–220. [Google Scholar] [CrossRef]
- Franckx, L.; Kampas, A. On the regulatory choice of refunding rules to reconcile the ‘polluter pays principle’ and Pigovian taxation: An application. Environ. Plan. C 2008, 231, 141–152. [Google Scholar]
- International Energy Agency (IEA). Projected Costs of Generating Electricity; IEA and OECD: Paris, France, 2010. [Google Scholar]
- Chris, N.; Ho, M. (Eds.) Clearer Skies over China: Reconciling Air Quality, Climate and Economic Goals; MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Gómez, C.M.; Tirado, D.; Rey-Maquieira, J. Water exchanges versus water works: Insights from a computable general equilibrium model for the Balearic Islands. Water Resour. Res. 2004, 4010, 287–301. [Google Scholar] [CrossRef]
- Lan, L.; Xin, Y. Feasibility Study of the Water Pollution “Fee to Tax” change in China. Environ. Prot. Technol. 2016, 226, 29–33. [Google Scholar]
- Fujimori, S.; Hanasaki, N.; Masui, T. Projections of industrial water withdrawal under shared socioeconomic pathways and climate mitigation scenarios. Sustain. Sci. 2017, 122, 275–292. [Google Scholar] [CrossRef] [PubMed]
- Llop, M.; Ponce-Alifonso, X. Water and Agriculture in a Mediterranean Region: The Search for a Sustainable Water Policy Strategy. Water 2016, 82, 66. [Google Scholar] [CrossRef]
- Chen, W.; Hao, X.; Shu, Z. Water Pollution Taxes in Hunan Province: A General Equilibrium Analysis of Its Design and Effects. Financ. Theory Appl. 2012, 331, 73–77. [Google Scholar]
- Yijun, Y.; Ying, M.; Ronghui, X. An Environmental-CGE Model Evaluation of the Performance of Water Pollution Tax Policy. Sci. Technol. Manag. 2016, 3, 6–11. [Google Scholar]
- Cao, J.; Ho, M. Appendix A. Economic-Environmental Model of China (Version 18); ETS-Hybrid Tax Application. Harvard China Project Working Paper. 2018. Available online: https://chinaproject.harvard.edu/files/chinaproject/files/chinaces-hhmodel.2018.pdf (accessed on 25 October 2017).
- Wang, C.; Wu, J.; Zhang, B. Environmental regulation, emissions and productivity: Evidence from Chinese COD-emitting manufacturers. J. Environ. Econ. Manag. 2018. [Google Scholar] [CrossRef]
- Hsieh, C.T.; Klenow, P.J. Misallocation and manufacturing TFP in China and India. Q. J. Econ. 2009, 124, 1403–1448. [Google Scholar] [CrossRef]
- Garbaccio, R.; Ho, M.; Jorgenson, D. Controlling Carbon Emissions in China. Environ. Dev. Econ. 1999, 44, 493–518. [Google Scholar] [CrossRef]
- Sue Wing, I.; Daenzer, K.; Fisher-Vanden, K.; Calvin, K. Phoenix Model Documentation. PNNL Joint Global Change Research Institute, 2011. Available online: http://www.globalchange.umd.edu/models/phoenix/ (accessed on 23 August 2011).
- Wu, H.X.; Yue, X.; Zhang, G. Constructing Annual Employment and Compensation Matrices and Measuring Labor Input in China; Discussion Paper 15-E.-005; Research Institute of Economy, Trade and Industry (RIETI): Tokyo, Japan, 2015.
- Tsinghua IEEE. China and the New Climate Economy, Tsinghua University Institute for Energy and Environmental Economics. 2015. Available online: http://newclimateeconomy.net/content/china-and-new-climate-economy (accessed on 25 July 2015).
- Parry, I.W.H. Pollution Taxes and Revenue Recycling. J. Environ. Econ. Manag. 1995, 293, 64. [Google Scholar] [CrossRef]
- Ma, Z. Fundamental Issues: Industrial Wastewater. Available online: http://chinawaterrisk.org/interviews/fundamental-issues-in-industrial-wastewater/ (accessed on 12 March 2014).
- IEA (2017) World Economic Outlook; International Energy Agency: Paris, France, 2017.


| Sector | COD Concentration | COD Intensity | Wastewater Discharge | COD Discharge |
|---|---|---|---|---|
| Sj,tCOD (10−3) | Ij,tCOD (kg/1000 yuan) | (billion ton) | (million ton) | |
| Coal mining | 0.57 | 0.64 | 2.46 | 1.40 |
| Oil mining | 0.57 | 0.89 | 1.50 | 0.85 |
| Natural gas mining | 0.57 | 0.89 | 0.35 | 0.20 |
| Non-energy mining | 0.56 | 1.14 | 3.97 | 2.23 |
| Food products and tobacco processing | 0.57 | 0.28 | 5.23 | 2.96 |
| Textile goods | 0.53 | 0.93 | 7.54 | 4.02 |
| Wearing apparel, leather, furs, down and related products | 0.53 | 0.66 | 4.54 | 2.38 |
| Sawmills and furniture | 0.50 | 0.24 | 1.12 | 0.56 |
| Paper and products, printing and record medium reproduction | 0.45 | 0.61 | 5.18 | 2.32 |
| Petroleum processing and coking | 0.42 | 0.03 | 0.34 | 0.14 |
| Chemical | 0.39 | 0.27 | 10.01 | 3.90 |
| Nonmetal mineral products | 0.41 | 0.35 | 5.17 | 2.12 |
| Metals smelting and pressing | 0.39 | 0.10 | 3.10 | 1.20 |
| Metal products | 0.39 | 0.23 | 2.47 | 0.95 |
| Machinery | 0.39 | 0.41 | 8.97 | 3.47 |
| Transportation equipment | 0.39 | 0.11 | 2.29 | 0.88 |
| Electrical machinery | 0.39 | 0.09 | 1.39 | 0.54 |
| Communication equipment, computer, Electronic | 0.39 | 0.08 | 1.73 | 0.67 |
| Instruments | 0.20 | 0.28 | 0.52 | 0.10 |
| Other manufacturing products | 0.22 | 0.20 | 0.73 | 0.16 |
| Electricity, steam and hot water production and supply | 0.20 | 0.20 | 3.80 | 0.75 |
| Gas production and supply | 0.20 | 0.24 | 0.59 | 0.12 |
| National | 0.42 | 0.41 | 73.0 | 31.90 |
| Variable | 2018 | 2030 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Base | 4 Times | 8 Times | 20 Times | Hybrid | Base | 4 Times | 8 Times | 20 Times | Hybrid | |
| % Change from Base Case | % Change from Base Case | |||||||||
| Population (million) | 1393 | 1416 | ||||||||
| Real GDP (billion 2014 yuan) | 82,316 | 0.02 | 0.04 | 0.09 | 0.06 | 150,957 | 0.06 | 0.13 | 0.32 | 0.42 |
| Consumption (billion 2014 yuan) | 34,818 | −0.02 | −0.04 | −0.23 | −0.12 | 75,507 | 0.06 | 0.13 | 0.32 | 0.24 |
| Investment (billion 2014 yuan) | 35,425 | 0.07 | 0.16 | 0.41 | 0.45 | 56,593 | 0.16 | 0.36 | 0.89 | 1.09 |
| Wastewater Use (billion ton) | 82.7 | −0.37 | −0.85 | −2.20 | −1.91 | 111.1 | −0.61 | −1.38 | −3.48 | −2.66 |
| COD Discharge (billion kg) | 36.0 | −0.44 | −1.00 | −2.58 | −2.41 | 48.0 | −0.72 | −1.62 | −4.02 | −3.42 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Ho, M.S.; You, L.; Cao, J.; Fang, Y.; Tu, T.; Hong, Y. Industrial Water Pollution Discharge Taxes in China: A Multi-Sector Dynamic Analysis. Water 2018, 10, 1742. https://doi.org/10.3390/w10121742
Guo X, Ho MS, You L, Cao J, Fang Y, Tu T, Hong Y. Industrial Water Pollution Discharge Taxes in China: A Multi-Sector Dynamic Analysis. Water. 2018; 10(12):1742. https://doi.org/10.3390/w10121742
Chicago/Turabian StyleGuo, Xiaolin, Mun Sing Ho, Liangzhi You, Jing Cao, Yu Fang, Taotao Tu, and Yang Hong. 2018. "Industrial Water Pollution Discharge Taxes in China: A Multi-Sector Dynamic Analysis" Water 10, no. 12: 1742. https://doi.org/10.3390/w10121742
APA StyleGuo, X., Ho, M. S., You, L., Cao, J., Fang, Y., Tu, T., & Hong, Y. (2018). Industrial Water Pollution Discharge Taxes in China: A Multi-Sector Dynamic Analysis. Water, 10(12), 1742. https://doi.org/10.3390/w10121742





