Effect of Density and Total Weight on Flow Depth, Velocity, and Stresses in Loess Debris Flows
Abstract
1. Introduction
2. Experimental Materials and Sample Preparation
2.1. Similarity Principle
2.1.1. Geometric Similarity
2.1.2. Material Similarity
2.1.3. Velocity Similarity
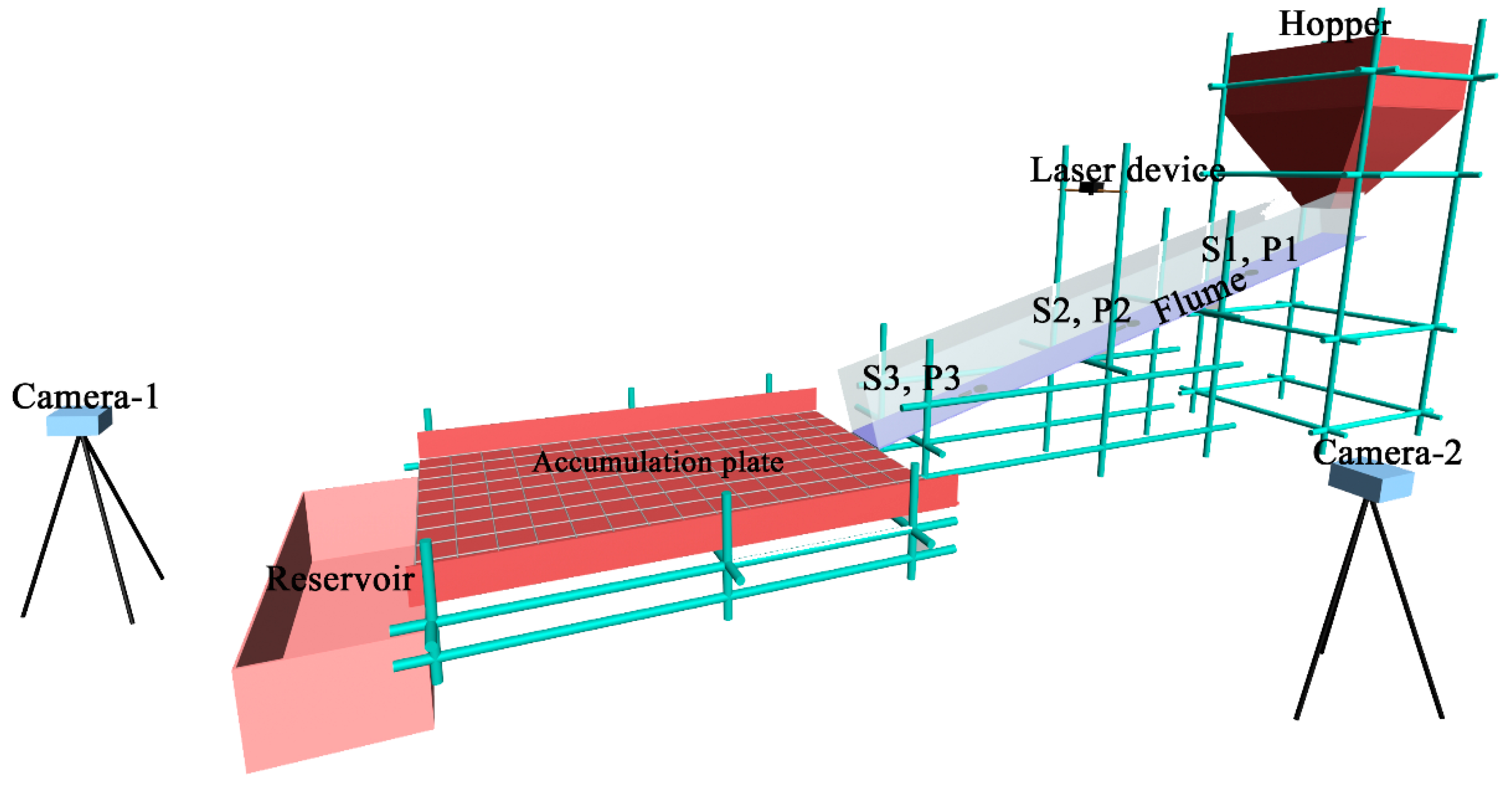
2.2. Experimental Apparatus
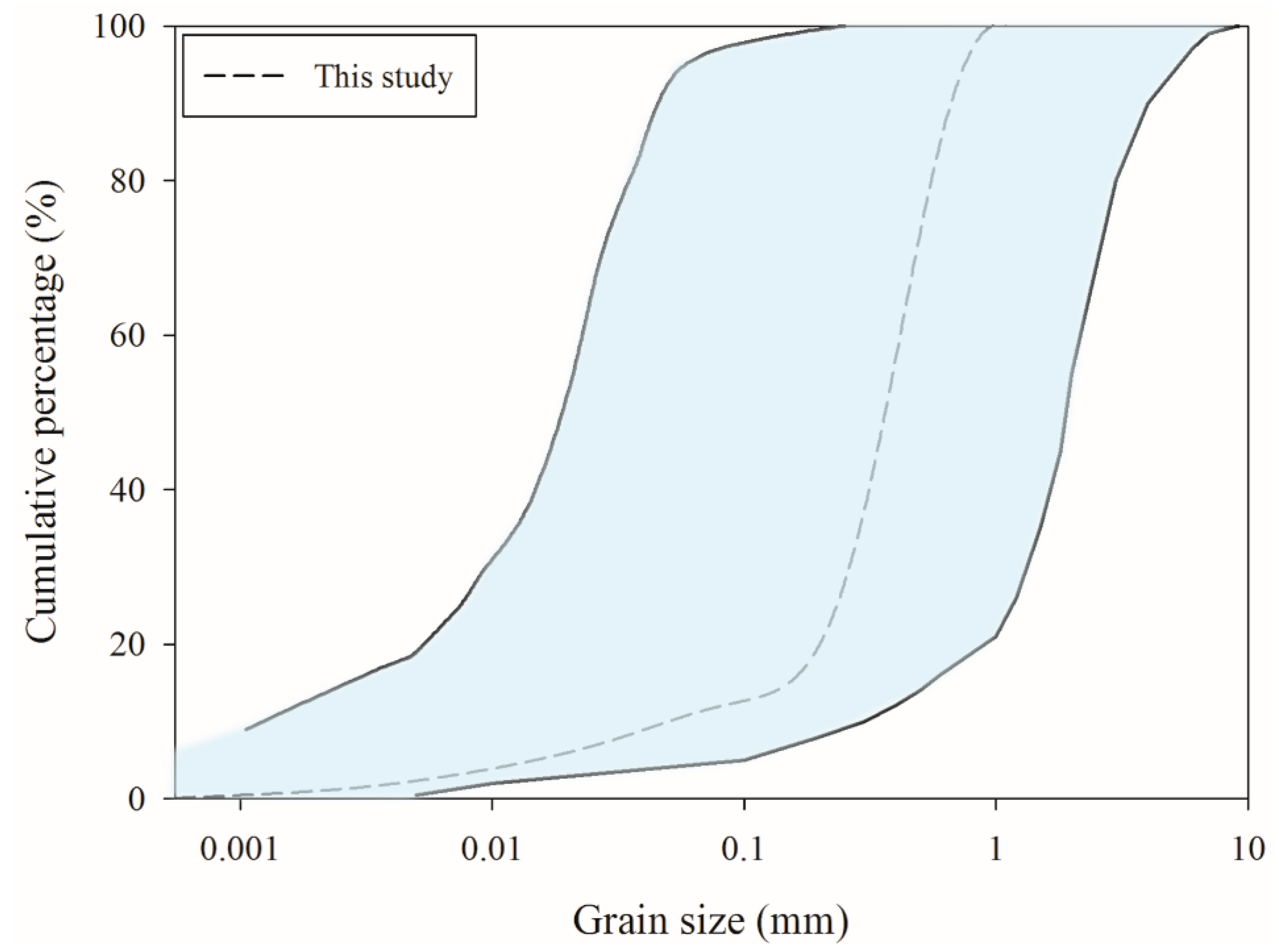
2.3. Sample Preparation
3. Results and Discussion
3.1. General Flow Patterns
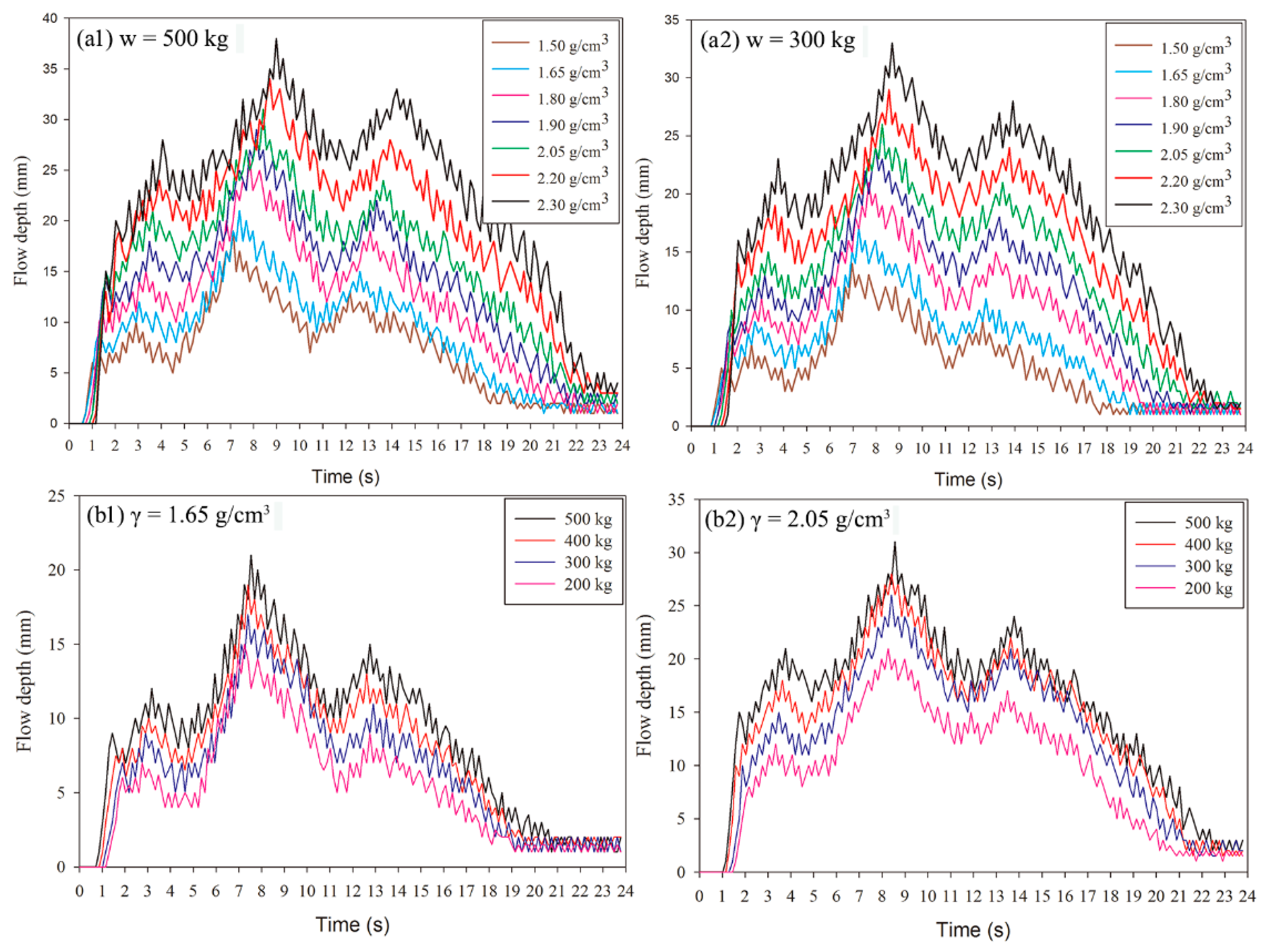
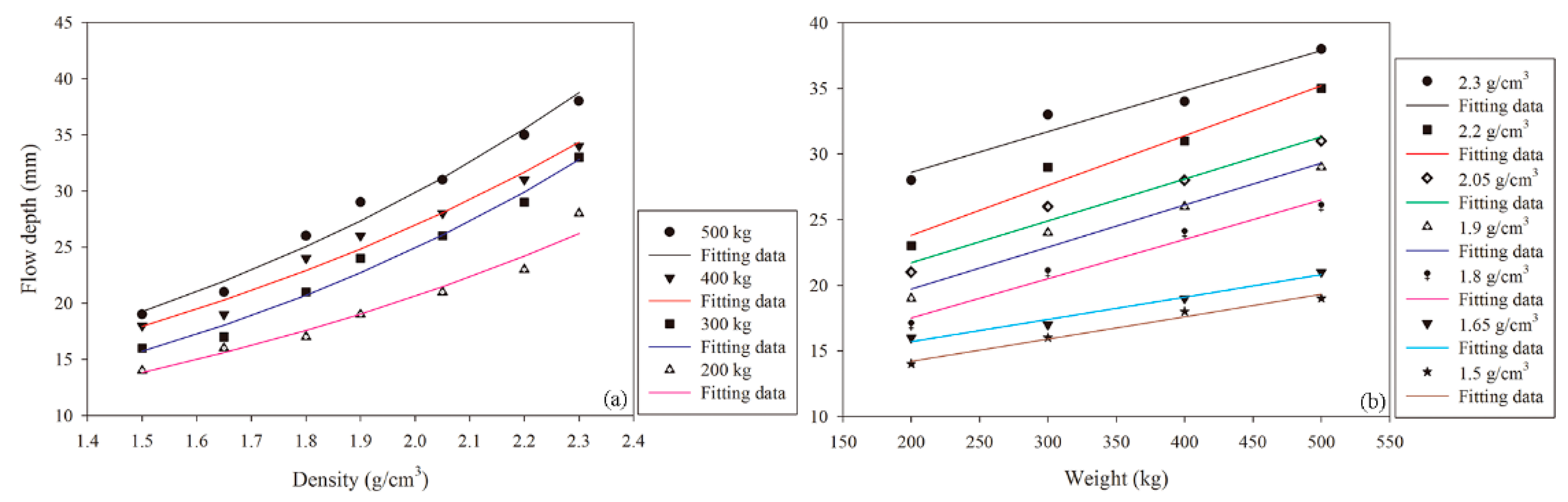
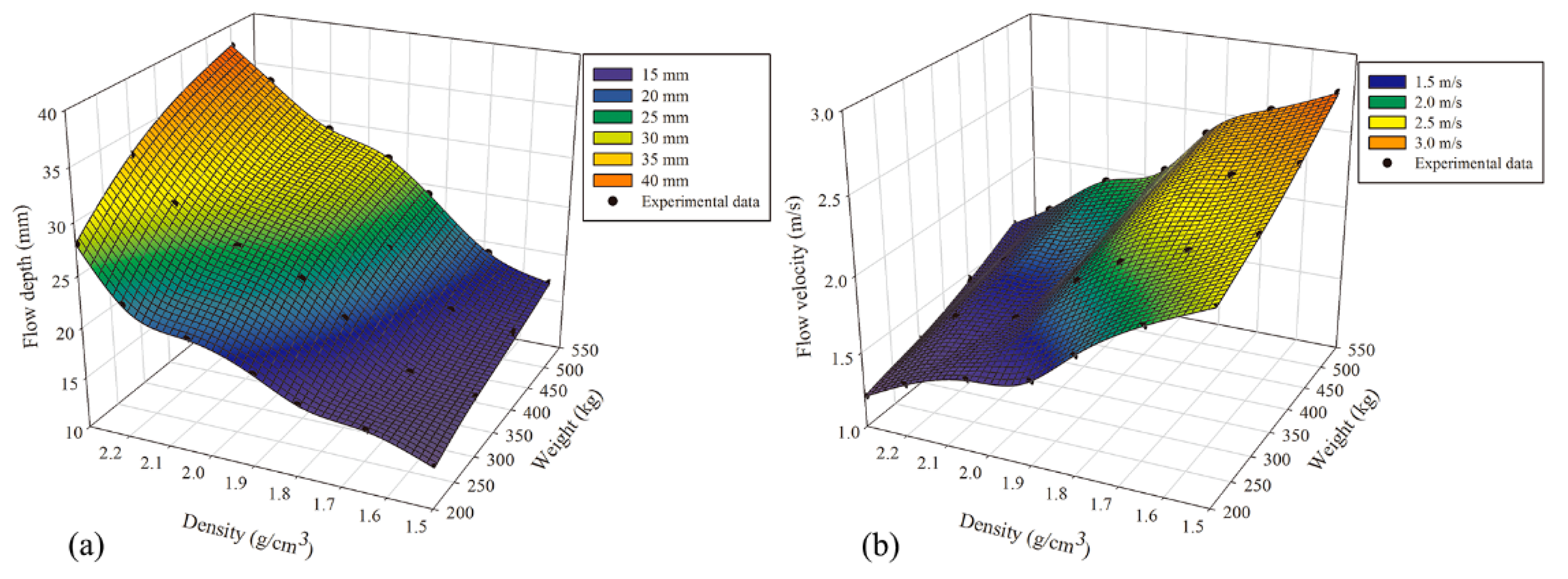
3.2. Flow Depth
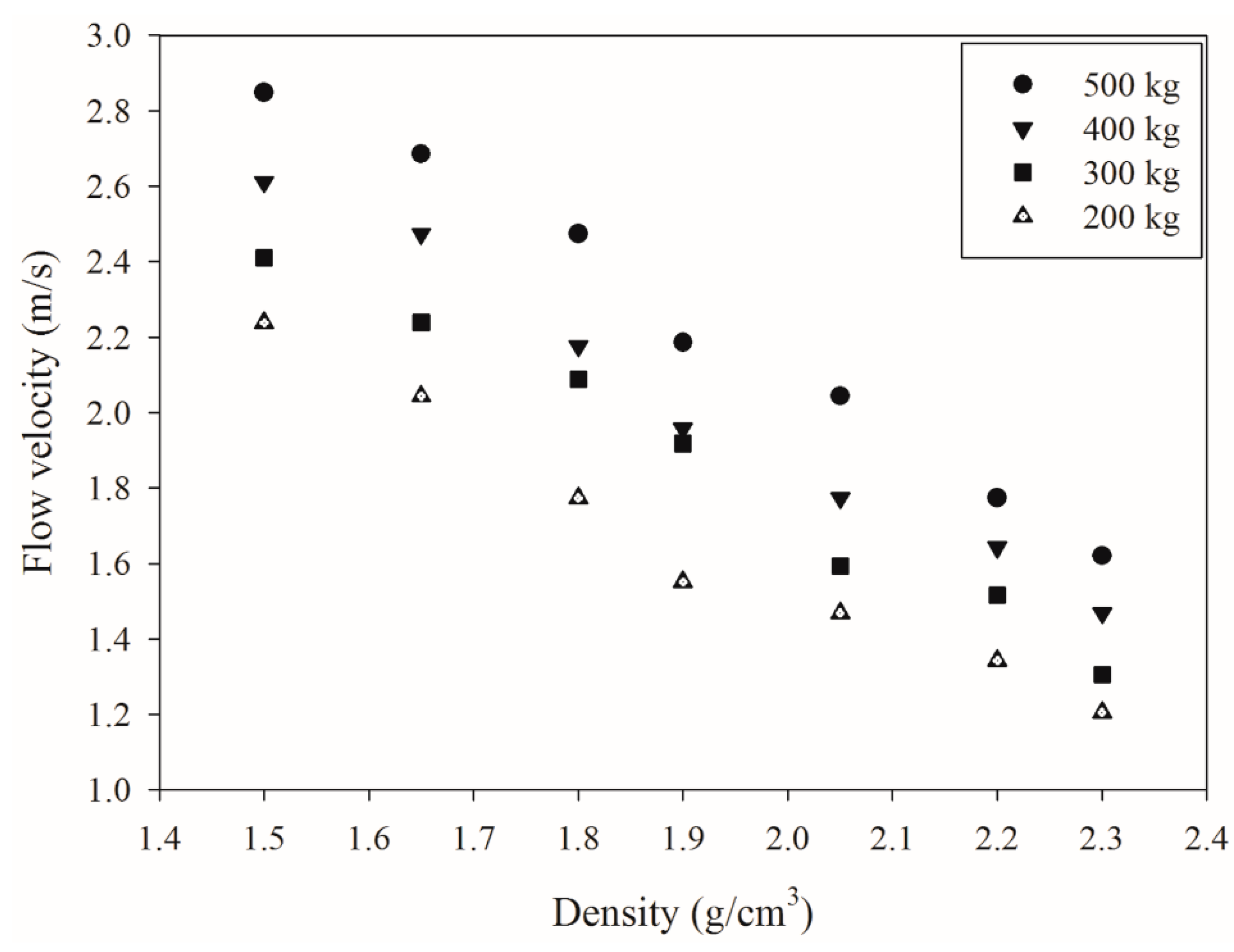
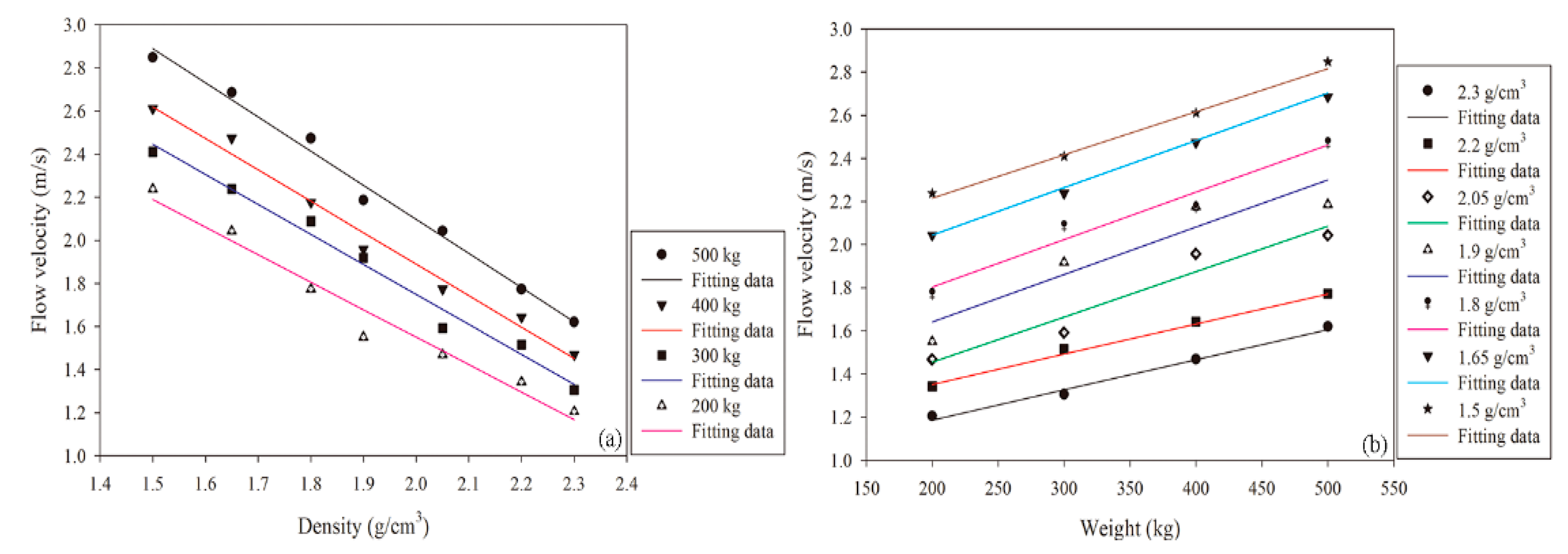
3.3. Flow Velocity
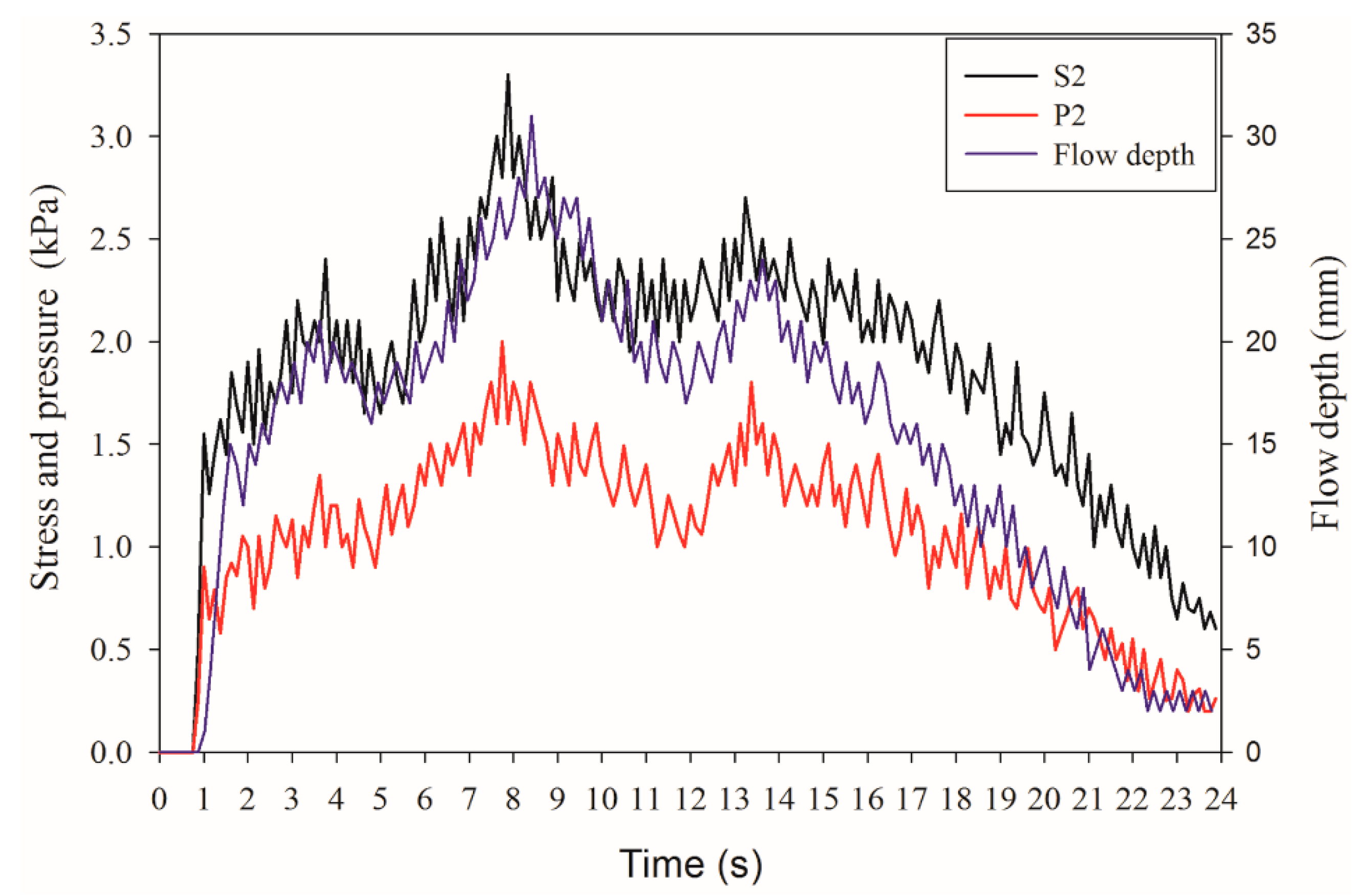
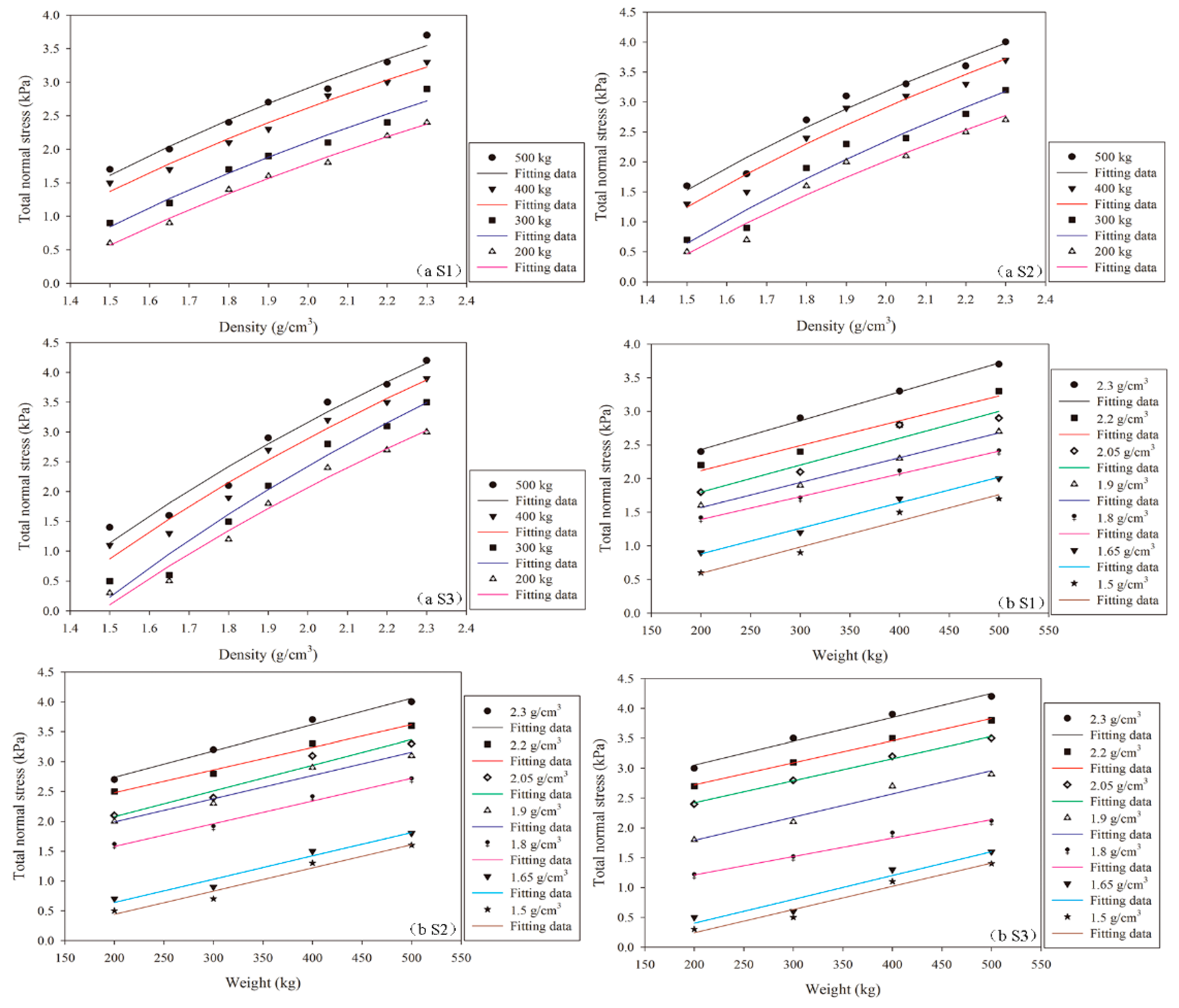
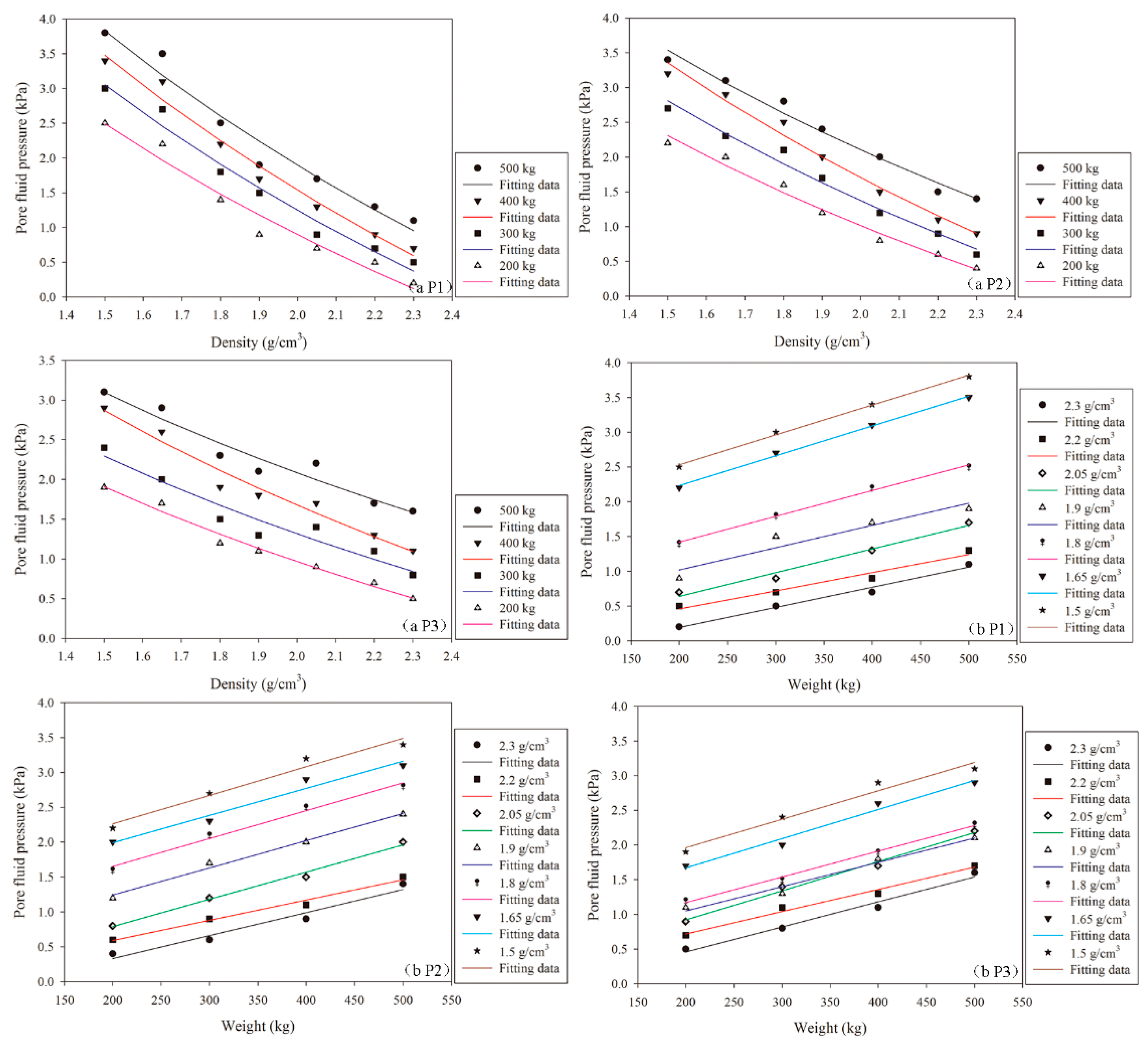
3.4. Stress and Pressure Measurements
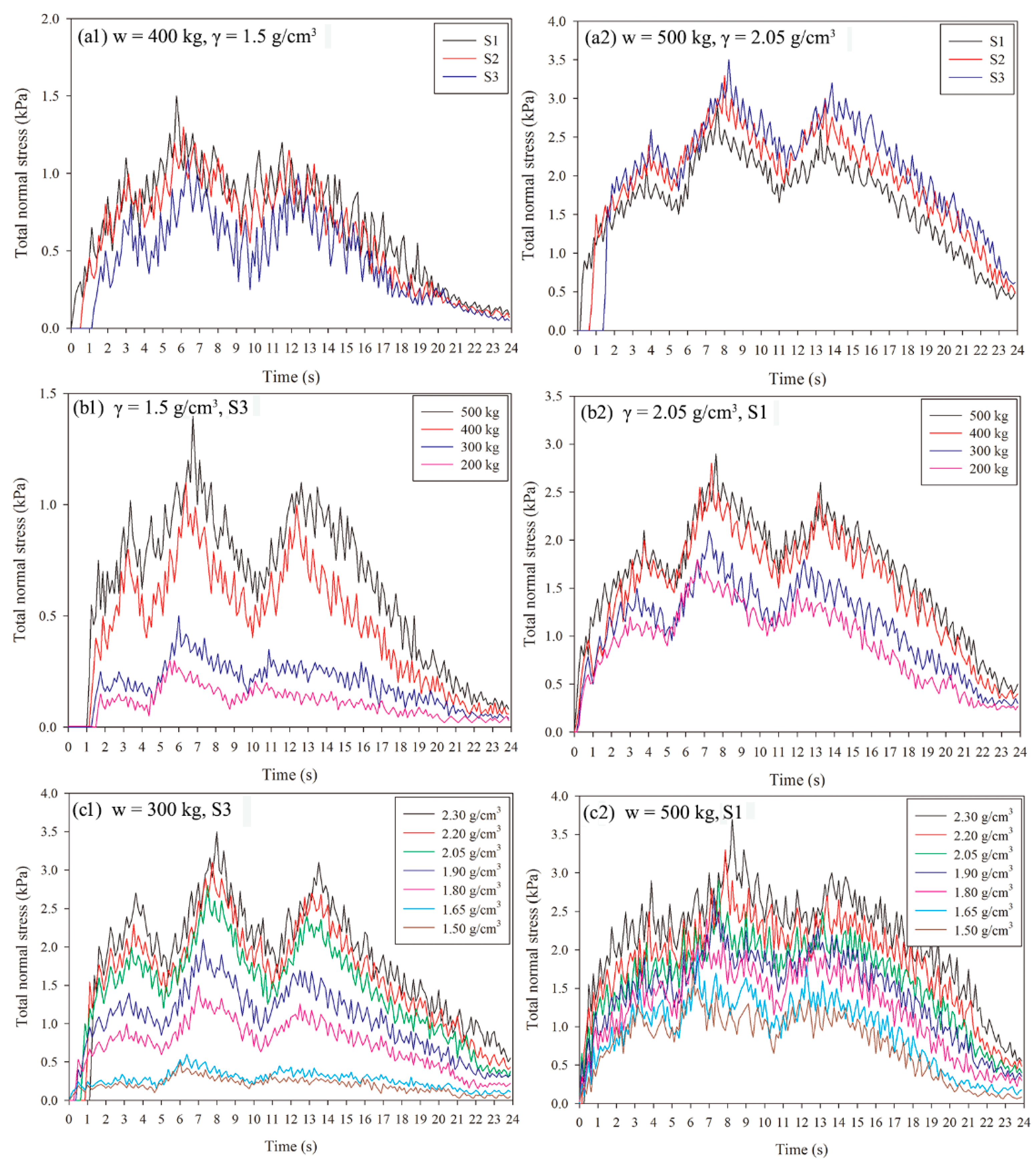
3.4.1. Total Normal Stress
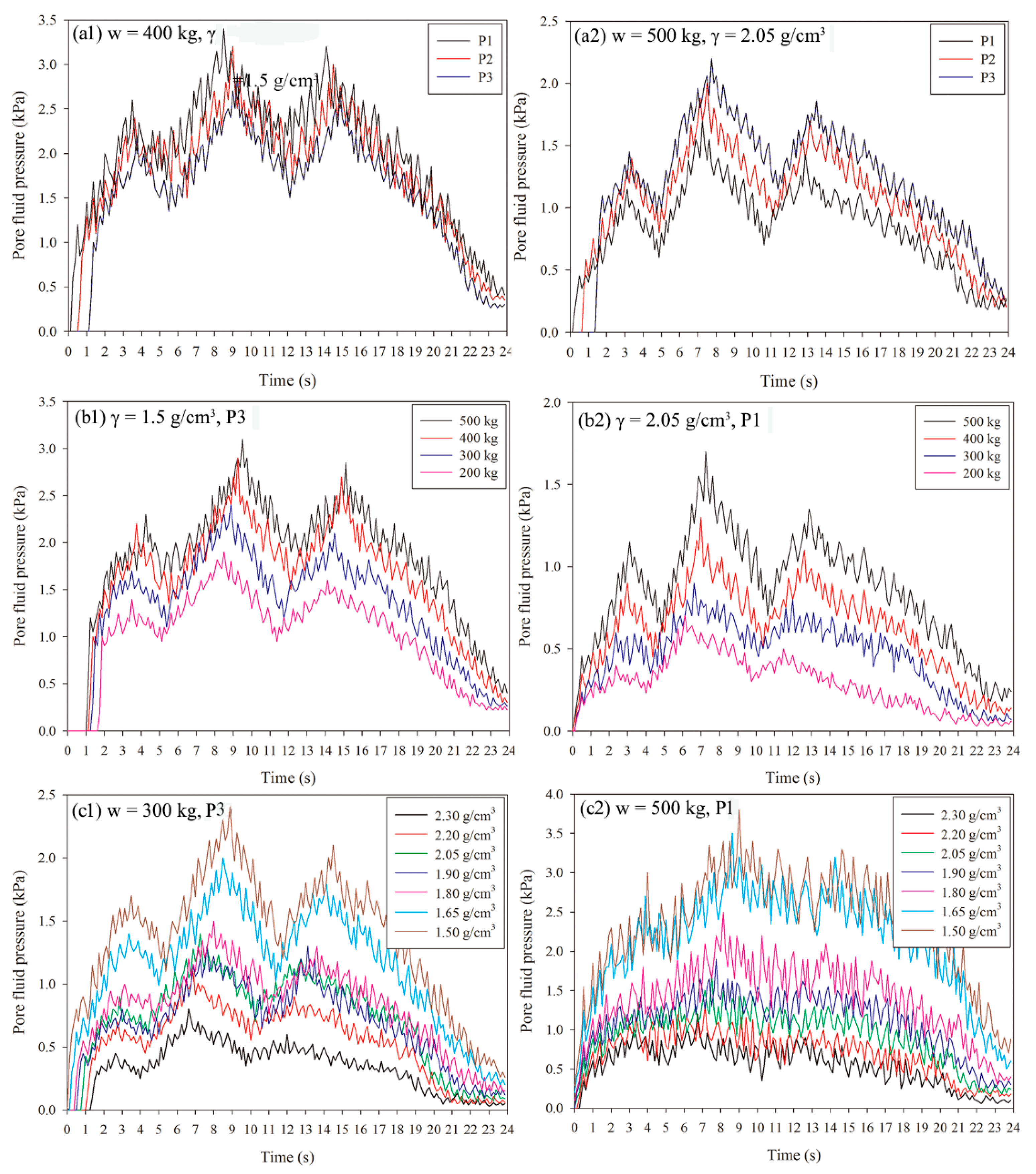
3.4.2. Pore Fluid Pressure
3.5. Development of Predictive Functions Based on the Study Data
3.5.1. Parameterization of the Fitting Functions
3.5.2. Parameterized Functions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hungr, O.; Evans, S.; Bovis, M.; Hutchinson, J. A review of the classification of landslides of the flow type. Environ. Eng. Geosci. 2001, 7, 221–238. [Google Scholar] [CrossRef]
- Godt, J.W.; Coe, J.A. Alpine debris-flows triggered by a 28 July 1999 thunderstorm in the Central Front Range, Colorado. Geomorphology 2007, 84, 80–97. [Google Scholar] [CrossRef]
- Pudasaini, S.P. A general two-phase debris flow model. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Takahashi, T. Debris Flow: Mechanics, Prediction and Counter-Measures, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014; p. 574. [Google Scholar]
- Wang, F.; Chen, X.Q.; Chen, J.G.; You, Y. Experimental study on a debris-flow drainage channel with different types of energy dissipation baffle. Eng. Geol. 2017, 220, 43–51. [Google Scholar] [CrossRef]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- Iverson, R.M.; Reid, M.E.; Logan, M.; Lahusen, R.G.; Godt, I.W.; Groswold, J.P. Positive feedback and momentum growth during debris-flow entrainment of wet bed sediment. Nat. Geosci. 2011, 4, 116–121. [Google Scholar] [CrossRef]
- VanDine, D.F.; Bovis, M. History and goals of Canadian debris-flow research. Nat. Hazards 2002, 26, 67–80. [Google Scholar] [CrossRef]
- Tang, C.; Zhu, J.; Li, W.L.; Liang, J.T. Rainfall-triggered debris flows following the Wenchuan earthquake. Bull. Eng. Geol. Environ. 2009, 68, 187–194. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, S.; Li, W.L.; van Asch, T.W.J. The 13 August 2010 catastrophic debris flows after the 2008 Wenchuan earthquake, China. Nat. Hazards Earth Syst. Sci. 2012, 12, 201–216. [Google Scholar] [CrossRef]
- Cui, P.; Zhou, G.G.D.; Zhu, X.H.; Zhang, J.Q. Scale amplification of natural debris flows caused by cascading landslide dam failures. Geomorphology 2013, 182, 173–189. [Google Scholar] [CrossRef]
- Han, Z.; Wang, W.D.; Li, Y.G.; Huang, J.L.; Su, B.; Tang, C.; Chen, G.Q.; Qu, X. An integrated method for rapid estimation of the valley incision by debris flows. Eng. Geol. 2018, 232, 34–35. [Google Scholar] [CrossRef]
- Jakob, M.; Friele, P. Frequency and magnitude of debris flows on Cheekye River, British Columbia. Geomorphology 2010, 114, 382–395. [Google Scholar] [CrossRef]
- Stoffel, M.; Mendlik, T.; Schneuwly-Bollschweiler, M.; Gobiet, A. Possible impacts of climate change on debris-flow activity in the Swiss Alps. Clim. Chang. 2014, 122, 141–155. [Google Scholar] [CrossRef]
- Li, Y.; Ma, C.; Wang, Y. Landslides and debris flows caused by an extreme rainstorm on 21 July 2012 in mountains near Beijing, China. Bull. Eng. Geol. Environ. 2017, 1–16. [Google Scholar] [CrossRef]
- Lyu, H.M.; Shen, J.S.; Arulrajah, A. Assessment of geohazards and preventative countermeasures using AHP incorporated with GIS in Lanzhou, China. Sustainability 2018, 10, 304. [Google Scholar] [CrossRef]
- Jakob, M. Debris-Flow Hazard Analysis. In Debris-Flow Hazards and Related Phenomena; Jakob, M., Hungr, O., Eds.; Springer: Berlin, Germany, 2005; pp. 411–443. [Google Scholar]
- Hürlimann, M.; Copons, R.; Altimir, J. Detailed debris flow hazard assessment in Andorra: A multidisciplinary approach. Geomorphology 2006, 78, 359–372. [Google Scholar] [CrossRef]
- Cavalli, M.; Marchi, L. Characterisation of the surface morphology of an alpine alluvial fan using airborne LiDAR. Nat. Hazards Earth Syst. Sci. 2008, 8, 323–333. [Google Scholar] [CrossRef]
- Jeong, S.; Kim, Y.; Lee, J.K.; Kim, J. The 27 July 2011 debris flows at Umyeonsan, Seoul, Korea. Landslides 2015, 12, 799–813. [Google Scholar] [CrossRef]
- Bai, S.; Xu, Q.; Wang, J.; Zhou, P. Pre-conditioning factors and susceptibility assessments of Wenchuan earthquake landslide at the Zhouqu segment of Bailongjiang basin, China. J. Geol. Soc. India 2013, 82, 575–582. [Google Scholar] [CrossRef]
- Fan, X.; Xu, Q.; Scaringi, G.; Li, S.; Peng, D. A chemo-mechanical insight into the failure mechanism of frequently occurred landslides in the Loess Plateau, Gansu Province, China. Eng. Geol. 2016, 228, 337–345. [Google Scholar] [CrossRef]
- Yuan, B.; Chen, W.W.; Tang, Y.Q.; Li, J.P.; Yang, Q. Experimental study on gully-shaped mud flow in the loess area. Environ. Earth Sci. 2015, 74, 759–769. [Google Scholar] [CrossRef]
- Derbyshire, E. Geological hazards in loess terrain, with particular reference to the loess regions of China. Earth Sci. Rev. 2001, 54, 231–260. [Google Scholar] [CrossRef]
- Cui, P.; Zeng, C.; Lei, Y. Experimental analysis on the impact force of viscous debris flow. Earth Surf. Process. Landf. 2015, 40, 1644–1655. [Google Scholar] [CrossRef]
- Chen, J.G.; Chen, X.Q.; Li, Y.; Wang, F. An experimental study of dilute debris flow characteristics in a drainage channel with an energy dissipation structure. Eng. Geol. 2015, 193, 224–230. [Google Scholar] [CrossRef]
- Hubl, J.; Suda, J.; Proske, D.; Kaitna, R.; Scheidl, C. Debris flow impact estimation. In Proceedings of the 11th International Symposium on Water Management and Hydraulic Engineering, Ohrid, Macedonia, 8–12 September 2009; Volume 1, pp. 137–148. [Google Scholar]
- Armanini, A.; Larcher, M. Rational criterion for designing opening of slit-check dam. J. Hydraul. Eng. 2001, 127, 94–104. [Google Scholar] [CrossRef]
- Huebl, J.; Fiebiger, G. Debris-Flow Mitigation Measures. In Debris-Flow Hazards and Related Phenomena; Jakob, M., Hungr, O., Eds.; Springer: Berlin, Germany, 2005; pp. 445–466. [Google Scholar]
- Hassanli, A.M.; Nameghi, A.E.; Beecham, S. Evaluation of the effect of porous check dam location on fine sediment retention (a case study). Environ. Monit. Assess. 2009, 152, 319–326. [Google Scholar] [CrossRef] [PubMed]
- Takahisa, M. Structural countermeasures for debris flow disasters. Int. J. Eros. Control Eng. 2008, 1, 8–43. [Google Scholar] [CrossRef]
- You, Y.; Pan, H.L.; Liu, J.F.; Ou, G.Q. The optimal cross-section design of the “Trapezoid-V” shaped drainage channel of viscous debris flow. J. Mt. Sci. 2011, 8, 103–107. [Google Scholar] [CrossRef]
- Wendeler, C.; McArdell, B.; Volkwein, A.; Denk, M.; Gröner, E. Debris flow mitigation with flexible ring net barriers—Field tests and case studies. WIT Trans. Eng. Sci. 2008, 60, 23–31. [Google Scholar] [CrossRef]
- Volkwein, A.; Baumann, R.; Rickli, C.; Wendeler, C. Standardization for Flexible Debris Retention Barriers; Lollino, G., Giordan, D., Crosta, G.B., Corominas, J., Azzam, R., Wasowski, J., Sciarra, N., Eds.; Springer: Berlin, Germany, 2011; Volume 2, pp. 193–196. [Google Scholar]
- Liu, J.F.; Nakatani, K.; Mizuyama, T. Effect assessment of debris flow mitigation works based on numerical simulation by using Kanako 2D. Landslides 2013, 10, 161–173. [Google Scholar] [CrossRef]
- Okano, K.; Suwa, H.; Kanno, T. Characterization of debris flows by rainstorm condition at a torrent on the Mount Yakedake volcano, Japan. Geomorphology 2012, 136, 88–94. [Google Scholar] [CrossRef]
- Navratil, O.; Liébault, F.; Bellot, H.; Travaglini, E.; Theule, J.; Chambon, G.; Laigle, D. High-frequency monitoring of debris-flow propagation along the Réal Torrent, Southern French Prealps. Geomorphology 2013, 201, 157–171. [Google Scholar] [CrossRef]
- Rickenmann, D. Empirical relationships for debris flows. Nat. Hazards 1999, 19, 47–77. [Google Scholar] [CrossRef]
- Song, E.; Sang, J.I.; Dongyeob, K.D.; Kun, W.C. Flow and deposition characteristics of sediment mixture in debris flow flume experiments. For. Sci. Technol. 2017, 13, 61–65. [Google Scholar] [CrossRef]
- Suwa, H.; Okud, S.; Yokoya, K. Observation system on rocky mud-flow. Bull. Dis. Prev. Res. Inst. 1973, 23, 59–73. [Google Scholar]
- Hu, K.H.; Wei, F.Q.; Li, Y. Real-time measurement and preliminary analysis of debris-flow impact force at Jiangjia Ravine, China. Earth Surf. Process. Landf. 2011, 36, 1268–1278. [Google Scholar] [CrossRef]
- Wendeler, C.; Volkwein, A.; Roth, A.; Denk, M.; Wartmann, S. Field Measurements Used for Numerical Modelling of Flexible Debris Flow Barriers. In Debris-Flow Hazards Mitigation, Mechanics, Prediction, and Assessment; Chen, C.I., Major, J.J., Eds.; Millpress: Rotterdam, The Netherlands, 2007; pp. 681–687. [Google Scholar]
- Hürlimann, M.; Abancó, C.; Moya, J.; Vilajosana, I. Results and experiences gathered at the Rebaixader debris-flow monitoring site, Central Pyrenees, Spain. Landslides 2013, 11, 939–953. [Google Scholar] [CrossRef]
- Morino, C.; Conway, S.J.; Balme, M.R.; Hillier, J.; Jordan, C.; Saemundsson, Þ.; Argles, T. Debris-flow release processes investigated through the analysis of multi-temporal LiDAR datasets in north-western Iceland. Earth Surf. Process. Landf. 2018. [Google Scholar] [CrossRef]
- Bossi, G.; Cavalli, M.; Crema, S.; Frigerio, S.; Quan Luna, B.; Mantovani, M.; Marcato, G.; Schenato, L.; Pasuto, A. Multi-temporal LiDAR-DTMs as a tool for modelling a complex landslide: A case study in the Rotolon catchment (eastern Italian Alps). Nat. Hazards Earth Syst. Sci. 2015, 15, 715–722. [Google Scholar] [CrossRef]
- Cavalli, M.; Goldin, B.; Comiti, F.; Brardinoni, F.; Marchi, L. Assessment of erosion and deposition in steep mountain basins by differencing sequential digital terrain models. Geomorphology 2017, 291, 4–16. [Google Scholar] [CrossRef]
- D’Agostino, V.; Cesca, M.; Marchi, L. Field and laboratory investigations of runout distances of debris flows in the Dolomites (Eastern Italian Alps). Geomorphology 2010, 115, 294–304. [Google Scholar] [CrossRef]
- Scheidl, C.; Chiari, M.; Kaitna, R.; Müllegger, M.; Krawtschuk, A.; Zimmermann, T.; Proske, D. Analysing debris-flow impact models, based on a small scale modelling approach. Surv. Geophys. 2013, 34, 21–140. [Google Scholar] [CrossRef]
- Haas, T.; Braat, L.; Leuven, J.R.F.W.; Lokhorst, I.R.; Kleinhans, M.G. Effects of debris flow composition on runout, depositional mechanisms, and deposit morphology in laboratory experiments. J. Geophys. Res. Earth Surf. 2015, 120, 1949–1972. [Google Scholar] [CrossRef]
- Hürlimann, M.; Rickenmann, D.; Graf, C. Field and monitoring data of debris-flow events in the Swiss Alps. Can. Geotech. J. 2003, 40, 161–175. [Google Scholar] [CrossRef]
- Takahashi, T. A review of Japanese debris flow research. Int. J. Eros. Control Eng. 2009, 2, 1–14. [Google Scholar] [CrossRef]
- McCoy, S.W.; Kean, J.W.; Coe, J.A.; Staley, D.M.; Wasklewicz, T.A.; Tucker, G.E. Evolution of a natural debris flow: In situ measurements of flow dynamics, video imagery, and terrestrial laser scanning. Geology 2010, 38, 735–738. [Google Scholar] [CrossRef]
- Marchi, L.; Tecca, P.R. Dating Torrential Processes on Fans and Cones. In Debris-Flow Monitoring in Italy; Schneuwly-Bollschweiler, M., Stoffel, M., Rudolf-Miklau, F., Eds.; Springer: Berlin, Germany, 2013; pp. 309–318. [Google Scholar]
- Moriguchi, S.; Borja, R.; Yashima, A.; Sawada, K. Estimating the impact force generated by granular flow on a rigid obstruction. Acta Geotech. 2009, 4, 57–71. [Google Scholar] [CrossRef]
- Iverson, R.M. Scaling and design of landslide and debris-flow experiments. Geomorphology 2015, 244, 9–20. [Google Scholar] [CrossRef]
- Arattano, M.; Franzi, L. On the evaluation of debris flows dynamics by means of mathematical models. Nat. Hazards Earth Syst. Sci. 2003, 3, 539–544. [Google Scholar] [CrossRef]
- Armanini, A.; Larcher, M.; Odorizzi, M. Dynamic impact of a debris flow front against a vertical wall. In Proceedings of the 5th International Conference on Debris-flow Hazard Mitigation, Rome, Italy, 14–17 June 2011; Genevois, R., Douglas, L., Eds.; Casa Editrice Università La Sapienza: Roma, Italy, 2011; pp. 1041–1049. [Google Scholar]
- Wang, D.; Chen, Z.; He, S.; Liu, Y.; Tang, H. Measuring and estimating the impact pressure of debris flows on bridge piers based on large-scale laboratory experiments. Landslides 2018, 15, 1331–1345. [Google Scholar] [CrossRef]
- Egashira, S.; Honda, N.; Itoh, T. Experimental study on the entrainment of bed material into debris flow. Phys. Chem. Earth Part C 2001, 26, 645–650. [Google Scholar] [CrossRef]
- Acharya, G.; Cochrane, T.; Davies, T.; Bowman, E. Quantifying and modeling postfailure sediment yields from laboratory-scale soil erosion and shallow landslide experiments with silty loess. Geomorphology 2011, 129, 49–58. [Google Scholar] [CrossRef]
- Peng, J.; Huo, A.; Cheng, Y.; Dang, J.; Wei, H.; Wang, X.; Li, C. Submersion simulation in a typical debris flow watershed of Jianzhuangchuan catchment, Loess Plateau. Environ. Earth Sci. 2017, 76. [Google Scholar] [CrossRef]
- Peng, J.; Fan, Z.; Wu, D.; Zhuang, J.; Dai, F.; Chen, W.; Zhao, C. Heavy rainfall triggered loess-mudstone landslide and subsequent debris flow in Tianshui, China. Eng. Geol. 2015, 186, 79–90. [Google Scholar] [CrossRef]
- Tu, X.B.; Kwong, A.K.L.; Dai, F.C.; Tham, L.G.; Min, H. Field monitoring of rainfall infiltration in a loess slope and analysis of failure mechanism of rainfall induced landslides. Eng. Geol. 2009, 105, 134–150. [Google Scholar] [CrossRef]
- Shi, J.S.; Wu, L.Z.; Wu, S.R.; Li, B.; Wang, T.; Xin, P. Analysis of the causes of large-scale loess landslides in Baoji, China. Geomorphology 2016, 264, 109–117. [Google Scholar] [CrossRef]
- Tan, Q.M. Dimensional Analysis: With Case Studies in Mechanics; Springer: Berlin, Germany, 2011. [Google Scholar]
- Vagnon, F.; Segalini, A. Debris flow impact estimation on a rigid barrier. Nat. Hazards Earth Syst. Sci. 2016, 16, 1–17. [Google Scholar] [CrossRef]
- Choi, C.E.; Ng, C.W.W.; Au-Yeung, S.C.H.; Goodwin, G.R. Froude characteristics of both dense granular and water flows in flume modelling. Landslides 2015, 12, 1197–1206. [Google Scholar] [CrossRef]
- Ditzler, C.; Scheffe, K.; Monger, H.C. Soil Survey Manua, Soil Science Division Staff; USDA Handbook 18; Government Printing Office: Washington, DC, USA, 2017.
- Zhang, D.X.; Wang, G.H. Study of the 1920 Haiyuan earthquake-induced landslides in loess (China). Eng. Geol. 2007, 94, 76–88. [Google Scholar] [CrossRef]
- Xu, L.; Dai, F.C.; Tham, L.G.; Tu, X.B.; Min, H.; Zhou, Y.F.; Wu, C.X.; Xu, K. Field testing of irrigation effects on the stability of a cliff edge in loess, North-west China. Eng. Geol. 2011, 120, 10–17. [Google Scholar] [CrossRef]
- Wang, G.H.; Zhang, D.X.; Furuya, G.; Yang, J. Pore-pressure generation and fluidization in a loess landslide triggered by the 1920 Haiyuan earthquake, China: A case study. Eng. Geol. 2014, 174, 36–45. [Google Scholar] [CrossRef]
- Chen, J.G.; Chen, X.Q.; Wang, T.; Zou, Y.H.; Zhong, W. Types and causes of debris flow damage to drainage channels in the Wenchuan earthquake area. J. Mt. Sci. 2014, 11, 1406–1419. [Google Scholar] [CrossRef]
- Gaál, L.; Szolgay, J.; Kohnová, S.; Hlavčová, K.; Parajka, J.; Viglione, A.; Merz, R.; Blöschl, G. Dependence between flood peaks and volumes: A case study on climate and hydrological controls. Hydrol. Sci. J. 2015, 60, 968–984. [Google Scholar] [CrossRef]
- Kean, J.W.; McCoy, S.W.; Tucker, G.E.; Staley, D.M.; Coe, J.A. Runoff-generated debris flows: Observations and modeling of surge initiation, magnitude, and frequency. J. Geophys. Res. Earth Surf. 2013, 118, 2190–2207. [Google Scholar] [CrossRef]
- Lyu, L.; Wang, Z.; Cui, P.; Xu, M. The role of bank erosion on the initiation and motion of gully debris flows. Geomorphology 2017, 285, 137–151. [Google Scholar] [CrossRef]
- Ilstad, T.; Marr, J.G.; Elverhøi, A.; Harbitz, C.B. Laboratory studies of subaqueous debris flows by measurements of pore-fluid pressure and total stress. Mar. Geol. 2004, 213, 403–414. [Google Scholar] [CrossRef]
- Gujarati, D.N. Basic Econometrics; Tata McGraw-Hill Education: New Yrok, NY, USA, 2009. [Google Scholar]
- Song, F.; Wang, H.; Jiang, M.J. Analytically-based simplified formulas for circular tunnels with two liners in viscoelastic rock under anisotropic initial stresses. Constr. Build. Mater. 2018, 175, 746–767. [Google Scholar] [CrossRef]


| Index | a | B | c | d | Adj. R2 |
|---|---|---|---|---|---|
| Coefficient value | 0.0524 | 27.2243 | 0.1044 | 0.8405 | 0.9729 |
| Index | u | K | y | z | Adj. R2 |
|---|---|---|---|---|---|
| Coefficient values | 0.0009 | 0.6280 | −1.5142 | 4.9659 | 0.9834 |
| Position | sg | sh | Si | si | Adj. R2 |
|---|---|---|---|---|---|
| S1 | 0.0022 | 0.5259 | 3.2798 | −0.4498 | 0.9603 |
| S2 | 0.0019 | 0.5764 | 4.3714 | −0.9746 | 0.9370 |
| S3 | 0.0016 | 0.6155 | 5.8129 | −1.8288 | 0.9412 |
| Position | pl | pn | po | pq | Adj. R2 |
|---|---|---|---|---|---|
| P1 | 0.0017 | 0.4085 | −6.0102 | 5.5407 | 0.9548 |
| P2 | 0.0019 | 0.3766 | −4.6781 | 4.7382 | 0.9586 |
| P3 | 0.0021 | 0.2782 | −3.3683 | 3.8258 | 0.9423 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, H.; Ma, J.; Yu, H.; Hürlimann, M.; Zhang, P.; Liu, F.; Qi, S. Effect of Density and Total Weight on Flow Depth, Velocity, and Stresses in Loess Debris Flows. Water 2018, 10, 1784. https://doi.org/10.3390/w10121784
Shu H, Ma J, Yu H, Hürlimann M, Zhang P, Liu F, Qi S. Effect of Density and Total Weight on Flow Depth, Velocity, and Stresses in Loess Debris Flows. Water. 2018; 10(12):1784. https://doi.org/10.3390/w10121784
Chicago/Turabian StyleShu, Heping, Jinzhu Ma, Haichao Yu, Marcel Hürlimann, Peng Zhang, Fei Liu, and Shi Qi. 2018. "Effect of Density and Total Weight on Flow Depth, Velocity, and Stresses in Loess Debris Flows" Water 10, no. 12: 1784. https://doi.org/10.3390/w10121784
APA StyleShu, H., Ma, J., Yu, H., Hürlimann, M., Zhang, P., Liu, F., & Qi, S. (2018). Effect of Density and Total Weight on Flow Depth, Velocity, and Stresses in Loess Debris Flows. Water, 10(12), 1784. https://doi.org/10.3390/w10121784






