Evaluation and Hydrological Validation of GPM Precipitation Products over the Nanliu River Basin, Beibu Gulf
Abstract
1. Introduction
2. Study Region
3. Data and Method
3.1. Data
3.2. Hydrological Model
3.3. Performance Indicators
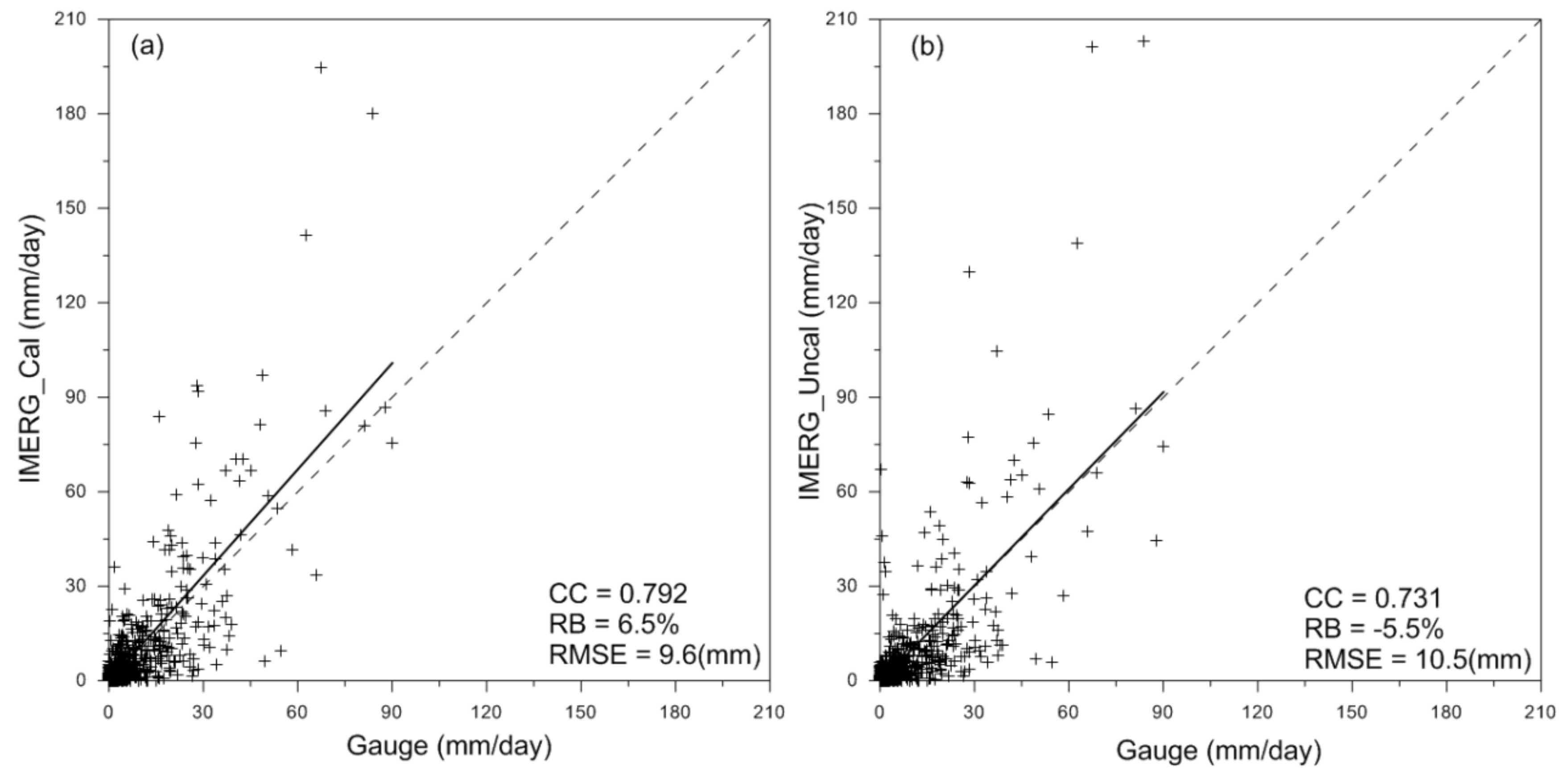
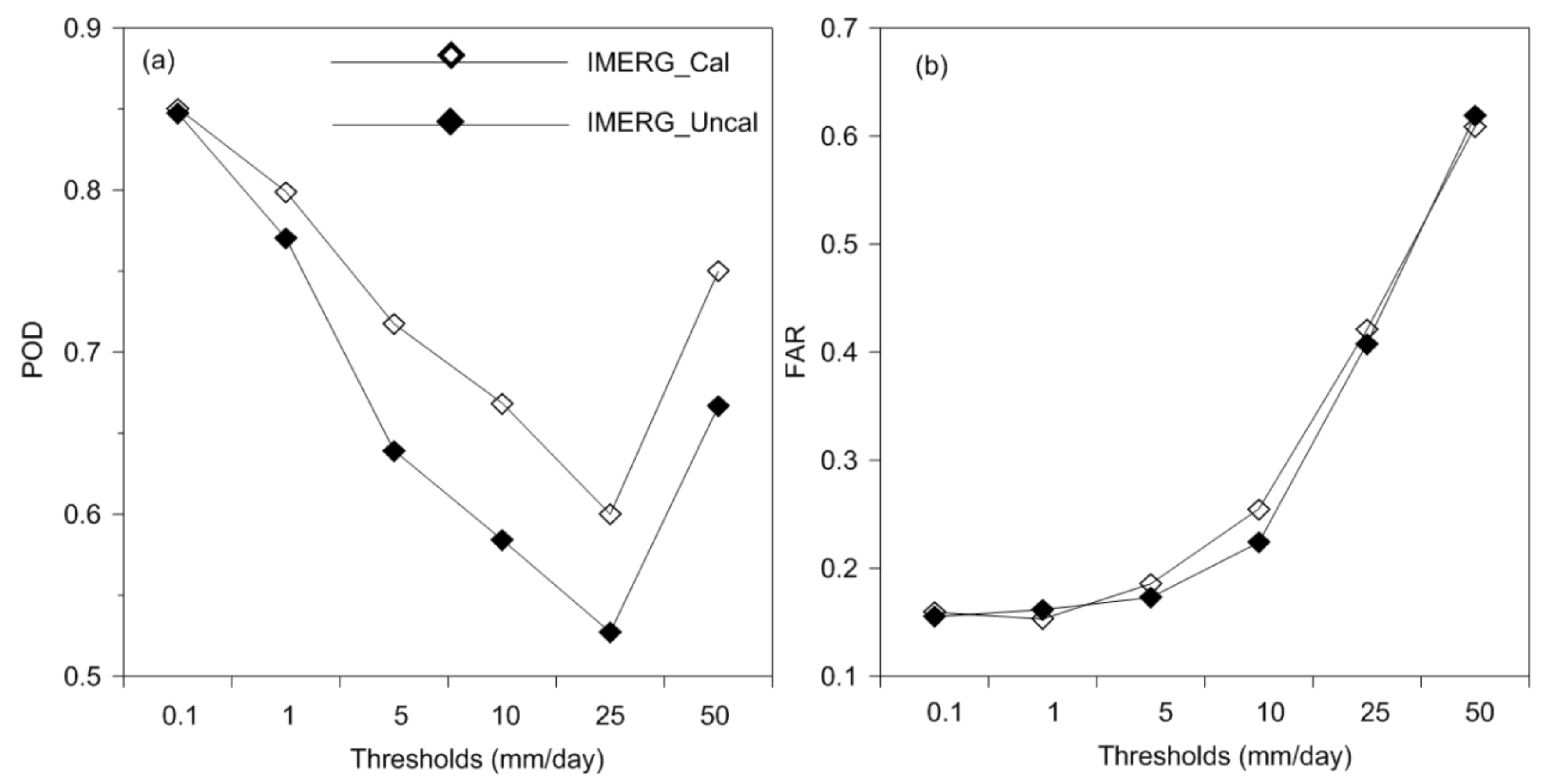
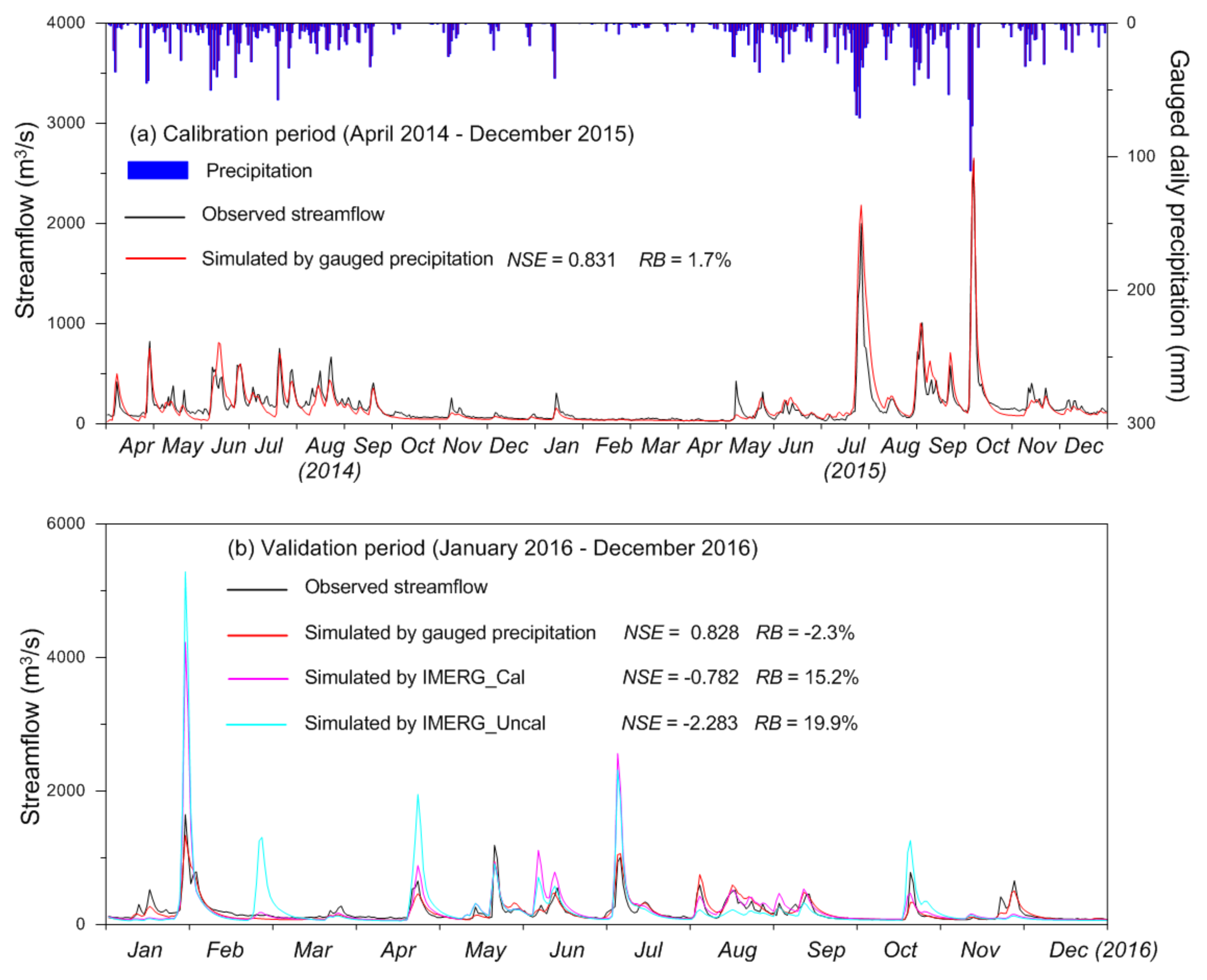
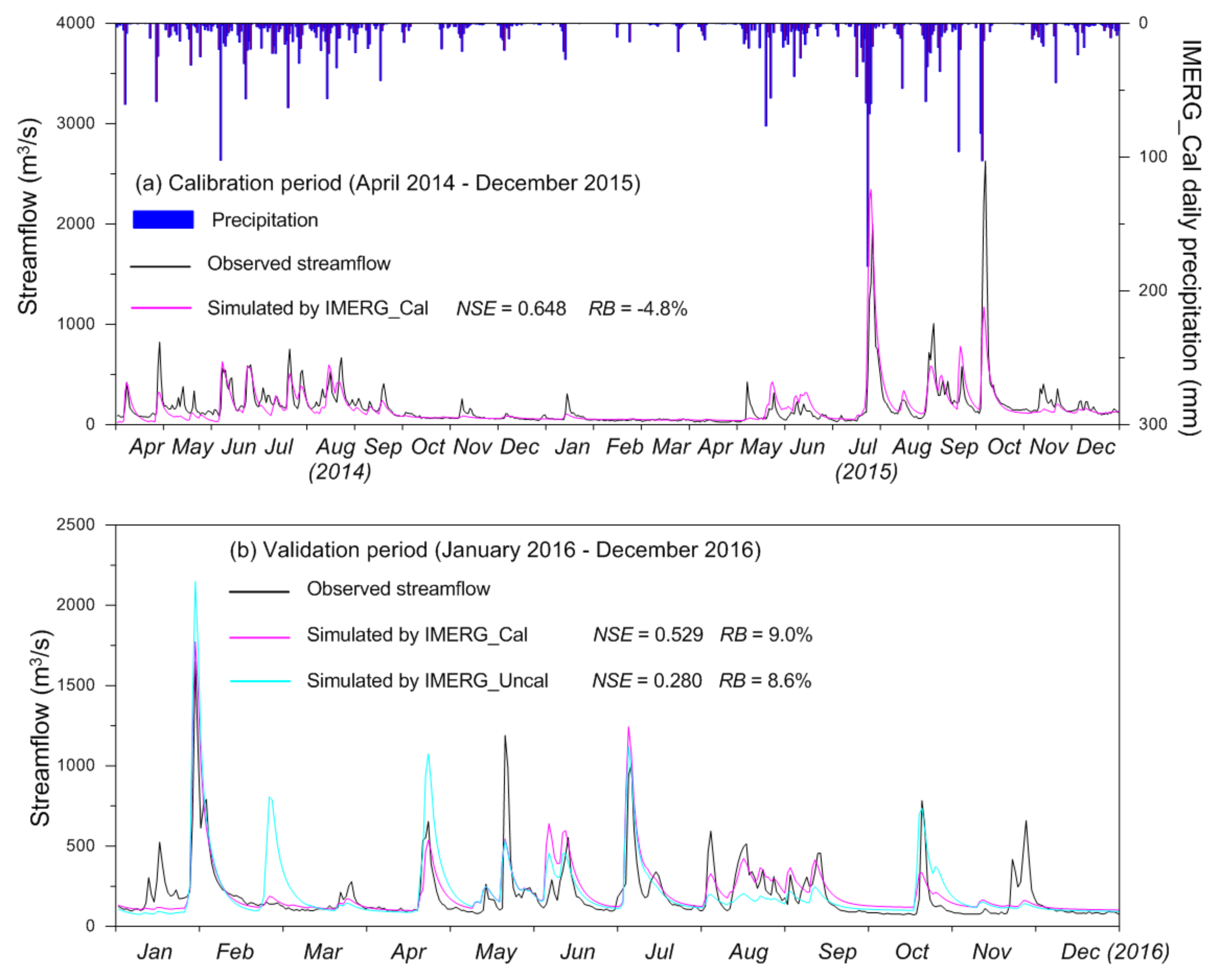
4. Results
5. Discussions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Hou, A.; Kakar, R.; Neeck, S.; Azarbarzin, A.; Kummerow, C.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; Mejía, J.M. The design of rainfall networks in time and space. Water Resour. Res. 1974, 10, 713–728. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Ciach, G.J.; Habib, E. An analysis of small-scale rainfall variability in different climatic regimes. Hydrol. Sci. J. 2003, 48, 151–162. [Google Scholar] [CrossRef]
- Gebremichael, M.; Krajewski, W.F. Assessment of the Statistical Characterization of Small-Scale Rainfall Variability from Radar: Analysis of TRMM Ground Validation Datasets. J. Appl. Meteorol. 2004, 43, 1180–1199. [Google Scholar] [CrossRef]
- Chen, F.; Li, X. Evaluation of IMERG and TRMM 3B43 Monthly Precipitation Products over Mainland China. Remote Sens. 2016, 8, 472. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Cressman, K.; Connor, S.J. Evaluating Detection Skills of Satellite Rainfall Estimates over Desert Locust Recession Regions. J. Appl. Meteorol. Climatol. 2010, 49, 1322–1332. [Google Scholar] [CrossRef]
- Zulkafli, Z.; Buytaert, W.; Onof, C.; Manz, B.; Tarnavsky, E.; Lavado, W.; Guyot, J. A Comparative Performance Analysis of TRMM 3B42 (TMPA) Versions 6 and 7 for Hydrological Applications over Andean–Amazon River Basins. J. Hydrometeorol. 2014, 15, 581–592. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Yang, D.; Hao, Z. Evaluation of satellite precipitation retrievals and their potential utilities in hydrologic modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Mishra, V. Climatic uncertainty in Himalayan water towers. J. Geophys. Res. Atmos. 2015, 120, 2689–2705. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN system satellite-based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.M.; Bolvin, D.T.; Curtis, S.; Joyce, R.; Mcgavock, B.; Susskind, J. Global precipitation at one-degree daily resolution from multisatellite observations. J. Hydrometeorol. 2001, 2, 36–50. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.G.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Simpson, J.; Kummerow, C.; Tao, W.-K.; Adler, R.F. On the Tropical Rainfall Measuring Mission (TRMM). Meteorol. Atmos. Phys. 1996, 60, 19–36. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Kummerow, C.; Simpson, J.; Thiele, O.; Barnes, W.; Chang, A.T.C.; Stocker, E.; Adler, R.F.; Hou, A.; Kakar, R.; Wentz, F.; et al. The status of the Tropical Rainfall Measuring Mission (TRMM) after two years in orbit. J. Appl. Meteorol. 2000, 39, 1965–1982. [Google Scholar] [CrossRef]
- NASA Rainfall Satellite Out of Fuel, but Continues to Provide Data. Available online: https://pmm.nasa.gov/articles/trmm-out-fuel-continues-provide-data (accessed on 3 December 2018).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-satellitE Retrievals for GPM (IMERG) Technical Documentation; NASA/GSFC: Greenbelt, MD, USA, 2014. [Google Scholar]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of Integrated Multi-satellite Retrievals for Global Precipitation Measurement over China. Atmos. Res. 2016, 121–133. [Google Scholar] [CrossRef]
- Liu, Z. Comparison of Integrated Multisatellite Retrievals for GPM (IMERG) and TRMM Multisatellite Precipitation Analysis (TMPA) Monthly Precipitation Products: Initial Results. J. Hydrometeorol. 2016, 17, 777–790. [Google Scholar] [CrossRef]
- Ma, Y.; Tang, G.; Long, D.; Yong, B.; Zhong, L.; Wan, W.; Hong, Y. Similarity and Error Intercomparison of the GPM and Its Predecessor-TRMM Multisatellite Precipitation Analysis Using the Best Available Hourly Gauge Network over the Tibetan Plateau. Remote Sens. 2016, 8, 569. [Google Scholar] [CrossRef]
- Sahlu, D.; Nikolopoulos, E.; Moges, S.A.; Anagnostou, E.N.; Hailu, D. First Evaluation of the Day-1 IMERG over the Upper Blue Nile Basin. J. Hydrometeorol. 2016, 17, 2875–2882. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhang, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Asong, Z.E.; Razavi, S.; Wheater, H.S.; Wong, J.S. Evaluation of Integrated Multisatellite Retrievals for GPM (IMERG) over Southern Canada against Ground Precipitation Observations: A Preliminary Assessment. J. Hydrometeorol. 2017, 18, 1033–1050. [Google Scholar] [CrossRef]
- Sungmin, O.; Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG Early, Late, and Final rainfall estimates using WegenerNet gauge data in southeastern Austria. Hydrol. Earth Syst. Sci. 2017, 21, 6559–6572. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and Hydrological Comparisons between TRMM and GPM Level-3 Products over a Midlatitude Basin: Is Day-1 IMERG a Good Successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- He, Z.; Yang, L.; Tian, F.; Ni, G.; Hou, A.; Lu, H. Intercomparisons of Rainfall Estimates from TRMM and GPM Multisatellite Products over the Upper Mekong River Basin. J. Hydrometeorol. 2017, 413–430. [Google Scholar] [CrossRef]
- Sharif, H.O.; Al-Zahrani, M.; El Hassan, A. Physically, Fully-Distributed Hydrologic Simulations Driven by GPM Satellite Rainfall over an Urbanizing Arid Catchment in Saudi Arabia. Water 2017, 9, 163. [Google Scholar] [CrossRef]
- Zubieta, R.; Getirana, A.; Espinoza, J.C.; Lavado-Casimiro, W.; Aragon, L. Hydrological modeling of the Peruvian–Ecuadorian Amazon Basin using GPM-IMERG satellite-based precipitation dataset. Hydrol. Earth Syst. Sci. 2017, 21, 3543–3555. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Hogue, T.S.; Hsu, K.-L.; Sorooshian, S. Intercomparison of rain gauge, radar, and satellite-based precipitation estimates with emphasis on hydrologic forecasting. J. Hydrometeorol. 2005, 6, 497–517. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Kirstetter, P.E.; Tian, Y. Performance of IMERG as a Function of Spatiotemporal Scale. J. Hydrometeorol. 2017, 18, 307–319. [Google Scholar] [CrossRef] [PubMed]
- Che, L.; Hu, B.; Li, Y. Spatial and Temporal Variations of Vegetation Cover Degrees in the Nanliujiang River Watershed from 1991 to 2009. J. Guangxi Teach. Educ. Univ. 2012, 29, 52–59. (In Chinese) [Google Scholar]
- Nachtergaele, F.; Velthuizen, H.V.; Verelst, L. Harmonized World Soil Database; Food and Agriculture Organization of the United Nations: Rome, Italy, 2008. [Google Scholar]
- Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Sohlberg, R. Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. Remote Sens. 2000, 21, 1331–1364. [Google Scholar] [CrossRef]
- Li, S.; Dai, Z.; Mei, X.; Huang, H.; Wei, W.; Gao, J. Dramatic variations in water discharge and sediment load from Nanliu River (China) to the Beibu Gulf during 1960–2013. Quat. Int. 2017, 440, 12–23. [Google Scholar] [CrossRef]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-SatelliE Retrievals for GPM (IMERG); Algorithm Theoretical Basis Document, Version 4.5; NASA: Greenbelt, MD, USA, 2015. [Google Scholar]
- Zhao, R.; Wang, P. Parameter analysis for Xinanjiang model. J. China Hydrol. 1988, 6, 2–9. (In Chinese) [Google Scholar]
- Zhao, R. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Thiessen, A.H. Precipitation Averages for Large Areas. Mon. Weather Rev. 1911, 39, 1082–1084. [Google Scholar] [CrossRef]
- Tabios, G.Q.; Salas, J.D. A comparative analysis of techniques for spatial interpolation of precipitation. J. Am. Water Resour. Assoc. 1985, 21, 365–380. [Google Scholar] [CrossRef]
- Nijssen, B.; Lettenmaier, D.P. Effect of precipitation sampling error on simulated hydrological fluxes and states: Anticipating the Global Precipitation Measurement satellites. J. Geophys. Res. 2004, 109, D02103. [Google Scholar] [CrossRef]
- Su, F.; Hong, Y.; Lettenmaier, D.P. Evaluation of TRMM Multisatellite Precipitation Analysis (TMPA) and its utility in hydrologic prediction in the La Plata Basin. J. Hydrometeorol. 2008, 9, 622–640. [Google Scholar] [CrossRef]
- Artan, G.; Gadain, H.; Smith, J.L.; Bandaragoda, C.J.; Verdin, J.P. Adequacy of satellite derived rainfall data for stream flow modeling. Nat. Hazards 2007, 43, 167–185. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M.; Ghebremichael, L.T.; Bayissa, Y.A. Evaluation of high-resolution satellite rainfall products through streamflow simulation in a hydrological modeling of a small mountainous watershed in Ethiopia. J. Hydrometeorol. 2012, 13, 338–350. [Google Scholar] [CrossRef]
- Gao, J.; Tang, G.; Hong, Y. Dual-Frequency Precipitation Radar (DPR) upon TRMM Precipitation Radar (PR) in global precipitation rate estimation, type classification and vertical profiling. Remote Sens. 2017, 9, 1142. [Google Scholar] [CrossRef]
- Zhao, Y.; Xie, Q.; Lu, Y.; Hu, B. Hydrologic Evaluation of TRMM Multisatellite Precipitation Analysis for Nanliu River Basin in Humid Southwestern China. Sci. Rep. 2017, 7, 2470. [Google Scholar] [CrossRef]
- Jin, X.; Shao, H.; Zhang, C.; Yan, Y. The Applicability Evaluation of Three Satellite Products in Tianshan Mountains. J. Nat. Resour. 2016, 31, 2074–2085, (In Chinese with English Abstract). [Google Scholar]
- Kim, K.; Park, J.; Baik, J.; Choi, M. Evaluation of topographical and seasonal feature using GPM IMERG and TRMM 3B42 over Far-East Asia. Atmos. Res. 2007, 187, 95–105. [Google Scholar] [CrossRef]
- Manz, B.; Páez-Bimos, S.; Horna, N.; Buytaert, W.; Ochoa-Tocachi, B.; Lavado-Casimiro, W.; Willems, B. Comparative Ground Validation of IMERG and TMPA at Variable Spatiotemporal Scales in the Tropical Andes. J. Hydrometeorol. 2017, 18, 2469–2489. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Win, K.W.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM Multi-Satellite Precipitation Products in Streamflow Simulations in a Data-Sparse Mountainous Watershed in Myanmar. Remote Sens. 2017, 9, 302. [Google Scholar] [CrossRef]
- Hamada, A.; Takayabu, Y. Improvements in Detection of Light Precipitation with the Global Precipitation Measurement Dual-Frequency Precipitation Radar (GPM DPR). J. Atmos. Ocean. Technol. 2016, 33, 653–667. [Google Scholar] [CrossRef]
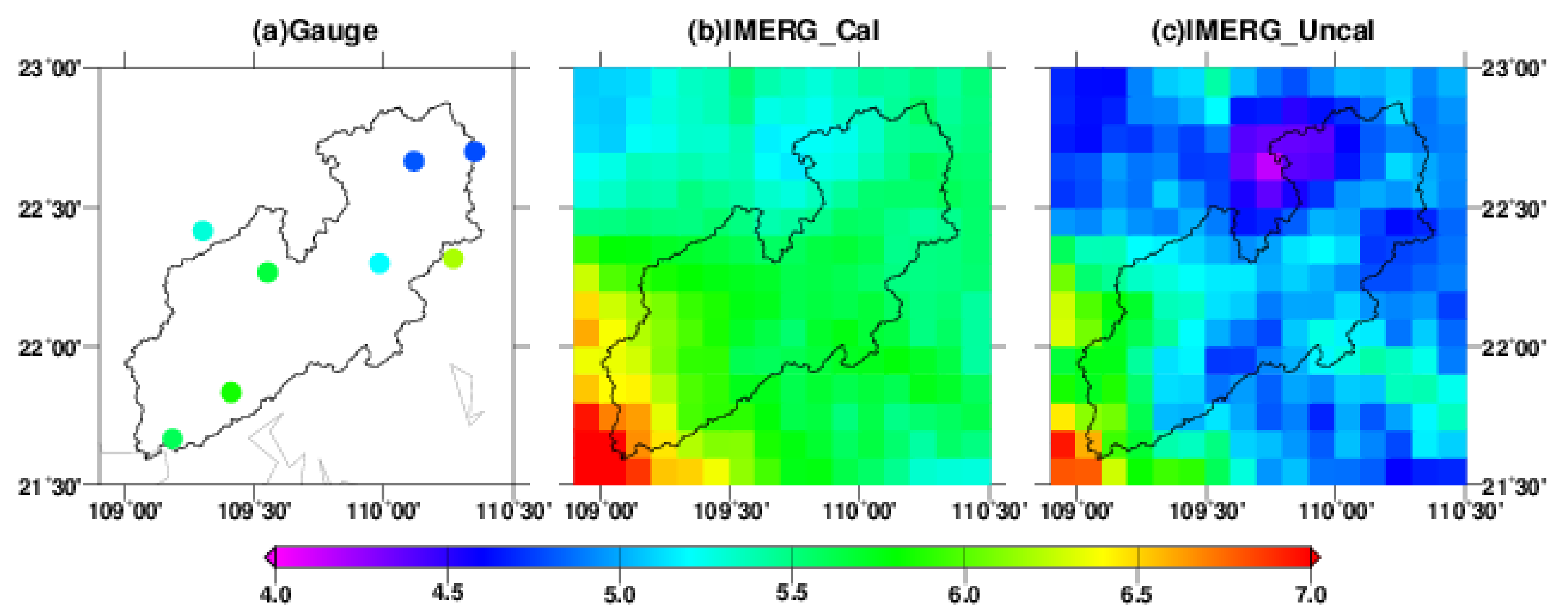
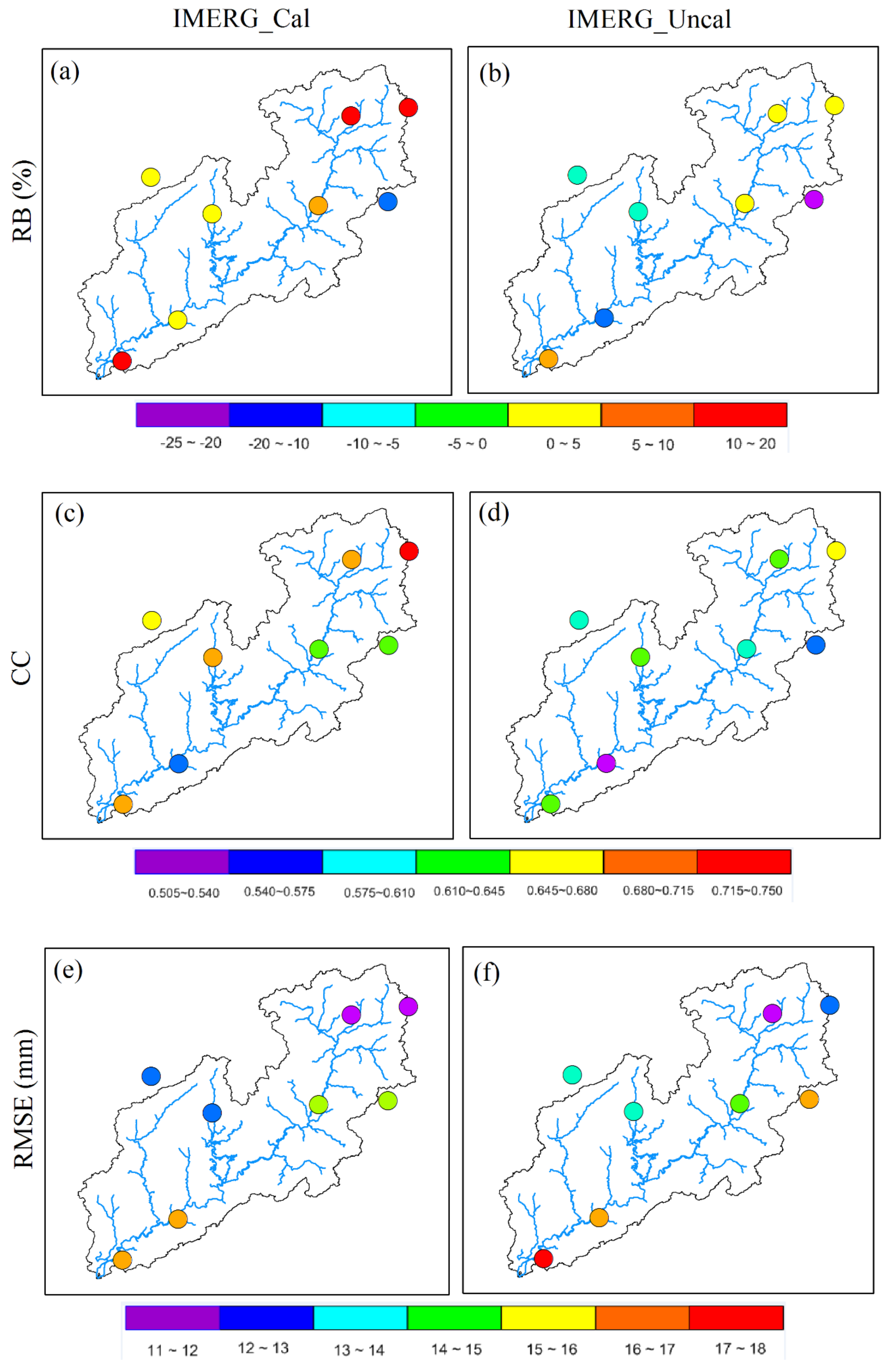
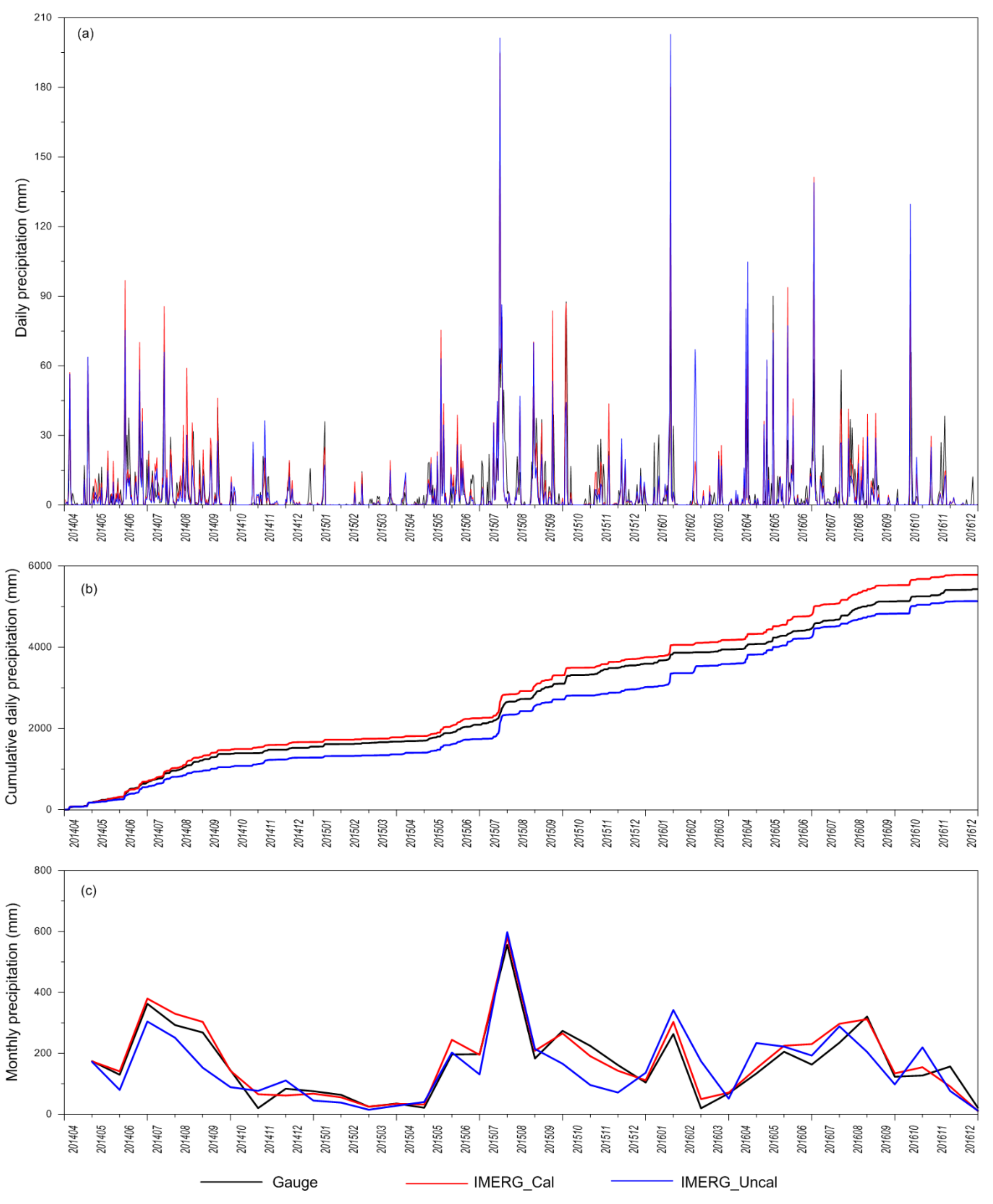
| Station Number | Station Name | Latitude (N) | Longitude (E) | Elevation (m) |
|---|---|---|---|---|
| 59,446 | Lingshan | 22°25′ | 109°18′ | 67 |
| 59,448 | Pubei | 22°16′ | 109°33′ | 69 |
| 59,449 | Bobai | 22°18′ | 109°59′ | 56 |
| 59,451 | Beiliu | 22°42′ | 110°21′ | 105 |
| 59,453 | Yulin | 22°39′ | 110°10′ | 82 |
| 59,457 | Luchuan | 22°19′ | 110°16′ | 113 |
| 59,640 | Hepu | 21°40′ | 109°11′ | 12 |
| Changle * | 21°50′ | 109°25′ | 32 |
| Stations | RB (%) | CC | RMSE (mm) | |||
|---|---|---|---|---|---|---|
| IMERG_Cal | IMERG _Uncal | IMERG_Cal | IMERG _Uncal | IMERG_Cal | IMERG _Uncal | |
| Beiliu | 16.1 | 4.5 | 0.744 | 0.662 | 11.3 | 12.6 |
| Bobai | 9.3 | 1.2 | 0.624 | 0.590 | 14.1 | 14.3 |
| Changle | 1.2 | −12.6 | 0.557 | 0.521 | 16.7 | 16.9 |
| Hepu | 18.9 | 5.9 | 0.686 | 0.636 | 16.4 | 17.5 |
| Lingshan | 4.0 | −7.3 | 0.679 | 0.599 | 12.2 | 13.5 |
| Luchuan | −11.4 | −23.3 | 0.637 | 0.550 | 14.7 | 16.2 |
| Pubei | 1.1 | −9.0 | 0.696 | 0.643 | 12.9 | 13.8 |
| Yulin | 14.0 | 0.8 | 0.691 | 0.625 | 11.5 | 11.9 |
| No. | Parameters/Units | Definition | Value |
|---|---|---|---|
| 1 | K | Pan evaporation coefficient | 1.27 |
| 2 | WUM (mm) | Tension water capacity from upper layer | 20 |
| 3 | WLM (mm) | Tension water capacity from lower layer | 80 |
| 4 | WDM (mm) | Tension water capacity from deep layer | 20 |
| 5 | C (dimensionless quantity) | Evapotranspiration coefficient from deep layer | 0.15 |
| 6 | B (dimensionless quantity) | Exponential number of storage capacity distribution curve | 0.4 |
| 7 | SM (mm) | Areal mean free water storage capacity | 100 |
| 8 | EX | Parameter in the distribution of free water storage capacity | 1.0 |
| 9 | KG | Outflow coefficient of the ground water from free water | 0.3 |
| 10 | KSS | Outflow coefficient of the interflow from free water | 0.4 |
| 11 | KKG | Groundwater recession coefficient | 0.9972 |
| 12 | KKSS | Interflow recession coefficient | 0.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, K.; Zhao, Y.; Wei, Y.; Hu, B.; Lu, Y. Evaluation and Hydrological Validation of GPM Precipitation Products over the Nanliu River Basin, Beibu Gulf. Water 2018, 10, 1777. https://doi.org/10.3390/w10121777
Tong K, Zhao Y, Wei Y, Hu B, Lu Y. Evaluation and Hydrological Validation of GPM Precipitation Products over the Nanliu River Basin, Beibu Gulf. Water. 2018; 10(12):1777. https://doi.org/10.3390/w10121777
Chicago/Turabian StyleTong, Kai, Yinjun Zhao, Yongping Wei, Baoqing Hu, and Yuan Lu. 2018. "Evaluation and Hydrological Validation of GPM Precipitation Products over the Nanliu River Basin, Beibu Gulf" Water 10, no. 12: 1777. https://doi.org/10.3390/w10121777
APA StyleTong, K., Zhao, Y., Wei, Y., Hu, B., & Lu, Y. (2018). Evaluation and Hydrological Validation of GPM Precipitation Products over the Nanliu River Basin, Beibu Gulf. Water, 10(12), 1777. https://doi.org/10.3390/w10121777






