Evaluating the Road-Bioretention Strip System from a Hydraulic Perspective—Case Studies

Abstract

The two-dimensional overland flow simulation program, FullSWOF_2D, was revised to include submodules of determining infiltration by zones (Z) and grate-inlet (G) drainage from a 2D surface to a 1D pipe flow. The updated program, FullSWOF-ZG, was used to evaluate the performance of a road-bioretention strip (RBS) system and explore/understand key parameters of continuous RBS design. The program was validated using eight pervious surfaces under simulated rainfall events and tested with 20 experimental cases of a locally depressed curb inlet. The mean difference of simulated interception efficiencies (36.6%–86.0%) and observed interception efficiencies (34.8%–84.0%) of the curb inlet was 3.5%, which proves the program predicts the curb-inlet interception efficiency accurately. The 20 road-only and 20 RBS modeling cases were designed and modeled using the FullSWOF-ZG program. These case studies have different road lengths, curb inlet lengths, longitudinal slopes, cross slopes, bioretention-overflow inlet heights, and bioretention soil infiltration parameters. Only 34.6%–48.4% of the total runoff volume is intercepted by the RBS’s curb inlet under heavy rainfall (250 mm/h) and the remaining part of the runoff flows downstream along the road, which may cause local inundation and become a safety hazard. The curb inlet becomes the bottleneck of the RBS system that could impede the runoff flowing into the bioretention strip for detention and infiltration to improve the stormwater quality.

1. Introduction

Over the past 40 years to 2016, China’s urban population rose from 17.6% in 1977 to 57.4% of its total population, which led to rapid urbanization, and this trend will keep increasing by 1% per year to reach approximately 60% by 2020 [1,2]. Consequently, different city syndromes, such as water shortage, water pollution, flood inundation, and ecologic deterioration, have happened frequently over the past decades, causing huge economic loss and becoming large obstacles to sustainable development in China [1,3] as well as in other parts of the world [4,5,6]. The national New-type Urbanization Plan (2014–2020) was launched in March 2014 by the Chinese central government and emphasized environmental-friendly and sustainable urbanization approaches as an important component of the blueprint [7]. In order to endorse the sustainable urbanization plan, the Sponge City (SPC, a summary of definitions or descriptions of all acronyms and symbols used in the paper is given in Appendix A) paradigm based on green/gray stormwater management infrastructure integration was announced in 2013 as a relief countermeasure to city syndromes in China [8,9,10].

An important component of the low impact development (LID), bioretention best management practice (BMP) in Prince George’s County, Maryland [11] is a stormwater quantity and quality control practice that facilitates decreasing surface runoff, increasing groundwater recharge, and treating various pollutants through a variety of processes [12,13,14]. Many bioretention cells were used in LID practices and studied by many researchers in the past. These bioretention cells receive the runoff from different small drainage areas, such as parking lots and a few urban buildings. Bioretention BMP has been applied to diverse sites, including residential gardens [15], parking lots [16,17,18], and along urban roads and highways [19,20,21,22,23]. Typical bioretention design includes a vegetation layer (ponding area), a soil layer (organic or mulch layer plus planting soil), a storage layer filled with gravels, an overflow inlet, and an optional underdrain (perforated pipe) (Figure 1). When saturated hydraulic conductivity is less than 13 mm/h, an underdrain system for infiltrated water is required, which flows to the outfall point [14]. As an important and typical practice, a continuous road-bioretention strip (RBS) (Figure 1 and Figure 2), which combines green/gray infrastructures to facilitate road runoff control through infiltration and storage as well as decreasing road local flood inundation risk, is widely used in the pilot SPC construction [9]. A continuous RBS is built along an urban road or street over s relatively long distance and could be separated into several cells/units by check dams (berms) when the longitudinal slope is large enough. The slope and distance between two check dams control the ponding depth and length in the RBS. When the slope is small, the RBS could be one single elongated cell containing tree planters (Figure 2).

Figure 2 shows four RBS projects in four SPC pilot cities, indicating that road-bioretention systems are widely built in China. Figure 2a is a continuous RBS built in the Beijing Economic-Technological Development Area. The vegetation in the bioretention strip is very dense and its vegetation volume is a large fraction of the bioretention ponding volume. The concern is that dense vegetation may affect the ponding process of runoff. Figure 2b,c present two projects built in Shenzhen, Guangdong province and Jinan, Shandong province, respectively. The bioretention strips with tree planters were constructed on the right-of-way. Figure 2d presents a road-bioretention project in Ningbo, Zhejiang province; its bioretention curb inlet was designed mainly from the landscape perspective rather than for the flow intercepting function purpose. Different from right-of-way bioretention cells constructed in the USA, road-bioretention projects in SPC pilot cities are always very long along the roadside and are combined with tree planters [9]. Different types of curb inlets (outlined by red rectangles in Figure 2) have been used in different projects while no guidance for designing curb inlets of the RBS systems is available. These RBS curb inlets were designed from the landscape and safety perspective and based on experience rather than research findings on RBS’ curb inlet interception efficiencies. Continuous RBS performance on intercepting road runoff and reducing local flooding under different rainfall events or upstream inflows is still unclear. Key design parameters of continuous RBS also need to be explored and determined.

Normally, each RBS cell has an overflow grate inlet at the downstream end and near the berm, and the overflow height (h_b), as an important design parameter, is the grate inlet height above the ground surface of the RBS (Figure 1). When the rainfall starts, runoff generated from the road flows into the RBS through curb inlets and infiltrates into the soil first. Then, after the soil is saturated, surface ponding occurs inside the RBS. When the ponding depth is greater than the overflow height, the runoff begins to flow into the grate inlet and then to the underground stormwater sewage system. When the infiltrated runoff reaches the storage layer of the RBS it can drain through the perforated pipe.

Most previous studies indicate that bioretention BMPs have a good hydrologic performance and pollutant removal efficiency in treating urban road runoff based on experimental and monitored data [24]. There was limited guidance and study on RBS design in China [25,26]. In the study conducted by Manganka et al. [27], the influence of rainfall characteristics, and inflow and outflow discharge on bioretention pollutant treatment performance was explored using conceptual model simulation data. Manganka et al. [24] found that the antecedent dry period is the most important factor affecting bioretention pollutant treatment efficiency while the study did not link the bioretention performance to actual design parameters directly. To evaluate and design RBS, the influence of design parameters, including the catchment area, longitudinal slope, road/street cross slope, curb inlet length, bioretention overflow height, and infiltration capacity, on RBS performance still needs to be explored.

Much more attention and focus should be paid to studying the curb inlet interception efficiency and its design because the curb inlet is an important hydraulic infrastructure for RBS. The curb inlet allows surface runoff on the road to get into bioretention cells and influences the road-bioretention strip’s performance directly [25]. Some previous studies have explored the curb inlet interception efficiency evaluation [28], efficiency limitation [29], and influence factors [30] in urban drainage while not much research was found on curb inlets in RBS. An evidence-based curb inlet design guide for RBS is of great importance and urgency because current practices do not address RBS’ hydraulic performance needs [26]. It is important to design a continuous RBS with a high curb-inlet interception efficiency and grate-inlet capacity to reduce the runoff on roads, ensure traffic safety, and relieve local flood inundation.

To understand the influence of design parameters for RBS, a performance evaluation of RBS is particularly important [31]. The main purpose of the study is to understand how the runoff generated from the upstream road is intercepted by the curb inlet and the grate inlet on the road and how the flow interception further influences the hydrological performance of the RBS system. In this study, the submodules for determining infiltration by zones (pervious and impervious zones in the simulation domain, Figure 2) and grate-inlet drainage from the 2D surface to the 1D pipe were added to the open source FullSWOF_2D (version 1.07, Lab. J. A. Dieudonné & EPU Nice Sophia, Nice, France) [32] program to explore the continuous RBS performance and design concerns; the updated program was called FullSWOF-ZG. FullSWOF_2D means full shallow-water equations (SWEs) for overland flow in two-dimensional (2D) analysis which is programmed using C++ to fully describe the rainfall-runoff and flow distribution progress on the surface in two-dimensional domains [33]. Therefore, the FullSWOF-ZG program can simulate impervious and pervious surfaces (different infiltration parameters/capabilities in different zones) in the RBS domain simultaneously under rainfall events. The 2D-1D grate-inlet drainage submodule enables the program to simulate the 2D overland runoff flowing into a grate inlet then to a 1D underground drainage pipe using the weir equation [34].

2. Materials and Methods

2.1. Road-Bioretention Strip (RBS) Design

The continuous RBS is mainly designed to remove runoff from the road, reduce local flood inundation, and improve runoff quality through bioretention. Curb inlet interception efficiency, bioretention ponding volume, bioretention infiltration capacity, and road grate inlet capacity should be taken into consideration when designing a continuous RBS.

2.1.1. Curb Inlet Interception Efficiency Calculation

There are three types of curb inlets commonly used in the USA. The undepressed curb inlet, which has one cross slope for the road and gutter so that the curb inlet has the same elevation as the nearby road surface (Figure 2), is also widely used in China [26]. The continuously depressed curb inlet is placed in gutters of streets with a composite cross slope [35]. The locally depressed curb inlet has an adjacent depression in the gutter near the inlet for effective flow interception, such as type C (Figure 3) and type D curb inlets designed and constructed by the Texas Department of Transportation [36].

Current curb inlet designs in the USA are based on Hydraulic Engineering Circular No. 22 (HEC-22) from the Federal Highway Administration [37] and the Urban Street Stormwater Guide from the National Association of City Transportation Officials [25]. Design procedures of commonly-used inlet types are presented in HEC-22 and other specific design guidance is provided in different studies [28,36]. The interception efficiency (E_ci) of undepressed curb inlets is calculated using the following Equations (1)–(3) adopted from HEC-22:

$$Q=\left(0.376/n\right) S_x^{1.67} S_0^{0.5}{T}^{2.67}$$

(1)

$$L_T=0.817Q^{0.42}{S}_0^{0.3}{\left[1/\left(n{S}_x\right)\right]}^{0.6}$$

(2)

$$E_{ci}=1-{\left[1-\left(L_{ci}/L_T\right)\right]}^{1.8}$$

(3)

where L_T (m) is the theoretical curb-inlet length required to intercept 100% of the flow; E_ci (%) is the inlet interception efficiency; L_ci (m) is the curb inlet length; S_x and S₀ are the cross slope and longitudinal slope of the road/street, Q is the flow rate on the road/street surface; T is the spread width of the flow on the road/street surface; and n (-) is Manning’s roughness of the road surface.

2.1.2. Bioretention Ponding Volume and Infiltration Capacity

Overflow height/ponding depth provides a temporary storage space for stormwater runoff before it filters downward through the bioretention facility. The temporary ponding depth for bioretention facilities ranges from 5 cm (for mitigating sidewalk runoff alone, or in fast-draining soils) to up to 30 cm (for mitigating roadway runoff, or in slower-draining soils) [25]. The Delaware Green Technologies Design Manual and Model provides design guidance for bioretention systems, and allows a maximum ponding depth of 45 cm [38]. Allen et al. [14] declared the overall principles of the bioretention ponding volume and infiltration capacity design in their study. The ponding volume is designed by the corresponding catchment area and the design’s rainfall depth.

The initial bioretention design specifications suggested the use of natural soils with high permeability [11]. Three soil textural classifications were specified, which include: Loamy sand, sandy loam, and loam. The Green-Ampt model was adopted to simulate the bioretention infiltration process in this study. The infiltration parameters included the saturated hydraulic conductivity (K), moisture deficit (Δθ), and suction head (φ). RBS with three different soils were studied here: Loamy sand (K = 51 mm/h, Δθ = 0.410, φ = 0.09 m), sandy loam (K = 25 mm/h, Δθ = 0.435, φ = 0.218 m), and loam (K = 13 mm/h, Δθ = 0.451, φ = 0.478 m); and their infiltration parameter values were adopted based on the soil type [14]. The thickness of the soil layer was 0.45 m according to the bioretention design cases [39].

2.2. FullSWOF-ZG Program and Model Test

In this study, the open-source FullSWOF_2D program was revised and improved, and the updated program is called FullSWOF-ZG. The simplified SWEs model, as a Saint-Venant system [40], is widely used to simulate the incompressible Navier–Stokes flow occurring in rivers, channels, oceans, and land surfaces [41]. The 2D SWEs for the FullSWOF_2D program, including the continuity equation and two momentum equations in the x and y directions, are stated as the following equations for each computational cell (center coordinates x and y):

$$\frac{\partial h}{\partial t}+\frac{\partial hu}{\partial x}+\frac{\partial hv}{\partial y}=R_i\left(x,y\right)-f\left(x,y\right)$$

(4)

$$\frac{\partial hu}{\partial t}+\frac{\partial }{\partial x}\left(h{u}^2+\frac{g{h}^2}{2}\right)+\frac{\partial }{\partial y}\left(huv\right)=-gh\left(\frac{\partial z}{\partial x}+S_{fx}\right)$$

(5)

$$\frac{\partial hv}{\partial t}+\frac{\partial }{\partial x}\left(huv\right)+\frac{\partial }{\partial y}\left(h{v}^2+\frac{g{h}^2}{2}\right)=-gh\left(\frac{\partial z}{\partial y}+ S_{fy}\right)$$

(6)

where R_i(x, y) (m/s) is the cell’s rainfall intensity; f(x, y) (m/s) is the cell’s infiltration rate; h (m) is the cell’s water depth; z (m) is the cell topography elevation as a function of the cell location or x and y coordinates; u (m/s) and v (m/s) are the cell’s depth-averaged velocities in the x and y directions, respectively; S_fx and S_fy are the cell’s friction slopes in the x and y directions, respectively; g (m/s²) is the gravity acceleration; and t (s) is time.

The FullSWOF_2D program fully solves SWEs on a structured mesh (square cells) in two dimensions using the finite volume method that ensures mass conservation compared to the finite difference method [42]. A well-balanced numerical scheme was adopted to guarantee the positivity of water depth and the preservation of steady states for specific hydrological features such as during wet-dry transitions and tiny water depths [32,43]. Different boundary conditions, friction laws, and numerical schemes were developed that make the program a very powerful overland flow simulation software. A modified bi-layer (crust- and soil-layer) Green–Ampt infiltration model [44] to calculate f(x, y) for Equation (4) was coded in the FullSWOF_2D [42], which enables the program to simulate the overland flow on impervious and pervious surfaces simultaneously.

The updated FullSWOF-ZG program includes the rainfall input and the infiltration determination by zone and a new 2D-1D drainage inlet submodule. Therefore, the program can simulate impervious road (Figure 3 and Figure 4) and pervious bioretention surfaces (Figure 4) with different infiltration capabilities simultaneously. The simulation domain can have several grate inlets (Figure 4); therefore, the 2D overland flow can drain into these 2D grate inlets (rectangles) to become a 1D flow in underground drainage pipes. Currently, the FullSWOF-ZG program does not further simulate the 1D flow in the drainage pipes, assuming the pipe capability is large enough to accept all inflow from inlets [37]. The simulation domain has curb inlets connecting the road (impervious surface) and the RBS (Figure 2 and Figure 4). Normally, the runoff on the road flows through the curb inlet(s) into the RBS. Only under extreme conditions would the runoff in the RBS be able to flow back to the road, but the extreme conditions were not simulated in this study.

The grate-inlet flow-intercepting capacity (Q_gr, m³/s) from the 2D overland flow to the 1D drainage pipe flow is calculated using the weir Equation (7) [34] applied to the k cells within the grate inlet:

$$Q_{gr}={\displaystyle \sum }_{i=1}^k{k}_w\sqrt{2g}{L}_w{h}_{2D\left(i\right)}^{3/2}$$

(7)

where k_w (-) is the discharge coefficient of the weir flow = 0.368 [45]; g (m/s²) is the gravity acceleration; L_w (m) is the flow length (=cell size); h_2D(i) (m) is the overland-flow water depth for the ith cell; and k is the total number of the cells within the grate inlet. Each grate inlet in the simulation domain is considered to have an elevation difference (e.g., 5 cm lower) from the surrounding road cells.

The FullSWOF_2D program was previously tested and verified for overland flow on pervious surfaces [46]. In this study, FullSWOF-ZG was tested separately using two kinds of modeling cases: eight pervious surfaces under indoor simulated rainfall events and twenty curb inlets with local depression and inflow from upstream. The inlet geometry was represented by the detailed high-resolution digital elevation model (DEM). These testing cases are described below in detail separately.

2.2.1. Pervious Surface Modeling Cases

FullSWOF-ZG was validated using eight pervious surfaces under indoor simulated rainfall events as testing cases to demonstrate that it can be used to accurately simulate overland flow on pervious surfaces. The experiment was conducted at Texas A&M University to investigate the travel time and runoff characteristics of overland flow on pervious clay surfaces. The data from indoor tests consist of the discharge rate and surface runoff depth under a varying rainfall intensity and slope of the surface.

The tests were conducted on a steel-framed bed 1.83 m (6 ft) wide, 9.14 m (30 ft) long, and 0.36 m (14 in) deep. The test bed was filled with clay and compacted with a lawn roller and left outdoors for over a month for natural compaction. The experiments were conducted using a rainfall simulator with a maximum capacity of up to 114.3 mm/h (4.5 in/h). Two samplers equipped with bubbler flow modules were used to collect discharge depths and surface runoff depths near the outlet with 2.54 × 10⁻⁶ m (0.0001 in) resolution every minute. The discharge depth was measured with a 22.5° V-notch weir box. The rainfall intensity was monitored using an inline flowmeter connected to the rainfall simulator. The tipping bucket rain gauge was also used to double check the rainfall depth. The rainfall was stopped at 10 min after the peak discharge was attained and the discharge measurement was done until the runoff ceased. The slope of the test bed was 0.02%, 0.1%, 0.2%, 0.5%, and 1.04%. Different slopes for the overland flow were achieved by raising or lowering the steel-framed bed. Six rainfall events were tested for each slope, with a total of 30 events for the experiment.

Eight of the 30 rainfall events were chosen as the test cases in this study. Four test cases had a slope of 0.1%, three cases of 0.2%, and one case of 0.5%. The cell size in the x- and y-directions of the simulation domain was 0.15 m (0.5 ft). The Manning’s friction formula with n = 0.02 was selected among three friction formulas of FullSWOF-ZG. The Green-Ampt model was used to simulate the infiltration process of the experiment. The saturated hydraulic conductivity (K = 1.524 mm/h), moisture deficit (Δθ = 0.15), and suction head (φ = 0.208 m) parameters’ values were adopted in the simulation based on the field survey.

The goodness of fit for the simulated hydrograph was evaluated using the Nash-Sutcliffe efficiency (NSE) coefficient [47]:

$$NSE=1-\frac{{{\displaystyle \sum }}_{i=1}^m{\left(Q_{oi}-Q_{si}\right)}^2}{{{\displaystyle \sum }}_{i=1}^m{\left(Q_{oi}-\overline{Q}\right)}^2}$$

(8)

where Q_oi (m³/s) is the ith observed runoff rate, Q_si (m³/s) is the corresponding simulated runoff rate, $\overline{Q}$ (m³/s) is the mean observed runoff rate, and m (-) is the total number of observed runoff rates. The NSE values for eight rainfall events were calculated to evaluate the FullSWOF-ZG performance.

2.2.2. Curb Inlet Modeling Cases

Hammonds and Holley [36] performed a series of laboratory experiments of Texas type C and type D locally depressed curb inlets to quantify the interception efficiencies of these inlets under different longitudinal slopes, cross slopes, and upstream inflows. Only the type C curb inlet geometry (Figure 3) and monitored data were used in this study to evaluate the FullSWOF-ZG model.

According to the dimensions of the experimental facility, the length and width of the simulation domain were 15.55 m (51 ft, x-direction) and 4.57 m (15 ft, y-direction), respectively, and the curb inlet was 4.57 m (15 ft) long in total. The type C inlet included a 1.52 m (5 ft) opening and 1.52 m (5 ft) upstream and downstream transition sections that change elevation or depression gradually from the undepressed section into the fully depressed inlet section over the 1.52 m (5 ft) length. The total width of the curb inlet depression was 0.457 m (1.5 ft) with a depressed depth of 0.010 m (0.33 ft) and a depression width of 0.368 m (1.2 ft) for the type C inlet [30,48]. The simulation domain was represented by a detailed and high-resolution DEM (Figure 3b) with a cell size equal to 0.076 m (0.25 ft). The elevation of every computation cell was calculated by considering the longitudinal slope, cross slope, local depressed slope of the curb inlet, and slopes of the inlet’s upstream and downstream transition parts.

The Manning’s law among the three friction choices (Manning’s law, Darcy-Weisbach law, and Laminar law) in FullSWOF-ZG was used in the simulation, and the roughness coefficient determined for the laboratory roadway was 0.018, as reported by Hammonds and Holley [36]. The longitudinal (x-direction) and cross (y-direction) slopes for the simulation domain were from left to right and bottom to top, respectively (Figure 3).

The imposed discharge condition among five available boundary condition choices (imposed water height, wall condition, Neumann condition, periodic condition, and imposed discharge) in FullSWOF-ZG was chosen as the left or upstream boundary condition of the domain. The imposed discharge for the boundary cells within the spread (T) was approximately assumed as the total inflow rate (Q_i) divided by the number of the cells within the spread and was equal to 0 for other boundary cells outside of the spread. The top and right (downstream) boundary of the simulation domain were set as a Neumann condition that allows the flow to get out of the simulation domain. At the top of the simulation domain, those cells outside the curb inlet had higher elevations to prevent the outflow. The bottom boundary of the simulation domain (Figure 3b) had the highest elevation along the y-direction and was set as a wall boundary condition to guarantee that the flow would not pass through the bottom boundary.

2.3. Road-Bioretention Modeling Cases

Figure 4, as an example, shows the plan view and high-resolution DEM for the modeling case RBS04 (

Table 1. Parameter values of 20 modeling cases of the road-bioretention strip (RBS) systems with an undepressed curb inlet and grate inlets (Figure 4a).

Case No.	L	S0	Sx	Lci	Db	K	φ	Δθ	Vpc
	(m)	(-)	(-)	(m)	(m)	(mm/h)	(m)	(-)	(m3)
RBS01	40	0.001	0.010	1.20	0.25	51	0.090	0.410	7.44
RBS02	30	0.001	0.015	0.90	0.30	25	0.218	0.435	7.33
RBS03	20	0.001	0.020	0.60	0.35	13	0.478	0.451	6.08
RBS04	10	0.001	0.030	0.45	0.45	51	0.090	0.410	4.28
RBS05	40	0.003	0.015	1.20	0.25	51	0.090	0.410	5.68
RBS06	30	0.003	0.020	0.90	0.30	25	0.218	0.435	6.33
RBS07	20	0.003	0.030	0.60	0.35	13	0.478	0.451	5.62
RBS08	10	0.003	0.040	0.45	0.45	51	0.090	0.410	4.16
RBS09 1	40	0.005	0.020	1.20	0.25	51	0.090	0.410	3.93
RBS10	30	0.005	0.030	0.90	0.30	25	0.218	0.435	5.32
RBS11	20	0.005	0.040	0.60	0.35	13	0.478	0.451	5.16
RBS12	10	0.005	0.045	0.45	0.45	51	0.090	0.410	4.03
RBS13 1	40	0.007	0.030	1.20	0.25	51	0.090	0.410	2.79
RBS14	30	0.007	0.040	0.90	0.30	25	0.218	0.435	4.32
RBS15	20	0.007	0.045	0.60	0.35	13	0.478	0.451	4.71
RBS16	10	0.007	0.055	0.45	0.45	51	0.090	0.410	3.91
RBS17 1	40	0.010	0.040	1.20	0.25	51	0.090	0.410	1.93
RBS18 1	30	0.010	0.045	0.90	0.30	25	0.218	0.435	3.04
RBS19	20	0.010	0.055	0.60	0.35	13	0.478	0.451	4.02
RBS20	10	0.010	0.065	0.45	0.45	51	0.090	0.410	3.72

Note: ¹—for the modeling case, L × S₀ ≥ h_b Equation (9). L (m) is the length of the road and the RBS upstream of the curb inlet (Figure 4), L_ci (m) is the opening length of the curb inlet, h_b (m) is the overflow height of the grate inlet inside the RBS, and the bioretention depth, D_b = h_b + 0.05 m, K (mm/h) is the saturated hydraulic conductivity, φ (m) is the soil suction head, and Δθ is the soil moisture deficit, V_pc (m³) is the calculated bioretention ponding volume when overflow occurs.

) with an undepressed curb inlet. Figure 4a includes the different parts of the RBS system: The road with longitudinal and cross slopes, the RBS, a curb inlet, a grate inlet on the road, an overflow grate inlet and a berm at the end of the RBS, and the curb separating the road and RBS. The RBS performance of ponding and infiltrating the runoff is affected by the longitudinal slope (S₀), cross slope (S_x), curb inlet interception efficiency (E_ci), bioretention depth (D_b), overflow height (h_b), and the RBS’s soil infiltration parameters, such as the saturated hydraulic conductivity (K), suction head (φ), and moisture deficit (Δθ). Different modeling cases were established to explore the influence of these design parameters on the RBS performance. Even when the RBS was flat in the y-direction with a lower elevation (i.e., bioretention depth, D_b) than the road surface, the RBS had the same length and longitudinal slope, S₀, in the x-direction as the road did (Figure 4).

There was a grate inlet at the end of the RBS where the grate inlet opening was h_b above the RBS ground surface. The elevation difference between the grate inlet opening and the RBS ground surface is called the overflow height, h_b, ranging from 0.25 m (10 in) to 0.45 m (18 in) in this study (Table 1). In the USA, the initial concept of bioretention has a shallow ponding depth of 0.15 m (6 in), but recent green infrastructure design manuals allow for 0.30 m (12 in) to 0.45 m (18 in) of ponding depth [14]. Only when the water depths near the grate inlet are greater than h_b, will the runoff in RBS flow into the grate inlet then to the underground drainage pipe system. There is a berm at the end of the RBS (Figure 1 and Figure 4) to pond the runoff inside the RBS, which facilitates infiltration downward and possible overflow into the grate inlet. The berm height was set as the same as the bioretention depth, D_b, to prevent the longitudinal outflow from the RBS since D_b > h_b.

The simulation domain is divided into two zones by an imaginary dividing line (Figure 4a): The upstream or left of the line has uniform rainfall and the downstream or right of the line has no rainfall. A part of the runoff generated on the road surface is intercepted by the curb inlet (Q_ci in Figure 4), then, a part of the bypass runoff from the inlet is captured by the grate inlet on the road (Q_rg) and leaves the simulated road surface through the grate inlet. Finally, the remainder of the runoff is discharged downstream along the road (Q_bp). The runoff into the bioretention infiltrates downward or overflows through the bioretention grate inlet (Q_og) when the ponding depth is greater than h_b.

The bioretention ponding volume (V_pc) was calculated for each modeling case in this study when the overflow occurred, and did not consider the vegetation volume fraction of the bioretention facility. The impact of the longitudinal slope was included when calculating V_pc using the following Equation (9). The V_pc is calculated with two situations: (1) The ponding length is larger than the upstream catchment length, L ($L\times S_0<h_b$); and (2) the ponding length is equal to or smaller than the upstream catchment length ($L\times S_0\ge h_b$):

$$V_{pc}=\{\begin{array}{c}\left(L\times h_b-\frac{L^2\times S_0}{2}\right)\times w_b-h_b\times A_{gr} L\times S_0<h_b\\ \frac{h_b}{S_0}\times \frac{h_b}{2}\times w_b-h_b\times A_{gr} L\times S_0\ge h_b \end{array}$$

(9)

where V_pc (m³) is the calculated ponding volume based on the RBS geometry; w_b (m) is the RBS width (1 m); L (m) is the RBS length, which is the same as the road length; S₀ is the RBS’s longitudinal slope; h_b (m) is the RBS overflow height; and A_gr (m²) is the overflow grate inlet area.

Twenty cases of the RBS systems were modeled in this study by having four contributing-watershed lengths (10–40 m, 32.8–131.2 ft) and five longitudinal slopes (0.001–0.01) (Table 1). When the road length and longitudinal slope were increased, the cross slope and the curb-inlet length, L_ci, were increased also as real design situations for the curb inlet to intercept a similar amount of the runoff. When the contributing watershed was enlarged by increasing L, a longer L_ci allowed more runoff to flow into the RBS. Other corresponding RBS’s parameter values were changed correspondingly as shown/summarized in Table 1. The RBS system has eight key modeling parameters, and to fully understand the RBS system performance and the influence from each parameter, a large number of modeling cases is required, which was not studied here. For all 20 cases (Table 1), the roadway width was 10 m (y-direction, Figure 4) for a two-lane road, including necessary space for shoulders and gutters [49]. The curb width, which was the same as the curb-inlet width, was 0.1 m (4 in) to separate the road and the RBS. The RBS width was 1.0 m (40 in), and the maximum ponding depth or the bioretention depth, D_b, was set as 0.05 m above the grate-inlet overflow height, h_b, i.e., D_b = h_b + 0.05 m for all 20 modeling cases. The road grate inlet was a rectangle of 0.75 m (30 in, along with the x-direction) by 0.45 m (18 in) and was made to be 0.05 m (2 in) lower than the surrounding road-surface cells for the model simulation here. The grate inlet in the RBS was the same size for all modeling cases.

For the modeling case, RBS04 (Figure 4), the simulation domain length was 13 m (43 ft, x-direction), including 10 m (33 ft) of road surface before the inlet and a width of 10 m (33 ft), which was the curb-inlet runoff contributing watershed that received the rainfall (Figure 4). The computational cell/grid size for the simulation domain was 0.05 m (3 in) both in the x- and y- directions with a total of 57,200 cells for the case, RBS04. There was a total of 135 cells in each grate inlet [(0.75/0.05) × (0.45/0.05)] or k = 135 in Equation (7), and the curb inlet (L_ci = 0.45 m) was 18 cells [(0.45/0.05) × (0.1/0.05)] in the simulation domain of RBS04.

To compare the effect of different design parameters of the RBS systems, there were another 20 modeling cases (Rd01–Rd20) that had the same road surface without a curb inlet and RBS. Thus, all Rd modeling cases were the road only in the simulation domain. Each Rd modeling case was the same length (L), and longitudinal and cross slopes (S₀ and S_x) for the road surface as the corresponding RBS modeling case (Table 1).

All cell’s elevations were calculated when the bottom left corner reference cell’s elevation (the highest in the domain) was assumed to be 10 m as shown in Figure 4b. The road surface and bioretention ground elevations, therefore, vary with the longitudinal and cross slopes set for each modeling case (Table 1). All cells for the 0.1 m curb were set 0.2 m higher than the road surface cells. The cell’s elevations inside the curb inlet cells were calculated using the same cross slope of the road surface, which helps and allows the runoff to flow into the RBS. The uniform rainfall intensity was 6.94 × 10⁻⁵ m/s (250 mm/h, 10 in/h) and lasted 1200 s (20 min) to generate enough runoff reach the ponding volume, but the total simulation period was 2400 s. A portion (virtual road-surface in Figure 4a) of the simulation domain just downstream of the curb inlet was simulated without rainfall because the focus of the study was to investigate the impact of the runoff generated upstream of the curb inlet.

3. Results and Discussion

3.1. FullSWOF-ZG Testing Results

In a previous study [46], FullSWOF_2D was updated and tested with published rainfall-runoff data on pervious surfaces adopted from Esteves’s study [44]. It showed that the updated program provided consistent simulation results with observed data during the whole rainfall period. The details of the testing results for FullSWOF-ZG for pervious surfaces with data collected in Texas A&M University and type C curb inlet cases with data from the published report are introduced below.

3.1.1. Results for Pervious Surfaces

The comparison of observed and simulated discharge hydrographs of one pervious surface under four rainfall events is shown in Figure 5. The simulated hydrographs closely follow with the observed hydrographs for the sample results. The discharge NSE values ranged from 0.79 to 0.93 (

Table 2. Comparison of simulated and observed discharge and volume results for eight rainfall events.

Events	S0	NSE	Vr	Vob	Vsi	∆Vp	Qpo	Qps	∆Qp
	(-)	(-)	(m3)	(m3)	(m3)	(%)	(L/s)	(L/s)	(%)
S01R1	0.001	0.85	0.35	0.20	0.25	22.2	0.18	0.21	15.4
S01R2	0.001	0.93	0.32	0.20	0.21	4.9	0.18	0.19	5.4
S01R3	0.001	0.83	0.32	0.19	0.22	14.6	0.15	0.19	23.5
S01R4	0.001	0.92	0.20	0.13	0.11	−16.7	0.12	0.12	0.0
S02R5	0.002	0.83	0.21	0.12	0.12	0.0	0.12	0.15	22.2
S02R6	0.002	0.84	0.27	0.15	0.15	0.0	0.12	0.15	22.2
S02R7	0.002	0.79	0.25	0.16	0.14	−13.3	0.15	0.14	−6.9
S05R8	0.005	0.87	0.19	0.09	0.10	10.5	0.12	0.16	28.6

Note: S₀ (-) is the testing bed’s surface slope, V_r (m³) is the calculated rainfall volume, V_ob (m³) is the observed total runoff volume, V_si (m³) is the simulated total runoff volume, ∆V_p (%) is the percent difference of the simulated runoff volume = (V_si − V_ob)/[(V_ob + V_si)/2] × 100%, Q_po (L/s) is the observed peak runoff rate, Q_ps (L/s) is the simulated peak runoff rate, ∆Q_p (%) is the percent difference of the simulated peak discharge = (Q_ps − Q_po)/[(Q_po + Q_ps)/2] × 100%.

, average ± standard deviation as 0.86 ± 0.05) for three pervious surfaces (slopes) under eight rainfall events. Table 2 also presents the comparison results of the simulated and observed runoff volume and peak discharges. The percent differences of the simulated runoff volume and peak discharges were 2.8 ± 13.3% (average ± standard deviation) and 13.8 ± 12.8%, respectively. Figure 5a is the case with the highest runoff-volume percent difference and Figure 5c is the case with the second highest peak-discharge percent difference. The indoor testing bed was 0.36 m deep, which was much larger than the cumulative infiltration depth during the experiment. The indoor testing bed was deep and provided enough soil space for the infiltrated runoff. The results for all eight rainfall events (Table 2 and Figure 5) show that the FullSWOF-ZG program predicted the rainfall–runoff process of overland flows on a pervious surface with reasonable accuracy.

3.1.2. Results of Curb Inlet Interception

Twenty modeling cases for the type C inlet on the road surfaces (

Table 3. Curb inlet test cases’ setting parameters and simulation results.

Case No.	S0	Sx	T	Qin	Qcio	Ecio	Qcis	Ecis	∆E	PDE
	(-)	(-)	(m)	(m3/s)	(m3/s)	(%)	(m3/s)	(%)	(%)	(%)
C01	0.004	0.0208 (1:48)	4.27	0.2400	0.1256	52.3	0.1306	54.4	2.1	3.9
C02	0.004	0.0208	4.27	0.1076	0.0829	77.0	0.0872	81.0	4.0	5.0
C03	0.010	0.0208	4.27	0.2361	0.1098	46.5	0.1185	50.2	3.7	7.7
C04	0.010	0.0208	4.27	0.1806	0.0983	54.4	0.1047	58.0	3.5	6.3
C05	0.020	0.0208	3.45	0.1246	0.0741	59.5	0.0793	63.6	4.2	6.8
C06	0.020	0.0208	4.27	0.2424	0.0979	40.4	0.1139	47.0	6.6	15.1
C07	0.040	0.0208	4.07	0.1281	0.0698	54.5	0.0734	57.3	2.8	5.1
C08	0.040	0.0208	4.07	0.1589	0.0762	48.0	0.0823	51.8	3.8	7.7
C09	0.060	0.0208	4.07	0.1166	0.0653	56.0	0.0615	52.8	−3.2	−6.0
C10	0.060	0.0208	4.27	0.2451	0.0853	34.8	0.0896	36.6	1.8	4.9
C11	0.004	0.0417 (1:24)	3.87	0.2316	0.1488	64.2	0.1539	66.4	2.2	3.4
C12	0.004	0.0417	3.21	0.1439	0.1182	82.1	0.1194	83.0	0.8	1.0
C13	0.010	0.0417	2.84	0.1433	0.1133	79.1	0.1145	79.9	0.9	1.1
C14	0.010	0.0417	3.37	0.2320	0.1369	59.0	0.1436	61.9	2.9	4.8
C15	0.020	0.0417	2.97	0.2433	0.1215	49.9	0.1359	55.9	5.9	11.2
C16	0.020	0.0417	2.28	0.1031	0.0870	84.4	0.0886	86.0	1.6	1.9
C17	0.050	0.0417	2.16	0.1724	0.0874	50.7	0.0983	57.0	6.3	11.7
C18	0.050	0.0417	3.09	0.2381	0.0940	39.5	0.1255	52.7	13.2	28.7
C19	0.070	0.0208	4.07	0.1542	0.0700	45.4	0.0682	44.2	−1.2	−2.6
C20	0.070	0.0417	3.05	0.1535	0.0803	52.3	0.0927	60.4	8.1	14.3

Note: S₀ (-) is the road longitudinal slope, S_x (-) is the road cross slope, T (m) is the upstream flow spread width, Q_in (m³/s) is the upstream inflow rate, Q_cio (m³/s) is the observed curb inlet intercepted flow rate, E_cio (%) is the observed curb inlet intercepted efficiency, Q_cis (m³/s) is the simulated curb inlet intercepted flow rate, E_cis (%) is the simulated curb inlet intercepted efficiency, ∆E (%) is the difference of the simulated intercepted efficiency = E_cis − E_cio, PD_E (%) is the percent difference of the simulated intercepted efficiency = (E_cis − E_cio)/[(E_cis + E_cio)/2] × 100%.

) covered six longitudinal slopes (0.004–0.07), two cross slopes (0.0208 and 0.0407), and 12 spreads (2.16–4.27 m), and 20 upstream inflows (Q_in 0.1031–0.2453 m³/s). All these model input parameter values were exactly the same as the experimental setup information [36,48]. The curb inlet interception efficiency (E_ci) was evaluated with the curb intercepted flow rate (observed Q_cio or simulated Q_cis) divided by the upstream inflow rate (Q_in) after the system reached equilibrium.

Table 3 shows that the simulated intercepted flows and inlet efficiencies of type C curb inlets on the road surfaces with different longitudinal and cross slopes have great consistency with the observed results from the laboratory experiments conducted by Hammonds and Holley [36]. The coefficient of determination (R²) of the linear relationship between the simulated and observed curb inlet interception efficiencies was 0.94. The high R² value with lower differences (∆E) is evidence to support that the FullSWOF-ZG model, which predicted the curb inlet interception efficiency with good performance.

The differences of the simulated and observed interception efficiencies (∆E) ranged from −3.2% to 13.2%, with an average ± standard deviation of 3.5 ± 3.5%. The percent differences (PD_E) of the simulated and observed intercepted efficiencies ranged from −6.0% to 28.7%, with an average ± standard deviation of 6.6 ± 7.3%. In a previous study by Fang et al. [48], a three-dimensional fluid simulation software, FLOW-3D, was applied to simulate complex 3D shallow flow over the drainage pavement and flow leaving through type C and type D inlets. The differences (∆E) ranged from −7.0% to 17.6%, with an average ± standard deviation of 1.0 ± 4.87% for type C cases in their 3D simulations. The percent differences (PD_E) for Fang’s study ranged from −19.7% to 6.1%, with an average ± standard deviation of −0.8 ± 5.7%. These 2D SWEs models using the FullSWOF-ZG program were almost as good as the FLOW-3D models used in the previous study when trying to simulate the interception efficiency of the type C curb inlet under different operation conditions. The results for all 20 modeling cases (Table 3) showed that the FullSWOF-ZG program was not only able to simulate the complicated flow over type C curb inlets, but also predicted the curb inlet interception efficiency well.

3.2. Results of Rd and RBS Modeling Cases

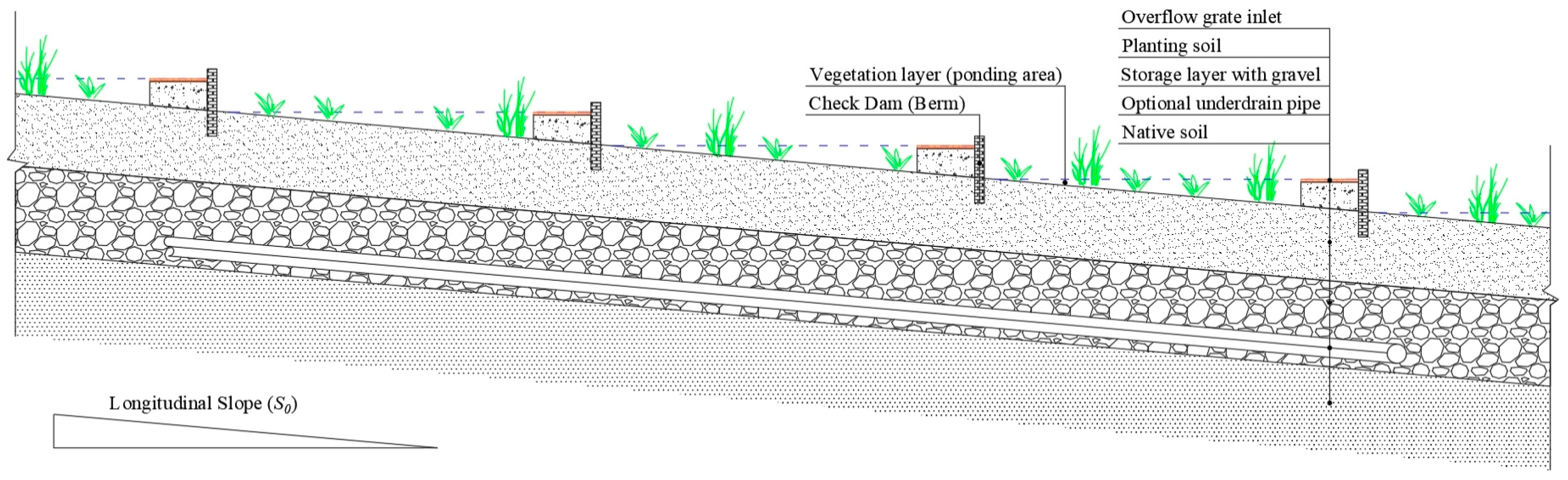
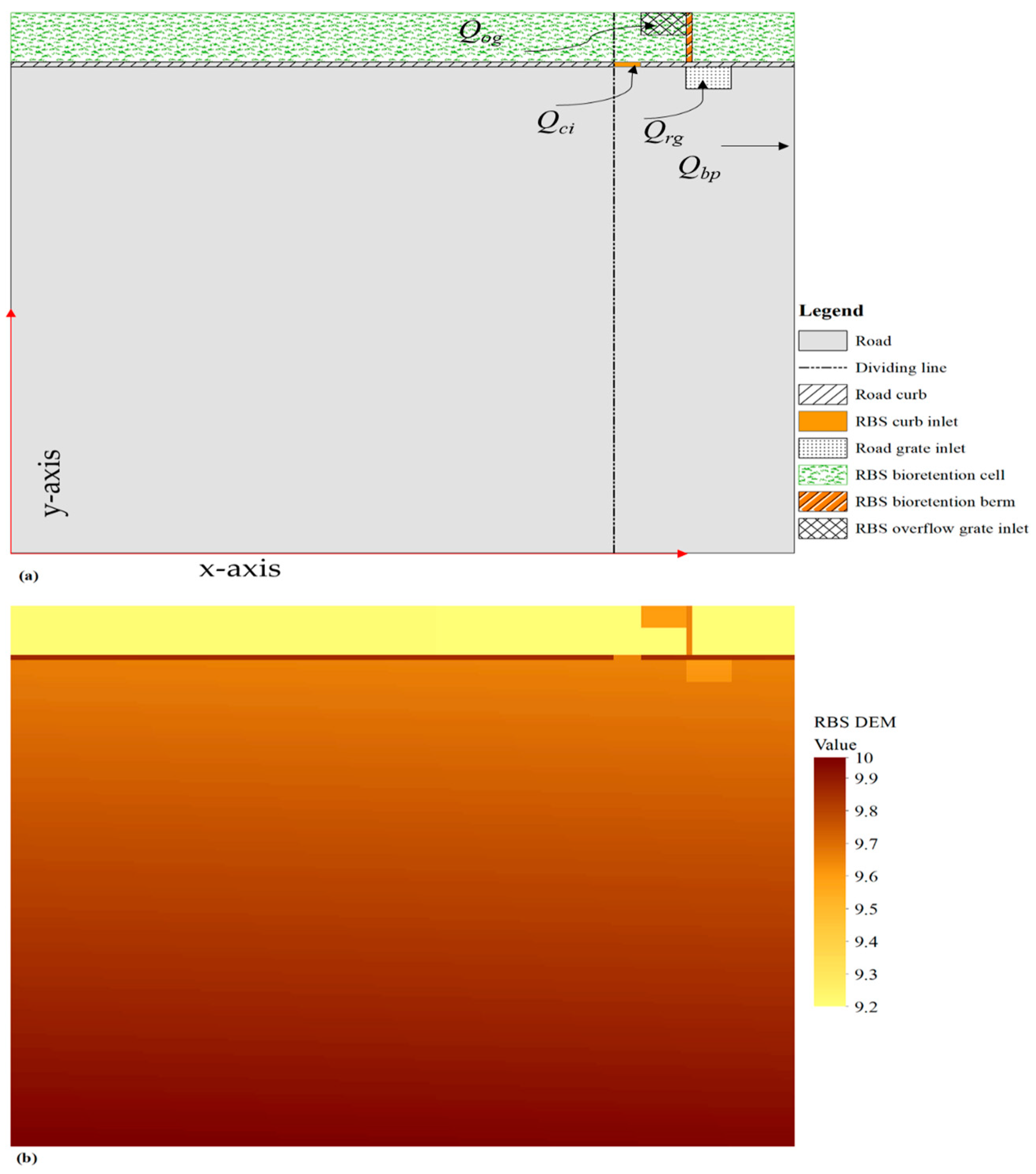
3.2.1. Example Modeling Results

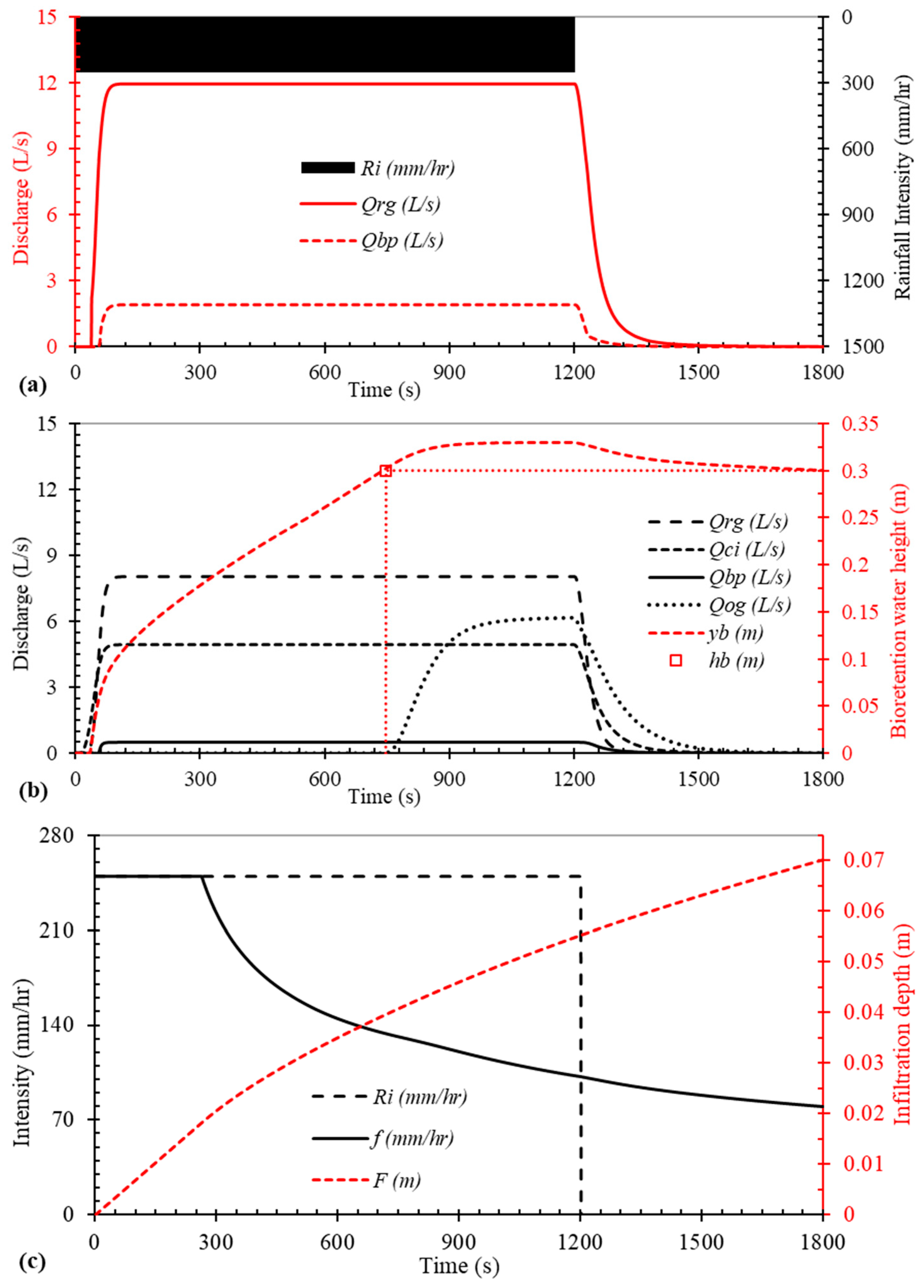
As an example of modeling results for the RBS systems, the performance of the case, RBS19, was first evaluated and compared with the modeling case, Rd19, that has no curb inlet. Figure 6 shows the simulated hydrographs for the Rd19 and RBS19 cases, the ponding depth in the RBS, infiltration rate, and cumulative infiltration depth for the RBS19 case (Table 1). A summary of the results for all modeling cases for the road-only and the RBS is given in

Table 4. Summary of simulation results of 20 road-only modeling cases (grouped by L).

Case No.	Vrd	Vsrd	∆Vrd	Vrg	Prg	Vbp	Pbp	Qprg	Qpbp
	(m3)	(m3)	(%)	(m3)	(%)	(m3)	(%)	(L/s)	(L/s)
Rd04 (10 m) 1	8.33	8.24	−1.02	8.10	98.3	0.14	1.7	6.81	0.13
Rd08	8.33	8.30	−0.34	8.16	98.3	0.14	1.7	6.82	0.12
Rd12	8.33	8.31	−0.21	8.06	97.0	0.25	3.0	6.74	0.20
Rd16	8.33	8.31	−0.17	7.92	95.3	0.39	4.7	6.62	0.32
Rd20	8.33	8.31	−0.18	7.67	92.3	0.64	7.7	6.42	0.52
Rd03 (20 m)	16.66	16.45	−1.25	14.85	90.3	1.60	9.7	12.43	1.45
Rd07	16.66	16.60	−0.33	13.10	78.9	3.50	21.1	10.80	3.08
Rd11	16.66	16.63	−0.17	13.81	83.0	2.82	17.0	11.43	2.45
Rd15	16.66	16.63	−0.13	14.05	84.5	2.58	15.5	11.66	2.22
Rd19	16.66	16.64	−0.11	14.39	86.5	2.25	13.5	11.97	1.91
Rd02 (30 m)	24.98	24.49	−2.00	21.52	87.9	2.97	12.1	18.01	2.81
Rd06	24.98	24.84	−0.58	19.98	80.4	4.86	19.6	16.55	4.27
Rd10	24.98	24.92	−0.24	17.00	68.2	7.93	31.8	13.94	6.88
Rd14	24.98	24.95	−0.13	18.50	74.1	6.45	25.9	15.25	5.57
Rd18	24.98	24.96	−0.10	19.18	76.8	5.78	23.2	15.86	4.96
Rd01 (40 m)	33.31	32.22	−3.28	22.85	70.9	9.37	29.1	19.02	8.73
Rd05	33.31	33.02	−0.88	21.87	66.2	11.15	33.8	17.97	9.79
Rd09	33.31	33.16	−0.44	17.71	53.4	15.45	46.6	14.38	13.38
Rd13	33.31	33.24	−0.22	20.61	62.0	12.62	38.0	16.87	10.89
Rd17	33.31	33.27	−0.13	22.96	69.0	10.31	31.0	18.89	8.87

Note: ¹—the road length, L, is given in brackets and there is the same length for other modeling cases in the same group, V_rd (m³) is the total rainfall volume fell on the road surface, V_rg (m³) is the runoff volume captured by the road grate inlet, V_bp (m³) is the bypass runoff volume (to the road downstream), P_rg (%) is the percent of runoff captured by the grate inlet = V_rg/(V_rg + V_bp) = V_rg/V_srd, P_bp (%) is the percent of the bypass runoff = V_bp/V_srd, ∆V_rd (%) is the percent difference of the simulated runoff volume = (V_srd − V_rd)/V_rd × 100%, Q_prg (L/s) is the peak discharge of the runoff captured by the road grade inlet, Q_pbp (L/s) is the peak discharge of the bypass runoff.

and

Table 5. Simulation results of road-bioretention cases (grouped by L).

Case No.	Vci	Pci	Vrg	Prg	Vbp	Pbp	Vrb	Vinf	Vbog	Vbio	∆V	∆Vrd	∆Vrb
	(m3)	(%)	(m3)	(%)	(m3)	(%)	(m3)	(m3)	(m3)	(m3)	(%)	(%)	(%)
RBS04 (10 m) 1	3.30	40.8	4.76	58.9	0.02	0.3	0.83	1.24	0.00	3.13	0.0	−2.9	5.8
RBS08	3.33	41.2	4.64	57.5	0.10	1.3	0.83	1.25	0.00	3.16	0.0	−3.0	5.9
RBS12	3.22	39.9	4.62	57.2	0.23	2.9	0.83	1.24	0.00	3.06	0.0	−3.0	6.1
RBS16	3.27	40.5	4.42	54.7	0.39	4.8	0.83	1.25	0.00	3.10	0.0	−3.0	5.9
RBS20	3.21	39.8	4.22	52.3	0.64	8.0	0.83	1.24	0.00	3.05	0.0	−3.0	6.0
RBS03 (20 m)	5.61	34.6	10.00	61.7	0.60	3.7	1.67	1.63	0.26	5.83	0.0	−2.7	6.1
RBS07	5.85	36.1	9.89	61.1	0.44	2.7	1.67	1.63	1.03	5.33	0.0	−2.8	6.3
RBS11	6.09	37.7	9.76	60.4	0.32	2.0	1.67	1.62	1.73	4.89	0.0	−2.9	6.3
RBS15	5.99	37.1	9.76	60.4	0.41	2.6	1.67	1.61	2.09	4.45	0.0	−3.0	6.4
RBS19	6.04	37.4	9.50	58.8	0.61	3.8	1.67	1.58	2.82	3.80	0.0	−3.0	6.5
RBS02 (30 m)	9.24	38.0	14.28	58.7	0.80	3.3	2.50	2.70	2.66	7.03	0.0	−2.6	5.5
RBS06	9.13	37.5	13.61	56.0	1.59	6.5	2.50	2.65	3.72	5.91	0.0	−2.6	5.6
RBS10	10.05	41.4	12.57	51.7	1.68	6.9	2.50	2.60	5.69	4.94	0.0	−2.7	5.4
RBS14	10.78	44.4	12.59	51.8	0.92	3.8	2.50	2.54	7.45	3.98	0.0	−2.8	5.2
RBS18	10.49	43.2	12.89	53.1	0.89	3.7	2.50	2.30	8.60	2.80	0.0	−2.8	5.4
RBS01 (40 m)	12.18	37.5	16.87	52.0	3.40	10.5	3.33	4.28	5.01	7.06	−0.1	−2.6	5.4
RBS05	12.47	38.4	15.81	48.7	4.19	12.9	3.33	4.12	7.45	5.07	0.0	−2.5	5.2
RBS09	12.96	39.9	15.64	48.2	3.87	11.9	3.33	3.85	9.85	3.43	0.0	−2.5	5.1
RBS13	14.75	45.4	14.34	44.2	3.37	10.4	3.33	3.42	13.09	2.42	0.0	−2.6	4.7
RBS17	15.72	48.4	14.67	45.2	2.06	6.3	3.33	3.09	15.14	1.68	0.0	−2.6	4.5

Note: ¹—the road length, L, is given in brackets and there is the same length for other modeling cases in the same group, V_ci (m³) is the runoff volume intercepted by the curb inlet, V_rg (m³) is the runoff volume captured by the road grate inlet, V_bp (m³) is the bypass runoff volume, P_ci (%) is the percentage of the total runoff volume that is intercepted by the curb inlet (V_ci/V_rd), P_rg (%) is the road grate inlet captured runoff percentage, P_bp (%) is the road end bypass runoff percentage, V_rb (m³) is the runoff generated on the bioretention surface from the rainfall, V_inf (m³) is the bioretention infiltrated runoff volume, V_bog (m³) is the bioretention overflow grate inlet discharge volume, V_bio (m³) is the runoff ponded in bioretention at the end of the simulation, ∆V (%) is the runoff volume percent difference of the whole simulation domain = (V_rg + V_bp + V_inf + V_bog + V_bio − V_rd − V_rb)/(V_rd + V_rb) × 100%, ∆V_rd (%) is the runoff volume percent difference of the road surface = (V_ci + V_bp + V_rg − V_rd)/V_rd × 100%, ∆V_rb (%) is the runoff volume percent difference of the bioretention cell = (V_inf + V_bog + V_bio − V_ci − V_rb)/(V_ci + V_rb) × 100%, P_inf (%) is the infiltrated runoff percentage = V_inf/(V_ci + V_rb) × 100%.

, respectively. Figure 6a shows the rainfall intensity over 20 min, hydrographs of the bypass flow (Q_bp), and the flow into the road grate inlet (Q_rg) of the 30 min simulation period. The runoff generated from the road surface took 32 s to reach the grate inlet, the discharge into the grate inlet then increased rapidly to a 98% peak in 85 s, and reached the equilibrium discharge of 11.96 L/s at 180 s under the constant rainfall. The grate inlet discharge took about 300 s to decrease to 0 L/s after the rainfall stopped. The rest part of the overland runoff that was not captured by the grate inlet discharges to the downstream as the bypass flow, which had a peak discharge of 1.91 L/s at 91 s. The sum of the peak flows of Q_rg and Q_bp was 13.87 L/s, which was the same as the peak discharge from the rational formula.

In comparison, Figure 6b shows simulated hydrographs for Q_rg, Q_bp, the curb inlet intercepted flow (Q_ci), and the overflow from the grate inlet in bioretention (Q_og) as well as the bioretention water depth (y_b) of the modeling case, RBS19. The peak or equilibrium discharges of Q_rg, Q_ci, and Q_bp were 8.03 L/s, 4.94 L/s, and 0.50 L/s, respectively. The flow interception by the curb inlet seemed to slow down the flow a little bit to make more runoff into the grate inlet. Therefore, the sum of the peak Q_rg and Q_ci for RBS 19 was 12.97 L/s, which was larger than the Q_rg of 11.96 L/s for the Rd19 case.

Under a rainfall event, the interception efficiency, E_ci, of a curb inlet is not constant, but changes with time. For RBS19, the runoff first reached the curb inlet at 11 s, and E_ci was 100% when the runoff rate was small at 11 s < t < 31 s, then E_ci decreased with time and became 36.7% when Q_ci reached the equilibrium discharge. At the end of the 40-min simulation, the runoff volume, intercepted by the curb inlet and generated from the road, can be computed and the volumetric interception efficiency was computed as 37.4% for the RBS19 case, which will be further discussed later using Table 5. Therefore, for RBS19, the grate inlet on the road still intercepted a large percent (~60%) of the incoming runoff and only about 2.6% of the runoff volume was bypassed downstream. This is important information to the road and bioretention design since many designers think the curb inlet can intercept all runoff and adding or keeping the grate inlet on the road is not necessary. Figure 6 also shows that the geometry of the experiment and the model allowed for a fully developed flow by the time the flow reached the inlet. This was true for all modeling cases.

Under 250 mm/h rainfall over 20 min, the bioretention overflow Q_og started at 748 s, reached the peak discharge of 6.16 L/s (at 1200s), and decreased after the rainfall stopped (Figure 6b). The red dash line in Figure 6b shows that the ponding depth (y_b) adjacent to the bioretention overflow grate inlet increased to become higher than the bioretention overflow height (h_b = 0.3 m) at 748 s and decreased to 0.3 m slowly after the rainfall stopped. There was a time period when Q_og was larger than Q_ci, which seemed impossible in the first impression. This was because the grate inlet discharge capacity was usually higher than the curb inlet capacity. In this study, the corresponding overflow weir length of the grate inlet [2 × (0.45 + 0.75) m] was much larger than the curb inlet opening (0.6 m) and the hydraulic head above the grate inlet could be larger also. It was verified that the mass conservation of the runoff in the simulation domain was valid (Figure 6) and the simulated larger Q_og was correct.

Figure 6c shows the bioretention infiltration rate (f) and cumulative infiltration (F) over time. The infiltration rate was calculated using the Green-Ampt method in FullSWOF-ZG, which considers the soil infiltration parameters, runoff ponding depth, and rainfall intensity (R_i) at every time step. The bioretention infiltration rate was equal to the rainfall intensity, R_i, when the calculated soil infiltration capacity was larger than R_i. The infiltration rate started to decrease at 263 s and decreased to 80.1 mm/h at the end of the simulation. The cumulative infiltration, F, kept increasing during the simulation period and reached 0.07 m at 30 min, which seemed small, but the infiltration continued at ~80 mm/h to gradually deplete all ponding water in the bioretention cell. The heavy rainfall (250 mm/h) over 20 min was used for the simulation in order to generate the overflow in the grate inlet at the RBS so that FullSWOF-ZG was fully tested.

3.2.2. Modeling Results for Road-Only (Rd) Cases

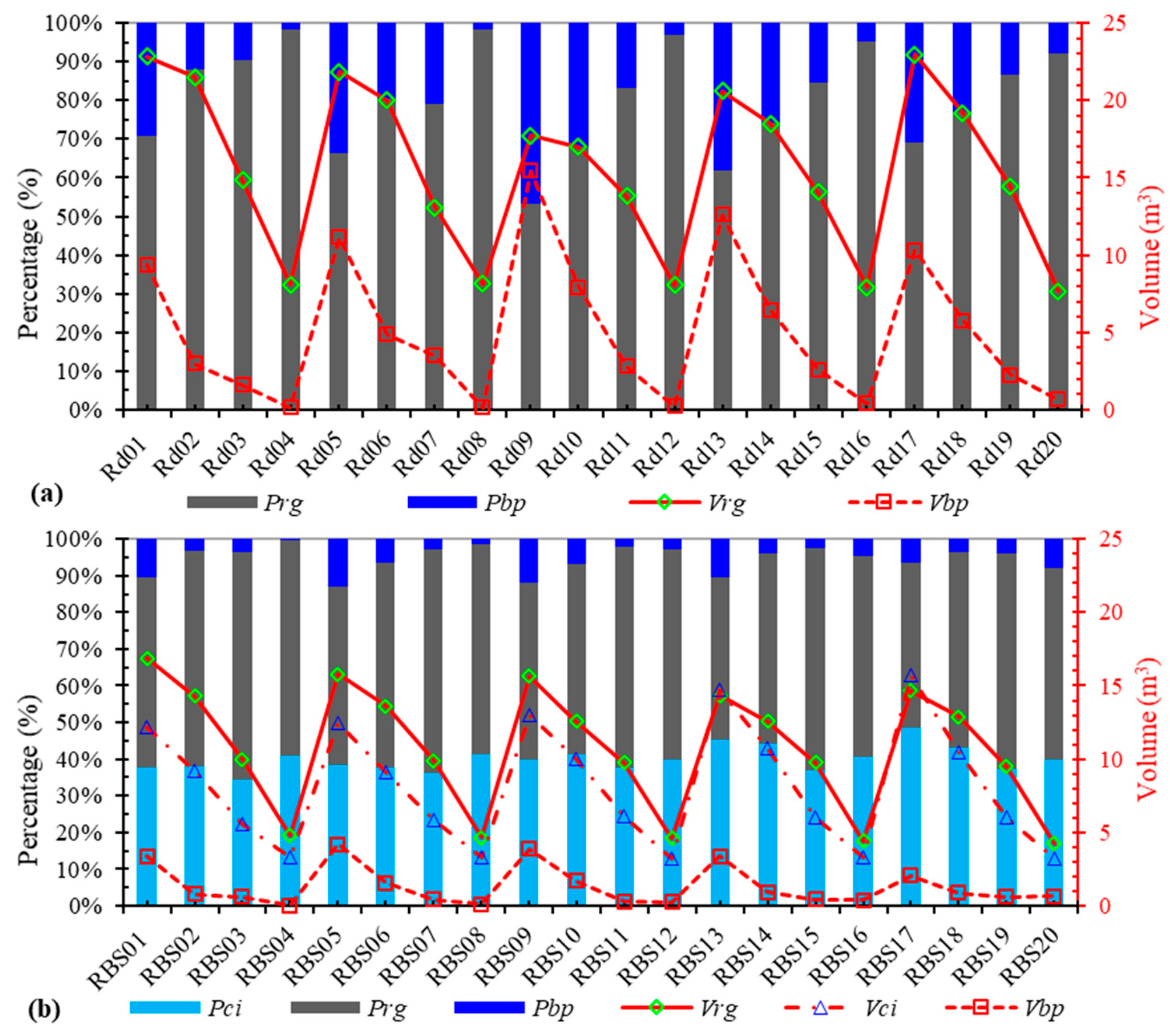
Modeling results for 20 road-only cases are first presented in Figure 7a and summarized in Table 4 to compare them with modeling results for the road-bioretention cases (Figure 7b, Table 5 and

Table 6. Mean and standard deviation (numbers inside brackets) of parameters calculated from each of the five road-bioretention cases with the same L (10 m–40 m).

Length (L)	Vci	Pci	Vrg	Prg	Vbp	Pbp	Vrb	Vinf	Vbog	Vbio
	(m3)	(%)	(m3)	(%)	(m3)	(%)	(m3)	(m3)	(m3)	(m3)
10 m RBS 1	3.27	40.5	4.53	56.1	0.28	3.4	0.83	1.24	0.00	3.10
	(0.05)	(0.6)	(0.21)	(2.6)	(0.25)	(3.1)	(0.00)	(0.00)	(0.00)	(0.05)
20 m RBS 2	5.91	36.6	9.78	60.5	0.48	2.95	1.67	1.61	1.59	4.86
	(0.19)	(1.2)	(0.18)	(1.1)	(0.12)	(0.8)	(0.00)	(0.02)	(0.98)	(0.78)
30 m RBS 3	9.94	40.9	13.19	54.3	1.17	4.8	2.50	2.56	5.62	4.93
	(0.74)	(3.07)	(0.74)	(3.0)	(0.42)	(1.7)	(0.00)	(0.16)	(2.48)	(1.65)
40 m RBS 4	13.62	42.0	15.46	47.6	3.38	10.4	3.33	3.75	10.11	3.93
	(1.54)	(4.76)	(1.00)	(3.1)	(0.81)	(2.5)	(0.00)	(0.50)	(4.10)	(2.16)

Note: ¹ for RBS04, 08, 12, 16, and 20; ² for RBS03, 07, 11, 15, and 19; ³ for RBS02, 06, 10, 14, and 18; and ⁴ for RBS01, 05, 09, 13, and 17.

) in the next section. For the road-only cases, the rainfall volume, V_rd, was transformed into the runoff volume captured by the road grate inlet (V_rg) and the bypass runoff volume (V_bp). The percent differences (∆V_rd) between the simulated runoff volume, V_srd = V_rg + V_bp, and the rainfall volume V_rd for 20 road-only cases ranged from −3.3% to 0.1%. The average ± standard deviation of ∆V_rd was −0.6 ± 0.8% for 20 road-only cases (Table 4), which indicated FullSWOF-ZG had a higher accuracy in mass balance. These 20 modeling cases were regrouped into five groups (by alternating two colors in Table 4): The road length L decreased from 40 m to 10 m as the modeling case number increased when S₀ is the same in each group (Table 1). Since the same rainfall was used for all modeling cases, all runoff volumes decreased with the decrease of the road length (Table 4), e.g., V_rg decreased from 22.96 m³ (Rd17, L = 40 m) to 7.67 m³ (Rd20, L = 10 m); and the corresponding V_bp decreased from 10.31 m³ to 0.64 m³. Because of the volume decrease or less flow velocity due to less L, the percent of V_rg (P_rg = V_rg/V_srd) increased with the additional influence of the increase of the cross slope, e.g., Rd01–Rd04 from 70.9% to 98.3% (Figure 7a). The percent of V_rg ranged from 53.4% (Rd09, S_x = 2%) to 98.3% (Rd08, S_x = 4%), with an average ± standard deviation of 80.7 ± 21.5%. The percent of V_bp (P_bp = V_bp/V_srd) ranged from 1.7% (Rd08) to 46.6% (Rd09), with an average ± standard deviation of 19.3 ± 13.0%. The relatively large variations of P_rg and P_bp were due to the change of the road length or upstream inflow.

If sorting the modeling cases by the road length, L (Table 4), the average P_rg for the same L cases decreased from 96.2% to 64.3% for L increases from 10 to 40 m, but the standard deviation from the mean increased from 2.5% to 7.0%. Therefore, L had more influence on P_rg than S₀ did. When L was smaller, the incoming runoff from the upstream road was small, more runoff as intercepted by the grate inlet, and less runoff was bypassed downstream. Only 20 individual road-only cases (4 L × 5 S₀) were modeled here; when S₀ was increased, the cross slope, S_x, was also increased to allow and guide more runoff to the grate inlet. S_x ranged from 3.0%–6.5% at L = 10 m to 1.0%–4.0% at L = 40 m (Table 1). For Rd09, both V_bp and P_bp were the highest and indicated a high potential of the local flooding on the road. For all road-only cases, the peak discharges of the grate inlet (Q_prg) were 6.68 ± 0.17 L/s for the L = 10 m group, 11.66 ± 0.61 L/s for the L = 20 m group, 15.92 ± 1.51 L/s for the L = 30 m group, and 17.43 ± 1.91 L/s for the L = 40 m group. The peak discharges of the bypass flow (Q_pbp) were 0.26 ± 0.17 L/s for the L = 10 m group, 2.22 ± 0.61 L/s for the L = 20 m group, 4.90 ± 1.51 L/s for the L = 30 m group, and 10.33 ± 1.91 L/s for the L = 40 m group. Both Q_prg and Q_pbp increased with the increase of the catchment length.

3.2.3. Modeling Results for Road-Bioretention Strip (RBS) Cases

1. Mass Balance on the Road with a Curb Inlet

First, we studied the mass (i.e., runoff volume) balance or redistribution on the road with a curb inlet for the RBS, which was compared with the road-only cases. Results are summarized in columns 2 to 7 in Table 5 and plotted on Figure 7b. For the corresponding 20 bioretention modeling cases (Figure 7b), a part of the road runoff (V_srd) was intercepted by the curb inlet (V_ci), resulting in a reduction of the runoff incepted by the road grate inlet (V_rg) and bypass runoff (V_bp). For the 20 RBS cases (Table 5), V_ci increased from 3.27 ± 0.05 m³ (L = 10 m) to 13.6 ± 1.54 m³ (L = 40 m) (Table 6), but the percentage (P_ci = V_ci/V_srd = V_ci/(V_ci + V_rg + V_bp)) of runoff volume intercepted by the curb inlet (or curb inlet efficiency by volume) was similar: 40.0 ± 3.3%. This was because the curb inlet length, L_ci, was also increased from 0.45 m to 1.2 m for L = 10–40 m. The corresponding runoff volume (V_rg) captured by the road grate inlet increased from 4.53 ± 0.21 m³ (L = 10 m) to 15.46 ± 1.00 m³ (L = 40 m); the bypass runoff volume (V_bp) from 0.28 ± 0.25 m³ to 3.38 ± 0.81 m³. The percentage of the runoff captured by the grate inlet on the road (P_rg = V_rg/V_srd) decreased from 56.1 ± 2.6% (L = 10 m) to 47.6 ± 3.1% (L = 40 m), with an overall average ± standard deviation of 54.6 ± 5.2%. Due to the curb inlet interception, each RBS system diverted a part of the runoff from the impervious road to the bioretention strip for infiltration and treatment (e.g., to allow sediments to settle and improve water quality), therefore, less runoff flowed into the grate inlet on the road, and then the P_rg for the RBS (Table 5) was always smaller than for the corresponding road-only case (Table 4). The differences of P_rg between the road-only and corresponding RBS modeling cases ranged from 5.2%–40.8%, with an average difference of 26.0 ± 9.6%.

For all RBS cases under 250 mm/h rainfall, the road surface runoff was not be 100% intercepted by the curb inlet, which indicated that the curb inlet was the bottleneck of the RBS system and impeded the runoff flowing into the bioretention strip for detention and infiltration to improve the stormwater quality. Therefore, the grate inlet was necessary to capture the road surface runoff and discharge into an underground drainage pipe to relieve road local flood inundation and ensure traffic safety. The bypass runoff percentage, P_bp, for the RBS cases (Figure 7 and Table 5) ranged from 0.3% (RBS04) to 12.9% (RBS05), with an average ± standard deviation of 5.4 ± 3.6%. The V_bp and P_bp for all RBS cases (Table 5) were lower than them for the corresponding road-only cases (Table 4), which means the curb inlet and grate inlet combination was more efficient than the grate inlet only for intercepting the road surface runoff. The mass balance as percent differences of the whole simulation domain (∆V), on the road (∆V_rd) and in the bioretention strip (∆V_rb), were small (Table 5).

2. Mass Balance in the Bioretention Strip

The mass (i.e., runoff volume) balance or redistribution in the bioretention strip are summarized in columns 8 to 11 in Table 5. For RBS systems, the inflow to the bioretention strip included the runoff intercepted by the curb inlet (V_ci) and generated on the bioretention surface from rainfall (V_rb). The bioretention outflow included the infiltration (V_inf) and the overflow through the grate inlet near the check dam (Figure 1, V_bog in Table 5). The difference between the inflow and the outflow was the ponding volume (V_bio) in the bioretention strip. V_rb was the rainfall depth (250 mm/h × 20 min) times the area (L × 1 m) of the bioretention strip and linearly increased from 0.83 m³ to 3.33 m³ for L = 10 m to 40 m.

The cumulative infiltration volume of bioretention (V_inf) was calculated (Table 5) and the mean V_inf ranged from 1.24 m³ for the L = 10 m group to 3.75 m³ for the L = 40 m group over 40 min simulation periods. To understand the soil infiltration performance of the bioretention, loamy sand was used for the L of 10 m and 40 m cases, sandy loam for L of 20 m cases, and loam for L of 30 m cases. The average and standard deviation of the infiltrated runoff percentage, i.e., V_inf/(V_ci + V_rb), were 30.4 ± 0.3% for loamy sand (L = 10 m group), 21.3 ± 0.8% for sandy loam (L = 20 m group), 20.7 ± 6.5% for loam (L = 30 m group), and 22.5 ± 8.5% for loamy sand (L = 40 m group).

The infiltration in the bioretention cell is influenced by the runoff inflow, the soil infiltration capacity, and the ponding depth as FullSWOF_2D considers the water depth when applying the Green-Ampt method [32]. Under small rainfall intensity and higher infiltration rate, it was possible for all runoff to infiltrate downward and the bioretention cell did not have any ponding. The infiltrated runoff volume, V_inf, decreased from RBS01 (4.28 m³) to RBS17 (3.09 m³, Table 5, L = 40 m group), mainly because the smaller longitudinal slope, S₀, increased the ponding area, since h_b and the infiltration parameters were the same for these five modeling cases. For RBS01, RBS05, and RBS09, L × S₀ ≤ h_b, so that the maximum ponding area was 40 m × 1 m (width of the bioretention strip); for RBS13 and RBS17, L × S₀ > h_b, so that the maximum ponding area was less than 40 m × 1 m (only covered 28.6 m and 20 m, respectively).

There was no overflow through the grate inlet in the bioretention strip for the modeling cases of L = 10 m (V_bog = 0) because the overflow height of the grate inlet (h_b) was the largest (0.4 m, D_b—0.05 in Table 1), but the maximum ponding depth (h_max,

Table 7. Mean and standard deviation (numbers inside brackets) of additional simulation results calculated from each of the five road-bioretention cases with the same L (10–40 m).

Length (L)	hmax	Tbog	Qpog	Vpc	Vbio(40)/Vpc	Qprgb	Qprgb/Qprg
	(m)	(s)	(L/s)	(m3)	(-)	(L/s)	(-)
10 m RBS 1	0.36	-	0.00	4.02	0.77	3.84	0.57
	(0.02)		(0.00)	(0.22)	(0.03)	(0.19)	(0.02)
20 m RBS 2	0.32	975	4.81	5.12	0.95	8.30	0.71
	(0.01)	(188)	(2.17)	(0.80)	(0.01)	(0.19)	(0.04)
30 m RBS 3	0.29	650	9.43	5.27	0.93	11.23	0.71
	(0.00)	(255)	(1.15)	(1.67)	(0.02)	(0.72)	(0.03)
40 m RBS 4	0.24	392	12.65	4.36	0.89	13.14	0.76
	(0.01)	(252)	(1.81)	(2.22)	(0.03)	(0.92)	(0.10)

Note: ¹ for RBS04, 08, 12, 16, and 20; ² for RBS03, 07, 11, 15, and 19; ³ for RBS02, 06, 10, 14, and 18; ⁴ for RBS01, 05, 09, 13, and 17; h_max (m) is the maximum ponding depth (water height) in the bioretention, T_bog (s) is the time when the bioretention overflow starts, Q_pog (L/s) is the bioretention overflow peak discharge, V_pc (m³) is the calculated maximum bioretention ponding volume based on bioretention-strip geometry, V_bio(40)/V_pc is the percentage of the bioretention ponding volume at the end of the 40-min simulation to the calculated bioretention ponding volume, Q_prgb (L/s) is the road grate inlet peak discharge for RBS cases, Q_prgb/Q_prg is the ratio of the road grate inlet peak discharge for RBS case to corresponding Rd case.

) was less than h_b for these cases. All other three modeling groups (L = 20, 30, and 40 m) overflowed through the grate inlet in the bioretention (h_max > h_b, Table 7). The increase of the overflow grate-inlet volume V_bog (Table 5) was mainly because of the increase of the longitudinal slope (S₀) when L and h_b were unchanged. The mean V_bog increased from 1.59 m³ (L = 20 m group) to 10.11 m³ (L = 40 m group) when h_b decreased from 0.3 to 0.2 m. This indicated that the overflow height, h_b, was a key design parameter of the RBS to retain the runoff inside the bioretention.

The mean V_bog percentage, i.e., V_bog/(V_ci + V_rb), increased when h_b decreased: 20.7 ± 12.7% for the L = 20 m group (h_b = 0.30 m), 44.4 ± 8.8% for the L = 30 m group (h_b = 0.25 m), and 58.4 ± 10.2% for the L = 40 m group (h_b = 0.20 m). When h_b was small, the grate-inlet overflow became the main mechanism to remove the extra runoff in the bioretention strip as indicated by the larger V_bog percentage.

The mean overflow peak discharge, Q_pog, increased from 4.81 L/s to 12.65 L/s for L = 20–40 m groups (Table 7) when the total inflow (V_ci + V_rb) increased, h_b decreased also. The bioretention overflow-start-time, (T_bog) and Q_pog, were mainly related to V_ci and h_b. T_bog decreased from 974.8 ± 188.2 s (L = 20 m group) to 391.6 ± 252.5 s (L = 40 m group). The bioretention overflow was delayed when the overflow height, h_b, increased. The bioretention overflow was first projected to start at 163 s in the RBS17 modeling case and reached the peak discharge of 14.92 L/s. The main reason was the largest curb inlet intercepted runoff volume of RBS17 (15.72 m³) due to the large L and S_x and the lowest h_b = 0.20 m.

For all 20 RBS cases (Table 5), the mean ponding volume in the bioretention (V_bio) were 3.10 m³ for the L = 10 m group, 4.86 m³ for the L = 20 m group, 4.93 m³ for the L = 30 m group, and 3.93 m³ for the L = 40 m group when the rainfall intensity was large (250 mm/h). V_bio is a function of time and shows the integrated/cumulative effects of different flow processes (inflow from curb inlet, outflow through the overflow grate inlet, rainfall, and infiltration). V_bio(t) is also related to the bioretention strip’s ponding capacity, which was determined by the bioretention-strip geometry as shown in Equation (9). There are four modeling cases (RBS09, 13, 17, and 18; Table 1) with L × S₀ ≥ h_b; therefore, the overflow height, h_b, was the only controlling factor for V_bio(t), independent of L × S₀ for these four cases.

From the beginning of the simulation, when the ponding depth was zero (more infiltration and zero runoff), V_bio(t) was zero. When the ponding depth increased from zero to h_b, V_bio(t)/V_pc increased from zero to 1.0, since V_pc (Equation (9) is the calculated maximum bioretention ponding volume at h_b. When the overflow through the grate inlet took place in the bioretention strip, V_bio(t)/V_pc was greater than 1.0. After the rainfall stopped, eventually, V_bio(t) was zero when the ponding depth decreased to zero. In this study, V_bio(t) at the end of the simulation (t = 40 min) for each RBS case is shown in Table 5 and was used to calculate the runoff-volume mass-balance percent difference (∆V) in the whole simulation domain. These percent differences (Table 5) were very small, with an average of −0.02%, and indicated that the RBS simulation results were reasonable.

The average V_bio(40) percentage, V_bio(40)/(V_ci + V_rb) at the end of simulation, t = 40 min, was larger when h_b was larger: 75.6 ± 0.2% for the L = 10 m group (h_b = 0.4 m), 64.3 ± 11.8% for the L = 20 m group, 40.3 ± 26.7% for the L = 30 m group, and 24.2 ± 26.3% for the L = 40 m group (h_b = 0.2 m). The higher V_bio(40) percentage means that more runoff was ponded and waited for infiltration when the simulation ended. The ponding volume, V_bio(40), for each case was compared with V_pc, and the ratio ranged from 0.73 to 0.96 (Table 7).

At the end of the simulation, V_bio(40) was smaller than V_pc, and the mean ratios of V_bio/V_pc were 0.77–0.95 for the changing L. The results in Table 7 and Equation (9) indicate that it is necessary to consider three parameters, S₀, L, and h_b, when calculating the ponding capacity of the bioretention; this was especially important in the continuous RBS system when these three parameters changed in different RBSs. In this study, the vegetation volume fraction was not considered when calculating V_pc, therefore, we need to use a safety factor to calculate the actual ponding volume based on the bioretention geometry and vegetation volume fraction when designing a continuous RBS system.

3.3. Implications of the Simulation Results on RBS Design

In this study, three implications can be drawn through the detailed analysis of the simulation results of the 20 RBS cases.

(1) The curb inlet could be the bottleneck of a continuous road-bioretention facility that impedes the runoff generated from the road flowing into the bioretention to infiltrate, detain (pond), and improve the stormwater quality. The analysis of 20 RBS performance indicated only 34.6–48.4% of the total runoff volume (Table 5) was intercepted by the curb inlet when the intensity was 250 mm/h for 20 min and the remaining part of the runoff flowed downstream along the road, which may cause local inundation and become a safety hazard. Many bioretention system designs do not pay much attention to the curb inlet interception efficiency, but only focus on the bioretention BMP itself. It is necessary to appropriately design the curb inlet to intercept enough stormwater runoff to improve the performance of RBS based on detailed hydraulic calculations, for example, using the HEC-22 method. Equations (1)–(3) indicate that HEC-22 considers the effects of the road longitudinal slope, cross slope, surface roughness, incoming flow or spread, and the inlet length on the curb inlet interception efficiency. The HEC-22 method has been widely used in the USA for drainage inlet design, but is seldom used for designing inlets for LID facilities. The HEC-22 calculated and FullSWOF-ZG simulated curb inlet efficiencies will be compared and evaluated in a future study.

(2) Bioretention BMP is intended to detain the runoff intercepted by the inlet under frequent rainfall events (e.g., the 95th percentile rainfall), and some current practices of the RBS design in China that eliminate necessary grate inlets on the road could cause local flooding (inundation) on the road under heavy rainfall events. The analysis of 20 RBS’s performances indicated that the runoff generated from the road, but could not be intercepted by the curb inlet, thus it needed to be captured by the grate inlet downstream from the curb inlet (Figure 4). In this study, the percent of runoff captured by the road grate inlet for the RBS system ranged from 44.2% to 61.7% (Table 5) under 250 mm/h heavy rainfall over 20 min. This indicated the importance of the grate inlet downstream of the curb inlet for the RBS system. The curb inlet intercepted the runoff for the bioretention strip and the grate inlet intercepted the bypassed flow after the curb inlet.

The peak discharges of the road grate inlet for 20 RBS modeling cases (Q_prgb, Table 7) were compared with the corresponding Q_prg for the road-only modeling cases. For all 20 RBS cases, the average Q_prgb increased from 3.84 L/s to 13.14 L/s for an L increase from 10 to 40 m. Comparing with Q_prg, the average ratio of Q_prgb/Q_prg were from 0.57 to 0.76 for L = 10–40 m groups. The overall average ± standard deviation of Q_prgb/Q_prg for 20 modeling cases was 0.69 ± 0.09, which indicates that the curb inlet and grate inlet combination could reduce the road grate inlet peak discharge and help to relieve road local flood inundation. Therefore, the curb inlet and grate inlet combination greatly benefits the runoff control, local flood inundation relief, and traffic safety, especially for continuous road-bioretention. Eliminating the grate inlets on the road for the RBS system is not a recommended design practice.

(3) A safety factor should be adopted to calculate the bioretention ponding volume when designing the RBS system. The actual ponding volume should be equal to the ponding volume calculated based on the bioretention geometry (V_pc) multiplied by the safety factor used for RBS design. The berm at the end of a bioretention cell (Figure 1 and Figure 2) is typically to pond the runoff for infiltration and to ensure that the overflow discharges through the grate inlet rather than flowing into the bioretention downstream. For the RBS13, RBS17, and RBS18 modeling cases, L × S₀ > h_b, so that the maximum ponding and infiltration area was less than the total bioretention surface area (e.g., 40 m × 1 m in this study), which is not a recommended design configuration for the bioretention strip. The distance between the ditch dikes should be small enough to have L × S₀ ≤ h_b or pond the runoff in the whole bioretention area. The bioretention ponding volume is influenced by the bioretention cells’ geometry, including the length, longitudinal slope, and overflow height; it can be computed using Equation 9, but the vegetation volume fraction can be important when the vegetation density in the bioretention is very high (Figure 2a) so that a ponding volume safety factor should be introduced. The EPA-SWMM model suggests the vegetation volume fraction of 0.1–0.2, therefore, the safety factor used for RBS design in computing the ponding volume should be 0.8–0.9.

4. Conclusions

The open-source Full Shallow-Water equations for Overland Flow in the two-dimensional (FullSWOF_2D) program, which applies the uniform rainfall and infiltration parameters to the whole simulation domain, was revised to include 2D plane zones (Z) with different rainfall and infiltration parameters and a 2D-1D grate-inlet (G) drainage module. The FullSWOF-ZG program was tested with the overland flow of eight pervious surface rainfall-runoff events and 20 impervious roads with a type C curb inlet to study whether the program could accurately simulate the overland flow on a pervious and impervious surface and accurately predict the curb inlet interception efficiency. Twenty road-bioretention strip or RBS modeling cases were designed based on the commonly used parameters (longitudinal and cross slopes, curb opening length, soil infiltration parameters, the bioretention depression depth, and the overflow height) and evaluated with FullSWOF-ZG. The simulation results were analyzed and demonstrated that the RBS hydrological performance, i.e., to intercept then infiltrate the runoff, was jointly influenced by several parameters. Even if the complex relationship between the RBS performance and all input parameters were not fully explored by using only 20 cases, we suggest three main points resulting from this study. (1) The RBS’s curb inlet could be the bottleneck of its hydrologic performance and should be designed to improve inlet interception efficiency, e.g., using procedures and equations in HEC-22; (2) The curb inlet and road grate inlet combination is necessary for continuous RBS because the road surface runoff could not be 100% intercepted by the curb inlet alone; and (3) it is necessary to consider the safety factor of the high-density vegetation and the relationship of overflow height, bioretention cell length, and longitudinal slope when calculating the ponding volume for the RBS design. The RBS performance evaluation and design under different rainfall distribution and intensity situations will be conducted in a future study. The performance improvement of RBS with different types of curb inlet will also be conducted in a future study to provide suggestions for SPC construction in China and LID practices (especially bioretention BMPs) over the world.