An Insight into the Projection Characteristics of the Soil-Water Retention Surface
Abstract
:1. Introduction
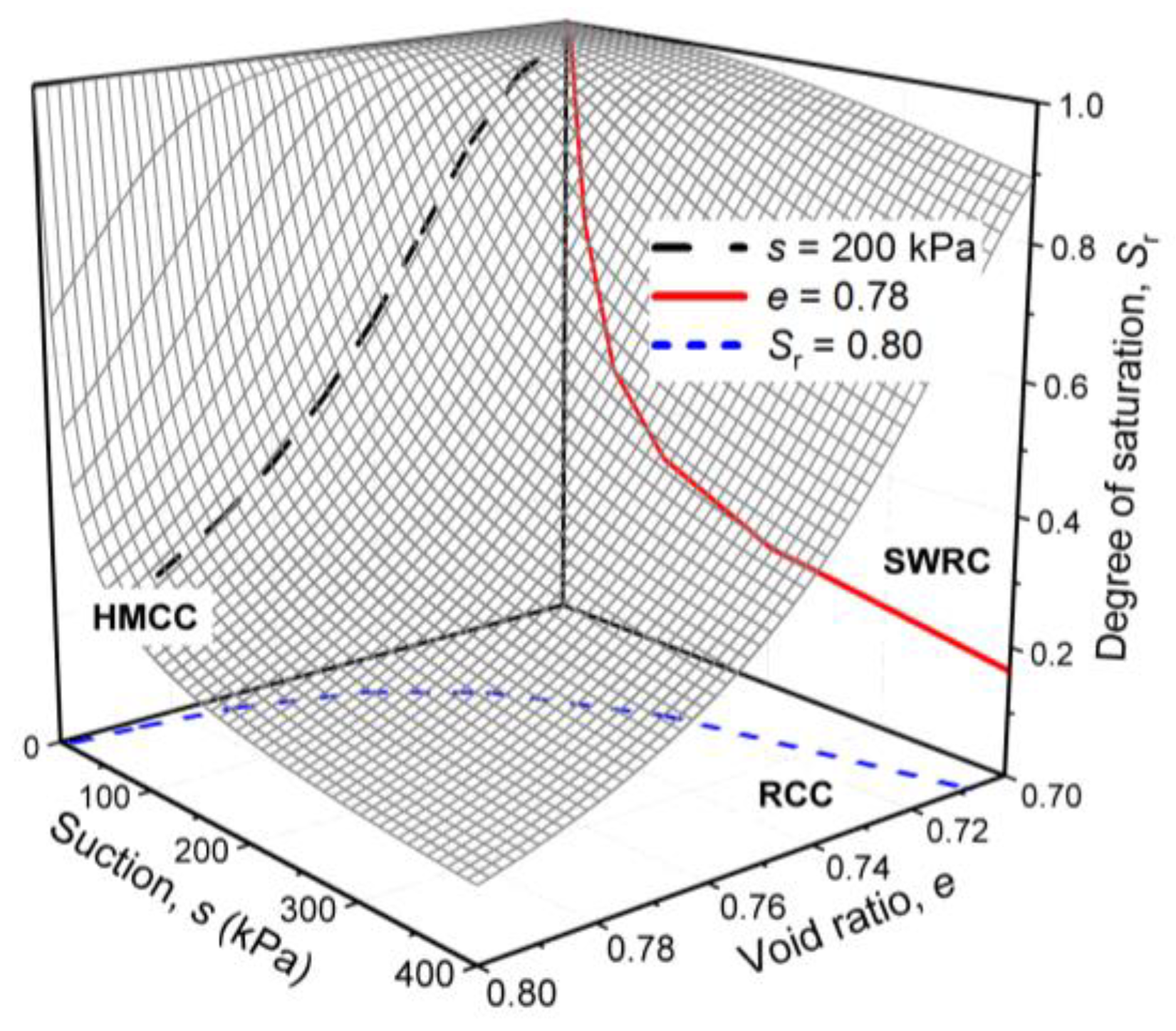
2. Projections of the SWRS
- (i)
- The SWRCs: the Sr versus s plot at constant e (referred to as plane e).
- (ii)
- The Sr versus e plot where s is constant (referred as plane s). It is denoted as the hydro-mechanical coupling curves (HMCCs) in this paper.
- (iii)
- The s versus e plot at constant Sr (referred to as plane Sr). It is commonly referred to as the retention consolidation curves (RCCs).
3. Characteristics of the Projections of the SWRS
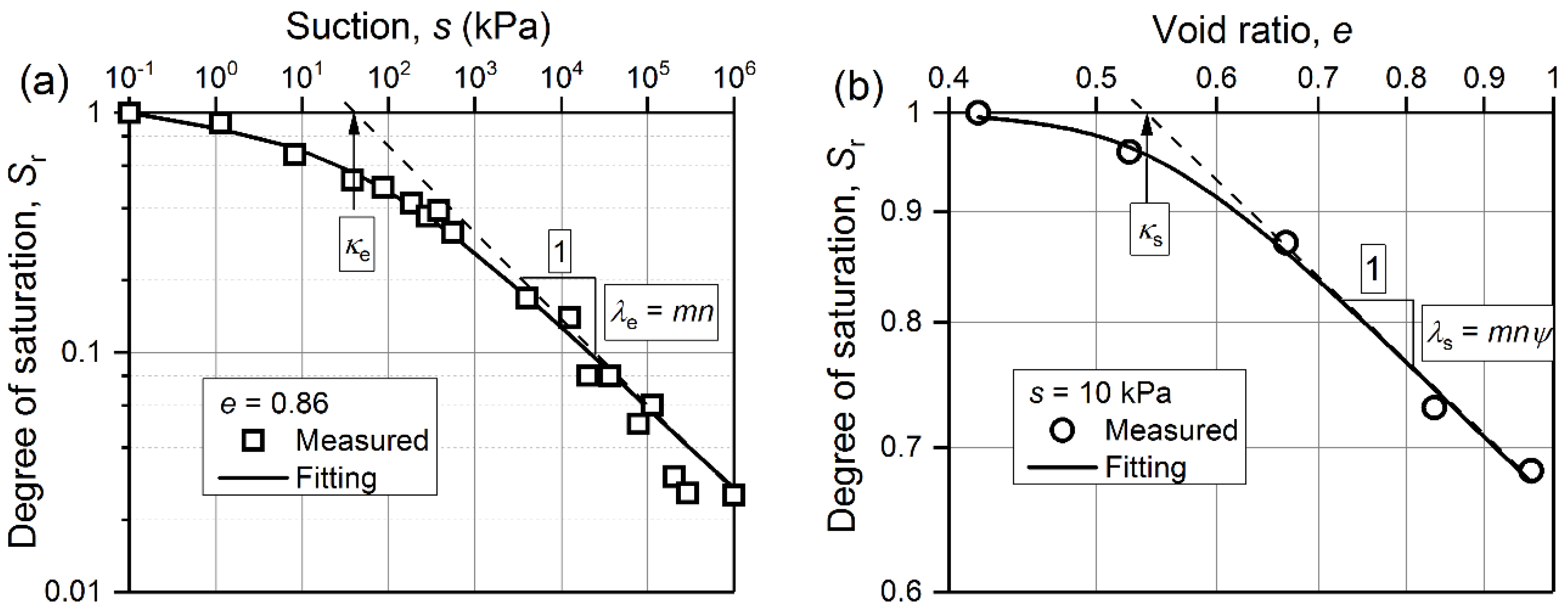
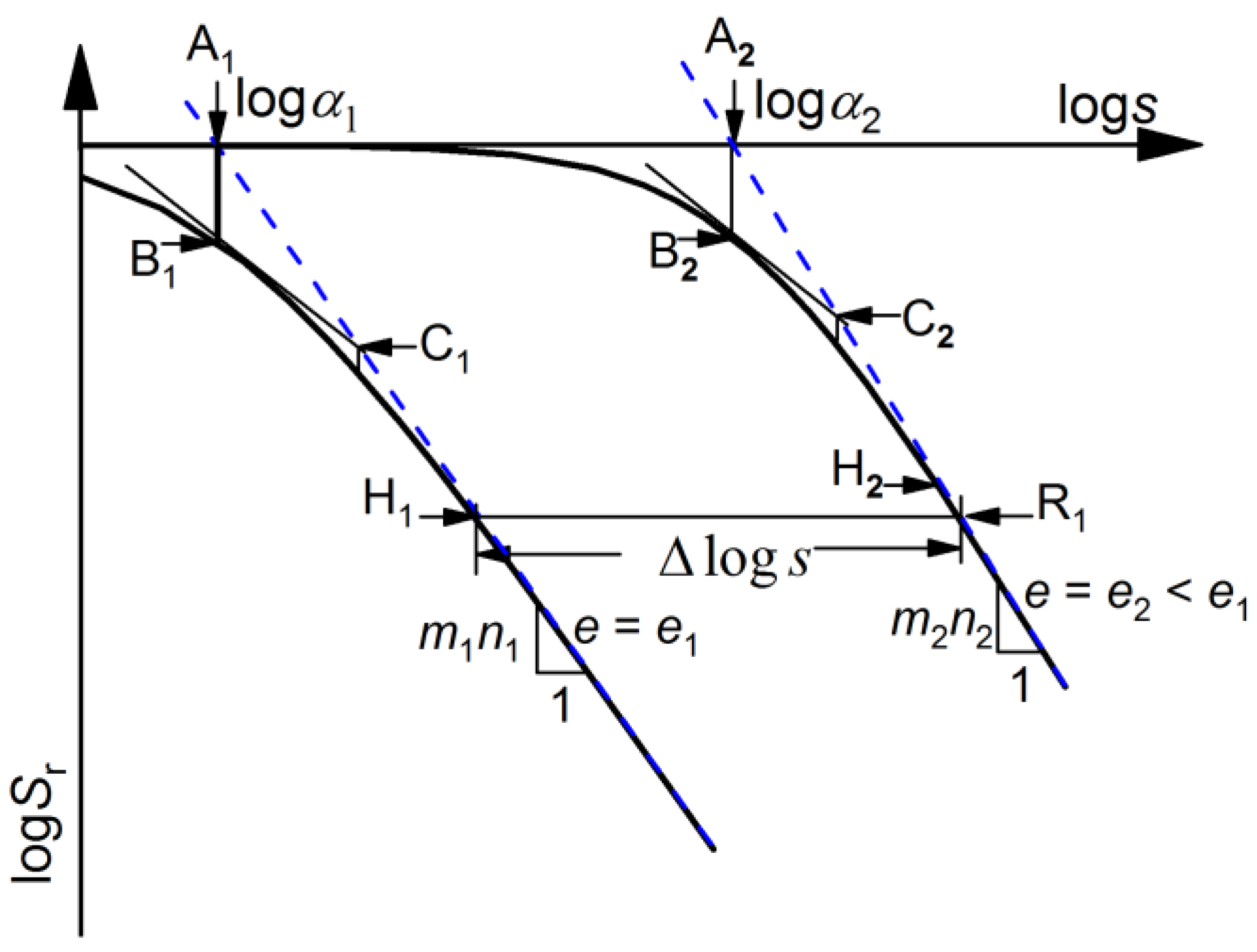
3.1. Soil-Water Retention Curves (SWRCs)
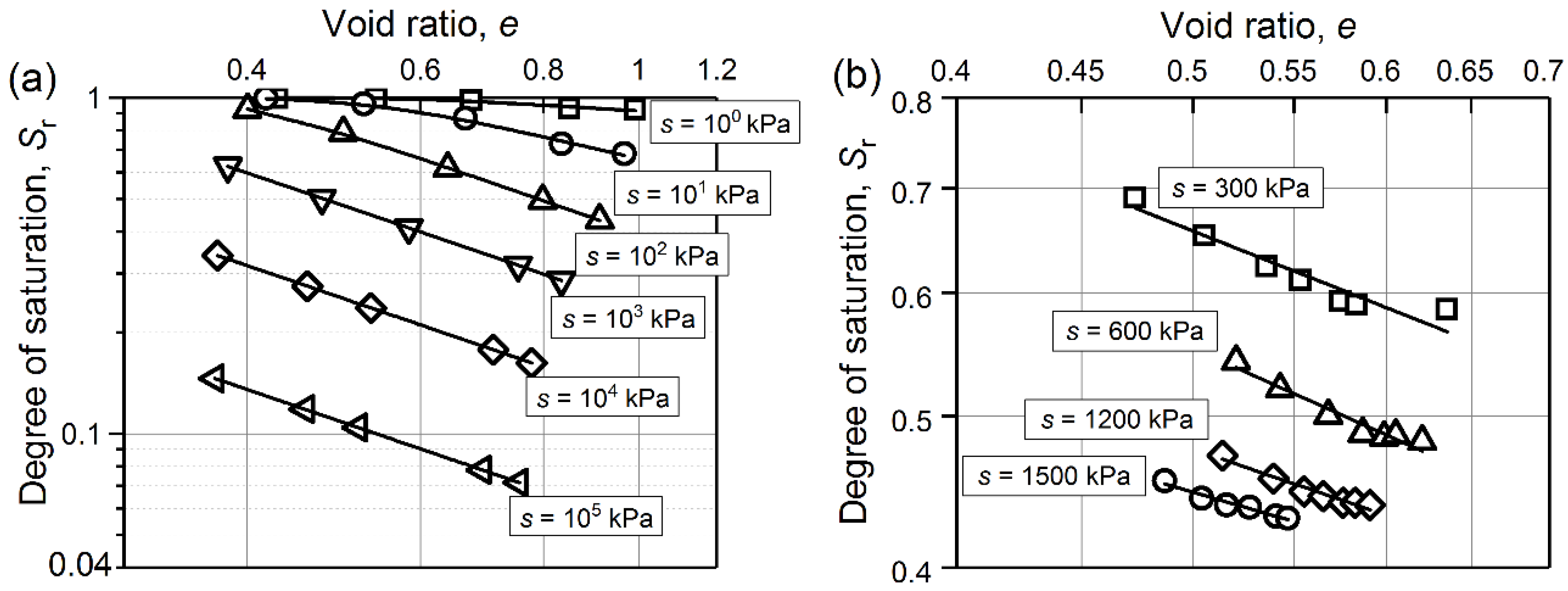
3.2. Hydro-Mechanical Coupling Curves (HMCCs)
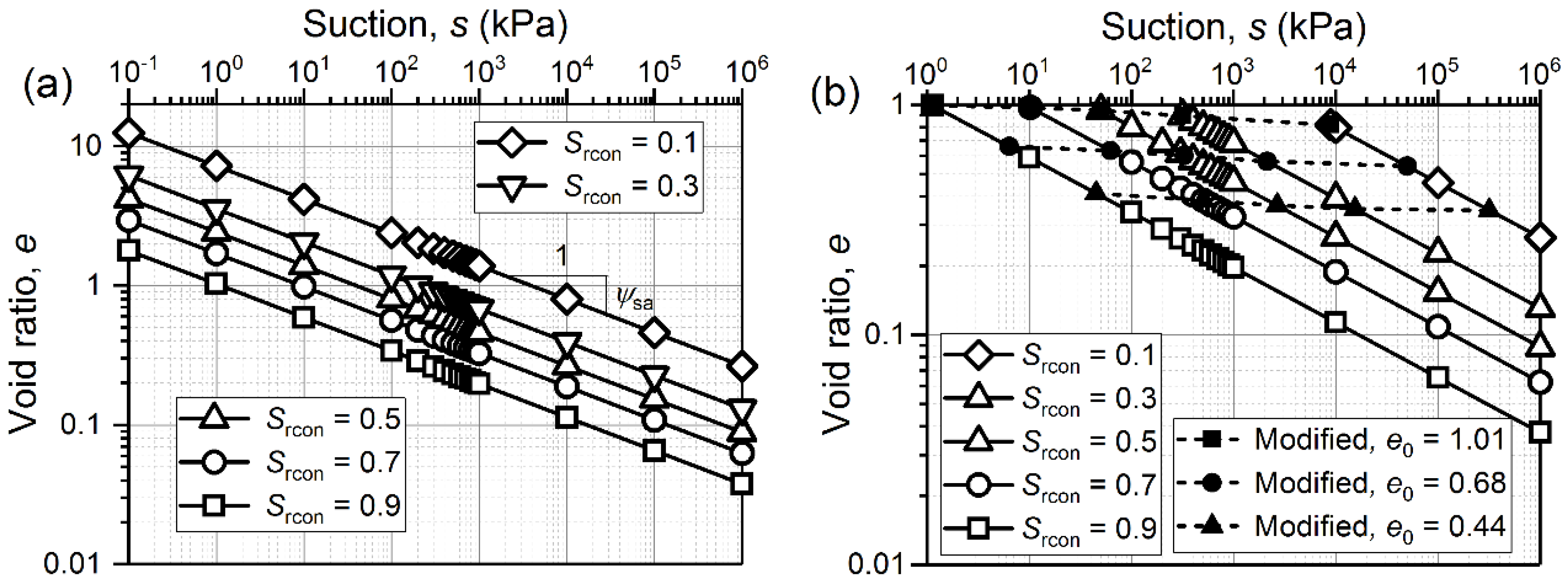
3.3. Retention Consolidation Curves (RCCs)
4. Conclusions
- (1)
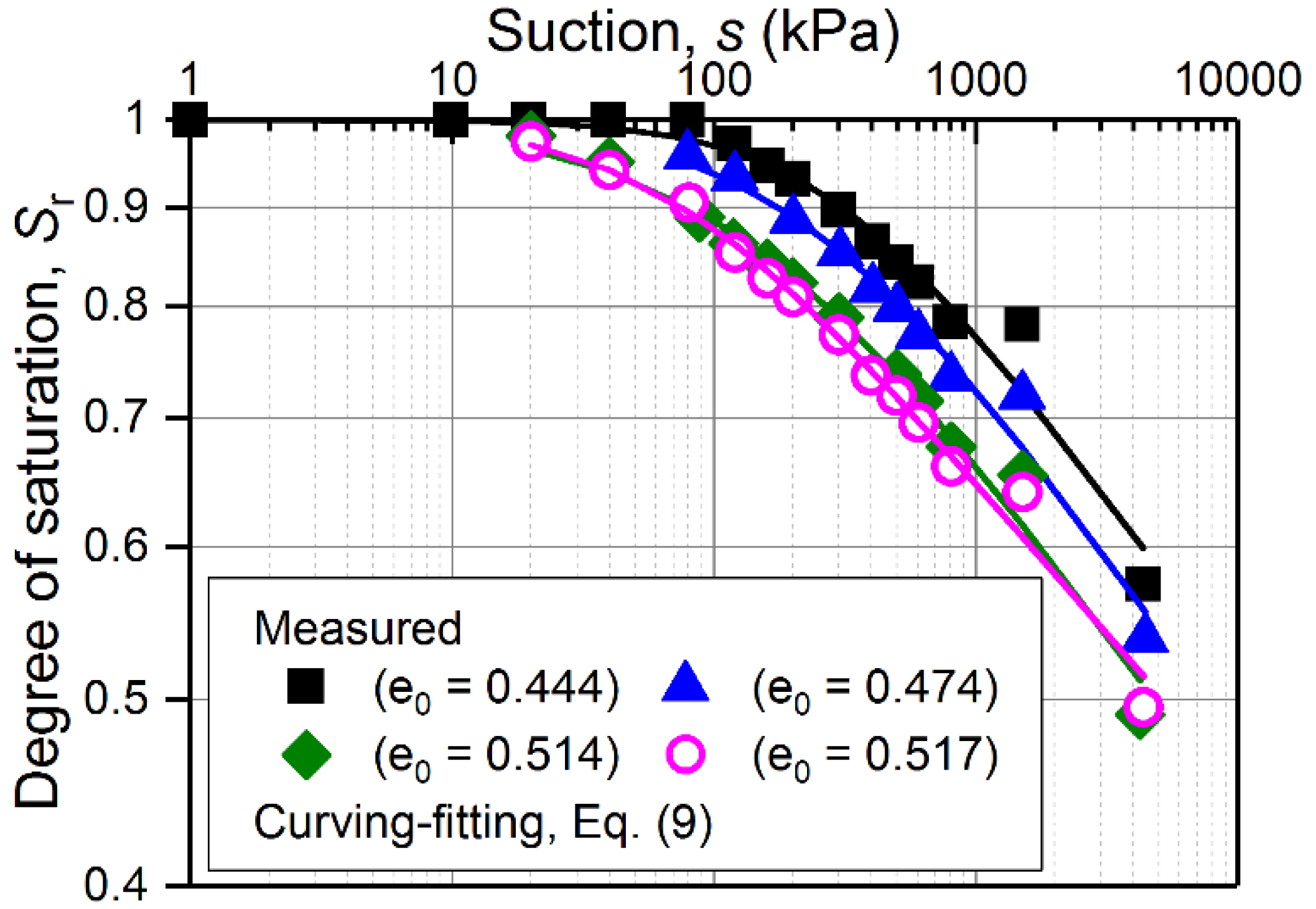
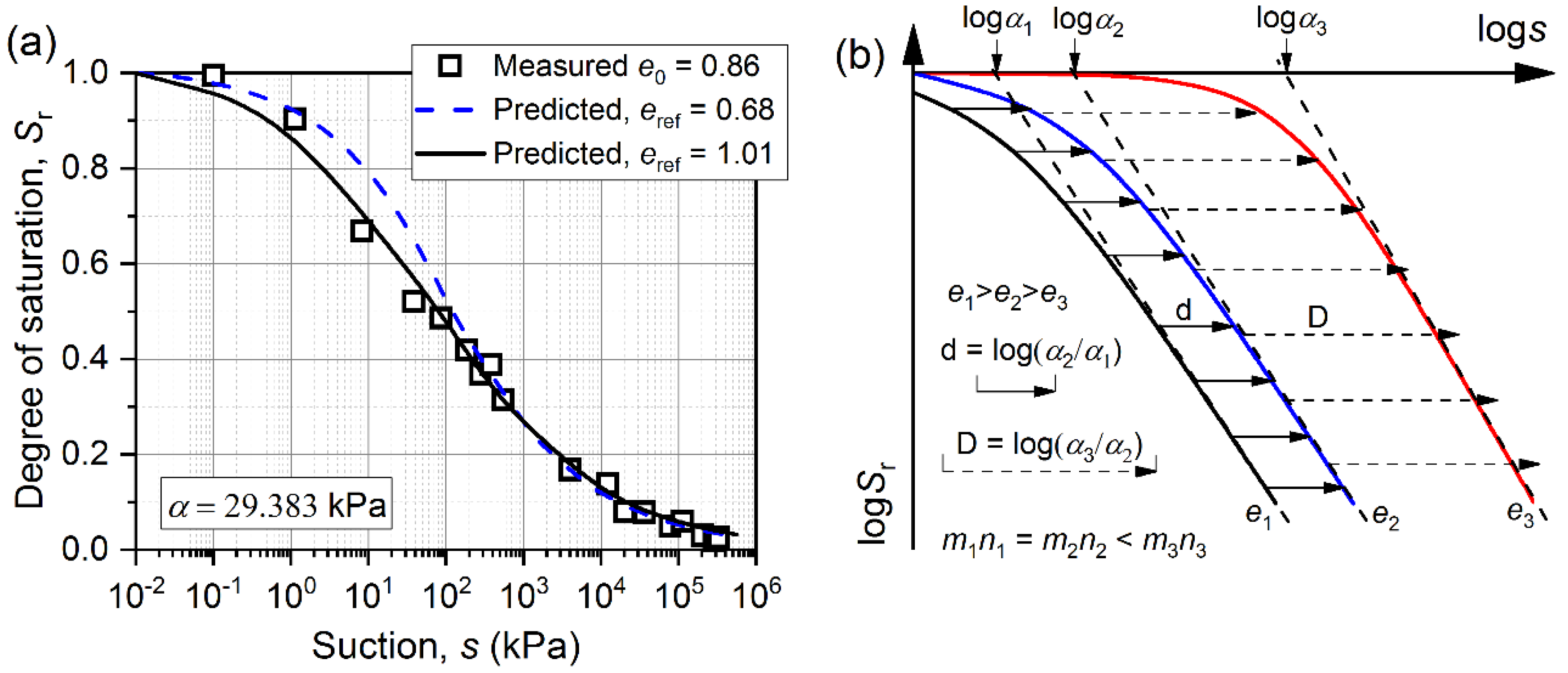
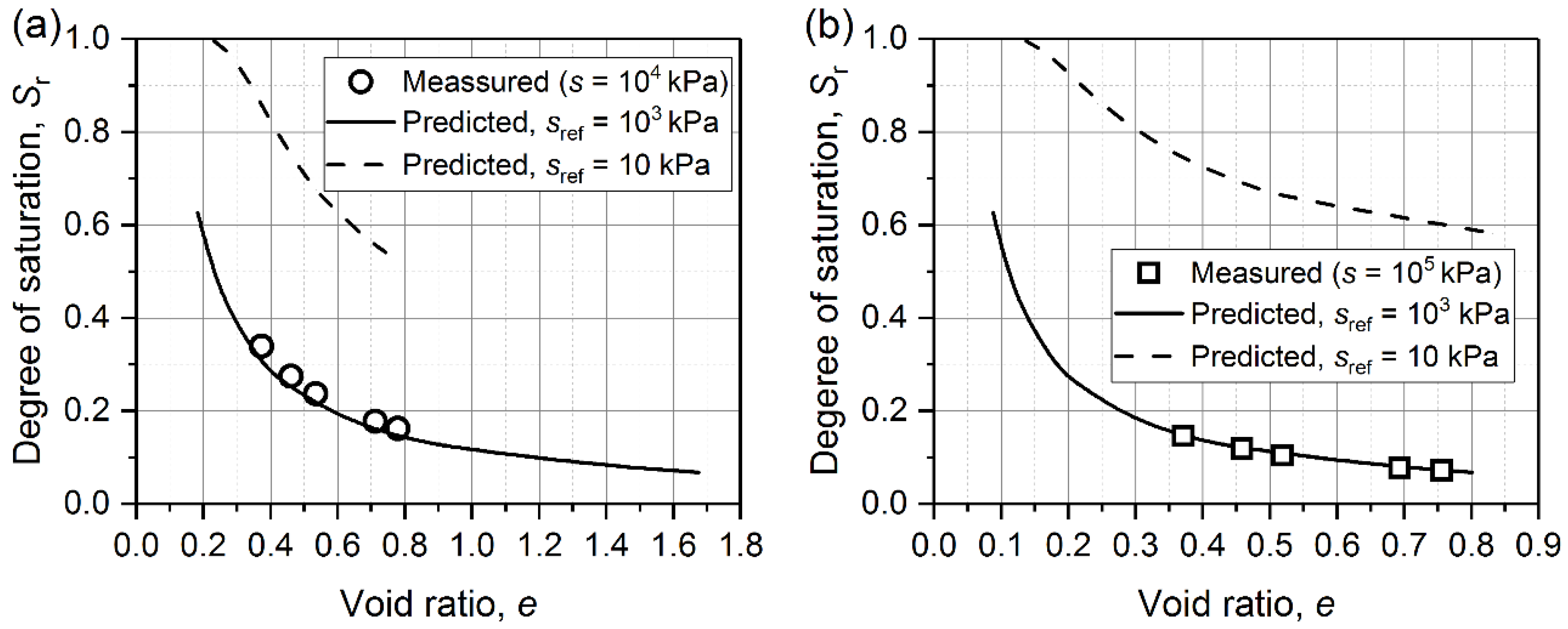
- The SWRCs tend to move towards the left-hand direction along the s axis on a log-log scale with the increase in initial e. When the gap of initial e values between the predicted SWRCs and reference SWRCs is as small as possible, SWRCs at different initial e can be obtained by a rigid translation of a reference SWRC alone the s axis in the logs-logSr plane.
- (2)
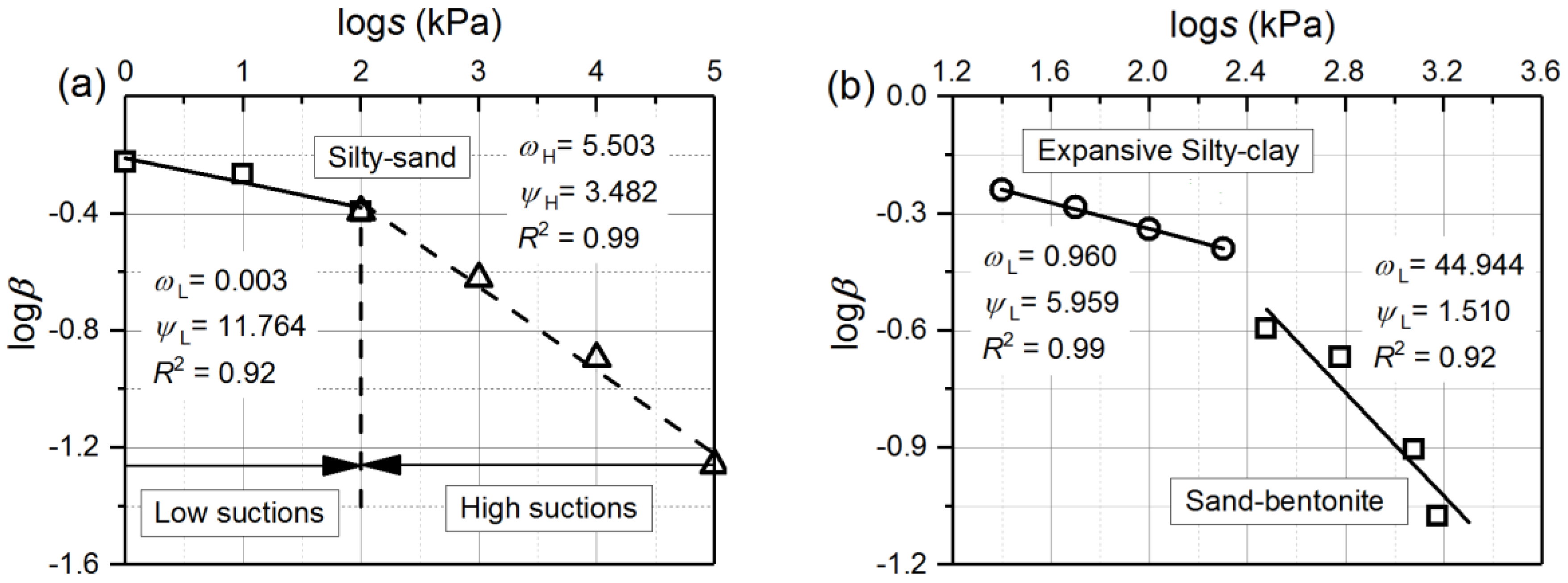
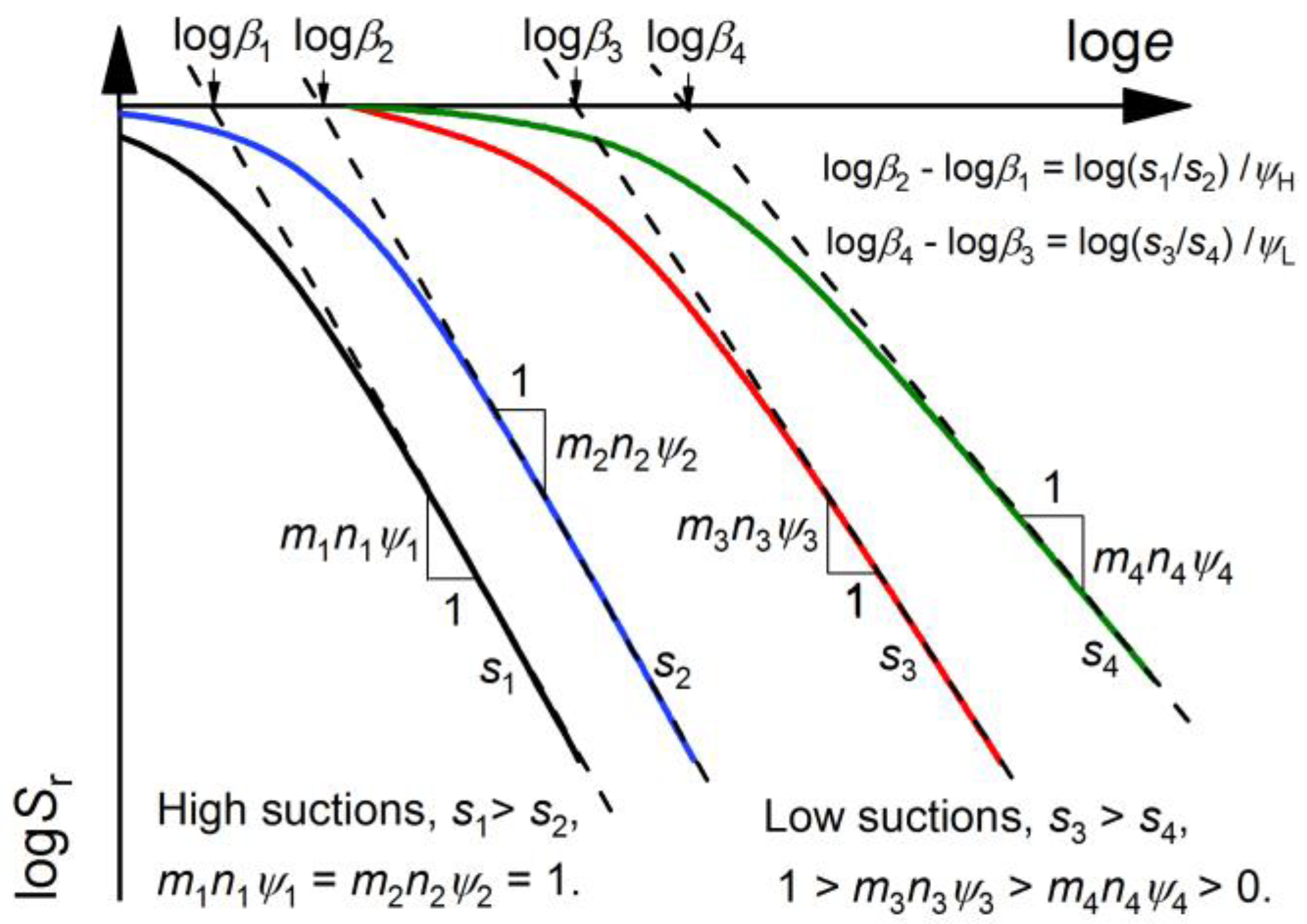
- Similarly, the HMCCs and the RCCs move towards the left-hand direction along the e axis on a log-log scale with the increase in s and Sr, respectively. HMCCs at high suctions cannot be obtained from a rigid translation of a reference HMCC at low suctions. The constant suctions imposed on the HMCCs are suggested to be high suctions when the mnψ = 1 and low suctions when 0 < mnψ < 1 (i.e., m, n, and ψ are the Gallipoli et al. [26] model parameters).
- (3)
- The RCC equation proposed is capable of describing the relationship between e and s on the constant Sr plane. The modified RCCs show that the initial suction increases with the reducing constant Sr. Moreover, the initial suction is reducing as initial e increases at equal values of Sr.
Author Contributions
Funding
Conflicts of Interest
References
- Alonso, E.E.; Gens, A.; Josa, A. A constitutive model for partially saturated soils. Geotechnique 1990, 40, 405–430. [Google Scholar] [CrossRef] [Green Version]
- Vaunat, J.; Romero, E.; Jommi, C. An elastoplastic hydromechanical model for unsaturated soils. In International Workshop on Unsaturated Soils: Experimental Evidence and Theoretical Approaches in Unsaturated Soils; Tarantino, A., Mancuso, C., Eds.; Springer: Balkema, Rotterdam, 2000; pp. 121–138. [Google Scholar]
- Wheeler, S.; Sharma, R.; Buisson, M. Coupling of hydraulic hysteresis and stress-strain behavior in unsaturated soils. Geotechnique 2003, 53, 41–53. [Google Scholar] [CrossRef]
- Khalili, N.; Habte, M.; Zargarbash, S. A fully coupled flow deformation model for cyclic analysis of unsaturated soils including hydraulic and mechanical hystereses. Comput. Geotech. 2008, 35, 872–889. [Google Scholar] [CrossRef]
- Gens, A. Soil–environment interactions in geotechnical engineering. Geotechnique 2010, 60, 3–74. [Google Scholar] [CrossRef]
- Sheng, D.C.; Zhou, A.N. Coupling hydraulic with mechanical models for unsaturated soils. Can. Geotech. J. 2011, 48, 826–840. [Google Scholar] [CrossRef]
- Sun, D.A.; Cui, H.B.; Matsuoka, H.; Sheng, D.C. A three-dimensional elastoplastic model for unsaturated compacted soils with hydraulic hysteresis. Soils Found. 2007, 47, 253–264. [Google Scholar] [CrossRef]
- Fuentes, W.; Triantafyllidis, T. Hydro-mechanical hypoplastic models for unsaturated soils under isotropic stress conditions. Comput. Geotech. 2013, 51, 72–82. [Google Scholar] [CrossRef]
- Masin, D. Double structure hydromechanical coupling formalism and a model for unsaturated expansive clays. Eng. Geol. 2013, 165, 73–88. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, D.A.; Zhou, A.N. Hydro-mechanical behaviour of unsaturated soil with different specimen preparations. Can. Geotech. J. 2016, 53, 909–917. [Google Scholar] [CrossRef]
- Ghasemzadeh, H.; Sojoudi, M.H.; Amiri, S.A.G.; Karami, M.H. Elastoplastic model for hydro-mechanical behavior of unsaturated soils. Soils Found. 2017, 57, 371–383. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, S.; Sivakumar, V. An elasto-plastic critical state framework for unsaturated soils. Géotechnique 1995, 45, 35–53. [Google Scholar] [CrossRef]
- Cui, Y.; Delage, P. Yielding and plastic behaviour of an unsaturated compacted silt. Geotechnique 1996, 46, 291–311. [Google Scholar] [CrossRef]
- Gardner, W.R. Some steady state solutions of the unsaturated moisture flow equation with application to evaporation from a water-table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soil. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A.Q. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Pang, Y.W. Influence of stress state on soil-water characteristics and slope stability. J. Geotech. Geoenviron. 2000, 126, 157–166. [Google Scholar] [CrossRef]
- Assouline, S. Modeling the relationship between soil bulk density and the water retention curve. Vadose Zone J. 2006, 5, 554–562. [Google Scholar] [CrossRef]
- Sun, D.A.; Sheng, D.C.; Xu, Y.F. Collapse behaviour of unsaturated compacted soil with different initial densities. Can. Geotech. J. 2007, 44, 673–686. [Google Scholar] [CrossRef]
- Miller, G.A.; Khoury, C.N.; Muraleetharan, K.K.; Liu, C.; Kibbey, T.C.G. Effects of soil skeleton deformations on hysteretic soil water characteristic curves: Experiments and simulations. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Masin, D. Predicting the dependency of a degree of saturation on void ratio and suction using effective stress principle for unsaturated soils. Int. J. Numer. Anal. Methods Geomech. 2010, 34, 73–90. [Google Scholar] [CrossRef]
- Zhou, A.N.; Sheng, D.; Carter, J.P. Modelling the effect of initial density on soil-water characteristic curves. Geotechnique 2012, 62, 669–680. [Google Scholar] [CrossRef]
- Han, Z.; Vanapalli, S.K.; Zou, W.L. Integrated approaches for predicting soil-water characteristic curve and resilient modulus of compacted fine-grained subgrade soils. Can. Geotech. J. 2017, 54, 646–663. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Barbour, S.L.; Fredlund, D.G. Development and verification of a coefficient of permeability function for a deformable unsaturated soil. Can. Geotech. J. 1998, 35, 411–425. [Google Scholar] [CrossRef]
- Gallipoli, D.; Wheeler, S.; Karstunen, M. Modelling the variation of degree of saturation in a deformable unsaturated soil. Geotechnique 2003, 53, 105–112. [Google Scholar] [CrossRef] [Green Version]
- Thu, T.M.; Rahardjo, H.; Leong, E.C. Elastoplastic model for unsaturated soil with incorporation of the soil-water characteristic curve. Can. Geotech. J. 2007, 44, 67–77. [Google Scholar] [CrossRef]
- Nuth, M.; Laloui, L. Advances in modelling hysteretic water retention curve in deformable soils. Comput. Geotech. 2008, 35, 835–844. [Google Scholar] [CrossRef]
- Karube, D.; Kawai, K. The role of pore water in the mechanical behaviour of unsaturated soils. Geotech. Geol. Eng. 2001, 19, 211–241. [Google Scholar] [CrossRef]
- Tsiampousi, A.; Zdravkovic, L.; Potts, D.M. A three-dimensional hysteretic soil-water retention curve. Geotechnique 2013, 63, 155–164. [Google Scholar] [CrossRef] [Green Version]
- Pasha, A.Y.; Khoshghalb, A.; Khalili, N. Hysteretic model for the evolution of water retention curve with void ratio. J. Eng. Mech. 2017, 143, 04017030. [Google Scholar] [CrossRef]
- Tarantino, A. A water retention model for deformable soils. Geotechnique 2009, 59, 751–762. [Google Scholar] [CrossRef]
- Gallipoli, D. A hysteretic soil-water retention model accounting for cyclic variations of suction and void ratio. Geotechnique 2012, 62, 605–616. [Google Scholar] [CrossRef]
- Salager, S.; Ei Youssoufi, M.S.; Saix, C. Definition and experimental determination of a soil-water retention surface. Can. Geotech. J. 2010, 47, 609–622. [Google Scholar] [CrossRef] [Green Version]
- Qi, S.; Simms, P.H.; Vanapalli, S.K. Piecewise-linear formulation of coupled large-strain consolidation and unsaturated flow i: Model development and implementation. J. Geotech. Geoenviron. 2017, 143, 1–11. [Google Scholar] [CrossRef]
- Salager, S.; El Youssoufi, M.S.; Saix, C. Experimental study of the water retention curve as a function of void ratio. In Proceedings of the International Conference Geo-Denver, Denver, CO, USA, 18–21 February 2007. [Google Scholar]
- Vanapalli, S.K.; Pufahl, D.E.; Fredlund, D.G. The influence of soil structure and stress history on the soil-water characteristic of a compacted till. Geotechnique 1999, 49, 143–159. [Google Scholar] [CrossRef]
- Sun, W.J.; Liu, S.; Sun, D.; Fang, L.; Zhou, A. Hydraulic and Mechanical Behavior of GMZ Ca-Bentonite; Geotechnical Special Publication: Reston, VA, USA, 2014; pp. 125–134. [Google Scholar]
- Aubertin, M.; Ricard, J.F.; Chapuis, R.P. A predictive model for the water retention curve: Application to tailings from hard-rock mines. Can. Geotech. J. 1998, 35, 55–69. [Google Scholar] [CrossRef]
- Laliberte, G.E.; Corey, A.T.; Brooks, R.H. Properties of Unsaturated Porous Media; Hydrology Paper No. 17; Colorado State University: Fort Collins, CO, USA, 1996. [Google Scholar]
- Sun, W.J.; Sun, D. Coupled modelling of hydro-mechanical behaviour of unsaturated compacted expansive soils. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 1002–1022. [Google Scholar] [CrossRef]
- Zhan, L. Field and laboratory study of an unsaturated expansive soil associated with rain-induced slope instability. Ph.D. Thesis, Hong Kong University of Science and Technology, Hong Kong, China, 2003. [Google Scholar]
- Stange, C.F.; Horn, R. Modeling the soil water retention curve for conditions of variable porosity. Vadose Zone J. 2005, 4, 602–613. [Google Scholar] [CrossRef]

| Soil Name | wL (%) | wp (%) | Sand (%) | Silt (%) | Clay (%) | USCS | Reference |
|---|---|---|---|---|---|---|---|
| Silty sand | 25 | 14.5 | 72 | 18 | 10 | CL | Salager et al. [36] |
| Compacted till | 35.5 | 16.8 | 28 | 42 | 30 | CL | Vanapalli et al. [37] |
| Ca-Bentonite | 99 | 41 | n/a | n/a | n/a | CH | Sun et al. [38] |
| Tailing sand | n/a | n/a | 30.1 | 55.7 | 14.2 | ML | Aubertin et al. [39] |
| Sandy loam | n/a | n/a | 54 | 35 | 11 | SM | Laliberte et al. [40] |
| Sand-Bentonite | 473.9 | 26.6 | n/a | n/a | n/a | n/a | Sun & Sun [41] |
| Expansive Silty-Clay | 50 | 31 | 3 | 48 | 39 | CL | Zhan [42] |
| Nonexpansive-Clay | 49 | 22 | 0 | 50 | 50 | CL | Sun et al. [20] |
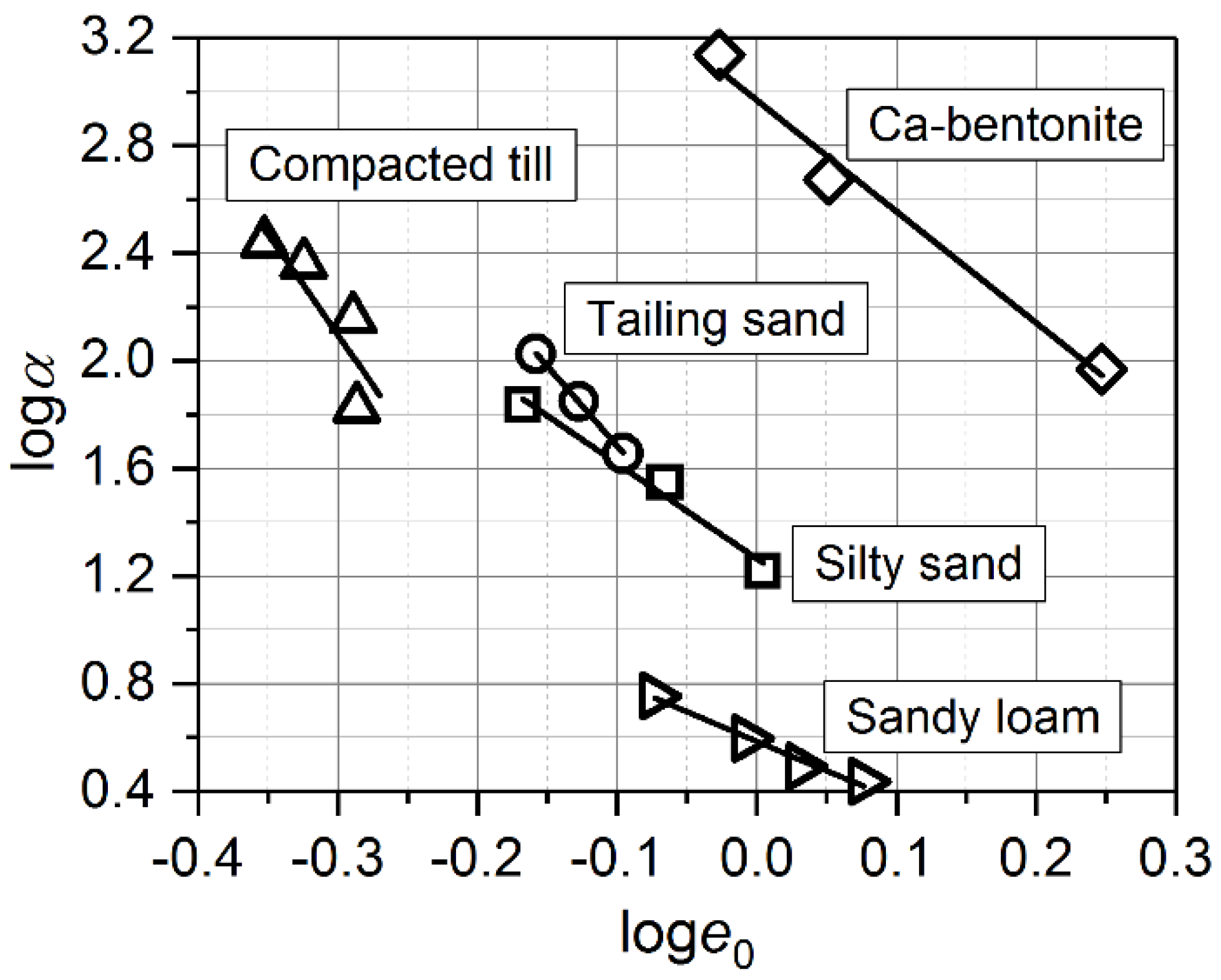
| Soil Type | e0 | me | ne | logα | κe | mene | λe |
|---|---|---|---|---|---|---|---|
| Silty sand (Salager et al. [36]) | 0.680 | 0.542 | 0.671 | 1.835 | 1.803 | 0.364 | −0.362 |
| 0.860 | 0.792 | 0.446 | 1.547 | 1.585 | 0.353 | −0.364 | |
| 1.010 | 0.710 | 0.488 | 1.217 | 1.326 | 0.347 | −0.357 | |
| Compacted till (Vanapalli et al. [37]) | 0.444 | 0.135 | 1.358 | 2.438 | 2.376 | 0.184 | −0.176 |
| 0.474 | 0.185 | 1.061 | 2.359 | 2.253 | 0.196 | −0.184 | |
| 0.514 | 0.222 | 0.878 | 2.157 | 2.009 | 0.195 | −0.179 | |
| 0.517 | 0.137 | 1.161 | 1.824 | 1.824 | 0.159 | −0.158 | |
| Ca-Bentonite (Sun et al. [38]) | 0.940 | 0.253 | 1.162 | 3.135 | 3.138 | 0.293 | −0.291 |
| 1.126 | 0.207 | 1.261 | 2.673 | 2.803 | 0.261 | −0.264 | |
| 1.765 | 0.213 | 1.271 | 1.969 | 2.040 | 0.271 | −0.276 | |
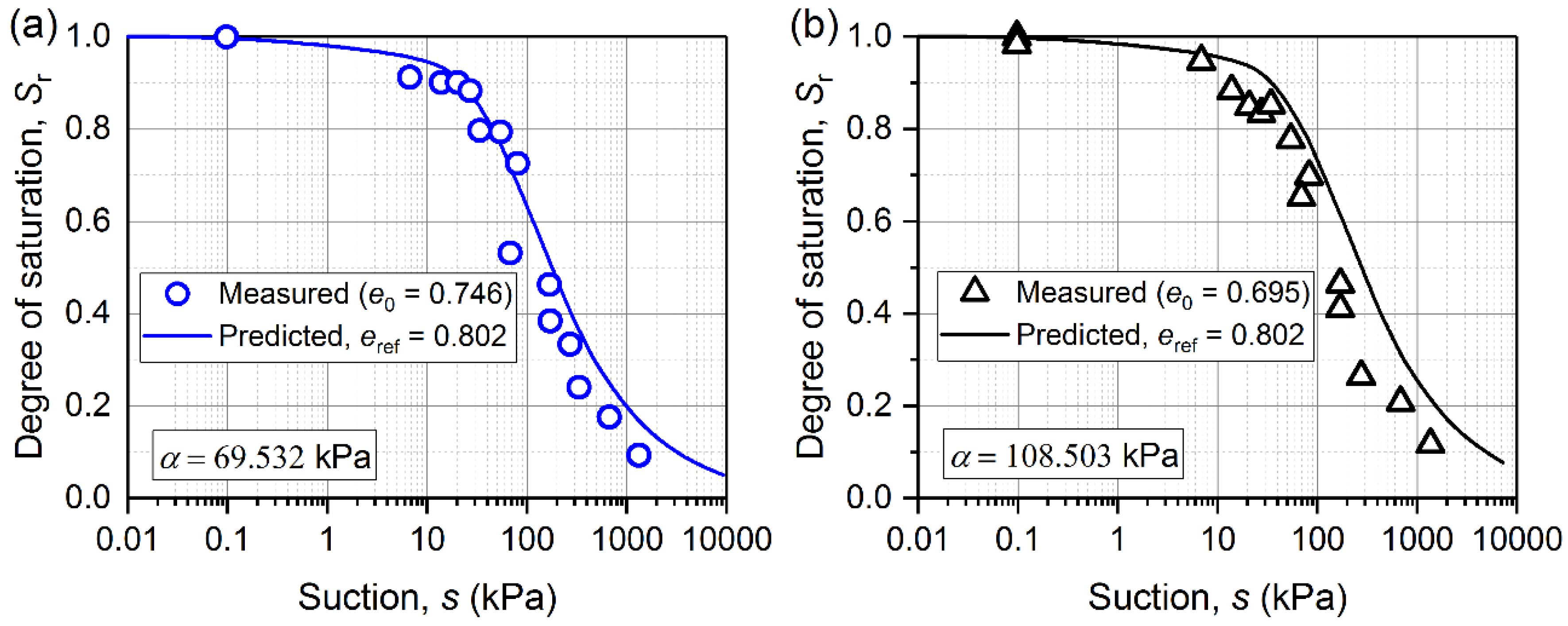
| Tailing sand (Aubertin et al. [39]) | 0.695 | 0.809 | 1.116 | 2.025 | 1.905 | 0.904 | −0.831 |
| 0.746 | 0.605 | 1.279 | 1.847 | 1.761 | 0.774 | −0.727 | |
| 0.802 | 0.479 | 1.272 | 1.655 | 1.598 | 0.609 | −0.588 | |
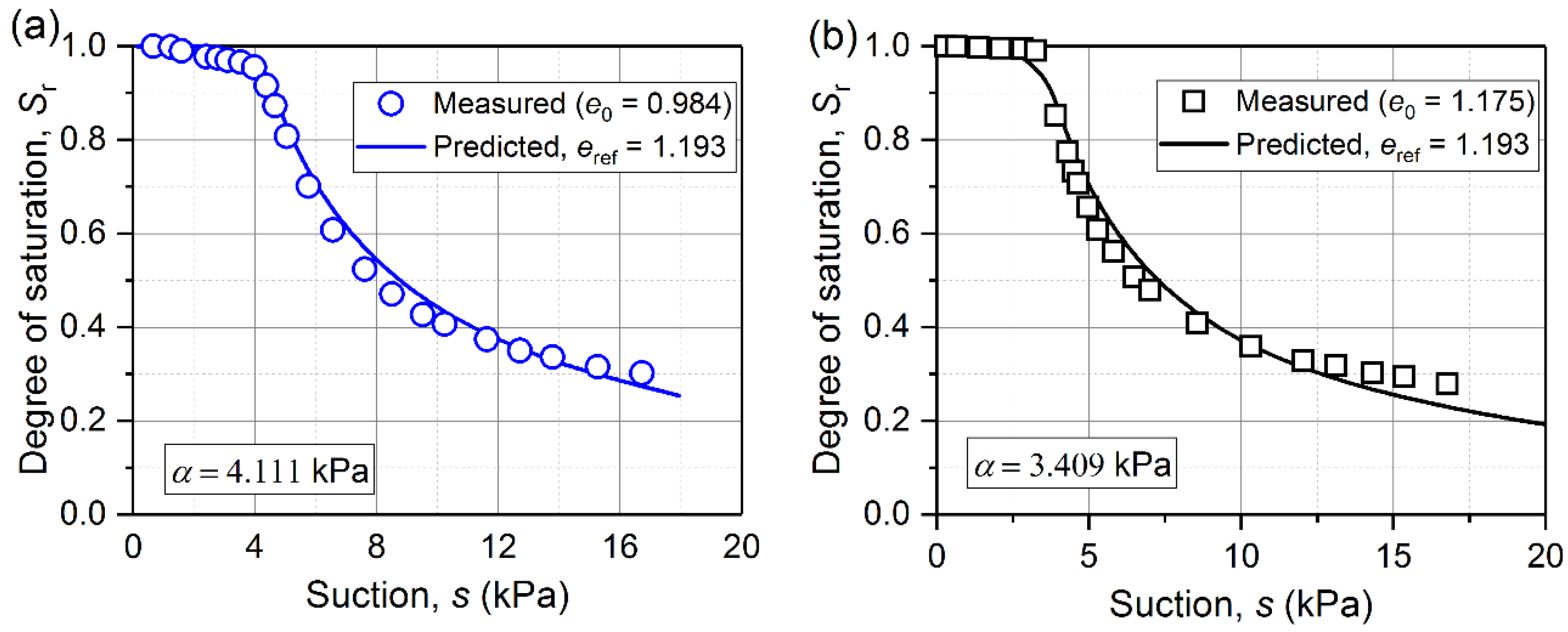
| Sandy loam (Laliberte [40]) | 0.845 | 0.115 | 11.417 | 0.754 | 0.749 | 1.317 | −1.284 |
| 0.984 | 0.064 | 14.239 | 0.596 | 0.596 | 0.913 | −0.913 | |
| 1.075 | 0.042 | 20.014 | 0.492 | 0.492 | 0.840 | −0.840 | |
| 1.193 | 0.031 | 30.311 | 0.437 | 0.437 | 0.930 | −0.930 |
| Soil Type | scon (kPa) | ms (10−2) | ns | logβ | msnsψs | λs | κs |
|---|---|---|---|---|---|---|---|
| Silty-Sand (Salager et al. [36]) | 1 | 0.358 | 7.456 | −0.224 | 0.173 | −0.173 | −0.224 |
| 10 | 6.65 | 2.383 | −0.266 | 0.680 | −0.675 | −0.268 | |
| 100 | 11.7 | 2.729 | −0.394 | 1.028 | −1.027 | −0.395 | |
| 1000 | 7.06 | 3.654 | −0.621 | 1.001 | −1.001 | −0.621 | |
| 10,000 | 16.4e | 4.234 | −0.895 | 1.002 | −1.002 | −0.895 | |
| 100,000 | 33.2 | 1.674 | −1.260 | 1.005 | −1.005 | −1.261 | |
| Sand-Bentonite (Sun & Sun [41]) | 300 | 2.68 | 4.446 | −0.595 | 0.620 | −0.620 | −0.595 |
| 600 | 6.65 | 2.383 | −0.669 | 0.700 | −0.669 | −0.700 | |
| 1200 | 4.77 | 3.373 | −0.905 | 0.533 | −0.905 | −0.533 | |
| 1500 | 5.66 | 2.643 | −1.076 | 0.451 | −0.452 | −1.076 | |
| Silty-Clay (Zhan [42]) | 25 | 1.22 | 5.491 | −0.240 | 0.749 | −0.749 | −0.240 |
| 50 | 5.79 | 3.461 | −0.284 | 0.786 | −0.781 | −0.285 | |
| 100 | 6.62 | 3.491 | −0.339 | 0.676 | −0.668 | −0.341 | |
| 200 | 7.45 | 1.882 | −0.390 | 0.625 | −0.621 | −0.393 | |
| Nonexpansive-Clay (Sun et al. [7]) | 98 | 1.17 | 3.609 | −0.203 | 0.804 | −0.804 | −0.203 |
| 147(CDG) | 2.88 | 4.737 | −0.314 | 0.606 | −0.606 | −0.314 | |
| 147(CDE) | 3.42 | 4.716 | −0.223 | 0.848 | −0.848 | −0.223 | |
| 196 | 2.31 | 2.926 | −0.247 | 0.924 | −0.924 | −0.247 | |
| 245 | 8.49 | 3.017 | −0.333 | 0.785 | −0.784 | −0.333 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.-x.; Zou, W.-l.; Han, Z. An Insight into the Projection Characteristics of the Soil-Water Retention Surface. Water 2018, 10, 1717. https://doi.org/10.3390/w10121717
Ye Y-x, Zou W-l, Han Z. An Insight into the Projection Characteristics of the Soil-Water Retention Surface. Water. 2018; 10(12):1717. https://doi.org/10.3390/w10121717
Chicago/Turabian StyleYe, Yun-xue, Wei-lie Zou, and Zhong Han. 2018. "An Insight into the Projection Characteristics of the Soil-Water Retention Surface" Water 10, no. 12: 1717. https://doi.org/10.3390/w10121717
APA StyleYe, Y.-x., Zou, W.-l., & Han, Z. (2018). An Insight into the Projection Characteristics of the Soil-Water Retention Surface. Water, 10(12), 1717. https://doi.org/10.3390/w10121717






