Use of WRF-Hydro over the Northeast of the US to Estimate Water Budget Tendencies in Small Watersheds
Abstract
1. Background
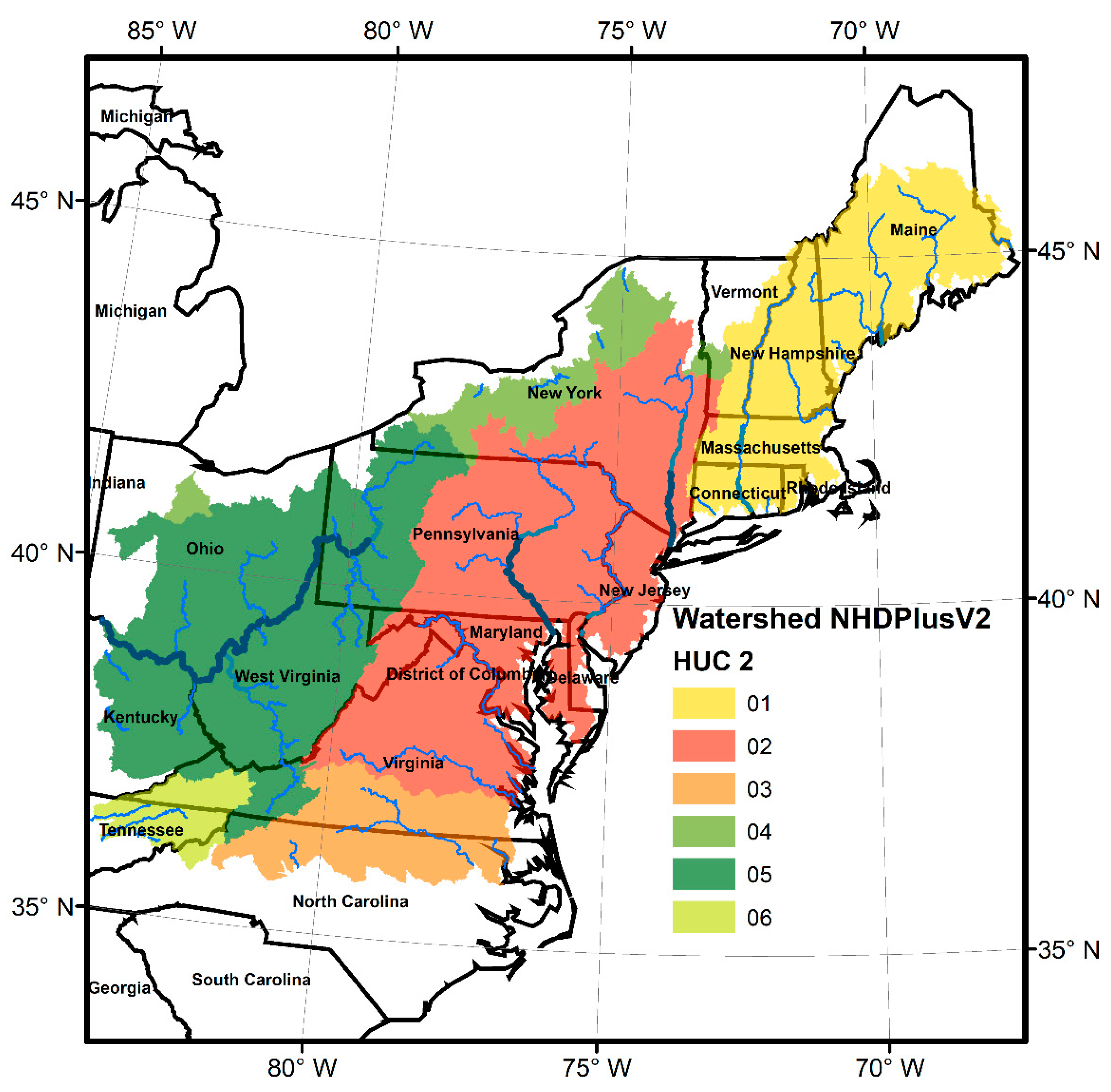
2. Study Area
3. Methods and Data
3.1. North American Land Data Assimilation System (NLDAS-2)
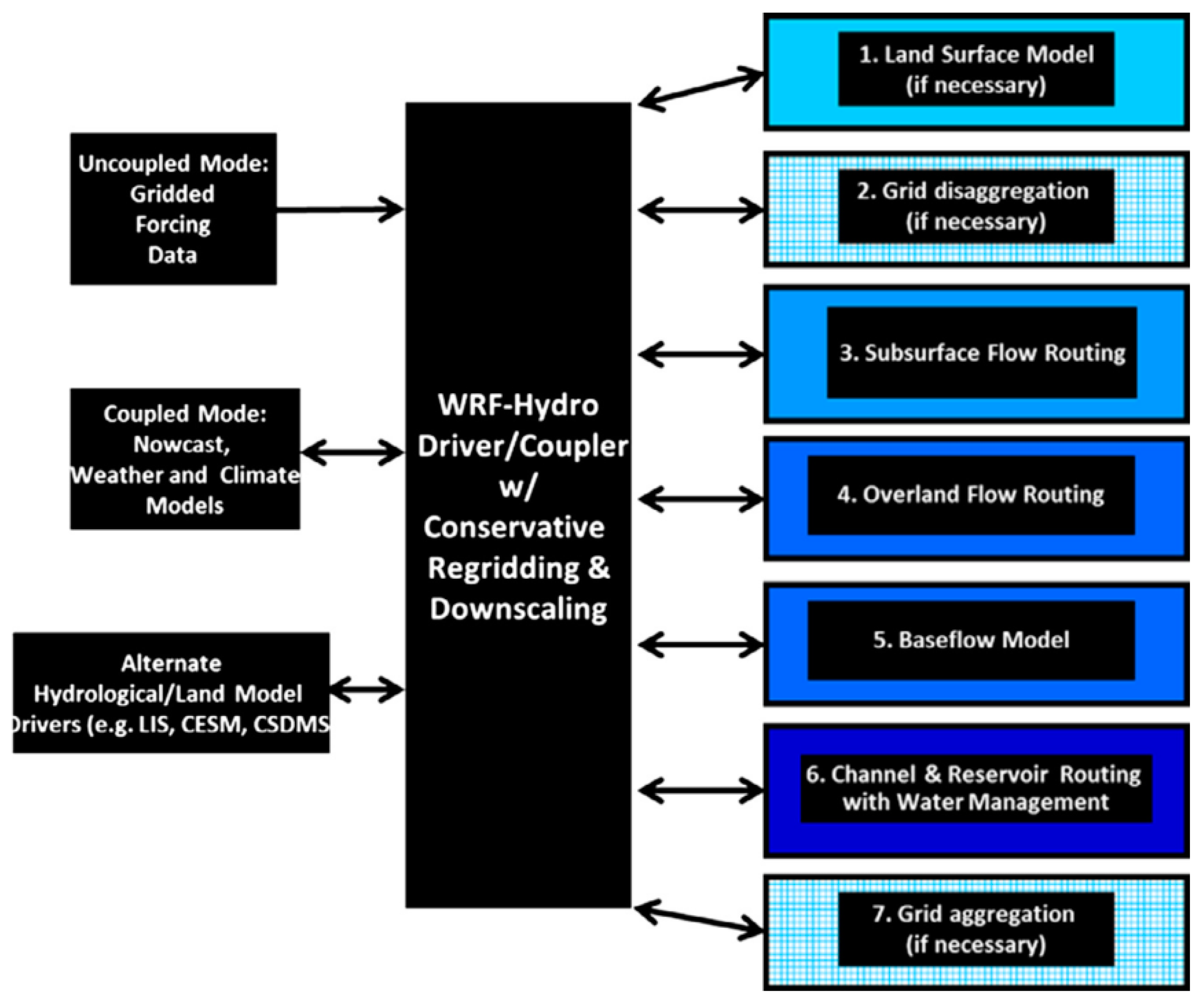
3.2. WRF-Hydro Model
3.3. National Hydrography Dataset Plus Version 2 (NHDplusV2) and RAPID
3.4. Streamflow Data, Calibration, and Spin-Up
3.5. Changes in Streamflow
3.6. Water Budget
4. Results
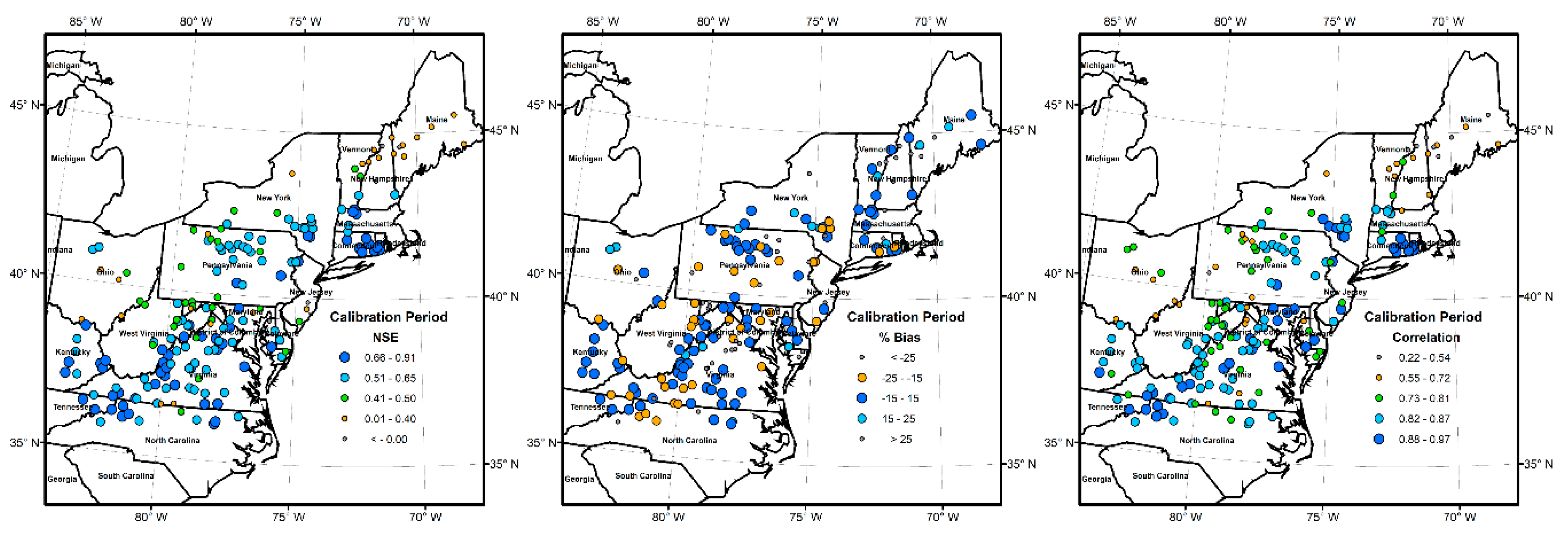
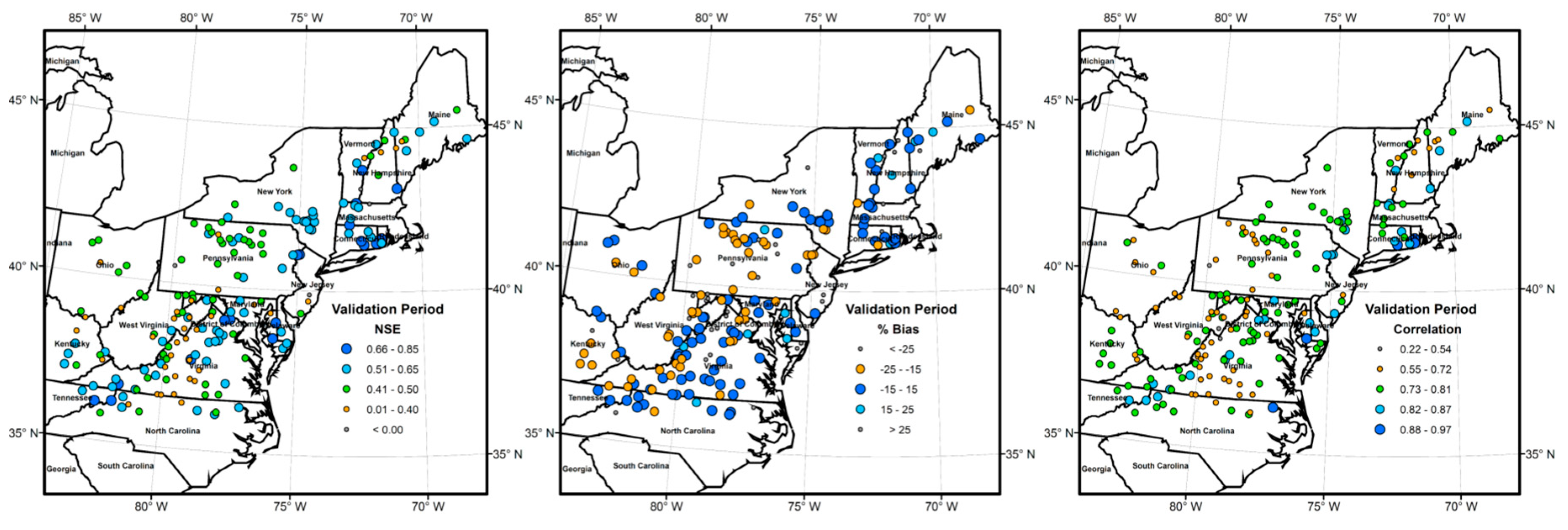
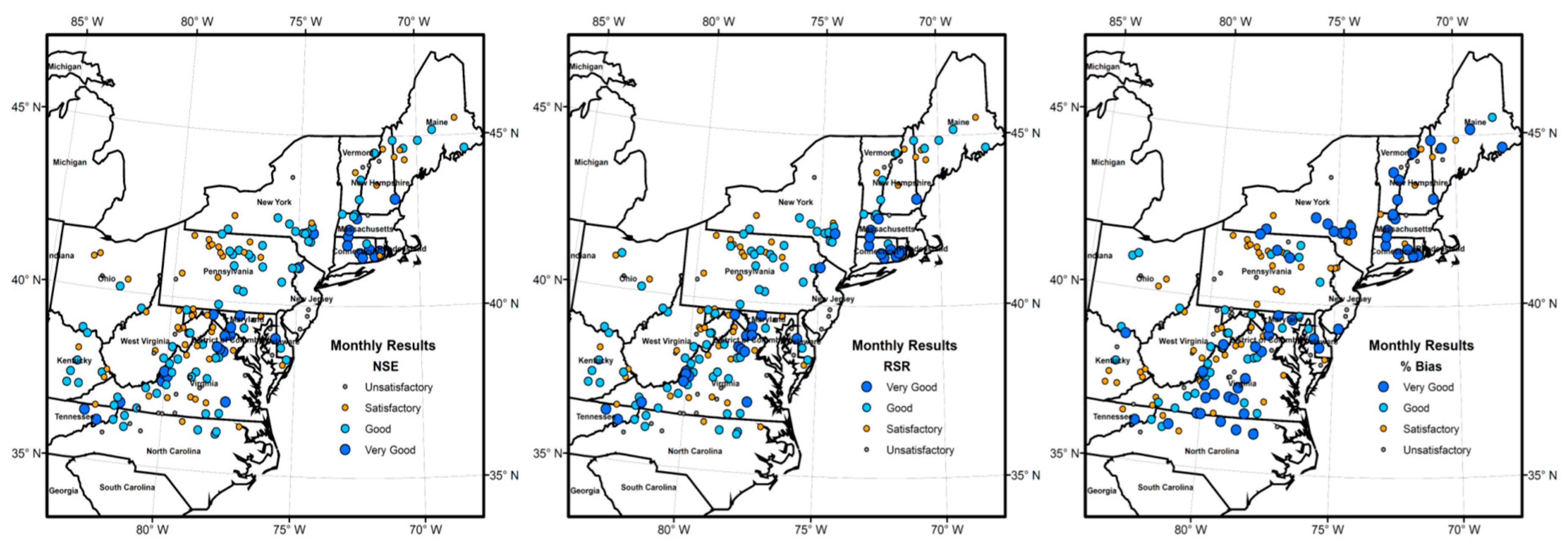
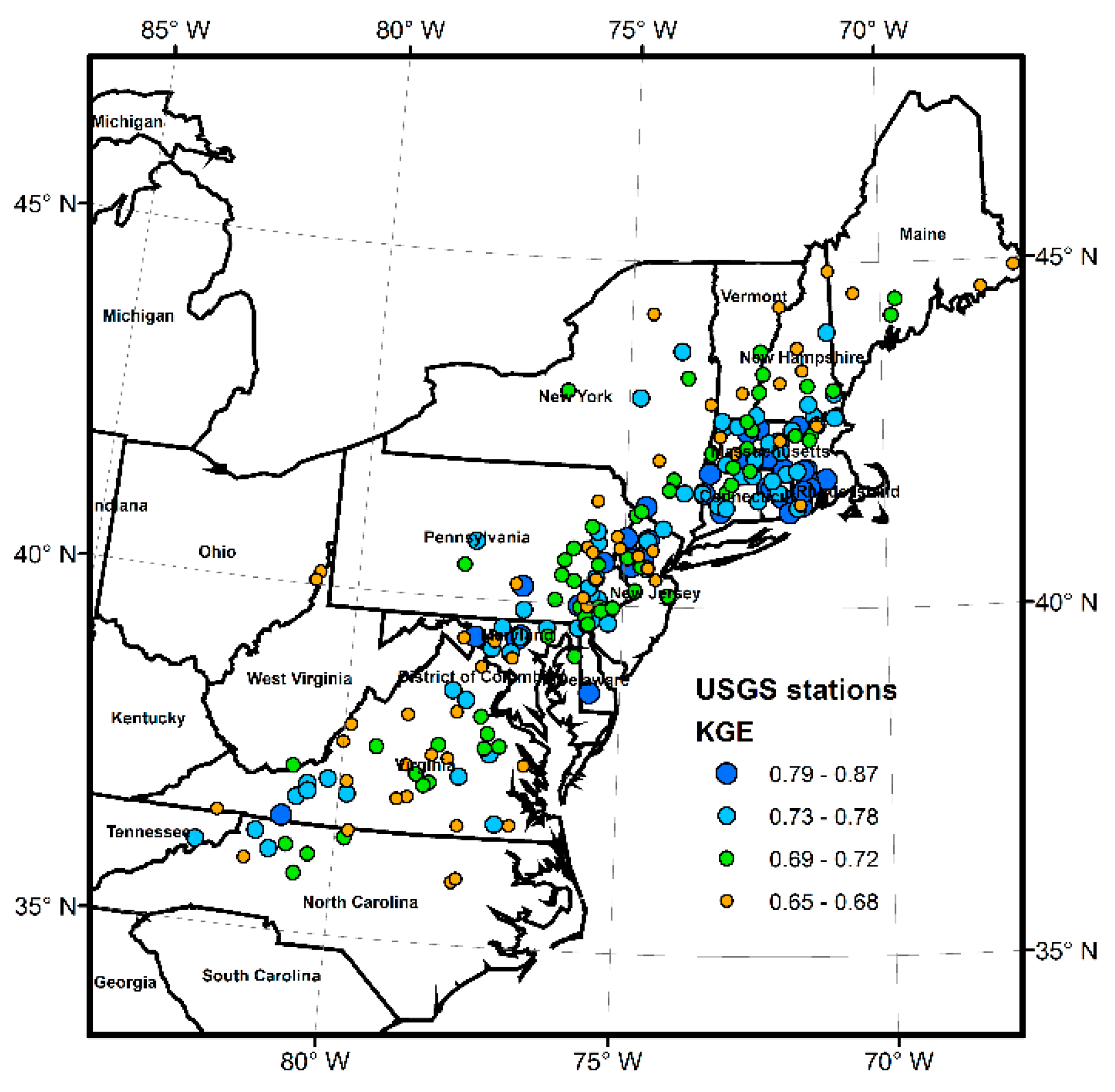
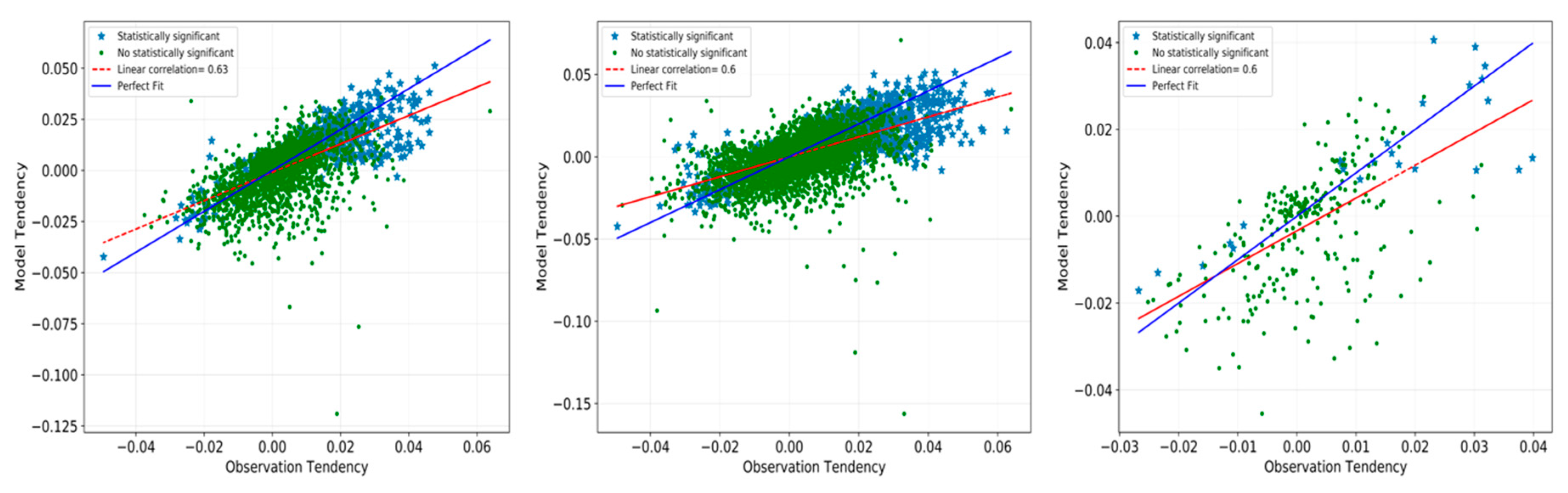
4.1. Performance of the Model
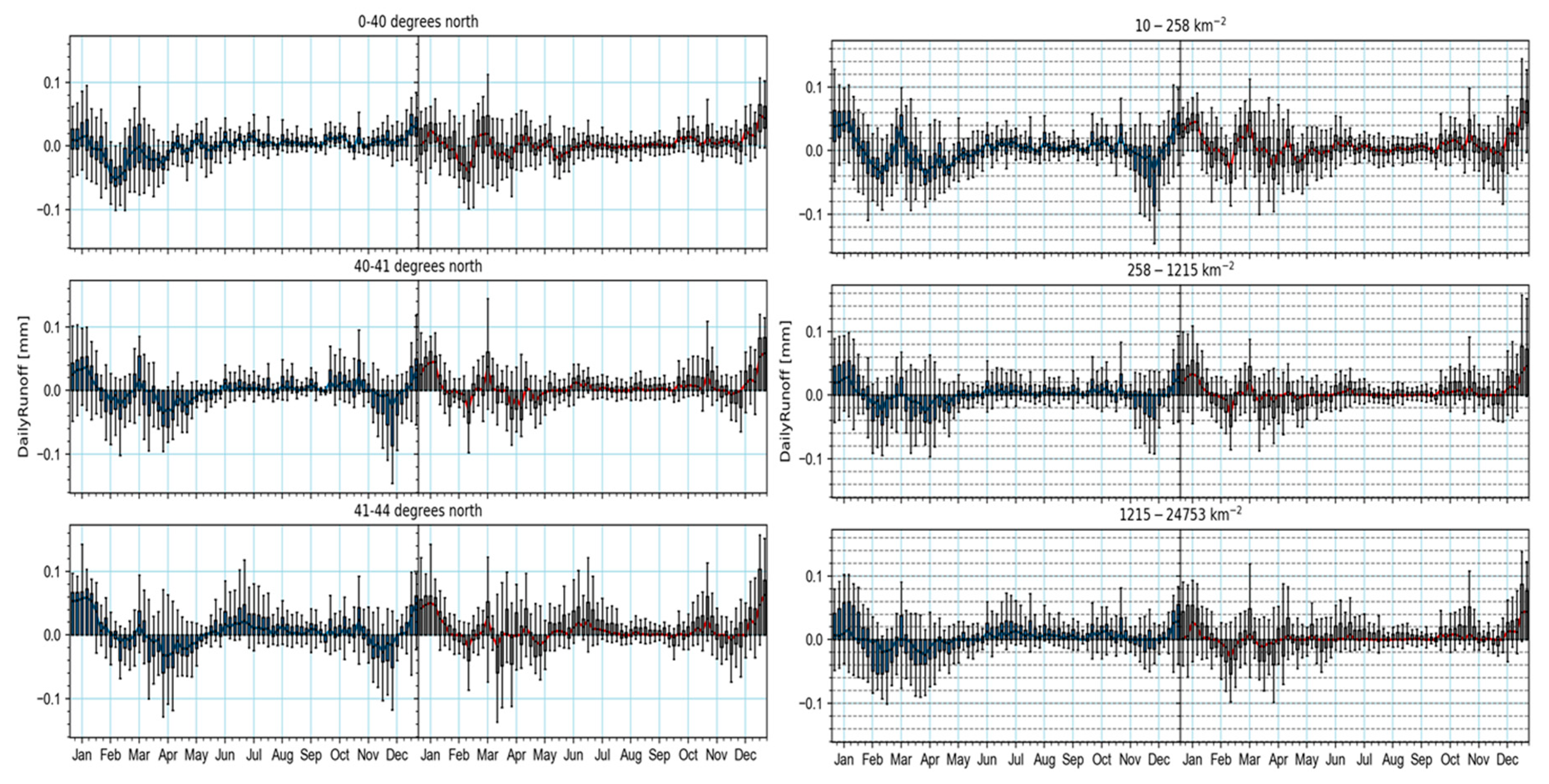
4.2. Changes in Streamflow and Water Budget Components
4.2.1. Three-Day Peak Flow (Q3)
4.2.2. Seven-Day Low Flow (Q7)
4.2.3. Five-Day Means (5)
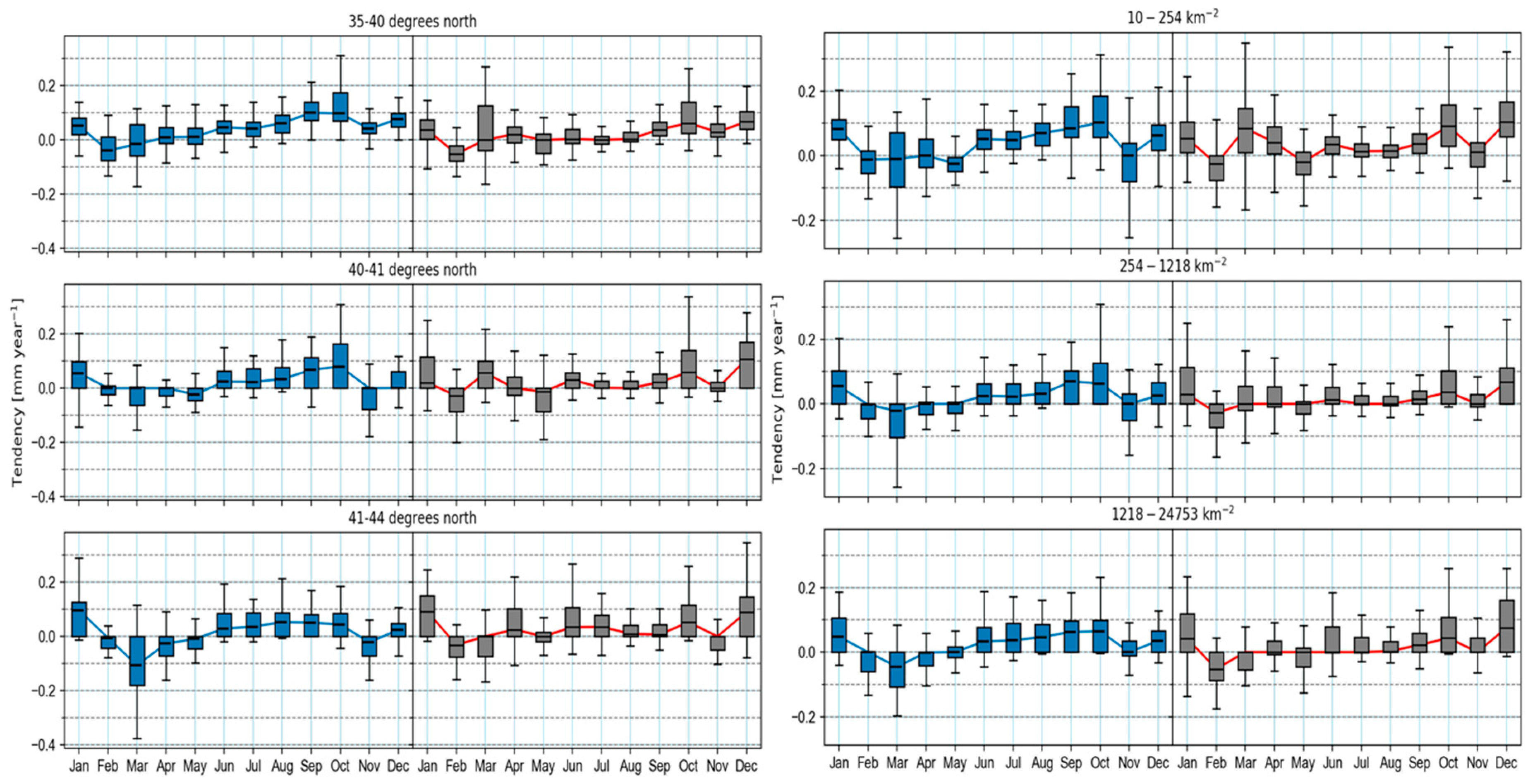
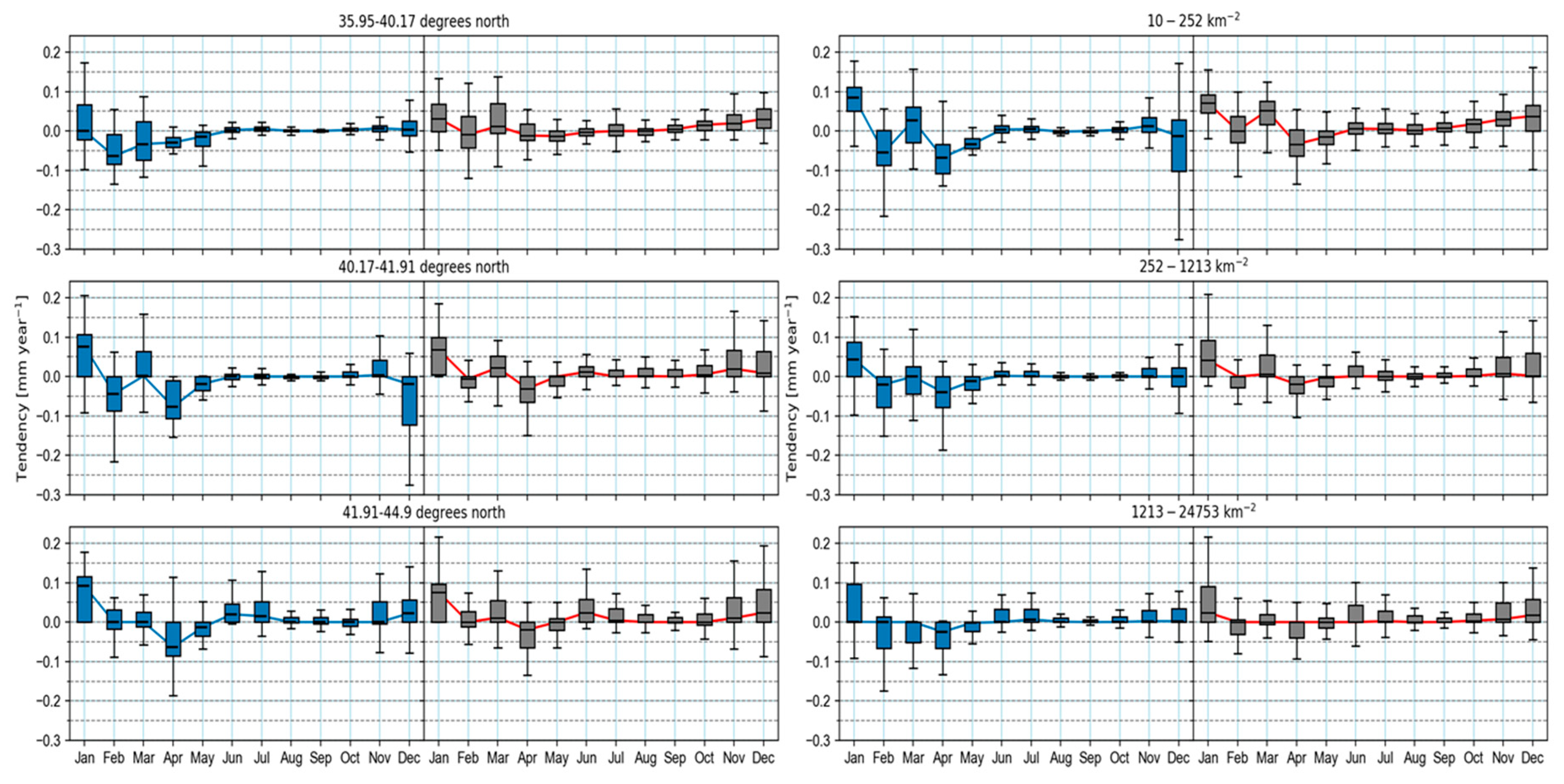
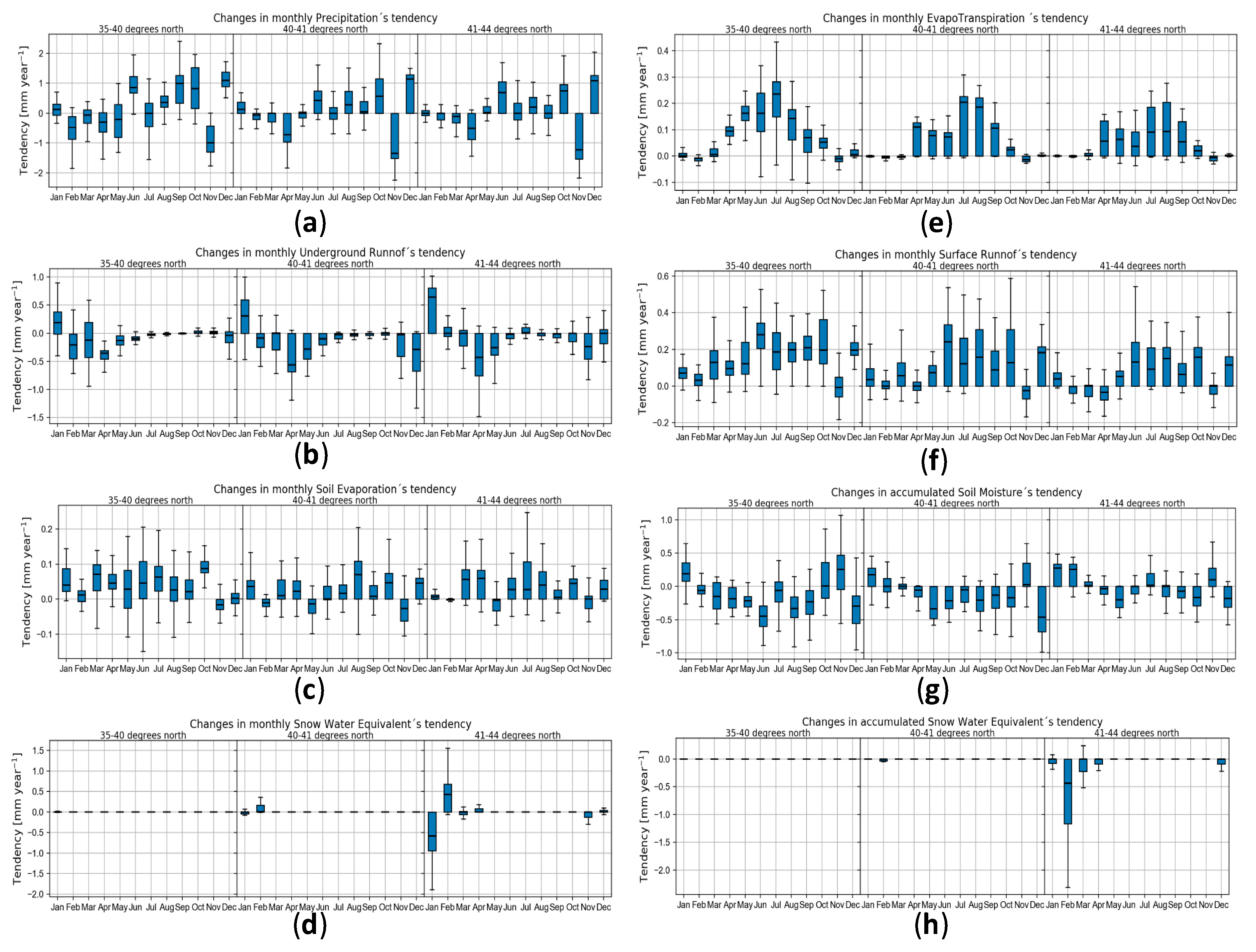
4.3. Water Budget
5. Discussion
5.1. Model Performance
5.2. Streamflow Tendency
5.3. Water Budget Tendencies
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karmalkar, A.V.; Bradley, R.S. Consequences of Global Warming of 1.5 °C and 2 °C for Regional Temperature and Precipitation Changes in the Contiguous United States. PLoS ONE 2017, 12, e0168697. [Google Scholar] [CrossRef] [PubMed]
- Berton, R.; Driscoll, C.T.; Chandler, D.G. Changing climate increases discharge and attenuates its seasonal distribution in the northeastern United States. J. Hydrol. Reg. Stud. 2016, 5, 164–178. [Google Scholar] [CrossRef]
- Hayhoe, K.; Wake, C.P.; Huntington, T.G.; Luo, L.; Schwartz, M.D.; Sheffield, J.; Wood, E.; Anderson, B.; Bradbury, J.; DeGaetano, A.; et al. Past and future changes in climate and hydrological indicators in the US Northeast. Clim. Dyn. 2007, 28, 381–407. [Google Scholar] [CrossRef]
- Dudley, R.W.; Hodgkins, G.A.; McHale, M.R.; Kolian, M.J.; Renard, B. Trends in snowmelt-related streamflow timing in the conterminous United States. J. Hydrol. 2017, 547, 208–221. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Knight, R.W.; Karl, T.R. Heavy precipitation and high streamflow in the contiguous United States: Trends in the twentieth century. Bull. Am. Meteorol. Soc. 2001, 82, 219–246. [Google Scholar] [CrossRef]
- Horton, R.; Yohe, G.; Easterling, W.; Kates, R.; Ruth, M.; Sussman, E.; Whelchel, A.; Wolfe, D.; Lipschultz, F. Chapter 16: Northeast. In Climate Change Impacts in the United States: The Third National Climate Assessment; Melillo, J.M., Richmond, T.T.C., Yohe, G.W., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2014. [Google Scholar]
- Bose, A.K.; Weiskittel, A.; Wagner, R.G. A three decade assessment of climate-associated changes in forest composition across the north-eastern USA. J. Appl. Ecol. 2017, 54, 1592–1604. [Google Scholar] [CrossRef]
- Sanders-DeMott, R.; McNellis, R.; Jabouri, M.; Templer, P.H. Snow depth, soil temperature and plant–herbivore interactions mediate plant response to climate change. J. Ecol. 2018, 106, 1508–1519. [Google Scholar] [CrossRef]
- Brin, L.D.; Goyer, C.; Zebarth, B.J.; Burton, D.L.; Chantigny, M.H. Changes in snow cover alter nitrogen cycling and gaseous emissions in agricultural soils. Agric. Ecosyst. Environ. 2018, 258, 91–103. [Google Scholar] [CrossRef]
- Contosta, A.R.; Burakowski, E.A.; Varner, R.K.; Frey, S.D. Winter soil respiration in a humid temperate forest: The roles of moisture, temperature, and snowpack. J. Geophys. Res. Biogeosci. 2016, 121, 3072–3088. [Google Scholar] [CrossRef]
- Patel, K.F.; Tatariw, C.; MacRae, J.D.; Ohno, T.; Nelson, S.J.; Fernandez, I.J. Soil carbon and nitrogen responses to snow removal and concrete frost in a northern coniferous forest. Can. J. Soil Sci. 2018, 12, 1–12. [Google Scholar] [CrossRef]
- Sanders-DeMott, R.; Sorensen, P.O.; Reinmann, A.B.; Templer, P.H. Growing season warming and winter freeze–thaw cycles reduce root nitrogen uptake capacity and increase soil solution nitrogen in a northern forest ecosystem. Biogeochemistry 2018, 137, 337–349. [Google Scholar] [CrossRef]
- Armstrong, W.H.; Collins, M.J.; Snyder, N.P. Hydroclimatic flood trends in the northeastern United States and linkages with large-scale atmospheric circulation patterns. Hydrol. Sci. J. 2014, 59, 1636–1655. [Google Scholar] [CrossRef]
- Armstrong, W.H.; Collins, M.J.; Snyder, N.P. Increased Frequency of Low-Magnitude Floods in New England. J. Am. Water Resour. Assoc. 2012, 48, 306–320. [Google Scholar] [CrossRef]
- Demaria, E.M.; Roundy, J.K.; Wi, S.; Palmer, R.N. The Effects of Climate Change on Seasonal Snowpack and the Hydrology of the Northeastern and Upper Midwest United States. J. Clim. 2016, 29, 6527–6541. [Google Scholar] [CrossRef]
- Chezik, K.A.; Anderson, S.C.; Moore, J.W. River networks dampen long-term hydrological signals of climate change. Geophys. Res. Lett. 2017, 44. [Google Scholar] [CrossRef]
- Hodgkins, G.A.; Dudley, R.W.; Huntington, T.G. Changes in the timing of high river flows in New England over the 20th Century. J. Hydrol. 2003, 278, 244–252. [Google Scholar] [CrossRef]
- Kam, J.; Sheffield, J. Changes in the low flow regime over the eastern United States (1962–2011): Variability, trends, and attributions. Clim. Chang. 2016, 135, 639–653. [Google Scholar] [CrossRef]
- Salas, F.R.; Somos-Valenzuela, M.A.; Dugger, A.; Maidment, D.R.; Gochis, D.J.; David, C.H.; Yu, W.; Ding, D.; Clark, E.P.; Noman, N. Towards Real-Time Continental Scale Streamflow Simulation in Continuous and Discrete Space. JAWRA J. Am. Water Resour. Assoc. 2017. [Google Scholar] [CrossRef]
- Lin, P.; Rajib, M.A.; Yang, Z.; Somos-Valenzuela, M.; Merwade, V.; Maidment, D.R.; Wang, Y.; Chen, L. Spatiotemporal Evaluation of Simulated Evapotranspiration and Streamflow over Texas using the WRF-Hydro-RAPID Modeling Framework. JAWRA J. Am. Water Resour. Assoc. 2017, 40–54. [Google Scholar] [CrossRef]
- Maidment, D.R. Conceptual Framework for the National Flood Interoperability Experiment. JAWRA J. Am. Water Resour. Assoc. 2017, 53, 245–257. [Google Scholar] [CrossRef]
- Gochis, D.; Yu, W.; Yates, D. WRF—Hydro Technical Description and User’s Guide Version 3; Center for Atmospheric Research (NCAR): Boulder, CO, USA, 2015. [Google Scholar]
- Yang, Z.; Cai, X.; Zhang, G.; Tavakoly, A.; Jin, Q.; Meyer, L.H.; Guan, X. The Community Noah Land Surface Model with Multi-Parameterization Options: Technical Description; Center for Integrated Earth System Science, The University of Texas at Austin: Austin, TX, USA, 2011. [Google Scholar]
- Yang, Z.-L.; Niu, G.-Y.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Longuevergne, L.; Manning, K.; Niyogi, D.; Tewari, M.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 2. Evaluation over global river basins. J. Geophys. Res. 2011, 116, D12110. [Google Scholar] [CrossRef]
- David, C.H.; Maidment, D.R.; Niu, G.-Y.; Yang, Z.-L.; Habets, F.; Eijkhout, V. River Network Routing on the NHDPlus Dataset. J. Hydrometeorol. 2011, 12, 913–934. [Google Scholar] [CrossRef]
- David, C.H.; Yang, Z.L.; Hong, S. Regional-scale river flow modeling using off-the-shelf runoff products, thousands of mapped rivers and hundreds of stream flow gauges. Environ. Model. Softw. 2013, 42, 116–132. [Google Scholar] [CrossRef]
- Lin, P.; Yang, Z.-L.; Gochis, D.J.; Yu, W.; Maidment, D.R.; Somos-Valenzuela, M.A.; David, C.H. Implementation of a vector-based river network routing scheme in the community WRF-Hydro modeling framework for flood discharge simulation. Environ. Model. Softw. 2018, 107, 1–11. [Google Scholar] [CrossRef]
- Lin, P.; Yang, Z.; Cai, X.; David, C.H. Regional Studies Development and evaluation of a physically-based lake level model for water resource management: A case study for Lake. J. Hydrol. 2015, 4, 661–674. [Google Scholar] [CrossRef]
- Cai, X.; Yang, Z.; Xia, Y.; Huang, M.; Wei, H.; Leung, L.R.; Ek, M.B. Assessment of simulated water balance from Noah, Noah-MP, CLM, and VIC over CONUS using the NLDAS test bed. J. Geophys. Res. Atmos. 2014, 119, 13–751. [Google Scholar] [CrossRef]
- Givati, A.; Gochis, D.; Rummler, T.; Kunstmann, H. Comparing One-Way and Two-Way Coupled Hydrometeorological Forecasting Systems for Flood Forecasting in the Mediterranean Region. Hydrology 2016, 3, 19. [Google Scholar] [CrossRef]
- Yucel, I.; Onen, A.; Yilmaz, K.K.; Gochis, D.J. Calibration and evaluation of a flood forecasting system: Utility of numerical weather prediction model, data assimilation and satellite-based rainfall. J. Hydrol. 2015, 523, 49–66. [Google Scholar] [CrossRef]
- Houska, T.; Kraft, P.; Chamorro-Chavez, A.; Breuer, L. SPOTting model parameters using a ready-made python package. PLoS ONE 2015, 10, e0145180. [Google Scholar] [CrossRef] [PubMed]
- Senatore, A.; Mendicino, G.; Gochis, D.J.; Yu, W.; Yates, D.N.; Kunstmann, H. Fully coupled atmosphere-hydrology simulations for the central Mediterranean: Impact of enhanced hydrological parameterization for short and long time scales. J. Adv. Model. Earth Syst. 2015, 7, 1693–1715. [Google Scholar] [CrossRef]
- Niu, G.-Y. The Community Noah Land Surface Model (LSM) with Multi-Physics Options, User’s Guide; Center for Integrated Earth System Science, The University of Texas at Austin: Austin, TX, USA, 2011. [Google Scholar]
- Mitchell, K.; Ek, M.; Wong, V.; Lohmann, D.; Koren, V.; Schaake, J.; Duan, Q.; Gayno, G.; Moore, B.; Grunmann, P.; et al. Noah Land Surface Model (LSM) User’s Guide; Noah: Corvallis, OR, USA, 2005. [Google Scholar]
- Déry, S.J.; Stahl, K.; Moore, R.D.; Whitfield, P.H.; Menounos, B.; Burford, J.E. Detection of runoff timing changes in pluvial, nival, and glacial rivers of western Canada. Water Resour. Res. 2009, 45, 1–11. [Google Scholar] [CrossRef]
- Demaria, E.M.; Palmer, R.N.; Roundy, J.K. Regional climate change projections of streamflow characteristics in the Northeast and Midwest U.S. J. Hydrol. Reg. Stud. 2016, 5, 309–323. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Andréassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420–421, 171–182. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Maurer, E.P.; Adam, J.C.; Wood, A.W. Climate model based consensus on the hydrologic impacts of climate change to the Rio Lempa basin of Central America. Hydrol. Earth Syst. Sci. 2009, 13, 183–194. [Google Scholar] [CrossRef]
- Maurer, E.P.; Brekke, L.D.; Pruitt, T. Contrasting lumped and distributed hydrology models for estimating climate change impacts on California watersheds. J. Am. Water Resour. Assoc. 2010, 46, 1024–1035. [Google Scholar] [CrossRef]
- Das, T.; Dettinger, M.D.; Cayan, D.R.; Hidalgo, H.G. Potential increase in floods in California’s Sierra Nevada under future climate projections. Clim. Chang. 2011, 109, 71–94. [Google Scholar] [CrossRef]
- WMO. Manual on Low-Flow Estimation and Prediction; WMO: Geneva, Switzerland, 2008; ISBN 9789263110299. [Google Scholar]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources. In Techniques of Water-Resources Investigations, Book 4; Chapter A3; U.S. Geological Survey: Reston, VA, USA, 2002. [Google Scholar]
- Liuzzo, L.; Freni, G. Analysis of Extreme Rainfall Trends in Sicily for the Evaluation of Depth-Duration-Frequency Curves in Climate Change Scenarios. J. Hydrol. Eng. 2015, 20, 04015036. [Google Scholar] [CrossRef]
- Seyednasrollah, B.; Swenson, J.J.; Domec, J.C.; Clark, J.S. Leaf phenology paradox: Why warming matters most where it is already warm. Remote Sens. Environ. 2018, 209, 446–455. [Google Scholar] [CrossRef]
| Physic’s Name | Model Selected in the Namelist |
|---|---|
| Dynamic Vegetation Option | 1-> Table LAI |
| Canopy Stomatal Resistance Option | 2-> Jarvis |
| Soil moisture factor for stomatal resistance | 1-> Noah |
| Runoff and groundwater | 3->Schaake96 |
| Surface layer drag coefficient | 1-> M-O |
| Frozen soil permeability | 1-> NY06 |
| Supercooled liquid water | 1-> NY06 |
| Radiation transfer | 1-> gap = F(3D, cosz) |
| Snow surface albedo | 2-> CLASS |
| Rainfall & snowfall | 1-Jordan91 |
| Lower boundary of soil temperature | 2-> Noah |
| snow/soil temperature time scheme | 1-> semi-implicit |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somos-Valenzuela, M.A.; Palmer, R.N. Use of WRF-Hydro over the Northeast of the US to Estimate Water Budget Tendencies in Small Watersheds. Water 2018, 10, 1709. https://doi.org/10.3390/w10121709
Somos-Valenzuela MA, Palmer RN. Use of WRF-Hydro over the Northeast of the US to Estimate Water Budget Tendencies in Small Watersheds. Water. 2018; 10(12):1709. https://doi.org/10.3390/w10121709
Chicago/Turabian StyleSomos-Valenzuela, Marcelo A., and Richard N. Palmer. 2018. "Use of WRF-Hydro over the Northeast of the US to Estimate Water Budget Tendencies in Small Watersheds" Water 10, no. 12: 1709. https://doi.org/10.3390/w10121709
APA StyleSomos-Valenzuela, M. A., & Palmer, R. N. (2018). Use of WRF-Hydro over the Northeast of the US to Estimate Water Budget Tendencies in Small Watersheds. Water, 10(12), 1709. https://doi.org/10.3390/w10121709





