Improved Forecasting of Extreme Monthly Reservoir Inflow Using an Analogue-Based Forecasting Method: A Case Study of the Sirikit Dam in Thailand
Abstract
1. Introduction
2. Study Area and Methods
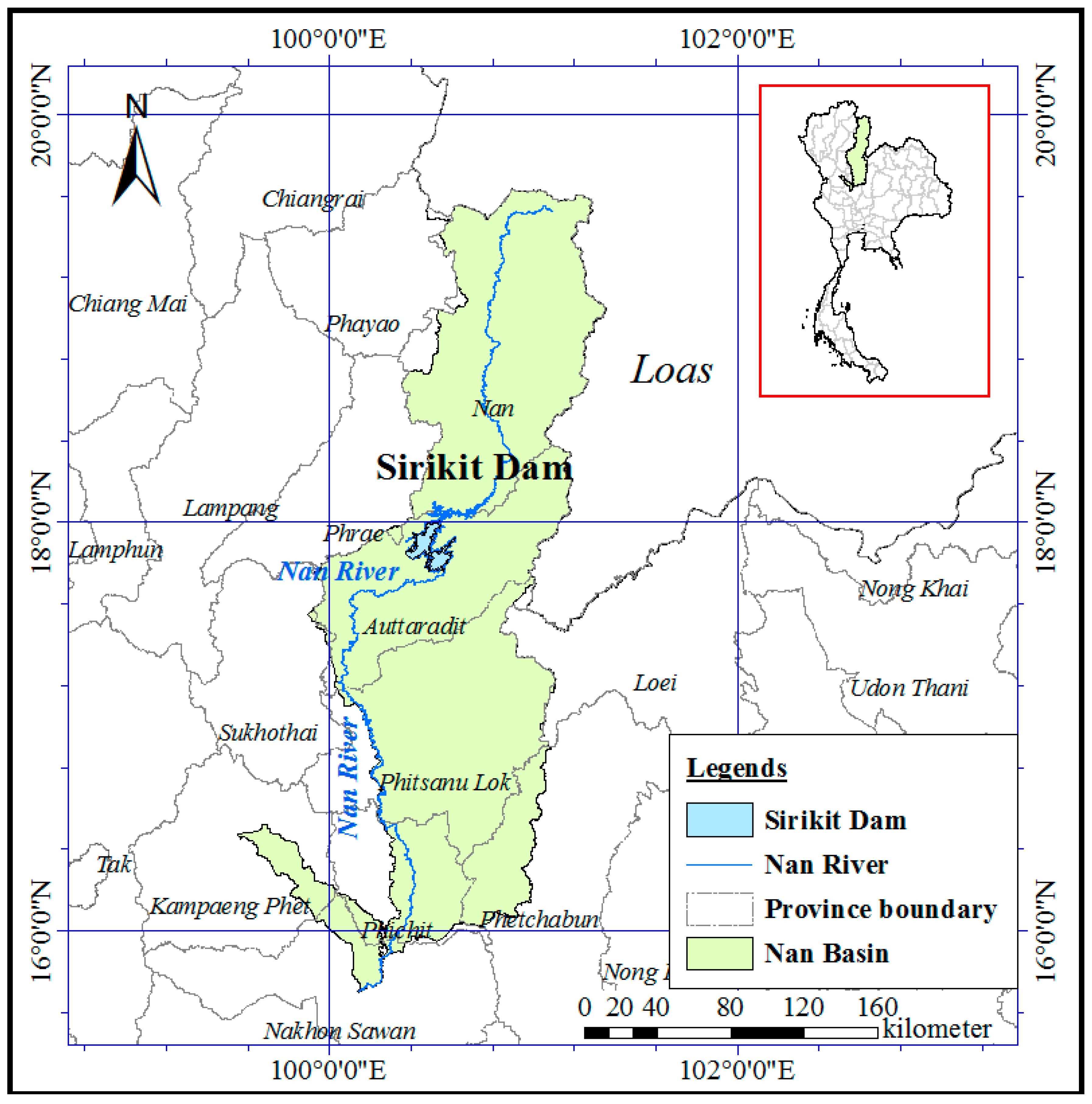
2.1. Study Area and Data
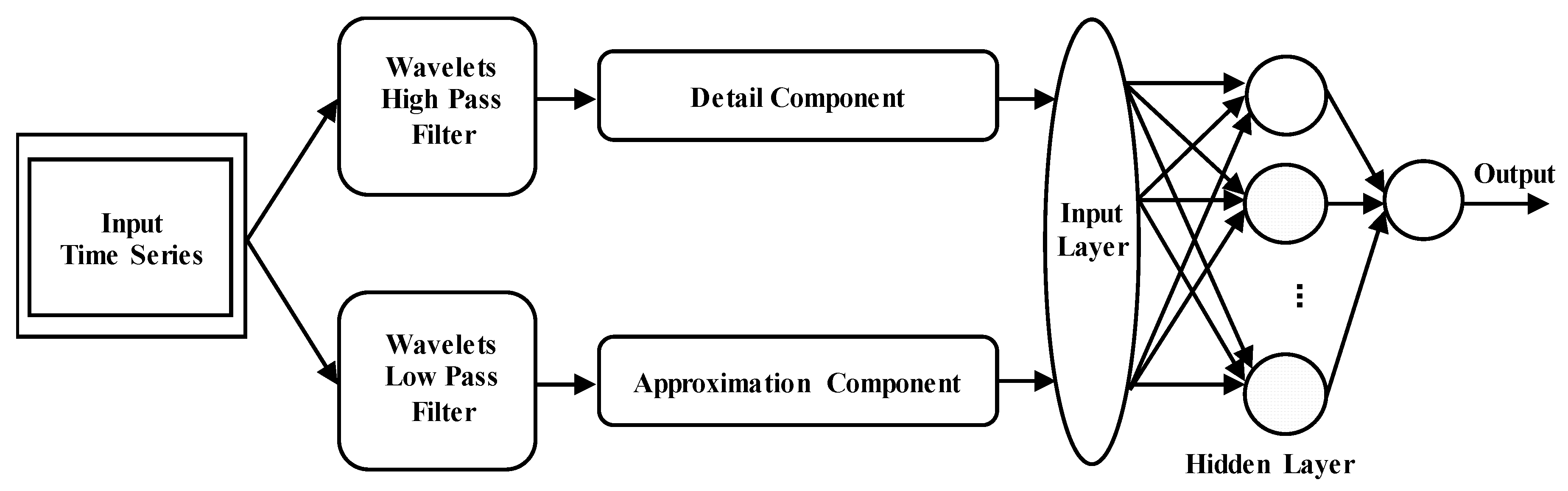
2.2. Wavelet Artificial Neural Network
2.3. Weighted Mean Analogue Method
2.4. Variation Analogue Method
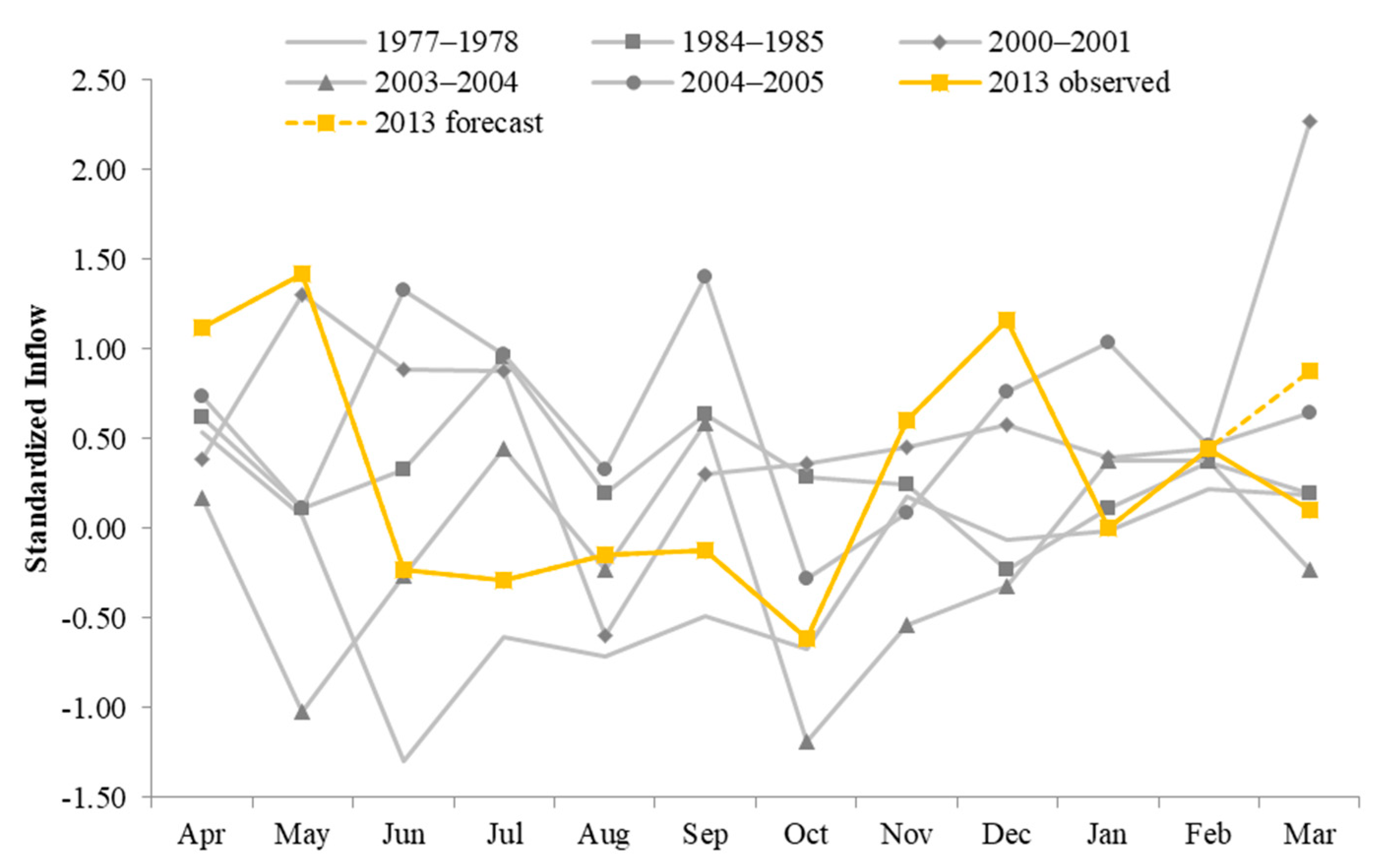
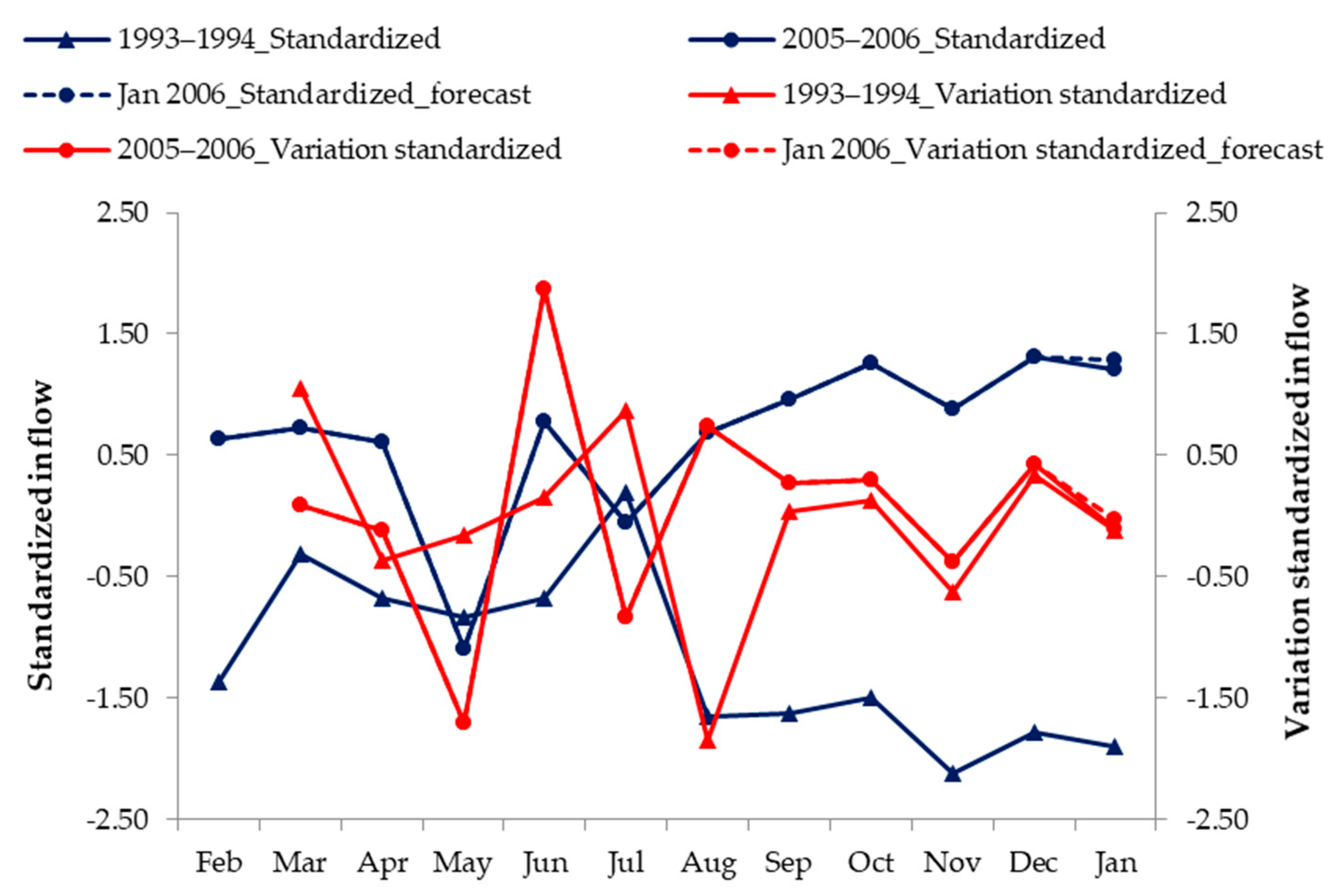
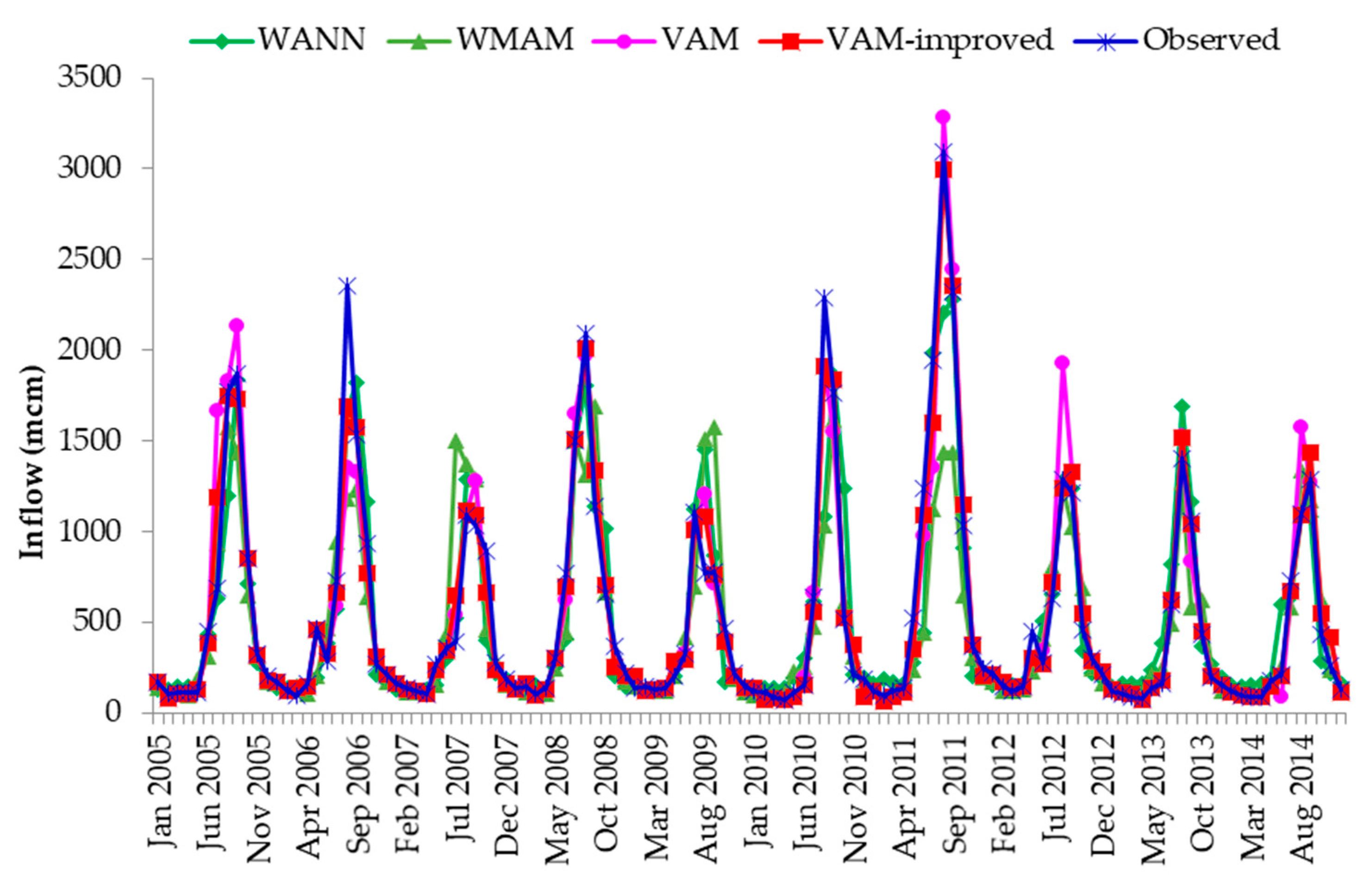
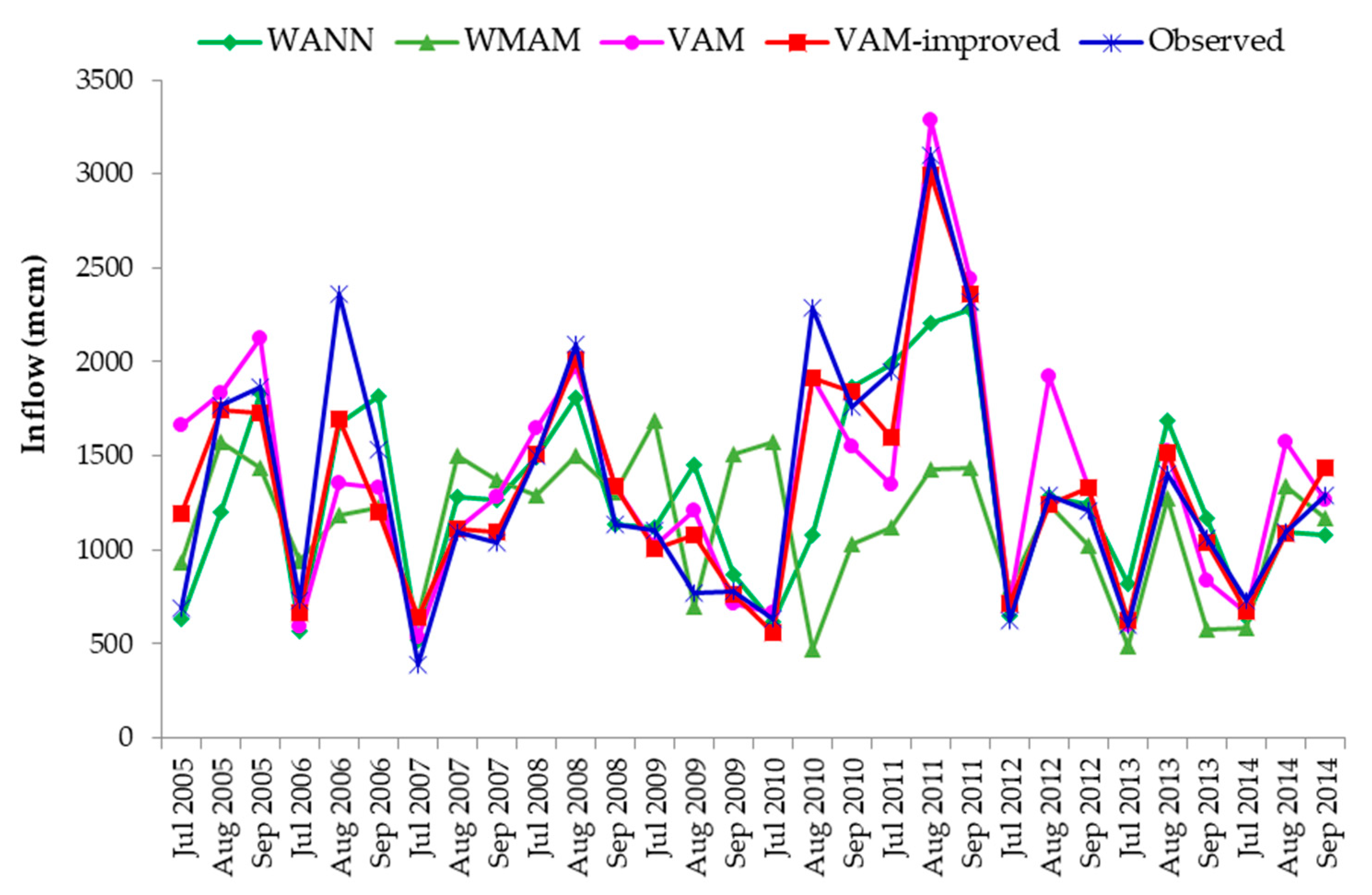
3. Results
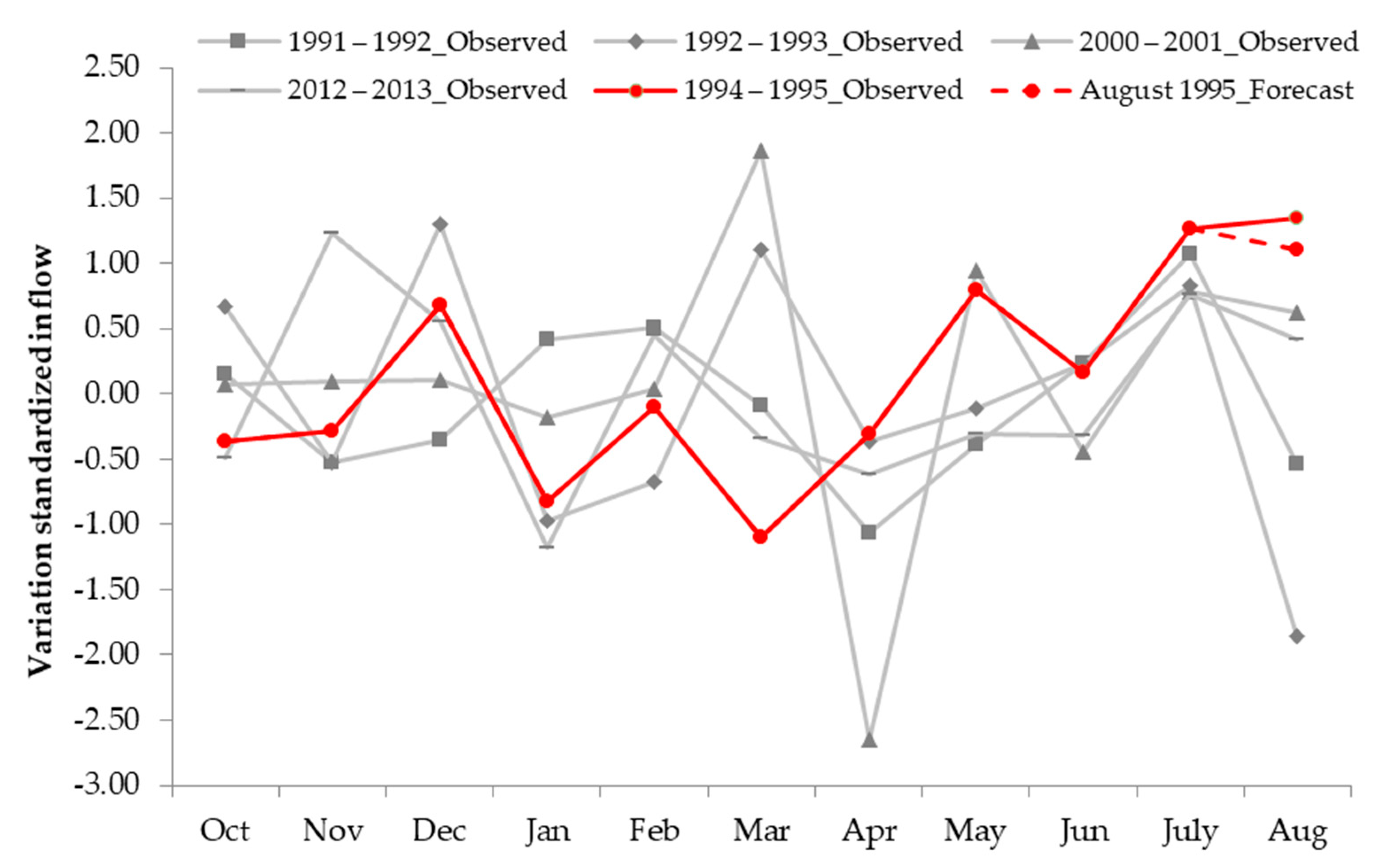
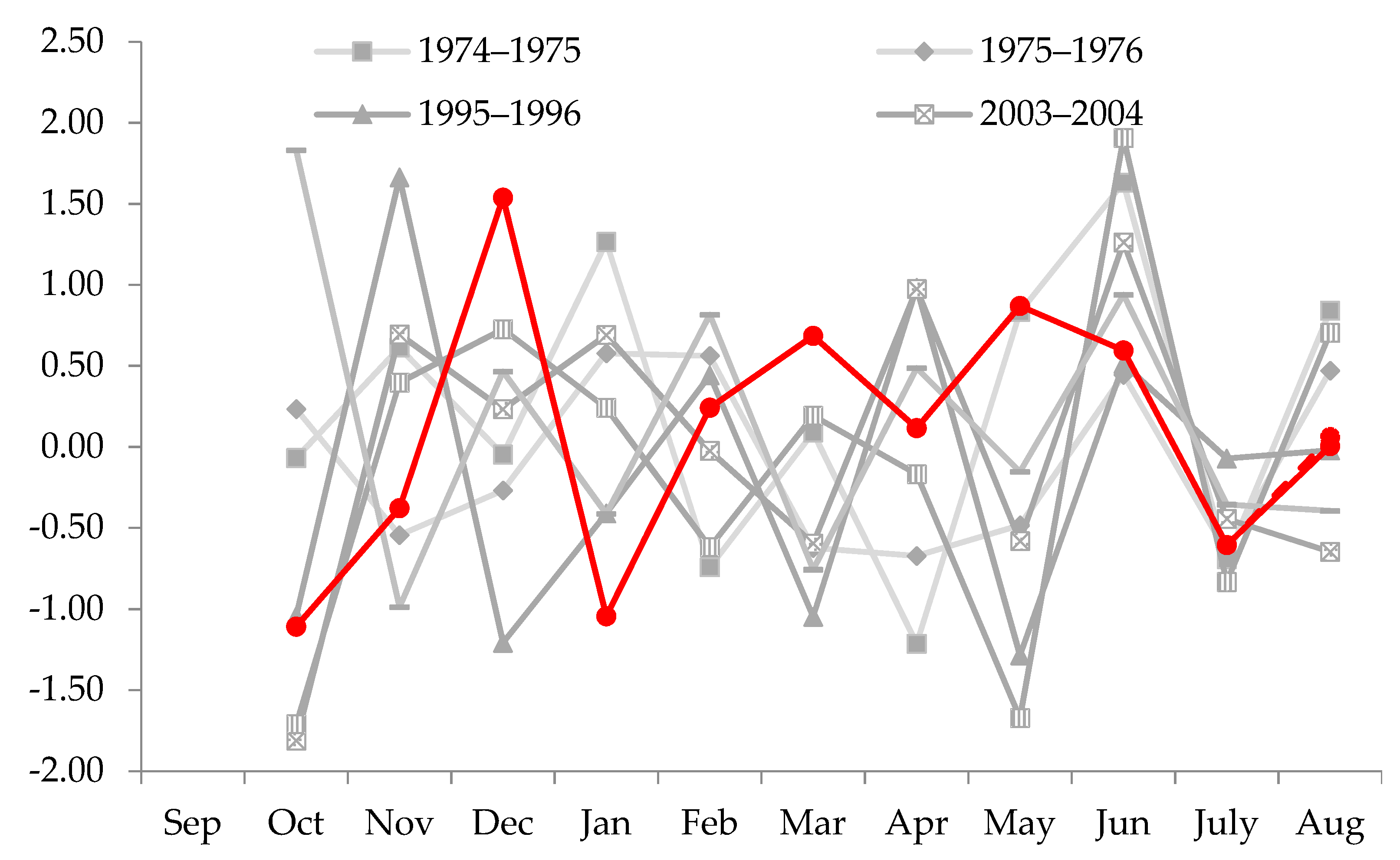
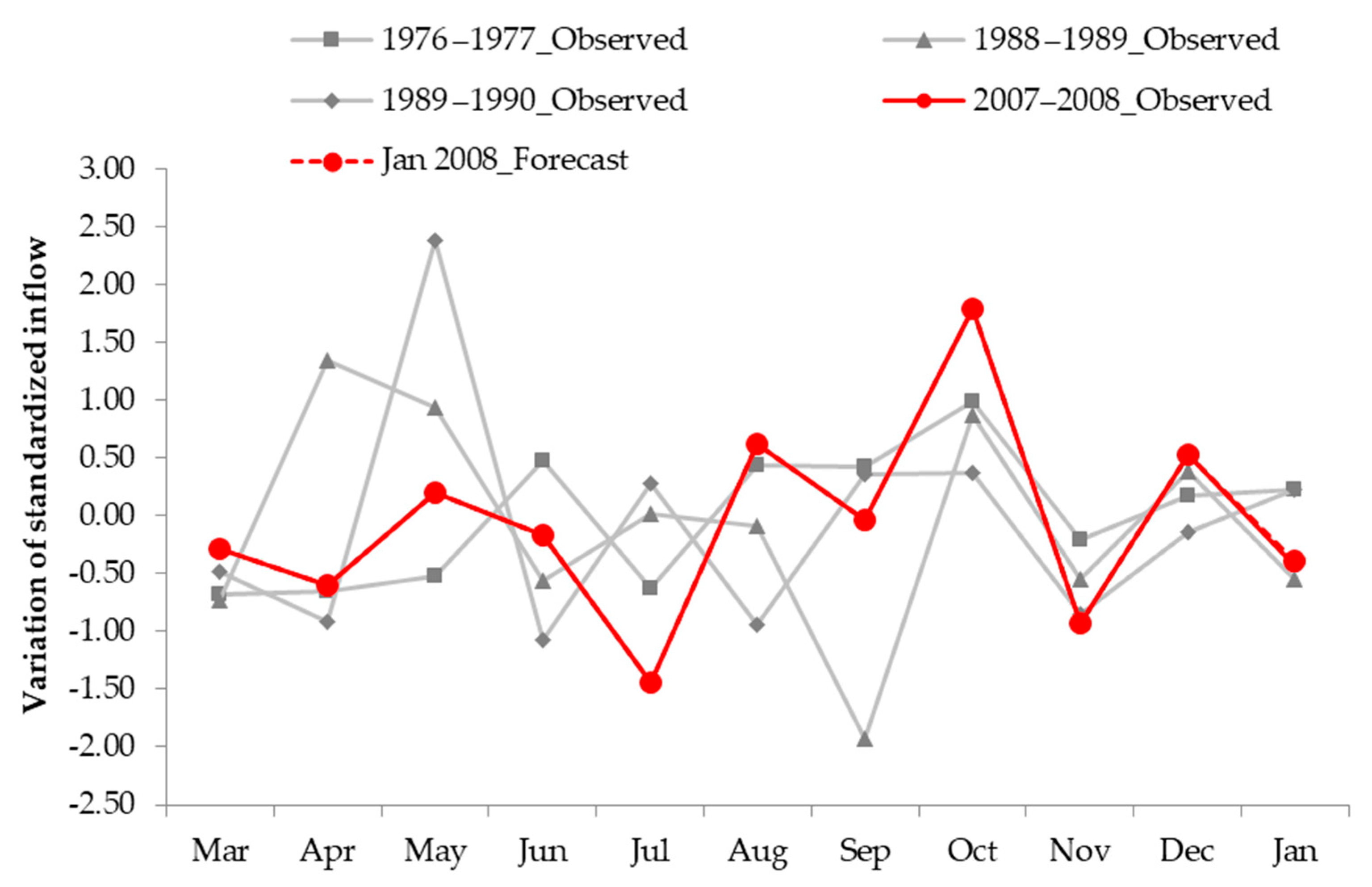
- The variations in standardized inflows for March to December 2007 are plotted along with the variations in standardized inflows for March to January of the available analogues. Potential analogues with variation patterns similar to that of December 2007 are selected. In this case, there are three historical analogue candidates: December 1976, December 1988, and December 1989 (Figure 6).
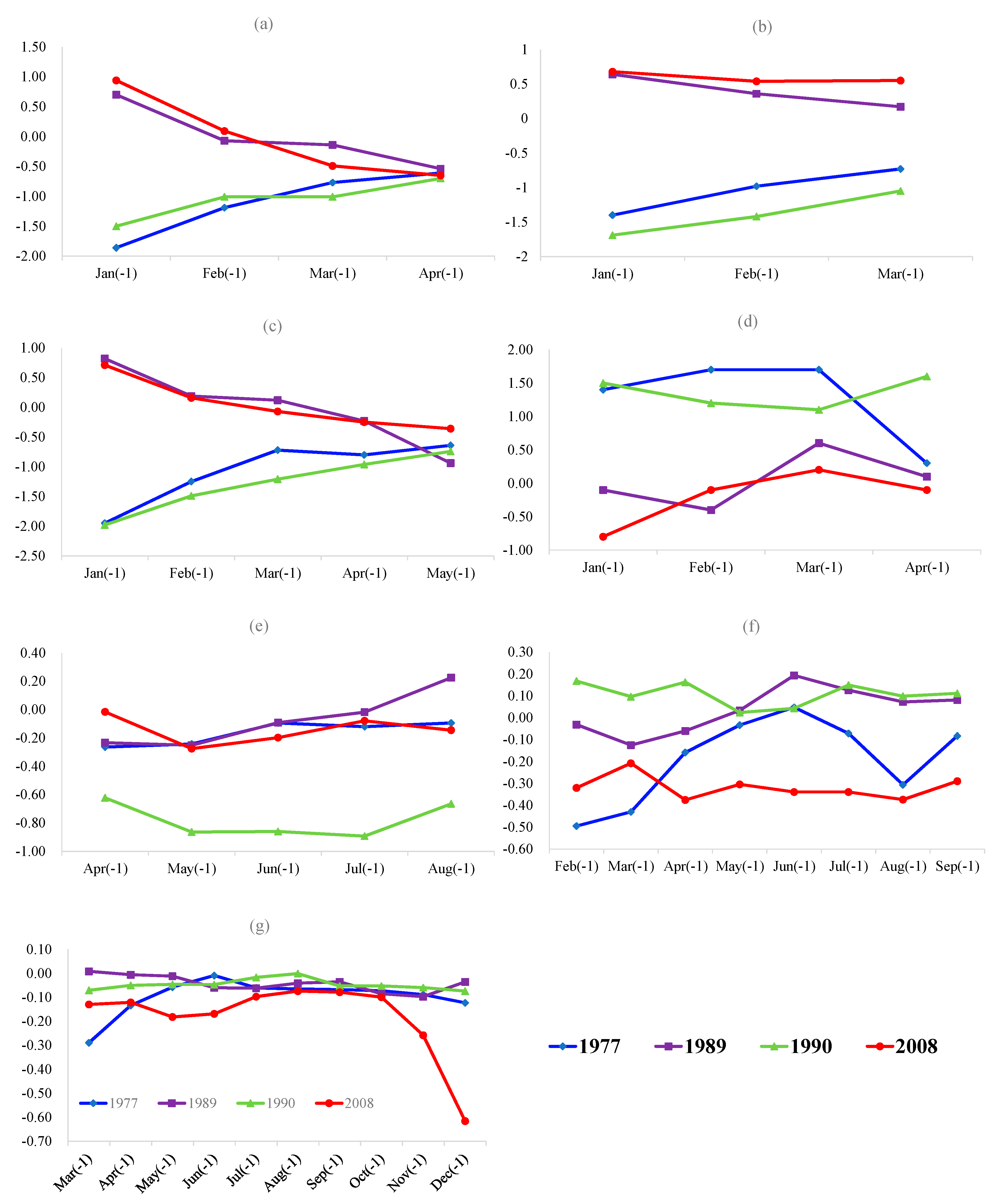
- To forecast the inflow for January 2008, the significant SSTs and climatic indices for inflows in January 2008, January 1977, January 1989, and January 1990 are plotted to assist in selection of the best potential analogue (see Appendix B). In this case, most of the significant climatic indices and SSTs for January 2008 are very similar to those for January 1989, and therefore January 1989 is selected as the best potential analogue.
- The forecast variation for January 2008 is calculated from the variation in January 1989 using Equation (6) and plotted as the red-dotted line in Figure 6.
- After obtaining the variation for January 2008, the standardized inflow is calculated using Equation (7) and converted to the normal form of inflow. The forecast inflow values calculated from this method and the observed inflow in January 2008 are 138.29 and 136.84 million cubic meters, respectively.
4. Discussion and Conclusions
- The WANN model, a hybrid of ANN and wavelet analysis, produced good results in forecasting the monthly reservoir inflow of Sirikit Dam. However, for the high-flow period it provided only satisfactory results. This indicated that the WANN model is weak in forecasting peak flows because such flows are rare compared to low- and moderate-flow events. As ANN-based models rely on learning from past events, the number of peak flow events is insufficient for ANN models to learn and produce good forecasting results. This characteristic of ANN-based models is a common issue that has been reported in the literature (e.g., Sudheer [34]; Yang et al. [35]). Wavelet analysis, a data pre-processing technique, generally improved the forecasting results, but the improvement was not enough to predict peak flow. In conclusion, the WANN method has a poor ability to forecast peak flows.
- The WMAM provided only reasonably satisfactory predictions for the whole-year period and its performance was markedly worse in the high-flow period. This may have been because the forecasting is dependent on the RMSE between historical and current inflows. The selection of historical analogues based on RMSE may result in the inclusion of all recent inflow patterns, even if they are not similar to the pattern of the current year. This leads to incorrect selection of analogues, especially for a high-response catchment such as the Sirikit Dam. This characteristic of analogue-based methods such as the WMAM was reported previously by Svensson [31], who concluded that the uncertainty of the historical analogue approach can be large, especially in catchments with a fast response.
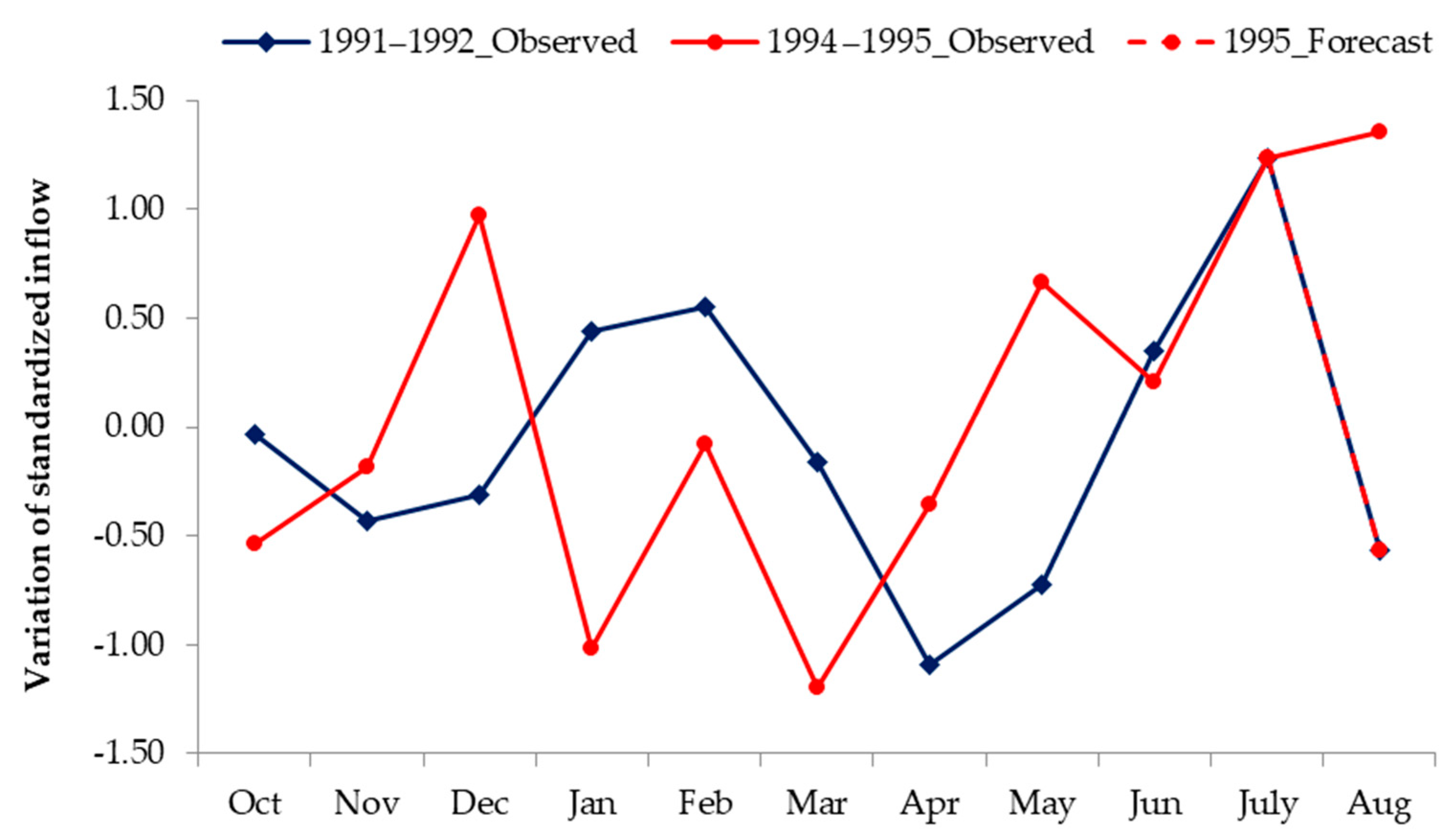
- The developed VAM provided excellent predictions of the monthly reservoir inflow of the Sirikit Dam. Its ability to forecast extreme peak flow represented an advantage over the other methods. However, it has the drawback that it relies on past observation data. Therefore, in the absence of a similar historical analogue it may not provide good results. This is especially important in the case of events with return periods that may be longer than the record length, making rare situations that have not been observed in the past very difficult to forecast. The example of this situation is the case of forecasting the inflow in August 1995 described earlier. In addition, changes in land use, urbanization processes, or changes in the morphology of the rivers may affect the discharge arriving to the reservoirs. The study of the effect of those changes should be further conducted to clarify this issue.
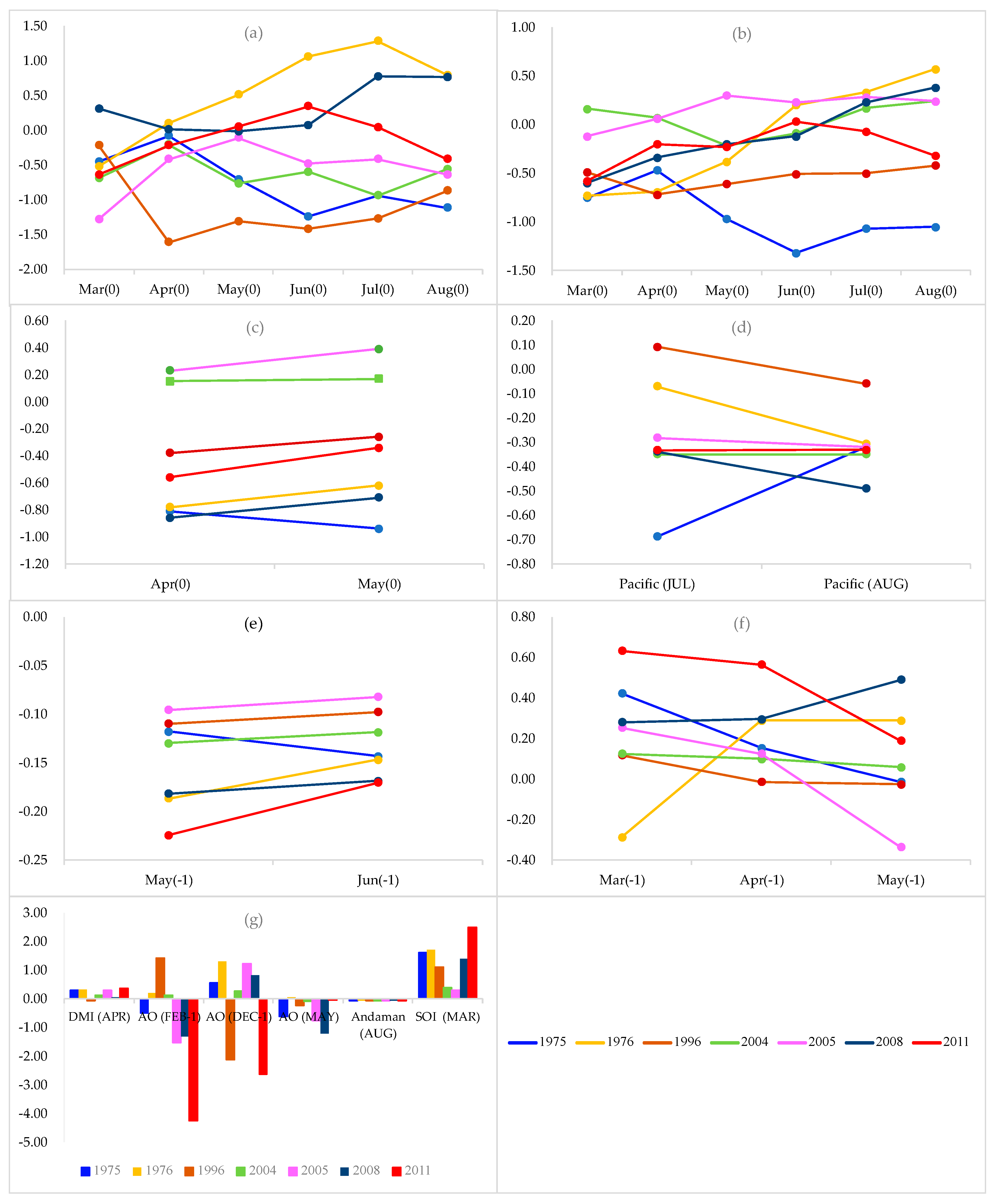
- The incorporation of SSTs and climatic indices in the WANN model and the VAM significantly improved forecasts. In the WANN model, SSTs and climatic indices were used as an input to the model. In the VAM, significant SSTs and climatic indices for the inflow each month were plotted and compared to aid in selecting appropriate historical analogues. The idea behind investigating use of SSTs and climatic indices as guidelines for selection of the most suitable historical analogues was derived from the results of several previous studies that indicated that SSTs and climatic indices were associated with the Thai climate and rainfall (e.g., Singharattna et al. [36]; Bejranonda and Koch [37]; Chansaengkrachang [38]; Bridhikitti [39]; and Manusthiparom [40]). The improvement in forecasts in this study after incorporation of SSTs and climatic indices supports these previous reports. However, future studies should clarify the individual contributions of SSTs and the climate indexes.
- Although the VAM could provide excellent predictions of the reservoir inflow of the Sirikit Dam, the leading time of prediction in this study is only one month, which may not be enough for the open large reservoir where prediction times of longer than one month are often needed. The further study of longer lead-time prediction using the VAM is hence needed for better reservoir operation.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| January | August | ||
|---|---|---|---|
| Significant SSTs/Indices | Correlation | Significant SSTs/Indices | Correlation |
| Andaman (MAR-1) | −0.404 | Andaman (AUG) | −0.321 |
| Andaman (APR-1) | −0.366 | Andaman (MAY-1) | −0.372 |
| Andaman (MAY-1) | −0.400 | Andaman (JUN-1) | −0.336 |
| Andaman (JUN-1) | −0.320 | AO (FEB-1) | −0.345 |
| Andaman (JUL-1) | −0.342 | AO (DEC-1) | −0.308 |
| Andaman (AUG-1) | −0.556 | AO (MAY) | −0.356 |
| Andaman (SEP-1) | −0.499 | DMI (APR) | 0.312 |
| Andaman (OCT-1) | −0.303 | DMI (MAR-1) | 0.325 |
| Andaman (NOV-1) | −0.371 | DMI (APR-1) | 0.421 |
| Andaman (DEC-1) | −0.325 | DMI (MAY-1) | 0.324 |
| Niño 3 (JAN-1) | −0.375 | SOI (MAR) | 0.448 |
| Niño 3 (FEB-1) | −0.422 | Niño 1 + 2 (MAR) | −0.316 |
| Niño 3 (MAR-1) | −0.391 | Niño 1 + 2 (APR) | −0.440 |
| Niño 3 (APR-1) | −0.388 | Niño 1 + 2 (MAY) | −0.404 |
| Niño 3.4 (Jan-1) | −0.398 | Niño 1 + 2 (JUN) | −0.342 |
| Niño 3.4 (FEB-1) | −0.403 | Niño 1 + 2 (JUL) | −0.307 |
| Niño 3.4 (MAR-1)) | −0.422 | Niño 1 + 2 (AUG) | −0.334 |
| Niño 3.4 (APR-1) | −0.459 | Niño 3 (MAR) | −0.330 |
| Niño 3.4 (MAY-1) | −0.327 | Niño 3 (APR) | −0.421 |
| Niño 4 (JAN-1) | −0.327 | Niño 3 (MAY) | −0.439 |
| Niño 4 (FEB-1) | −0.321 | Niño 3 (JUN) | −0.357 |
| Niño 4 (MAR-1) | −0.322 | Niño 3 (JUL) | −0.310 |
| Pacific (FEB-1) | −0.339 | Niño 3 (AUG) | −0.329 |
| Pacific (MAR-1) | −0.327 | Niño 3.4 (APR) | −0.318 |
| Pacific (APR-1) | −0.325 | Niño 3.4 (MAY) | −0.353 |
| Pacific (MAY-1) | −0.394 | Pacific (JUL) | −0.409 |
| Pacific (JUN-1) | −0.487 | Pacific (AUG) | −0.355 |
| Pacific (JUL-1) | −0.591 | ||
| Pacific (AUG-1) | −0.544 | ||
| Pacific (SEP-1) | −0.354 | ||
| SCS (APR-1) | −0.334 | ||
| SCS (MAY-1) | −0.320 | ||
| SCS (JUN-1) | −0.346 | ||
| SCS (JUL-1) | −0.361 | ||
| SCS (AUG-1) | −0.340 | ||
| SOI (JAN-1) | 0.362 | ||
| SOI (FEB-1) | 0.412 | ||
| SOI (MAR-1) | 0.531 | ||
| SOI (APR-1) | 0.398 | ||
Appendix B
Appendix C
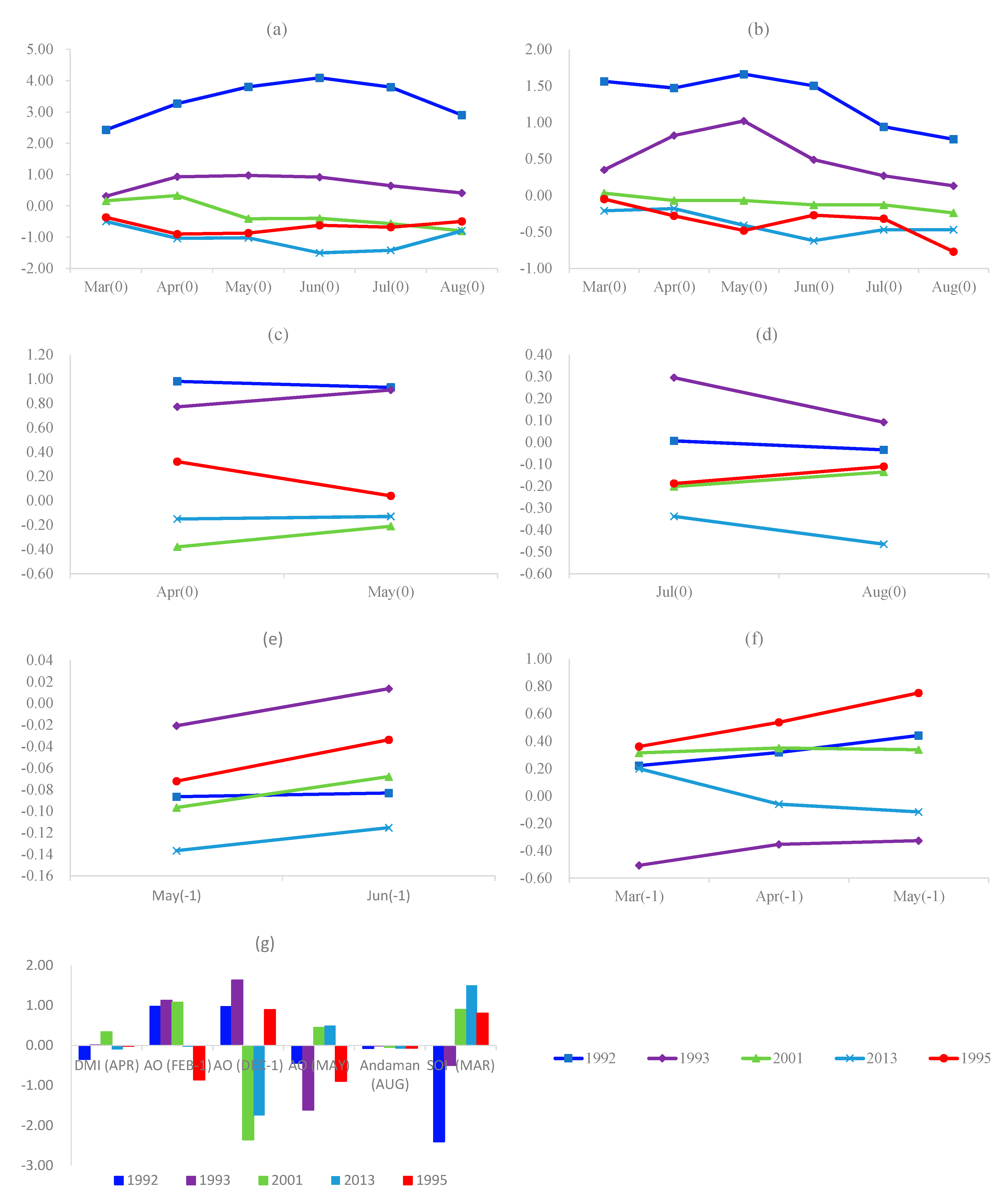
Appendix D
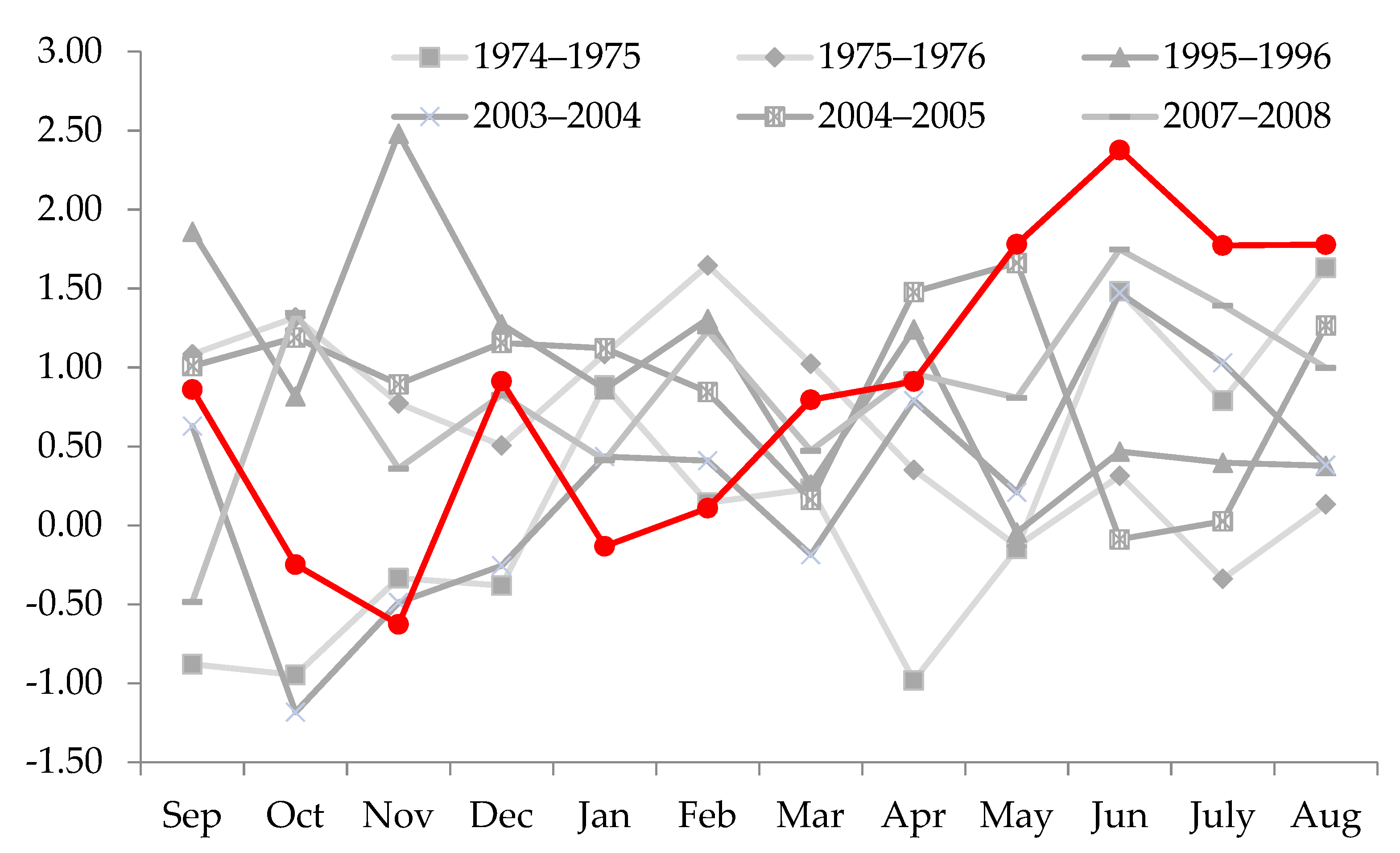
References
- Anand, J.; Gosain, A.K.; Khosa, R. Optimisation of multipurpose reservoir operation by coupling SWAT and genetic algorithm for optimal operating policy (case study: Ganga River basin). Preprints 2018. [Google Scholar] [CrossRef]
- Schleiss, A.J.; Franca, M.J.; Juez, C.; De Cesare, G. Reservoir sedimentation vision paper. J. Hydraul. Res. 2016. [Google Scholar] [CrossRef]
- US Army Corps of Engineers. Forecast-Based Advance Release at Folsom Dam: Effectiveness and Risk-Phase 1; PR-48; Hydrologic Engineering Center: Davis, CA, USA, 2002; pp. 1–111.
- Kumar, T. Operations Research in Water Quality Management; Harvard Water Resources Group: Cambridge, UK, 2013. [Google Scholar]
- Lin, S.-C.; Wu, R.-S.; Chen, S.-W. Study on optimal operating rule curves including hydropower purpose in parallel multireservoir systems. WIT Trans. Ecol. Environ. 2005, 83, 151–160. [Google Scholar]
- Mateo, C.M.R.; Hanasaki, N.; Komori, D.; Yoshimura, K.; Kiguchi, M.; Champathong, A.; Yamazaki, D.; Sukhapunnaphan, T.; Oki, T. A simulation study on modifying reservoir operation rules: Tradeoffs between flood mitigation and water supply. IAHS Publ. 2013, 362, 33–40. [Google Scholar]
- Mythili, B.; Devi, U.G.; Raviteja, A.; Kumar, P.S. Study of optimizing techniques of reservoir operation. Int. J. Eng. Res. Gen. Sci. 2013, 1, 2091–2730. [Google Scholar]
- Heydari, M.; Othman, F.; Taghieh, M. Optimization of multipurpose reservoir system operations by using matrix structure (case study: Karun and Dez Reservoir Dams). PLoS ONE 2016, 10, e0156276. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, J.M. Recalibration of Kainji Reservoir operating rules for optimal operation. Ann. Rev. Res. 2018, 1, 1–7. [Google Scholar]
- Sivapragasam, C.; Vasudevan, G.; Vincent, P. Effect of inflow forecast accuracy and operating time horizon in optimizing irrigation releases. Water Resour. Manag. 2007, 21, 933–945. [Google Scholar] [CrossRef]
- Dong, X.; Dohmen-Janssen, C.M.; Booij, M.; Hulscher, S. Effect of flow forecasting quality on benefits of reservoir operation. A case study for the Geheyan reservoir (China). Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 3771–3814. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, S.; Chen, H.; Zhou, Y. Comparative study of monthly inflow prediction methods for the Three Gorges Reservoir. Stoch. Environ. Res. Risk Assess. 2013, 28, 555–570. [Google Scholar] [CrossRef]
- Mohammadi, K.; Eslami, H.R.; Dardashti, S.D. Comparison of regression, ARIMA and ANN models for reservoir inflow forecasting using snowmelt equivalent (a case study of Karaj). J. Agric. Sci. Technol. 2005, 7, 17–30. [Google Scholar]
- ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial neural networks in hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial neural networks in hydrology. II: Hydrologic applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar] [CrossRef]
- Kim, T.; Choi, G.; Heo, J.-H. Inflow Forecasting for real-time reservoir operation using artificial neural network. In Proceedings of the World Environmental and Water Resources Congress, Kansas City, MO, USA, 17–21 May 2009; pp. 4947–4955. [Google Scholar]
- Zhang, J.; Cheng, C.-T.; Liao, S.-L.; Wu, X.-Y.; Shen, J.-J. Daily reservoir inflow forecasting combining QPF into ANNs model. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 121–150. [Google Scholar] [CrossRef]
- Othman, F.; Naseri, M. Reservoir inflow forecasting using artificial neural network. Int. J. Phys. Sci. 2011, 6, 434–440. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Monthly inflow forecasting using autoregressive artificial neural network. J. Appl. Sci. 2012, 12, 2139–2147. [Google Scholar] [CrossRef]
- Vijayakumar, N.; Vennila, S. Reservoir inflow forecasting at Krishnagiri Reservoir Project using artificial neural network. In Proceedings of the National Conference on Contemporary Advancements in Civil Engineering Practices—CACEP, P.S.G College of Technology, Coimbatore, India, 23 May 2016. [Google Scholar]
- Muluye, G.Y.; Coulibaly, P. Seasonal reservoir inflow forecasting with low-frequency climatic indices: A comparison of data-driven methods. Hydrol. Sci. J. 2007, 52, 508–522. [Google Scholar] [CrossRef]
- Kim, T.-W.; Valdés, J.B. A nonlinear model for drought forecasting based on conjunction of wavelet transforms and neural networks. J. Hydrol. Eng. 2003, 8, 319–328. [Google Scholar] [CrossRef]
- Amnatsan, S.; Kuribayashi, D.; Jayawadena, A.W. Application of artificial neural networks and wavelet analysis in prediction of water level in Nan River of Thailand. In Proceedings of the Annual Conference 23rd Annual Conference, Hosei University, Tokyo, Japan, 7 September 2010. [Google Scholar]
- Zhao, Z.; Giannakis, D. Analog forecasting with Dynamics-Adapted Kernels. Nonlinearity 2016, 29, 2888–2939. [Google Scholar] [CrossRef]
- Zhao, B.; Zhai, P. A new forecast model based on the analog method for persistent extreme precipitation. Weather Forecast. 2016, 31, 1325–1341. [Google Scholar] [CrossRef]
- Horton, P.; Obled, C.; Jaboyedoff, M. The analogue method for precipitation prediction: Finding better analogue situations at a sub-daily time step. Hydrol. Earth Syst. Sci. 2017, 21, 3307–3323. [Google Scholar] [CrossRef]
- Matulla, C.; Zhang, X.; Wang, X.L.; Wang, J.; Zorita, E.; Wagner, S.; Storch, H.V. Influence of similarity measures on the performance of the analog method for downscaling daily precipitation. Clim. Dyn. 2008, 30, 133–144. [Google Scholar] [CrossRef]
- Obled, C.; Bontron, G.; Garçon, R. Quantitative precipitation forecasts: A statistical adaptation of model outputs through an analogue sorting approach. Atmos. Res. 2002, 63, 303–324. [Google Scholar] [CrossRef]
- Diomede, T.; Nerozzi, F.; Paccagnella, T.; Todini, E. The use of meteorological analogues to account for LAM QPF uncertainty. Hydrol. Earth Syst. Sci. 2008, 12, 141–157. [Google Scholar] [CrossRef]
- Bellier, J.; Zin, I.; Siblot, S.; Bontron, G. Probabilistic flood forecasting on the Rhone River: Evaluation with ensemble- and analogue-based precipitation forecasts. E3S Web Conf. 2016, 7, 1–11. [Google Scholar] [CrossRef]
- Svensson, C. Seasonal river flow forecasts for the United Kingdom using persistence and historical analogues. Hydrol. Sci. J. 2016, 61, 19–35. [Google Scholar] [CrossRef]
- Panagoulia, D. Artificial neural networks and high and low flows in various climate regimes. Hydrol. Sci. J. 2006, 51, 563–587. [Google Scholar] [CrossRef]
- Komori, D.; Nakamura, S.; Kiguchi, M.; Nishijima, A.; Yamazaki, D.; Suzuki, S.; Kawasaki, A.; Oki, K.; Oki, T. Characteristics of the 2011 Chao Phraya River flood in Central Thailand. HRL 2012, 6, 41–46. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Nayak, P.C.; Ramasastri, K.S. Improving peak flow estimates in artificial neural network river flow models. Hydrol. Process. 2003, 17, 677–686. [Google Scholar] [CrossRef]
- Yang, T.; Asanjan, A.A.; Welles, E.; Gao, X.; Sorooshian, S.; Liu, X. Developing reservoir monthly inflow forecasts using artificial intelligence and climate phenomenon information. Water Resour. Res. 2017, 53, 2786–2812. [Google Scholar] [CrossRef]
- Singhrattna, N.; Babel, M.S.; Perret, S.R. Hydroclimate variability and its statistical links to the large-scale climate indices for the Upper Chao Phraya River Basin, Thailand. Hydrol. Earth Syst. Sci. Disscuss. 2009, 6, 6659–6690. [Google Scholar] [CrossRef]
- Bejranonda, W.; Koch, M. The role of ocean state indices in seasonal and inter-annual climate variability of Thailand. In Proceedings of the 1st Symposium on Sustainable Water Management and Climate Change, Nakhon Pathom, Thailand, 16–17 June 2010. [Google Scholar]
- Chansaengkrachang, K. Empirical orthogonal function analysis of rainfall over Thailand and its relationship with the Indian Ocean Dipole. Chiangmai Univ. Int. Conf. 2011, 1, 47–54. [Google Scholar]
- Bridhikitti, A. Connections of ENSO/IOD and aerosols with Thai rainfall anomalies and associated implications for local rainfall forecasts. Int. J. Climatol. 2013, 33, 2836–2845. [Google Scholar] [CrossRef]
- Manusthiparom, C. Hydroclimatic Prediction for Integrated Water Resources Management in the Chao Phraya River Basin in Thailand. Ph.D. Thesis, University of Tokyo, Tokyo, Japan, September 2003. [Google Scholar]
- Panagoulia, D.; Tsekouras, G.J.; Kousiouris, G. A multi-stage methodology for selecting input variables in ANN forecasting of river flows. Glob. Nest J. 2017, 19, 49–57. [Google Scholar]
- Wang, G.; Guo, L.; Duan, H. Wavelet Neural Network Using Multiple Wavelet Functions in Target Threat Assessment. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Vidakovic, B.; Mueller, P. Wavelets for Kids: A Tutorial Introduction; Duke University: Durham, NC, USA, 1991; pp. 1–28. [Google Scholar]
- Boslaugh, S. Statistics in a Nutshell, 2nd ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2013; pp. 173–192. ISBN 978-1-449-31682-2. [Google Scholar]
| Data Used | SST Regions/Ocean Index Name | Source |
|---|---|---|
| Sea-surface temperature (SST) | Niño 1 + 2 | The U.S. National Oceanic and Atmospheric Administration (NOAA) |
| Niño 3 | ||
| Niño 3.4 | ||
| Niño 4 | ||
| Pacific Ocean | ||
| South China Sea | ||
| Andaman Sea | ||
| Ocean index | Southern Oscillation Index (SOI) | |
| Dipole Mode Index (DMI) | Japan Agency for Marine-Earth Science and Technology (JAMSTEC) | |
| Monthly reservoir inflow | Electricity Generating Authority of Thailand (EGAT) |
| Input Parameter | SST Region/Ocean Index Name | Lag Used (Month) |
|---|---|---|
| Sea-surface temperature | Niño 1+2 | 5, 17, 18 |
| Niño 3 | 4, 16, 17 | |
| Niño 3.4 | 5, 15, 16 | |
| Pacific Ocean | 6, 7, 18 | |
| South China Sea | 6, 18, 19 | |
| Andaman Sea | 7, 18, 19 | |
| Ocean index | SOI | 5 |
| DMI | 16 | |
| Reservoir inflow | - | 1, 12 |
| Model Period | Model Performance Indicators | |||
|---|---|---|---|---|
| RMSE | R | EI | CD | |
| Training | 179.85 | 0.95 | 0.90 | 0.89 |
| Validation | 248.68 | 0.90 | 0.81 | 0.85 |
| Testing | 210.80 | 0.95 | 0.89 | 0.77 |
| Forecasting Period | Method | Model Performance Indicator | |||
|---|---|---|---|---|---|
| RMSE | R | EI | CD | ||
| Whole year (January–December) | WANN | 234.20 | 0.92 | 0.85 | 0.81 |
| WMAM | 335.45 | 0.84 | 0.69 | 0.62 | |
| VAM | 186.33 | 0.95 | 0.90 | 1.01 | |
| VAM-improved | 115.55 | 0.98 | 0.96 | 0.92 | |
| High flow (July–September) | WANN | 366.78 | 0.83 | 0.67 | 0.60 |
| WMAM | 627.42 | 0.37 | 0.04 | 0.37 | |
| VAM | 305.59 | 0.84 | 0.84 | 0.87 | |
| VAM-improved | 215.55 | 0.95 | 0.92 | 0.86 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amnatsan, S.; Yoshikawa, S.; Kanae, S. Improved Forecasting of Extreme Monthly Reservoir Inflow Using an Analogue-Based Forecasting Method: A Case Study of the Sirikit Dam in Thailand. Water 2018, 10, 1614. https://doi.org/10.3390/w10111614
Amnatsan S, Yoshikawa S, Kanae S. Improved Forecasting of Extreme Monthly Reservoir Inflow Using an Analogue-Based Forecasting Method: A Case Study of the Sirikit Dam in Thailand. Water. 2018; 10(11):1614. https://doi.org/10.3390/w10111614
Chicago/Turabian StyleAmnatsan, Somchit, Sayaka Yoshikawa, and Shinjiro Kanae. 2018. "Improved Forecasting of Extreme Monthly Reservoir Inflow Using an Analogue-Based Forecasting Method: A Case Study of the Sirikit Dam in Thailand" Water 10, no. 11: 1614. https://doi.org/10.3390/w10111614
APA StyleAmnatsan, S., Yoshikawa, S., & Kanae, S. (2018). Improved Forecasting of Extreme Monthly Reservoir Inflow Using an Analogue-Based Forecasting Method: A Case Study of the Sirikit Dam in Thailand. Water, 10(11), 1614. https://doi.org/10.3390/w10111614




