Design of A Streamwise-Lateral Ski-Jump Flow Discharge Spillway
Abstract
1. Introduction
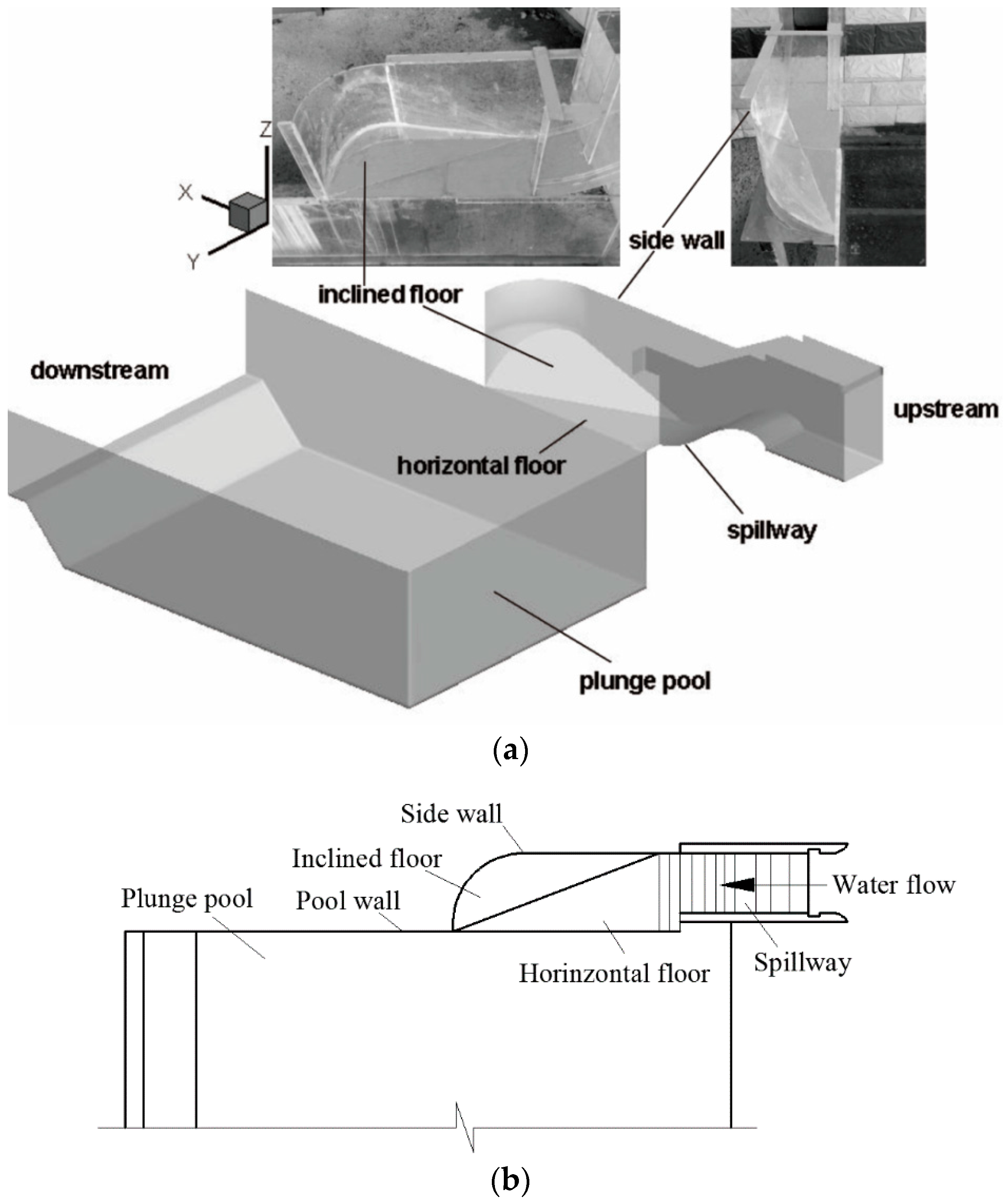
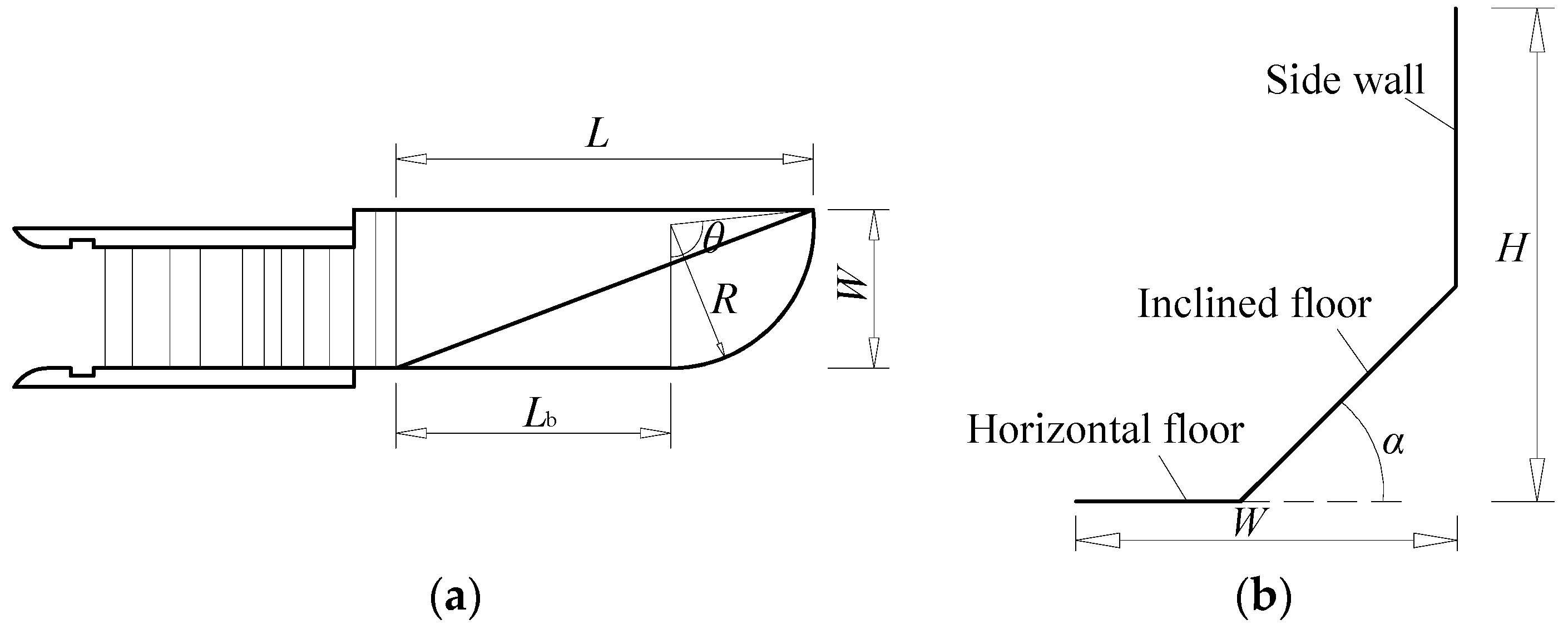
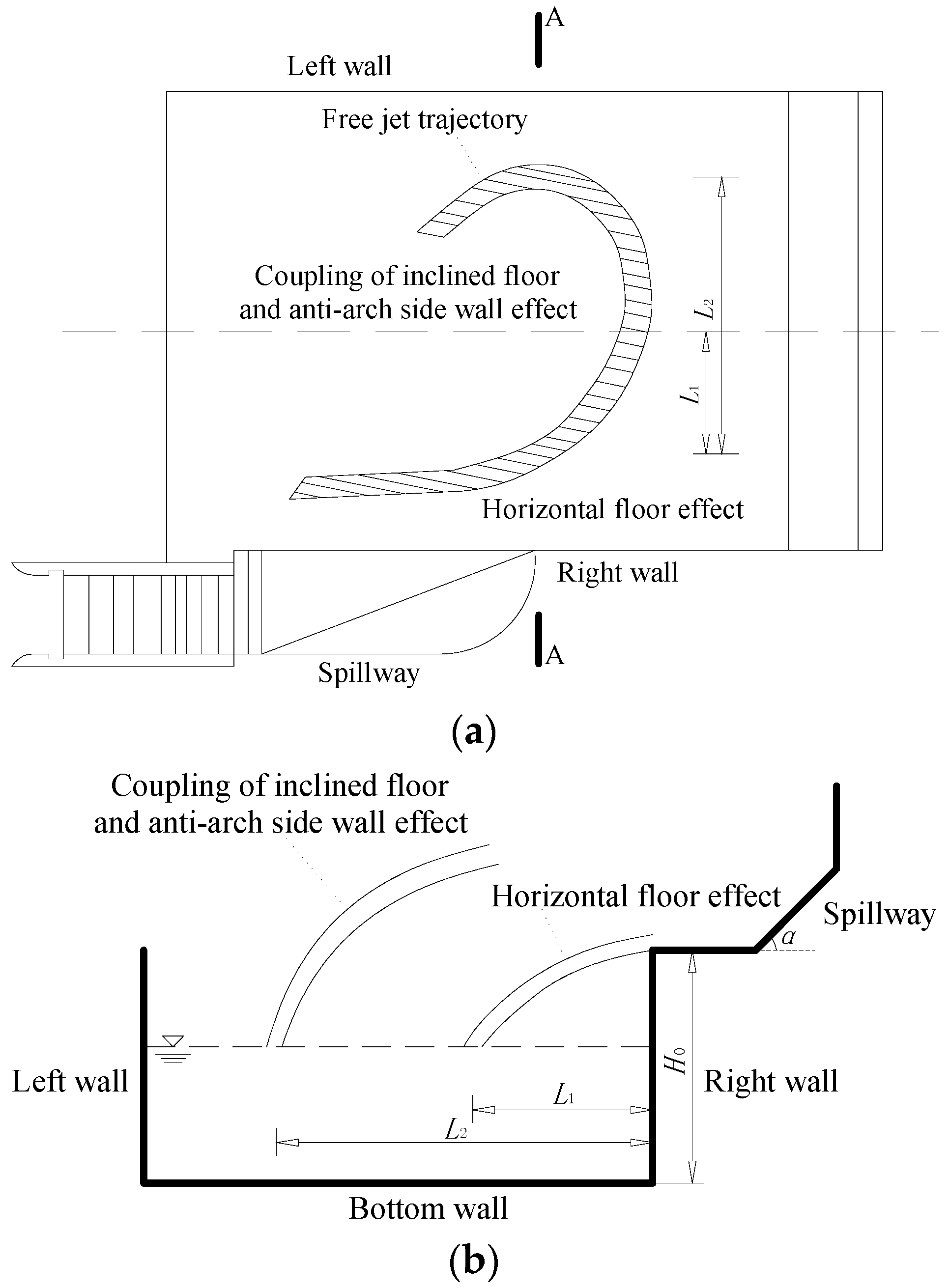
2. Physical Structure of the Streamwise-Lateral Discharge Spillway
3. Investigation Methods and Definition of the Free Jet Flow Pattern
3.1. Physical Model
3.2. Numerical Simulation
- Continuity equation:
- Momentum equation:
- k (turbulent kinetic energy) equation:
- ε (dissipation rate of turbulent kinetic energy) equation:where t is time. ρ and μ are the average density of the volume fraction and molecular viscosity, respectively. p is the pressure and Gk represents the generation of turbulence kinetic energy due to the mean velocity gradients. μt is the turbulent viscosity which can be deduced for the turbulence intensity k and energy dissipation rate ε:where S is the modulus of the mean strain rate tensor. The detailed values are shown in Table 1.
4. Results and Discussion
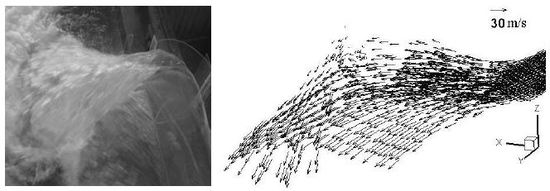
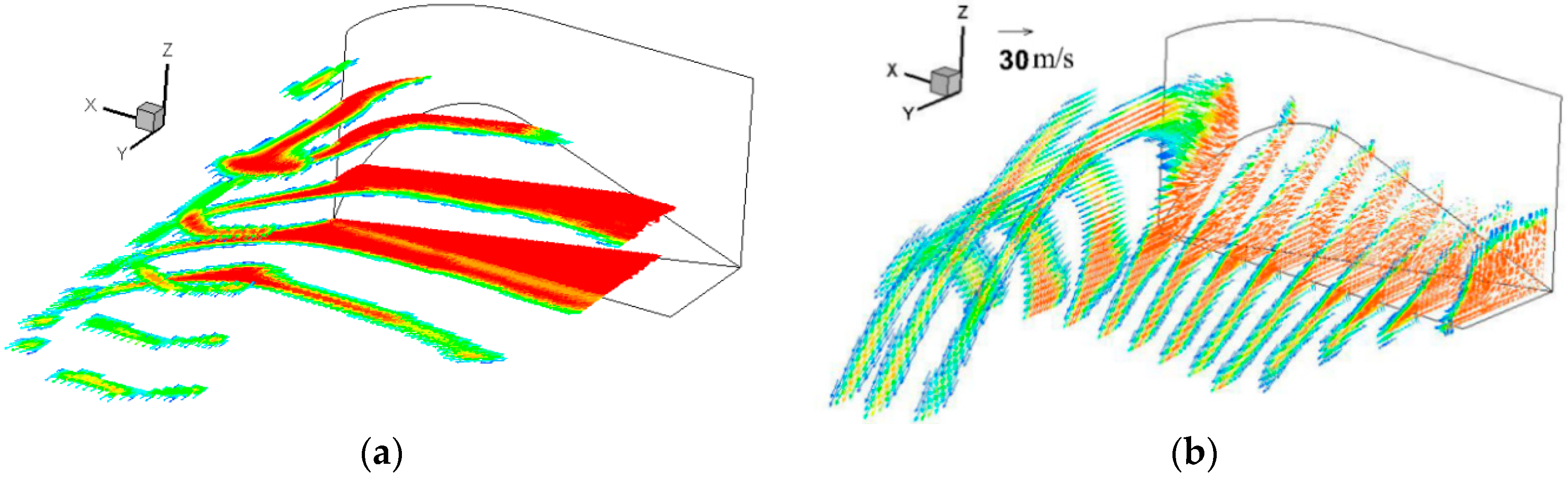
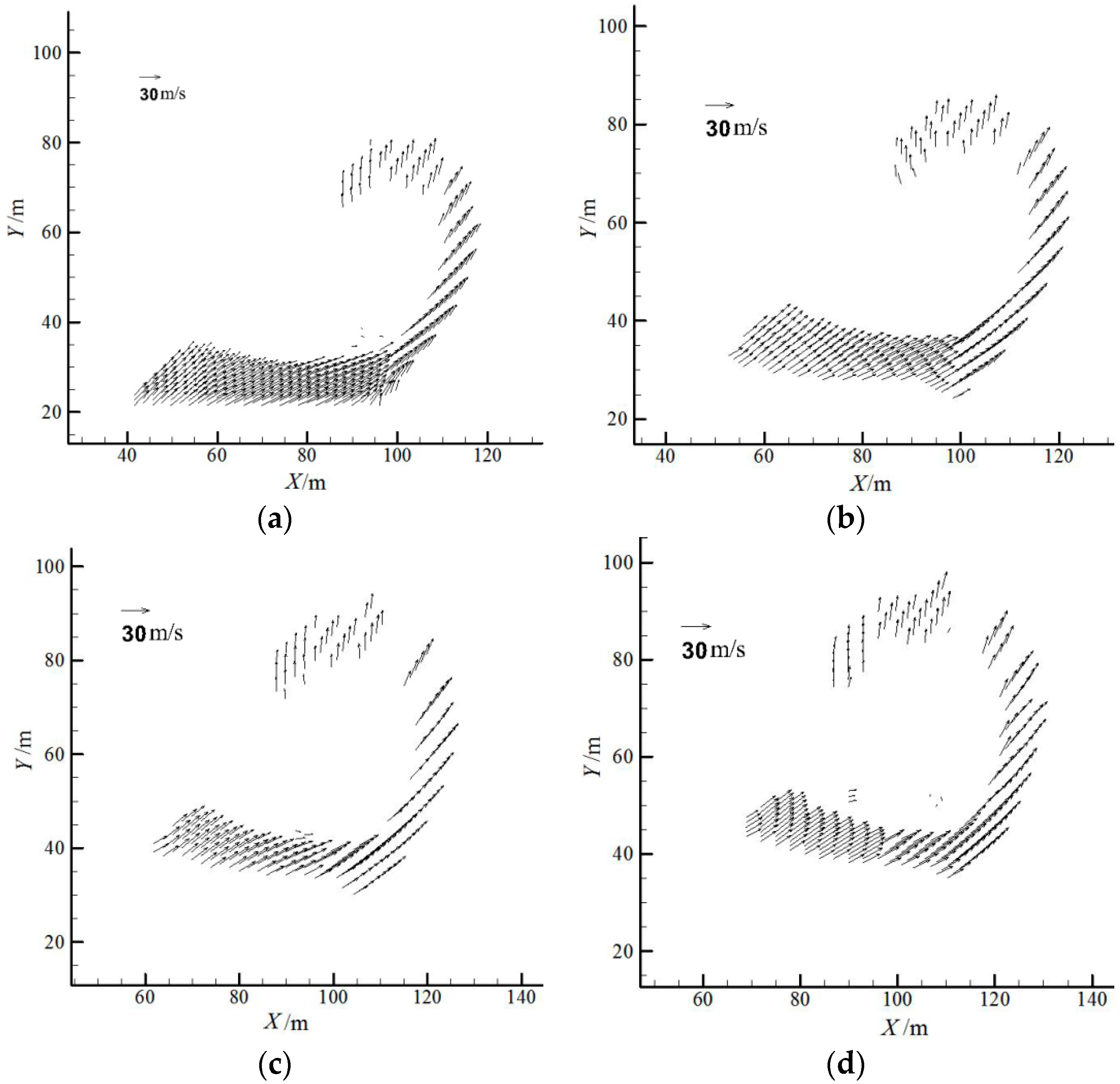
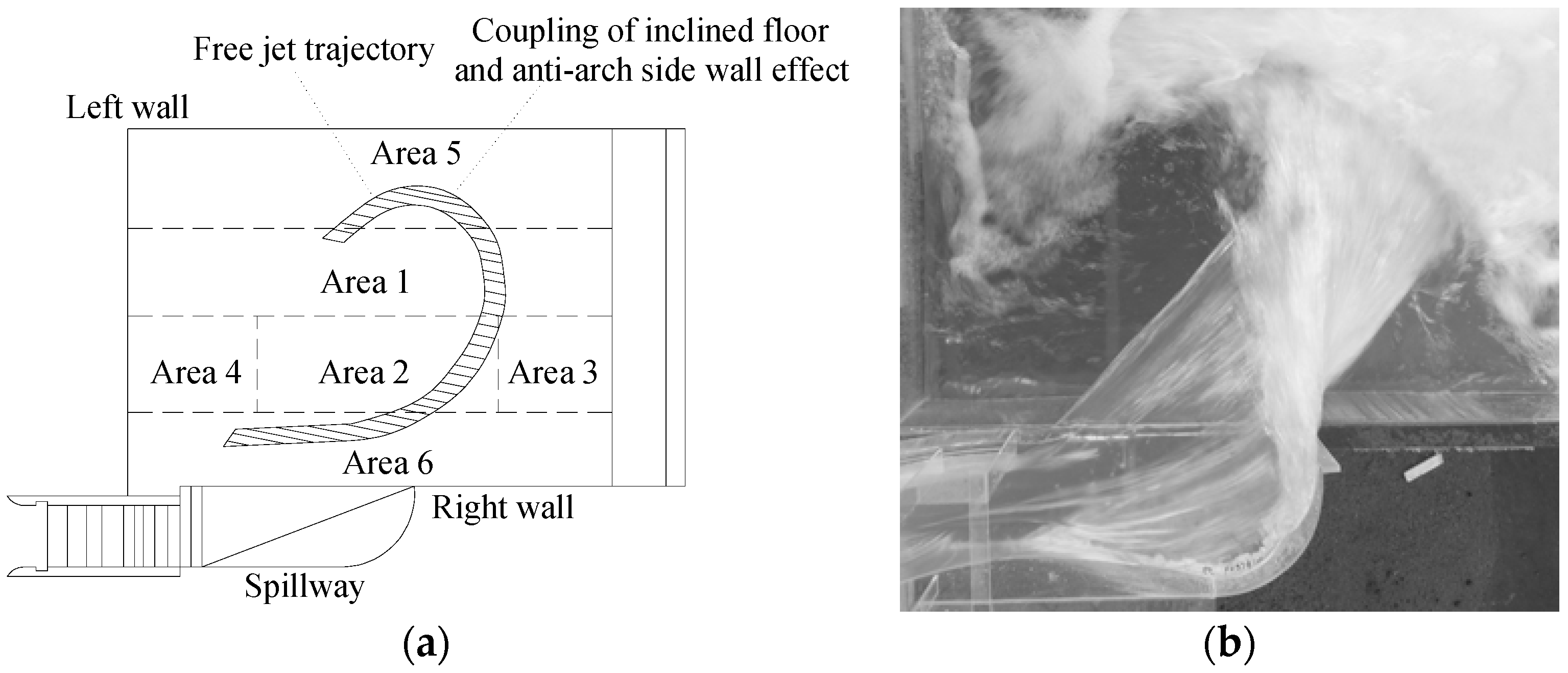
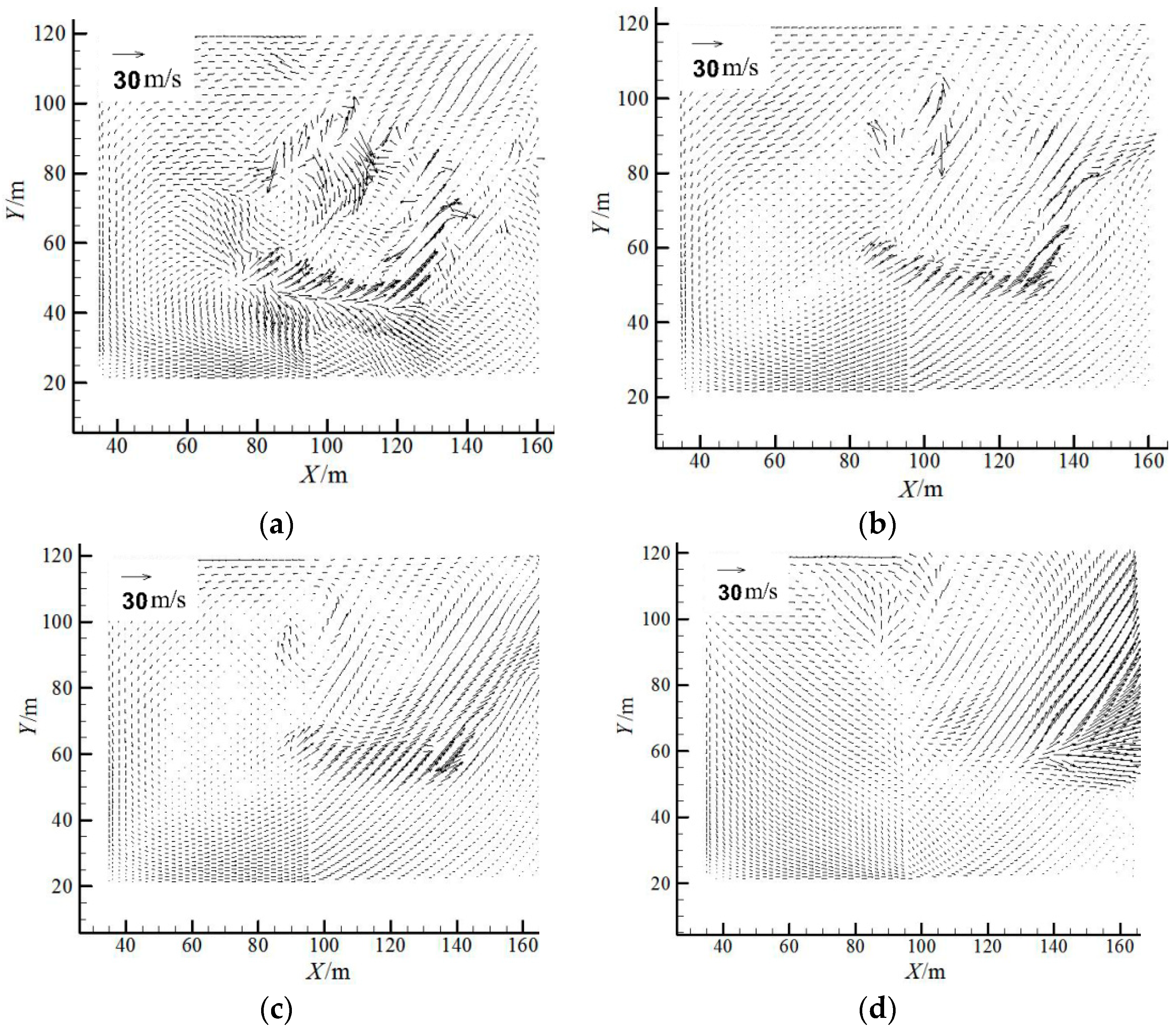
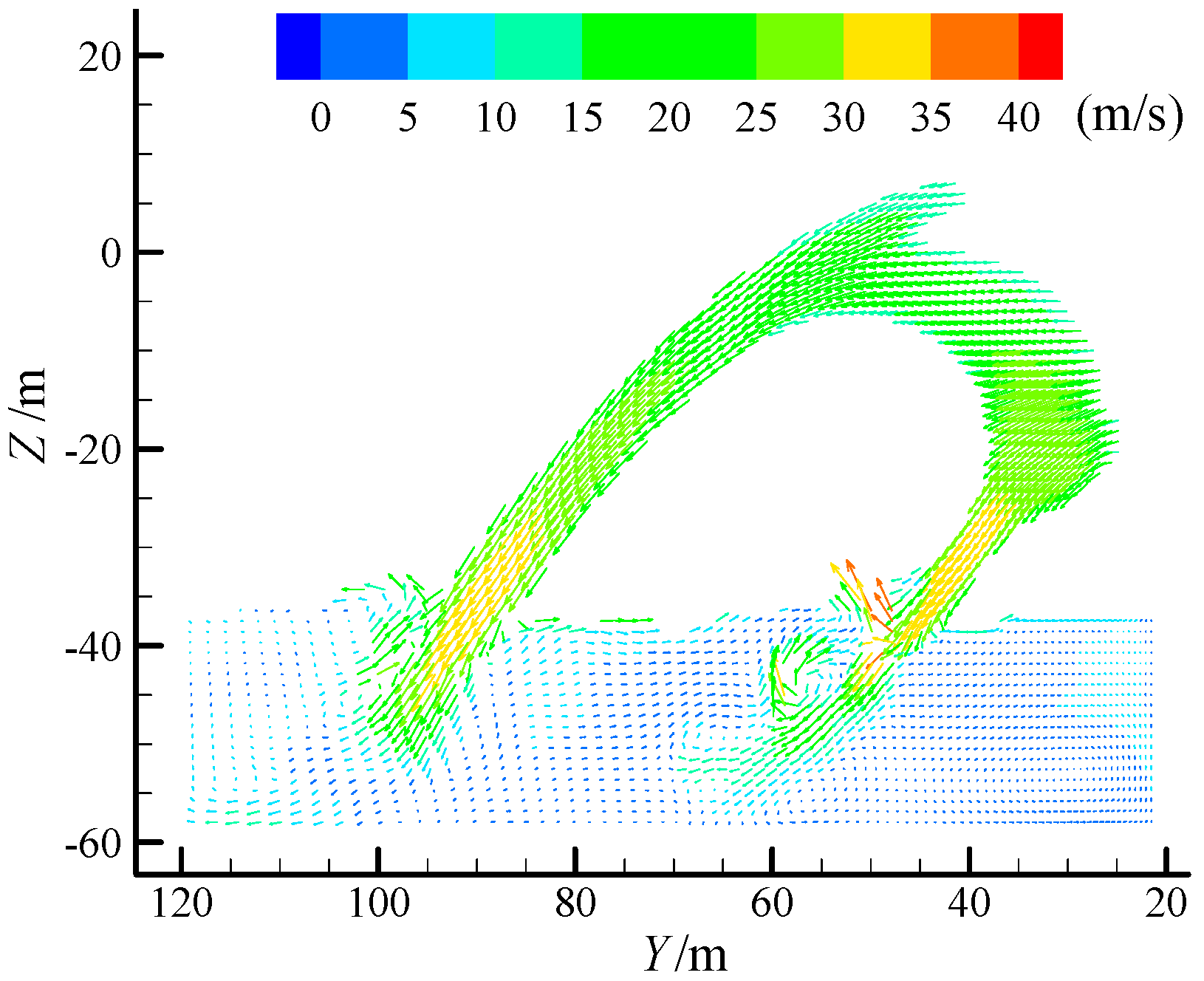
4.1. Ski-Jump Flow Pattern
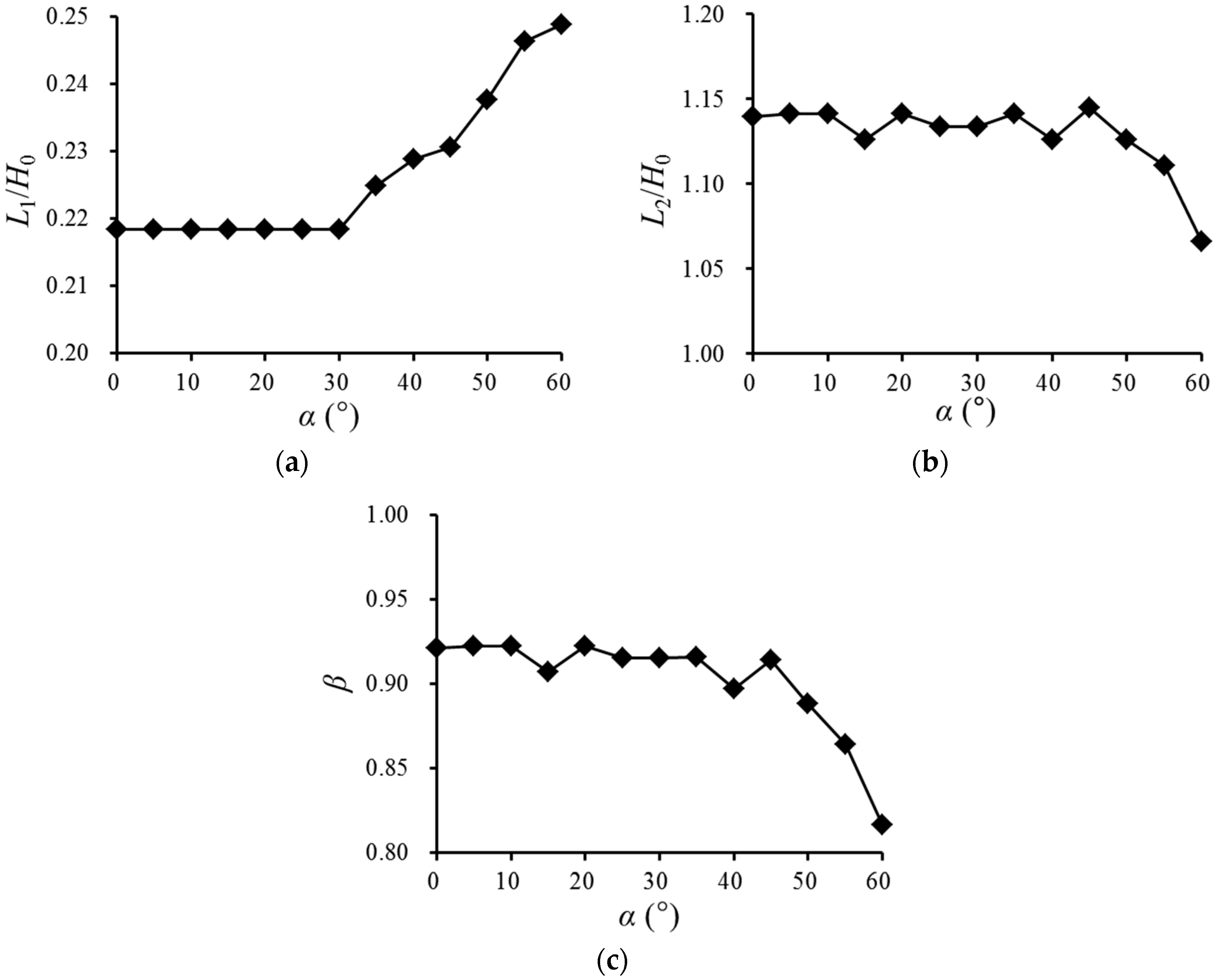
4.2. Effect of Inclined Floor on Jet Length
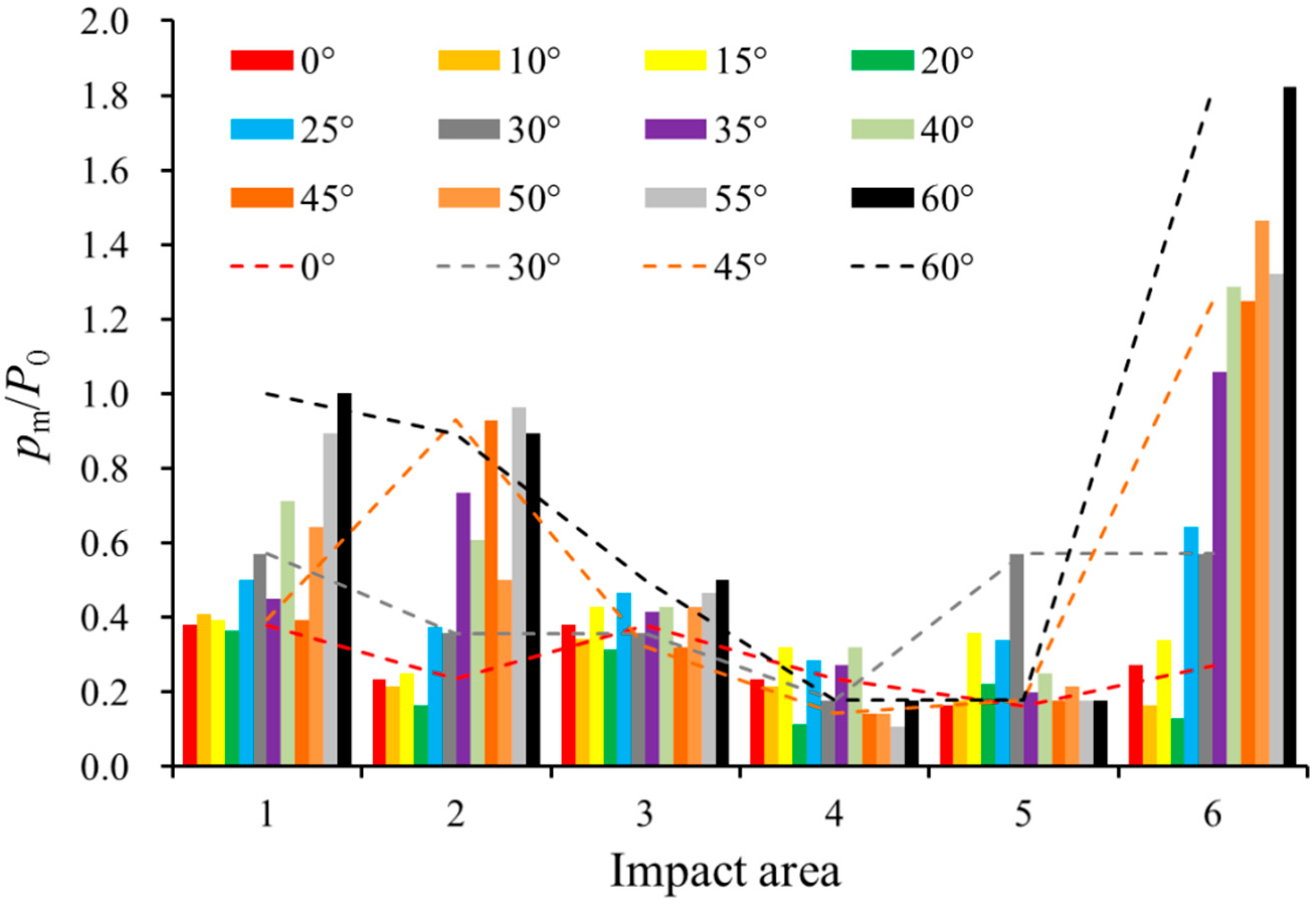
4.3. Effect of Inclined Floor on Jet Impact Pressure
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xu, W.L.; Luo, S.J.; Zheng, Q.W.; Luo, J. Experimental study on pressure and aeration characteristics in stepped chute flows. Sci. China Technol. Sci. 2015, 58, 720–726. [Google Scholar] [CrossRef]
- Chanson, H. Energy Dissipation in Hydraulic Structures; IAHR Monograph; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Liu, P.Q. Energy Dissipater Theory of Modern Dam Construction; Science Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Heller, V.; Hager, W.H.; Minor, H.E. Ski jump hydraulics. J. Hydraul. Eng. 2005, 131, 347–355. [Google Scholar] [CrossRef]
- Hager, W.H.; Boes, R.M. Hydraulic structures: A positive outlook into the future. J. Hydraul. Res. 2014, 52, 299–310. [Google Scholar] [CrossRef]
- Chanson, H. Aeration of a free jet above a spillway. J. Hydraul. Res. 1991, 29, 655–667. [Google Scholar] [CrossRef]
- Lenau, C.W.; Cassidy, J.J. Flow through spillway flip bucket. J. Hydraul. Div. 1969, 95, 633–648. [Google Scholar]
- Mason, P.J.; Arumugam, K. Free jet scour below dams and flip buckets. J. Hydraul. Eng. 1985, 111, 220–235. [Google Scholar] [CrossRef]
- Juon, R.; Hager, W.H. Flip bucket without and with deflectors. J. Hydraul. Eng. 2000, 126, 837–845. [Google Scholar] [CrossRef]
- Erpicum, S.; Archambeau, P.; Dewals, B.; Pirotton, M. Experimental investigation of the effect of flip bucket splitters on plunge pool geometry. Wasserwirtschaft 2010, 4, 73–80. [Google Scholar]
- Mason, P.J. Practical guidelines for the design of flip buckets and plunge pools. Water Power Dam Constr. 1993, 45, 40–45. [Google Scholar]
- Li, S.; Liang, Z. Gravity-affected potential flows past spillway flip buckets. J. Hydraul. Eng. 1988, 114, 409–427. [Google Scholar]
- Rajan, B.H.; Shivashankara, R.K.N. Design of trajectory buckets. J. Irrig. Power 1980, 37, 63–76. [Google Scholar]
- Steiner, R.; Heller, V.; Hager, W.H.; Minor, H.E. Deflector Ski Jump Hydraulics. J. Hydraul. Eng. 2008, 134, 562–571. [Google Scholar] [CrossRef]
- Alias, N.A.; Mohamed, T.A.; Ghazali, A.H.; Noor, M.J.M.M. Impact of takeoff angle of bucket type energy dissipater on scour hole. Am. J. Appl. Sci. 2008, 5, 117–121. [Google Scholar] [CrossRef]
- Wu, J.H.; Ma, F.; Yao, L. Hydraulic characteristics of slit-type energy dissipaters. J. Hydrodyn. 2012, 24, 883–887. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H. Deflector-generated jets. J. Hydraul. Res. 2010, 47, 466–475. [Google Scholar] [CrossRef]
- Li, N.W.; Liu, C.; Deng, J.; Zhang, X.Z. Theoretical and experimental studies of the flaring gate pier on the surface spillway in a high-arch dam. J. Hydrodyn. 2012, 24, 496–505. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, H.; Xu, W.L. Allotypic hybrid type flip bucket. II: Effect of contraction ratio on hydraulic characteristics and local scour. J. Hydroelec. Eng. 2013, 32, 140–146. (In Chinese) [Google Scholar]
- Felder, S.; Chanson, H. Scale effects in microscopic air-water flow properties in high-velocity free-surface flows. Exp. Therm. Fluid Sci. 2017, 83, 19–36. [Google Scholar] [CrossRef]
- Xu, W.L.; Liao, H.S.; Yang, Y.Q.; Wu, C.G. Computational and Experimental Investigation on the 3-D Flow Feature and Energy Dissipation Characteristics of Plunge Pools. Chin. J. Theor. Appl. Mech. 1998, 30, 35–42. [Google Scholar]
- Deng, J.; Xu, W.L.; Zhang, J.M.; Qu, J.X.; Yang, Y.Q. A new type of plunge pool―Multi-horizontal submerged jets. Sci. China Technol. Sci. 2008, 51, 2128–2141. [Google Scholar] [CrossRef]
- Deng, J.; Yang, Z.L.; Tian, Z.; Zhang, F.X.; Wei, W.R.; You, X.; Xu, W.L. A new type of leak-floor flip bucket. Sci. China Technol. Sci. 2016, 59, 565–572. [Google Scholar] [CrossRef]
- Wei, W.R.; Deng, J.; Liu, B. Influence of aeration and initial water thickness on axial velocity attenuation of jet flows. J. Zhejiang Univ. Sci. A 2013, 14, 362–370. [Google Scholar] [CrossRef]
- Yu, T.; Deng, J.; Xia, Y.; He, C.L.; Xu, W.L. Numerical simulation of turbulent trajectory flow with turnover nappe. Water Resour. Hydropower Eng. 2005, 36, 37–39. (In Chinese) [Google Scholar]


| Parameters | η0 | β | Cμ | C1ε | C2ε | σk | σε |
|---|---|---|---|---|---|---|---|
| Value | 4.38 | 0.012 | 0.0845 | 1.42 | 1.68 | 0.7179 | 0.7179 |
| Pressure on the Sidewall of Spillway (m) | Water Depth along the Side Wall of Spillway (m) | |||||||
|---|---|---|---|---|---|---|---|---|
| Y = 15 m | Y = 18 m | |||||||
| H | Simulation | Test | H | Simulation | Test | X | Simulation | Test |
| 8.9 | 23.7 | 23.4 | 6.7 | 25.4 | 24.3 | 4.1 | 11.1 | 10.3 |
| 11.3 | 17.0 | 17.6 | 9.2 | 19.6 | 19.1 | 14.1 | 10.5 | 10.3 |
| 12.4 | 13.6 | 12.6 | 11.7 | 13.4 | 13.6 | 23.8 | 11.3 | 11.2 |
| 14.8 | 8.5 | 9.7 | 15.3 | 6.3 | 5.6 | 33.1 | 13.0 | 13.0 |
| 17.1 | 4.8 | 4.5 | 17.8 | 2.4 | 2.7 | 41.5 | 15.4 | 14.6 |
| 19.5 | 1.9 | 1.6 | 21.5 | 1.4 | 0.9 | 49.5 | 19.7 | 19.3 |
| 23.0 | 0.5 | 0.6 | 22.8 | 1.0 | 0.9 | 55.1 | 25.5 | 25.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, J.; Wei, W.; Tian, Z.; Zhang, F. Design of A Streamwise-Lateral Ski-Jump Flow Discharge Spillway. Water 2018, 10, 1585. https://doi.org/10.3390/w10111585
Deng J, Wei W, Tian Z, Zhang F. Design of A Streamwise-Lateral Ski-Jump Flow Discharge Spillway. Water. 2018; 10(11):1585. https://doi.org/10.3390/w10111585
Chicago/Turabian StyleDeng, Jun, Wangru Wei, Zhong Tian, and Faxing Zhang. 2018. "Design of A Streamwise-Lateral Ski-Jump Flow Discharge Spillway" Water 10, no. 11: 1585. https://doi.org/10.3390/w10111585
APA StyleDeng, J., Wei, W., Tian, Z., & Zhang, F. (2018). Design of A Streamwise-Lateral Ski-Jump Flow Discharge Spillway. Water, 10(11), 1585. https://doi.org/10.3390/w10111585