An Improved Method to Estimate Soil Hydrodynamic and Hydraulic Roughness Parameters by Using Easily Measurable Data During Flood Irrigation Experiments and Inverse Modelling
Abstract
1. Introduction
2. Materials and Methods
2.1. Model of Flood Irrigation: Streamflow Advance and Infiltration
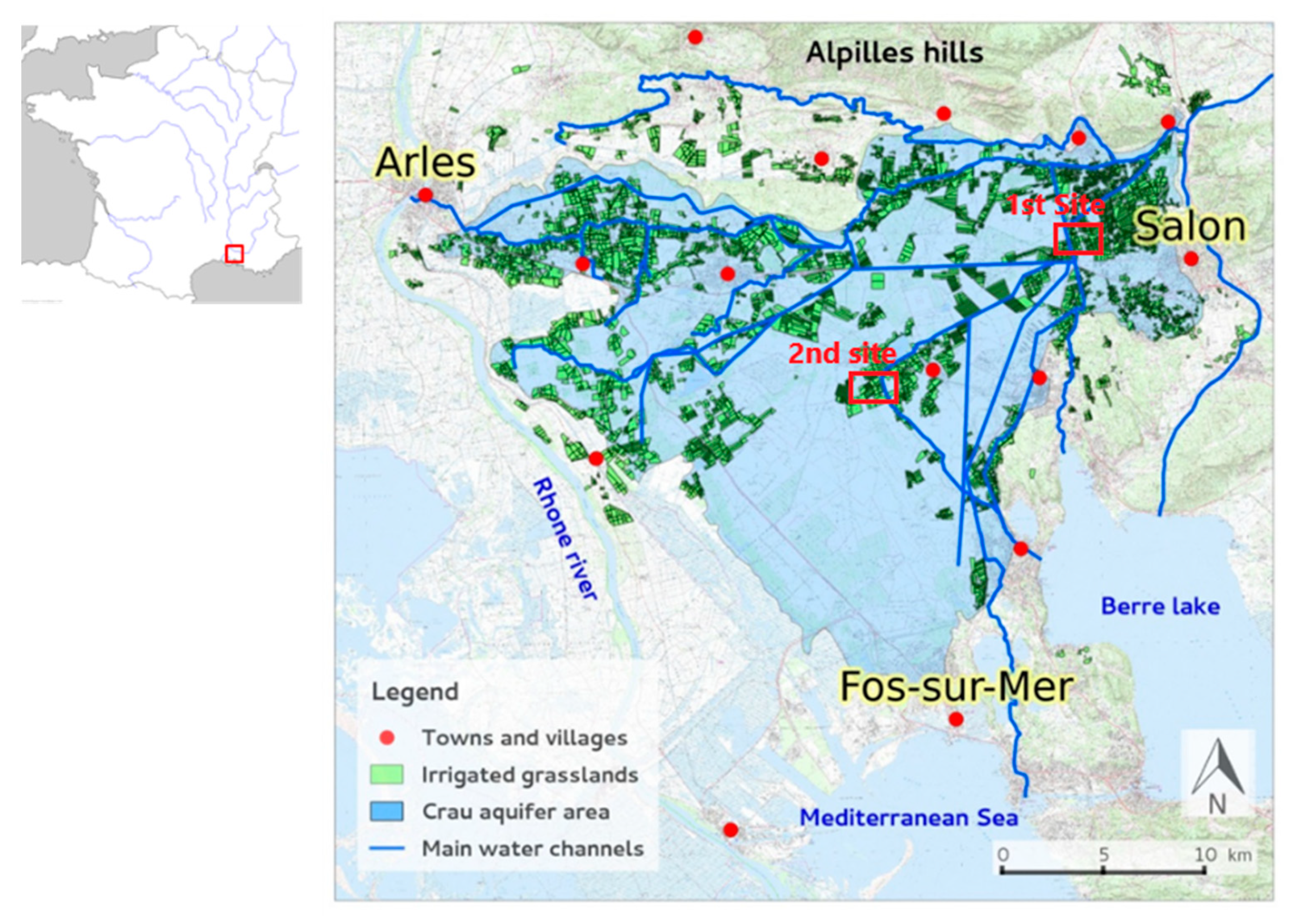
2.2. Site of Measurements
2.2.1. Field Location
2.2.2. Soil Description
2.3. Monitoring of the Flow Depth at the Field Surface
2.4. Measurement of Soil Characteristics
2.5. Measurement of Irrigation Characteristics
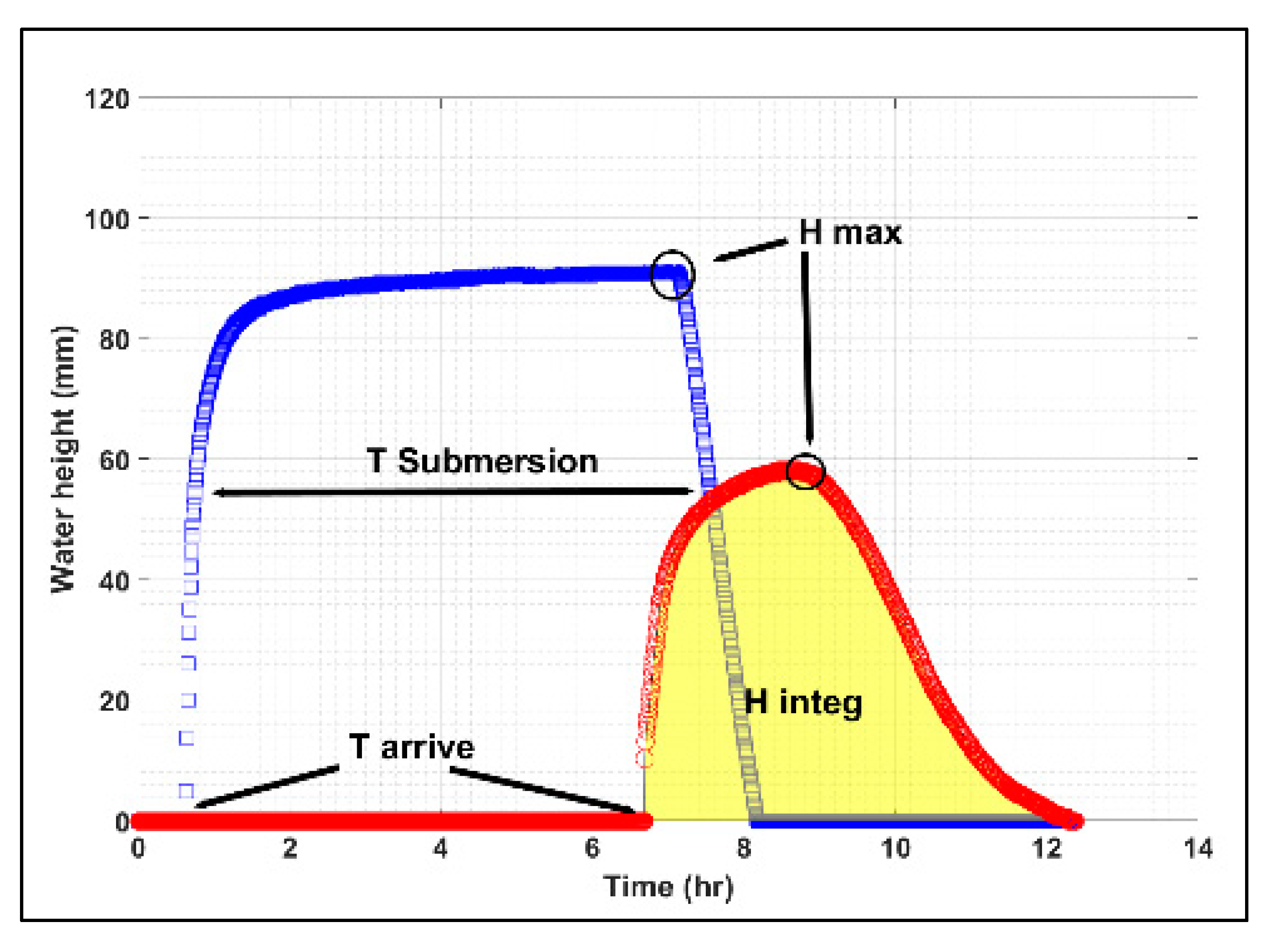
2.6. Experimental Data Used for the Fitting Algorithm (“Proxy-Data”)
- T_arrive (h) is the arrival time of the surface water front at each measurement location,
- T_submersion (h) is the time interval between the arrival time and the end of the recession phase of the surface water front at a given measurement location in the field,
- H_max (mm) is the maximum measured value of the flow depth,
- H_integral (mm·h) is defined as: , computed directly using the trapezoidal method function.
2.7. Inverse Modelling Approach
2.8. Evaluation of the Estimated Parameters
2.8.1. Coherence and Physical Meaning of the Fitted Parameters
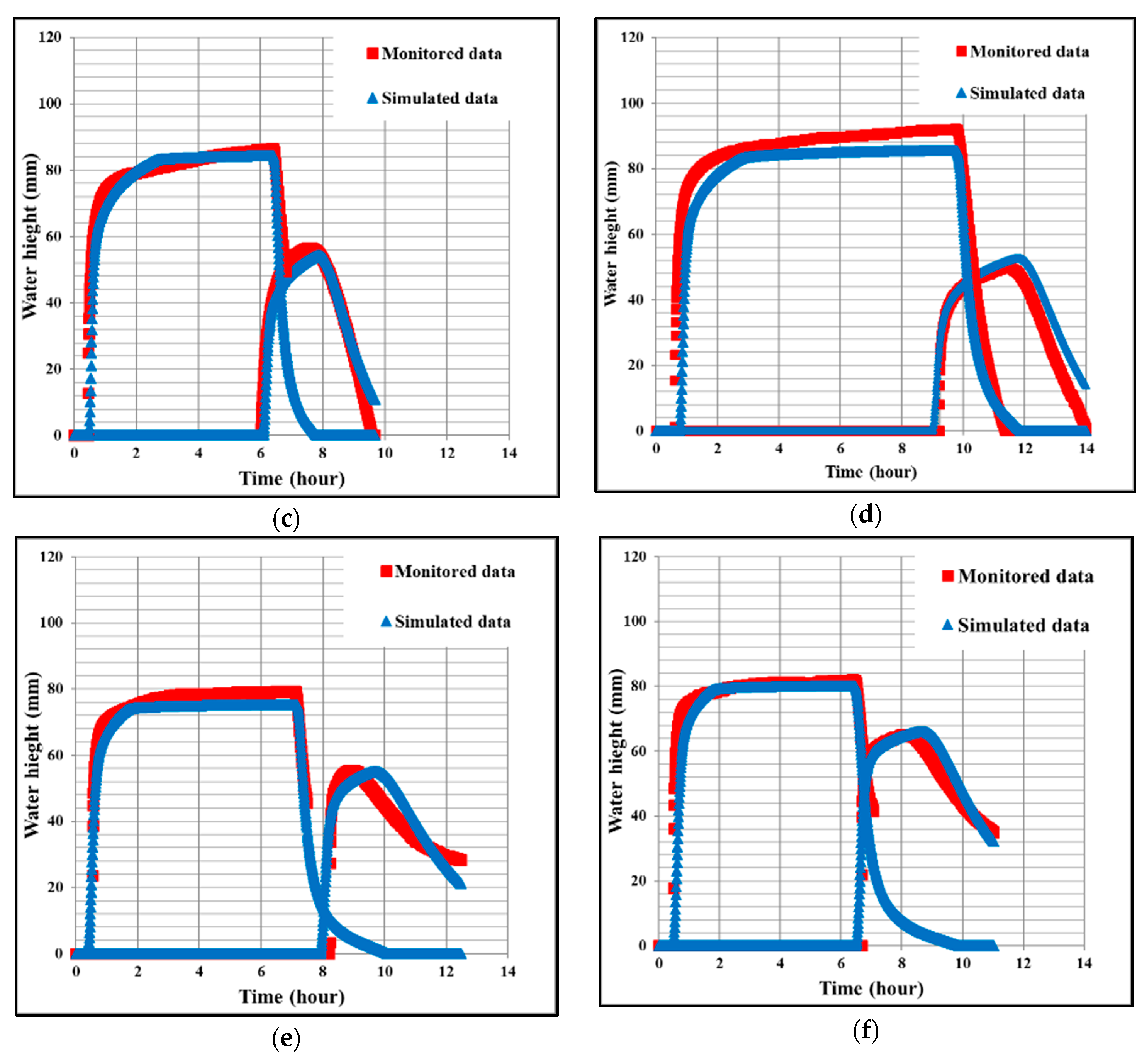
2.8.2. Evaluation of the Simulated Hydrograph and Surface Water Front from Irrigation Events Used for Calibration
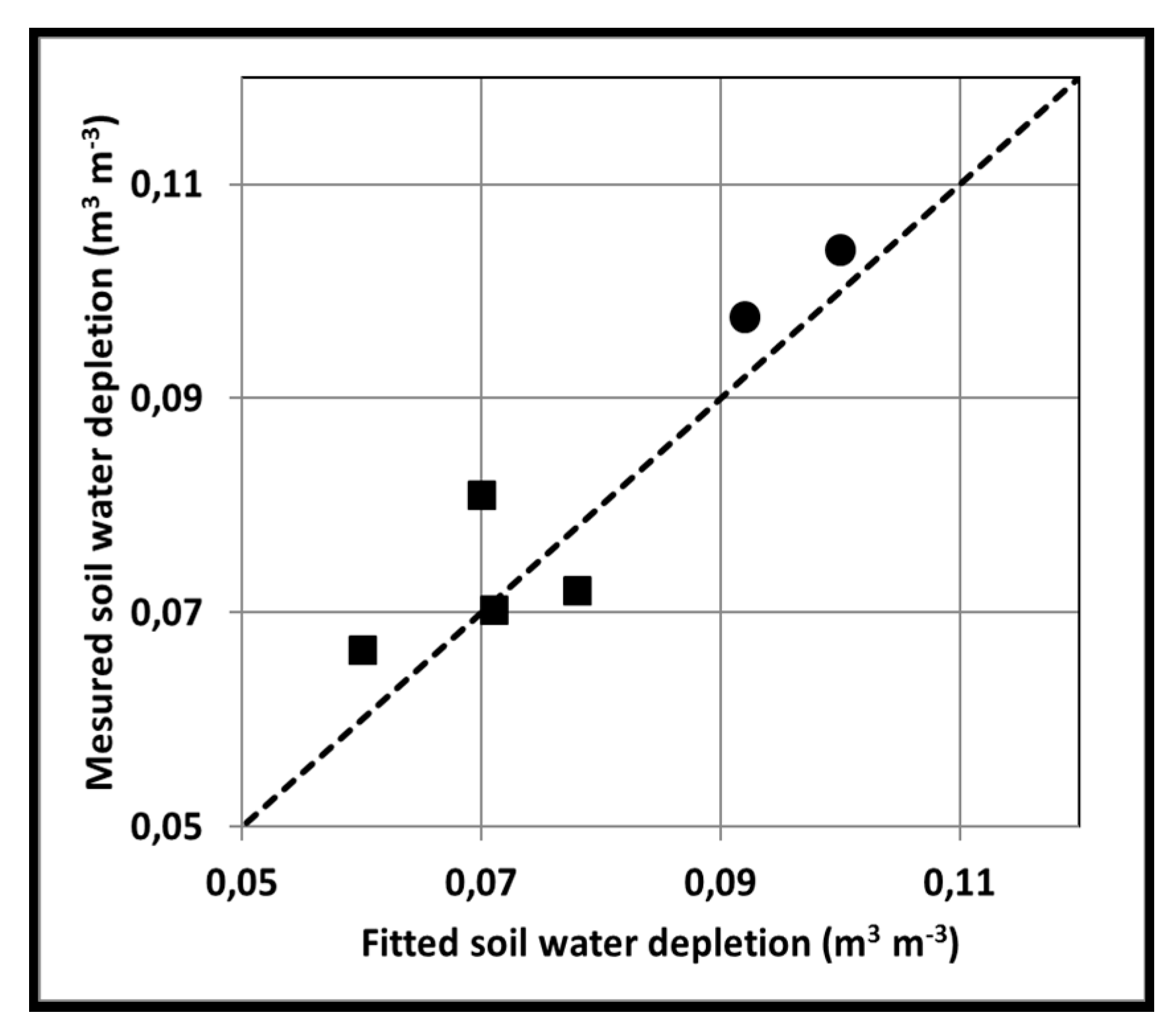
- Estimated and the measured soil water depletion ∆θ
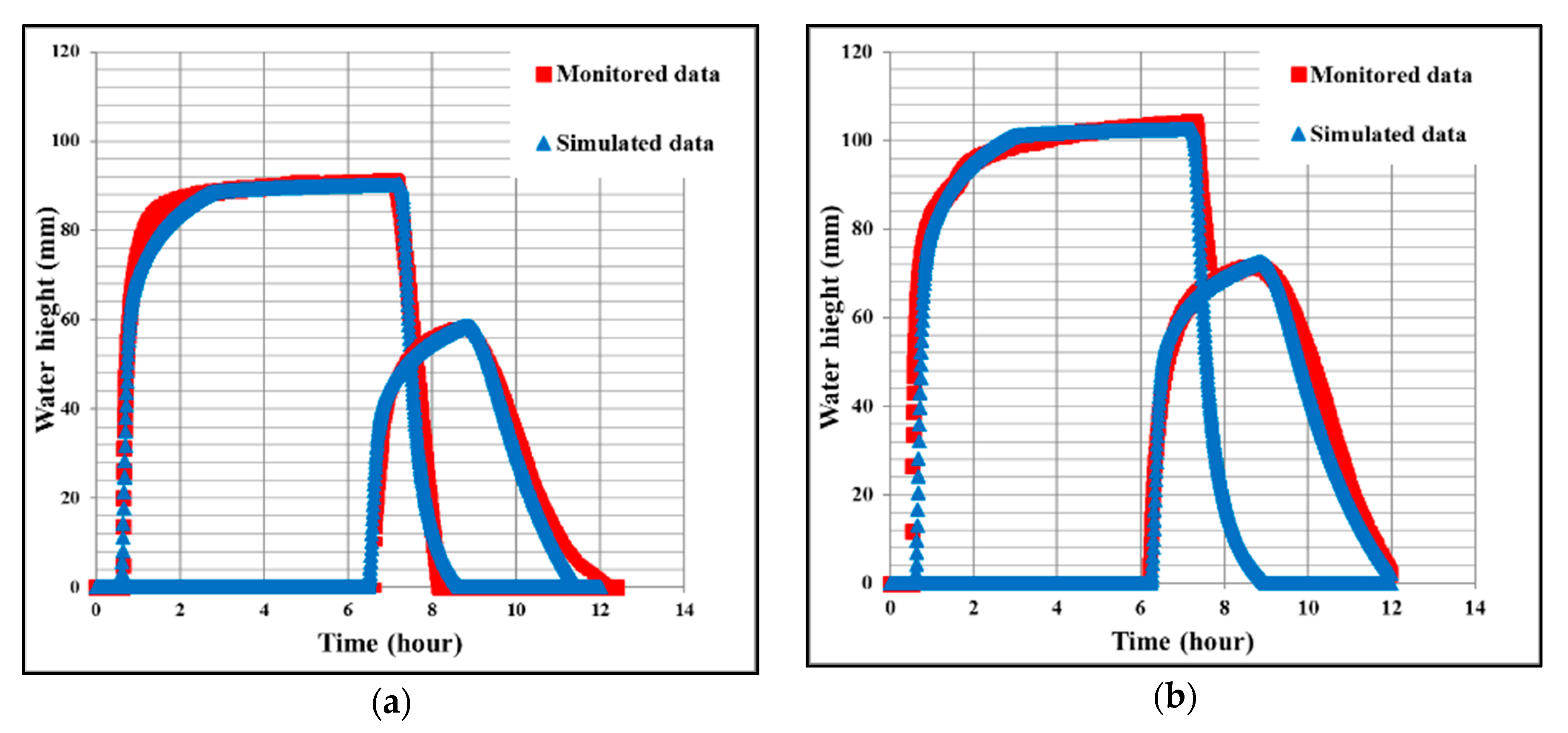
- Simulated and monitored time flow depth hydrograph H(t) in two cross sections of the field
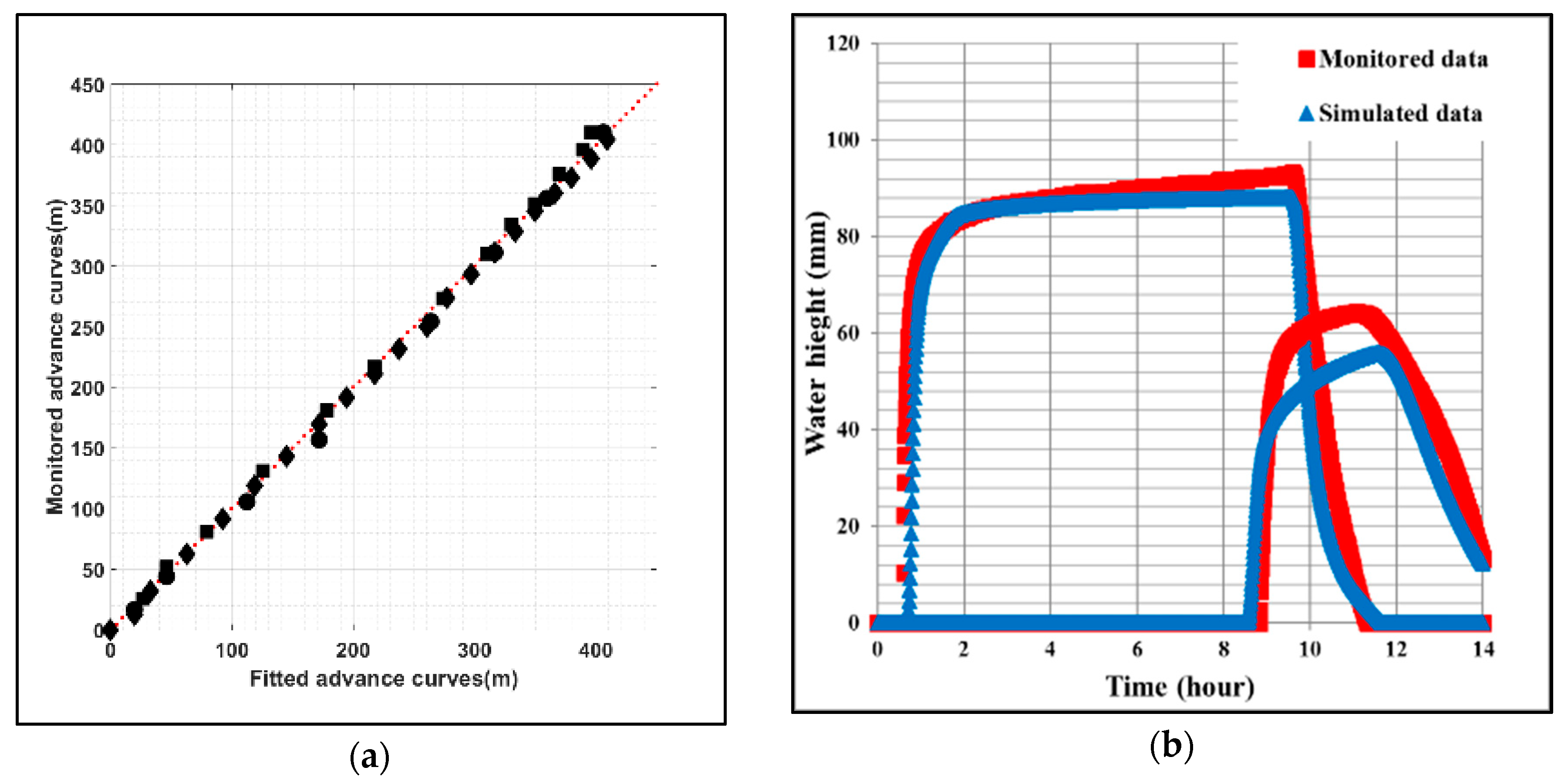
- Simulated and monitored advancement of surface water front
2.8.3. Evaluation of the Simulated Hydrograph and Surface Water Front for Cases Not Used for Calibration
- We simulated irrigation A4 that was not used during the calibration process. Parameters Ks, k, H0 and ∆θ used for this direct simulation were derived from the parameters obtained from irrigation A5. The comparison between the simulated and measured data was performed upon the advancement of the surface water and the water depth hydrographs H(t) at the two selected sections of the field.
- Two irrigation experiments referred to in [5] were obtained. They were monitored in the first experimental site and labelled irrigation A6 and A7. The first one occurred after the 1st mowing with a leaf area index (LAI) of about 1.3 and similar to those of irrigation A3 in our dataset. The second occurred before the 2nd mowing: the development of the vegetation was maximum with a LAI of about 7.7 and similar to that of irrigation A2. Therefore, we used the parameters fitted on irrigation A3 and A2 to simulate outputs of irrigation A6 and A7 respectively.
- Overall compared data for validation were also evaluated with RMSE and Nash criterion.
3. Results and Discussion
3.1. Coherence and Physical Meaning of the Fitted Parameters
3.2. Evaluation of the Performance of the Proposed Approach for Parameter Estimation
3.3. Evaluation of the New Parameter Estimation Approach
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FAO. AQUASTAT Main Database, Food and Agriculture Organization of the United Nations (FAO 2016). Available online: http://www.fao.org/nr/water/aquastat/main/index.stm (accessed on 3 June 2016).
- Clemmens, A.J. Errors in Surface Irrigation Evaluation from Incorrect Model Assumptions. J. Irrig. Drain. Eng. 2009, 135, 556–565. [Google Scholar] [CrossRef]
- Moravejalahkami, B.; Mostafazadeh-Fard, B.; Heidarpour, M.; Abbasi, F. Furrow infiltration and roughness prediction for different furrow inflow hydrographs using a zero-inertia model with a multilevel calibration approach. Biosyst. Eng. 2009, 103, 374–381. [Google Scholar] [CrossRef]
- Varella, H.; Buis, S.; Launay, M.; Guérif, M. Global sensitivity analysis for choosing the main soil parameters of a crop model to be determined. Agric. Sci. 2012, 3, 949–961. [Google Scholar] [CrossRef]
- Mailhol, J.C.; Merot, A. SPFC: A tool to improve water management and hay production in the Crau region. Irrig. Sci. 2008, 26, 289–302. [Google Scholar] [CrossRef]
- Bautista, E.; Clemmens, A.J.; Strelkoff, T.S.; Schlegel, J. Modern analysis of surface irrigation systems with WinSRFR. Agric. Water Manag. 2009, 96, 1146–1154. [Google Scholar] [CrossRef]
- Bader, J.C.; Saos, J.L.; Charron, F. Model of border irrigation runoff, advance and infiltration on a soil covering a very permeable subsoil. Hydrol. Sci. J. 2010, 55, 177–191. [Google Scholar] [CrossRef]
- Gillies, M.H.; Smith, R.J. SISCO: Surface irrigation simulation, calibration and optimisation. Irrig. Sci. 2015, 33, 339–355. [Google Scholar] [CrossRef]
- Cahoon, J. Kostiakov infiltration parameters from kinematic wave model. J. Irrig. Drain. Eng. 1998, 124, 127–130. [Google Scholar] [CrossRef]
- Sedaghatdoost, A.; Ebrahimian, H. Calibration of infiltration, roughness and longitudinal dispersivity coefficients in furrow fertigation using inverse modelling with a genetic algorithm. Biosyst. Eng. 2015, 136, 129–139. [Google Scholar] [CrossRef]
- Amoah, J.K.O.; Amatya, D.M.; Nnaji, S. Quantifying watershed surface depression storage: Determination and application in a hydrologic model. Hydrol. Process 2013, 27, 2401–2413. [Google Scholar] [CrossRef]
- Elliott, R.L.; Walker, W.R. Field evaluation of furrow infiltration and advance functions [irrigation; Colorado]. Trans. ASAE 1982, 25, 396–400. [Google Scholar] [CrossRef]
- Gillies, M.H.; Smith, R.J. Infiltration parameters from surface irrigation advance and run-off data. Irrig. Sci. 2005, 24, 25–35. [Google Scholar] [CrossRef]
- Walker, W.R. Multilevel calibration of furrow infiltration and roughness. J. Irrig. Drain. Eng. 2005, 131, 129–136. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies on soil physics: The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Bautista, E.; Strelkoff, T.S.; Clemmens, A.J. Improved Surface Volume Estimates for Surface Irrigation Volume-Balance Calculations. J. Irrig. Drain. Eng. 2012, 138, 715–726. [Google Scholar] [CrossRef]
- Bautista, E.; Schlegel, J.L. A flexible system for estimation of infiltration and hydraulic resistance parameters in surface irrigation. Trans. ASABE 2017, 60, 1223–1234. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Liaghat, A.; Ghanbarian-Alavijeh, B.; Abbasi, F. Evaluation of various quick methods for estimating furrow and border infiltration parameters. Irrig. Sci. 2010, 28, 479–488. [Google Scholar] [CrossRef]
- Gillies, M.H.; Smith, R.J.; Raine, S.R. Accounting for temporal inflow variation in the inverse solution for infiltration in surface irrigation. Irrig. Sci. 2006, 25, 87–97. [Google Scholar] [CrossRef]
- Mailapalli, D.R.; Wallender, W.W.; Raghuwanshi, N.S.; Singh, R. Quick method for estimating furrow infiltration. J. Irrig. Drain. Eng. 2008, 134, 788–795. [Google Scholar] [CrossRef]
- Shepard, J.S.; Wallender, W.W.; Hopmans, J.W. One-point method for estimating furrow infiltration. Trans. ASAE 1993, 36, 395–404. [Google Scholar] [CrossRef]
- Katopodes, N.K. Observability of surface irrigation advance. J. Irrig. Drain. Eng. 1990, 116, 656–675. [Google Scholar] [CrossRef]
- Weibo, N.; Liangjun, F.; Xiaoyi, M. Estimated Infiltration Parameters and Manning Roughness in Border Irrigation. Irrig. Drain. 2012, 61, 231–239. [Google Scholar] [CrossRef]
- Buis, S.; Wallach, D.; Guillaume, S.; Varella, H.; Lecharpentier, P.; Launay, M.; Guérif, M.; Bergez, J.E.; Justes, E. The STICS Crop Model and Associated Software for Analysis, Parameterization, and Evaluation. In Methods of Introducing System Models into Agricultural Research; American Society of Agronomy: Madison, SD, USA, 2011. [Google Scholar]
- Merot, A.; Wery, J.; Isberie, C.; Charron, F. Response of a plurispecific permanent grassland to border irrigation regulated by tensiometers. Eur. J. Agron. 2008, 28, 8–18. [Google Scholar] [CrossRef]
- Bouteyre, G.; Duclos, G. Carte Pédologique de la France à 1/100000; INRA: Arles, France, 1994. [Google Scholar]
- Galbiati, G.; Savi, F. Evaluation of the comparative influence of soil hydraulic properties and roughness on overland flow at the local scale. J. Agric. Eng. Res. 1995, 61, 183–190. [Google Scholar] [CrossRef]
- Risse, L.M.; Nearing, M.A.; Savabi, M.R. Determining the Green-Ampt effective hydraulic conductivity from rainfall-runoff data for the WEPP model. Trans. ASAE 1994, 37, 411–418. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Saxton, K.E. Estimation of soil water properties. Trans. ASAE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Charnes, A.; Frome, E.L.; Yu, P.-L. The equivalence of generalized least squares and maximum likelihood estimates in the exponential family. J. Am. Stat. Assoc. 1976, 71, 169–171. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Algorithm in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Rasoulzadeh, A.; Sepaskhah, A.R. Scaled Infiltration Equations for Furrow Irrigation. Biosyst. Eng. 2003, 86, 375–383. [Google Scholar] [CrossRef]
- Michael, A.M. Irrigation: Theory and Practice; Vikas Publishing House Pvt Ltd.: Noida, India, 2009. [Google Scholar]
- Davis, C.A.; Collins, H.G.; Portland, O.R.; Woodward, G.; Humpherys, A.S.; Hart, W.E. Design and Operation of Farm Irrigation Systems; The American Society of Agricultural and Biological Engineers: Joseph, MI, USA, 1980. [Google Scholar]
- Robertson, D.; Wood, M.; Wang, Q.J. Estimating hydraulic parameters for a surface irrigation model from field conditions. Aust. J. Exp. Agric. 2004, 44, 173–179. [Google Scholar] [CrossRef]
- Khattabi, A.A.; Hablous, A.A.; Elnemry, M.M. The Relation between the Coefficient of Friction and Pressure Drop by Using the Different Reynolds Number in a Circular Tube. J. Fluid Dyn. 2015, 5, 99–105. [Google Scholar] [CrossRef]
- Kamphorst, E.C.; Jetten, V.; Guérif, J.; Iversen, B.V.; Douglas, J.T.; Paz, A. Predicting depressional storage from soil surface roughness. Soil Sci. Soc. Am. J. 2000, 64, 1749–1758. [Google Scholar] [CrossRef]
- Kamphorst, E.C.; Duval, Y. Validation of a numerical method to quantify depression storage by direct measurements on moulded surfaces. Catena 2001, 43, 1–14. [Google Scholar] [CrossRef]
- Álvarez-Mozos, J.; Campo, M.Á.; Giménez, R.; Casalí, J.; Leibar, U. Implications of scale, slope, tillage operation and direction in the estimation of surface depression storage. Soil Till. Res. 2011, 111, 142–153. [Google Scholar] [CrossRef]
- Paz-Ferreiro, J.; Bertol, I.; Vidal Vázquez, E. Quantification of tillage, plant cover, and cumulative rainfall effects on soil surface microrelief by statistical, geostatistical and fractal indices. Nonlinear Process. Geophys. 2008, 15, 575–590. [Google Scholar] [CrossRef]
- Tiscareno-Lopez, M.; Lopes, V.L.; Stone, J.J.; Lane, L.J. Sensitivity analysis of the WEPP watershed model for rangeland applications I: Hillslope processes. Trans. ASAE 1993, 36, 1659–1672. [Google Scholar] [CrossRef]

| N | L | W (m) | I (‰) | Q (L·s−1·m−1) | ∆θ (m3·m−3) | Z (mm) | Ti (h) | Date | |
|---|---|---|---|---|---|---|---|---|---|
| (m) | |||||||||
| 1st site | A1 | 410 | 49 | 2.8 | 2.85 | 0.070 | 450 | 7.16 | 10 days before 1st mowing |
| A2 | 3 | 0.066 | 7.15 | 48 days before 2nd mowing | |||||
| A3 | 3.02 | 0.072 | 6.35 | 10 days after a 2nd mowing | |||||
| A4 | 2.28 | 0.072 | 9.5 | 21 days after a 2nd mowing | |||||
| A5 | 2.08 | 0.081 | 9.68 | 31 days after a 2nd mowing | |||||
| 2nd site | B6 | 60 | 4.8 | 1.48 | 0.097 | 200 | 7.12 | 20 days after a 2nd mowing | |
| B7 | 1.65 | 0.103 | 6.45 | 39 days after a 2nd mowing |
| log [KS (m·s−1)] | k (m·s−1/3) | ∆θ (m3·m−3) | H0 | |
|---|---|---|---|---|
| Min | −7.2 | 1.5 | 0.06 | 0 |
| Max | −5.6 | 4.5 | 0.12 | 20 |
| Experiment | Coherence of Fitted Parameters | Evaluation with Data Didn’t Used in Fitting Process | Evaluation Using Data from Independent Experiments |
|---|---|---|---|
| A1, A2, A3, A5, B6, B7 | - Temporal Stability of Ks | - Measured/fitted ∆θ. | |
| - f (Hay development, k). | - Measured/simulated H(t) | ||
| A5 | - Measured/simulated streamflow advance curve. | ||
| A4, A6, A7 [5] | - H(t) in A4 simulated with fitted parameters from A5 - Streamflow advance curve in A4, A6 and A7 using fitted parameters from A5, A3 and A2 respectively. |
| A1 | A2 | A3 | A5 | B6 | B7 | |
|---|---|---|---|---|---|---|
| Ks (m·s−1) | 1.5 × 10−6 (1.08–2.07) × 10−6 | 1.34 × 10−6 (0.9–1.99) × 10−6 | 1.36× 10−6 (0.98–1.88) × 10−6 | 1.41× 10−6 (0.94–2.1) × 10−6 | 1.15× 10−7 (0.83–1.59) × 10−7 | 1.11× 10−7 (0.8–1.53) × 10−7 |
| k (m·s−1/3) | 2.94 (2.43–3.44) | 2.61 (2.15–3.06) | 3.54 (3.15–3.92) | 2.53 (1.99–3.06) | 1.69 (1.58–1.79) | 1.65 (1.45–1.85) |
| ∆θ (m3·m−3) | 0.071 (0.05–0.09) | 0.06 (0.04–0.08) | 0.078 (0.06–0.09) | 0.07 (0.05–0.09) | 0.1 (0.08–0.12) | 0.092 (0.07–0.11) |
| H0 (mm) | 0.3 (0–6.3) | 1.9 (0–5.6) | 2.6 (0–6.13) | 4.2 (0–10.2) | 3.3 (0–7.1) | 2.6 (0–4.8) |
| Experiments | A1 | A2 | A3 | A5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
| Cnash (−) | Upstream | 0.99 | 0.85 | 0.86 | 0.89 | 0.85 | 0.96 |
| Downstream | 0.97 | 1.00 | 0.98 | 0.94 | 0.98 | 0.94 | |
| RMSE (mm) | Upstream | 3.63 | 10.12 | 8.18 | 10.29 | 8.61 | 4.13 |
| Downstream | 3.78 | 1.57 | 3.41 | 4.63 | 3.55 | 4.74 | |
| Streamflow Advanced Curve | Streamflow Hydrograph | ||||
|---|---|---|---|---|---|
| Experiments | A4 | A6 | A7 | Upstream | Downstream |
| CNASH (−) | 1.00 | 1.00 | 1.00 | 0.90 | 0.95 |
| RMSE (m) | 5.10 | 5.38 | 7.32 | 8.96 | 5.86 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkassem Alosman, M.; Ruy, S.; Buis, S.; Lecharpentier, P.; Bader, J.C.; Charron, F.; Olioso, A. An Improved Method to Estimate Soil Hydrodynamic and Hydraulic Roughness Parameters by Using Easily Measurable Data During Flood Irrigation Experiments and Inverse Modelling. Water 2018, 10, 1581. https://doi.org/10.3390/w10111581
Alkassem Alosman M, Ruy S, Buis S, Lecharpentier P, Bader JC, Charron F, Olioso A. An Improved Method to Estimate Soil Hydrodynamic and Hydraulic Roughness Parameters by Using Easily Measurable Data During Flood Irrigation Experiments and Inverse Modelling. Water. 2018; 10(11):1581. https://doi.org/10.3390/w10111581
Chicago/Turabian StyleAlkassem Alosman, Mohamed, Stéphane Ruy, Samuel Buis, Patrice Lecharpentier, Jean Claude Bader, François Charron, and Albert Olioso. 2018. "An Improved Method to Estimate Soil Hydrodynamic and Hydraulic Roughness Parameters by Using Easily Measurable Data During Flood Irrigation Experiments and Inverse Modelling" Water 10, no. 11: 1581. https://doi.org/10.3390/w10111581
APA StyleAlkassem Alosman, M., Ruy, S., Buis, S., Lecharpentier, P., Bader, J. C., Charron, F., & Olioso, A. (2018). An Improved Method to Estimate Soil Hydrodynamic and Hydraulic Roughness Parameters by Using Easily Measurable Data During Flood Irrigation Experiments and Inverse Modelling. Water, 10(11), 1581. https://doi.org/10.3390/w10111581





