Urban Irrigation Suppresses Land Surface Temperature and Changes the Hydrologic Regime in Semi-Arid Regions
Abstract
1. Introduction
2. Methods
2.1. Area of Interest
2.2. Landsat Land Surface Temperature
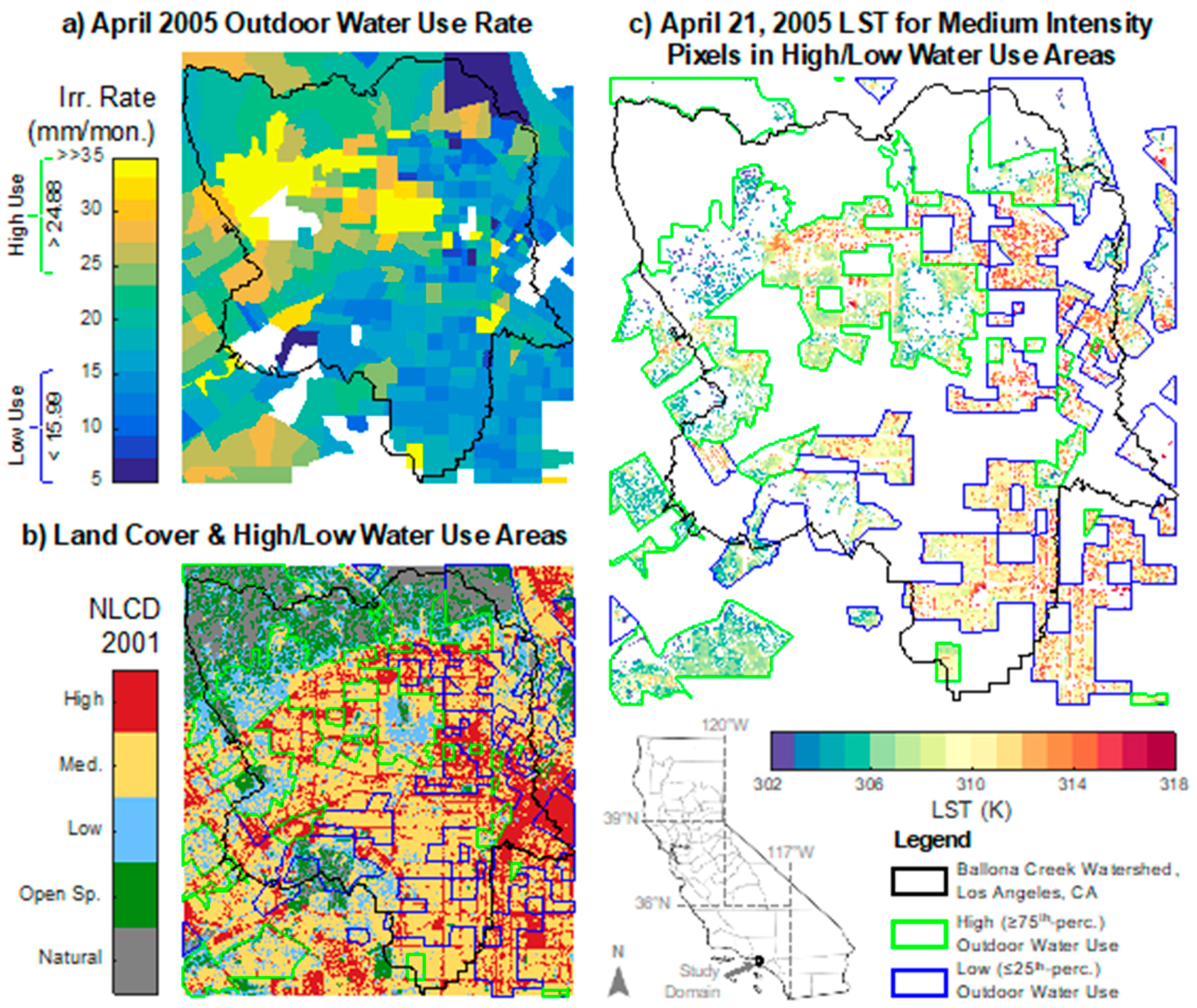
2.3. Outdoor Water Use Data and LST Classification
2.4. Land Cover, Irrigation and Model Used
2.5. Model Forcings
3. Results
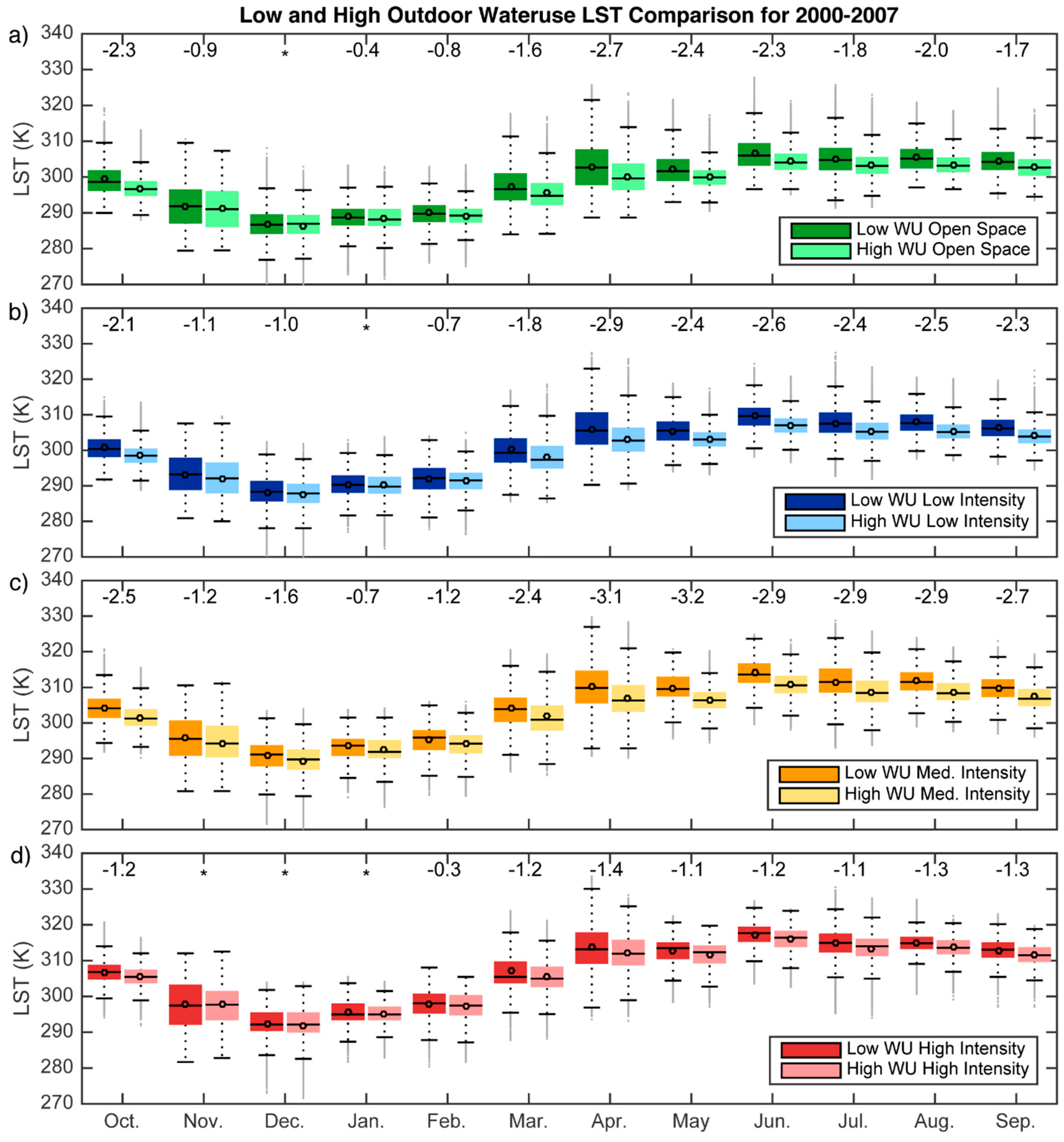
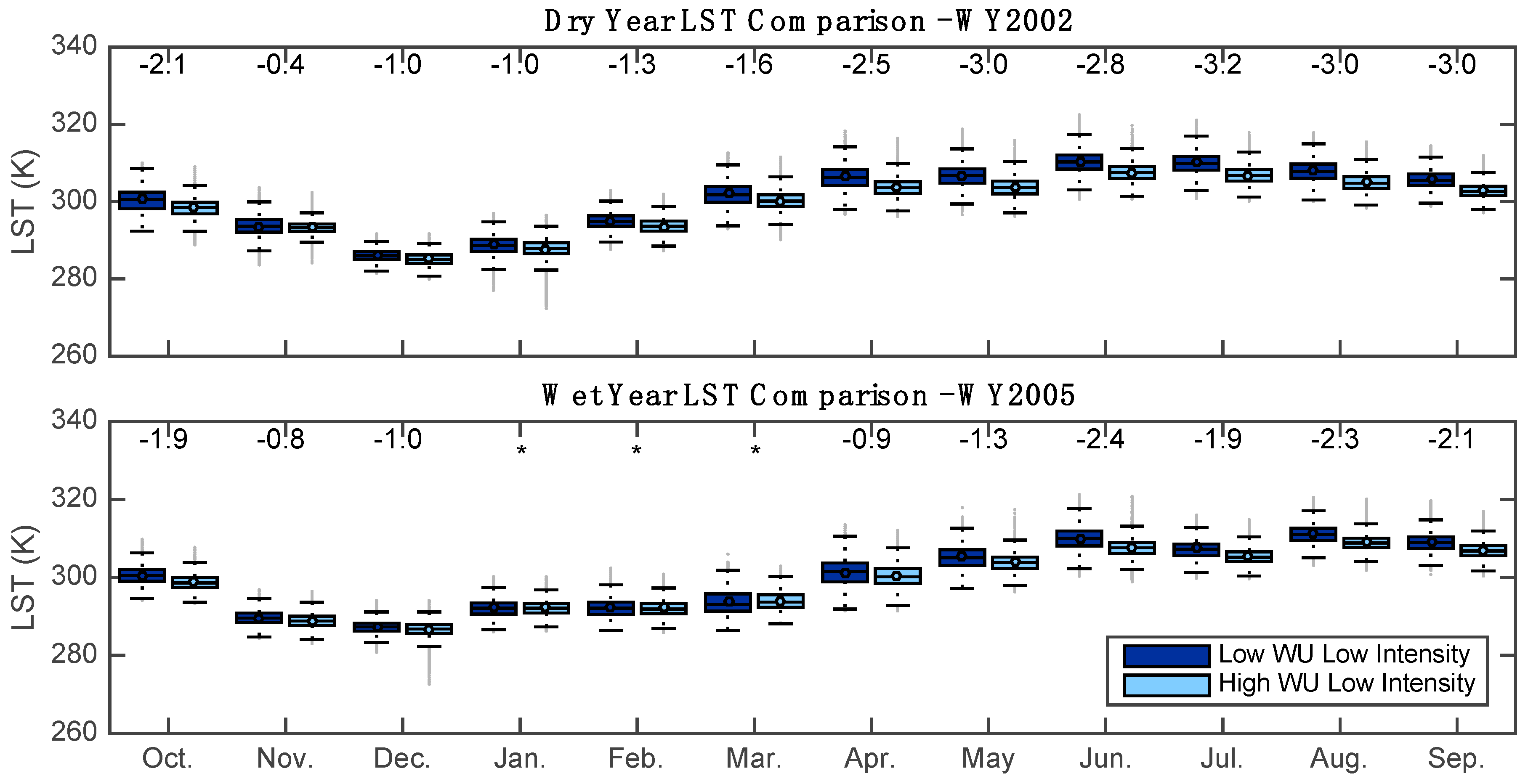
3.1. Irrigation Impact on LST
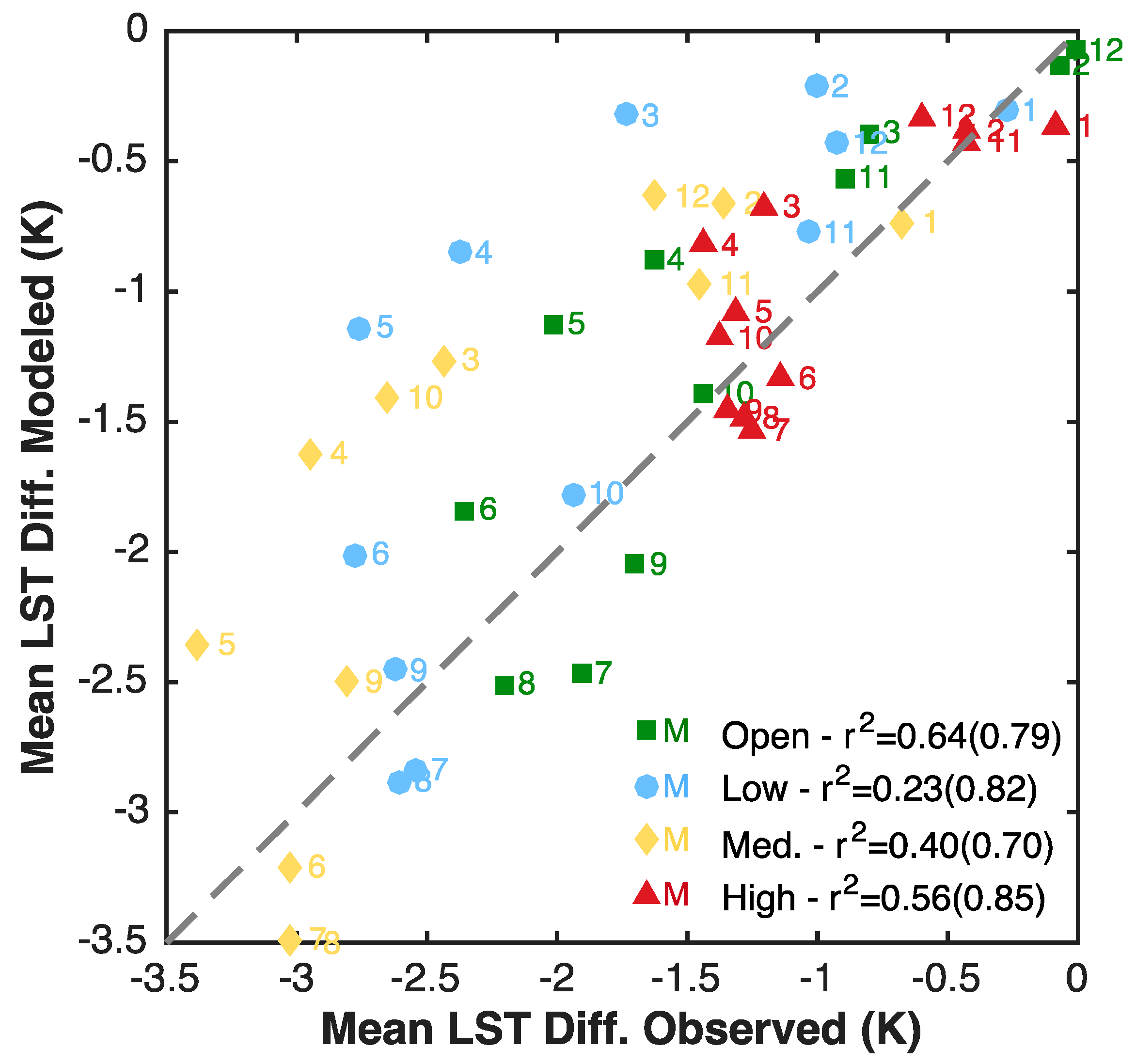
3.2. Simulated LST Change
3.3. Sensitivities of Hydrologic Fluxes and Regime Change
4. Discussion and Conclusions
- LST decreases with higher outdoor water use within similar LC type throughout our study period and at all times of the year. A larger impact on LST is seen in the spring and summer months, hypothesized to be a result of both larger irrigation volumes and increased prevailing LST during these months. Furthermore, by analyzing the LST difference during a wet year and a dry year we conclude that the cooling effect is largely caused by the irrigation flux, rather than any changes in regional meteorology.
- We are able to capture the relative change in LST caused by irrigation given that our simulations implement a constant irrigation pattern as opposed to higher irrigation rates in the spring and summer months. Furthermore, we capture the observed relative behavior of each urban LC type indicating fairly realistic representation of the urban land surface using our parameterization. However, these models consistently underestimate LST as compared to values of remotely sensed LST throughout the study period and for each LC type, with more developed LCs causing larger biases. This points to possible systematic errors in both model parameterization and in the method used to estimate LST from the remote sensing observations.
- The urban irrigation flux causes significant changes to the hydrologic regime of the urban semi-arid environment. The timing of irrigation only has a small impact on hydrologic fluxes for urban LC; the largest impact (±2%) occurs at high irrigation volumes for developed open space. At low volumes (less than ~75% of mean precipitation), the irrigation flux is partitioned into ET and into vegetation growth with runoff held relatively constant. At higher volumes, closer to estimated values in Los Angeles for the study period, the flux moves the system into a sub-humid regime with implications for increased runoff and infiltration. The model results presented here show some deficiencies in recreation of land surface temperatures by the land surface model used. However, adding the irrigation flux is shown to have a clear advantage in simulating the difference in LST between high and low water use areas of otherwise similar land cover.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Friedman, K.; Heaney, J.P.; Morales, M.; Palenchar, J.E. Predicting and managing residential potable irrigation using parcel-level databases. J. Am. Water Works Assoc. 2013, 105, E372–E386. [Google Scholar] [CrossRef]
- Mini, C.; Hogue, T.S.; Pincetl, S. Estimation of residential outdoor water use in Los Angeles, California. Landsc. Urban Plan. 2014, 127, 124–135. [Google Scholar] [CrossRef]
- United Nations. World Urbanization Prospects; United Nations Population Division, Department of Economic and Social Affairs: New York, NY, USA, 2011. [Google Scholar]
- Kaushal, S.; McDowell, W.; Wollheim, W.; Johnson, T.; Mayer, P.; Belt, K.; Pennino, M.; Kaushal, S.S.; McDowell, W.H.; Wollheim, W.M.; et al. Urban Evolution: The Role of Water. Water 2015, 7, 4063–4087. [Google Scholar] [CrossRef]
- Kim, H.; Son, J.; Lee, S.; Koop, S.; van Leeuwen, K.; Choi, Y.; Park, J.; Kim, H.; Son, J.; Lee, S.; et al. Assessing Urban Water Management Sustainability of a Megacity: Case Study of Seoul, South Korea. Water 2018, 10, 682. [Google Scholar] [CrossRef]
- Feingold, D.; Koop, S.; van Leeuwen, K. The City Blueprint Approach: Urban Water Management and Governance in Cities in the U.S. Environ. Manag. 2018, 61, 9–23. [Google Scholar] [CrossRef] [PubMed]
- Mini, C.; Hogue, T.S.; Pincetl, S. Patterns and controlling factors of residential water use in Los Angeles, California. Water Policy 2014, 16, 1054–1069. [Google Scholar] [CrossRef]
- Bonfils, C.; Lobell, D. Empirical evidence for a recent slowdown in irrigation-induced cooling. PNAS 2007, 104, 13582–13587. [Google Scholar] [CrossRef] [PubMed]
- Kueppers, L.M.; Snyder, M.A.; Sloan, L.C. Irrigation cooling effect: Regional climate forcing by land-use change. Geophys. Res. Lett. 2007, 34, L03703. [Google Scholar] [CrossRef]
- Lobell, D.B.; Bonfils, C.J.; Kueppers, L.M.; Snyder, M.A. Irrigation cooling effect on temperature and heat index extremes. Geophys. Res. Lett. 2008, 35, L09705. [Google Scholar] [CrossRef]
- Puma, M.J.; Cook, B.I. Effects of irrigation on global climate during the 20th century. J. Geophys. Res. Atmos. 2010, 115, D16120. [Google Scholar] [CrossRef]
- Sorooshian, S.; Li, J.; Hsu, K.; Gao, X. How significant is the impact of irrigation on the local hydroclimate in California’s Central Valley? Comparison of model results with ground and remote-sensing data. J. Geophys. Res. Atmos. 2011, 116, D06102. [Google Scholar] [CrossRef]
- Sorooshian, S.; AghaKouchak, A.; Li, J. Influence of Irrigation on Land Hydrological Processes over California: Influence of Irrigation on hydrology. J. Geophys. Res. Atmos. 2014, 119, 137–152. [Google Scholar] [CrossRef]
- Lu, Y.; Kueppers, L. Increased heat waves with loss of irrigation in the United States. Environ. Res. Lett. 2015, 10, 064010. [Google Scholar] [CrossRef]
- Jaeger, E.B.; Seneviratne, S.I. Impact of soil moisture–atmosphere coupling on European climate extremes and trends in a regional climate model. Clim. Dyn. 2011, 36, 1919–1939. [Google Scholar] [CrossRef]
- Kollet, S.J.; Maxwell, R.M. Capturing the influence of groundwater dynamics on land surface processes using an integrated, distributed watershed model. Water Resour. Res. 2008, 44, W02402. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Kollet, S.J. Interdependence of groundwater dynamics and land-energy feedbacks under climate change. Nat. Geosci. 2008, 1, 665–669. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Sharp, J.M.; Krothe, J.N.; Mather, J.D.; Garcia-Fresca, B.; Stewart, C.A. Effects of Urbanization on Groundwater Systems. In Earth Science in the City: A Reader; Heiken, G., Fakundiny, R., Sutter, J., Eds.; American Geophysical Union: Washington, DC, USA, 2003; pp. 257–278. [Google Scholar]
- Garcia-Fresca, B.; Sharp, J.M. Hydrogeologic considerations of urban development: Urban-induced recharge. Rev. Eng. Geol. 2005, 16, 123–136. [Google Scholar] [CrossRef]
- Sharp, J.M. The impacts of urbanization on groundwater systems and recharge. AQUA Mundi 2010, 1, 51–56. [Google Scholar] [CrossRef]
- Hibbs, B.J.; Sharp, J.M. Hydrogeological Impacts of Urbanization. Environ. Eng. Geosci. 2012, 18, 3–24. [Google Scholar] [CrossRef]
- Passarello, M.C.; Sharp, J.M.; Pierce, S.A. Estimating Urban-Induced Artificial Recharge: A Case Study for Austin, TX. Environ. Eng. Geosci. 2012, 18, 25–36. [Google Scholar] [CrossRef]
- Bhaskar, A.S.; Welty, C. Water Balances along an Urban-to-Rural Gradient of Metropolitan Baltimore, 2001–2009. Environ. Eng. Geosci. 2012, 18, 37–50. [Google Scholar] [CrossRef]
- Bhaskar, A.S.; Welty, C.; Maxwell, R.M.; Miller, A.J. Untangling the effects of urban development on subsurface storage in Baltimore. Water Resour. Res. 2015, 51, 1158–1181. [Google Scholar] [CrossRef]
- Lerner, D.N. Groundwater Recharge in Urban Areas. Atmos. Environ. 1990, 24, 29–33. [Google Scholar] [CrossRef]
- Lerner, D.N. Identifying and quantifying urban recharge: A review. Hydrogeol. J. 2002, 10, 143–152. [Google Scholar] [CrossRef]
- Delleur, J.W. The evolution of urban hydrology: Past, present, and future. J. Hydraul. Eng. 2003, 129, 563–573. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Schirmer, M.; Leschik, S.; Musolff, A. Current research in urban hydrogeology—A review. Adv. Water Resour. 2013, 51, 280–291. [Google Scholar] [CrossRef]
- Barrett, M.H.; Hiscock, K.M.; Pedley, S.; Lerner, D.N.; Tellam, J.H.; French, M.J. Marker species for identifying urban groundwater recharge sources: A review and case study in Nottingham, UK. Water Res. 1999, 33, 3083–3097. [Google Scholar] [CrossRef]
- Yang, Y.; Lerner, D.N.; Barrett, M.H.; Tellam, J.H. Quantification of groundwater recharge in the city of Nottingham, UK. Environ. Geol. 1999, 38, 183–198. [Google Scholar] [CrossRef]
- Barron, O.V.; Barr, A.D.; Donn, M.J. Effect of urbanisation on the water balance of a catchment with shallow groundwater. J. Hydrol. 2013, 485, 162–176. [Google Scholar] [CrossRef]
- Bhaskar, A.S.; Beesley, L.; Burns, M.J.; Fletcher, T.D.; Hamel, P.; Oldham, C.E.; Roy, A.H. Will it rise or will it fall? Managing the complex effects of urbanization on base flow. Freshw. Sci. 2016, 35, 293–310. [Google Scholar] [CrossRef]
- Vahmani, P.; Hogue, T.S. High-resolution land surface modeling utilizing remote sensing parameters and the Noah UCM: a case study in the Los Angeles Basin. Hydrol. Earth Syst. Sci. 2014, 18, 4791–4806. [Google Scholar] [CrossRef]
- Vahmani, P.; Hogue, T.S. Incorporating an Urban Irrigation Module into the Noah Land Surface Model Coupled with an Urban Canopy Model. J. Hydrometeorol. 2014, 15, 1440–1456. [Google Scholar] [CrossRef]
- Lintner, B.R.; Gentine, P.; Findell, K.L.; Salvucci, G.D. The Budyko and complementary relationships in an idealized model of large-scale land–atmosphere coupling. Hydrol. Earth Syst. Sci. 2015, 19, 2119–2131. [Google Scholar] [CrossRef]
- Wang, C.; Wang, S.; Fu, B.; Zhang, L. Advances in hydrological modelling with the Budyko framework A review. Prog. Phys. Geogr. 2016, 40, 409–430. [Google Scholar] [CrossRef]
- Renner, M.; Brust, K.; Schwärzel, K.; Volk, M.; Bernhofer, C. Separating the effects of changes in land cover and climate: A hydro-meteorological analysis of the past 60 yr in Saxony, Germany. Hydrol. Earth Syst. Sci. 2014, 18, 389–405. [Google Scholar] [CrossRef]
- Jaramillo, F.; Destouni, G. Developing water change spectra and distinguishing change drivers worldwide. Geophys. Res. Lett. 2014, 41, 8377–8386. [Google Scholar] [CrossRef]
- Taha, H. Urban climates and heat islands: Albedo, evapotranspiration, and anthropogenic heat. Energy Build. 1997, 25, 99–103. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Clim. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Masson, V. Urban surface modeling and the meso-scale impact of cities. Theor. Appl. Climatol. 2006, 84, 35–45. [Google Scholar] [CrossRef]
- Roth, M. Review of urban climate research in (sub)tropical regions. Int. J. Clim. 2007, 27, 1859–1873. [Google Scholar] [CrossRef]
- Lamptey, B. An analytical framework for estimating the urban effect on climate. Int. J. Clim. 2010, 30, 72–88. [Google Scholar] [CrossRef]
- Wang, J.; Feng, J.; Yan, Z.; Hu, Y.; Jia, G. Nested high-resolution modeling of the impact of urbanization on regional climate in three vast urban agglomerations in China. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef] [PubMed]
- Taleghani, M.; Sailor, D.; Ban-Weiss, G.A. Micrometeorological simulations to predict the impacts of heat mitigation strategies on pedestrian thermal comfort in a Los Angeles neighborhood. Environ. Res. Lett. 2016, 11, 024003. [Google Scholar] [CrossRef]
- Vahmani, P.; Ban-Weiss, G. Climatic consequences of adopting drought tolerant vegetation over Los Angeles as a response to California drought. Geophys. Res. Lett. 2016, 43, 8240–8249. [Google Scholar] [CrossRef]
- Kumar, R.; Mishra, V.; Buzan, J.; Kumar, R.; Shindell, D.; Huber, M. Dominant control of agriculture and irrigation on urban heat island in India. Sci. Rep. 2017, 7, 14054. [Google Scholar] [CrossRef] [PubMed]
- Collier, C.G. The impact of urban areas on weather. Q. J. Roy. Meteorol. Soc. 2006, 132, 1–25. [Google Scholar] [CrossRef]
- Fischer, E.M.; Oleson, K.W.; Lawrence, D.M. Contrasting urban and rural heat stress responses to climate change. Geophys. Res. Lett. 2012, 39, L03705. [Google Scholar] [CrossRef]
- Li, D.; Bou-Zeid, E. Quality and sensitivity of high-resolution numerical simulation of urban heat islands. Environ. Res. Lett. 2014, 9, 055001. [Google Scholar] [CrossRef]
- Bounoua, L.; Zhang, P.; Mostovoy, G.; Thome, K.; Masek, J.; Imhoff, M.; Marshall, S.; Quattrochi, D.; Santanello, J.; Silva, J.; Wolfe, R.; et al. Impact of urbanization on US surface climate. Environ. Res. Lett. 2015, 10, 084010. [Google Scholar] [CrossRef]
- Liu, S.; Hogue, T.S.; Stein, E.D.; Barco, J. Contempory and Historical Hydrologic Analysis of the Ballona Creek Watershed; Southern California Coastal Water Research Project: Costa Mesa, CA, USA, 2011; p. 49. [Google Scholar]
- LADWP. 2010 Urban Water Management Plan; Los Angeles Department of Water and Power: Los Angeles, CA, USA, 2010; p. 539. [Google Scholar]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Artis, D.A.; Carnahan, W.H. Survey of emissivity variability in thermography of urban areas. Remote Sens. Environ. 1982, 12, 313–329. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Stathopoulou, M.; Cartalis, C.; Petrakis, M. Integrating Corine Land Cover data and Landsat TM for surface emissivity definition: application to the urban area of Athens, Greece. Int. J. Remote Sens. 2007, 28, 3291–3304. [Google Scholar] [CrossRef]
- Homer, C.; Dewitz, J.; Fry, J.; Coan, M.; Hossain, N.; Larson, C.; Herold, N.; McKerrow, A.; VanDriel, J.N.; Wickham, J. Completion of the 2001 National Land Cover Database for the conterminous United States. Photogramm. Eng. Remote Sens. 2007, 73, 337–341. [Google Scholar]
- Fry, J.A.; Xian, G.; Jin, S.; Dewitz, J.A.; Homer, C.G.; Yang, L.; Barnes, C.A.; Herold, N.D.; Wickham, J.D. Completion of the 2006 National Land Cover Database for the conterminous United States. Photogramm. Eng. Remote Sens. 2011, 77, 858–864. [Google Scholar]
- Gleick, P.H.; Wolff, G.H.; Cushing, K.K. Waste Not, Want Not: The Potential for Urban Water Conservation in California; Pacific Institute for Studies in Development, Environment, and Security: Oakland, CA, USA, 2003; ISBN 1-893790-09-6. [Google Scholar]
- Maxwell, R.M.; Miller, N.L. Development of a Coupled Land Surface and Groundwater Model. J. Hydrometeorol. 2005, 6, 233–247. [Google Scholar] [CrossRef]
- Jefferson, J.L.; Gilbert, J.M.; Constantine, P.G.; Maxwell, R.M. Active subspaces for sensitivity analysis and dimension reduction of an integrated hydrologic model. Comput. Geosci. 2015, 83, 127–138. [Google Scholar] [CrossRef]
- Jefferson, J.L.; Maxwell, R.M. Evaluation of simple to complex parameterizations of bare ground evaporation. J. Adv. Model. Earth Syst. 2015, 7, 1075–1092. [Google Scholar] [CrossRef]
- Ferguson, I.M.; Jefferson, J.L.; Maxwell, R.M.; Kollet, S.J. Effects of root water uptake formulation on simulated water and energy budgets at local and basin scales. Environ. Earth Sci. 2016, 75, 1–15. [Google Scholar] [CrossRef]
- Ashby, S.F.; Falgout, R.D. A parallel multigrid preconditioned conjugate gradient algorithm for groundwater flow simulations. Nucl. Sci. Eng. 1996, 124, 145–159. [Google Scholar] [CrossRef]
- Jones, J.E.; Woodward, C.S. Newton–Krylov-multigrid solvers for large-scale, highly heterogeneous, variably saturated flow problems. Adv. Water Resour. 2001, 24, 763–774. [Google Scholar] [CrossRef]
- Kollet, S.J.; Maxwell, R.M. Integrated surface-groundwater flow modeling: A free-surface overland flow boundary condition in a parallel groundwater flow model. Adv. Water Resour. 2006, 29, 945–958. [Google Scholar] [CrossRef]
- Maxwell, R.M. A terrain-following grid transform and preconditioner for parallel, large-scale, integrated hydrologic modeling. Adv. Water Resour. 2013, 53, 109–117. [Google Scholar] [CrossRef]
- Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G.; et al. The Common Land Model. Bull. Am. Meteorol. Soc. 2003, 84, 1013–1023. [Google Scholar] [CrossRef]
- Zeng, X.; Shaikh, M.; Dai, Y.; Dickinson, R.E.; Myneni, R. Coupling of the Common Land Model to the NCAR Community Climate Model. J. Clim. 2002, 15, 1832–1854. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Ferguson, I.M.; Maxwell, R.M. Hydrologic and land–energy feedbacks of agricultural water management practices. Environ. Res. Lett. 2011, 6, 014006. [Google Scholar] [CrossRef]
- Condon, L.E.; Maxwell, R.M. Feedbacks between managed irrigation and water availability: Diagnosing temporal and spatial patterns using an integrated hydrologic model. Water Resour. Res. 2014, 50, 2600–2616. [Google Scholar] [CrossRef]
- Condon, L.E.; Maxwell, R.M. Groundwater-fed irrigation impacts spatially distributed temporal scaling behavior of the natural system: A spatio-temporal framework for understanding water management impacts. Environ. Res. Lett. 2014, 9, 034009. [Google Scholar] [CrossRef]
- Reyes, B.; Maxwell, R.M.; Hogue, T.S. Impact of lateral flow and spatial scaling on the simulation of semi-arid urban land surfaces in an integrated hydrologic and land surface model. Hydrol. Process. 2016, 30, 1192–1207. [Google Scholar] [CrossRef]
- Ajami, H.; McCabe, M.F.; Evans, J.P.; Stisen, S. Assessing the impact of model spin-up on surface water-groundwater interactions using an integrated hydrologic model. Water Resour. Res. 2014, 50, 2636–2656. [Google Scholar] [CrossRef]
- Mitchell, K.E.; Lohmann, D.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Cosgrove, B.A.; Sheffield, J.; Duan, Q.; Luo, L.; et al. The multi-institution North American Land Data Assimilation System (NLDAS): Utilizing multiple GCIP products and partners in a continental distributed hydrological modeling system. J. Geophys. Res. Atmos. 2004, 109, D7. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degré, A. Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth Syst. Sci. 2011, 15, 2259–2274. [Google Scholar] [CrossRef]
- Gesch, D.; Oimoen, M.; Greenlee, S.; Nelson, C.; Steuck, M.; Tyler, D. The national elevation dataset. Photogramm. Eng. Remote Sens. 2002, 68, 5–11. [Google Scholar]
- Cayan, D.R.; Maurer, E.P.; Dettinger, M.D.; Tyree, M.; Hayhoe, K. Climate change scenarios for the California region. Clim. Chang. 2008, 87, 21–42. [Google Scholar] [CrossRef]
- Mini, C.; Hogue, T.S.; Pincetl, S. The effectiveness of water conservation measures on summer residential water use in Los Angeles, California. Resour. Conserv. Recycl. 2015, 94, 136–145. [Google Scholar] [CrossRef]
- Ponce, V.M.; Pandey, R.P.; Ercan, S. Characterization of Drought across Climatic Spectrum. J. Hydrol. Eng. 2000, 5, 222–224. [Google Scholar] [CrossRef]
- Arora, V.K. The use of the aridity index to assess climate change effect on annual runoff. J. Hydrol. 2002, 265, 164–177. [Google Scholar] [CrossRef]

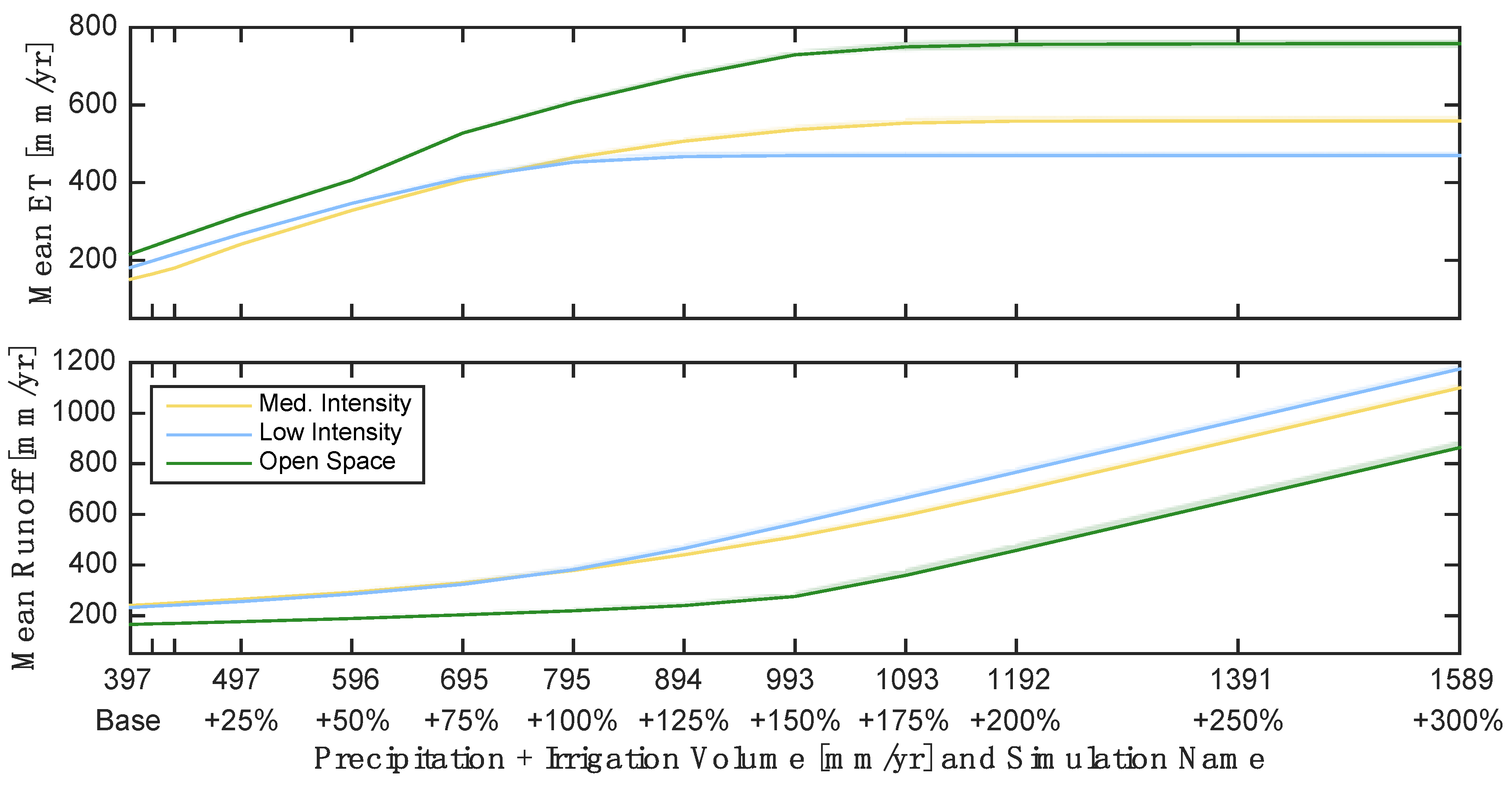
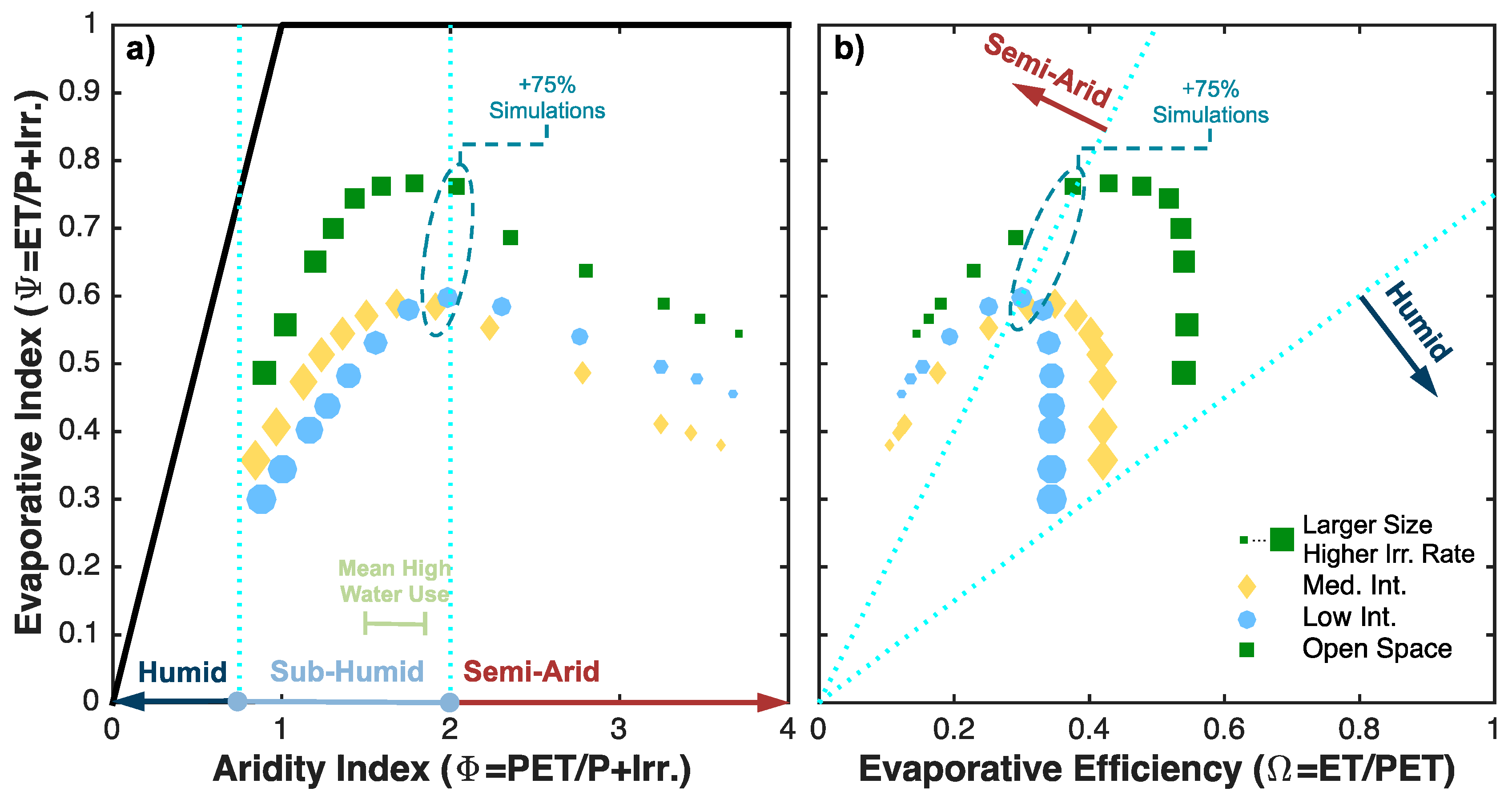
| Scenario | Base | 5% | 10% | 25% | 50% | 75% | 100% | 125% | 150% | 175% | 200% | 250% | 300% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Irrigation Rate (mm yr−1) | 0 | 20 | 40 | 99 | 199 | 298 | 397 | 496 | 596 | 695 | 794 | 993 | 1192 |
| Precipitation + Irrigation (mm yr−1) | 397 | 417 | 437 | 496 | 596 | 695 | 794 | 893 | 993 | 1092 | 1191 | 1390 | 1588 |
| Land Cover | Open Space | Low Intensity | Med. Intensity | High Intensity | ||||
|---|---|---|---|---|---|---|---|---|
| Month | Dry | Wet | Dry | Wet | Dry | Wet | Dry | Wet |
| October | −3.9 | −1.9 | −2.1 | −1.9 | −2.7 | −2.5 | −0.6 | −1.2 |
| November | −0.6 | −0.9 | −0.4 | −0.8 | −0.7 | −1.5 | * | −0.9 |
| December | −1.3 | −1.1 | −1.0 | −1.0 | −1.4 | −1.3 | * | −0.8 |
| January | −2.3 | * | −1.0 | * | −1.1 | * | * | * |
| February | −1.3 | * | −1.3 | * | −1.6 | −1.2 | −0.6 | −0.3 |
| March | −1.4 | * | −1.6 | * | −2.5 | −1.9 | −1.4 | −1.4 |
| April | −2.4 | −0.7 | −2.5 | −0.9 | −3.4 | −1.4 | −1.2 | * |
| May | −2.8 | −0.8 | −3.0 | −1.3 | −3.8 | −2.4 | −1.7 | −0.6 |
| June | −2.6 | −1.7 | −2.8 | −2.4 | −3.5 | −3.7 | −1.2 | −2.0 |
| July | −2.6 | −1.2 | −3.2 | −1.9 | −3.7 | −2.2 | −1.9 | −1.0 |
| August | −2.6 | −1.7 | −3.0 | −2.3 | −3.4 | −2.6 | −1.6 | −1.4 |
| September | −2.5 | −1.3 | −3.0 | −2.1 | −3.2 | −2.4 | −1.3 | −1.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reyes, B.; Hogue, T.; Maxwell, R. Urban Irrigation Suppresses Land Surface Temperature and Changes the Hydrologic Regime in Semi-Arid Regions. Water 2018, 10, 1563. https://doi.org/10.3390/w10111563
Reyes B, Hogue T, Maxwell R. Urban Irrigation Suppresses Land Surface Temperature and Changes the Hydrologic Regime in Semi-Arid Regions. Water. 2018; 10(11):1563. https://doi.org/10.3390/w10111563
Chicago/Turabian StyleReyes, Bryant, Terri Hogue, and Reed Maxwell. 2018. "Urban Irrigation Suppresses Land Surface Temperature and Changes the Hydrologic Regime in Semi-Arid Regions" Water 10, no. 11: 1563. https://doi.org/10.3390/w10111563
APA StyleReyes, B., Hogue, T., & Maxwell, R. (2018). Urban Irrigation Suppresses Land Surface Temperature and Changes the Hydrologic Regime in Semi-Arid Regions. Water, 10(11), 1563. https://doi.org/10.3390/w10111563





