Abstract
Detecting droughts as early as possible is important in avoiding negative impacts on economy, society, and environment. To improve drought monitoring, we studied drought propagation (i.e., the temporal manifestation of a precipitation deficit on soil moisture and streamflow). We used the Standardized Precipitation Evapotranspiration Index (SPEI), Standardized Streamflow Index (SSI), and Standardized Soil Moisture Index (SSMI) in three drought-prone regions: Sonora (Mexico), Maipo (Chile), and Mendoza-Tunuyán (Argentina) to study their temporal interdependence. For this evaluation we use precipitation, temperature, and streamflow data from gauges that are managed by governmental institutions, and satellite-based soil moisture from the ESA CCI SM v03.3 combined data set. Results confirm that effective drought monitoring should be carried out (1) at river-basin scale, (2) including several variables, and (3) considering hydro-meteorological processes from outside its boundaries.
1. Introduction
Droughts are extreme hydrometeorological events that cannot be avoided, whose severe consequences must be kept to a minimum by water managers and policy. Negative impacts that are related to drought events are manifold; particularly, in the agricultural sector, they are related to soil moisture and irrigation deficits, reduced yields and pasture, livestock, and decreased feed and forage. On the other side, on the non-agricultural sector, natural water bodies and ecosystems are affected, impacting important sectors, such as the municipal water supply and tourism [1,2]. Hence, one of the main areas of drought research is aimed at understanding the underlying processes and dynamics that affect socioecological systems to minimize their negative effects on society, economy and the environment. This research field is complex and involves several aspects, such as drought detection and the development of suitable monitoring methods, data analysis from multiple sources, impacts assessment, and drought forecasting.
Studying drought propagation using variables that describe drought processes at a river basin scale is a challenging yet necessary task to provide a basis for drought understanding and its management. Examples are the Californian Drought and the Millennium Drought in Australia, two recent and severe drought events, as they occurred not only due to a precipitation deficit, hence they serve as examples for the importance of monitoring more than one variable and the linkage between them. The latest Californian Drought caused by precipitation deficit and record-breaking temperatures, produced in 2015 statewide losses of around 2.7 billion US$ and 18,600 jobs [3]. Drought impacts on ecosystems, society, and economy are far-reaching and long-lasting, as trees need to be replanted, groundwater systems need to recover, and agricultural areas must be cultivated. Another example is the Millennium Drought in Australia (1997–2009), a precipitation deficit that is linked to El Niño conditions, which changed interactions in the hydrological cycle for years. Mitigation programs that were implemented during the event minimized losses (e.g., open water markets, public water restrictions, new desalination plants) and initiated a paradigm shift in the perception of Australians society towards a pro-active behaviour [3,4]. These are only two examples which highlight the importance of drought monitoring as one component of drought management. We understand drought monitoring as an essential part of drought management, and studying drought propagation as part of drought monitoring, as it incorporates the relation between variables in the study area. Hence, as drought propagation patterns are studied, drought monitoring could be improved as warning signals can be noticed. Further, the monitoring systems of the United States (US) and Australia are guiding examples for drought monitoring worldwide, and still, negative impacts occur and even exceed previous ones. Taking those two examples, for which the causes (combination of high temperatures in California and El Niño–Southern Oscillation (ENSO) influence in Australia) were detected afterwards, are serving as examples for the necessity of broadening drought monitoring and including propagation patterns.
Recently, larger-scale drought monitoring is growing and improving, with initiatives like the Latin-American Drought and Flood Monitor, or the African Drought Monitor being good examples at continental scale. Similarly, nationwide initiatives are setting up timely and online drought status tools. The US Drought Monitor operating since 1999 still serves as guiding example for other regions with weekly updates on drought status across the US, merging in-situ measurements and observations with satellite information (http://droughtmonitor.unl.edu/). Drought monitoring in the countries that were considered in this study (Mexico, Chile and Argentina) are carried out in similar ways, with different responsibilities. The drought monitor of Mexico (Monitor de Sequía en México, https://smn.cna.gob.mx/es/climatologia/monitor-de-sequia/monitor-de-sequia-en-mexico) started in 2002, and it provides bi-weekly maps for the entire country. This monitoring is a collaboration between the Mexican government and the US Drought Monitor, using the same indices and severity categories. In Chile, the Agroclimatic Observatory provides information on drought alerts, forecasts, and vulnerability maps for agricultural drought, which are monthly updated for all communes (http://www.climatedatalibrary.cl/UNEA/maproom/Monitoring/index.html). Also, Argentina works with drought monitoring maps on monthly basis, available online. Monitoring is carried out by the Center for Surveying and Assessment of Agriculture and Natural Resources (http://www.crean.unc.edu.ar/monitoreo-de-sequias/), in cooperation with the Secretary of Environment and Sustainable Development and the Nacional Meteorological Service. Statewide monitoring is a necessary and useful tool for governmental institutions to keep track of drought development, and maps that are published online offer transparent information for farmers and the public. Nevertheless, despite the progress in the development of monitoring systems, more research is needed to better understand river basin processes and how the involved hydro-climatic variables are intertwined, to anticipate the severity of drought events and to implement mitigation measures. When considering the complexity of each location, this is an ambitious task that involves interdisciplinary research, as each drought event as such is unique.
The starting point of a drought event is commonly defined by a prolonged precipitation deficit, impacting soil moisture and affecting vegetation, and further influencing streamflow volumes and groundwater recharge. However, the dynamics of such interconnections and the lag experienced in its expression in each different subsystem is not unique. Drought propagation refers to the pattern of spatial and/or temporal development of a prolonged precipitation deficit through the hydrological cycle [5]. Propagation patterns are explained by catchment properties and the capacity to store water in lakes, snow packs, or in the soil [6]. For example, a very large river basin might have a longer propagation process (i.e., months and years) from precipitation to streamflow than in smaller basins, where propagation takes place in the order of days or weeks. A seminal study on drought propagation was carried out by Changnon [7], starting from the lack of precipitation and through runoff, soil moisture, streamflow, and groundwater levels in Illinois, USA. From this work, the conceptual description of drought behaviour and propagation (see Figure 1) became the starting point to other studies. Followed by contributions, such as those by van Lanen [8], who analysed two river basins in Europe based on different hydrological models, those information obtained by propagation patterns can improve monitoring, as more details are known, and variables can be related accordingly. Or by Peters et al. [5], who focused on processes of groundwater drought by simulated groundwater patterns in the Pang catchment (UK). Also, Tallaksen et al. [9], who modelled the space-time characteristics of drought in the same catchment, and concluded that the linkages of different variables are necessary and that they should be read in the purpose of the study, as obtained data can be valuable for models. Another important study on hydrological drought processes was that by van Loon [10], who analysed four different types of European river basins using hydrological models to overcome data gaps. This study highlights in detail the diversity of underlying processes related to temperature and storage. More recently, barker et al. [11] studied the detection of drought processes in the UK using Standardized Precipitation Index (SPI) and Standardized Streamflow Index (SSI), in which two different accumulation periods and extended frame as three variables are considered. Still, studies on drought propagation processes based on station data are rare, and specific studies with a regional focus on Latin America are missing, providing the motivation for this paper, especially for snow-melt driven river basins.
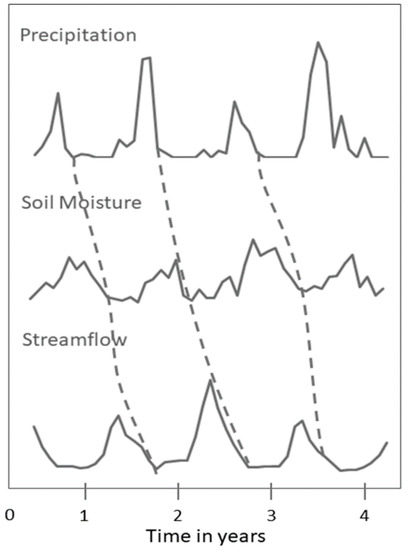
Figure 1.
Sketch to illustrate a drought propagation, as proposed by Changnon, 1987 [7].
Motivated by the conceptual description of Changnon [7], the objective of this work is to study drought processes and to characterize drought propagation in four river basins in Latin America, a region with a variety of climates and reliefs that exhibits an important dryland area. In this paper, we analyse the temporal relationship of a precipitation deficit, and its effects on soil moisture and streamflow in semi-arid basins. Hence, we use the term propagation here to describe the impacts of precipitation deficits on soil moisture and streamflow in time. We therefore want to test the suitability of standardized indices for the identification of propagation patterns in semi-arid river basins, to identify repetitive characteristics for each basin, to detect influences of the El Niño–Southern Oscillation (ENSO) on drought events, and finally to present results in a graphical approach as a river-basin summary. The river basins that were used for analysis are the Sonora in Mexico, the Maipo in Chile, and the Mendoza-Tunuyán in Argentina. All of them are strongly influenced by human activities, and are prone to droughts when considering recent urban and economic developments. For this purpose, we use three standardized drought indices, the Standardized Precipitation Evapotranspiration Index (SPEI), Standardized Soil Moisture Index (SSMI), and Standardized Streamflow Index (SSI), which allow for characterizing meteorological, agricultural, and hydrological drought events, respectively, and evaluate the potential connections among them. Input data are taken from hydro-meteorological stations provided by governmental institutions, and soil moisture is obtained from satellite data provided by the ESA SM v.3.03 (http://www.esa-soilmoisture-cci.org) [12,13,14]. Using satellite data to detect agricultural drought events is a very active research field and as more data from different satellite missions are available, valuable insights are provided on the linkage of soil moisture and meteorological variables [15,16,17,18]. Moreover, we evaluated the link between the resulting standardized indices and ENSO, an irregular recurring shift in sea surface temperature and winds in the Pacific strongly linked with climate and hydrological regimes, mainly in the tropics and subtropics. This evaluation helps to identify and assess ENSO as a possible driving force of drought. We applied the same framework to each river basin, to identify drought propagation patterns among the river basins, while keeping river basin specific features. Moreover, having different study cases allows for testing our approach to assess its replicability elsewhere.
2. Data and Methods
2.1. River Basins
The area under study encompasses three different semi-arid regions in Mexico, Chile, and Argentina. Selected river basins share important features, such as challenges that are associated with growing populations, and the relevance of agricultural sector both as major consumer of water resources, and as relevant contributor to the regional or national gross domestic product. Maps of the basins obtained from 30 m digital elevation models (DEM) are shown in Figure 2. In the following subsections we briefly describe each river basin, highlighting their main specific characteristics.
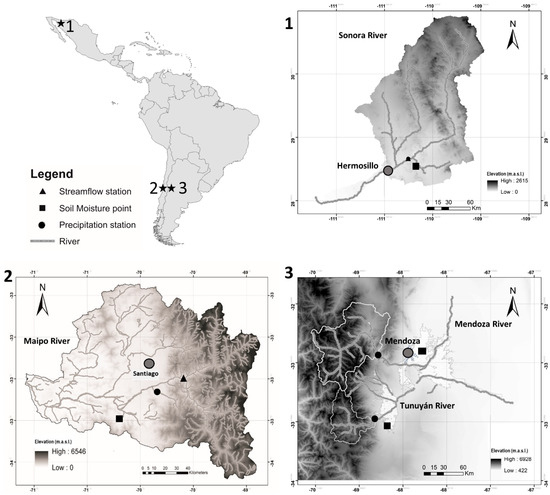
Figure 2.
Maps of selected river basins: (1): Sonora, (2): Maipo, and (3): Mendoza-Tunuyán.
2.1.1. Sonora, Mexico
The Sonoran river basin has an area of about 21,000 km² and it is one of the most important rivers in the Sonora State in arid northwest Mexico, with a population of 860,000 people [19]. The annual average temperature is approximately 20 °C, with summer temperatures reaching 45 °C and dropping to below 0 °C values in winter. Total annual precipitation is approximately 380 mm, concentrated mainly between June and August, and the total annual streamflow volume is around 274 million m³ [20,21]. Elevations range from 2400 m a.s.l. in the northeast of the basin and the sea level, with the lowest portion (i.e., <400 m a.s.l.) being located on the coast at the Gulf of Californian.
The San Miguel and Zanjón rivers are the main tributaries, which converge with the Sonora River at the Abelardo Rodríguez dam near Hermosillo, the main city of the region. The dam allows flow regulation and provides surface water for the city and the coast of Hermosillo, where the main agricultural activities take place. Surface water corresponds to 60% of the total allocated water volume (the remaining 40% is extracted from groundwater), and it is the main source for the lower part of the river basin [22]. Main agricultural and socio-economic activities are concentrated in the lower and flat part of the river basin [23]. Agriculture is the main water user in the basin, as it consumes approximately 90% of total surface water. Since the mid 1990-ies, the agricultural area has increased from 13,000 to 18,000 ha and crops have changed substantially, as cereals were replaced by grapes, nuts, citrus fruits, and fresh vegetables [24]. Nevertheless, groundwater over-exploitation has led to salinity intrusion with loss of agricultural areas in the coast [21]. Water related conflicts and challenges are recognized by the regional government, but established solutions or programs are often short-term or politically conflicting [22].
2.1.2. Maipo, Chile
The Maipo river basin lies in central Chile and it has an area of approximately 15,000 km². The basin contains Santiago, the capital of Chile covers an urban area of ~640 km² and it has a population of around seven million people (i.e., 40% of the Chilean population) [25]. The basin has a Mediterranean climate with a mean annual temperature of 14 °C and total precipitation of 350 mm in the valley. Precipitation falls mainly during winter months (June–September), with snow accumulation above 1500 m a.s.l., while streamflow reaches peak values during spring/summer months (September–March) [26]. This strong seasonality makes the basin vulnerable to extreme events, such as droughts. The recent megadrought in the river basin started in 2009 and some impacts currently taken place can still be related to this drought event [27]. Furthermore, future projections show an increasing vulnerability to drought events due to climate change, as well as larger drinking water demands due to urban growing, which intensifies the competition with agriculture on limited water resources. Regional agriculture depends on irrigation and it is thus the main water user with a share of 80% of freshwater resources. Main crops are fruits, vegetables, grapes for wine, and cereals. Natural vegetation in the lower part of the river basin is characterized by grass and shrublands with some native forests [28].
2.1.3. Mendoza-Tunuyán, Argentina
The Mendoza-Tunuyán areas are two independent but neighbouring river basins, and as such, they considered under the General Irrigation Department (DGI); nevertheless, they share common characteristics. Both originate in the Andes Mountains in Midwest Argentina. The two river basins are also similar in size, the Mendoza has an area of ~19,500 km² [29], and the Tunuyán covers an area of ~19,000 km² [30]. Both rivers originate at elevations above 6000 m a.s.l. and have outlets located at elevations of ~600 m a.s.l. The climate is semi-arid, with annual precipitation of around 500 mm in the higher mountains [31,32] and 200 mm in the lower part of the basins, where the temperatures range between 35 °C in summer and around 0 °C in winter [32]. Streamflow is driven by snow accumulation and melting; thus, water availability depends both on precipitation and temperatures in the mountain range. In particular, snowmelt from November to February accounts for 60% of annual discharge [31]. Given the semi-arid and arid conditions in the lower part of the river basin, agriculture depends on irrigation. Both rivers provide water to the wine industry and the metropolitan region of Mendoza with around one million inhabitants. This city is the urban and industrial centre of the region, and the fourth most important one at national scale [33]. Water consumption reflects the importance of the wine production with 91.5% of the withdrawals for irrigation, 7.3% for drinking water, and 1–3% for industrial purposes [31]. Water supply depends mainly on surface water, but also on groundwater, which provides 27% of irrigation needs, and cover entirely water demands for the urban sector [33]. The whole region socially and economically depends on the wine industry, and thus, the region is highly vulnerable to climate variabilities. Other factors influencing water availability include illegal groundwater pumping and weak water regulations, especially their controls [31,33], and increasing salt intrusion and the pollution of groundwater [32].
2.2. Data
We used data provided freely by governmental institutions utilized for official water management purposes. Data availability (for daily or monthly time series) and access is improving, but (complete) long-term measures are still sporadic. Precipitation, temperature (Tmax, Tmin), and streamflow records correspond to gauged data in situ, while soil moisture data was obtained from satellites. We used the ESA SM v.3.03 version, which provides daily soil moisture data from 1978–2016. This data set offers active, passive, or combined soil moisture retrievals. As the combined package provides more data points, it was used in this study. Because of specific database characteristics, and to ensure the most complete dataset, we used different starting years for the study sites (i.e., 1992 for Sonora, 1995 for Maipo, Tunuyán, and Mendoza). Table 1 summarized the input data and sources that are used in the calculation of drought indices.

Table 1.
Monthly input variables and their sources used in this study (filling methods are identified by * for linear regression and ** for linear interpolation).
To fit distributions to monthly data, it is recommended to use data sets of minimum 30 years [34]. But, as datasets not always meet this recommendation, nowadays a minimum period of 20 years is suggested [35,36] and is applied to this study. The meteorological stations and the point for soil moisture data were chosen following criteria of maximum proximity between them, whereas streamflow gauges were chosen in the upper part of the river basins, to avoid the influence of human activities. We processed the gathered data to use monthly time series for the calculation of the indices, and gap filling procedures were applied when necessary. Percentages of missing values and applied filling method are listed in Table 1. When possible, a linear regression with the closest neighbour (R² > 0.7) was used to fill data gaps [37], marked by an asterisk in Table 1. If needed, we also used linear interpolation (marked by ** in Table 1). With the given data, we want to introduce and test an easy replicable method, which is still conform with research standards to detect drought propagation patterns, therefore applied data is as less as possible modified, as no models are used.
2.3. Standardized Indices
Since the introduction of the Standardized Precipitation Index by McKee et al. [38] to detect drought events, standardized indices have become very popular in drought management. One main feature of standardized indices is their comparability among time, space, and variables. Studies on standardized indices as drought detection tools are manifold and they provide a solid basis for their application for drought analyses [6,39,40,41]. The calculation procedure is the same, independently of the input variable used, i.e., precipitation, soil moisture, streamflow. The main steps of the calculation are (e.g., McKee et al. [38], Guttman [42], Sivakumar et al. [43]):
- obtaining the time series of the desired variable at a given time step (e.g., monthly),
- fitting a probability distribution function to monthly data aggregated using different cumulative periods (e.g., 1-, 3-, 6-, 12-month),
- converting to a cumulative distribution function, and
- use an inverse function to obtain standardized gaussian values (i.e., values that follow a normal distribution with mean 0 and standard deviation 1).
The first selected index for our study is the Standardized Precipitation Evapotranspiration Index (SPEI), developed by Vicente-Serrano et al. [44]. This index is based on a simple water balance given by the difference (D) of precipitation (P) and reference evapotranspiration (ET0).
D = P − ET0
For this study, we obtained ET0 using the modified Hargreaves equation by Droogers and Allan [45], as this method is more precise and preferred to more simple approaches.
where RA (MJm-2d-1) corresponds to extra-terrestrial radiation (i.e., radiation reaching the top of the atmosphere), Tavg (°C) is the average temperature obtained from Tmax (°C) and Tmin (°C), and TD (°C) is the temperature range (difference between Tmax and Tmin).
ET0 = 0.0013 × 0.408RA × (Tavg + 17) × (TD − 0.0123P)0.76
Cumulative monthly values of D are then fitted to a probability distribution function. According to recent recommendations in literature [46,47,48,49], we used the Generalized Extreme Values (GEV) function, as it fits well to our data. Differences in results of the indices (by GEV and Log-logistic) were negligible. In fact, R²-values of 0.99 are obtained when relating index values to each other; moreover, there were no influence on the detection of drought events.
Standardized index values based on soil moisture data are relatively new, as longer data sets are still sporadic. Nevertheless, approaches to used standardized values of soil moisture for drought detection can be found in Carrão et al. [50] or Hao and AghaKouchak [51]. For the calculation of the Standardized Soil Moisture Index (SSMI), no recommendations on distribution fitting, similar to the SPEI are currently available. Nevertheless, the Log-logistic distribution fitted all soil moisture data sets very well and it was applied in this study.
Finally, the Standardized Streamflow Index (SSI) was used for hydrological drought detection. Previous uses of this index include two streamflow indices based on the SPI-calculation procedure developed by Shukla and Wood [52] and Nalbantis [53]. For the calculation of SSI, we used the GEV distribution, recommended for this purpose [54]. Figure 3 provides exemplary probability plots for distribution fitting process for SPEI (Mendoza), SSMI (Sonora), and SSI (Maipo). Despite the huge variety of distribution functions, it is challenging to choose the most appropriate one for each month, accumulation period, and variable. Parameters in this study were obtained by probably weighted moments. We compared results of index values that were obtained by best-fit distributions against recommended ones, and found as higher the accumulation period, the lesser the difference between index results. Therefore, we calculated the indices presented in this study with recommended distributions by literature. All of the indices were calculated using the SCI-package in R [55].
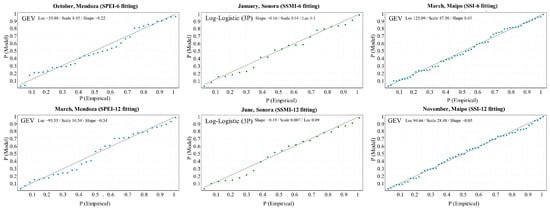
Figure 3.
Examples of P-Plots for distribution fitting.
2.4. Drought Propagation
To evaluate relations between the standardized indices reflecting the hydrologic variables, we used the Pearson correlation coefficient (denoted by r) between SPEI and SSMI, SPEI and SSI, and SSMI and SSI. The Pearson correlation coefficient is used to investigate relationships between variables and also for studies on drought propagation [10]. In this paper, we use the correlations as an indicator between the variables of interest (precipitation, soil moisture, and streamflow), and to deviate propagation patterns. These correlations considered lag-times of 0 (i.e., concurrent), 1, 2, …, and up to 12 months, to identify delays in the response variable. The statistical significance of the results was assessed using a t-test with a 5% level of significance [56]. We analysed cumulative periods of 6- and 12-months for all indices, as they are more suitable to detect the long-term behaviour of the river basins and the persistence of drought conditions.
2.5. ENSO Influence
To identify and assess the potential influence of El Niño Southern Oscillation (ENSO) phenomenon on the indexes, we computed the Pearson correlations coefficient between sea surface temperature anomaly values in region Niño 3.4 (ENSO 3.4), obtained from the National Oceanic and Atmospheric Administration (NOAA), and the corresponding SPEI, SSMI, and SSI values. Influences of ENSO on precipitation patterns in several parts in the world are well documented [57]. The influence itself does not describe the propagation process itself, but it can provide useful information on the development of a drought event (e.g., severity during La Nina phase), and further support drought management decisions. As in the results section, we provide correlation coefficients for each river basin, we would like to mention for completeness ENSO years from 1995 to 2015: El Niño 1995, 1998, 2003, 2007, 2010/2011, and 2015/2016 and La Niña 1999, 2000, 2008, 2011, and 2012 (Source: https://www.esrl.noaa.gov/psd/enso/past_events.html). Correlations were calculated for March and September (i.e., relevant months representative of the entire year). Statistical significance of the results was assessed using t-test with a 5% significance level.
3. Results
Graphical summaries were prepared to illustrate drought propagation for each river basin using the standardized indices (Figure 4, Figure 5 and Figure 6). These summary figures show results for 6- and 12-months accumulation periods (left and right respectively). A plot showing annual precipitation and streamflow patterns from observations is located in the middle upper part. Calculated SPEI, SSMI, and SSI-indices are shown for the same period (i.e., 1995–2015) to allow visual comparisons of all the metrics. Coloured bars across the indices are to exemplify drought events and their response in the other two indices, besides they highlight the uniqueness of each drought event. In the figures, we also provide a table with the correlation coefficients between the ENSO anomaly index and each drought index for March and September, and marked years of ENSO with ‘*’ for El Niño events and ‘o’ for La Niña years in the time line of the indices. Furthermore, below the plots, heatmaps of the SPEI, SSMI, and SSI are shown for the same period 1995–2015, for easier comparison of magnitudes (by colours) and durations (one line per calendar year) among the indices. Finally, the bottom part of the graphical summary shows Pearson correlation coefficients among the indices for 0-lag, 1-lag, 3-lag, and 6-lag in a matrix format: statistical significance is expressed through bold values and the asterisk symbol is used to denote maximum correlation coefficients. Additionally, Table 2 summarizes the highest correlation coefficients for all analysed indices in all river basins, and provide a first glance about propagation patterns, especially at the lag with highest observed correlation. Note that negative correlation coefficients between SPEI and SSI in the Mendoza and Tunuyán river basins are small, meaning that, in this area, the hydrological regime cannot be explained by local precipitation only. This is due to the influence of the precipitation falling on the western side of the Andes, hence precipitation patterns of the Maipo river basin have a higher influence on the streamflow of the Mendoza and Tunuyán river basin as precipitation falling within them. Further details are provided in the results section of each river basin, especially for the “Interconnected river basin” presented in the discussion section.
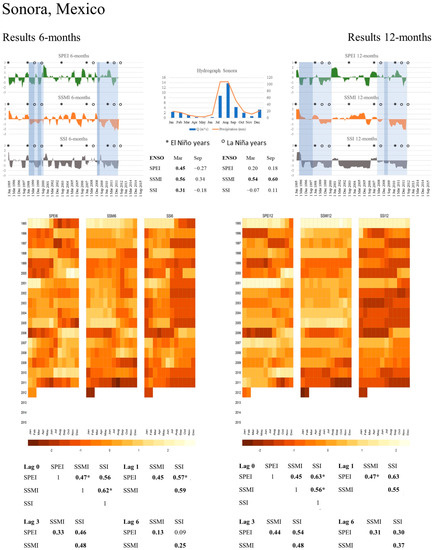
Figure 4.
Graphical summary of results for the Sonora river basin.
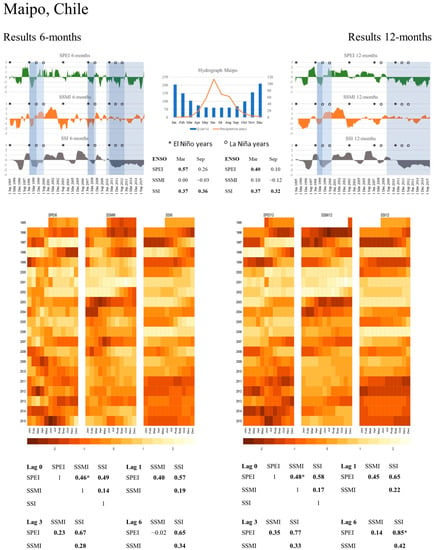
Figure 5.
Graphical summary of results for the Maipo river basin.
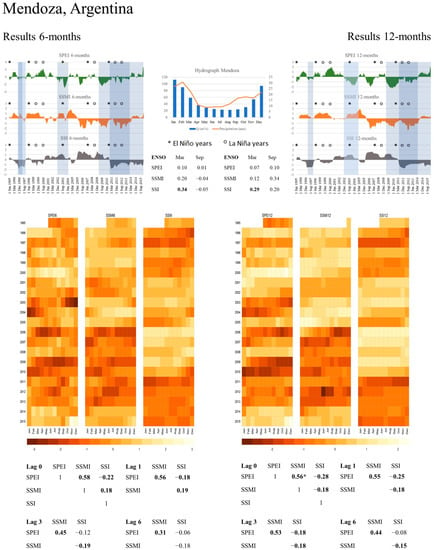
Figure 6.
Graphical summary of results for the Mendoza river basin.

Table 2.
Highest Pearson correlations between indices with lagged months (all statistical significant p ≤ 0.05).
3.1. Sonora, Mexico
The hydrograph describes the pluvial regime of the Sonoran river basin. Main precipitation events occur in July and August, and lower precipitation events during winter months in the northern hemisphere. A strong ENSO influence on the six-months accumulation period is detected for March for all three drought indices, with highest r = 0.56 between SSMI and ENSO. Thus, an ENSO influence can be detected, although the obtained correlation coefficients suggest that other influencing factors take place as well. For instance, for the 12-months accumulation period only correlations between ENSO and SSMI are statistically significant, and no influences on SPEI or SSI are visible. Using a threshold of −1 for the SPEI values, we detect six drought events for SPEI-6, and five for the SPEI-12. Applying the same threshold for SSMI values, four drought events are found at 6-months, and two at 12-months. Detected events by SPEI do not overlap completely with SSMI detected events. By looking at the correlation coefficients between both indices, we can identify a rapid response of soil moisture to precipitation. Although significant, this relation is moderate, with the highest r = 0.47 for lag 0. The same applies for SPEI with SSI values, even though the highest r is obtained with lag-1, showing a rapid response of streamflow to precipitation, as seen on the hydrograph. SPEI and SSI resulting values highlight that hydrological drought events persist longer, indicating that longer recovery times take place. Soil moisture responds to streamflow immediately (r = 0.62 at lag-0), demonstrating that SSMI-values are linked to SSI-values as well. For example, for the drought event starting in 2009, SSMI values are constantly below average, even if SPEI values are above average at the end of 2009 for nearly one and a half year. During the same period, SSI values were below average, overlapping with SSMI values in duration and magnitude. Thus, we can argue that soil moisture is an important variable to understand drought processes within the river basin as it is correlated with ENSO and the other indices. Hence, the beginning of drought events that are detected by SPEI are similar, but the duration and streamflow and soil moisture patterns, are captured differently. This can be due to other variables, such as human influences (e.g., irrigation and water extraction). The heatmaps reflect the rapid response of soil moisture and streamflow respond to precipitation, as well as longer recovery periods.
3.2. Maipo, Chile
The Maipo river basin has a nival regime, hence streamflow peaks occur during summer months, as temperatures are high and snow-melt processes take place. The hydrograph in the graphical summary precisely shows the opposite behaviour between precipitation and streamflow. Highest correlation coefficients are found between the ENSO and SPEI for both accumulation periods in March (r = 0.57 for SPEI-6 and r = 0.4 for SPEI-12). These results are in agreement with previous studies showing the high influence of ENSO on the basin [57]. On the other hand, r-values between ENSO and SSI differ only marginally between March and September for both accumulation periods. As these values are all significant but lower than the correlation coefficients between ENSO and SPEI, we conclude that ENSO influence on streamflow patterns, but not to the same extent than precipitation. Finally, no significant correlation between SSMI and ENSO was found. A visual comparison among the indices shows a rapid response in soil moisture to changes in precipitations, and a much slower response of the streamflow, with delays of up to six months. The highest correlations among the indices is detected between SPEI and SSMI at lag-0 (r = 0.46 for 6-months and r = 0.48 for 12-months). Furthermore, the correlation between SPEI 6-months and SSI 6-months is maximum for a lag-4 (r = 0.69), while for the 12-months indices, this maximum occurs for lag-6 the (r = 0.85). Finally, the highest correlation coefficients between SSMI and SSI are noted with lag-7 for 6-months (r = 0.35) and lag-8 for 12-months (r = 0.43). This slower response of streamflow is expected due to the nival regime of the river basin. Applying a threshold of −1 to SPEI-6, seven values were below that threshold, although not indicating seven independent drought events. In fact, for the time period associated with the recent Mega-Drought that started in 2009, the SPEI-6 values were predominantly negative, with minimum values below −2. Thus, values above the threshold do not necessarily notify the end of a drought event, if other indices keep negative as well. Drought events that were detected by SPEI-12 are the same as for SPEI-6, illustrating connected dry spells more clearly, as shown in the time series graphs in Figure 5, marked by grey bars. Further, a comparison of the indices dynamics shows that hydrologic drought events are not only typically delayed with respect to the start of a meteorological drought event, but also, they last longer before returning to average values. In the case of the recent drought, SSI-values were positive again in May 2016 for the 6-months accumulation period (and in January 2017 for 12-months), whereas SPEI values were positive from November 2015 for the 6-months accumulation period (and from April 2016 for 12-months). The heatmaps for both accumulation periods show only a few months with index values above 0 during the last decade for the SPEI and SSI.
3.3. Mendoza, Argentina
The Mendoza river basin has a nival regime, with high peak flows from snowmelt taking place during summer months of the southern hemisphere. In fact, the ~200 mm of rain falling during spring and summer have a minor impact on streamflow volumes. ENSO influences are only statistically significant for SSI values in March, although the corresponding correlation coefficients are weak (i.e., r = 0.34 for SSI-6, and r = 0.29 for SSI-12). From the dynamics of the SPEI, SSMI, and SSI, a drought propagation type completely different to that of the other river basins is observed and it is hard to clearly identify the propagation features. To some extent, the SPEI seems to behave in the opposite direction than the SSMI and SSI. Thus, the highest r-values are those between SPEI and SSMI with lag-0 for 6-months (r = 0.58) and 12-months (r = 0.56). On the other hand, SPEI and SSI correlate negatively for lags up to ten months. The same occurs for the correlation coefficients between SSMI and SSI; in this case the coefficients tend to 0 with larger lags. Thus, only persisting meteorological droughts events are also detected by SSI. SSMI and SSI results for 6- and 12-month cumulative periods only overlap from 2011 until 2014. SPEI values are negative during this period, indicating a longer drought. Our results support the idea that local drought propagation characteristics can be related to regional factors beyond the river basin. Streamflow depends on snow accumulation in the Andes, and precipitation in the mountain range is driven by circulations of the Pacific Ocean. Considering streamflow volumes in comparison to precipitation amounts in the Mendoza river basin, we argue that streamflow is the determining variable for drought processes. Hence, streamflow is the most relevant variable for drought management purposes.
3.4. Tunuyán, Argentina
The Tunuyán river basin is a snowmelt dominated basin next to the Mendoza basin, whose main river provides resources to irrigate the same agricultural areas. Therefore, we carried out the same analysis as for the previous river basins (Figure 7). The Tunuyán river basin streamflow amounts are lower, and precipitation amounts are higher as compared to the Mendoza River, but the shapes of the hyetograph and hydrograph are similar. ENSO influences are detected for SPEI values at both accumulation periods, although for March and September the influences are still weak. For SSI values the ENSO influence is statistical significant only during March, with values of r = 0.32 at 6-months and r = 0.28 at 12-months. For SSMI values, no influence of ENSO is detected. Form the comparison of the index results we easily detect the relationship between SPEI and SSMI values. Nevertheless, detected drought events by SPEI and SSMI do not overlap, with the exemption of the drought event starting in 2009 (indicated by SPEI and SSMI), for which an overlap is explicit from 2011 on, similar to the Mendoza river basin. Highest Pearson correlation coefficients between SPEI and SSMI are found at lag-0 for 6-months (r = 0.77) and 12-months (r = 0.82). Like the Mendoza river basin, streamflow patterns are better explained by precipitation from the Maipo river basin, as for both we obtained negative correlations between SPEI and SSI values (Table 2), which is contrary to the expected connection of both indices. As for the Mendoza river basin negative correlations are also found between SSMI and SSI values, this is not the case for the Tunuyán river basin, where correlation values are moderate. This direct comparison with a neighbouring basin shows that even in spatially close river basins differences in drought propagation are detected, highlighting the uniqueness of each river basin as such.
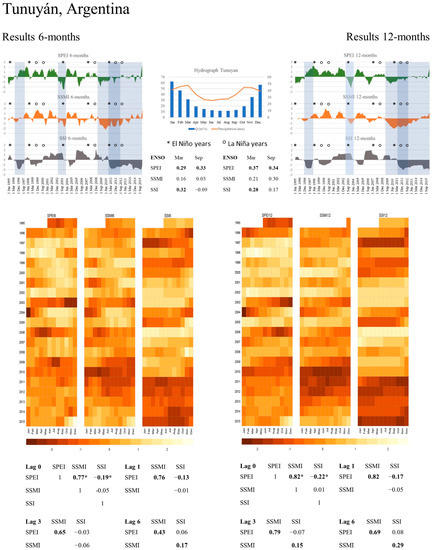
Figure 7.
Graphical summary of results for the Tunuyán river basin.
4. Discussion
4.1. “Interconnected” Andes
We decided to discuss our findings with a further application of the provided results and to better describe the influence of mountain precipitation in the Mendoza river basin, we enlarge our study and simulate a hybrid river basin, referred to as “Interconnected”, based on merged data of the Maipo (precipitation) and Mendoza (temperature, streamflow, and soil moisture). The graphical summary for the “Interconnected” river basin is slightly different (Figure 8), as it presents correlation coefficients of SPEI with SSI and SPEI with SSMI in chart format for lags up to ten months, together with the corresponding results from the Maipo and Mendoza cases. As expected, the hydrograph mirrors the same shape as in the case of the Maipo river basin, with the difference that streamflow values are nearly halved. Graphical comparisons of SPEI for 6- and 12-months between the Maipo, and the “Interconnected” demonstrate similar patterns due to same precipitation input for calculation; hence, differences between results reflect the influence of temperature on SPEI values. Results for the SSMI-, and SSI-Interconnected are the same as for the Mendoza river basin. Moreover, visual propagation is noticeable, as the SSI drought event starting in 1996 is not detected by the SPEI-Mendoza (6- and 12-months), but by the SPEI-Interconnected, supporting the common understanding of drought development from meteorological to hydrological drought. Correlation coefficients between SPEI and SMMI, and SPEI and SSI are low; SPEI/SSMI values for the Interconnected are weaker than the SPEI/SSMI for Mendoza. Nevertheless, SPEI with SSI values are positively related with lag-7, accounting for snow-melt processes in the mountain range. This additional analysis allows for a better description of the interconnectivity between the two river basins that are separated by the Andes but are connected by snow, to represent the physical connectivity of precipitation, snow, and streamflow [58,59,60]. Precipitation, which accounts for snow accumulation depends on moisture from frontal systems of the Pacific. Hence, we emphasize on the inclusion of hydrological processes taking place beyond a river basin to understand occurring processes within it.
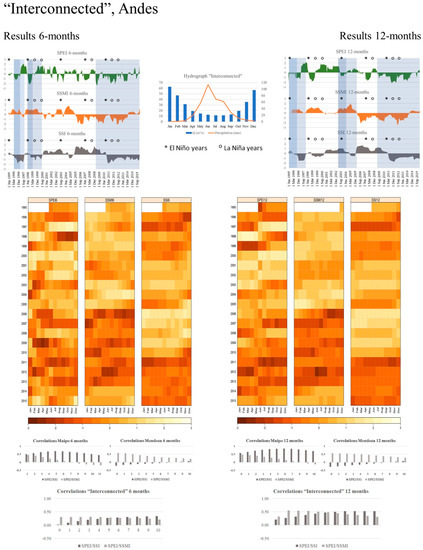
Figure 8.
Graphical summary of results for the “Interconnected” river basin.
4.2. Drought Propagation via Standardized Indices
Reflecting this study, we confirm the suitability of standardized indices as tools to detect drought processes. Moreover, due to the standardization procedure, they allow for comparisons among variables and across time and different river basins. The applied method is easy replicable and may serve further investigations in other river basins. Although we are aware that propagation is not alone described by Pearson correlations, other influences (e.g., soil types, vegetation cover, permeability of soils) should be considered—if possible—to obtain a holistic picture of drought processes in a river basin. Given the data use in this study and the comparative approach, we used the Pearson correlation coefficient to assess relationships among the variables (precipitation, soil moisture, and streamflow). We kept the same calculation of the coefficients to provide homogeneous and comparable results, using them as an indicator of existing relations between the variables. As we were interested in the relation among the variables, we used the entire time series of the standardized indices, and not only those time windows that were identified as drought events by one or another index. Still, drought events identified by SPEI values with a chosen threshold of −1 are compared in the graphs and heatmaps in the results section. Besides, the analysis among obtained index values helps to identify the driving variable that is relevant for drought management purposes. For the Sonora river basin, soil moisture (as closely related to precipitation), is important to be considered for drought detection, whereas streamflow detects drought processes in the Mendoza and Tunuyán river basins. Note though that the application of standardized indices may be limited due to data availability, as at least 20 years of data are required to identify the most suitable probability distribution [61]. In general, data availability is a limiting factor for the analysis of drought processes, as historical data is often rare, particularly in Latin America. For this reason, drought processes related to groundwater are not analysed in this study. Groundwater is an important variable, especially as it is used to supply urban and agricultural water demands in all the river basins. Thus, our study provides the detection of ‘surface’ drought events, serving as initial point for further analysis. The same holds true for snow, as measuring stations in the upper mountains are missing. Further, the chosen streamflow gauges for this study were installed before human interventions took place, which could modify streamflow measurements. On the other hand, precipitation measures are not human influenced, and soil moisture points are chosen in non-irrigated areas. We are aware that drought analysis needs to include human influences, as the river basins in this study face similar challenges while population is growing, agricultural activities are intensified, and more extreme weather events are expected. Still, to investigate the link between drought processes that were detected by hydro-meteorological data with social (including economic and agricultural aspects) developments is challenging [62], as the concept of ‘anthropogenic droughts’ or ‘human-influenced drought’ is just in its beginning [63,64]. We therefore urge to include in further research land use changes, as urban growth influence hydrological processes, and hence drought processes.
5. Conclusions
The aim of this study is to detect drought propagation features using standardized drought indices, and to evaluate drought processes of semi-arid basins in Latin America. We analysed four river basins with competing water users in drought prone regions. Our results show that the Sonoran (Mexico) basin responds rapidly to meteorological processes and droughts, connecting precipitation, soil moisture, and streamflow simultaneously. In contrast, the Maipo basin (Chile), with its nival regime, is a slow response river basin where streamflow responds with a delay of four months or more (for 6-months accumulation period) to precipitation. However, soil moisture responds with no lag to precipitation in all study basins, confirming the close relation between the two variables. A third type of drought propagation was identified for the Mendoza river basin. In this case, the SPEI and SSMI are related as expected, but the SSI-values seem uncoupled, as negative correlations with SPEI and SSI are observed.
In summary, our study confirms the suitability of standardized indices to identify drought processes between variables. Results of indices permit the identification of drought propagation types, i.e., if a rapid or a slow response between precipitation and streamflow is observed. As we carried out the same methodology for four different river basins across Latin America, this study provides a starting point for further drought propagation analysis as applied methods are intentionally easiy replicable.
Author Contributions
Conceptualization, M.O., F.J.M. and J.G.; Data curation, M.O. and F.R.; Formal analysis, M.O., F.J.M. and J.G.; Funding acquisition, F.J.M., C.A.S. and N.P.-P.; Investigation, M.O.; Supervision, F.J.M.; Validation, J.G. and F.R.; Writing–original draft, M.O.; Writing–review & editing, F.J.M., J.G., C.A.S. and N.P.-P.
Funding
The research is funded by Becas Conicyt, Programa de Formación de Capital Humano Avanzado, Ministerio de Educación de Chile. Further this work was carried out with the aid of a grant from the Inter-American Institute for Global Change Research (IAI) CRN3056 which is supported by the US National Science Foundation (Grant GEO-1128040). Authors would like to acknowledge the support from the Lloyd’s Register Foundation (a charitable foundation helping to protect life and property by supporting engineering-related education, public engagement and the application of research).
Acknowledgments
The authors would like to thank the anonymous reviewers for their comments and suggestions to improve this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ding, Y.; Hayes, M.J.; Widhalm, M. Measuring economic impacts of drought: A review and discussion. Disaster Prev. Manag. 2011, 20, 434–446. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding the drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- AghaKouchak, A. Recognize anthropogenic drought. Nature 2015, 524, 409–411. [Google Scholar] [CrossRef] [PubMed]
- Van Dijk, A.I.J.M.; Beck, H.E.; Crosbie, R.S.; de Jeu, R.A.M.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The Millennium Drought in southeast Australia (2001–2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
- Peters, E.; Bier, G.; van Lanen, H.A.J.; Torfs, P.J.J.F. Propagation and spatial distribution of drought in a groundwater catchment. J. Hydrol. 2006, 321, 257–275. [Google Scholar] [CrossRef]
- Wood, E.F.; Sheffield, J. Drought: Past Problems and Future Scenarios; Taylor and Francis: Hoboken, NJ, USA, 2012. [Google Scholar]
- Changnon, S.A. Detecting Drought Conditions in Illinois; Department of Energy and Natural Resources: Springfield, IL, USA, 1987. [Google Scholar]
- Van Lanen, H.A.J. Drought propagation through the hydrological cycle. In Climate Variability and Change, Proceedings of the Fifth Friend World Conference, Havana, Cuba, 27 November–1 December 2006; IAHS Press: Wallingford, UK, 2006. [Google Scholar]
- Tallaksen, L.M.; Hisdal, H.; van Lanen, H.A.J. Space–time modelling of catchment scale drought characteristics. J. Hydrol. 2009, 375, 363–372. [Google Scholar] [CrossRef]
- Van Loon, A.F. On the Propagation of Drought. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 2013. [Google Scholar]
- Barker, L.J.; Hannaford, J.; Chiverton, A.; Svensson, C. From meteorological to hydrological drought using standardised indicators. Hydrol. Earth Syst. Sci. 2016, 20, 2483–2505. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Dorigo, W.A.; Parinussa, R.M.; de Jeu, R.A.M.; Wagner, W.; McCabe, M.F.; Evans, J.P.; van Dijk, A.I.J.M. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sens. Environ. 2012, 123, 280–297. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.A.; Crow, W.; Wagner, W. Triple Collocation-Based Merging of Satellite Soil Moisture Retrievals. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6780–6792. [Google Scholar] [CrossRef]
- Keshavarz, M.R.; Vazifedoust, M.; Alizadeh, A. Drought monitoring using a Soil Wetness Deficit Index (SWDI) derived from MODIS satellite data. Agric. Water Manag. 2014, 132, 37–45. [Google Scholar] [CrossRef]
- Mishra, A.; Vu, T.; Veettil, A.V.; Entekhabi, D. Drought monitoring with soil moisture active passive (SMAP) measurements. J. Hydrol. 2017, 552, 620–632. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A.; Herrero-Jiménez, C.M. Satellite soil moisture for agricultural drought monitoring: Assessment of the SMOS derived Soil Water Deficit Index. Remote Sens. Environ. 2016, 177, 277–286. [Google Scholar] [CrossRef]
- Kędzior, M.; Zawadzki, J. SMOS data as a source of the agricultural drought information: Case study of the Vistula catchment, Poland. Geoderma 2017, 306, 167–182. [Google Scholar] [CrossRef]
- Instituto Nacional de Estadística y Geografía (INEGI). Censo de Población y Vivienda 2010. 2016. Available online: http://www.beta.inegi.org.mx/proyectos/ccpv/2010/ (accessed on 19 January 2018).
- Robles-Morua, A.; Halvorsen, K.E.; Mayer, A.S.; Vivoni, E.R. Exploring the application of participatory modeling approaches in the Sonora River Basin, Mexico. Environ. Model. Softw. 2014, 52, 273–282. [Google Scholar] [CrossRef]
- Romo-Leon, J.R.; van Leeuwen, W.J.D.; Castellanos-Villegas, A. Using remote sensing tools to assess land use transitions in unsustainable arid agro-ecosystems. J. Arid Environ. 2014, 106, 27–35. [Google Scholar] [CrossRef]
- Pineda-Pablos, N.; Moreno-Váquez, J.-L.; Salazar-Adams, A.; Lutz-Ley, A.N. Derechos de agua y gestión por cuencas en México. El caso del río Sonora. Espiral Estud. Sobre Estado Soc. 2014, 21, 191–225. [Google Scholar]
- Comisión Nacional del Agua (CONAGUA). Programas de Medidas Preventivas y de Mitigación de la Sequía: Guía de Elaboración para Usuarios Urbanos de agua Potable y Sanemiento; Versión 1.0; Comisión Nacional del Agua: Mexico City, Mexico, 2014. [Google Scholar]
- Adams, A.; Vázquez, J.L.; Ley, A.N. Agricultura y manejo sustentable del acuífero de la Costa de Hermosillo. Reg. Soc. 2012, 54, 155–179. [Google Scholar]
- Meza, F.J.; Vicuña, S.; Jelinek, M.; Bustos, E.; Bonelli, S. Assessing water demands and coverage sensitivity to climate change in the urban and rural sectors in central Chile. J. Water Clim. Chang. 2014, 5, 192. [Google Scholar] [CrossRef]
- Meza, F.; Wilks, D.; Gurovich, L.; Bambach, N. Impacts of climate change on irrigated agriculture in the Maipo Basin, Chile: Reliability of water rights and changes in the demand for irrigation. J. Water Resour. Plan. Manag. 2012, 138, 421–430. [Google Scholar] [CrossRef]
- Garreaud, R.; Alvarez-Garreton, C.; Barichivich, J.; Boisier, J.P.; Christie, D.; Galleguillos, M.; LeQuesne, C.; McPhee, J.; Zambrano-Bigiarini, M. The 2010–2015 mega drought in Central Chile: Impacts on regional hydroclimate and vegetation. Hydrol. Earth Syst. Sci. 2017, 21, 6307–6327. [Google Scholar] [CrossRef]
- Bustos, E.; Meza, F.J. A method to estimate maximum and minimum air temperature using MODIS surface temperature and vegetation data: Application to the Maipo Basin, Chile. Theor. Appl. Climatol. 2015, 120, 211–226. [Google Scholar] [CrossRef]
- Departamento General de Irrigación (DGI). Plan Director del Rio Mendoza; Gobierno de Mendoza, Secretaría de Agricultura, Ganadería, Pesca y Alimentación de la Nación, Proyecto PNUD/FAO/ARG/00/008; DGI: Mendoza, Argentina, 2006. [Google Scholar]
- Departamento General de Irrigación (DGI). Plan Director del Rio Tunuyán; Gobierno de Mendoza, Secretaría de Agricultura, Ganadería, Pesca y Alimentación de la Nación, Proyecto PNUD/FAO/ARG/00/008; DGI: Mendoza, Argentina, 2006. [Google Scholar]
- Castex, V.; Tejeda, E.M.; Beniston, M. Water availability, use and governance in the wine producing region of Mendoza, Argentina. Environ. Sci. Policy 2015, 48, 1–8. [Google Scholar] [CrossRef]
- Salatino, S.; Morábito, J.; Bermejillo, A.; Dediol, C.; Stocco, A.; Tapia, O.; Miralles, S.; Hernández, R.; Mastrantonio, L.; Genovese, D.; et al. Calidad de aguas y análisis de la contaminación en el Río Tunuyán Superior (Mendoza, Argentina) en el periodo 2007–2014: Water quality and analysis of contamination in upper Tunuyán River (Mendoza, Argentina) in period 2007–2014. Augmdomus 2017, 9, 67–82. [Google Scholar]
- Salas, S.; Jiménez, E.; Montaña, E.; Garay-Flühmann, R.; Gauthier, D.; Polo Díaz, H. Vulnerabilidad al Cambio Climático: Desafíos para la Adaptación en las Cuencas de Elqui y Mendoza; Inter-American Institute for Global Change Research: Montevideo, Uruguay, 2012. [Google Scholar]
- Guttmann, N. Accepting the standardized precipitation index: A calculation algorithm. J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Standardized Precipitation Index User Guide; Svoboda, M., Hayes, M., Wood, D., Eds.; World Meteorological Organization: Geneva, Switzerland, 2012. [Google Scholar]
- Otkin, J.A.; Anderson, M.C.; Hain, C.; Svoboda, M. Using temporal changes in drought indices to generate probabilistic drought intensification forecasts. J. Hydrometeorol. 2014. [Google Scholar] [CrossRef]
- Pappas, C.; Papalexiou, S.M.; Koutsoyiannis, D. A quick gap filling of missing hydrometeorological data. J. Geophys. Res. Atmos. 2014, 119, 9290–9300. [Google Scholar] [CrossRef]
- McKee, T.; Doesken, N.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the Eight Conference, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Heim, R.R. A review of twentieth-century drought indices used in the United States. Bull. Am. Meteorol. Soc. 2002, 1149–1165. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Quiring, S.M. Developing objective operational definitions for monitoring drought. J. Appl. Meteorol. Climatol. 2009, 48, 1217–1229. [Google Scholar] [CrossRef]
- Guttman, N.B. Comparing the palmer drought index and the standardized precipitation index. J. Am. Water Resour. Assoc. 1998, 34, 113–121. [Google Scholar] [CrossRef]
- Sivakumar, M.V.K.; Motha, R.P.; Wilhite, D.A.; Wood, D.A. (Eds.) Agricultural Drought Indices, 1572nd ed.; World Meteorological Organization: Geneva, Switzerland, 2011. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; van Loon, A.F.; Stahl, K. Candidate distributions for climatological drought indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; van Loon, A.F.; Stahl, K. Response to comment on ‘Candidate distributions for climatological drought indices (SPI and SPEI)’. Int. J. Climatol. 2016, 36, 2132–2138. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S. Comment on ‘Candidate distributions for climatological drought indices (SPI and SPEI)’ by James H. Stagge et al. Int. J. Climatol. 2016, 36, 2120–2131. [Google Scholar] [CrossRef]
- Carrão, H.; Russo, S.; Sepulcre-Canto, G.; Barbosa, P. An empirical standardized soil moisture index for agricultural drought assessment from remotely sensed data. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 74–84. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. Multivariate standardized drought index: A parametric multi-index model. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Nalbantis, I. Evaluation of a hydrological drought index. Eur. Water 2008, 23/24, 67–77. [Google Scholar]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Accurate computation of a streamflow drought index. J. Hydrol. Eng. 2012, 17, 318–331. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Stagge, J.H. SCI: Standardized Climate Indices such as SPI, SRI or SPEI, R-Package Version 1.0-2. 2016. Available online: https://cran.r-project.org/web/packages/SCI/index.html (accessed on 1 November 2018).
- Rodgers, J.L.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Urdiales, D.; Meza, F.; Gironás, J.; Gilabert, H. Improving stochastic modelling of daily rainfall using the ENSO index: Model development and application in Chile. Water 2018, 10, 145. [Google Scholar] [CrossRef]
- Saavedra, F.A.; Kampf, S.K.; Fassnacht, S.R.; Sibold, J.S. Changes in Andes snow cover from MODIS data, 2000–2016. Cryosphere 2018, 12, 1027–1046. [Google Scholar] [CrossRef]
- Masiokas, M.H.; Villalba, R.; Luckman, B.H.; Mauget, S. Intra- to multidecadal variations of snowpack and streamflow records in the Andes of Chile and Argentina between 30° and 37° S. J. Hydrometeorol. 2010, 11, 822–831. [Google Scholar] [CrossRef]
- Masiokas, M.H.; Villalba, R.; Luckman, B.H.; Le Quesne, C.; Aravena, J.C. Snowpack variations in the Central Andes of Argentina and Chile, 1951–2005: Large-scale atmospheric influences and implications for water resources in the region. J. Clim. 2006, 19, 6334–6352. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Wilhite, D.A.; Svoboda, M.D. The effect of the length of record on the standardized precipitation index calculation. Int. J. Climatol. 2005, 25, 505–520. [Google Scholar] [CrossRef]
- Rangecroft, S.; van Loon, A.F.; Maureira, H.; Verbist, K.; Hannah, D.M. Multi-method assessment of reservoir effects on hydrological droughts in an arid region. Earth Syst. Dynam. Discuss. 2016. [Google Scholar] [CrossRef]
- Van Lanen, H.A.J.; Laaha, G.; Kingston, D.G.; Gauster, T.; Ionita, M.; Vidal, J.-P.; Vlnas, R.; Tallaksen, L.M.; Stahl, K.; Hannaford, J.; et al. Hydrology needed to manage droughts: The 2015 European case. Hydrol. Process. 2016, 30, 3097–3104. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Stahl, K.; Di Baldassarre, G.; Clark, J.; Rangecroft, S.; Wanders, N.; Gleeson, T.; van Dijk, A.I.J.M.; Tallaksen, L.M.; Hannaford, J.; et al. Drought in a human-modified world: Reframing drought definitions, understanding, and analysis approaches. Hydrol. Earth Syst. Sci. 2016, 20, 3631–3650. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).