Optimal Design of Circular Baffles on Sloshing in a Rectangular Tank Horizontally Coupled by Structure
Abstract
1. Introduction
2. Mathematical Model
Setup
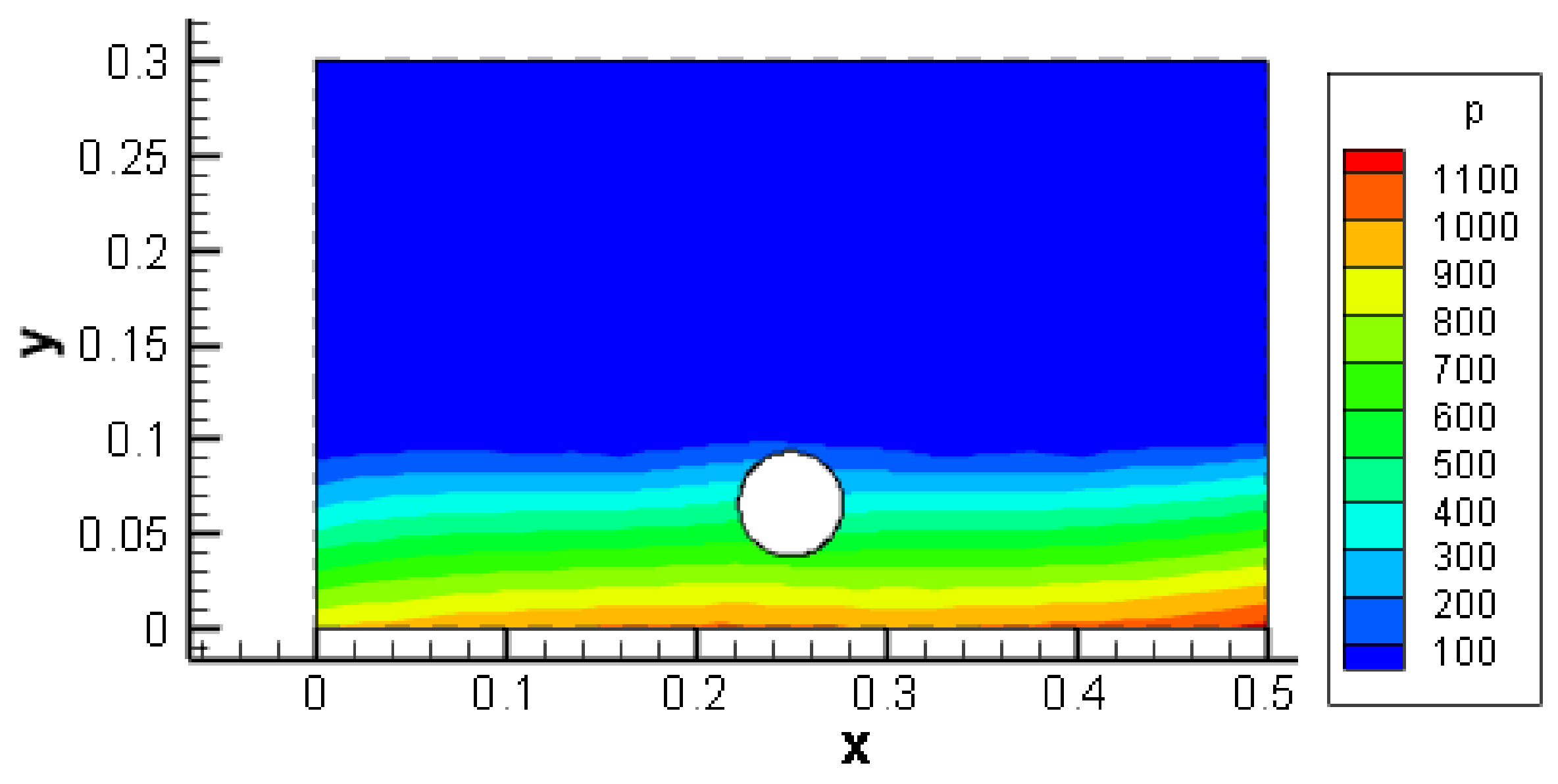
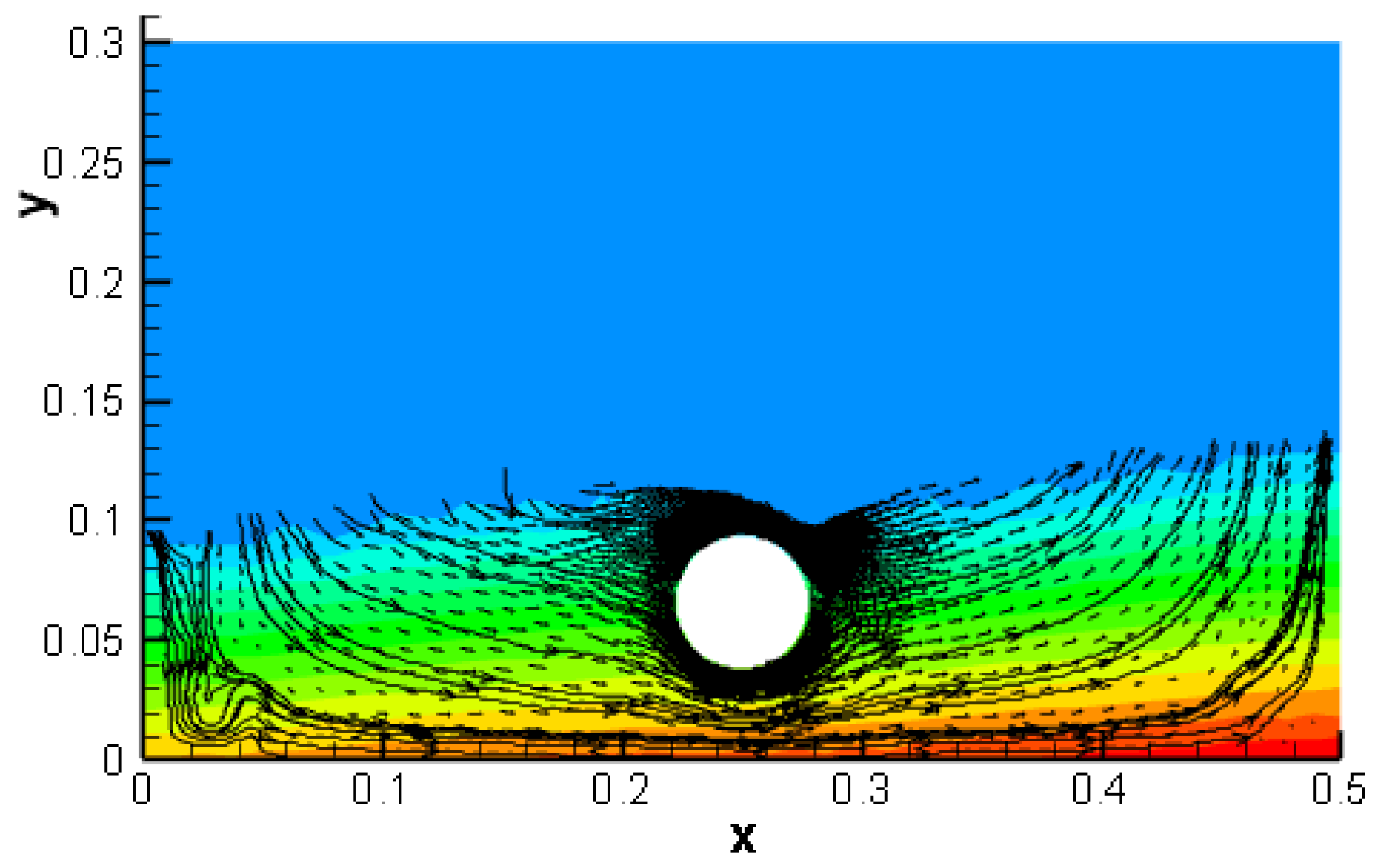
3. Results and Discussion
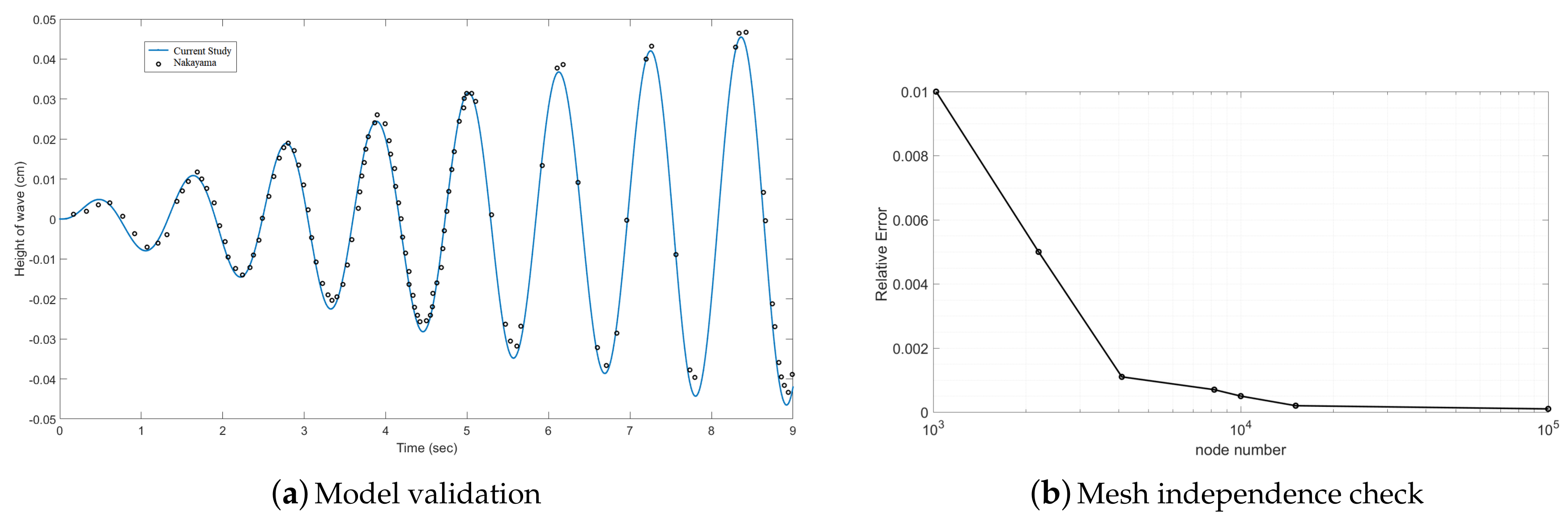
3.1. Validation and Grid Independence
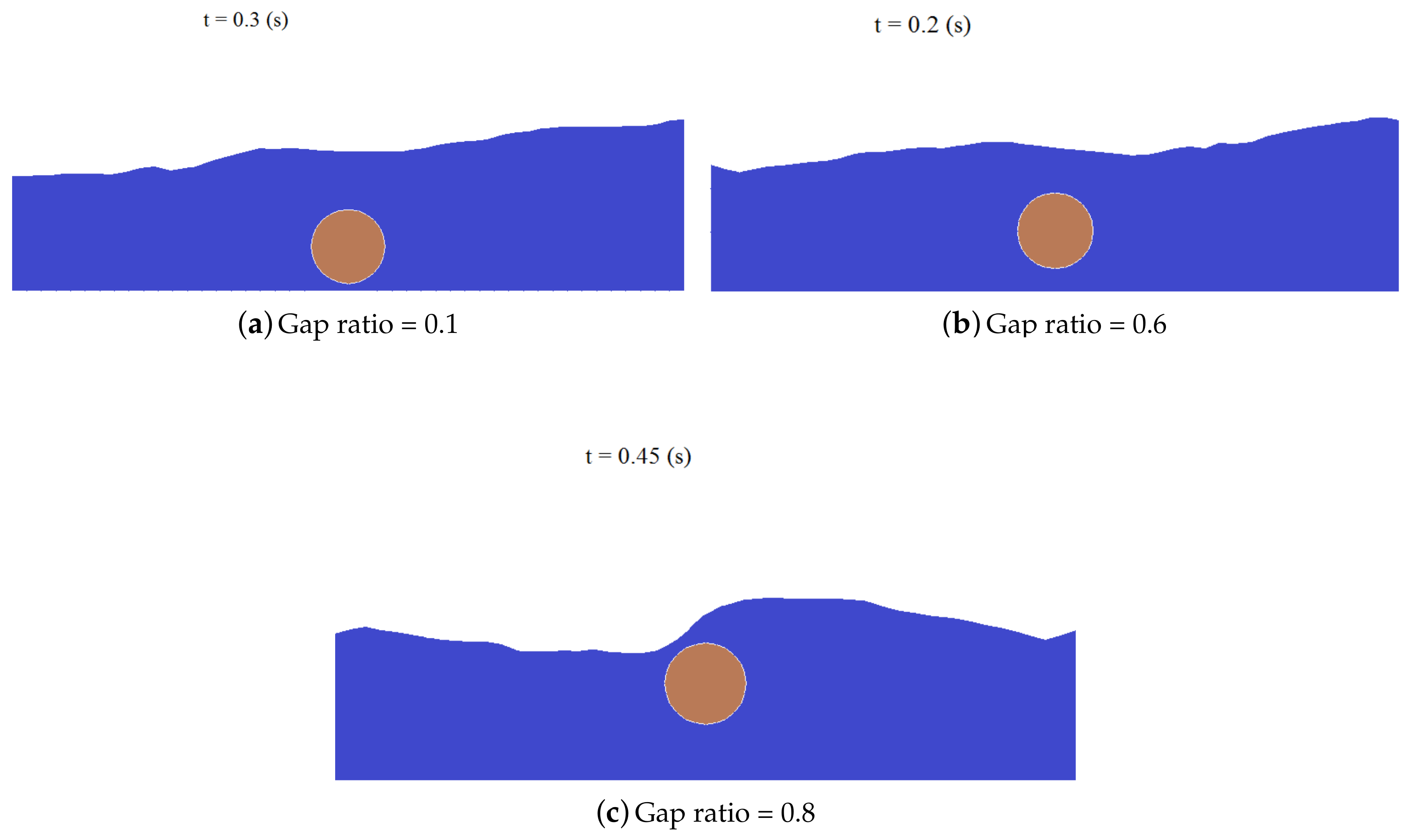
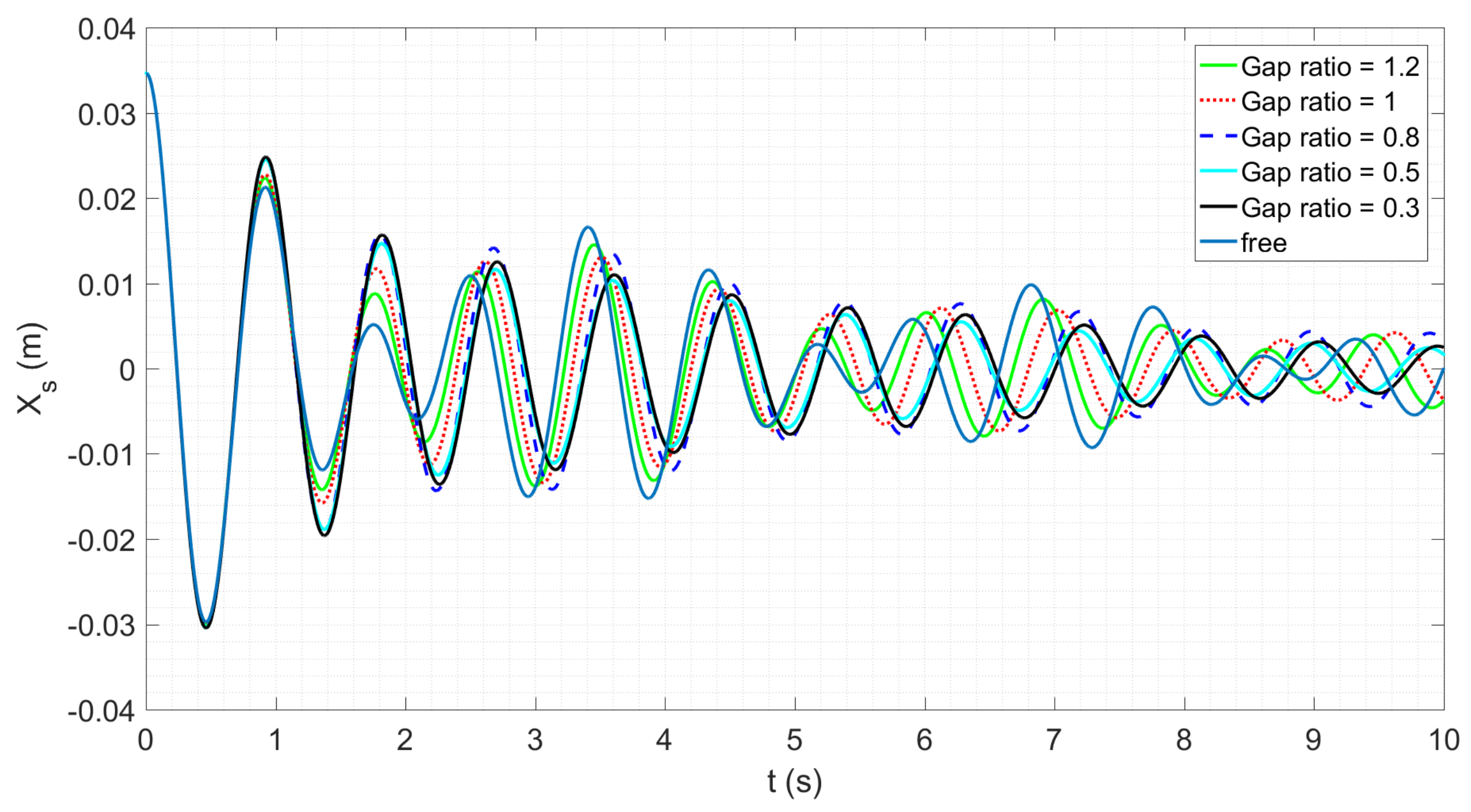
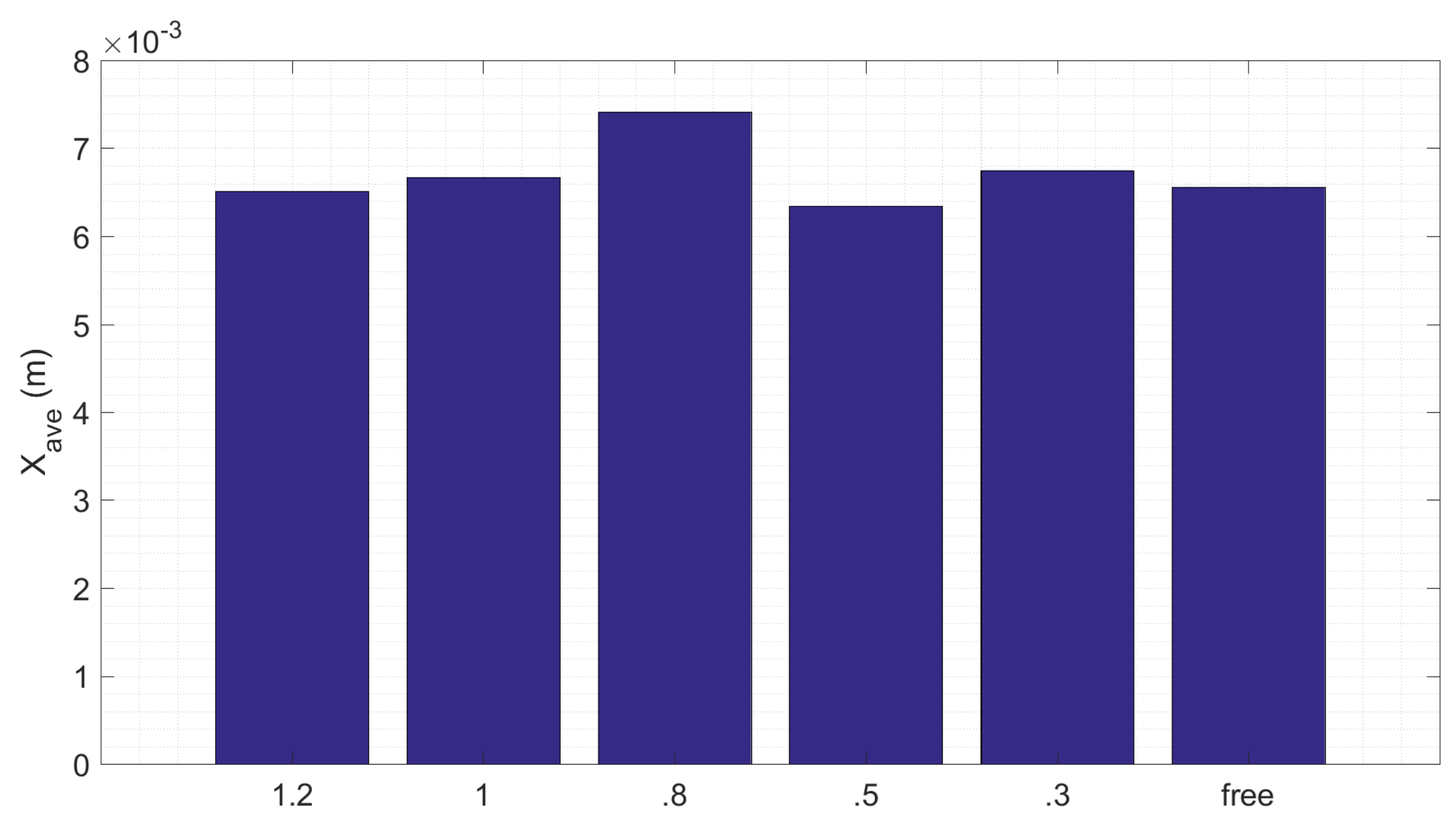
3.2. Effect of Gap with the Bottom Wall
3.3. Effect of Filling Level
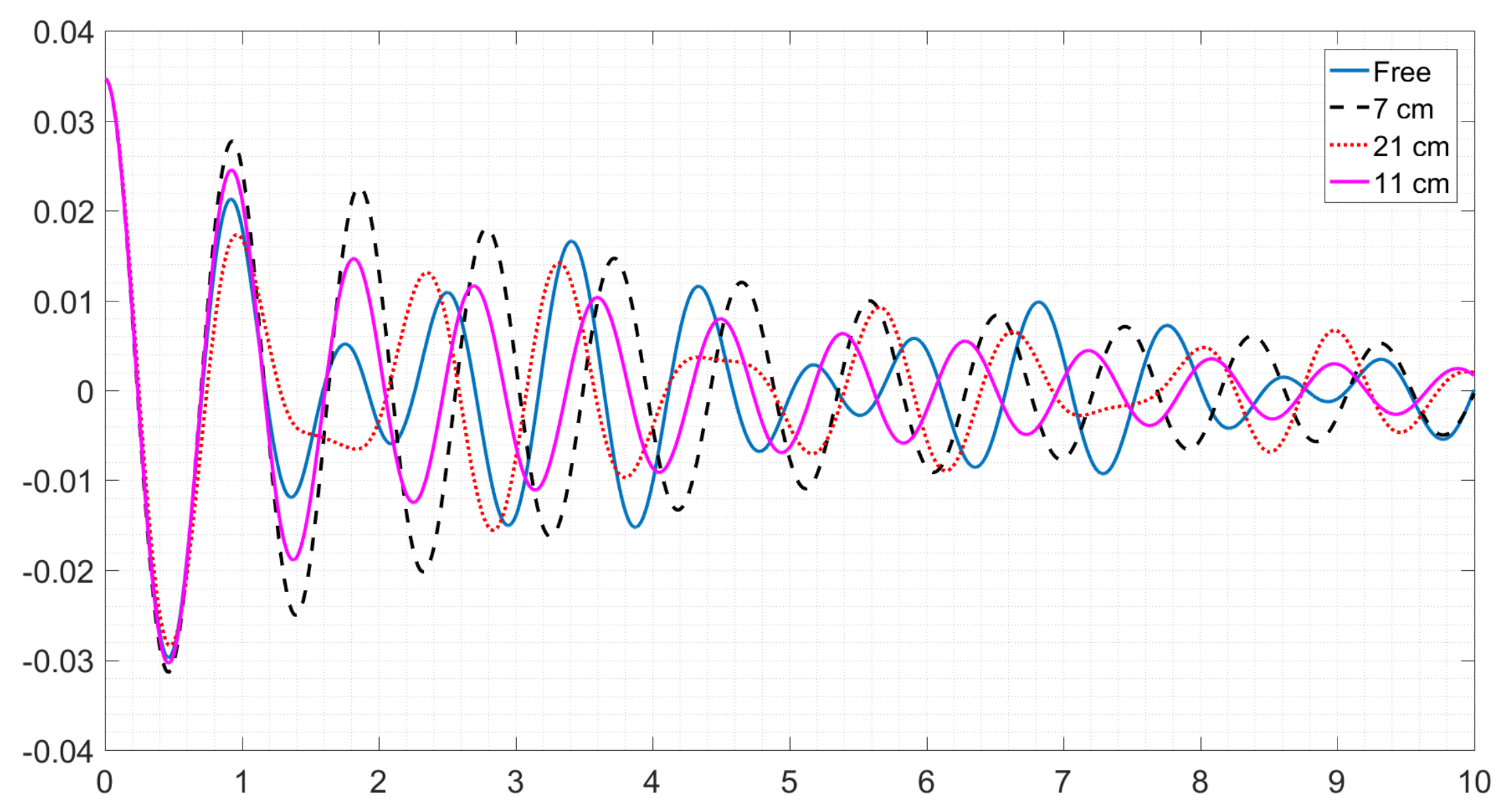
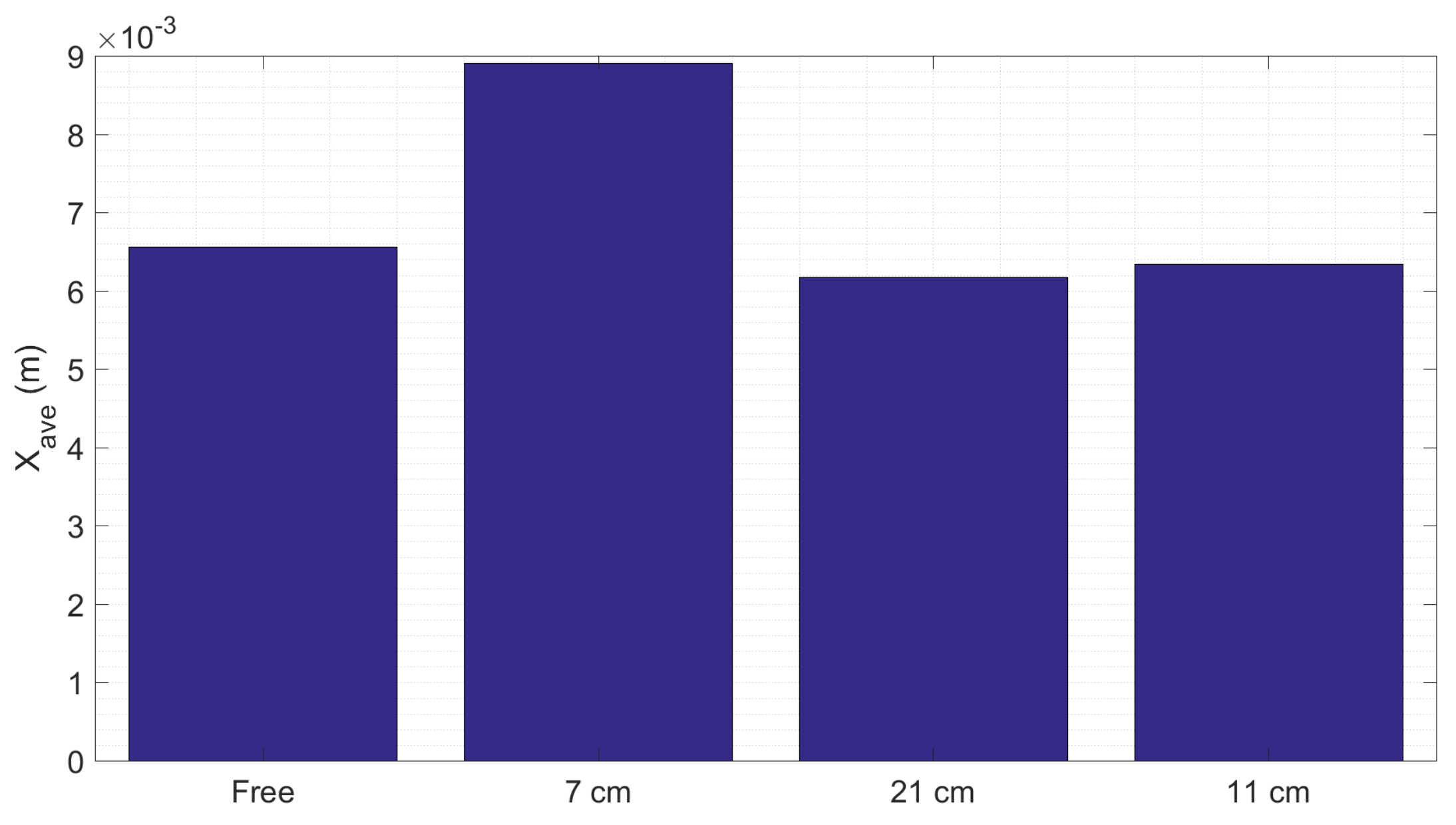
3.4. Distance from the Side Wall
4. Conclusions
- The near wall zone plays an important role in dampening the fluid momentum in the tank.
- The baffle located close to the free surface is effective in control of surface fluctuations, as well as concomitant force and pressure.
- The filling ratio affects the wet wall fraction and sloshing frequency.
- The existence of distances from the wall influences the wet wall area (surface tension effect), and liquid can climb up to the baffle if the baffle is near the surface.
- As the sloshing in the tank is steady, baffles can do little with wave breaking and have no influence on the behavior of liquid.
- The liquid thickness has more importance in slosh damping than wet area.
- The parameter studied here based on importance are the distances, filling ratio, and gaps of the baffle
- Based on a detailed study of transient structure motion coupled with sloshing dynamics, and by optimizing the parameters of baffle, optimal baffle location was achieved.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Velocity | m/s | |
| Density | kg· m | |
| p | Dynamic pressure | Pa |
| L | Length of fluid tank | m |
| Kinematic viscosity | m/s | |
| Thermal expansion coefficient | 1/K | |
| H | Vertical height of fluid tank | m |
| Viscosity | Pa·s | |
| Reference density | kg· m | |
| Buoyancy ratio |
References
- Nasiri, H.; Abdollahzadeh Jamalabadi, M.Y.; Sadeghi, R.; Nguyen, T.K.; Safdari Shadloo, M. A smoothed particle hydrodynamics approach for numerical simulation ofnano-fluid flows: Application to forced convection heat transfer over a horizontal cylinder. J. Therm. Anal. Calorim. 2018, 1–19. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A.; Daqiqshirazi, M.; Nasiri, H.; Safaei, M.R.; Nguyen, T.K. Modeling and analysis ofbiomagnetic blood Carreau fluid flow through astenosis artery with magnetic heat transfer: A transient study. PLoS ONE 2018, 484, e0192138. [Google Scholar]
- Abdollahzadeh Jamalabadi, M.Y.; Safaei, M.R.; Alrashed, A.A.A.A.; Nguyen, T.K.; Filho, E.P.B. Entropy generation in thermalradiative loading of structures with distinct heaters. Entropy 2017, 19, 506. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y.; Bidokhti, A.A.A.; Rah, H.K.; Vaezi, S.; Hooshmand, P. Numerical investigation of oxygenated anddeoxygenated blood flow through a taperedstenosed arteries in magnetic field. PLoS ONE 2016, 12, e0167393. [Google Scholar]
- Abdollahzadeh Jamalabadi, M.Y. Microrobots propulsion system design for drug delivery. J. Chem. Pharm. Res. 2016, 8, 448–496. [Google Scholar]
- Abdollahzadeh Jamalabadi, M.Y.; Keikha, A.J. Fluid–solid interaction modeling ofcerebrospinal fluid absorption inarachnoid villi. J. Chem. Pharm. Res. 2016, 8, 428–442. [Google Scholar]
- Sadeghi, R.; Shadloo, M.S.; Hopp-Hirschler, M.; Hadjadj, A.; Nieken, U. Three-dimensional lattice Boltzmann simulations of high density ratio two-phase flows in porous media. Comput. Math. Appl. 2018, 75, 2445–2465. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Weiss, R.; Yildiz, M.; Dalrymple, R.A. Numerical Simulations of the Breaking and Non-breaking Long Waves. Int. J. Offshore Polar Eng. 2015, 25, 1–7. [Google Scholar]
- Shadloo, M.S.; Rahmat, A.; Yildiz, M. A Smoothed Particle Hydrodynamics Study on theElectrohydrodynamic Deformation of a Droplet Suspended in a Neutrally Buoyant Newtonian Fluid. Comput. Mech. 2013, 52, 693–707. [Google Scholar] [CrossRef]
- Sadeghi, R.; Shadloo, M.S. Three-dimensional Numerical Investigation of Film Boiling by Lattice Boltzmann Method. Numer. Heat Transf. Part A Appl. 2017, 71, 374–385. [Google Scholar] [CrossRef]
- Sadeghi, R.; Shadloo, M.S.; Hooman, K. Numerical Investigation of Natural Convection Film Boiling Around Elliptical Tubes. Numer. Heat Transf. Part A Appl. 2016, 70, 707–722. [Google Scholar] [CrossRef]
- Fatehi, R.; Shadloo, M.S.; Manzari, M.T. Numerical Investigation of Two-Phase Secondary Kelvin-Helmholtz Instability. J. Mech. Eng. Sci. 2014, 228, 1913–1924. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Yildiz, M. Numericalmodelling of Kelvin-Helmholtz Instability Using Smoothed Particle Hydrodynamics Method. Int. J. Numer. Methods Eng. 2011, 87, 988–1006. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Oger, G.; le Touze, D. Smoothed Particle Hydrodynamics Method for Fluid Flows, Towards Industrial Applications: Motivations, Current state, and Challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Rahmat, A.; Tofighi, N.; Shadloo, M.S.; Yildiz, M. Numerical Simulation of Wall Bounded and Electrically Excited Rayleigh Taylor Instability Using Incompressible Smoothed Particle Hydrodynamics. Colloids Surf. A 2014, 460, 60–70. [Google Scholar] [CrossRef]
- Lebon, B.; Nguyen, M.Q.; Peixinho, J.; Shadloo, M.S.; Hadjadj, A. A new mechanism for the periodic bursting of therecirculation region of the flow through a sudden expansion in a circular pipe. Phys. Fluids 2018, 30, 031701. [Google Scholar] [CrossRef]
- Nguyen, M.Q.; Lebon, B.; Shadloo, M.S.; Peixinho, J.; Hadjadj, A. New features of transition to turbulence in a sudden expansion pipe flow. arXiv, 1807; arXiv:1807.10665. [Google Scholar]
- Sumner, I.; Lacovic, R.; Stofan, A. Experimental Investigation of Liquid Sloshing in a Scale-Model Centaur Liquid-Hydrogen Tank; National Aeronautics and Space Administration: Washington, DC, USA, 1966. [Google Scholar]
- Panzarella, C.; Kassemi, M. On the validity of purely thermodynamic descriptions of two-phase cryogenic fluid storage. J. FluidMech. 2003, 484, 41–68. [Google Scholar] [CrossRef]
- Yoon, S.-H.; Park, K.-J. Effect of baffles on sloshing mitigation in liquid storage tanks. Adv. Sci. Technol. Lett. 2015, 108, 1–5. [Google Scholar]
- Hasheminejad, S.; Mohammadi, M.M. Effect of anti-slosh baffles on free liquid oscillations in partially filled horizontal circular tanks. Ocean Eng. 2011, 38, 49–62. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Aghabeigi, M. Sloshing characteristics in half-full horizontal elliptical tanks with vertical baffles. Appl. Math. Model. 2012, 36, 57–71. [Google Scholar] [CrossRef]
- Dodge, F.T. The New “Dynamic Behavior of Liquids in Moving Containers”; Southwest Research Instution: San Antonio, TX, USA, 2000. [Google Scholar]
- Kannape, M.; Przekwa, A.; Singhal, A.; Costes, N. Liquid oxygen sloshing in space shuttle external tank. In Proceedings of the 23rd Joint Propulsion Conference, San Diego, CA, USA, 24–27 June 1987; p. 2019. [Google Scholar]
- Dogde, F. The New dynamic Behavior of Liquids in Moving Containers; Southwest Reserach Inst.: San Antonio, TX, USA, 2000. [Google Scholar]
- Adam, P.; Leachman, J. Design of areconfigurable liquid hydrogen fuel tank for use in the genii unmanned aerial vehicle. AIP Conf. Proc. 2014, 1573, 1299–1304. [Google Scholar]
- Strauch, H.; Luig, K.; Bennani, S. Model based design environment for launcher upper stagegnc development. In Proceedings of the Workshop on Simulation for European Space Programmes SESP, Noordwijk, The Netherlands, 6–8 November 2014. [Google Scholar]
- Behruzi, P.; Konopka, M.; de Rose, F.; Schwartz, G. Cryogenic slosh modeling inlng ship tanks and spacecrafts. In Proceedings of the Twenty-Fourth International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014. [Google Scholar]
- Grayson, G.; Lopez, A.; Chandler, F.; Hastings, L.; Tucker, S. Cryogenic tank modeling for thesaturn as-203 experiment. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006; p. 5258. [Google Scholar]
- Seo, M.; Jeong, S. Analysis of self-pressurization phenomenon of cryogenic fluid storage tank with thermal diffusion model. Cryogenics 2010, 50, 549–555. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Y.; Zhu, K.; Wang, Y.; Wang, L.; Tan, H. Investigation on no-vent filling process of liquid hydrogen tank undermicrogravity condition. Int. J. Hydrogen Energy 2017, 42, 8264–8277. [Google Scholar] [CrossRef]
- Frandsen, J.B. Sloshing motions in excited tanks. J. Comput. Phys. 2004, 196, 53–87. [Google Scholar] [CrossRef]
- Chintalapati, S.; Kirk, D. Parametric study of a propellant tank slosh baffle. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008; p. 4750. [Google Scholar]
- Hirt, C.; Nichols, B.D. Volume of fluid (vof) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Nakayama, T.; Washizu, K. Boundary element analysis of nonlinear sloshing problems. In Developments in Boundary Element Method-3; Elsevier Applied Science Publishers: New York, NY, USA, 1984. [Google Scholar]
- Fries, N.; Behruzi, P.; Arndt, T.; Winter, M.; Netter, G.; Renner, U. Modelling of fluid motion in spacecraft propellant tanks-sloshing. In Proceedings of the Space Propulsion Conference, Bordedaux, France, 7–10 May 2012. [Google Scholar]
- Behruzi, P.; Rose, F.; Cirillo, F. Coupling sloshing, gnc and rigid body motions during ballistic flight phases. In Proceedings of the AIAA Joint Propulsion Conference (AIAA 2016-4586), Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar]
- Gerstmann, J.; Konopka, M. Cryo-laboratory for test and development of propellant management technologies. In Proceedings of the 2nd International Spacecraft Propulsion Conference (SP2015_3124996), Kyoto, Japan, 14–18 September 2015. [Google Scholar]
- Kartuzova, O.; Kassemi, M. Modeling interfacial turbulent heat transfer duringventless pressurization of a large scale cryogenic storage tank inmicrogravity. In Proceedings of the 47 th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011; p. 6037. [Google Scholar]
- Kurul, N.; Podowski, M.Z. Multidimensional effects in forced convectionsubcooled boiling. In Proceedings of the Ninth International Heat Transfer Conference, Jerusalem, Israel, 19–24 August 1990; Hemisphere Publishing: New York, NY, USA, 1990; Volume 2, pp. 19–24. [Google Scholar]
- Apkarian, P.; Dao, N.; Noll, D. Parametric robust structured control design. IEEE Trans. Autom. Control 2015, 60, 1857–1869. [Google Scholar] [CrossRef]
- Konopka, M.; De Rose, F.; Arndt, T.; Gerstmann, J. Large-scale tank active sloshing damping simulation and experiment. In Proceedings of the 3rd International Spacecraft Propulsion Conference (SP2016_3124606), Rome, Italy, 2–6 May 2016. [Google Scholar]
- Zhou, K.; Doyle, J. Essentials of Robust Control; Prentice-Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Hecker, S.; Varga, A. Generalized lft-based representation of parametric uncertain models. Eur. J. Control 2004, 10, 326–337. [Google Scholar] [CrossRef]
- Falcoz, A.; Pittet, C.; Bennani, S.; Guignard, A.; Bayart, C.; Frapard, B. Systematic design methods of robust and structured controllers for satellites. CEAS Space J. 2015, 7, 319–334. [Google Scholar] [CrossRef]
- Achenbach, E. Influence of Surface Roughness on the Cross-Flow Around a Circular Cylinder. J. Fluid Mech. 1971, 46, 321–335. [Google Scholar] [CrossRef]
- Basara, B.; Krajnović, S.; Girimaji, S.; Pavlovic, Z. Near-Wall Formulation of the Partially Averaged Navier–Stokes Turbulence Model. Am. Inst. Aeronaut. Astronaut. J. 2011, 49, 2627–2636. [Google Scholar] [CrossRef]
- Bloor, M.S. The Transition to Turbulence in the Wake of a Circular Cylinder. J. Fluid Mech. 1964, 19, 290–304. [Google Scholar] [CrossRef]
- Chaouat, B.; Schiestel, R. A New Partially Integrated Transport Model forSubgrid-Scale Stresses and Dissipation Rate for Turbulent Developing Flows. Phys. Fluids 2005, 17, 065106. [Google Scholar] [CrossRef]
- Fage, A.; Warsap, J.H. The Effects of Turbulence and Surface Roughness on the Drag of a Circular Cylinder. Aeronaut. Res. Comm. 1929, 39, 335–342. [Google Scholar]
- Fasel, H.F.; Seidel, J.; Wernz, S. A Methodology for Simulations for Complex Turbulent Flows. J. Fluids Eng. 2002, 124, 933–942. [Google Scholar] [CrossRef]
- Gatski, T.B.; Speziale, C.G. On Explicit Algebraic Stress Models for Complex Turbulent Flows. J. Fluid Mech. 1993, 254, 59–78. [Google Scholar] [CrossRef]
- Gerich, D.; Eckelmann, H. Influence of End Plates and Free Ends on the Shedding Frequency of Circular Cylinders. J. Fluid Mech. 1982, 122, 109–121. [Google Scholar] [CrossRef]
- Germano, M. Turbulence: The Filtering Approach. J. Fluid Mech. 1992, 238, 325–336. [Google Scholar] [CrossRef]
- Girimaji, S.S. Fully Explicit and Self-Consistent Algebraic Reynolds Stress Model. Theor. Comput. Fluid Dyn. 1996, 8, 387–402. [Google Scholar] [CrossRef]
- Reyes, D.A.; Cooper, J.M.; Girimaji, S.S. Characterizing Velocity Fluctuations in Partially Resolved Turbulence Simulations. Phys. Fluids 2014, 26, 085106. [Google Scholar] [CrossRef]
- Girimaji, S.S. Pressure-Strain Correlation Modelling of Complex Turbulent Flows. J. Fluid Mech. 2000, 422, 91–123. [Google Scholar] [CrossRef]
- Girimaji, S.S. Lower-Dimensional Manifold (Algebraic) Representation of Reynolds Stress Closure Equations. Theor. Comput. Fluid Dyn. 2001, 14, 259–281. [Google Scholar] [CrossRef]
- Girimaji, S. Partially-Averaged Navier–Stokes Model for Turbulence: A Reynolds-AveragedNavier–Stokes to Direct Numerical Simulation Bridging Method. J. Appl. Mech. 2005, 73, 413–421. [Google Scholar] [CrossRef]
- Girimaji, S.S.; Abdol-Hamid, K.S. Partially-Averaged Navier Stokes Model for Turbulence: Implementation and Validation. In Proceedings of the 43rd American Institute of Aeronautics and Astronautics (AIAA) Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Girimaji, S.S.; Jeong, E.; Srinivasan, R. Partially Averaged Navier–Stokes Method for Turbulence: Fixed Point Analysis and Comparison With Unsteady Partially Averaged Navier–Stokes. J. Appl. Mech. 2005, 73, 422–429. [Google Scholar] [CrossRef]
- Güven, O.; Farrel, C.; Patel, V.C. Surface-Roughness Effects on the Mean Flow Past Circular Cylinder. J. Fluid Mech. 1980, 98, 673–701. [Google Scholar] [CrossRef]
- Huang, Y.-N.; Rajagopal, K.R. On a Generalized Nonlinear k-ϵ Model for Turbulence that Models Relaxation Effects. Theor. Comput. Fluid Dyn. 1996, 8, 275–288. [Google Scholar]
- Hussain, A.K.M.F.; Reynolds, W.C. The Mechanics of an Organized Wave in Turbulent Shear Flow. J. Fluid Mech. 1970, 41, 241–258. [Google Scholar] [CrossRef]
- Kok, J.C. A Stochastic Backscatter Model for Grey-Area Mitigation in Detached Eddy Simulations. Flow Turbul. Combust. 2017, 99, 119–150. [Google Scholar] [CrossRef]
- Pereira, F.S.; Vaz, G.; Eça, L. An Assessment of Scale-Resolving Simulation Models for the Flow Around a Circular Cylinder. Turbul. Heat Mass Transf. (THMT) 2015, 8. [Google Scholar]
- Kok, J.C.; Dol, H.S.; Oskam, B.; der Ven, H.V. Extra-Large Eddy Simulation of Massively Separated Flows. In Proceedings of the 42nd American Institute of Aeronautics and Astronautics (AIAA) Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar]
- Muschinski, A. A Similarity Theory of Locally Homogeneous and Isotropic Turbulence Generated by aSmagorinsky-Type LES. J. Fluid Mech. 1996, 325, 239–260. [Google Scholar] [CrossRef]
- Mishra, A.A.; Girimaji, S.S. Intercomponent Energy Transfer inIncompressible Homogeneous Turbulence: Multi-Point Physics and Amenability to One-Point Closures. J. Fluid Mech. 2013, 731, 639–681. [Google Scholar] [CrossRef]
- Koopmann, G.H. The Vortex Wake of Vibrating Cylinders at Low Reynolds Numbers. J. Fluid Mech. 1967, 28, 501–512. [Google Scholar] [CrossRef]
- Lehmkuhl, O.; Rodriguez, I.; Borrel, R.; Oliva, A. Low-Frequency Unsteadiness in the Vortex Formation of a Circular Cylinder. Phys. Fluids 2013, 25, 085109. [Google Scholar] [CrossRef]
- Lakshmipathy, S.; Girimaji, S.S. Partially-AveragedNavier–Stokes Method for Turbulent Flows: k-ω Model Implementation. In Proceedings of the 44th American Institute of Aeronautics and Astronautics (AIAA) Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Schiestel, R. Multiple-Time-Scale Modeling of Turbulent Flows in One-Point Closures. Phys. Fluids 1987, 30, 722–731. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the Scale-Determining Equation for Advanced Turbulence Models. Am. Inst. Aeronaut. Astronaut. J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Schiestel, R.; Dejoan, A. Towards a New Partially Integrated Transport Model for Coarse Grid and Unsteady Flow Simulation. Theor. Comput. Fluid Dyn. 2005, 18, 443–468. [Google Scholar] [CrossRef]
- Pope, S.B. A More General Effective-Viscosity Hypothesis. J. Fluid Mech. 1975, 72, 331–340. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.Kh.; Travin, A.K. A HybridRANS-LES Approach with Delayed-DES and Wall-Modelled LES Capabilities. Int. J. Heat Fluid Flow 2008, 29, 1639–1649. [Google Scholar] [CrossRef]
- Spalart, P.R.; Jou, W.-H.; Strelets, M.; Allmaras, S. Comments on the Feasibility of LES for Wings and on the HybridRANS/LES Approach. In Proceedings of the 1st Air Force Office of Scientific Research (AFOSR) International Conference onDNS/LES-Advances inDNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Speziale, C. Computing Non-Equilibrium Turbulent Flow with Time-Dependent RANS and VLES. In Proceedings of the 15th International Conference on Numerical Methods in Fluid Dynamics, Monterey, CA, USA, 24–28 June 1996. [Google Scholar]
- Mishra, A.A.; Girimaji, S.S. Pressure-Strain Correlation Modeling: Towards Achieving Consistency with Rapid Distortion Theory. Flow Turbul. Combust. 2010, 85, 593–619. [Google Scholar] [CrossRef]
- Mishra, A.A.; Girimaji, S.S. Toward Approximating Non-Local Dynamics in Single-Point Pressure-Strain Correlation Closures. J. Fluid Mech. 2017, 811, 168–188. [Google Scholar] [CrossRef]
- Speziale, C.G.; Sarkar, S.; Gatski, T.B. Modelling the Pressure Strain-Rate Correlation of Turbulence: An Invariant Dynamical Systems Approach. J. Fluid Mech. 1991, 227, 245–272. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. In Turbulence, Heat and Mass Transfer, 4th ed.; Hanjalić, K., Nagano, Y., Tummers, M., Eds.; Begell House, Inc.: Antalya, Turkey, 2003. [Google Scholar]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the Development of a Reynolds-Stress Turbulence Closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Rodi, W. A New Algebraic Relation for Calculating the Reynolds Stresses. Z. Angew. Math. Mech. (ZAMM) 1976, 56, 219–221. [Google Scholar]
- Lin, J.-C.; Vorobieff, P.; Rockwell, D. Three-Dimensional Patterns ofStreamwise Vorticity in the Near-Wake of a Cylinder. J. Fluids Struct. 1995, 9, 231–234. [Google Scholar] [CrossRef]
- Prasad, A.; Williamson, C.H.K. Three-Dimensional Effects in Turbulent Bluff-Body Wake. J. Fluid Mech. 1997, 343, 235–265. [Google Scholar] [CrossRef]
- Mansy, H.; Yang, P.-M.; Williams, D.R. Quantitative Measurements of Three-Dimensional Structures in the Wake of a Circular Cylinder. J. Fluid Mech. 1994, 270, 277–296. [Google Scholar] [CrossRef]
- Roshko, A. On the Development of Turbulent Wake from Vortex Streets; Tech. Rep. 1191; National Advisory Committee for Aeronautics: Washington, DC, USA, 1954. [Google Scholar]
- Sadeh, W.Z.; Saharon, D.B. Turbulence Effect on Crossflow Around a Circular Cylinder at Subcritical Reynolds Numbers; NASA Contractor Report 3622; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1982. [Google Scholar]
- West, G.S.; Apelt, C.J. The Effects of Tunnel Blockage and Aspect Ratio on the Mean Flow Past a Circular Cylinder with Reynolds Numbers Between 104 and105. J. Fluid Mech. 1982, 114, 361–377. [Google Scholar] [CrossRef]
- Norberg, C. An Experimental Investigation of the Flow Around a Circular Cylinder: Influence of Aspect Ratio. J. Fluid Mech. 1994, 258, 287–319. [Google Scholar] [CrossRef]
- Szepessy, S.; Bearman, P.W. Aspect Ratio and End Plate Effects on Vortex Shedding From a Circular Cylinder. J. Fluid Mech. 1992, 234, 191–217. [Google Scholar] [CrossRef]
- Norberg, C. LDV-Measurements in the Near Wake of a Circular Cylinder. Advances in Understanding of Bluff Body Wakes and Vortex-Induced Vibration; Washington, DC, USA, 1998. Available online: http://www.ht.energy.lth.se/fileadmin/ht/Norberg-FEDSM98-5202.pdf (accessed on 9 October 2018).
- Norberg, C. Pressure Distributions around a Circular Cylinder in Cross-Flow. In Proceedings of the Symposium on Bluff Body Wakes and Vortex-Induced Vibrations (BBVIV3), Port Arthur, Australia, 17–20 December 2002. [Google Scholar]
- Norberg, C. Fluctuating Lift on a Circular Cylinder: Review and New Measurements. J. Fluids Struct. 2003, 17, 59–96. [Google Scholar] [CrossRef]
- Norberg, C.; Sundén, B. Turbulence and Reynolds Number Effects on the Flow and Fluid Forces on a Single Cylinder in Cross Flow. J. Fluids Struct. 1987, 1, 337–357. [Google Scholar] [CrossRef]
- Parnaudeau, P.; Carlier, J.; Heitz, D.; Lamballais, E. Experimental and Numerical Studies of the Flow over a Circular Cylinder at Reynolds Number 3900. Phys. Fluids 2008, 20, 085101. [Google Scholar] [CrossRef]
- Pereira, F.S.; Vaz, G.; Eça, L.; Girimaji, S.S. Simulation of the Flow Around a Circular Cylinder at Re = 3900 with Partially-Averaged Navier–Stokes Equations. Int. J. Heat Fluid Flow 2017, 69, 234–246. [Google Scholar] [CrossRef]
- Prasad, A.; Williamson, C.H.K. The Instability of the Shear Layer Separating from a Bluff Body. J. Fluid Mech. 1997, 333, 375–402. [Google Scholar] [CrossRef]
- Unal, M.F.; Rockwell, D. On Vortex Shedding from a Cylinder. Part 1. The Initial Instability. J. Fluid Mech. 1988, 190, 419–512. [Google Scholar] [CrossRef]
- Rajagopalan, S.; Antonia, R.A. Flow Around a Circular Cylinder-Structure of the Near Wake Shear Layer. Exp. Fluids 2005, 38, 393–402. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Vortex Dynamics in the Cylinder Wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Flow Around Circular Cylinder Volume 1: Fundamentals; Oxford Science Publications: Oxford, UK, 1997. [Google Scholar]
- Rayleigh, L. Investigation of the Character of the Equilibrium of anIncompressible Heavy Fluid of Variable Density. Lond. Math. Soc. 1883, 14, 170–177. [Google Scholar]
- Rivlin, R.S. The Relation Between the Flow of Non-Newtonian Fluids and Turbulence Newtonian Fluids. Q. Appl. Math. 1957, 15, 212–215. [Google Scholar] [CrossRef]
- Tokumaru, P.T.; Dimotakis, P.E. Rotary Oscillation Control of a Cylinder Wake. J. Fluid Mech. 1991, 224, 77–90. [Google Scholar] [CrossRef]
- Zacharioudaki, M.; Kouris, C.; Dimakopoulos, Y.; Tsamopoulos, J. A direct comparison between volume and surface tracking methods with a boundary-fitted coordinate transformation and third-orderupwinding. J. Comput. Phys. 2007, 227, 1428–1469. [Google Scholar] [CrossRef]
- Fraggedakis, D.; Kouris, C.; Dimakopoulos, Y.; Tsamopoulos, J. Flow of twoimmiscible fluids in a periodically constricted tube: Transitions to stratified, segmented, churn, spray or segregated flow. Phys. Fluids 2015, 27, 082102. [Google Scholar] [CrossRef]
- Leschziner, M.A.; Drikakis, D. Turbulence and turbulent flow computation in aeronautics. Aeronaut. J. 2002, 106, 349–384. [Google Scholar]
- Shapiro, E.; Drikakis, D. Artificial compressibility, characteristics-based schemes for variable density, incompressible, multi-species flows. Part I. Derivation of different formulations and constant density limit. J. Comput. Phys. 2005, 210, 584–607. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitlydiscretized fluid flow equations by operator splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Meldi, M.; Poux, A. A reduced order model based onKalman filtering for sequential data assimilation of turbulent flows. J. Fluids Struct. 2017, 347, 207–234. [Google Scholar]
- Hill, S.; Deising, D.; Acher, T.; Klein, H.; Bothe, D.; Marschall, H. Boundedness-preserving implicit correction of mesh-induced errors for VOF based heat and mass transfer. J. Fluids Struct. 2017, 352, 285–300. [Google Scholar] [CrossRef]


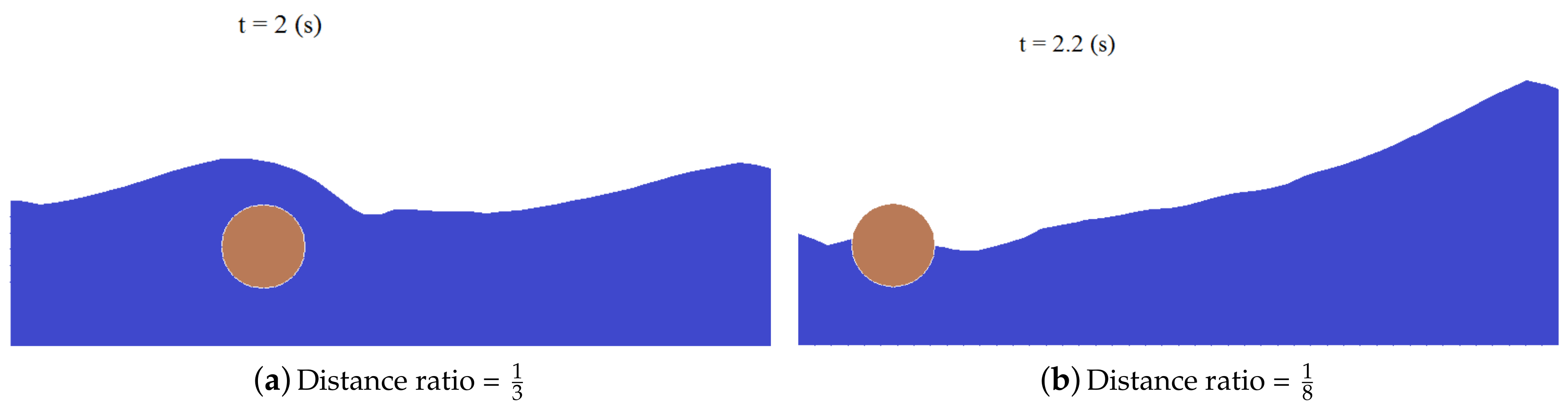
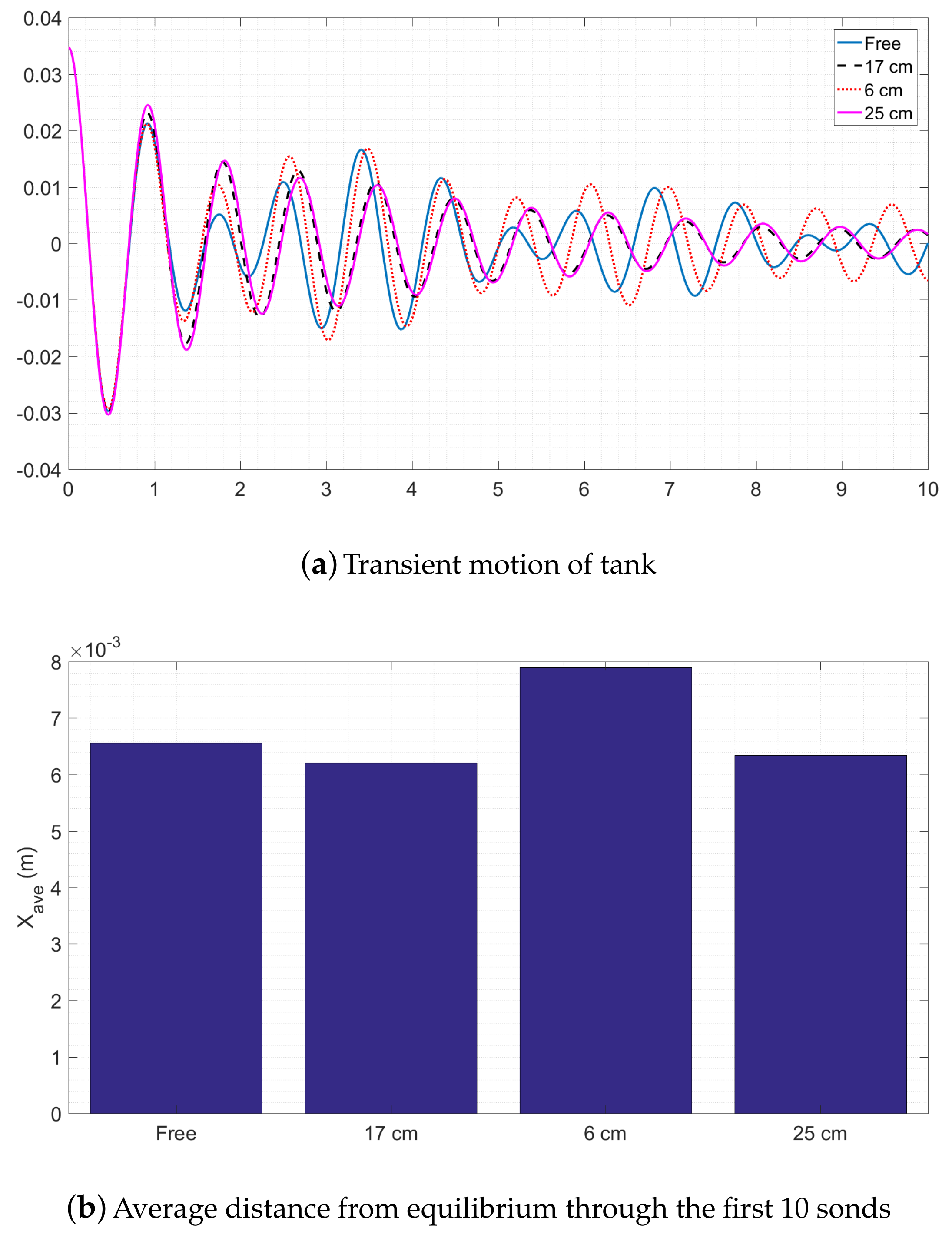
| Parameters | Group of Setups |
|---|---|
| Fill level | 6 cm, 11 cm, 20 cm |
| Distance from left | 10 cm, 25 cm |
| Gap | 1 cm, 2 cm, 3 cm, 5 cm, 10 cm |
| Flow Regimes | |
|---|---|
| fully laminar | < 180–200 |
| transition in the wake | < 350–400 |
| transition in the free shear-layer | |
| transition in the boundary-layer | |
| fully turbulent boundary-layer |
| Parameter | Value |
|---|---|
| Mass | 18.9 kg |
| Natural frequency | 1.09 1/s |
| Damping ratio | 0.0019 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamalabadi, M.Y.A.; Ho-Huu, V.; Nguyen, T.K. Optimal Design of Circular Baffles on Sloshing in a Rectangular Tank Horizontally Coupled by Structure. Water 2018, 10, 1504. https://doi.org/10.3390/w10111504
Jamalabadi MYA, Ho-Huu V, Nguyen TK. Optimal Design of Circular Baffles on Sloshing in a Rectangular Tank Horizontally Coupled by Structure. Water. 2018; 10(11):1504. https://doi.org/10.3390/w10111504
Chicago/Turabian StyleJamalabadi, Mohammad Yaghoub Abdollahzadeh, Vinh Ho-Huu, and Truong Khang Nguyen. 2018. "Optimal Design of Circular Baffles on Sloshing in a Rectangular Tank Horizontally Coupled by Structure" Water 10, no. 11: 1504. https://doi.org/10.3390/w10111504
APA StyleJamalabadi, M. Y. A., Ho-Huu, V., & Nguyen, T. K. (2018). Optimal Design of Circular Baffles on Sloshing in a Rectangular Tank Horizontally Coupled by Structure. Water, 10(11), 1504. https://doi.org/10.3390/w10111504






