Abstract
The Mediterranean climate is marked by arid climate conditions in summer; therefore, crop irrigation is crucial to sustain plant growth and productivity in this season. If groundwater is utilized for irrigation, an impressive water pumping system is needed to satisfy crop water requirements at catchment scale. Consequently, irrigation water quality gets worse, specifically considering groundwater salinization near the coastal areas due to seawater intrusion, as well as triggering soil salinization. With reference to an agricultural coastal area in the Mediterranean basin (southern Italy), close to the Adriatic Sea, an assessment of soil salinization risk due to processing tomato cultivation was carried out. A simulation model was first arranged, then validated, and finally applied to perform a water and salt balance along a representative soil profile on a daily basis. In this regard, long-term weather data and physical soil characteristics of the considered area (both taken from international databases) were utilized in applying the model, as well as considering three salinity levels of irrigation water. Based on the climatic analysis performed and the model outputs, the probability of soil salinity came out very high, such as to seriously threaten tomato yield. Autumn–winter rainfall frequently proved to be insufficient to leach excess salts away from the soil profile and reach sustainable conditions of tomato cultivation. Therefore, alternative cropping strategies were investigated.
1. Introduction
Salinization is one of the major threats of land degradation [1] that negatively impacts on agricultural sustainability and environmental health, leading to severe losses of soil productivity and desertification processes [2,3]. The accumulation of water-soluble salts in the soil is occurring worldwide, with the most prominent areas being the arid and semi-arid climatic zones [4]. In Europe, salt-affected soils cover an area of about 3.8 million ha, particularly concentrated in the Mediterranean basin [5,6]. Here, salinization is most often caused by the use of highly saline irrigation water, such as groundwater salinized due to seawater intrusion, frequently coupled with poor soil drainage conditions [5,7].
Mediterranean regions are characterized by a semi-arid climate, with high temperatures and limited rains in summer, mild winter periods, and frequent drought. The lower rainfall occurring during the summer season, coupled with the high air temperatures and the consequent high potential evapotranspiration, results in a serious water deficit. Therefore, the systematic support of irrigation in summer is essential to sustain crop growth and production. This is of particular relevance in the Apulia region (southern Italy), where the economy of the agricultural system is strongly based on irrigation farming [8]. Moreover, the Apulia region is one of the European regions that is most heavily affected by a chronic water shortage [9]. Groundwater, if optimally managed, may represent a useful alternative to surface water collected in artificial reservoirs, thus narrowing the gap between summer water demand for agricultural uses and actual water availability [7]. Unfortunately, the large water requirement of summer crops has often forced intensive exploitation of groundwater, causing the progressive lowering of the water table and the consequent gradual intrusion of the marine water “cone”, bringing about a significant increase in water salinity. This condition is particularly critical along the coastal areas of the Apulian region, where the use of saline groundwater for irrigation has become a serious threat to the sustainability of the cropping systems [10]. In these areas, irrigated agriculture should take into account that the increase of groundwater salinization inevitably triggers the risk of secondary soil salinization, with the consequent soil quality degradation [11], possible soil alkalization, osmotic imbalance, and specific ion toxicity. These conditions can severely affect crop growth and yield [12,13] and become even more stringent if considering that the Mediterranean climate is warming up and becoming increasingly arid [14,15]. Precipitation has begun to decrease in the long term, mainly in the dry season, with more frequent extreme heat and drought events [16].
In order to preserve agricultural soils and crop production potential, the application of management techniques able to reduce soil salinity or prevent the continuous accumulation of salts in the soil root layer is required [17]. Leaching, the movement of excess soluble salts from the upper to the lower soil depths or out of the root zone due to draining water, is the key operation to control salinity. Under semi-arid climate conditions, salt leaching could be also performed naturally by fall–winter rains, if their seasonal amount is satisfactory. However, rainfall alone is often insufficient to move salt downward through the soil profile. Therefore, the application of extra-irrigation water to promote salt leaching and maintain agricultural productivity has become a common practice [18,19,20,21,22,23,24,25].
Tomato is among the most important crops in the considered area and a significant agro-industrial sector of tomato processing was developed in the region [8,26,27], having a large economic impact. On the one hand, farmers are encouraged to grow processing tomato every year to increase their profits; on the other hand, the large application of usually saline irrigation water to fulfil the high tomato water requirements [10] represents an increasing risk of soil salinization. The higher the soil salinization, the lower the tomato yield and the consequent farmers’ profits. A proper trade-off between these two opposing trends should be identified and, for this purpose, an important feature to be detected is the climatic capability of fall–winter rains to leach out the salt in excess from the soil.
The aim of the present study was to evaluate, over a long simulation period, the probability of soil salinization due to irrigation use of saline groundwater in a coastal area close to the Mediterranean Sea. More specifically, the salinization risk assessment was intended to estimate two consecutive components:
- (i)
- the annual probability of soil salinization below a considered threshold at the start of the tomato spring–summer cropping season. This probability is inversely related to the total amount of rainfall that occurred in the previous fall–winter period, which acts in promoting salt leaching;
- (ii)
- the consequent damage to the tomato cultivation caused by soil salinization in terms of crop yield reduction with respect to the expected maximum yield.
A climatic analysis based on an existing dataset was performed over a long-term period (1975–2017), during which processing tomato was assumed to be regularly cultivated during every spring–summer season, as well as considering different salinity levels of applied irrigation water. From the combined effect of both annual rainfall and water salinities, different scenarios of soil salinization risk resulted. Moreover, a modified version of the Mass and Hoffman [28] model allowed us to estimate the relative decrease in tomato yield due to soil salinity.
These outcomes were obtained through the application of a spreadsheet simulation model, performing the water and the salt balance along a 0–800 mm soil profile. The model represents an easy-to-use and friendly tool, which can be ordinarily used by farmers in order to make decisions and address a correct cropping management, and by decision makers (such as irrigation district managers) to define proper land planning strategies in mitigating the soil salinity build-up.
Possible high levels of salinity risk should call for special management interventions, at both farm-size and catchment scale.
2. Materials and Methods
2.1. Reference Area
The simulation study was carried out with reference to an agricultural area in the Mediterranean basin, placed in the north-eastern part of the Apulia region (southern Italy), close to the Manfredonia gulf (Adriatic sea). This area is in the municipality of Margherita di Savoia (Figure 1), located in a large plain that represents a highly developed agricultural land in the Capitanata district. More specifically, the farming system of the area is mostly characterized by extensive and rainfed winter cereals such as durum wheat or, conversely, intensive and irrigated vegetable crops, such as processing tomato, depending on the availability of irrigation water. In the reference area, farmers commonly adopt drip irrigation method when horticultural crops are cultivated. Considering the geographical district of Capitanata, tomato crop covers a cultivation area of 17,000 ha [29] and accounts for 33% of the total national production [30]. Tomato is among the most representative crops in the area, characterized by high water requirements during the arid summer months. At district scale, fresh water delivered through huge irrigation infrastructures diverting water from artificial reservoirs can be used to satisfy these on-farm crop requirements. Unfortunately, these fresh water resources are not available in all the potential farming areas; therefore, groundwater resources pumped from private wells are largely exploited [30]. As a result of this massive water withdrawal, the level of the water table is progressively lowering and, by consequence, the hydraulic gradient near the coastline is reversed, thus causing seawater intrusion and groundwater salinization [31].
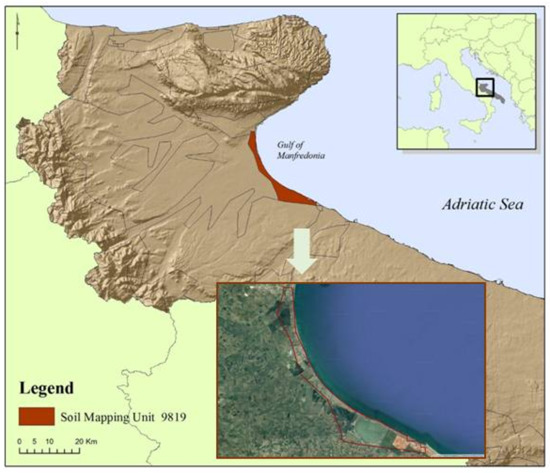
Figure 1.
Reference area, identified by the soil mapping unit N° 9819 of the Harmonized World Soil Database [32].
2.2. Dynamic of Aquifer and Soil Salinity in the Reference Area
The water electrical conductivity (ECw) in the aquifer usually increases nearing the coastline. Water salinity is usually higher as the distance from the sea is smaller, although the degree of seawater infiltration could be different from zone to zone along the same coastline, mostly because of the aquifer karst nature.
Under the conditions observed in the area, groundwater is placed at a depth of 25–30 m (depending on the season). During the wet season, in the fall–winter months, a recharge of groundwater occurs, with the consequent rising of the water table level, an increase of the hydrostatic pressure, and the resulting regression of the frontline between fresh and salt water towards the sea. During the dry summer months, the reverse process takes place and seawater is wedged inside the aquifer, progressing inwards. Considering these recursive seasonal pulses and their effects on the aquifer, the thickness of the fresh water layer superimposed to the salt water of marine origin will decrease and then increase, in pace with the rainfall regime. If this condition of hydrological equilibrium is altered, a drastic change in the relationship between fresh and salt water inevitably occurs. An intense and prolonged drought period, as well as intense groundwater pumping, lowers the level of the water table, at least locally, causing a progressive flow of saline water from the sea into the aquifer as a result of a new hydrostatic balance. The greater the depth reached by the well inside the aquifer below the sea level and the more intense the groundwater pumping, the more easily the well will be invaded by saline water. The aquifer salinity will also increase, now predominantly enriched in seawater. These kinds of overall dynamics have been represented in a flow chart (Figure 2) describing the complex and multi-factorial conditions that can alter or modify the level of soil salinity.
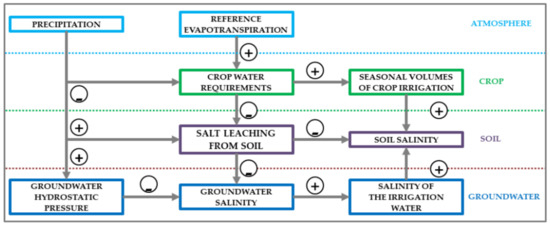
Figure 2.
Cause–effect relationships among the factors related to weather, crop, soil, and groundwater, affecting soil salinity. Precipitation always favours a decrease in soil salinity by reducing the irrigation supply, promoting soil salt leaching, and avoiding the seawater intrusion into groundwater. The plus and minus signs identify positive and negative correlations, respectively. The final effect of one certain factor on soil salinity is obtained by multiplying the signs along the path.
Earlier soil salinity monitoring in the reference area [10] showed that the aquifer salinity is generally quite low at the beginning of the irrigation season (in the first half of May), a very favorable condition with respect to the growth of crops. However, it increases along the season, even doubling its value by the middle of August. This seasonal oscillation in water salinity is usually correlated to the average annual salinity value; the higher the average, the higher this seasonal fluctuation. The time-course of water salinity used for tomato irrigation and pumped from the aquifer can be accounted for by a sine-wave curve. The sinusoid curve describes a smooth periodic oscillation; its mathematical formulation as follows:
where ECw is the electrical conductivity of irrigation water, ECwAV is the annual average value of the electrical conductivity of irrigation water, ΔECw is the amplitude of the curve (i.e., the upper and lower peak deviation of the sine-wave function from the avergage), Ph is the annual shifting phase (expressed in day-units over 365 days in a year), and T the time of the year (from 1 to 365).
ECw = ECwAV + ΔECw × Sin [(T − Ph)/365] (dS m−1)
According to the detected local conditions, Ph is equal to 130 DY (days from the beginning of the year), corresponding to 10 May. This means that the peak in water salinity is reached on 10 August, while the lowest value is achieved on 7 February.
2.3. Environmental Data
The weather data utilized in the simulation procedure were acquired from the Agri4Cast database [33]. This is part of the Crop Growth Monitoring System developed by the Joint Research Centre and contains meteorological data from weather stations interpolated on a 25 × 25 km grid, available on a daily basis starting from 1975. Maximum, average, and minimum air temperature (T, °C); precipitation (P, mm d−1); potential evaporation from a free water surface (E, mm d−1); potential evaporation from a moist bare soil surface (ES, mm d−1); and potential evapotranspiration from a reference crop canopy cover (ET0, mm d−1) were the acquired from weather data. The grid cell covering the reference area is identified as N° 60130 and data refer to a 43-year period, from 1 January 1975 to 31 December 2017. The reference area is characterized by a Mediterranean kind of climate. The monthly average of maximum air temperatures in the hottest month (31.13 °C, std err ± 0.26 °C) is reached in July, while the monthly average of minimum air temperatures in the coldest month (4.89 °C, std err ± 0.30 °C) is detected in February. The annual precipitation average is 458.5 mm (std err ± 18.37 mm) with a rather high coefficient of variation (26.27%), thus indicating a large interannual variability of rains. The largely erratic annual rain totals prevent the capture of a statistically significant climatic trend over the 43-year period, although a decreasing rate in the amount of rains (−1.22 mm y−1) was detected. A high correlation (r = 0.90**) was observed between the annual rain totals and the number of rainy days in the year (with p > 5 mm). The average number of rainy days were 25.54 per year (std err ± 1.14) with an average precipitation of 13.64 mm per rainy day (std err ± 0.30 mm). The number of rainy days contributes 87% of the annual rainfall, while the amounts of daily rainfall contribute only 13%. The main feature of the Mediterranean climate is the strong seasonality of precipitation and the marked aridity of the summer months. Figure 3 reports the monthly time-course of P and ET0 (Figure 3a) and De Martonne aridity index (AI) (Figure 3b). Strong aridity conditions (ET0 > 2P) are detected from the second half of March to the first half of September (Figure 3a); semi-arid conditions (10 < AI < 20) are detected in April, May, June, and September (Figure 3b); and stronger arid conditions (AI < 10) are observed in July and August (Figure 3b). The average annual value of AI is 17.32 (std err ± 0.73), which corresponds to semi-arid conditions on an annual basis. The total annual ET0 (Figure 3a) is 1147.35 mm (std err ± 11.24 mm), which, compared with the total annual rainfall, highlights a remarkable climatic water deficit (ET0—P) on annual basis equal to 688.85 mm (std err ± 25.13 mm). The highest monthly water cumulative deficit is observed in July (190.71 mm) and the second highest in June and August (155.34 and 155.91 mm, respectively). The highest water cumulative surplus is detected in November and December (27.15 and 29.83 mm, respectively).
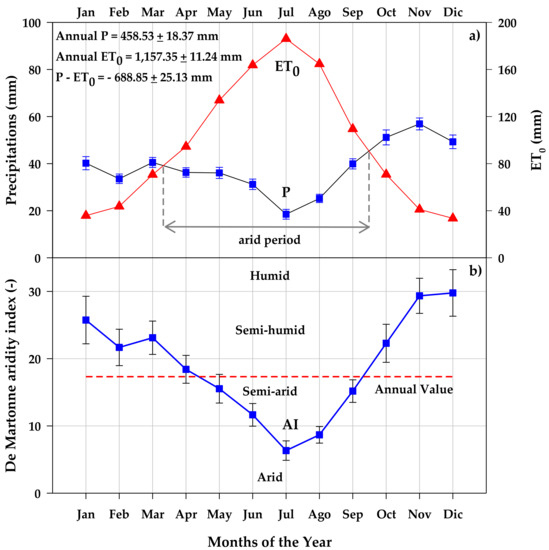
Figure 3.
Climatic characterization of the reference area. Monthly averages of long-term climatic data (1975–2017) are reported. (a) Reference evapotranspiration (ET0) and precipitation (P); (b) De Martonne aridity index (AI).
Data on soil characteristics utilized in the assessment procedure were acquired from the Harmonized World Soil Database (HWSD) [32], which is a raster database with over 15,000 different soil mapping units. HWSD provides information on the soil unit composition and standardized soil parameters for both topsoil and subsoil, for each soil mapping unit. The soil parameters considered in this study are those strictly related to the hydraulic soil properties, such as soil fractions of textural classes, including gravel (Ø > 2 mm); water content at soil saturation (WST); field capacity (WFC); and crop wilting point (WWP). Other relevant data about the soil hydrology are soil drainage condition, soil hydraulic conductivity, soil salinity, base saturation, and sodicity (sodium exchange percentage). The latter parameters are not directly used in the simulation, but should be considered very useful in order to define the soil characteristics and apply the consequent irrigation management. The main representative soil unit of the reference area is identified as N° 9819 (Figure 1). The dominant soil group is Fluvisol (FL) (young soils in alluvial deposits). The physico–chemical soil attributes obtained from the database are shown in Table 1.

Table 1.
Soil, water, and crop attributes utilized in the simulation.
2.4. Simulation Model of Water and Soil Salinity Balance
An easy-to-apply model of water and salinity balance was arranged, mostly based on a simplified functional approach (i.e., the numerical solution of the Richard’s equation is not implemented). The model works on a daily time step and uses rainfall (P) and reference evapotranspiration (ET0) as inputs (together with E and ES). Soil and crop characteristics, such as soil moisture parameters, crop root depth, and ET crop coefficients, are also required as inputs. The soil profile was divided into four consecutive layers (L1, L2, L3, and L4), with a depth of 200 mm each. Every soil layer forms a water reservoir, connected to the one placed immediately below. The soil water balance was based on the Ritchie’s concept of soil drainage upper and lower limit [34,35,36]. The upper water content corresponds to soil field capacity (water potential of −0.33 bar), while the lower water content corresponds to the wilting point (water potential of −15 bar). The approach is a simple water accounting procedure performed downward consecutively in each layer of the soil profile [37]. The water in the upper layer cascades to the lower ones, mimicking the process of a series of linear reservoirs. Internal drainage takes place if the water present in a soil layer exceeds its water holding capacity. The water drainage of the deepest layer is the drainage at the bottom of the soil profile (external drainage). A schematic representation of the model structure is reported in Figure 4.
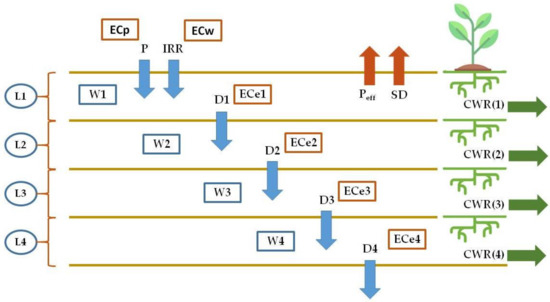
Figure 4.
Schematic representation of the water and salt balance model used to simulate the long-term scenarios of soil salinity risk. Wi = water content in the ith soil layer (with i = 1, 2, 3, and 4, respectively); ECe i = electrical conductivity of the soil saturated water extract in the ith soil layer (with i = 1, 2, 3, and 4, respectively); CWR = crop water requirement; ECp = electrical conductivity of precipitation; ECw = electrical conductivity of irrigation water; Peff = effective precipitation; SD = soil drying.
Some simplifying assumptions were the following. Water completely infiltrates through the soil surface and no run-off takes place (e.g., the soil is levelled out and its infiltration rate is not a constraint). In the case of rain or irrigation, in the first stage, the water wetting the soil surface can be directly evaporated (proportionally to the potential evaporation from a free water surface), while in the second stage (soon after the surface drying), the upper soil layer can be progressively dried out according to a negative exponential function over time [38]. The soil profile was assumed to not limit the drainage and to not interact with the groundwater placed far below (i.e., no capillary rise is allowed in the upper 800 mm of soil profile and only vertical downwards water fluxes are observed).
According to the matter conservation law, the water content of a given soil layer cannot increase without addition from the outside, nor can it diminish unless transported to deeper soil layer by drainage or lost by crop transpiration or by soil evaporation into the atmosphere [39]. In its simplest form, the water balance equation states that changes in soil volumetric water content over a period of time are equal to the difference between the amount of water added (WIN) and withdrawn (WOUT), respectively, during the same period.
ΔW = WIN − WOUT (mm d−1)
All the terms of the water balance are expressed in daily units of volume per unit area (e.g., mm d−1). Just considering the soil upper layer, the added amount of water is represented by precipitation (or better, the effective fraction of P, equal to PEFF) and irrigation (IRR), while water losses may be the result of drainage (D), soil evaporation (ES), soil drying (ED), and crop transpiration (T). Apart from the upper one, and considering the other soil layers placed below, water is supplied by drainage from above and is removed by the crop root system according to the corresponding transpiration rate (T) in that layer.
The maximum crop evapotranspiration rate (ETC) is determined by multiplying the reference crop evapotranspiration (ET0) by a crop coefficient (KC), according to the well-known FAO approach [40].
ETC = ET0 × KC (mm d−1)
The time course of KC along the tomato crop cycle was defined by a curvilinear equation based on specific coefficients: the initial KC value (KCin); the maximum KC value (KCmax); the inflection time FK; and the ascending and descending rates of the curve, G1 and G2, respectively, with t being the cropping day.
A logistic equation was applied in order to compute the progressive deepening of the tomato root system (H) along the soil profile, considering the starting and final root depth (Hin and Hmax, respectively), as well as the inflection time (FH) and the rate coefficient (G).
The values assigned to the empirical coefficients of Equations (4) and (5) are listed in Table 1.
The daily value of ETC represents the daily crop water requirements (CWR). Irrigation (IRR) is applied whenever the consumptive water depletion in each soil layer is greater than a predetermined fraction (α) of the total available water (WAV), defined as readily available water (WRA).
For the tomato crop, WRA is assumed equal to 40% of the WAV, that is, the soil water content between field capacity and wilting point. Considering each soil layer, the fraction of CWR currently uptaken and transpired by the crop is proportional to the root density along the soil profile.
In the course of the tomato cropping cycle, irrigation is performed every time the WRA is depleted by the cumulated daily values of CWR, net of the effective precipitation Peff that temporarily recharges the reservoir. In this way, the soil field capacity is restored. Amounts of water exceeding the soil field capacity produce a downward draining water flow in the soil layer placed below.
Let us define, with Z (g m−2), the amount of salts in the soil. Similar to the water balance, the salt balance assumes that if the quantity of salts in a defined soil layer at the start of a considered period (Z T−1) differs from the final value at the end of the same period (Z T), then we can write the following:
that is,
ΔZ = Z T − Z T−1 (g m−2)
Z T = Z T−1 + (ZIN − ZOUT) (g m−2)
The assumptions of this salt balance are that no salts are dissolved or conversely precipitated in the considered soil volume, while salts from agricultural inputs (fertilizers), or those absorbed by the crop, can be considered negligible.
We can regard the amount of salt in a soil layer as being dissolved in the circulating soil water according to a corresponding salt concentration C (g m−3). However, salts can only be moved along the soil profile through a water flow, either in or out of each layer; therefore,
Z T = Z T−1 + 10−3 × (WIN × CIN − WOUT × COUT) (g m−2)
Because the downward movements of water and salt generally take place at water contents near or just above field capacity, we can logically consider Z to be dissolved in an amount of water equal to WFC. Therefore, at field capacity, the salt concentration (CFC) of the water in the soil layer is as follows:
CFC = 103 × Z/WFC (g m−3)
If, in every considered layer, all the incoming water (WIN) is mixing thoroughly with the soil water, the salt concentration in the outgoing water (WOUT) percolating from the rootzone will be equal to the average salt concentration in the soil water at field capacity (i.e., COUT = ĈFC). In contrast, salt concentrations of the outgoing water can be computed, assuming leaching or salt mixing efficiencies (γ), to be assigned as input data (i.e., COUT = γ × ĈFC). This coefficient varies between 1 and 0 and the effect of a different leaching efficiency can be simulated by varying this critical input value through a calibration process followed by validation. If γ = 1 is imposed, complete mixing is assumed.
Considering a period in which Z changes from ZT−1 to ZT, according to van Hoorn and van Alphen [41], the average salt concentration ĈFC of the soil water at field capacity during that period is as follows:
or,
COUT = γ × ĈFC = γ × 103 × ½ (ZT−1 + ZT)/WFC (g m−3)
‘COUT = COUT/(γ × 103) = ½ (ZT−1 + ZT)/WFC (g m−3)
With reference to a generic soil layer (I), excluding the upper one (i.e., I > 1), it is possible to write the following:
WIN = D(I−1); WOUT = D(I); CIN = COUT (I−1); and COUT = COUT (I)
For I > 1, Equation (8) can be modified accordingly:
Z T = Z T−1 + γ × 10−3 × [ D(I−1) × ‘COUT (I−1) − D(I) × ‘COUT(I))] (g m−2)
For I = 1 (i.e., considering the upper soil layer), we have to remind that WIN × CIN = IRR × CIR + P × CP. Where CIR and CP are the salt concentrations of irrigation and rain water, respectively. Therefore, Equation (8) can be modified accordingly:
Z T = Z T−1 + γ × 10−3 × (IRR × CIR + P × CP − D(I) × ‘COUT(I)) (g m−2)
Equations (12)–(14) are the salt equations applied in the model. They can be used either to model salt storage due to irrigation and salt leaching due to rainfalls.
The value of Z can be converted and expressed in terms of electrical conductivity of the saturated soil-paste extract (ECe), keeping in mind the following relationships:
whereby
that is,
EC (dS m−1) = 1/640 C (g m−3)
ECe (dS m−1) = 0.5 × EC (dS m−1)
ECe (dS m−1) = 0.5 × (1/640) × CFC (g m−3)
ECe = 0.5 × (1/640) × 103 × Z/WFC (dS m−1)
A leaching fraction (λ) can be eventually applied at every irrigation. When λ > 0, the irrigation volume is increased by this fraction with respect to the volume needed to restore the soil field capacity in order to allow drainage and, therefore, salt leaching.
Finally, the relative reduction in the actual tomato yield compared with the potential yield (Yact/Ymax) as a consequence of the buildup of soil salinity due to saline irrigation water can be estimated by several salinity-dependent functions. The well-known linear model from Maas and Hoffman [28] can be rearranged into the van Genuchten and Hoffman [42] alternative S-shaped function, according to the following equation:
where ECe 50 is the soil salinity at which yield is reduced by 50 percent, and δ is an empirical, crop-dependent, and dimensionless parameter. For many crops, the value of δ was found to be about 3 when the S-shape function was applied to salinity stress data. Equation (19) was found to describe crop salt tolerance data equally well or even better than the Maas and Hoffman model [43]. This was applied to estimate the relative tomato yield reduction (Yact/Ymax) due to soil salinity (ECe), according to parameter values reported in Table 1. A weighted average of daily values was computed according to the fraction of water uptake by the crop root system at the three soil layers (L1, L2, and L3). This calculation started from the 60th day of the crop cycle, corresponding approximately with the beginning of flowering, followed by fruit setting and ripening, until fruit commercial maturity.
Yact/Ymax = 1/(ECe/ECe 50) δ (-)
The simulation model was set up as a spreadsheet; its validation passed through the calibration of the leaching efficiency coefficient (γ), followed by a testing procedure on an independent set of data. Data for calibration and validation were obtained from a previous experimental trial conducted on lysimeters with very similar soil characteristics [23]. For a deeper understanding of the validation procedure, the reader is referred to the annexed Supplementary Material (Figure S1).
2.5. Simulation Conditions and Scenarios of Salinity Risk
In order to assess the risk of soil salinization in the reference area, three increasing groundwater salinity conditions were assumed, accordingly to the values generally detected in the aquifer. These conditions are the following: S3 = 3, S4 = 4, and S5 = 5 dS m−1, considering the annual ECw average value (ECwAV); 0.5, 1.0, and 1.5 dS m−1, respectively, are the values assigned to the sine-wave amplitude (ΔECw).
Over the time-frame from 1975 to 2017, a fixed, annual, 120-day cultivation period of processing tomato (Solanum lycopersicum L.) cultivation was simulated over every spring–summer season, from 110 to 230 DY (i.e., from 2 May to 18 August).
During the tomato growing cycle, a leaching fraction λ = 15% was systematically applied as soon as salinity at soil saturation reached the salinity of irrigation water. Considering soil texture and its drainage conditions, a value of 15% was assumed as the maximum applicable leaching fraction.
Finally, as a consequence of the calibration and validation process, a leaching efficiency of γ = 80% was assigned and used in performing the model.
2.6. Procedure to Assess the Soil Salinization Risk
The quantitative risk assessment of soil salinization was intended to estimate two different components, that is, the occurrence probability of soil salinization and the consequent damage it can produce in terms of tomato yield reduction.
The selected 43-year reference period (1975–2017) should be considered a long enough period to perform a climatic analysis of soil salinity from data obtained by the simulated scenarios and to capture possible climatic trends. Frequency distribution analysis and probability charts were the analytical tools applied to investigate soil salinization.
A threshold salinity value corresponding to the start of tomato yield decrease was identified and the probabilistic exceeding occurrence at the very beginning of the cultivation cycle was determined under the three different scenarios of irrigation water quality (S3, S4, and S5, respectively).
3. Results
3.1. Climatic and Irrigation Trends
With respect to the 43-year period of climatic analysis, the time trend of both reference evapotranspiration (ET0) and crop water requirements (CRW) was shown to be statistically significant (p < 0.01) and an annual increase rate of 3.76 and 2.57 mm y−1, respectively, was detected (Figure 5).
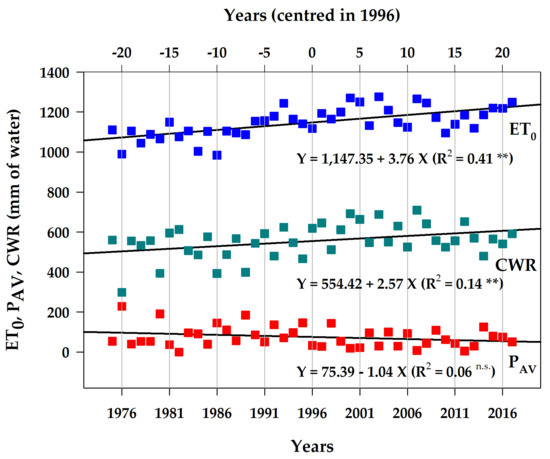
Figure 5.
Time trends of reference evapotranspiration (ET0), available precipitation (PAV), and crop water requirement (CWR) determined over a 43-year period (from 1975 to 2017). Annual data are related to the tomato crop cycle (from 110° to 230° days of each year).
Conversely, the annual amount of rainfall occurring along the tomato crop cycle showed a decreasing time trend (−1.04 mm y−1), although not statistically significant (p < 0.10). Considering that the predicted seasonal irrigation volume was 554.42 mm in 1996, and became 605.82 mm twenty years later, in 2016, the predicted value for the next twenty-year period is 657.23 mm (i.e., increase of 51.40 mm every 20 years). Indeed, the double effect of an increase in the climatic evaporation request (water losses) and, in the same period, the reduction of precipitation (water gains), clearly determined a relevant water imbalance in tomato cultivation and a consequent increase in the climatic estimate of the seasonal irrigation volume. If the irrigation water shows a high salinity level, it follows that the risk of soil salinization is largely increased by increasing the irrigation volume (Figure 2).
3.2. Time-Course of Soil Salinity
In general, the soil salinity dynamics closely reflect the considerable addition of salts by irrigation during the tomato-growing season (Figure 6). Salinity starts to increase on the eleventh ten-day period of the year (TDP), and reaches the maximum value on the twenty-third TDP, at the time of tomato transplanting and harvesting, respectively. A two-TDY lag-time is observed in the salinity build-up, proceeding from one soil layer to the lower one; irrigation water gradually moves the salts downwards, and very soon, the amount of salts in the deeper soil layers becomes much higher than that in the upper one. While the first soil layer is strongly leached by irrigation water, transferring the salts downwards, the second and the third soil layers are not, and their salinity level sharply increases (Figure 6).
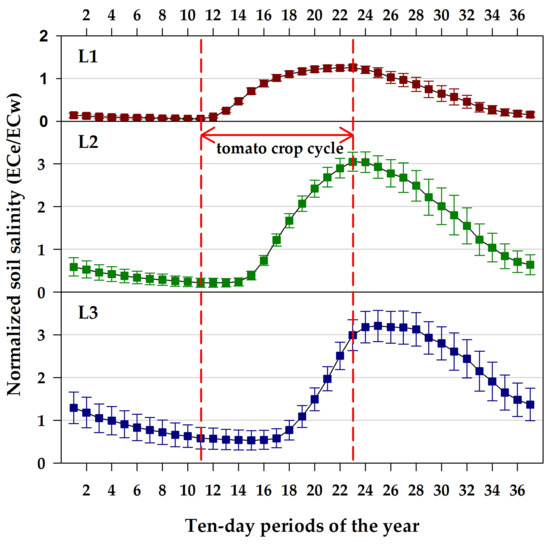
Figure 6.
Temporal dynamics of soil salinity considering three consecutive soil layers (L1: 0–200; L2: 200–400; L3: 400–600 mm of depth). The annual time scale is expressed in ten-day units (36.5 per year). The salinity values are normalized with respect to the average salinity level of the irrigation water (ECw). The vertical bars represent the standard deviation of the estimates obtained by 43 annual runs of the hydro-saline simulation model.
The highest soil salinity levels are strongly affected by the quality of irrigation water; 3.46, 8.50, and 9.80 dS m−1 are the soil salinity estimates for S3 at the three L1, L2, and L3 soil layers, respectively; 4.88, 11.87, and 12.57 dS m−1 for S4; and 6.30, 15.24, and 16.05 dS m−1 for S5. These values are represented in normalized units in Figure 6 with respect to the average salinity level of the irrigation water (i.e., the normalized values for S5 are determined by dividing the soil ECe by the ECw value of 5 dS m−1, and in the same way for S3 and S4).
Soon after tomato harvesting, soil salinity starts to decrease due to rainfalls, mostly occurring in the autumn season (Figure 6). Salinity reduction also proceeds in the following winter period, until springtime in the subsequent year. The higher the rainfalls, the higher the chance to move salinity along the soil profile and, possibly, far below the deepest soil layer. The variability of soil salinity estimates in the fall–winter period is larger as compared with the variability observed during the summer cropping cycle; this is the result of the erratic nature of rainfalls. Conversely, irrigations are systematic and regularly performed, therefore, the consequent soil salinity estimates are much less variable. The variability of these estimates also greatly increases along the soil profile, from the upper to the deeper soil layers, again considering that abundant rainfalls are less likely to occur than lighter ones and that the former may produce a deeper leaching than the latter (Figure 6).
Steady state conditions were imposed in the simulation, in order to set a general salinity balance over the entire long period considered in the analysis. These conditions have been established through consecutive simulation runs, being the salinity estimates at the end of the period used repeatedly as initial values of the subsequent simulation, until stabilization of the long-term salinity estimates at each soil depth was achieved. Under these conditions, the annual average amount of the incoming salinity load (ZIN), due to irrigation, was exactly equal to the average amount of salts moving downwards (ZOUT), at each soil depth, and carried away by drainage along the soil profile.
The annual salinity load was, on average, 1293.48 in S3, 1806.44 in S4, and 2319.50 in S5 g m−2 (std dev of ±121.21, ±170.32, and ±219.45 g m−2, respectively). As can be observed from Table 2, the annual average of soil salinity increases with the increasing salinity level of the irrigation water applied, as well as with the soil depth.

Table 2.
Estimates of the average annual values of soil salinity under the effect of the three irrigation water salinities (S3 = 3, S4 = 4, and S5 = 5 dS m−1) and along the four considered soil layers.
In contrast to the general observation, the L4 soil layer showed an average salinity estimate lower than L3, thus indicating that, over the year, leaching is not sufficient to move the accumulated salts away from L3, in L4, or further below. As was clear already from Figure 6, it can be argued that critical conditions are observed mostly in L2 and L3. Indeed, both rainfalls and irrigation water easily leach away salts from L1, while in L4, summer irrigation does not affect its salinity level, although a salt build-up is usually observed in autumn (and not in summer) due to the salt load coming from the upper soil layers leached by rainfalls.
3.3. Distribution of Precipitation in the Fallow Period and Salt Leaching Capacity by Rainfall
The fallow period is the fraction of time the soil is left bare, without any kind of cultivation. In our case study, this period lasts from tomato harvesting (day 230 of year Y) to tomato transplanting in the following year (day 110 of year Y + 1). The average total precipitation detected in this period was equal to 350.55 mm (std dev = 116.87 mm) and the probability distribution of this statistic is represented very well by a “log-normal” density function (Figure 7a). In response to a largely variable annual precipitation height, soil salinity at the start of the tomato growing season (DY 110) is greatly uneven, although quite predictable according to a probabilistic analysis shown in Figure 7. Like in Figure 6, soil salinity is expressed in normalized units; this data conversion allowed for representing a single curve for all possible salinity levels of irrigation water (Figure 7b). This means that the salinity level of irrigation water (S3, S4, and S5) largely affected the maximum salt content of soil layers in the absence of leaching, while salt leaching was totally controlled by rainfalls occurring in the fallow period, according to the observed climatic variability. No kind of interaction occurred between the two factors (i.e., water salinity and rainfall amounts). Conversely, different distribution curves represent the three consecutive soil layers (L1, L2, and L3); soil salinity at the start of the tomato-growing season and without leaching by rainfalls is much lower in L1 and is increasingly higher in L2 and L3. The distribution function is markedly a sigmoid curve, well described by a three-parameter “logistic” equation (M: maximum value, R: decreasing rate, and F: inflection point). Apart from the value of M, the other function parameters (R and F, respectively) have the same statistical values for all the soil layers (L1, L2, and L3), thus offering to consider exactly the same shape and dynamic behavior with respect to rainfalls. For each soil layer, a double-curve is shown in Figure 7b, representing 95% of all possible model outcomes included in it. From Figure 7, it is possible to detect that as the amount of rainfall increases, the initial level of soil salinity also decreases. Moreover, the estimated values at the three soil depths gradually approach one another, until they merge. Again, similar to Figure 6, it is worth noting that the double-curve is much larger in L3 and much smaller in L1; indeed, estimates related to deeper soil layers are much more uncertain and variable than estimates concerning upper soil layers.
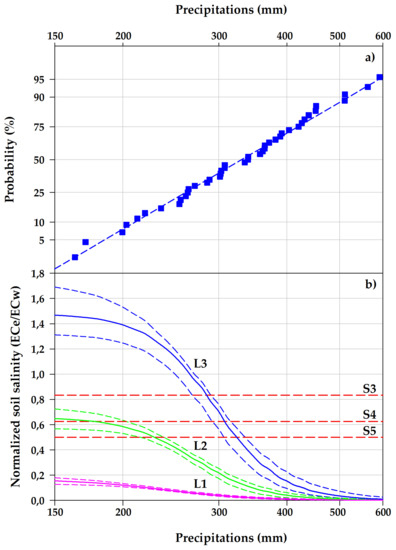
Figure 7.
(a) Log-normal probability distribution of rainfalls detected in the fallow period (time lapse between two consecutive tomato cropping cycles) over the 43-year period of reference. (b) Consequent soil salinity (ECe) distribution at the start of the tomato-growing season (DY 110), expressed in normalized values with respect to the average salinity level of the irrigation water (ECw) and considering the three consecutive soil layers (L1, L2, and L3). Horizontal lines represent the threshold salinity values (corresponding to ECe = 2.5 d m−1) for S3, S4, and S5, respectively. Salinity values above the threshold reduce the potential yield of tomato cultivation.
According to the salinity model proposed by Mass and Hoffman [28], a damage threshold of soil ECe equal to 2.5 dS m−1 should be considered as the salinity level at which tomato yield starts decreasing. If this salinity level is observed since the beginning of the tomato cropping period, there is no reason at all to cultivate this relevant cash crop, considering the very limited yield due to salinity damage. Figure 7b shows this threshold value (ECe = 2.5 dS m−1) considering the three quality levels of irrigation water (S3, S4, and S5, respectively). Soil salinity in L1 is always below the threshold, irrespective of the considered water quality. In contrast, soil salinity in L2 is always below threshold S3, but above the S4 and S5 thresholds with a 10 and 20% expected probability, respectively. In other words, we can say that soil salinity in 1 year out of 10 is totally unsuited to tomato cultivation already at the start of the tomato growing cycle, considering an irrigation water of ECi = 4 dS m−1; similarly, soil salinity in 2 years out of 10 is totally unsuited to tomato cultivation, considering an irrigation water of ECi = 5 dS m−1. Finally, concerning L3, even the best S3 water quality is frequently unsuited for tomato cultivation; indeed, there is approximately 25% probability that soil salinity in L3 is above the damage threshold for the S3 water quality, while it is 40–50% for S4 and S5.
3.4. Simulated Decrease of Tomato Yields Due to Water Salinity
Tomato yield reduction was not significantly altered by the starting level of soil salinity at the beginning of the tomato growing cycle; the total amount of water delivered to the crop and the level of salinity of the irrigation water applied were the only relevant factors that affected the yield penalty.
Assuming that irrigation is routinely and constantly operated by applying the S3 water quality, the consequent tomato yield was reduced to 48.84% (std dev = 3.62%). On condition that S4 water is constantly applied, the yield reduction reached 40.66% (std dev = 5.05%). Finally, when S5 water is used in tomato irrigation, the resulting yield reduction further decreased to 33.00% (std dev = 5.83%).
Applying the simulation model, it is possible to detect that irrigation salinity must remain below the ECi value of 1 dS m−1 in order to avoid that soil salinity exceeds the ECe damage threshold of 2.5 dS m−1. The actual operating conditions of S3, S4, and S5 (currently observed in some places of the considered area) are thus very far from an acceptable level of sustainable agriculture.
4. Discussion
Considering the climatic trend, it was observed that both reference evapotranspiration and crop water requirements showed significant annual increase rates, while annual rainfalls along the tomato crop cycle revealed a decreasing rate over time, although not statistically significant. In this respect, it is possible to suggest that the risk of soil salinization is getting higher. This is because of the possible display of a double effect. On the one hand, larger water volumes are withdrawn from the aquifer in order to meet the increasing crop water requirements and, therefore, higher amounts of salts are progressively brought into the soil through irrigation. On the other hand, groundwater salinity and, consequently, salinity of irrigation water are also getting higher as a result of seawater intrusion along the coastline. For this reason, three possible water salinity levels were considered in the analysis.
Meanwhile, the long-term observed fall–winter rains are also decreasing, although this value was not statistically relevant, thus reducing their capability to operate salt leaching from the cultivated soil.
Soil salinity under steady state conditions was largely influenced by the salinity level of the irrigation water applied along the tomato cropping cycle, and only secondarily was it affected by the amount of autumn–winter rainfalls occurring during the fallow period. These rainfalls are the main factors influencing the soil salinity at the beginning of the tomato cultivation; the more abundant are these rains, the lower the soil salinity, according to a well-defined and fully detected probability chart.
The first soil layer was usually well leached, while salt accumulation is particularly relevant in the second and third soil layers, up to a level seriously hampering crop growth and productivity. The total amounts of autumn–winter rainfalls are unable to operate a sufficient salt leaching from the second and third soil layers. The associated probability was indeed quite high. This probability sharply increases with the increasing salinity level of irrigation water.
Because of irrigation with saline water, potential tomato yield is severely affected and, at worst, totally compromised since the beginning of the summer cropping cycle, according to the unpredictable amounts of the autumn–winter rainfalls. Estimated yield reduction is in the range 30–50%. Under the assumed ECw values of irrigation water (S3, S4, and S5), tomato cultivation was clearly unsustainable. Of course, these critical conditions will only worsen if the contribution of rainwater in autumn and winter will tend to decrease and, conversely, if the irrigation volumes required by summer crops will continue to increase (Figure 2).
When high saline water is the only water available for irrigation, extra efforts should be applied in order to control the salt build-up in the soil and special techniques should be routinely introduced in mitigating the salinity effects on plant growth and productivity.
Apart from intentional leaching operated in the course of the cultivation cycle, and often proven to be rather ineffective [44], the double cropping strategy to be applied is the following:
- (a)
- considerably reduce the total amount of salts brought into the soil with irrigation; this means reducing the total amount of irrigation water and applying water with a lower salt concentration;
- (b)
- make the most of the amount of fresh water (i.e., rainfall) in benefitting the soil through salt leaching.
The first strategy (a) can be performed by shifting the cultivation of horticultural crops from the summer to the autumn–winter period. In the case of tomato cultivation showing a very high risk of soil salinization, the only chance is to focus on alternative horticultural species that can be cultivated later on, in autumn and winter (such as spinach, broccoli, lettuce, chicory, etc.). The advantage is that the crop water requirement is significantly lower (due to a lower ET0), while the rain contribution is significantly higher [10]. Both factors contribute to reducing the seasonal irrigation volumes. Moreover, the ECw values observed in autumn and winter are much lower than in spring or summer. This also contributes to decreasing the total yearly amount of salts brought into the soil with irrigation. An even more radical solution would be to cultivate wheat under totally rainfed conditions or, at least, with only supplemental irrigations. In this case, a rainfed cultivation does not involve any salt addition to the soil.
Concerning the second strategy (b), it should be accomplished when tomato is still considered an irreplaceable cultivation. A close succession of an irrigated summer crop and a rainfed crop could be applied [22]. In this way, the leaching effect of winter rainfall could be better exploited. Under these conditions, tomato cultivation must be performed not every year, but in alternate years (i.e., one over two), thus allowing that the total amount of precipitation able to operate salt leaching is roughly doubled and favoring the removal of excess salts from the active soil [10,23].
5. Conclusions
Climatic trends, together with cropping management strategies and operations, are factors seriously affecting soil salinity, triggering positive feedback processes towards a worsening of agricultural sustainability conditions practiced along the coastal irrigated areas of southern Italy.
Intensification of the cropping systems, the greater incidence of summer horticultural crops compared with winter ones, the relevant increase in seasonal irrigation requirements, and the quality deterioration of irrigation water withdrawn from the aquifer are “tesserae” of a worrying picture leading to intolerable levels of soil salinity. At catchment scale, this complex picture must be promptly addressed, through salinity monitoring, detailed land risk assessment of salinization, a more strict and severe regulation of groundwater use for irrigation purposes, innovative agricultural management criteria aimed at the reduction of the total salt load carried into the soil with irrigation, and an increased efficiency in the application of salt leaching.
This work, having defined the overall operating framework and having proposed a set of salinity management strategies, together with some specific interventions, should be considered as a step forward along the recovery path, needed for a more sustainable agricultural production.
Supplementary Materials
The following are available online at http://www.mdpi.com/2073-4441/10/11/1503/s1, Figure S1. Graphical representation of the simulation performance of the model prepared and used in this work. The model was applied to an experimental lysimetric data set reproducing a leaching process carried out through the daily application of 20 mm of water during 15 consecutive days (300 mm of water in totale were applied). (A) Soil salinity in the course of the leaching process considering a low-salinized soil. (B) Soil salinity in the course of the leaching process considering a high-salinized soil. (C) Predicted vs. observed ECe values to judge the performance of the simulation model.
Author Contributions
A.L., M.M., and A.R.B.C. conceived the research idea. M.M. designed the methodology. A.R.B.C. collected and prepared the data set. M.M. performed data processing. All authors equally contributed to the interpretations of the results, their discussion, and conclusions. A.L. and M.M. wrote the first manuscript. All the authors amended and revised the manuscript and approved the final version.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bless, A.E.; Colin, F.; Crabit, A.; Devaux, N.; Philippon, O.; Follain, S. Landscape evolution and agricultural land salinization in coastal area: A conceptual model. Sci. Total Environ. 2018, 625, 647–656. [Google Scholar] [CrossRef] [PubMed]
- Rengasamy, P. World salinization with emphasis on Australia. J. Exp. Bot. 2006, 57, 1017–1023. [Google Scholar] [CrossRef] [PubMed]
- Tóth, G.; Montanarella, L.; Rusco, E. (Eds.) Threats to Soil Quality in Europe EUR 23438—Scientific and Technical Research Series; Office for Official Publications of the European Communities: Luxembourg, 2008; pp. 61–74. [Google Scholar]
- Nachshon, U. Cropland Soil Salinization and Associated Hydrology: Trends, Processes and Examples. Water 2018, 10, 1030. [Google Scholar] [CrossRef]
- Joint Research Centre (JRC). The State of Soil in Europe; JRC Reference Reports; European Environment Agency, European Union, Publications Office of the European Union: Luxembourg, 2012; p. 71. [Google Scholar]
- Daliakopoulos, I.N.; Tsanis, I.K.; Koutroulis, A.; Kourgialas, N.N.; Varouchakis, A.E.; Karatzas, G.P.; Ritsema, C.J. The threat of soil salinity: A European scale review. Sci. Total Environ. 2016, 573, 727–739. [Google Scholar] [CrossRef] [PubMed]
- European Environment Agency (EEA). Europe’s Environment, the Third Assessment; Environmental Assessment Report No. 10; Office for Official Publications of the European Communities: Luxembourg, 2003; p. 341. [Google Scholar]
- Libutti, A.; Gatta, G.; Gagliardi, A.; Vergine, P.; Pollice, A.; Beneduce, L.; Disciglio, G.; Tarantino, E. Agro-industrial wastewater reuse for irrigation of a vegetable crop succession under Mediterranean conditions. Agric. Water Manag. 2018, 196, 1–14. [Google Scholar] [CrossRef]
- Xiloyannis, C.; Montanaro, G.; Sofo, A. Water emergency. Proposal in order to contain drought damages in fruit crops [Apulia—Basilicata]. Frutticoltura 2002, 7–8, 19–27. (In Italian) [Google Scholar]
- Libutti, A.; Monteleone, M. Irrigation management in Mediterranean salt affected agriculture: How leaching operates. Ital. J. Agron. 2012, 7, e5. [Google Scholar] [CrossRef]
- Perez-Sirvent, C.; Martınez-Sanchez, M.J.; Vidal, J.; Sanchez, A. The role of low-quality irrigation water in the desertification of semi-arid zones in Murcia, SE Spain. Geoderma 2003, 113, 109–125. [Google Scholar] [CrossRef]
- Bahri, H.; Annabi, M.; Houot, S.; Bougzala, M.; Latiri, K. Effet du type des résidus de cultures et de la salinité de l’eau sur la minéralisation du carbone organique dans un sol cultivé. Annales de L’inrgref 2010, 14, 117–124. [Google Scholar]
- Chaganti, V.N.; Crohn, D.M.; Simunek, J. Leaching and reclamation of a biochar and compost amended saline-sodic soil with moderate SAR reclaimed water. Agric. Water Manag. 2015, 255–265. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I.; Sabate, S.; Gracia, C. Natural systems: Terrestrial ecosystems. In Report on Climate Change in Catalonia; Llebot, J.E., Ed.; Institut d’estudis Catalans: Barcelona, Spain, 2005; pp. 517–553. [Google Scholar]
- IPCC. Summary for Policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Eds.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Penuelas, J.; Sardans, J.; Estiarte, M.; Ogaya, R.; Carnicer, J.; Coll, M.; Barbeta, A.; RivasUbach, A.; Llusià, J.; Garbulsky, M.; et al. Evidence of current impact of climate change on life: A walk from genes to the biosphere. Glob. Chang. Biol. 2013, 19, 2303–2338. [Google Scholar] [CrossRef] [PubMed]
- Díaz, F.J.; Grattan, S.R.; Reyes, J.A.; de la Roza-Delgado, B.; Benes, S.E.; Jiménez, C.; Dorta, M.; Tejedor, M. Using saline soil and marginal quality water to produce alfalfa in arid climates. Agric. Water Manag. 2018, 199, 11–21. [Google Scholar] [CrossRef]
- Abrol, I.P.; Yadav, J.S.P.; Massoud, F.I. Salt-Affected Soils and Their Management. FAO Soils Bulletin No. 39; Soil Resources Management and Conservation Service, FAO Land and Water Development Division; Food and Agriculture Organization of the United Nations: Rome, Italy, 1988. [Google Scholar]
- Ayers, R.S.; Westcot, D.W. Water Quality for Agriculture; FAO Irrigation and Drainage Paper No. 29 Rev. 1; Food and Agriculture Organization of the United Nations: Rome, Italy, 1994. [Google Scholar]
- Barnard, J.H.; van Rensburg, L.D.; Bennie, A.T.P. Leaching irrigated saline sandy to sandy loam apedal soils with water of a constant salinity. Irrig. Sci. 2010, 28, 191–201. [Google Scholar] [CrossRef]
- Corwin, D.L.; Rhoades, D.J.; Simunek, J. Leaching requirement for soil salinity control: Steady-state versus transient models. Agric. Water Manag. 2007, 90, 165–180. [Google Scholar] [CrossRef]
- Letey, J.; Hoffman, G.J.; Hopmans, J.W.; Grattan, S.R.; Suarez, D.; Corwin, D.L.; Oster, J.D.; Wu, L.; Amrhein, C. Evaluation of soil salinity leaching requirement guidelines. Agric. Water Manag. 2011, 98, 502–506. [Google Scholar] [CrossRef]
- Monteleone, M.; Libutti, A. Salt leaching due to rain in Mediterranean climate: Is it enough? Ital. J. Agron. 2012, 7, e6. [Google Scholar] [CrossRef]
- Moreno, F.; Cabera, F.; Andreu, L.; Vaz, R.; Martinaranda, J.; Vachaud, G. Water movement and salt leaching in drained and irrigated marsh soils of southwest Spain. Agric. Water Manag. 1995, 27, 25–44. [Google Scholar] [CrossRef]
- Qadir, M.; Ghafoor, A.; Murtaza, G. Amelioration strategies for saline soils: A review. Land Degrad. Dev. 2000, 11, 501–521. [Google Scholar] [CrossRef]
- Gatta, G.; Libutti, A.; Gagliardi, A.; Beneduce, L.; Brusetti, L.; Borrusso, L.; Disciglio, G.; Tarantino, E. Treated agro-industrial wastewater irrigation of tomato crop: Effects on qualitative/quantitative characteristics of production and microbiological properties of the soil. Agric. Water Manag. 2015, 149, 33–43. [Google Scholar] [CrossRef]
- Vergine, P.; Salerno, C.; Libutti, A.; Beneduce, L.; Gatta, G.; Gerardi, G.; Pollice, A. Closing the water cycle in the agro-i ndustrial sector by reusing treated wastewater for irrigation. J. Clean. Prod. 2017, 164, 587–596. [Google Scholar] [CrossRef]
- Maas, E.V.; Hoffman, G.J. Crop salt tolerance-current assessment. J. Irrig. Drain. Div. 1977, 103, 115–134. [Google Scholar]
- ISTAT. Electronic Information System on Agriculture and Livestock; Italian National Statistical Institute (ISTAT): Rome, Italy. Available online: http://agri.istat.it/ (accessed on 14 May 2018).
- Zingaro, D.; Portoghese, I.; Giannoccaro, G. Modelling crop pattern changes and water resources exploitation: A case study. Water 2017, 9, 685. [Google Scholar] [CrossRef]
- Mahlknecht, J.; Merchán, D.; Rosner, M.; Meixner, A.; Ledesma-Ruiz, R. Assessing seawater intrusion in an arid coastal aquifer under high anthropogenic influence using major constituents, Sr and B isotopes in groundwater. Sci. Total Environ. 2017, 587–588, 282–295. [Google Scholar] [CrossRef] [PubMed]
- HWSD Harmonized World Soil Database v. 1.2. Available online: http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/harmonized-world-soil-database-v12/it/ (accessed on 24 May 2018).
- AGRI4CAST Interpolated Meteorological Data. Available online: http://mars.jrc.ec.europa.eu/mars/About-us/AGRI4CAST/Data-distribution/AGRI4CAST-Interpolated-Meteorological-Data (accessed on 21 May 2018).
- Ritchie, J.T. A model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- Ritchie, J.T. Water dynamics in the soil-plant-atmosphere. Plants Soil 1981, 58, 81–96. [Google Scholar] [CrossRef]
- Ritchie, J.T. Soil water availability. Plants Soil 1981, 58, 327–338. [Google Scholar] [CrossRef]
- Ritchie, J.T.; Singh, U.; Godwin, D.C.; Bowen, W.T. Cereal growth, development and yield. In Understanding Options of Agricultural Production; Tsuji, G.Y., Hoogenboom, G., Thornton, P.K., Eds.; Kluwer Academic Publishers and International Consortium for Agricultural Systems Applications: Dordrecht, The Netherlands, 1998; pp. 79–98. [Google Scholar]
- Loomis, R.S.; Connor, D.J. Crop Ecology: Productivity and Management in Agricultural Systems; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Hillel, D. Soil and Water, Physical Principles and Processes; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage, Paper No. 56; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998. [Google Scholar]
- Van Hoorn, J.W.; van Alphen, J.G. Salinity control. In Drainage Principles and Applications; Ritzema, H.P., Ed.; Int. Inst. of Land Reclamation (ILRI): Wageningen, The Netherlands, 1994; pp. 553–600. [Google Scholar]
- Van Genuchten, M.T.; Hoffman, G.J. Analysis of crop salt tolerance data. In Soil Salinity under Irrigation-Process and Management; Ecological Studies 51; Shainberg, I., Shalhevet, J., Eds.; Springer: New York, NY, USA, 1984; pp. 258–271. [Google Scholar]
- Van Genuchten, M.T.; Gupta, S.K. A reassessment of the crop tolerance response function. J. Indian Soc. Soil Sci. 1993, 41, 730–737. [Google Scholar]
- Libutti, A.; Monteleone, M. Soil vs. groundwater: The quality dilemma. Managing nitrogen leaching and salinity control under irrigated agriculture in Mediterranean conditions. Agric. Water Manag. 2017, 186, 40–50. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).