Irradiance Variability Quantification and Small-Scale Averaging in Space and Time: A Short Review
Abstract
1. Introduction
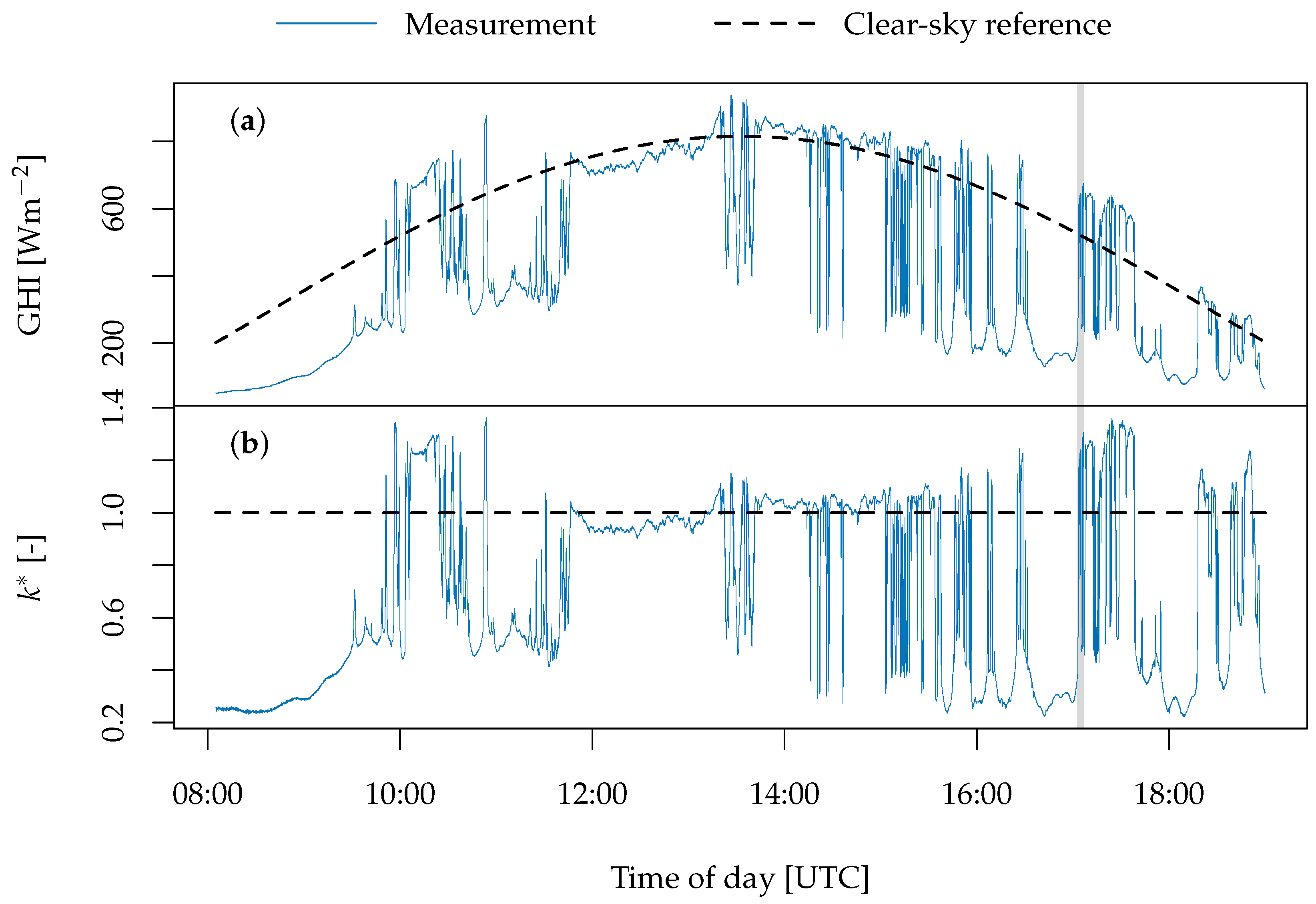
2. Irradiance Normalization and Time-Scale-Specific Changes
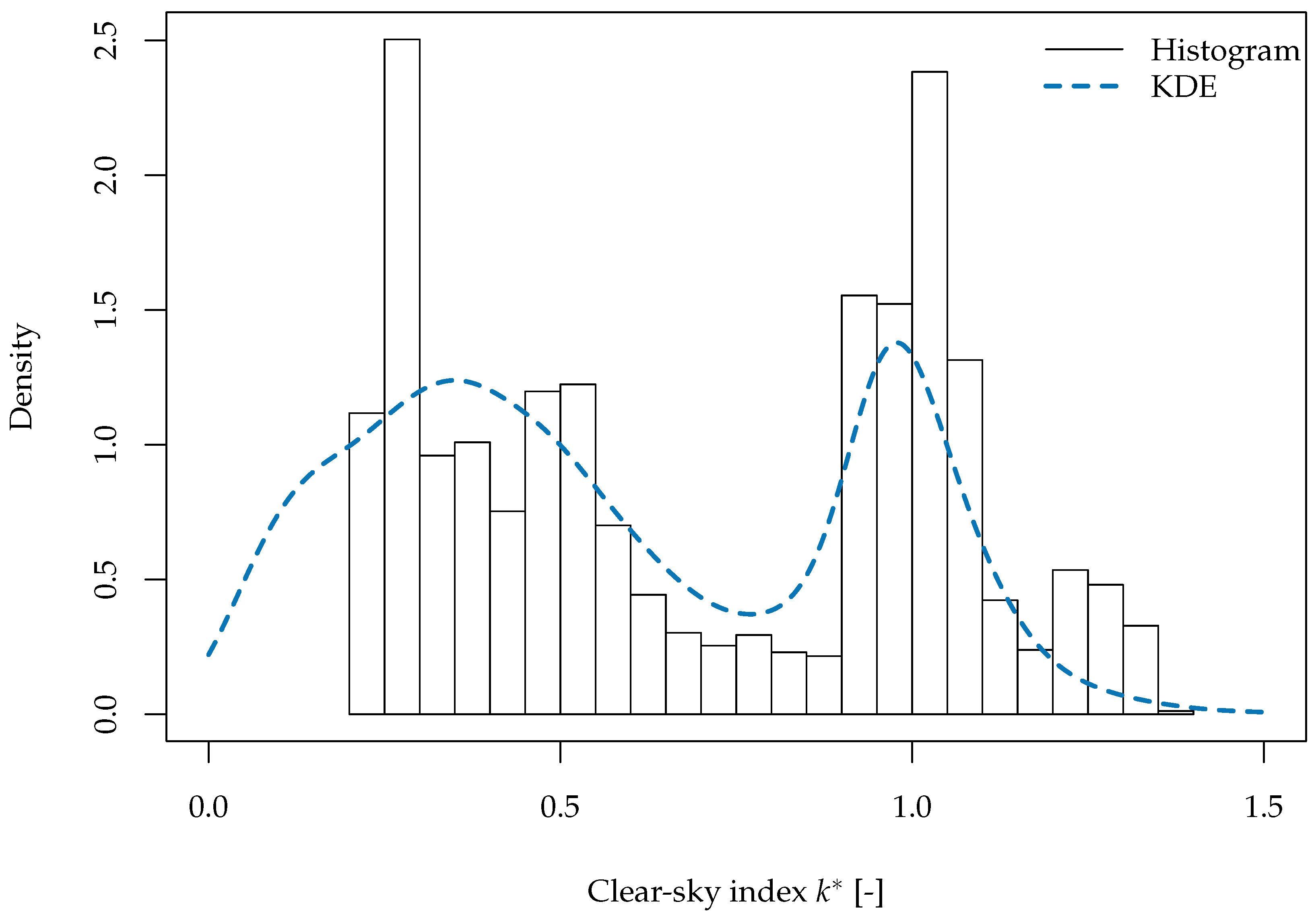
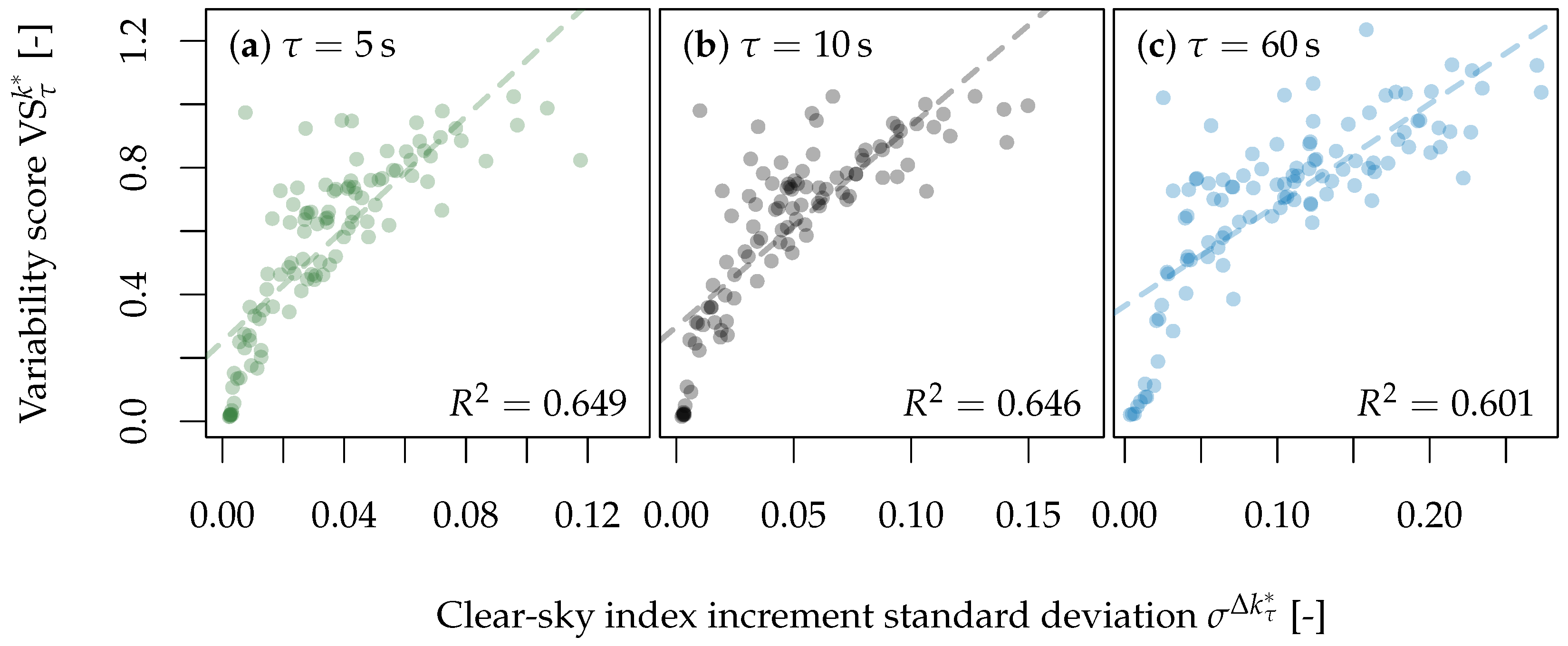
3. Variability Quantification
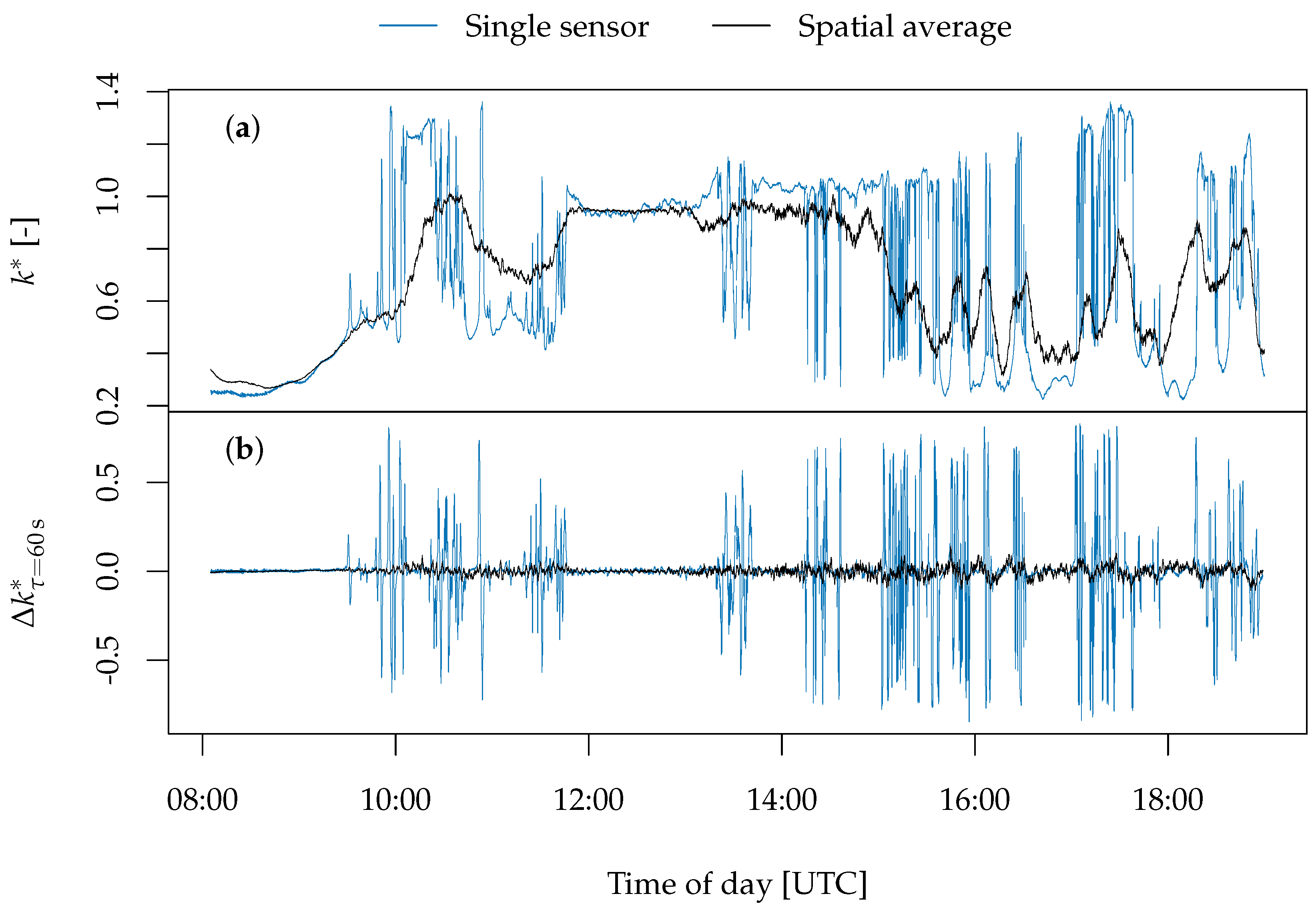
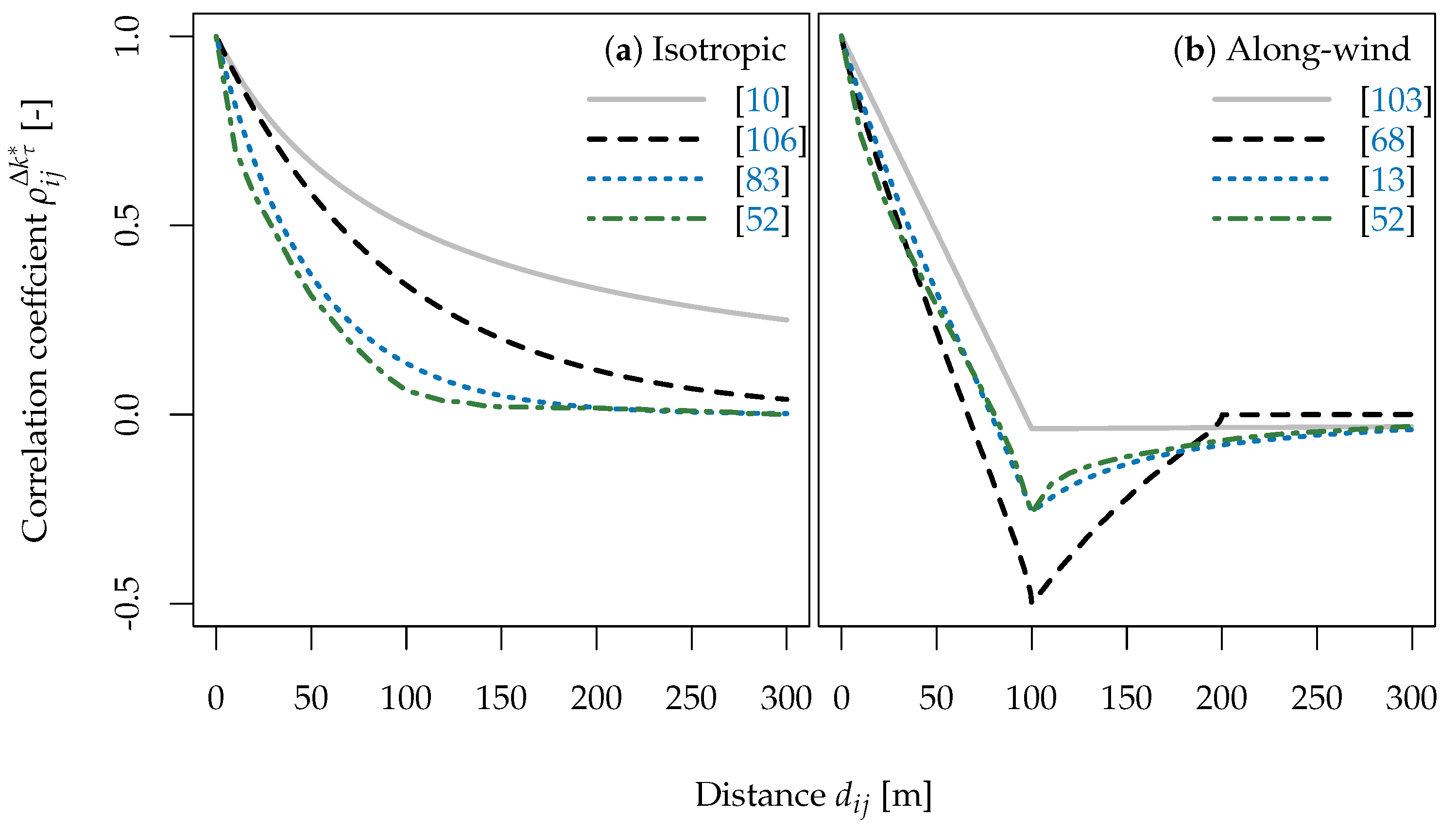
4. Spatial Averaging
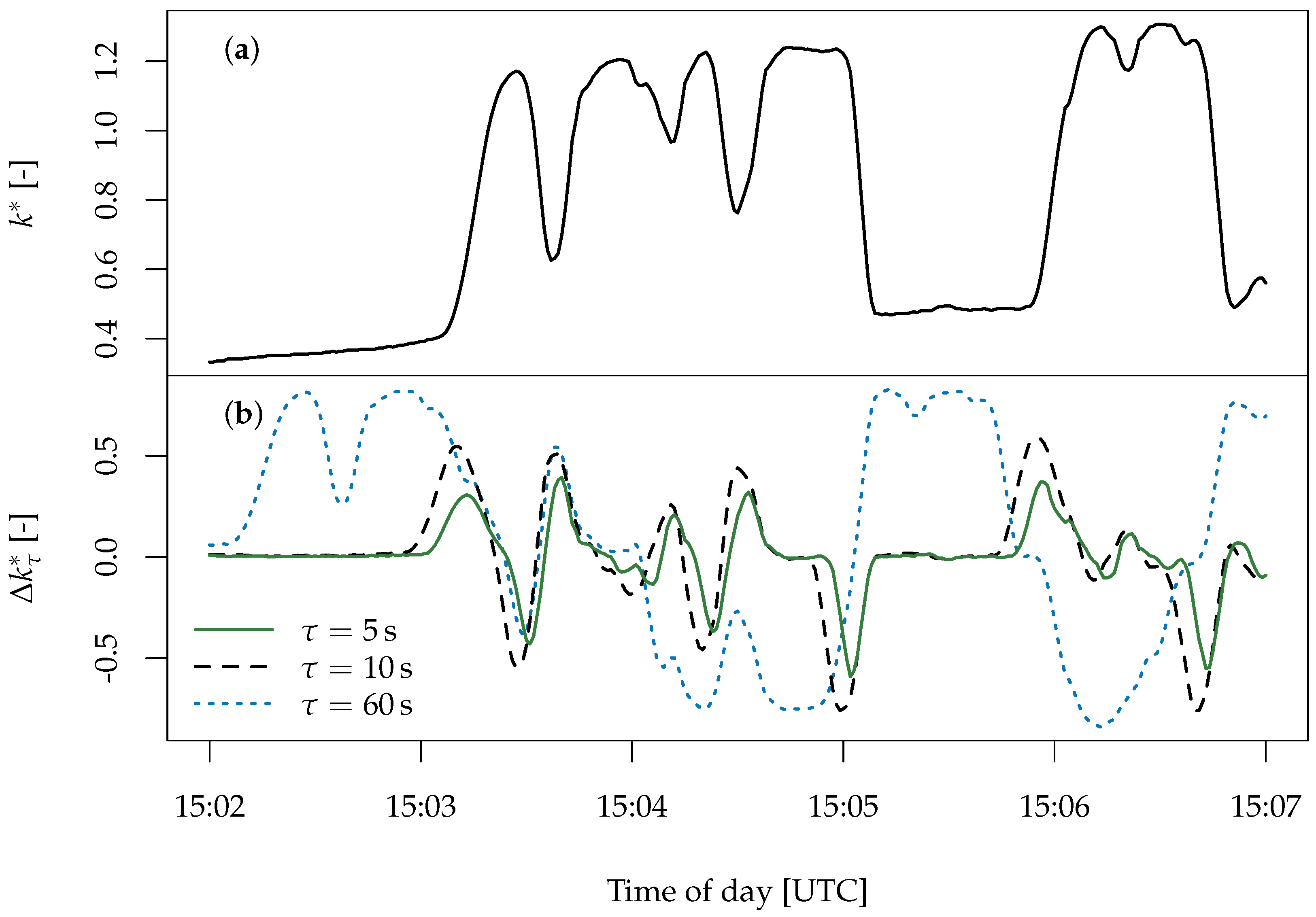
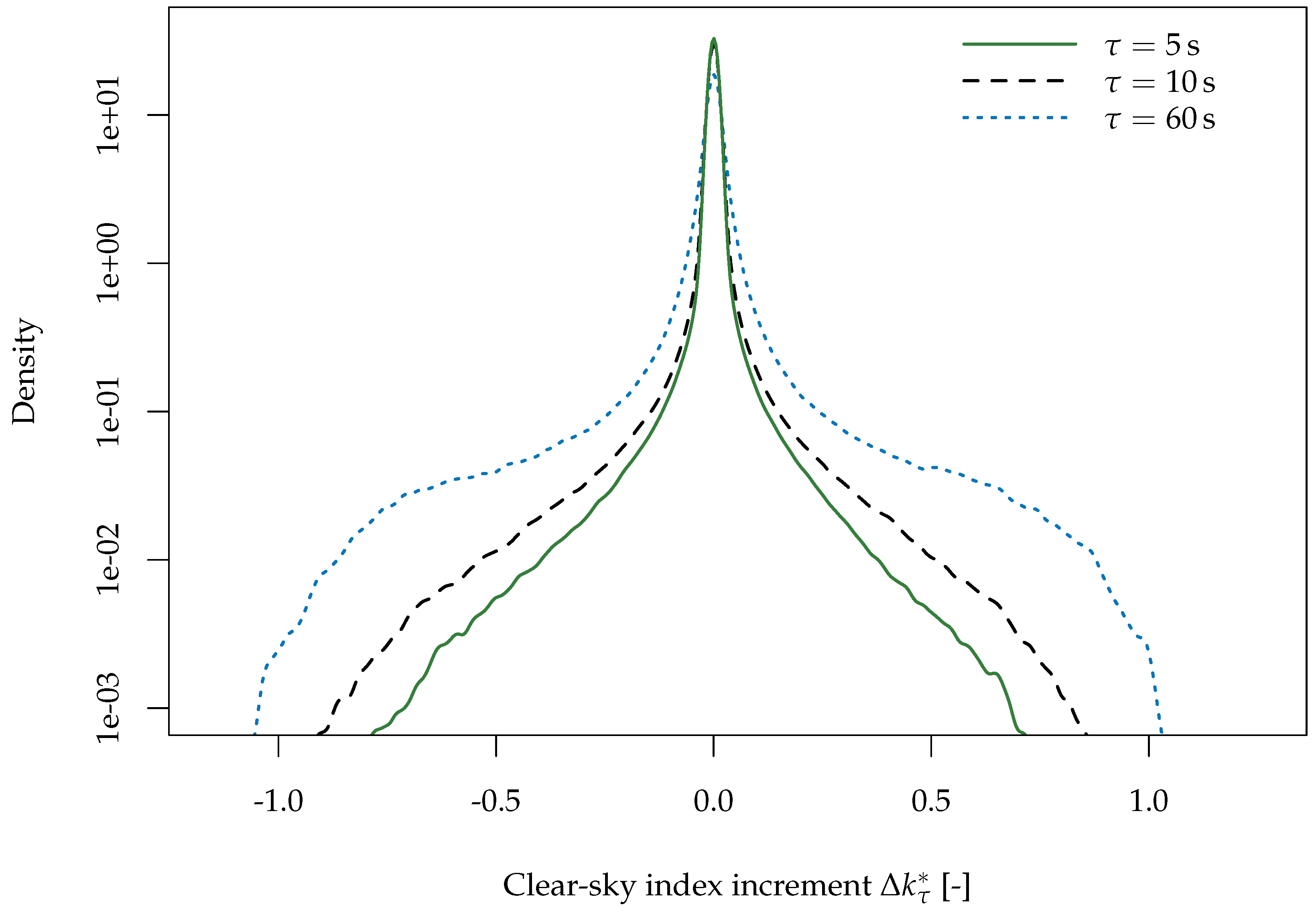
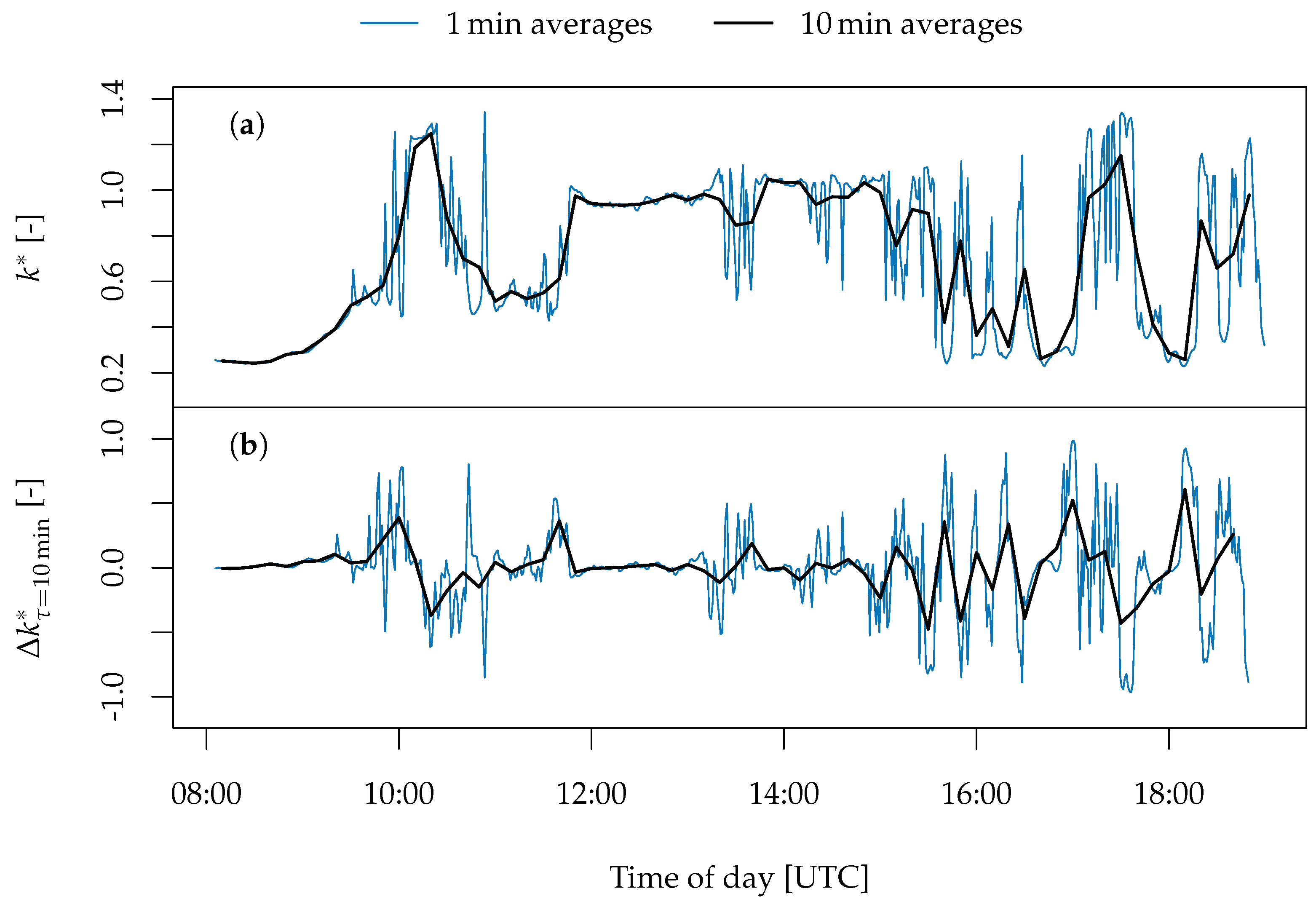
5. Temporal Averaging
- determining instantaneous irradiance variations for each of a few hundred days in spring and summer by calculating the second temporal derivative of each observation, considering the minimum (i.e., negative) value of a day’s derivatives to represent the day’s most severe fluctuation, and then computing an ideal averaging time by assuming the variations to feature parabolic shapes and accepting an error of 10 Wm−2 in the measurements [17];
- assessing the reduction of the standard deviation of an irradiance time series (measured during 7 h on a single summer’s day) as a function of increasing averaging time scales [63];
- separately studying the variability index and the variability score of irradiance for seven selected days as functions of increasing averaging time scales [16]; and
- characterizing the changes of and standard deviations as a function of averaging time using thousands of hours worth of irradiance observations with raw temporal resolutions ranging from 0.01 through 1 s [111].
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Solar Power Europe (SPE). Solar Market Report & Membership Directory; Publishing Events Ltd.: London, UK, 2016. [Google Scholar]
- REN21. Renewables 2016 Global Status Report; Technical report; REN21 Secretariat: Paris, France, 2016. [Google Scholar]
- Haegel, N.M.; Margolis, R.; Buonassisi, T.; Feldman, D.; Froitzheim, A.; Garabedian, R.; Green, M.; Glunz, S.; Henning, H.M.; Holder, B.; et al. Terawatt-scale photovoltaics: Trajectories and challenges. Science 2017, 356, 141–143. [Google Scholar] [CrossRef] [PubMed]
- Stetz, T.; von Appen, J.; Niedermeyer, F.; Scheibner, G.; Sikora, R.; Braun, M. Twilight of the grids: The impact of distributed solar on Germany’s energy transition. IEEE Power Energy Mag. 2015, 13, 50–61. [Google Scholar] [CrossRef]
- Perez, R.; Rábago, K.R.; Trahan, M.; Rawlings, L.; Norris, B.; Hoff, T.; Putnam, M.; Perez, M. Achieving very high PV penetration—The need for an effective electricity remuneration framework and a central role for grid operators. Energy Policy 2016, 96, 27–35. [Google Scholar] [CrossRef]
- Suri, M.; Huld, T.; Dunlop, E.; Albuisson, M.; Lefevre, M.; Wald, L. Uncertainties in solar electricity yield prediction from fluctuation of solar radiation. In Proceedings of the 22nd European Photovoltaic Solar Energy Conference, Milan, Italy, 3–7 September 2007. [Google Scholar]
- Bridier, L.; David, M.; Lauret, P. Optimal design of a storage system coupled with intermittent renewables. Renew. Energy 2014, 67, 2–9. [Google Scholar] [CrossRef]
- Denholm, P.; Hand, M. Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energy Policy 2011, 39, 1817–1830. [Google Scholar] [CrossRef]
- Widén, J.; Wäckelgård, E.; Paatero, J.; Lund, P. Impacts of distributed photovoltaics on network voltages: Stochastic simulations of three Swedish low-voltage distribution grids. Electr. Power Syst. Res. 2010, 80, 1562–1571. [Google Scholar] [CrossRef]
- Hoff, T.E.; Perez, R. Modeling PV fleet output variability. Solar Energy 2012, 86, 2177–2189. [Google Scholar] [CrossRef]
- Mills, A.; Ahlstrom, M.; Brower, M.; Ellis, A.; George, R.; Hoff, T.; Kroposki, B.; Lenox, C.; Miller, N.; Milligan, M.; et al. Dark Shadows. IEEE Power Energy Mag. 2011, 9, 33–41. [Google Scholar] [CrossRef]
- Perez, R.; Kivalov, S.; Schlemmer, J.; Hemker, K., Jr.; Hoff, T.E. Short-term irradiance variability: Preliminary estimation of station pair correlation as a function of distance. Solar Energy 2012, 86, 2170–2176. [Google Scholar] [CrossRef]
- Widén, J. A model of spatially integrated solar irradiance variability based on logarithmic station-pair correlations. Solar Energy 2015, 122, 1409–1424. [Google Scholar] [CrossRef]
- Lave, M.; Kleissl, J.; Arias-Castro, E. High-frequency irradiance fluctuations and geographic smoothing. Solar Energy 2012, 86, 2190–2199. [Google Scholar] [CrossRef]
- Widén, J.; Carpman, N.; Castellucci, V.; Lingfors, D.; Olauson, J.; Remouit, F.; Bergkvist, M.; Grabbe, M.; Waters, R. Variability assessment and forecasting of renewables: A review for solar, wind, wave and tidal resources. Renew. Sustain. Energy Rev. 2015, 44, 356–375. [Google Scholar] [CrossRef]
- Gagné, A.; Turcotte, D.; Goswamy, N.; Poissant, Y. High resolution characterisation of solar variability for two sites in Eastern Canada. Solar Energy 2016, 137, 46–54. [Google Scholar] [CrossRef]
- Yordanov, G.; Saetre, T.; Midtgard, O.M. Optimal temporal resolution for detailed studies of cloud-enhanced sunlight (Overirradiance). In Proceedings of the 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC), Tampa, Fl, USA, 16–21 June 2013; pp. 985–988. [Google Scholar] [CrossRef]
- Klima, K.; Apt, J. Geographic smoothing of solar PV: Results from Gujarat. Environ. Res. Lett. 2015, 10, 104001. [Google Scholar] [CrossRef]
- Perez, R.; David, M.; Hoff, T.E.; Jamaly, M.; Kivalov, S.; Kleissl, J.; Lauret, P.; Perez, M. Spatial and temporal variability of solar energy. Found. Trends Renew. Energy 2016, 1, 1–44. [Google Scholar] [CrossRef]
- Liu, B.Y.; Jordan, R.C. The interrelationship and characteristic distribution of direct, diffuse and total solar radiation. Solar Energy 1960, 4, 1–19. [Google Scholar] [CrossRef]
- Bendt, P.; Collares-Pereira, M.; Rabl, A. The frequency distribution of daily insolation values. Solar Energy 1981, 27, 1–5. [Google Scholar] [CrossRef]
- Jurado, M.; Caridad, J.; Ruiz, V. Statistical distribution of the clearness index with radiation data integrated over five minute intervals. Solar Energy 1995, 55, 469–473. [Google Scholar] [CrossRef]
- Skartveit, A.; Olseth, J. The probability density and autocorrelation of short-term global and beam irradiance. Solar Energy 1992, 49, 477–487. [Google Scholar] [CrossRef]
- Suehrcke, H.; McCormick, P.G. The frequency distribution of instantaneous insolation values. Solar Energy 1988, 40, 413–422. [Google Scholar] [CrossRef]
- Tomson, T.; Tamm, G. Short-term variability of solar radiation. Solar Energy 2006, 80, 600–606. [Google Scholar] [CrossRef]
- Van Haaren, R.; Morjaria, M.; Fthenakis, V. Empirical assessment of short-term variability from utility-scale solar PV plants. Prog. Photovolt. Res. Appl. 2014, 22, 548–559. [Google Scholar] [CrossRef]
- Munkhammar, J.; Widén, J. An autocorrelation-based copula model for generating realistic clear-sky index time-series. Solar Energy 2017, 158, 9–19. [Google Scholar] [CrossRef]
- Hoff, T.E.; Perez, R. Quantifying PV power output variability. Solar Energy 2010, 84, 1782–1793. [Google Scholar] [CrossRef]
- Perez, R.; Kivalov, S.; Schlemmer, J.; Hemker, K.; Hoff, T. Parameterization of site-specific short-term irradiance variability. Solar Energy 2011, 85, 1343–1353. [Google Scholar] [CrossRef]
- Soriga, I.; Badescu, V. Thermal inertia of flat-plate solar collectors in different radiative regimes. Energy Convers. Manag. 2016, 111, 27–37. [Google Scholar] [CrossRef]
- Badescu, V.; Budea, S. How significant is the stability of the radiative regime when the best operation of solar DHW systems is evaluated? Renew. Energy 2016, 88, 346–358. [Google Scholar] [CrossRef]
- Brabec, M.; Paulescu, M.; Badescu, V. Statistical properties of clear and dark duration lengths. Solar Energy 2017, 153, 508–518. [Google Scholar] [CrossRef]
- Brabec, M.; Badescu, V.; Paulescu, M. Cloud shade by dynamic logistic modeling. J. Appl. Stat. 2014, 41, 1174–1188. [Google Scholar] [CrossRef]
- Brabec, M.; Paulescu, M.; Badescu, V. Generalized additive models for nowcasting cloud shading. Solar Energy 2014, 101, 272–282. [Google Scholar] [CrossRef]
- Badescu, V.; Paulescu, M. Statistical properties of the sunshine number illustrated with measurements from Timisoara (Romania). Atmos. Res. 2011, 101, 194–204. [Google Scholar] [CrossRef]
- Paulescu, M.; Badescu, V.; Brabec, M. Tools for PV (photovoltaic) plant operators: Nowcasting of passing clouds. Energy 2013, 54, 104–112. [Google Scholar] [CrossRef]
- Brabec, M.; Badescu, V.; Paulescu, M. Nowcasting sunshine number using logistic modeling. Meteorol. Atmos. Phys. 2013, 120, 61–71. [Google Scholar] [CrossRef]
- Badescu, V.; Paulescu, M. Autocorrelation properties of the sunshine number and sunshine stability number. Meteorol. Atmos. Phys. 2011, 112, 139–154. [Google Scholar] [CrossRef]
- Paulescu, M.; Badescu, V. New approach to measure the stability of the solar radiative regime. Theor. Appl. Climatol. 2011, 103, 459–470. [Google Scholar] [CrossRef]
- Paulescu, M.; Badescu, V.; Brabec, M. Retrieval of effective cloud field parameters from radiometric data. Theor. Appl. Climatol. 2018, 133, 437–446. [Google Scholar] [CrossRef]
- Munkhammar, J.; Widén, J.; Hinkelman, L.M. A copula method for simulating correlated instantaneous solar irradiance in spatial networks. Solar Energy 2017, 143, 10–21. [Google Scholar] [CrossRef]
- Woyte, A.; Van Thong, V.; Belmans, R.; Nijs, J. Voltage fluctuations on distribution level introduced by photovoltaic systems. IEEE Trans. Energy Convers. 2006, 21, 202–209. [Google Scholar] [CrossRef]
- Woyte, A.; Belmans, R.; Nijs, J. Localized spectral analysis of fluctuating power generation from solar energy systems. EURASIP J. Adv. Signal Process. 2007, 2007. [Google Scholar] [CrossRef]
- Anvari, M.; Lohmann, G.; Wächter, M.; Milan, P.; Lorenz, E.; Heinemann, D.; Tabar, M.R.R.; Peinke, J. Short term fluctuations of wind and solar power systems. New J. Phys. 2016, 18, 063027. [Google Scholar] [CrossRef]
- Barry, J.; Munzke, N.; Thomas, J. Power fluctuations in solar-storage clusters: Spatial correlation and battery response times. Energy Procedia 2017, 135, 379–390. [Google Scholar] [CrossRef]
- Bosch, J.; Kleissl, J. Cloud motion vectors from a network of ground sensors in a solar power plant. Solar Energy 2013, 95, 13–20. [Google Scholar] [CrossRef]
- Calif, R.; Schmitt, F.G.; Huang, Y.; Soubdhan, T. Intermittency study of high frequency global solar radiation sequences under a tropical climate. Solar Energy 2013, 98, 349–365. [Google Scholar] [CrossRef]
- Dyreson, A.R.; Morgan, E.R.; Monger, S.H.; Acker, T.L. Modeling solar irradiance smoothing for large PV power plants using a 45-sensor network and the Wavelet Variability Model. Solar Energy 2014, 110, 482–495. [Google Scholar] [CrossRef]
- Hinkelman, L.M. Differences between along-wind and cross-wind solar irradiance variability on small spatial scales. Solar Energy 2013, 88, 192–203. [Google Scholar] [CrossRef]
- Lave, M.; Reno, M.J.; Broderick, R.J. Characterizing local high-frequency solar variability and its impact to distribution studies. Solar Energy 2015, 118, 327–337. [Google Scholar] [CrossRef]
- Lohmann, G.M.; Monahan, A.H.; Heinemann, D. Local short-term variability in solar irradiance. Atmos. Chem. Phys. 2016, 16, 6365–6379. [Google Scholar] [CrossRef]
- Lohmann, G.M.; Hammer, A.; Monahan, A.H.; Schmidt, T.; Heinemann, D. Simulating clear-sky index increment correlations under mixed sky conditions using a fractal cloud model. Solar Energy 2017, 150, 255–264. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Holmgren, W.F.; Cronin, A.D. Irradiance forecasts based on an irradiance monitoring network, cloud motion, and spatial averaging. Solar Energy 2015, 122, 1158–1169. [Google Scholar] [CrossRef]
- Madhavan, B.L.; Deneke, H.; Witthuhn, J.; Macke, A. Multiresolution analysis of the spatiotemporal variability in global radiation observed by a dense network of 99 pyranometers. Atmos. Chem. Phys. 2017, 17, 3317–3338. [Google Scholar] [CrossRef]
- Marcos, J.; Marroyo, L.; Lorenzo, E.; Alvira, D.; Izco, E. From irradiance to output power fluctuations: The PV plant as a low pass filter. Prog. Photovolt. Res. Appl. 2011, 19, 505–510. [Google Scholar] [CrossRef]
- Marcos, J.; Marroyo, L.; Lorenzo, E.; Alvira, D.; Izco, E. Power output fluctuations in large scale PV plants: One year observations with one second resolution and a derived analytic model. Prog. Photovolt. Res. Appl. 2011, 19, 218–227. [Google Scholar] [CrossRef]
- Monger, S.H.; Morgan, E.R.; Dyreson, A.R.; Acker, T.L. Applying the kriging method to predicting irradiance variability at a potential PV power plant. Renew. Energy 2016, 86, 602–610. [Google Scholar] [CrossRef]
- Perpiñán, O.; Lorenzo, E. Analysis and synthesis of the variability of irradiance and PV power time series with the wavelet transform. Solar Energy 2011, 85, 188–197. [Google Scholar] [CrossRef]
- Schmidt, T.; Kalisch, J.; Lorenz, E.; Heinemann, D. Evaluating the spatio-temporal performance of sky-imager-based solar irradiance analysis and forecasts. Atmos. Chem. Phys. 2016, 16, 3399–3412. [Google Scholar] [CrossRef]
- Tabar, M.R.R.; Anvari, M.; Lohmann, G.; Heinemann, D.; Wächter, M.; Milan, P.; Lorenz, E.; Peinke, J. Kolmogorov spectrum of renewable wind and solar power fluctuations. Eur. Phys. J. Spec. Top. 2014, 223, 1–8. [Google Scholar] [CrossRef]
- Widén, J.; Shepero, M.; Munkhammar, J. On the properties of aggregate clear-sky index distributions and an improved model for spatially correlated instantaneous solar irradiance. Solar Energy 2017, 157, 566–580. [Google Scholar] [CrossRef]
- Yordanov, G.H.; Saetre, T.O.; Midtgård, O.M. Extreme overirradiance events in Norway: 1.6 suns measured close to 60° N. Solar Energy 2015, 115, 68–73. [Google Scholar] [CrossRef]
- Torres Lobera, D.; Mäki, A.; Huusari, J.; Lappalainen, K.; Suntio, T.; Valkealahti, S. Operation of TUT solar PV power station research plant under partial shading caused by snow and buildings. Int. J. Photoenergy 2013, 2013. [Google Scholar] [CrossRef]
- Yordanov, G.; Midtgård, O.M.; Saetre, T.; Nielsen, H.; Norum, L. Overirradiance (cloud enhancement) events at high latitudes. IEEE J. Photovolt. 2013, 3, 271–277. [Google Scholar] [CrossRef]
- Yordanov, G.H.; Saetre, T.O.; Midtgard, O.M. 100-millisecond Resolution for Accurate Overirradiance Measurements. IEEE J. Photovolt. 2013, 3, 1354–1360. [Google Scholar] [CrossRef]
- Driesse, A.; Stein, J.S.; Riley, D.; Carmignani, C. Sampling and Filtering in Photovoltaic System Performance Monitoring; Sandia National Laboratories: Albuquerque, NM, USA, 2014; Volume 12, p. 2016.
- Lave, M.; Broderick, R.J.; Reno, M.J. Solar variability zones: Satellite-derived zones that represent high-frequency ground variability. Solar Energy 2017, 151, 119–128. [Google Scholar] [CrossRef]
- Arias-Castro, E.; Kleissl, J.; Lave, M. A Poisson model for anisotropic solar ramp rate correlations. Solar Energy 2014, 101, 192–202. [Google Scholar] [CrossRef]
- Bright, J.M.; Babacan, O.; Kleissl, J.; Taylor, P.G.; Crook, R. A synthetic, spatially decorrelating solar irradiance generator and application to a LV grid model with high PV penetration. Solar Energy 2017, 147, 83–98. [Google Scholar] [CrossRef]
- Lave, M.; Kleissl, J. Cloud speed impact on solar variability scaling—Application to the wavelet variability model. Solar Energy 2013, 91, 11–21. [Google Scholar] [CrossRef]
- Elsinga, B.; van Sark, W.G. Analytic model for correlations of cloud induced fluctuations of clear-sky index. Solar Energy 2017, 155, 985–1001. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Holmgren, W.F.; Cronin, A.D. Irradiance Monitoring Network Data and Wind Motion Vectors; Zenodo: Geneva, Switzerland, 2015. [Google Scholar] [CrossRef]
- Natural Resources Canada. High-Resolution Solar Radiation Datasets; Natural Resources Canada: Ottawa, ON, Canada, 2016. Available online: http://www.nrcan.gc.ca/energy/renewable-electricity/solar-photovoltaic/18409 (accessed on 13 June 2017).
- Standardized Atmospheric Measurement Data. HD(CP)2 Short Term Observations, sw Broadband Downwelling Radiation (Surface) Data of Pyranometer Network (no. 00), HOPE Campaign by TROPOS, Data Version 00. PID: Madhavan Bomidi. 2017. Available online: https://icdc.cen.uni-hamburg.de/index.php?id=hopetroppyrnet00l1rsds (accessed on 13 June 2017).
- Sengupta, M.; Andreas, A. Oahu Solar Measurement Grid (1-Year Archive): 1-s Solar Irradiance; Oahu, Hawaii (Data); Technical report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010. [CrossRef]
- Schmidt, T.; Lohmann, G.M. A 10 Hz Irradiance Dataset from Oldenburg, Germany; Zenodo: Geneva, Switzerland, 2018. [Google Scholar] [CrossRef]
- Curtright, A.E.; Apt, J. The character of power output from utility-scale photovoltaic systems. Prog. Photovolt. Res. Appl. 2008, 16, 241–247. [Google Scholar] [CrossRef]
- Lave, M.; Kleissl, J. Solar variability of four sites across the state of Colorado. Renew. Energy 2010, 35, 2867–2873. [Google Scholar] [CrossRef]
- Madanchi, A.; Absalan, M.; Lohmann, G.; Anvari, M.; Reza Rahimi Tabar, M. Strong short-term non-linearity of solar irradiance fluctuations. Solar Energy 2017, 144, 1–9. [Google Scholar] [CrossRef]
- Anvari, M.; Werther, B.; Lohmann, G.; Wächter, M.; Peinke, J.; Beck, H.P. Suppressing power output fluctuations of photovoltaic power plants. Solar Energy 2017, 157, 735–743. [Google Scholar] [CrossRef]
- Schmietendorf, K.; Peinke, J.; Kamps, O. The impact of turbulent renewable energy production on power grid stability and quality. Eur. Phys. J. B 2017, 90, 222. [Google Scholar] [CrossRef]
- Vindel, J.; Polo, J. Intermittency and variability of daily solar irradiation. Atmos. Res. 2014, 143, 313–327. [Google Scholar] [CrossRef]
- Lave, M.; Kleissl, J.; Stein, J.S. A wavelet-based variability model (WVM) for solar PV power plants. IEEE Trans. Sustain. Energy 2013, 4, 501–509. [Google Scholar] [CrossRef]
- Woyte, A.; Nijs, J.; Belmans, R. Partial shadowing of photovoltaic arrays with different system configurations: Literature review and field test results. Solar Energy 2003, 74, 217–233. [Google Scholar] [CrossRef]
- Pareek, S.; Dahiya, R. Enhanced power generation of partial shaded photovoltaic fields by forecasting the interconnection of modules. Energy 2016, 95, 561–572. [Google Scholar] [CrossRef]
- Belhaouas, N.; Cheikh, M.S.A.; Agathoklis, P.; Oularbi, M.R.; Amrouche, B.; Sedraoui, K.; Djilali, N. PV array power output maximization under partial shading using new shifted PV array arrangements. Appl. Energy 2017, 187, 326–337. [Google Scholar] [CrossRef]
- Kurtz, B.; Kleissl, J. Measuring diffuse, direct, and global irradiance using a sky imager. Solar Energy 2016. [Google Scholar] [CrossRef]
- Urquhart, B.; Kurtz, B.; Dahlin, E.; Ghonima, M.; Shields, J.E.; Kleissl, J. Development of a sky imaging system for short-term solar power forecasting. Atmos. Meas. Tech. 2015, 8, 875–890. [Google Scholar] [CrossRef]
- Yang, H.; Kurtz, B.; Nguyen, D.; Urquhart, B.; Chow, C.W.; Ghonima, M.; Kleissl, J. Solar irradiance forecasting using a ground-based sky imager developed at UC San Diego. Solar Energy 2014, 103, 502–524. [Google Scholar] [CrossRef]
- Chauvin, R.; Nou, J.; Thil, S.; Grieu, S. Modelling the clear-sky intensity distribution using a sky imager. Solar Energy 2015, 119, 1–17. [Google Scholar] [CrossRef]
- Gohari, M.; Urquhart, B.; Yang, H.; Kurtz, B.; Nguyen, D.; Chow, C.; Ghonima, M.; Kleissl, J. Comparison of solar power output forecasting performance of the Total Sky Imager and the University of California, San Diego Sky Imager. Energy Procedia 2014, 49, 2340–2350. [Google Scholar] [CrossRef]
- Schmidt, T.; Calais, M.; Roy, E.; Burton, A.; Heinemann, D.; Kilper, T.; Carter, C. Short-term solar forecasting based on sky images to enable higher PV generation in remote electricity networks. Renew. Energy Environ. Sustain. 2017, 2, 23. [Google Scholar] [CrossRef]
- Jazayeri, M.; Jazayeri, K.; Uysal, S. Generation of spatially dispersed irradiance time-series based on real cloud patterns. Solar Energy 2017, 158, 977–994. [Google Scholar] [CrossRef]
- Nou, J.; Chauvin, R.; Eynard, J.; Thil, S.; Grieu, S. Towards the intrahour forecasting of direct normal irradiance using sky-imaging data. Heliyon 2018, 4, e00598. [Google Scholar] [CrossRef] [PubMed]
- Anagnostos, D.; Schmidt, T.; Cavadias, S.; Soudris, D.; Poortmans, J.; Catthoor, F. A Method for Detailed, Short-Term Energy Yield Forecasting of Photovoltaic Installations. Renew. Energy 2018. [Google Scholar] [CrossRef]
- Stein, J.S.; Hansen, C.W.; Reno, M.J. The variability index: A new and novel metric for quantifying irradiance and PV output variability. In Proceedings of the World Renewable Energy Forum, Denver, CO, USA, 13–17 May 2012; pp. 13–17. [Google Scholar]
- Perpiñán, O.; Marcos, J.; Lorenzo, E. Electrical power fluctuations in a network of DC/AC inverters in a large PV plant: Relationship between correlation, distance and time scale. Solar Energy 2013, 88, 227–241. [Google Scholar] [CrossRef]
- Lenox, C.; Nelson, L. Variability comparison of large-scale photovoltaic systems across diverse geographic climates. In Proceedings of the 25th European Photovoltaic Solar Energy Conference, Valencia, Spain, 6–10 September 2010. [Google Scholar]
- Watanabe, T.; Oishi, Y.; Nakajima, T.Y. Characterization of surface solar-irradiance variability using cloud properties based on satellite observations. Solar Energy 2016, 140, 83–92. [Google Scholar] [CrossRef]
- Hummon, M.; Ibanez, E.; Brinkman, G.; Lew, D. Sub-Hour Solar Data for Power System Modeling From Static Spatial Variability Analysis: Preprint; Technical report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2012.
- Wolff, B.; Kühnert, J.; Lorenz, E.; Kramer, O.; Heinemann, D. Comparing support vector regression for PV power forecasting to a physical modeling approach using measurement, numerical weather prediction, and cloud motion data. Solar Energy 2016, 135, 197–208. [Google Scholar] [CrossRef]
- Elsinga, B.; van Sark, W. Spatial power fluctuation correlations in urban rooftop photovoltaic systems. Prog. Photovolt. Res. Appl. 2014. [Google Scholar] [CrossRef]
- Lonij, V.P.; Brooks, A.E.; Cronin, A.D.; Leuthold, M.; Koch, K. Intra-hour forecasts of solar power production using measurements from a network of irradiance sensors. Solar Energy 2013, 97, 58–66. [Google Scholar] [CrossRef]
- Mills, A. Implications of Wide-Area Geographic Diversity for Short-Term Variability of Solar Power 2010. Available online: https://cloudfront.escholarship.org/dist/prd/content/qt9mz3w055/qt9mz3w055.pdf (accessed on 3 May 2013).
- Munkhammar, J.; Widén, J. A Markov-chain probability distribution mixture approach to the clear-sky index. Solar Energy 2018, 170, 174–183. [Google Scholar] [CrossRef]
- Perez, R.; Hoff, T.; Kivalov, S. Spatial & temporal characteristics of solar radiation variability. In Proceedings of the International Solar Energy (ISES) World Congress, Kassel, Germany, 28 August–2 September 2011. [Google Scholar]
- Schwarz, M.; Folini, D.; Hakuba, M.Z.; Wild, M. Spatial representativeness of surface-measured variations of downward solar radiation: Spatiotemporal representativeness of SSR. J. Geophys. Res. Atmos. 2017. [Google Scholar] [CrossRef]
- Bengulescu, M.; Blanc, P.; Wald, L. Characterizing Temporal Variability in Measurements of Surface Solar Radiation and its Dependence on Climate. Energy Procedia 2016, 97, 164–171. [Google Scholar] [CrossRef]
- Bright, J.; Smith, C.; Taylor, P.; Crook, R. Stochastic generation of synthetic minutely irradiance time series derived from mean hourly weather observation data. Solar Energy 2015, 115, 229–242. [Google Scholar] [CrossRef]
- Hansen, C.W.; Stein, J.S.; Riley, D. Effect of Time Scale on Analysis of PV System Performance; SANDIA Report; Sandia National Laboratories: Albuquerque, NM, USA, 2012.
- Lohmann, G.M.; Monahan, A.H. Effects of temporal averaging on short-term irradiance variability under mixed sky conditions. Atmos. Meas. Tech. 2018, 11, 3131–3144. [Google Scholar] [CrossRef]
- Kim, I. Markov chain Monte Carlo and acceptance–rejection algorithms for synthesising short-term variations in the generation output of the photovoltaic system. IET Renew. Power Gener. 2017, 11, 878–888. [Google Scholar] [CrossRef]
- Perry, M.; Troccoli, A. An approach for generating synthetic fine temporal resolution solar radiation time series from hourly gridded datasets. Meteorol. Z. 2017, 26, 265–276. [Google Scholar] [CrossRef]
- Riley, D.M.; Cameron, C.P.; Jacob, J.A.; Granata, J.E.; Galbraith, G.M. Quantifying the effects of averaging and sampling rates on PV system and weather data. In Proceedings of the 2009 34th IEEE Photovoltaic Specialists Conference (PVSC), Washington, DC, USA, 7–12 June 2009; pp. 456–461. [Google Scholar]
- Huang, J.; Davy, R.J. Predicting intra-hour variability of solar irradiance using hourly local weather forecasts. Solar Energy 2016, 139, 633–639. [Google Scholar] [CrossRef]
- Lave, M.; Weekley, A. Comparison of high-frequency solar irradiance: Ground measured vs. satellite-derived. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 1101–1106. [Google Scholar]
- Hummon, M.; Weekley, A.; Searight, K.; Clark, K. Downscaling Solar Power Output to 4-Seconds for Use in Integration Studies: Preprint; Technical repor; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2013.
- Wegener, J.; Lave, M.; Luoma, J.; Kleissl, J. Temporal Downscaling of Irradiance Data via Hidden Markov Models on Wavelet Coefficients: Application to California Solar Initiative Data; Technical report; University of California San Diego: La Jolla, CA, USA, 2012. [Google Scholar]
- Kleissl, J. Solar Energy Forecasting and Resource Assessment; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Inman, R.H.; Pedro, H.T.; Coimbra, C.F. Solar forecasting methods for renewable energy integration. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Badescu, V. Modeling Solar Radiation at the Earth’s Surface; Springer: New York, NY, USA, 2014. [Google Scholar]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Solar Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.; Coimbra, C.F. History and trends in solar irradiance and PV power forecasting: A preliminary assessment and review using text mining. Solar Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Barbieri, F.; Rajakaruna, S.; Ghosh, A. Very short-term photovoltaic power forecasting with cloud modeling: A review. Renew. Sustain. Energy Rev. 2017, 75, 242–263. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z.; Lin, J.; Hu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2015, 1, 38–46. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de Pison, F.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Solar Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Van der Meer, D.; Widén, J.; Munkhammar, J. Review on probabilistic forecasting of photovoltaic power production and electricity consumption. Renew. Sustain. Energy Rev. 2018, 81, 1484–1512. [Google Scholar] [CrossRef]
- Graabak, I.; Korpås, M. Variability Characteristics of European Wind and Solar Power Resources—A Review. Energies 2016, 9, 449. [Google Scholar] [CrossRef]
- Qazi, A.; Fayaz, H.; Wadi, A.; Raj, R.G.; Rahim, N.; Khan, W.A. The artificial neural network for solar radiation prediction and designing solar systems: A systematic literature review. J. Clean. Prod. 2015, 104, 1–12. [Google Scholar] [CrossRef]
- Kashyap, Y.; Bansal, A.; Sao, A.K. Solar radiation forecasting with multiple parameters neural networks. Renew. Sustain. Energy Rev. 2015, 49, 825–835. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Beyer, H.G. Handling of Small Scale Structures of the Irradiance Field for Solar Energy System Analysis—A Review. Energy Procedia 2016, 97, 141–148. [Google Scholar] [CrossRef]
- Badescu, V.; Gueymard, C.A.; Cheval, S.; Oprea, C.; Baciu, M.; Dumitrescu, A.; Iacobescu, F.; Milos, I.; Rada, C. Computing global and diffuse solar hourly irradiation on clear sky. Review and testing of 54 models. Renew. Sustain. Energy Rev. 2012, 16, 1636–1656. [Google Scholar] [CrossRef]
- Gueymard, C.A. Clear-sky irradiance predictions for solar resource mapping and large-scale applications: Improved validation methodology and detailed performance analysis of 18 broadband radiative models. Solar Energy 2012, 86, 2145–2169. [Google Scholar] [CrossRef]
- Reno, M.J.; Hansen, C.W.; Stein, J.S. Global Horizontal Irradiance Clear Sky Models: Implementation and Analysis. In SANDIA Report SAND2012-2389; 2012. Available online: http://prod.sandia.gov/techlib/access-control.cgi/2012/122389.pdf (accessed on 4 December 2017).
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
- Madhavan, B.L.; Kalisch, J.; Macke, A. Shortwave surface radiation network for observing small-scale cloud inhomogeneity fields. Atmos. Meas. Tech. 2016, 9, 1153–1166. [Google Scholar] [CrossRef]
- Macke, A.; Seifert, P.; Baars, H.; Barthlott, C.; Beekmans, C.; Behrendt, A.; Bohn, B.; Brueck, M.; Bühl, J.; Crewell, S.; et al. The HD(CP)2 Observational Prototype Experiment (HOPE)—An overview. Atmos. Chem. Phys. 2017, 17, 4887–4914. [Google Scholar] [CrossRef]
- Dumortier, D. Modelling Global and Diffuse Horizontal Irradiances under Cloudless Skies with Different Turbidities; Daylight II, JOU2-CT92-0144, Final Report; CNRS-ENTPE: Vaulx-en-Velin, France, 1995. [Google Scholar]
- Schade, N.H.; Macke, A.; Sandmann, H.; Stick, C. Enhanced solar global irradiance during cloudy sky conditions. Meteorol. Z. 2007, 16, 295–303. [Google Scholar] [CrossRef]
- Piacentini, R.D.; Salum, G.M.; Fraidenraich, N.; Tiba, C. Extreme total solar irradiance due to cloud enhancement at sea level of the NE Atlantic coast of Brazil. Renew. Energy 2011, 36, 409–412. [Google Scholar] [CrossRef]
- Pecenak, Z.K.; Mejia, F.A.; Kurtz, B.; Evan, A.; Kleissl, J. Simulating irradiance enhancement dependence on cloud optical depth and solar zenith angle. Solar Energy 2016, 136, 675–681. [Google Scholar] [CrossRef]
- Gueymard, C.A. Cloud and albedo enhancement impacts on solar irradiance using high-frequency measurements from thermopile and photodiode radiometers. Part 1: Impacts on global horizontal irradiance. Solar Energy 2017, 153, 755–765. [Google Scholar] [CrossRef]
- Tovar, J.; Olmo, F.J.; Alados-Arboledas, L. One-minute global irradiance probability density distributions conditioned to the optical air mass. Solar Energy 1998, 62, 387–393. [Google Scholar] [CrossRef]
- Olseth, J.A.; Skartveit, A. A probability density model for hourly total and beam irradiance on arbitrarily orientated planes. Solar Energy 1987, 39, 343–351. [Google Scholar] [CrossRef]
- Ripley, B.D. Modern Applied Statistics with S; Springer: New York, NY, USA, 2002. [Google Scholar]
- Friedrich, R.; Peinke, J.; Sahimi, M.; Reza Rahimi Tabar, M. Approaching complexity by stochastic methods: From biological systems to turbulence. Phys. Rep. 2011, 506, 87–162. [Google Scholar] [CrossRef]
- Nikulin, M.S. Three-sigma rule. In Encyclopedia of Mathematics; Facts On File, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Woyte, A.; Richter, M.; Moser, D.; Mau, S.; Reich, N.; Jahn, U. Monitoring of photovoltaic systems: Good practices and systematic analysis. In Proceedings of the 28th European Photovoltaic Solar Energy Conference, Paris, France, 30 September–4 October 2013; pp. 3686–3694. [Google Scholar]
- Ngoko, B.; Sugihara, H.; Funaki, T. Synthetic generation of high temporal resolution solar radiation data using Markov models. Solar Energy 2014, 103, 160–170. [Google Scholar] [CrossRef]
- Hansen, C.W.; Stein, J.S.; Ellis, A. Simulation of One-Minute Power Output from Utility-Scale Photovoltaic Generation Systems; Technical Report SAND 2011-5529; Sandia National Laboratories: Albuquerque, NM, USA, 2011.
- Morf, H. The stochastic two-state solar irradiance model (STSIM). Solar Energy 1998, 62, 101–112. [Google Scholar] [CrossRef]
- Morf, H. A stochastic solar irradiance model adjusted on the Ångström–Prescott regression. Solar Energy 2013, 87, 1–21. [Google Scholar] [CrossRef]
- Pfenninger, S. Energy scientists must show their workings. Nat. News 2017, 542, 393. [Google Scholar] [CrossRef] [PubMed]
- Perpiñán, O. Statistical analysis of the performance and simulation of a two-axis tracking PV system. Solar Energy 2009, 83, 2074–2085. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Ruiz-Arias, J.A. Performance of separation models to predict direct irradiance at high frequency: Validation over arid areas. In Proceedings of the EuroSun 2014 ISES Conference, Aix-les-Bains, France, 16–19 September 2014. [Google Scholar]
- Gueymard, C.A.; Ruiz-Arias, J.A. Extensive worldwide validation and climate sensitivity analysis of direct irradiance predictions from 1-min global irradiance. Solar Energy 2016, 128, 1–30. [Google Scholar] [CrossRef]
- Engerer, N. Minute resolution estimates of the diffuse fraction of global irradiance for southeastern Australia. Solar Energy 2015, 116, 215–237. [Google Scholar] [CrossRef]
- Gueymard, C.A. Temporal variability in direct and global irradiance at various time scales as affected by aerosols. Solar Energy 2012, 86, 3544–3553. [Google Scholar] [CrossRef]
- Xia, X.; Chen, H.; Li, Z.; Wang, P.; Wang, J. Significant reduction of surface solar irradiance induced by aerosols in a suburban region in northeastern China. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Mukkavilli, S.K.; Prasad, A.A.; Taylor, R.A.; Troccoli, A.; Kay, M.J. Mesoscale Simulations of Australian Direct Normal Irradiance, Featuring an Extreme Dust Event. J. Appl. Meteorol. Climatol. 2018, 57, 493–515. [Google Scholar] [CrossRef]
- Alfadda, A.; Rahman, S.; Pipattanasomporn, M. Solar irradiance forecast using aerosols measurements: A data driven approach. Solar Energy 2018, 170, 924–939. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Gueymard, C.A.; Santos-Alamillos, F.J.; Pozo-Vázquez, D. Worldwide impact of aerosol’s time scale on the predicted long-term concentrating solar power potential. Sci. Rep. 2016, 6, 30546. [Google Scholar] [CrossRef] [PubMed]
- Mueller, R.; Träger-Chatterjee, C. Brief Accuracy Assessment of Aerosol Climatologies for the Retrieval of Solar Surface Radiation. Atmosphere 2014, 5, 959–972. [Google Scholar] [CrossRef]
- Mueller, R.; Pfeifroth, U.; Traeger-Chatterjee, C. Towards Optimal Aerosol Information for the Retrieval of Solar Surface Radiation Using Heliosat. Atmosphere 2015, 6, 863–878. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Gueymard, C.A.; Santos-Alamillos, F.J.; Pozo-Vázquez, D. Do spaceborne aerosol observations limit the accuracy of modeled surface solar irradiance: Aerosol limits modeled solar radiation. Geophys. Res. Lett. 2015, 42, 605–612. [Google Scholar] [CrossRef]
- Alonso-Blanco, E.; Gómez-Moreno, F.; Artíñano, B.; Iglesias-Samitier, S.; Juncal-Bello, V.; Piñeiro-Iglesias, M.; López-Mahía, P.; Pérez, N.; Brines, M.; Alastuey, A.; et al. Temporal and spatial variability of atmospheric particle number size distributions across Spain. Atmos. Environ. 2018. [Google Scholar] [CrossRef]
- Nikitidou, E.; Kazantzidis, A.; Salamalikis, V. The aerosol effect on direct normal irradiance in Europe under clear skies. Renew. Energy 2014, 68, 475–484. [Google Scholar] [CrossRef]
- Polo, J.; Estalayo, G. Impact of atmospheric aerosol loads on Concentrating Solar Power production in arid-desert sites. Solar Energy 2015, 115, 621–631. [Google Scholar] [CrossRef]
- Law, E.W.; Prasad, A.A.; Kay, M.; Taylor, R.A. Direct normal irradiance forecasting and its application to concentrated solar thermal output forecasting–A review. Solar Energy 2014, 108, 287–307. [Google Scholar] [CrossRef]
- Nickovic, S.; Cuevas, E.; Baldasano, J.; Terradellas, E.; Nakazawa, T.; Baklano, A. Sand and Dust Storm Warning Advisory and Assessment System (SDS-WAS) Science and Implementation Plan: 2015–2020; World Meteorological Organization (WMO): Geneva, Switzerland, 2015. [Google Scholar]
- Lohmann, G.M. Solar Irradiance Variability on Small Spatial and Temporal Scales. Ph.D. Thesis, Carl von Ossietzky Universität Oldenburg, Oldenburg, Germany, 2017. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lohmann, G.M. Irradiance Variability Quantification and Small-Scale Averaging in Space and Time: A Short Review. Atmosphere 2018, 9, 264. https://doi.org/10.3390/atmos9070264
Lohmann GM. Irradiance Variability Quantification and Small-Scale Averaging in Space and Time: A Short Review. Atmosphere. 2018; 9(7):264. https://doi.org/10.3390/atmos9070264
Chicago/Turabian StyleLohmann, Gerald M. 2018. "Irradiance Variability Quantification and Small-Scale Averaging in Space and Time: A Short Review" Atmosphere 9, no. 7: 264. https://doi.org/10.3390/atmos9070264
APA StyleLohmann, G. M. (2018). Irradiance Variability Quantification and Small-Scale Averaging in Space and Time: A Short Review. Atmosphere, 9(7), 264. https://doi.org/10.3390/atmos9070264




