Does Marine Surface Tension Have Global Biogeography? Addition for the OCEANFILMS Package
Abstract
1. Introduction
2. Background
3. Methods and Theory
- List observed (2D) surface pressure ranges and influence on: (Section 4)
- Define a surface pressure range (0.3 to 3 mN/m) encompassing all effects (Table 1)
- Segregate and prioritize global biomacromolecules by their likely functionality (Section 5) [30,31,32,33,37]
- ◦
- It is concluded that proteins and lipids dominate air-water interfaces
- ◦
- Albumin (protein) and stearic acid (lipids)
- ◦
- Standard commercial alternatives are rejected
- Construct a 2D equation of state to provide surface pressure values as a function of surfactant occupancy (Section 8 and Appendix A) [36,38]
- We address the two introductory questions: (Section 9 and remainder)
- ◦
- Distributions of 2D pressure are entirely coherent
- ◦
- Aerosol to energy fluxes are directly in play
4. Observed Surface Tension Effects
5. Compound Identities
6. Surrogates or Proxies
7. Mixed Layer Concentrations
8. Spreading Exercises
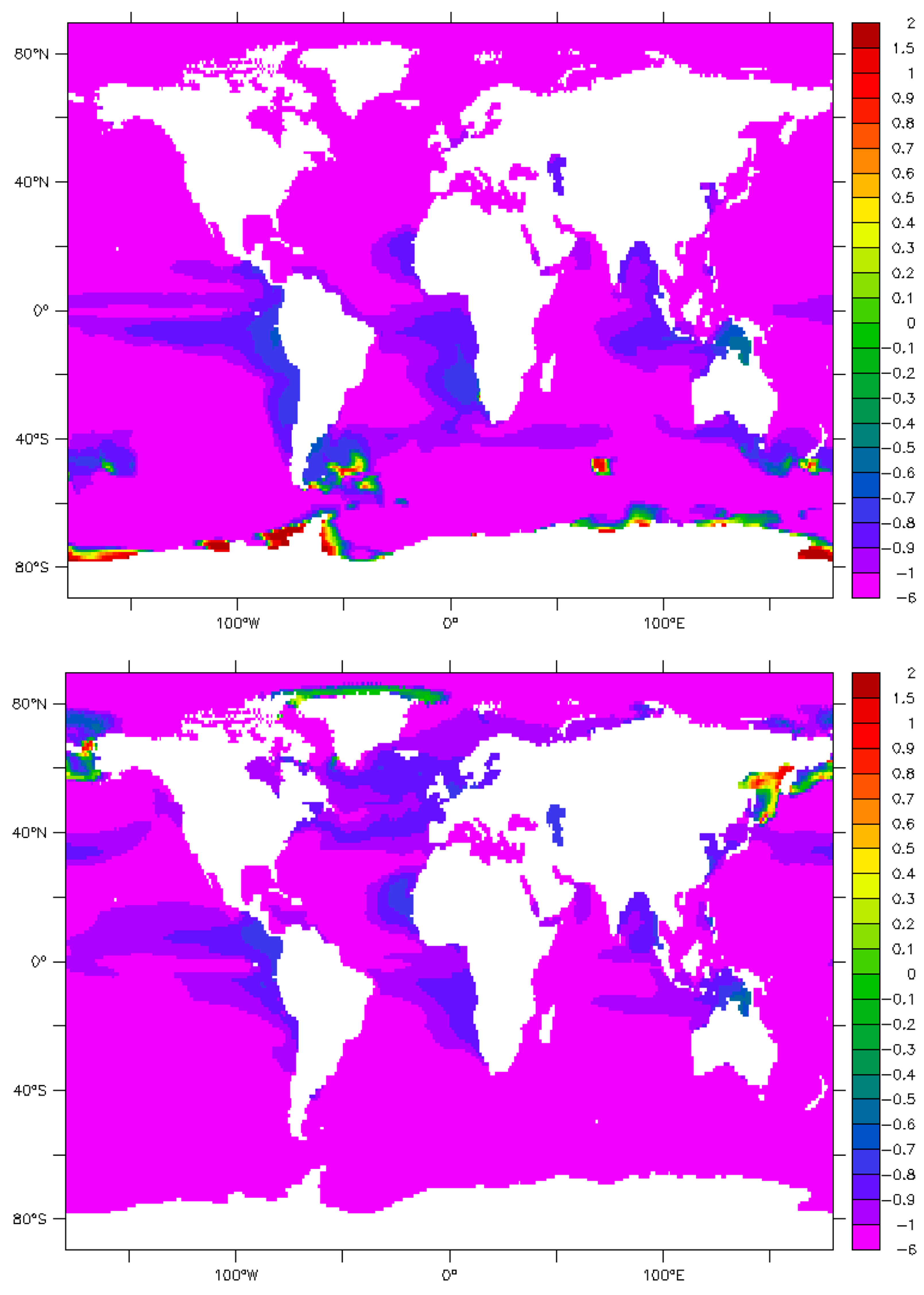
9. Maps and Sensitivity
10. Uncertainties
- Effects on the surfactant equilibria:
11. Summary and Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Equations
| Surrogate | Reference Concentrations 1/2 Max, all μM Carbon | Maxima (Γ mg/m2, π as mN/m) | Exponents Values for n | |||
|---|---|---|---|---|---|---|
| Excess | 2D Pressure | Excess | 2D Pressure | Excess | 2D Pressure | |
| Protein (Albumin) | 10 | 30 | 2 | 20 | 0.5 | 1 |
| Lipid (Stearate) | 0.5 | 2 | 2.5 | 50 | 1 | 8 |

References
- Jarvis, N. Adsorption of surface-active material at the sea-air interface. Limnol. Oceanogr. 1967, 12, 213–221. [Google Scholar] [CrossRef]
- Liss, P. Chemistry of the sea surface microlayer. In Chemical Oceanography; Riley, J., Skirrow, G., Eds.; Academic Press: New York, NY, USA, 1975; Volume 2. [Google Scholar]
- Barger, W.; Daniel, W.; Garrett, W. Surface chemical properties of banded sea slicks. Deep Sea Res. Oceanogr. Abstr. 1974, 21, 83–89. [Google Scholar] [CrossRef]
- Barger, W.; Garrett, W. Surface active organic material in air over the Mediterranean and the Eastern Equatorial Pacific. J. Geophys. Res. 1976, 81, 3151–3163. [Google Scholar] [CrossRef]
- Barger, W.; Means, J. Clues to the structure of marine organic material from the study of physical properties of surface films. In Marine and Estuarine Geochemistry; Sigleo, A., Haitori, A., Eds.; Lewis Publishers: Chelsea, MI, USA, 1985. [Google Scholar]
- Goldman, J.; Dennett, M.; Frew, N. Surfactant effects on air-sea exchange under turbulent conditions. Deep Sea Res. 1988, 35, 1953–1970. [Google Scholar] [CrossRef]
- Ermakov, S.; Salashin, S.; Panchenko, A. Film slicks on the sea surface and some mechanisms of their formation. Dyn. Atmos. Oceans 1992, 16, 279–304. [Google Scholar] [CrossRef]
- Peltzer, R.; Griffin, O.; Barger, W.; Kaiser, J. High resolution measurement of surface active film redistribution in ship wakes. J. Geophys. Res. 1992, 97, 5231–5252. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, J. In situ measurements of surface tension wave damping and wind properties modified by natural films. J. Geophys. Res. 1992, 97, 5307–5313. [Google Scholar] [CrossRef]
- Riley, W.; Skirrow, G. Chemical Oceanography; Academic Press: New York, NY, USA, 1975; Volume 1 & 2. [Google Scholar]
- Herr, F.; Williams, J. Role of Surfactant Films on the Interfacial Properties of the Sea Surface; Office of Naval Research: London, UK, 1986. [Google Scholar]
- Liss, P.; Duce, R. The Sea Surface and Global Change; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Jones, I.; Toba, Y. Wind Stress over the Ocean; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Lewis, E.; Schwartz, S. Sea Salt Aerosol Production; American Geophysical Union: Washington, DC, USA, 2004. [Google Scholar]
- Gade, M.; Huhnerfuss, H.; Korenowski, G. Marine Surface Films; Springer: Berlin, Germany, 2006. [Google Scholar]
- Frew, N.; Nelson, R. Isolation of marine microlayer film surfactants for ex situ study of their physical and chemical properties. J. Geophys. Res. 1992, 97, 5281–5290. [Google Scholar] [CrossRef]
- Bock, E.; Frew, N. Static and dynamic response of natural ocean surface films to compression and dilation: Laboratory and field observations. J. Geophys. Res. 1993, 98, 14599–14617. [Google Scholar] [CrossRef]
- Frew, N. The role of organic films in air-sea gas exchange. In The Sea Surface and Global Change; Liss, P., Duce, R., Eds.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Frew, N.; Nelson, R.; Johnson, C. Correlation studies of mass spectral patterns and elasticity of sea-slick materials. In Marine Surface Films; Gade, M., Huhnerfuss, H., Korenowski, G., Eds.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Asher, W. The sea-surface microlayer and its effect on global air-sea gas transfer. In The Sea Surface and Global Change; Liss, P., Duce, R., Eds.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Tsai, W.; Liu, K. An assessment of the effect of sea surface surfactant on atmosphere-ocean CO2 flux. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Ito, A.; Kawamiya, M. Potential impact of ocean ecosystem changes due to global warming on marine organic aerosols. Glob. Biogeochem. Cycles 2010, 24. [Google Scholar] [CrossRef]
- Vignati, E.; Facchini, M.; Scannel, C.; Ceburnis, D.; Sciare, J.; Kanakidou, M.; Dentener, F.; O’Dowd, C. Global scale emission and distribution of sea-spray aerosol: Sea-salt and organic enrichment. Atmos. Environ. 2010, 44, 610–677. [Google Scholar] [CrossRef]
- Meskhidze, N.; Xu, J.; Gantt, B.; Nenes, Y.; Ghan, S.; Liu, X.; Easter, R.; Zaveri, R. Global contribution and climate forcing of marine organic aerosol 1: Model improvements and evaluation. Atmos. Chem. Phys. 2011, 11, 11689–11705. [Google Scholar] [CrossRef]
- Detwiler, A.; Blanchard, D. Aging and bursting bubbles in trace-contaminated water. Chem. Eng. Sci. 1978, 33, 9–13. [Google Scholar] [CrossRef]
- Gagosian, R.; Zafiriou, O.; Peltzer, E.; Alford, J. Lipids in aerosols from the tropical North Pacific: Temporal variability. J. Geophys. Res. 1982, 87, 11133–11144. [Google Scholar] [CrossRef]
- O’Dowd, C.; Facchini, M.; Cavalli, F.; Ceburnis, D.; Mircea, M.; Decesari, S.; Fuzzi, S.; Putaud, J. Biogenically driven organic contribution to marine aerosol. Nature 2004, 431, 676–681. [Google Scholar] [CrossRef] [PubMed]
- Modini, R.; Russell, L.; Deane, G.; Stokes, M. Effect of soluble surfactant on bubble persistence and bubble produced aerosol particles. J. Geophys. Res. 2013, 118. [Google Scholar] [CrossRef]
- Alpert, P.; Kilthau, W.; Bothe, D.; Radway, J.; Aller, J.; Knopf, D. The influence of marine microbial activities on aerosol production: A laboratory mesocosm study. J. Geophys. Res. 2015, 120. [Google Scholar] [CrossRef]
- Burrows, S.; Ogunro, O.; Frossard, A.; Russell, L.; Rasch, P.; Elliott, S. A physically based framework for modeling the organic fractionation of sea spray aerosol from bubble film Langmuir equilibria. Atmos. Chem. Phys. 2014, 14, 13601–13629. [Google Scholar] [CrossRef]
- Burrows, S.; Gobrogge, E.; Fu, L.; Link, K.; Elliott, S.; Rasch, P.; Wang, H.; Walker, R. OCEANFILMS-2: Representing co-adsorption of marine surfactants and soluble polysaccharides improves simulation of marine aerosol chemistry. Geophys. Res. Lett. 2016, 43, 8306–8313. [Google Scholar] [CrossRef]
- McCoy, D.; Burrows, S.; Wood, R.; Grosvenor, D.; Elliott, S.; Ma, P.; Rasch, P.; Hartmann, D. Natural aerosols explain seasonal and spatial patterns of Southern Ocean cloud albedo. Sci. Adv. 2015. [Google Scholar] [CrossRef] [PubMed]
- Ogunro, O.; Burrows, S.; Elliott, S.; Frossard, A.; Hoffman, F.; Letscher, R.; Moore, J.; Russell, L.; Wang, S.; Wingenter, O. Global distribution and surface activity of macromolecules in offline simulations of marine organic chemistry. Biogeochemistry 2015, 126, 25–56. [Google Scholar] [CrossRef]
- Szyszkowski, B. Experimentelle Studien uber kapillare Eigenschaften der wassrigen Losungen von Fettsauren. Z. Phys. Chem. 1908, 64, 385–414. [Google Scholar] [CrossRef]
- Langmuir, I. The constitution and fundamental properties of solids and liquids II. Liquids. J. Am. Soc. 1917, 39, 1848–1906. [Google Scholar] [CrossRef]
- Adamson, A. Physical Chemistry of Surfaces; Interscience: Easton, PA, USA, 1960. [Google Scholar]
- Elliott, S.; Burrows, S.; Deal, C.; Liu, X.; Long, M.; Ogunro, O.; Russell, L.; Wingenter, O. Prospects for simulating macromolecular surfactant chemistry at the ocean-atmosphere boundary. Environ. Res. Lett. 2014, 9, 064012. [Google Scholar] [CrossRef]
- Davies, J.; Rideal, E. Interfacial Phenomena; Academic Press: London, UK, 1963. [Google Scholar]
- Longhurst, A. Ecological Geography of the Sea; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Longhurst, A. Ecological Geography of the Sea; Elsevier: San Diego, CA, USA, 2007. [Google Scholar]
- Moore, J.; Doney, S.; Kleypas, J.; Glover, D.; Fung, I. An intermediate complexity marine ecosystem model for the global domain. Deep-Sea Res. II 2002, 49, 403–462. [Google Scholar] [CrossRef]
- Moore, J.; Doney, S.; Lindsay, K. Upper ocean ecosystem dynamics and iron cycling in a global three dimensional model. Glob. Biogeochem. Cycles 2004, 18, 18. [Google Scholar] [CrossRef]
- Letscher, R.; Moore, J. Preferential remineralization of dissolved organic phosphorus and non-Redfield DOM dynamics in the global ocean. Global Biogeochem. Cycles 2015, 29, 325–340. [Google Scholar] [CrossRef]
- Franklin, B. Of the stilling of waves by means of oils. Philos. Trans. R. Soc. Lond. B 1774, 64, 445–460. [Google Scholar] [CrossRef]
- Wang, D.; Steiglitz, H.; Marden, J.; Tamm, L. Philadelphia’s favorite son was a membrane biophysicist. Biophys. J. 2013, 104, 287–291. [Google Scholar] [CrossRef] [PubMed]
- Cox, C.; Zhang, X.; Duda, T. Suppressing breakers with polar oil films: Using an epic sea rescue to model wave energy budgets. Geophys. Res. Lett. 2016, 44. [Google Scholar] [CrossRef]
- Sverdrup, H.; Johnson, M.; Fleming, R. The Oceans: Their Physics, Chemistry and General Biology; Prentice-Hall: New York, NY, USA, 1942. [Google Scholar]
- Cox, C.; Munk, W. Statistics of the sea surface derived from sun glitter. J. Mar. Res. 1954, 16, 231–240. [Google Scholar]
- Blanchard, D. The electrification of the atmosphere by particles from bubbles in the sea. Prog. Oceanogr. 1963, 1, 73–202. [Google Scholar] [CrossRef]
- Davies, J. The effects of surface films in damping eddies at a free surface of a turbulent liquid. Proc. R. Soc. Lond. A 1966, 290, 515–526. [Google Scholar] [CrossRef]
- Jarvis, N. The effect of monomolecular films on surface temperature and convective motion at the water/air interface. J. Colloid Sci. 1962, 17, 512–522. [Google Scholar] [CrossRef]
- Garrett, W. The influence of monomolecular surface films on the production of condensation nucleii from bubbed sea water. J. Geophys. Res. 1968, 73, 5145–5150. [Google Scholar] [CrossRef]
- Paterson, M.; Spillane, K. Surface films and the production of sea salt aerosol. Q. J. R. Meterol. Soc. 1969, 95, 526–534. [Google Scholar] [CrossRef]
- Hoffman, E.; Duce, R. Factors influencing the organic carbon content of marine aerosols: A laboratory study. J. Geophys. Res. 1976, 81, 3667–3670. [Google Scholar] [CrossRef]
- Liss, P.; Slater, P. Flux of gases across the air-sea interface. Nature 1974, 247, 181–184. [Google Scholar] [CrossRef]
- Levich, V. Physicochemical Hydrodynamics; Prentice Hall: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]
- Lucassen-Reynders, E.; Lucassen, J. Properties of capillary waves. Adv. Colloid Interface Sci. 1969, 2, 347–395. [Google Scholar] [CrossRef]
- Jenkinson, I. Oceanographic implications of non-Newtonian properties found in phytoplankton cultures. Nature 1986, 323, 435–437. [Google Scholar] [CrossRef]
- Ermakov, S.; Zujkova, A.; Panchenko, A.; Salashin, S.; Talipova, T.; Titov, V. Surface film effects of short wind waves. Dyn. Atmos. Oceans 1986, 10, 31–50. [Google Scholar] [CrossRef]
- Piexoto, J.; Oort, A. Physics of Climate; Springer: Berlin, Germany, 1992. [Google Scholar]
- Dysthe, K. On surface renewal and sea slicks. In Marine Surface Films; Gade, M., Huhnerfuss, H., Korenowski, G., Eds.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Garrett, W. Organic chemical composition of the ocean surface. Deep-Sea Res. 1967, 14, 221–227. [Google Scholar] [CrossRef]
- Jarvis, N.; Garrett, W.; Scheiman, M.; Timmons, C. Surface chemical characterization of surface active material in seawater. Limnol. Oceanogr. 1967, 12, 88–96. [Google Scholar] [CrossRef]
- Wu, J. Suppression of ripples by surfactant: Spectral effects deduced from sun glitter, wave staff and microwave measurements. J. Phys. Oceanogr. 1989, 19, 238–245. [Google Scholar] [CrossRef]
- Mitsuyasu, H.; Bock, E. The influence of surface tension. In Wind Stress over the Ocean; Jones, I., Toba, Y., Eds.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Brunke, M.; Zeng, X.; Anderson, S. Uncertainties in sea surface turbulent flux algorithms and data. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Brunke, M.; Zeng, X.; Misra, V.; Beljaars, A. Integration of a prognostic sea surface skin temperature scheme into weather and climate models. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Lodziana, Z.; Topsoe, N.; Norskov, J. A negative surface energy for alumina. Nat. Mater. 2004, 3, 289–293. [Google Scholar] [CrossRef] [PubMed]
- Tuckermann, R. Surface tension of aqueous solutions of water-soluble organic and inorganic compounds. Atmos. Environ. 2007, 41, 6265–6275. [Google Scholar] [CrossRef]
- Ulabanathan, V.; Fainerman, V.; Gochev, G.; Aksenenko, E.; Gunes, D.; Gehin-Delval, C.; Miller, R. Evidence of negative surface pressure induced by beta lactoglobulin and casein at the water/air interface. Food Hydrocolloids 2014, 34, 10–14. [Google Scholar] [CrossRef]
- Atkins, P. Physical Chemistry, 2nd ed.; W.H. Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Adamson, A.; Gast, A. Physical Chemistry of Surfaces, 6th ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Wurl, O.; Holmes, D. The gelatinous nature of the sea-surface microlayer. Mar. Chem. 2008, 110, 89–97. [Google Scholar] [CrossRef]
- Cunliffe, M.; Upstill-Goddard, R.; Murrell, J. Microbiology of aquatic surface microlayers. FEMS Microbiol. Rev. 2011, 35, 233–246. [Google Scholar] [CrossRef] [PubMed]
- Wurl, O.; Miller, L.; Vagle, S. Production and fate of transparent exopolymer particles in the ocean. J. Geophys. Res. 2011, 116, C00H13. [Google Scholar] [CrossRef]
- Rossignol, S.; Tinel, L.; Bianco, A.; Passananti, M.; Donaldson, J.; George, C. Atmospheric chemistry at a fatty acid-coated air-water interface. Science 2016, 353, 699–702. [Google Scholar] [CrossRef] [PubMed]
- Van Vleet, E.; Williams, P. Surface potential and film pressure measurements in seawater systems. Limnol. Oceanogr. 1983, 28, 401–414. [Google Scholar] [CrossRef]
- Davies, J. Turbulence Phenomena; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Bell, T.; De Bruyn, W.; Miller, S.; Ward, B.; Christensen, K.; Saltzman, E. Air-sea dimethylsulfide (DMS) gas transfer in the North Atlantic. Atmos. Chem. Phys. 2013, 13, 11073–11087. [Google Scholar] [CrossRef]
- Garrett, W. Damping of capillary waves at the air-sea interface by organic surface-active material. J. Mar. Res. 1967, 25, 279–291. [Google Scholar]
- Hunter, K. Chemistry of the sea surface microlayer. In The Sea Surface and Global Change; Liss, P., Duce, R., Eds.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Hicks, B.; Drinkrow, R.; Grauze, G. Drag and bulk transfer coefficients associated with a shallow water surface. Bound. Layer Met. 1974, 6, 287–297. [Google Scholar] [CrossRef]
- Deacon, E. The role of coral mucus in reducing the wind drag over coral reefs. Bound. Layer Met. 1979, 17, 517–521. [Google Scholar] [CrossRef]
- Simpson, I.; Shaw, T.; Seager, R. Diagnosis of the seasonally and longitudinally varying midlatitude circulation response to global warming. J. Atmos. Sci. 2014, 71, 2489–2515. [Google Scholar] [CrossRef]
- Callaghan, A.; Deane, G.; Stokes, D. Two regimes of laboratory whitecap foam decay: Bubble plume controlled and surfactant stabilized. J. Phys. Oceanogr. 2013, 43, 1114–1126. [Google Scholar] [CrossRef]
- Clift, M.; Grace, J.; Webber, M. Bubbles, Drops and Particles; Dover: New York, NY, USA, 1978. [Google Scholar]
- Leifer, I.; Patro, R. The bubble mechanism for methane transport from the shallow sea bed to the surface: A review and sensitivity study. Cont. Shelf Res. 2002, 22, 2409–2428. [Google Scholar] [CrossRef]
- Deane, G.; Stokes, D. Scale dependence of bubble creation mechanisms in breaking waves. Nature 2002, 418, 839–844. [Google Scholar] [CrossRef] [PubMed]
- Friedlingstein, P.; Cox, P.; Betts, R.; Bopp, L.; Von Bloh, W.; Brovkin, V.; Cadule, P.; Doney, S.; Eby, M.; Fung, I.; et al. Carbon cycle feedback analysis: Results from the C4MIP model intercomparison. J. Clim. 2006, 19, 3337–3353. [Google Scholar] [CrossRef]
- Liu, X.; Easter, R.; Ghan, S.; Zaveri, R.; Rasch, P.; Shi, X.; Lamarque, J.; Gettelman, A.; Morrison, H.; Vitt, F.; et al. Toward a minimal representation of aerosols in climate models: description and evaluation of the Community Atmosphere Model CAM5. Geosci. Model Dev. 2012, 5, 703–739. [Google Scholar] [CrossRef]
- Six, K.; Kloster, S.; Ilyina, T.; Archer, S.; Zhang, K.; Maier-Reimer, E. Global warming amplified by reduced sulfur fluxes as a result of ocean acidification. Nat. Clim. Chang. 2013, 3, 975–978. [Google Scholar] [CrossRef]
- Edson, J.; Jampana, V.; Weller, R.; Bigorre, S.; Plueddemann, A.; Fairall, C.; Miller, S.; Mahrte, L.; Vickers, D.; Hersbach, H. On the exchange of momentum over the open ocean. J. Phys. Oceanogr. 2013, 43, 1589–1610. [Google Scholar] [CrossRef]
- Brunke, M.; Fairall, C.; Zeng, X.; Eymard, L.; Curry, J. Which bulk aerodynamic algorithms are least problematic in computing ocean surface turbulent fluxes? J. Clim. 2003, 16, 619–635. [Google Scholar] [CrossRef]
- Christodoulou, A.; Rosano, H. Effect of pH and nature of monovalent cations on surface isotherms of C16 to C22 saturated soap monolayers. Adv. Chem. 1968, 84, 210–234. [Google Scholar]
- Graham, D.; Phillips, M. Proteins at liquid interfaces II. Adsorption isotherms. J. Colloid Int. Sci. 1979, 70, 415–426. [Google Scholar] [CrossRef]
- Hansell, D.; Carlson, C.; Schlitzer, R. Net removal of major marine dissolved organic carbon fraction in the subsurface ocean. Glob. Biogeochem. Cycles 2012, 26. [Google Scholar] [CrossRef]
- Letscher, R.; Moore, J.; Teng, Y.; Primeau, F. Variable C:N:P stoichiometry of dissolved organic matter in the Community Earth System Model. Biogeosciences 2015, 12, 209–221. [Google Scholar] [CrossRef]
- Kumar, M. A review of chitin and chitosan applications. React. Funct. Polym. 2000, 46, 1–27. [Google Scholar] [CrossRef]
- Dittmar, T.; Kattner, G. Recalcitrant dissolved organic matter in the ocean: Major contribution of small amphiphilics. Mar. Chem. 2003, 82, 115–123. [Google Scholar] [CrossRef]
- Tuckermann, R.; Cammenga, H. Surface tension of aqueous solutions of some atmospheric water soluble organic compounds. Atmos. Environ. 2004, 38, 6135–6138. [Google Scholar] [CrossRef]
- Aluwihare, L.; Repeta, D.; Pantoja, S.; Johnson, C. Two chemically distinct pools of organic nitrogen accumulate in the ocean. Science 2005, 308, 1007–1010. [Google Scholar] [CrossRef] [PubMed]
- Petters, M.; Kreidenweis, S. A single parameter representation of hygroscopic growth and cloud condensation nucleus activity. Atmos. Chem. Phys. 2007, 7, 1961–1971. [Google Scholar] [CrossRef]
- Petters, S.; Petters, M. Surfactant effect on cloud condensation nuclei for two-component internally mixed aerosols. J. Geophys. Res. 2016, 121. [Google Scholar] [CrossRef]
- Parsons, T.; Takahashi, M.; Hargrave, B. Biological Oceanographic Processes; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Wakeham, S.; Lee, C.; Hedges, J.; Hernes, P.; Petersen, M. Molecular indicators of diagenetic status in marine organic matter. Geochim. Cosmochim. Acta 1997, 61, 5363–5369. [Google Scholar] [CrossRef]
- Nagata, T.; Meon, B.; Kirchman, D. Microbial degradation of peptidoglycan in seawater. Limnol. Oceanogr. 2003, 48, 745–754. [Google Scholar] [CrossRef]
- Fasham, M.; Sarmiento, J.; Slater, R.; Ducklow, H.; Williams, R. Ecosystem behavior at Bermuda Station “S” and ocean weather station “India”: A general circulation model and observational analysis. Glob. Biogeochem. Cycles 1993, 7, 379–415. [Google Scholar] [CrossRef]
- Sarmiento, J.; Slater, R.; Fasham, M.; Ducklow, H.; Toggweiler, J.; Evans, G. Seasonal three dimensional ecosystem model of nitrogen cycling in the North Atlantic euphotic zone. Glob. Biogeochem. Cycles 1993, 7, 415–450. [Google Scholar] [CrossRef]
- Benner, R. Chemical composition and reactivity. In Biogeochemistry of Dissolved Organic Matter; Hansell, D., Carlson, C., Eds.; Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Stumm, W.; Morgan, J. Aquatic Chemistry; Wiley Interscience: New York, NY, USA, 1981. [Google Scholar]
- Malcolm, R. The uniqueness of humic substances in each of soil, stream and marine environments. Geochim. Cosmochim. Acta 1990, 232, 19–30. [Google Scholar] [CrossRef]
- Kaiser, K.; Benner, R. Biochemical composition and size distribution of organic matter at the Pacific and Atlantic time series stations. Mar. Chem. 2009, 113, 63–77. [Google Scholar] [CrossRef]
- Parrish, C. Dissolved and particulate marine lipid classes: A review. Mar. Chem. 1988, 23, 17–40. [Google Scholar] [CrossRef]
- Alpers, W.; Huhnerfuss, H. The damping of ocean wave by surface films: A new look at an old problem. J. Geophys. Res. 1989, 94, 6251–6252. [Google Scholar] [CrossRef]
- Mitsuyasu, H.; Honda, T. Wind induced growth of water waves. J. Fluid Mech. 1982, 123, 425–442. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Oceanic primary production: Estimation by remotes sensing at local and regional scales. Science 1988, 241, 1613–1620. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Bada, J. Dissolved amino acids in the equatorial Pacific, the Sargasso Sea and Biscayne Bay. Limnol. Oceanogr. 1977, 22, 502–510. [Google Scholar] [CrossRef]
- Chavez, F.; Ryan, J.; Lluch-Cota, S.; Niquen, M. From anchovies to sardines and back: Multidecadal change in the Pacific Ocean. Science 2003, 299, 217–221. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Cameron-Smith, P.; Russell, L.; Ghan, S.; Liu, Y.; Elliott, S.; Yang, Y.; Lou, S.; Lamjiri, M.; Manizza, M. Role of dimethyl sulfide in the ENSO cycle of the tropics. J. Geophys. Res. 2016, 121, 13527–13558. [Google Scholar]
- Lumby, J.; Folkard, A. Variation in the surface tension of seawater in situ. Bull. Inst. Oceanogr. Monaco 1956, 1080, 1–19. [Google Scholar]
- Sieburth, J.; Conover, J. Slicks associated with Trichodesmium blooms in the Sargasso Sea. Nature 1965, 205, 830–831. [Google Scholar] [CrossRef]
- Garrett, W. Collection of slick forming materials from the sea surface. Limnol. Oceanogr. 1965, 10, 602–605. [Google Scholar] [CrossRef]
- Sturdy, G.; Fischer, W. Surface tension of slick patches near kelp beds. Nature 1966, 211, 951–952. [Google Scholar] [CrossRef]
- Hunter, K.; Liss, P. Organic sea surface films. In Marine Organic Chemistry; Duursma, E., Dawson, R., Eds.; Elsevier: Amsterdam, the Netherlands, 2002. [Google Scholar]
- Elliott, S.; Maltrud, M.; Reagan, M.; Moridis, G.; Cameron-Smith, P. Marine methane cycle simulations for the period of early global warming. J. Geophys. Res. 2011, 116, 495. [Google Scholar] [CrossRef]
- Large, W.; Pond, S. Open ocean flux measurements in moderate to strong winds. J. Phys. Oceanogr. 1981, 11, 324–337. [Google Scholar] [CrossRef]
- Jones, I.; Volkov, Y.; Toba, Y. Overview. In Wind Stress over the Ocean; Jones, I., Toba, Y., Eds.; Cambridge University Press: Cambridge, UK, 2001; pp. 1–34. [Google Scholar]
- Krembs, C.; Eicken, H.; Deming, J. Exopolymer alteration of physical properties of sea ice and implication for ice habitability and biogeochemistry in a warmer Arctic. Proc. Natl. Acad. Sci. USA 2011, 108, 3653–3658. [Google Scholar] [CrossRef] [PubMed]
- Nada, H.; Furukawa, Y. Antifreeze proteins: Computer simulation studies of the mechanism of ice growth inhibition. Polym. J. 2012, 44, 690–698. [Google Scholar] [CrossRef]
- Pruppacher, H.; Klett, J. Microphysics of Clouds and Precipitation; D. Reidel: Dordrecht, The Netherlands, 1978. [Google Scholar]
- Hassler, C.; Schoemann, V. The availability of organically bound Fe to model phytoplankton of the Southern Ocean. Biogeosciences 2009, 6, 2281–2296. [Google Scholar] [CrossRef]
- Hassler, C.; Schoemann, V.; Nichols, C.; Butler, E.; Boyd, P. Saccharides enhance iron bioavailability to Southern Ocean phytoplankton. Proc. Natl. Acad. Sci. USA 2011, 108, 1076–1081. [Google Scholar] [CrossRef] [PubMed]
- Alldredge, A.; Passow, U.; Logan, B. The abundance and significance of a class of large, transparent organic particles in the ocean. Deep-Sea Res. I 1993, 40, 1131–1140. [Google Scholar] [CrossRef]
- Passow, U.; Alldredge, A.; Logan, B. The role of particulate carbohydrate exudates in the flocculation of diatom blooms. Deep-Sea Res. I 1994, 41, 335–357. [Google Scholar] [CrossRef]
- Chin, W.; Orellana, M.; Verdugo, P. Spontaneous assembly of marine dissolved organic matter into polymer gels. Nature 1998, 391, 568–571. [Google Scholar]
- Wells, M. Marine colloids and trace metals. In Biogeochemistry of Dissolved Organic Matter; Hansell, D., Carlson, C., Eds.; Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Verdugo, P.; Alldredge, A.; Azam, F.; Kirchman, D.; Passow, U.; Santschi, P. The oceanoic gel phase: A bridge in the DOM-POM continuum. Mar. Chem. 2004, 92, 67–85. [Google Scholar] [CrossRef]
- Kraus, E.; Turner, J. A one-dimensional model of the seasonal thermocline. Tellus 1967, 19, 98–106. [Google Scholar] [CrossRef]
- Bowden, K. Oceanic and estuarine mixing processes. In Chemical Oceanography Vol. II; Riley, J., Skirrow, G., Eds.; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Johnson, J. The lifetime of carbonyl sulfide in the troposphere. Geophys. Res. Lett. 1981, 8, 938–940. [Google Scholar] [CrossRef]
- Woolf, D. Bubbles and their role in gas exchange. In The Sea Surface and Global Change; Liss, P., Duce, R., Eds.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Babak, V.; Skotnikova, E.; Lukina, I.; Pelletier, S.; Hubert, P.; Dellach, E. Hydrophobically associating alginate derivatives: Surface tension properties of their mixed aqueous solutions with oppositely charged surfactants. J. Colloid Int. Sci. 2000, 225, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Dutcher, C.; Wexler, A.; Clegg, S. Tensions of inorganic multicomponent aqueous electrolyte solutions and melts. J. Phys. Chem. 2010, 114, 12216–12230. [Google Scholar] [CrossRef] [PubMed]
- Dutcher, C.; Ge, W.; Wexler, A.; Clegg, S. Statistical mechanics of multilayer sorption: 2. Systems containing multiple solutes. J. Phys. Chem. 2012, 116, 1850–1864. [Google Scholar] [CrossRef]
- Erickson, D. A stability dependent theory for air-sea gas exchange. J. Geophys. Res. 1993, 98, 8471–8488. [Google Scholar] [CrossRef]
- Hardy, J. Biological effects of chemicals in the sea surface microlayer. In The Sea Surface and Global Change; Liss, P., Duce, R., Eds.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Callaghan, A.; Deane, G.; Stokes, D. Observed physical and environmental causes of scatter in white cap coverage values in a fetch-limited coastal zone. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Ward, A.; Tordai, L. Standard entropy of adsorption. Nature 1946, 158, 416–424. [Google Scholar] [CrossRef]
- Parra-Barraza, H.; Burboa, M.; Sanchez-Vazquez, M.; Goycoolea, F.; Valdez, M. Chitosan-cholesterol and chitosan-stearic acid interactions at the air-water interface. Biomacromolecules 2005, 6, 2416–2426. [Google Scholar] [CrossRef] [PubMed]
- Kanicky, J.; Shah, D. Effect of degree, type and position of unsaturation on the pKa of long-chain fatty acids. J. Colloid Int. Sci. 2002, 256, 201–207. [Google Scholar] [CrossRef]
- Peltzer, R.; Griffin, M. Stability of a three dimensional foam layer in seawater. J. Geophys. Res. 1988, 93, 10804–10812. [Google Scholar] [CrossRef]
- Sellegri, K.; O’Dowd, C.; Yoon, Y.; Jennings, S. Surfactants and submicron sea spray generation. J. Geophys. Res. 2006, 111, D22215. [Google Scholar] [CrossRef]
- Blanchard, D. Sea to air transport of surface active material. Science 1964, 146, 396–397. [Google Scholar] [CrossRef] [PubMed]
- Callaghan, A.; Deane, G.; Stokes, D.; Ward, B. Observed variation in the decay time of oceanic whitecap foams. J. Geophys. Res. 2012, 117, C09015. [Google Scholar] [CrossRef]
- Zhuang, G.; Yi, Z.; Duce, R.; Brown, P. Link between iron and sulphur cycles suggested by detection of Fe(II) in remote marine aerosols. Nature 1992, 355, 537–539. [Google Scholar] [CrossRef]
- Meskhidze, N.; Chameides, W.; Nenes, A. Dust and pollution: A recipe for enhanced ocean fertilization. J. Geophys. Res. 2005, 110, D03301. [Google Scholar] [CrossRef]
- Novakov, T.; Corrigan, E.; Penner, J.; Chuang, J.; Rosario, O.; Mayo-Bracero, O. Organic aerosols in Caribbean trade winds: A natural source? J. Geophys. Res. 1997, 97, 21307–21314. [Google Scholar] [CrossRef]
- Callaghan, A.; Stokes, D.; Deane, G. The effect of water temperature on air entrainment, bubble plumes and surface foam in a laboratory breaking-wave analog. J. Geophys. Res. 2014, 119, 7463–7482. [Google Scholar] [CrossRef]
- Meskhidze, N.; Nenes, A. Phytoplankton and cloudiness in the Southern Ocean. Science 2006, 314, 1419–1423. [Google Scholar] [CrossRef] [PubMed]
- Boyer, H.; Dutcher, C. Statistical thermodynamic model for surface tension of aqueous organic acids with consideration of partial dissociation. J. Phys. Chem. 2016, 120, 4368–4375. [Google Scholar] [CrossRef] [PubMed]
- Singer, S. Note on an equation of state for linear macromolecules in monolayers. J. Chem. Phys. 1948, 16, 872–876. [Google Scholar] [CrossRef]
- Bull, H. Determination of molecular weights of proteins in spread monolayers. J. Biol. Chem. 1950, 185, 27–38. [Google Scholar] [PubMed]
- Kirkwood, J.; Buff, F. The statistical mechanical theory of surface tension. J. Chem. Phys. 1949, 17, 338–343. [Google Scholar] [CrossRef]
- Salter, S.; Davis, H. Statistical mechanical calculations of the surface tension of fluids. J. Chem. Phys. 1975, 63, 3295–3307. [Google Scholar] [CrossRef]
- Kujawinski, E.; Soule, M.; Valentine, D.; Boysen, A.; Longnecker, K.; Redmond, M. Fate of dispersants associated with the Deepwater Horizon oil spill. Environ. Sci. Tech. 2011, 45, 1298–1306. [Google Scholar] [CrossRef] [PubMed]
- Sarupria, S.; Debenedetti, P. Homogenous nucleation of methane hydrate in microsecond molecular dynamics simulations. J. Phys. Chem. Lett. 2012, 3, 2942–2947. [Google Scholar] [CrossRef] [PubMed]
- Tan, L.; Pratt, L.; Chaudhari, M. Molecular-scale description of SPAN80 desorption from the squalane-water interface. J. Phys. Chem. B 2017, 122, 3378–3383. [Google Scholar] [CrossRef] [PubMed]
- Krummel, O. Handbook of Oceanography; J. Engelhorn: Stuttgart, Germany, 1911. [Google Scholar]
- Fleming, R.H.; Revelle, R. Physical processes in the ocean. In Recent Marine Sediments; Trask, P., Ed.; American Association of Petroleum Geologists: Tulsa, OK, USA, 1939. [Google Scholar]
- Guastalla, J. Diluted films of some proteins; Determination of molecular masses. C. R. 1939, 208, 1078–1080. [Google Scholar]
- Freundlich, H. Colloid and Capillary Chemistry; Methuen and Co.: London, UK, 1926. [Google Scholar]
- Laidler, K. Chemical Kinetics; McGraw Hill: New York, NY, USA, 1965. [Google Scholar]
- Ter Minassian-Saraga, L. Recent work on spread monolayers, adsorption and desorption. J. Colloid Sci. 1956, 11, 398–418. [Google Scholar] [CrossRef]
- Brzozowska, A.; Duits, M.; Mugele, F. Stability of stearic acid monolayers on artificial sea water. Colloid Surf. 2012, 407, 38–48. [Google Scholar] [CrossRef]
- Nilsson, L.; Bergenstahl, B. Adsorption of hydrophobically modified starch at oil-water interfaces during emulsification. Langmuir 2006, 22, 8770–8776. [Google Scholar] [CrossRef] [PubMed]
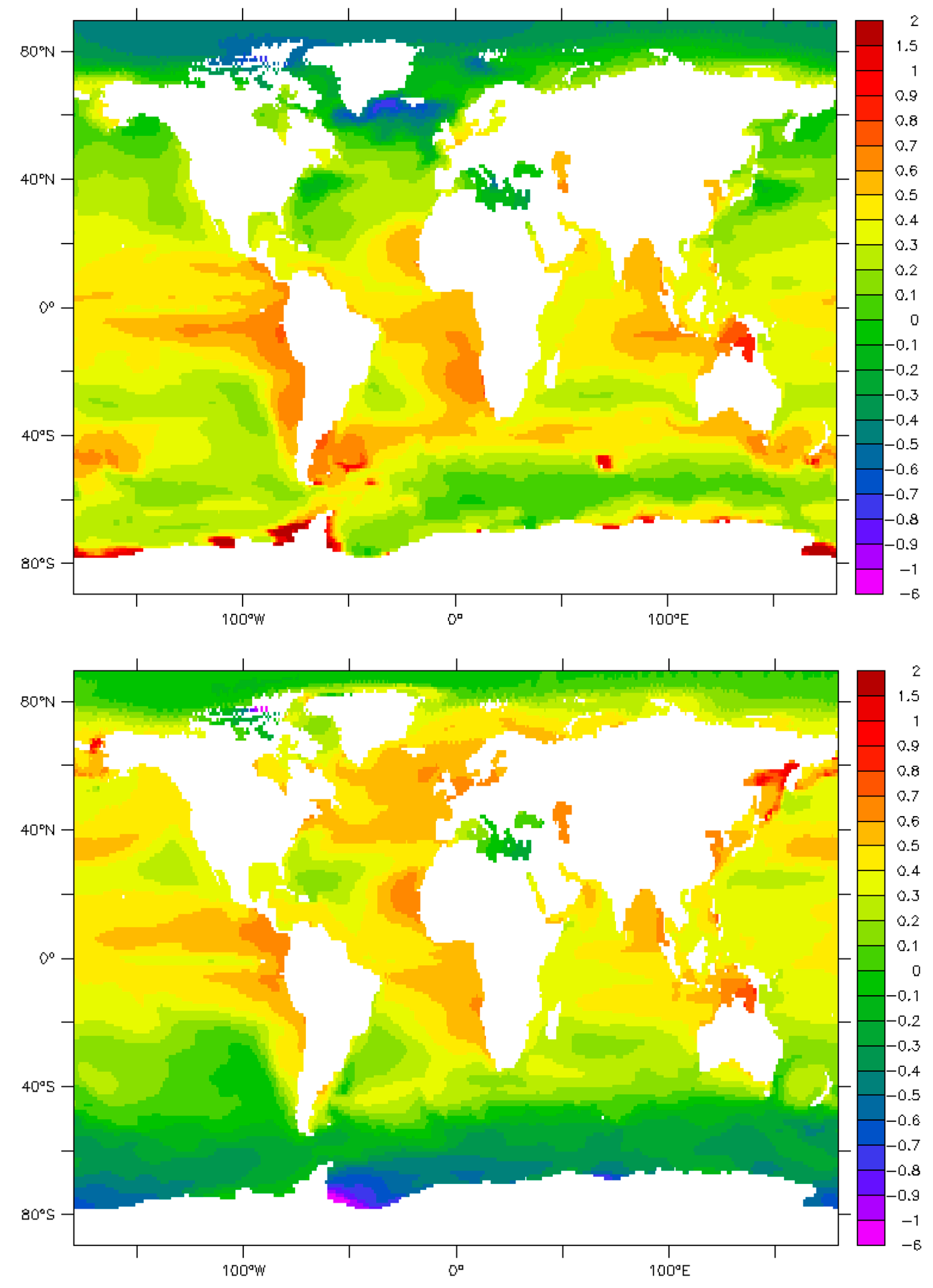
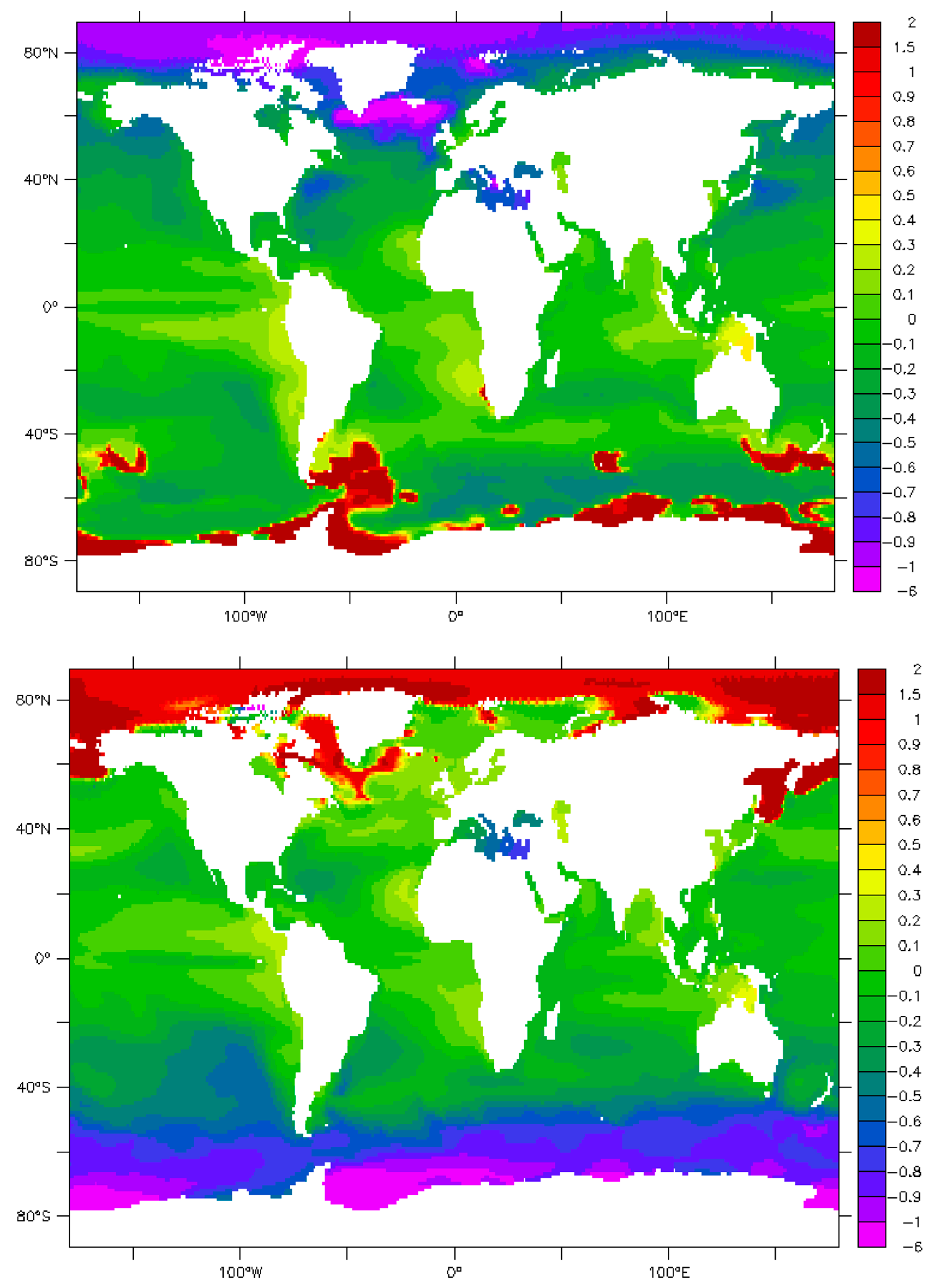
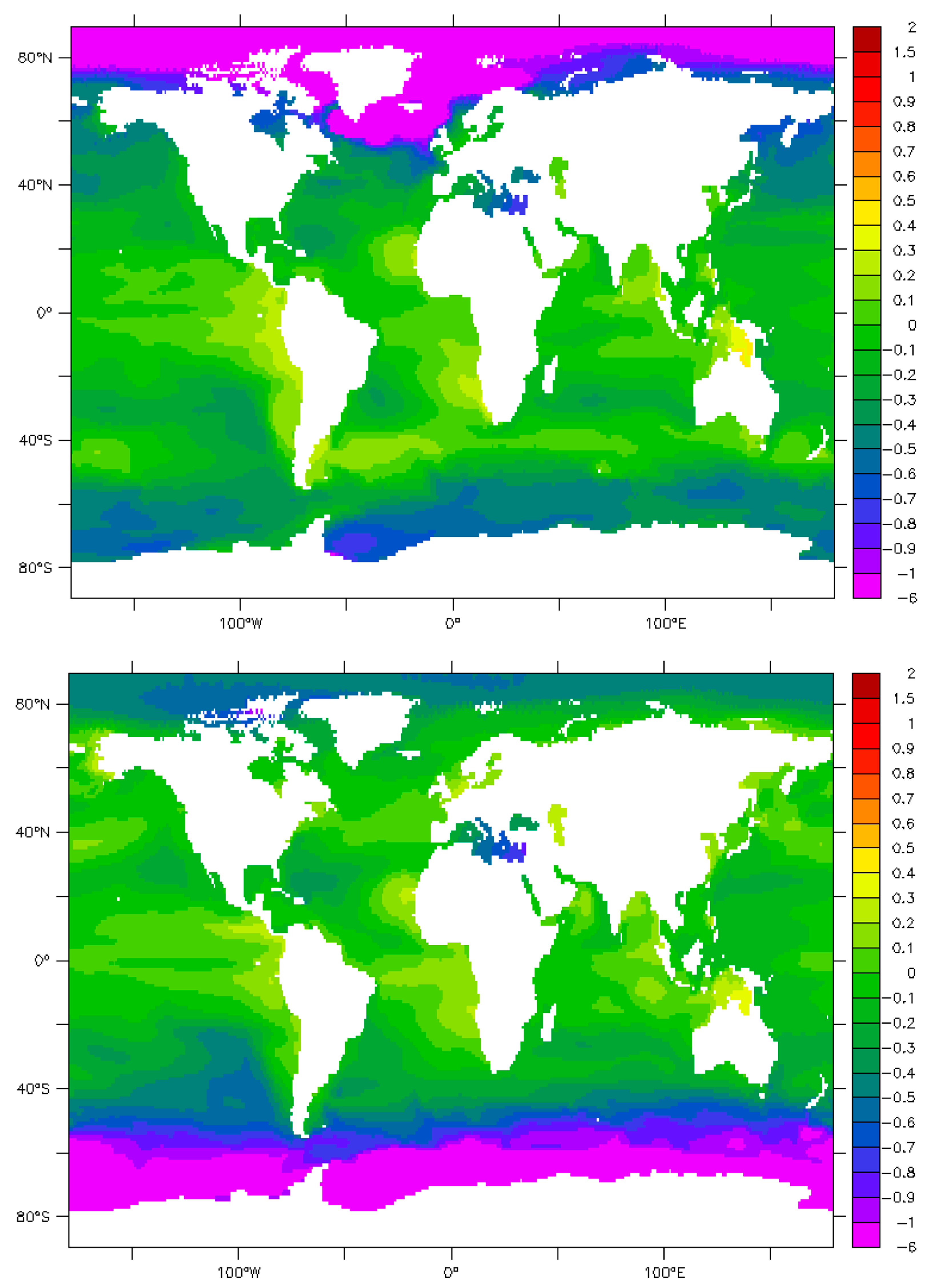
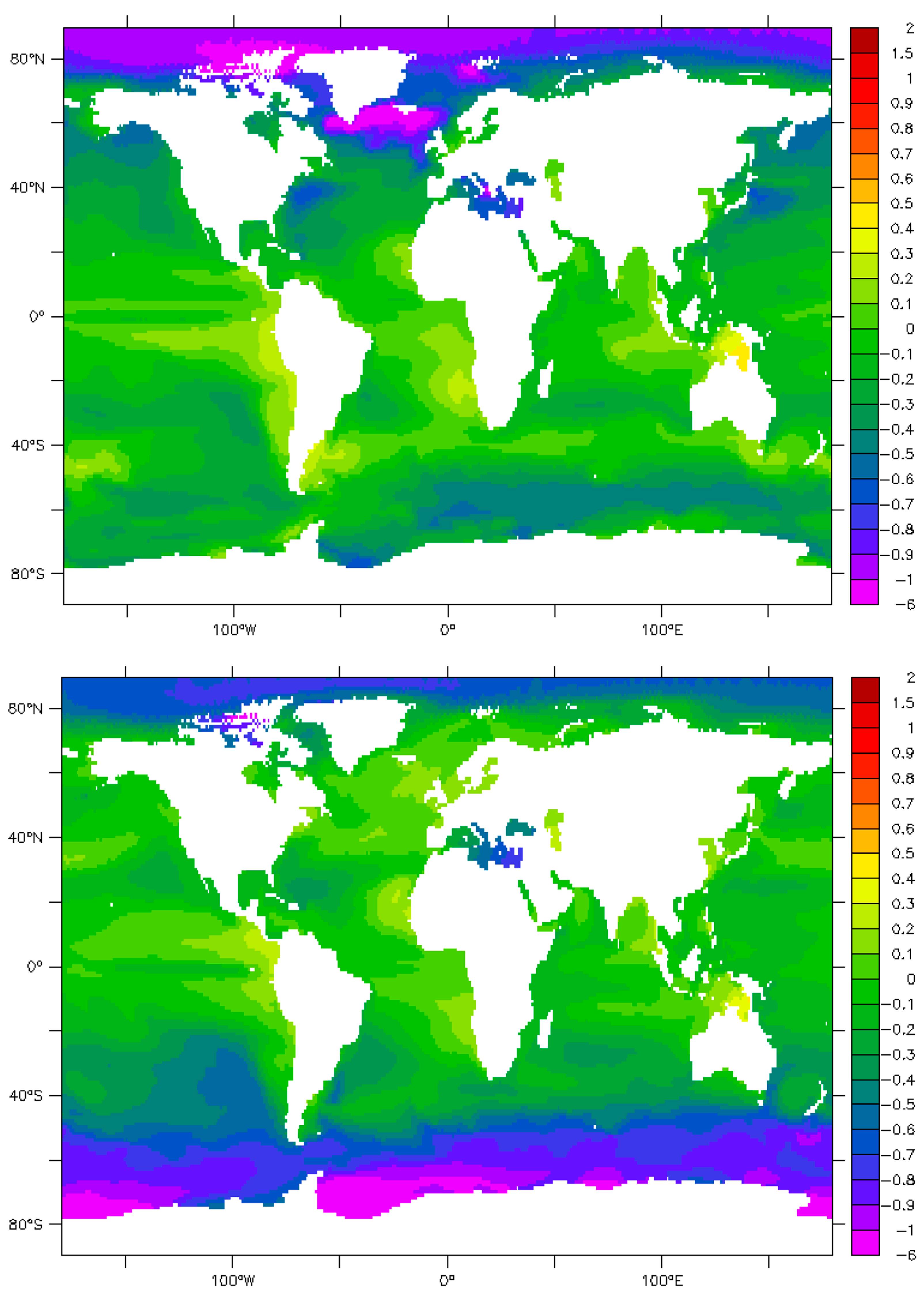
| Phenomenon | Measured π | Parameter | Effect | References/Authors |
|---|---|---|---|---|
| Trace Gas Transfer | 0.3–3 mN/m | Piston Velocity | Lower 3x | Davies 1966 and 1972; Goldman et al. 1988; Frew 1997; Tsai and Liu 2003, Frew et al. 2006; Bell et al. 2013 |
| Sea Spray Flux | 1–10 mN/m | Number or Efficiency | ±3x | Blanchard 1963; Garrett 1968; Paterson and Spillane 1969; Detwiler and Blanchard 1978; Lewis and Schwartz 2004; Modini et al. 2013; Alpert et al. 2015 |
| Ripples/Capillaries | 0.3–3 mN/m | Damping e-Fold Distance | Lower 3x | Garrett 1967; Jarvis et al. 1967; Ermakov et al. 1986; Wei and Wu 1992; Bock and Frew, 1993; Hunter 1997; Dysthe 2006 |
| Boundary Wind | >1 mN/m (so above background) | Drag Coefficient | Lower 3x | Hicks et al. 1974; Deacon 1979; Ermakov et al. 1986; Asher 1997; Mitsuyasu and Bock 2001; Simpson et al. 2014; Cox et al. 2016 |
| Chemistry | Monomeric Units | Examples | C (1/2 π max) (μM) | Surface Phase |
|---|---|---|---|---|
| Protein | Amino Acids | Enzymes, Collagen and structural | 101–102 | 2D gas |
| Polysaccharide | Sugars | Alginates, Uronics | 105 | (soluble) |
| Lipid | (aliphatic with some double bonding) | Fatty Acids, Sterols, Triglycerides | 100 (estimate) | 2D solid (often) |
| Aminosugars | Replace OH by N in the saccharide | Chitin, Chitosan | (insoluble) | 2D solid (Chitos) |
| Hybrids of above | Combined | Peptidoglycan, Lipopolysaccharide | 104 (Peptido) | Planar mixing interactions |
| Humic/Fulvic | Recondensates | Suwannee River, Deep Arctic | 105 | 2D liquid |
| Atmospheric | (C chains, rings) | Levoglucosan, dicarboxylics, lipids, then oxidation | >106 (Levo) | (soluble, Levo) |
| Provinces | CALC CNRY | CAMR PNEC ARAB | BPLR BERS ARCT | KURO NPPF GFST | PEQD ETRA | WARM WTRA MONS | NPTG NAST NATR |
|---|---|---|---|---|---|---|---|
| Surfactomes | Coastal (Mid-Lat) | Coastal (Low-Lat) | Polar | Westerly | Equator (East) | Equator (West) | Gyre |
| Protein | |||||||
| Longhurst | 4 (22) | 6 (20) | 1.5 (27) | 0.8 (8) | 5 | 1 | 0.8 |
| Ogunro 2015 | 3 (10) | 3 (10) | 1 (10) | 3 (7) | 3–10 | 1–3 | 1 |
| Letscher 2015 | 5 (10) | 5 (7) | 1 (10) | 3 (7) | 3–10 | 7 | 3 |
| Measurements | - | - | 1 (na) | 0.3 (3) | 0.5–1 | - | 0.5–1 |
| Carry forward | 4 (15) | 5 (15) | 1 (15) | 1 (5) | 5 | 3 | 1 |
| Lipid | |||||||
| Longhurst | 0.1 (0.7) | 0.2 (0.7) | 0.03 (0.9) | 0.03 (0.3) | 0.2 | 0.05 | 0.03 |
| Ogunro 2015 | 0.03 (1) | 0.01 (0.05) | 0 (3) | 0.01 (0.3) | 0.03–3 | 0.01 | 0.01–0.03 |
| Letscher 2015 | 0.01 (0.3) | 0.01 (0.03) | 0 (3) | 0 (1) | 0.03–0.3 | <0.01 | 0.01 |
| Measurements | 0.3 (3) | - | - | - | 0.1–3 | - | 0.003–0.3 |
| Carry forward | 0.1 (1) | 0.03 (0.1) | 0 (3) | 0.01 (0.3) | 1 | 0.03 | 0.01 |
| Surfactomes | Coastal (Mid-Lat) | Coastal (Low-Lat) | Polar | Westerly | Equator (East) | Equator (West) | Gyre |
|---|---|---|---|---|---|---|---|
| Surface Pressure and Modulus, units mN/m both Cases | |||||||
| π (Appendix) | 2.4 (9.4) | 2.9 (6.7) | 0.65 (50) | 0.65 (2.9) | 6.5 | 1.8 | 0.65 |
| π (data) | 0.3 (23) | 0.1 (10) | 0.1 (5) | 0.1–1 | |||
| ε (local) | 6.6 (25) | 8.0 (18.1) | 1.6 (175) | 1.5 (8.2) | 10 | 4.9 | 1.6 |
| 2D Phase | |||||||
| Model | g (l-s) | g (g) | g (s) | g (l) | s | g | g |
| Data | g-l (l) | g-l (l) | l-s | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elliott, S.; Burrows, S.; Cameron-Smith, P.; Hoffman, F.; Hunke, E.; Jeffery, N.; Liu, Y.; Maltrud, M.; Menzo, Z.; Ogunro, O.; et al. Does Marine Surface Tension Have Global Biogeography? Addition for the OCEANFILMS Package. Atmosphere 2018, 9, 216. https://doi.org/10.3390/atmos9060216
Elliott S, Burrows S, Cameron-Smith P, Hoffman F, Hunke E, Jeffery N, Liu Y, Maltrud M, Menzo Z, Ogunro O, et al. Does Marine Surface Tension Have Global Biogeography? Addition for the OCEANFILMS Package. Atmosphere. 2018; 9(6):216. https://doi.org/10.3390/atmos9060216
Chicago/Turabian StyleElliott, Scott, Susannah Burrows, Philip Cameron-Smith, Forrest Hoffman, Elizabeth Hunke, Nicole Jeffery, Yina Liu, Mathew Maltrud, Zachary Menzo, Oluwaseun Ogunro, and et al. 2018. "Does Marine Surface Tension Have Global Biogeography? Addition for the OCEANFILMS Package" Atmosphere 9, no. 6: 216. https://doi.org/10.3390/atmos9060216
APA StyleElliott, S., Burrows, S., Cameron-Smith, P., Hoffman, F., Hunke, E., Jeffery, N., Liu, Y., Maltrud, M., Menzo, Z., Ogunro, O., Van Roekel, L., Wang, S., Brunke, M., Jin, M., Letscher, R., Meskhidze, N., Russell, L., Simpson, I., Stokes, D., & Wingenter, O. (2018). Does Marine Surface Tension Have Global Biogeography? Addition for the OCEANFILMS Package. Atmosphere, 9(6), 216. https://doi.org/10.3390/atmos9060216







