Spatial Estimation of Thermal Indices in Urban Areas—Basics of the SkyHelios Model
Abstract
1. Introduction
- Provide a detailed and comprehensive description of the extensions to the diagnostic SkyHelios model,
- Describe the models capabilities in the course of a small case study,
- Indicate opportunities and limitations analyzing the results,
- Identify the most suitable shading type for the reduction of heat stress.
2. Materials and Methods
2.1. Radiation Modeling
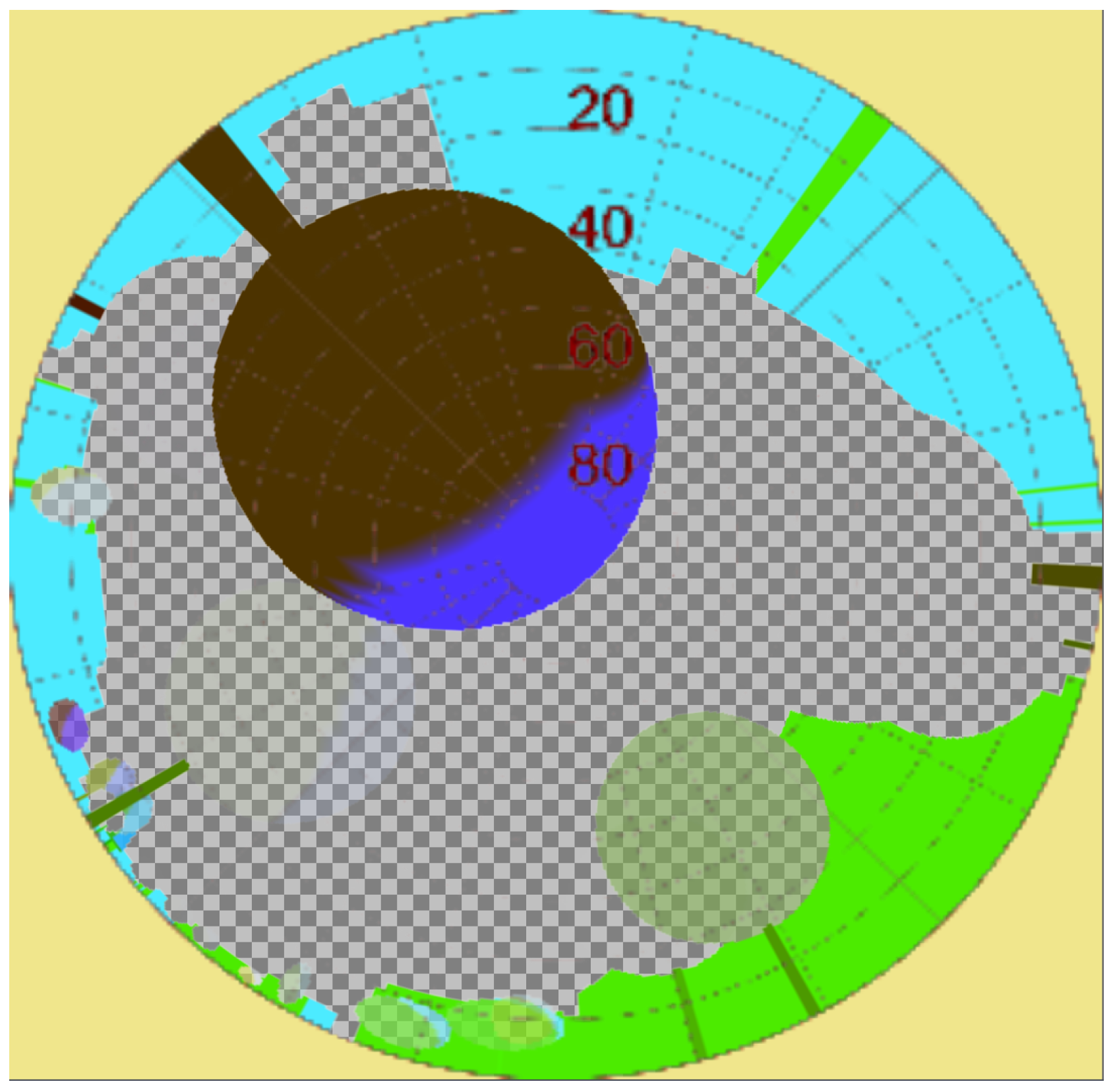
2.1.1. Sky View Factor
2.1.2. Shortwave Radiation
Direct Shortwave Irradiation
Diffuse Shortwave Irradiation
2.1.3. Longwave Radiation
2.1.4. Mean Radiant Temperature
2.2. Wind Modeling
2.2.1. Upwind Stagnation Zone
2.2.2. Downwind Recirculation Zone
2.2.3. Street Canyon Parametrization
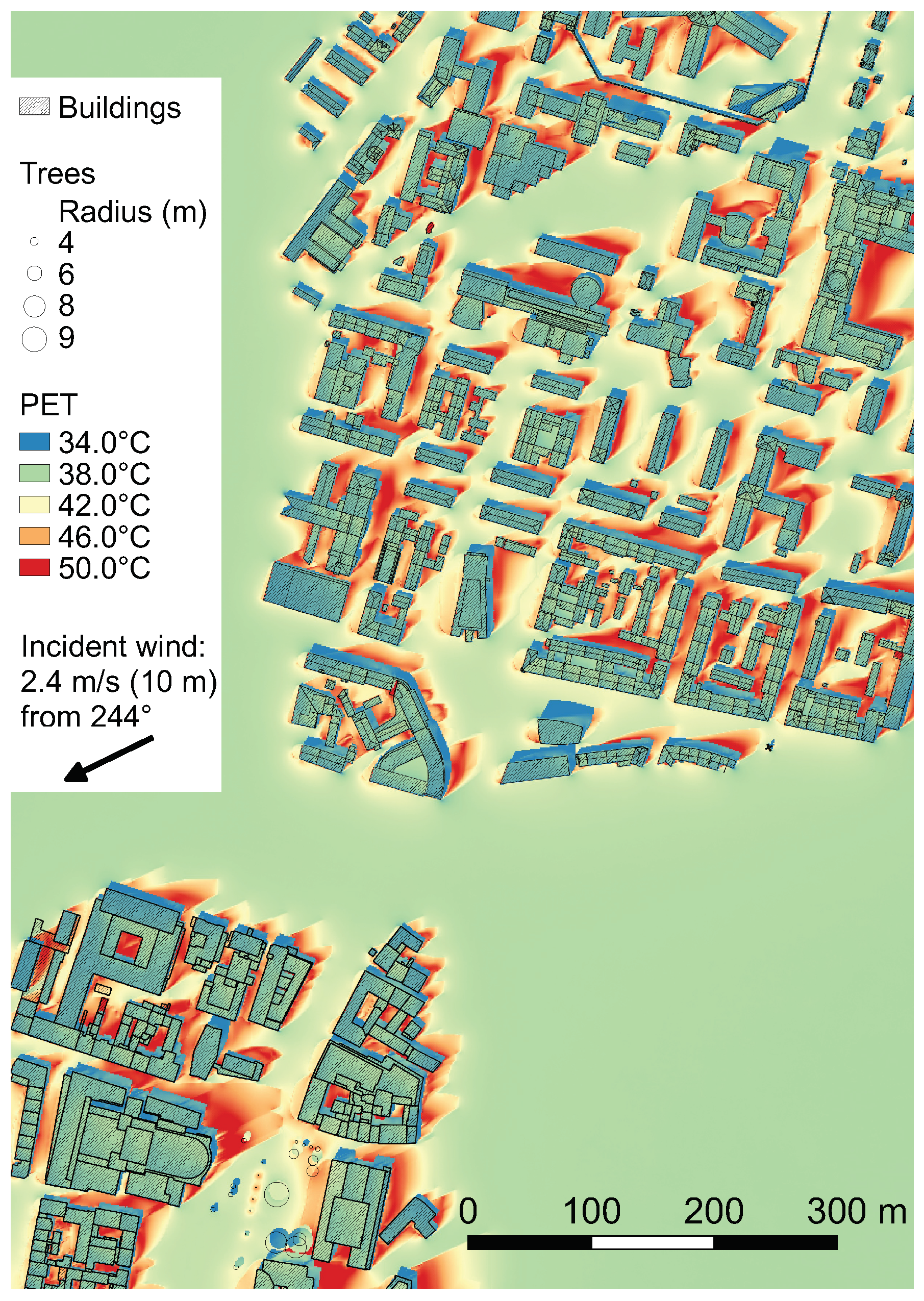
2.3. Area of Interest and Data
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Matzarakis, A.; Muthers, S.; Koch, E. Human-biometeorological evaluation of summer mortality in Vienna. Theor. Appl. Climatol. 2011, 105, 1–10. [Google Scholar] [CrossRef]
- Ketterer, C.; Matzarakis, A. Comparison of Different Methods for the Assessment of the Urban Heat Island in Stuttgart, Germany. Int. J. Biometeorol. 2015, 59, 1299–1309. [Google Scholar] [CrossRef] [PubMed]
- Fröhlich, D.; Matzarakis, A. Modeling of changes in human thermal bioclimate resulting from changes in urban design—Examples based on a popular place in Freiburg, SW-Germany. In Proceedings of the MettoolsVIII, 8. Fachtagung des Ausschusses Umweltmeteorologie der Deutschen Meteorologischen Gesellschaft, Leipzig, Germany, 20–22 March 2012; pp. 1–8. [Google Scholar]
- Lopes, A.; Lopes, S.; Matzarakis, A.; Alcoforado, M.J. The influence of the summer sea breeze on thermal comfort in Funchal (Madeira). A contribution to tourism and urban planning. Meteorol. Z. 2011, 20, 553–564. [Google Scholar] [CrossRef]
- Lin, T.P.; Matzarakis, A.; Hwang, R.L. Shading effect on long-term outdoor thermal comfort. Build. Environ. 2010, 45, 213–221. [Google Scholar] [CrossRef]
- Hwang, R.L.; Lin, T.P.; Matzarakis, A. Seasonal effects of urban street shading on long-term outdoor thermal comfort. Build. Environ. 2011, 46, 863–870. [Google Scholar] [CrossRef]
- Fröhlich, D.; Matzarakis, A. Modeling of changes in thermal bioclimate: Examples based on urban spaces in Freiburg, Germany. Theor. Appl. Climatol. 2013, 111, 547–558. [Google Scholar] [CrossRef]
- Lin, T.P.; Tsai, K.T.; Liao, C.C.; Huang, Y.C. Effects of thermal comfort and adaptation on park attendance regarding different shading levels and activity types. Build. Environ. 2013, 59, 599–611. [Google Scholar] [CrossRef]
- Charalampopoulos, I.; Tsiros, I.; Chronopoulou-Sereli, A.; Matzarakis, A. A note on the evolution of the daily pattern of thermal comfort-related micrometeorological parameters in small urban sites in Athens. Int. J. Biometeorol. 2015, 59, 1223–1236. [Google Scholar] [CrossRef] [PubMed]
- VDI. VDI Guideline 3787, Part 2: Environmental Meteorology. Methods for the Human Biometeorological Evaluation of Climate and Air Quality for Urban and Regional Planning at Regional Level. Part I: Climate; Technical Report 1b; VDI: Düsseldorf, Germany, 2008. [Google Scholar]
- Herrmann, J.; Matzarakis, A. Mean radiant temperature in idealized urban canyons—Examples from Freiburg, Germany. Int. J. Biometeorol. 2012, 56, 199–203. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.P.; Matzarakis, A.; Hwang, R.L.; Huang, Y.C. Effect of pavements albedo on long-term outdoor thermal comfort. In Proceedings of the 7th Conference on Biometeorology, Freiburg, Germany, 12–14 April 2010; Volume 20, pp. 498–504. [Google Scholar]
- Shashua-Bar, L.; Pearlmutter, D.; Erell, E. The influence of trees and grass on outdoor thermal comfort in a hot-arid environment. Int. J. Climatol. 2011, 31, 1498–1506. [Google Scholar] [CrossRef]
- Bruse, M.; Fleer, H. Simulating surface–plant–air interactions inside urban environments with a three dimensional numerical model. Environ. Model. Softw. 1998, 13, 373–384. [Google Scholar] [CrossRef]
- Bruse, M. Die Auswirkungen Kleinskaliger Umweltgestaltung auf das Mikroklima. Entwicklung des Prognostischen Numerischen Modells ENVI-met zur Simulation der Wind-, Temperatur- und Feuchteverteilung in StäDtischen Strukturen. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 1999. [Google Scholar]
- Lindberg, F.; Grimmond, C.S.B.; Gabey, A.; Huang, B.; Kent, C.W.; Sun, T.; Theeuwes, N.E.; Jarvi, L.; Ward, H.C.; Capel-Timms, I.; et al. Urban Multi-scale Environmental Predictor (UMEP): An integrated tool for city-based climate services. Environ. Model. Softw. 2018, 99, 70–87. [Google Scholar] [CrossRef]
- Lindberg, F.; Holmer, B.; Thorsson, S. SOLWEIG 1.0—Modelling spatial variations of 3D radiant fluxes and mean radiant temperature in complex urban settings. Int. J. Biometeorol. 2008, 52, 697–713. [Google Scholar] [CrossRef] [PubMed]
- Matzarakis, A.; Matuschek, O. Sky view factor as a parameter in applied climatology—Rapid estimation by the SkyHelios model. Meteorol. Z. 2011, 20, 39–45. [Google Scholar] [CrossRef]
- Staiger, H.; Laschewski, G.; Graetz, A. The perceived temperature - a versatile index for the assessment of the human thermal environment. Part A: Scientific basics. Int. J. Biometeorol. 2012, 56, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Jendritzky, G.; de Dear, R.; Havenith, G. UTCI-Why another thermal index? Int. J. Biometeorol. 2012, 421–428. [Google Scholar] [CrossRef] [PubMed]
- Bröde, P.; Fiala, D.; Blazejczyk, K.; Holmér, I.; Jendritzky, G.; Kampmann, B.; Tinz, B.; Havenith, G. Deriving the operational procedure for the Universal Thermal Climate Index (UTCI). Int. J. Biometeorol. 2012, 56, 481–494. [Google Scholar] [CrossRef] [PubMed]
- Höppe, P.R. The physiological equivalent temperature—A universal index for the biometeorological assessment of the thermal environment. Int. J. Biometeorol. 1999, 43, 71–75. [Google Scholar] [CrossRef] [PubMed]
- MOGRE Community. Managed Open Graphics Rendering Engine; MOGRE Community, 2016; Available online: http://wiki.ogre3d.org/MOGRE (accessed on 18 November 2017).
- Open Source Geospatial Foundation. GDAL/OGR Geospatial Data Abstraction Software Library; Open Source Geospatial Foundation, 2018; Available online: http://gdal.org (accessed on 18 March 2018).
- Matzarakis, A.; Rutz, F.; Mayer, H. Modelling radiation fluxes in simple and complex environments—Application of the RayMan model. Int. J. Biometeorol. 2007, 51, 323–334. [Google Scholar] [CrossRef] [PubMed]
- Matzarakis, A.; Rutz, F.; Mayer, H. Modelling radiation fluxes in simple and complex environments: Basics of the RayMan model. Int. J. Biometeorol. 2010, 54, 131–139. [Google Scholar] [CrossRef] [PubMed]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge: London, UK; New York, NY, USA, 1995. [Google Scholar]
- Hämmerle, M.; Gál, T.; Unger, J.; Matzarakis, A. Comparison of models calculating the Sky View Factor used for urban climate investigations. Theor. Appl. Climatol. 2011, 105, 521–527. [Google Scholar] [CrossRef]
- Jendritzky, G.; Menz, H.; Schirmer, H.; Schmidt-Kessen, W. Methodik zur Raumbezogenen Bewertung der Thermischen Komponente im Bioklima des Menschen (Fortgeschriebenes Klima-Michel-Modell); Akad für Raumforschung und Landesplanung: Hannover, Germany, 1990. [Google Scholar]
- VDI. VDI Guideline 3789, Part 1: Climate. Environmental Meteorology, Interactions between Atmosphere and Surface; Calculation of Short-and Long Wave Radiation. Part 2: VDI/DIN-Handbuch Reinhaltung der Luft; Technical Report 1b; VDI: Düsseldorf, Germany, 1994. [Google Scholar]
- Kasten, F.; Young, A. Revised optical air-mass tables and approximation formula. Appl. Opt. 1989, 28, 4735–4738. [Google Scholar] [CrossRef] [PubMed]
- Kasten, F. A simple parametrization of the pyrheliometric formula for determining the linke turbidity factor. Meteorol. Rundsch. 1980, 33, 124–127. [Google Scholar]
- Krayenhoff, E.S.; Voogt, J.A. A microscale three-dimensional urban energy balance model for studying surface temperatures. Bound.-Layer Meteorol. 2007, 123, 433–461. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y. Development of a Three-Dimensional Urban Energy Model for Predicting and Understanding Surface Temperature Distribution. Bound.-Layer Meteorol. 2013, 149, 303–321. [Google Scholar] [CrossRef]
- Resler, J.; Krč, P.; Belda, M.; Juruš, P.; Benešová, N.; Lopata, J.; Vlček, O.; Damašková, D.; Eben, K.; Derbek, P.; et al. PALM-USM v1.0: A new urban surface model integrated into the PALM large-eddy simulation model. Geosci. Model Dev. 2017, 10, 3635–3659. [Google Scholar] [CrossRef]
- Valko, P. Die Himmelsstrahlung in ihrer Beziehung zu verschiedenen Parametern. Arch. Meteorol. Geophys. Bioklimatol. Ser. B 1966, 14, 336–359. [Google Scholar] [CrossRef]
- Fanger, P. Thermal Comfort; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Staiger, H.; Matzarakis, A. Evaluation of atmospheric thermal radiation algorithms for daylight hours. Theor. Appl. Climatol. 2010, 102, 227–241. [Google Scholar] [CrossRef]
- Brunt, D. Notes on radiation in the atmosphere. I. Q. J. R. Meteorol. Soc. 1932, 58, 389–420. [Google Scholar] [CrossRef]
- Swinbank, W.C. Long-wave radiation from clear skies. Q. J. R. Meteorol. Soc. 1963, 89, 339–348. [Google Scholar] [CrossRef]
- Satterlund, D. Improved equation for estimating long-wave-radiation from the atmosphere. Water Resour. Res. 1979, 15, 1649–1650. [Google Scholar] [CrossRef]
- Crawford, T.M.; Duchon, C.E. An Improved Parameterization for Estimating Effective Atmospheric Emissivity for Use in Calculating Daytime Downwelling Longwave Radiation. J. Appl. Meteorol. 1999, 38, 474–480. [Google Scholar] [CrossRef]
- Iziomon, M.G.; Mayer, H.; Matzarakis, A. Downward atmospheric longwave irradiance under clear and cloudy skies: Measurement and parameterization. J. Atmos. Sol.-Terr. Phys. 2003, 65, 1107–1116. [Google Scholar] [CrossRef]
- Duarte, H.F.; Dias, N.L.; Maggiotto, S.R. Assessing daytime downward longwave radiation estimates for clear and cloudy skies in Southern Brazil. Agric. For. Meteorol. 2006, 139, 171–181. [Google Scholar] [CrossRef]
- Kantor, N.; Unger, J. The most problematic variable in the course of human-biometeorological comfort assessment—The mean radiant temperature. Cent. Eur. J. Geosci. 2011, 3, 90–100. [Google Scholar] [CrossRef]
- Chen, Y.C.; Lin, T.P.; Matzarakis, A. Comparison of mean radiant temperature from field experiment and modelling: A case study in Freiburg, Germany. Theor. Appl. Climatol. 2014, 118, 535–551. [Google Scholar] [CrossRef]
- Der Luft, V.K.R. Stadtklima und Luftreinhaltung: Ein Wissenschaftliches Handbuch für die Praxis in der Umweltplanung; mit 47 Tabellen; Technical Report; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Helbig, A.; Baumüller, J.; Kerschgens, M.J. Stadtklima und Luftreinhaltung. 2., VollstäNdig üBerarbeitete und ErgäNzte Auflage mit 200 Abbildungen und 79 Tabellen, 2th ed.; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Matzarakis, A. Die thermische Komponente des Stadtklimas; Number 6 in Berichte des Meteorologischen Institutes der Universität Freiburg; Meteorologisches Inst.: Freiburg, Germany, 2001. [Google Scholar]
- Röckle, R. Bestimmung der Strömungsverhältnisse im Bereich Komplexer Bebauungsstrukturen. Ph.D. Thesis, Fachbereich Mechanik der Technischen Hochschule Darmstadt, Darmstadt, Germany, 1990. [Google Scholar]
- Bagal, N.; Pardyjak, E.; Brown, M. Improved Upwind Cavity Parameterizations for a Fast Response Urban Wind Model. In Proceedings of the AMS Symposium on Planning, Nowcasting, and Forecasting in the Urban Zone, Seattle, WA, USA, 11–15 January 2004. [Google Scholar]
- Taylor, P.A.; Salmon, J.R. A model for the correction of surface wind data for sheltering by upwind obstacles. J. Appl. Meteorol. 1993, 49, 226–239. [Google Scholar] [CrossRef]
- Pardyjak, E.R.; Brown, M.J.; Bagal, N. Improved Velocity Deficit Parameterizations for a Fast Response Urban Wind Model. In Proceedings of the AMS Symposium on Planning, Nowcasting, and Forecasting in the Urban Zone, Seattle, WA, USA, 11–15 January 2004. [Google Scholar]
- Singh, B.; Hansen, B.S.; Brown, M.J.; Pardyjak, E.R. Evaluation of the QUIC-URB fast response urban wind model for a cubical building array and wide building street canyon. Environ. Fluid Mech. 2008, 8, 281–312. [Google Scholar] [CrossRef]
- Fröhlich, D. Development of a Microscale Model for the Thermal Environment in Complex Areas. Ph.D. Thesis, Albert-Ludwigs-Universität, Freiburg, Germany, 2017. [Google Scholar] [CrossRef]
- Matzarakis, A.; Mahlau, F.; Mayer, H. Online-visualisierung von meteorologischen Daten im Internet—Meteorologische Stadtstation Freiburg. In Proceedings of the Fachtagung Mettools IV, Bonn, Germany, 4–6 October 2000; pp. 150–152. [Google Scholar]
- Emmanuel, R.; Johansson, E. Influence of urban morphology and sea breeze on hot humid microclimate: The case of Colombo, Sri Lanka. Clim. Res. 2006, 30, 189–200. [Google Scholar] [CrossRef]
- Matzarakis, A.; Mayer, H.; Iziomon, M.G. Applications of a universal thermal index: Physiological equivalent temperature. Int. J. Biometeorol. 1999, 43, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Mayer, H.; Kuppe, S.; Holst, J.; Imbery, F. Human thermal comfort below the canopy of street trees on a typical Central European summer day. In Proceedings of the 5th Japanese-German Meeting on Urban Climatology, Freiburg, Germany, 6–8 October 2008; in Number 18 in Berichte des Meteorologischen Institutes der Universität Freiburg; Meteorologisches Inst.: Freiburg, Germany, 2009; pp. 211–219. [Google Scholar]
- Nouri, A.S.; Fröhlich, D.; Silva, M.M.; Matzarakis, A. The Impact of Tipuana tipu Species on Local Human Thermal Comfort Thresholds in Different Urban Canyon Cases in Mediterranean Climates: Lisbon, Portugal. Atmosphere 2018, 9, 12. [Google Scholar] [CrossRef]
- Mayer, H.; Holst, J.; Dostal, P.; Imbery, F.; Schindler, D. Human thermal comfort in summer within an urban street canyon in Central Europe. Meteorol. Z. 2008, 17, 241–250. [Google Scholar] [CrossRef]
- De Abreu-Harbicha, L.V.; Labakia, L.C.; Matzarakis, A. Effect of tree planting design and tree species on human thermal comfort in the tropics. Landsc. Urban Plan. 2015, 138, 99–109. [Google Scholar] [CrossRef]
- Fröhlich, D.; Matzarakis, A. A quantitative sensitivity analysis on the behaviour of common thermal indices under hot and windy conditions in Doha, Qatar. Theor. Appl. Climatol. 2016, 124, 179–187. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fröhlich, D.; Matzarakis, A. Spatial Estimation of Thermal Indices in Urban Areas—Basics of the SkyHelios Model. Atmosphere 2018, 9, 209. https://doi.org/10.3390/atmos9060209
Fröhlich D, Matzarakis A. Spatial Estimation of Thermal Indices in Urban Areas—Basics of the SkyHelios Model. Atmosphere. 2018; 9(6):209. https://doi.org/10.3390/atmos9060209
Chicago/Turabian StyleFröhlich, Dominik, and Andreas Matzarakis. 2018. "Spatial Estimation of Thermal Indices in Urban Areas—Basics of the SkyHelios Model" Atmosphere 9, no. 6: 209. https://doi.org/10.3390/atmos9060209
APA StyleFröhlich, D., & Matzarakis, A. (2018). Spatial Estimation of Thermal Indices in Urban Areas—Basics of the SkyHelios Model. Atmosphere, 9(6), 209. https://doi.org/10.3390/atmos9060209




