Nitric Oxide Production by Centimeter-Sized Meteoroids and the Role of Linear and Nonlinear Processes in the Shock Bound Flow Fields

Abstract

Nitric oxide (NO) is a critical indicator of energy deposition in the lower thermosphere because of its formational pathways. Thus, it is important to constrain sources of NO, such as meteoroid generated hypersonic flows below 95 km altitude. This paper aims to examine the process of and place the upper estimate on NO production in high temperature flow fields of strongly ablating meteoroids. For centimeter-sized meteoroids, the production of NO is bound within the dynamically stable volume of bright meteor plasma trains in the region of 80–95 km. Our estimate of the upper limit of the cumulative mass of NO produced annually by centimeter-sized meteoroids is significantly lower than that reported in previous early studies. In the context of shock waves, we explored the reasons why centimeter-sized meteoroids are the most efficient producers of NO. Effects of nonlinear processes on meteoric NO production are discussed.

1. Introduction

Estimates of total annual mass influx of interplanetary dust and particles (collectively defined as meteoroids) in the upper atmosphere varies broadly from 5 to 300 tons/day [1], with the most recent estimate suggesting 30 tons/day [2]. The initial high incident velocity of those particles and subsequent collisional and thermal interaction with the upper mesosphere and lower thermosphere (MLT) region of the atmosphere result in a range of physico-chemical effects [1,3,4]. The corresponding luminous phenomena accompanying the meteoroid passage thorough the atmosphere is generally referred to as a meteor. An example of modification of the upper atmosphere by meteor induced physico-chemical effects is the deposition of the metallic layer in the MLT [1,3,4,5,6,7]. Meteor induced chemistry, such as ozone destruction by thermalized meteoric metal ions, is well understood from laboratory, modeling and remote sensing studies [1,3]. However, thermally driven chemical and physical processes, such as nitric oxide (NO) production related to meteor phenomena, are less understood, especially in the context of larger object sizes and velocity distributions capable of such atmospheric modification. Indeed, understanding hyperthermal chemistry associated with such events is a highly difficult and nontrivial task (e.g., [8]). Consequently, any estimates of meteoric NO production depend not only on a quantifiable meteoroid population with a size capable of producing high temperature flows, but also on understanding the physical properties of these flows along with their thermal history. These factors were the sources of significant uncertainties in assessing meteoric NO production in the MLT region in the early studies (e.g., [9]).

The size distribution of meteoroids impacting the Earth’s upper atmosphere (with recurring annual frequency) ranges widely from dust size particles to meter size objects (e.g., [2]) with the highest mass influx centered around 2 × 10⁻⁵ kg [1]. For pedantic reasons, we digress and note that a different naming scheme applies to objects that are greater in size than 0.1 m.

Nevertheless, only limited subsets of those events have sufficient sizes and velocities to generate and sustain high temperature hypersonic flows (e.g., [10]) conducive to NO production [9]. At this point, we should recall that all objects in the transitional–continuum flow regimes [11] traveling with velocities exceeding ~5 km/s produce NO in their flow fields [12]. Considering that meteoroids have much greater velocities (11.2–72.5 km/s), they are expected to produce NO more efficiently, provided that they have sufficient sizes to satisfy the flow regime constraints [13,14]. Given that the Earth’s atmosphere is continuously bombarded by meteoroids (especially those in the centimeter-size regime), it is important to place an upper boundary of NO production by these objects. Another point to consider in the context of meteoric NO production are nonlinear processes intrinsically associated with hypersonic flows [11].

To date, results from only two early studies of meteoric NO production in the upper atmosphere exist in the literature [9,13]. Interestingly, despite intriguing findings by those authors that show significant NO production by meteors, current models of NO in the upper atmosphere do not explicitly include meteoric contribution (e.g., [15,16,17,18,19,20]).

In principle, the natural production mechanisms responsible for generating an NO reservoir between 100 and 110 km are comparatively less efficient below 95 km altitude [9,13,21,22]. However, dynamic vertical transport around the poles reaching a maximum during winter months facilitates the transport of NO from its peak altitudes in the lower thermosphere downward to the mesospheric region (e.g., [17,23,24]). Moreover, at high latitudes, energetic particle precipitation may produce notable effects as far down as the stratosphere during solar proton events (e.g., [20,25]) and geomagnetic storms (e.g., [19]), although these events are intermittent (not continuously present). The contribution of such events to the NO budget in the atmosphere is reasonably well understood and well covered in the literature (e.g., [20,23,24,25]). The role of solar proton events and geomagnetic storms are not discussed further because they are infrequent and latitude-dependent (compared to the continuous bombardment of centimeter-sized meteoroids globally), and are well beyond the general aim of this paper. Instead, in this paper, we focus solely on NO produced as a by-product of meteor generated shock waves.

Therefore, it is important to understand and evaluate the meteor related production mechanisms that may contribute significantly to the NO budget in the region of MLT below 95 km and could be responsible for significant and yet unresolved variations observed at 85 km (i.e., [26,27]). The significance of this lies in the fact that NO plays a critical role in the structure and energetics of the upper atmosphere (e.g., [15]). Following up-to-date estimates of meteoric masses and sizes impacting the Earth’s atmosphere [2], along with a more comprehensive understanding of meteor flow field temperatures (e.g., [10]) and flight dynamics [14], this preliminary study examines the role of common centimeter-sized meteoroids in NO production. The meteoric objects in this size range (~0.01 m) are the most efficient in NO production and have the highest contribution to overall meteor related NO [9]. This work aims to place the constraint on the upper boundary of NO production by these shock-generating meteoroids, capable of sustaining high temperature flow fields, at altitudes between 80 and 95 km.

The paper is structured as follows: Section 2 presents a brief overview of the production mechanisms and importance of NO in the upper atmosphere, and subsequently discusses the mechanism of NO production in hypersonic flows. Section 3 examines the fundamentals of theoretical reasoning necessary for evaluation of NO production in high temperature meteor flow fields. In particular, this section covers ablation, hydrodynamic shielding, shock waves, the role of initial radii of adiabatically formed high temperature meteor plasma trains and the role of light and ionization curves in the context of NO production and maximum energy deposition by a meteoroid per unit length. Section 4 describes the methodology to estimate meteor produced NO at specified altitudes. Section 5 presents the results and the general discussion in the context of identifying effects of nonlinear and linear processes on NO production as a function of temporal and spatial evolution of the flow. We also identify the reasons why centimeter-sized meteoroids, compared to other sizes, are the most efficient producers of NO. We conclude the paper in Section 6.

2. Sources of NO in the Upper Atmosphere

2.1. Production of NO in the Lower Thermosphere

Nitric oxide in the lower thermosphere exhibits the highest concentration around 110 km altitude [15,16]. Typical NO density in that region is about 10¹² m⁻³, although it is highly variable both spatially and temporally (e.g., [15,28,29]).

Production of NO in the lower thermosphere depends directly on the availability of excited atomic nitrogen and is controlled by the energy input in the form of solar radiation and auroral high energy electrons, required to break the strong molecular bond of N₂ [15,29]. Consequently, the abundance of NO is a critical indicator of energy deposition in the upper atmosphere [15] despite the fact that, in terms of number density, NO is a minor species.

Nitric oxide in the lower thermosphere is generally produced through the reaction of the excited atomic nitrogen with molecular oxygen N(²D) + O₂ = NO + O. At lower latitudes, the solar radiation (soft X-rays and UV) is a primary energy source for producing NO [29,30]. At high latitudes, the main energy source for N₂ dissociation and subsequent NO production are high energy auroral electrons which exhibit strong temporal variability [31,32]. Correspondingly, NO strongly varies with solar and auroral activity in the lower thermosphere [29].

Nitric oxide is very sensitive to UV radiation, and its loss mechanism is primarily via photodissociation. Subsequently, further destruction of NO takes place via ground state nitrogen which is released during the UV dissociation of NO (e.g., [15]). Consequently, the production and loss of NO clearly depends on the relative amounts of excited and ground state atomic nitrogen. A comprehensive summary of processes that govern production and loss of NO in the upper atmosphere is given by Bailey et al. [15].

A nitric oxide molecule has a fairly long lifetime of about 19 h under illuminated conditions [33], while the lifetime of the NO molecule in diffusive transport is approximately one day [34]. Nitric oxide is a heteronuclear molecule and emits efficiently in infrared at 5.3 μm which is an important source of radiative cooling in the upper atmosphere (e.g., [35,36]). Consequently, NO plays an important role in the energy budget and temperature structure of the MLT.

Additionally, photoionization of NO by the solar Lyman-α emissions is responsible for the electron density profile that characterizes the D region (70−95 km) [37] and, at higher altitudes, the low ionization potential of NO controls the ion composition of the ionospheric E region. This illustrates the important role of NO in controlling the structure and energetics of the upper atmosphere. Enhanced NO polar transport to lower altitudes takes place during winter months (e.g., [17,22,23,24,38,39,40]) and may in general play an important role in a coupling mechanism between the thermosphere and the middle atmosphere (stratosphere–mesosphere).

2.2. Formation of NO in Hypersonic Flows

Nitric oxide is produced in all hypersonic flows exceeding a velocity of around 5 km/s [11], where shock-heated (read collisionally-heated) atmospheric gasses are subject to rapid and immense changes in density and temperature [41]. The latter mechanism is principally responsible for an increase in vibrational energy of atmospheric molecules and the subsequent dissociation (e.g., [14]). Of course, strong shock waves, which are an integral part of hypersonic flows, are further characterized by different degrees of excitation, ionization and other non-equilibrium processes (cf. [14,42]), all of which are highly nonlinear processes. In this context, it has been suggested that dissociation may also have a stabilizing effect on hypersonic flows (e.g., [42]). It should be noted that both ascending and re-entering space vehicles are known to produce immense amounts of NO [12].

The production of NO in hypersonic flows is closely correlated to the degree of dissociation of N₂ and O₂, in addition to thermal history in different regions of the flow field. Nitric oxide formation in shock forming hypersonic flows has been intensively investigated in recent years (e.g., [43,44,45,46,47]). In rarefied air, O₂ generally dissociates in the range of 2000 to 4000 K [11,41]. Nitrogen molecules start to dissociate at 4000 K and the dissociation is complete at about 9000 K, after which ionization effects start to take place [48]. Following the initial rapid dissociation, two main reactions (collectively known as the Zel’dovich mechanism) that are primarily responsible for the NO production in the incipient high temperature hypersonic flows, in the range of approximately 2000–10,000 K, can be written as follows:

N₂ + O → NO + N

(1)

N + O₂ → NO + O

(2)

The rate of NO production is governed by the first endothermic reaction which requires an activation energy of 3.3 eV to proceed [41]. It is also the main mechanism for production of NO in hypersonic flows (cf. [42]). However, its efficiency is controlled by the limited residence time and thermal history of the reacting species. The reverse process of Reaction (1) is efficient in removing NO in the upper atmosphere:

NO + N → N₂ + O

(3)

However, Menees and Park [9] determined that Reaction (3) has a negligible effect on the overall concentration of NO in hypersonic rarefied flows. Reaction (2) proceeds at a rate that is weakly temperature dependent above several thousand kelvin [9], removing the available N atoms provided that a sufficient supply of O₂ is available in expanding flows. Reactions (1) and (2) are coupled in hypersonic flows, because, as soon as the nitrogen atom is liberated by Reaction (1), it proceeds to immediately react with the available oxygen. In shock generating hypersonic flows, NO reaches the peak mole fraction at about 3500 K [11,42]. The large amount of NO that forms as a result of hypersonic flows remains deposited in the ambient air for a long time, mainly because there is no time to decompose in the rapidly cooled flows [41]. In the MLT, rapid rarefication of the initial hypersonic continuum flows (in the case of a strongly ablating meteoroid) renders the three-body processes, such as the reverse of initial shock induced dissociation, unimportant.

The amount of NO produced in hypersonic flows depends strongly on the flow thermal evolution and history, but in general does not exceed several percent of the mole fraction [41]. An additional factor controlling the abundance of NO in high temperature flows is the Damköhler number (the ratio of the flow residence time to the chemical reaction time for reactions) [49]. The spatial and temporal importance of Reactions (1) and (2) in the context of the meteor generated shock waves, flow field evolution and diffusive processes are revisited in the next section.

3. Theoretical Considerations for the Understanding of Meteoric NO Formation

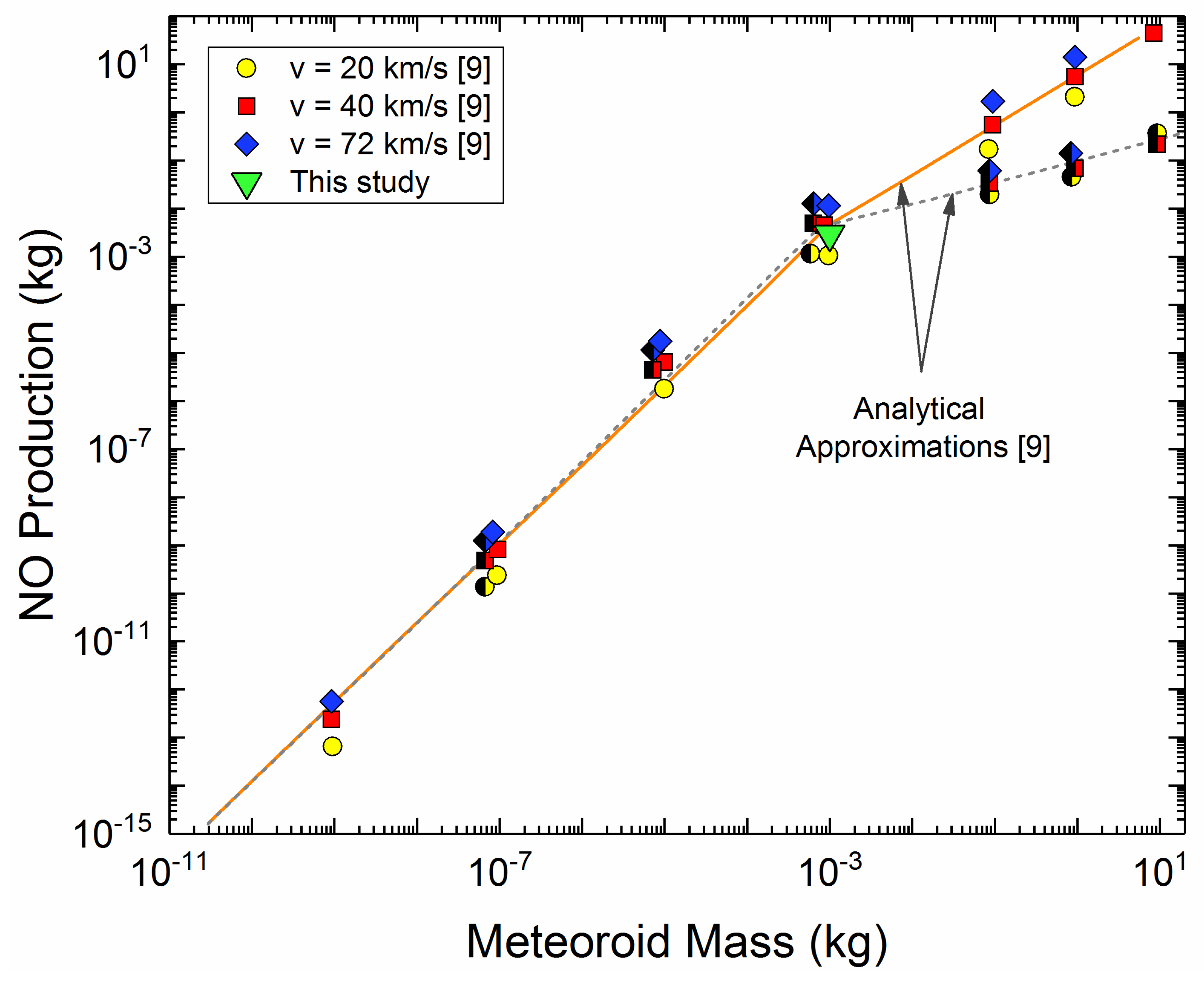
3.1. Role of Meteor Masses, Ablation and Vapor Shielding in NO Production

We start this section with a brief overview of meteoric masses, as these have important implications for ablation, formation of vapor shielding, formation and strength of meteor generated shock waves, and consequently impact NO meteoric production. In the past several decades since the work of Menees and Park [9], there have been significant advances in meteor science, especially in terms of estimating overall meteor mass influx. In this study, we only consider meteoroid sizes of about 10⁻² m (corresponding to masses of ~10⁻³ kg), due to their reasonably reliable annual frequency and long term trends [2] and because of the ability of this meteoroid size segment to generate shock waves and high flow field temperatures. These meteoroid sizes can generate ablationally amplified continuum flows (around and aft of the meteoroid) bound by the initial shock envelope and are consequently conducive to NO production.

Sizes above 10⁻² m exhibit strong uncertainty in terms of overall flux density [2,50] and we chose to neglect them. In this study, we also neglected the millimeter- and submillimeter-sized particles, as these particles are inefficient producers of NO compared to the sizes of meteoroids considered in this work [9]. The main reasons are: (i) heating of these small meteoroids (d ≤ 10⁻⁶ m) is inefficient because the radiative heat loss does not allow heating to reach evaporation temperatures [51]; and (ii) small sizes (e.g., mm-sized bodies) do not permit for sufficient mass loss per unit length and subsequent formation of high temperature flow fields [9,13]. Admittedly, the exclusion of these sizes from our study may somewhat skew attempts at estimating the total NO production by the cumulative meteoroid mass entering the Earth’s atmosphere annually. However, this wider spectrum of meteoroid sizes, including very large Chelyabinsk (albeit rare) type events [52] (as very efficient producers of NO), should be addressed in future work.

Meteor flight dynamics in the upper atmosphere (similar to that of any hypersonic body) is best described using the characterization of the flow regimes which are generally defined in terms of the Knudsen number (Kn) (the ratio of the mean free path in the ambient atmosphere and the characteristic dimension of the hypersonic object) (e.g., [11,53,54]).

However, assigning the Knudsen number to the meteoroid, purely based on its characteristic dimensions, may not be sufficient (e.g., see [53]). That is evident in the case of meteor generated shock waves which appear at significantly higher altitudes than predicted using the classical Knudsen number [55,56]. Before we revisit this point, let us overview some fundamentals.

As the meteoroids enter the rarefied atmosphere (corresponding to the free molecular flow or Kn ≥ 1), they collide with individual atmospheric molecules. Those collisions are highly energetic [57] and cause meteoroid heating and mass loss by sputtering [58,59,60]. Because the kinetic energy of impinging atmospheric molecules far exceeds the surface potential barrier (or binding energy), each collision results in a large number of meteoric atoms (or ions if ionized during the impact) to escape the lattice of the meteoroid surface [59,61]. Depending on the meteoroid composition, the number of the ejected meteoric atoms can be up to two orders of magnitude greater than the number of impacting molecules (cf. [62]). Following a collision with the meteoroid surface, the atmospheric molecules are mostly dissociated (dissociating energy is at least an order of magnitude smaller than the initial kinetic energy) and subsequently reflected and mixed with the ejected meteoroid atoms into the vapor–air mixture in front of and around the meteoroid (cf. [63,64]). This phenomenon, generally defined as the vapor cap, begins to play an important role in reducing the collisions with meteoroid surface as the mean free path of the vapor–air mix within that region starts to increase with decreasing altitude [65]. However, depending on the impact parameters, a small fraction of impinging atmospheric molecules may get reflected outward and consequently may not end up entrained in the meteor flow field [66].

Notably, the vapor shielding by the reflected and dissociated atmospheric species also appears in re-entry vehicles, despite the absence of appreciable ablation [67]. When the mean free path of the vapor cap is about ten times smaller than the ambient mean free path, the shielding becomes efficient in preventing direct collisions of free stream molecules with the meteoroid surface [64]. At lower altitudes, the density within the vapor cap increases as atmospheric density increases. The vapor shielding is also characterized by large pressure, density and temperature gradients. Pressure in the vapor cap generally exceeds the dynamic loading forces and can be up to four orders of magnitude greater than the pressure of the ambient local atmosphere [64]. At the point where the vapor shielding is sufficiently dense to prevent direct collisions with the meteoroid surface, all initial redistribution of energy imparted by the colliding atmospheric molecules takes place within the vapor cloud. This indicates that the number of dissociated N₂ and O₂ molecules is approximately proportional to the size of the vapor shielding. Consequently, the size of vapor shielding has a direct impact on meteoric NO production.

In principle, the vapor cap size is proportional to the cube of the meteoroid velocity [68] and recent numerical models show that the size of vapor shielding volume is about one to two orders of magnitude greater than the characteristic meteoroid dimensions [51,62,64,69]. Observational evidence suggests that the vapor shielding takes on an even larger size, at least in the case of fast meteors [70,71], but there are still large uncertainties in terms of constraining the parameters and the exact size of the vapor shielding. On the other hand, the presence of vapor shielding is the main reason the Knudsen numbers of meteoroids do not correspond to particle dimensions. Correspondingly, the vapor shielding shifts the flow regimes to higher altitudes [53]. This presents a significant uncertainty in accurately constraining the meteor flow regimes relative to their actual sizes and velocities [65]. To see why, consider that with increasing ablation (cf. [72]), the meteoroid vapor cloud results in the meteoroid behaving like a significantly larger body (with a larger cross-sectional area that sweeps the ambient atmosphere). The implication of this point in the context of meteor generated shock waves is discussed further in the shock wave section.

The vapor cap starts to play an important role as early as 114 km altitude for meteoroids with sizes 1 × 10⁻⁵–1 × 10⁻¹ m, and for these particles, the vapor pressure is always greater than that of the ambient atmosphere. Moreover, the size of the vapor shielding volume scales down with the increasing atmospheric density in a similar manner as the initial radius of the plasma train (e.g., [73]). Similar behavior is observed in a meteor head echo (MHE) [74]. Moreover, the density distribution of the vapor may not be Gaussian, and is likely analogous to the distribution of plasma density in a volume of initial radius [75] or in the meteor head echo [76]. As we shown below, this has important implications for the assumptions taken in our modeling and toward the total estimate of NO production by centimeter-sized meteoroids.

Moreover, the vapor shielding size increases with the presence of ablation [63,77]. Ablation (generally term for intensive mass loss) starts at the onset of the transitional flow regime when the surface of meteoroid reaches high temperature [72,78] and its efficiency depends on the meteoroid velocity and heat of evaporation [61]. The onset of strong ablation coincides with the presence of strong vapor shielding, which enhances radiative heat transfer to the body. Because the body is protected from direct impacts, yet intensely heated, the evaporation is a dominant mechanism of mass loss for most meteoroids with the vapor shielding. Strong ablation contributes to the increase of the vapor shielding region [62,77] and is conducive to the presence of higher temperature in the meteor flow fields [62]. Moreover, the strong ablation decreases the rate of thermalization in meteor wakes, while limited or no ablation promotes rapid cooling [10,69].

Thus, a higher rate of ablation of bodies in a hypersonic flow enables higher NO production efficiency in meteor flow fields. In the general case, the temperature history in the flow field, which is a function of both axial and radial distance from the central axis in the meteor wake, is important in determining the peak NO production, as we are going to see soon.

At the moment of its formation along the meteor path, the vapor cloud has two components of the velocity: (i) the incipient axial velocity, higher or similar to that of the meteoroid; and (ii) the radial component, about one order of magnitude slower and instrumental in formation of the initial radius [61,79]. The vapor cloud can be fundamentally regarded as a fluid element because of its high density relative to the ambient atmosphere, and it can be considered to expand much like a hydrodynamic flow into a vacuum [51]. When the meteoroid sizes are in the range 1–4 × 10⁻⁴ m, there is a strong ablation and vapor cap, but no onset of the shock wave (or a comparatively very weak one). In such case, when the vapor starts slowing down after collisions with the ambient atmosphere and subsequently enters the flow field behind the meteoroid, it quickly expands and transitions into the rarefied flow field in the immediate wake (the assumption of near or continuum flow no longer applies), and cools rapidly (i.e., [9]). Contrary to that, thermalization of the flow fields generated by larger ablating bodies (e.g., d~10⁻² m) is much slower, and the production of NO is not limited within the boundaries diffusive and turbulent high temperature flows in the immediate meteoroid wake (see [80]). Rather, NO production proceeds even after the formation of a more dynamically stable volume of meteor plasma and vapor, with the initial radius (r₀) [61,75]. This takes place during the so-called diffusive regime of NO formation where Reaction (2) dominates. The overall relevance of the initial radius in the context of meteoric NO production is discussed below.

Meteoroid fragmentation, while playing an important role in mass loss, was neglected in this study. One of the main reasons is that, in the meteoroid sizes considered here, the presence of fragmentation may not impact the efficiency of NO production [9].

3.2. Meteor Generated Shock Waves

Conceptually, we can think of a meteor generated shock wave as a paraboloid surface that starts as a hemispheric region in front of the meteoroid and extends to the meteor wake, and separates regions of high density, temperature and energy from the ambient atmosphere [65]. The meteor shock wave can be approximated as a typical blunt body shock wave (or bow shock). The strongest shock is in front of the meteoroid (bow shock) and it propagates with the velocity of the body. This hemispherical surface of extremely strong temperature, pressure and density gradients transitions into the radially expanding cylindrical component of the meteor bow shock wave. This is generally defined as the cylindrical shock wave. That term originates from approximating the meteor shock wave as the shock wave resulting from the “instantaneous” energy release by a line source [14,81,82,83,84,85,86]. The typical meteor shock morphology was described by Silber et al. [14,65].

A meteor shock wave forms when the increase in density and temperature in the compressed vapor shielding is sharp and large enough such that it satisfies the Rankine–Hugoniot relations, which relate the upstream and downstream values of density, bulk velocity, and temperature in an ideal compressible fluid [65]. Because of its strength, the bow shock in front of the meteoroid dissociates, excites and ionizes the swept atmospheric molecules that impact the shock envelope. However, all these processes are highly nonlinear [11]. The cylindrical shock wave, however, depends on the energy deposition per unit length (i.e., ablated mass deposition in the form of vapor and plasma) and its radial expansion rate can be approximated reasonably close by a thermal velocity (e.g., [79]). However, the actual radial rate of expansion of the meteor generated cylindrical shock wave is governed by the initial pressure differential with the ambient atmosphere that drives the cylindrical shock wave [14]. That pressure difference is a function of meteor velocity and mass loss per unit length.

For pedantic reasons, it should be mentioned that smaller meteoroids, with diameters in the range 1–4 × 10⁻⁴ m, may be capable of forming only a “weak” shock wave at an altitude at around 80 km in the MLT. That can be evidenced by comparing the mass deposition per unit length and calculating the radius of maximum energy deposition (R₀) based on the energy relation (e.g., [14,81,87]):

R₀ = (E₀/p₀)^0.5

(4)

where E₀ is the energy deposited per unit path length and p₀ is the ambient pressure (e.g., [55]). The shock from these meteoroids will not appreciably modify (e.g., dissociate) and may only heat the limited volume of the ambient atmosphere surrounding the meteor axis of propagation. The energy deposition estimates per unit length (E₀) are obtained by determining the mass of ablationally deposited species corresponding to the given meteoroid size and its electron line density (e.g., [88,89,90]). This is done using the typical value of ionization coefficient (β ≈ 0.1) [91].

On the other hand, the meteoroids with sizes of about 10⁻² m have sufficient energy to dissociate O₂ and minor species such as O₃, but not N₂ in any appreciable quantities [14]. This is a very important distinction because, in such scenarios, there is an abundant amount of atomic oxygen available to react thermally with N₂ in Reaction (1), which enables a higher rate of NO production in the boundaries of turbulently diffusing flows prior to and coinciding with the formation of the initial meteor plasma train. For centimeter-sized bodies, the shock wave appears in the region of 90–95 km altitude [77]. In principle, the shock wave has appreciable strength when the ablation rate exceeds the density of the ambient atmosphere.

Beside significantly higher temperature, density and energy values that characterize the shock wave, the main difference between the strong vapor shielding and the shock is the existence of coherent flow fields within the shock layer around the body. These are governed by the temperature, density and viscous forces and are regions where collisional history within the flow field impacts distribution of internal energy modes (i.e., rotational, vibrational and electronic) [65]. Chemical reactions that lead to the production of NO among other species are the result of those initial high energy intermolecular collisions.

In principle, it is important to emphasize that, while the strong ablation takes place at the onset of the transitional flow, a blunt hypersonic body in the late transitional regimes is characterized by a strong, detached bow shock (e.g., [65]). The meteor velocity and rate of ablation have a significant impact on the shock stand-off distance [42,77] and overall size of the hemispherical region of the bow shock in the front of the meteoroid (see [65] for discussion). The ablation amplified initial volume of the meteoroid bow shock envelope scales down with the atmospheric density (e.g., [92]) in a way that is analogous to the behavior of the vapor cap, meteor head echoes [74] and initial radius [73].

Considering the strong effect of ablation and dissociation in the shock layer [42], it is reasonable to expect that the bow shock dimensions are similar to the dense non-Gaussian region of the vapor cloud. This is because the size of the initial flow field bound by an initial shock envelope is a function of energy of ablated vapor and plasma ($\frac{dm}{dt}\frac{V^2}{2}$) (e.g., [9,79]) and inversely proportional to atmospheric density. This reasoning is indeed consistent with the results of a numerical model presented by Zinn et al. [79] and it also agrees well with recent simulations [92].

It follows that the meteoroids in the size range 10⁻² m not only form the shock waves, but the size of the initial atmospheric region swept (dissociated, excited and ionized) by the front hemispheric shock surface is at least an order of magnitude larger than the characteristic meteoroid dimensions at the height of 95 km (e.g., [62,79]). This is an important consideration for the production of NO because the number of dissociated N₂ molecules, initially swept by the ablation amplified shock envelope (and subsequently entrained in the meteor the flow field), greatly exceeds the number that would be swept by the meteoroid alone. Therefore, this behavior, characteristic of ablating meteoroids, must be considered in any computational model that aims to constrain the number of thermally produced species.

Furthermore, the strong ablation and presence of the continuum flow in the flow field bound by the initial shock surface generated by ablating meteoroids results in a significantly larger spatial and longer temporal extension of the high temperature flow fields. Because high temperatures persist for much longer (e.g., [10]), the assessment of production of NO by these meteoroids must be approached somewhat differently than in the case of rapidly cooling smaller meteoroids flow fields. This implies that the region of NO formation is markedly larger than the initial dimensions of the shock envelope. Consequently, the NO production still takes place by Reaction (2) under a colder regime and at the time when the adiabatically expanding ablated meteor plasma forms a train bound by the radius r₀. This consideration may be used to reliably constrain the spatial extent of the NO production estimates in meteor trains.

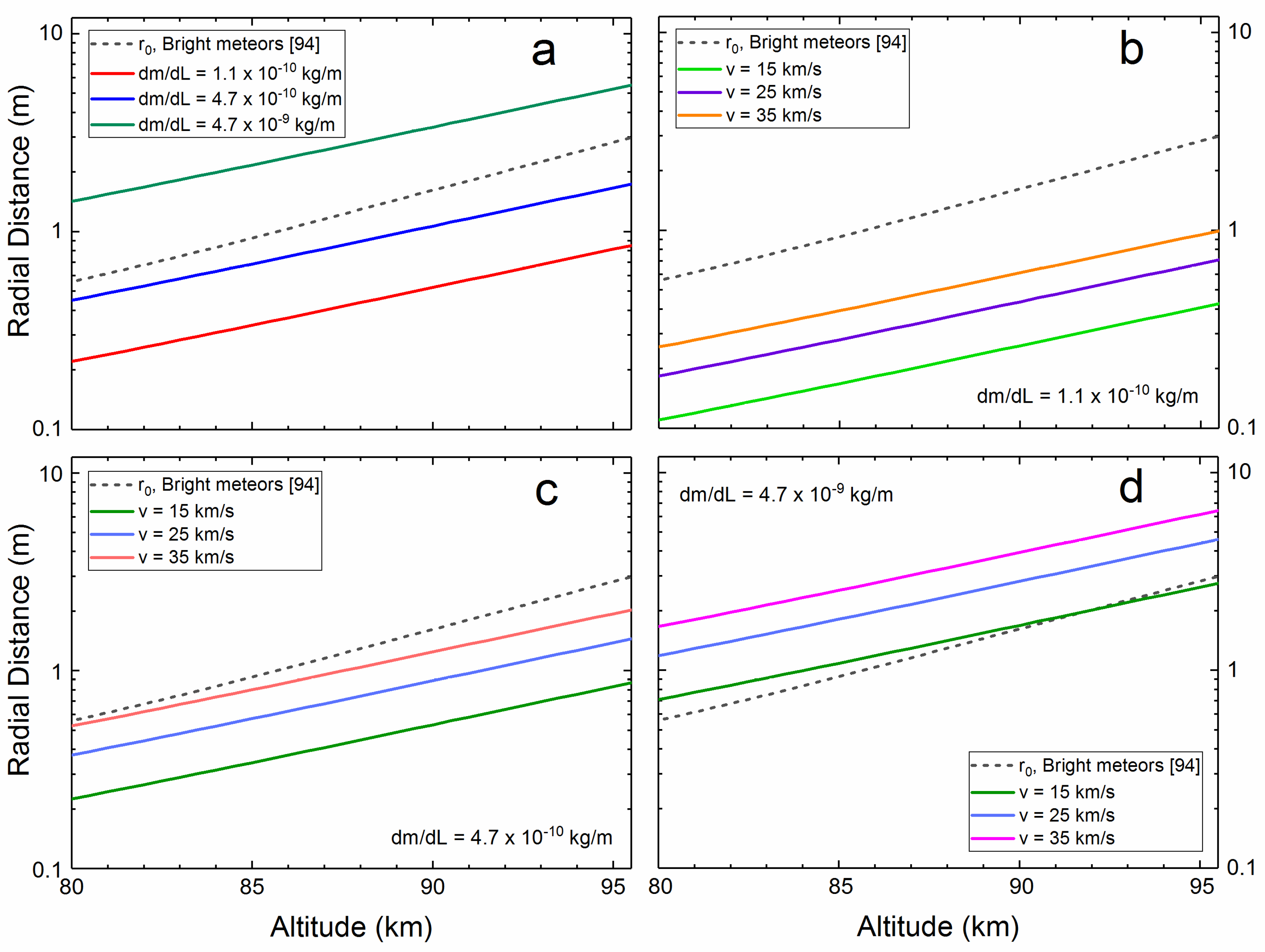
3.3. The Role of Initial Radius, Light and Ionization Curves in the Framework of NO Production

The role of the initial radius is surprisingly important in the production of NO, as briefly indicated in the earlier section. Here we expand on the fundamentals that support such reasoning. The high temperature ablated meteor vapor and plasma initially enclosed by the shock envelope expand adiabatically (~10⁻⁴ s) during the turbulent and rapid diffusive stage in the near meteor wake to form a more dynamically stable volume that is in pressure equilibrium, but not in thermal one, with the ambient atmosphere (e.g., [14,61,80]). The volume of this initial plasma–vapor train has a radius of r₀. The formation of such initial plasma cylinder with the radius r₀ lags significantly behind the departure of the cylindrical shock wave (~10⁻⁵ s). The evolution of the plasma train coincides with the radiative meteor stage, where ablated vapor–plasma mixture has a strong axial and much slower radial component of its velocity.

The electron distribution in this initial plasma volume is assumed to be Gaussian. However, a numerical simulation demonstrates that electron density might be higher around the axis and less concentrated toward the outer boundary of the train as defined by the initial radius [91]. This plasma volume is generally detected by meteor radars, which distinguish meteor trains based on the initial electron line densities and subsequent reflection characteristics (e.g., [93]). Generally, meteor trains generated by centimeter-sized ablating bodies considered in this study can be defined as overdense, based on their electron line density (α ≥ 10¹⁶ electrons/m) (e.g., [93]).

However, the importance of the initial radius for this work is that it marks a physical boundary at which high temperature driven processes inside the meteor train cease. Another important aspect of the initial radius of overdense meteor trains is that there is no observable variance with increasing electron densities and only weak dependence on meteor velocity. This has been observationally confirmed for bright (overdense) meteor trains [94]. That means that it is reasonable to use r₀ as the boundary of the plasma volume at which efficient production of NO stops. This approach is valid for the meteoroid sizes in this study.

The reasoning is simple. Prior to the formation of the meteor train, the initial strong turbulence trailing the region of recompression of vapor and plasma (with both axial and radial expansion) in the immediate meteor wake promotes relatively uniform mixing of the shock modified and entrained atmospheric species (see [14]). However, we need to digress for a moment. Of course, in hypersonic rarefied flow when Reynolds number is low, the region of strong turbulence is not likely to exist. However, in the case of strongly ablating meteoroids that have the continuum flow within the shock bound flow field, the turbulent region is assumed to exist.

The expansion of meteor plasma and vapor that leads to the formation of the meteor train coincides with the optimal range of temperatures required for NO formation in the meteor wake [13]. It should be noted, however, that the diffusive and chemical processes (governed by the Damköhler number) are much faster in the immediate high temperature wake then further down in the flow stream when the meteor plasma train is formed and only governed by the ambipolar expansion (e.g., [89]). However, we need to emphasize that, following the formation of the meteor plasma train with the initial radius r₀ (when T ≥ 4000 K), temperature drops relatively quickly below 2000 K (~10⁻² s) and the only mechanism of NO production in this “cold regime”, taking place in the train or at the train boundaries, is controlled by Reaction (2).

For the sizes of meteoroids considered in this work, with the average velocity of about 30 km/s, both ionization and light curves are likely to extend well over the region between 80–95 km (e.g., [95,96,97,98,99,100]). This is important as the presence of bright luminous phenomena (as delineated by a light curve) and strong ionization (from ionization curves) present in meteor trains [95], signifies the strong ablation amplified flow fields and very high temperatures. These conditions are conducive to NO production.

Nevertheless, the production of NO trails behind the onset of light curves [9] and the same behavior can be assumed for the ionization curves. In general, the production of NO is proportional to the behavior of both ionization and light curve [9]. However, accounting for and modeling the behavior of each individual meteor event, for different velocities and masses, is not computationally possible at the moment. Therefore, some compromises need to be made in terms of approximations that simplify our analytical approach (discussed in the next section).

3.4. The Assumptions

The complexity of the task that requires evaluation of NO produced by meteors is best seen through the cumulative variability and uncertainty in meteoroid parameters. All of those parameters such as size, composition, density, velocity, associated altitudes of maximum ablation, the size of the initial meteor shock envelope and flow field can influence NO production. The determination of exact NO production by meteoroids would need to account for all these factors, including large annual and seasonal variations corresponding to the meteoroid influx.

This led Menees and Park [9] and Park and Menees [13] to impose a number of simplifying assumptions used in their model (herein referred to as the MP model). Rather than using the flow over a body, Menees and Park [9] used a point source model to introduce flow field that simulates the meteoric flow environment. The model is ingenious in its conception because the simulated meteoroid is independent of its own Knudsen number, as long as the flow region of consideration was situated in the meteor wake. Moreover, the MP model allows external restrictions on the Knudsen number before the significant changes in chemical composition takes place. Additionally, the model is suited for body sizes up to 10⁻¹ m.

Our study is different in that we employed up-to-date knowledge of meteor physics and used an analytical approach to evaluate the upper boundary of the NO production. Before we discuss several reasonable approximations that need to be implemented, we note that the production of NO does not appreciably depend on chemical reactions involving species from ablated high temperature meteoric plasma and vapor (e.g., [8,13]). For example, the production of metal oxides in high temperature meteor trails begins only at 3000 K, which is significantly below the peak production temperature of NO. This led us to introduce the assumptions used in our work to estimate the production of NO by centimeter-sized meteoroids. These assumptions were fundamentally based on the discussion, physical and theoretical reasoning presented in the previous sections. Our assumptions are also justified with the fact that we are estimating the upper boundary of NO production by a particular meteoroid size segment, rather than precise NO production.

• The size of the initial and ablation amplified shock region in front of the meteoroid (or initial vapor cloud) is about twenty times that of the meteoroid diameter at 95 km and around ten times the meteoroid diameter at 80 km. This is consistent with the height dependent scaling behavior of the initial radius or MHE, discussed earlier.
• The production of NO is constant between 80 and 95 km for 1 cm meteoroids. We have discussed the main aspects that contribute to this assumption in the previous section. However, for the purpose of this exposition, here we briefly summarize that reasoning again. The ionization and light curves are assumed not to change significantly between 80 and 95 km (e.g., [101]), and consequently we assume that the production rate of NO is constant in that region. Accordingly, we also assume that the velocity change is negligible during NO production in that region of the MLT. Of course, meteoroids in our considered size range do not ablate at a constant rate between 80–95 km altitudes, as mass loss and deceleration also play a critical role (e.g., [102]). However, consider that a typical 1 cm meteoroid (m~10⁻³ kg) loses about 1.5 × 10⁻⁶ kg if it ablates in that part of the atmosphere at a constant rate that produces its maximum electron line density. This is not significantly different from the mass loss as a function of variable ionization or light curve. Finally, the variability of heights of maximum ablation (signifying the maximum peaks in ionization and light curves [101]) for example, as a function of velocity and composition justifies the approximation as the constant ablation and constant rate of NO production is in this region.
• The NO production is bound by the initial radius of the bright meteor plasma train (e.g., [94]). Irrespective of the size of the area of the initial shock region, the maximum production of meteoric NO for body sizes of about 1 cm is limited by the initial radius r₀ of the dynamically stable plasma volume of the meteor train. The process of flow field cooling negates Reaction (1) and favors Reaction (2). During the stage of turbulent diffusion and expansion of high temperature recompression region behind the meteoroid (see [14]), the available N species react with O₂ that survived the passage of the cylindrical shock wave. However, at the r₀ boundary, Reaction (2) is impeded by the limited supply of the N species at the moment when the meteor train starts to expand under the effects of ambipolar diffusion.
• The effects of fragmentation are excluded. In this meteoroid size regime, the fragmentation may only potentially reduce the total NO production [13].
• The effects of UV radiation from the shock layer are ignored.
• Only vertical meteor entry is considered. The variation of zenith angle would not significantly impact the overall estimates in this study. This was shown by Menees and Park [9].

4. Methods

Following Bose and Candler [44], we assumed that the value of mass fraction of NO production remains constant (0.01) for both endothermic Reaction (1) and weakly temperature dependent Reaction (2), and that the NO production is bound within the volume of the bright meteor plasma train with an initial radius r₀ [94]. Bose and Candler [44] modeled the flow fields at 5.1 km/s and obtained the peak mass fractions ranging from 10⁻³ at 80 km altitude to 10⁻⁵ at 87.5 km altitude. Our approximation is thus reasonable, because much faster, strongly ablating meteoroids will have substantially higher peak mass fractions. In fact, a more recent modeling study [103] on the re-entry of spherules produced and ejected by the Chuxculub impact has shown that the NO mole fraction is consistent with the value adopted in our study. Consequently, the mass of produced NO is computed from 80 to 95 km within the volume corresponding to the initial radius of a bright meteor train. This volume is governed by the height dependent initial radius (e.g., [73]). The mass of NO produced by a single event was then integrated over the cumulative annual number of events corresponding to the cm-size meteoroid segment [2].

The validation of our assumption regarding the upper NO production boundary governed by the initial radius of bright meteors was done in the following way. We determined the characteristic radius (R₀) of maximum energy deposition (E₀) per unit length according to three different sizes of an ablating meteoroid capable of generating a shock, corresponding to transitional, strong transitional and overdense meteors with electron densities α = 2.4 × 10¹⁴, 10¹⁵ and 10¹⁶ electrons/m, respectively. The mass loss is intrinsically related to the characteristic radius through the energy (E₀) term in Equation (4). Therefore, it is possible to examine how R₀ varies from 80 to 95 km altitude. The masses of ablated species were determined employing the commonly used value of 0.1 for the ionization coefficient [91] and adopting the typical chondritic composition of the meteoroid, which makes it straightforward to obtain the mass of ablated atoms. We incorporated the altitude dependent pressure profile from the U.S. Standard Atmosphere [104] to tabulate R₀ between 80 and 95 km altitude for a meteoroid traveling at 30 km/s. To also investigate the effect of the impact velocity, we applied the same approach again, but varied the impact velocity, 15, 25 and 35 km/s. Only centimeter-sized overdense meteors have the sufficient energy deposition within the characteristic radius (R₀) that matches or exceeds the initial radius of bright meteor trains. Thus, this approach is robust for centimeter-sized meteoroids. However, for smaller meteoroids (mm-size) that generate a comparatively weaker shock wave, R₀ is significantly smaller than r₀. It then follows that this method of calculating NO production by centimeter-sized meteoroids, using the initial radius of bright meteor trains is not appropriate for smaller meteoroid sizes.

5. Results and Discussion

5.1. The Upper Bound of NO Produced by Centimeter-Sized Meteoroids

As described above, to account for velocity, density and compositional variations in the peak of ionization and light curve discussed in the previous sections, we assume that a typical 1 cm meteoroid with velocities 25–35 km/s ablates at a constant rate from 95 km down to 80 km altitude. We also assume an average mass deposition about 10⁻⁹ kg/m, characteristic of mass deposition of strong overdense (d~10⁻² m) meteors. Using the boundary of the initial radius of bright meteor plasma trains [94], and the average rate of NO production corresponding to the mole fraction of 0.01, we estimate that NO produced by a single centimeter-sized meteoroid is about three times its mass. Thus, for a 0.9 × 10⁻³ kg meteoroid, this is about 2.9 × 10⁻³ kg. This agrees well with the results obtained by Menees and Park [9] and Park and Menees [13] (Figure 1).

After integrating the amount of NO produced by one meteoroid within the plasma and vapor volume bound by the initial radius from 80 to 95 km, with respect to the number of events in that size segment [2], we obtain the upper bound of the mass of total NO produced. For a centimeter-sized body, that number does not exceed 100 tons/year. Of course, the variation of individual meteor parameters such as the velocity, density and composition may increase or decrease that value somewhat, but the divergence from the value stated above will not be significant. This value is by two orders of magnitude less than the estimates by Park and Menees [13]. Considering that this meteoroid size segment contributes the most toward overall meteoric NO production, it is easy to see that the total meteoric NO across all sizes cannot exceed 1000 tons/year (even after accounting for larger and less frequent events). This is insignificant comparing to the early estimates of 40,000 tons/year (e.g., [13]). The main reason for this divergence is a largely reduced estimate of the cumulative annual meteoroid influx [2], and the correspondingly reduced number of events in each segment size capable of NO production.

5.2. Implications

Nearly all aspects of hypersonic flows in the rarefied gas are highly nonlinear. This is apparent by considering high temperature chemically reacting flows, viscous interactions in the shock layer and the presence of entropy layers in the flow field around a body [11].

Comprehensive modeling of meteor flows in a rarefied environment of the MLT is extremely difficult as the classical Navier–Stokes equations are not valid in such conditions. A suitable model would need to include the effect of strong ablation while accounting for nonlinear heat transfer to the body (e.g., [105]). Consequently, such a simulation would also need to account for typical shock layer related effects such as vibrational excitation, dissociation, electronic excitation, ionization and radiation phenomena in the rarefied gas. All of these effects associated with the rarefied and hypersonic flows are a consequence of the nonequilibrium real gas effects and are nonlinear, implying that their simplifications can lead to significant errors in the model predictions.

An additional challenging and difficult modeling task in the near wake of the meteoroid is simulating the flow of ablated vapor and plasma that starts rapidly expanding as it emerges from the “recompression” region. This flow forms a high temperature turbulent diffusive region which is highly nonlinear (fundamentally, a mean a state of spatiotemporal chaos) that eventually leads to the formation of the dynamically stable volume of meteor plasma with initial radius r₀. Principally, this region facilitates mixing the ablated and entrained species that participate in temperature driven chemistry. A computational approach should be able to include a detailed description of such a non-linear dynamical system and to account for all physico-chemical phenomena. To date, no such comprehensive model exists that accounts for all the effects associated with the rarefied hypersonic flow of a typical meteoroid.

Although different from that used by Menees and Park [9] and Park and Menees [13], the approach implemented in this work is robust, and it also produces the same ratio of meteoroid mass to NO produced for a 1 cm-size meteoroid. This validates our approach and the assumptions made in this study. Of course, the stark difference in overall estimated meteoric NO production as obtained by Park and Menees [13] comes primarily from the extensively reduced estimate of meteoric masses impacting the Earth annually [2]. On the other hand, for centimeter-sized objects, this methodology is relatively robust and can be applied to estimate the number of other potentially interesting species formed during the thermal chemistry stage of bright meteors. However, caution needs to be exercised here. First, let us see why this methodology is a successful way to approximate NO production in a bright shock producing meteor. This becomes clear when we consider the comparison of the radius of the maximum energy deposition (R₀) and the initial radius of the meteor train (r₀) formed by an average bright (overdense) meteor with ablation rate in the range of 10⁻⁹ kg/m (Figure 2). For clarity, we plotted R₀ for smaller meteoroids still capable of shock production (d~4 × 10⁻⁴ m). The radius of maximum energy deposition is easily derived for specific altitudes using Equation (4) and letting the average ionization coefficient be equal to 0.1 (e.g., [91]).

Let us digress for a moment to make one important distinction. The energy relation in Equation (4) only applies to the shock producing events; therefore, it is not appropriate to use it for smaller meteoroids that are not capable of generating shock. The maximum energy deposition per unit length exceeds or is comparable to the initial radius of bright meteor trains (Figure 2a,d). On the other hand, R₀ from smaller objects is always smaller than the initial radius (Figure 2b,c). This is significant because it shows that only larger bodies are capable of generating the cylindrical shock that modifies the ambient atmosphere (in the form of heating and dissociation) on the scale comparable to or exceeding that of the initial radius of bright meteor trains as observed by Baggaley and Fisher [94]. This is one of the main reasons why centimeter-sized meteoroids are the most efficient in NO production [9].

The reasons for such behavior of centimeter-sized meteoroids become clear when we consider the dynamics of NO production in three distinct meteoroid size regimes. These regimes correspond to centimeter-sized meteoroids studied in this work, and much smaller and much larger bodies. Here, we present the analysis of the highly nonlinear nature of NO production in the context of each meteoroid size category.

Recall that Reactions (1) and (2) are the most important in the production of NO in the shock generating high temperature hypersonic flows. On the other hand, general production of NO is very small in comparison to the amount of N₂ and O₂ that enter the shock envelope [44]. This is principally because there is a very limited supply of N₂ versus abundant atomic O in the main flow field as a result of shock dissociation. The presence of N₂ required for endothermic and nonlinear production of NO via Reaction (1) only comes from the outer boundaries of the flow field, where ambient N₂ enters the peripheral shock envelope and gets entrained in the flow streamline without dissociation (cf. [11] for a more comprehensive presentation). This can be understood in the context of the distribution of vibrational energy of molecules across the shock surface. Consequently, dissociation, which depends on the collisional history of the molecules, is highly nonlinear (e.g., [47,106]). We can visualize this by considering that the impacting air molecules pass through the approximately hemispherical shock front of the meteoroid at different angles and subsequently end up entrained in the flow streams controlled by significantly different density-velocity-temperature gradients. In principle, the non-equilibrium chemistry dominates in the flow field behind the shock envelope and extends into the meteor wake.

Another source of N₂ comes from outside the initial bow shock envelope and gets mixed into the high temperature flow as a result of rapid turbulent diffusion of meteor plasma and vapor, consequently leading to the formation of the more stable meteor plasma volume with initial radius r₀. Reaction (1) depends on the temperature, and thus thermalization and rarefaction of the flow field make it effective only up to 10⁻⁴–10⁻³ s. On the other hand, Reaction (2) depends on the quantity of O₂, which is only available in appreciable quantities outside of the initial flow field. This reaction only plays a complimentary role and becomes appreciably effective in NO production during the rapid turbulent diffusive regime (just prior to and at the time of formation of the plasma train with the initial radius r₀) (see [80] for extensive discussion). In principle, the production of NO through both reactions also depends on the Damköhler number, which makes it highly nonlinear. It is important to note that, despite recent studies (e.g., [46,47]), the exact contribution of Reaction (3) in the removal of NO from hypersonic high temperature rarefied flows remains poorly constrained due to the lack of comprehensive experimental and theoretical data at high altitudes. However, Reaction (3) is considered to have an insufficient contribution to the NO removal from the rarefied flows [9], and thus does not affect our estimates of the upper boundary of NO production.

In this context, it important to note that the mixing times at altitudes above 80 km are shorter than chemical reaction times [8], and the main component of the NO production is appreciably further in the meteor wake [9]. However, one critical point left unmentioned in this discussion is the role of the meteor generated cylindrical shock wave. For centimeter-sized bodies, the cylindrical shock wave (approximated as the shock from a line source) is strong enough to heat the region of the ambient atmosphere within the characteristic radius R₀ and dissociate a significant amount of O₂ (and most of minor species such as O₃). However, these shock waves are not strong enough to dissociate N₂ (see [14]). This indeed ensures the optimal supply of N₂ and O₂ for Reactions (1) and (2) and makes NO production efficient. However, this is not the case for larger or smaller bodies, as we shall see.

In the case of large meteoroids, the initial shock bound flow field is larger, but the cylindrical shock wave is very strong and capable of dissociating most of O₂ and N₂ in the wider region of the ambient atmosphere surrounding the axis of the meteor propagation (e.g., [79]). In this case, the supply of N₂ and O₂ is very limited, thereby reducing the efficiency of NO production, as noted by Menees and Park [9]. In this scenario, the production of NO via Reaction (1) is significantly greater, while Reaction (2) only plays a minor role in the limit of the ambipolar diffusion-controlled outer regions of the thermalized (and comparably larger) plasma train. This was also demonstrated by Menees and Park [9] who showed that the decrease in NO production efficiency with increasing mass (above 10⁻³ kg) is highly nonlinear.

For small meteoroids, the situation is reversed. The efficiency of NO production is reduced because of the diminished role of Reaction (1). The absence of a shock wave indicates the absence of the continuum flow behind the meteoroid. The flow rarefies and cools rapidly behind the meteoroid. Ambient O₂ surrounding the boundaries of the initial flow is preserved, and N that results from the collisional dissociation in the vapor cap reacts with ambient O₂ at the rate controlled by the diffusion regime. Subsequently, for small meteoroids, Reaction (2) is dominant in the production of NO. Considering that the rate of NO production is controlled by diffusion alone, the NO production (for the time of diffusion duration) can be approximated to have a linear dependence. However, considering that the initial size of the area corresponding to the vapor shielding where the impinging molecules dissociate is relatively small (as discussed earlier, an order of magnitude greater than the characteristic meteoroid dimensions), the supply of N is limited. This consequently makes the production of NO by small meteoroids very inefficient. Menees and Park [9] arrived to the same conclusion, albeit using different reasoning, and determined that the efficiency rate decreases exponentially with decreasing mass.

The method used in this work is robust enough and it can be used to approximate the production of other species of potential interest that are produced by centimeter-sized bright meteors below 95 km. However, it only applies to the centimeter-sized segment, because the initial radius of bright meteor trains is known from experimental considerations [94]. For both smaller and larger sizes, the consideration must be different due to a highly nonlinear decrease in NO production efficiency, as shown by Menees and Park [9]. For smaller meteoroids (say mm-sized), the region in which NO is produced should be about an order of magnitude larger than the characteristic dimension of the meteoroid. However, for large events, the main contribution will not come from the region inside the plasma train. Rather, this contribution comes from the outer boundaries during the early stage of expansion governed by ionic diffusion. This, however, awaits further computational validation in future work.

Our results indicate that the upper boundary of the meteoric NO production is small, compared to early estimates [9]; this is supported by atmospheric chemistry models (e.g., [19,20]). While atmospheric chemistry models do not include the meteoric NO contribution, they reproduce reasonably well the observed NO in the MLT. Indeed, this confirms that the meteoric production of NO is relatively minor.

The biggest uncertainty in our cumulative estimates of NO production comes from an uncertainty in the influx of meteoroids in a particular size segment [2] capable of generating conditions for NO formation. Another significant source or uncertainty may come from the radiative effects that have been observed in centimeter-sized meteoroids (e.g., [70,71]). These effects are well known to be associated with hypersonic flows (e.g., [107,108]). In principle, the radiation from the shock layer (especially in the UV band) may modify and dissociate a region of the ambient atmosphere in front of and surrounding the meteoroid’s axis of propagation. Such a process will inevitably impact the NO production relative to the meteoroid size. However, the contribution of the radiative phenomena on meteoric NO production remains unclear for the time.

The cumulative effect of all uncertainties will need to be more rigorously considered in future studies that may seek to constrain the exact amount of NO produced by centimeter-sized meteoroids. In this study, we only sought to determine the upper boundary of annual NO production by cm size meteoroids.

6. Summary and Conclusions

Nitric oxide is a very important minor species in the upper atmosphere. It plays an important role in the structure and energetics of that region, especially in the lower thermosphere where it exhibits the highest concentration [16]. Nitric oxide is also an important source of radiative cooling in the upper atmosphere, as it emits efficiently in infrared at 5.3 μm (e.g., [15]). The formational pathways of NO require input from high energy sources such as soft X-rays, UV radiation and high energy auroral electrons, which are the mechanisms responsible for N₂ dissociation [15,16,30]. However, some of these mechanisms are less efficient in the MLT below 95 km. Events that could promote the injection of NO to lower altitudes, such as strong solar proton events and geomagnetic storms, are confined to polar regions and are intermittent. Therefore, other sources of NO below 95 km altitude, meteoroid high temperature flow fields in particular, require better quantification.

We examined the capacity of centimeter-sized meteoroid hypersonic flow fields to produce NO via the Zel’dovich mechanism, at altitudes of 80–95 km and sought to establish the upper mass boundary of meteoric NO deposited in that region of atmosphere. We applied an analytical approach to achieve this. Therefore, it was important to make some simplifying assumptions in this study. We note that, to date, no comprehensive computational model exists that accounts for all the complexities (e.g., ablation, radiation, and thermally driven chemistry) in the rarefied flow regime. Indeed, modeling of the high temperature flow field evolution and dynamics of a meteoroid in a rarefied atmosphere and related thermally driven chemical processes is a nontrivial task, because it needs to account for the strong ablation, continuum conditions in the initial shock bound flow field and chaos regime during rapid expansion of the region in the meteoroid wake, dominated by turbulent mixing.

Zel’dovich reactions are complementary; Reaction (1) is the dominant NO production pathway during the high temperature regime in the meteor flow field, while Reaction (2) dominates in the cold regime below 3000 K. This regime is characterized by the rapid expansion of the turbulent region in the near meteor wake which leads to the formation of a more dynamically stable volume of meteor plasma with initial radius r₀. For centimeter-sized meteoroids, the volume of the meteor plasma train limited by the initial radius of bright meteors [94] is determined to be the boundary of NO production.

The total mass of NO produced by centimeter-sized meteoroids was obtained by integrating the mass of NO produced by a single event, between 80 and 95 km altitude, over the number of events corresponding to that size segment. The mass of NO produced by a single event was calculated using the value of NO fraction which was assumed to be constant in the initial plasma train volume governed by r₀. The cumulative annual meteoric mass influx and number of events per size segment were derived from the updated data [2].

The upper mass limit for NO produced by centimeter-sized meteoroids, based on the most recent estimates of the annual influx [2], was estimated to be in the range of 100 tons/year. The interpretation of our results shows that the maximum cumulative annual production of NO by meteoroids with sizes capable of sustaining high temperature flows cannot exceed 1000 tons. This value is significantly less than the mass determined in early studies [9,13], primarily due to a drastically revised meteoroid annual mass influx [2].

Future work should aim to resolve a more exact mass of NO produced by meteoroids, as well as a more thorough analysis of NO number densities or mixing ratios. Moreover, the correlation between meteor showers and high resolution NO satellite data should be examined.