Abstract
Considering recent weather events in Serbia (especially the floods in 2014), a need has arisen for research that would help in identifying extreme weather phenomena. Therefore, the aim of this paper is to determine the thresholds above which intense precipitation can be considered as extreme precipitation events in Serbia. In this study, we determined the frequency of precipitation occurring at an intensity above the threshold of an extreme phenomenon (1961–2015), as well as the frequency of precipitation occurring at or above the absolute daily maximum in the reference period (1961–1990). The study sample included daily rainfall observations from 28 stations from the national meteorological network in Serbia. Applying a decile method, all the stations recording precipitation above the threshold of dangerous phenomena on the same day are classified into the corresponding decile. The threshold value was determined as the average value of the extreme annual precipitation in the analyzed period. The cases that are due to the high prevalence listed in the last decile are considered extreme. The results showed that the critical number of observation points above which an event is considered extreme precipitation event is 6.21, and a warning of the danger could be ensured only in the case of neighboring stations in the network. The threshold of extreme precipitation events for the individual stations ranges up to 130 mm. The obtained results might be used to mitigate the effects of extreme precipitation events in Serbia in the future.
1. Introduction
In order to predict extreme weather events, it is essential to know the thresholds of unfavorable weather phenomena. Many studies have been carried out regarding the impact of these weather phenomena upon different aspects of the environment and human activity within modern climate changes [1,2,3,4,5,6,7,8]. These studies suggest that climate change has a tendency to increase the frequency of extreme precipitation, thus causing natural hazards. Serbia and surrounding countries, due to extreme precipitation, suffer particular damage from floods, especially within the Danube River Basin and sub-basins of the Sava, Morava, Kolubara, and Nišava rivers [9,10,11,12,13].
Floods and fluvial erosion are serious threats to many economic activities [14,15,16]. The biggest flood in Serbia and the surrounding regions since the second half of the 20th century occurred in 2014. In the period from 14 to 18 May, more than 300 L/m2 of rainfall was observed locally. It was estimated that the total damage was 1.525 million Euros [17]. Additionally, floods occurred in the two following years, causing natural disasters in certain regions of Serbia. It is assumed that during these events, the thresholds of extreme precipitation were significantly exceeded.
Different studies have investigated precipitation extremes in Europe [18,19,20]. Their results have shown that the frequency of heavy rainfall has generally increased [21,22,23,24,25,26]. Specifically, the analysis of rainfall and extremes in Serbia has been the subject of several studies. Gocić and Trajković [27,28] found an increasing trend for the mean annual precipitation in most of the area. Luković et al. [29] analyzed the rainfall trend in Serbia and its spatial pattern annually, seasonally, and monthly. They detected very slight tendencies towards drier conditions on a seasonal scale during spring, and wetter conditions during autumn. The results of Milanović-Milićević et al. [30] showed that the amount and intensity of precipitation showed a statistically significant increase only during autumn, and this was most pronounced in the northern and western parts of the country. The variability of precipitation and extreme events was investigated by Tošić and Unkašević [31]. They studied only extreme daily precipitation and its link with the prevailing directions of the air trajectories at Belgrade. Milanović et al. [32] carried out an analysis of extreme climatic indices for just two stations, one in Belgrade and the other in Niš. Additionally, Tošić et al. [33] studied two exceptional cases of extreme precipitation in Serbia in 2014. The study by Milanović-Milićević et al. [30] on recent changes in Serbian climate extreme indices showed that the most pronounced increase in the daily amount of precipitation and short-term precipitation intensity was recorded in the north and the west of the country.
The aim of this paper is to determine the thresholds above which precipitation could be considered as a dangerous. According to the Global Change Glossary from the U.S. Global Change Research Program [34], extreme precipitation events are defined as: “An episode of abnormally high rain or snow”. Furthermore, “The definition of “extreme” is a statistical concept that varies depending on location, season, and length of the historical record”. In this study, such events are considered at daily levels. They are divided according to statistical criteria into two hazard categories (danger levels): heavy precipitation events, and very heavy precipitation events. The first type of event is a minor hazard, and the second causes significant hazards in the environment (this work can be the basis for research regarding adaption, vulnerability and resilience). However, the real consequences depend mainly on the readiness of society to protect themselves against the threats. Some categorizations of extreme precipitation events in Serbia have been made by Radinović and Maksimović [35], as well as Anđelković [36], to a limited extent. This study represents an addition to the previous studies of extreme weather conditions, with the aim of better understanding the impacts of climate change in Serbia.
2. Materials and Methods
2.1. Study Area and Data
Serbia is located in southern Europe between 41°43′ N and 46°11′ N, and 18°49′ E and 23°00′ Е. The geographical position of Serbia in Europe is shown in Figure 1. The study area is within the territory of Serbia, and is 88.361 km2. Altitudes in Serbia vary in elevation from 28 m in the north-eastern parts of the country at the mouth of the Veliki Timok River to the Danube River near the borders between Bulgaria and Romania, up to 2656 m at the Prokletije Mountains [37]. The mean altitude is 473 m. The northern part of the country is entirely located within the Pannonian Plain. The Dinaric Alps run through the western and south-western regions, and the Carpathians, Balkans, and Rhodope Mountains occupy the eastern and south-eastern regions.
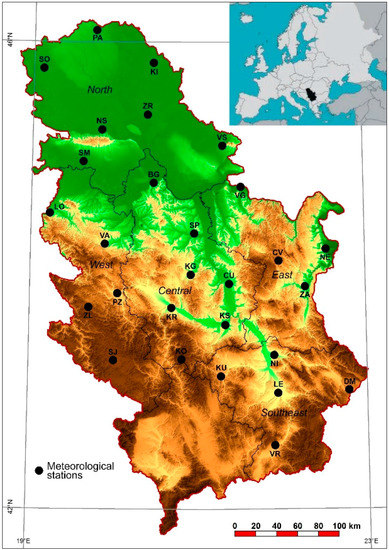
Figure 1.
Geographical position of Serbia in Europe, and the map of Serbia with orography and position of meteorological stations (explanation of the abbreviations can be found in Table 1).
There are three main types of climate in Serbia. A typical continental climate characterizes the northern parts of the country. A moderate continental climate occurs in the largest part of the territory (central, western, eastern, and southern parts of the country), while the south and southwestern regions of the country are subjected to Mediterranean influences with a modified Mediterranean climate [38,39]. The average annual amount of precipitation for the entire country is 739 mm [40]. Most of the terrain is exposed to the penetration of moist air masses from the west. The annual precipitation varies throughout the Serbian region as a consequence of the climatic and relief heterogeneity of the study area (Figure 2). An average annual precipitation of 500–700 mm is characteristic of Vojvodina (the Northern Province of Serbia) and smaller parts of the Južna and Velika Morava valleys. Precipitation of 700–1000 mm is characteristic of central Serbia and parts of the lower mountain terrains of eastern, southern, and southeastern Serbia. An average annual precipitation amount of 1000–1200 mm mainly characterizes the westernmost and the furthest southwestern mountainous parts of the country. The highest amount of rainfall occurs in southwestern mountains of Serbia, with the average amount exceeding 1300 mm [41]. The precipitation regime is continental across almost the whole country, with two maxima (the primary in May or June and the secondary in November or December), and two minima (the primary in January or February and the secondary in September or October) [39]. The spatial distribution of precipitation in June and February, as the rainiest and the driest months of the year respectively, is very similar to the annual spatial distribution. The precipitation ranges from 60–140 mm in June, and from 30–100 mm in February, for the largest part of Serbia [41].
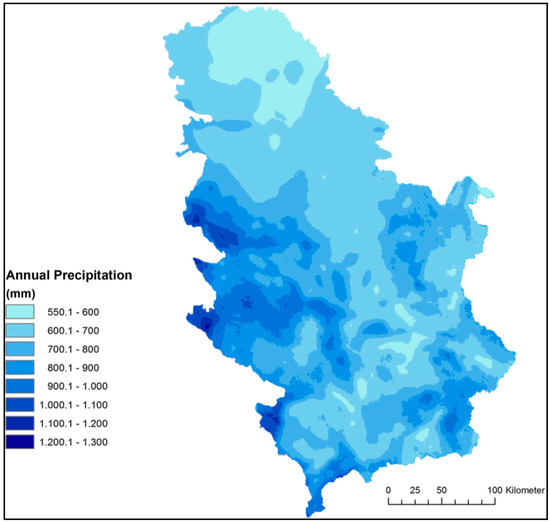
Figure 2.
The map of annual precipitation in Serbia (1961–2010) [41].
Daily rainfall observations from 28 stations from the national Met office were used (Table 1) [42]. The network includes stations that are evenly distributed throughout the country, excluding Kosovo and Metohija (for which data were not available). The period analyzed is 1961–2015. The sequences of daily precipitation from all stations were analyzed monthly; the series of data of each month were created over 55 years. Such classification has been carried out due to the fact that the rainfall regime in Serbia has the tendency to change month by month.

Table 1.
Geographical descriptions of 28 meteorological stations in Serbia.
Severe precipitation is always extremely difficult to differentiate in a small area, and even at some nearby areas with different geographical characteristics, different values could occur. Hence, our analysis has been carried out in five administrative-geographical regions (Table 1): Northern Serbia (seven meteorological stations), Central Serbia (seven meteorological stations), Western Serbia (five meteorological stations), Eastern Serbia (four meteorological stations) and South-eastern Serbia (five meteorological stations).
2.2. Methods
The daily maximum of precipitation is a parameter with no Gaussian distribution [2,6,43,44]. Two methods are used for analysis: the method of peaks over threshold (POT), and the decile method (D) [6,43,44]. These two statistical methods were used in this study for calculating the thresholds of extreme intensity of precipitation.
For calculating thresholds of heavy precipitation events at single stations, the method of peaks was used. This is a model of interrupted distribution, and is also known as a method of partial duration series. Here, the value of the threshold was defined as the average value (arithmetic mean) of maximal daily precipitation (Mi) for each year (i) during n years (55 years in this case) of the analyzed climate period of 1961–2015.
This method enables the analysis of three basic characteristics of extreme precipitation: maximum daily precipitation, the number of peaks (observed values above the threshold), and the height of peaks.
Also, an autocorrelation test of the MDP (Maximum Daily Precipitation) series was performed using the Neyman test squares of successive differences, and the Anderson autocorrelation test of the first order [45,46]. The results show that almost all MDP series do not have autocorrelation. The exception is the series for Požega and Vranje, because in both sets of Neyman and Anderson tests, they show values greater than critical (1.96): Požega 1.99785 (Neyman test), 1.962725 (Anderson test) and Vranje 2.64182 (Neyman test), 2.62251 (Anderson test). Additionally, in Novi Sad the Neyman test showed that the series is not random (2.26224).
The non-parametric Mann-Kendall (MK) test was applied to detect and evaluate the statistical significance of maximum daily precipitation trends, while Sen’s method was used for assessing slope trends [47,48]. To detect the changing point (transition year), the Pettitt test was applied [49]. The confidence level (α) of the Pettitt test in this study was set to 0.05, which is a common value.
For analyzing very heavy precipitation events, the starting point is the fact that heavy precipitation distributed over a huge territory can give rise to harmful consequences, based on spatial criterion. For the distribution of the frequency of points of the observation network (synoptic stations), which describes the distribution of precipitation, the decile method was used [6,43,50]. This method was used for studying extreme precipitation throughout the entire territory of Serbia, and for defining the size of the territory as the threshold for a very heavy precipitation event. Deciles (Dx) were derived when the members of the population were distributed into ten equal parts (x), per 10% of the total number of members (N), in which LD is a low level of decile class, fk is the cumulative frequency of the class preceding the decile class, and fa is the frequency of the decile class.
The area included in the frequency curve was divided into ten equal parts. Each scope defines a 10% probability of the observed event occurring. As can be seen from Table 2, the last (tenth) decile includes extreme events that belong to the category of extraordinary above normal [50].

Table 2.
Frequency distribution presented by decile method.
The procedure was carried so that the number of stations in which the observed precipitation on the same day was above the threshold of a heavy precipitation event (already defined by the method of peaks) were classified into appropriate deciles; the higher the decile, the bigger the distribution of the phenomena. Very heavy precipitation events represent extreme precipitation that was, according to the territorial distribution, classified into the last decile (extraordinary above normal).
Finally, the analysis of the length of the interval between extremes was carried out. These are extremes that, if they occur on the same day, produce very heavy precipitation events. The periods are several years long between two thresholds that were both exceeded, as defined by the method of peaks. Additionally, the length of the interval between two such events was analyzed in each monthly sequence. Out of 336 analyzed sequences of data, we singled out only the sequences in which the thresholds of extreme precipitation were exceeded two or three times. Our research was carried out in this way due to the fact that it is possible to compare at least two inter-periods.
Apart from spatial criterion, the criterion for detection of precipitation that can cause the highest level of harmful effects at only one place was also analyzed. These events are also considered as heavy precipitation events, but registered only at single stations. We analyzed situations in which daily precipitation was higher than the absolute daily maximum. In order to study these extremes for each station, the sub-period 1990–2015 was analyzed in relation to normal of 1961–1990.
3. Results and Discussion
3.1. Spatial Analysis of Maximum Daily Precipitation (MDP)
Maximal daily precipitation in Serbia, was first analyzed. The results showed that daily precipitation maxima appear mostly in May, June, and July. Table 3 shows that the territories of Northern Serbia and Central Serbia are primarily at risk of extreme precipitation. Out of five observed regions, only in Western Serbia and Eastern Serbia did the absolute maximum not appear in July, but in September; this is due to the continental precipitation regime. The highest value of measured daily precipitation of 189.7 mm was registered in Vršac on 18 July 1995, and is considered as the upper limit of extreme precipitation.

Table 3.
Absolute maximum daily precipitation (mm) in Serbia (period 1961–2015).
Extreme precipitation that exceeded previous records affected southeastern Europe, including Serbia, in May and September 2014. Precipitation exceeded 200 mm in 72 h, producing the most catastrophic floods in the recent history of Serbia [33]. In May 2014, the Balkans was hit by a Vb-type cyclone that brought disastrous flooding and severe damage to Serbia. The maximum daily precipitation (MDP) for 2014 was the highest for the period 1961–2015 at seven stations in Serbia (Sremska Mitrovica: 69.1 mm, Beograd: 109.8 mm, Loznica: 110.0 mm, Valjevo: 108.2 mm, Negotin: 161.3 mm, Kuršumlija: 71.2 mm, and Niš: 74.5 mm) and broke previous historical records (Figure 3). These results are in accordance with the results of Tošić et al. [33]. Furthermore, Tošić et al. [33] concluded that the value of 161.3 mm, observed on 16 September 2014 in Negotin, would be expected only once in 200 years.
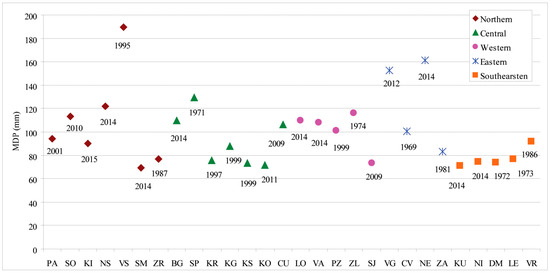
Figure 3.
Maximum daily precipitation (MDP) for 28 stations grouped in five regions for the period of 1961–2015 in Serbia.
MDPs occurred in the 21st century at a majority of stations (54%), but if the last five years of the 20th century are included in the analysis, MDPs were recorded at 71% of stations. The southeastern region experienced maximum values. In comparison to other regions, the largest variations are seen in the northern region, where measured maxima apart from the station at Vršac occurred in the 21st century. In the central and western regions, six stations out of 12 had their maxima in the 21st century, and four more stations had maxima in the last five years of the 20th century.
3.2. Time Series Analysis of Maximum Daily Precipitation (MDP)
Calculations show that Serbia has a tendency towards an increase in maximum daily precipitation (Table 4). Applying the Mann–Kendall test, a non-significant positive trend for MDPs was found for 23 stations. At only two station—Pozega and Valjevo (in the western region)—a non-significant negative trend was found. A significant positive trend was found for three stations. An increasing trend at a significance level of 0.01 was registered at Novi Sad. For Loznica, significant increase trends were detected at the level of 0.05, and for Sremska Mitrovica at the level of 0.1. The Sen’s slope shows that the average increase of MDPs for these stations are 0.423 mm/year, 0.288 mm/year, and 0.153 mm/year, respectively. Generally, it can be concluded that positive significant trends were detected in the northwestern area of Serbia.

Table 4.
Geographical descriptions and results of the Mann-Kendall (MK) tests for maximum daily precipitation at meteorological stations over the period 1961–2015.
Results of the Pettit test showed, at a confidence level of 0.05, that there was a significant sudden shift upward for the research period, but only for the station at Loznica (Figure 4). As a transition year for MDP, the year 1981 was detected. The average annual values of MDP were 39.8 mm before the transition year, and 54.6 mm after the transition year.
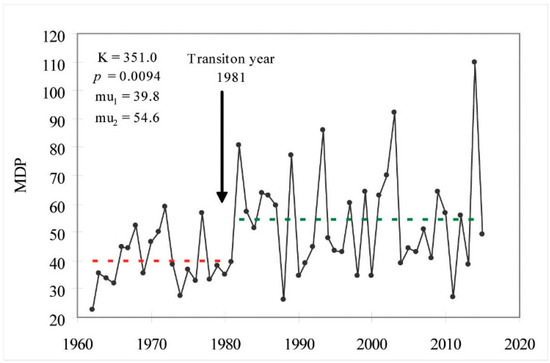
Figure 4.
Results of the Pettit test for maximum daily precipitation (MDP) with a significant change point at the significance level (α = 0.05) for the meteorological station at Loznica. (mu1 is the average value in the period before the transition year, mu2 is the average value in the period after the transition year).
3.3. Thresholds of Extreme Precipitation
The threshold for heavy precipitation events, determined by the method of peaks, is in the range of 36.6–52.5 mm (Figure 5) in Serbia. Applying the method of decile to the time series of daily precipitation in Belgrade, Radinović, and Ćurić [44], we calculated the value of this threshold to be 33.7 mm. If the daily intensity of precipitation is above the calculated thresholds, it is likely that river discharge and the water level will increase, mechanical water erosion will occur, leading to damage to agricultural areas and settlements
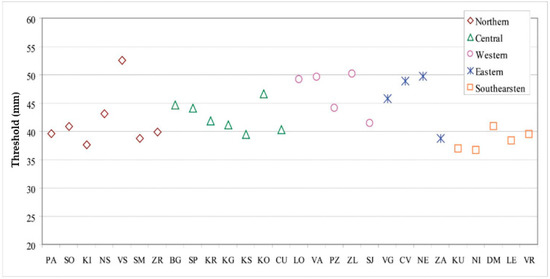
Figure 5.
Average value thresholds (mm) for very heavy precipitation events for meteorological stations grouped in five regions for the period 1961–2015 in Serbia.
Regional differences are presented in Figure 5. Dry southeastern Serbia is most susceptible to precipitation events (even at a precipitation level of 36.6 mm), while northern Serbia is slightly less at risk. The more protected parts of the country include the western and central regions, in which the threshold values move to above 40 mm (Table 5). At mountainous meteorological stations (Kopaonik, Zlatibor, and Crni Vrh), the thresholds of dangerous precipitation were higher than at lowland stations; the lowest threshold was registered at the meteorological station at Kopaonik (46.7 mm). As a result, the threshold of warning for a territory above an altitude of 1000 m should be set at about 45 mm. According to these results, it can be concluded that, in case of extreme rainfall in Serbia, warnings should be spatially differentiated in accordance with the weather forecast and the lowest value of the defined thresholds for heavy precipitation events.

Table 5.
Thresholds for heavy precipitation events by region in Serbia.
In the study period (1961–2015) in Serbia, 416 cases of threshold exceedance for heavy precipitation events were registered. The occurrence of these cases at several stations on the same day is a spatial criterion for registering very heavy precipitation events. Analyzing the distribution of occurrences, the results indicate that 6.21 is the critical number of stations for registering heavy precipitation events on the same day. This result is calculated from Equation (2) for calculating deciles. It includes the parameters of the distribution of the 416 cases when the threshold of heavy precipitation is exceeded in one day.
All values above this number are considered to represent levels of precipitation that fall into a higher category of hazard. This result is very significant, mainly due to the fact that such research has not been done so far. Taking into consideration the fact that each meteorological station theoretically covers 2.767 km2 of territory (77.472 km2/28 stations), it can be concluded that very heavy precipitation events occur when they cover over 22.17% of the studied territory of Serbia (2.767 km2 × 6.21 = 17.183 km2). The critical number of stations (namely at least 7 stations) is extraordinarily above normal, since it can cause extremely harmful consequences of national significance in the environment (Figure 6). In the study period, seven catastrophic floods occurred when the threshold of extreme precipitation was registered at seven or more meteorological stations: in 1967 (seven stations); in 1978 (seven stations); in 1985 (eight stations); in 1987 (11 stations); in 1999 (11 stations); in 2009 (eight stations) and in 2014 (14 stations). During the time period in which the largest floods occurred in May 2014, 50% of the meteorological stations in Serbia registered exceedance of the threshold for extreme precipitation. Out of that number, 12 stations were in the area of northern Serbia (covering 33.204 km2 or 42.85% of the territory) which, of all regions, suffered the most from the floods. The consequences of the floods were upsetting: 51 people died, 31,879 people were evacuated, and 1.6 million people were directly or indirectly hurt [17].
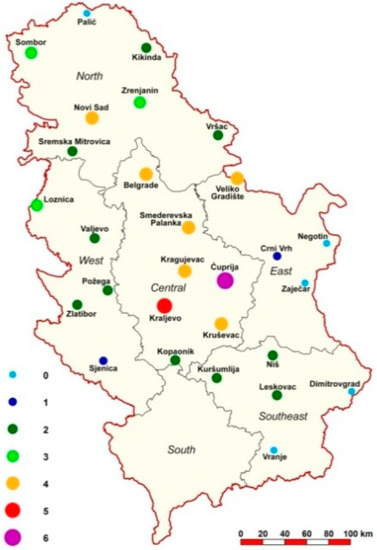
Figure 6.
The frequencies of very heavy precipitation events defined by the method of decile at metrological stations in Serbia with consequences of national significance (1961–2015).
This study has been carried out on statistical sequences (series) of daily precipitation distributed per month; a total of 336 series at meteorological stations in Serbia were utilized. Out of this number, 129 series were registered with three and more exceedances of extreme thresholds (Table 6). Their frequency indicates the probability of co-occurrence at several stations causing very heavy precipitation events in Serbia. The series for the first three months in the year did not include any threshold exceedance. From April, the number of such cases increased quickly, and in July, all stations registered a threshold exceedance. During autumn, the number of these cases decreased, so that in December, there was no threshold exceedance registered at any station. The largest number of threshold exceedance occurrences in one month was registered in the period of 1961–2015 in northern Serbia, at the meteorological station at Kikinda in June (from a total number of 12 situations, or 11 subintervals for the research). Northern Serbia is known for significant flooding of large rivers, and June is the wettest month.

Table 6.
Basic parameters of the variability of intervals between exceedance of extreme precipitation thresholds defined by the method of peaks (heavy precipitation events) in Serbia.
The frequency of extreme precipitation in the period of the studied 55 years varied significantly. Numerous researchers have shown that the parameters of extreme precipitation in Europe are very variable, both spatially and across seasons [21,51,52,53,54,55]. In general, the frequency of precipitation that occurred above the extreme level during the 55 years was very low, only exceeding five occurrences in one series of data 15 times. Therefore, the results from Table 6 should be carefully considered (especially in terms of the change of the intervals between extreme occurrences). This example is the largest registered shortening of the interval between extremes in 13.5 successive years for August (given that Sombor is placed in northern Serbia), in which the conclusion was reached only on the basis of four registered extremes. Additionally, it should be taken into consideration that Northern Serbia is lowland, and known for huge spatial and time variations of precipitation and hydrological parameters (floods or droughts). Although it is apparent in the data that extremes, in many cases, become more frequent, it is difficult to precisely predict extreme events due to the low frequency of extremes. It is very likely, however, that the shortening of the interval between exceedances of two thresholds in a series increases the risk to the environment.
In support of the conclusion that extremes have become more frequent is the fact that there were threshold exceedances in successive years at the end of the studied period of 55 years in 22 situations. Out of this number, there were three situations of threshold exceedance in three successive years (station Crni Vrh in the period 2012–2014, and stations Kragujevac and Kuršumlija in the period 2013–2015), and one situation of threshold exceedance in four successive years (station Kikinda in the period 2007–2010). These results indicate an increase in the probability of co-occurrences of threshold exceedances on the same day, causing situations with the potential for very dangerous consequences for the environment. Therefore, the community is obliged to be ready with an adequate response.
Moreover, results were also obtained for the cases in which harmful consequences of very heavy precipitation events covered only a small area, or only a local community. This happened in cases when precipitation at one station exceeded the absolute daily maximum of the previous climate period (1961–1990). Such received thresholds of extreme precipitation were in the range of 54.5 mm–129.3 mm. Among them, 17 thresholds, or 60% of the data had a value in the range of 70 mm–100 mm, which were approximate values of their arithmetic means for the whole territory (85 mm); these were very high intensities of rainfall for one day. These values are even higher than the average monthly amount of precipitation in Serbia, which is 75 mm (according to the Republic Hydrometeorological Service of Serbia).
In the period of 1991–2015, 18 measured stations exceeded the values of their thresholds. The exceeding value was approximately 18.3 mm (Table 7). Very heavy precipitation events mostly caused damage to places in the northern and western parts of Serbia, since they were the most exposed to the moisture from the west.

Table 7.
Meteorological stations at which very heavy precipitation events occurred in the period of 1990–2015, exceeding the absolute maximum of the previous climate period (1961–1990), with occurrence frequencies.
The threshold was exceeded 27 times, mainly in May, June, and July. Only at the stations in Western Serbia and one station in Eastern Serbia was the threshold exceeded in autumn. This fact is in keeping with the research of Petrović et al. [56], and Ristic et al. [57], stating that the largest number of torrential floods in Serbia occurs exactly in June (27.5%), May (21%), and July (10.4%).
4. Conclusions
The results of the research regarding thresholds of extreme precipitation have both local and national significance, and are important for developing readiness strategies which would allow communities to react in situations of crisis. The spatial distribution of very heavy precipitation events has the most significant impact upon the occurrence of dangerous outcomes in the environment. The consequences of precipitation of the first level of hazard are not too dangerous, since they are not widely distributed.
In this paper, we calculated that the critical number of stations above which an event is considered a very heavy precipitation event, or a climate extreme of national significance, is 6.21 (theoretically containing above 22.17% of the total territory). This means that when, on one day at seven or more stations, heavy precipitation events occur, these events are extraordinarily above normal in nature, and are likely to cause very harmful consequences for the environment. In the study period, seven such events were registered in Serbia. The biggest flood—that of May, 2014—was initiated by extreme precipitation that occurred at 14 stations. In other words, the thresholds of extreme precipitation defined in this paper were exceeded at half of the meteorological stations in Serbia during this event. This was the single most dangerous recorded situation, and the subsequent results (a high number of threshold exceedances) indicate the significance of the calculated threshold criteria for emergency preparedness aimed at preventing harmful consequences.
A denser network of meteorological stations, especially in higher mountainous regions, would give more reliable and precise results when using the method of peaks and the method of decile. In forecasting and predicting very heavy precipitation events, apart from statistical indices, it is also necessary to take into consideration the spatial distribution of stations that are classified in the last decile, since it is extremely important to consider whether they, in territorial terms, cover a continual area.
Expected domination of a decreasing trend of the length of interval between threshold exceedances of heavy precipitation events indicates an increasing danger of co-occurrence of extremes at more stations in the future, which may lead to very dangerous outcomes.
Author Contributions
G.A. is a first author. G.A., S.J. and S.M. wrote the manuscript with extensive comments and input by all authors during all stages. G.A., I.S., L.Ž., D.Š., D.G. and M.D. designed the study. G.A., S.J., S.M., and I.S. collected and analysed the data for precipitation in Serbia while L.Ž., D.Š., D.G. and M.D. collected and analysed data for geographical descriptions of meteorological stations in Serbia. All authors approved the final version of the manuscript.
Acknowledgments
This study was supported by the Ministry of Education, Science andTechnological Development of the Republic of Serbia, No. 176008, No. 176017, No. 43007.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Changnon, S.; Changnon, R.; Fosse, R.; Hoganson, D.; Roth, R.; Totsch, J. Effects of recent weather extremes on the insurance industry: Major implications for the atmospheric sciences. Bull. Am. Meteorol. Soc. 1997, 78, 425–435. [Google Scholar] [CrossRef]
- Changnon, S. Evalution of weather catastrophe data for use in climate change investigation. Clim. Chang. 1998, 38, 435–445. [Google Scholar] [CrossRef]
- Kumkel, K.; Pielke, R.; Changnon, S. Temporal fluctuations in weather and climate extremes that cause economic and human health impacts: A review. Bull. Am. Meteorol. Soc. 1999, 80, 1077–1098. [Google Scholar] [CrossRef]
- WMO. Climate extremes: Early warnings are critical for socio-economic development. Bull. WMO 2006, 55, 21–26. [Google Scholar]
- Oikonomou, C.; Flocas, H.A.; Hatzaki, M.; Asimakopoulos, D.N.; Giannakopoulos, C. Future changes in the occurrence of extreme precipitation events in eastern Mediterranean. Glob. NEST J. 2008, 10, 255–262. [Google Scholar]
- Radinović, D.; Ćurić, M. Deficit and surplus of precipitation as a continuous function of time. Theor. Appl. Climatol. 2009, 98, 197–200. [Google Scholar] [CrossRef]
- Leblois, A.; Quirion, P. Agricultural insurances based on meteorological indices: Realizations, methods and research challenges. Meteorol. Appl. 2011, 18, 186–198. [Google Scholar] [CrossRef]
- Wendler, G.; Gordon, T.; Stuefer, M. On the Precipitation and Precipitation Change in Alaska. Atmosphere 2017, 8, 253. [Google Scholar] [CrossRef]
- Anđelković, G.; Živković, N. Precipitation as adverse climatic phenomenon in Negotin. Bull. Serbian Geogr. Soc. 2007, 87, 51–62. [Google Scholar] [CrossRef]
- Dragićević, S.; Živković, N.; Ducić, V. Factors of flooding on the territory of the municipality of Obrenovac. Collect. Pap. Fac. Geogr. Univ. Belgrade 2007, 55, 39–54. [Google Scholar]
- Ocokoljić, M. The historical maximal precipitations in Belgrade and their urban aspect. Bull. Serbian Geogr. Soc. 2007, 87, 63–68. [Google Scholar] [CrossRef]
- Milanović, A.; Urošev, M.; Milijašević, D. Floods in Serbia in the 1999–2009 period: Hydrological analysis and flood protection measures. Bull. Serbian Geogr. Soc. 2010, 90, 109–121. [Google Scholar] [CrossRef]
- Mustafić, S.; Manojlović, P.; Milošević, M. Extreme Erosion Rates in the Nišava River Basin (Eastern Serbia) in 2010. In Geomorphological Impacts off Ekstreme Weather; Case Studies from Central and Eastern Europe; Loczy, D., Ed.; Springer: Dordrecht, The Netherland, 2013; pp. 171–187. ISBN 978-94-007-6301-2. [Google Scholar]
- Rousta, I.; Nasserzadeh, M.H.; Jalali, M.; Haghighi, E.; Ólafsson, H.; Ashrafi, S.; Doostkamian, M.; Ghasemi, A. Decadal Spatial-Temporal Variations in the Spatial Pattern of Anomalies of Extreme Precipitation Thresholds (Case Study: Northwest Iran). Atmosphere 2017, 8, 135. [Google Scholar] [CrossRef]
- Ge, G.; Shi, Z.; Yang, X.; Hao, Y.; Guo, H.; Kossi, F.; Xin, Z.; Wei, W.; Zhang, Z.; Zhang, X.; et al. Analysis of Precipitation Extremes in the Qinghai-Tibetan Plateau, China: Spatio-Temporal Characteristics and Topography Effects. Atmosphere 2017, 8, 127. [Google Scholar] [CrossRef]
- Caloiero, T.; Pasqua, A.A.; Petrucci, O. Damaging hydrogeological events: A procedure for the assessment of severity levels and an application to Calabria (Southern Italy). Water 2014, 6, 3652–3670. [Google Scholar] [CrossRef]
- Government of the Republic of Serbia. Available online: http://www.obnova.gov.rs (accessed on 17 September 2017).
- Fowler, H.; Kilsby, C. A regional frequency analysis of United Kingdom extreme rainfall from 1961 to 2000. Int. J. Climatol. 2003, 23, 1313–1334. [Google Scholar] [CrossRef]
- Groisman, P.; Knight, R.; Easterling, D.; Karl, T.; Hegerl, G.; Razuvaev, V. Trends in intense precipitation in the climate record. J. Clim. 2005, 18, 1326–1350. [Google Scholar] [CrossRef]
- Pujol, N.; Neppel, L.; Sabatier, R. Regional tests for trend detection in maximum precipitation series in the French Mediterranean region. Hydrol. Sci. J. 2007, 52, 956–973. [Google Scholar] [CrossRef]
- Klein Tank, A.; Können, G. Trends in indices of daily temperature and precipitation extremes in Europe, 1946–99. J. Clim. 2003, 16, 3665–3680. [Google Scholar] [CrossRef]
- Zolina, O.; Simmer, C.; Belyaev, K.; Kapala, A.; Gulev, S. Improving estimates of heavy and extreme precipitation using daily records from European rain gauges. J. Hydrometeorol. 2009, 10, 701–716. [Google Scholar] [CrossRef]
- Van den Besselaar, E.J.M.; Klein Tank, A.M.G.; Buishand, T.A. Trends in European precipitation extremes over 1951–2010. Int. J. Climatol. 2013, 33, 2682–2689. [Google Scholar] [CrossRef]
- Kostopoulou, E.; Jones, P.D. Assessment of climate extremes in the Eastern Mediterranean. Meteorol. Atmos. Phys. 2005, 89, 69–85. [Google Scholar] [CrossRef]
- Ducić, V.; Luković, J.; Burić, D.; Stanojević, G.; Mustafić, S. Precipitation extremes in the wettest Mediterranean region (Krivošije) and associated atmospheric circulation types. Nat. Hazards Earth Syst. Sci. 2012, 12, 687–697. [Google Scholar] [CrossRef]
- Burić, D.; Luković, J.; Bajat, B.; Kilibarda, M.; Živković, N. Recent trends in daily rainfall extremes over Montenegro (1951–2010). Nat. Hazards Earth Syst. Sci. 2015, 15, 2069–2077. [Google Scholar] [CrossRef]
- Gocić, M.; Trajković, S. Analysis of precipitation and drought data in Serbia over the period 1980–2010. J. Hydrol. 2013, 494, 32–42. [Google Scholar] [CrossRef]
- Gocić, M.; Trajković, S. Spatio-temporal patterns of precipitation in Serbia. Theor. Appl. Climatol. 2014, 117, 419–431. [Google Scholar] [CrossRef]
- Luković, J.; Bajat, B.; Blagojević, D.; Kilibarda, M. Spatial pattern of recent rainfall trends in Serbia (1961–2009). Reg. Environ. Chang. 2014, 14, 1789–1799. [Google Scholar] [CrossRef]
- Milanović-Milićević, S.; Radovanović, M.; Stanojević, G.; Milovanović, B. Recent changes in Serbian climate extreme indices from 1961 to 2010. Theor. Appl. Climatol. 2017, 124, 1089–1098. [Google Scholar] [CrossRef]
- Tošić, I.; Unkašević, M. Extreme daily precipitation in Belgrade and their links with the prevailing directions of the air trajectories. Theor. Appl. Climatol. 2013, 111, 97–107. [Google Scholar] [CrossRef]
- Milanović, M.; Gocić, M.; Trajković, S. Analysis of Extreme Climatic Indices in the Area of Nis and Belgrade for the Period between 1974 and 2003. Agric. Agric. Sci. Procedia 2015, 4, 408–415. [Google Scholar] [CrossRef]
- Tošić, I.; Unkašević, M.; Putniković, S. Extreme daily precipitation: The case of Serbia in 2014. Theor. Appl. Climatol. 2017, 128, 785–794. [Google Scholar] [CrossRef]
- Global Change Glossary. Available online: https://definedterm.com/extreme_precipitation_events (accessed on 23 January 2018).
- Radinović, D.; Maksimović, S. Proposal for Methodology Detecting and Researching of Extreme Weather and Climate Events; Urbanistički zavod Republike Srpske: Banja Luka, Bosnia and Hercegovina, 2002; pp. 21–32. [Google Scholar]
- Anđelković, G. Climatic extremes in Serbia—Definitions, types and classificationgoran. Bull. Serbian Geogr. Soc. 2010, 90, 125–146. [Google Scholar] [CrossRef]
- Manojlović, P.; Dragićević, S.; Mustafić, S. The basic morphometric characteristics of Serbian relief. Bull. Serbian Geogr. Soc. 2004, 84, 11–20. [Google Scholar] [CrossRef]
- Unkašević, M.; Radinović, D. Statistical analysis of daily maximum and monthly precipitation at Belgrade. Theor. Appl. Climatol. 2000, 66, 241–249. [Google Scholar] [CrossRef]
- Ducić, V.; Radovanović, M. Climate of Serbia; Zavod za Udzbenike i Nastavna Sredstva: Belgrade, Serbia, 2005; pp. 1–212. ISBN 86-17-12290-0. [Google Scholar]
- Bajat, B.; Pejović, M.; Luković, J.; Manojlović, P.; Ducić, V.; Mustafić, S. Mapping average annual precipitation in Serbia (1961–1990) by using regression kriging. Theor. Appl. Climatol. 2013, 112, 1–13. [Google Scholar] [CrossRef]
- Milovanović, B.; Schuster, P.; Radovanović, M.; Ristić Varanjac, V.; Schneider, C. Spatial and temporal variability of precipitation in Serbia for the period 1961–2010. Theor. Appl. Climatol. 2017, 130, 687–700. [Google Scholar] [CrossRef]
- Republic Hydrometeorological Service of Serbia. Available online: http://www.hidmet.gov.rs (accessed on 15 October 2016).
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; p. 154. [Google Scholar]
- Radinović, D.; Ćurić, M. Measuring scales for daily temperature extremes, precipitation and wind velocity. Meteorol. Appl. 2014, 21, 461–465. [Google Scholar] [CrossRef]
- Von Neumann, J. Distribution of the Ratio of the Mean Square Successive Difference to the Variance. Ann. Math. Stat. 1941, 12, 367–395. [Google Scholar] [CrossRef]
- Anderson, R.L. Distribution of the serial correlation coefficients. Ann. Math. Stat. 1942, 13, 1–13. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975; ISBN 10 0852641990. [Google Scholar]
- Pettitt, A.N. A non-parametric approach to the change-point problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Gibbs, W.J. Defining climate. Bull. WMO 1987, 36, 290–296. [Google Scholar]
- Frei, C.; Schöll, R.; Fukutome, S.; Schmidli, J.; Vidale, L.P. Future change of precipitation extremes in Europe: Intercomparison of scenarios from regional climate models. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Lupikasza, E. Spatial and temporal variability of extreme precipitation in Poland in the period 1951–2006. Int. J. Climatol. 2010, 30, 991–1007. [Google Scholar] [CrossRef]
- Sanderson, M. Changes in the Frequency of Extreme Rainfall Events for Selected Towns and Cities; Met Office of United Kingdom: Exeter, UK, 2010; pp. 1–39.
- Rajczak, R.; Pall, P.; Schär, C. Projections of extreme precipitation events in regional climate simulations for Europe and the Alpine Region. J. Geophys. Res. 2013, 118, 3610–3626. [Google Scholar] [CrossRef]
- Rulfová, Z.; Beranová, R.; Kyselý, J. Climate change scenarios of convective and large-scale precipitation in the Czech Republic based on EURO-CORDEX data. Int. J. Climatol. 2017, 37, 2451–2465. [Google Scholar] [CrossRef]
- Petrović, A.; Kostadinov, S.; Dragićević, S. The inventory and characterisation of torrential flood phenomenon in Serbia. Pol. J. Environ. Stud. 2014, 23, 823–830. [Google Scholar]
- Ristić, R.; Kostadinov, S.; Albomasov, B.; Dragićević, S.; Trivan, G.; Radić, B.; Trifunović, M.; Radosavljević, Z. Torrential floods and town and country planning in Serbia. Nat. Hazards Earth Syst. Sci. 2012, 12, 23–35. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).