Evaluation of Fog and Low Stratus Cloud Microphysical Properties Derived from In Situ Sensor, Cloud Radar and SYRSOC Algorithm
Abstract
1. Introduction
2. Observational Dataset and Synergistic Remote Sensing of Clouds (SYRSOC) Algorithm
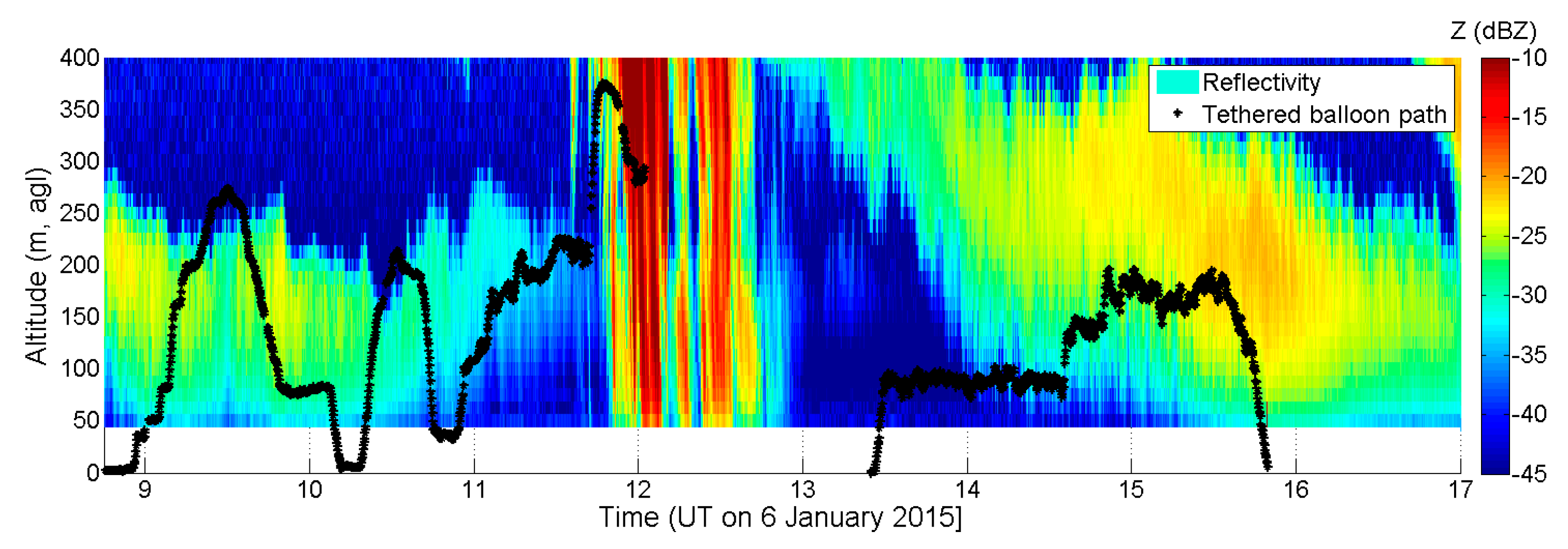
2.1. Intensive Observational Periods (IOP) and Three Tethered Balloon Flights
2.2. Remote-Sensing Instruments and In Situ Sensor
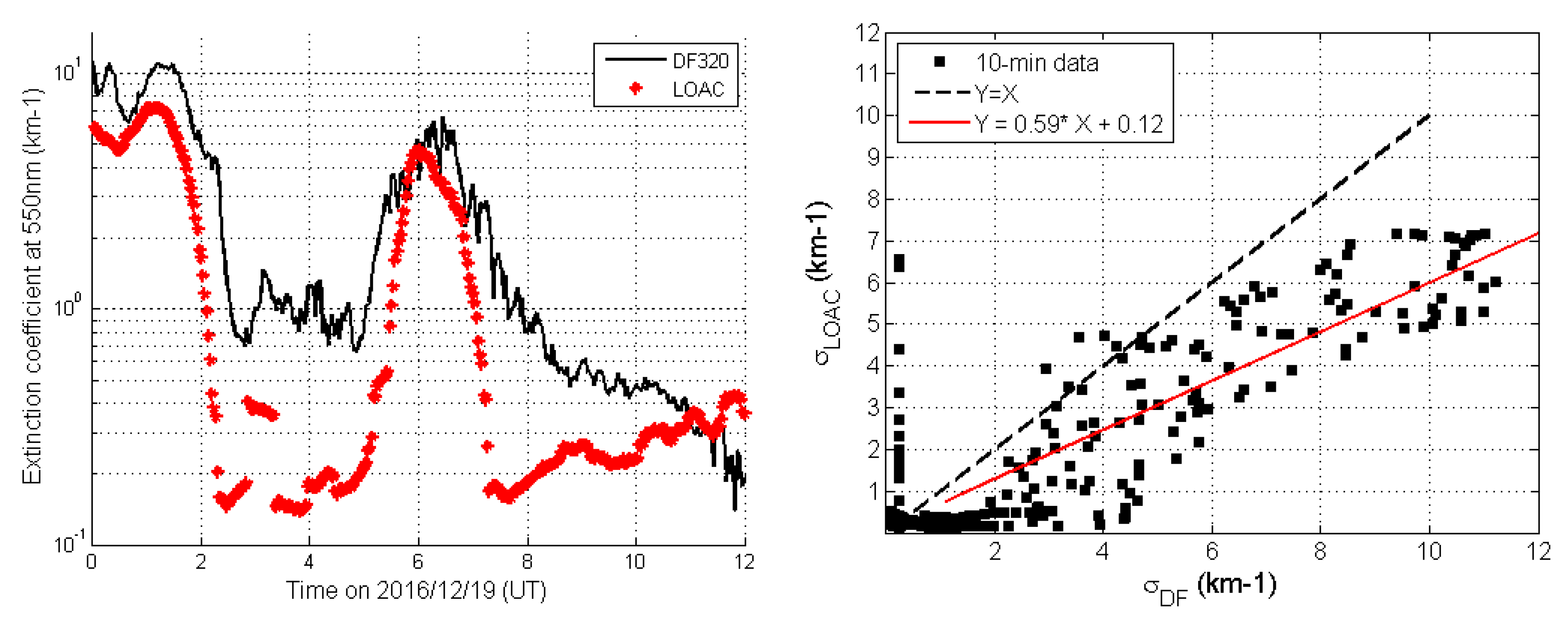
2.3. Visible Extinction Normalisation for Light Optical Aerosol Counter (LOAC) Validation
2.4. SYRSOC Algorithm
3. Liquid Water Content (LWC), Effective Radius (Re) and Cloud Droplet Number Concentration (CDNC) Retrievals
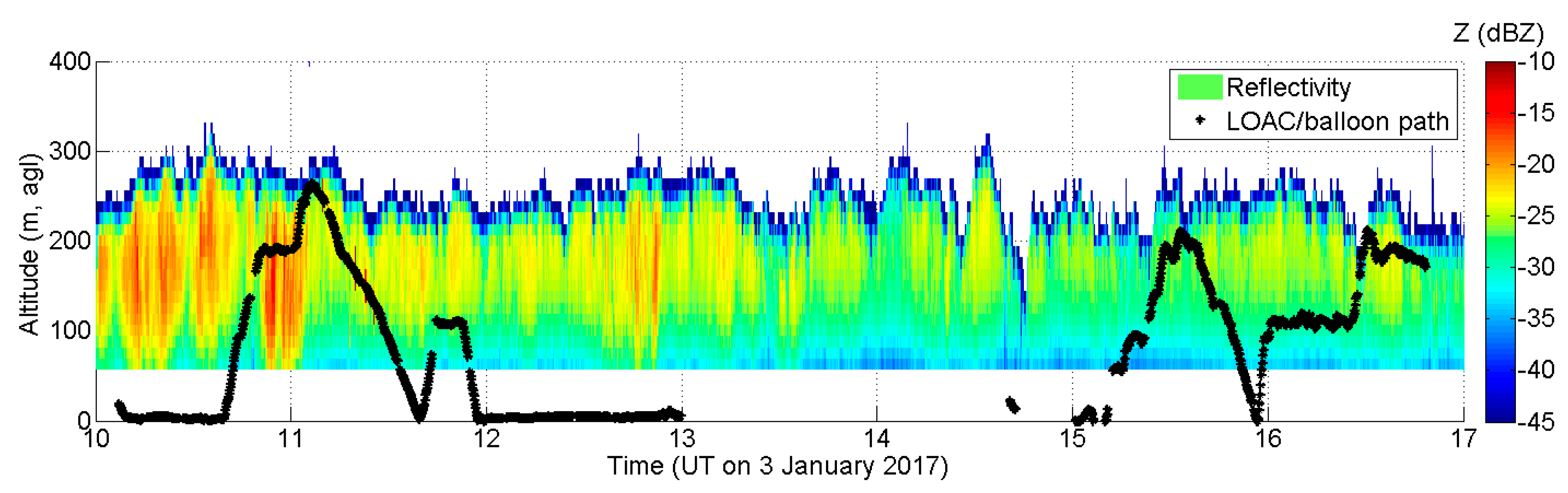
3.1. Pairing of Radar and In Situ Observations Along the Flight Path
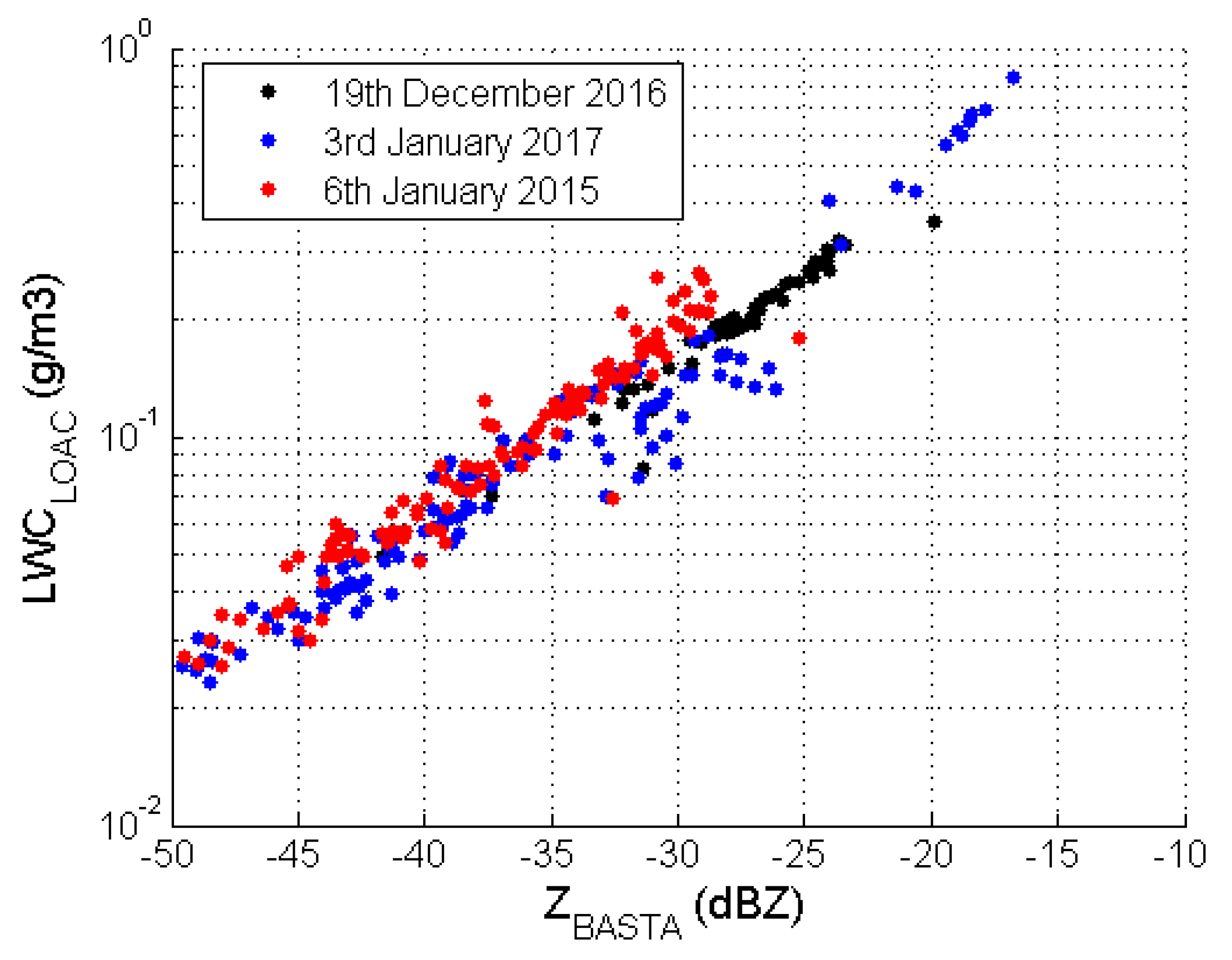
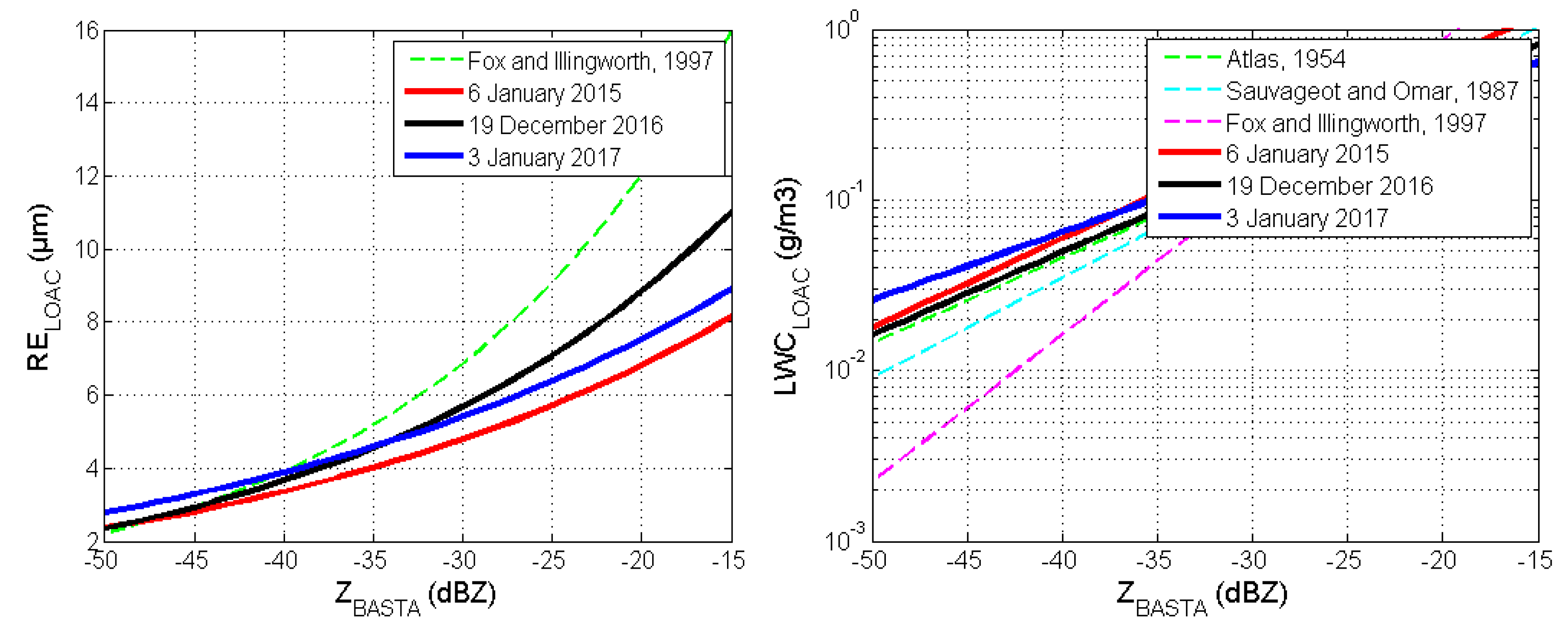
3.2. Doppler Cloud Radar Reflectivity (Z)–LWC Relationship
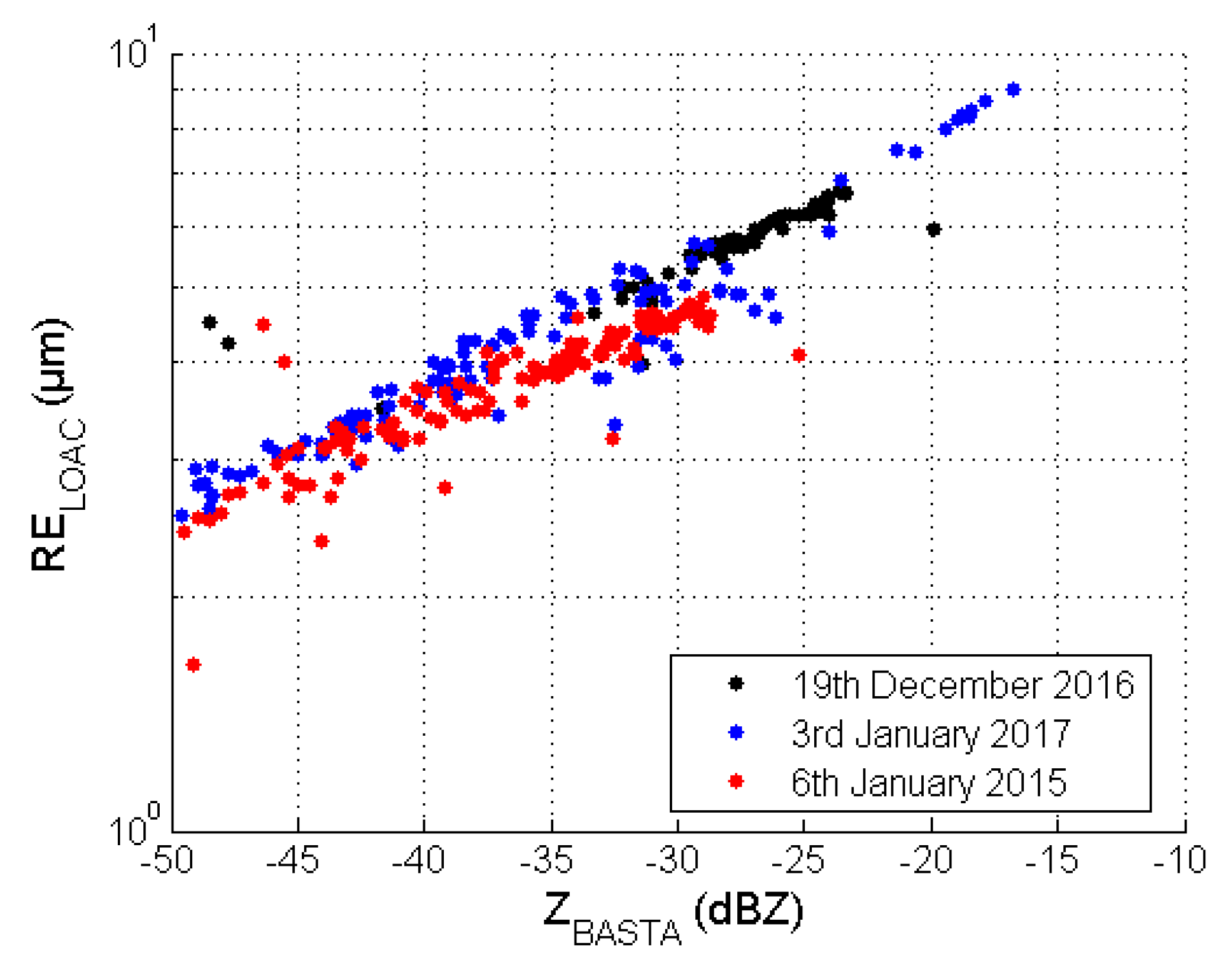
3.3. Z–Re Relationship
3.4. Cloud Droplet Number Concentration (CDNC)
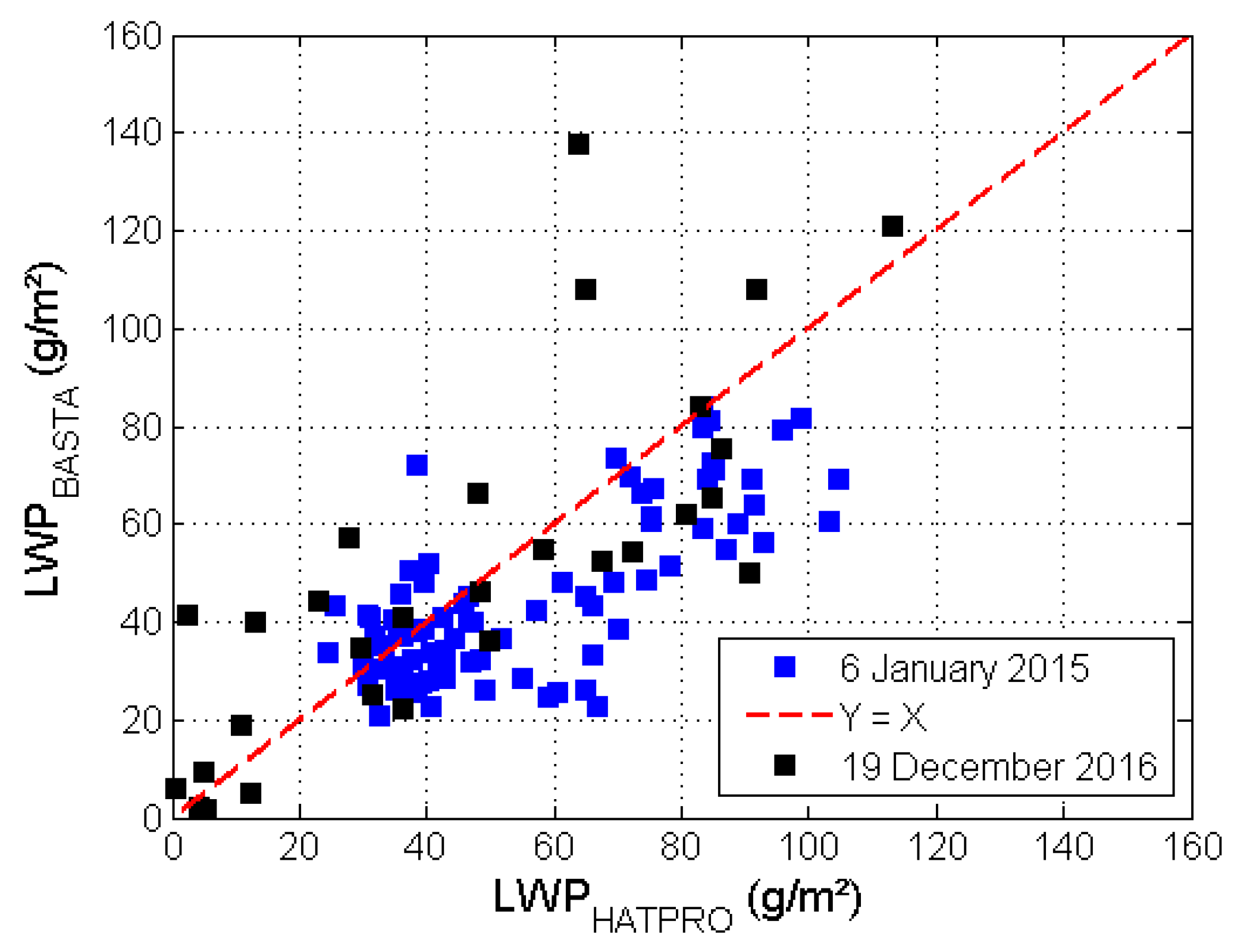
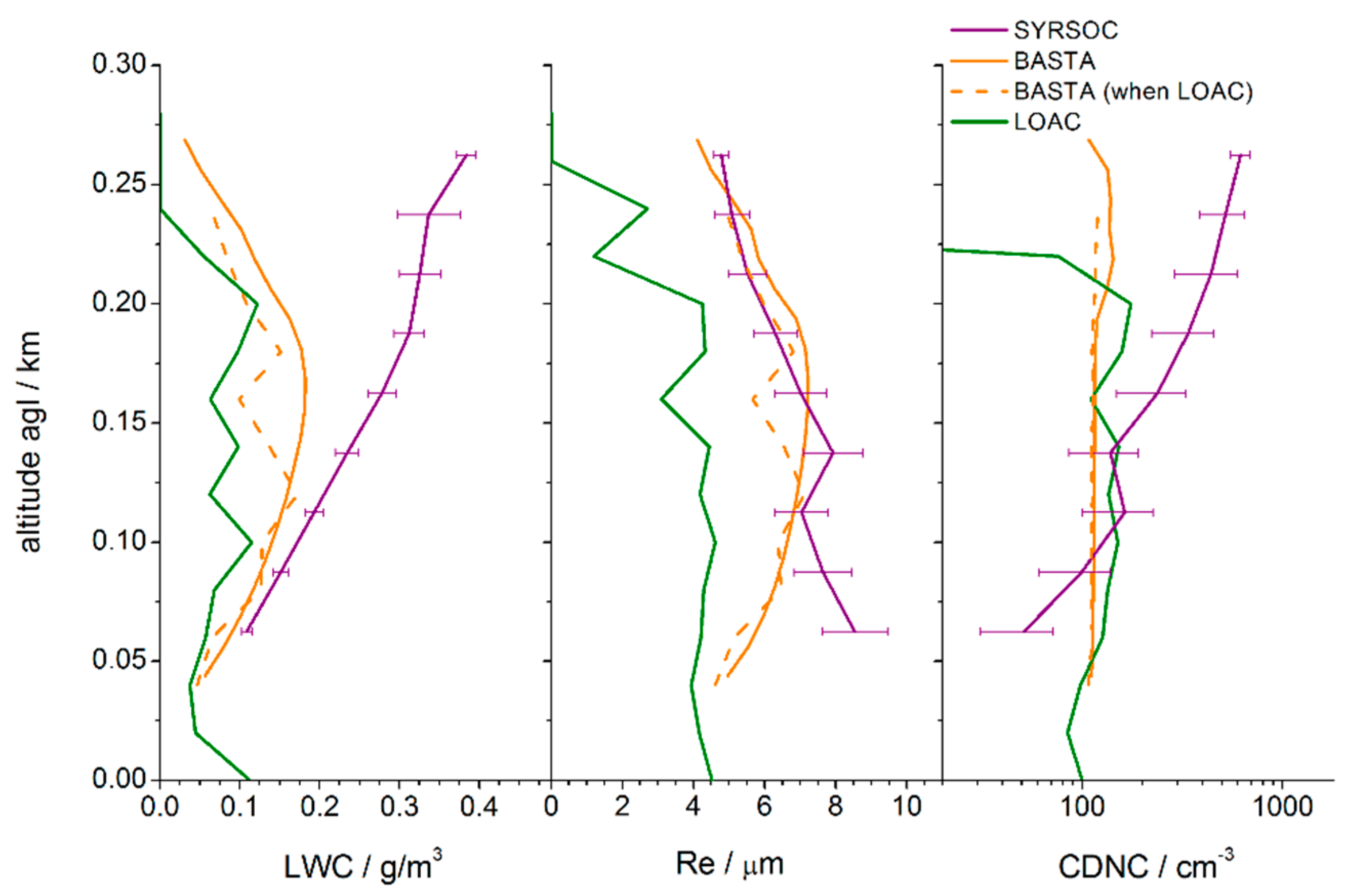
3.5. Liquid Water Closure
3.6. Discussion on the Validity of these Relationships
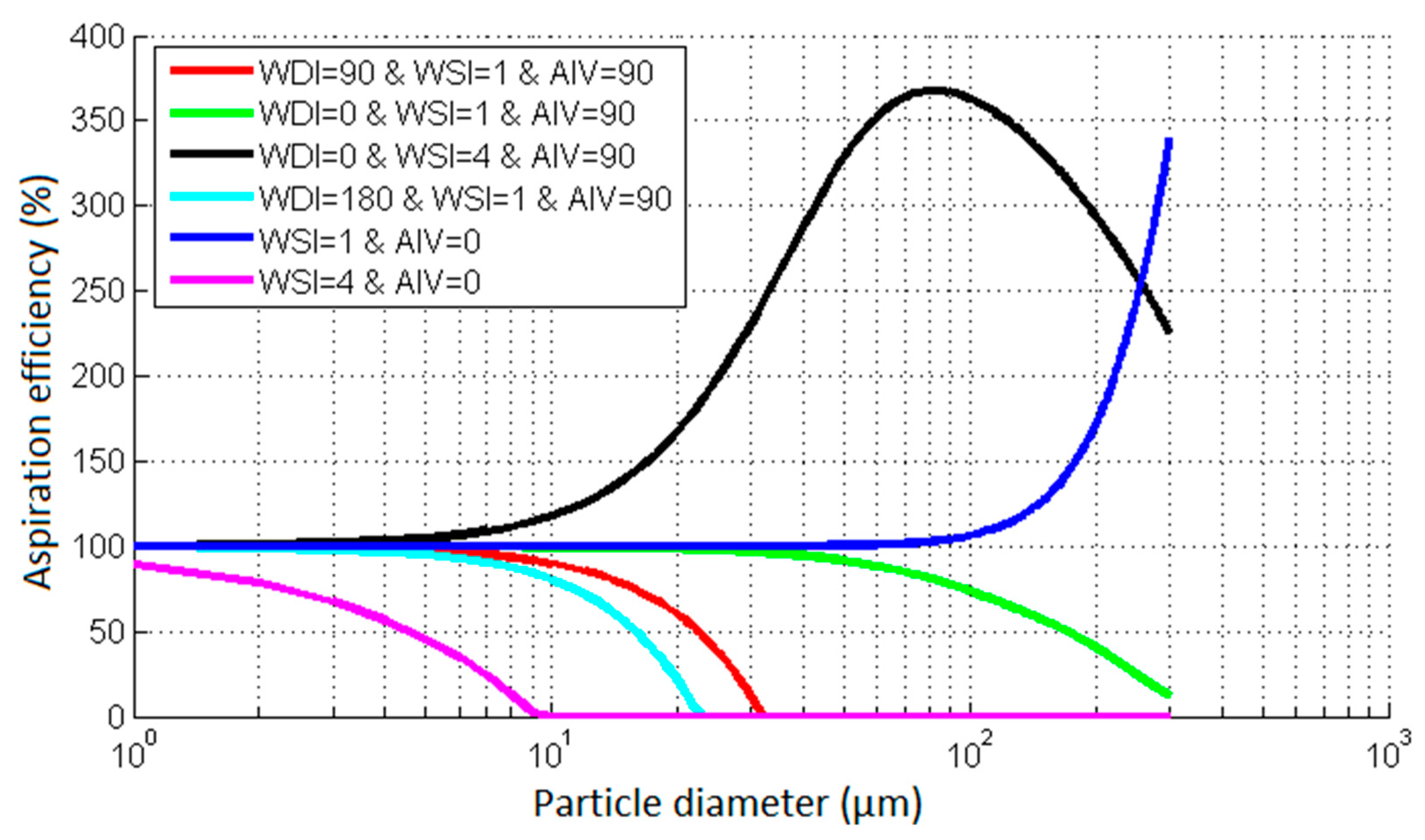
3.6.1. Impact of Aspiration Efficiency
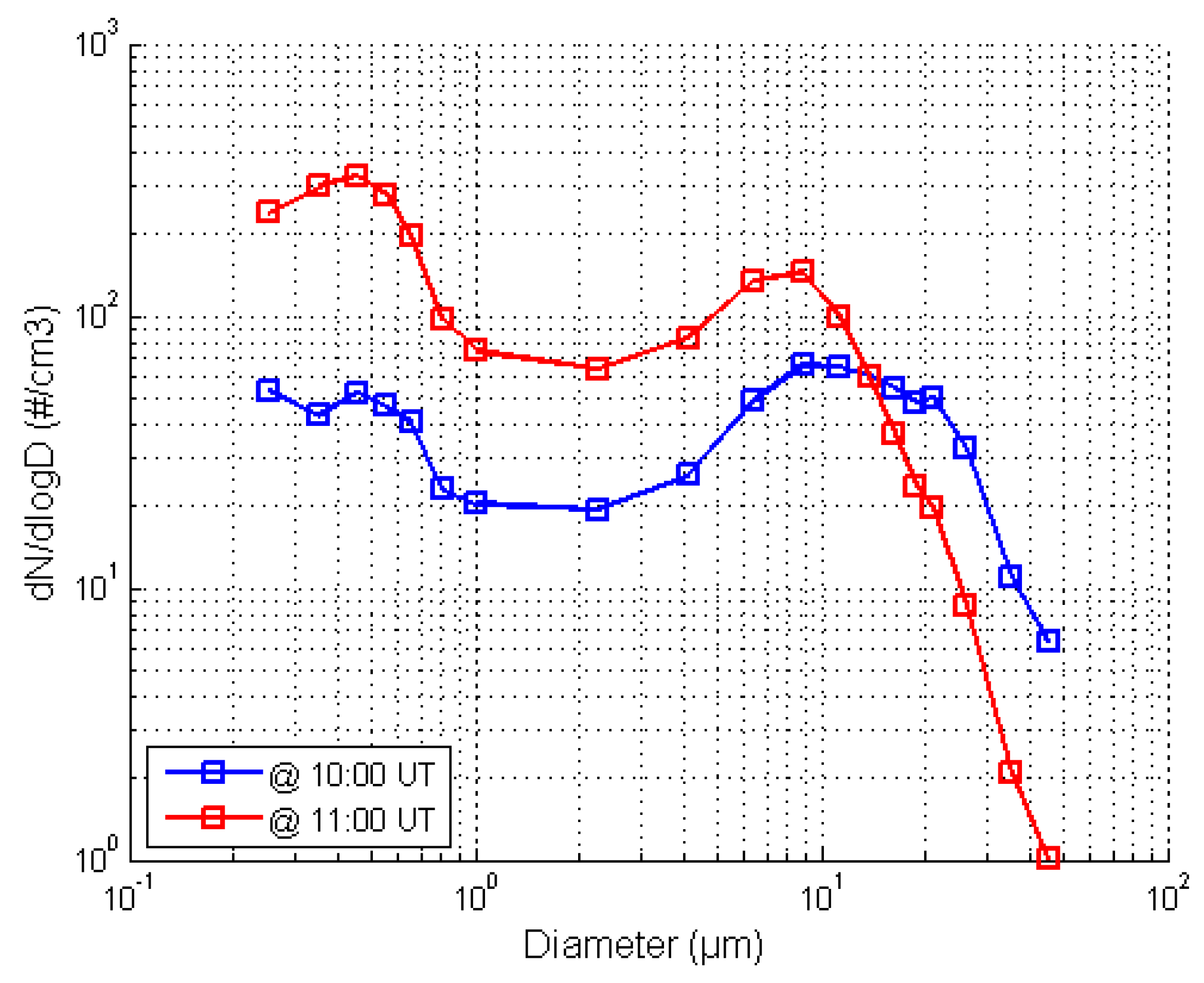
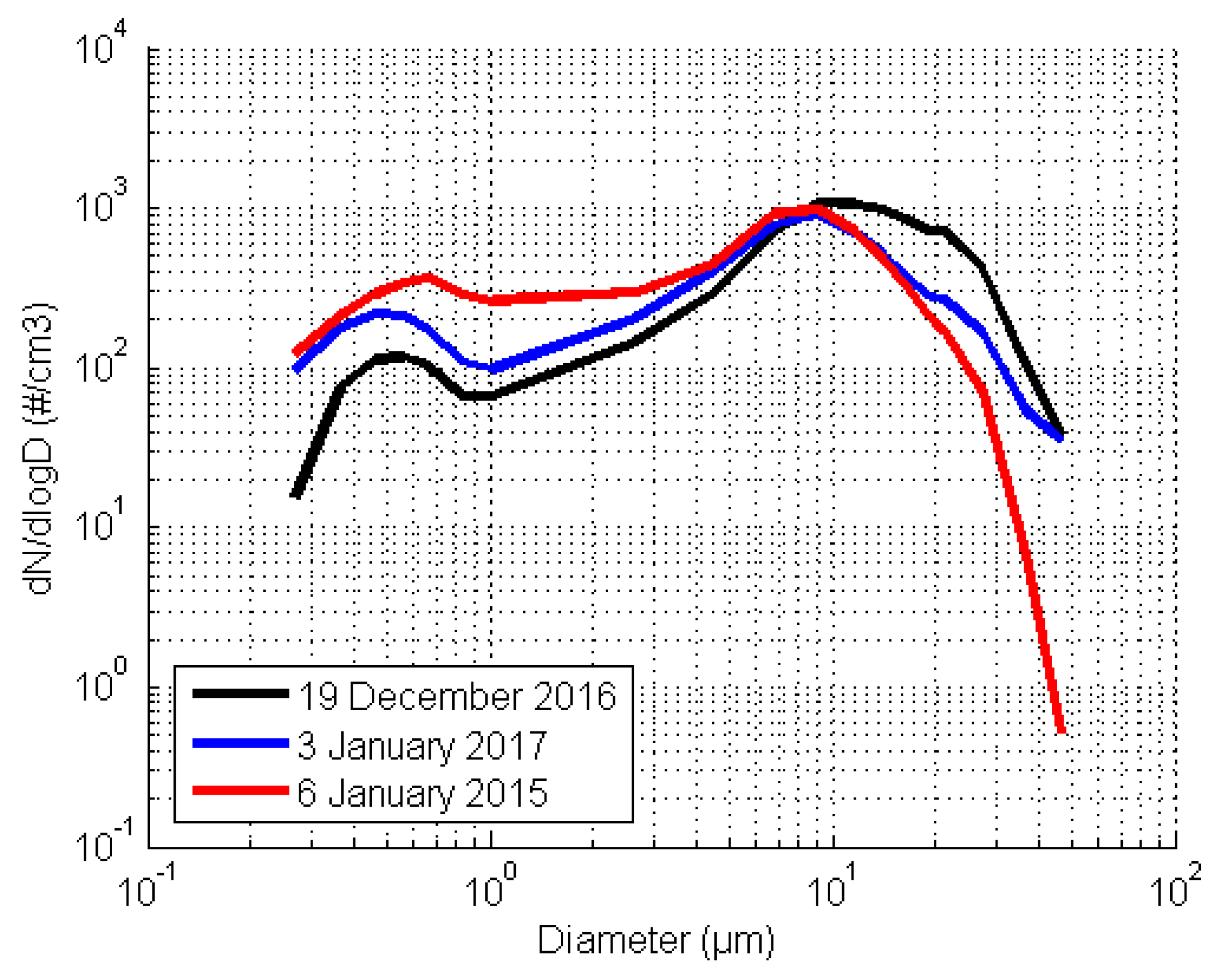
3.6.2. Variability of Droplet-Size Distribution
3.6.3. Variability of Parametrical Relationships and Impact on Profiles
4. Comparison and Discussion of Two Stratus-Fog Events
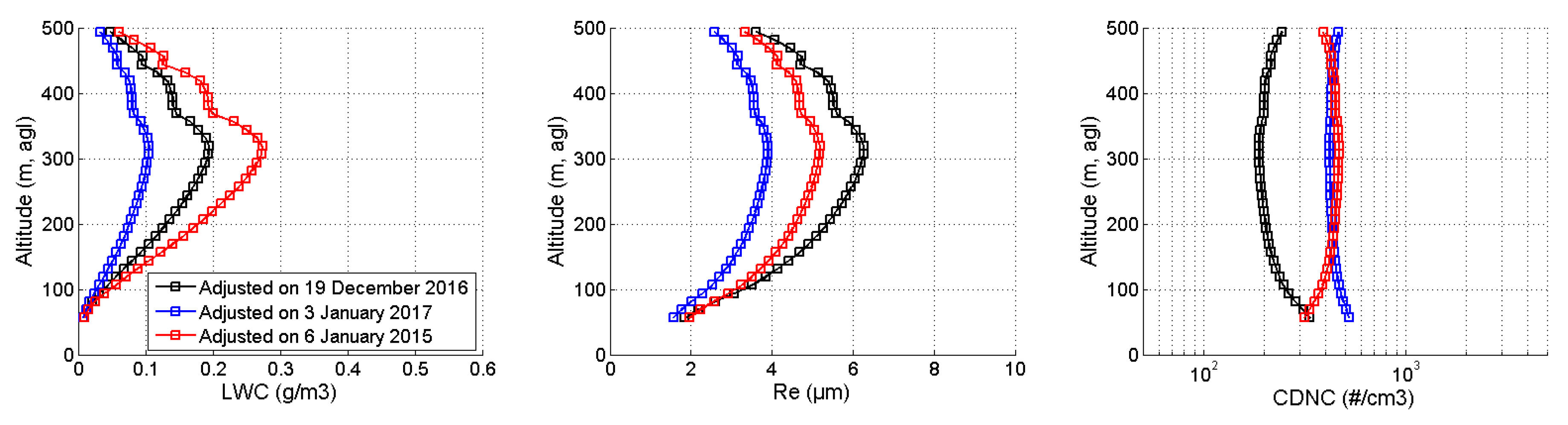
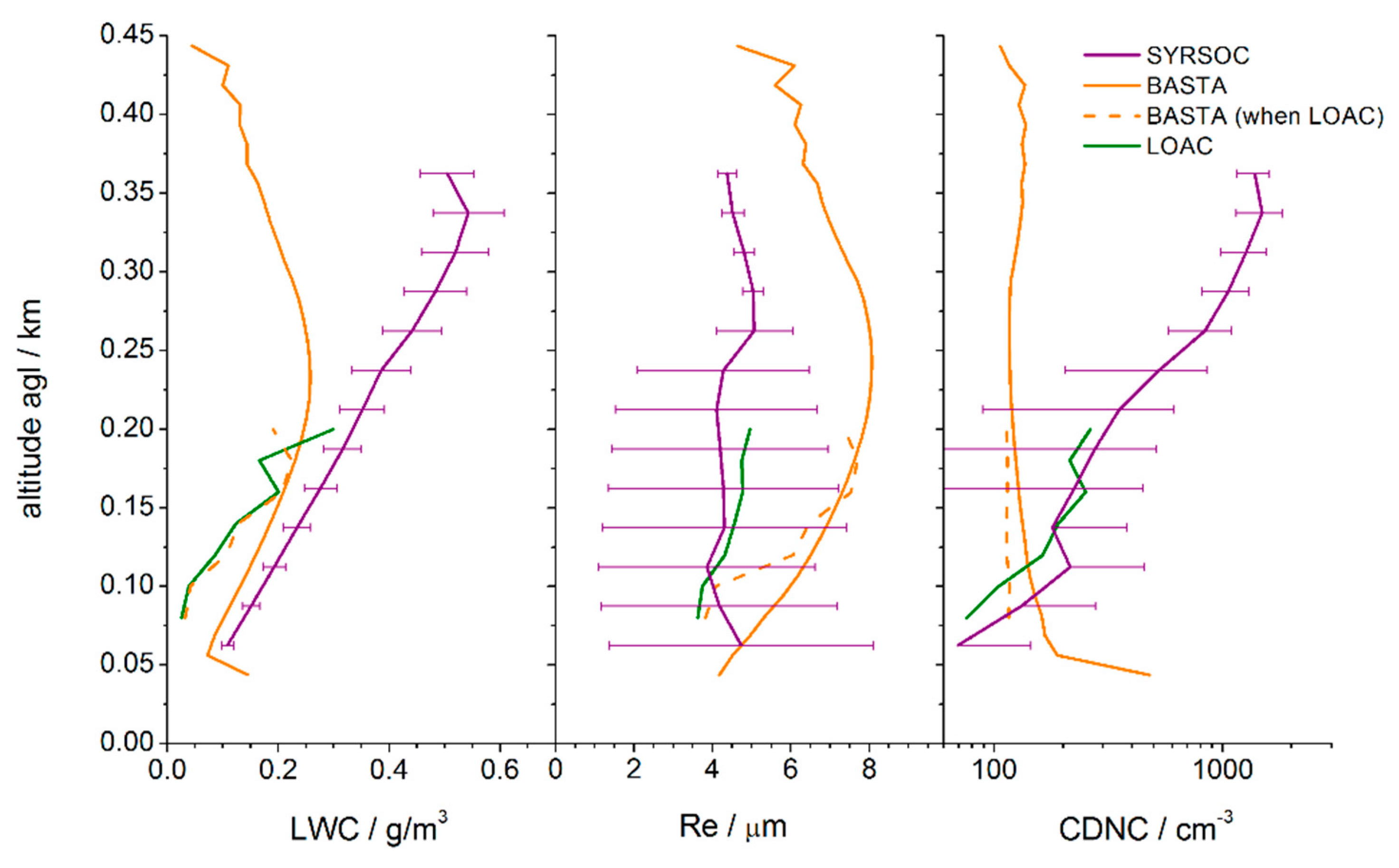
4.1. Vertical Profiles of Microphysical Properties on 6 January 2015
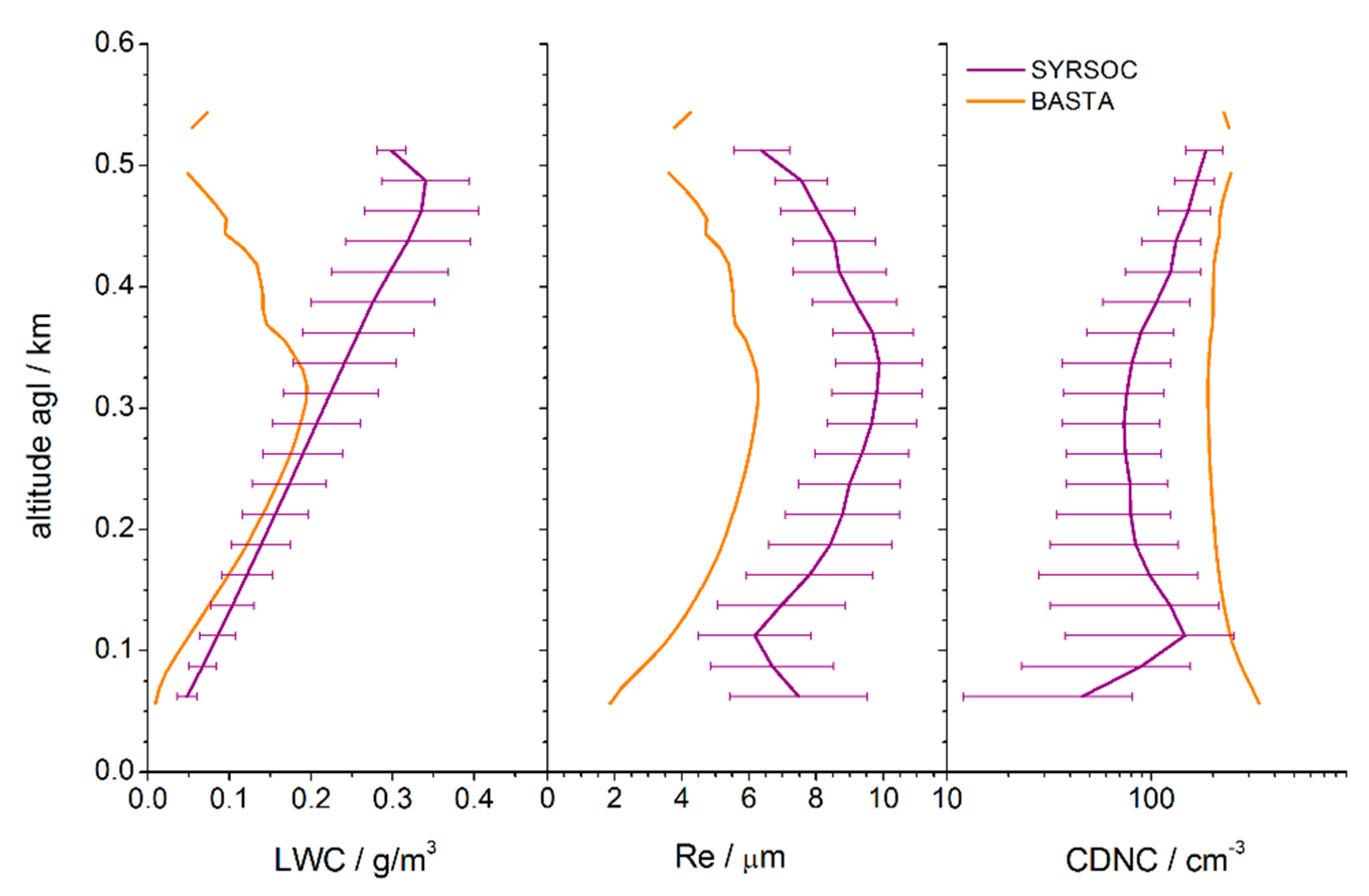
4.2. Vertical Profiles of Microphysical Properties on 19 December 2016
4.3. Discussion of SYRSOC Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bergot, T.; Terradellas, E.; Cuxart, J.; Mira, A.; Liechti, O.; Mueller, M.; Nielsen, N.W. Intercomparison of single-column numerical models for the prediction of radiation fog. J. Appl. Meteorol. 2007, 46, 504–521. [Google Scholar] [CrossRef]
- Delanoe, J.; Protat, A.; Vinson, J.P.; Brett, W.; Caudoux, C.; Bertrand, F.; Parent du Chatelet, J.; Hallali, R.; Barthes, L.; Haeffelin, M.; et al. BASTA: A 95-GHz FMCW Doppler radar for cloud and fog studies. J. Atmos. Ocean. Technol. 2016, 33, 1023–1038. [Google Scholar] [CrossRef]
- Donovan, D.P.; van Lammeren, A.C.A.P. Cloud effective particle size and water content profile retrievals using combined lidar and radar observations: 1. Theory and examples. J. Geophys. Res. 2001, 106, 27425–27448. [Google Scholar] [CrossRef]
- Dupont, J.C.; Haeffelin, M.; Protat, A.; Bouniol, D.; Boyouk, N.; Morille, Y. Stratus fog formation and dissipation. A 6-day case study. Bound.-Layer Meteorol. 2012, 143, 207–225. [Google Scholar] [CrossRef]
- Dupont, J.C.; Haeffelin, M.; Stolaki, S.; Elias, T. Analysis of Dynamical and Thermal Processes Driving Fog and Quasi-Fog Life Cycles Using the 2010–2013 ParisFog Dataset. Pure Appl. Geophys. 2016, 173, 1337–1358. [Google Scholar] [CrossRef]
- Elias, T.; Haeffelin, M.; Drobinski, P.; Gomes, L.; Rangognio, J.; Bergot, T.; Chazette, P.; Raut, J.C.; Colomb, M. Particulate contribution to extinction of visible radiation: Pollution, haze, and fog. Atmos. Res. 2012, 92, 443–454. [Google Scholar] [CrossRef]
- Fox, N.I.; Illingworth, A.J. The retrieval of stratocumulus cloud properties by ground-based cloud radar. J. Appl. Meteorol. 1997, 36, 485–492. [Google Scholar] [CrossRef]
- Grinshpun, S.; Willeke, K.; Kalatoor, S. A general equation for aerosol aspiration by thin-walled sampling probes in calm and moving air. Atmos. Environ. A-Gen. 1993, 27, 1459–1470. [Google Scholar] [CrossRef]
- Gultepe, I.; Tardif, R.; Michaelides, S.C.; Cermak, J.; Bott, A.; Bendix, J.; Müller, M.D.; PagowskiI, M.; Hansen, B.; Ellrod, G.; et al. Fog research: A review of past achievements and Future perspectives. Pure Appl. Geophys. 2007, 164, 1121–1159. [Google Scholar] [CrossRef]
- Haeffelin, M.; Barthès, L.; Bock, O.; Boitel, C.; Bony, S.; Bouniol, D.; Chepfer, H.; Chiriaco, M.; Cuesta, J.; Delanoe, J.; et al. SIRTA, a ground-based atmospheric observatory for cloud and aerosol research. Ann. Geophys. 2005, 23, 253–275. [Google Scholar] [CrossRef]
- Hogan, R.J.; Bouniol, D.; Ladd, D.N.; O’Connor, E.J.; Illingworth, A.J. Absolute calibration of 94/95-GHz radars using rain. J. Atmos. Ocean. Technol. 2003, 20, 572–580. [Google Scholar] [CrossRef]
- Koschmieder, H. Theorie der horizontalen Sichtweite. Beitraege Physicae Freiberger Atmos. 1924, 12, 33–55. [Google Scholar]
- Liao, L.; Sassen, K. Investigation of relationships between Ka-band radar reflectivity and ice and liquid water contents. Atmos. Res. 1994, 34, 231–248. [Google Scholar] [CrossRef]
- Löhnert, U.; Crewel, S.; Simmer, C.; Macke, A. Profiling cloud liquid water by combining active and passive microwave measurements with cloud model statistics. J. Atmos. Ocean. Technol. 2001, 18, 1354–1366. [Google Scholar] [CrossRef]
- Martucci, G.; O’Dowd, C.D. Ground-based retrieval of continental and marine warm cloud microphysics. Atmos. Meas. Technol. 2011, 4, 2749–2765. [Google Scholar] [CrossRef]
- Maier, F.; Bendix, J.; Thies, B. Simulating Z-LWC relations in natural fogs with radiative transfer calculations for future application to a cloud radar profiler. Pure Appl. Geophys. 2012, 169, 793–807. [Google Scholar] [CrossRef]
- Niu, S.J.; Lu, C.S.; Yu, H.Y.; Zhao, L.; Lü, J. Fog research in China: An overview. Adv. Atmos. Sci. 2010, 27, 639–661. [Google Scholar] [CrossRef]
- Pagowski, M.; Gultepe, I.; King, P. Analysis and modelling of an extremely dense fog event in southern Ontario. J. Appl. Meteorol. 2004, 43, 3–16. [Google Scholar] [CrossRef]
- Preißler, J.; Martucci, G.; Saponaro, G.; Ovadnevaite, J.; Vaishya, A.; Kolmonen, P.; Ceburnis, D.; Sogacheva, L.; Leeuw, G.; O’Dowd, C. Six years of surface remote sensing of stratiform warm clouds in marine and continental air over Mace Head, Ireland. J. Geophys. Res. Atmos. 2016, 121, 538–557. [Google Scholar] [CrossRef]
- Renard, J.B.; Dulac, F.; Berthet, G.; Lurton, T.; Vignelles, D.; Jégou, F.; Dupont, J.C.; Verdier, N. LOAC: A light aerosols counter for ground-based and balloon measurements of the size distribution and of the main nature of atmospheric particles, 2. First results from balloon and unmanned aerial vehicle flights. Atmos. Meas. Technol. 2016, 9, 3673–3686. [Google Scholar] [CrossRef]
- Renard, J.B.; Dulac, F.; Berthet, G.; Lurton, T.; Vignelles, D.; Jégou, F.; Dupont, J.C.; Verdier, N. LOAC: A light aerosols counter for ground-based and balloon measurements of the size distribution and of the main nature of atmospheric particles, 1. Principle of measurements and instrument evaluation. Atmos. Meas. Technol. 2016, 9, 1721–1742. [Google Scholar] [CrossRef]
- Sauvageot, H.; Omar, J. Radar reflectivity of cumulus clouds. J. Atmos. Ocean. Technol. 1987, 4, 264–272. [Google Scholar] [CrossRef]
- Sekelsky, S.M. Near-field reflectivity and antenna boresight gain corrections for millimeter-wave atmospheric radars. J. Atmos. Ocean. Technol. 2002, 19, 468–477. [Google Scholar] [CrossRef]
- Stolaki, S.; Pytharoulis, I.; Karacostas, T. A study of fog characteristics using a coupled WRF-COBEL model over Thessaloniki airport, Greece. Pure Appl. Geophys. 2012, 169, 961–981. [Google Scholar] [CrossRef]
- Tardif, R. The impact of vertical resolution in the explicit numerical forecasting of radiation fog: A case study. Pure Appl. Geophys. 2007, 164, 1221–1240. [Google Scholar] [CrossRef]
- Thies, B.; Egli, S.; Bendix, J. The Influence of Drop Size Distributions on the Relationship between Liquid Water Content and Radar Reflectivity in Radiation Fogs. Atmosphere 2017, 8, 142. [Google Scholar] [CrossRef]
- Wærsted, E.G.; Haeffelin, M.; Dupont, J.-C.; Delanoë, J.; Dubuisson, P. Radiation in fog: Quantification of the impact on fog liquid water based on ground-based remote sensing. Atmos. Chem. Phys. 2017, 17, 10811–10835. [Google Scholar] [CrossRef]
- Wendisch, M.; Mertes, S.; Heintzenberg, J.; Wiedensohler, A.; Schell, D.; Wobrock, W.; Frank, G.; Martinsson, B.G.; Fuzzi, S.; Orsi, G.; et al. Drop size distribution and LWC in Po Valley fog. Contrib. Atmos. Phys. 1998, 71, 87–100. [Google Scholar]
| Type of Instrument | Name | Parameters | Sampling | Uncertainty |
|---|---|---|---|---|
| Remote-sensing instruments | Bistatic Radar System for Atmospheric Studies (BASTA) cloud radar (95 GHz) | Reflectivity, Doppler velocity, cloud top height | 12 s | 0.5 dBZ, 0.2 m/s |
| Humidity and Temperature Profiler (HATPRO) microwave radiometer | Liquid water path (LWP) | 5 min | LWP ± 20 g/m² | |
| CL31 Ceilometer | Cloud base height | 1 min | 7.5 m | |
| CHM15K Ceilometer | Cloud base height | 1 min | 7.5 m | |
| In situ sensors | Degreane DF320 diffusometer | Horizontal visibility (km) at 4 m agl | 1 min | ±10–25% |
| Light optical aerosol counter (LOAC) granulometer | Particle-size distribution for particles ranging from 0.2 to 50 µm (in diameter) | 1 min Sampling 2.5 L/min |
| Normalization Procedure | Slope | # | ρ | Average Temp. (°C) | Average Wind Speed (m/s) | Average CDNC (#/cm3) Total, and >10 µm | Average Visibility (m) |
|---|---|---|---|---|---|---|---|
| 6 January 2015 | 8.2 | 86 | 0.93 | −1.2 | 2.2 | 840/40 | 670 |
| 19 December 2016 | 0.59 | 76 | 0.88 | 3.4 | 0.5 | 465/55 | 500 |
| 3 January 2017 | 0.92 | 157 | 0.73 | 0.9 | 1.8 | 930/35 | 180 |
| 17 February 2017 * | 4.2 | 45 | 0.83 | 7.6 | 1.1 | 270/110 | 320 |
| Equation (3) | α | β | # | ρ | Average Z (min, max) (dBZ) | Average LWC (min, max) (g/m3) |
|---|---|---|---|---|---|---|
| Atlas, 1954 | 0.048 | 2 | / | / | / | |
| Sauvageot and Omar, 1987 | 0.030 | 1.7 | / | 0.67 | / | / |
| Fox and Illingworth, 1997 | 0.012 | 1.16 | / | 0.82 | / | / |
| Flight 1. 6 January 2015 | 0.020 | 1.91 | 62 | 0.79 | −38.4 (−57.5, −25.1) | 0.07 (0.03, 0.26) |
| Flight 2. 19 December 2016 | 0.049 | 2.06 | 43 | 0.88 | −27.7 (−48.5, −19.8) | 0.19 (0.02, 0.35) |
| Flight 3. 3 January 2017 | 0.097 | 2.51 | 81 | 0.74 | −25.1 (−43.4, −11.5) | 0.1 (0.01, 0.85) |
| Equation (4) | γ | δ | Average Re * (min, max) (µm) | # | ρ | Average Z (min, max) (dBZ) | Average Re (min, max) (µm) |
|---|---|---|---|---|---|---|---|
| Fox and Illingworth, 2007 | 40.9 | −64.2 | 4 | / | / | / | / |
| Flight 1. 6 January 2015 | 65.0 | −74.2 | 3.6 (1.1, 4.9) | 62 | 0.74 | −38.4 (−57.5, −25.1) | 4.9 (0.8, 8.6) |
| Flight 2. 19 December 2016 | 52.0 | −69.2 | 5.7 (2.1, 7.2) | 43 | 0.86 | −27.7 (−48.5, −19.8) | 6.8 (1.1, 9.4) |
| Flight 3. 3 January 2017 | 69.2 | −80.7 | 4.3 (1.7, 9.5) | 81 | 0.78 | −25.1 (−43.4, −11.5) | 5 (0.8, 12.6) |
| Equation (4) | CDNC * (#/cm3) | Average Z (min, max) (dBZ) | Average CDNC (min, max) (#/cm3) |
|---|---|---|---|
| Flight 1. 6 January 2015 | 108 | −33.4 (−52.5, −20.1) | 113 (95, 166) |
| Flight 2. 19 December 2016 | 58 | −22.7 (−43.5, −14.8) | 65 (62, 97) |
| Flight 3. 3 January 2017 | 154 | −25.1 (−43.4, −11.5) | 133 (5, 155) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dupont, J.-C.; Haeffelin, M.; Wærsted, E.; Delanoe, J.; Renard, J.-B.; Preissler, J.; O’Dowd, C. Evaluation of Fog and Low Stratus Cloud Microphysical Properties Derived from In Situ Sensor, Cloud Radar and SYRSOC Algorithm. Atmosphere 2018, 9, 169. https://doi.org/10.3390/atmos9050169
Dupont J-C, Haeffelin M, Wærsted E, Delanoe J, Renard J-B, Preissler J, O’Dowd C. Evaluation of Fog and Low Stratus Cloud Microphysical Properties Derived from In Situ Sensor, Cloud Radar and SYRSOC Algorithm. Atmosphere. 2018; 9(5):169. https://doi.org/10.3390/atmos9050169
Chicago/Turabian StyleDupont, Jean-Charles, Martial Haeffelin, Eivind Wærsted, Julien Delanoe, Jean-Baptiste Renard, Jana Preissler, and Colin O’Dowd. 2018. "Evaluation of Fog and Low Stratus Cloud Microphysical Properties Derived from In Situ Sensor, Cloud Radar and SYRSOC Algorithm" Atmosphere 9, no. 5: 169. https://doi.org/10.3390/atmos9050169
APA StyleDupont, J.-C., Haeffelin, M., Wærsted, E., Delanoe, J., Renard, J.-B., Preissler, J., & O’Dowd, C. (2018). Evaluation of Fog and Low Stratus Cloud Microphysical Properties Derived from In Situ Sensor, Cloud Radar and SYRSOC Algorithm. Atmosphere, 9(5), 169. https://doi.org/10.3390/atmos9050169






