Abstract
The cloud longwave (LW) scattering effect has been ignored in most current climate models. To investigate its climate impact, we apply an eight-stream DIScrete Ordinates Radiative Transfer (DISORT) scheme to include the cloud LW scattering in the General circulation model version of the LongWave Rapid Radiative Transfer Model (RRTMG_LW) and the Community Atmospheric Model Version 5 (CAM5). Results from the standalone RRTMG_LW and from diagnostic runs of CAM5 (no climate feedback) show that the cloud LW scattering reduces the upward flux at the top of the atmosphere and leads to an extra warming effect in the atmosphere. In the interactive runs with climate feedback included in CAM5, the cloud LW scattering effect is amplified by the water vapor-temperature feedback in a warmer atmosphere and has substantial influences on cloud fraction and specific humidity. The thermodynamic feedbacks are more significant in the northern hemisphere and the resulting meridional temperature gradient is different between the two hemispheres, which strengthens the southern branch of Hadley circulation, and modulates the westerly jet near 50° S and the upper part of Walker circulation. Our study concludes that the cloud LW scattering effect could have complex impacts on the global energy budget and shall be properly treated in future climate models.
1. Introduction
Longwave (LW) radiation plays an indispensable role in modulating the global radiative budget and maintaining the Earth climate system. On one hand, increases in water vapor and greenhouse gases trap more LW radiation in the earth-atmosphere system and generate more LW emission from the atmosphere to the surface, which results in a warming condition in climate [1]. On the other hand, the cloud effect in LW is similar to the greenhouse effect, especially for high and thin ice clouds on trapping terrestrial radiation [2,3]. Since temperature is decreased with height in the troposphere and LW emission is proportional to the fourth power of temperature, the outgoing LW radiation (OLR) at the top of the atmosphere (TOA) is much less than that would have emitted from the earth surface, thus keeping energy in the earth-atmosphere system. In addition, clouds and moisture increases in anomaly convective regions can lead to a reduced OLR, and an extra diabatic heating in the atmosphere [4]. Calculation of the LW cloud effect involves absorbing, scattering, and emitting processes in radiation. However, the importance of LW scattering is regarded as uncompetitive to that of absorption [5,6,7,8,9] and less attention has been paid to the proper treatment of scattering processes in numerical models. The computational expense of LW scattering calculation is another reason for neglecting it in radiative transfer models and particularly in global climate models.
With the demand for accurate calculation of radiative fluxes and heating rates, the effect of LW scattering by clouds has been studied in the last two decades. Several methods were proposed, such as δ-two- and δ-four-stream combination approximations [5], a parameterization with scaling approximation based on discrete-ordinate calculation [6], perturbation solution [7,10], and four-stream adding method [11]. However, the cloud LW scattering effect is still ignored in most of the current General Circulation Models (GCMs). In the inter-comparison study of radiation algorithms [12], only four standalone radiative transfer models [7,13,14,15] handle the full LW scattering. All the other models use the absorption approximation method [5,10] for the LW radiative transfer calculation, which is highly simplified in the LW scattering processes. The overall LW scattering effect on upward flux at TOA can reach −4 W m−2 for cloudy cases [7,10]. Other theoretical studies obtain the results with a similar magnitude. Stephens et al. [16] and Joseph and Min [17] demonstrated that the OLR could be overestimated by about 8 W m−2 when neglecting the multiple LW scattering in thin cirrus clouds. Costa and Shine [8] showed that the LW scattering effect by low clouds could reduce the estimated OLR by 0.9 W m−2 and the reduction in OLR is 3 W m−2 over mid-latitudes and tropics for all clouds. In addition to the broadband results, some studies also specified the spectral ranges, in which the cloud LW scattering effect dominates, such as the atmospheric window range (8–12 μm) [8] and far infrared range at around 25 μm [8,9,13,18].
Cloud is strongly coupled with the LW radiation. Since the simulation of cloud has large uncertainty in GCMs [19], most previous studies [19,20,21,22] focus on improving the cloud macro- or micro-physical scheme and investigating the resulted impacts on LW radiation and climate, but seldom consider the LW scattering effect on radiation and climate. Secondarily, the LW radiation studies are extensively related to the feedbacks induced by surface temperature, water vapor, greenhouse gases, anomalous convections, and other climate forcings [4,23,24,25]. For example, OLR is usually taken as a detectable proxy to understand tropical convective processes and greenhouse gas effects [26,27,28], the consideration of cloud LW scattering could inevitably influence on the relevant analysis. To the authors’ knowledge, few studies investigate the impact of cloud LW scattering on the climate system so far.
Although the cloud LW scattering effect has been recognized, the comprehensive quantification and understanding of the effect in the climate system still lack, which will be achieved in this study by analyzing the LW scattering effect using a standalone radiative transfer model and a GCM. In Section 2, the LW radiative transfer theory and the schemes for water/ice cloud optical properties used in this study are described. The design of model experiments is also given. Section 3 exhibits the LW scattering effects on band-by-band fluxes and heating rates simulated in a standalone radiative transfer model. Section 4 analyzes the results from GCM runs with and without the climate feedbacks included. Finally, a summary is given in Section 5.
2. Theory and Methodology
2.1. Radiative Transfer in Longwave
In a plane-parallel homogeneous atmosphere, the azimuth-averaged diffuse longwave intensity I (τ, μ) is governed by the equation,
where µ = cos θ, θ is the zenith angle, τ is the cloud optical depth, is the single scattering albedo, B(T) is the Planck function for the substance with temperature T, and P (µ, µ′) is the azimuthal-independent phase function. The above phase function can be expanded in Legendre polynomials as
According to the Gauss quadrature, the discrete-ordinates approximation can be expressed as (Fu et al., 1997),
where i = ±1, …, ±n, quadrature point µ−j = −µj, j ≠ 0, weight a−j = aj. By setting the value of n, discrete-ordinates 2n-stream approximation can be obtained [29]. Using a higher number of streams can describe the scattering process more reasonably.
Another way is using the δ-Eddington approximation [30] to present the phase function as,
where f is the fractional scattering into the forward direction, g is the asymmetry factor. When LW absorption is strong enough to overwhelm scattering, the process can be simplified by setting f = 1. That means only the forward-scattering peak is kept (and enhanced) and scattering in all the other directions is completely neglected. Then Equation (1) can be rearranged as
Equation (5) is referred as an absorption approximation (AA) [5,10]. It is worthy to emphasize that AA is already more accurate than the method that completely ignores the scattering effect, i.e., ignoring the second term on the right side of Equation (1). Because AA keeps only the forward scattering, upward flux and downward flux can be calculated independently. In a single layer of atmosphere with optical depth Δτ, the downward (upward) flux at the bottom (top) of the layer is [7]:
where is the outgoing flux, is the incoming flux, is the effective Planck function, = 1/1.6487 is the diffuse factor [31].
In RRTMG_LW (the General circulation model version of Rapid Radiative Transfer Model for LongWave, [32,33]) (available from http://rtweb.aer.com), the averaged outgoing longwave radiation is expressed as:
where and are the beginning and ending wavenumbers of spectra, is the transmittance for the layer of atmosphere, Δz is the vertical thickness of the layer of atmosphere, ρ is the density of absorber in the layer, k (, p, T) is the absorption coefficient at pressure p, and k (, p, T) ρ Δz = Δτ. Therefore, the radiative transfer calculation used in RRTMG_LW follows the AA method (i.e., Equation (5)), which keeps scattering only in the forward peak but ignores multi-scattering in all the other directions. Despite this existing deficiency, RRTMG_LW still has reasonable performances and acceptable computational costs. RRTMG_LW is currently applied in the Community Atmospheric Model Version 5 (CAM5) to conduct LW radiative calculations [34].
To study the cloud LW scattering effect, we introduce an 8-stream discrete ordinates radiative transfer (DISORT) solver [29] into RRTMG_LW as a benchmark scheme for the LW radiation calculation. The original radiative transfer scheme and that with the 8-stream DISORT (DISORT_8S) exhibit almost the same results under the clear-sky condition in RRTMG_LW (not shown). The differences in cloudy sky are essentially attributed to the cloud LW scattering effects, i.e.,
where RRRTMG_DISORT_8S is the result obtained from RRTMG_LW with DISORT_8S, indicating a benchmark by including the LW scattering effect as described with Equation (3). RRRTMG_LW represents the result from RRTMG_LW as currently used in CAM5, which is described by Equation (7). EScattering_Effect is noted as the cloud LW scattering effect.
Because LW radiance is less anisotropic compared to that of solar radiation, a radiative transfer scheme with a small number of streams is capable of achieving reasonably accurate results. Kuo et al. [18] have shown that the difference in fluxes between 16-stream and more precise 128-stream DISORT is within 1%. We also checked that the difference between 8-stream and 16-stream DISORT is less than 0.3% (not shown). Therefore, it is appropriate to choose 8-stream DISORT as a benchmark for LW radiation. Although the DISORT_8S costs about 7 times more computational time than the original RRTMG_LW in CAM5, we introduce this algorithm only for quantifying the LW scattering effect in an accurate way. Actually, several analytical schemes for LW scattering can be applied to GCM by requiring less computational costs than DISORT_8S but having lower accuracy (e.g., the perturbation method [7]).
In RRTMG_LW of CAM5, sixteen LW bands are applied and the spectral band boundaries are listed in Table 1. Identically, the implementation of DISORT_8S is also accommodated to the band configuration in CAM5 for simulations.

Table 1.
LongWave Rapid Radiative Transfer Model (RRTMG_LW) spectral band boundaries in wavelength (µm) and in wave number (cm−1) respectively (Same as Table 4.7 in Neale et al. [34]).
2.2. Experiments Design
To investigate the cloud LW scattering effect and its impact on radiation and climate, we design three types of model simulations. First, we run RRTMG_LW independently by prescribing a certain set of atmospheric profiles and idealized cloud cases. Results of the standalone RRTMG_LW run are used to estimate the LW scattering effect on fluxes and heating rates under the given atmospheric and cloud conditions (more details in Section 3).
Second, we make the GCM simulations using CAM5, in which water and ice cloud properties are calculated online in the cloud microphysical scheme. We conduct a reference run of CAM5 with the original RRTMG_LW calculation, and call DISORT_8S in parallel for the LW calculation. The radiative results from the original RRTMG_LW advance the model integration to proceed the reference run. At the same time, the radiative results from DISORT_8S are only diagnosed for output but have no effect on the model integration (i.e., have no climate impacts/feedbacks). By looking at the difference in the model outputs from the original RRTMG_LW and from DISORT_8S, we will be able to quantify the instantaneous LW scattering effect on radiation without perturbing the simulated climate system. This type of GCM simulation is called a diagnostic run (more details in Section 4.1).
Third, we conduct a different type of GCM simulations by running CAM5 twice separately. One is the reference run only including the original RRTMG_LW. The other is the interactive run with DISORT_8S replacing the original LW calculation in RRTMG. The radiative results from DISORT_8S advance the model integration in the interactive run, thus the LW scattering effect does exert a perturbation on the simulated climate system. By looking at the differences in radiative results and climatological fields between the reference run and the interactive run, we will quantify the perturbation of LW scattering effect to the climate system and investigate the related impacts and feedbacks (more details in Section 4.2).
Note that the inclusion of LW scattering effect in the interactive run will certainly regulate the model simulated cloud properties. However, certain discrepancies still exist between the cloud properties simulated in the released CAM5 and observations [35,36,37]. It is beyond the scope of this study to modify or tune the cloud microphysical scheme to obtain a reasonably simulated cloud field in the interactive run. But we realize the strong interactions between the LW radiation calculation and the cloud microphysical scheme. Discussions on these issues are presented in Section 4.3.
2.3. LW Optical Properties of Water and Ice Clouds
Cloud optical properties in LW are determined by its macro- and micro-physical characteristics such as cloud amount, cloud top height, cloud particle size, cloud water content and so on [3,38,39,40,41,42,43,44,45,46,47,48]. In this subsection we present the variation of cloud optical properties in LW spectral bands, providing a base to demonstrate the longwave scattering ability of water/ice cloud particles.
The optical properties of water clouds with assumed spherical particle shape are parameterized in terms of liquid water content (LWC) and the particle size distribution parameters of spectral shape (µ*) and slope (λ*). The latter two microphysical parameters can be transferred into effective radius (re), that is given by [34]
where Γ is the Gamma function, μ* = 1/η2 − 1 (2 < μ* < 15) and η represents the radius dispersion in particle size distribution, which is empirically parameterized as an increasing function of cloud particle number concentration. These optics are computed by the MIEV0 program [49].
For ice clouds, the optical properties are parameterized in terms of ice water content (IWC) and generalized effective size (Dge) following the scheme developed in Fu and Liou [40] and Fu et al. [41], in which the ice cloud particle shape is assumed as hexagonal, and Dge can be expressed as
where αν is the extinction coefficient at wavenumber ν and ρi = 917 kg m−3 is the pure ice density.
Using the above two schemes, the calculated water and ice cloud optical properties for selected particle sizes are plotted to examine the LW scattering abilities. Figure 1 shows the LW optical properties (mass extinction/absorption coefficients, single scattering albedo, and asymmetry factor) for water cloud droplets with the selected re of 5.6 µm and 10 µm (representing typical particle sizes according to observations [39,43,44]), and for ice cloud crystals with the selected Dge of 40 µm and 60 µm (according to satellite observations [45]). The scattering ability of cloud particles is represented by the proportion of scattering coefficients to extinction coefficients, i.e., single scattering albedo (SSA). Generally speaking, smaller water cloud droplets have stronger extinction and absorption coefficients compared to the larger ones [46], and the same is applied for ice crystals. SSA of water cloud is sensitive to the wavelength (wave band) [47]. Bands 1–6 (10.2–1000.0 µm) show obviously lower values of SSA compared to the other spectral ranges, which indicates a substantially strong absorption. On the other hand, SSA of ice cloud varies with ice crystal size and wave band [41]. The largest SSA (i.e., weakest absorption) occurs at band 2 (20–28.57 µm) [18]. For asymmetry factor, both water and ice particles with larger size generally have a larger asymmetry factor [41,46,48] indicating that larger particles have stronger forward scattering ability for both water and ice clouds.

Figure 1.
Band-by-band cloud optical properties: mass coefficients of extinction and absorption (black and red symbols in panels a, (d); single scattering albedo (panels b,e); and asymmetry factor (panels c,f) for water and ice clouds (left and right columns) respectively. The different symbols represent two selected particle sizes: re of 5.6 µm and 10 µm (circles and triangles in left column) for water clouds and Dge of 40 µm and 60 µm (circles and triangles in right column) for ice clouds.
3. Standalone Radiative Transfer Model Results
The LW scattering effects on broadband radiative fluxes and heating rates have been discussed in previous studies using the standalone radiative transfer model (e.g., [7,10,11,16,17]). We show here the band-by-band results with prescribed clouds in three typical atmospheric profiles to examine the cloud LW scattering effect in different wavelength ranges and in certain atmospheric and cloud conditions. The standalone radiative transfer model RRTMG_LW is set with vertical resolution of 59 levels for a sub-arctic winter profile, 60 levels for a tropical profile, and 60 levels for a mid-latitude winter profile, respectively [32,33]. According to Fu et al. [5], three idealized cloud cases are considered in the profiles. The low cloud (LWC = 0.22 g m−3, re = 5.89 μm) is about 1 km thick and located from 700 hPa to 800 hPa. The middle cloud (LWC = 0.28 g m−3, re = 6.2 μm) is about 1.5 km thick and located from 500 hPa to 650 hPa. The high ice cloud (IWC = 0.0048 g m−3, Dge = 41.1 μm) is about 1 km thick and located from 230 hPa to 300 hPa. RRTMG_LW runs with the original LW radiation calculation and with DISORT_8S (RRTMG_DISORT_8S) respectively. As indicated by Equation (8), the difference between the two runs is regarded as the cloud LW scattering effect under certain atmosphere and cloud conditions.
The left column of Figure 2 shows the cumulative band-by-band results of upward fluxes at TOA and downward fluxes at the surface with the three idealized cloud cases in each of the three atmospheric profiles in RRTMG_LW. Note that the upward flux at TOA is equivalent to OLR. For the same cloud case, the simulated fluxes are different for the three atmospheric profiles due to the different vertical temperature distributions among the profiles. The fluxes at the first three bands (15.87–1000 µm) possess a significant proportion of LW energy, followed by band 5 (12.2–14.29 µm) and the atmospheric window region (bands 6–9, 7.19–12.2 µm). The right column of Figure 2 shows the difference in each band between RRTMG_LW and RRTMG_DISORT_8S, that is the cloud LW scattering effect. For the upward flux at TOA, the cloud LW scattering effect reduces the transmission; thus RRTMG_DISORT_8S produces less OLR in all bands (mostly negative values in the right column of Figure 2). Though the scattering ability of water cloud particles is relatively weak in the first three bands than the other bands (see the left column of Figure 1), a large fraction of energy occupies in this spectral range, thus the radiative effect of the LW cloud scattering is significant. On the other hand, Figure 1 shows that ice cloud generally has the strongest LW scattering ability in band 2 (20–28.57 µm), which results in the greatest reduction in upward fluxes in the same band. It is confirmed by the negative values with magnitudes larger than 2 W m−2 in band 2 simulated for the high ice cloud case in all the three atmospheric profiles. In our study, the cumulative LW scattering effect on OLR is 2–6 W m−2, and it is comparable with 4–8 W m−2 in Chou et al. [6], 4 W m−2 in Li [7] and Li and Fu [10], and 6–8 W m−2 in Joseph and Min [17]. Kuo et al. [18] demonstrated that the LW scattering in the far-infrared and atmospheric window regions (10–1390 cm−2) mainly contribute to the biases in spectral fluxes, which is consistent with our results in Figure 2.

Figure 2.
Cumulative band-by-band downward LW fluxes at the surface (dash lines) and upward LW fluxes at top of the atmosphere (TOA) (solid lines) from RRTMG_LW with the original LW calculation (left column) and the difference caused by the LW scattering effect in each band (right column). The red, blue and green lines represent the respective results with low, middle, and high cloud cases prescribed in the given atmospheric profiles in tropics (panel a,d); middle latitude winter (panel b,e); and subarctic winter (panel c,f).
The downward flux at the surface is more complicated than that at the TOA. The backscattering from the upward radiance would enhance the downward flux at the surface, but the backscattering from downward radiance has an opposite effect. The enhancement-reduction partitioning of LW scattering effect depends on the competition between these two backscattering effects and causes a weaker cloud LW scattering effect on the downward flux at the surface than the effect on the upward flux at TOA. In Fu et al. [5], a multiple-stream scheme is compared with AA in a radiative transfer model. The results showed a weak impact on downward flux at the surface as well. The spectral results of the cloud LW scattering effect on flux in Figure 2 are consistent with the band-by-band LW flux biases by neglecting scattering in Kuo et al. [18].
Additionally, the LW cloud scattering ability is sensitive to the particle size as shown in Figure 1 and smaller cloud particles generally have stronger scattering abilities. To test it, we conduct another pair of RRTMG_LW and RRTMG_DISORT_8S runs with the high ice cloud case in the tropical profile by changing the prescribed ice cloud particle size Dge only (results are shown in Figure S1). It does show a larger reduction of OLR for smaller ice particles under a given cloud ice water content, which agree with the result in Joseph and Min [17]. However, as the cloud water content (or say the cloud optical depth) increases, the sensitivity to particle size obviously decreases because the LW scattering becomes less anisotropic.
The cloud LW scattering effect on heating rate is exhibited in Figure 3 (dotted area indicates the location of prescribed cloud cases). As the effects in the three atmospheric profiles are very similar, only the results in the tropical profile are shown. The upper row of Figure 3 plots the heating rate simulated with RRTMG_LW and the lower row plots the differences in the heating rate between RRTMG_LW and RRTMG_DISORT_8S (i.e., the LW cloud scattering effect on heating rate). The LW cooling appears above water clouds (left and middle panels in the upper row of Figure 3) and dominates in the first four bands (14.29–1000 µm). The warming at the bottom of water clouds is mainly in bands 6–9 (7.19–12.2 µm). The LW cooling in the atmosphere is due to the energy loss to the outer space (i.e., OLR). While cloud shelters the upward flux from losing and causes a warming effect below.
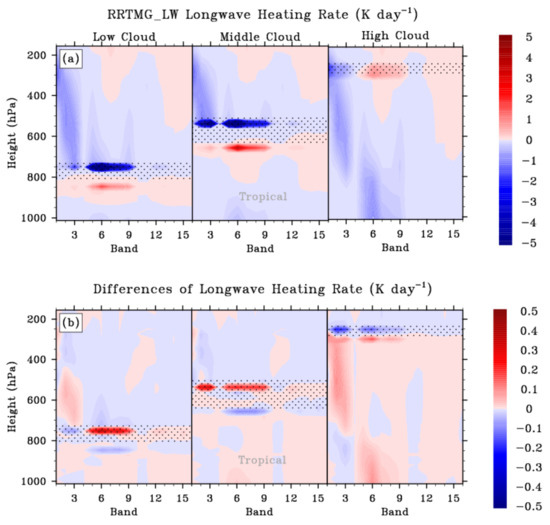
Figure 3.
Band-by-band LW heating rates from RRTMG_LW run (upper panels) and the difference in LW heating rate (lower panels) between RRTMG_LW and RRTMG_DISORT_8S runs (i.e., caused by the LW scattering effect) for respective results with the prescribed low (left) and middle (middle) water cloud, and high (right) ice cloud cases in the tropical profile; dotted area indicates the location of the prescribed cloud cases.
The left and middle panels in the lower row of Figure 3 show the water cloud LW scattering effect on heating rates. The LW scattering effect leads to an overall warming in the atmosphere. This result is consistent with Figure 2, as the cloud LW scattering effect reduces the upward flux at TOA but has a weak impact on downward flux at the surface. Therefore the atmosphere gains a positive net energy and the warming is mostly below the cloud.
An interesting feature is seen in the atmospheric window region (bands 6–9, 7.19–12.2 µm) that the water cloud exerts a prominent warming below cloud (left and middle panels in the upper row of Figure 3). The atmosphere is almost transparent in the window region, thus the upward thermal flux from the surface can easily reach the cloud base. Cloud then reemits radiation downward from its bottom. The window region contains a large portion of energy from the terrestrial radiation around the cloud base. Therefore, the re-emission in the bands of the atmospheric window region is more significant than the other bands, which leads to a stronger warming effect below cloud than the other bands too. However, the cloud LW scattering effect causes a cooling below cloud (left and middle panels in the lower row of Figure 3), that is, reduces the warming in the atmospheric window region. It is because the LW cloud scattering reduces the downward reemitted radiation and thus weakens the warming below the cloud base.
The LW heating rate and the scattering effect of ice cloud show different features from the results of water clouds. The warming effect caused by the ice cloud is only obvious in and below the cloud in the atmospheric window region (upper right panel in Figure 3). Because a large portion of energy reaches the high ice cloud only in the atmospheric window region, thus a stronger reemission of cloud results in a warming in and below the ice cloud. When the LW scattering effect is included, it enhances the anisotropic radiance caused by multi-direction scattering within the cloud layer. Therefore extra cooling and warming are exerted above and below the ice cloud respectively. The strengthening of warming effect below the high ice cloud is quite noticeable. The spectral results of the cloud LW scattering effect on heating rates shown here have seldom been discussed before.
4. Global Climate Model Results
As described in Section 2.2, DISORT_8S is implemented in RRTMG of CAM5 to investigate the cloud LW scattering effect in the global climate model. Two types of GCM experiments are conducted. One is the diagnostic run. A reference run of CAM5 includes the original RRTMG_LW radiative transfer scheme to advancing the model integration while RRTMG_DISORT_8S is run in parallel but its radiative results are only diagnostic outputs and do not have climate impacts/feedbacks. Differences in the radiative results between RRTMG_LW and RRTMG_DISORT_8S imply the instantaneous cloud LW scattering effect in the diagnostic run of CAM5. The other is a pair of CAM5 runs. The reference run and the interactive run are separately conducted with RRTMG_LW and RRTMG_DISORT_8S respectively. Differences in the radiative results and climatological fields between the two runs will quantify the perturbation of LW scattering effect to the climate system and show the climate impacts and feedbacks. As commonly configured for an atmospheric GCM simulation [19], CAM5 is run with 1.9° × 2.5° horizontal resolution and 31 vertical levels in this study. The model is driven by the prescribed climatological sea surface temperature and sea ice fraction for the year 2000 as an AMIP (Atmospheric Model Inter-comparison Project [50]) type run (As mentioned in Section 3 the cloud LW scattering has little effect on the downward flux at the surface thus we expect negligible impacts on the energy exchange between the atmosphere and ocean surface). The cloud microphysical properties in GCM runs are simulated online in the cloud microphysical scheme [51] of CAM5. The diagnostic run is integrated for 5 years and the results in the last 4 years are taken for analysis. As multiple-year climatology is necessary for statistical significance, the interactive runs are integrated for 11 years and results in the last ten years are taken for analysis on the climate impacts.
4.1. Diagnostic Run
Results of the diagnostic run indicate the instantaneous radiative effect of cloud LW scattering. Figure 4a plots the annual mean global difference in the upward LW flux at TOA between RRTMG_LW and RRTMG_DISORT_8S under the all-sky condition in CAM5. The globally averaged value of instantaneous effect is −1.8 W m−2. On the contrary the instantaneous effect on the downward flux at the surface is less than +0.5 W m−2 (not shown). This is consistent with the standalone RRTMG_LW result in Figure 2 and the estimation from Fu et al. [5], in which the cloud LW scattering has a more significant effect at TOA than that at the surface. Figure 4a also shows that the cloud LW scattering effect is relatively strong in the tropical regions, especially over the Pacific warm pool and Indian monsoon regions.
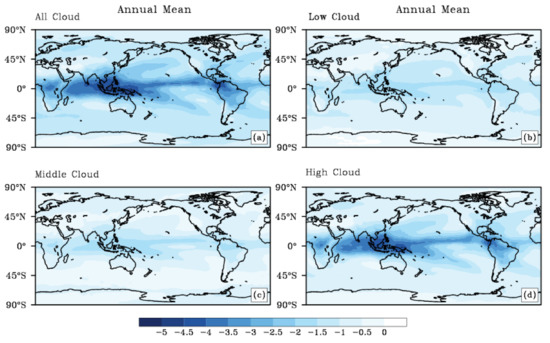
Figure 4.
Diagnostic run: annual mean global distributions of instantaneous cloud LW scattering effect on the upward LW flux at TOA (W m−2) for all-sky (panel a); low clouds (panel b); middle clouds (panel c); and high clouds (panel d).
To understand the role of cloud at different vertical levels, we further analyze the LW scattering effect of low, middle, and high clouds respectively. In the diagnostic run, the radiative transfer calculations are applied separately for low clouds (700–1200 hPa), middle clouds (400–700 hPa), and high clouds (50–400 hPa), and the respective differences between RRTMG_LW and RRTMG_DISORT_8S are plotted in Figure 4b–d. The instantaneous LW scattering effects of low and middle clouds are −1.0 W m−2 and −0.8 W m−2, respectively. Its distribution highlights in the western Pacific and storm track regions, where the marine stratocumulus mostly occurs in low and middle levels [52,53]. The LW scattering effect of high cloud is stronger than that of low and middle clouds, with a global mean of −1.4 W m−2. The simulated values here show good agreements with the results estimated from a radiative transfer model by using observed cloud data [8], which are −0.9, −0.7, and −1.4 W m−2 for low, middle, and high clouds respectively. It is worth noting that the distribution of high cloud effect is very similar to that of the all-sky in Figure 4a, which implies that the cloud LW scattering effect is mostly attributed to high clouds. It is consistent with the standalone RRTMG results in Figure 2 and Figure 3 that the cloud LW scattering effect of high ice cloud is more significant than that of low and middle water clouds. It is also understandable when high cloud overlaps low or middle cloud. Because the upward LW fluxes emitting from the top of low or middle cloud are mostly shaded by high cloud in GCM due to the extra absorption or backscattering of LW radiation from high cloud. Intuitively, only a few parts of the radiance from low and middle clouds penetrate through and influences on the upward fluxes at TOA. Although Figure 4 indicates that high clouds composing of ice crystals play a dominant role in the cloud LW scattering effect, the multi-scattering processes between multi-layer clouds could account for the potential effects of low and middle clouds. It may explain why the LW scattering effects of low and middle clouds prevail in the similar regions as the high cloud, where deep convective clouds commonly overlap with low and middle-level stratocumulus [45]. Therefore, high ice clouds play a dominant role in the cloud LW scattering effect, which prevails in the Pacific warm pool, monsoon areas with frequent convective clouds, and storm tracks [45]. But the effects of low and middle clouds may not be simply ignored.
Figure 5a shows the instantaneous cloud LW scattering effect on heating rates under the all-sky condition in the diagnostic run. A warming effect is in most of the troposphere and peaks below 800 hPa in the low latitudes, which is due to more energy kept from escaping to outer space by the cloud LW scattering effect. In Figure 5b–d, changes in heating rate caused by LW scattering effect of low, middle and high clouds are plotted respectively. The LW scattering effect of high clouds on heating rates is very similar to that in the all-sky condition (Figure 5a), especially in tropical regions. It confirms the primary role of high clouds in the LW scattering process in GCM. On the other hand, the LW scattering of low and middle clouds exert a stronger warming effect than that of high clouds in the lower troposphere in tropics but the warming effect damps rapidly with the elevation (Figure 5b,c). It again indicates the potential contribution of low and middle clouds to the LW scattering effect in tropical regions.
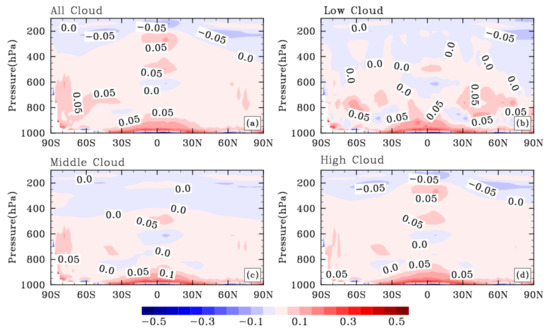
Figure 5.
Diagnostic run: annual zonal mean distributions of instantaneous cloud LW scattering effect on LW heating rate (K day−1) by all-sky (panel a), low clouds (panel b), middle clouds (panel c) and high clouds (panel d).
4.2. Interactive Runs
Figure 4 and Figure 5 have shown that the instantaneous cloud LW scattering effect reduces the upward LW fluxes at TOA and enhances the LW warming in the troposphere. The warmer atmosphere could store more water vapor and lead to further influences on atmospheric thermal structures and dynamic processes related to precipitation and evaporation. In this subsection, results of the interactive run include the cloud LW scattering effect and its impacts/feedbacks in the perturbed climate system. Note that the difference between reference and interactive runs indicates a bias due to the missing LW scattering process in the simulated climate system with CAM5, but not a forcing. Because the climate forcing only refers to an external perturbation and the forcing agent must originate from outside the climate system [50].
Figure 6a shows the climate impact of the cloud LW scattering on the upward flux at TOA. The global annual mean upward flux is reduced by 2.6 W m−2 at TOA, which is about 45% higher than the reduction estimated in the diagnostic run (Figure 4a). It indicates that climate feedbacks considerably enhance the LW scattering effect and cause an additional reduction of OLR. Comparing Figure 4a and Figure 6a, the cloud LW scattering effects on the upward flux show different patterns between diagnostic and interactive runs. The peak effects are still in the Pacific warm pool and monsoon regions. But substantial impacts also occur in the African continent and northern Latin America (Figure 6a), which could be related to the water vapor feedback and resulted changes in cloud distributions over these areas. In the region with the strongest effect such as the Pacific warm pool, the cloud LW scattering effect on the upward flux is up to −10 W m−2, accounting for about 5% of the total outgoing upward flux at TOA (shown as contour lines) in this region. Figure 6b shows the cloud LW scattering effect on the downward flux at the surface. A global mean downward flux is increased by 1.1 W m−2, which doubles the instantaneous result in the diagnostic run (mentioned in Section 4.1). The enhanced effect on downward LW flux is mainly attributed to the cloud feedback as the cloud LW scattering leads to a warmer and wetter atmosphere thus increases the cloud amount. Figure S2 shows the increased fractions of low, middle and high clouds caused by the LW scattering effect. The enhanced effect on downward LW flux is mainly due to the increased fraction of low clouds as most downward fluxes to the surface are emitted from the bottom of low clouds. The peak effect of LW scattering on downward flux is at about 40° N (Figure 6b), where the increase in low cloud fraction is also significant (see Figure S2).
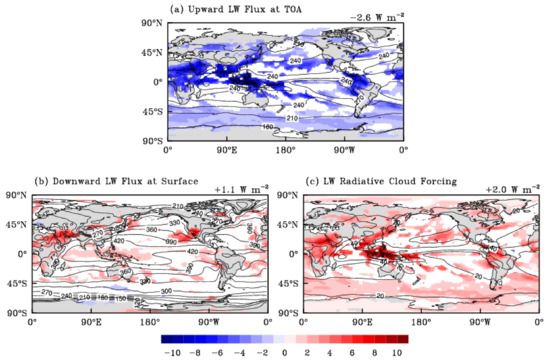
Figure 6.
Interactive runs: the color contours show the cloud LW scattering effect on annual global distributions of upward LW flux at TOA (panel a); downward LW flux at the surface (panel b); and LW cloud forcing at TOA (panel c). Results from the reference run with original RRTMG_LW are plotted as solid contour lines. (Results shown with colors are significant at the 90% confidence level using the Student’s t test; the global mean value is given in the top-right corner of each panel).
The LW scattering effect on LW cloud radiative forcing (LWCF) at TOA is shown in Figure 6c. Clouds exert a positive LW forcing on the climate and the cloud LW scattering effect further enhances LWCF. The peak effect is over the Pacific warm pool and monsoon regions, and the secondary effect is over the African continent and northern Latin America, which is similar to the pattern of Figure 6a. The global mean enhancement of LWCF due to the cloud LW scattering effect is about 2 W m−2 which is roughly comparable to the magnitude of the radiative forcing by doubling carbon dioxide [18,54]. The increase in LWCF exceeds 10 W m−2 in the Pacific warm pool and the local LWCF is 60 W m−2, indicating that the cloud LW scattering effect can lead to a considerable enhancement in the local LWCF. Figure 7 shows the zonal mean distributions of the cloud LW scattering effect on longwave heating rate, temperature, and specific humidity respectively. The longwave cooling is strengthened near the tropopause by more than −0.1 K day−1 but weakened in the troposphere. The reduction in the LW cooling is specifically strong in the lower troposphere at tropics and the local value even exceeds +0.16 K day−1. Comparing to the instantaneous effect on heating rate in Figure 5a, the warming effect caused by the cloud LW scattering is more obvious in extratropical regions in Figure 7a, which is consistent with the extra reduction in upward flux at TOA in the same region from Figure 4a to Figure 6a. As mentioned before, the climate feedbacks on the increased water vapor and cloud amount explain for the enhanced effect of cloud LW scattering from the diagnostic run to the interactive run.
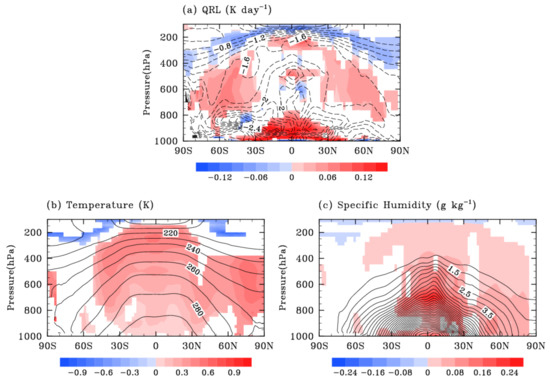
Figure 7.
Interactive runs: the color contours show the cloud LW scattering effect on annual zonal mean distributions of LW heating rate (panel a), temperature (panel b) and specific humidity (panel c). Results from the reference run with original RRTMG_LW are plotted as dashed (panel a) or solid (panels b,c) contour lines. (Results shown with colors are significant at the 90% confidence level using the Student’s t test).
The cloud LW scattering effect on atmospheric temperature is shown in Figure 7b. Comparing Figure 7a,b, we see that temperature can be modified not only by radiative heating but also by thermodynamic heating. The cloud LW scattering effect on radiative heating is strong in the lower tropical atmosphere, while the effect on temperature is weak near the surface. It is because the temperature change is inversely proportional to air density. The cloud LW scattering effect causes a decrease in zonal mean temperature near the tropopause by −0.5 K and increases almost everywhere in the troposphere. The largest increase in temperature appears in the tropical upper troposphere, with a value up to +0.8 K.
Resulted from the raised temperature, water vapor in the atmosphere also increases (Figure 7c) because the warmer environment can store more moisture. The more water vapor enhances the trapping of LW radiation, which further warms and humidifies the atmosphere resulting in a positive feedback. However, the water vapor-temperature feedback is not uniform everywhere. Kang et al. [55] show that the high specific humidity during monsoon seasons over Asia and North America contrasts to descending and dry air in anticyclone over the southern hemisphere, it makes an overall stronger LW trapping effect of water vapor over land than ocean for any given temperature. Hence, the water vapor feedback is more significant in the northern hemisphere than the southern hemisphere (as shown in Figure 7c) and so is the cloud LW scattering effect on thermodynamics. Figures S3 and S4 confirm the dominated LW scattering effect during the monsoon period of warm seasons over the northern hemisphere.
As shown in Figure 7b,c, the thermodynamic feedback caused by cloud LW scattering effect increases temperature at almost all latitudes in the northern hemisphere but only at low latitudes in the southern hemisphere. Therefore, the meridional temperature gradient becomes greater in the southern hemisphere compared to the northern hemisphere. Additionally, the meridional temperature gradient becomes larger in the upper troposphere because the temperature change due to the cloud LW scattering effect is more significant in high levels than near the surface (see Figure 7b). The temperature gradient change affects the climate dynamics and global circulations, such as the variation of Hadley circulation is associated with the meridional temperature gradients [56,57]. Keeping this in mind, Figure 8a shows the change of zonal mean meridional stream function (a proxy for the strength of circulation) due to the cloud LW scattering effect. The Hadley circulation in the southern hemisphere is strengthened, which modulates the westerly jet over 30° S and 50° S (see Figure 8b). The increase of the baroclinicity resulted from the changed temperature distributions may have an impact on the jet stream as well [58]. The mean zonal wind (in Figure 8b) near the tropical tropopause is also modified and Figure 8c depicts the details in its meridional distribution. A significant westerly wind anomaly at about 200 hPa is between 120° E and 90° W, corresponding to the position of the upper branch of Walker circulation (in Figure 8c). It could be attributed to the increase of thermodynamic instability resulted from a decrease of temperature over the tropopause (see Figure 7b).
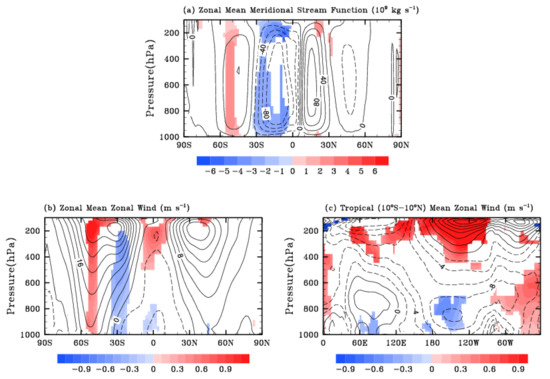
Figure 8.
Interactive runs: the color contours show the cloud LW scattering effect on annual zonal mean distributions of meridional stream function (panel a), zonal wind U (panel b), and tropical (10° S–10° N) mean zonal wind (panel c). Results from the reference run with original RRTMG_LW are plotted as solid (positive values indicate clockwise circulation in panel a or west wind in panels b and c) and dashed (negative values indicate anti-clockwise circulation in panel a or east wind in panels b and c) contour lines. (Results shown with colors are significant at the 90% confidence level using the Student’s t test).
The northward energy transport in the atmosphere is calculated following Equation (11) from Dargan and Hwang [59] and plotted in Figure 9.
where FA is the meridional northward energy transport in atmosphere (black curves in Figure 9), QS is the net downward shortwave flux at TOA, QL is the upward LW flux at TOA, QO is the net surface fluxes, including sensible heat flux, latent heat flux, net LW flux at the surface, and the net shortwave flux at the surface, λ is the longitude, φ is the latitude and, a is the radius of Earth. Since Hadley circulation dominates atmospheric cross equatorial energy transport, the net energy change between the two hemispheres is another indicator to understand the changes in large-scale circulation caused by the cloud LW scattering. Figure 9 shows the difference in the northward energy transport due to the cloud LW scattering effect. Less northward energy transports over tropics in the southern hemisphere but more energy transports over 40° S–50° S, which can partly explain the strengthening of Hadley circulation (see Figure 8a) and the modulation of the westerly jet in the southern hemisphere (see Figure 8b). Previous studies show that the northward cross-equatorial energy transport always co-occurs with a southward-shifting of ITCZ (Intertropical Convergence Zone) and the moistening in the south of the equator [59,60,61] and vice versa. Therefore, the cloud LW scattering effect on the precipitation (red curves in Figure 9) shows a significant reduction near the equator corresponding to the decreased northward cross-equatorial energy transport. It adds evidence to the changed Hadley circulation and perturbed energy budget in the atmosphere. On the other hand, Figure S5 shows that the reduced rainfall could partly lead to the reduction of latent heat flux, which has a contribution to the change of heat transport in Equation (11). Knowing that the warm and moist air converging near the equator should cause heavy precipitation, and the released latent heat drives strong rising motions [62]. An extra warmer atmosphere resulted from the cloud LW scattering effect in the middle of the troposphere near the equator may inhibit the convergence of moist air, leading to less latent heat release and reduced precipitation.
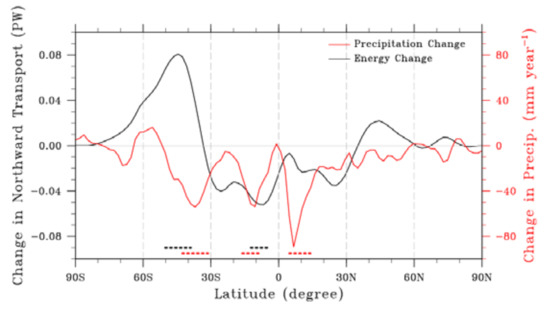
Figure 9.
Interactive runs: cloud LW scattering effect on annual zonal averaged precipitation (mm year−1) (red curves) and northward energy transport in the atmosphere (PW, i.e., 1015 W) (black curves) (The dashed lines underneath mark the significances for each variable at the 90% confidence level using the Student’s t test).
In summary, the cloud LW scattering exerts a warming effect in the troposphere. The cloud, water vapor, and temperature feedbacks amplify the warming non-uniformly between different vertical levels and between the two hemispheres, leading to complex impacts on the large-scale circulations and energy budget in the atmosphere. Since the large proportion of high clouds occurs over tropics, the LW scattering effects and climate impacts are most significant in this region. Our simulation with CAM5 shows a strong extra warming in the northern hemisphere and cooling in the upper troposphere, which results in a strengthening of Hadley circulation and reduction in precipitation near the equator.
4.3. Discussions
The cloud inhomogeneity (sub-grid cloud) and its effect on the radiation calculation are well handled by McICA (Monte-Carlo Independent Column Approximation [63]) in CAM5. Here we briefly discuss the impact of cloud inhomogeneity effect on cloud LW scattering. Generally speaking, the effect of cloud inhomogeneity is larger than that of LW scattering [17]. If excluding the LW scattering, the effect of cloud inhomogeneity simulated in the model can be even larger. On the other hand, the effect of cloud geometry can be much more significant than scattering process when the cloud optical depth is high [64]. These effects might be partly cumulative or offsetting, but not simply additive. The overall effect must be sensitive to the presentation of cloud properties and atmospheric conditions.
This study aims to quantify the bias of missing LW scattering in CAM5 and investigate the resulted impacts and feedbacks in climate. The reference run with original RRTMG_LW has been well tuned but the interactive run including the LW scattering could potentially introduce a perturbation to the tuned-to-balanced climate and cause a small imbalance of energy at TOA (Table S1). However, it is common to analyze the unbalanced model results to understand perturbing factors in the climate [19,65]. A few watts per square meter of imbalances can be removed afterward by empirically tuning certain parameters in cloud micro- or macro-physical scheme [65]. Therefore, we quantify the LW cloud scattering effect and analyze the resulted impacts and feedbacks in a perturbed climate system as simulated with CAM5 in Section 4.2. Additionally, we further tune one microphysical and one macrophysical cloud parameters in the interactive run to reach the energy balance at the TOA (see Table S1). The LW cloud scattering effects on the upward flux at TOA and on temperature (Figures S6 and S7) in the two tuned runs show similar patterns as Figure 6a and Figure 7b, confirming the significance of the LW cloud scattering effect on climate and the robustness of our results in Section 4.2. However, as the cloud parameterizations in the released CAM5 are still under development by other modelers, their tuning could be very different from the cloud parameters we tune here. The magnitude of LW scattering effect alone and its potential climate influence in this study could provide a reference to modelers for future simulation by combining the LW scattering effect with new cloud scheme tunings.
5. Summary
This study investigates the cloud LW scattering effect on radiative budget and climate impacts by using a standalone radiative transfer model RRTMG and a global climate model CAM5. Firstly, the band-by-band scattering optical properties of water and ice clouds for selected typical particle sizes are calculated. Ice clouds show stronger scattering ability than water clouds in bands 1–6 (10.2–1000.0 µm), and especially in band 2 (20.0–28.57 µm).
Next, the cloud LW scattering effect is estimated with a standalone RRTMG by prescribing cloud cases in low, middle and high levels of certain atmospheric profiles. Results show that the LW scattering effect exerts less (more) cooling at the top of the water (ice) clouds and less (more) warming below water (ice) cloud bottom. The cloud LW scattering effect has a negligible impact on the downward LW flux at the surface. In general, standalone RRTMG results indicate that the cloud LW scattering reduces the outgoing LW radiation at TOA and has an additional warming effect on the atmosphere. The instantaneous LW scattering effect is estimated in the diagnostic run without including its climate impacts in CAM5. The global LW scattering effect by high cloud is more significant than low and middle clouds, indicating a dominant role of high cloud in the LW scattering effect in all-sky condition. The spatial distribution of the cloud LW scattering effect peaks in tropical regions. The instantaneous LW scattering effect causes a reduction of 1.8 W m−2 in the annual global mean upward LW flux at the TOA.
The LW cloud scattering effect and its impacts/feedbacks in the perturbed climate system are estimated in the interactive run of CAM5. The reduction of upward flux at TOA is significantly amplified compared to the instantaneous result. It is caused by the increased cloud fraction responding to the feedback of a warming atmosphere. The missing LW cloud scattering leads to a reduction of 2.6 W m−2 in the upward LW flux at TOA and an increase of 2 W m−2 in the annual global mean LWCF. As the LW cloud forcing is enhanced, both air temperature and specific humidity increase in the northern hemisphere as a result of the thermodynamic feedback that higher temperature favors more water vapor and traps more energy in the earth-atmosphere system. On the contrary, the positive water vapor-temperature feedback has negligible impact in mid- and high-latitudes in the southern hemisphere. Therefore, non-uniform meridional temperature gradient in the two hemispheres strengthens the southern branch of Hadley circulation, and modulates the westerly jet near 50° S and upper part of Walker circulation.
The cloud LW scattering effect on the climate system may cause modifications on Madden Julian Oscillation, monsoon activities, and some other seasonal or decadal variations. The complex feedbacks related to these climate indices are worth being understood with more quantitative analysis in future studies. The cloud LW scattering effect on climate system has an equivalent strength to that of doubling carbon dioxide [18], as documented in this study. Noting that RRTMG is a popular radiative transfer algorithm widely used in state-of-the-art climate models, our work calls attention that the proper treatment on LW radiative transfer is an essential issue in future climate modeling research.
Supplementary Materials
The following are available online at http://www.mdpi.com/2073-4433/9/4/153/s1.
Acknowledgments
This work is supported by China National 973 Program (Grant No. 2014CB441302). Authors thank the three anonymous reviewers for their constructive comments.
Author Contributions
Wenjie Zhao and Yiran Peng have done all the model experiments and result analysis. Bin Wang has helped with the analysis of CAM5 results in terms of climate feedbacks and global circulations. Jiangnan Li has designed all the experiments and decided the layout of manuscript. All authors have contributed to the formation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Donohoe, A.; Armour, K.C.; Pendergrass, A.G.; Battisti, D.S. Shortwave and longwave radiative contributions to global warming under increasing CO2. Proc. Natl. Acad. Sci. USA 2014, 111, 16700–16705. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.; Liu, G.; Li, J.-L.F. Assessing the radiative effects of global ice clouds based on CloudSat and CALIPSO measurements. J. Clim. 2016, 29, 7651–7674. [Google Scholar] [CrossRef]
- Baran, A.J. From the single-scattering properties of ice crystals to climate prediction: A way forward. Atmos. Res. 2012, 112, 45–69. [Google Scholar] [CrossRef]
- Kim, D.; Ahn, M.-S.; Kang, I.-S.; Genio, A. Role of longwave cloud-radiation feedback in the simulation of the Madden-Julian oscillation. J. Clim. 2015, 28, 6979–6993. [Google Scholar] [CrossRef]
- Fu, Q.; Liou, K.N.; Cribb, M.C.; Charlock, T.P.; Grossman, A. On multiple scattering in thermal infrared radiative transfer. J. Atmos. Sci. 1997, 54, 2799–2812. [Google Scholar] [CrossRef]
- Chou, M.D.; Lee, K.T.; Tsay, S.C.; Fu, Q. Parameterization for cloud longwave scattering for use in atmospheric models. J. Clim. 1999, 12, 159–169. [Google Scholar] [CrossRef]
- Li, J. Accounting for unresolved clouds in a 1D infrared radiative transfer model. Part I: Solution for radiative transfer, including cloud scattering and overlap. J. Atmos. Sci. 2002, 59, 3302–3320. [Google Scholar] [CrossRef]
- Costa, S.M.S.; Shine, K.P. An estimate of the global impact of multiple scattering by clouds on outgoing long-wave radiation. Q. J. R. Meteorol. Soc. 2006, 132, 885–895. [Google Scholar] [CrossRef]
- Chen, X.; Huang, X.; Flanner, M.G. Sensitivity of modeled far-IR radiation budgets in polar continents to treatments of snow surface and ice cloud radiative properties. Geophys. Res. Lett. 2014, 41, 6530–6537. [Google Scholar] [CrossRef]
- Li, J.; Fu, Q. Absorption approximation with scattering effect for infrared radiation. J. Atmos. Sci. 2000, 57, 2905–2914. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, K.; LI, J.; Yang, Q.; Zhao, J.; Li, J. Analytical infrared delta-four-stream adding method from invariance principle. J. Atmos. Sci. 2016, 73, 4171–4188. [Google Scholar] [CrossRef]
- Oreopoulos, L.; Mlawer, E.; Delamere, J.; Shippert, T.; Cole, J.; Fomin, B.; Iacono, M.; Jin, Z.; Li, J.; Manners, J.; et al. The Continual Intercomparison of Radiation Codes: Results from Phase I. J. Geophys. Res. 2012, 117, D06118. [Google Scholar] [CrossRef]
- Edwards, J.M.; Slingo, A. Studies with a flexible new radiation code. I: Choosing a configuration for a large-scale model. Q. J. R. Meteorol. Soc. 1996, 122, 689–719. [Google Scholar] [CrossRef]
- Zhang, Y.; Rossow, W.B.; Lacis, A.A.; Oinas, V.; Mishchenko, M.I. Calculation of radiative fluxes from the surface to top of atmosphere based on ISCCP and other global data sets: Refinements of the radiative transfer model and the input data. J. Geophys. Res. 2004, 109, D19105. [Google Scholar] [CrossRef]
- Fomin, B.A. Monte-Carlo algorithm for line-by-line calculations of thermal radiation in multiple scattering layered atmospheres. J. Quant. Spectrosc. Radiat. Transf. 2006, 98, 107–115. [Google Scholar] [CrossRef]
- Stephens, G.L.; Gabriel, P.M.; Partain, P.T. Parameterization of atmospheric radiative transfer. Part I: Validity of simple models. J. Atmos. Sci. 2001, 58, 3391–3409. [Google Scholar] [CrossRef]
- Joseph, E.; Min, Q. Assessment of multiple scattering and horizontal inhomogeneity in IR radiative transfer calculations of observed thin cirrus clouds. J. Geophys. Res. 2003, 108, 4380. [Google Scholar] [CrossRef]
- Kuo, C.-P.; Yang, P.; Huang, X.; Feldman, D.; Flanner, M.; Kuo, C.; Mlawer, E.J. Impact of Multiple scattering on longwave radiative transfer involving clouds. J. Adv. Model. Earth Syst. 2017, 9, 3082–3098. [Google Scholar] [CrossRef]
- Park, S.; Bretherton, C.S.; Rasch, P.J. Integrating cloud processes in the community atmosphere model, version 5. J. Clim. 2014, 27, 6821–6856. [Google Scholar] [CrossRef]
- Tao, W.-K.; Simpson, J.; Sui, C.-H.; Ferrier, B.; Lang, S.; Scala, J.; Chou, M.-D.; Pickering, K. Heating, moisture, and water budgets of tropical and midlatitude squall lines: Comparisons and sensitivity to longwave radiation. J. Atmos. Sci. 1993, 50, 673–690. [Google Scholar] [CrossRef]
- Shupe, M.D.; Intrieri, J.M. Cloud radiative forcing of the arctic surface: The influence of cloud properties, surface albedo, and solar zenith angle. J. Clim. 2004, 17, 616–628. [Google Scholar] [CrossRef]
- Zelinka, M.D.; Klein, S.A.; Taylor, K.E.; Andrews, T.; Webb, M.J.; Gregory, J.M.; Forster, P.M. Contributions of different cloud types to feedbacks and rapid adjustments in CMIP5. J. Clim. 2013, 26, 5007–5027. [Google Scholar] [CrossRef]
- Huang, Y.; Ramaswamy, V.; Soden, B. An investigation of the sensitivity of the clear-sky outing longwave radiation to atmospheric temperature and water vapor. J. Geophys. Res. 2007, 112, D05104. [Google Scholar] [CrossRef]
- Huang, Y. A simulated climatology of spectrally decomposed atmospheric infrared radiation. J. Clim. 2012, 26, 1702–1715. [Google Scholar] [CrossRef]
- Huang, Y. On the longwave climate feedbacks. J. Clim. 2013, 26, 7603–7610. [Google Scholar] [CrossRef]
- Harries, J.E.; Brindley, H.E.; Sagoo, P.J.; Bantges, R.J. Increases in greenhouse forcing inferred from the outgoing longwave radiation spectra of the Earth in 1970–1997. Nature 2001, 410, 355–357. [Google Scholar] [CrossRef] [PubMed]
- Sandeep, S.; Stordal, F. Use of daily outgoing longwave radiation (OLR) data in detecting precipitation extremes in the tropics. Remote Sens. Lett. 2013, 6, 570–578. [Google Scholar] [CrossRef]
- Kiladis, G.N.; Dias, J.; Straub, K.H.; Wheeler, M.C.; Tulich, S.N.; Kikuchi, K.; Weickmann, K.M.; Ventrice, M.J. A Comparison of OLR and Circulation-Based Indices for Tracking the MJO. Mon. Weather Rev. 2014, 142, 1697–1715. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef] [PubMed]
- Joseph, J.H.; Wiscombe, W.J.; Weinman, J.A. The delta Eddington approximation for radiative flux transfer. J. Atmos. Sci. 1976, 33, 2452–2459. [Google Scholar] [CrossRef]
- Li, J. Gaussian quadrature and its application to infrared radiation. J. Atmos. Sci. 2000, 57, 753–765. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by longlived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Neale, R.B.; Chen, C.-C.; Gettelman, A.; Lauritzen, P.H.; Park, S.; Williamson, D.L.; Conley, A.J.; Garcia, R.; Kinnison, D.; Lamarque, J.-F.; et al. Description of the NCAR Community Atmosphere Model (CAM 5.0); NCAR Tech. Note NCAR/TN-486+STR. 2012. Available online: http://www.cesm.ucar.edu/models/cesm1.0/cam/docs/description/cam5_desc.pdf (accessed on 29 January 2018).
- Eidhammer, T.; Morrison, H.; Bansemer, A.; Gettelman, A.; Heymsfield, A.J. Comparison of ice clod properties simulated by the Community Atmosphere Model (CAM5) with in-situ observations. Atmos. Chem. Phys. 2014, 14, 10103–10118. [Google Scholar] [CrossRef]
- Kay, J.E.; Wall, C.; Yettella, V.; Medeiros, B.; Hannay, C.; Caldwell, P.; Bitz, C. Global climate impacts of fixing the Southern Ocean shortwave radiation bias in the Community Earth System Model (CESM). J. Clim. 2016, 29, 4617–4636. [Google Scholar] [CrossRef]
- Kay, J.E.; Bourdages, L.; Miller, N.B.; Morrison, A.; Yettella, V.; Chepfer, H.; Eaton, B. Evaluating and improving cloud phase in the Community Atmosphere Model version 5 using spaceborne lidar observations. J. Geophys. Res. Atmos. 2016, 121, 4162–4176. [Google Scholar] [CrossRef]
- Baran, A.J. A review of the light scattering properties of cirrus. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1239–1260. [Google Scholar] [CrossRef]
- Slingo, A.; Schrecker, H.M. On the shortwave radiative properties of stratiform water clouds. Q. J. R. Meteorol. Soc. 1982, 108, 407–426. [Google Scholar] [CrossRef]
- Fu, Q.; Liou, K.N. Parameterization of the radiative properties of cirrus clouds. J. Atmos. Sci. 1993, 50, 2008–2025. [Google Scholar] [CrossRef]
- Fu, Q.; Yang, P.; Sun, W.B. An accurate parameterization of the infrared radiative properties of cirrus clouds for climate models. J. Clim. 1998, 11, 2223–2237. [Google Scholar] [CrossRef]
- Foot, J.S. Some observations of the optical properties of clouds. II: Cirrus. Q. J. R. Meteorol. Soc. 1988, 114, 141–164. [Google Scholar] [CrossRef]
- Herman, G.F.; Curry, J.A. Observational and theoretical studies of solar radiation in arctic stratus clouds. J. Clim. Appl. Meteorol. 1984, 23, 5–24. [Google Scholar] [CrossRef]
- Slingo, A. A GCM parameterization for the shortwave radiative properties of water clouds. J. Atmos. Sci. 1989, 46, 1419–1427. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, G. The characteristics of ice cloud properties derived from CloudSat and CALIPSO measurements. J. Clim. 2015, 28, 3880–3901. [Google Scholar] [CrossRef]
- Hu, Y.X.; Stamnes, K. An accurate parameterization of the radiative properties of water clouds suitable for use in climate models. J. Clim. 1993, 6, 728–742. [Google Scholar] [CrossRef]
- Lindner, T.H.; Li, J. Parameterization of the optical properties for water clouds in the infrared. J. Clim. 2000, 13, 1797–1805. [Google Scholar] [CrossRef]
- Yi, B.; Yang, P.; Baum, B.A.; L’Ecuyer, T.; Oreopoulos, L.; Mlawer, E.J.; Heymsfield, A.J.; Liou, K.-N. Influence of ice particle surface roughening on the global cloud radiative effect. J. Atmos. Sci. 2013, 70, 2794–2807. [Google Scholar] [CrossRef]
- Wiscombe, W.J. Mie Scattering Calculations: Advances in Technique and Fast, Vector-Speed Computer Codes; Technical Report Tech. Note. NCAR/TN-140+STR. 1996. Available online: http://dust.ess.uci.edu/ppr/ppr_Wis79.pdf (accessed on 29 January 2018).
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Morrison, H.; Gettelman, A. A New Two-Moment Bulk Stratiform Cloud Microphysics Scheme in the Community Atmosphere Model, Version 3 (CAM3). Part I: Description and Numerical Tests. J. Clim. 2008, 21, 3642–3659. [Google Scholar] [CrossRef]
- Li, J.; Chylek, P.; Zhang, F. The dissipation structure of extratropical cyclones. J. Atmos. Sci. 2014, 71, 69–88. [Google Scholar] [CrossRef]
- Muhlbauer, A.; McCoy, I.L.; Wood, R. Climatology of stratocumulus cloud morphologies: Microphysical properties and radiative effects. Atmos. Chem. Phys. 2014, 14, 6695–6716. [Google Scholar] [CrossRef]
- Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Forster, P.; Kerminen, V.-M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. Clouds and Aerosols. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Kang, S.M.; Seager, R.; Frierson, D.M.W.; Liu, X. Croll revisited: Why is the northern hemisphere warmer than the southern hemisphere? Clim. Dyn. 2015, 44, 1457–1472. [Google Scholar] [CrossRef]
- Lu, J.; Vecchi, G.A.; Reichler, T. Expansion of the Hadley cell under global warming. Geophys. Res. Lett. 2007, 34, L06805. [Google Scholar]
- Adam, O.; Schneider, T.; Harnik, N. Role of changes in mean temperatures versus temperature gradients in the recent widening of the Hadley circulation. J. Clim. 2014, 27, 7450–7461. [Google Scholar] [CrossRef]
- Ceppi, P.; Shepherd, T.G. Contributions of climate feedbacks to changes in atmospheric circulation. J. Clim. 2017, 30, 9097–9118. [Google Scholar] [CrossRef]
- Dargan, M.D.F.; Hwang, Y.T. Extratropical influence on ITCZ shifts in slab ocean simulations of global warming. J. Clim. 2011, 25, 720–733. [Google Scholar]
- Hawcroft, M.; Haywood, J.M.; Collins, M.; Jones, A.; Jones, A.C.; Stephens, G. Southern ocean albedo, inter-hemispheric energy transports and the double ITCZ: Global impacts of biases in a coupled model. Clim. Dyn. 2016, 48, 2279–2295. [Google Scholar] [CrossRef]
- Loeb, N.G.; Wang, H.; Cheng, A.; Kato, S.; Fasullo, J.T.; Xu, K.M.; Allan, R.P. Observational constraints on atmospheric and oceanic cross-equatorial heat transports: Revisiting the precipitation asymmetry problem in climate models. Clim Dyn. 2016, 46, 3239–3257. [Google Scholar] [CrossRef]
- Holton, J. An Introduction to Dynamic Meteorology; Academic Press: Cambridge, MA, USA, 2004; p. 372. [Google Scholar]
- Räisänen, P.; Barker, H.W.; Khairoutdinov, M.; Li, J. Stochastic generation of subgrid-scale cloudy columns for large-scale models. Q. J. R. Meteorol. Soc. 2004, 130, 2047–2068. [Google Scholar] [CrossRef]
- Takara, E.E.; Ellingson, R.G. Broken cloud field longwave-scattering effects. J. Atmos. Sci. 2000, 57, 1298–1310. [Google Scholar] [CrossRef]
- Bacmeister, J.T.; Wehner, M.F.; Neale, R.B.; Gettelman, A.; Hannay, C.; Lauritzen, P.H.; Caron, J.M.; Truesdale, J.E. Exploratory High-Resolution Climate Simulations using the Community Atmosphere Model (CAM). J. Clim. 2014, 27, 3073–3099. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).