Modelling of Basin Wide Daily Evapotranspiration with a Partial Integration of Remote Sensing Data
Abstract
1. Introduction
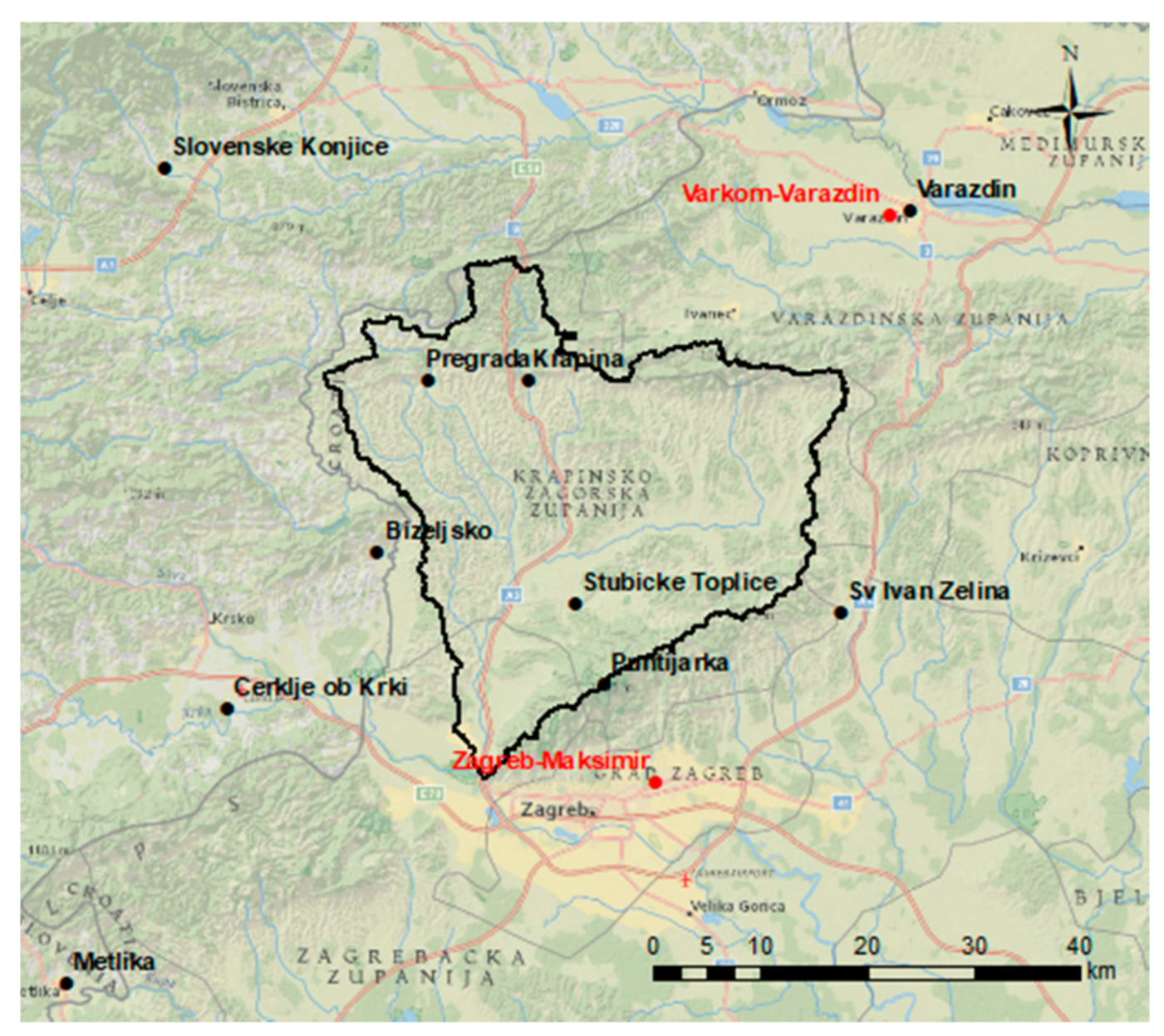
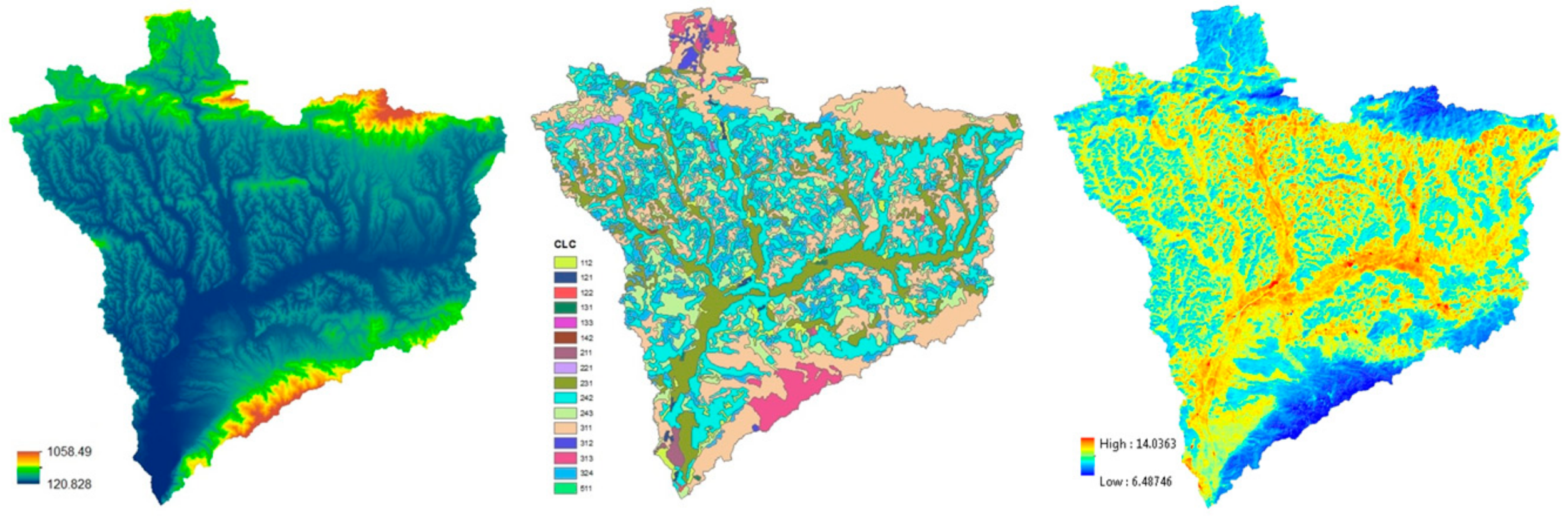
2. Study Area and Data
3. Methodology
3.1. SEBAL ET Estimates
3.2. Obtaining Daily ET by Using Interpolated Evaporative Fraction
3.3. Validation and Sensitivity Analysis
4. Results
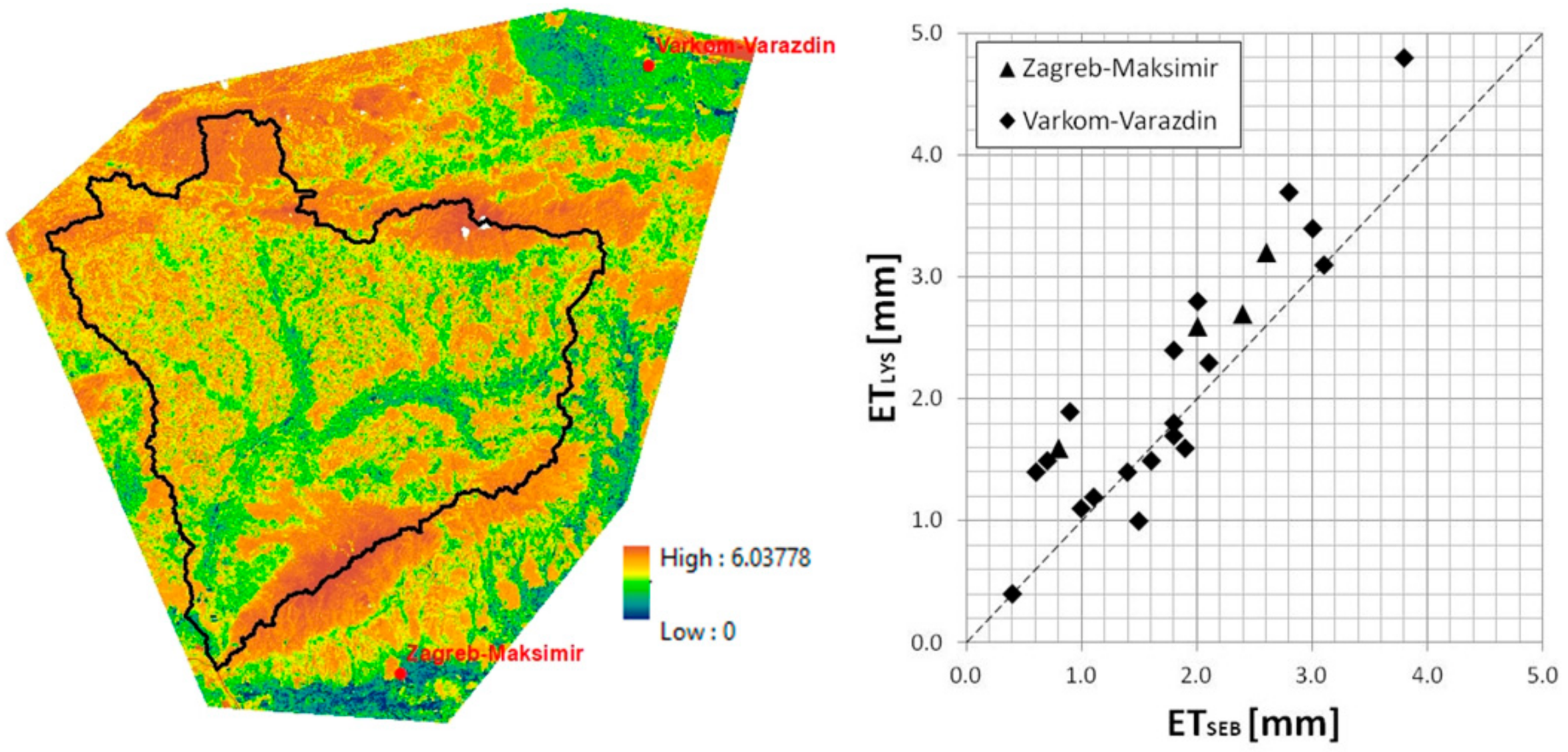
4.1. Measured ET in the Krapina River Basin
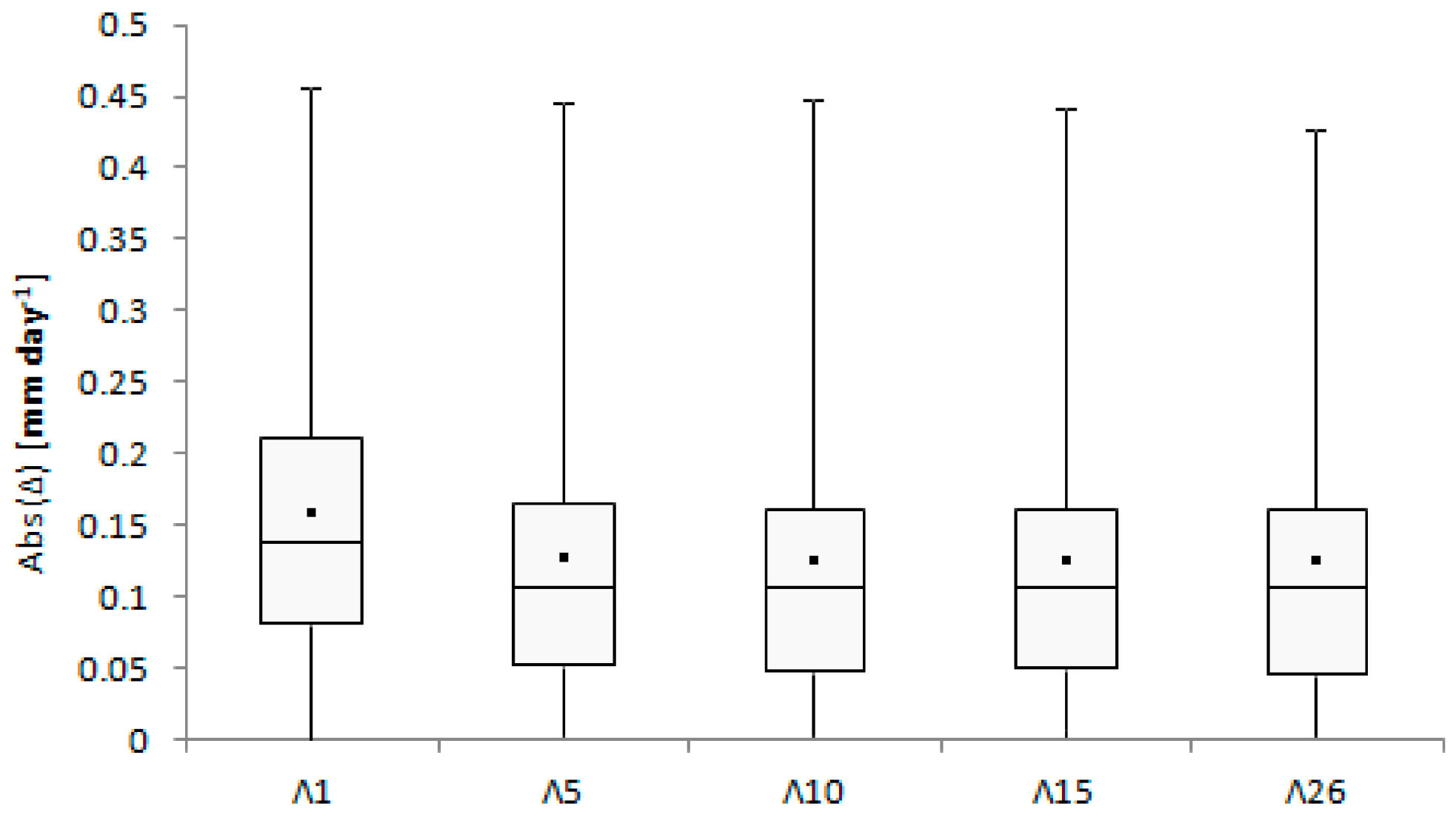
4.2. Evaporative Fraction Variability and Interpolation
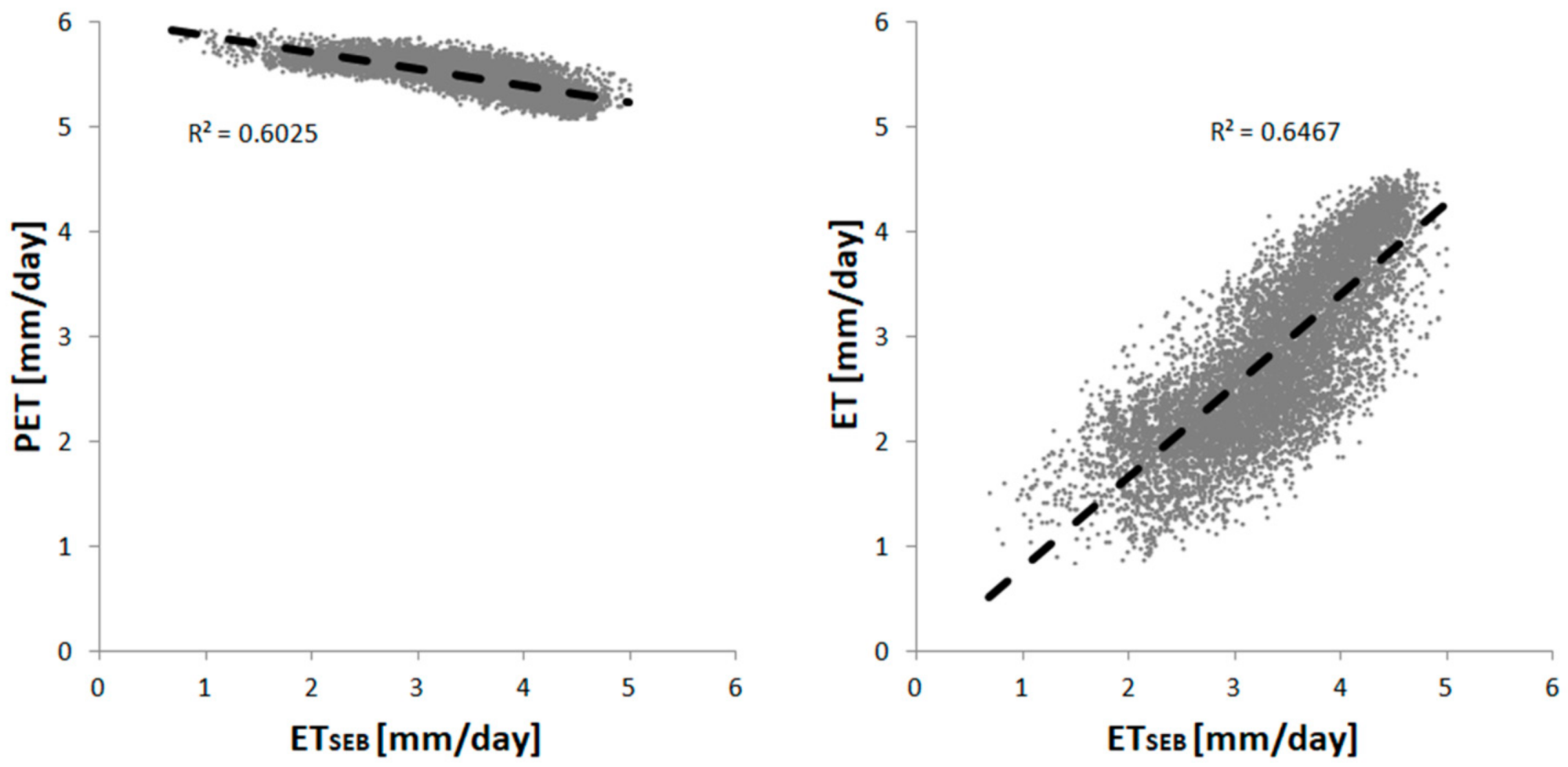
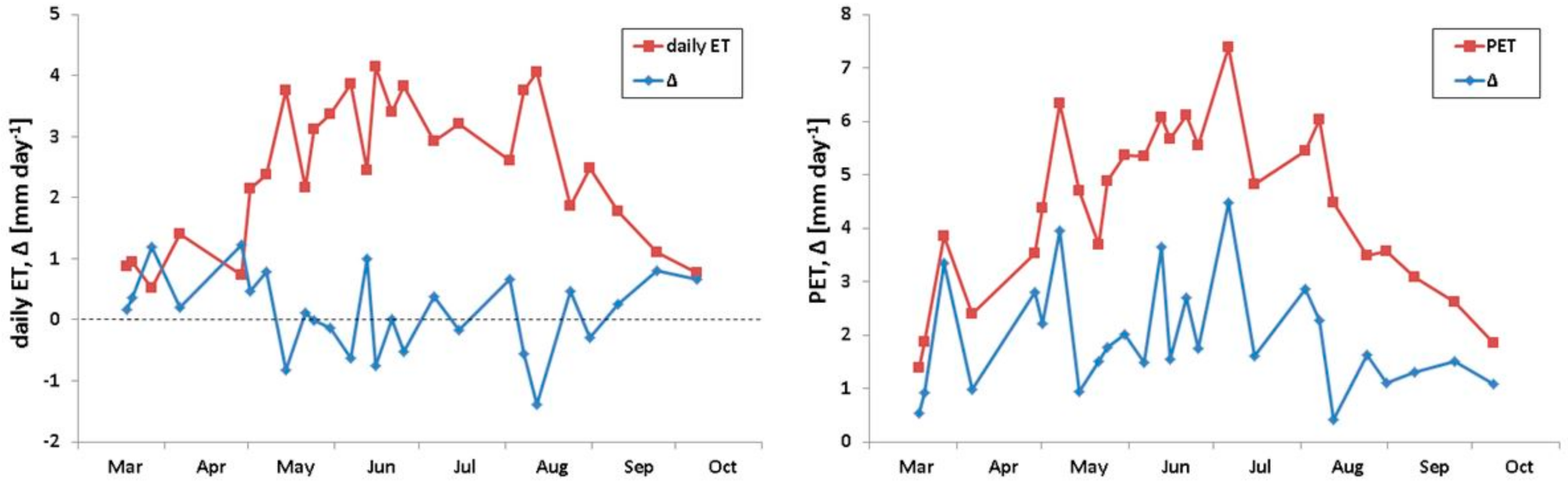
4.3. Daily ET Modelling Based on PET Variation
4.4. Validation of Proposed Concept
4.5. Standard PET Methods
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- UN-Water. Managing Water under Uncertainty and Risk; Report 4; The United Nations World Water Development: Paris, France, 2012. [Google Scholar]
- European Parliament. Policy Department, Economic and Scientific Policy, Water Scarcity and Droughts; European Parliament’s Committee on the Environment, Public Health and Food Safety: London, UK, 2008. [Google Scholar]
- Senay, G.B.; Leake, S.; Nagler, P.L.; Artan, G.; Dickinson, J.; Cordova, J.T.; Glenn, E.P. Estimating basin scale evapotranspiration (ET) by water balance and remote sensing methods. Hydrol. Process. 2011, 25, 4037–4049. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. WIREs Water 2016. [Google Scholar] [CrossRef]
- Cristobal, J.; Poyatos, R.; Ninyerola, M.; Llorens, P.; Pons, X. Combining remote sensing and GIS climate modelling to estimate daily forest evapotranspiration in a Mediterranean mountain area. Hydrol. Earth Syst. Sci. 2011, 15, 1563–1575. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface balance algorithm for land (SEBAL). J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Gamage, N.; Smakhtin, V.; Perera, B.J.C. Estimation of Actual Evapotranspiration using Remote Sensing data. In Proceedings of the 19th International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011; pp. 3356–3362. [Google Scholar]
- Samain, B.; Simons, G.W.H.; Voogt, M.P.; Defloor, W.; Bink, N.-J.; Pauwels, V.R.N. Consistency between hydrological model, large aperture scintillometer and remote sensing based evapotranspiration estimates for a heterogeneous catchment. Hydrol. Earth Syst. Sci. 2012, 16, 2095–2107. [Google Scholar] [CrossRef]
- Horvat, B. Spatial dynamics of actual daily evapotranspiration. Gradjevinar 2013, 65, 693–705. [Google Scholar]
- Zhang, L.; Potter, N.; Hickel, K.; Zhang, Y.; Shao, Q. Water balance modeling over variable time scales based on the Budyko framework—Model development and testing. J. Hydrol. 2008, 360, 117–131. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Chen, D. Comparison of seven models for estimation of evapotranspiration and groundwater recharge using lysimeter measurement data in Germany. Hydrol. Process. 2005, 19, 3717–3734. [Google Scholar] [CrossRef]
- Douglas, E.M.; Jacobs, J.M.; Sumner, D.M.; Ray, R.L. A comparison of models for estimating potential evapotranspiration for Florida land cover types. J. Hydrol. 2009, 373, 366–376. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)-Model. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. A two-source energy balance approach using directional radiometric temperature observations for sparse canopy covered surfaces. Agron. J. 2000, 92, 847–854. [Google Scholar] [CrossRef]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Sanchez, J.M.; Kustas, W.P.; Caselles, V.; Anderson, M.C. Modelling surface energy fluxes over maize using a two-source patch model and radiometric soil and canopy temperature observations. Remote Sens. Environ. 2008, 112, 1130–1143. [Google Scholar] [CrossRef]
- Bhattarai, N.; Quackenbush, L.J.; Dougherty, M.; Marzen, L.J. A simple Landsat–MODIS fusion approach for monitoring seasonal evapotranspiration at 30 m spatial resolution. Int. J. Remote Sens. 2014, 36, 115–143. [Google Scholar] [CrossRef]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2015. [Google Scholar] [CrossRef]
- Schuurmans, J.M.; Troch, P.A.; Veldhuizen, A.A.; Bastiaanssen, W.G.M.; Bierkens, M.F.P. Assimilation of remotely sensed latent heat flux in a distributed hydrological model. Adv. Water Resour. 2003, 26, 151–159. [Google Scholar] [CrossRef]
- Neale, C.M.U.; Geli, H.M.E.; Kustas, W.P.; Alfieri, J.G.; Gowda, P.H.; Evett, S.R.; Prueger, J.H.; Hipps, L.E.; Dulaney, W.P.; Chávez, J.L.; et al. Soil water content estimation using a remote sensing based hybrid evapotranspiration modeling approach. Adv. Water Resour. 2012, 50, 152–161. [Google Scholar] [CrossRef]
- Parr, D.; Wang, G. Integrating Remote Sensing Data on Evapotranspiration and Leaf Area Index with Hydrological Modeling: Impacts on Model Performance and Future Predictions. J. Hydrometeorol. 2015, 16, 2086–2100. [Google Scholar] [CrossRef]
- Campos, I.; González-Piqueras, J.; Carrara, A.; Villodre, J.; Calera, A. Estimation of total available water in the soil layer by integrating actual evapotranspiration data in a remote sensing-driven soil water balance. J. Hydrol. 2016, 534, 427–439. [Google Scholar] [CrossRef]
- SEBAL (Surface Energy Balance Algorithms for Land). Advanced Training and Users Manual, Version 1.0; Waters Consulting: Nelson, BC, Canada; University of Idaho: Kimberly, Idaho; WaterWatch Inc.: Wageningen, The Netherlands, 2002. [Google Scholar]
- Singh, R.K.; Liu, S.; Tieszen, L.L.; Suyker, A.E.; Verma, S.B. Estimating seasonal evapotranspiration from temporal satellite images. Irrig. Sci. 2012, 30, 303–313. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, X.; Vogelmann, J.E.; Gao, F.; Jin, S. A simple and effective method for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Kar, S.K. Evapotranspiration Estimation with Remote Sensing and Various Surface Energy Balance Algorithms-A Review. Energies 2014, 7, 2821–2849. [Google Scholar] [CrossRef]
- Nouri, H.; Beecham, S.; Kazemi, F.; Hassanli, A.M.; Anderson, S. Remote sensing techniques for predicting evapotranspiration from mixed vegetated surfaces. Hydrol. Earth Syst. Sci. 2013, 10, 3897–3925. [Google Scholar] [CrossRef]
- Alemu, H.; Kaptue, A.T.; Senay, G.B.; Wimberly, M.C.; Henebry, G.M. Evapotranspiration in the Nile Basin: Identifying Dynamics and Drivers, 2002–2011. Water 2015, 7, 4914–4931. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL Model with Remotely Sensed Data to Improve Water-Resources Management under Actual Field Conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Thoreson, B.; Clark, B.; Davids, G. Discussion of “Application of SEBAL Model for Mapping Evapotranspiration and Estimating Surface Energy Fluxes in South-Central Nebraska” by Singh, Irmak, Irmak, and Martin. J. Irrig. Drain. Eng. 2010, 136, 282–283. [Google Scholar] [CrossRef]
- Gao, Y.C.; Long, D.; Li, Z.L. Estimation of daily actual evapotranspiration from remotely sensed data under complex terrain over the upper Chao river basin in North China. Int. J. Remote Sens. 2008, 29, 3295–3315. [Google Scholar] [CrossRef]
- Sun, Z.; Wei, B.; Su, W.; Shen, W.; Wang, C.; You, D.; Liu, Z. Evapotranspiration estimation based on the SEBAL model in the Nansi Lake Wetland of China. Math. Comput. Model. 2011, 54, 1086–1092. [Google Scholar] [CrossRef]
- Lu, J.; Tang, R.; Tang, H.; Li, Z.-L.; Zhou, G.; Shao, K.; Bi, Y.; Labed, J. Daily Evaporative Fraction Parameterization Scheme Driven by Day-Night Differences in Surface Parameters: Improvement and Validation. Remote Sens. 2014, 6, 4369–4390. [Google Scholar] [CrossRef]
- Nutini, F.; Boschetti, M.; Candiani, G.; Bocchi, S.; Brivio, P.A. Evaporative Fraction as an Indicator of Moisture Condition and Water Stress Status in Semi-Arid Rangeland Ecosystems. Remote Sens. 2014, 6, 6300–6323. [Google Scholar] [CrossRef]
| Image No. | Acquisition Date | Λ1 | Λ5 | Λ10 | Λ15 | Λ26 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Δ [mm day−1] | σ [mm day−1] | Δ [mm day−1] | σ [mm day−1] | Δ [mm day−1] | σ [mm day−1] | Δ [mm day−1] | σ [mm day−1] | Δ [mm day−1] | σ [mm day−1] | ||
| 1 | 6 July 1999 | 0.03 | 0.25 | 0.17 | 0.14 | 0.19 | 0.16 | 0.18 | 0.17 | 0.17 | 0.16 |
| 2 | 15 July 1999 | −0.20 | 0.19 | −0.06 | 0.10 | −0.04 | 0.11 | −0.04 | 0.12 | −0.06 | 0.11 |
| 3 | 7 August 1999 | −0.19 | 0.21 | −0.06 | 0.10 | −0.03 | 0.13 | −0.04 | 0.13 | −0.06 | 0.13 |
| 4 | 24 September 1999 | −0.10 | 0.18 | 0.04 | 0.10 | 0.06 | 0.11 | 0.05 | 0.11 | 0.04 | 0.11 |
| 5 | 18 March 2000 | −0.21 | 0.34 | −0.08 | 0.30 | −0.05 | 0.31 | −0.06 | 0.31 | −0.07 | 0.32 |
| 6 | 28 April 2000 | 0.14 | 0.30 | 0.28 | 0.31 | 0.30 | 0.28 | 0.30 | 0.28 | 0.28 | 0.27 |
| 7 | 14 May 2000 | −0.32 | 0.18 | −0.19 | 0.15 | −0.16 | 0.11 | −0.17 | 0.11 | −0.18 | 0.11 |
| 8 | 21 May 2000 | −0.13 | 0.20 | 0.01 | 0.26 | 0.04 | 0.20 | 0.03 | 0.20 | 0.02 | 0.20 |
| 9 | 6 June 2000 | −0.26 | 0.17 | −0.13 | 0.12 | −0.10 | 0.08 | −0.11 | 0.09 | −0.12 | 0.08 |
| 10 | 15 June 2000 | −0.30 | 0.18 | −0.16 | 0.16 | −0.13 | 0.12 | −0.14 | 0.13 | −0.15 | 0.12 |
| 11 | 2 August 2000 | 0.00 | 0.00 | 0.14 | 0.18 | 0.16 | 0.13 | 0.15 | 0.12 | 0.14 | 0.12 |
| 12 | 10 September 2000 | −0.10 | 0.16 | 0.04 | 0.24 | 0.06 | 0.19 | 0.05 | 0.18 | 0.04 | 0.18 |
| 13 | 6 April 2001 | −0.10 | 0.16 | 0.04 | 0.16 | 0.07 | 0.13 | 0.06 | 0.12 | 0.04 | 0.12 |
| 14 | 1 May 2001 | −0.03 | 0.16 | 0.10 | 0.17 | 0.13 | 0.13 | 0.12 | 0.11 | 0.11 | 0.12 |
| 15 | 24 May 2001 | −0.16 | 0.16 | −0.02 | 0.18 | 0.00 | 0.13 | −0.01 | 0.12 | −0.02 | 0.13 |
| 16 | 25 June 2001 | −0.31 | 0.20 | −0.16 | 0.17 | −0.15 | 0.15 | −0.15 | 0.14 | −0.17 | 0.13 |
| 17 | 12 August 2001 | −0.45 | 0.21 | −0.32 | 0.14 | −0.29 | 0.14 | −0.30 | 0.15 | −0.31 | 0.14 |
| 18 | 8 October 2001 | 0.04 | 0.16 | 0.17 | 0.12 | 0.20 | 0.10 | 0.19 | 0.10 | 0.18 | 0.09 |
| 19 | 12 June 2002 | −0.02 | 0.21 | 0.12 | 0.14 | 0.15 | 0.14 | 0.14 | 0.15 | 0.12 | 0.13 |
| 20 | 21 June 2002 | −0.14 | 0.18 | 0.00 | 0.17 | 0.02 | 0.14 | 0.02 | 0.14 | 0.00 | 0.13 |
| 21 | 24 August 2002 | −0.09 | 0.15 | 0.05 | 0.17 | 0.07 | 0.14 | 0.06 | 0.14 | 0.05 | 0.13 |
| 22 | 31 August 2002 | −0.21 | 0.16 | −0.07 | 0.14 | −0.05 | 0.12 | −0.05 | 0.12 | −0.07 | 0.10 |
| 23 | 20 March 2003 | −0.02 | 0.18 | 0.11 | 0.17 | 0.14 | 0.15 | 0.13 | 0.14 | 0.12 | 0.14 |
| 24 | 27 March 2003 | 0.29 | 0.17 | 0.42 | 0.15 | 0.45 | 0.13 | 0.44 | 0.12 | 0.43 | 0.12 |
| 25 | 7 May 2003 | 0.08 | 0.14 | 0.21 | 0.15 | 0.24 | 0.11 | 0.23 | 0.09 | 0.22 | 0.10 |
| 26 | 30 May 2003 | −0.15 | 0.18 | −0.01 | 0.20 | 0.02 | 0.15 | 0.01 | 0.15 | −0.01 | 0.15 |
| MAE | 0.16 | 0.18 | 0.14 | 0.17 | 0.13 | 0.15 | 0.13 | 0.14 | 0.13 | 0.14 | |
| Min | −0.45 | 0.00 | −0.32 | 0.10 | −0.29 | 0.08 | −0.30 | 0.09 | −0.31 | 0.08 | |
| Max | 0.29 | 0.34 | 0.42 | 0.31 | 0.45 | 0.31 | 0.44 | 0.31 | 0.43 | 0.32 | |
| Image No. | Acquisition Date | ETSEB,MEAN [mm day−1] | ΛMEAN [1] | Δ [1] | σ [1] | Δ [1] | σ [1] | Δ [1] | σ [1] | Δ [1] | σ [1] | Δ [1] | σ [1] | Δ [1] | σ [1] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Altitude Class (m a.s.l.) | Basin | 68–163 | 163–195 | 195–228 | 228–302 | 302–1053 | |||||||||
| 1 | 6 July 1999 | 2.92 | 0.35 | 0.17 | 0.14 | 0.07 | 0.14 | 0.13 | 0.16 | 0.18 | 0.16 | 0.2 | 0.16 | 0.28 | 0.13 |
| 2 | 15 July 1999 | 3.21 | 0.58 | −0.06 | 0.10 | −0.07 | 0.11 | −0.07 | 0.12 | −0.06 | 0.12 | −0.06 | 0.12 | −0.04 | 0.09 |
| 3 | 7 August 1999 | 3.75 | 0.6 | −0.06 | 0.10 | −0.12 | 0.11 | −0.08 | 0.13 | −0.05 | 0.13 | −0.05 | 0.14 | 0.01 | 0.11 |
| 4 | 24 September 1999 | 1.11 | 0.5 | 0.04 | 0.10 | 0.03 | 0.11 | 0.06 | 0.11 | 0.06 | 0.12 | 0.05 | 0.11 | 0.02 | 0.1 |
| 5 | 18 March 2000 | 0.87 | 0.67 | −0.08 | 0.30 | 0.07 | 0.32 | −0.04 | 0.35 | −0.07 | 0.33 | −0.13 | 0.32 | −0.22 | 0.2 |
| 6 | 28 April 2000 | 0.73 | 0.22 | 0.28 | 0.31 | 0.18 | 0.3 | 0.27 | 0.27 | 0.3 | 0.26 | 0.34 | 0.23 | 0.32 | 0.22 |
| 7 | 14 May 2000 | 3.75 | 0.7 | −0.19 | 0.15 | −0.23 | 0.13 | −0.18 | 0.12 | −0.16 | 0.1 | −0.16 | 0.1 | −0.15 | 0.07 |
| 8 | 21 May 2000 | 2.17 | 0.46 | 0.01 | 0.26 | 0.04 | 0.19 | 0.06 | 0.21 | 0.0 | 0.2 | 0.01 | 0.2 | −0.06 | 0.18 |
| 9 | 6 June 2000 | 3.86 | 0.66 | −0.13 | 0.12 | −0.12 | 0.09 | −0.13 | 0.09 | −0.13 | 0.08 | −0.13 | 0.08 | −0.09 | 0.06 |
| 10 | 15 June 2000 | 4.15 | 0.67 | −0.16 | 0.16 | −0.15 | 0.13 | −0.16 | 0.12 | −0.15 | 0.11 | −0.15 | 0.13 | −0.13 | 0.11 |
| 11 | 2 August 2000 | 2.6 | 0.4 | 0.14 | 0.18 | 0.19 | 0.12 | 0.15 | 0.13 | 0.13 | 0.12 | 0.13 | 0.12 | 0.09 | 0.09 |
| 12 | 10 September 2000 | 1.77 | 0.5 | 0.04 | 0.24 | 0.14 | 0.17 | 0.05 | 0.18 | 0.01 | 0.17 | 0.02 | 0.19 | −0.04 | 0.18 |
| 13 | 6 April 2001 | 1.4 | 0.5 | 0.04 | 0.16 | 0.09 | 0.12 | 0.05 | 0.12 | 0.04 | 0.12 | 0.02 | 0.12 | 0.0 | 0.13 |
| 14 | 1 May 2001 | 2.15 | 0.43 | 0.10 | 0.17 | 0.06 | 0.15 | 0.12 | 0.13 | 0.12 | 0.12 | 0.12 | 0.11 | 0.11 | 0.08 |
| 15 | 24 May 2001 | 3.11 | 0.55 | −0.02 | 0.18 | −0.07 | 0.15 | 0.0 | 0.13 | 0.0 | 0.12 | 0.01 | 0.12 | −0.04 | 0.08 |
| 16 | 25 June 2001 | 3.82 | 0.67 | −0.16 | 0.17 | −0.24 | 0.18 | −0.19 | 0.13 | −0.18 | 0.11 | −0.15 | 0.1 | −0.13 | 0.09 |
| 17 | 12 August 2001 | 4.06 | 0.83 | −0.32 | 0.14 | −0.3 | 0.15 | −0.33 | 0.14 | −0.32 | 0.14 | −0.33 | 0.14 | −0.27 | 0.09 |
| 18 | 8 October 2001 | 0.77 | 0.35 | 0.17 | 0.12 | 0.17 | 0.1 | 0.17 | 0.1 | 0.19 | 0.09 | 0.19 | 0.09 | 0.18 | 0.08 |
| 19 | 12 June 2002 | 2.45 | 0.41 | 0.12 | 0.14 | 0.11 | 0.13 | 0.13 | 0.13 | 0.14 | 0.13 | 0.12 | 0.14 | 0.08 | 0.13 |
| 20 | 21 June 2002 | 3.41 | 0.52 | 0.00 | 0.17 | 0.02 | 0.16 | −0.01 | 0.13 | −0.01 | 0.12 | 0.0 | 0.13 | 0.01 | 0.1 |
| 21 | 24 August 2002 | 1.86 | 0.48 | 0.05 | 0.17 | 0.12 | 0.14 | 0.06 | 0.13 | 0.03 | 0.12 | 0.01 | 0.13 | 0.01 | 0.11 |
| 22 | 31 August 2002 | 2.48 | 0.58 | −0.07 | 0.14 | −0.04 | 0.16 | −0.08 | 0.1 | −0.09 | 0.09 | −0.08 | 0.08 | −0.07 | 0.06 |
| 23 | 20 March 2003 | 0.95 | 0.47 | 0.11 | 0.17 | 0.11 | 0.15 | 0.1 | 0.15 | 0.12 | 0.14 | 0.14 | 0.14 | 0.12 | 0.14 |
| 24 | 27 March 2003 | 0.52 | 0.12 | 0.42 | 0.15 | 0.39 | 0.09 | 0.42 | 0.11 | 0.44 | 0.11 | 0.45 | 0.11 | 0.41 | 0.16 |
| 25 | 7 May 2003 | 2.37 | 0.32 | 0.21 | 0.15 | 0.22 | 0.12 | 0.23 | 0.11 | 0.22 | 0.1 | 0.22 | 0.09 | 0.2 | 0.07 |
| 26 | 30 March 2003 | 3.37 | 0.53 | −0.01 | 0.20 | −0.02 | 0.18 | 0.02 | 0.15 | 0.0 | 0.13 | 0.0 | 0.14 | −0.05 | 0.12 |
| Avg | 2.45 | 0.5 | 0.02 | 0.17 | 0.02 | 0.15 | 0.03 | 0.14 | 0.03 | 0.14 | 0.03 | 0.14 | 0.02 | 0.11 | |
| Min | 0.52 | 0.12 | −0.32 | 0.10 | −0.3 | 0.09 | −0.33 | 0.09 | −0.32 | 0.08 | −0.33 | 0.08 | −0.27 | 0.06 | |
| Max | 4.15 | 0.83 | 0.42 | 0.31 | 0.39 | 0.32 | 0.42 | 0.35 | 0.44 | 0.33 | 0.45 | 0.32 | 0.41 | 0.22 | |
| Image No. | Acquisition Date | Δ [mm Day−1] | σ [mm Day−1] | NSE | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | HS | PM | M | PT | T | HS | PM | M | PT | T | HS | PM | M | PT | ||
| 1 * | 6 July 1999 | 0.39 | 0.28 | 1.08 | 0.38 | 0.58 | 1.08 | 0.98 | 1.22 | 1.08 | 1.09 | 0.3 | 0.11 | −0.8 | −0.03 | 0.11 |
| 2 * | 15 July 1999 | −0.25 | −0.72 | −0.61 | −0.17 | 0 | 0.6 | 0.55 | 0.57 | 0.62 | 0.63 | 0.1 | 0.54 | 0.24 | 0.56 | 0.53 |
| 3 * | 7 August 1999 | −0.54 | −0.96 | −0.46 | −0.55 | −0.42 | 0.74 | 0.61 | 0.76 | 0.74 | 0.75 | −0.42 | 0.05 | 0.11 | 0.17 | 0.07 |
| 4 * | 24 September 1999 | 0.83 | 0.41 | 0.29 | 0.81 | 0.51 | 0.31 | 0.29 | 0.26 | 0.31 | 0.27 | 0.07 | −1.82 | 0.42 | −0.24 | −1.94 |
| 5 * | 18 March 2000 | −0.97 | −0.16 | −0.12 | 0.17 | −0.07 | 0.85 | 0.51 | 0.5 | 0.47 | 0.49 | 0.15 | 0.26 | 0.22 | 0.29 | −3.88 |
| 6 | 28 April 2000 | 1.24 | 1.34 | 1.11 | 1.23 | 1.34 | 0.79 | 0.79 | 0.78 | 0.79 | 0.8 | −2.61 | −2.2 | −1.74 | −2.61 | −2.23 |
| 7 | 14 May 2000 | −1.01 | −1.17 | −1.23 | −0.83 | −0.89 | 0.6 | 0.62 | 0.59 | 0.61 | 0.61 | −0.76 | −0.08 | −0.87 | −0.17 | −0.38 |
| 8 | 21 May 2000 | −0.11 | 0.16 | −0.22 | 0.12 | 0.19 | 0.92 | 0.93 | 0.91 | 0.85 | 0.84 | 0.57 | 0.64 | 0.57 | 0.63 | 0.58 |
| 9 | 6 June 2000 | −0.66 | −0.76 | −0.99 | −0.63 | −0.41 | 0.47 | 0.44 | 0.44 | 0.49 | 0.52 | 0.11 | 0.28 | −0.33 | 0.49 | 0.24 |
| 10 | 15 June 2000 | −0.79 | −1.24 | −1.16 | −0.75 | −0.51 | 0.77 | 0.76 | 0.75 | 0.78 | 0.8 | −0.41 | 0.22 | −0.26 | 0.39 | 0.18 |
| 11 | 2 August 2000 | 0.63 | 0.3 | 0.36 | 0.66 | 0.71 | 0.85 | 1.04 | 0.87 | 0.84 | 0.87 | 0.55 | 0.57 | 0.66 | 0.52 | 0.57 |
| 12 | 10 September 2000 | 0.2 | 0 | −0.14 | 0.26 | −0.05 | 0.68 | 0.8 | 0.74 | 0.65 | 0.72 | 0.5 | 0.61 | 0.55 | 0.59 | 0.61 |
| 13 | 6 April 2001 | −0.1 | 0 | −0.11 | 0.2 | 0.02 | 0.43 | 0.42 | 0.39 | 0.36 | 0.38 | 0.59 | 0.59 | 0.6 | 0.65 | 0.54 |
| 14 | 1 May 2001 | 0.44 | 0.39 | 0.21 | 0.46 | 0.47 | 0.61 | 0.68 | 0.62 | 0.6 | 0.61 | 0.48 | 0.51 | 0.63 | 0.49 | 0.52 |
| 15 | 24 May 2001 | −0.16 | −0.52 | −0.48 | −0.01 | −0.03 | 0.74 | 0.83 | 0.78 | 0.72 | 0.72 | 0.48 | 0.72 | 0.55 | 0.72 | 0.69 |
| 16 | 25 June 2001 | −0.59 | −1.02 | −0.91 | −0.53 | −0.33 | 0.73 | 0.67 | 0.69 | 0.75 | 0.77 | −0.48 | 0.16 | −0.31 | 0.29 | 0.12 |
| 17 | 12 August 2001 | −1.52 | −2.1 | −1.68 | −1.38 | −1.47 | 0.59 | 0.52 | 0.55 | 0.63 | 0.62 | −6.14 | −2.52 | −3.78 | −2−.91 | −3.06 |
| 18 | 8 October 2001 | 0.72 | 0.37 | 0.22 | 0.67 | 0.31 | 0.23 | 0.22 | 0.2 | 0.22 | 0.2 | −0.18 | −2.03 | 0.43 | 0.14 | −2.55 |
| 19 | 12 June 2002 | 0.94 | 0.41 | 0.76 | 1 | 0.87 | 0.84 | 0.81 | 0.81 | 0.84 | 0.87 | 0.35 | −0.34 | 0.05 | −0.78 | −0.23 |
| 20 | 21 June 2002 | 0.01 | −0.14 | −0.15 | 0 | 0.38 | 0.79 | 0.87 | 0.81 | 0.79 | 0.79 | 0.62 | 0.69 | 0.67 | 0.62 | 0.69 |
| 21 | 24 August 2002 | 0.47 | 0.04 | −0.01 | 0.46 | 0.53 | 0.48 | 0.54 | 0.52 | 0.48 | 0.48 | 0.6 | 0.39 | 0.62 | 0.29 | 0.37 |
| 22 | 31 August 2002 | −0.27 | −0.76 | −0.56 | −0.29 | −0.34 | 0.43 | 0.44 | 0.43 | 0.43 | 0.43 | −0.08 | 0.63 | 0.3 | 0.58 | 0.64 |
| 23 | 20 March 2003 | −0.07 | 0.16 | 0.06 | 0.36 | 0.05 | 0.41 | 0.4 | 0.35 | 0.33 | 0.35 | 0.26 | 0.03 | 0.49 | 0.5 | 0.3 |
| 24 | 27 March 2003 | 1.03 | 0.97 | 1.59 | 1.19 | 0.77 | 0.52 | 0.58 | 0.5 | 0.5 | 0.53 | −1.16 | −1.81 | −3.64 | −0.49 | −1.27 |
| 25 | 7 May 2003 | 0.78 | 0.85 | 1.05 | 0.78 | 0.67 | 0.82 | 0.99 | 0.79 | 0.81 | 0.85 | 0.29 | 0.47 | 0.28 | 0.51 | 0.46 |
| 26 | 30 May 2003 | −0.19 | −0.99 | −0.54 | −0.14 | 0.02 | 0.96 | 1.06 | 1.01 | 0.95 | 0.94 | 0.14 | 0.62 | 0.47 | 0.64 | 0.61 |
| Avg (only *) | −0.11 | −0.23 | 0.04 | 0.13 | 0.12 | 0.72 | 0.59 | 0.66 | 0.64 | 0.65 | 0.04 | −0.17 | 0.04 | 0.15 | −1.02 | |
| Min (only *) | −0.97 | −0.96 | −0.61 | −0.55 | −0.42 | 0.31 | 0.29 | 0.26 | 0.31 | 0.27 | −0.42 | −1.82 | −0.80 | −0.24 | −3.88 | |
| Max (only *) | 0.83 | 0.41 | 1.08 | 0.81 | 0.58 | 1.08 | 0.98 | 1.22 | 1.08 | 1.09 | 0.30 | 0.54 | 0.42 | 0.56 | 0.53 | |
| Avg | 0.02 | −0.19 | −0.10 | 0.13 | 0.11 | 0.66 | 0.67 | 0.65 | 0.64 | 0.65 | −0.23 | −0.10 | −0.15 | 0.07 | −0.30 | |
| Min | −1.52 | −2.10 | −1.68 | −1.38 | −1.47 | 0.23 | 0.22 | 0.20 | 0.22 | 0.20 | −6.14 | −2.52 | −3.78 | −2.91 | −3.88 | |
| Max | 1.24 | 1.34 | 1.59 | 1.23 | 1.34 | 1.08 | 1.06 | 1.22 | 1.08 | 1.09 | 0.62 | 0.72 | 0.67 | 0.72 | 0.69 | |
| Image No. | Acquisition Date | Δ [mm Day−1] | σ [mm Day−1] | NSE |
|---|---|---|---|---|
| 6 | 28 April 2000 | 1.23 | 0.79 | −2.61 |
| 7 | 14 May 2000 | −0.83 | 0.61 | −0.17 |
| 8 | 21 May 2000 | 0.12 | 0.85 | 0.63 |
| 9 | 6 June 2000 | −0.63 | 0.49 | 0.49 |
| 10 | 15 June 2000 | −0.75 | 0.78 | 0.39 |
| 11 | 2 August 2000 | 0.66 | 0.84 | 0.52 |
| 12 | 10 September 2000 | 0.26 | 0.65 | 0.59 |
| 13 | 6 April 2001 | 0.2 | 0.36 | 0.65 |
| 14 | 1 May 2001 | 0.46 | 0.6 | 0.49 |
| 15 | 24 May 2001 | −0.01 | 0.72 | 0.72 |
| 16 | 25 June 2001 | −0.53 | 0.75 | 0.29 |
| 17 | 12 August 2001 | −1.38 | 0.63 | −2.91 |
| 18 | 8 October 2001 | 0.67 | 0.22 | 0.14 |
| 19 | 12 June 2002 | 1 | 0.84 | −0.78 |
| 20 | 21 June 2002 | 0 | 0.79 | 0.62 |
| 21 | 24 August 2002 | 0.46 | 0.48 | 0.29 |
| 22 | 31 August 2002 | −0.29 | 0.43 | 0.58 |
| 23 | 20 March 2003 | 0.36 | 0.33 | 0.5 |
| 24 | 27 March 2003 | 1.19 | 0.5 | −0.49 |
| 25 | 7 May 2003 | 0.78 | 0.81 | 0.51 |
| 26 | 30 May 2003 | −0.14 | 0.95 | 0.64 |
| Avg | 0.13 | 0.64 | 0.05 | |
| Min | −1.38 | 0.22 | −2.91 | |
| Max | 1.23 | 0.98 | 0.72 | |
| Image No. | Acquisition Date | Δ [mm Day−1] | σ [mm Day−1] | NSE | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | HS | PM | M | PT | T | HS | PM | M | PT | T | HS | PM | M | PT | ||
| 1 | 6 July 1999 | 3.22 | 3.16 | 4.47 | 3.19 | 3.58 | 1.10 | 1.40 | 1.06 | 1.09 | 1.13 | −7.00 | −6.62 | −13.11 | −8.42 | −6.76 |
| 2 | 15 July 1999 | 2.30 | 1.49 | 1.61 | 2.42 | 2.77 | 0.91 | 1.08 | 0.86 | 0.86 | 0.90 | −2.65 | −6.14 | −2.62 | −8.16 | −5.61 |
| 3 | 7 August 1999 | 2.17 | 1.49 | 2.28 | 2.15 | 2.39 | 0.80 | 1.03 | 0.79 | 0.78 | 0.80 | −2.63 | −4.74 | −5.40 | −5.98 | −4.88 |
| 4 | 24 September 1999 | 2.49 | 1.77 | 1.50 | 2.45 | 1.89 | 0.52 | 0.71 | 0.55 | 0.50 | 0.50 | −12.37 | −21.92 | −8.41 | −12.99 | −22.86 |
| 5 | 18 March 2000 | −0.88 | 0.48 | 0.53 | 1.09 | 0.62 | 1.07 | 0.70 | 0.66 | 0.65 | 0.63 | −1.12 | −3.76 | −1.10 | −1.30 | −4.59 |
| 6 | 28 April 2000 | 3.03 | 3.28 | 2.80 | 2.99 | 3.19 | 0.93 | 1.08 | 1.00 | 0.91 | 0.91 | −16.68 | −13.53 | −12.14 | −15.30 | −13.88 |
| 7 | 14 May 2000 | 1.36 | 1.14 | 0.94 | 1.67 | 1.57 | 1.02 | 1.25 | 0.98 | 0.97 | 0.99 | −1.88 | −2.72 | −0.85 | −2.45 | −1.91 |
| 8 | 21 May 2000 | 1.75 | 2.33 | 1.51 | 2.18 | 2.32 | 1.46 | 1.62 | 1.38 | 1.40 | 1.41 | −2.92 | −2.25 | −1.04 | −2.58 | −1.53 |
| 9 | 6 June 2000 | 2.05 | 1.95 | 1.48 | 2.11 | 2.51 | 0.94 | 1.19 | 1.01 | 0.90 | 0.91 | −4.91 | −4.96 | −2.62 | −7.03 | −4.78 |
| 10 | 15 June 2000 | 2.20 | 1.47 | 1.54 | 2.27 | 2.71 | 1.15 | 1.47 | 1.23 | 1.12 | 1.12 | −1.87 | −3.26 | −1.60 | −4.70 | −3.10 |
| 11 | 2 August 2000 | 3.39 | 2.87 | 2.85 | 3.42 | 3.55 | 1.66 | 1.98 | 1.57 | 1.63 | 1.74 | −3.59 | −4.41 | −2.99 | −4.91 | −4.37 |
| 12 | 10 September 2000 | 1.96 | 1.64 | 1.31 | 2.07 | 1.48 | 1.19 | 1.38 | 1.17 | 1.16 | 1.16 | −2.60 | −3.41 | −1.41 | −1.77 | −3.12 |
| 13 | 6 April 2001 | 1.07 | 1.26 | 0.99 | 1.62 | 1.28 | 0.80 | 0.81 | 0.68 | 0.70 | 0.71 | −4.23 | −6.18 | −2.36 | −3.95 | −3.12 |
| 14 | 1 May 2001 | 2.65 | 2.66 | 2.22 | 2.67 | 2.71 | 1.08 | 1.38 | 1.08 | 1.05 | 1.07 | −6.61 | −5.95 | −4.16 | −6.17 | −5.93 |
| 15 | 24 May 2001 | 2.35 | 1.76 | 1.77 | 2.62 | 2.70 | 1.38 | 1.56 | 1.39 | 1.32 | 1.32 | −1.97 | −3.63 | −1.72 | −3.85 | −3.00 |
| 16 | 25 June 2001 | 2.35 | 1.61 | 1.75 | 2.45 | 2.84 | 1.00 | 1.20 | 1.03 | 0.97 | 0.99 | −3.00 | −5.90 | −3.11 | −7.94 | −5.47 |
| 17 | 12 August 2001 | 0.68 | −0.36 | 0.41 | 0.92 | 0.74 | 0.77 | 0.82 | 0.85 | 0.71 | 0.70 | −0.23 | −1.08 | −0.38 | −0.60 | −0.63 |
| 18 | 8 October 2001 | 2.00 | 1.40 | 1.08 | 1.89 | 1.24 | 0.42 | 0.56 | 0.42 | 0.40 | 0.39 | −12.90 | −21.64 | −7.19 | −9.34 | −24.49 |
| 19 | 12 June 2002 | 3.94 | 3.06 | 3.64 | 4.05 | 4.50 | 1.15 | 1.44 | 1.26 | 1.12 | 1.13 | −7.86 | −12.64 | −10.50 | −15.66 | −12.02 |
| 20 | 21 June 2002 | 2.96 | 2.81 | 2.70 | 2.93 | 3.67 | 1.41 | 1.81 | 1.50 | 1.39 | 1.42 | −4.46 | −4.15 | −3.66 | −6.56 | −4.25 |
| 21 | 24 August 2002 | 2.53 | 1.78 | 1.63 | 2.49 | 2.64 | 0.91 | 1.05 | 0.97 | 0.88 | 0.87 | −4.79 | −8.50 | −3.89 | −9.47 | −8.83 |
| 22 | 31 August 2002 | 1.61 | 0.72 | 1.10 | 1.58 | 1.48 | 0.78 | 0.81 | 0.82 | 0.76 | 0.76 | −0.62 | −3.24 | −1.60 | −2.85 | −3.44 |
| 23 | 20 March 2003 | 0.71 | 1.18 | 0.93 | 1.50 | 0.91 | 0.67 | 0.74 | 0.56 | 0.56 | 0.55 | −6.76 | −9.18 | −3.74 | −3.52 | −2.81 |
| 24 | 27 March 2003 | 2.36 | 2.29 | 3.35 | 2.64 | 1.87 | 0.81 | 0.95 | 0.71 | 0.77 | 0.78 | −9.29 | −11.67 | −18.59 | −5.91 | −9.49 |
| 25 | 7 May 2003 | 3.47 | 3.75 | 3.96 | 3.46 | 3.27 | 1.56 | 2.06 | 1.57 | 1.53 | 1.62 | −6.57 | −4.94 | −6.52 | −4.53 | −5.00 |
| 26 | 30 May 2003 | 2.63 | 1.15 | 2.01 | 2.71 | 2.04 | 1.57 | 1.63 | 1.65 | 1.53 | 1.53 | −0.61 | −2.91 | −1.72 | −3.67 | −2.79 |
| Avg | 2.17 | 1.85 | 1.94 | 2.37 | 2.33 | 1.04 | 1.22 | 1.03 | 0.99 | 1.00 | −5.00 | −6.90 | −4.71 | −6.14 | −6.49 | |
| Min | −0.88 | −0.36 | 0.41 | 0.92 | 0.62 | 0.42 | 0.56 | 0.42 | 0.40 | 0.39 | −16.68 | −21.92 | −18.59 | −15.66 | −24.49 | |
| Max | 3.94 | 3.75 | 4.47 | 4.05 | 4.50 | 1.66 | 2.06 | 1.65 | 1.63 | 1.74 | −0.23 | −1.08 | −0.38 | −0.60 | −0.63 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivezic, V.; Bekic, D.; Horvat, B. Modelling of Basin Wide Daily Evapotranspiration with a Partial Integration of Remote Sensing Data. Atmosphere 2018, 9, 120. https://doi.org/10.3390/atmos9040120
Ivezic V, Bekic D, Horvat B. Modelling of Basin Wide Daily Evapotranspiration with a Partial Integration of Remote Sensing Data. Atmosphere. 2018; 9(4):120. https://doi.org/10.3390/atmos9040120
Chicago/Turabian StyleIvezic, Vedran, Damir Bekic, and Bojana Horvat. 2018. "Modelling of Basin Wide Daily Evapotranspiration with a Partial Integration of Remote Sensing Data" Atmosphere 9, no. 4: 120. https://doi.org/10.3390/atmos9040120
APA StyleIvezic, V., Bekic, D., & Horvat, B. (2018). Modelling of Basin Wide Daily Evapotranspiration with a Partial Integration of Remote Sensing Data. Atmosphere, 9(4), 120. https://doi.org/10.3390/atmos9040120




