Hazardous Source Estimation Using an Artificial Neural Network, Particle Swarm Optimization and a Simulated Annealing Algorithm
Abstract
:1. Introduction
2. Models and Methods
2.1. Structure of ANN
2.2. Solution Algorithm
| Algorithm 1. Hybrid algorithm of PSO and SA |
|
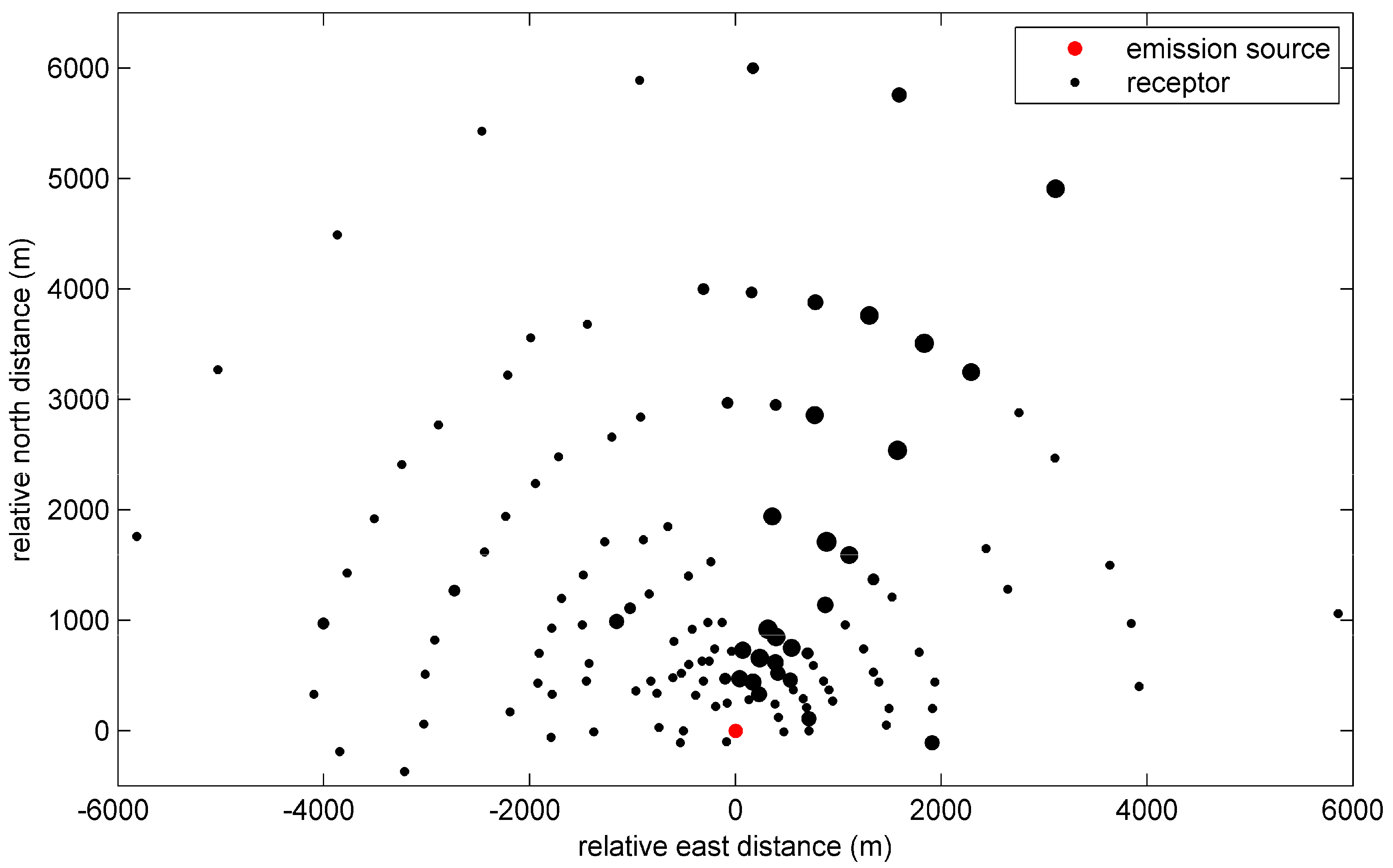
3. Numerical Case Study
- Define a number of leak scenarios in PHAST, and extract training data and test data from these scenarios.
- Train the ANN and adjust the neuron numbers of two hidden layers according to the performance. Test the performance of the trained ANN on the test data.
- Define scenarios and generate receptor data for the source estimation.
- Apply the proposed hybrid algorithm with an ANN to the source estimation and compare its performance with another two algorithms mentioned above.
- Analyze the influence of receptor configuration and measurement noise on estimation result.
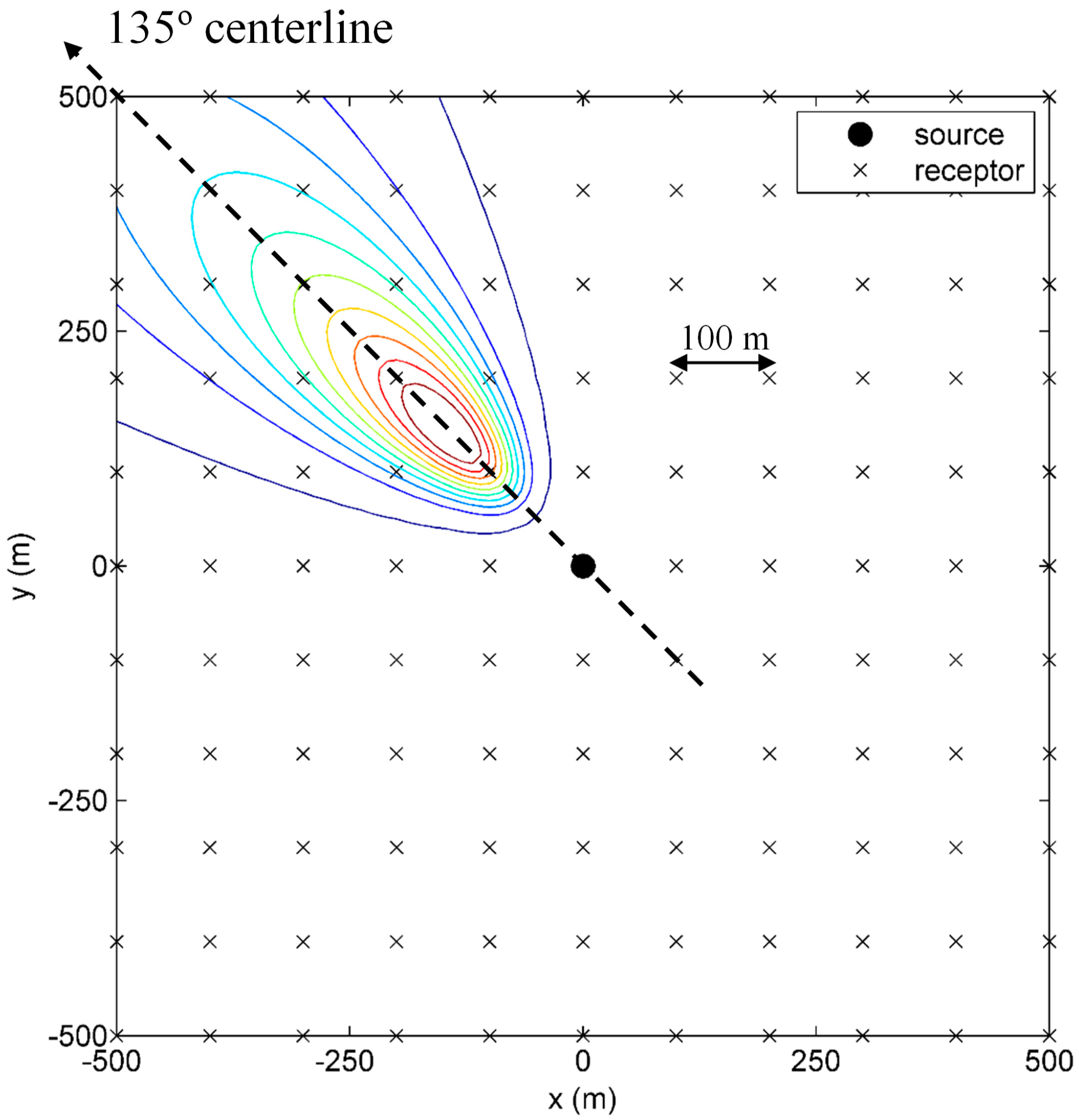
3.1. Synthetic Scenario
- A set of downwind and crosswind distance of the target points from the release point: and , where is the number of receptors;
- The gas concentration at targets points (i.e., receptor data): ;
- The wind direction (), speed (), and atmospheric stability class ();
- The source location () and strength ().
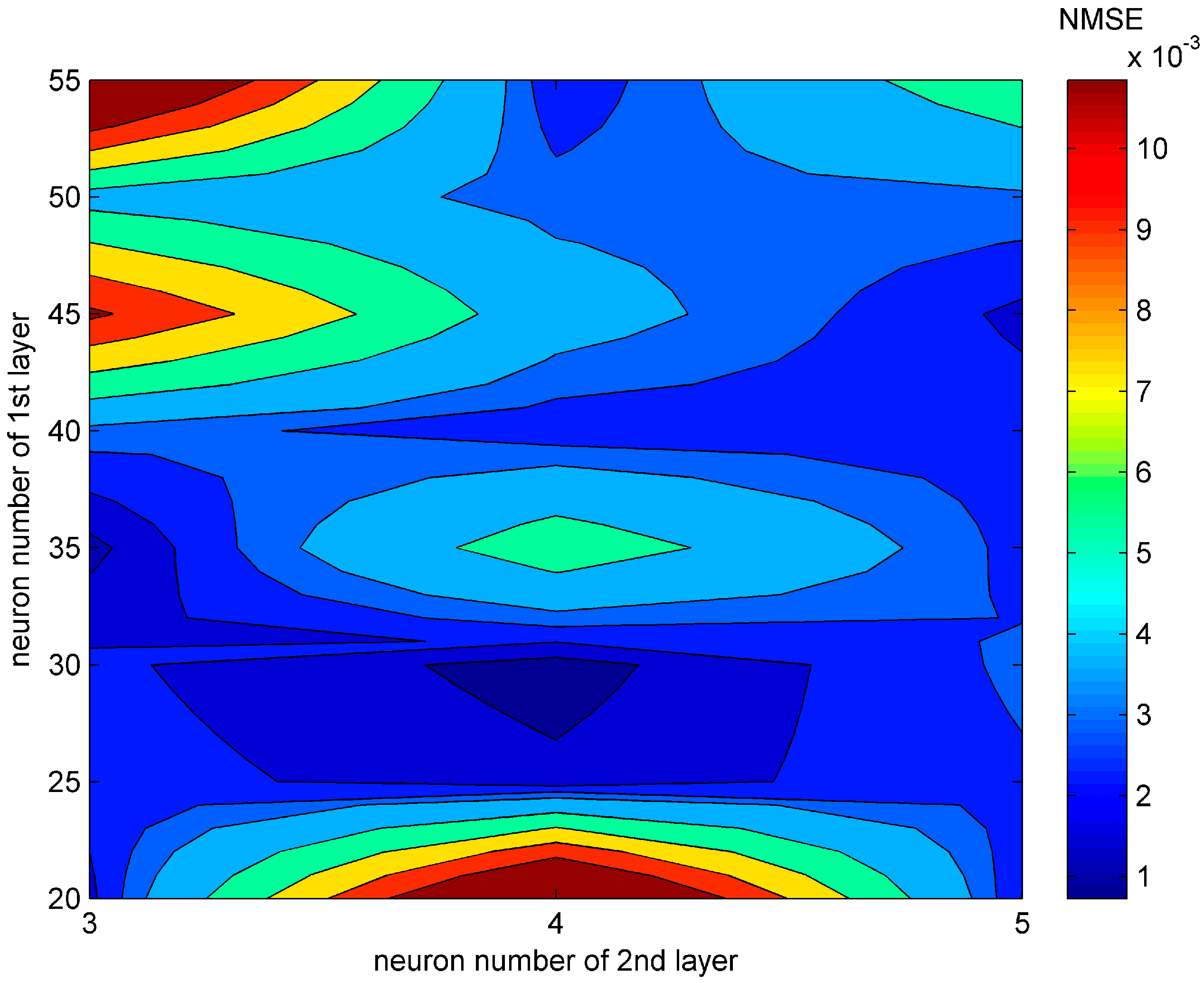
3.2. Configurations of the Artificial Neural Network and Optimization Algorithms
3.3. Skill Score
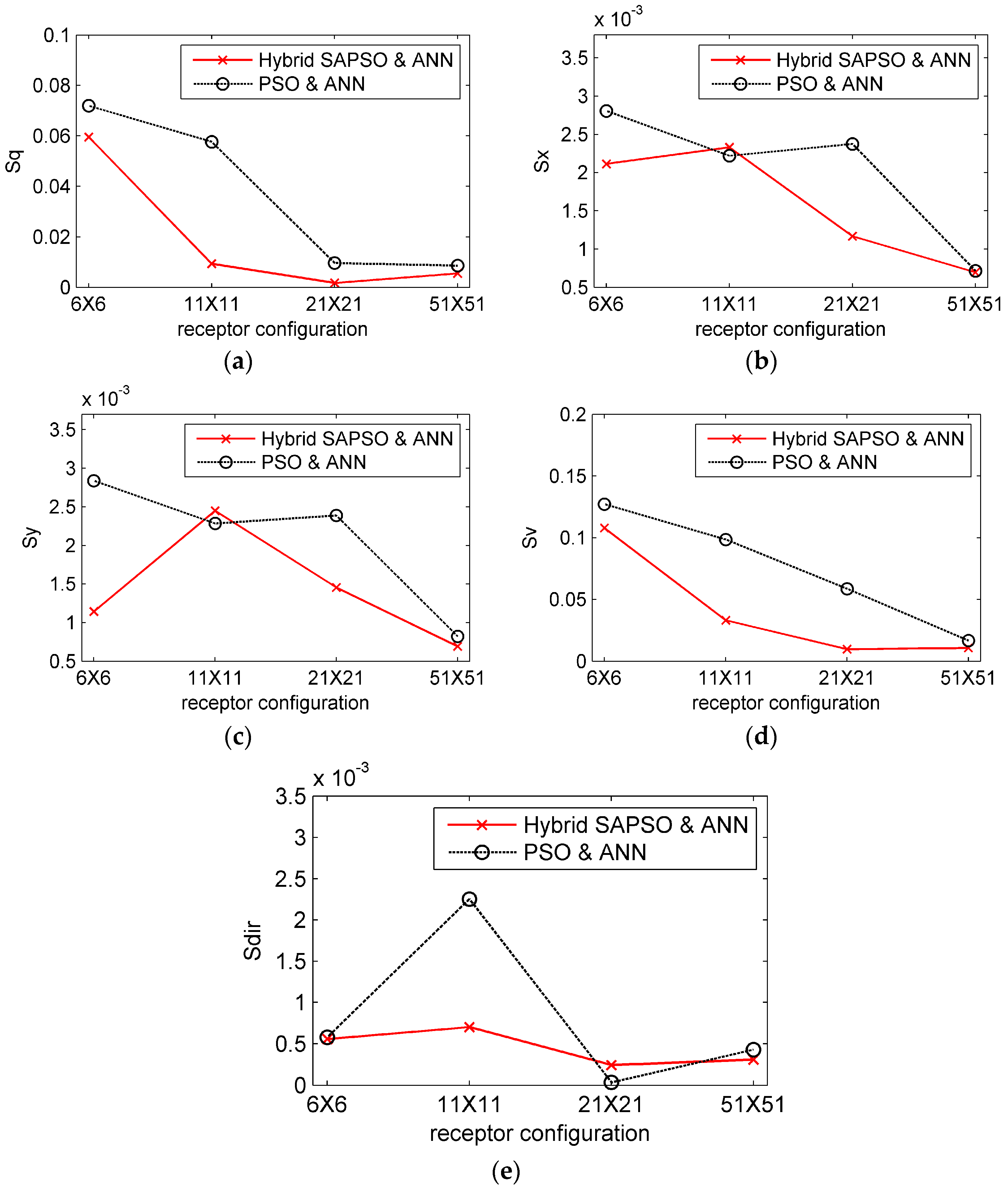
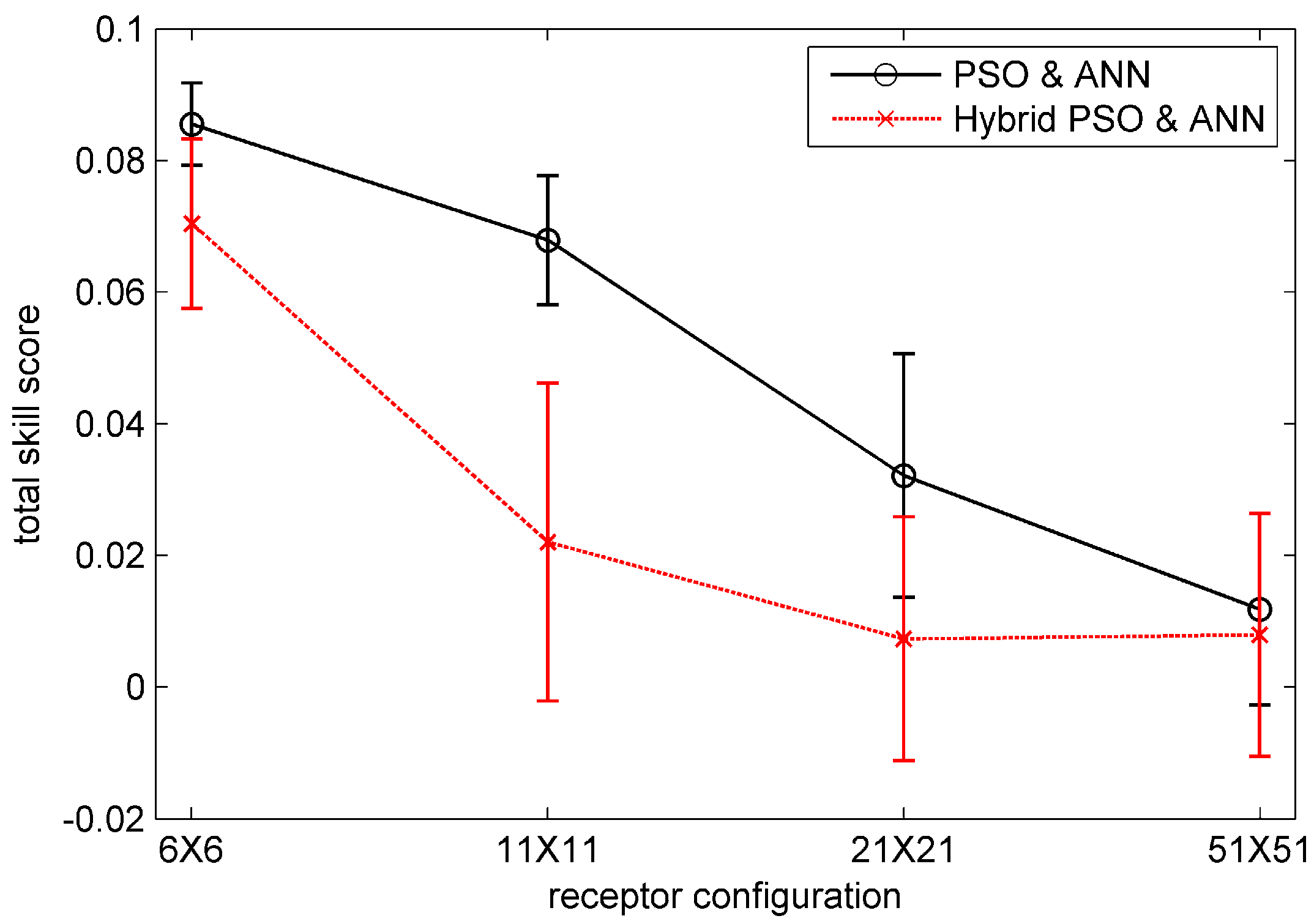
3.4. Results and Analysis
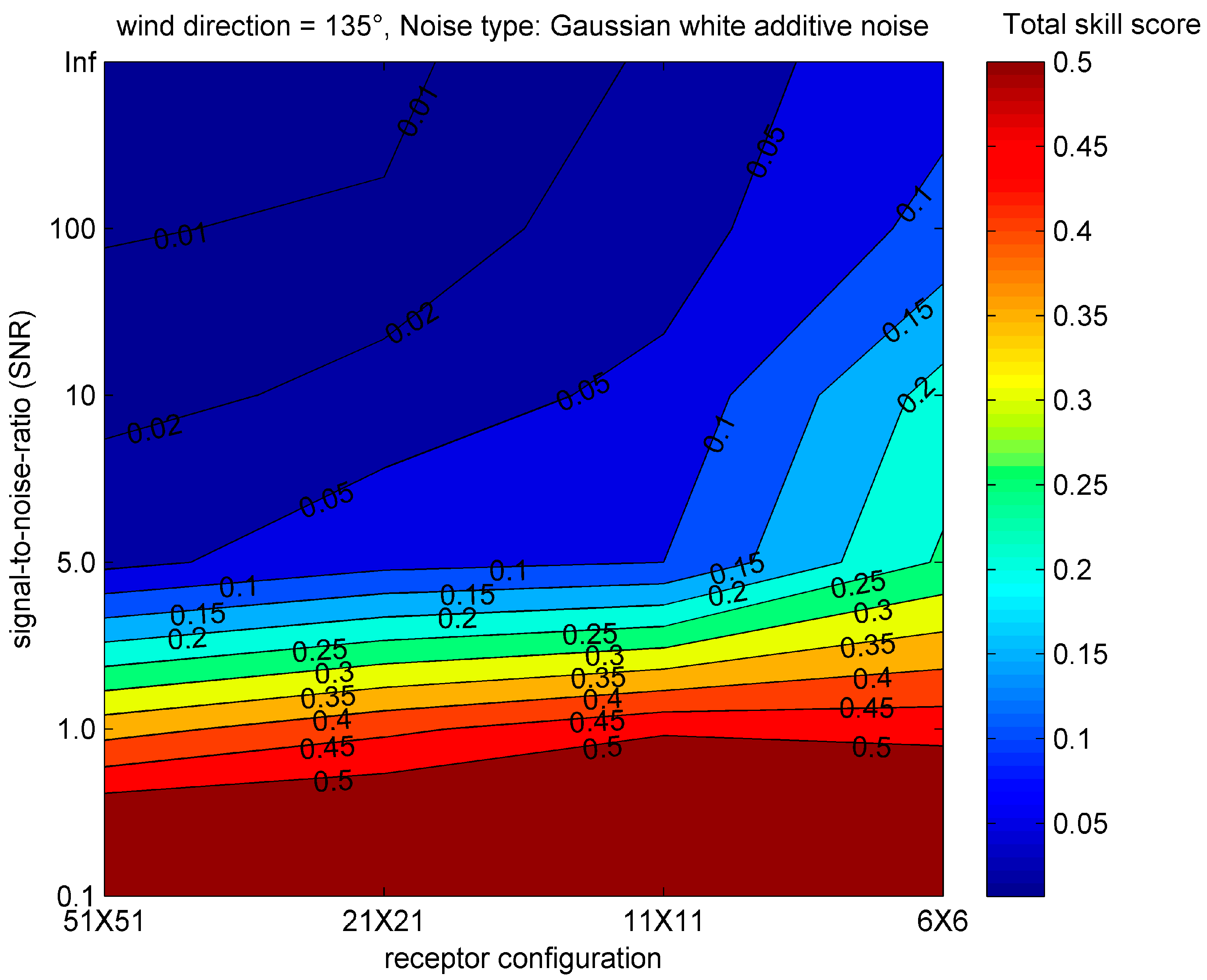
3.5. The Influence of Noisy Observation
4. Indianapolis Field Study
4.1. Introduction of the Indianapolis Tracer Experiment
4.2. Configurations of the Artificial Neural Network and the Solution Algorithm
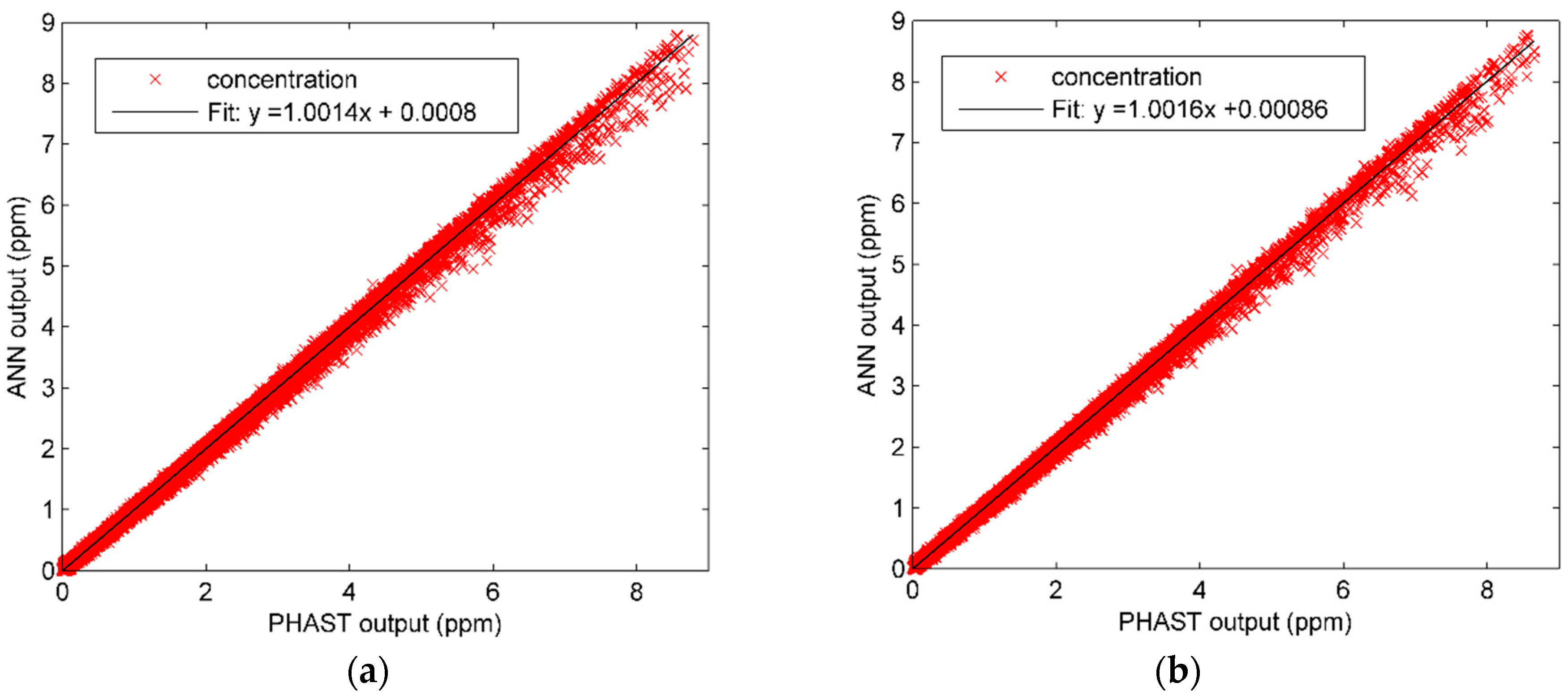
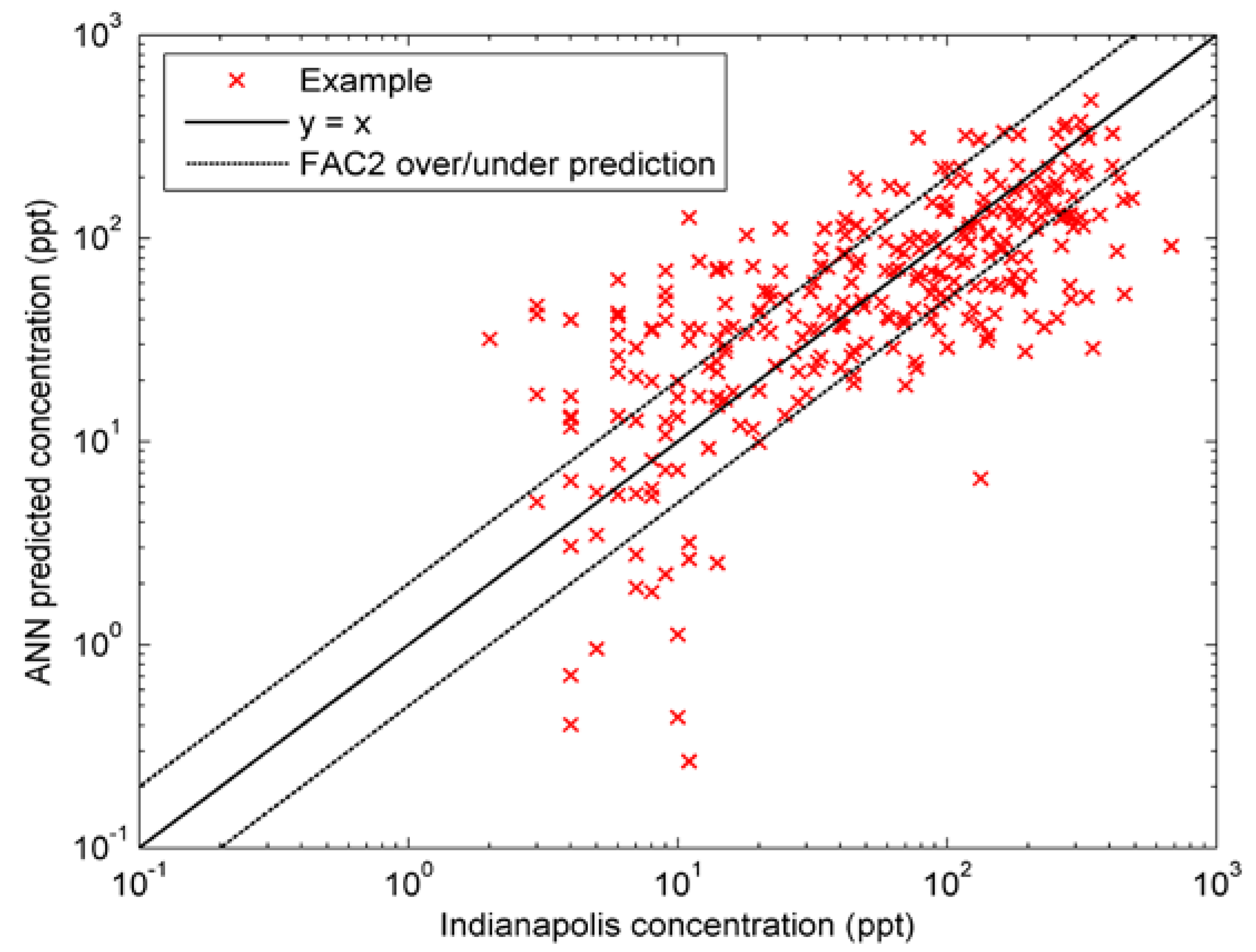
4.3. Results and Analysis
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhu, Z.; Chen, B.; Reniers, G.; Zhang, L.; Qiu, S.; Qiu, X. Playing chemical plant environmental protection games with historical monitoring data. Int. J. Environ. Res. Public Health 2017, 14, 1155. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Zhang, L.; Guo, G.; Qiu, X. KD-ACP: A software framework for social computing in emergency management. Math. Probl. Eng. 2015, 2015, 27. [Google Scholar] [CrossRef]
- Hutchinson, M.; Oh, H.; Chen, W.-H. A review of source term estimation methods for atmospheric dispersion events using static or mobile sensors. Inf. Fusion 2017, 36, 130–148. [Google Scholar] [CrossRef]
- Wang, R.; Chen, B.; Qiu, S.; Zhu, Z.; Qiu, X. Data assimilation in air contaminant dispersion using a particle filter and expectation-maximization algorithm. Atmosphere 2017, 8, 170. [Google Scholar] [CrossRef]
- Briggs, G.A. Diffusion Estimation for Small Emissions. Preliminary Report; Atmospheric Turbulence and Diffusion Laboratory; NOAA: Silver Spring, MD, USA, 1973.
- Hanna, S.R.; Briggs, G.A.; Hosker, R.P.; Smith, J.S.; United States. Department of Energy. Office of Energy Research; United States. Department of Energy. Office of Health and Environmental Research. Handbook on Atmospheric Diffusion; U.S. Department of Energy: Washington, DC, USA, 1982; p. 102.
- Flesch, T.K.; Wilson, J.D.; Yee, E. Backward-time lagrangian stochastic dipsersion models and their application to estimate gaseous emissions. J. Appl. Meteorol. 1995, 34, 1320–1332. [Google Scholar] [CrossRef]
- Wilson, J.D.; Sawford, B.L. Review of lagrangian stochastic models for trajectories in the turbulent atmosphere. Bound. Layer Meteorol. 1996, 78, 191–210. [Google Scholar] [CrossRef]
- Pontiggia, M.; Derudi, M.; Busini, V.; Rota, R. Hazardous gas dispersion: A CFD model accounting for atmospheric stability classes. J. Hazard. Mater. 2009, 171, 739–747. [Google Scholar] [CrossRef] [PubMed]
- Xing, J.; Liu, Z.; Huang, P.; Feng, C.; Zhou, Y.; Zhang, D.; Wang, F. Experimental and numerical study of the dispersion of carbon dioxide plume. J. Hazard. Mater. 2013, 256–257, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Bieringer, P.E.; Rodriguez, L.M.; Vandenberghe, F.; Hurst, J.G.; Bieberbach, G.; Sykes, I.; Hannan, J.R.; Zaragoza, J.; Fry, R.N. Automated source term and wind parameter estimation for atmospheric transport and dispersion applications. Atmos. Environ. 2015, 122, 206–219. [Google Scholar] [CrossRef]
- Pelliccioni, A.; Tirabassi, T. Air dispersion model and neural network: A new perspective for integrated models in the simulation of complex situations. Environ. Model. Softw. 2006, 21, 539–546. [Google Scholar] [CrossRef]
- Podnar, D.; Koračin, D.; Panorska, A. Application of artificial neural networks to modeling the transport and dispersion of tracers in complex terrain. Atmos. Environ. 2002, 36, 561–570. [Google Scholar] [CrossRef]
- Boznar, M.; Lesjak, M.; Mlakar, P. A neural network-based method for short-term predictions of ambient SO2 concentrations in highly polluted industrial areas of complex terrain. Atmos. Environ. Part B Urban Atmos. 1993, 27, 221–230. [Google Scholar] [CrossRef]
- Bing, W.; Bingzhen, C.; Jinsong, Z. The real-time estimation of hazardous gas dispersion by the integration of gas detectors, neural network and gas dispersion models. J. Hazard. Mater. 2015, 300, 433–442. [Google Scholar]
- Ma, D.; Zhang, Z. Contaminant dispersion prediction and source estimation with integrated gaussian-machine learning network model for point source emission in atmosphere. J. Hazard. Mater. 2016, 311, 237–245. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Chen, B.; Wang, R.; Zhu, Z.; Wang, Y.; Qiu, X. Estimating contaminant source in chemical industry park using UAV-based monitoring platform, artificial neural network and atmospheric dispersion simulation. RSC Adv. 2017, 7, 39726–39738. [Google Scholar] [CrossRef]
- Qiu, S.; Chen, B.; Wang, R.; Zhu, Z.; Wang, Y.; Qiu, X. Atmospheric dispersion prediction and source estimation of hazardous gas using artificial neural network, particle swarm optimization and expectation maximization. Atmos. Environ. 2018, 178, 158–163. [Google Scholar] [CrossRef]
- Johannesson, G.; Hanley, B.; Nitao, J. Dynamic Bayesian Models via Monte Carlo—An Introduction with Examples; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2004. [Google Scholar]
- Keats, A.; Yee, E.; Lien, F.S. Bayesian inference for source determination with applications to a complex urban environment. Atmos. Environ. 2007, 41, 465–479. [Google Scholar] [CrossRef]
- Wawrzynczak, A.; Kopka, P.; Borysiewicz, M. Sequential monte carlo in bayesian assessment of contaminant source localization based on the sensors concentration measurements. In Parallel Processing and Applied Mathematics, Revised Selected Papers, Part II, Proceedings of the 10th International Conference, PPAM 2013, Warsaw, Poland, 8–11 September 2013; Wyrzykowski, R., Dongarra, J., Karczewski, K., Waśniewski, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 407–417. [Google Scholar]
- Zheng, X.; Chen, Z. Back-calculation of the strength and location of hazardous materials releases using the pattern search method. J. Hazard. Mater. 2010, 183, 474–481. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Ma, D.; Deng, J.; Zhang, Z. Comparison and improvements of optimization methods for gas emission source identification. Atmos. Environ. 2013, 81, 188–198. [Google Scholar] [CrossRef]
- Qiu, S.; Chen, B.; Zhu, Z.; Wang, Y.; Qiu, X. Source term estimation using air concentration measurements during nuclear accident. J. Radioanal. Nucl. Ch. 2017, 311, 165–178. [Google Scholar] [CrossRef]
- Thomson, L.C.; Hirst, B.; Gibson, G.; Gillespie, S.; Jonathan, P.; Skeldon, K.D.; Padgett, M.J. An improved algorithm for locating a gas source using inverse methods. Atmos. Environ. 2007, 41, 1128–1134. [Google Scholar] [CrossRef]
- Allen, C.T.; Young, G.S.; Haupt, S.E. Improving pollutant source characterization by better estimating wind direction with a genetic algorithm. Atmos. Environ. 2007, 41, 2283–2289. [Google Scholar] [CrossRef]
- Allen, C.T.; Haupt, S.E.; Young, G.S. Source characterization with a genetic algorithm coupled dispersion backward model incorporating scipuff. J. Appl. Meteorol. Climatol. 2007, 46, 273–287. [Google Scholar] [CrossRef]
- Long, K.J.; Haupt, S.E.; Young, G.S. Assessing sensitivity of source term estimation. Atmos. Environ. 2010, 44, 1558–1567. [Google Scholar] [CrossRef]
- Haupt, S.E.; Young, G.S.; Allen, C.T. A genetic algorithm method to assimilate sensor data for a toxic contaminant release. J. Comput. 2007, 2, 85–93. [Google Scholar] [CrossRef]
- Carrascal, M.D.; Puigcerver, M.; Puig, P. Sensitivity of gaussian plume model to dispersion specifications. Theor. Appl. Climatol. 1993, 48, 147–157. [Google Scholar] [CrossRef]
- Vogt, K.J. Empirical investigations of the diffusion of waste air plumes in the atmosphere. Nucl. Technol. 1977, 34, 43–57. [Google Scholar] [CrossRef]
- Steven Hanna, J.C.; Olesen, H.R. Indianapolis Tracer Data and Meteorological Data; National Environmental Research Institute: Roskilde, Denmark, 2005. [Google Scholar]
- Phast. Available online: https://www.dnvgl.com/services/process-hazard-analysis-software-phast-1675 (accessed on 29 December 2017).
- Henk, W.M.; Witloxa, M.H.; Pitbladob, R. Validation of phast dispersion model as required for USA lng siting applications. Chem. Eng. Trans. 2013, 31, 49–54. [Google Scholar]
- Li, X. A comparison between information transfer function sigmoid and tanh on neural. J. Wuhan Univ. Technol. 2004, 28, 312–314. [Google Scholar]
- Lauret, P.; Heymes, F.; Aprin, L.; Johannet, A. Atmospheric dispersion modeling using artificial neural network based cellular automata. Environ. Model. Softw. 2016, 85, 56–69. [Google Scholar] [CrossRef]
- Chang, J.C.; Hanna, S.R. Air quality model performance evaluation. Meteorol. Atmos. Phys. 2004, 87, 167–196. [Google Scholar] [CrossRef]
- Hajek, B. Cooling schedules for optimal annealing. Math. Oper. Res. 1988, 13, 311–329. [Google Scholar] [CrossRef]
- Cimorelli, A.J.; Perry, S.G.; Lee, R.F.; Paine, R.J.; Venkatram, A.; Weil, J.C.; Wilson, R.B. Aermod Description of Model Formulation Version; EPA: Washington, DC, USA, 1998.
- Scire, J.S.; Strimaitis, D.G.; Yamartino, R. A User’s Guide for the Calpuff Dispersion Model; Earth Tech, Inc.: Somerset, PA, USA, 2000. [Google Scholar]
- TRC Environmental Consultants. Urban Power Plant Plume Studies; EPRI: Palo Alto, CA, USA, 1986. [Google Scholar]
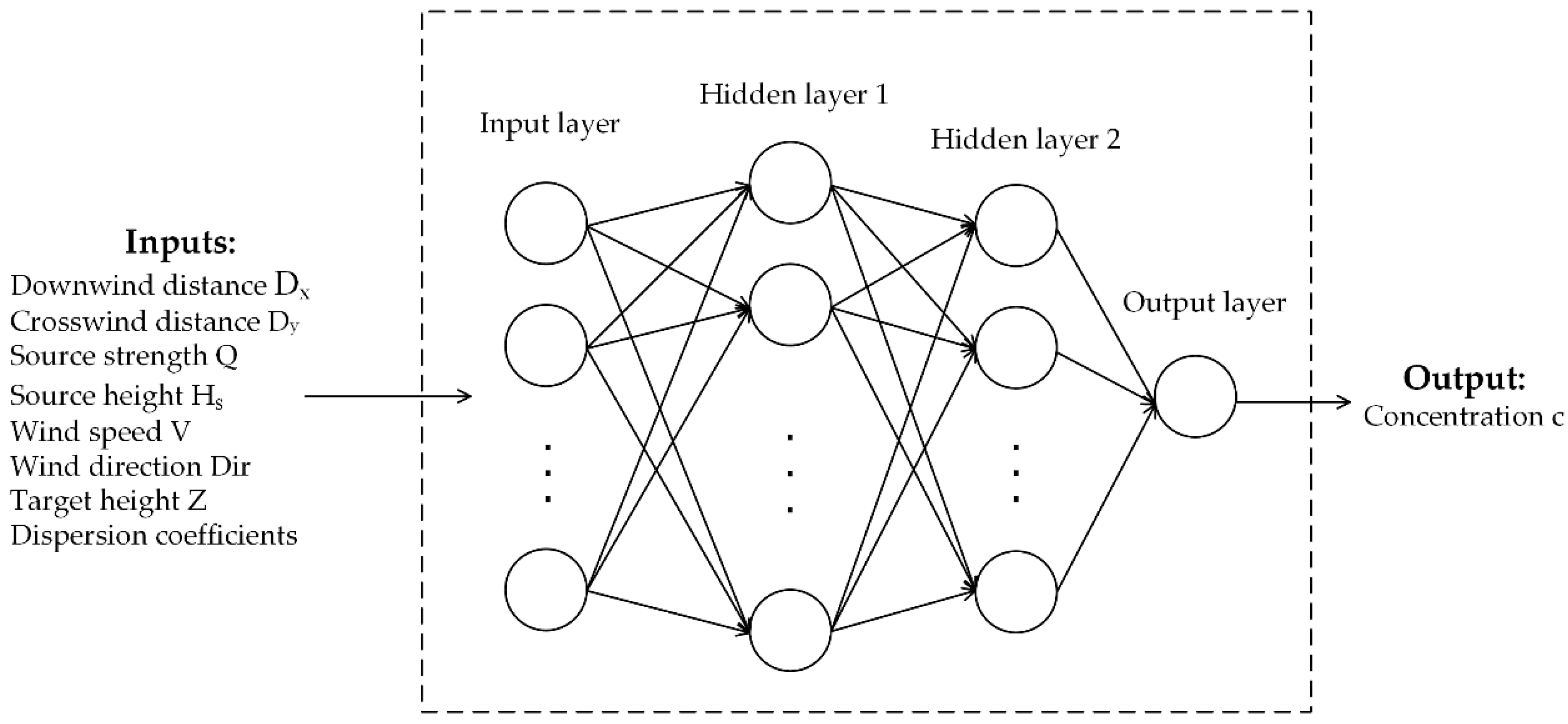

| Parameter | Symbol | Unit |
|---|---|---|
| Downwind distance | m | |
| Crosswind distance | m | |
| Source strength | g·s−1 | |
| Source stack height | m | |
| Wind speed | m·s−1 | |
| Wind direction | deg | |
| Atmospheric stability | / | |
| Temperature | °C | |
| Target height | m | |
| Mixing height | m | |
| Cloud height | m | |
| Cloud cover | % |
| Parameter | Symbol | Range | Step |
|---|---|---|---|
| Source strength | (g·s−1) | 1–30 | 5 |
| Average wind speed | (m·s−1) | 1–6 | 2 |
| Average wind direction | (deg) | 100–200 | 10 |
| Atmospheric stability | A–F | / |
| Scenarios | Source Strength (g·s−1) | Source Location (m) | Wind Speed (m·s−1) | Wind Direction (deg) | Atmospheric Stability Class |
|---|---|---|---|---|---|
| 1 | 25 | (0, 0) | 4 | 135 | C |
| 2 | 15 | (300, −300) | 2 | 180 | C |
| Parameter | Symbol | Minimum | Maximum |
|---|---|---|---|
| Source strength | (g·s−1) | 0 | 30 |
| Source x coordinate | (m) | −500 | 500 |
| Source y coordinate | (m) | −500 | 500 |
| Wind speed | (m·s−1) | 0 | 6 |
| Wind direction | (deg) | 90 | 180 |
| Method | Receptor Configuration | Source Strength (g·s−1) | Source Location (m) | Wind Speed (m·s−1) | Wind Direction (deg) | Total Skill Score | Computing Time (s) |
|---|---|---|---|---|---|---|---|
| Actual values | / | 25 | (0, 0) | 4 | 135 | 0 | / |
| PSO & ANN | 6 × 6 | 1.7980 | (−1.4035, 1.4196) | 0.5084 | −0.0523 | 0.0855 | 82.14 |
| SAPSO & ANN | 6 × 6 | 1.4883 | (−1.0564, 0.5712) | 0.4313 | 0.0502 | 0.0704 | 84.01 |
| PSO & ANN | 11 × 11 | −1.4410 | (1.1102, −1.1424) | −0.3941 | 0.2029 | 0.0679 | 83.53 |
| SAPSO & ANN | 11 × 11 | −0.2331 | (1.1648, −1.2247) | −0.1322 | 0.0632 | 0.0220 | 84.02 |
| PSO & ANN | 21 × 21 | −0.2406 | (1.1871, −1.1937) | −0.2347 | 0.0031 | 0.0321 | 83.17 |
| SAPSO & ANN | 21 × 21 | 0.0430 | (0.5835, −0.7272) | 0.0385 | −0.0219 | 0.0073 | 84.77 |
| PSO & ANN | 51 × 51 | −0.2406 | (0.3576, −0.4107) | −0.0668 | 0.0387 | 0.0118 | 85.66 |
| SAPSO & ANN | 51 × 51 | −0.1365 | (0.3473, −0.3454) | −0.0426 | −0.0279 | 0.0079 | 88.64 |
| Method | Receptor Configuration | Source Strength (g·s−1) | Source Location (m) | Wind Speed (m·s−1) | Wind Direction (deg) | Total Skill Score | Computing Time (s) |
|---|---|---|---|---|---|---|---|
| Actual values | / | 15 | (300, −300) | 2 | 180 | 0 | / |
| PSO & ANN | 6 × 6 | 2.4246 | (−0.6221, 3.1990) | 0.4384 | 0.0061 | 0.1306 | 81.76 |
| SAPSO & ANN | 6 × 6 | 2.0661 | (0.6618, 1.9660) | 0.3646 | −0.1068 | 0.1070 | 83.13 |
| PSO & ANN | 11 × 11 | 0.7587 | (−1.3977, 0.6910) | −0.1721 | 0.0518 | 0.0494 | 82.57 |
| SAPSO & ANN | 11 × 11 | 0.4615 | (−0.4273, 0.8910) | −0.1230 | 0.0565 | 0.0333 | 83.89 |
| PSO & ANN | 21 × 21 | 0.2697 | (−0.3100, 0.4310) | 0.1100 | −0.0204 | 0.0302 | 83.56 |
| SAPSO & ANN | 21 × 21 | 0.1917 | (−0.0492, 0.3830) | 0.0140 | 0.0177 | 0.0085 | 85.04 |
| PSO & ANN | 51 × 51 | 0.2630 | (0.2070, 0.2600) | 0.0289 | 0.0321 | 0.0089 | 85.13 |
| SAPSO & ANN | 51 × 51 | 0.1506 | (0.0222, 0.2330) | 0.0267 | 0.0027 | 0.0063 | 88.33 |
| Method | Source Strength (g·s−1) | Source Location (m) |
|---|---|---|
| Actual value | 4.6600 | (0, 0) |
| PSO & ANN1 | 4.6844 | (57.6866, 74.5629) |
| SAPSO & ANN1 | 4.6805 | (57.2595, 73.7221) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Chen, B.; Qiu, S.; Ma, L.; Zhu, Z.; Wang, Y.; Qiu, X. Hazardous Source Estimation Using an Artificial Neural Network, Particle Swarm Optimization and a Simulated Annealing Algorithm. Atmosphere 2018, 9, 119. https://doi.org/10.3390/atmos9040119
Wang R, Chen B, Qiu S, Ma L, Zhu Z, Wang Y, Qiu X. Hazardous Source Estimation Using an Artificial Neural Network, Particle Swarm Optimization and a Simulated Annealing Algorithm. Atmosphere. 2018; 9(4):119. https://doi.org/10.3390/atmos9040119
Chicago/Turabian StyleWang, Rongxiao, Bin Chen, Sihang Qiu, Liang Ma, Zhengqiu Zhu, Yiping Wang, and Xiaogang Qiu. 2018. "Hazardous Source Estimation Using an Artificial Neural Network, Particle Swarm Optimization and a Simulated Annealing Algorithm" Atmosphere 9, no. 4: 119. https://doi.org/10.3390/atmos9040119
APA StyleWang, R., Chen, B., Qiu, S., Ma, L., Zhu, Z., Wang, Y., & Qiu, X. (2018). Hazardous Source Estimation Using an Artificial Neural Network, Particle Swarm Optimization and a Simulated Annealing Algorithm. Atmosphere, 9(4), 119. https://doi.org/10.3390/atmos9040119





