3.1. Descending Motions over the EM Region
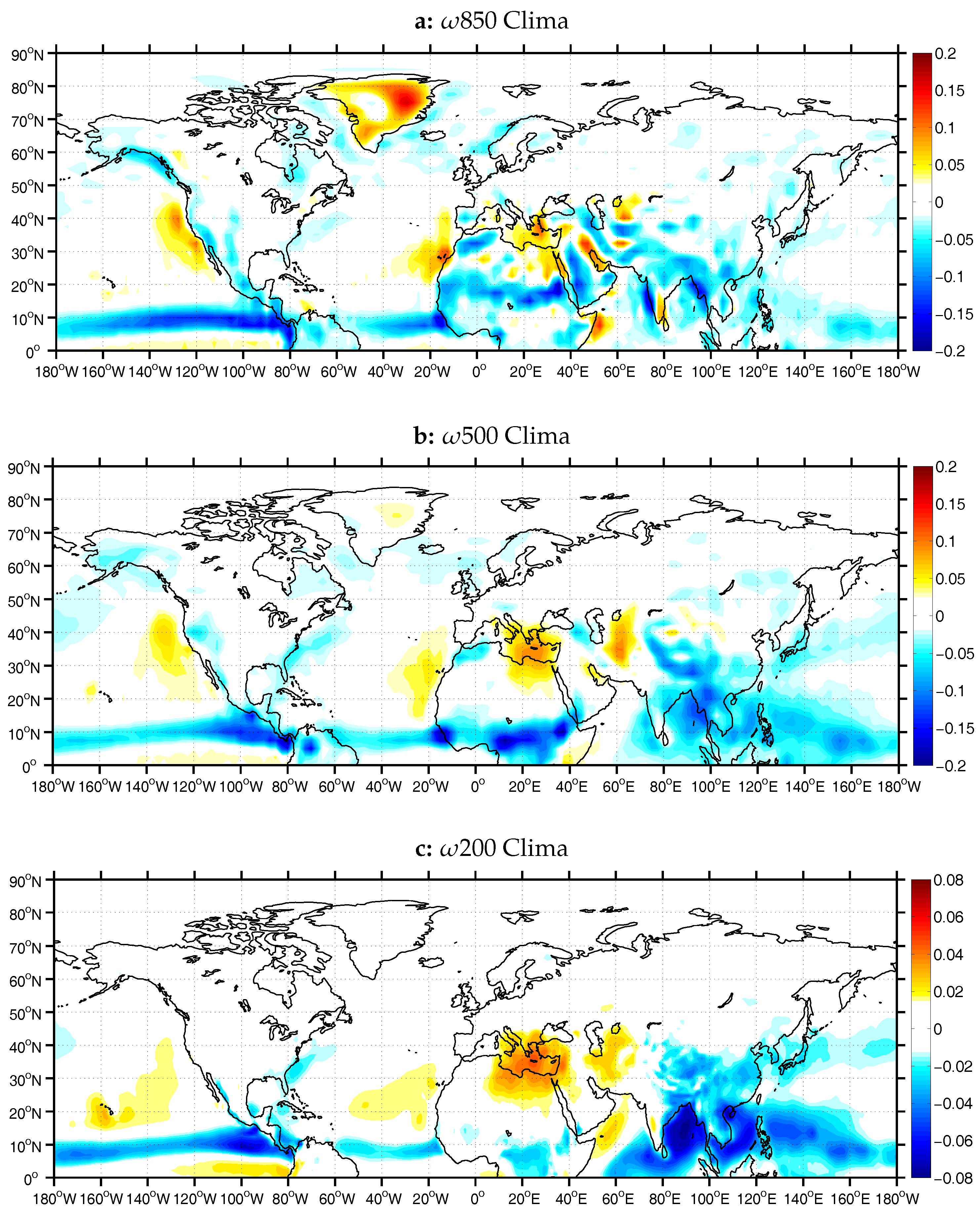
Figure 1 depicts the observed climatology of vertical velocity
for boreal summer (JJAS) in the lower (a), middle (b) and upper (c) troposphere. One can notice the band of ascent over the tropics throughout the troposphere, which is interrupted by the West Arabian Sea, and the most prominent regions of ascending motion due to monsoon activity east of 70
E. The deepest monsoon-induced ascent is found over the Bay of Bengal, Myammar and Nepal where a monsoon high forms at the upper levels and a monsoon low at the low levels, being spatially in quadrature along with the divergence regime [
19]. On the other hand, subsidence appears to be stronger over the central and eastern Mediterranean in both middle and upper troposphere, whereas a secondary subsidence core is found over Iran, Turkmenistan and Afghanistan. Topography modifies the flow and localizes the EM descending motion in the lower troposphere over the Aegean, the Red Sea and the Persian Gulf regions [
4,
6,
15].
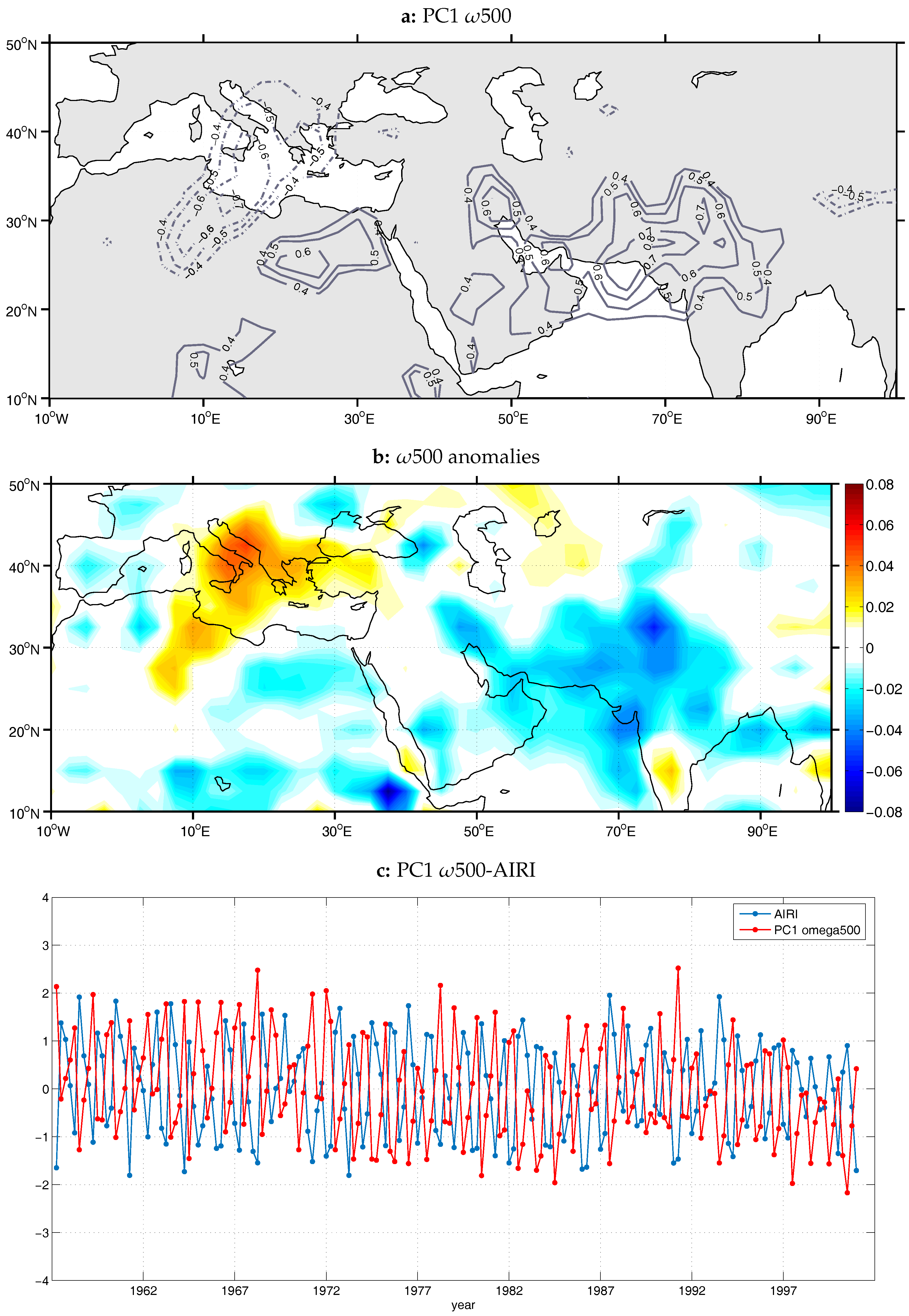
For the case of vertical velocity at the middle troposphere (500 hPa;
500) over the area of the Mediterranean and South Asia (10
W–100
E, 10
N–50
N), PCA led to 42 principal components, which explain about 75% of total variability of the examined field. The time series of the first principal component (PC) was found to be best correlated with the All India Rainfall Index, with
r = −0.83 (significant at the 0.05 level), explaining 9.5% of the total variability of
500 on the specific area. The two time series appear to anti-correlate on intraseasonal and interannual time scales (
Figure 2c). The spatial pattern of loadings of the first PC is shown in
Figure 2a. Loadings indicate the correlation between the anomalies of the initial variable at each grid point and the temporal variation (scores) of the PC, thus the spatial distribution of loadings reveals the regions that are strongly associated with the specific PC. Having in mind that each PC has a positive and a negative phase, every spatial map of loadings can be interpreted in two ways. In
Figure 2a, two main poles of opposite sign are apparent, i.e., one center of negative
500 anomalies over the central Mediterranean and west EM, with an expansion to the south over Algeria and Libya as well as a positive anomaly center over an extended area covering Iraq, Iran, the Persian Gulf, Pakistan, NW India and the North Arabian Sea. A secondary positive center is found over Egypt and East Libya, denoting weaker than normal descent over the region. The negative phase of the respective pattern is associated with strong descent over the central Mediterranean and west EM and with stronger than normal ascent over the North Arabian Sea, Northwest India and north central India, north of 20
N. Sixty-nine percent of the variability of the first PC is attributed to ISM activity. The results associated with the first principal component of middle troposphere vertical movements confirm the findings of Tyrlis et al. [
15] about the connection of the subsidence over EM with the ISM activity.
In order to obtain a realistic and physical view of the negative phase of the first 500 PC and to confirm the mathematical products of PCA, months with absolute standardized scores greater than 1.5 were selected and the respective maps of 500 composite anomalies were constructed. (The negative phase of PC1 was selected as it is the one that correlates with stronger monsoon activity). Principal component scores reflect the strength of coherence between the monthly pattern of the field and the specific principal component pattern over the examined area, meaning that the higher the score value the greater the resemblance of the one with the other. The value of ±1.5 was defined after a sensitivity test was conducted regarding the coherence and physical interpretation of the composite patterns that resulted from the selection of different threshold values. The chosen threshold is 1.5 times the standard deviation greater than the mean value of the PC time series; therefore, it is associated with the most representative months of the specific principal component. The same threshold value was employed for the construction of all anomaly composites displayed in the following, in accordance with the procedure described above.
The distribution derived from the study of the scores of the first PC (
Figure 2b) reveals two distinct regions with opposite signs. One center of positive anomalies is found over the central and eastern Mediterranean, with maximum values over the Italian peninsula and the Adriatic Sea, whereas the center of negative values lies over NW India and the Himalayas, northern Arabian Sea as well as Pakistan and South Iran. The anomalous ascent over the Himalayas and Tibet region represents the orographic rainfall of the area. The specific pattern is in agreement with the results of Tyrlis et al. [
15], who found that both the subsidence and northerly flow over the EM start intensifying simultaneously with the appearance of enhanced convection over the northern Arabian Sea and the Indian summer monsoon core.
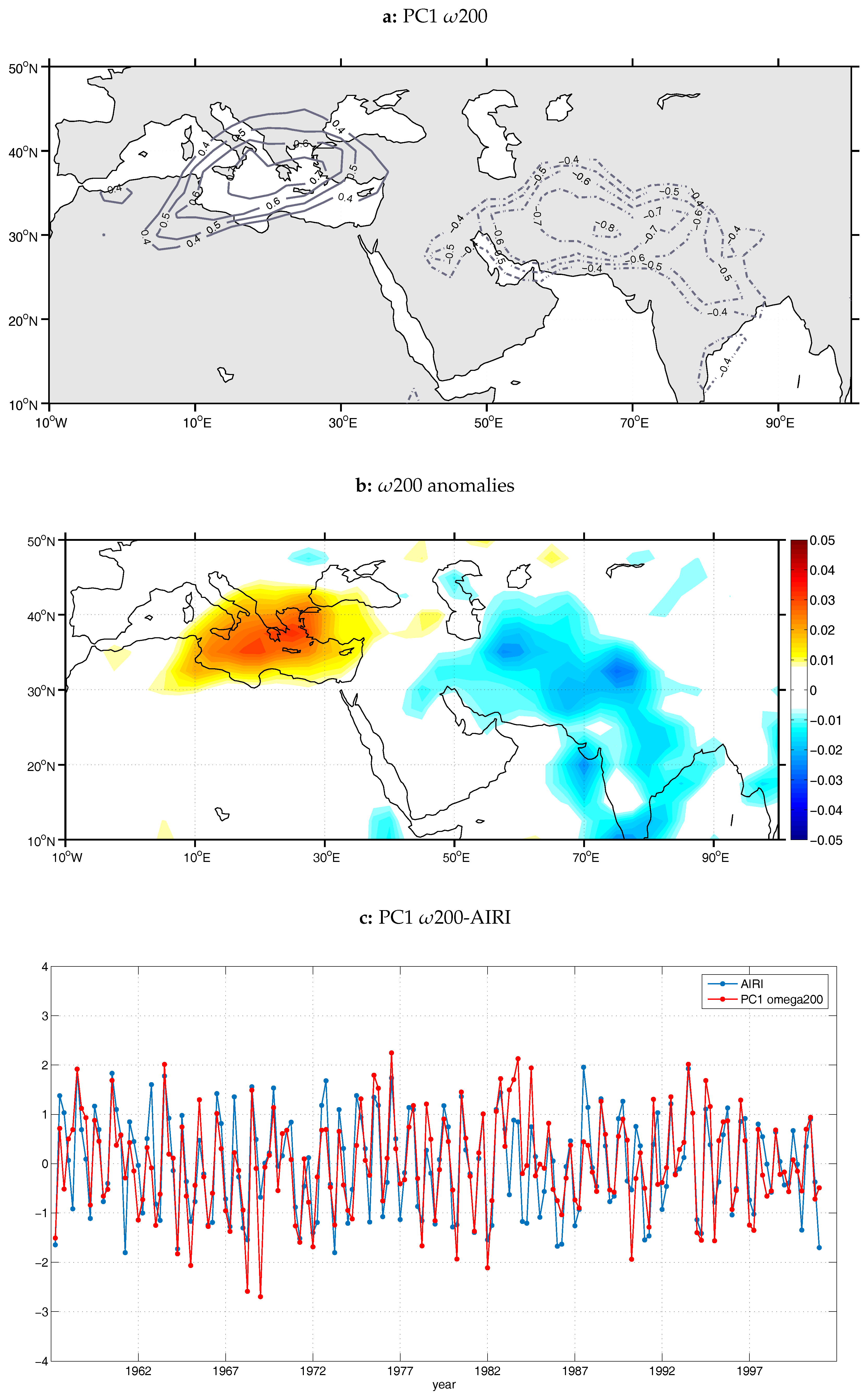
Similarly, for the case of vertical velocity at the upper troposphere (200 hPa;
200) 35 principal components arose from PCA application, accounting for approximately 74% of the total variance. The corresponding
200 loadings map of the first PC is presented in
Figure 3a. This was the PC that exhibited the highest correlation with AIRI (
r = 0.79, significant at the 0.05 level), explaining 62% of the variability of
200 at the centers of action of PC1. It is apparent that this pattern resembles the
500 PC1 pattern, where the positive correlation center covers the central and eastern Mediterranean with a SW to NE direction and the negative correlations extend over northern India, Pakistan and Afghanistan. The correlation coefficients are above
r = 0.6 over the EM and below
r = −0.7 (significant at the 0.05 level) over Pakistan. The PC1 score time series approximates the temporal variations of
200 at the above centers and exhibits similar behavior to the time series of the negative phase of
500 PC1, but in occasions with slightly larger amplitudes (
Figure 3c) . In order to facilitate the interpretation of the PC1 pattern, the composite anomaly map for the positive phase of PC1 is displayed in
Figure 3b. From this map, it is apparent that the positive phase of PC1 is connected with enhanced subsidence over the central and eastern Mediterranean simultaneously with enhanced ascending motion over NW India and the Himalayas, west-central India, Arabian Sea and West Bay of Bengal. Consistent with 500 hPa and 200 hPa results, the findings from the examined 850 hPa vertical velocity revealed one center of action over the central and eastern Mediterranean and another prominent center over the Arabian Sea and Pakistan (not shown). However, the subsidence center over EM in the lower troposphere is less extensive and with lower loading values than the ones found in the middle and upper troposphere and thus the dipole pattern over EM and India appears to be less coherent.
The results regarding the vertical velocity suggest that, although the strongest magnitude of ascent in the region of the ISM is observed over the Bay of Bengal (
Figure 1b,c), ascending motions over the northern Arabian Sea, NW India and Pakistan synchronize the most with the descending motions over the central and eastern Mediterranean. Such off-equatorial heat sources could excite Rossby waves, able to interact with the midlatitude westeries. Tyrlis et al. [
15] reached a similar conclusion, i.e., the subsidence over the EM is mostly correlated with the monsoon convection activity over the North Arabian Sea.
In order to facilitate the investigation of the dynamics related to the subsidence over the EM region, the upper troposphere circulation was examined with the aid of the PCA technique. Many previous researchers have studied the interrelationship between the ISM and the mid-latitude anomalous climate conditions, either by examining the impact of mid-latitudes on the ISM variability [
23,
29,
30,
31] or by investigating the influence of the ISM on the climate or weather conditions in the middle latitude regions [
4,
6,
22,
32,
33]. In most of these cases, Rossby waves were found to regulate the revealed teleconnections.
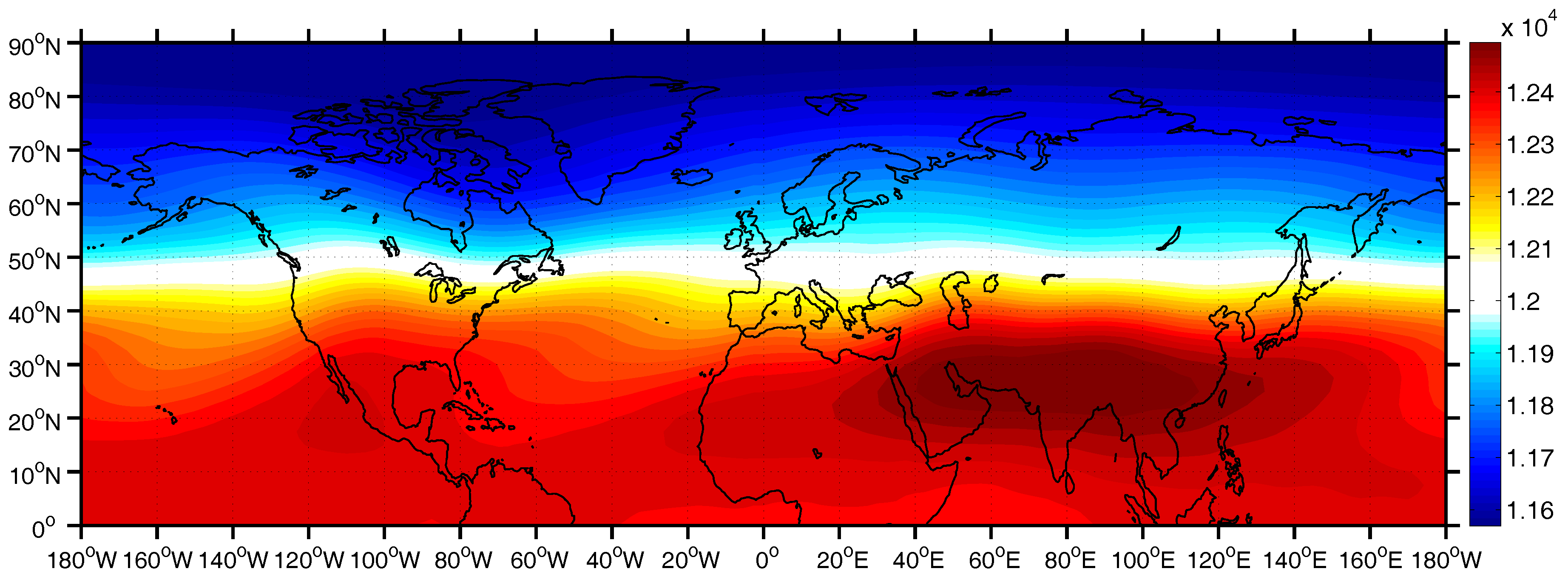
Figure 4 displays the 200 hPa geopotential height climatology. The high pressure band over tropical and subtropical latitudes, whose western flank covers the Middle East and N. Africa, is distinguished and an extended ridge forms over the ISM and the western North Pacific summer monsoon regions, corresponding to divergence areas and following the basic monsoon features described by [
19]. Moreover, these ridges coincide with the diabatic heating of the monsoon systems.
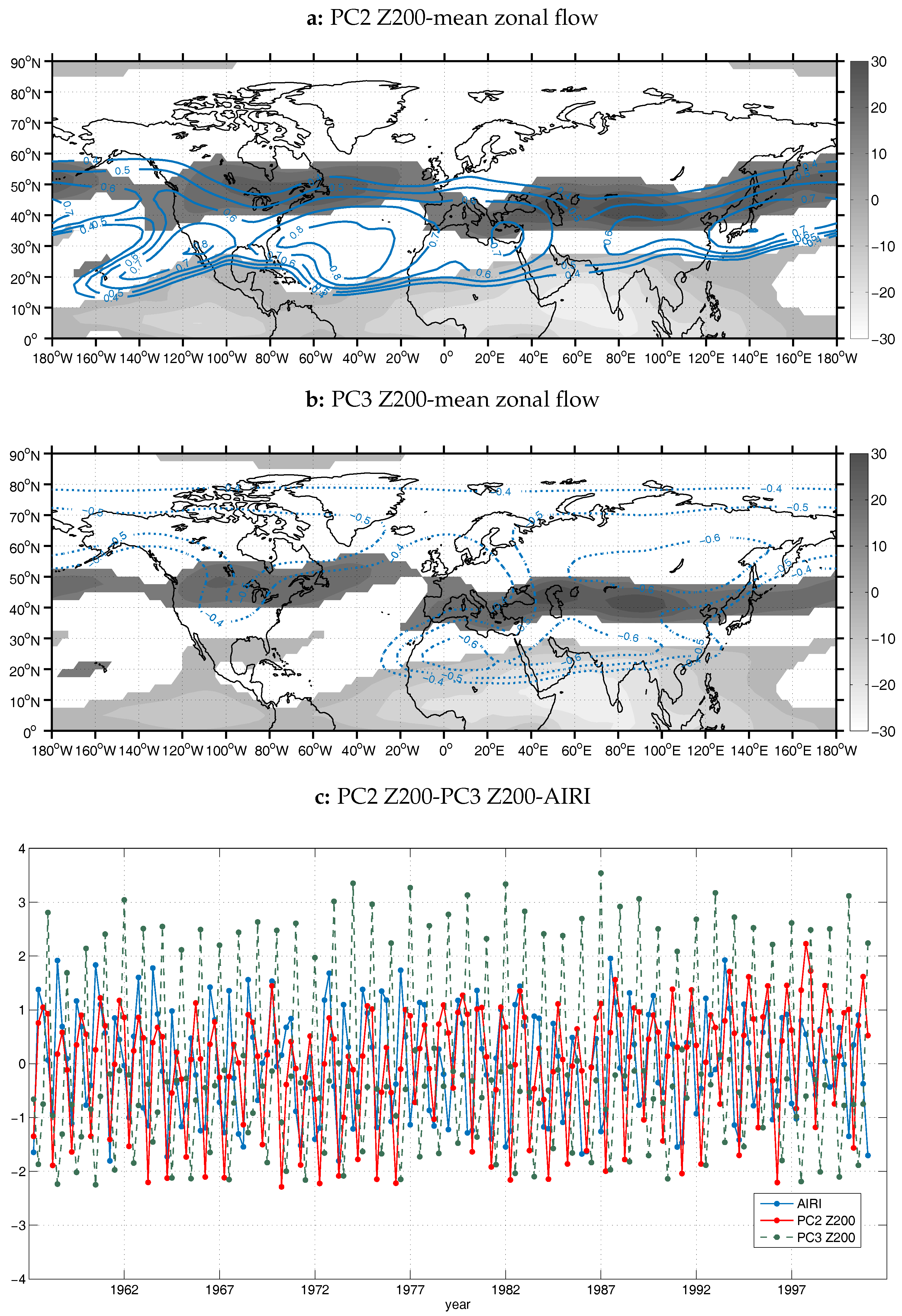
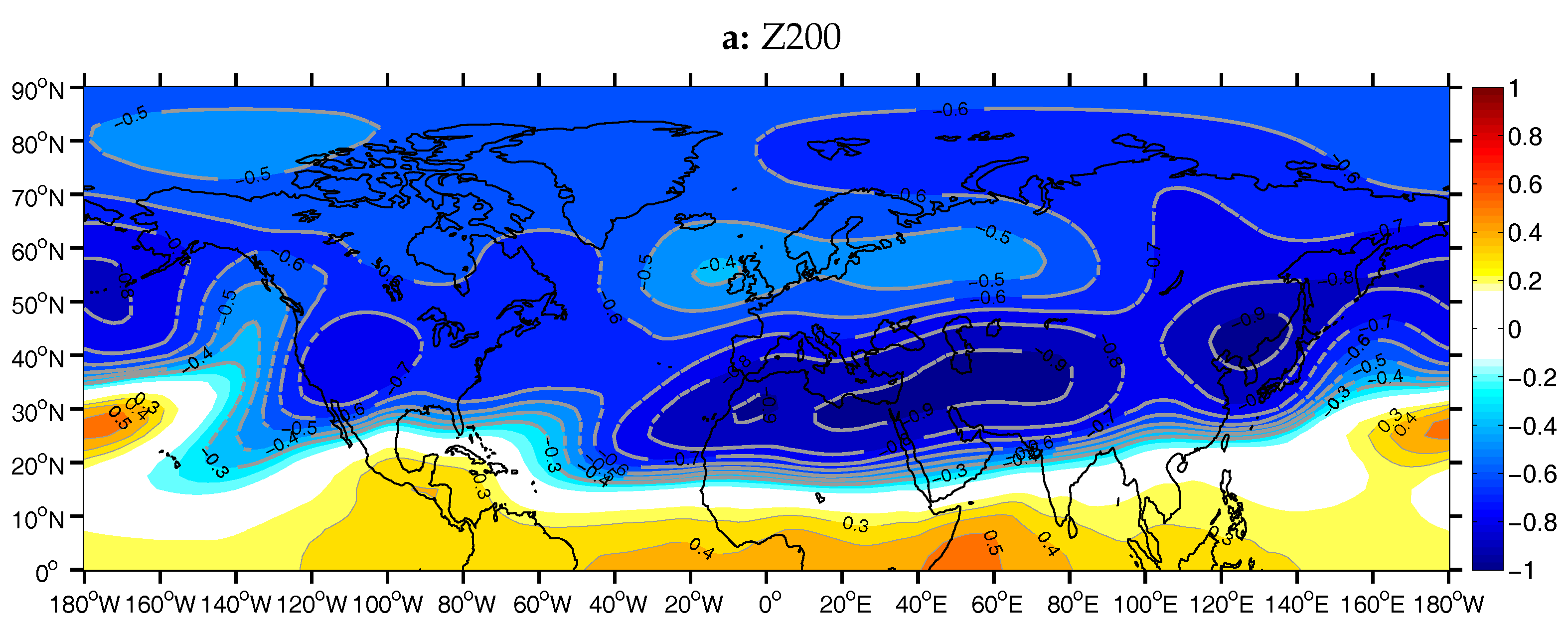
PCA resulted in five main components for the case of geopotential height at 200 hPa (Z200) over the NH, which share approximately 80% of total variability. The correlation coefficient between the second and third component and AIRI is
r = 0.52 and
r = −0.56 respectively (significant at the 0.05 level) and it is worth noting that the Z200 PC3 signal presents larger amplitudes compared to the corresponding Z200 PC2 time series (
Figure 5c). The PC2 loadings spatial pattern (22.6% of total variance) is characterized by positive geopotential height anomalies along the subtropical latitudes of the NH (
Figure 5a). Specifically, significant correlations appear along subtropical and extratropical latitudes (40
–50
N) over the Pacific region, western N. America coast and eastern Asia coast and along 30
N over the Atlantic and Eurasia. This wave pattern, that resulted from the application of RPCA in the Z200 field, looks very similar to the circumglobal teleconnection pattern (CGT) observed by Ding and Wang [
22] and Ding and Wang [
23] in the summertime midlatitude circulation of the NH, on the interannual and intraseasonal time scales of upper-tropospheric circulation. The third PC for the field of geopotential height at 500 hPa (not shown) was found almost identical, with slightly higher loadings.
The negative phase of PC3 for the Z200 field (21.7% of total variance), which correlates with AIRI, consists of three main anticyclonic anomaly centers over N. Africa, west-central Asia and NE Asia (
Figure 5b). The two anticyclonic centers of PC3 located over Asia, belong to the CGT pattern, which is attributed to the combined contribution of both middle latitude circulation and ISM activity. As for the extended anticyclonic center found over N. Africa and west-central Asia, it resembles in structure the NH branch of an equatorially trapped Rossby wave of the upper troposphere, which is regarded as the response to a tropical source of diabatic heating near India [
34]. According to previous studies [
4,
32,
35], this wave train is excited due to the perturbation created by the release of massive amounts of diabatic heating in the area of ISM, it is located at the subtropical latitudes of both Hemispheres, symmetric relative to the Equator, and it propagates zonally to the west, reaching the coasts of Central America. The anticyclonic center over west-central Asia is part of the CGT wave, that develops north of the equatorially Rossby wave gyre, along the westerly flow of the midlatitudes.
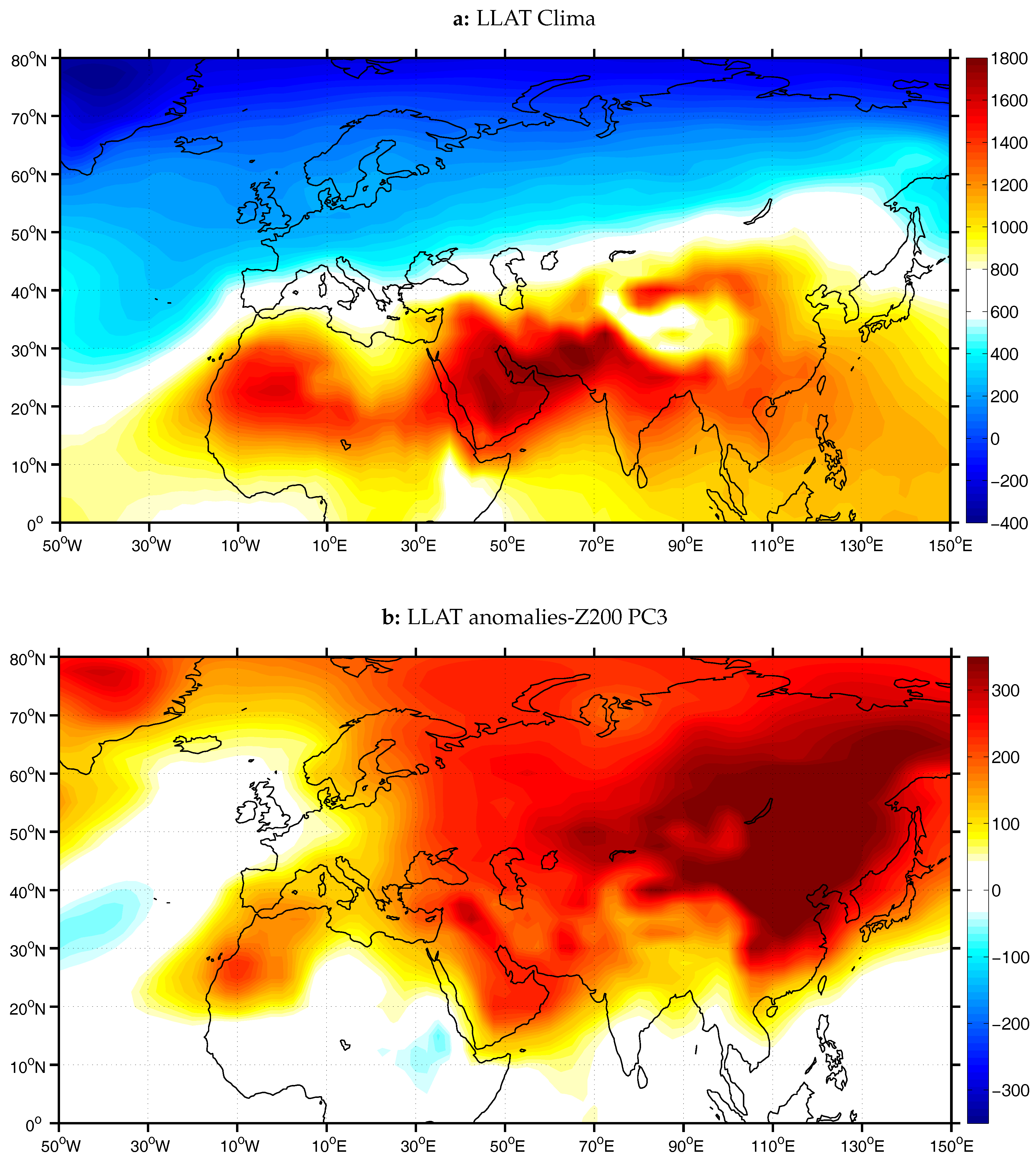
The anomalies of the low-level atmospheric thickness (LLAT) between the pressure levels of 700 hPa and 925 hPa, associated with months when the negative phase of PC3 for Z200 field prevails, are depicted in
Figure 6b. The LLAT describes the heat-induced dilatation of the low levels and it is thus utilized to identify the areas where significant heat lows develop near the surface due to the lower troposphere heating [
36]. The 0600 UTC reanalysis geopotential fields were used, as suggested by Lavaysse et al. [
36], in order to minimize the effect of convective clouds and surface albedo on the radiative budget in the lower troposphere. During months with high Z200 PC3 score values, the Sahara heat low over West Africa appears to be enhanced compared to its climatology (
Figure 6a) and moreover positive anomalies of LLAT, and hence of mean temperature of the tropospheric layer, are found over the Anatolian plateau, the Arabian peninsula, the Kyzylkum desert and the region east of the Caspian Sea as well as over the Thar desert in India and Pakistan and over Mongolia (Gobi desert) and China. The thermal influence of the most prominent desert regions of Eurasia, found west of the Indian subcontinent, may be of great importance for the modulation of the westward propagating Rossby waves. Rodwell and Hoskins [
4], in their idealized simulations, investigated the effect of the local diabatic forcing of the east Sahara region on the intensity of descent observed over the EM. However, the effect of the desert heat lows on the formation and propagation of these westward moving waves has not been investigated thoroughly.
The development of this westward moving equatorial Rossby wave, which is associated with the ISM forcing, depends primarily on the relative position of the diabatic heating source in respect to the upper easterly jet over South Asia [
20], as the amplitude of the tropical disturbance-response is directly related to the basic mean zonal flow. According to Lin [
32] calculations and to the Doppler shifting effect of a mean zonal flow on forced equatorial waves [
37,
38], the Rossby wave response is very strong for a perturbation with wavenumber 6 and basic state zonal wind between O and 15 m/s. When the basic background flow consists of easterlies or strong westerlies, the response to the tropical diabatic heating is quite weak. In line with the above, when the tropical forcing of the ISM is located on latitudes with the aforementioned favorable conditions, that is, near zero or weak westerly background flow, then the NH Rossby wave gyre response can easily develop to the west and have a great intensity.
Figure 5 represents the second and third main components of Z200 along with the mean state of the zonal wind speed component at 200 hPa. The colored contours correspond to zonal wind speeds over 15 m/s and below 0 m/s, following the calculations of Lin [
32] for simplicity, with dark gray colors corresponding to westerlies and light gray colors to easterlies. The subtropical jet over central Asia and Europe is depicted, as well as the polar jet over N. America and the easterly jet over South Asia. For the case of Z200 PC2, the northern flanks of the wave disturbance lie over the mid-latitude westerlies and follow the movement of the subtropical jet over Eurasia and the polar jet over N. America and northern Atlantic, with a greater consistency over the Eurasia continent. The latter indicates the significant contribution of the subtropical jet stream in the development of the Rossby wave response in the extratropical latitudes [
24]. The two anticyclonic centers of Z200 PC3 in the subtropics and especially the Rossby wave gyre over N. Africa are located within the area of weak westerlies, where the equatorial response to the ISM heating anomaly is favored to develop with a high amplitude. In the middle troposphere, no such geopotential pattern as in Z200 PC3 is recognized among its principal components.
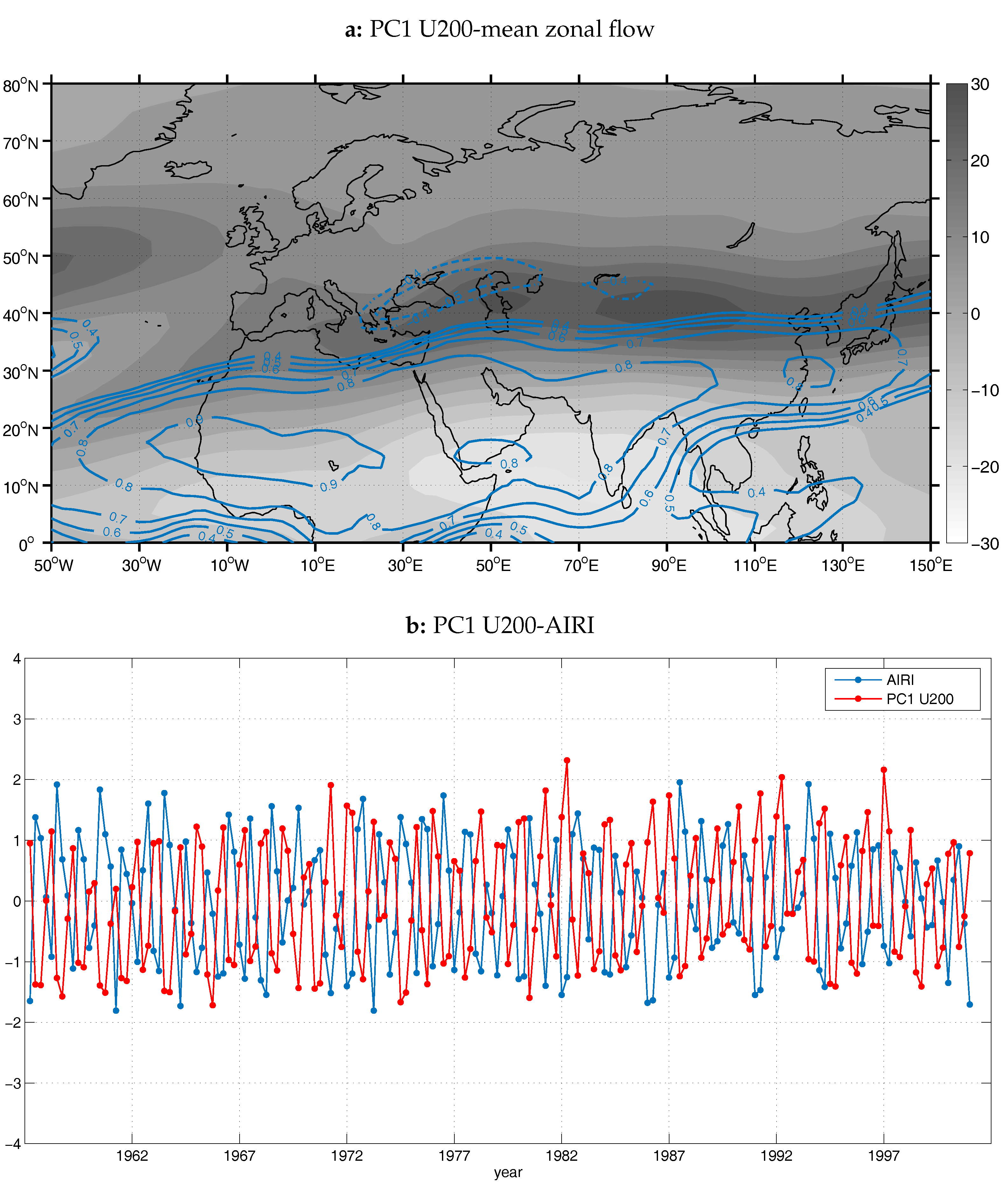
Based on the above analysis, it is inferred that a necessary condition for the development of the equatorial Rossby wave response west of the ISM tropical force source, is the retreat of the Eurasian subtropical jet poleward of its climatological mean position [
32]. The retreat of the jet creates a zone of weak westerlies between the subtropical westerly jet and the easterly tropical jet. This phenomenon is depicted on the spatial pattern of the first component (
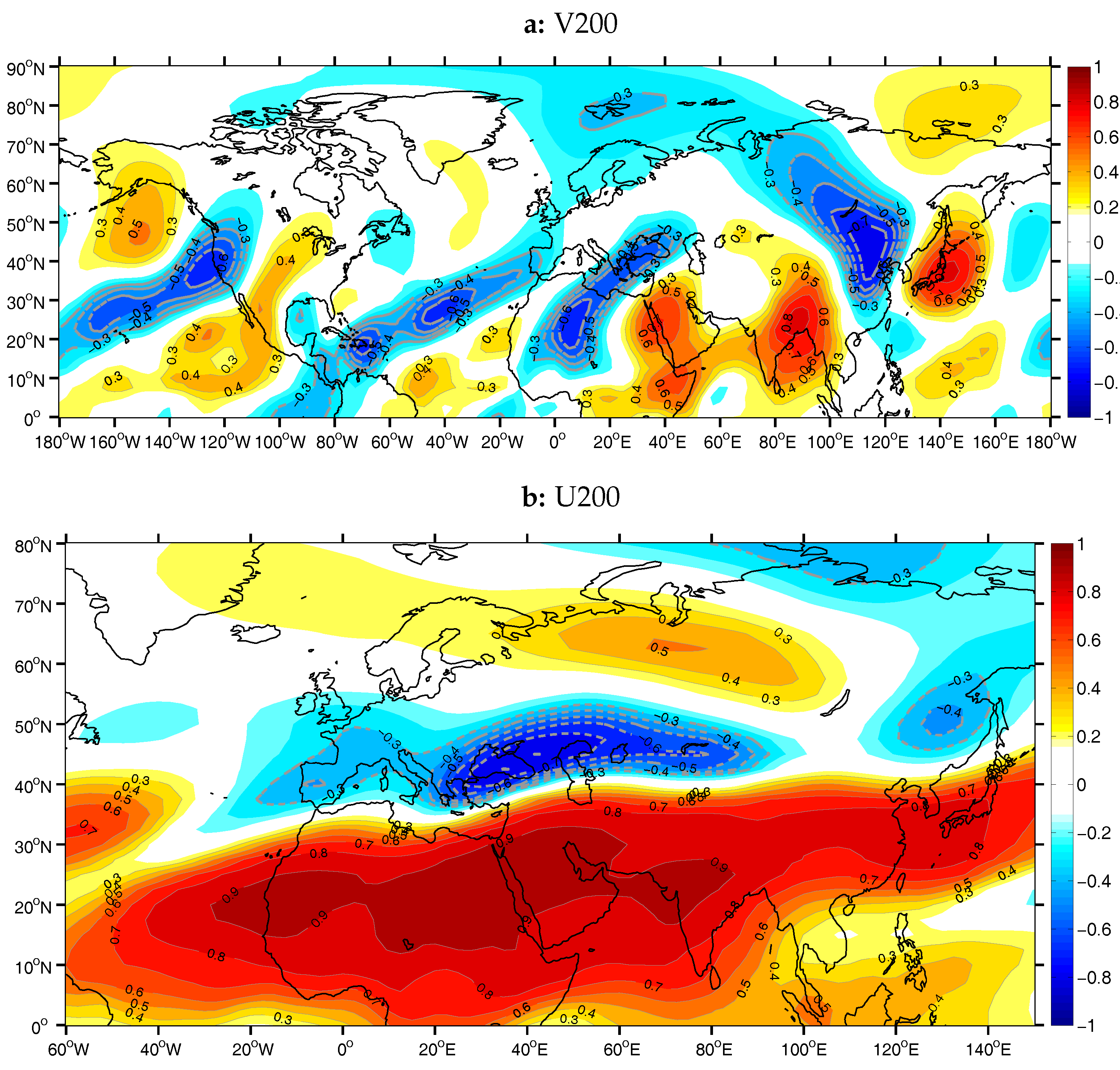
Figure 7a) of zonal wind speed at 200 hPa (U200). PCA was applied on the field of U200 in the domain 0
–80
N and 60
W–150
E and from the resultant components the 12 first main PCs were retained (75% of total variance). The first PC was the only one to have a statistically significant correlation with AIRI (
r = −0.84, significant at the 0.05 level,
Figure 7b).
The pattern of PC1 anomalies is bi-polar, consisting of a center of weak negative anomalies over EM and the Caspian Sea and a center of strong and extended positive anomalies, which covers South Asia, south of 40
N, the Middle East and North Africa, as well as the adjacent Atlantic Ocean, south of 30
N. The negative phase of PC1 can be interpreted as a strengthening and poleward displacement of the subtropical jet core over the EM region and central Asia, in combination with an enhancement of the tropical easterly jet over India, the Arabian Sea, Arabian peninsula and N. Africa along with a slight poleward displacement of it (
Figure 7a). The latitudinal displacement of the two jets results in favorable conditions for the equatorial Rossby wave development and propagation towards N. Africa and EM, in an area away from the two jet cores.
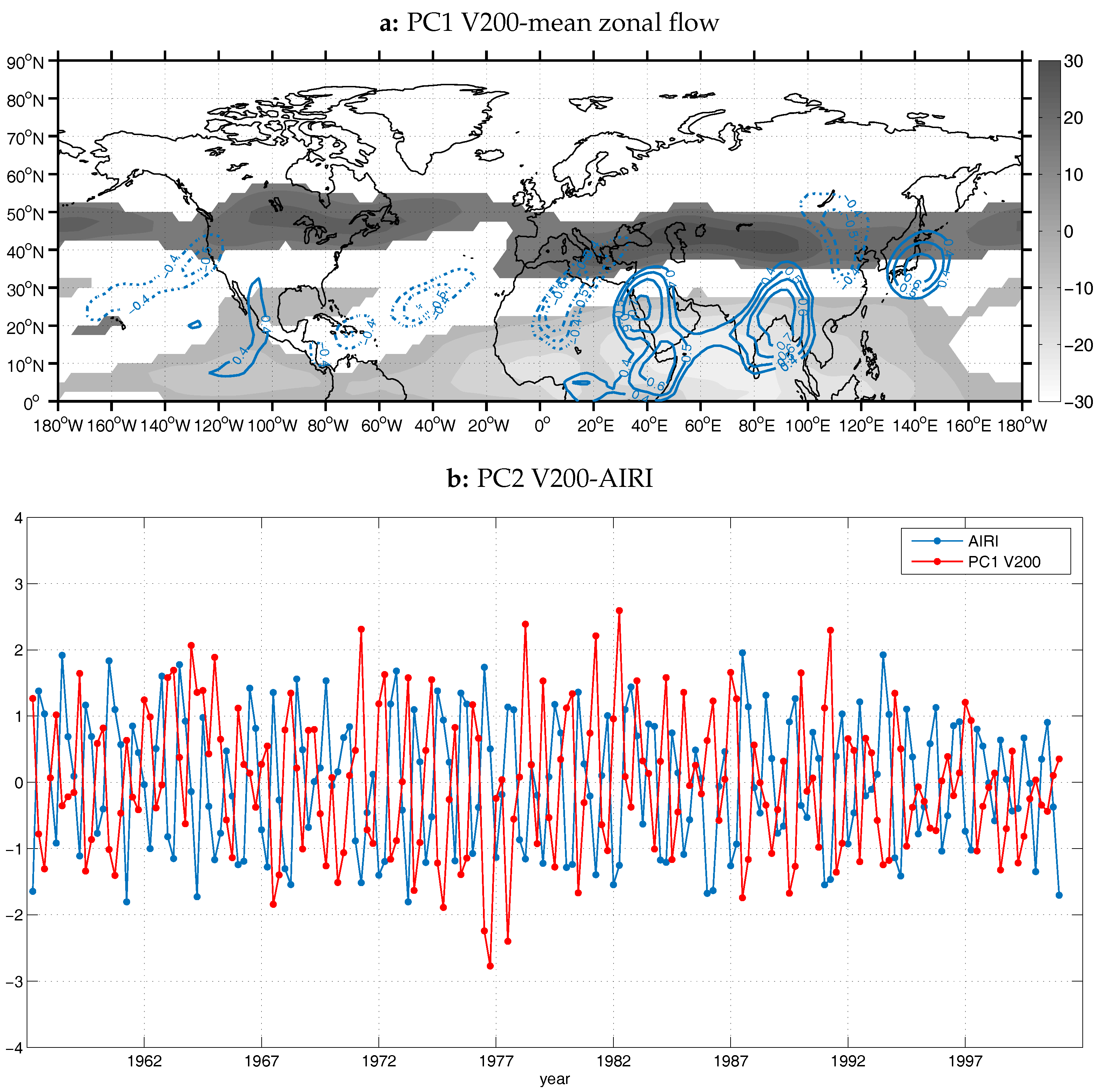
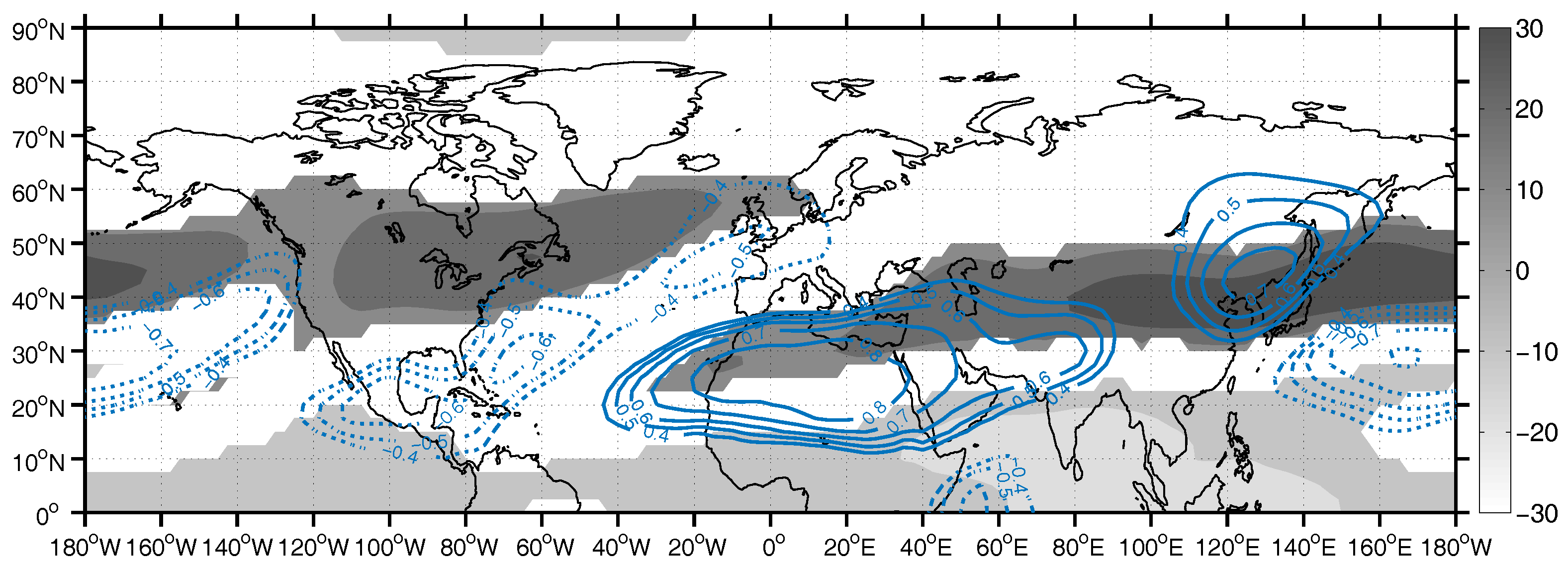
The first PC (PC1; 8% of total variance) that arose for the case of meridional wind speed component at 200 hPa (V200) was found to have a very good correlation with AIRI (
r = −0.72, significant at the 0.05 level,
Figure 8b). From the application of PCA on the data of V200 for the whole NH, 36 components were retained and rotated, corresponding to 76% of the total variance. The PC1 spatial pattern consists of alternating positive and negative meridional wind anomalies (
Figure 8), i.e., southerlies and northerlies, extending over almost all the NH. The wave of anomalies is found at the tropical and subtropical latitudes over Asia, Africa, Atlantic Ocean and the American continent, whereas over eastern Asia and the western Pacific Ocean, the wave shifts poleward, over the middle latitudes. The stronger anomaly centers are located over Eurasia, where two systems are detected. One is found over the subtropical latitudes, extending from the northern Bay of Bengal to the central Atlantic to the west, and the other is found over the middle latitudes of eastern Asia, with two action centers along the westerly jet. The system over the India and Africa region is located over an area characterized by low westerlies and easterlies (
Figure 8) and it can be concluded that it resembles the tropical Rossby wave response to the monsoon heating of the atmosphere. Accordingly, the two anomaly centers over the eastern Asia are considered to belong to the CGT pattern, that follows the waveguide of the westerly jet.
PCA was once more applied on the Z200 field, but this time, prior to its application, the mean zonal state of Z200 was removed from the initial data, so that the deviation from the mean zonal flow becomes more apparent and the tropical Rossby wave can be isolated. The resulting pattern (
Figure 9) is a combination of Z200 PC2 and PC3 that we discussed earlier in
Figure 5. The most intense action center is an anomalous subtropical anticyclone over west-central Asia and N. Africa, which represents the tropical Rossby wave—response to the ISM forcing. The secondary anticyclonic center over eastern Asia, constitutes along with the midlatitude cyclonic centers, the footprint of the CGT pattern [
22].
3.2. Persistent Northerly Flow over the EM Region
Etesians are the second major climatic feature in the region of EM during summer. As mentioned above, Etesians along with the vertical movement over EM, are considered a manifestation of the remote effect of the ISM [
4] and they are also correlated with each other. In
Figure 10, the climatology of the lower troposphere circulation components are presented. The two prominent dynamical factors of the lower troposphere geopotential field, the ISM thermal low and the Azores anticyclone, are apparent in
Figure 10a. On the other hand, in
Figure 10b, a persistent northerly air component over the central and eastern Mediterranean is depicted, with an expansion over western Libya and Egypt, and additionally a respective northerly flow is distinguished over the Red Sea, Iraq and the Persian Gulf as well as over the region south of the Aral Sea. As for the zonal wind speed field (
Figure 10c), the values over the EM are significantly low, indicative of the prevailing northerly flow; the wind is of an eastern direction over the Black Sea and of a western direction over the Levantine Sea.
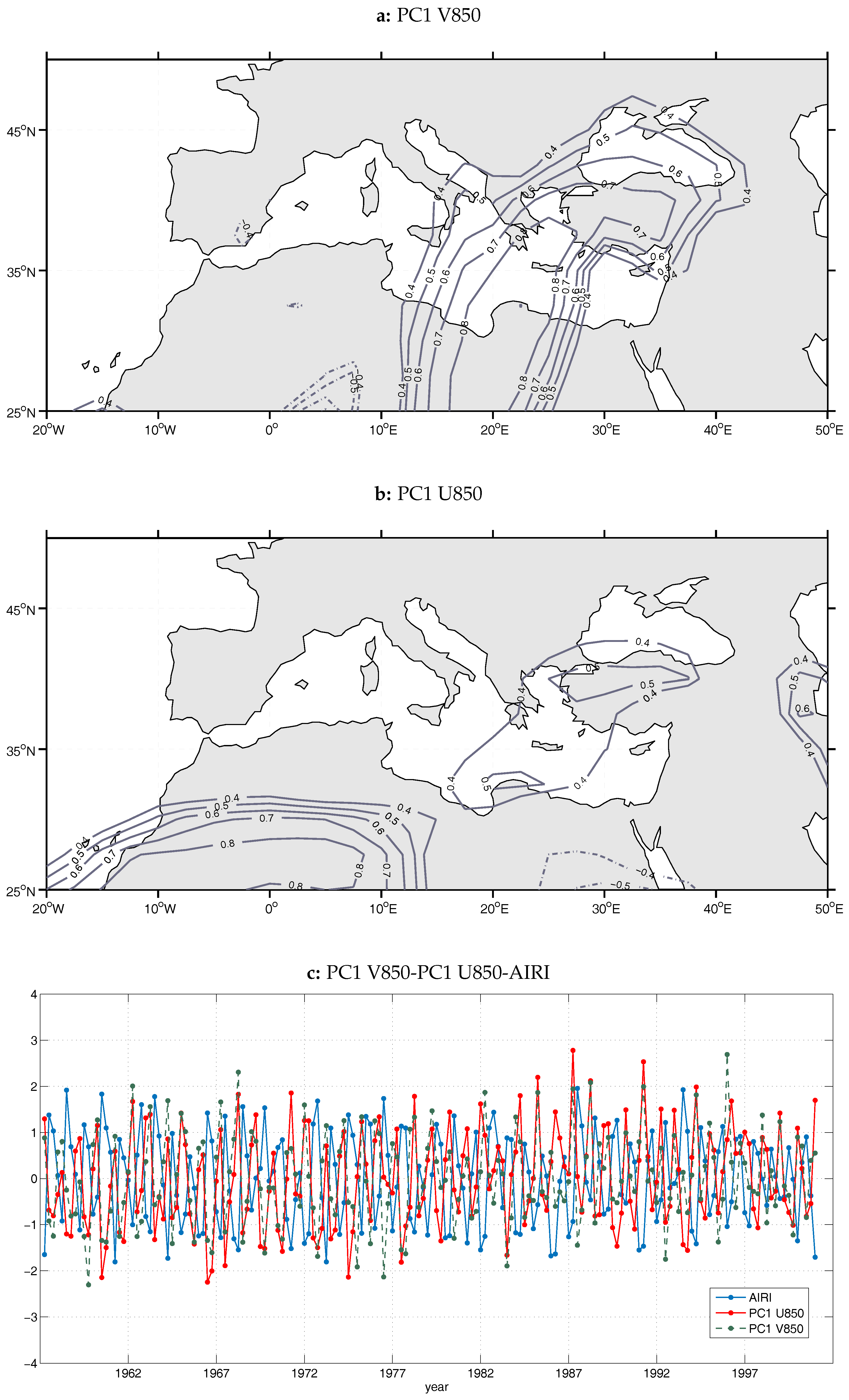
In the case of the meridional wind component at 850 hPa (V850), nine main components were retained and rotated, which together account for 73% of the total variability of the field over the region of 25
–50
N and 20
W–50
E. The pattern of the correlation isolines of the first component (13% of total variability) resembles the characteristic pattern of Etesians during summer, which comprises northeasterly winds over the northern Aegean and northerly winds over the central and southern Aegean. Hence, the spatial pattern of PC1 shows that the center of action is located over the Aegean Sea and the western coast of Turkey, extending to the north over the Black Sea and to the south over Libya (
Figure 11a). The correlation coefficient between the PC1 scores time series and the monsoon index AIRI is equal to
r = −0.71 (significant at the 0.05 level), confirming that there is a connection between the PC1 pattern and the ISM and indicating that the intraseasonal variability of the Etesians is controlled by the ISM activity in accordance with the findings of Tyrlis et al. [
15]. The center of action for the case of the Etesians, that is depicted in
Figure 11a, is located right beneath the subsidence centers of the middle and upper troposphere (
Figure 2a and
Figure 3a), as was pointed out in the results of the idealized simulations of Rodwell and Hoskins [
6]. According to them and the satisfaction of the Sverdrup vorticity balance, the Etesians can be considered as the equatorward flow that forms below the subsidence region over the EM.
As for the zonal component of wind speed at 850 hPa (U850), nine principal components were retained, which share approximately 77% of total variance. Based upon the loadings of the first component of U850, which exhibited the strongest correlation with AIRI (
r = −0.72, significant at the 0.05 level), a spatial pattern with two action centers has resulted. The first and strongest center is located over NW Africa, between latitudes 25
and 30
N and is associated with the Harmattan winds, i.e the northeasterly trade winds that dominate over N. Africa in boreal summer, whereas the secondary center is a much weaker center of positive anomalies over the EM, with a SW–NE direction and with the higher loadings of the pattern being spotted over the southern region of the Black Sea. This means that during the months associated with the negative phase of U850 PC1, enhanced easterlies appear over NW Africa, reflecting the Harmattan circulation over the western Sahara and probably the mid-tropospheric easterly African jet [
20]. The first principal components of V850 and U850 fields, which have the highest correlation with AIRI, fluctuate quite concurrently in time (
Figure 11c) and thus present a significant correlation coefficient with a magnitude of
r = 0.74.
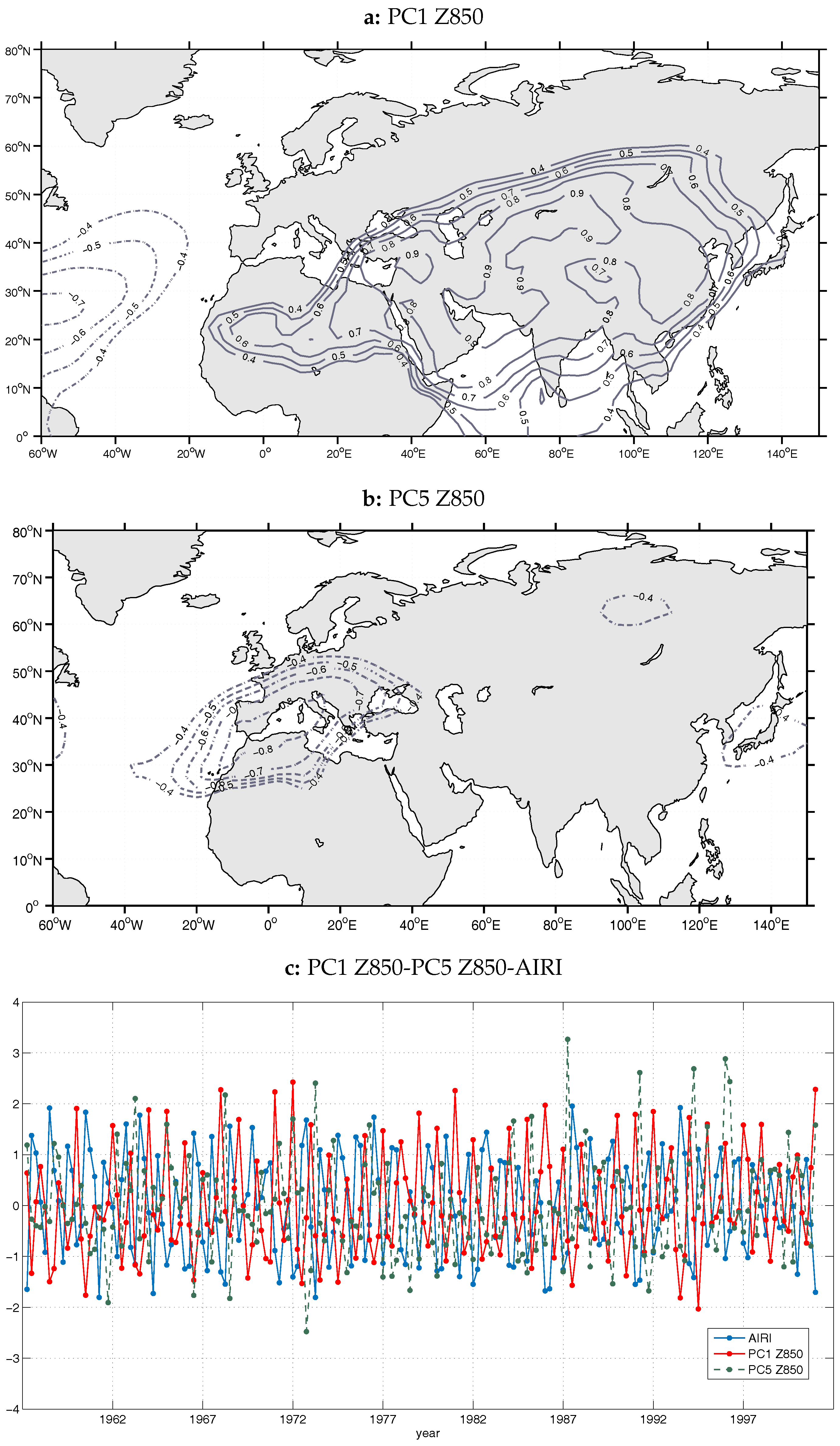
In order to seek out the low-level circulation regime mostly related to the ISM activity, the PCA was performed based on monthly anomalies of 850 hPa geopotential height (Z850) in the domain 0
–80
N and 60
W–150
E. Thirteen main components were retained and rotated, accounting for 83% of the total variance. The first and fifth main components exhibited a statistically significant correlation with AIRI (
r = −0.6/
r = −0.45, significant at the 0.05 level). The first PC depicts a dipole of correlations with an opposite sign (
Figure 12a). The most prominent and extended center of the PC1 pattern covers almost all South Asia, south of 50
N, extends to the west over EM at a latitude of 40
N and at even lower latitudes over Africa, at the regions of great descent and deserts (15
–25
N). The second pole, which consists of negative correlations, is found over the western Atlantic, between 20
and 30
N and is connected with the inner area of the subtropical Azores anticyclone. The strongest positive correlations are found over the northern Arabian Sea, Pakistan and Afghanistan as well as over Syria, Iraq and the Levantine. The AIRI index is correlated with the negative phase of PC1, thus in the months related to the negative PC1 phase, ISM strengthening coincides with enhanced cyclonic activity over the South Asia thermal low and Anatolian thermal low region and at the same time with enhanced anticyclonic activity over the negative correlation pole of the PC1 pattern. The strengthening of the South Asian thermal low and its expansion to the west, the Persian trough, is naturally connected to the ISM strength. On the other hand, the strengthening of the Azores anticyclone concurrently with the enhancement of ISM could be explained by the influence of a common element of low-frequency variability. The influence of the tropical Atlantic Ocean decadal variability and specifically of the Atlantic Multidecadal Oscillation on the Indian monsoon rainfall, via various physical mechanisms, has been studied extensively [
39]. There are various studies that have emphasized the role of the North Atlantic Oscillation (NAO) in the teleconnections of circulation and sea surface temperature anomalies in the North Atlantic with the Indian monsoon [
31,
40]. More specifically, there is evidence that the Atlantic Multidecadal Oscillation is responsible for the decadal variability of the monsoon by modulating the frequency of occurrence of strong NAO events [
41].
The spatial map of Z850 PC5 loadings (
Figure 12b) is characterized by a monopole of negative correlations. The center of anomalies stretches over NW Africa, central and northern Europe and further to the east over EM, Greece and the Balkans. The negative phase of the component reflects an anomalous anticyclonic system over the area, which can be associated with the western center of action that contributes to the pressure gradient over the EM, necessary for the appearance of the Etesians. The surface anticyclone over central Europe and the Balkans has been considered by many as an expansion of the Azores anticyclone towards Europe. However, the findings of many researchers [
7,
9] suggest that, in most cases, the Azores and the central European anticyclones are of different origin and have no connection to each other, but are two separate systems with the central European/Balkan anticyclone being basically the result of negative vorticity advection by a wave disturbance originating over the N. Atlantic [
42]. The correlation between the PC5 scores time series and AIRI could be attributed to the upstream influence of mid-latitude systems on the ISM variability on intraseasonal and interannual time scales [
22,
43,
44]. It is interesting to note that no statistically significant correlation was found between the two GP850 principal components, which suggests that the two distinctive patterns they represent are unrelated.
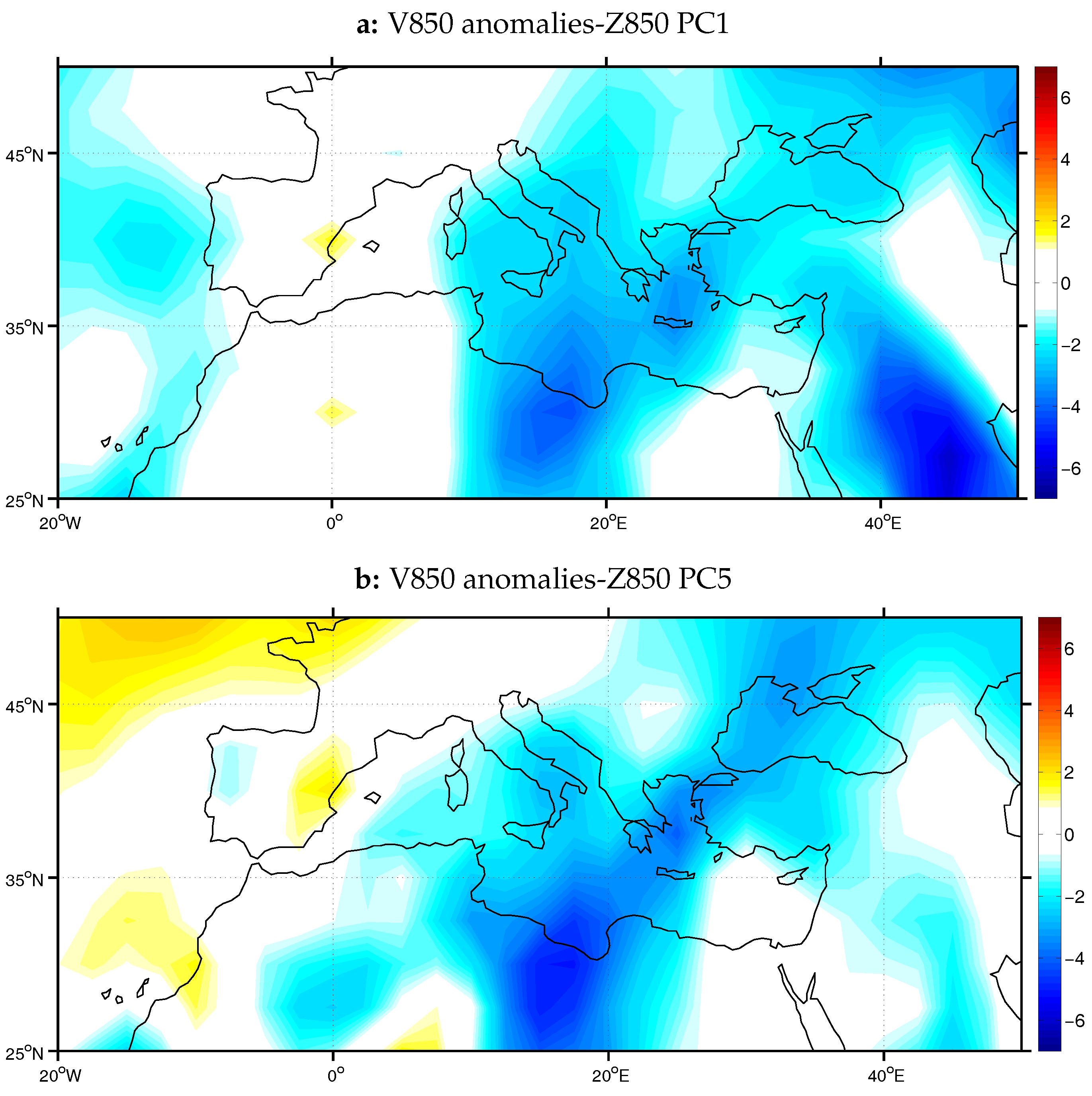
In order to gain insight into the surface wind regimes connected to these two Z850 components, the composite anomalies of V850 were constructed, corresponding to months belonging to the negative phase of the first and fifth PC of Z850 (
Figure 13). The two resulting anomaly maps exhibit similar patterns of northerlies over central and eastern Mediterranean, with the main difference that for the case of the PC1 composite map the strongest northerlies appear to be over the Middle East and secondary over the central and eastern Mediterranean and Libya, whereas in the case of the PC5 composite map only the northerly winds over the Aegean and Libya can be seen. The above findings point to the results of Tyrlis et al. [
15] and Tyrlis and Lelieveld [
42], who in their studies concluded that the South Asian monsoon may indeed control the seasonality and arrival of the Etesian winds and subsidence movements over EM, as well as their interannual variability, but the middle latitude dynamics control the high-frequency variability of the Etesians specifically.
By combining the resulting PCs for the upper troposphere (Z200–Z500), that were mentioned above, and the first component of the lower troposphere (Z850), we can conclude that the Rossby wave response to the Indian monsoon heating has a baroclinic structure. The Rossby wave response is constituted primarily by an upper level ridge that extends over South Asia, North Africa and the Mediterranean, expanding to the west of the monsoon heating source, from the northern Bay of Bengal to the central Atlantic, and by a low level trough that expands westward from the monsoon region towards the EM and N. Africa via the Persian Gulf. The upper level ridge and the mid and upper tropospheric warming, that propagate westward from the diabatic heating source, constitute the structure that facilitates the subsidence over the EM, whereas the low level trough, in conjunction with the Balkan anticyclone, builds the steep gradient of surface pressure that produces the Etesian winds. Thus, both subsidence and Etesians appear to be connected with the atmospheric response to the monsoon activity.