Evaluating the Sensitivity of the Mass-Based Particle Removal Calculations for HVAC Filters in ISO 16890 to Assumptions for Aerosol Distributions
Abstract
1. Introduction
2. Methods
3. Results
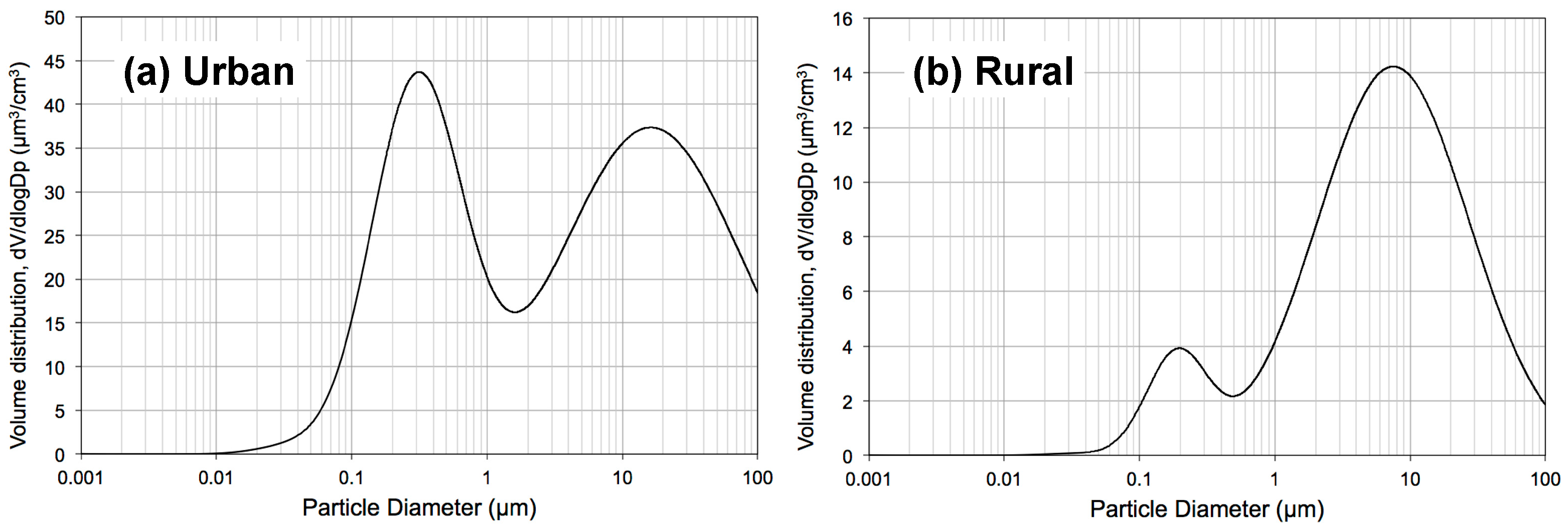
3.1. Origin of the Historical Ambient Aerosol Distributions Used in ISO 16890
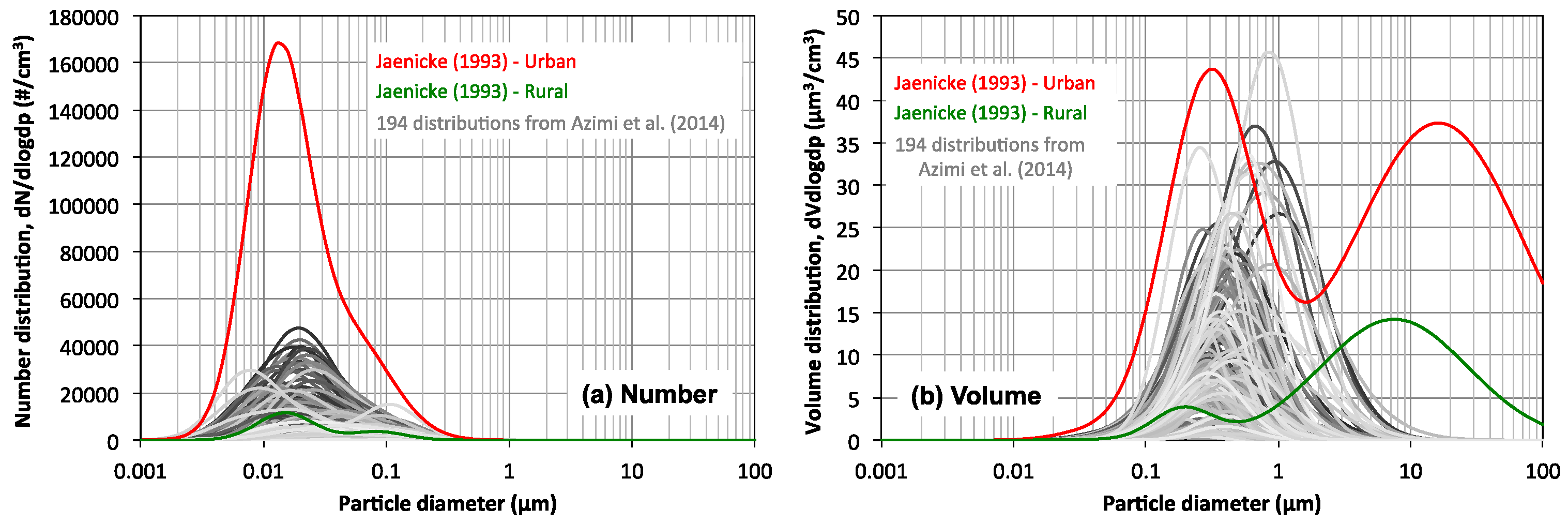
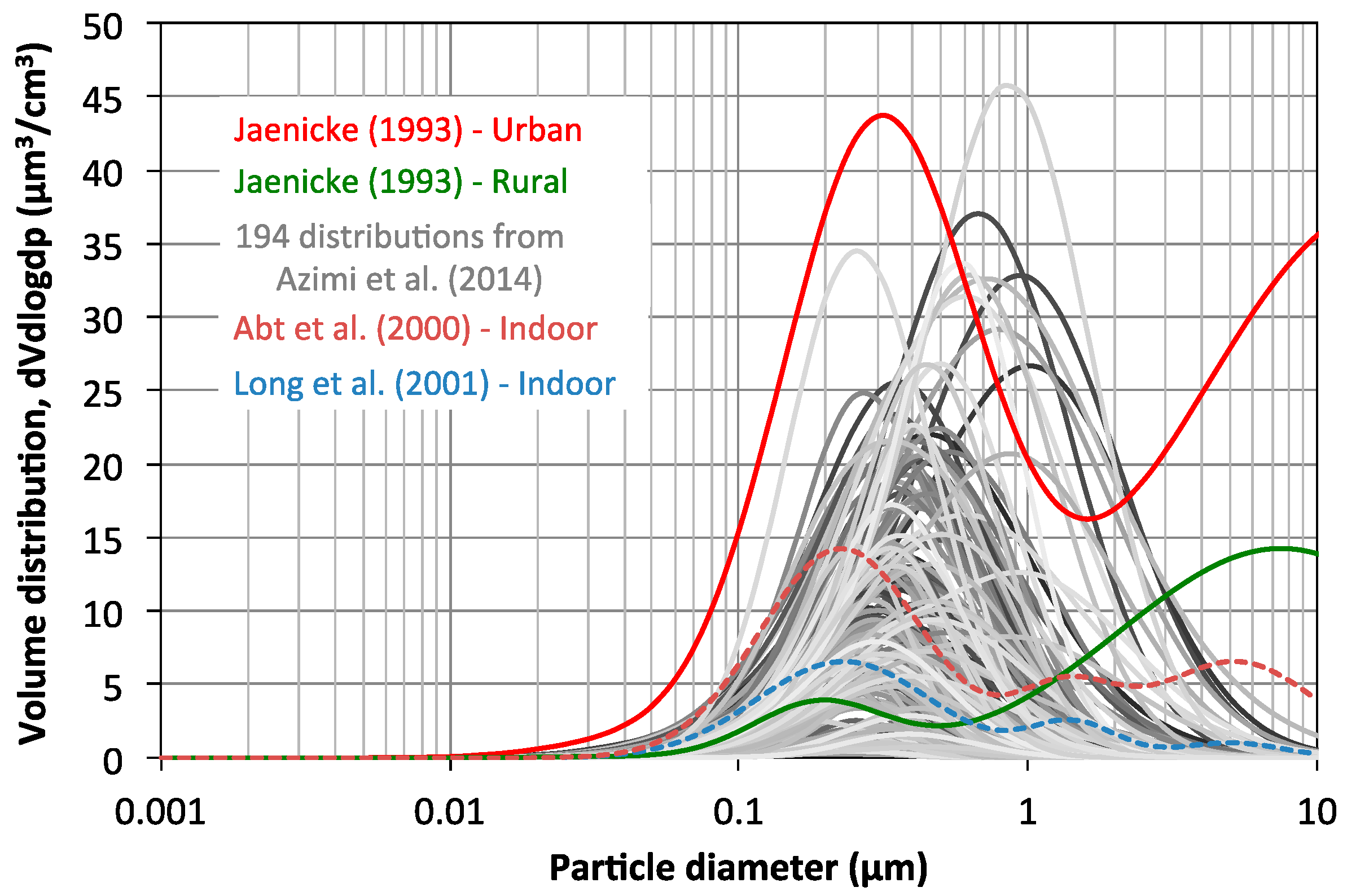
3.2. How Relevant Are the Historical Ambient Aerosol Distributions Used in ISO 16890 Today?
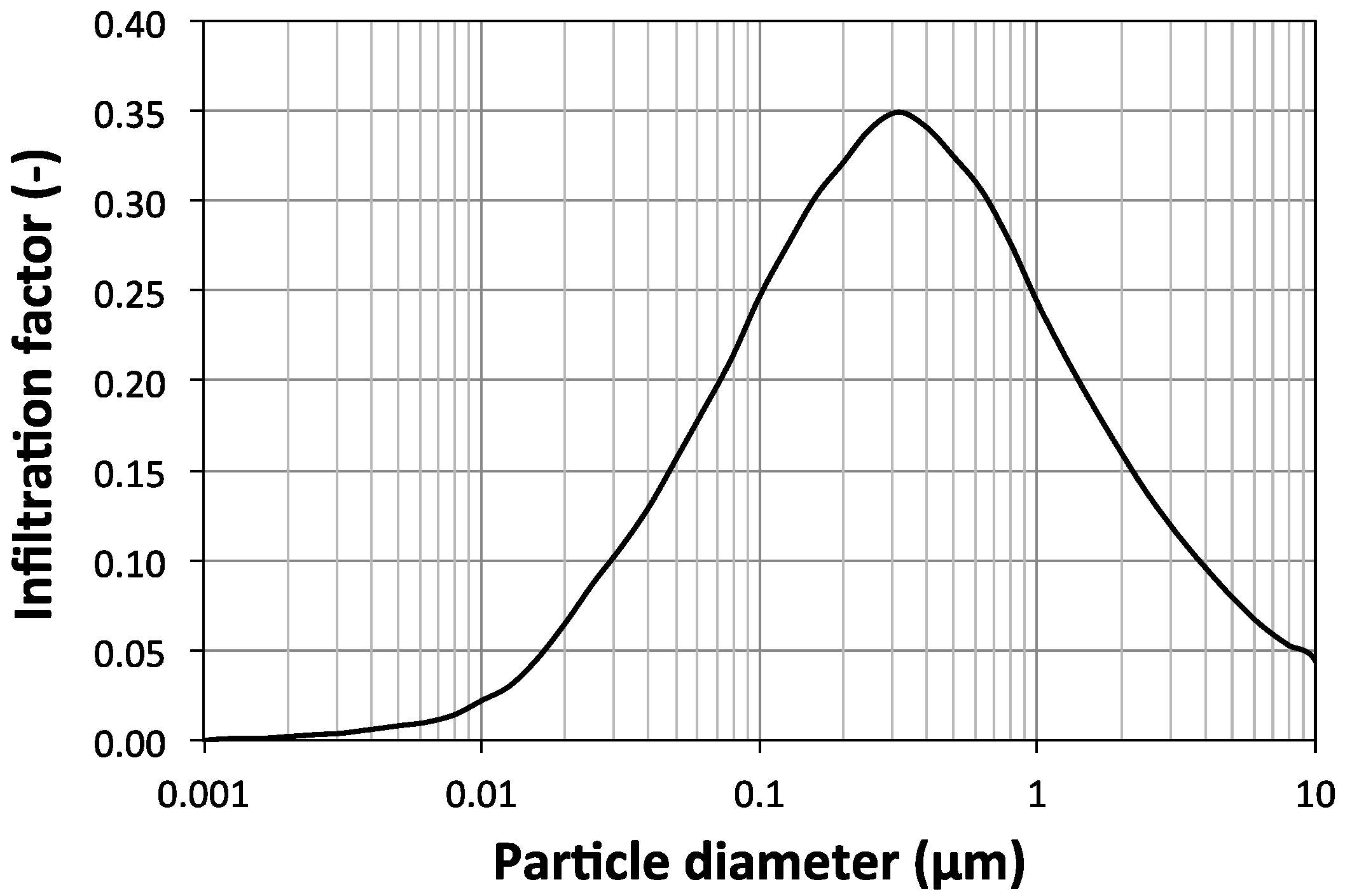
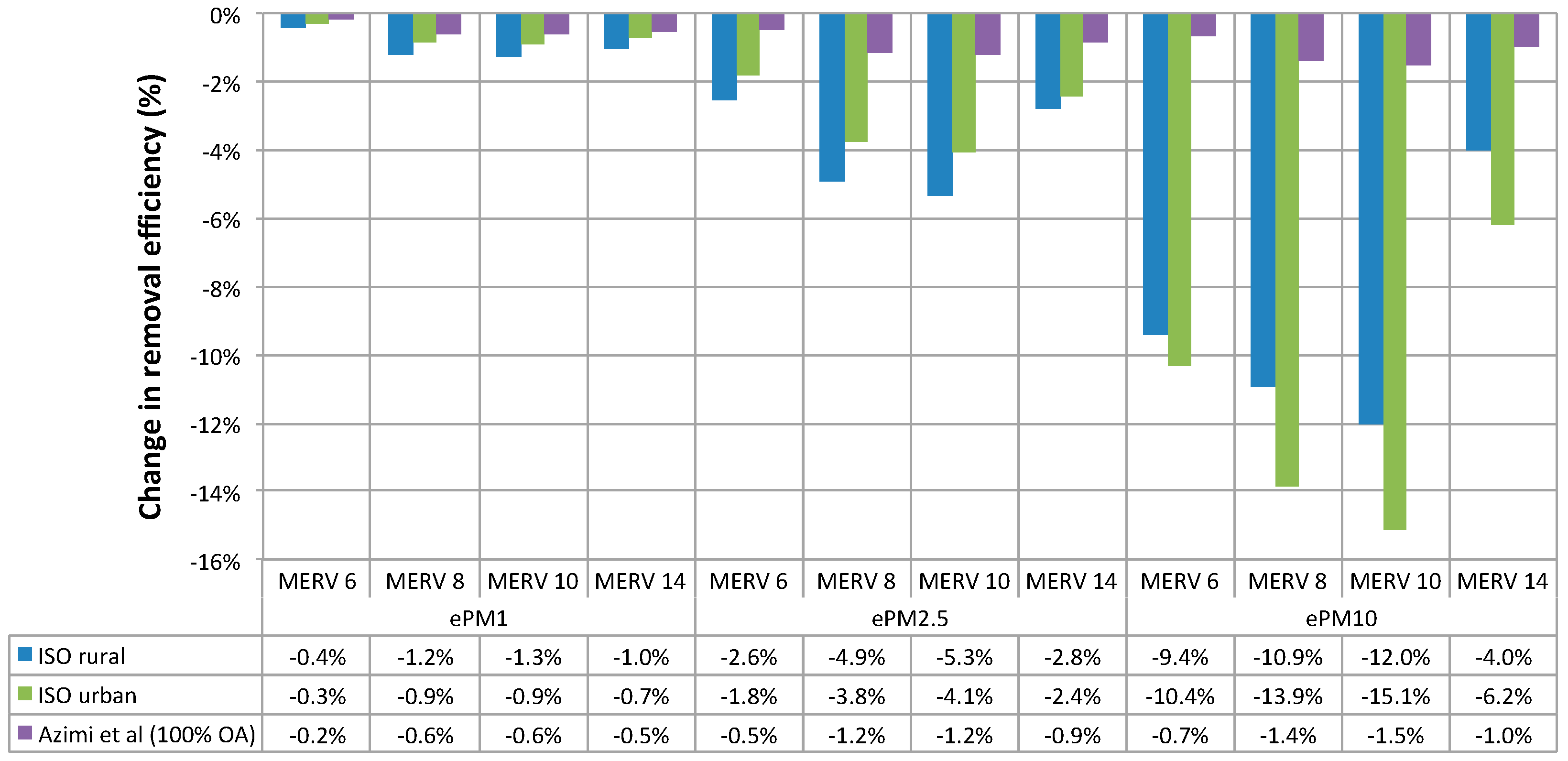
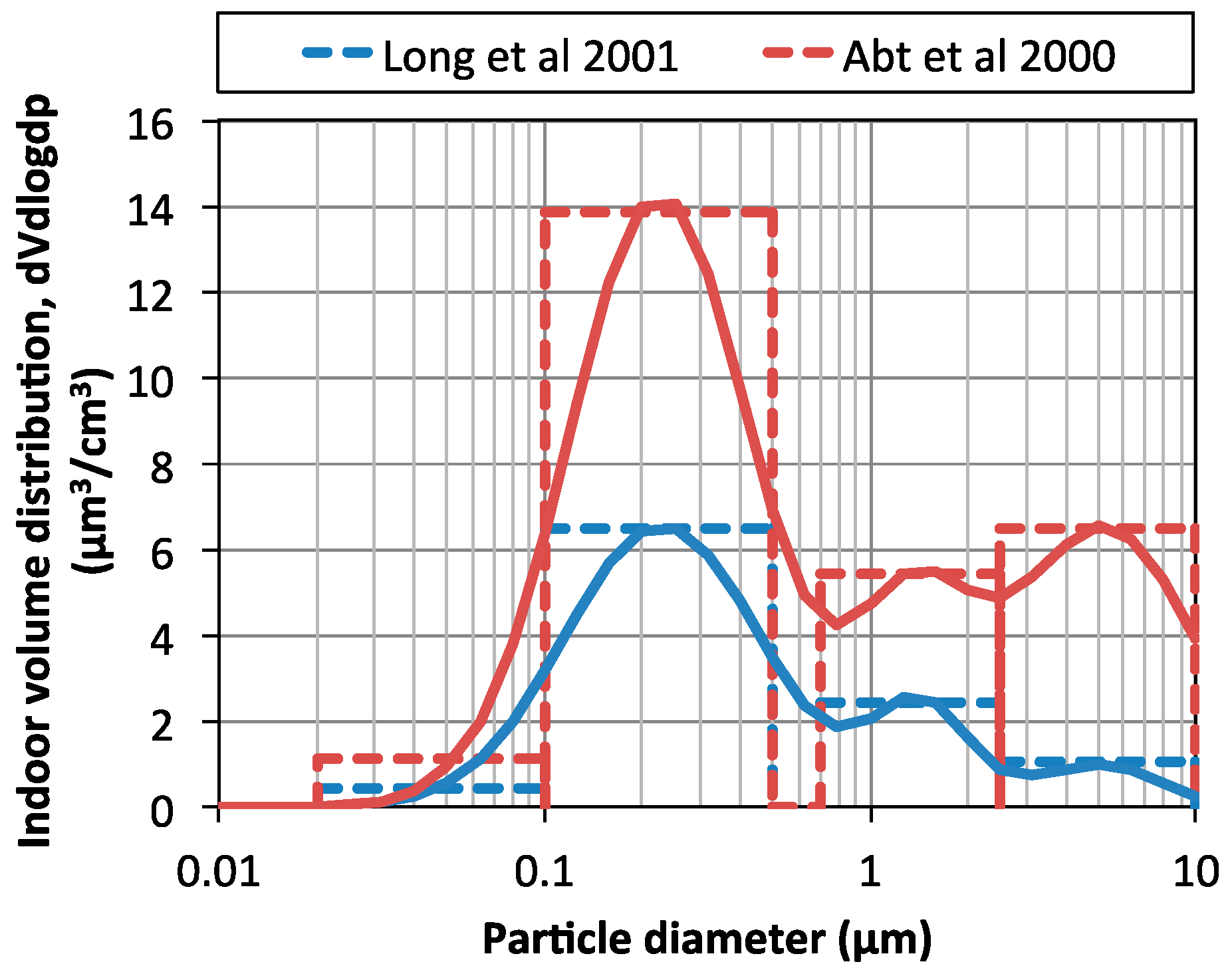
3.3. How Does the Outdoor-to-Indoor Transport of Ambient Aerosol Distributions Affect Estimates of ePM for Particles of Outdoor Origin?
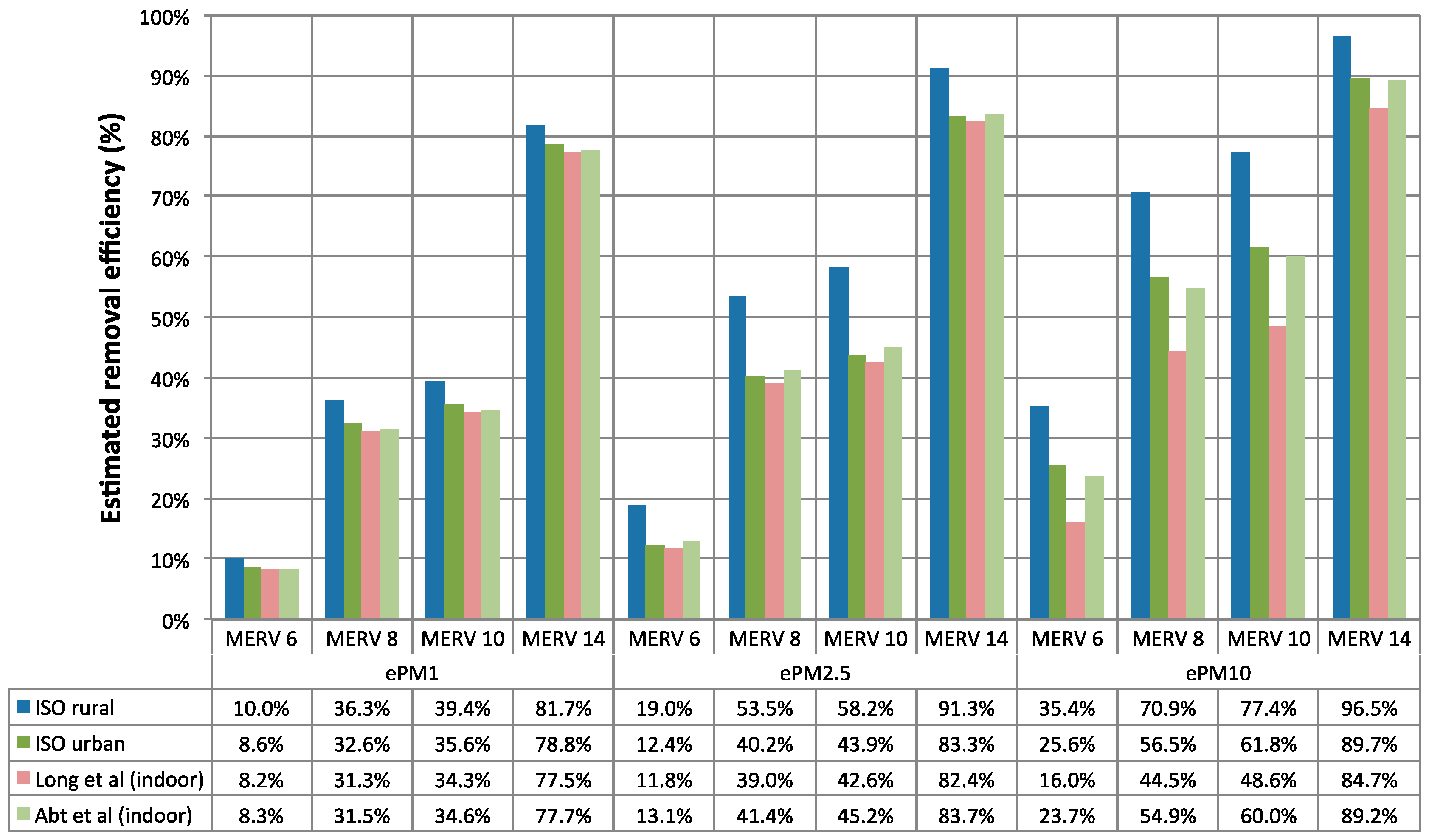
3.4. How Does the Use of Indoor Aerosol Distributions Affect Estimates of ePM?
4. Discussion
- The urban and rural ambient aerosol distributions used in ISO 16890 date back to the 1970s, and have number concentrations that greatly exceed most recent ambient aerosol distributions. However, the shape of the number distributions are somewhat similar to more recent ambient distributions, albeit with some deviations in the ~0.05–0.5 µm size range.
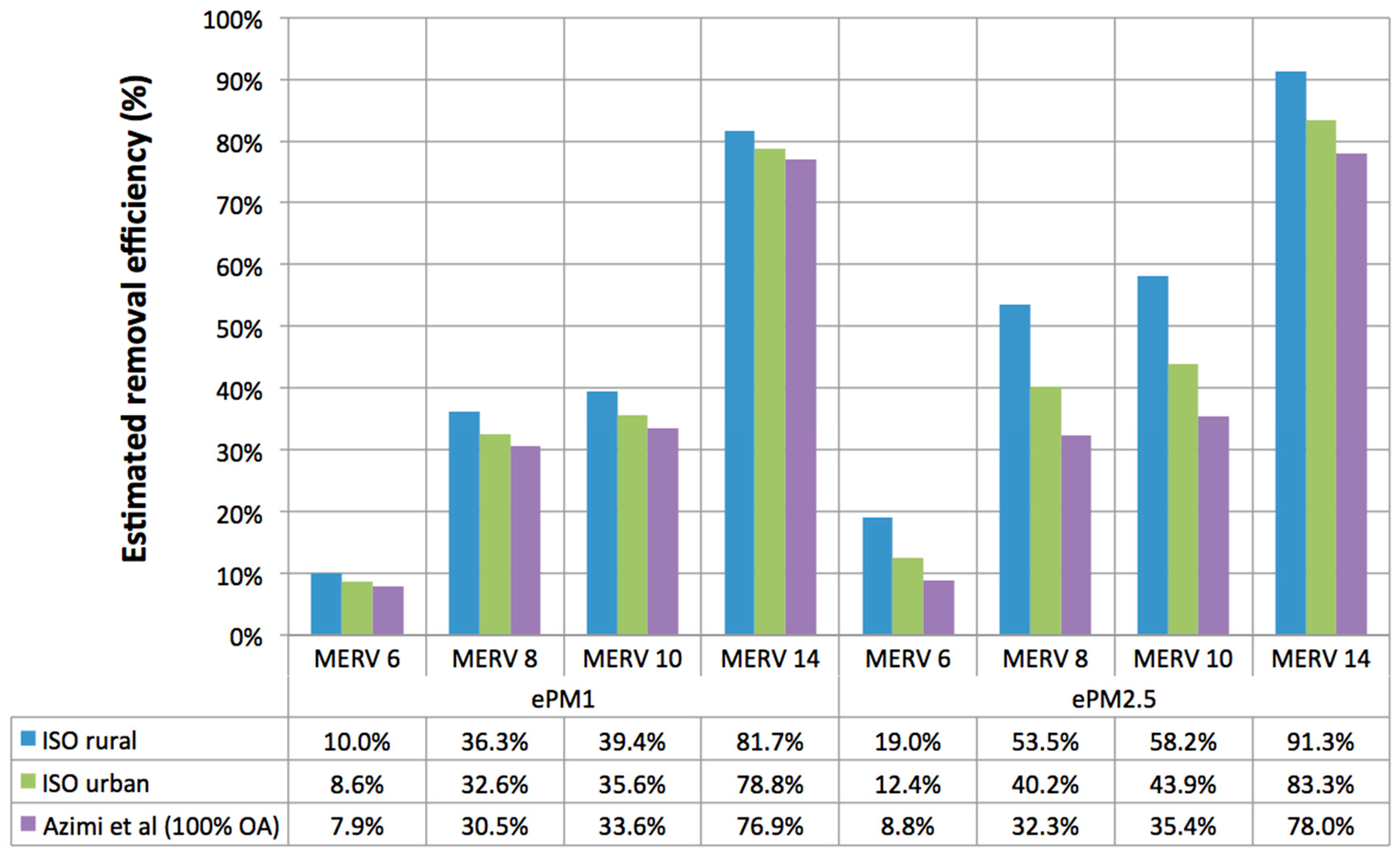
- Differences in estimates of ePM for filtration of 100% outdoor air made using the historical ambient aerosol distributions in ISO 16890 and more modern ambient distributions can be substantial (particularly for ePM2.5).
- Failing to account for size-resolved transformations that typically occur during outdoor-to-indoor transport, particularly in residential buildings, yields estimates of ePM for indoor particles of outdoor origin that are overestimated by as much as ~15% (on a relative basis) for the four HVAC filters investigated herein.
- The use of indoor aerosol distributions to represent indoor particulate matter that is a mixture of indoor and outdoor sources rather than assuming filtration of 100% outdoor air yields relatively large differences in estimates of ePM10, but estimates of ePM1 and ePM2.5 were actually quite similar.
- The historical and static ambient aerosol distributions should be updated to reflect more modern ambient environments.
- The standard should reconsider its use of the somewhat artificial distinction that filters that were designed to filter primarily PM1 and PM2.5 size fractions be characterized using only the urban aerosol distribution, and that filters designed to filter primarily PM10 be characterized using only on the rural volume distribution. Given that HVAC filters are currently marketed and sold to consumers without the distinction of whether the filter should be used in an urban or rural environment, and that suburban and other environments are not explicitly addressed, this practice will likely lead to more confusion than clarity.
- The standard should be modified in order to allow for estimations of ePM based on other commonly used HVAC system configurations in addition to 100% outdoor, including 100% recirculation systems, and mixed outdoor/recirculation systems with variable outdoor air fractions in which indoor PM is a mixture of aerosols that are generated indoors and transported from outdoors (often through building envelopes, particularly in residences, but not always).
- To support item #3 above, further research should be conducted in order to more robustly characterize indoor aerosol distributions in a wide variety of building types and under a variety of conditions (e.g., varying emission sources, ventilation rates, etc.).
- Although not explicitly address herein, the vast majority of particles in both indoor and outdoor environments (on a number basis) are typically smaller than 0.3 µm (and typically ultrafine particles, or UFPs, smaller than 0.1 µm) [36,54,55]. Therefore, ISO 16890 and other standards should consider adopting measures of removal efficiency for size-resolved and/or total UFPs to better characterize the impact that filters can have on IAQ.
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Stephens, B.; Brennan, T.; Harriman, L. Selecting ventilation air filters to reduce PM2.5 of outdoor origin. ASHRAE J. 2016, 9, 12–20. [Google Scholar]
- Singer, B.C.; Delp, W.W.; Black, D.R.; Walker, I.S. Measured performance of filtration and ventilation systems for fine and ultrafine particles and ozone in an unoccupied modern California house. Indoor Air 2016, 27, 780–790. [Google Scholar] [CrossRef] [PubMed]
- Chan, W.R.; Parthasarathy, S.; Fisk, W.J.; McKone, T.E. Estimated effect of ventilation and filtration on chronic health risks in U.S. offices, schools, and retail stores. Indoor Air 2016, 26, 331–343. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, M.C.; Ludwig, J.F.; Brown, S.G.; Vaughn, D.L.; Roberts, P.T. Filtration effectiveness of HVAC systems at near-roadway schools. Indoor Air 2013, 23, 196–207. [Google Scholar] [CrossRef] [PubMed]
- Polidori, A.; Fine, P.M.; White, V.; Kwon, P.S. Pilot study of high-performance air filtration for classroom applications. Indoor Air 2013, 23, 185–195. [Google Scholar] [CrossRef] [PubMed]
- MacIntosh, D.L.; Minegishi, T.; Kaufman, M.; Baker, B.J.; Allen, J.G.; Levy, J.I.; Myatt, T.A. The benefits of whole-house in-duct air cleaning in reducing exposures to fine particulate matter of outdoor origin: A modeling analysis. J. Expo. Sci. Environ. Epidemiol. 2010, 20, 213–224. [Google Scholar] [CrossRef] [PubMed]
- Brown, K.W.; Minegishi, T.; Allen, J.; McCarthy, J.F.; Spengler, J.D.; MacIntosh, D.L. Reducing Patients’ Exposures to Asthma and Allergy Triggers in their Homes: An Evaluation of Effectiveness of Grades of Forced Air Ventilation Filters. J. Asthma 2014, 51, 585–594. [Google Scholar] [CrossRef] [PubMed]
- ASHRAE Standard 52.2: Method of Testing General Ventilation Air-Cleaning Devices for Removal Efficiency by Particle Size; ASHRAE: Atlanta, GA, USA, 2017.
- ISO 16890: Air Filters for General Ventilation 2016; ISO: Geneva, Switzerland, 2016.
- Brook, R.D.; Rajagopalan, S.; Pope, C.A.; Brook, J.R.; Bhatnagar, A.; Diez-Roux, A.V.; Holguin, F.; Hong, Y.; Luepker, R.V.; Mittleman, M.A.; et al. Particulate matter air pollution and cardiovascular disease. Circulation 2010, 121, 2331–2378. [Google Scholar] [CrossRef] [PubMed]
- Di, Q.; Wang, Y.; Zanobetti, A.; Wang, Y.; Koutrakis, P.; Choirat, C.; Dominici, F.; Schwartz, J.D. Air Pollution and Mortality in the Medicare Population. N. Engl. J. Med. 2017, 376, 2513–2522. [Google Scholar] [CrossRef] [PubMed]
- Dockery, D.W.; Pope, C.A., 3rd; Xu, X.; Spengler, J.D.; Ware, J.H.; Fay, M.E.; Ferris, B.G., Jr.; Speizer, F.E. An association between air pollution and mortality in six U.S. cities. N. Engl. J. Med. 1993, 329, 1753–1759. [Google Scholar] [CrossRef] [PubMed]
- Gharibvand, L.; Shavlik, D.; Ghamsary, M.; Beeson, W.L.; Soret, S.; Knutsen, R.; Knutsen, S.F. The Association between Ambient Fine Particulate Air Pollution and Lung Cancer Incidence: Results from the AHSMOG-2 Study. Environ. Health Perspect. 2017, 125, 378–384. [Google Scholar] [CrossRef] [PubMed]
- Krewski, D.; Jerrett, M.; Burnett, R.T.; Ma, R.; Hughes, E.; Shi, Y.; Turner, M.C.; Pope, C.A., III; Thurston, G.; Calle, E.E.; et al. Extended follow-up and spatial analysis of the American Cancer Society study linking particulate air pollution and mortality. Res. Rep. Health Eff. Inst. 2009, 140, 5–114. [Google Scholar]
- Pope, C.A.; Burnett, R.T.; Thun, M.J.; Calle, E.E.; Krewski, D.; Ito, K.; Thurston, G.D. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution. JAMA J. Am. Med. Assoc. 2002, 287, 1132–1141. [Google Scholar] [CrossRef]
- Pope, C.A.; Dockery, D.W. Health effects of fine particulate air pollution: Lines that connect. J. Air Waste Manag. Assoc. 2006, 56, 709–742. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Zanobetti, A.; Kloog, I.; Coull, B.A.; Koutrakis, P.; Melly, S.J.; Schwartz, J.D. Low-Concentration PM2.5 and Mortality: Estimating Acute and Chronic Effects in a Population-Based Study. Environ. Health Perspect. 2015, 124, 46–52. [Google Scholar] [CrossRef] [PubMed]
- U.S. Environmental Protection Agency. Integrated Science Assessment for Particulate Matter; U.S. EPA: Washington, DC, USA, 2009.
- Logue, J.M.; Price, P.N.; Sherman, M.H.; Singer, B.C. A method to estimate the chronic health impact of air pollutants in U.S. residences. Environ. Health Perspect. 2012, 120, 216–222. [Google Scholar] [CrossRef] [PubMed]
- McDonnell, W.F.; Nishino-Ishikawa, N.; Petersen, F.F.; Chen, L.H.; Abbey, D.E. Relationships of mortality with the fine and coarse fractions of long-term ambient PM10 concentrations in nonsmokers. J. Expo. Sci. Environ. Epidemiol. 2000, 10, 427–436. [Google Scholar] [CrossRef]
- CEN EN 779: Particulate Air Filters for General Ventilation—Determination of the Filtration Performance; European Committee for Standardization: Brussels, Belgium, 2012.
- Neusüss, C.; Wex, H.; Birmili, W.; Wiedensohler, A.; Koziar, C.; Busch, B.; Brüggemann, E.; Gnauk, T.; Ebert, M.; Covert, D.S. Characterization and parameterization of atmospheric particle number-, mass-, and chemical-size distributions in central Europe during LACE 98 and MINT. J. Geophys. Res. 2002, 107, LAC 91–LAC 913. [Google Scholar] [CrossRef]
- Pitz, M.; Schmid, O.; Heinrich, J.; Birmili, W.; Maguhn, J.; Zimmermann, R.; Wichmann, H.-E.; Peters, A.; Cyrys, J. Seasonal and Diurnal Variation of PM2.5 Apparent Particle Density in Urban Air in Augsburg, Germany. Environ. Sci. Technol. 2008, 42, 5087–5093. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Peng, J.; Sun, K.; Yue, D.; Guo, S.; Wiedensohler, A.; Wu, Z. Estimation of Size-Resolved Ambient Particle Density Based on the Measurement of Aerosol Number, Mass, and Chemical Size Distributions in the Winter in Beijing. Environ. Sci. Technol. 2012, 46, 9941–9947. [Google Scholar] [CrossRef] [PubMed]
- Riley, W.J.; McKone, T.E.; Lai, A.C.K.; Nazaroff, W.W. Indoor particulate matter of outdoor origin: Importance of size-dependent removal mechanisms. Environ. Sci. Technol. 2002, 36, 200–207. [Google Scholar] [CrossRef] [PubMed]
- Waring, M.S.; Siegel, J.A. Particle loading rates for HVAC filters, heat exchangers, and ducts. Indoor Air 2008, 18, 209–224. [Google Scholar] [CrossRef] [PubMed]
- El Orch, Z.; Stephens, B.; Waring, M.S. Predictions and determinants of size-resolved particle infiltration factors in single-family homes in the U.S. Build. Environ. 2014, 74, 106–118. [Google Scholar] [CrossRef]
- Zaatari, M.; Novoselac, A.; Siegel, J. The relationship between filter pressure drop, indoor air quality, and energy consumption in rooftop HVAC units. Build. Environ. 2014, 73, 151–161. [Google Scholar] [CrossRef]
- Azimi, P.; Zhao, D.; Stephens, B. Estimates of HVAC filtration efficiency for fine and ultrafine particles of outdoor origin. Atmos. Environ. 2014, 98, 337–346. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Jaenicke, R. Chapter 1 Tropospheric Aerosols. In International Geophysics; Elsevier: San Diego, CA, USA, 1993; Volume 54, pp. 1–31. [Google Scholar]
- Hobbs, P.V.; Bowdle, D.A.; Radke, L.F. Particles in the Lower Troposphere over the High Plains of the United States. Part I: Size Distributions, Elemental Compositions and Morphologies. J. Clim. Appl. Meteorol. 1985, 24, 1344–1356. [Google Scholar] [CrossRef]
- Jaenicke, R.; Junge, C. Studien zur oberen Grenzgröße des natürlichen Aerosols. Beitr. Phys. Atmos. 1967, 40, 129–142. (In German) [Google Scholar]
- Whitby, K.T. The physical characteristics of sulfur aerosols. Atmos. Environ. 1978, 12, 135–159. [Google Scholar] [CrossRef]
- Hecker, R.; Hofacre, K.C. Development of Performance Data for Common Building Air Cleaning Devices; U.S. Environmental Protection Agency: Washington, DC, USA, 2008.
- Wallace, L. Indoor sources of ultrafine and accumulation mode particles: Size distributions, size-resolved concentrations, and source strengths. Aerosol Sci. Technol. 2006, 40, 348–360. [Google Scholar] [CrossRef]
- Kearney, J.; Wallace, L.; MacNeill, M.; Xu, X.; VanRyswyk, K.; You, H.; Kulka, R.; Wheeler, A.J. Residential indoor and outdoor ultrafine particles in Windsor, Ontario. Atmos. Environ. 2010. [Google Scholar] [CrossRef]
- Chan, W.R.; Logue, J.M.; Wu, X.; Klepeis, N.E.; Fisk, W.J.; Noris, F.; Singer, B.C. Quantifying fine particle emission events from time-resolved measurements: Method description and application to 18 California low-income apartments. Indoor Air 2017, 28, 89–101. [Google Scholar] [CrossRef] [PubMed]
- MacNeill, M.; Kearney, J.; Wallace, L.; Gibson, M.; Héroux, M.E.; Kuchta, J.; Guernsey, J.R.; Wheeler, A.J. Quantifying the contribution of ambient and indoor-generated fine particles to indoor air in residential environments. Indoor Air 2014, 24, 362–375. [Google Scholar] [CrossRef] [PubMed]
- Morawska, L.; Afshari, A.; Bae, G.N.; Buonanno, G.; Chao, C.Y.H.; Hänninen, O.; Hofmann, W.; Isaxon, C.; Jayaratne, E.R.; Pasanen, P.; et al. Indoor aerosols: From personal exposure to risk assessment. Indoor Air 2013, 23, 462–487. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.W.; Adar, S.D.; Avol, E.; Cohen, M.; Curl, C.L.; Larson, T.; Liu, L.-J.S.; Sheppard, L.; Kaufman, J.D. Modeling the residential infiltration of outdoor PM2.5 in the Multi-Ethnic Study of Atherosclerosis and Air Pollution (MESA Air). Environ. Health Perspect. 2012, 120, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhao, B. Review of relationship between indoor and outdoor particles: I/O ratio, infiltration factor and penetration factor. Atmos. Environ. 2011, 45, 275–288. [Google Scholar] [CrossRef]
- Meng, Q.Y.; Turpin, B.J.; Korn, L.; Weisel, C.P.; Morandi, M.; Colome, S.; Zhang, J.; Stock, T.; Spektor, D.; Winer, A.; et al. Influence of ambient (outdoor) sources on residential indoor and personal PM2.5 concentrations: Analyses of RIOPA data. J. Expo. Anal. Environ. Epidemiol. 2005, 15, 17–28. [Google Scholar] [CrossRef] [PubMed]
- Nazaroff, W.W. Indoor particle dynamics. Indoor Air 2004, 14, 175–183. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Azimi, P.; Stephens, B. Evaluating the long-term health and economic impacts of central residential air filtration for reducing premature mortality associated with indoor fine particulate matter (PM2.5) of outdoor origin. Int. J. Environ. Res. Public Health 2015, 12, 8448–8479. [Google Scholar] [CrossRef] [PubMed]
- Azimi, P.; Zhao, D.; Stephens, B. Modeling the Impact of Residential HVAC Filtration on Indoor Particles of Outdoor Origin (RP-1691). Sci. Technol. Built Environ. 2016, 22, 431–462. [Google Scholar] [CrossRef]
- Montgomery, J.F.; Reynolds, C.C.O.; Rogak, S.N.; Green, S.I. Financial implications of modifications to building filtration systems. Build. Environ. 2015, 85, 17–28. [Google Scholar] [CrossRef]
- Bekö, G.; Clausen, G.; Weschler, C. Is the use of particle air filtration justified? Costs and benefits of filtration with regard to health effects, building cleaning and occupant productivity. Build. Environ. 2008, 43, 1647–1657. [Google Scholar] [CrossRef]
- Fisk, W.J.; Chan, W.R. Effectiveness and cost of reducing particle-related mortality with particle filtration. Indoor Air 2017, 27, 909–920. [Google Scholar] [CrossRef] [PubMed]
- Abt, E.; Suh, H.H.; Allen, G.; Koutrakis, P. Characterization of indoor particle sources: A study conducted in the metropolitan Boston area. Environ. Health Perspect. 2000, 108, 35–44. [Google Scholar] [CrossRef] [PubMed]
- Long, C.M.; Suh, H.H.; Catalano, P.J.; Koutrakis, P. Using time- and size-resolved particulate data to quantify indoor penetration and deposition behavior. Environ. Sci. Technol. 2001, 35, 2089–2099. [Google Scholar] [CrossRef] [PubMed]
- Hussein, T.; Glytsos, T.; Ondracek, J.; Dohanyosova, P.; Zdimal, V.; Hameri, K.; Lazaridis, M.; Smolik, J.; Kulmala, M. Particle size characterization and emission rates during indoor activities in a house. Atmos. Environ. 2006, 40, 4285–4307. [Google Scholar] [CrossRef]
- Afshari, A.; Matson, U.; Ekberg, L.E. Characterization of indoor sources of fine and ultrafine particles: A study conducted in a full-scale chamber. Indoor Air 2005, 15, 141–150. [Google Scholar] [CrossRef] [PubMed]
- Wallace, L.; Ott, W. Personal exposure to ultrafine particles. J. Expo. Sci. Environ. Epidemiol. 2011, 21, 20–30. [Google Scholar] [CrossRef] [PubMed]
- Health Effects Institute. Understanding the Health Effects of Ambient Ultrafine Particles; Health Effects Institute: Boston, MA, USA, 2013. [Google Scholar]

| Distribution | Mode 1 | Mode 2 | Mode 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| N (#/cm3) | Dg (µm) | logσg | N (#/cm3) | Dg (µm) | logσg | N (#/cm3) | Dg (µm) | logσg | |
| Urban | 9.93 × 104 | 0.013 | 0.245 | 1.1 × 103 | 0.014 | 0.666 | 3.64 × 104 | 0.050 | 0.337 |
| Rural | 6650 | 0.015 | 0.225 | 147 | 0.054 | 0.557 | 1990 | 0.084 | 0.266 |
| Distribution | Mode 1 | Mode 2 | Mode 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| N (#/cm3) | Dg (µm) | logσg | N (#/cm3) | Dg (µm) | logσg | N (#/cm3) | Dg (µm) | logσg | |
| Abt et al. (2000) | 10,700 | 0.065 | 0.280 | 3.5 | 0.8 | 0.180 | 0.4 | 1.5 | 0.280 |
| Long et al. (2001) | 6660 | 0.055 | 0.300 | 1 | 1 | 0.150 | 0.15 | 3.0 | 0.180 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stephens, B. Evaluating the Sensitivity of the Mass-Based Particle Removal Calculations for HVAC Filters in ISO 16890 to Assumptions for Aerosol Distributions. Atmosphere 2018, 9, 85. https://doi.org/10.3390/atmos9030085
Stephens B. Evaluating the Sensitivity of the Mass-Based Particle Removal Calculations for HVAC Filters in ISO 16890 to Assumptions for Aerosol Distributions. Atmosphere. 2018; 9(3):85. https://doi.org/10.3390/atmos9030085
Chicago/Turabian StyleStephens, Brent. 2018. "Evaluating the Sensitivity of the Mass-Based Particle Removal Calculations for HVAC Filters in ISO 16890 to Assumptions for Aerosol Distributions" Atmosphere 9, no. 3: 85. https://doi.org/10.3390/atmos9030085
APA StyleStephens, B. (2018). Evaluating the Sensitivity of the Mass-Based Particle Removal Calculations for HVAC Filters in ISO 16890 to Assumptions for Aerosol Distributions. Atmosphere, 9(3), 85. https://doi.org/10.3390/atmos9030085