Abstract
We examine the capability of thirteen Coupled Model Intercomparison Project (CMIP) phase 5 (CMIP5) models in simulating climatology and interannual variability of Winter North Pacific Storm Track (WNPST). It is found that nearly half of the selected models can reproduce the spatial pattern of WNPST climatology. However, the strength and spatial variation of WNPST climatology are weak in most of the models. Most differences among the models are in the northeast of the simulated multi-model ensemble (MME) climatology, while it is more consistent in the south. The MME can reflect not only the center position, but also the strength and spatial distribution of interannual variation of the WNPST amplitude. Except for CNRM-CM5, the interannual standard deviations of simulated WNPST strength and spatial variation in all other models are weak. ACCESS1-3 and CanESM2 have a better capability in simulating the spatial modes of WNPST, while the simulated second and third modes in some models are in opposite order with those in NCEP (National Centers for Environmental Prediction) reanalysis. Only five models and MME can capture “midwinter suppression” feature in their simulations. Compared with NCEP reanalysis, the winter longitude index is larger and latitude index is smaller in most of the models, indicating the simulated storm track is further east and south. CNRM-CM5, MME and CMCC-CM could be used to evaluate interannual variation of strength index, longitude index and latitude index respectively. Nevertheless, only INM-CM4 and CNRM-CM5 can simulate southward drift of WNPST.
1. Introduction
Meridional transport of heat and kinetic energy by synoptic-scale transient eddies plays an important role in maintaining atmospheric circulation. As midlatitude storm track (MST) is the most active region for mid-latitude synoptic transient eddies, its variation reflects not only some aspects of synoptic transient eddy itself but also a close relationship between the storm track and developing baroclinic waves [1,2,3,4]. As a bridge for exchange of water vapor, heat and kinetic energy between ocean and atmosphere, MST is crucial for energy transport between tropics and mid-higher latitude. MST is also a focus for climate dynamics [5], and its variation is one of major components in studying climate change. It interacts with large-scale atmospheric circulation, and exhibits various features in a broad range of temporal scales including monthly, seasonal, interannual, decadal and interdecadal variation [6,7,8,9,10,11,12,13].
Characteristics about MST variability have been substantially revealed in previous studies. It has been proposed that two wave guides exist in the strong baroclinic region in mid-latitude North Pacific for transporting synoptic scale vortices [14], which is consistent with the recent finding of double storm tracks in the lower troposphere [15]. Nakamura [2] demonstrated that seasonal variation of MST exhibits a “midwinter suppression” feature. In decadal scale, some previous studies indicate variation of MST is a response to ENSO [16]. Nakamura et al. [17] found interannual variation of MST is related to anomalous winter monsoon and the strength of its corresponding East Asia jet as well as heat transport of stationary/transient wave.
With the advancement of climate models, it has become a very important method to use model to study and simulate the impact of MST on anomalous climate [18,19]. Through numerical simulation, Cai and Mak [20] demonstrated that atmospheric low-frequency variability is related to synoptic scale vortex. Chang [21] successfully simulated interannual variation of WNPST (Winter North Pacific Storm Track) through a dry nonlinear model, and found the structure of storm track is determined by the mean flow. Chang and Guo [22] studied interannual variation of MST with a stationary wave model and an ideal General Circulation Model and pointed out that not only the interaction between the local wave and mean flow but also the remote forcing from large-scale planetary wave should be included to account for the variability. Yao et al. [23] used WRFV3.4 to verify the “baroclinic ocean adjustment” mechanism proposed by Nakamura et al. [24,25], that is, the offset of heat transport from both sides of Kuroshio Oyashio Extension and poleward transport so that baroclinicity is maintained, which is required for continuous development of storm track.
However, many uncertainties still exist in the models, and large model bias is one of the common features for all the models. Besides, there are significant differences among models. Therefore, evaluating the capability of models in simulating the storm track and analyzing model biases is crucial for the application of models to the prediction of storm tracks variability and the response to climate change. The outputs from the latest climate system models for Coupled Model Intercomparison Project (CMIP) phase 5 (CMIP5) have been extensively investigated and compared with the earlier CMIP3 results [26]. Compared with CMIP phase 3 (CMIP3) models, CMIP5 models have higher resolution and better representation of the earth system [27]. Chang et al. [28] evaluated 23 models in simulating the storm track based on CMIP5 outputs and compared the results with those from 17 models in CMIP3 [29]. The comparison revealed that the climatology of storm track in most of CMIP5 models is weaker and the simulated storm track is closer to the equator than that in the CMIP3 models. Possible implications of model biases in storm-track climatology have been investigated by Chang et al. [29], and they found that biases in storm-track amplitudes in general circulation model simulations are not primarily due to horizontal resolution. With 12 CMIP5 models and ERA-Interim data, Booth et al. [5] examined interaction of surface storm tracks and western boundary current. As for under a global warming climate, the weaker the simulated climatology of storm track, the more uncertainties of the projected climate of the middle 21th century (2041–2060), and for the Northern Hemisphere, the models project some poleward shift and upward expansion of the storm track in the upper troposphere, but mainly weakening of the storm track toward its equatorward flank in the troposphere [28].
All these previous studies paid more attention on the aspects of the projected storm track, with a broad focus not only on the storm track in the northern hemisphere, but also on the storm track in the whole globe, and the methods they used to evaluate the climatology of storm track are also limited. In addition, few studies involved discussion about the interannual variability of the storm track. In this study, we select 13 CMIP5 models and, with a focus on meridional transport of heat flux, we aim to provide a relatively more complete evaluation of the WNPST climatology and interannual variability and provide reference for Intercomparison between the models and further improvements. In the following, Section 2 includes a brief description about reanalysis dataset, CMIP5 models, and the methods used in this study. Section 3 presents the assessments of the climatology and interannual variability of WNPST in the models. A summary is given in Section 4.
2. Data and Methods
2.1. Data
The daily reanalysis data are from NCEP/NCAR global reanalysis dataset. The primary variables we used include zonal wind and temperature at 850 hPa. The horizontal resolution of the data is 2.5° × 2.5°, and the period is 1955–2005. In this study, the winter refers to the time period of December to February. The 13 CMIP5 models are listed in Table 1. The simulation data used are outputs from “long-term” historical experiments, Taylor et al. [26] gave a detailed introduction about the experiments.

Table 1.
List of 13 selected Coupled Model Intercomparison Project (CMIP) phase 5 (CMIP5) climate models.
2.2. Methods
MST can be represented by variance of geopotential height, meridional transport of heat flux or eddy kinetic energy [4]. In this study, we use meridional transport of heat flux (, is meridional wind speed, is temperature) to represent WNPST. Because WNPST has a three-dimensional structure from sea surface to the tropopause. Thus, it can be well represented by the variable at different level. As the maximum of the heat flux is located at the lower level of the troposphere (usually 850 hPa), at 850 hPa is selected for this study. On the other hand, due to various resolution of the model outputs, for convenience of comparison, we interpolate all the data into 2.5° × 2.5° grid before calculation. We use a Lanzcos band-pass filter to isolate synoptic scale (2.5–6-day) disturbance from NCEP/NCAR reanalysis daily data, and calculate with the formula showed below:
In this formula, and represent 2.5–6-day filtered synoptic component, represents the days in the time series. The climatological mean and in this study are the monthly climatology based on the daily meridional wind speed and temperature anomaly after filtering, respectively.
In order to further evaluate the capability of each CMIP5 model in simulating strength and location of WNPST, a couple of WNPST indices are introduced in this paper. We adopted the method proposed by Li et al. [30] which can represent the WNPST dynamically and quantitatively. Specifically, we set a threshold which is the median of WNPST strength of all the grids within a domain (25°–65° N, 130° E–120° W). By doing so, the number of grids is same for all the samples, and WNPST is well represented by the selected grids. The mean of the values greater than this threshold in all the grids is defined as strength index of WNPST, conveniently, the average longitude/latitude is defined as longitude/latitude index. Strength, longitude and latitude index are expressed as follows:
N is the number of grid point, on which the strength is great than the median of WNPST strength of all the grids within a domain. Then, Str, Lon and Lat are the strength, longitude and latitude of WNPST on that grid point, respectively. A positive difference with NCEP in latitude (longitude) index mean northward (eastward) shift of storm track in CMIP5.
Considering North et al. [31] pointed out that EOF (empirical orthogonal function) analyses often result in pairs of equally important modes, we apply the EOF skill score (ESS) introduced by Timm and Diaz [32]. The calculation formula is as follows:
the correlations between ith spatial EOF pattern of CMIP5 models and the jth EOF of NCEP reanalysis are summed over a limited range of EOF combinations. Weight function is according to
with i, j representing the EOF modes 1, 2 3. The weights in the EOF skill score ESS also account for the explained variance and of the eigenmodes of the model and the reanalysis, respectively.
3. Results
3.1. Climatology
Figure 1 depicts the simulated WNPST climatology in selected 13 CMIP5 models and their differences to NCEP reanalysis (Figure 1a). Figure 1b shows the results of multi-model ensemble (MME) which represents the mean of the results from all the selected models. To better evaluate the capability of each model in simulating WNPST, Taylor diagram (Figure 2) is also adopted to display the relative information from multiple models concisely, so that the differences among the simulations from all the models are revealed clearly [33]. This diagram shows the ratio of the standard deviation calculated from simulation to that obtained in reanalysis, correlation coefficient and root mean square error (RMSE). The closer the point representing the model to REF (see Figure 2), the better capability of the model [34].
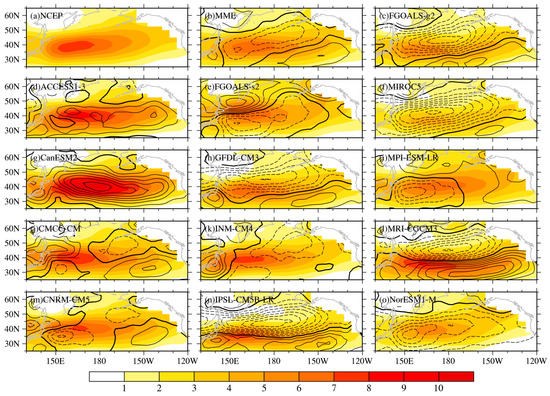
Figure 1.
Winter North Pacific Storm Track (WNPST) climatology (Shading) and the difference between each model and NCEP reanalysis (contour, with an interval of 0.5, black bold line represents the contour with the zero value) (unit: K∙ms−1). The value is not shown in blank areas to avoid data contamination by terrain effect.
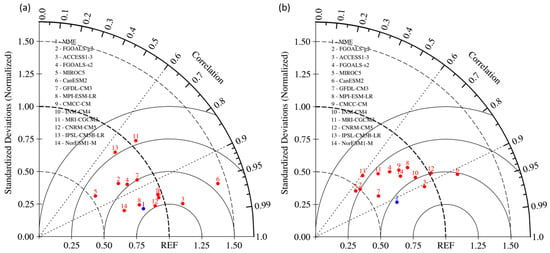
Figure 2.
Taylor diagrams of (a) WNPST Climatology and (b) interannual variation of its amplitude.
According to Figure 1, all these 13 models generally can reproduce WNPST climatology, yet large discrepancies exist about the strength and location of WNPST. The differences between the models are also significant. In terms of strength, the simulated WNPST in CanESM2 is the strongest, with a positive bias over 3 K∙ms−1 near the center. The stronger simulated WNPST can also be found in MRI-CGCM3 and IPSL-CM5B-LR models, they both show a bias exceeding 3 K∙ms−1 near the center. While the simulations of WNPST in FGOALS-g2, MIROC5 and NorESM-M are generally weak, especially for MIROC5, with a negative bias of 4 K∙ms−1 near the center of the storm track. Nevertheless, ACCESS1-3 and CNRM-CM5 generate better simulations, the absolute value of bias is less than 1 K∙ms−1 for most of the area. CanESM2, MIROC5, MRI-CGCM3 and IPSL-CM5B-LR show a large RMSE (Figure 2a), while the RMSEs of simulation in ACCESS1-3 and CNRM-CM5 are smaller.
Specifically, the center location of simulated WNPST in MRI-CGCM3, MIROC5, FGOALS-g2, GFDL-CM3 and IPSL-CM5B-LR is further south, which is reflected by negative bias in the north of the domain. The simulated WNPST in FGOALS-s2 is stronger in the north, and weaker in the south and east. While it is stronger in the west for the simulations in INM-CM4 and CMCC-CM. An obvious eastward extension can be found in the simulations of CanESM2 and ACCESS1-3. It seems most of the models have little capability in simulating the center location and strength of WNPST. The MME can generally reflect the center location of WNPST, but the strength of WNPST is still weak.
It can be learned from Figure 2a that the spatial pattern is well simulated in 7 models including CanESM2, ACCESS1-3 and CNRM-CM5, with a correlation coefficient greater than 0.9. Especially, the correlation coefficient for ACCESS1-3 is larger than 0.97, but is not well reproduced in several models including IPSL-CM5B-LR, MRI-CGCM3 and MIROC5. Figure 2a also shows that, for the standard deviation of WNPST climatology, large differences exist among the models. CanESM2, MIROC5 and NorESM-M are three models which are the most different from the reanalysis. While CMCC-CM, INM-CM4 and MRI-CGCM3 are three models which are closest to the reanalysis. It needs to mention that the standard deviation in most of the models is smaller compared with the reanalysis, indicating further improvement is needed for these models in simulating the spatial variation of WNPST climatology.
In general, CNRM-CM5 and ACCESS1-3 have stronger capability in simulating WNPST climatology. In addition, for some specific aspects, the MME of these 13 models is not as good as even a single model, but for overall evaluation in terms of spatial distribution, standard deviation and root mean square error, MME is still superior to most of the single models.
In order to further evaluate the difference of simulated WNPST climatology among CMIP5 models, the distributions of the standard deviation from these 13 models are displayed in Figure 3 which can clearly reveal the spatial differences. It can be seen that the major difference appears over midlatitude in the central North Pacific (especially within the area of 40°–45° N,150° E–170° W). The contour in Figure 3 is WNPST climatology from the MME. It shows large differences exist in the northeast of WNPST center, while there is only small difference in the south.
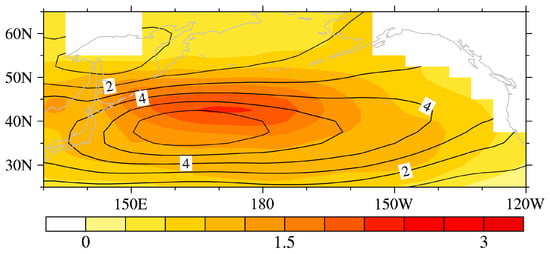
Figure 3.
The multi-model ensemble (MME) of simulated climatological WNPST amplitude (contour) and standard deviation (spread) of these 13 models (shading).
3.2. Interannual Variation of WNPST Strength
Figure 4 shows the distribution of the interannual standard deviation of WNPST amplitude from NCEP reanalysis and CMIP5 models. The capability of the models in simulating the interannual variation of WNPST amplitude can be evaluated by analyzing the interannual standard deviation. According to Figure 4a, the area with significant interannual variability is generally in a domain of 40°–45° N, 160° E–180°. While significant differences exist among these 13 models. ACCESS1-3 and CanESM2 can generally capture the center of interannual variability very well. In particular, ACCESS1-3 can even reproduce acclivous pattern of standard deviation distribution. The center of interannual variability in the simulations of CNRM-CM5, FGOALS-s2 and INM-CM4 is further west, while it is further east in the simulation of MPI-ESM-LR and further north in the simulation of CMCC-CM. the center positions are rather southwest in the simulations of GFDL-CM3, IPSL-CM5B-LR, MRI-CGCM3 and FGOALS-g2.
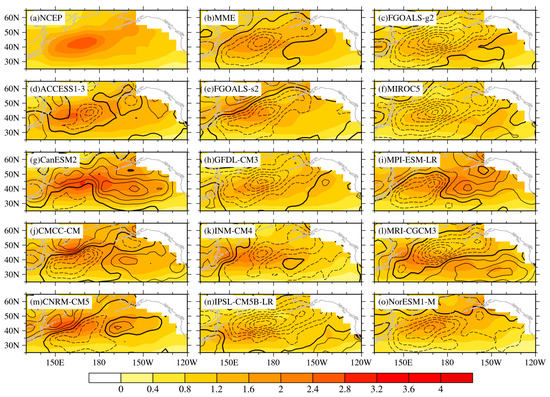
Figure 4.
Interannual standard deviation of the climatological WNPST amplitude (shading) from reanalysis and difference between each model and reanalysis (contour, with an interval of 0.2 and black bold contour represent zero line) (unit: K∙ms−1).
For interannual variation of WNPST strength, it is clear that WNPST is weaker west of 180° in most of the models. For IPSL-CM5B-LR, FGOALS-g2 and MIROC5, the overall simulations of interannual variation of WNPST amplitude are significantly weaker. The absolute value of the difference is over 1 K∙ms−1, their RMSEs are also larger (Figure 2b). On the other hand, the simulations of WNPST strength in CanESM2, CMCC-CM, MPI-ESM-LR and CNRM-CM5 are stronger in the east. The simulations in ACCESS1-3, CanESM2 and CNRM-CM5 generally have smaller bias and RMSE, which means they are more skillful in simulating the interannual variation of WNPST amplitude.
As showed in Figure 2b, ACCESS1-3 and CanESM2 perform very well in simulating the spatial pattern of interannual variation of WNPST amplitude, with a correlation coefficient greater than 0.9. For IPSL-CM5B-LR, MIROC5 and FGOALS-g2, they not only underestimate interannual variation of WNPST strength but also produce a spatial pattern that is markedly different from the reanalysis reference pattern. In addition, the interannual standard deviations of simulated WNPST amplitude in MIROC5 and FGOALS-g2 are much smaller, while the simulation in CNRM-CM5 is generally close to that in NCEP reanalysis. ACCESS1-3 is also able to generate an acceptable simulation. Given the fact that most of the models generate smaller interannual standard deviation compared with reanalysis, it is reasonable to believe that most of the models have less capability in simulating interannual variation of WNPST amplitude.
In general, ACCESS1-3, INM-CM4 and CNRM-CM5 all perform very well in simulating the spatial pattern, strength and interannual standard deviation of WNPST amplitude, especially for ACCESS1-3, while some simulation results (IPSL-CM5B-LR, MIROC5 and FGOALS-g2) are quite different from NCEP reanalysis. On the other hand, in spite of the individual model deficiencies the MME result can simulate the center position of interannual variation very well with a higher correlation coefficient exceeding 0.9 and a smaller RMSE. However, the standard deviation is not as good as that in ACCESS1-3 and CNRM-CM5.
3.3. Spatial Modes
Ren et al. [35] pointed out that three leading modes can generally reflect interannual variation of WNPST. To evaluate the capability of CMIP5 models in simulating these spatial modes, we carry out EOF (Empirical Orthogonal Function) analysis for the simulated WNPST amplitude in CMIP5 models during the period 1955–2004. Figure 5 shows the spatial modes of simulated WNPST amplitude and those from NCEP reanalysis. Table 2 lists the correlation coefficients corresponding to these modes. According to NCEP reanalysis, the first leading mode accounts for most variances of variability, with a percentage as large as 42%. The spatial pattern (Figure 5a1) shows the center is located at 170° E, 40° N. The contours exhibit a acclivous pattern toward northeast. It is overall positive to the north of the center, while the only area with negative values is in the southeast of the domain. The first leading mode reflects the universal variation of WNPST. We can learn from Figure 5 that most of the models can reproduce the center position and spatial pattern of the first leading mode. ACCESS1-3 and CNRM-CM5 are the best models in reproducing the first leading mode, with correlation coefficients of 0.95 and 0.93 respectively. The performance of CanESM2 is also acceptable. However, FGOALS-g2 and MRI-CGCM3 are two models that don not perform very well, the corresponding correlation coefficients are only 0.38 and 0.51 respectively. The variance contribution to the first leading mode in the simulations of CanESM2, CNRM-CM5 and INM-CM4 are close to that in NCEP reanalysis. But the variance contribution to the first leading mode in FGOALS-g2, IPSL-CM5B-LR and MIROC5 is only 20%. In general, CanESM2, CNRM-CM5 and INM-CM4 are skillful in simulating the spatial pattern and have similar variance contribution from the first leading mode to that in reanalysis
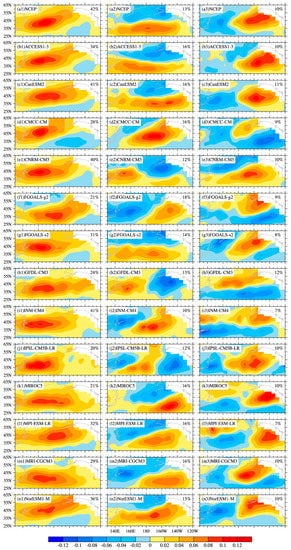
Figure 5.
The leading spatial modes of WNPST in reanalysis and CMIP5 models, variance contribution is showed in the upper right corner of each panel.

Table 2.
Correlation coefficients of the spatial modes between CMIP5 models and NCEP reanalysis. (Correlation coefficients between the second (third) and third (second) modes are listed in parenthesis).
The second leading mode in NCEP reanalysis (Figure 5a2) exhibits a dipole pattern with positive and negative portions are separated by 40° N. With a 13% contribution to total variance, this mode reflects the universally strengthening/weakening and southward/northward migration of WNPST [35]. There are large discrepancies among the CMIP5 models in reproducing the second leading mode. Only ACCESS1-3, CanESM2, FGOALS-s2 and NorESM1-M can generally capture the spatial pattern, and their correlation coefficients are 0.78, 0.85, 0.86 and 0.74 respectively. In spite of the larger correlation coefficients, the percentages of variance contribution in these four models are not all consistent with NCEP reanalysis except for FGOALS-s2 and NorESM1-M. It needs to be mentioned that, rather than a north-south orientated dipole pattern, many CMIP5 models produce an east-west orientated dipole, which results in smaller correlation coefficients. In particular, the simulated spatial pattern in IPSL-CM5B-LR exhibits an east-west orientated tripole mode, and the correlation between this spatial distribution and reanalysis is only 0.02.
The third leading mode in NCEP reanalysis only have 10% contribution to total variance. It exhibits an east-west orientated dipole mode with the positive center in the east located at (160° W, 45° N), and it reflects the eastward/westward migration of WNPST. It is easy to notice that CanESM2, IPSL-CM5B-LR and NorESM1-M all show a better skill in capturing this mode. The correlation coefficients are 0.87, 0.75 and 0.80 respectively. The variance contribution from the third mode in the simulations of CMIP5 models are generally consistent with the NCEP reanalysis. It is interesting to find that the spatial patterns of the third mode in FGOALS-g2, GFDL-CM3, CMCC-CM and INM-CM4 resemble the spatial patterns of the second mode in NCEP reanalysis, while the spatial patterns of the second mode in these models resemble the spatial patterns of the third mode in NCEP reanalysis. To verify this finding, we calculate the corresponding correlation coefficients between the patterns of the second/third mode in these models and those of the third/second mode in NCEP reanalysis, it turns out that five of the models obtain larger correlation coefficients (listed in parenthesis in Table 2), especially for GFDL-CM3. This implies that the order of the second and third leading modes in several CMIP5 models is opposite to that in reanalysis, which reflects some CMIP5 models have less skills in simulating WNPST migration as well as interannual variability.
Based on the simulations from all the selected CMIP5 models and the EOF skill score (see Table 3), it can be learned that CanESM2, ACCESS1-3, NorESM1-M and CNRM-CM5 have higher capability in simulating the spatial modes of WNPST, which is reflected by the better simulations of climatology, interannual variation of WNPST amplitude (Figure 1 and Figure 4).

Table 3.
The EOF skill score of CMIP5 models.
3.4. WNPST Indices
Figure 6 shows time series of climatological mean monthly WNPST strength index, longitude index and latitude index during the period 1955–2004. According to NCEP reanalysis (Figure 6a), significant seasonal variation of WNPST strength index is evident, and it is the strongest in winter and the weakest in summer with a minimum in July. It exhibits a bimodal curve which the strongest months are in November and March, representing a “midwinter suppression” effect. CMIP5 models are able to simulate the monthly variation of WNPST strength index. The discrepancies among the 13 models are the smallest during May–October, with the magnitude of the difference less than 1 K∙ms−1. The difference between the models and NCEP reanalysis is also smaller during this period. However, large discrepancies still exist among the models for the other months, with the magnitude of the difference greater than 3.5 K∙ms−1. It can also be found that only MIROC5, CNRM-CM5, FGOALS-g2, MPI-ESM-LR and GFDL-CM3 can reproduce the “midwinter suppression” effect. Though NorESM1-M also shows a bimodal curve, one of the peaks occurs in April rather than March. CMMCC-CM, ACCESS1-3 and IPSL-CM5B-LR can only generate the peak in March correctly, while the single peak in INM-CM4 occurs in November. On the other hand, the WNPST strength index is the strongest in spring in CanESM2, FGOALS-s2 and MRI-CGCM3. According to above analysis, we believe these models can somehow simulate the monthly variation of WNPST strength though only less than half of all the models can generate acceptable simulations. Nevertheless, the MME of strength index shows much better results, it can not only represent “midwinter suppression”, but also has similar magnitude to NCEP reanalysis and shows consistent variation, it is superior to all the single models.
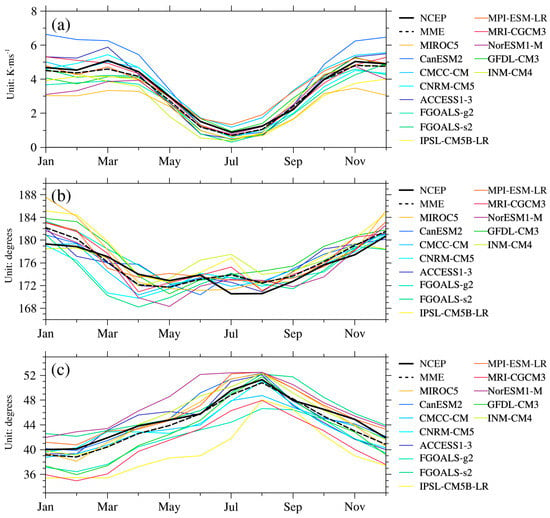
Figure 6.
Climatological monthly variation of (a) strength index (b) longitude index and (c) latitude index.
The major differences among the strength indices from these 13 models are in winter. Figure 7a shows the differences of winter climatological mean of strength index between these models and NCEP reanalysis. It is easy to find that the strength index is smaller in winter in most of the models. Specifically, the strength index from MIROC5 shows a negative bias of 1.6 K∙ms−1, while the strength index in CanESM2 shows a positive bias of 1.7 K∙ms−1. CNRM-CM5, FGOALS-s2 and MPI-ESM-LR show relatively smaller biases. The strength index from MPI-ESM-LR is very close to that from NCEP reanalysis, indicating this model can reproduce WNPST strength.
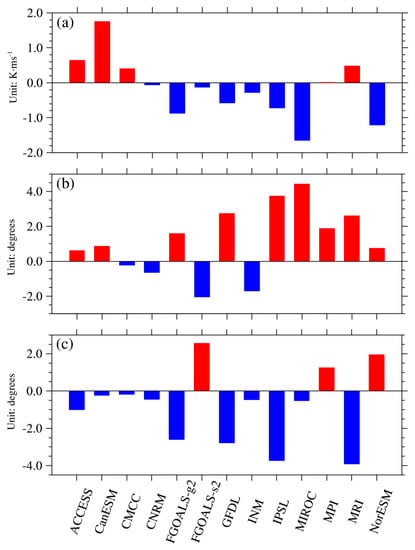
Figure 7.
Difference of (a) strength index, (b) longitude index and (c) latitude index of winter climatological mean between the CMIP5 models and NCEP reanalysis.
The monthly variation of longitude index from NCEP reanalysis (Figure 6b) indicates that the major part of WNPST experiences clear seasonal east-west migration between 170° E and 179° W. It starts moving eastward in June, reaches the eastern boundary around dateline in winter and retreats back to 170° E in summer. Overall, CMIP5 models can satisfactorily simulate the east-west seasonal migration, but large discrepancies still exist among the models. It is also clear that WNPST in most of the models is further east in winter (Figure 7b), especially in MIROC5 and IPSL-CM5B-LR. The simulated WNPST is about 4.2 degrees further east in winter in MIROC5, and even 8 degrees further east in January. In IPSL-CM5B-LR, it is 4 degrees further east of the observations in winter. While CMCC-CM is better in reproducing the eastern boundary of WNPST, with an error of only 0.2 degrees. Specifically, the eastward migration of WNPST in FGOALS-s2, CNRM-CM5, CMCC-CM and MPI-ESM-LRs starts in May, and it starts in July for CanESM2. For MRI-CGCM3, INM-CM4, IPSL-CM5B-LR and NorESM1-M, the eastward migration of WNPST continues until July. The correlation coefficients between the longitude indices in FGOALS-s2, INM-CM4 and NCEP reanalysis are 0.65 and 0.66, without passing significance test with a cutoff value of 0.01. In contrast, FGOALS-g2 and MIROC5 can simulate the monthly variation of longitude index very well. Most of the other models have a correlation coefficient less than 0.9, indicating some problems still exist for these models in simulating the east-west migration of WNPST. This is also probably related to the markedly difference of the third spatial mode between these models and NCEP reanalysis.
Similar to the strength and longitude indices, the latitude index also shows remarkable seasonal variation (Figure 6c). It exhibits northward migration in summer and southward migration in winter with a range between 39° and 51° N, reaching the furthest north in August. It is clear that all the 13 models can simulate monthly variation of the latitude index, especially for CMCC-CM and GFDL-CM3. Nearly all the models can reproduce the aspect that WNPST reaching the furthest north in August. However, large discrepancies exist among the models for all the months, especially for June (difference between the simulation in NorESM1-M and IPSL-CM5B-LR is about 14 degrees). The discrepancies are relatively not significant in fall. Figure 7c shows most of the models generate a smaller winter latitude index compared with NCEP, which means the simulated WNPST is further south. It is about 4 degrees further south compared with NCEP in MRI-CGCM3 and IPSL-CM5B-LR. While the simulated WNPST is further north in FGOALS-s2, MPI-ESM-LR and NorESM1-M.
Figure 8 shows the ratios of interannual standard deviations of WNPST winter strength index, longitude index and latitude index in these 13 models to those in NCEP reanalysis. The interannual variation of winter longitude index in the MME matches that in NCEP reanalysis very well. The longitude indices calculated from CNRM-CM5, FGOALS-s2 and MIROC5 are also acceptable. However, CMCC-CM produces a larger longitude index, IPSL-CM5B-LR instead produces a smaller longitude index variability. The winter strength index of CNRM-CM5 close to NCEP reanalysis, though most of the other models generate a smaller winter strength index, except for CanESM2. For interannual variation of winter latitude index, the simulations in CMCC-CM and CNRM-CM5 are generally consistent with NCEP reanalysis, while most of the other models simulate weak indices, especially for INM-CM4. The results from above analysis suggest we should use the MME and CNRM-CM5 to evaluate the interannual variation of WNPST longitude index and strength index respectively, but use CMCC-CM and CNRM-CM5 to evaluate interannual variation of latitude index.
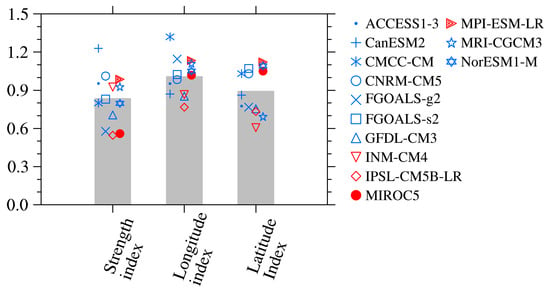
Figure 8.
Ratio of standard deviation of indices in each model to those in NCEP reanalysis. Gray bar represents the MME of the corresponding index.
Figure 9 shows time series of WNPST latitude index and its trend for the period 1955–2004. As seen from Figure 9a, WNPST drifts southward with a rate of 0.042°/a in NCEP reanalysis. The southward drift in FGOALS-g2, MIROC5, CanESM2 and three other models is not significant, with a small drift rate about 0.001°/a. While it has a northward drift with a rate of 0.01°/a in FGOALS-s2 and MRI-CGCM3. The northward drift rate is 0.039°/a in CMCC-CM. Only three models including ACCESS1-3, INM-CM4 and CNRM-CM5 simulate similar southward drift with a rate of 0.01°/a which is still slightly slower than that in NCEP reanalysis. Considering that scholars do not fully understand the reasons for the trend change, we discuss the meaning of the trend comparison from two different points of view: (a) if the observed trend is caused by an external forcing, our results indicate most of models have less skills in simulating southward drift of WNPST, but INM-CM4 and CNRM-CM5 show relatively better skills in this; (b) if the observed trend is caused by internal variability, it follows that models do not have to produce a matching trend behavior and thus this trend comparison provides a less strict model performance test than the other metrics (at least at this time with limited scientific knowledge regarding trend attribution ).
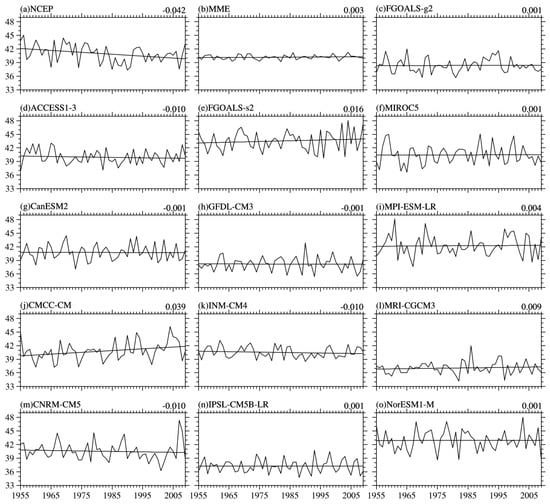
Figure 9.
Time series of winter latitude index in each model and its trend (linear trend is showed in upper right corner of each panel).
4. Summary
With WNPST represented by 850-hPa meridional eddy flux, 13 CMIP5 models are selected to simulate the climatology and interannual variation of WNPST, and the results are compared with NCEP reanalysis. To provide an intuitive understanding of the capability of CMIP5 models in simulating WNPST, a brief summary of the performance of individual model in simulating the WNPST is presented in Figure 10. The results indicate nearly half of all the selected models can satisfactorily simulate of the spatial distribution of WNPST climatology (correlation coefficient greater than 0.95, see the first column in Figure 10), especially for ACCESS1-3. However, two models (IPSL-CM5B-LR and MRI-CGCM3) show a relatively weak simulation capability in this. ACCESS1-3 and CNRM-CM5 show strong capabilities in simulating the WNPST amplitude. Most of the models reproduce a weaker WNPST except for CanESM2, which produce a apparent stronger WNPST in its simulation. Most of the models also reproduce weak spatial variations for WNPST climatology, but we still can use 3 models (CMCC-CM, INM-CM4 and MRI-CGCM3) to evaluate the spatial variation of climatological WNPST, as their difference with reanalysis are less than 5% (see the second column in Figure 10). The MME can reflect the spatial distribution of WNPST very well except for a slightly weak strength. In addition, the major differences among the 13 models are mainly concentrated in the northeast of the MME climatology.
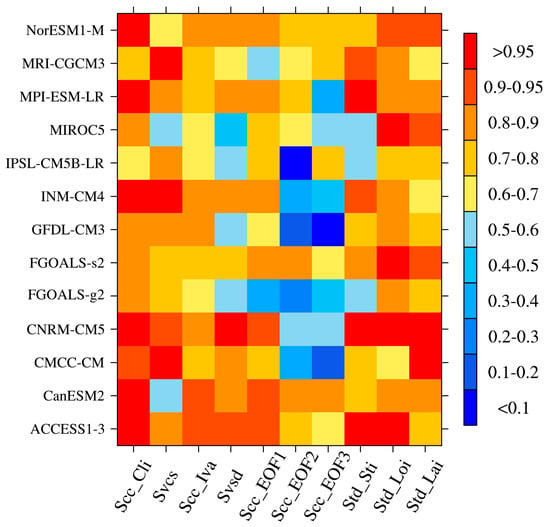
Figure 10.
Diagram indicating the relative ability of (top to bottom) the CMIP5 models in simulating the climatology and interannual variability of WNPST (Scc_Cli, Scc_Iva, Scc_EOF1, Scc_EOF2 and Scc_EOF3 on horizontal axis represents spatial correlation coefficients (Scc) of climatology (Cli), interannual variation of amplitude (Iva), the first mode (EOF1), the second mode (EOF2) and the third mode (EOF3) respectively; Svcs, Svsd, Std_Sti, Std_Loi and Std_Lai represents capability of model in simulating the spatial variation of climatology strength (Svcs), standard deviation (Svsd), and the interannual variability (Std) of the WNPST strength index (Sti), longitude index (Loi) and latitude index (Lai) respectively (represented by 1-deviation)).
For interannual variation of the WNPST amplitude, ACCESS1-3 and CanESM2 show more skills in simulating spatial distribution (correlation coefficient greater than 0.9, see the third column in Figure 10), and reasonably reproduce the center position of interannual variation of WNPST. In addition, ACCESS1-3, CanESM2 and CNRM-CM5 have smaller bias in simulating interannual variation of WNPST amplitude, also with a smaller RMSE. CNRM-CM5 almost reproduce similar pattern of standard deviation of the WNPST strength to NCEP reanalysis (bias less than 5%, see the fourth column in Figure 10), so does ACCESS1-3 (bias less than 10%). The MME not only can capture the center position of interannual variation, but also has a high correlation (>0.9) with reanalysis and small RMSE. But the MME is not as good as CNRM-CM5 and ACCESS1-3 in simulating the standard deviation.
ACCESS1-3, CNRM-CM5 and CanESM2 can simulate the first leading mode of spatial distribution of WNPST (correlation coefficient >0.9, see the fifth column in Figure 10) very well, while but the first mode is not well simulated in FGOALS-g2 and MRI-CGCM3. Only 3 models (CanESM2, CNRM-CM5 and INM-CM4) can better simulate the variance contribution of the first mode. Among these 13 models, FGOALS-s2 is better in simulating the spatial pattern and variance contribution of the second mode, and the correlations coefficients in 8 other models are less than 0.7 (see the sixth column in Figure 10). For the third mode, CanESM2 produces better simulation, but there are still 9 models whose correlation coefficients are less than 0.7 (see the seventh column in Figure 10). On the other hand, we find the second mode and third mode of WNPST in 5 models are opposite in order with those in NCEP reanalysis.
Large discrepancies still exist in simulated winter strength indices among the models, only the strength index from MPI-ESM-LR shows consistent features with NCEP, while the winter strength index is smaller in most of the models. Only 5 models and the MME can reproduce “midwinter suppression” aspect. CMCC-CM is better in simulating longitude index, with an error of only 0.2 degrees. FGOALS-s2 and INM-CM4 show less skills in simulating monthly variation of longitude index, while it is much better in the simulations from FGOALS-g2 and MIROC5. Most of the models produce larger longitude indices and smaller latitude indices compared with NCEP reanalysis. The MME and CNRM-CM5 can be used to evaluate interannual variation of the WNPST longitude index and latitude index. CMCC-CM and CNRM-CM5 can be used to evaluate interannual variation of latitude index (see the tenth column in Figure 10). Besides, most of the models cannot reproduce southward drift of WNPST, except for INM-CM4 and CNRM-CM5.
Acknowledgments
This research was supported by National Natural Science Foundation of China (41605051, 41490642, 41475070).
Author Contributions
Xin Li conceived the idea and designed the structure of this paper; Minghao Yang performed the experiments; Minghao Yang, Ruiting Zuo, Xiong Chen and Liqiong Wang analyzed the data; Minghao Yang wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Blackmon, M.L.; Wallace, J.M.; Lau, N.C.; Mullen, S.L. An observational study of the Northern Hemisphere wintertime circulation. J. Atmos. Sci. 1977, 34, 1040–1053. [Google Scholar] [CrossRef]
- Nakamura, H. Midwinter suppression of baroclinic wave activity in the Pacific. J. Atmos. Sci. 1992, 49, 1629–1642. [Google Scholar] [CrossRef]
- Chang, E.K.M. Downstream development of baroclinic waves as inferred from regression analysis. J. Atmos. Sci. 1993, 50, 2038–2053. [Google Scholar] [CrossRef]
- Chang, E.K.M.; Fu, Y. Interdecadal variations in Northern Hemisphere winter storm track intensity. J. Clim. 2002, 15, 642–658. [Google Scholar] [CrossRef]
- Booth, J.F.; Kwon, Y.O.; Ko, S.; Small, R.J.; Msadek, R. Spatial Patterns and Intensity of the Surface Storm Tracks in CMIP5 Models. J. Clim. 2017, 30, 4965–4981. [Google Scholar] [CrossRef]
- Nakamura, H.; Sampe, T. Trapping of synoptic-scale disturbances into the North-Pacific subtropical jet core in midwinter. Geophys. Res. Lett. 2002, 29, 8-1–8-4. [Google Scholar] [CrossRef]
- Chang, E.K.M. Assessing the increasing trend in Northern Hemisphere winter storm track activity using surface ship observations and a statistical storm track model. J. Clim. 2007, 20, 5607–5628. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Lim, G.H.; Kug, J.S. Influence of the East Asian winter monsoon on the storm track activity over the North Pacific. J. Geophys. Res. 2010, 115, D09102. [Google Scholar] [CrossRef]
- Deng, Y.; Jiang, T. Intraseasonal modulation of the North Pacific storm track by tropical convection in boreal winter. J. Clim. 2011, 24, 1122–1137. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Lim, G.H. Dependency of the North Pacific winter storm tracks on the zonal distribution of MJO convection. J. Geophys. Res. 2012, 117, D14101. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Kug, J.S.; Lim, G.H.; Watanabe, M. Eastward shift of the Pacific/North American pattern on an interdecadal time scale and an associated synoptic eddy feedback. Int. J. Climatol. 2011, 32, 1128–1134. [Google Scholar] [CrossRef]
- Straus, D.M.; Shukla, J. Variations of midlatitude transient dynamics associated with ENSO. J. Atmos. Sci. 1997, 54, 777–790. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Hurrell, J.W. Decadal atmosphere-ocean variations in the Pacific. Clim. Dyn. 1994, 9, 303–319. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Hodges, K.I. New perspectives on the Northern Hemisphere winter storm tracks. J. Atmos. Sci. 2002, 59, 1041–1061. [Google Scholar] [CrossRef]
- Booth, J.F.; Thompson, L.A.; Patoux, J.; Kelly, K.A.; Dickinson, S. The signature of the midlatitude tropospheric storm tracks in the surface winds. J. Clim. 2010, 23, 1160–1174. [Google Scholar] [CrossRef]
- Held, I.M.; Lyons, S.W.; Nigam, S. Transients and the extratropical response to El Niño. J. Atmos. Sci. 1989, 163–174. [Google Scholar] [CrossRef]
- Nakamura, H.; Izumi, T.; Sampe, T. Interannual and decadal modulations recently observed in the Pacific storm track activity and East Asian winter monsoon. J. Clim. 2002, 15, 1855–1874. [Google Scholar] [CrossRef]
- Yin, J.H. A consistent poleward shift of the storm tracks in simulations of 21st century climate. Geophys. Res. Lett. 2005, 32, L18701. [Google Scholar] [CrossRef]
- Ulbrich, U.; Pinto, J.G.; Kupfer, H.; Leckebusch, G.C.; Spangehl, T.; Reyers, M. Changing Northern Hemisphere storm tracks in an ensemble of IPCC climate change simulations. J. Clim. 2008, 21, 1669–1679. [Google Scholar] [CrossRef]
- Cai, M.; Mak, M. Symbiotic relation between planetary and synopticscale waves. J. Atmos. Sci. 1990, 47, 2953–2968. [Google Scholar] [CrossRef]
- Chang, E.K.M. An idealized nonlinear model of the Northern Hemisphere winter storm tracks. J. Atmos. Sci. 2006, 63, 1818–1839. [Google Scholar] [CrossRef]
- Chang, E.K.M.; Guo, Y.J. Dynamics of the stationary anomalies associated with the interannual variability of the midwinter Pacific storm track-The roles of tropical heating and remote eddy forcing. J. Atmos. Sci. 2007, 64, 2442–2461. [Google Scholar] [CrossRef]
- Yao, Y.; Zhong, Z.; Yang, X.Q. Numerical experiments of the storm track sensitivity to oceanic frontal strength within the Kuroshio/Oyashio Extensions. J. Geophys. Res. Atmos. 2016, 121, 2888–2900. [Google Scholar] [CrossRef]
- Nakamura, H.; Sampe, T.; Goto, A.; Ohfuchi, W.; Xie, S.P. On the importance of midlatitude oceanic frontal zones for the mean state and dominant variability in the tropospheric circulation. Geophys. Res. Lett. 2008, 35, L15709. [Google Scholar] [CrossRef]
- Nakamura, H.; Sampe, T.; Tanimoto, Y.; Shimpo, A. Observed associations among storm tracks, jet streams and midlatitude oceanic fronts. Geophys. Monogr. Ser. 2004, 147, 329–345. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Gong, H.; Wang, L.; Chen, W.; Wu, R.; Wei, K.; Cui, X. The Climatology and Interannual Variability of the East Asian Winter Monsoon in CMIP5 Models. J. Clim. 2014, 27, 1659–1678. [Google Scholar] [CrossRef]
- Chang, E.K.M.; Guo, Y.; Xia, X. CMIP5 multi-model ensemble projection of storm track change under global warming. J. Geophys. Res. 2012, 117, D23118. [Google Scholar] [CrossRef]
- Chang, E.K.M.; Guo, Y.; Xia, X.; Zheng, M. Storm track activity in IPCC AR4/CMIP3 model simulations. J. Clim. 2013, 26, 246–260. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, W.; Wei, J. Reappraisal and improvement of winter storm track indices in the North Pacific. Chin. J. Atmos. Sci. 2010, 34, 1001–1010. (In Chinese) [Google Scholar]
- North, G.; Bell, T.; Cahalan, R.; Moeng, F. Sampling errors in the estimation of empirical orthogonal functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Timm, O.; Diaz, H.F. Synoptic-Statistical Approach to Regional Downscaling of IPCC Twenty-First-Century Climate Projections: Seasonal Rainfall over the Hawaiian Islands. J. Clim. 2009, 22, 4261–4280. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Jiang, D.B.; Tian, Z.P. East Asian monsoon change for the 21st century: results of CMIP3 and CMIP5 models. Chin. Sci. Bull. 2012, 58, 1427–1435. [Google Scholar] [CrossRef]
- Ren, X.J.; Yang, X.Q.; Han, B.; Xu, G.Y. Storm track variations in the North Pacific in winter season and the coupled pattern with the midlatitude atmosphere-ocean system. Chin. J. Geophys. 2007, 50, 94–103. (In Chinese) [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).