Precipitation Extremes in Dynamically Downscaled Climate Scenarios over the Greater Horn of Africa
Abstract
1. Introduction
2. Data and Methods
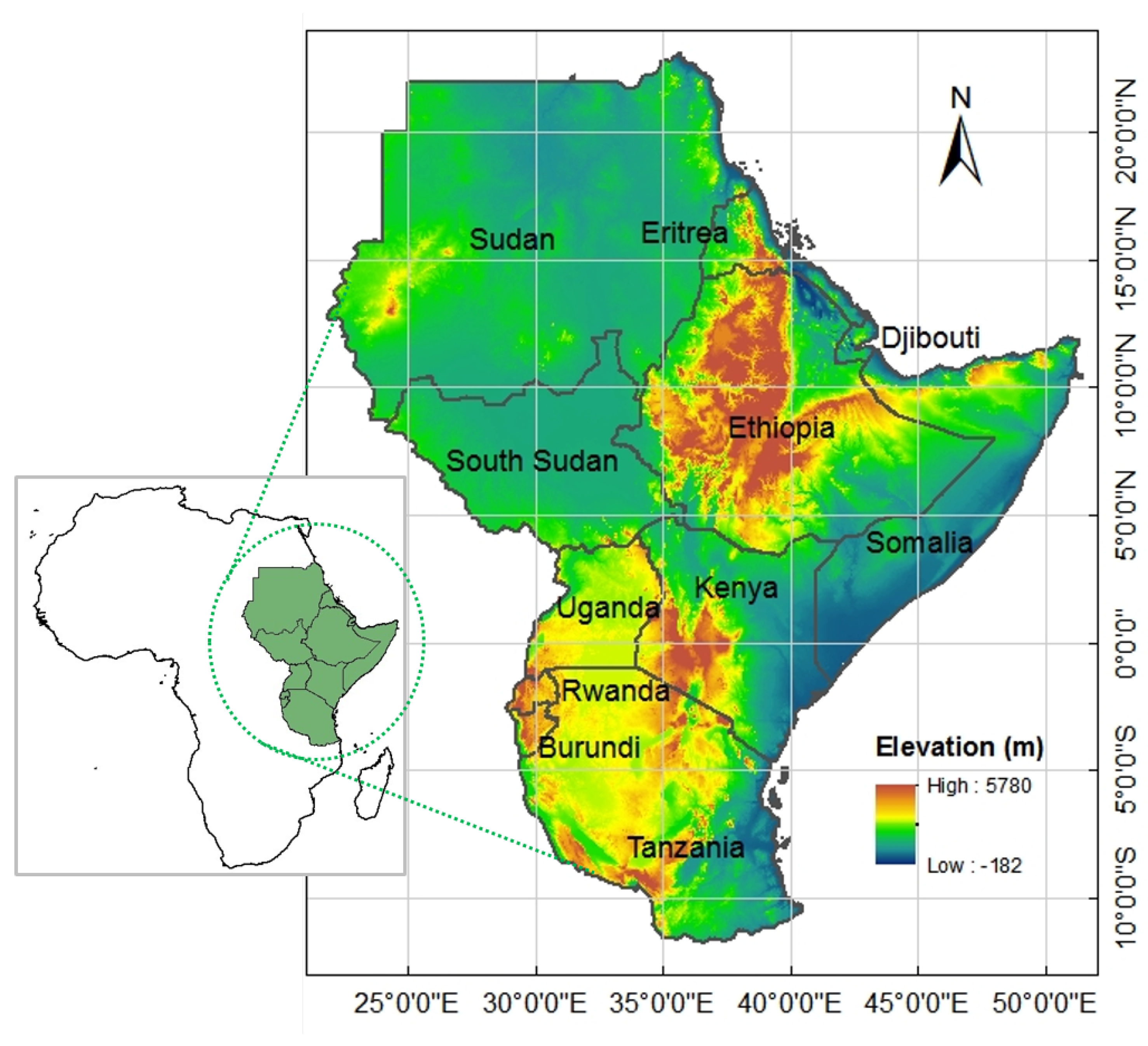
2.1. Model data
2.2. Observed Data
2.3. Indices
2.4. Analysis and Evaluation
3. Result and Discussion
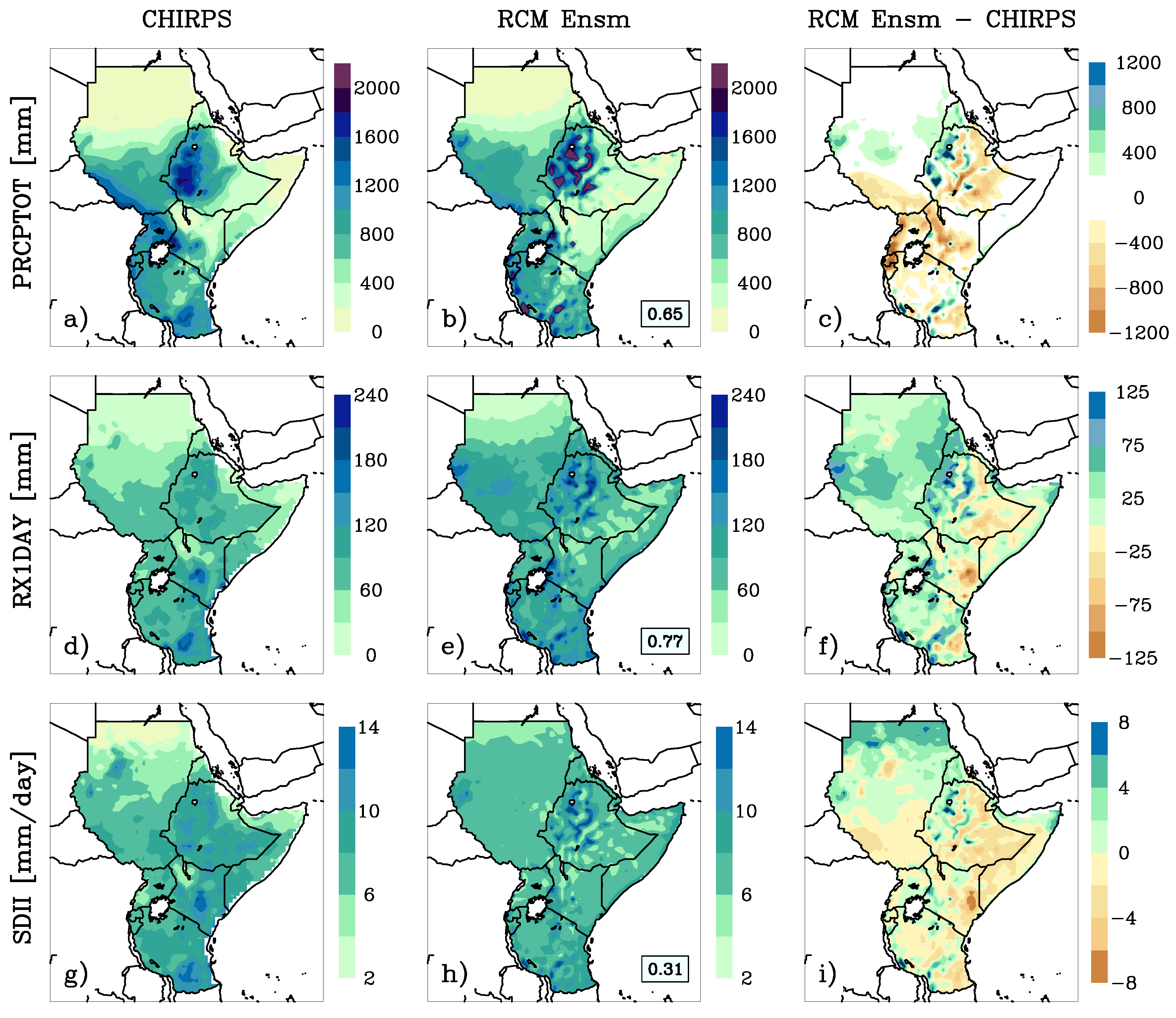
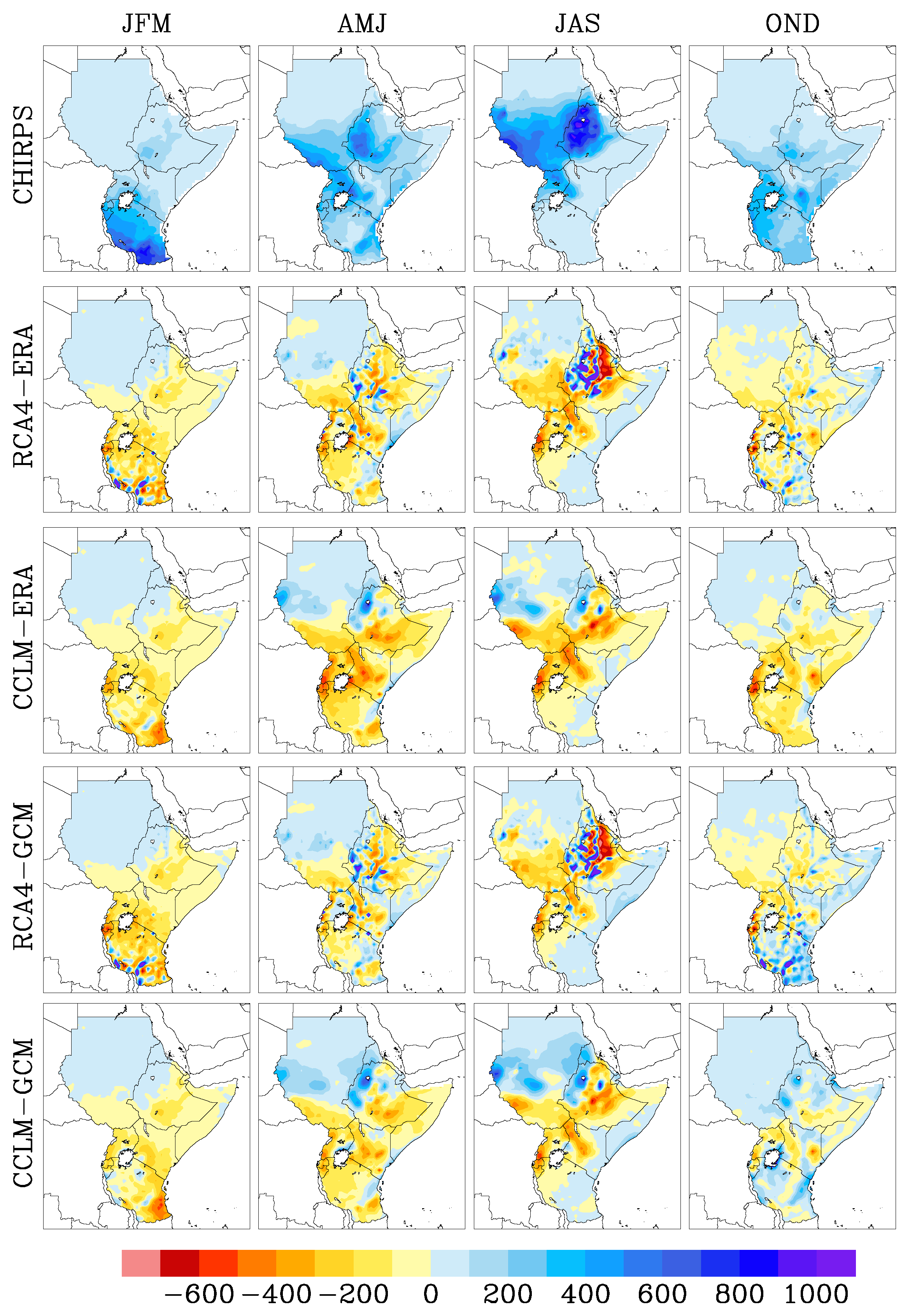
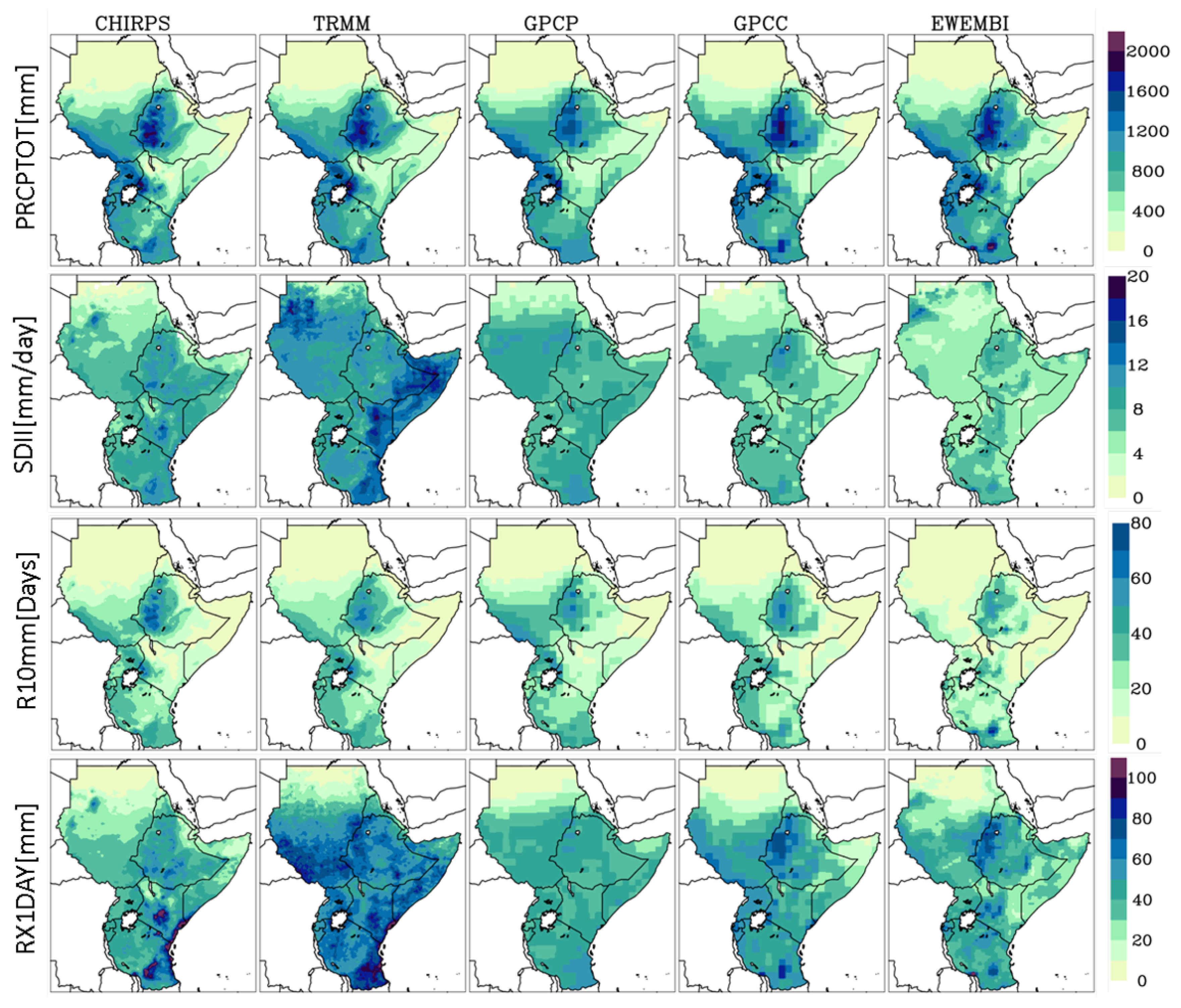
3.1. Comparison between Observed and Simulated Extremes
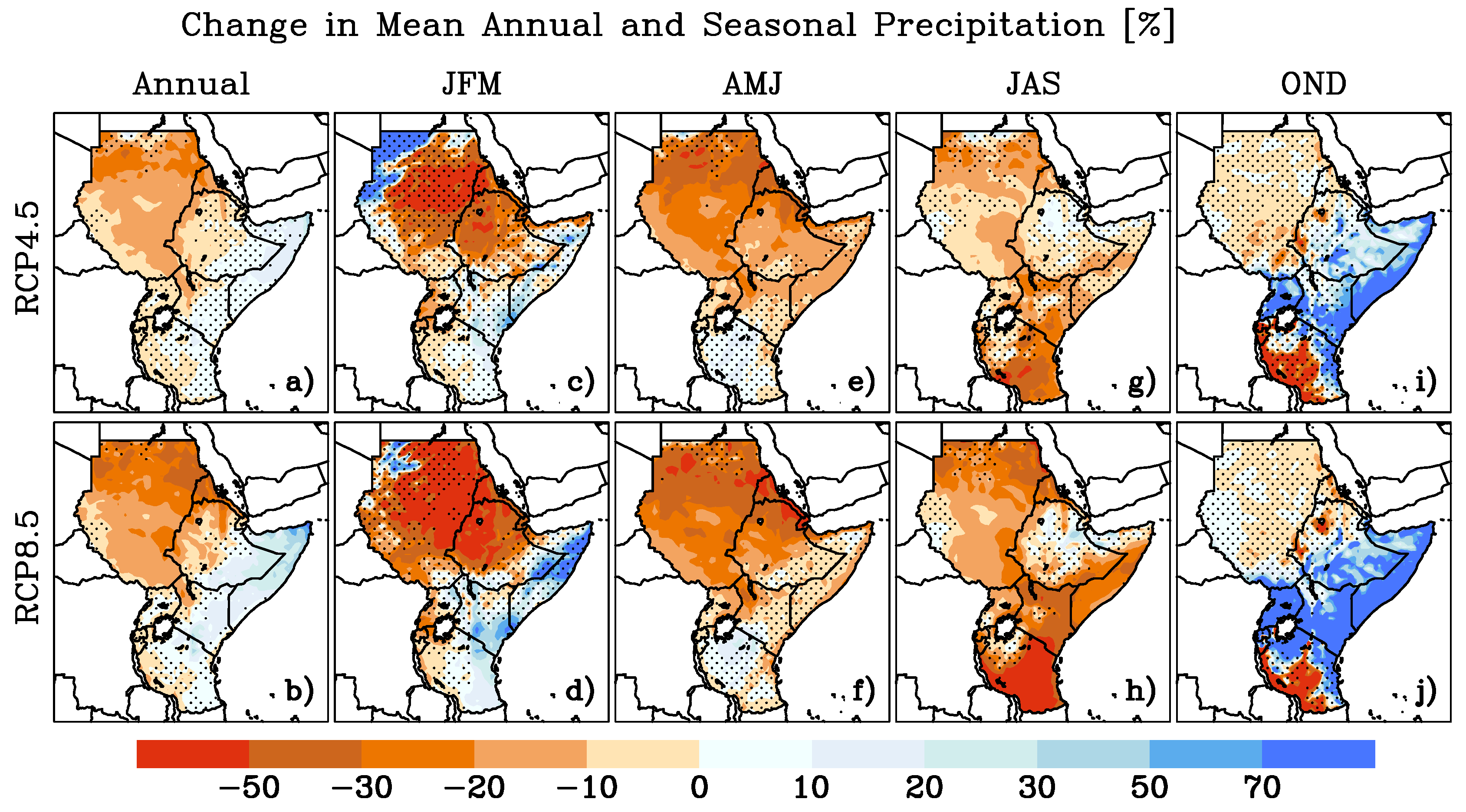
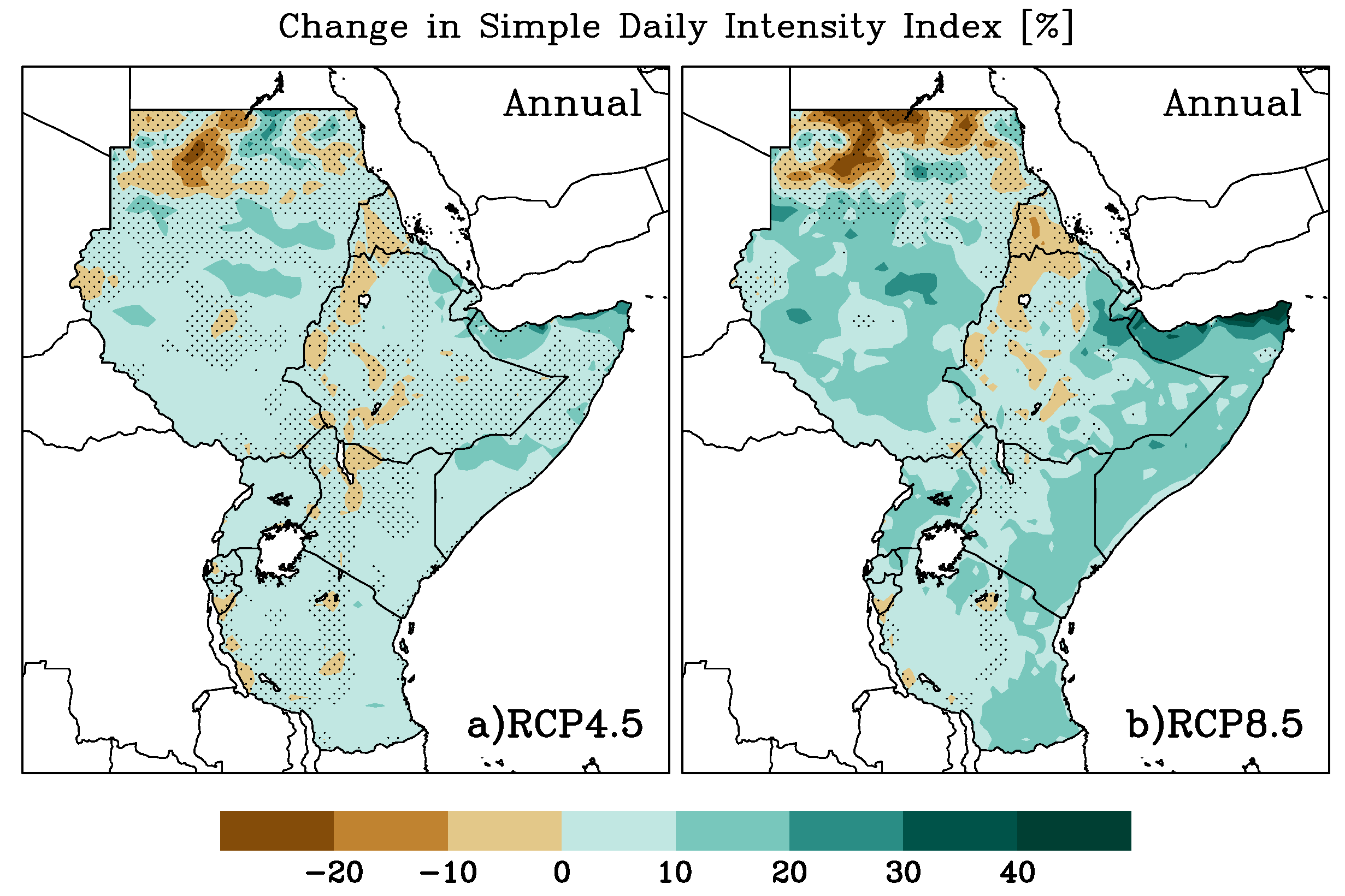
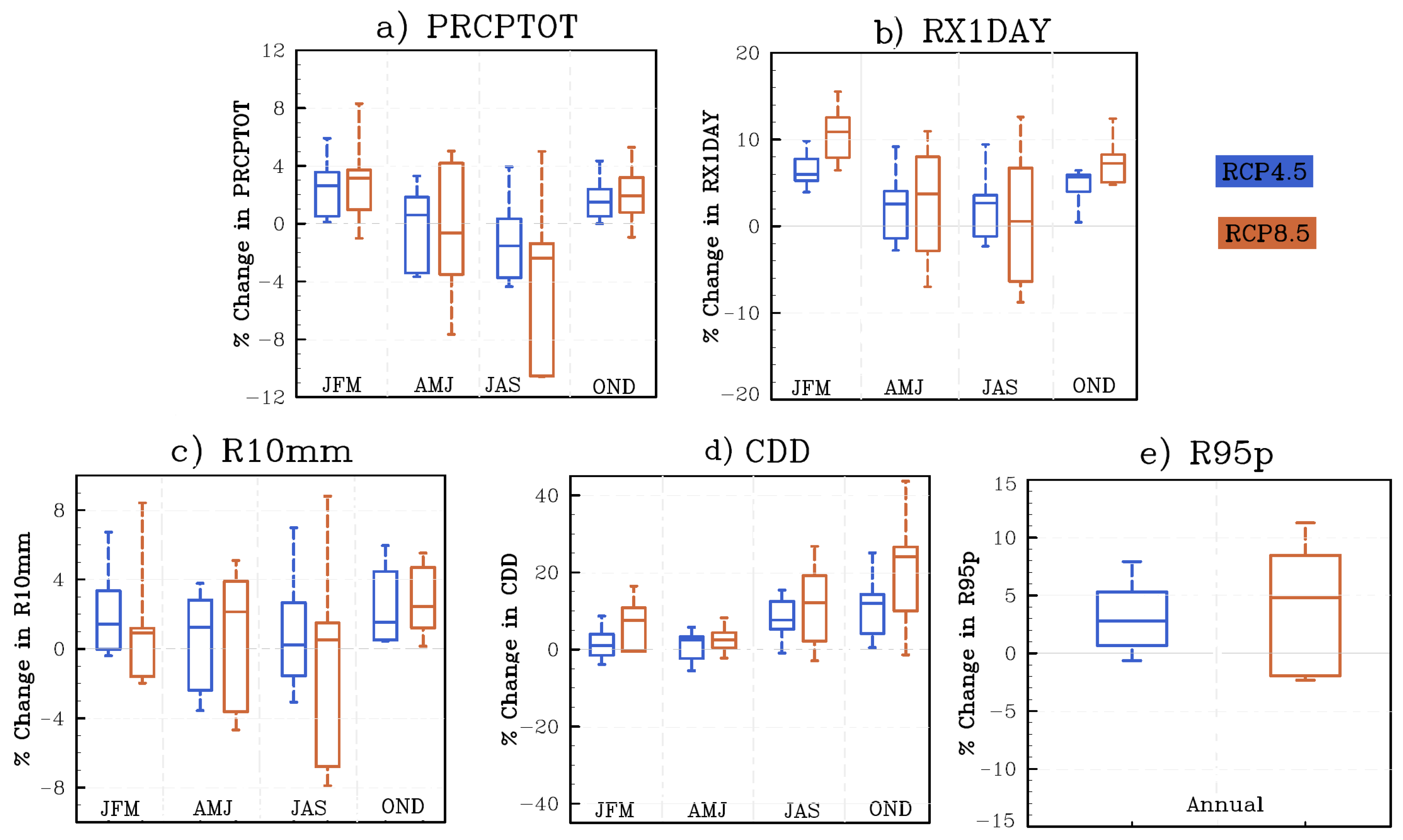
3.2. Projected Changes in PRCPTOT and SDII
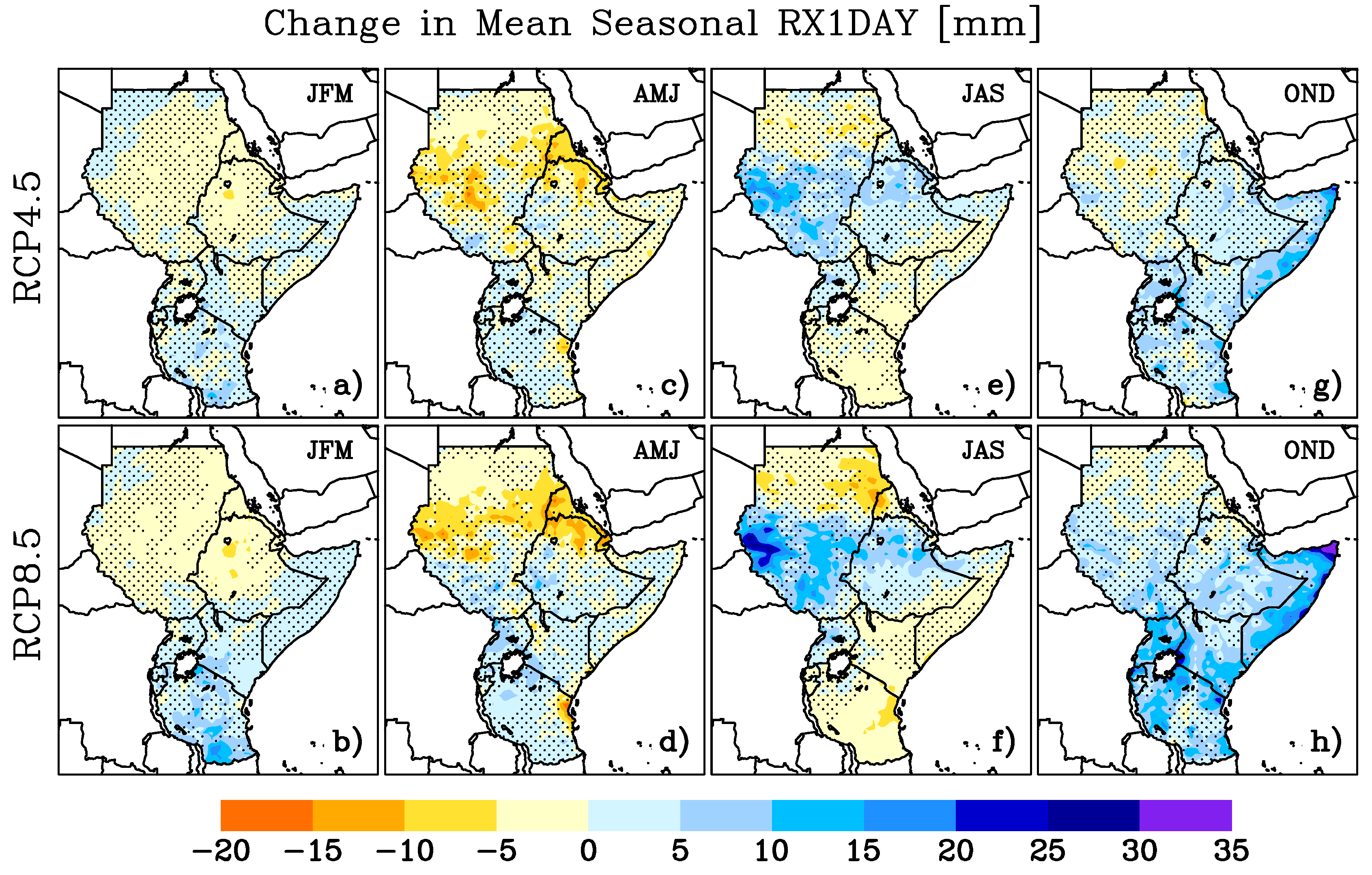
3.3. Projected Changes in RX1DAY and RX5DAY Precipitation
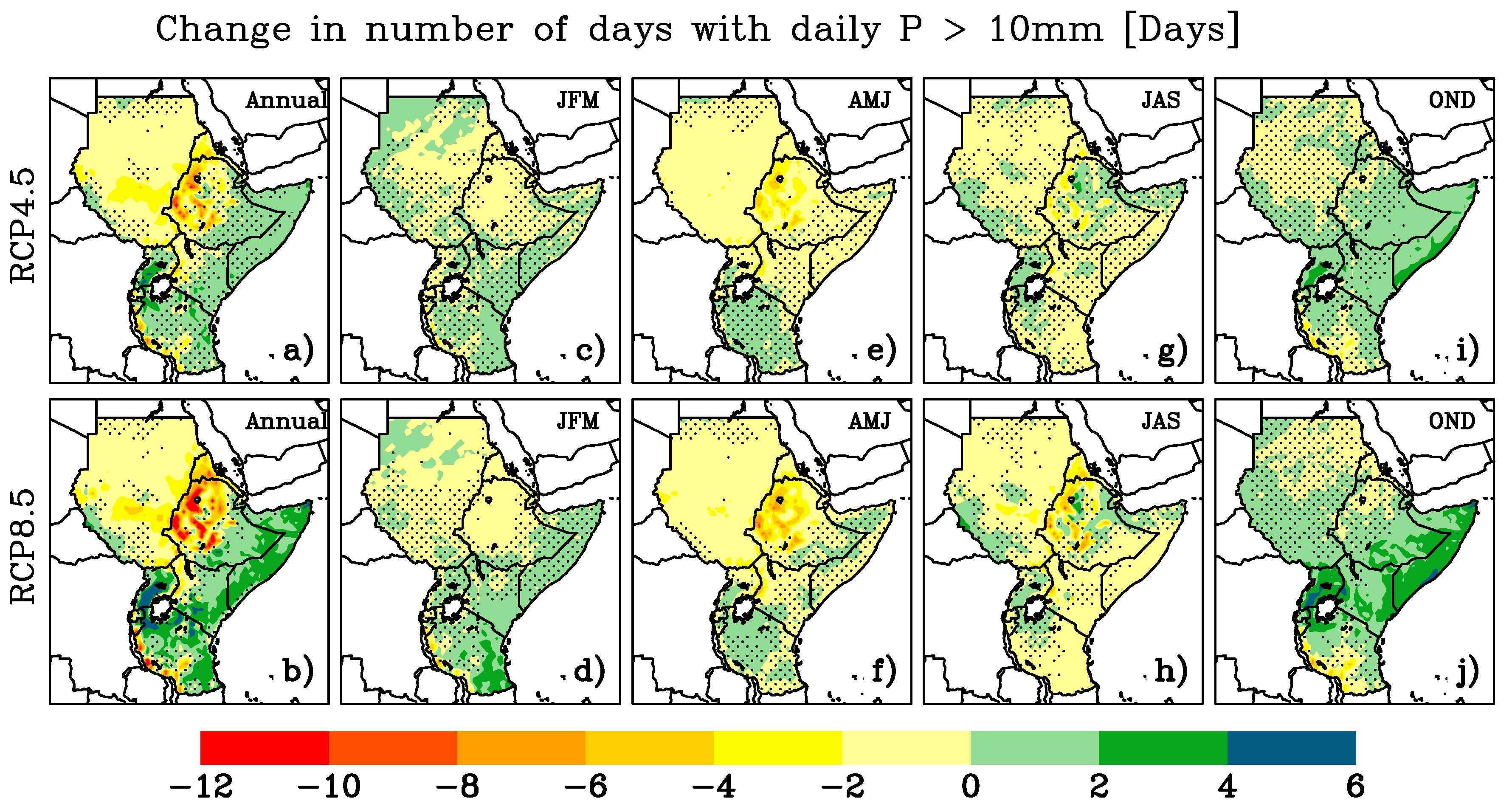
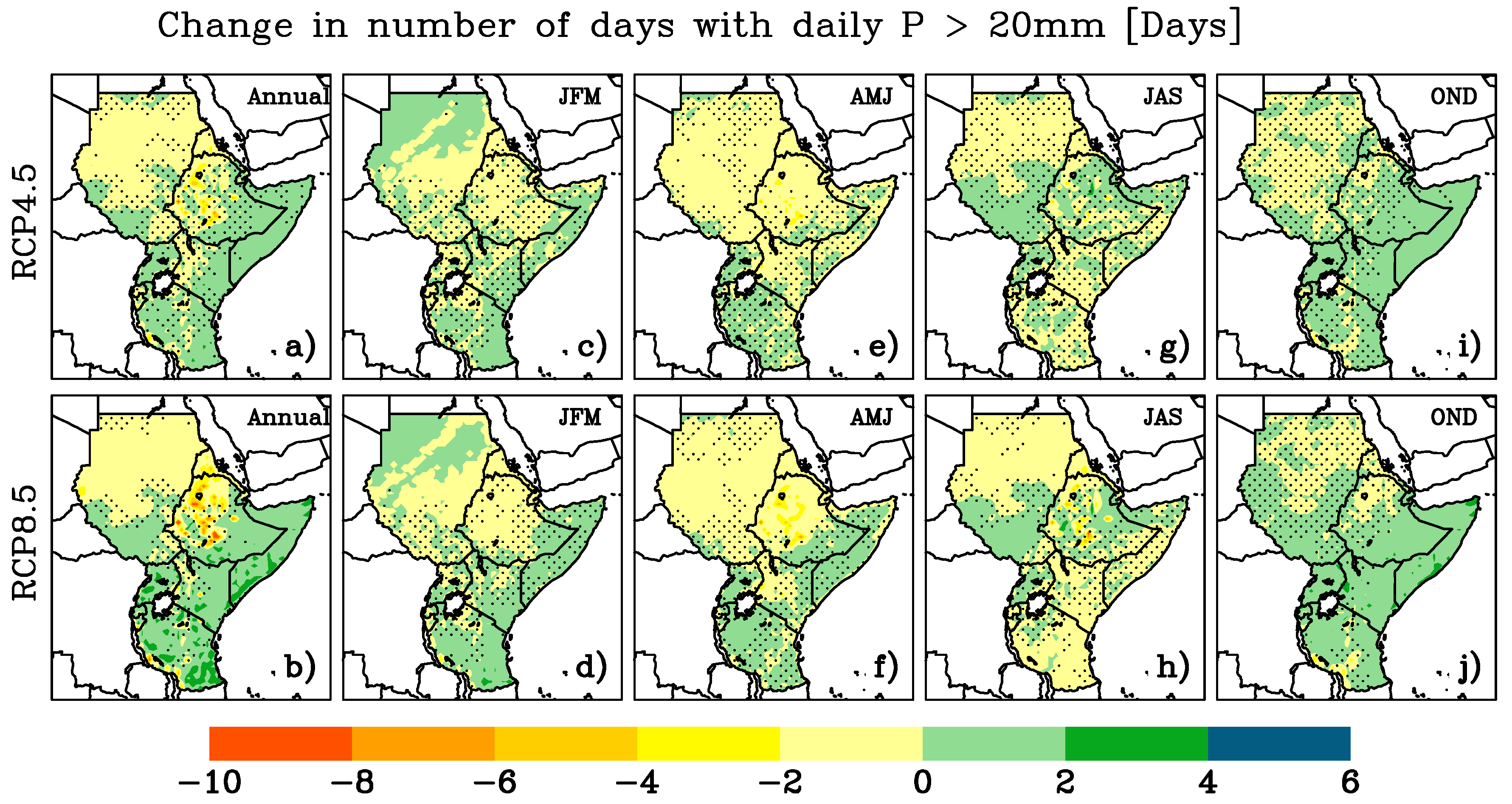
3.4. Projected Changes in Daily Precipitation Absolute Threshold Indices
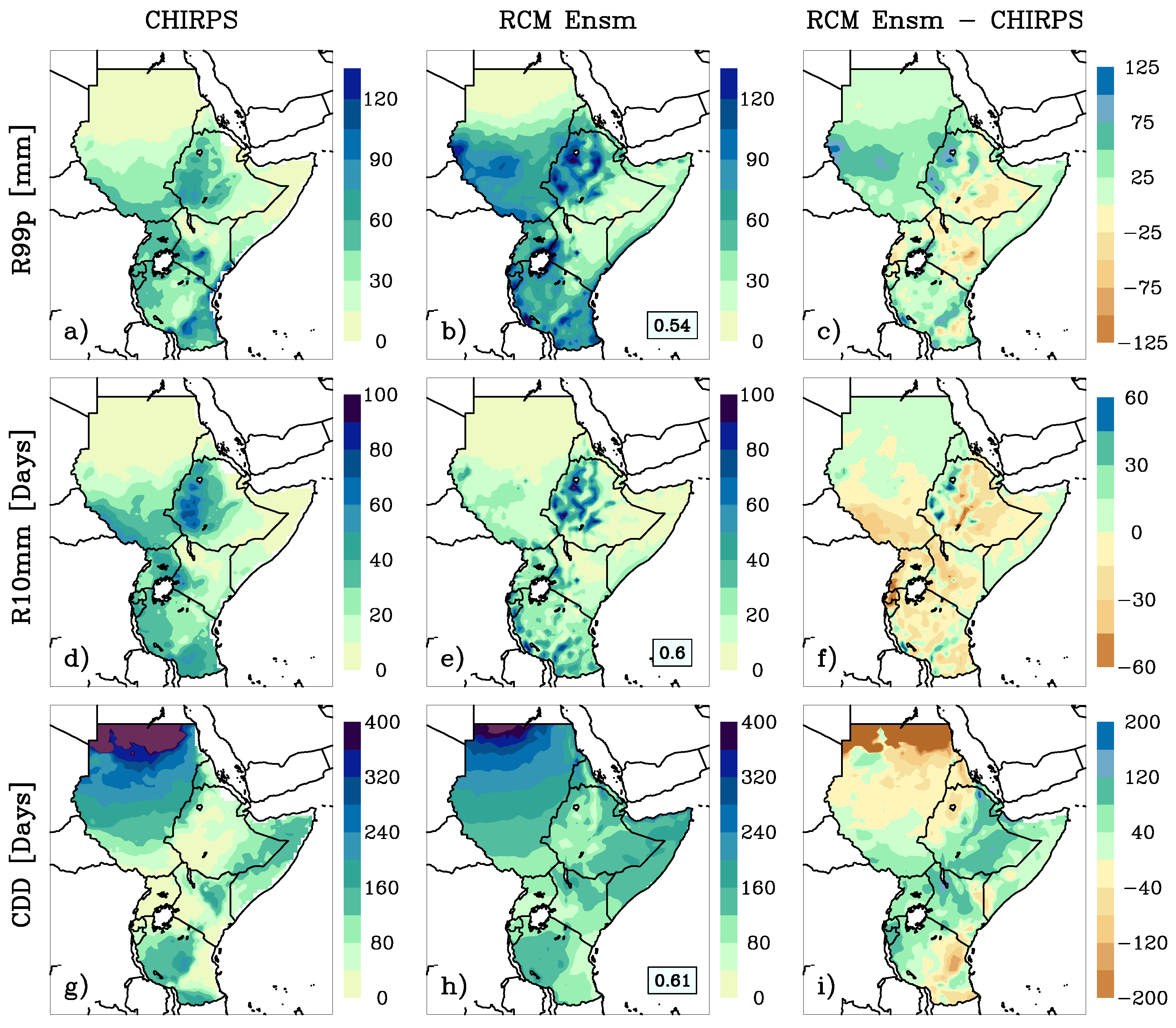
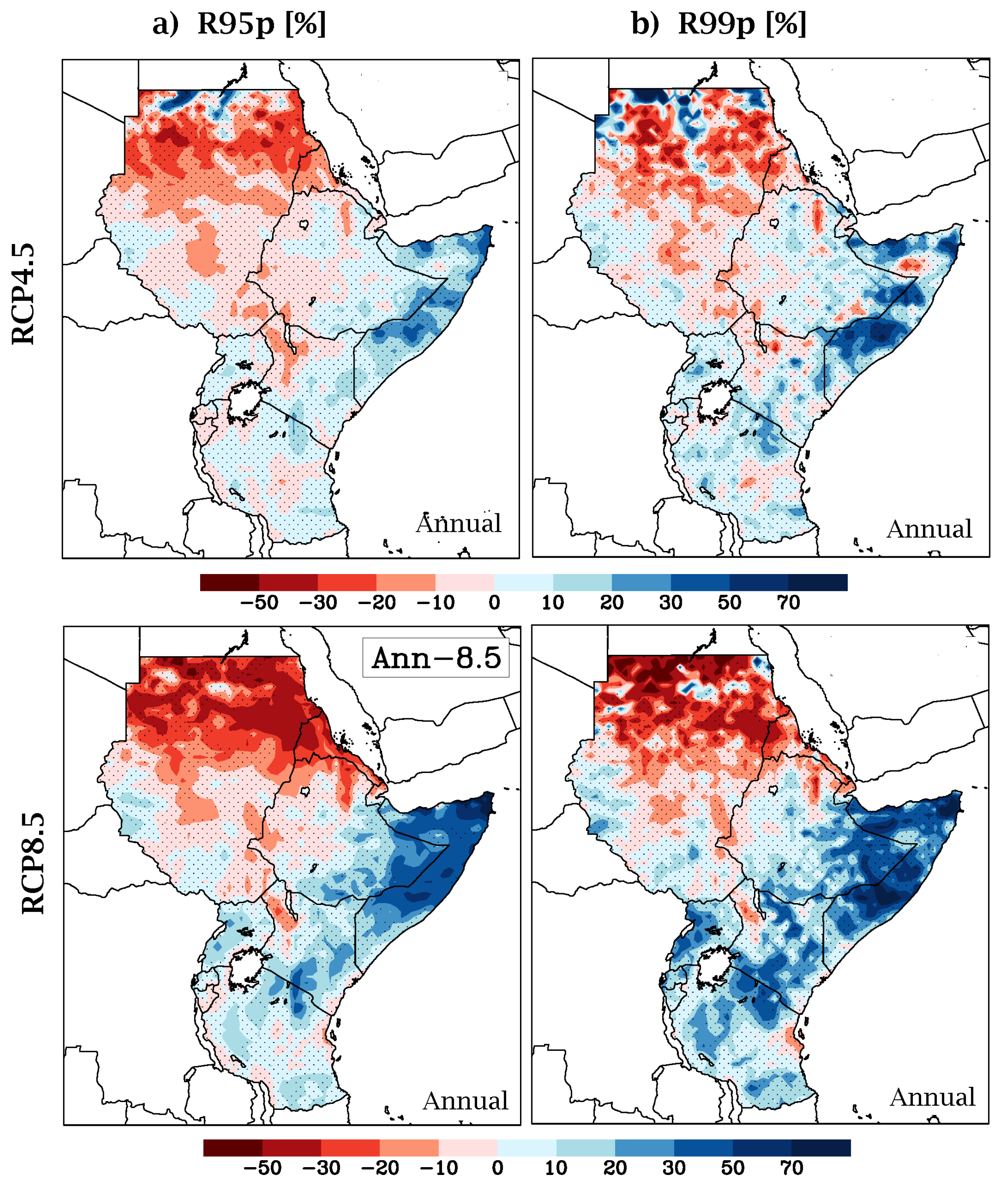
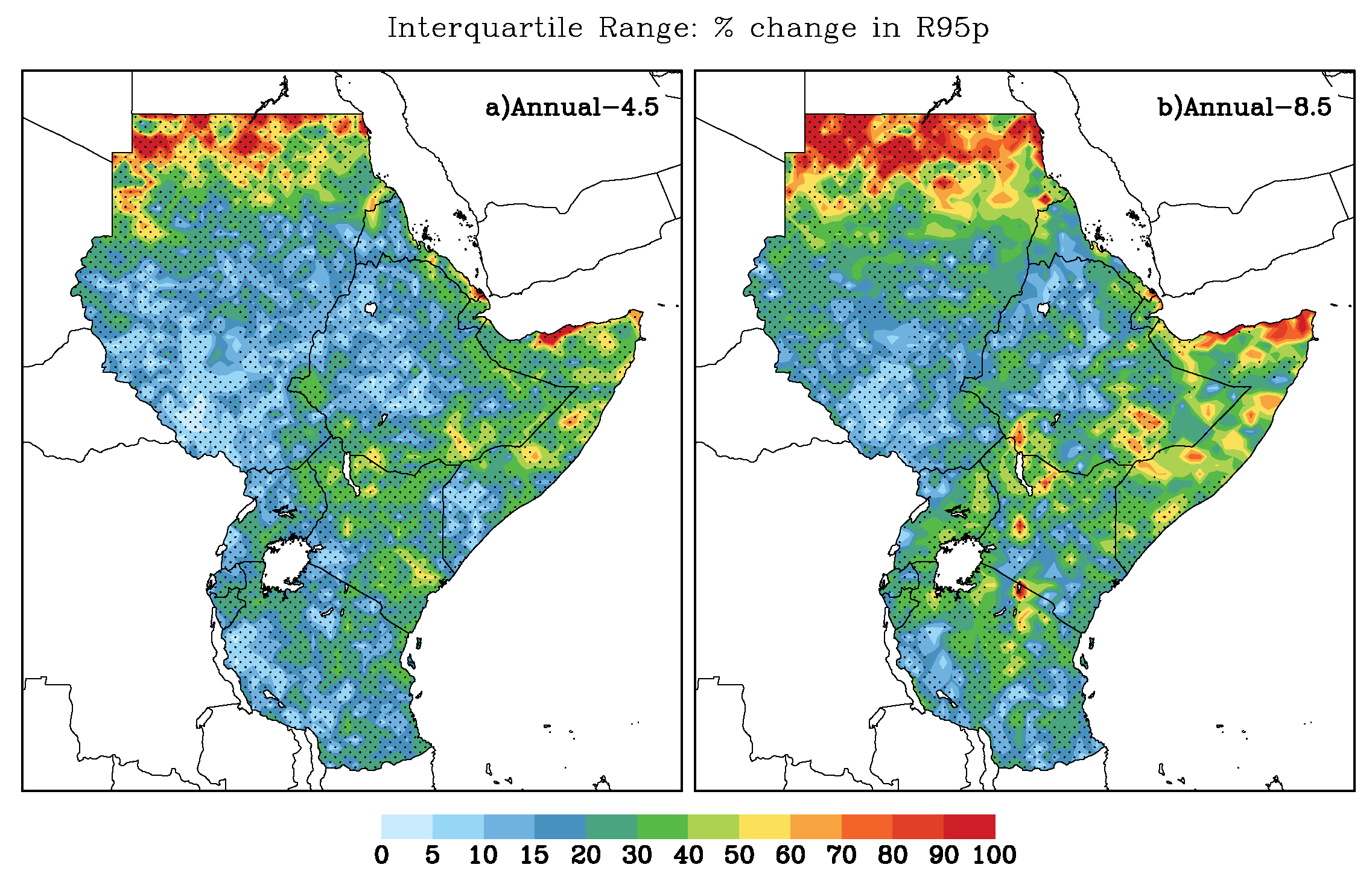
3.5. Projected Changes in Daily Precipitation Percentile Indices
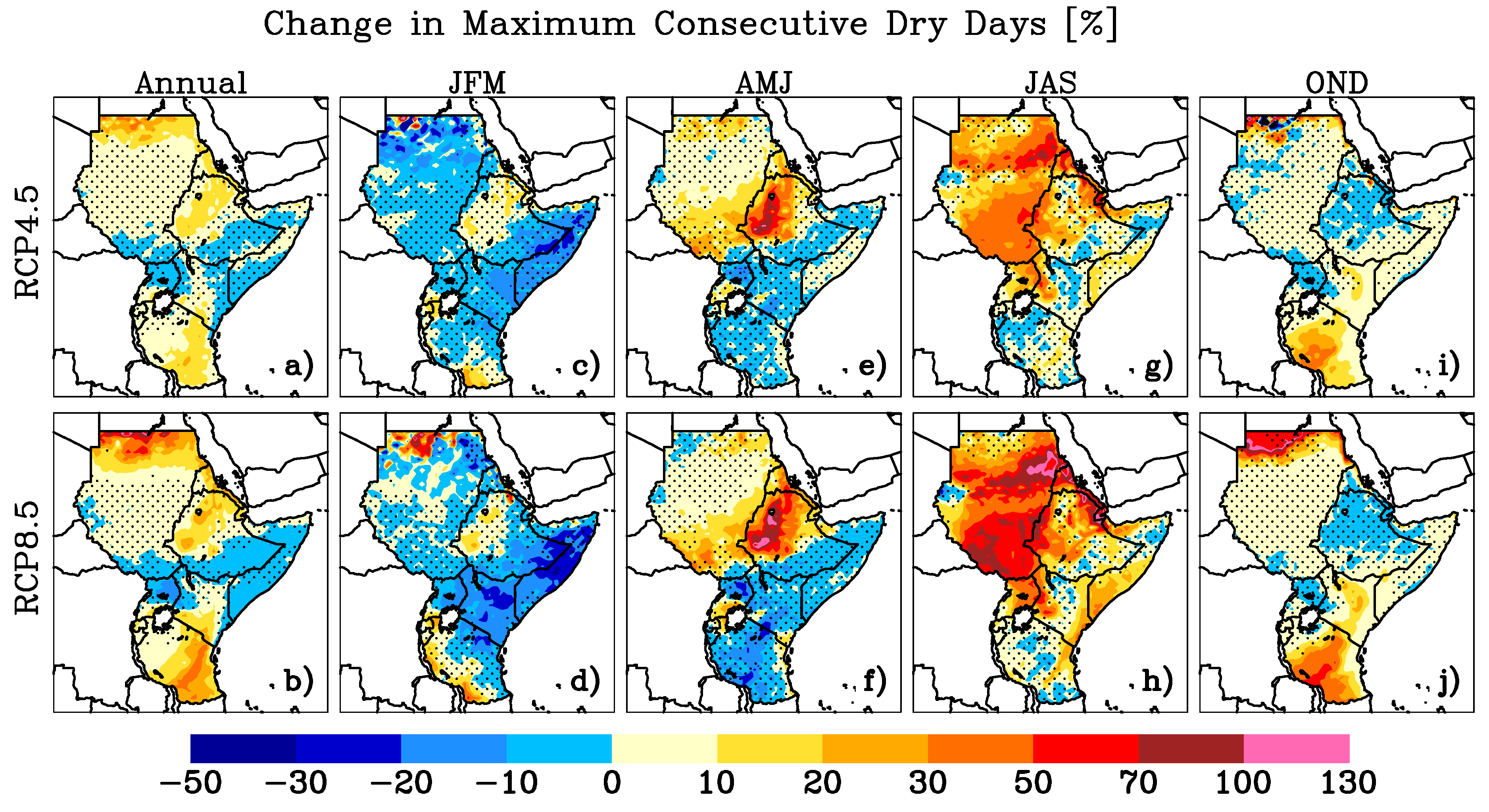
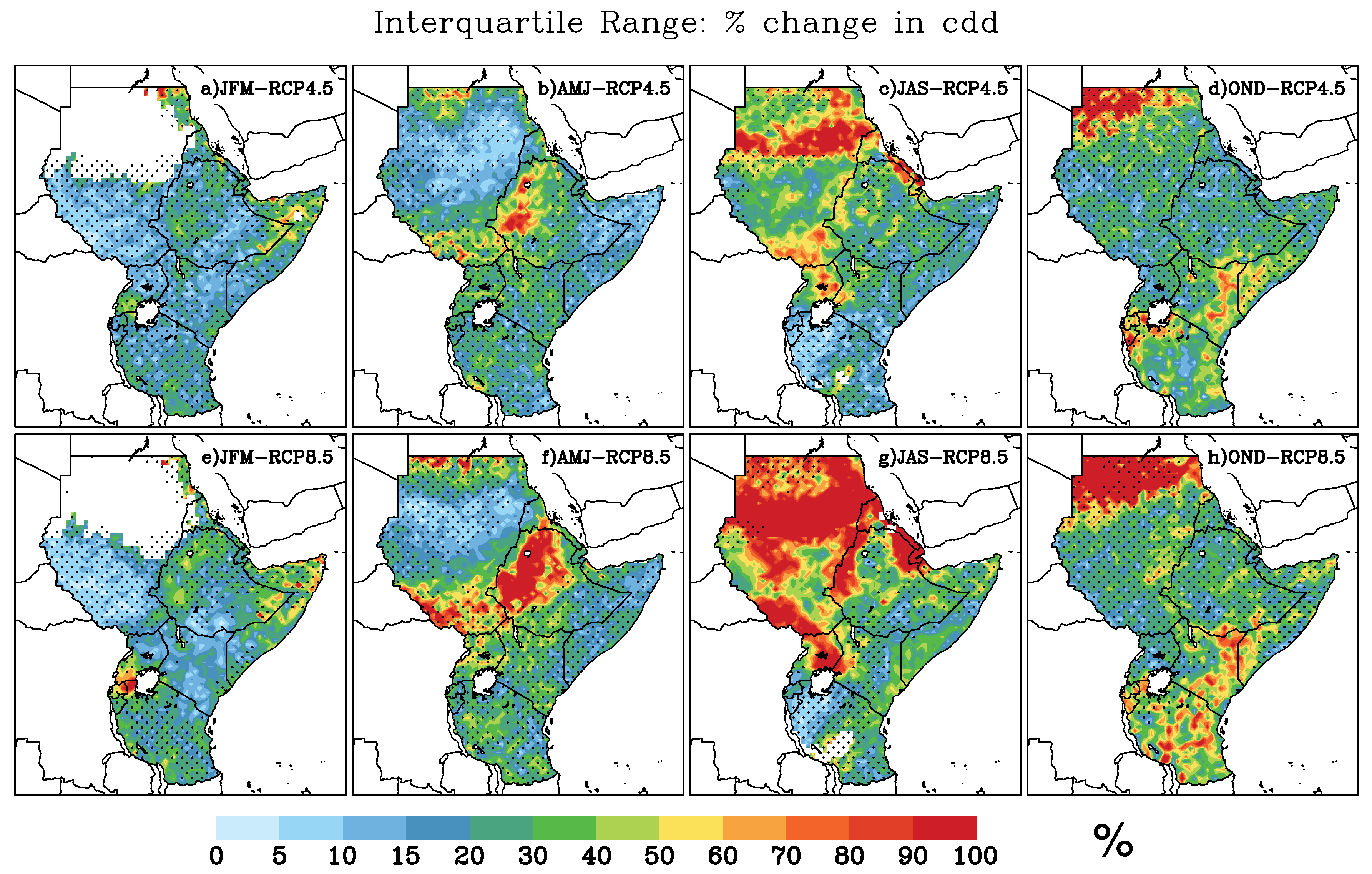
3.6. Projected Changes in Duration-Based Precipitation Indices
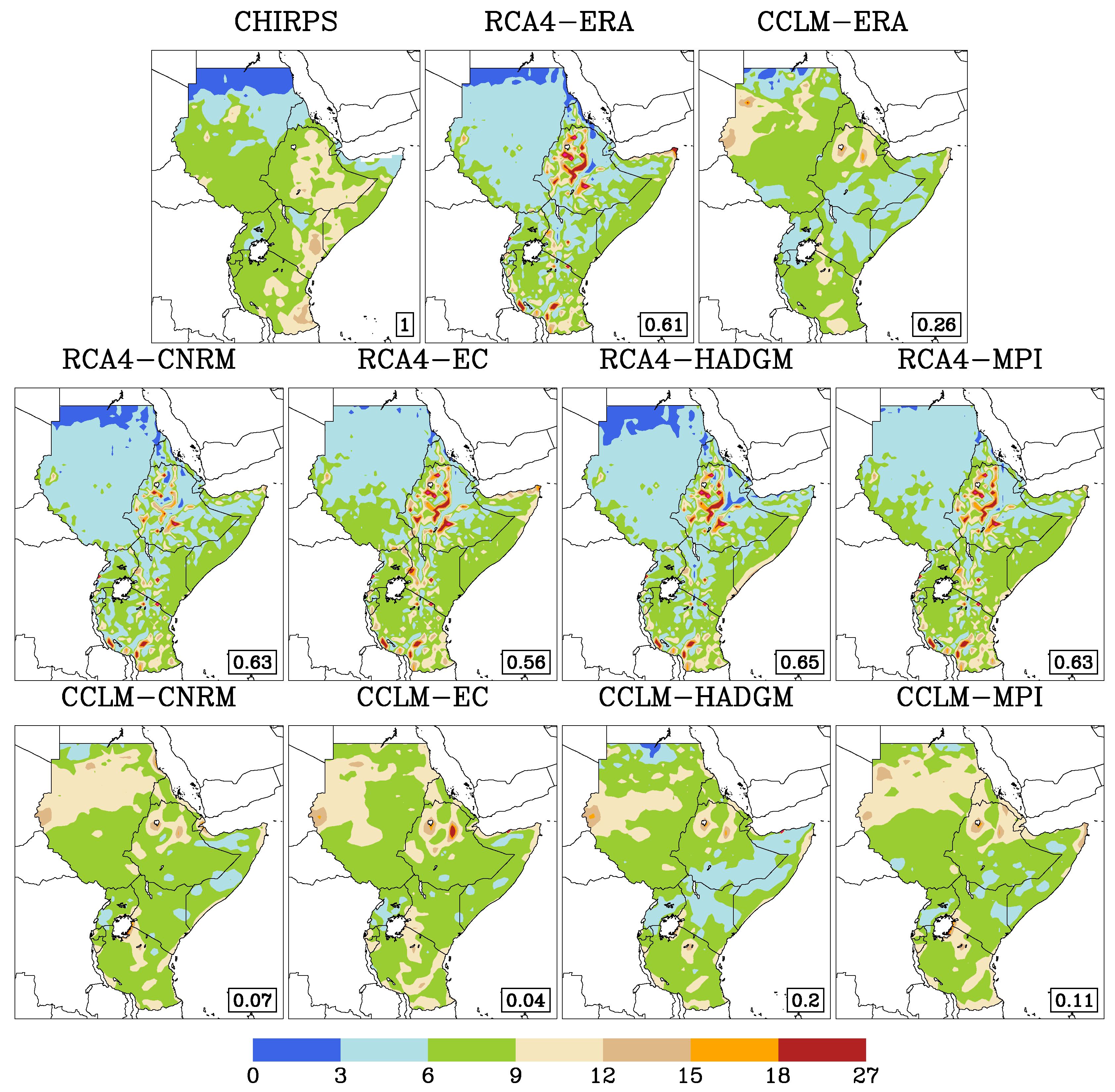
3.7. Model Agreement
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dosio, A. Projection of temperature and heat waves for Africa with an ensemble of CORDEX Regional Climate Models. Clim. Dyn. 2017, 49, 493–519. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Nicholls, N.; Easterling, D.; Goodess, C.M.; Kanae, S.; Kossin, J.; Luo, Y.; Marengo, J.; McInnes, K.; Rahimi, M.; et al. Changes in climate extremes and their impacts on the natural physical environment. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambridge University Press: Cambridge, UK, 2012; pp. 109–230. [Google Scholar]
- Stocker, T. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Mariotti, L.; Diallo, I.; Coppola, E.; Giorgi, F. Seasonal and intraseasonal changes of African monsoon climates in 21st century CORDEX projections. Clim. Chang. 2014, 125, 53–65. [Google Scholar] [CrossRef]
- Case, M. Climate Change Impacts on East Africa: A Review of the Scientific Literature; /hl2006. Available online: www.taccire.suanet.ac.tz/xmlui/bitstream/handle/123456789/138/east_africa_climate_change_impacts.pdf?sequence=1 (accessed on 15 March 2018).
- Endris, H.S.; Omondi, P.; Jain, S.; Lennard, C.; Hewitson, B.; Chang’a, L.; Awange, J.L.; Dosio, A.; Ketiem, P.; Nikulin, G.; et al. Assessment of the Performance of CORDEX Regional Climate Models in Simulating East African Rainfall. J. Clim. 2013, 26, 8453–8475. [Google Scholar] [CrossRef]
- Anyah, R.O.; Qiu, W. Characteristic 20th and 21st century precipitation and temperature patterns and changes over the Greater Horn of Africa. Int. J. Climatol. 2012, 32, 347–363. [Google Scholar] [CrossRef]
- Funk, C.; Dettinger, M.D.; Michaelsen, J.C.; Verdin, J.P.; Brown, M.E.; Barlow, M.; Hoell, A. Warming of the Indian Ocean threatens eastern and southern African food security but could be mitigated by agricultural development. Proc. Natl. Acad. Sci. USA 2008, 105, 11081–11086. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.P.; Funk, C. A westward extension of the warm pool leads to a westward extension of the Walker circulation, drying eastern Africa. Clim. Dyn. 2011, 37, 2417–2435. [Google Scholar] [CrossRef]
- Maidment, R.I.; Allan, R.P.; Black, E. Recent observed and simulated changes in precipitation over Africa. Geophys. Res. Lett. 2015, 42, 8155–8164. [Google Scholar] [CrossRef]
- Lyon, B.; DeWitt, D.G. A recent and abrupt decline in the East African long rains. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Mequanint, F.; Takele, R.; Shiferaw, A. Observed and Future Climate Variability and Extremes Over East Shoa Zone, Ethiopia. J. Climatol. Weather Forecast. 2016, 4, 1–9. [Google Scholar]
- Jury, M.R.; Funk, C. Climatic trends over Ethiopia: regional signals and drivers. Int. J. Climatol. 2013, 33, 1924–1935. [Google Scholar] [CrossRef]
- Pinto, I.; Lennard, C.; Tadross, M.; Hewitson, B.; Dosio, A.; Nikulin, G.; Panitz, H.; Shongwe, M. Evaluation and projections of extreme precipitation over southern Africa from two CORDEX models. Clim. Chang. 2016, 135, 655–668. [Google Scholar] [CrossRef]
- Bartholy, J.; Pongrácz, R.; Kis, A. Projected changes of extreme precipitation using multi-model approach. Q. J. Hung. Meteorol. Serv. 2015, 119, 129–142. [Google Scholar]
- Giorgi, F.; Jones, C.; Asrar, G. Addressing climate information needs at the regional level: The CORDEX framework. WMO Bull. 2009, 58, 175–183. [Google Scholar]
- Dosio, A. Projections of climate change indices of temperature and precipitation from an ensemble of bias-adjusted high-resolution EURO-CORDEX regional climate models. J. Geophys. Res. Atmos. 2016, 121, 5488–5511. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscipl. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Dieterich, C.; Schimanke, S.; Wang, S.; Väli, G.; Liu, Y.; Hordoir, R.; Höglund, A.; Meier, M. Evaluation of the SMHI Coupled Atmosphere-Ice-Ocean Model RCA4-NEMO; Technical Report 47; SMHI: Norrköping, Sweden, 2013. [Google Scholar]
- Rockel, B.; Will, A.; Hense, A. The Regional Climate Model COSMO-CLM (CCLM). Meteorol. Z. 2008, 17, 347–348. [Google Scholar] [CrossRef]
- Panitz, H.J.; Dosio, A.; Büchner, M.; Lüthi, D.; Keuler, K. COSMO-CLM (CCLM) climate simulations over CORDEX-Africa domain: Analysis of the ERA-Interim driven simulations at 0.44∘ and 0.22∘ resolution. Clim. Dyn. 2014, 42, 3015–3038. [Google Scholar] [CrossRef]
- Nikulin, G.; Jones, C.; Giorgi, F.; Asrar, G.; Büchner, M.; Ruth, C.; Christensen, O.; Déqué, M.; Fernandez, J.; Hänsler, A.; et al. Precipitation Climatology in an Ensemble of CORDEX-Africa Regional Climate Simulations. J. Clim. 2012, 25, 6057–6078. [Google Scholar] [CrossRef]
- Dosio, A.; Panitz, H.J.; Schubert-Frisius, M.; Lüthi, D. Dynamical downscaling of CMIP5 global circulation models over CORDEX-Africa with COSMO-CLM: Evaluation over the present climate and analysis of the added value. Clim. Dyn. 2015, 44, 2637–2661. [Google Scholar] [CrossRef]
- Baldauf, M. Stability analysis for linear discretisations of the advection equation with Runge—Kutta time integration. J. Comput. Phys. 2008, 227, 6638–6659. [Google Scholar] [CrossRef]
- Tiedtke, M. A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon. Weather Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef]
- Kain, J. Convective parameterization for mesoscale models: The Kain-Fritcsh scheme. In The Representation of Cumulus Convection in Numerical Models; American Meteorological Society: Boston, MA, USA, 1993. [Google Scholar]
- Ritter, B.; Geleyn, J.F. A comprehensive radiation scheme for numerical weather prediction models with potential applications in climate simulations. Mon. Weather Rev. 1992, 120, 303–325. [Google Scholar] [CrossRef]
- Savijärvi, H. Fast radiation parameterization schemes for mesoscale and short-range forecast models. J. Appl. Meteorol. 1990, 29, 437–447. [Google Scholar] [CrossRef]
- Sass, B.H.; Rontu, L.; Räisänen, P. HIRLAM-2 Radiation Scheme: Documentation and Tests; HIRLAM: Norrköping, Sweden, 1994. [Google Scholar]
- Herzog, H.J.; Vogel, G.; Schubert, U. LLM–a nonhydrostatic model applied to high-resolving simulations of turbulent fluxes over heterogeneous terrain. Theor. Appl. Climatol. 2002, 73, 67–86. [Google Scholar] [CrossRef]
- Cuxart, J.; Bougeault, P.; Redelsperger, J.L. A turbulence scheme allowing for mesoscale and large-eddy simulations. Q. J. R. Meteorol. Soc. 2000, 126, 1–30. [Google Scholar] [CrossRef]
- Buzzi, M.; Rotach, M.W.; Holtslag, M.; Holtslag, A.A. Evaluation of the COSMO-SC turbulence scheme in a shear-driven stable boundary layer. Meteorol. Z. 2011, 20, 335–350. [Google Scholar] [CrossRef]
- Doms, G.; Förstner, J.; Heise, E.; Herzog, H.; Raschendorfer, M.; Schrodin, R.; Reinhardt, T.; Vogel, G. A description of the non-hydrostatic regional model LM (version 3.20). In Part II: Physical Parameterization; Deutscher Wetterdienst: Offenbach, Germany, 2007. [Google Scholar]
- Baldauf, M.; Schulz, J. Prognostic precipitation in the Lokal-Modell (LM) of DWD. Cosmo Newslett. 2004, 4, 177–180. [Google Scholar]
- Rasch, P.; Kristjánsson, J. A comparison of the CCM3 model climate using diagnosed and predicted condensate parameterizations. J. Clim. 1998, 11, 1587–1614. [Google Scholar] [CrossRef]
- Samuelsson, P.; Gollvik, S.; Ullerstig, A. The Land-Surface Scheme of the Rossby Centre Regional Atmospheric Climate Model (RCA3); SMHI: Norrkoping, Sweden, 2006. [Google Scholar]
- Baldauf, M.; Seifert, A.; Förstner, J.; Majewski, D.; Raschendorfer, M.; Reinhardt, T. Operational Convective-Scale Numerical Weather Prediction with the COSMO Model: Description and Sensitivities. Mon.Weather Rev. 2011, 139, 3887–3905. [Google Scholar] [CrossRef]
- Jones, C.G.; Samuelsson, P.; Kjellström, E. Regional climate modelling at the Rossby Centre. Tellus A 2011, 63, 1–3. [Google Scholar] [CrossRef]
- Shongwe, M.E.; Van Oldenborgh, G.; Van Den Hurk, B.; De Boer, B.; Coelho, C.; Van Aalst, M. Projected changes in mean and extreme precipitation in Africa under global warming. Part I: Southern Africa. J. Clim. 2009, 22, 3819–3837. [Google Scholar] [CrossRef]
- Sylla, M.B.; Giorgi, F.; Coppola, E.; Mariotti, L. Uncertainties in daily rainfall over Africa: assessment of gridded observation products and evaluation of a regional climate model simulation. Int. J. Climatol. 2013, 33, 1805–1817. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- UCAR/NCAR/CISL/TDD. The NCAR Command Language (Version 6.3.0) [Software]; UCAR/NCAR/CISL/TDD: Boulder, Colorado, 2016. [Google Scholar]
- Alexander, L.; Yang, H.; Perkins, S. ClimPACT—Indices and Software. User Manual. 2013. Available online: http://www.wmo.int/pages/prog/wcp/ccl/opace/opace4/meetings/documents/ETCRSCI_software_documentation_v2a.doc (accessed on 17 January 2017).
- Frich, P.; Alexander, L.V.; Della-Marta, P.; Gleason, B.; Haylock, M.; Tank, A.K.; Peterson, T. Observed coherent changes in climatic extremes during the second half of the twentieth century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Yin, H.; Donat, M.G.; Alexander, L.V.; Sun, Y. Multi-dataset comparison of gridded observed temperature and precipitation extremes over China. Int. J. Climatol. 2015, 35, 2809–2827. [Google Scholar] [CrossRef]
- Diallo, I.; Giorgi, F.; Deme, A.; Tall, M.; Mariotti, L.; Gaye, A.T. Projected changes of summer monsoon extremes and hydroclimatic regimes over West Africa for the twenty-first century. Clim. Dyn. 2016, 47, 3931–3954. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 2. Future climate projections. J. Geophys. Res. Atmos. 2013, 118, 2473–2493. [Google Scholar] [CrossRef]
- Diro, G.T.; Toniazzo, T.; Shaffrey, L. Ethiopian rainfall in climate models. In African Climate and Climate Change; Springer: Berlin, Germany, 2011; pp. 51–69. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Pattern Correlation Coefficient. Available online: https://www.ncl.ucar.edu/Document/Functions/ Contributed/pattern_cor.shtml (accessed on 25 April 2017).
- Di Luca, A.; de Elía, R.; Laprise, R. Potential for small scale added value of RCM’s downscaled climate change signal. Clim. Dyn. 2013, 40, 601–618. [Google Scholar] [CrossRef]
- Endris, H.S.; Lennard, C.; Hewitson, B.; Dosio, A.; Nikulin, G.; Panitz, H.J. Teleconnection responses in multi-GCM driven CORDEX RCMs over Eastern Africa. Clim. Dyn. 2016, 46, 2821–2846. [Google Scholar] [CrossRef]
- Feser, F.; Rockel, B.; von Storch, H.; Winterfeldt, J.; Zahn, M. Regional climate models add value to global model data: a review and selected examples. Bull. Am. Meteorol. Soc. 2011, 92, 1181–1192. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.M.; Bolvin, D.T.; Curtis, S.; Joyce, R.; McGavock, B.; Susskind, J. Global Precipitation at One-Degree Daily Resolution from Multisatellite Observations. J. Hydrometeorol. 2001, 2, 36–50. Available online: https://doi.org/10.1175/1525-7541(2001)002<0036:GPAODD>2.0.CO;2 (accessed on 5 February 2018). [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. Available online: https://doi.org/10.1175/JHM560.1 (accessed on 5 February 2018). [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Ziese, M. GPCC Full Data Reanalysis Version 7.0: Monthly Land-Surface Precipitation from Rain Gauges built on GTS based and Historic Data. Available online: https://rda.ucar.edu/datasets/ds496.0/ (accessed on 5 February 2018).
- Lange, S. EartH2Observe, WFDEI and ERA-Interim data Merged and Bias-corrected for ISIMIP (EWEMBI): GFZ Data Services. Available online: http://dataservices.gfz-potsdam.de/pik/showshort.php?id=escidoc:1809891 (accessed on 5 February 2018).
- Cook, K.H.; Vizy, E.K. Projected Changes in East African Rainy Seasons. J. Clim. 2013, 130222102159002. [Google Scholar] [CrossRef]
- Otieno, V.O.; Anyah, R.O. CMIP5 simulated climate conditions of the Greater Horn of Africa (GHA). Part II: projected climate. Clim. Dyn. 2013, 41, 2099–2113. [Google Scholar] [CrossRef]
- Alexander, L.V.; Arblaster, J.M. Historical and projected trends in temperature and precipitation extremes in Australia in observations and CMIP5. Weather Clim. Extremes 2017, 15, 34–56. [Google Scholar] [CrossRef]

| CLMcom-CCLM4.8 | SMHI-RCA4 | |
|---|---|---|
| Institute | Climate Limited-Area Modelling Community(CLMcom) | Swedish Meteorological and Hydrological Institute(SMHI), Rossby Centre |
| Model Name | COSMO-Climate Limited-Area Modelling (COSMO-CLM) | Rossby Centre regional atmospheric model v4 (RCA4) |
| Short name | CCLM | RCA4 |
| Projection resolution | Rotated pole 0.44 | Rotated pole 0.44 |
| Vertical coordinate/levels | Terrain following/35 | hybrid/40 |
| Advection | Fifth-order upwind [24] | Semi-Lagrangian |
| Time step (s) | 240 | 1200 |
| Convective scheme | Tiedtke [25] | Kain and Fritsch [26,27] |
| Radiation scheme | Ritter and Geleyn [28] | Savijärvi [29,30] |
| Turbulence vertical | LLM [31] | Meso-NH [32] |
| diffusion | COSMO single column [33] | |
| Cloud microphysics scheme | COSMO [34] LM-DWD [35] | Rasch and Kristjansson [36] |
| Land surface scheme | TerraLib Modeling Language (TERRA-ML) [34] | LSS-RCA3 [37] |
| Latest reference | [20,38] | [39] |
| Model | Description | Modeling Center |
|---|---|---|
| CNRM-CM5 | Centre National de Météorologiques Coupled Model 5 | Centre National de Recherches Météorologiques/Centre Européen de Recherche et Formation (CERFACS)Avancée en Calcul Scientifique |
| EC-EARTH HadGEM2-ES | EC-EARTH Hadley Global Environmental Earth System Model 2 | EC-EARTH consortium Met Office Hadley Centre(MOHC) |
| MPI-ESM-LR | MPI Earth System Model running on low resolution grid | Max Planck Institute for Meteorology (MPI-M) |
| Index | Definition | Unit |
|---|---|---|
| PRCPTOT | Sum of daily precipitation ≥ 1 mm | mm |
| SDII | Annual total PRCP divided by the number of wet days (≥1 mm) | mm/day |
| CDD | Maximum number of Consecutive Dry Days (<1 mm) | mm |
| R10 mm | Number of days when precipitation ≥ 10 mm | days |
| R20 mm | Number of days when precipitation ≥ 20 mm | days |
| RX1DAY | Maximum 1-day precipitation total | mm |
| RX5DAY | Maximum 5-day precipitation total | mm |
| R95p | Annual sum of daily precipitation ≥95th percentile | mm |
| R99p | Annual sum of daily precipitation ≥99th percentile | mm |
| PRCPTOT | SDII | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| TRMM | GPCP | GPCC | EWEMBI | TRMM | GPCP | GPCC | EWEMBI | ||
| CHIRPS | 0.98 | 0.97 | 0.97 | 0.97 | CHIRPS | 0.55 | 0.71 | 0.71 | 0.40 |
| TRMM | 0.96 | 0.96 | 0.96 | TRMM | 0.62 | 0.37 | 0.41 | ||
| GPCP | 0.95 | 0.94 | GPCP | 0.74 | 0.35 | ||||
| GPCC | 0.97 | GPCC | 0.52 | ||||||
| R10 mm | RX1DAY | ||||||||
| TRMM | GPCP | GPCC | EWEMBI | TRMM | GPCP | GPCC | EWEMBI | ||
| CHIRPS | 0.90 | 0.89 | 0.95 | 0.78 | CHIRPS | 0.33 | 0.55 | 0.78 | 0.62 |
| TRMM | 0.95 | 0.89 | 0.83 | TRMM | 0.85 | 0.47 | 0.68 | ||
| GPCP | 0.89 | 0.77 | GPCP | 0.66 | 0.77 | ||||
| GPCC | 0.83 | GPCC | 0.79 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiferaw, A.; Tadesse, T.; Rowe, C.; Oglesby, R. Precipitation Extremes in Dynamically Downscaled Climate Scenarios over the Greater Horn of Africa. Atmosphere 2018, 9, 112. https://doi.org/10.3390/atmos9030112
Shiferaw A, Tadesse T, Rowe C, Oglesby R. Precipitation Extremes in Dynamically Downscaled Climate Scenarios over the Greater Horn of Africa. Atmosphere. 2018; 9(3):112. https://doi.org/10.3390/atmos9030112
Chicago/Turabian StyleShiferaw, Andualem, Tsegaye Tadesse, Clinton Rowe, and Robert Oglesby. 2018. "Precipitation Extremes in Dynamically Downscaled Climate Scenarios over the Greater Horn of Africa" Atmosphere 9, no. 3: 112. https://doi.org/10.3390/atmos9030112
APA StyleShiferaw, A., Tadesse, T., Rowe, C., & Oglesby, R. (2018). Precipitation Extremes in Dynamically Downscaled Climate Scenarios over the Greater Horn of Africa. Atmosphere, 9(3), 112. https://doi.org/10.3390/atmos9030112






