Evaluations of WRF Sensitivities in Surface Simulations with an Ensemble Prediction System
Abstract
1. Introduction
2. Model Setting, Experiments’ Design and Observation Data Sources
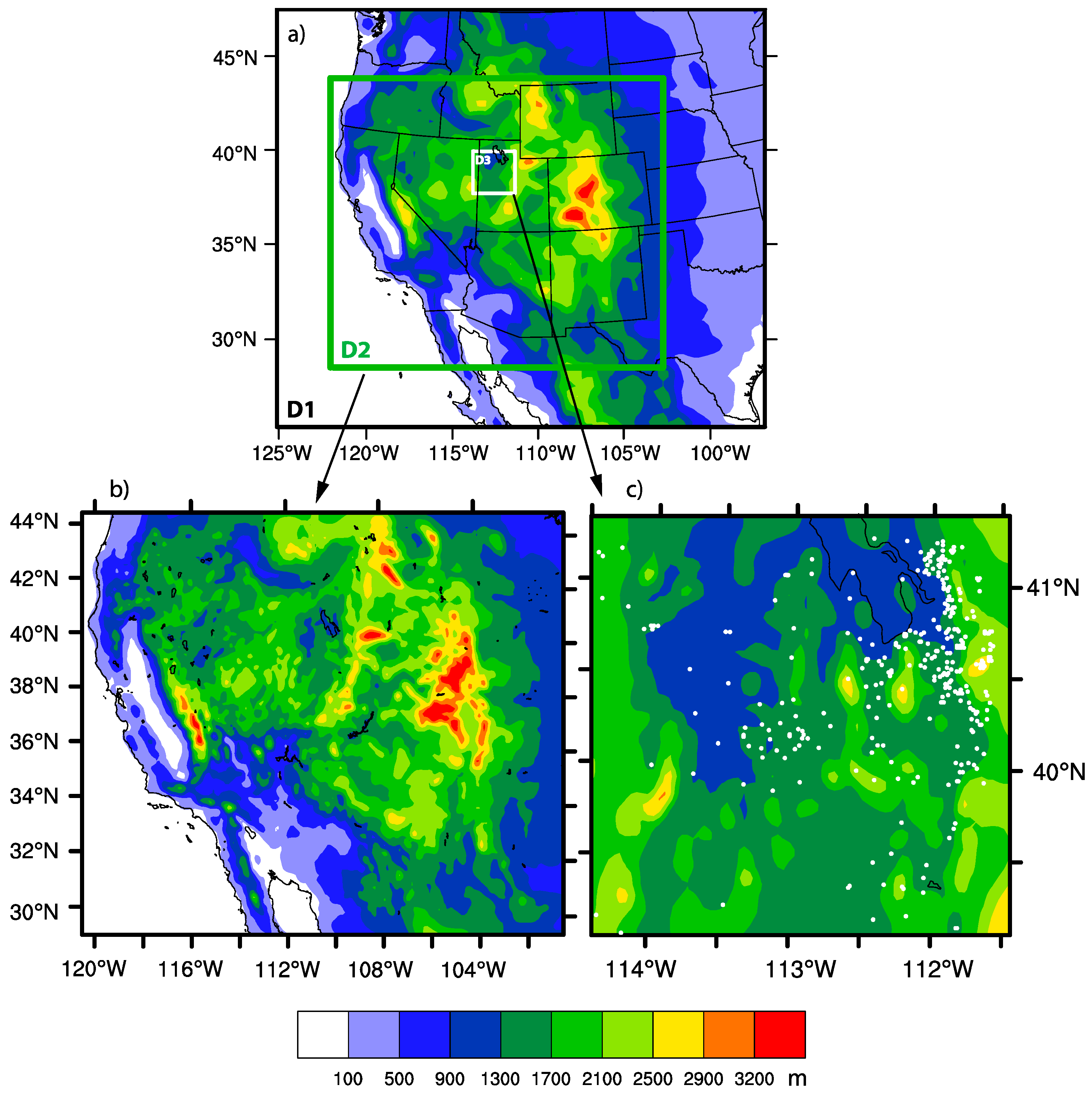
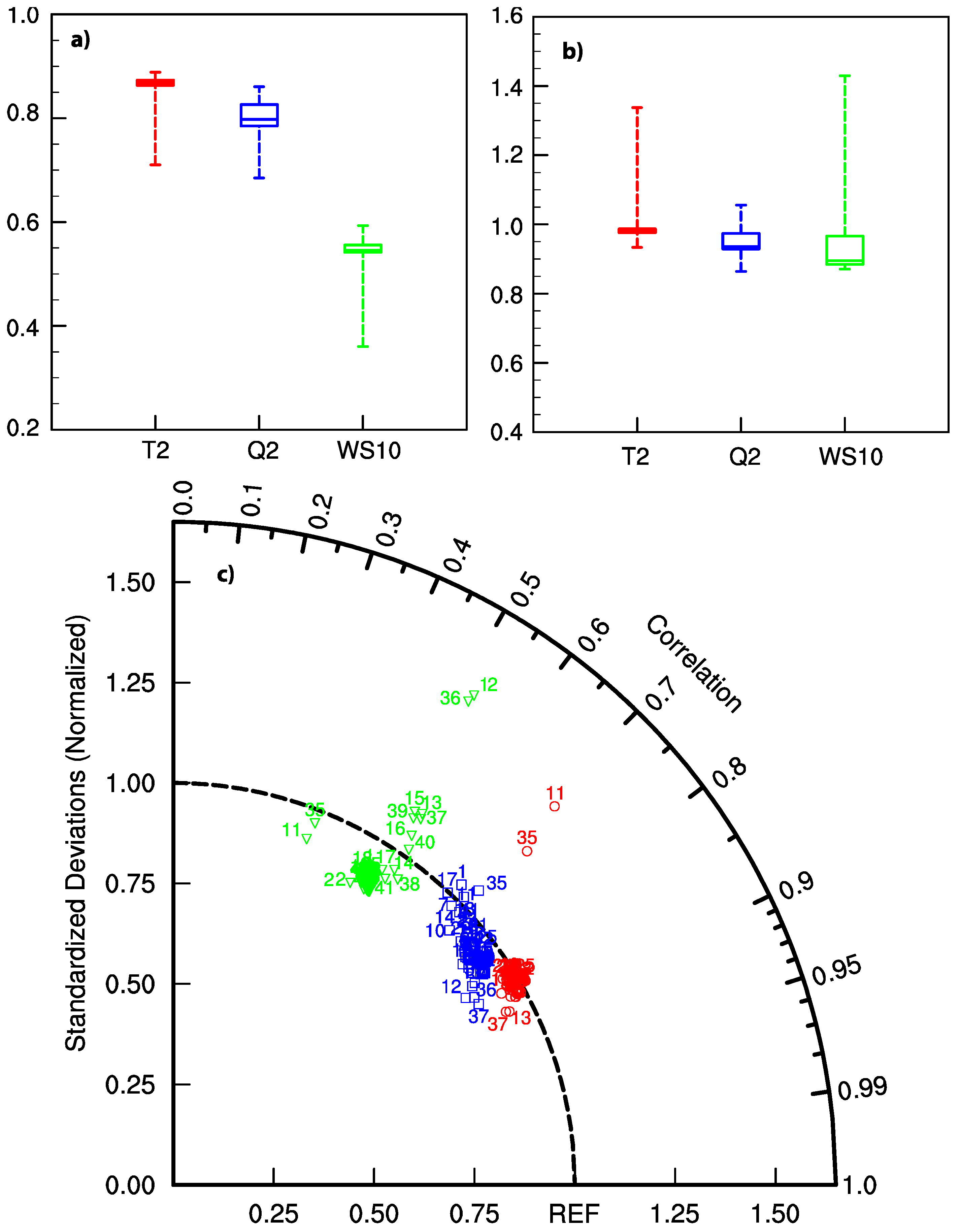
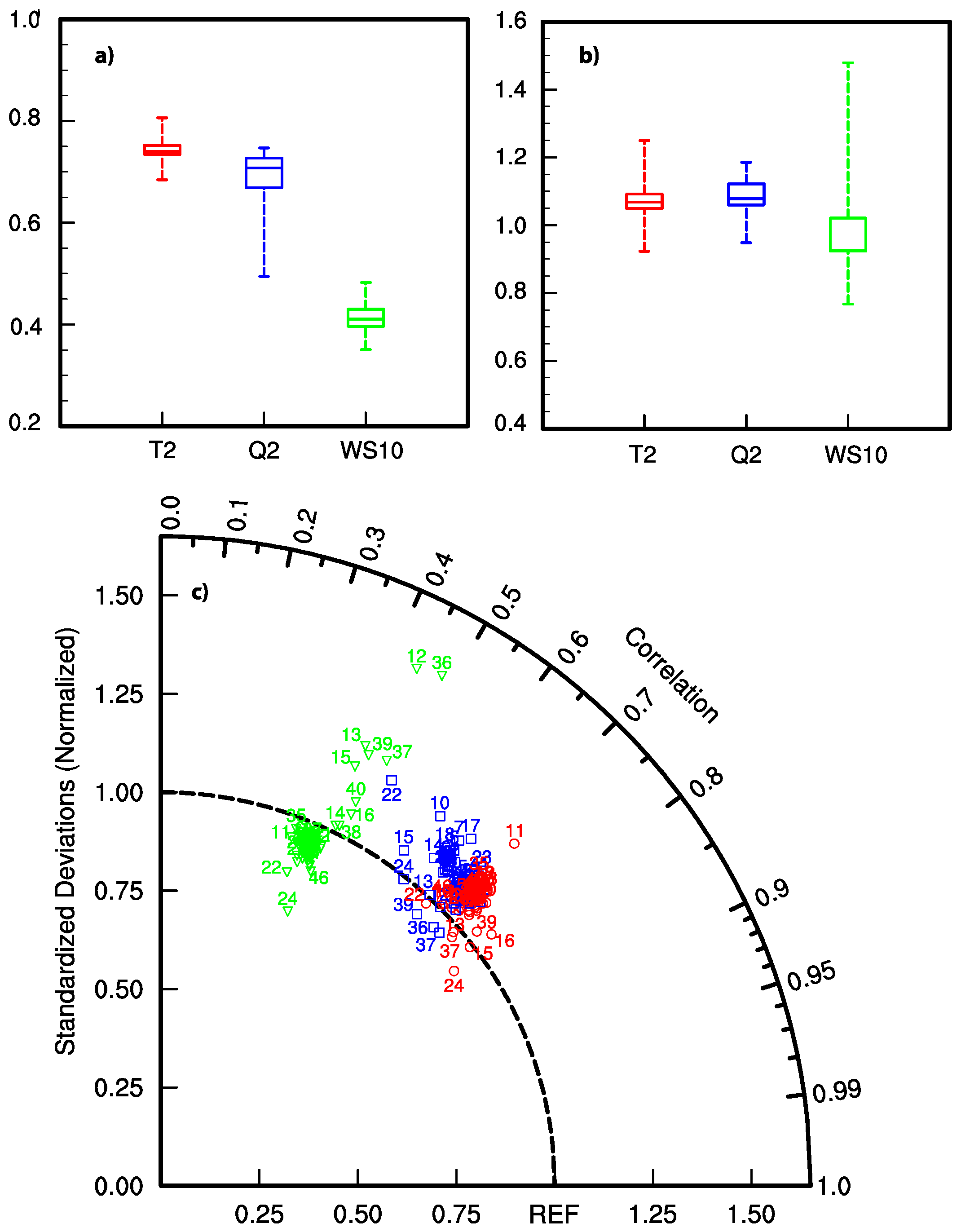
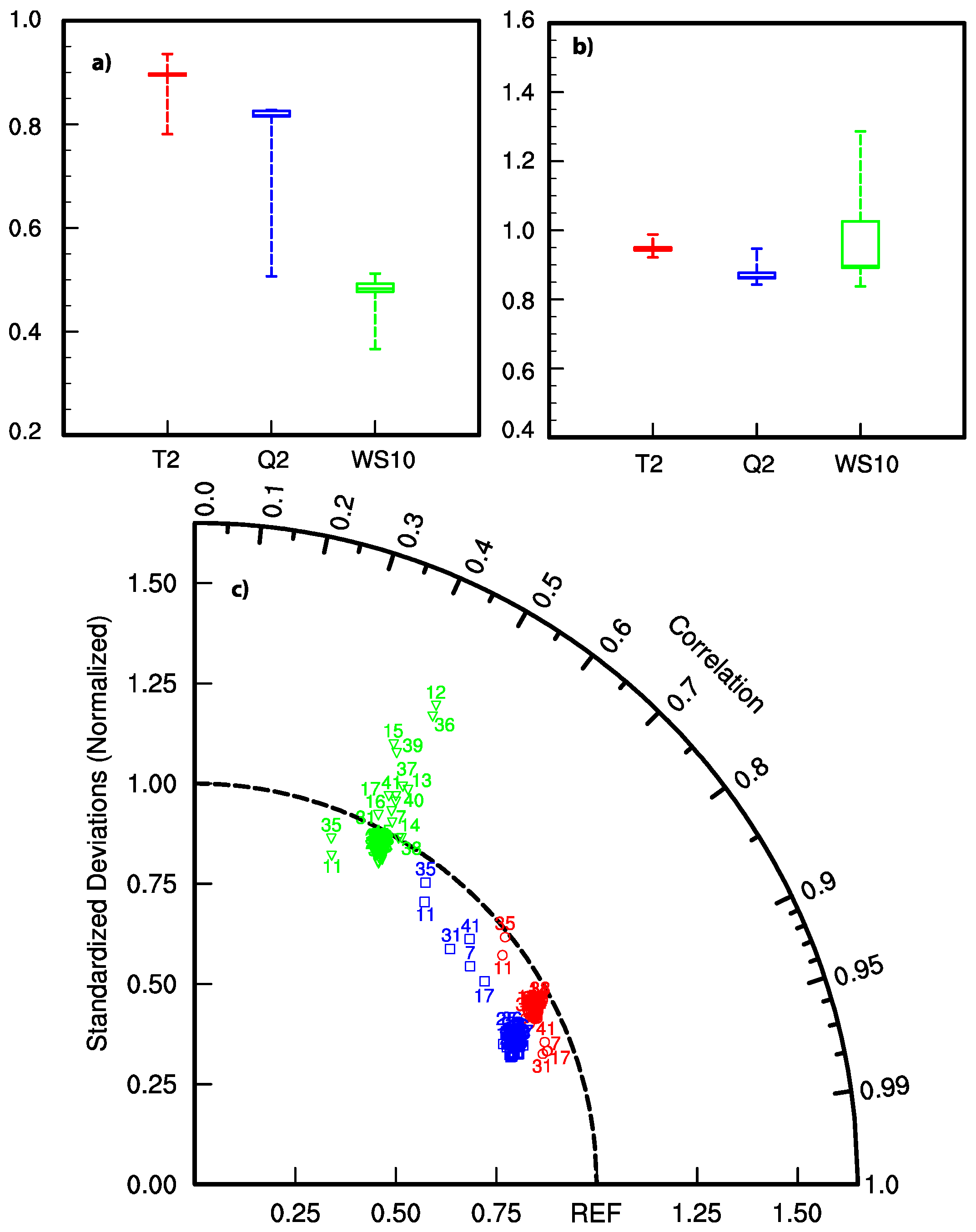
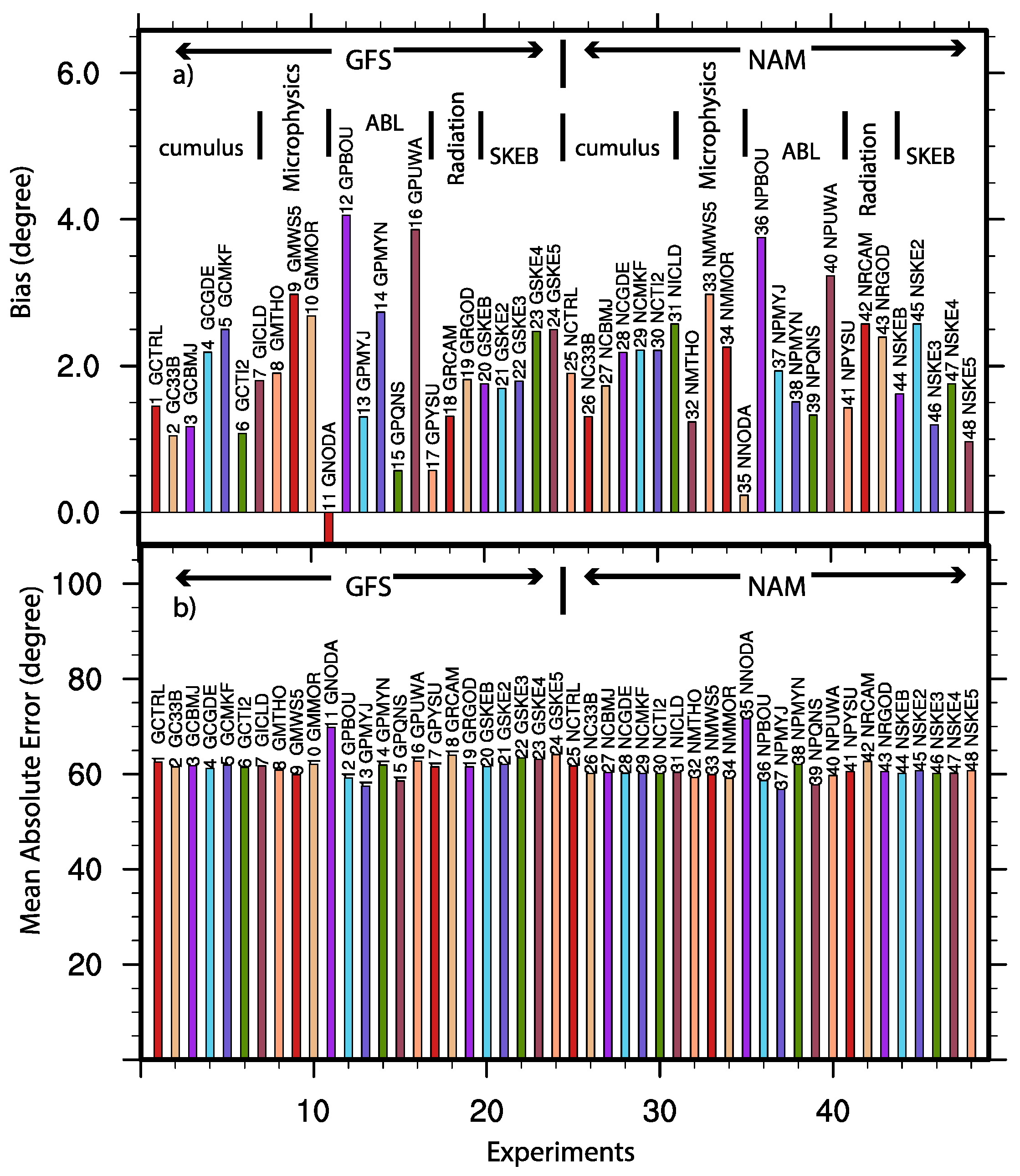
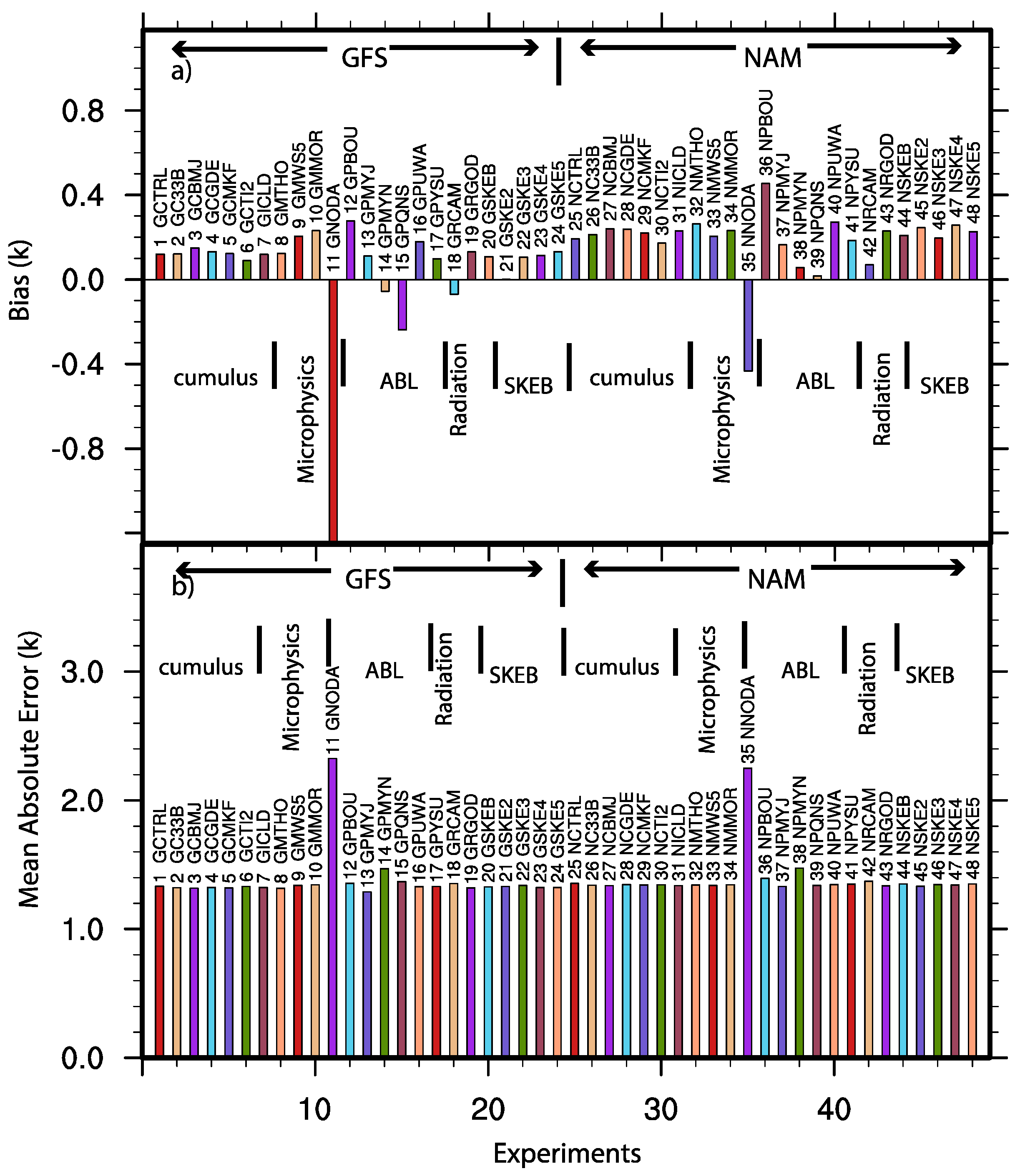
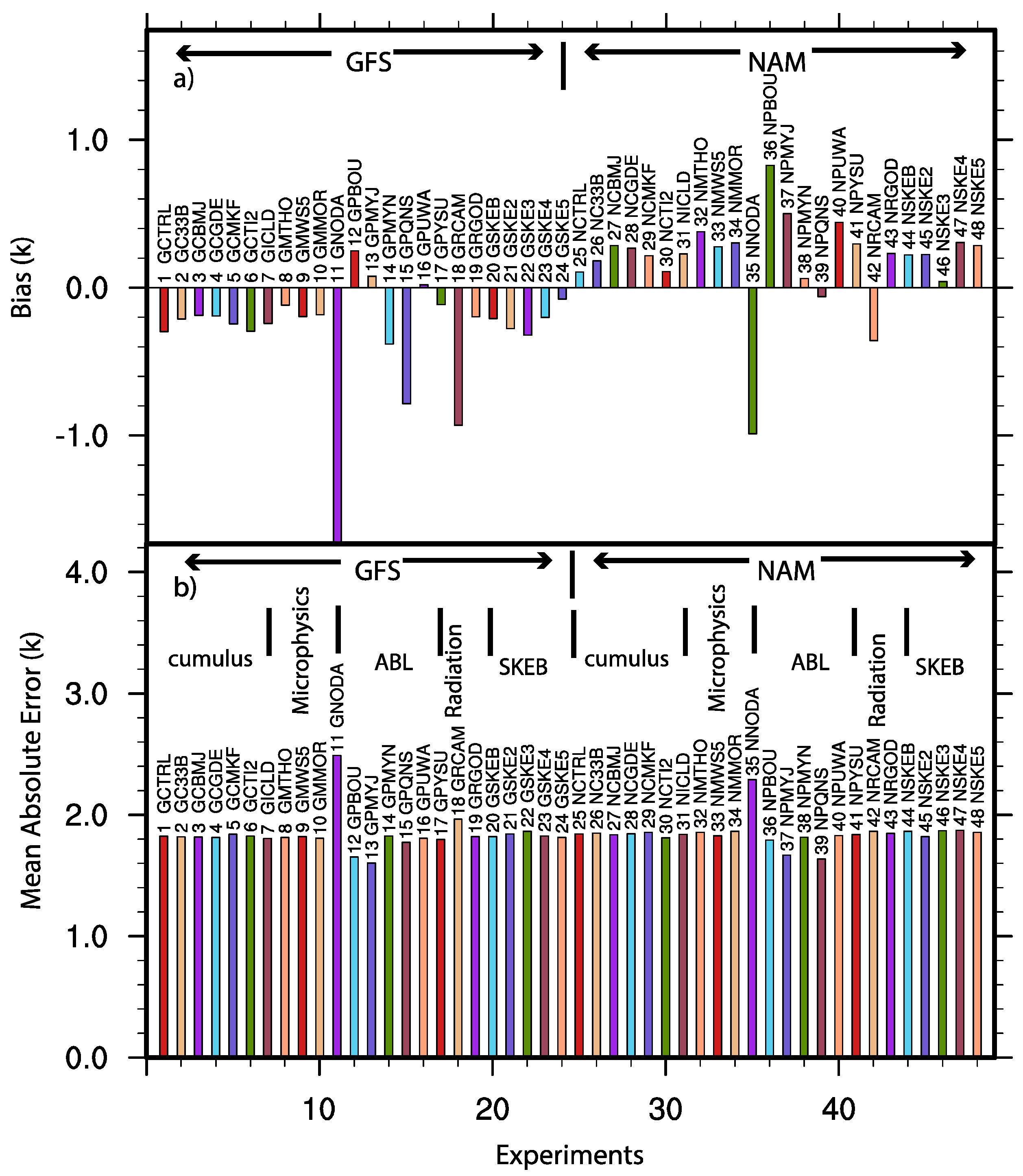
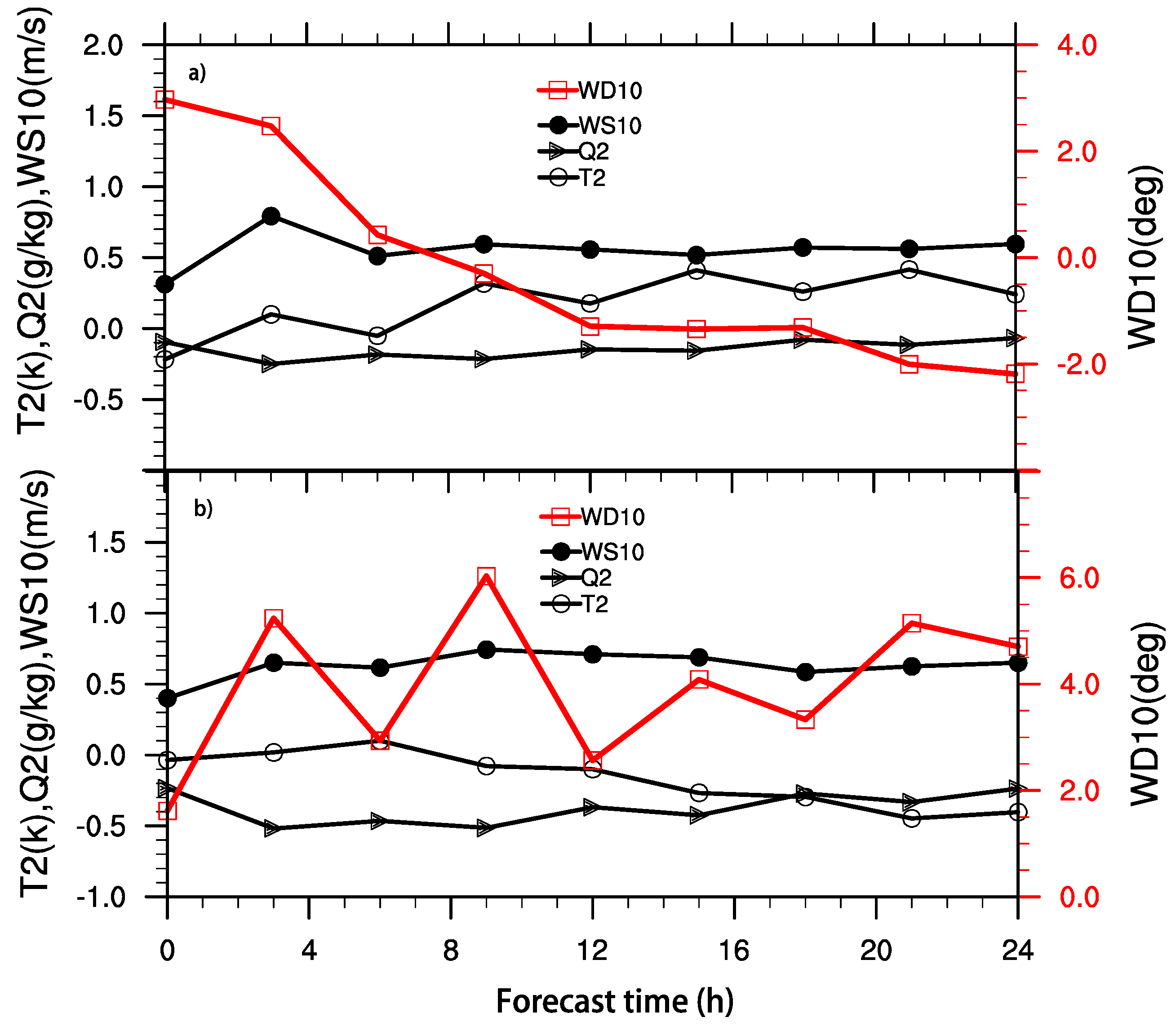
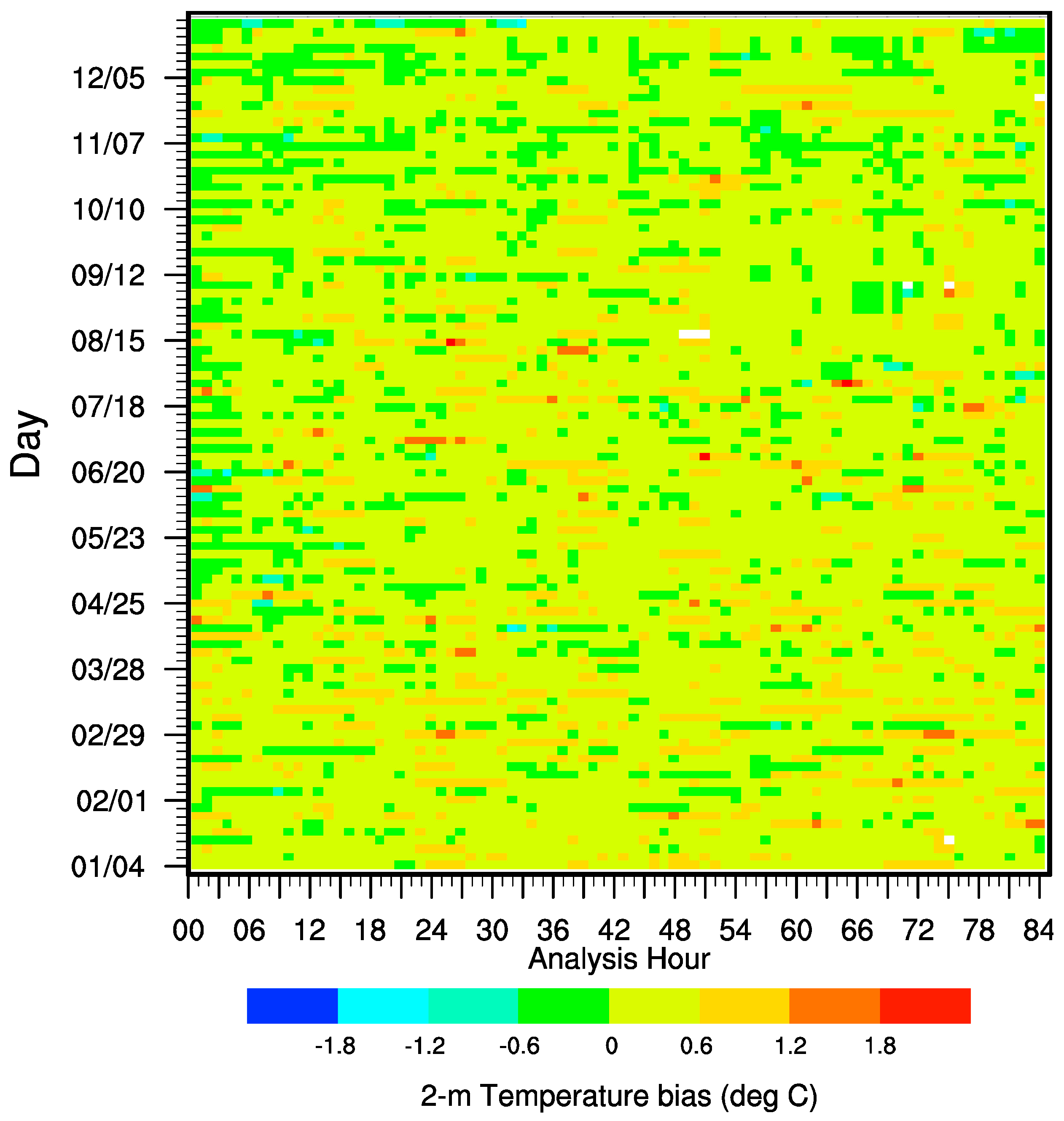
3. Evaluation of the Sensitivities of the System
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A description of the Advanced Research WRF Version 2. NCAR Tech. Notes 2005. NCAR/TN-468+STR. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gomez-Gesteira, M.; Santos, C. A sensitivity study of the WRF model in wind simulation for an area of high wind energy. Environ. Model. Softw. 2012, 33, 23–34. [Google Scholar] [CrossRef]
- Banks, R.F.; Tiana-Alsina, J.; MaríaBaldasano, J.; Rocadenbosch, F.; Papayannis, A.; Solomos, S.; Tzanis, C.G. Sensitivity of boundary-layer variables to PBL schemes in the WRF model based on surface meteorological observations, lidar, and radiosondes during the HygrA-CD campaign. Atmos. Res. 2016, 176, 185–201. [Google Scholar] [CrossRef]
- Hu, X.M.; Nielsen-Gammon, J.M.; Zhang, F. Evaluation of three planetary boundary layer schemes in the WRF model. J. Appl. Meteorol. Climatol. 2010, 49, 1831–1844. [Google Scholar] [CrossRef]
- Kleczek, M.A.; Steeneveld, G.J.; Holtslag, A.A.M. Evaluation of the Weather Research and Forecasting mesoscale model for GABLS3: Impact of boundary-layer schemes, Boundary Conditions and Spin-Up. Bound.-Layer Meteorol. 2014, 152, 213–243. [Google Scholar] [CrossRef]
- Gómez-Navarro, J.J.; Raible, C.C.; Die, S. Sensitivity of the WRF model to PBL parameterizations and nesting techniques: Evaluation of wind storms over complex terrain. Geosci. Model Dev. 2014, 8, 3349–3363. [Google Scholar] [CrossRef]
- Hariprasad, K.B.R.R.; Srinivas, C.V.; Bagavath Singh, A.; Vijaya Bhaskara Rao, S.; Baskaran, R.; Venkatraman, B. Numerical simulation and intercomparison of boundary layer structure with different PBL schemes in WRF using experimental observations at a tropical site. Atmos. Res. 2014, 145, 27–44. [Google Scholar] [CrossRef]
- Frediani, M.E.B.; Hacker, J.P.; Anagnostou, E.N.; Hopson, T. Evaluation of PBL Parameterizations for Modeling Surface Wind Speed during Storms in the Northeast United States. Weather Forecast. 2016, 31, 1511–1528. [Google Scholar] [CrossRef]
- Tymvios, F.; Charalambous, D.; Michaelides, S.; Lelieveld, J. Intercomparison of boundary layer parameterizations for summer conditions in the eastern Mediterranean island of Cyprus using the WRF—ARW model. Atmos. Res. 2017. [Google Scholar] [CrossRef]
- Hahmann, A.N.; Vincent, C.L.; Peña, A.; Lange, J.; Hasager, C.B. Wind climate estimation using WRF model output: Method and model sensitivities over the sea. Int. J. Climatol. 2015, 35, 3422–3439. [Google Scholar] [CrossRef]
- Ruiz, J.J.; Saulo, C. WRF Model Sensitivity to Choice of Parameterization over South America: Validation against Surface Variables. Mon. Weather Rev. 2010, 138, 3342–3355. [Google Scholar] [CrossRef]
- Chadee, X.; Seegobin, N.; Clarke, R. Optimizing the Weather Research and Forecasting (WRF) Model for Mapping the Near-Surface Wind Resources over the Southernmost Caribbean Islands of Trinidad and Tobago. Energies 2017, 10, 931. [Google Scholar] [CrossRef]
- Santos-Alamillos, F.J.; Pozo-Vázquez, D.; Ruiz-Arias, J.A.; Lara-Fanego, V.; Tovar-Pescador, J. Analysis of WRF Model Wind Estimate Sensitivity to Physics Parameterization Choice and Terrain Representation in Andalusia (Southern Spain). J. Appl. Meteorol. Climatol. 2013, 52, 1592–1609. [Google Scholar] [CrossRef]
- Di, Z.; Duan, Q.; Gong, W.; Wang, C.; Gan, Y.; Quan, J.; Li, J.; Miao, C.; Ye, A.; Tong, C. Assessing WRF model parameter sensitivity: A case study with 5 day summer precipitation forecasting in the Greater Beijing Area. Geophys. Res. Lett. 2015, 42, 579–587. [Google Scholar] [CrossRef]
- Pei, L.; Moore, N.; Zhong, S.; Luo, L.; Hyndman, D.W.; Heilman, W.E.; Gao, Z. WRF model sensitivity to land surface model and cumulus parameterization under short-term climate extremes over the southern Great Plains of the United States. J. Clim. 2014, 27, 7703–7724. [Google Scholar] [CrossRef]
- Rajeevan, M.; Kesarkar, A.; Thampi, S.B.; Rao, T.N.; Radhakrishna, B.; Rajasekhar, M. Sensitivity of WRF cloud microphysics to simulations of a severe thunderstorm event over Southeast India. Ann. Geophys. 2010, 28, 603–619. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Lim, K.-S.S.; Kim, J.-H.; Lim, J.-O.J.; Dudhia, J. Sensitivity Study of Cloud-Resolving Convective Simulations with WRF Using Two Bulk Microphysical Parameterizations: Ice-Phase Microphysics versus Sedimentation Effects. J. Appl. Meteorol. Clim. 2009, 48, 61–76. [Google Scholar] [CrossRef]
- Patil, R.; Kumar, P.P. WRF model sensitivity for simulating intense western disturbances over North West India, Model. Earth Syst. Environ. 2016, 2, 1–15. [Google Scholar] [CrossRef]
- Orr, A.; Listowski, C.; Couttet, M.; Collier, E.; Immerzeel, W.; Deb, P.; Bannister, D. Sensitivity of simulated summer monsoonal precipitation in Langtang Valley, Himalaya, to cloud microphysics schemes in WRF. J. Geophy. Res. Atmos. 2017, 122, 6298–6318. [Google Scholar] [CrossRef]
- García-Díez, M.; Fernández, J.; Vautard, R. An RCM multi-physics ensemble over Europe: Multi-variable evaluation to avoid error compensation. Clim. Dyn. 2015, 45, 3141–3156. [Google Scholar] [CrossRef]
- Jerez, S.; Montavez, J.P.; Jimenez-Guerrero, P.; Gomez-Navarro, J.J.; Lorente-Plazas, R.; Zorita, E. A multi-physics ensemble of present-day climate regional simulations over the Iberian Peninsula. Clim. Dyn. 2013, 40, 3023–4306. [Google Scholar] [CrossRef]
- Di Luca, A.; Flaounas, E.; Drobinski, P.; Brossier, C.L. The atmospheric component of the Mediterranean Sea water budget in a WRF multi-physics ensemble and observations. Clim. Dyn. 2014, 43, 2349–2375. [Google Scholar] [CrossRef]
- Zeng, X.-M.; Wang, N.; Wang, Y.; Zheng, Y.; Zhou, Z.; Wang, G.; Chen, C.; Liu, H. WRF-simulated sensitivity to land surface schemes in short and medium ranges for a high-temperature event in East China: A comparative study. J. Adv. Model. Earth Syst. 2015, 7, 1305–1325. [Google Scholar] [CrossRef]
- Nemunaitis-Berry, K.L.; Klein, P.M.; Basara, J.B.; Fedorovich, E. Sensitivity of Predictions of the Urban Surface Energy Balance and Heat Island to Variations of Urban Canopy Parameters in Simulations with the WRF Model. J. Appl. Meteorol. Clim. 2017, 56, 573–595. [Google Scholar] [CrossRef]
- Zeng, X.-M.; Wang, M.; Wang, N.; Yi, X.; Chen, C.; Zhou, Z.; Wang, G.; Zheng, Y. Assessing simulated summer 10-m wind speed over China: influencing processes and sensitivities to land surface schemes. Clim. Dyn. 2017. [Google Scholar] [CrossRef]
- Lorente-Plazas, R.; Jiménez, P.A.; Dudhia, J.; Montávez, J.P. Evaluating and Improving the Impact of the Atmospheric Stability and Orography on Surface Winds in the WRF Model. Mon. Weather Rev. 2016, 144, 2685–2693. [Google Scholar] [CrossRef]
- Jee, J.-B.; Kim, S. Sensitivity Study on High-Resolution Numerical Modeling of Static Topographic Data. Atmosphere 2016, 7, 86. [Google Scholar] [CrossRef]
- Santos-Alamillos, F.J.; Pozo-Vázquez, D.; Ruiz-Arias, J.A.; Tovar-Pescador, J. Influence of land-use misrepresentation on the accuracy of WRF wind estimates: Evaluation of GLCC and CORINE land-use maps in southern Spain. Atmos. Res. 2015, 157, 17–28. [Google Scholar] [CrossRef]
- Pan, L.; Liu, Y.; Li, L.; Jiang, J.; Cheng, W.; Roux, G. Impact of four-dimensional data assimilation (FDDA) on urban climate analysis. J. Adv. Model. Earth Syst. 2015, 7, 1997–2011. [Google Scholar] [CrossRef]
- Knievel, J.; Liu, Y.; Hopson, T.; Shaw, J.; Halvorson, S.; Fisher, H.; Roux, G.; Sheu, R.; Pan, L.; Wu, W.; et al. Mesoscale ensemble weather prediction at U. S. Army Dugway Proving Ground, Utah. Weather Forecast. 2017, 32, 2195–2216. [Google Scholar] [CrossRef]
- Wicker, L.J.; Skamarock, W.C. Time splitting methods for elastic models using forward time schemes. Mon. Weather Rev. 2002, 130, 729–747. [Google Scholar] [CrossRef]
- Klemp, J.B.; Skamarock, W.C.; Dudhia, J. Conservative split-explicit time integration methods for the compressible nonhydrostatic equations. Mon. Weather Rev. 2007, 135, 2897–2913. [Google Scholar] [CrossRef]
- Knievel, J.C.; Bryan, G.H.; Hacker, J.P. Explicit numerical diffusion in the WRF Model. Mon. Weather Rev. 2007, 135, 3808–3824. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. A one-dimensional entraining detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef]
- Lin, Y.-L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Clim. Appl. Meteorol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. 2011, 116, D12109. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Wang, W.; Powers, J.G. A description of the Advanced Research WRF Version 3. NCAR Tech. Notes 2008. NCAR/TN-475+STR. [Google Scholar] [CrossRef]

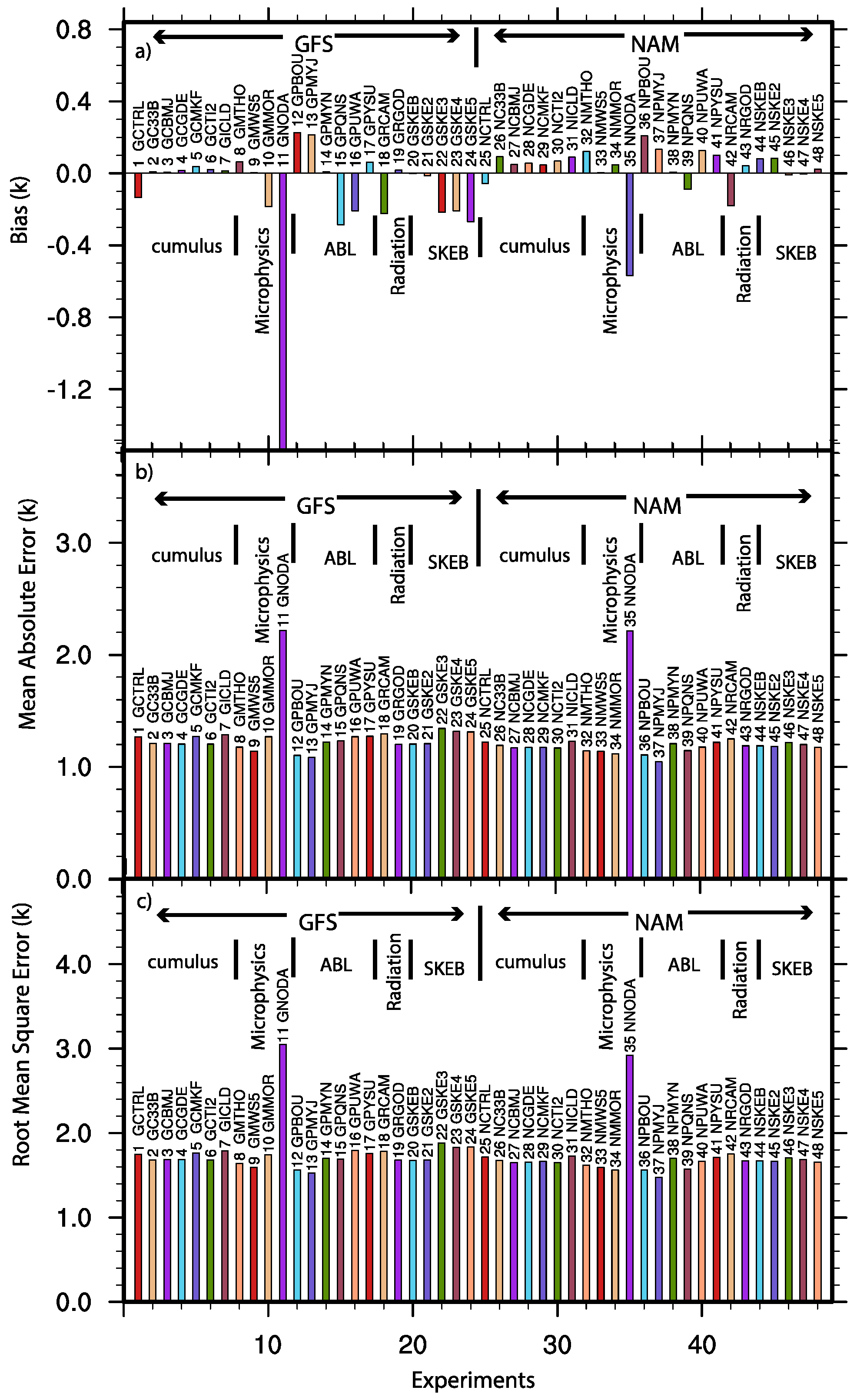
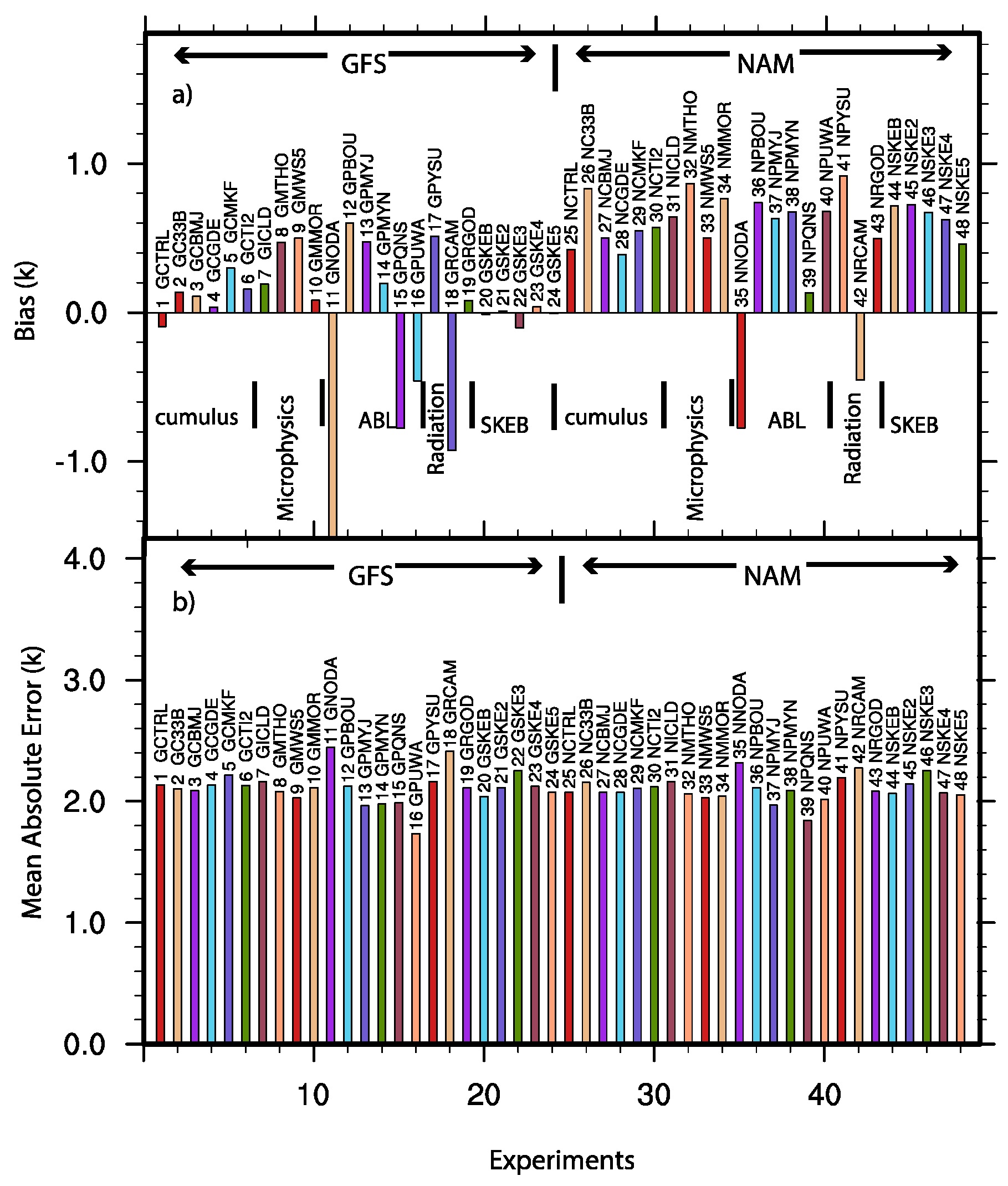
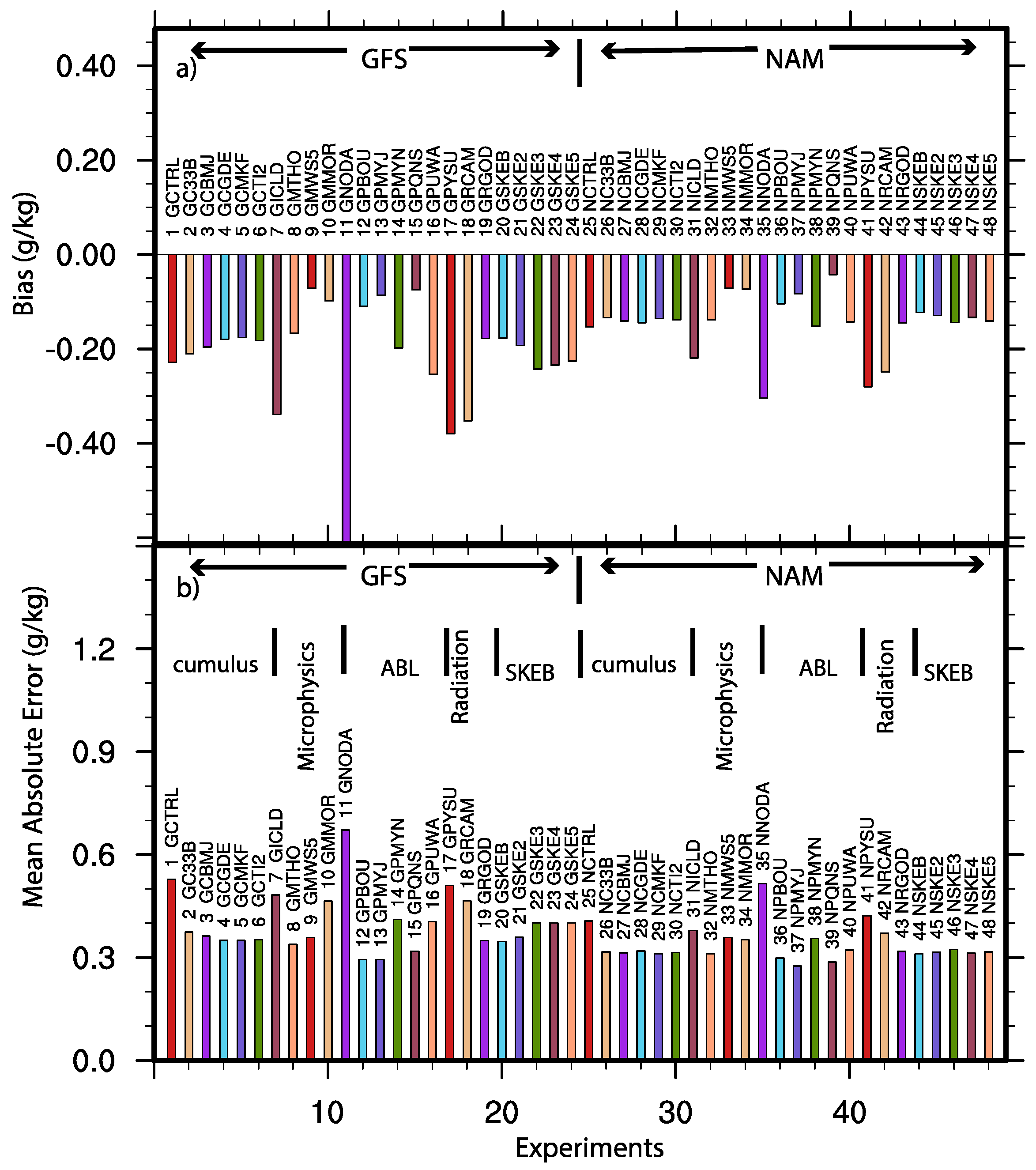
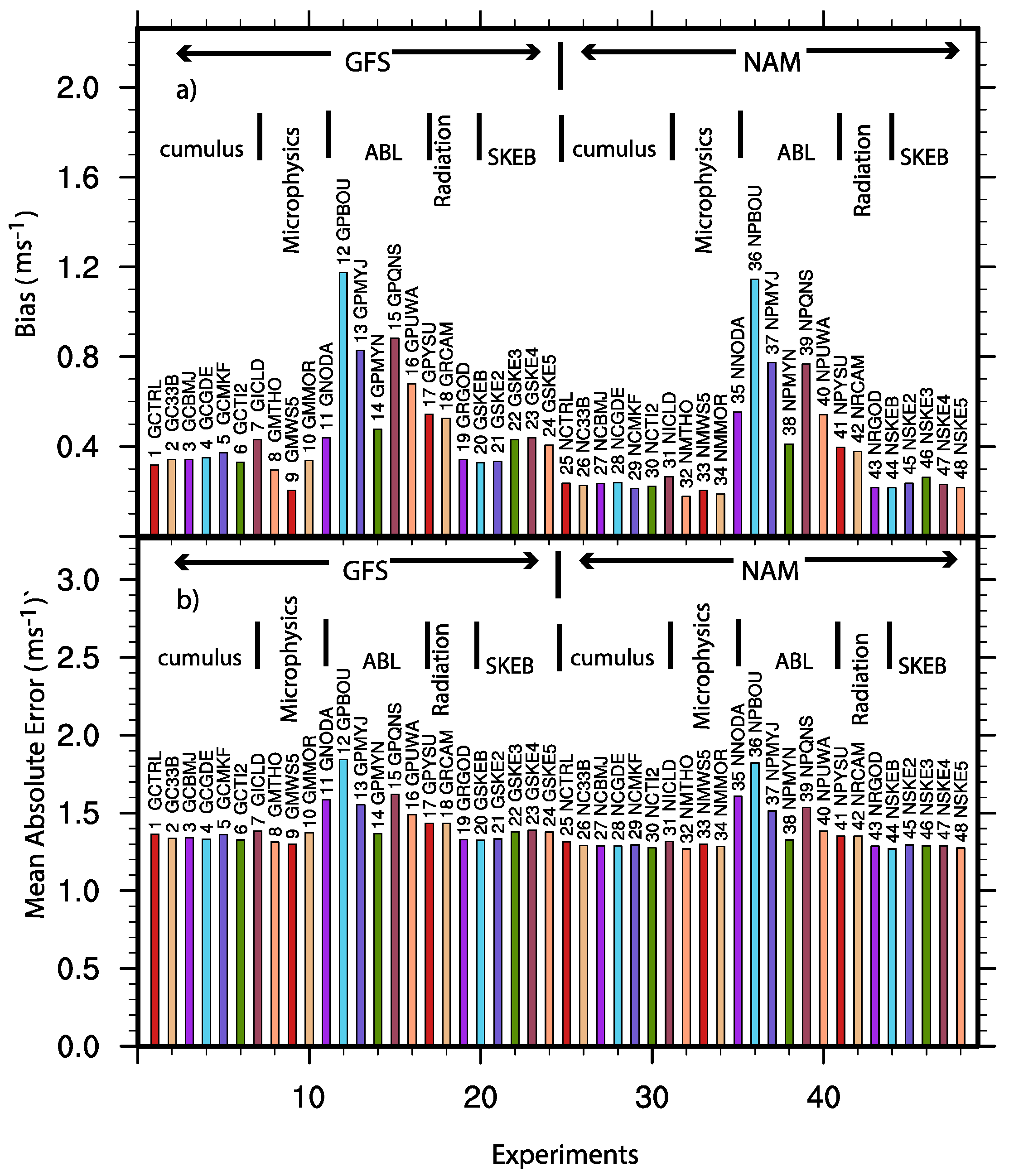
| Experiment | Descriptions of the Experiment Setting | Abbreviation | |
|---|---|---|---|
| Descriptions | Boundary Conditions | ||
| 1 | Control run with YSU ABL scheme, Kain–Fritsch cumulus scheme, single momentum 6-class microphysics, Dudhia Shortwave | GFS | GCTRL |
| 2 | Betts–Miller–Janjic cumulus scheme including D3 | GFS | GC33B |
| 3 | Betts–Miller–Janjic cumulus scheme | GFS | GCBMJ |
| 4 | Grell–Devenyi ensemble cumulus scheme | GFS | GCGDE |
| 5 | Multi-scale Kain–Fritsch cumulus scheme | GFS | GCMKF |
| 6 | New Tiedtke cumulus scheme | GFS | GCTI2 |
| 7 | Relative Humidity (RH)-based method for cloud fraction | GFS | GICLD |
| 8 | Thompson microphysics | GFS | GMTHO |
| 9 | WRF Double Momentum (WDM) 5-class scheme | GFS | GMWS5 |
| 10 | Morrison microphysics scheme | GFS | GMMOR |
| 11 | Similar to experiment 1 (GCTRL) except without data assimilation | GFS | GNODA |
| 12 | Bougeault and Lacarrere (BOU) ABL scheme | GFS | GPBOU |
| 13 | Mellor–Yamada–Janjic (Eta) Turbulent Kinetic Energy (TKE) ABL scheme | GFS | GPMYJ |
| 14 | Mellor-Yamada-Nakanishi-Niino (MYN) 2.5 level TKE ABL scheme | GFS | GPMYN |
| 15 | Quasi-Normal Scale Elimination (QNS) ABL scheme | GFS | GPQNS |
| 16 | University of Washington (UW) (Bretherton and Park) ABL scheme | GFS | GPUWA |
| 17 | YSU ABL scheme with modified mixing | GFS | GPYSU |
| 18 | Community Atmospheric Model (CAM) short wave radiation | GFS | GRCAM |
| 19 | Goddard shortwave scheme | GFS | GRGOD |
| 20 | Stochastic kinetic-energy backscatter Scheme (SKEBS) 1 | GFS | GSKEB |
| 21 | Stochastic kinetic-energy backscatter Scheme (SKEBS) 2 | GFS | GSKE2 |
| 22 | Stochastic kinetic-energy backscatter Scheme (SKEBS) 3 | GFS | GSKE3 |
| 23 | Stochastic kinetic-energy backscatter Scheme (SKEBS) 4 | GFS | GSKE4 |
| 24 | Stochastic kinetic-energy backscatter Scheme (SKEBS) 5 | GFS | GSKE5 |
| 25 | Control run with YSU ABL scheme, Kain–Fritsch cumulus scheme, single momentum 6-class microphysics scheme | NAM | NCTRL |
| 26 | Betts–Miller–Janjic cumulus scheme | NAM | NC33B |
| 27 | Betts–Miller–Janjic cumulus scheme | NAM | NCBMJ |
| 28 | Grell–Devenyi ensemble cumulus scheme | NAM | NCGDE |
| 29 | Multi-scale Kain–Fritsch cumulus scheme | NAM | NCMKF |
| 30 | New Tiedtke cumulus scheme | NAM | NCTI2 |
| 31 | RH-based method for cloud fraction | NAM | NICLD |
| 32 | Thompson microphysics | NAM | NMTHO |
| 33 | WDM 5-class scheme | NAM | NMWS5 |
| 34 | Morrison microphysics scheme | NAM | NMMOR |
| 35 | Similar to experiment 25 (NCTRL) except without data assimilation | NAM | NNODA |
| 36 | Bougeault and Lacarrere (BouLac) ABL scheme | NAM | NPBOU |
| 37 | Mellor–Yamada–Janjic (Eta) TKE ABL scheme | NAM | NPMYJ |
| 38 | MYNN 2.5 level TKE ABL scheme | NAM | NPMYN |
| 39 | Quasi-Normal Scale Elimination ABL scheme | NAM | NPQNS |
| 40 | UW (Bretherton and Park) ABL scheme | NAM | NPUWA |
| 41 | YSU ABL scheme with modified mixing | NAM | NPYSU |
| 42 | CAM short wave radiation | NAM | NRCAM |
| 43 | Goddard shortwave scheme | NAM | NRGOD |
| 44 | Stochastic kinetic-energy backscatter (SKEB) Scheme 1 | NAM | NSKEB |
| 45 | Stochastic kinetic-energy backscatter (SKEB) Scheme 2 | NAM | NSKE2 |
| 46 | Stochastic kinetic-energy backscatter (SKEB) Scheme 3 | NAM | NSKE3 |
| 47 | Stochastic kinetic-energy backscatter (SKEB) Scheme 4 | NAM | NSKE4 |
| 48 | Stochastic kinetic-energy backscatter Scheme (SKEBS) 5 | NAM | NSKE5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, L.; Liu, Y.; Knievel, J.C.; Delle Monache, L.; Roux, G. Evaluations of WRF Sensitivities in Surface Simulations with an Ensemble Prediction System. Atmosphere 2018, 9, 106. https://doi.org/10.3390/atmos9030106
Pan L, Liu Y, Knievel JC, Delle Monache L, Roux G. Evaluations of WRF Sensitivities in Surface Simulations with an Ensemble Prediction System. Atmosphere. 2018; 9(3):106. https://doi.org/10.3390/atmos9030106
Chicago/Turabian StylePan, Linlin, Yubao Liu, Jason C. Knievel, Luca Delle Monache, and Gregory Roux. 2018. "Evaluations of WRF Sensitivities in Surface Simulations with an Ensemble Prediction System" Atmosphere 9, no. 3: 106. https://doi.org/10.3390/atmos9030106
APA StylePan, L., Liu, Y., Knievel, J. C., Delle Monache, L., & Roux, G. (2018). Evaluations of WRF Sensitivities in Surface Simulations with an Ensemble Prediction System. Atmosphere, 9(3), 106. https://doi.org/10.3390/atmos9030106





