Comparative Evaluation of the Third-Generation Reanalysis Data for Wind Resource Assessment of the Southwestern Offshore in South Korea

Abstract

This study evaluated the applicability of long-term datasets among third-generation reanalysis data CFSR, ERA-Interim, MERRA, and MERRA-2 to determine which dataset is more suitable when performing wind resource assessment for the ‘Southwest 2.5 GW Offshore Wind Power Project’, which is currently underway strategically in South Korea. The evaluation was performed by comparing the reanalyses with offshore, onshore, and island meteorological tower measurements obtained in and around the southwest offshore. In the pre-processing of the measurement data, the shading sectors due to a meteorological tower were excluded from all observation data, and the measurement heights at the offshore meteorological towers were corrected considering the sea level change caused by tidal difference. To reflect the orographic forcing by terrain features, the reanalysis data were transformed by using WindSim, a flow model based on computational fluid dynamics and statistical-dynamic downscaling. The comparison of the reanalyses with the measurement data showed the fitness in the following order in terms of coefficient of determination: MERRA-2 > CFSR = MERRA > ERA-Interim. Since the measurement data at the onshore meteorological towers strongly revealed a local wind system such as sea-land breeze, it is judged to be inappropriate for use as supplementary data for offshore wind resource assessment.

1. Introduction

The opening of a wind power project is determined based on a feasibility study that estimates the profit of wind energy production, cost of wind farm construction, and operations and maintenance (O&M). The most significant risk in wind power projects, which are huge investment projects, is cost estimation, i.e., wind resource assessment, because a wind farm is to be operated for the next 20 to 30 years. Therefore, how to reduce uncertainty in relation to a long-term wind resource using short-term observation data of a year or more is the most important key. In this regard, the Korean Board of Audit and Inspection warned of the low economic feasibilities of the ‘Daejeong Offshore Wind Power Project’ on Jeju Island even though it is the wind resource-richest province in South Korea [1] and the USD 8-billion, three-stage ‘Southwest 2.5 GW Offshore Wind Power Project’ led by the Korean government. A number of studies on wind resource assessment have been conducted to promote the ‘Southwest Offshore Wind Project’ in the west to the Korean Peninsula and in the east to China (region marked with dashed line in Yellow Sea in Figure 1). Note, however, that it is necessary to have in-depth re-investigation since considerable discrepancies in wind resource prediction were reported. Kim et al. [2] pointed out that, if the ‘Southwest Offshore Wind Project’ depended on the short-term measurements of offshore meteorological towers only, uncertainties became larger due to the variability of wind resource, resulting in increases in project risk. Realistically, it is difficult to perform measurements at the offshore meteorological tower for five years or longer.

Nowadays, reanalysis data tend to be employed more as long-term reference data than meteorological observation data on nearby islands or onshore. Since orographic forcing by terrain features does not exist in offshore, reanalysis data shows more higher correlation in offshore than in the land [3]. Several high-resolution reanalysis data sets are now freely available for use in wind resource assessment, such as CFSR, ERA-Interim, MERRA, and MERRA-2. Compared to independent meteorological tower measurements, all four perform significantly better than the 1990s-era first generation and 2000s-era second generation reanalysis at all-time scales. Eichelberger et al. [4] evaluated the third-generation reanalysis data using high-rise meteorological tower measurements at 35 sites; the comparison result showed that R² of CFSR and ERA-Interim was about 17% higher than that of MERRA. (MERRA R² = 0.46, CFSR & ERA-Interim R² = 0.54) Brower et al. [5] reported the same result in their study, which was performed using measurements of high-rise meteorological towers at 37 sites around the world. R² of CFSR and ERA-Interim was about 9% higher than that of MERRA. (MERRA R² = 0.66, CFSR R² = 0.74, ERA-Interim R² = 0.73) Carvalho et al. [6] compared buoy measurements at five sites in the sea of the Iberian Peninsula with reanalysis data and reported MERRA R² = 0.87, CFSR R² = 0.87, and ERA Interim R² = 0.78. Chawla et al. [7] also reported buoy measurements at 12 sites in the sea of the Gulf of Mexico in the Atlantic and at 10 sites in the sea of Hawaii in the Pacific, showing CFSR R² of 0.84 and 0.87.

The Korean Peninsula located in the Far East Asia belongs to the monsoon climate zone characterized by complex seasonal and diurnal meteorological pattern due to the effect of the oceanic climate in summer and the continental climate in the winter. This study sought to determine data suitable for the southwest offshore wind resource assessment in the Korean Peninsula among third-generation reanalysis data CFSR, ERA-Interim, MERRA, and MERRA-2. To do this, a comparative evaluation was performed on the measurement data around the target site of the ‘Southwest Offshore Wind Project’—which are offshore, onshore, and island meteorological tower measurements—and the third-generation reanalysis data. Furthermore, pre-processing was conducted to take optimal measurements analysis. The variation of measurement heights caused by tidal change in the Yellow Sea and the meteorological tower shading effect were taken into consideration. Since meteorological towers installed on islands and coasts are affected by flow transform caused by terrain features, numerical analysis using CFD was conducted to correct the effect.

2. Research Data

2.1. Reanalysis Data

Reanalysis refers to a systematic approach for reproducing systematic and consistent meteorological data by accommodating 7–9 million observation data acquired through various sources (e.g., radiosonde, buoy, airplanes, ships, etc.) every 6–12 h in the invariant data assimilation structure and meteorological model in an integrated manner. The first-generation reanalysis data refers to the global reanalysis data produced at the National Center for Atmospheric Research/National Centers for Environmental Prediction (NCAR/NCEP) and Europe Center for Medium-Range Weather Forecast (ECMWF) in the 1990s [8]. The second-generation reanalysis data were then produced in the early 2000s by resolving several problems and adding the parametrization of physical processes in the same grid network [9]. In 2010s, third-generation reanalysis data such as CFSR, ERA-Interim, MERRA, and MERRA-2—which are significantly improved spatio-temporal resolution—were developed.

Table 1. Comparison of the third-generation reanalysis data.

Name	Source	Time Range	Assimilation	Model Resolution	Publicly Available Dataset Resolution	Dataset Output Times and Time Averaging
CFSR	NCEP	1979–present	3D-VAR	T382 L64	0.5 × 0.5 and 2.5 × 2.5	Hourly, 4 times daily
ERA Interim	ECMWF	1979–present	4D-VAR	TL255L60 and N128 reduced Gaussian	User-defined, down to 0.75 × 0.75	3 h for most surface fields; 6 h for upper-air fields
MERRA	NASA	1979–present	3D-VAR, with incremental update	2/3 lon. × 1/2 lat. deg.; 72 sigma levels	2/3 lon. × 1/2 lat. deg. 3D analysis and 2D variables; 1.25 deg. 3D diagnostics; 72 model levels and 42 pressure levels	2D diagnostics—1 h avg., centered on half hour; 3D diagnostics—3 h avg., centered on 01:30, 04:30 ... 22:30; 3D analysis -instantaneous 6-h; 2D diagnostics
MERRA-2	NASA GMAO	1980–present	3D-VAR with incremental update; Includes aerosol data assimilation	Native cube sphere grid output is interpolated to 5/8 lon. × 1/2 lat. deg.; 72 sigma levels	5/8 lon. × 1/2 lat. deg. 3D analysis and 2D variables; 3D diagnostics; 72 model levels and 42 pressure levels	2D Diagnostics—1 h avg., centered on half-hour; 3D diagnostics—3 h avg., centered on 0130, 0430 ... 2230; 3D analysis - Instantaneous 6-h; 2D diagnostics

Source: https://reanalyses.org/atmosphere/comparison-table (accessed on 16 February 2018).

shows the comparison of the specifications in the third-generation reanalysis data. The temporal resolution of MERRA, MERRA-2, and CFSR is one-hour interval, whereas ERA-Interim is three-hour interval. The spatial resolution is 0.5° × 0.5° for CFSR, 0.67° × 0.5° for MERRA, and 0.75° × 0.75° for ERA-Interim. This study employed the reanalysis data in the grid point closest to the location of offshore meteorological tower HeMOSU-1, a representative location of the southwest offshore where wind direction and wind speed data were extracted at 100 m above sea level to be compared with the observation data.

2.1.1. CFSR (Climate Forecast System Reanalysis)

CFSR (http://rda.ucar.edu/pub/cfsr.html) was produced by the atmosphere-ocean-surface-glacier coupled climate forecast system with global high resolution in the NCEP based on the same meteorological data and analysis model as that of MERRA [10].

2.1.2. ERA-Interim (European Center for Medium-Range Weather Forecasts Interim)

ERA-Interim (https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim) was produced as a prior step to producing next-generation reanalysis data following ERA-15 and ERA-40 among the reanalysis data series of the ECMWF. ERA-Interim applies a 12-h, 4-dimensional variation analysis (4D-Var) with adaptive estimation of biases in satellite radiance data (VarBC) based on the ECMWF Integrated Forecast Model [11].

2.1.3. MERRA (Modern Era Reanalysis for Research and Applications)

MERRA (http://gmao.gsfc.nasa.gov/merra/) refers to the reanalysis data of the National Aeronautics and Space Administration (NASA) for the satellite era. The official data production was launched in 2008 using the up-to-date GEOS-5 (Goddard Earth Observing System Data Assimilation System Version 5) produced in NASA GMAO (GSFC Global Modeling and Assimilation Office) [12].

2.1.4. MERRA-2 (Modern Era Reanalysis for Research and Applications Version 2)

MERRA-2 (https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/) is MERRA version 2 that improved the data assimilation of modern hyperspectral radiance and microwave observations, along with GPS-Radio Occultation datasets. In particular, it was designed such that space-based observations of aerosols including NASA ozone observations after 2005 were assimilated to represent their interactions with other physical processes in the climate system [13].

2.2. Meteorological Tower Measurements

The measurement data secured in the target area were offshore meteorological towers (HeMOSU-1 and HeMOSU-2), onshore meteorological tower (Gochang), island meteorological towers (Hoenggyeong-do, Wangdeung-do, Wangdeungyeo), and wind resource campaign database (Dongho, Sinsi-do, Julpo, and Saemangeum). Figure 2 shows the location of the in-situ measurement sites around the southwest offshore target area. The yellow lozenge in the map center is a proposed construction location of the pilot wind farm site as the first phase of the ‘Southwest Offshore Wind Project’.

Table 2. Summary of the meteorological tower measurements.

Site	Location	Coordinates	Meausrement Period	Data Average	Measurement Heights (m)
HeMOSU-1	Offshore	35°27′55.17′′ N, 126°07’43.30′′ E	October 2010~March 2016	10 min	26, 46, 56, 66, 76, 86, 96, 99
HeMOSU-2	Offshore	35°49′25.50′′ N, 126°12′23.06′′ E	January 2014~July 2015	10 min	40, 60, 80, 100, 107, 117
Hoenggyeong-do	Island	35°51′26′′ N, 126°25′03′′ E	December 2008~November 2009	Monthly	20, 30
Wangdeung-do	Island	35°39′43′′ N, 126°06′24′′ E	May 2011~April 2012	Monthly	12
Wangdeunyeo	Island	35°22′15′′ N, 126°07′50′′ E	January 2010~December 2011	10 min	20, 40, 60, 70, 80
Gochang	Onshore	35°27′43′′ N, 126°26′57′′ E	November 2008~May 2009	10 min	80, 100, 120
Dongho	Onshore	35°30′37′′ N, 126°28′48′′ E	April 1997~April 1998	Hourly	15, 30
Sinsi-do	Island	35°49′10′′ N, 126°28′40′′ E	December 1999~April 2000	Hourly	15, 30
Julpo	Onshore	35°34′58′′ N, 126°39′50′′ E	February 1998~August 2000	Hourly	15, 30
Saemangeum	Onshore	35°43′39′′ N, 126°31′41′′ E	August 1999~October 2001	Hourly	15, 30

summarizes the meteorological tower measurements used in this study.

2.2.1. Measurement Data of Offshore Meteorological Towers

The Korean Ministry of Trade, Industry & Energy announced the ‘Southwest 2.5 GW Offshore Wind Power Roadmap’ in October 2010. Next, the Korea Electric Power Research Institute installed Korea’s first offshore meteorological tower, HeMOSU (Herald of Meteorological and Oceanographic Special Unit) No. 1 unit (since October 2010) and No. 2 unit (since September 2013).

2.2.2. Measurement Data of Onshore Meteorological Tower

As the first phase of the ‘Southwest Offshore 2.5 GW Wind Project,’ the 80 MW-capacity pilot wind farm is under construction until 2018 and will be grid-connected to the Gochang Power Test Center of Korean Electric Power Corporation (KEPCO) located near the coast. The wind speed data for 34 months obtained from a 120 m-high transmission tower (altitude above sea level: 21 m) inside the Gochang Power Test Center were employed.

2.2.3. Measurement Data of Island Meteorological Towers

Meteorological towers were installed on nearby islands to alleviate the uncertainty in the wind resource assessment at the pilot wind farm. The measurement data for 12 months—which were measured by attaching sensors to a broadcasting tower (altitude above sea level: 184 m) in Wangdeung-do, which was 22 km away from the north of HeMOSU-1—were employed. Jeong et al. [14] installed an 80 m-high meteorological tower in Wangdeungyeo (altitude above sea level: 30 m), 8 km away from the south of HeMOSU-1; the monthly wind speed data for 24 months were adopted from their paper. In addition, Shim et al. [15] installed a 30 m-high meteorological tower in Hoenggyeon-do (altitude above sea level: 40 m) located north of Saemangeum Gogunsan-do; the monthly wind speed data for 12 months were adopted from their paper.

2.2.4. Wind Resource Database

The Korea Institute of Energy Research (KIER) disclosed the results of the wind resource assessment performed throughout South Korea through the web service of the renewable energy resource map (www.kier-atlas.org). Wind data measured at 30 m-high meteorological towers in Dongho, Sinsi-do, Julpo, and Saemangeum were used for comparison.

3. Analysis Methods

3.1. Comparative Evaluation between Reanalysis Data

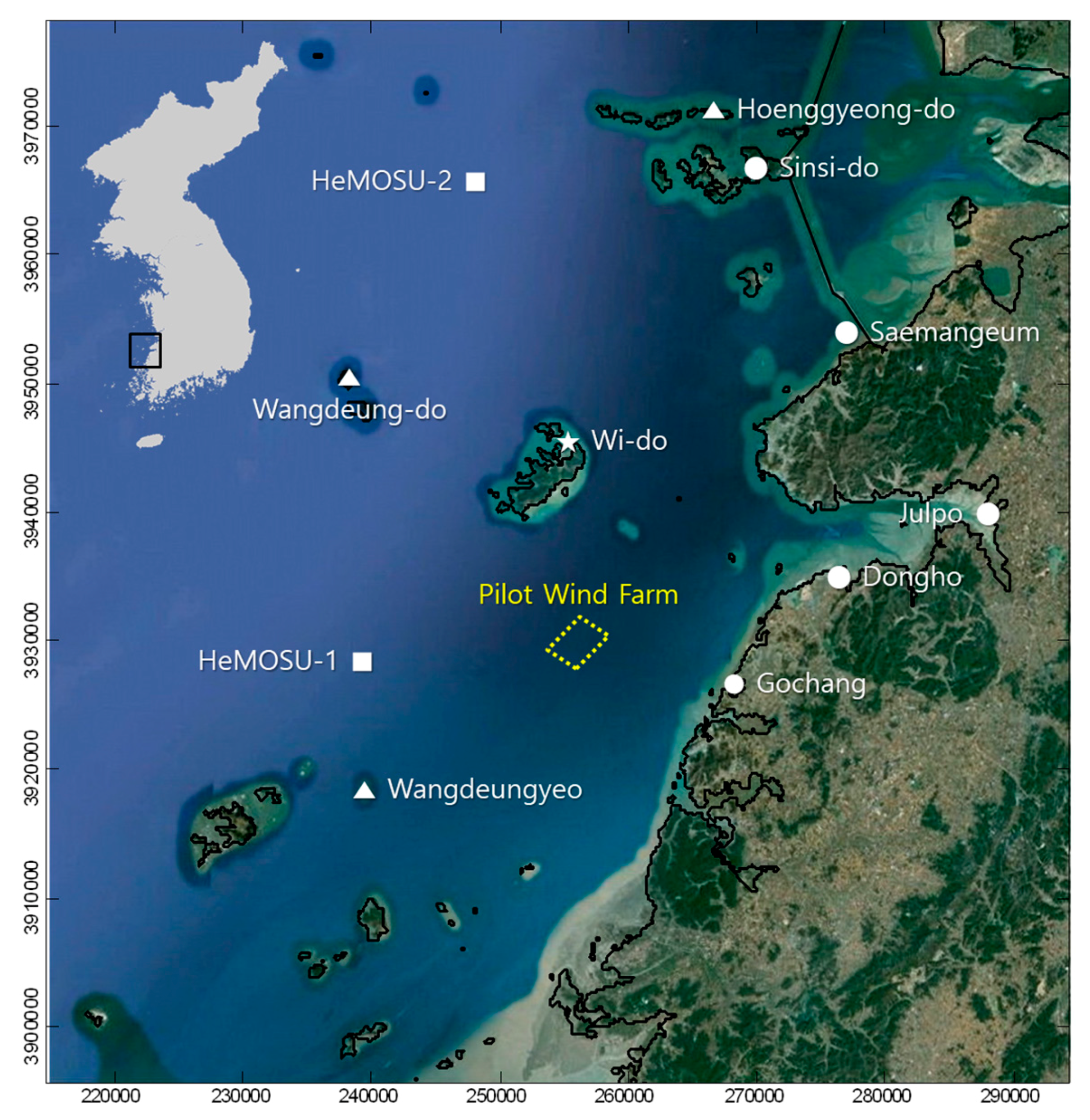
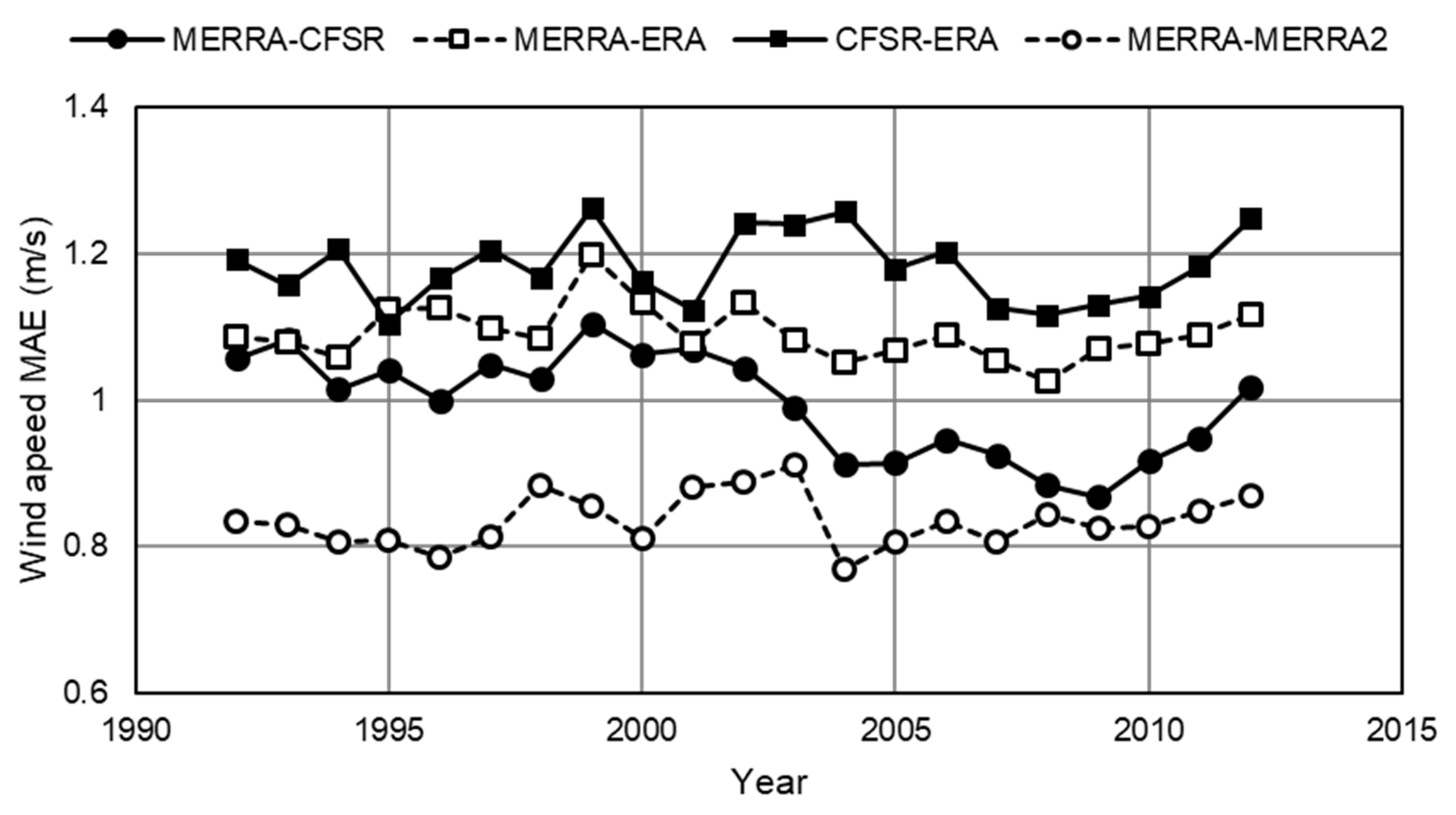
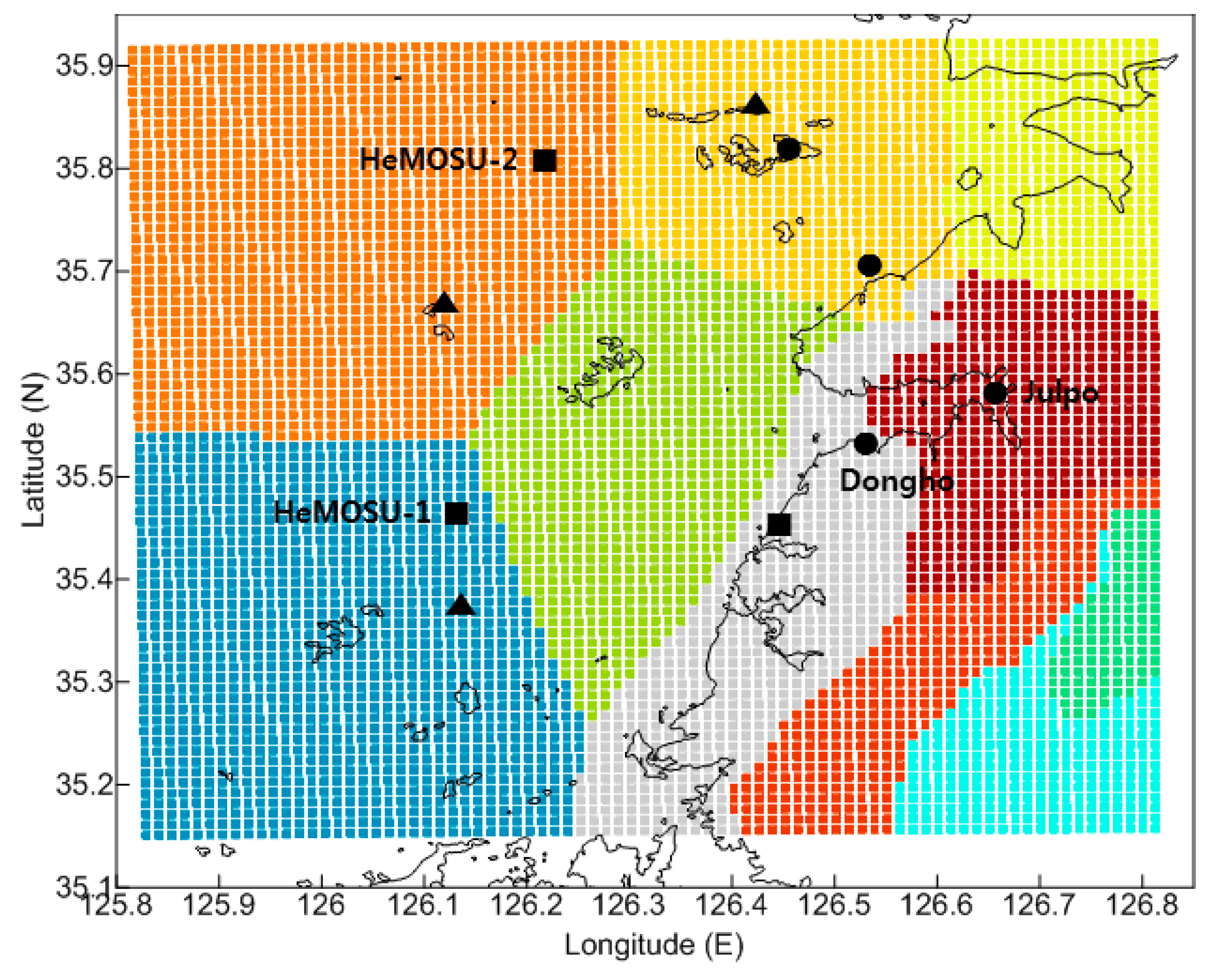
Four kinds of reanalysis data closest at the installation location of HeMOSU-1, which was regarded as a representative location of southwest offshore in Korea, were extracted to examine the differences between the reanalysis data systematically and were reconfigured into 1 h-averaged time series data.

The reference height was set to 100 m above sea level, which is the highest measurement height of HeMOSU-1. The mean average error (MAE) was calculated to evaluate the difference between the reanalysis data quantitatively as follows:

$$\mathrm{MAE}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|V_{1,i}-V_{2,i}\right|$$

(1)

In Equation (1), V refers to the wind speed in the reanalysis data; the data period was selected as 24 years (from 1992 to 2015, n = 24 × 8760), which included all measurement periods of observation data used in this study. Number 1 and 2 indicate two different reanalyses. The MAE of wind speed difference was calculated and an inter-annual pattern was compared.

3.2. Measurement Data Preprocessing

The measurement data around the pilot wind farm were pre-processed to remove uncertainty factors, and orographic forcing caused by terrain features at each of the meteorological tower locations was reflected on the reanalysis data using a flow model, WindSim (available online: www.winsim.com, accessed on 16 February 2018).

3.2.1. Exclusion of Tower Shading Sectors

Sensors were mounted at the end of a long horizontal boom attached to the meteorological tower to minimize flow interference caused by the tower structure following the IEC 61400-12-1 Annex G. [16] Note, however, that wind reaches an anemometer through the meteorological tower in a specific wind direction. Here, a measurement error due to the shading of the meteorological tower could occur. Thus, the wind direction sectors where meteorological tower shading occurred were identified and excluded.

3.2.2. Correction of Sea-Level Variation

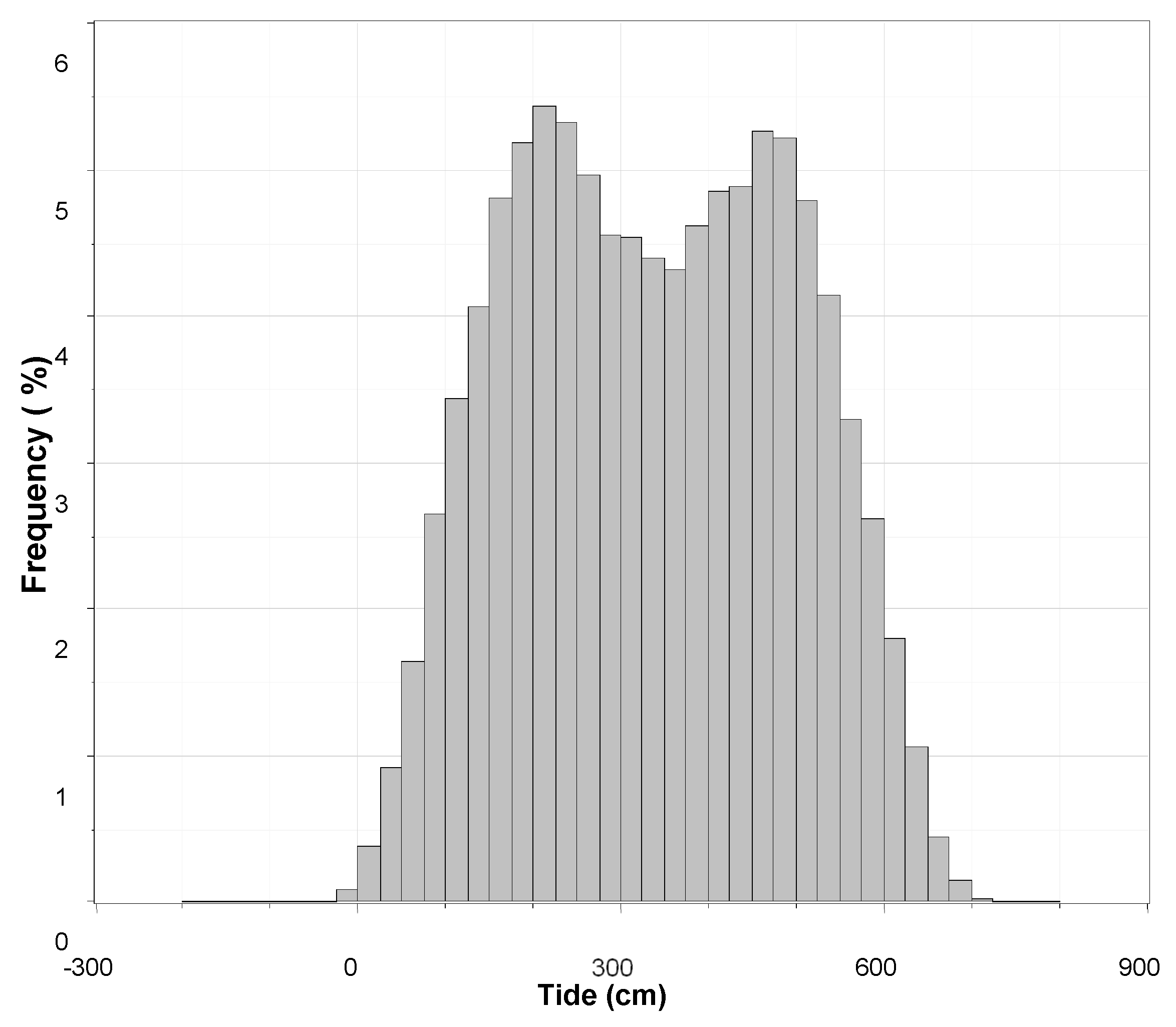
Because the West Sea of Korea (Yellow Sea in Figure 1) has tidal difference of more than 7 m, the measurement height of the sensors installed at the offshore meteorological tower should be corrected to the reference of sea level. The measurement height was corrected using hourly tidal data (Figure 3) in the Wi-do observation station (star mark in Figure 2) of the Korea Hydrographic & Oceanographic Administration, which is closest to the HeMOUS-1 offshore meteorological tower. In other words, the wind speed measured at the anemometer installed between the top of the offshore meteorological tower (99 m based on the mean sea level) and below (86 m) was corrected considering the tidal difference through linear interpolation.

3.2.3. CFD to reflect Orographic Forcing by Terrain Features

Since the spatial resolution of the reanalysis data (Table 1) is in order of dozens of km, orographic forcing of local scale by terrain features was not reflected. Moreover, since meteorological towers installed on islands and coasts are strongly affected by orographic forcing by terrain features, numerical analysis using the CFD software WindSim was conducted to reflect the effect. In other words, reanalysis data were inputted to ‘Climatology’ in the WindSim analysis and then ‘Transferred Climatology’, on which orographic forcing by terrain features was reflected at each of the measurement locations, was simulated.

3.3. Evaluation between Reanalysis Data and Measurement Data

Regression analysis on the four kinds of third-generation reanalysis data, which were transferred to meteorological tower locations by reflecting orographic forcing by terrain features, with the pre-processed measurement data was conducted. Here, superiority and inferiority among the reanalysis data were evaluated in terms of mean bias (BIAS), root mean square error (RMSE), and coefficient of determination (R²).

$$\mathrm{BIAS}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left(M_i-O_i\right)$$

(2)

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(M_i-O_i\right)}^2}$$

(3)

In Equations (2) and (3), M and O refer to the predicted and observed wind speed respectively.

The measurement data of meteorological towers were expected to have different characteristics depending on the installation location of the tower, such as offshore, onshore, and island. To examine the meteorological characteristics, the energy pattern factor [17], one-hour autocorrelation coefficient, and Weibull shape factor were compared. The energy pattern factor (EPF) is defined as presented in Equation (4).

$$K_e=\frac{1}{n{\overline{V}}^3}{\displaystyle \sum }_{i=1}^n{V}_i{}^3$$

(4)

Assuming that air density ($\mathsf{\rho }$) is a constant, EPF will be a ratio of wind power density ($\overline{P}/A$) calculated with mean wind speed ($\overline{V}$) to actual mean wind power density ($\overline{P}$). In other words,

$$\frac{\overline{P}}{A}=\frac{1}{2}\rho {\overline{V}}^3{K}_e$$

(5)

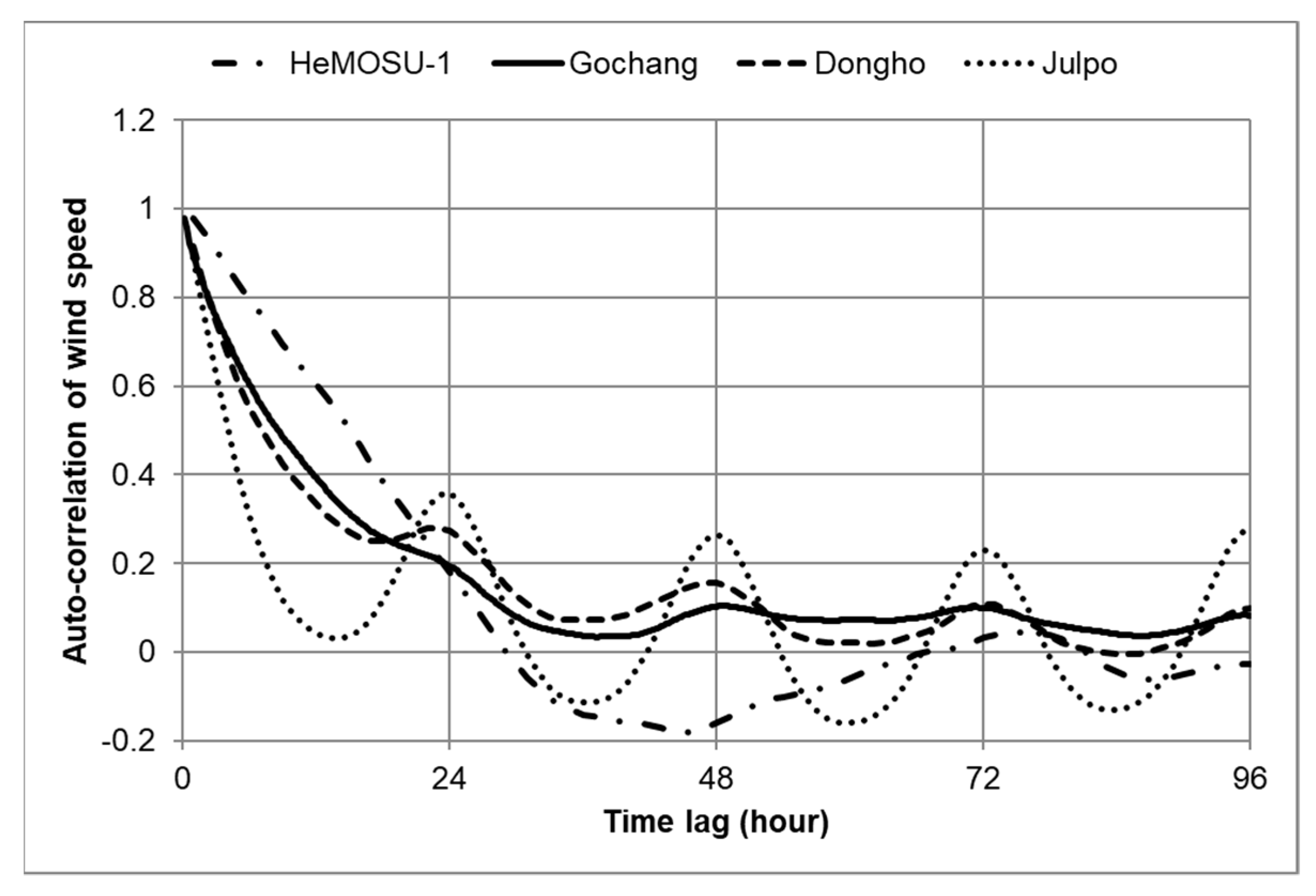
Thus, the larger EPF is, the larger the dispersion of wind speed distribution from the mean wind speed, which is then followed by a decreasing Weibull shape factor (k). This correlation is also expected to occur in the 1 h-autocorrelation coefficient. Since larger dispersion of wind speed means large wind speed variance, the 1 h-autocorrelation coefficient will tend to decrease.

4. Results and Discussion

4.1. Comparative Analysis on Reanalysis Data

Table 3. Wind statistics of hourly reanalysis data at HeMOSU-1 location (100 m above sea level).

Wind Statistics	CFSR	ERA-Interim	MERRA	MERRA-2
Mean wind speed (m/s)	6.9	6.9	6.6	6.4
Max wind speed	30.8	29.9	29.0	29.0
Weibull shape parameter (k)	1.96	1.99	1.98	1.95
Weibull scale parameter (c, m/s)	7.73	7.73	7.48	7.22
Mean wind power density (W/m2)	385	377	343	322

and

Table 4. Coefficient of determination (R²) among hourly reanalysis data at HeMOSU-1 location (left: wind speed, right: wind direction).

Reanalysis Data	ERA-Interim		MERRA		MERRA-2
CFSR	0.76	0.91	0.82	0.92	0.83	0.93
ERA-Interim	1		0.85	0.94	0.83	0.93
MERRA			1		0.89	0.95

present the statistical and correlation analysis results of hourly reanalysis data at HeMOSU-1 location, respectively. For the mean/maximum wind speed and Weibull factors, the difference between reanalysis data is within the range of 8%. The correlation among reanalysis data showed that air temperature has R² of more than 0.98, wind speed has R² of more than 0.76, and wind direction has R² of more than 0.91. From the meteor-statistics viewpoint, the four kinds of reanalysis data are very similar time-series data, but a difference in mean wind power density should be noted.

In other words, the maximum value (CFSR) and the minimum value (MERRA-2) of wind power density are almost 20% different, which cannot be ignored at all in wind resource assessment. This result implies that the economic feasibility results for the wind power project can be altered, depending on which reanalysis data are selected.

Noticeable differences between third-generation reanalysis data are seen mostly since satellite data were assimilated into the reanalyses after 2000s (see Figure 4). However, MERRA and MERRA-2 that use the same production scheme shows the smallest difference.

4.2. Comparative Analysis between Reanalysis Data and Measurement Data

4.2.1. Offshore Meteorological Tower Data

HeMOSU-1 and HeMOSU-2 are approximately 40 km away from each other; the R² between the two measurement data is 0.83 for wind speed and 0.94 for wind direction, respectively. The correction of tidal difference in all cases showed about 3% improvement of R². Wind power density was adjusted to 451 W/m² at 437 W/m², or an increase of approximately 3.2% (see

Table 5. Comparison between the HeMOSU-1 and HeMOSU-2 measurements and reanalysis data.

Site	Measure	CFSR	ERA-Interim	MERRA	MERRA-2
HeMOSU-1 100 m ASL		Tower shading correction
	BIAS (m/s)	−0.07	0.18	−0.09	−0.06
	RMSE (m/s)	2.10	2.22	2.20	2.08
	R2	0.76	0.70	0.73	0.76
		Tower shading correction + tide correction
	BIAS (m/s)	−0.07	0.10	−0.07	−0.05
	RMSE (m/s)	2.10	2.20	2.20	2.06
	R2	0.77	0.72	0.74	0.78
HeMOSU-2 100 m ASL		Tower shading correction + tide correction
	BIAS (m/s)	−0.13	−0.19	−0.19	−0.05
	RMSE (m/s)	2.03	2.17	2.06	2.01
	R2	0.72	0.69	0.71	0.73

). The highest reliable fitness with the highest representation of the southwest offshore area between offshore meteorological tower data and four kinds of reanalysis data was as follows: MERRA-2 = CFSR > MERRA > ERA-Interim.

4.2.2. Onshore Meteorological Tower Data

As presented in

Table 6. Comparison between onshore measurements and reanalysis data.

Site	Measure	CFSR	ERA-Interim	MERRA	MERRA-2
Gochang 100 m AGL	BIAS (m/s)	1.53	1.71	1.42	1.30
	RMSE (m/s)	2.77	2.94	2.69	2.44
	R2	0.60	0.57	0.58	0.61
Dongho 30 m AGL	BIAS (m/s)	0.86	0.85	0.60	0.60
	RMSE (m/s)	2.32	2.42	2.26	2.24
	R2	0.52	0.48	0.50	0.52
Sinsi-do 30 m AGL	BIAS (m/s)	0.40	0.44	0.01	0.01
	RMSE (m/s)	2.50	2.43	2.50	2.48
	R2	0.65	0.58	0.66	0.67
Julpo 30 m AGL	BIAS (m/s)	1.47	1.50	1.32	1.30
	RMSE (m/s)	2.88	2.88	2.78	2.71
	R2	0.25	0.25	0.25	0.26
Saemangeum 30 m AGL	BIAS (m/s)	0.50	0.50	0.30	0.30
	RMSE (m/s)	2.19	2.22	2.16	2.10
	R2	0.49	0.49	0.52	0.53

, which summarizes the comparative evaluations with the observation data of the onshore meteorological towers, MERRA-2 had the highest fitness in all cases. HeMOSU-1 and Gochang are approximately 30 km away from each other; the R² between the two measurement data is 0.68 for wind speed that is fairly lower than that between HeMOSU-1 and 2.

The rank of fitness in the reanalysis data was similar to that of the offshore meteorological towers: MERRA-2 > MERRA = CFSR > ERA-Interim.

4.2.3. Island Meteorological Tower Data

As presented in

Table 7. Comparison between island measurements and reanalysis data (R²).

Site	Correction	CFSR	ERA-Interim	MERRA	MERRA-2
Wangdeung-do 40 m AGL	No correction	0.64	0.55	0.59	0.60
	Tower shading correction	0.74	0.68	0.73	0.76
Wangdeungyeo 80 m AGL	–	0.56	0.65	0.58	0.74
Heonggueng-do 30 m AGL	–	0.76	0.70	0.79	0.82

, which compares the correlation factor between the observation data of island meteorological tower and reanalysis data, the correlation factor with the reanalysis data was the same order as shown above: MERRA-2 > MERRA = CFSR > ERA-Interim. For Wangdeung-do where sensors were mounted in the broadcasting tower, R² noticeably improved 16% to the 27% level with tower shading correction.

4.3. Offshore/Onshore Meteorology

The correlation between the onshore meteorological tower measurements and reanalysis data was relatively low. In particular, Julpo was the lowest. To investigate the reason for this low correlation, various meteor-statistical parameters were calculated as presented in

Table 8. Comparison of wind statistics of the meteorological tower measurements.

Site	Energy Pattern Factor	1 h Autocorrelation	Weibull Scale Factor, c (m/s)	Weibull Shape Factor, k
HeMOSU-1	2.18	0.98	7.85	1.81
HeMOSU-2	2.36	0.95	7.28	1.69
Gochang	2.39	0.93	5.97	1.65
Dongho	2.41	0.92	5.13	1.72
Sinsi-do	2.43	0.94	6.15	1.55
Julpo	3.22	0.89	3.76	1.31
Saemangeum	2.35	0.93	5.48	1.70

. It was clearly seen that EPF, 1 h autocorrelation coefficient, and Weibull factors in Julpo had highly different range of values compared to that of other meteorological towers. One interesting fact is that a strong negative correlation, −0.84 and −0.95, was revealed between EPF and 1 h autocorrelation coefficient and between EPF and Weibull shape factor, respectively. This is similar to the expectation in Section 3.3.

Figure 5 depicts the autocorrelation of the wind speed measurement data. The measurements at HeMOSU-1 influenced by oceanic weather with low variability, Gochang on the coast showed a reduction tendency in autocorrelation coefficient monotonically according to a lag time. In contrast, Julpo on the coast inside a bay located inwardly in the inland showed clear periodicity of 24 h due to the effect of the sea-land breeze system. Dongho located in the entry of the bay also has 24 h periodicity, although it is weaker than that in Julpo. Julpo is located 20 km inward to the inland from the bay entrance, and it has topographic characteristics shielded by 509 m-high and 444 m-high mountains in the north and south, respectively. Thus, ventilation would occur only through the open east-west direction.

From the analysis with Table 8 and Figure 5, it is conjectured that the intensity of local wind system increases as penetrates into inland from offshore through onshore. This implies that offshore wind resource assessment using onshore or inland measurement data would cause considerable misinterpretation. According to a wind sector clustering map shown in Figure 6, classified by a surface wind regionalization method proposed by Kim et al. [18], offshore meteorological towers HeMOSU-1 and HeMOSU-2 belong to a different wind sector, whereas Dongho and Gochang belong to the same wind sector along the coast; Julpo, which is located inland, is classified into a separate wind sector.

5. Conclusions

This study performed comparative analysis with the meteorological tower measurement data to evaluate the applicability of four kinds of third-generation reanalysis data when wind resource assessment on the ‘Southwest Offshore Wind Project,’ which is underway strategically in South Korea at present, is conducted. The following conclusions were derived through this study:

(1)

The difference in wind power density between four kinds of reanalysis data was more than 20% in the southwest offshore, and this level of difference cannot be ignored in the wind resource assessment. Accordingly, it is very important to select proper reanalysis data.

(2)

According to the comparison of offshore, onshore, and island meteorological tower measurements with the reanalysis data, MERRA-2 showed the best fitness among the four kinds of data. In terms of the mean of R² between the reanalysis data and all observation data, the fitness is in the following order: MERRA-2 (0.67) > CFSR (0.63) = MERRA (0.63) > ERA-Interim (0.61). For reference, the variance of R² was 0.10 for all reanalysis data.

(3)

Pre-processing is recommended when meteorological tower measurement data are used. For example, R² was improved by over 16% when tower shading correction was applied for Wangdeung-do case; the correction of the tidal difference of HeMOSU-1 also improved R² by over 2%.

(4)

According to the wind characteristics analysis such as energy pattern factor, 1 h autocorrelation, and surface wind regionalization, 24 h periodicity due to sea-land breeze was revealed to be stronger inland than on the coast. Therefore, onshore or inland measurements are inappropriate for use as supplementary data for offshore wind resource assessment in the Southwestern Offshore in South Korea.

Since many kinds of reanalysis data are available, the data selection criteria are not sufficiently clear. Thus, this study limited the locations to the southwest offshore in the Korean Peninsula and selected reanalysis data suitable for the wind resource assessment through comparative analysis with various types of observation data. For future studies, investigating an ensemble method that can reduce uncertainty by employing multiple reanalysis data is recommended.